SpikingDynamicMaskFormer: Enhancing Efficiency in Spiking Neural Networks with Dynamic Masking

Abstract

Spiking Neural Networks (SNNs) offer promising low-power alternatives to conventional neural models but often incur considerable redundancy in parameters and computations. To address these inefficiencies, we propose SpikingDynamicMaskFormer (SDMFormer), a novel framework that integrates dynamic masking and lightweight position encoding into a spike-based Transformer backbone. Specifically, our Dynamic Mask Encoder Block adaptively suppresses ineffective spike channels by learning mask parameters, reducing parameter count to 37.93–42.69% of the original Spikformer. Simultaneously, a redesigned lightweight position embedding replaces resource-intensive relative position convolutions, further lowering complexity. Experiments on three neuromorphic vision datasets—DVS128, CIFAR10-DVS and N-Caltech101—demonstrate that SDMFormer cuts energy consumption by 42.79–50.13% relative to Spikformer while maintaining or slightly surpassing accuracy. Moreover, compared with recent leading works, SDMFormer achieves competitive accuracy with substantially fewer parameters and delivers higher inference efficiency, reaching up to 196.20 img/s on CIFAR10-DVS. These results highlight the efficacy of combining event-driven attention with structured pruning and parameter-efficient position encoding, indicating the potential of SDMFormer for resource-efficient SNN deployment in low-power applications.

1. Introduction

Spiking Neural Networks (SNNs), often referred to as the “third generation” of neural networks, have garnered increasing attention due to their event-driven computation paradigm and low power consumption [1,2,3]. Inspired by the spike-based communication mechanisms in the brain, SNNs transmit information through discrete spikes, offering a biologically plausible and energy-efficient alternative to traditional Artificial Neural Networks (ANNs) [4]. Recent research has shown that by leveraging architectural innovations pioneered in ANNs—such as deep residual connections and recurrent structures—SNNs can achieve improved performance, although they still lag behind conventional ANNs on more complex tasks [5].

Concurrently, the Transformer model has redefined state-of-the-art approaches in deep learning [6,7]. Initially employed for natural language processing, its self-attention mechanism has also demonstrated remarkable success in computer vision tasks by effectively capturing long-range dependencies in the data. The capability to selectively focus on critical features endows the Transformer with powerful representational capacity. Given the inherent strengths of SNNs (low power consumption and event-driven computation) and Transformers (strong feature learning and representation), integrating these two paradigms has emerged as a compelling research direction. In this context, Spikformer was introduced with the goal of merging the spiking, event-driven nature of SNNs and the attention mechanism characteristic of Transformers, thereby constructing an efficient model that can handle more complex tasks while retaining the low-power advantage of SNNs [8].

Central to Spikformer is the Spiking Self-Attention (SSA) mechanism, designed to adapt the floating-point self-attention computations of standard Transformers into the SNN framework [8,9]. Within SSA, the Query, Key, and Value representations are all encoded as binary spike trains (0/1 sequences), rather than continuous-valued vectors. This spike-based approach naturally produces non-negative, sparse attention maps, eliminating the need for softmax normalization to scale attention weights. Consequently, Spikformer replaces computationally costly dot products and softmax operations with simple logical AND operations and spike accumulations, thereby avoiding floating-point multiplication entirely in its attention layers.

However, through systematic analysis of the Spikformer architecture, we found that the sparse spike multiplication mechanism in SSA modules causes significant intrinsic information redundancy within the model. More specifically, as shown in Figure 1a, the resulting inactive-channel ratio exhibits a clear distribution across test samples, with a mean of 0.223 and a median of 0.230 estimated from 100 CIFAR10-DVS test samples. To provide an intuitive view of this phenomenon, Figure 1b visualizes the per-channel spike firing rates for a representative CIFAR10-DVS test sample. Notably, 60 out of 256 channels that originally carry information exhibit spike firing rates that drop to zero after passing through a single SSA module, indicating that they no longer convey any information. These inactive spike channels, while contributing nothing to subsequent network operations, consume substantial computational resources during processing. Furthermore, the Relative Position Encoding (RPE) module, despite employing convolutional layers with residual structures for information extraction, accounts for approximately 20% of total parameters while delivering limited performance enhancement.

To address these limitations and enhance the efficiency–accuracy balance, we propose the SpikingDynamicMaskFormer (SDMFormer) framework. The core innovation involves strategically inserting Dynamic Mask Encoder Blocks into the original Spikformer architecture. Through dynamic adjustment of mask layer values during training, this mechanism suppresses pulse emission in non-contributing channels while preserving network performance, thereby substantially reducing both model parameters and computational overhead. Additionally, we introduce a lightweight positional encoding module that replaces the complex RPE structure. This redesign not only decreases overall parameter count but also synergizes with the Spiking Patch Splitting (SPS) module to amplify discriminative feature representation.

In the final stage, we conduct a systematic and comprehensive experimental evaluation of the proposed SDMFormer framework on several neuromorphic datasets. We deliberately do not use static frame-based datasets, as neuromorphic data provide a more systematic and faithful assessment of the temporal modeling capability of SNNs [10], thereby enabling a more effective evaluation of model latency and energy consumption. The results show that, compared to the original Spikformer, SDMFormer reduces the parameter count to 37.93–42.69% and lowers energy consumption by 42.79–50.13%. More importantly, despite significant reductions in model size and computational cost, SDMFormer maintains or even slightly improves classification accuracy across these datasets, achieving an optimal balance between efficiency and accuracy.

The principal contributions of this work can be summarized as follows:

(1)

We introduce SDMFormer, an improvement of Spikformer, aimed at significantly reducing the network’s parameters and energy consumption.

(2)

To address channel redundancy in Spikformer networks, we propose DMEB that dynamically learns and adjusts mask values during training to suppress spike emissions in ineffective channels. Pruning these redundant channels not only preserves model performance but also significantly reduces model parameters and inference energy consumption.

(3)

We redesign the original relative position encoding into a streamlined module through structural optimization and feature fusion enhancement. Integrated with SPS, LPE focuses computation on information-rich regions while maintaining parameter efficiency (20.3% reduction vs. conventional RPE modules).

2. Related Work

2.1. Spiking Convolutional Neural Networks

Ongoing advances in neuromorphic computing hardware and associated algorithmic research have led to remarkable progress in Spiking Convolutional Neural Networks (SCNNs) for computer vision [11,12,13]. Compared to conventional artificial neural networks, SCNNs employ an event-driven computing paradigm in which computations are performed only when neurons generate spikes, thereby allowing greater energy efficiency on large-scale parallel accelerators [14,15,16]. To maintain high accuracy while leveraging the advantages of spiking neural networks, researchers have mainly explored two directions: (1) converting ANNs—already widely used in the deep learning community—into SNNs which is called indirect training, and (2) directly training deep SNNs by employing spiking neuron models [4,12,17,18,19].

A widely adopted indirect training approach involves converting pre-trained ANN models into SNNs through carefully designed neuron thresholds and normalization strategies [20,21,22]. These methods fully leverage the mature training techniques and pre-trained weights of ANNs on large-scale datasets, while compensating for spike-related loss during conversion to minimize any drop in accuracy. For instance, some studies employ a “spike calibration” method to flexibly adjust spike frequencies across different layers, which significantly reduces latency while preserving accuracy [23]. Other efforts analyze the activation function and membrane potential distributions to propose quantization-aware conversion mechanisms, enabling near-ANN performance even with a limited number of timesteps [24]. Overall, ANN-to-SNN conversion offers reduced energy consumption through event-driven computation while largely preserving model performance; however, it still faces challenges regarding inference timesteps and certain constraints inherited from the original ANN architecture.

Another line of work directly utilizes the native dynamic model of spiking neurons and trains the network end-to-end by approximating the gradient of the spiking function [25,26,27,28,29]. Compared to indirect methods, this approach grants greater flexibility in network design and, in principle, better exploits the temporal information carried by spike signals. Along the way, various regularization strategies have been proposed to guide membrane potential distributions, further enhancing convergence speed and generalization. Some researchers have also experimented with “pseudo-spikes” during training, switching back to true binary spike firing in the inference phase to balance training efficiency and deployment performance [30]. In recent years, with the development of improved gradient approximations and optimization techniques, researchers have achieved accuracy on large-scale datasets that is highly competitive with ANNs, while also reducing inference latency by lowering the number of spikes required [21,31]. In parallel, Shen et al. introduce a temporal attention-guided adaptive fusion framework that enables energy-efficient multimodal SNNs by dynamically reweighting temporal features and balancing the contribution of different modalities [32]. A recent TTFS-based SNN framework shows that deep time-to-first-spike networks can closely match ReLU models while achieving extremely low firing rates [33]. Rather than reducing spikes per neuron while keeping the architectural width unchanged, our method enforces structured, channel-wise sparsity, which is complementary to TTFS sparsity, focusing on structured pruning and ViT-specific redundancy that translate more directly into memory and compute savings in practical implementations.

2.2. Spiking Transformer Architecture

Spiking transformers have made remarkable strides by addressing key architectural challenges in marrying Spiking Neural Networks with vision Transformers. Early efforts often relied on shallow SNN front-ends or ANN-to-SNN conversions, which limited performance and left the self-attention largely non-spiking [34,35,36]. The breakthrough came with Spikformer [8]—the first fully spike-based Vision Transformer—which introduced a Spiking Self-Attention mechanism eliminating expensive floating-point operations by using spike-form Q/K/V without softmax. This enabled direct SNN training on ImageNet with then state-of-the-art accuracy of 74.8%. Subsequent works further improved spiking attention and efficiency. Spike-Driven Transformer developed a linear-complexity attention using only binary masks and additions, and restructured residual connections to maintain purely spike-based activations—achieving higher accuracy of 77.1% with 87× lower computation than standard attention [37]. To better capture multi-scale visual features, SpikingResformer combined a ResNet-inspired multi-stage backbone with a novel Dual Spike Self-Attention that introduces proper scaling for larger feature maps [38]. This architecture set a new SNN record on ImageNet, which is up to 79.4%, while using fewer parameters and less energy than prior spiking ViTs. Biologically inspired attention mechanisms have further bridged the gap to ANNs—for instance, a Saccadic Spike Self-Attention module drew on ocular saccades to dynamically focus on salient regions over time, significantly enhancing spatio-temporal feature integration in SNN-ViTs [39]. Together, these architectural advances—from spike-based self-attention designs to hybrid convolution-Transformer layouts—have substantially improved the performance and efficiency of SNNs on vision tasks, rapidly closing the gap between neuromorphic and conventional deep vision models.

2.3. Model Pruning Techniques

Model pruning is a type of model compression technique that aims to remove redundant parts of neural networks, encompassing two main categories: unstructured pruning and structured pruning. Unstructured pruning removes individual weights with low importance, thereby producing highly sparse models that can dramatically reduce the number of parameters [40,41]. Although such methods can retain performance comparable to the original model after fine-tuning, the resulting irregular sparsity patterns often require specialized hardware or software support to realize actual acceleration. In contrast, structured pruning eliminates entire structural units of a network—such as convolutional channels or Transformer attention heads—making it more hardware-friendly and capable of delivering practical speedups without additional implementation costs. Many recent methods in Convolutional Neural Networks (CNNs) adopt criteria based on weight norms or output feature map information to identify and prune redundant filters with minimal impact on accuracy.These pruning techniques have also been extended to vision Transformer models. By removing redundant attention units, tokens, or even entire layers, researchers have effectively reduced computational overhead while maintaining accuracy [42].

Despite the rapid adoption of pruning in conventional CNNs and ViTs, research on pruning within Transformer-based Spiking Neural Networks is still in its infancy. The seminal Spikformer demonstrated how self-attention can be implemented with spike-form Q/K/V, but it left the compression question largely open [8]. Only a handful of subsequent works have begun to address it: SparseSpikformer jointly searches for winning tickets and removes low-firing tokens, achieving ⩾90% weight sparsity with only 20% GFLOP overhead reduction [43]; STAtten refines the spatial–temporal attention module yet reports pruning merely as a side experiment rather than a core contribution [44]. Taken together, these scattered efforts underscore how Transformer-SNN compression remains largely unexplored, with no consensus on effective token/weight co-design strategies.

The landscape of dynamic pruning is even sparser. In the non-spiking domain, dynamic token sparsification frameworks such as DynamicViT [45], A-ViT [46], Dynamic Token Pruning [47], illustrate the benefits of input-adaptive computation. Yet these methods remain confined to token-level gating, leaving channel-level dynamics mostly untapped.

3. Methods

To address the issue of channel redundancy in Spikformer, we propose SDMFormer, which integrates dynamic masking layers into Spikformer in an ordered manner. This modification prevents redundant channels from emitting spikes, thereby reducing the computational burden of the model while maintaining or improving accuracy. In the following sections, we provide a detailed explanation of the network architecture of SDMFormer.

3.1. LIF Neuron

The Leaky Integrate-and-Fire (LIF) neuron [48] is widely used in SNNs. Its biologically inspired yet mathematically simple membrane makes it a common choice for simulation of large-scale SNNs [4]. LIF neuron has neuronal dynamics that enables spatio-temporal information processing. The dynamics of spiking neurons can be characterized:

$$V^l[t+1]=\left(1-{\displaystyle \frac{1}{{\tau }_m}}\right)V^l\left[t\right]+{\displaystyle \frac{1}{{\tau }_m}}{W}^l{S}^{l-1}[t+1]$$

(1)

$$S^l[t+1]=\Theta \left(V^l[t+1]-V_{th}\right)$$

(2)

where $l=1,\dots ,L$ is the layer index, t is the timestep, $S^{l-1}\left[t\right]$ and $V^l[t-1]$ are the spatial input spikes and the temporal membrane potential input, respectively, $W^l$ is the synaptic weight, ${\tau }_m$ is the decay factor, and $V_{th}$ is the threshold. The Heaviside step function is denoted by $\Theta$. For every $x\ge 0$, $\Theta \left(x\right)=1$; otherwise, $\Theta \left(x\right)=0$. The input spatio-temporal information is incorporated into $V^l\left[t\right]$ and then compared with the threshold to decide whether to fire spikes.

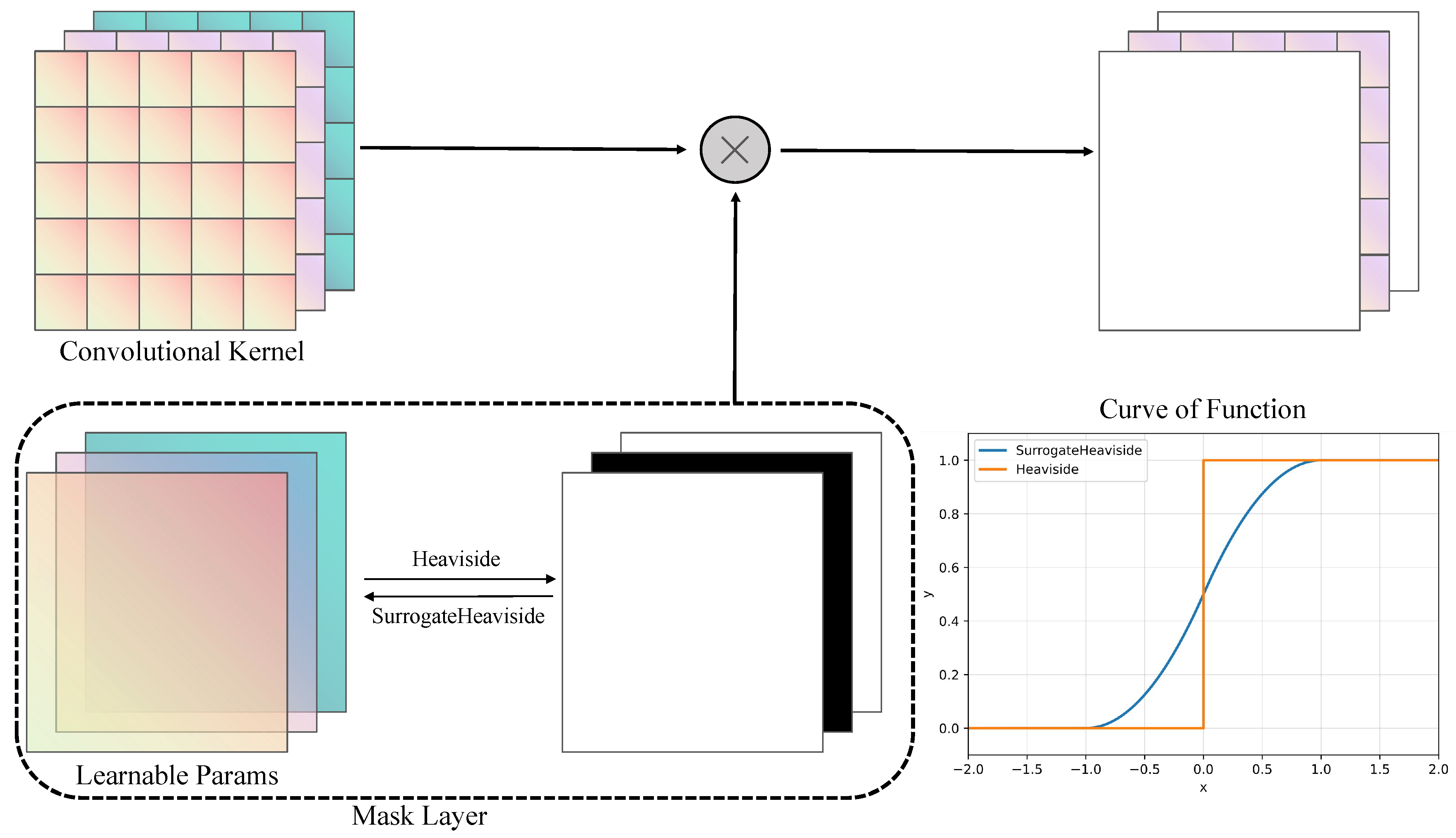
3.2. Mask Layer

As shown in Figure 2, the proposed mask layer is strategically positioned after the convolutional layer to dynamically prune redundant filters in an end-to-end learnable manner. Let C denote the number of output channels of the preceding convolution. The mask layer maintains a trainable parameter vector $m\in {\mathbb{R}}^C$, where each scalar $m_{\mathrm{c}}$ (for $c=1,\dots ,C$) corresponds to a channel-wise gating mechanism.

During backpropagation, the mask parameters are updated as continuous values through gradient descent. To ensure numerical stability, we constrain $m_c$ within $[-1,1]$ via a hyperbolic tangent activation. The differentiable binarization is achieved by applying the SurrogateHeaviside, a continuous piecewise-polynomial surrogate for the Heaviside function:

$$SurrogateHeaviside\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}x<-1,\hfill \\ {\displaystyle \frac{{(x+1)}^2}{2}}\hfill & \mathrm{if}-1\le x<0,\hfill \\ {\displaystyle \frac{2x-x^2+1}{2}}\hfill & \mathrm{if}0\le x<1,\hfill \\ 1\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

Crucially, $SurrogateHeaviside(·)$ exhibits non-vanishing gradients across the entire input domain, with its derivative:

$${\displaystyle \frac{\partial SurrogateHeaviside\left(x\right)}{\partial x}}=\left\{\begin{array}{cc}x+1\hfill & \mathrm{if}-1\le x<0,\hfill \\ 1-x\hfill & \mathrm{if}0\le x<1,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

During the forward pass of training and the inference phase, the trainable parameter vector $m_{\mathrm{c}}$ is binarized to {0, 1} by the Heaviside function, acting as a channel selector. Here is the mathematical definition of the Heaviside function:

$$Heaviside\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<0,\hfill \\ 1,\hfill & x\ge 0.\hfill \end{array}\right.$$

(5)

This surrogate formulation allows gradient signals to propagate through the mask layer during optimization by replacing the non-differentiable derivative of the Heaviside function with a well-behaved surrogate derivative, as commonly done in surrogate-gradient learning [49].

The final output tensor $Y\in {\mathbb{R}}^{H\times W\times C}$ is computed via element-wise multiplication:

$$Y=Heaviside\left(x\right)\odot Conv\left(X\right),$$

(6)

where $Heaviside(·)$ presents the operation of binarization, x presents the learnable parameters, ⊙ denotes channel-wise multiplication and X is the input feature map. Channels assigned a mask value of 0 are permanently deactivated, inducing structured sparsity in the network without architectural modification.

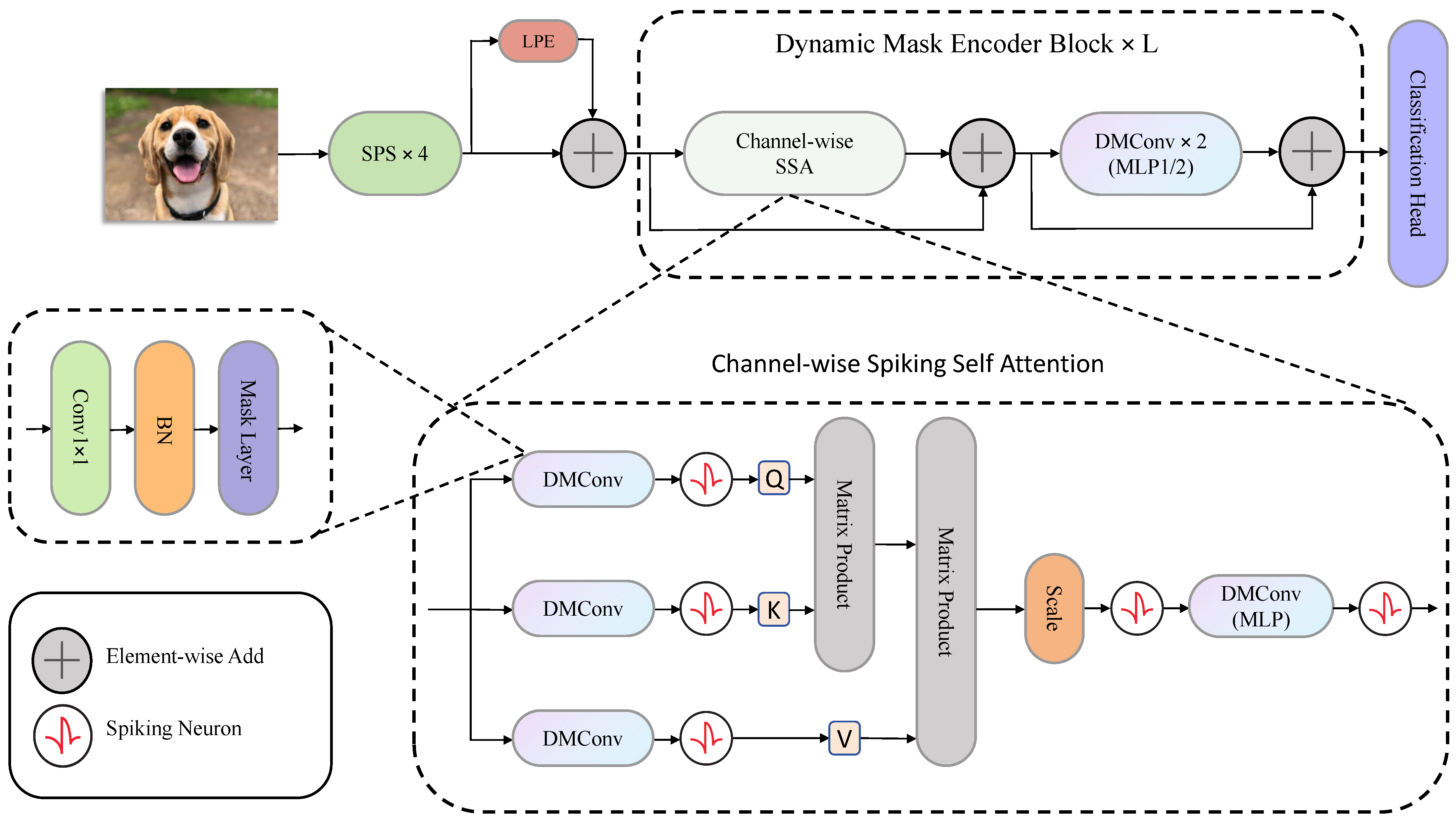
3.3. Dynamic Mask Encoder Block

To further enhance the efficiency and interpretability of the spike-based self-attention mechanism, we propose a novel Dynamic Mask Encoder Block (DMEB) based on the mask layer. This block adaptively prunes redundant channels by learning and applying a set of mask parameters to the convolutional layers within the encoding module during training. Unlike the conventional approach where all channels are treated equally in standard convolutions, DMEB introduces channel-wise masking operations in the network, enabling computational resources to focus on feature channels that have a greater influence on decision-making. Conceptually, this resembles unequal error protection in video transmission, where more important content units receive stronger protection [50]. For Spiking Neural Networks, this selective channel gating is particularly advantageous: by removing excessive discharges from uninformative or noisy channels, both computational complexity and efficiency are improved.

As shown in Figure 3, the core structure of DMEB consists of two main components: Channel-wise SSA and two Dynamic Mask Convolution (DMConv) modules, which replace traditional MLP layers. The Channel-wise SSA first generates query (Q), key (K), and value (V) tensors from the input. Each stage employs a $1\times 1$ convolution to map the input spike feature maps to a latent representation space, followed by batch normalization (BatchNorm) to stabilize and accelerate training. Unlike traditional attention modules, we insert a mask layer (parameterized by learnable tensors) after the BatchNorm operation. The masked features are then fed into the spiking neuron model (MultiStepLIFNode), which we refer to as DMConv. Finally, self-attention operations are performed on the generated spike activations, and another DMConv module completes the overall transformation.

Specifically, let the input tensor be $X\in R^{T\times B\times C\times N}$, where T represents the number of time steps, B is the batch size, C is the number of channels, and N is the spatial resolution (e.g., tokens or spatial positions). In each convolutional layer of DMEB, the channel dimension C is mapped back to its original dimension C. We denote the outputs of the convolution and batch normalization operations as $Q_{\mathrm{bn}},K_{\mathrm{bn}},V_{\mathrm{bn}}\in {\mathbb{R}}^{T·B\times C\times N}$. Subsequently, the mask layer generates a learnable gating function M and applies it to these tensors at the channel level:

The masked feature maps $\tilde{Q},\tilde{K},\tilde{V}$ are subsequently reshaped and passed through spiking neurons. By selectively zeroing out or scaling down less influential channels, this process effectively prevents unnecessary spike activity in uninformative channels, thereby reducing the overall computational load. After undergoing Channel-wise SSA processing, the data is further transmitted through two DMConv modules connected via residual links, replacing traditional MLP layers. This design not only reduces the number of network parameters but also enhances the efficiency of information processing within the network.

Our experimental results presented in Section 4 demonstrate that replacing the conventional spiking transformer architecture with DMEB leads to significant reductions in both parameter count and computational overhead across multiple benchmark datasets. Furthermore, due to the improved computational efficiency, the network performance is maintained or even enhanced in most cases. This underscores the substantial value of DMEB for SNNs operating in resource-constrained environments, emphasizing the importance of implementing dynamic channel gating within spike-based self-attention frameworks.

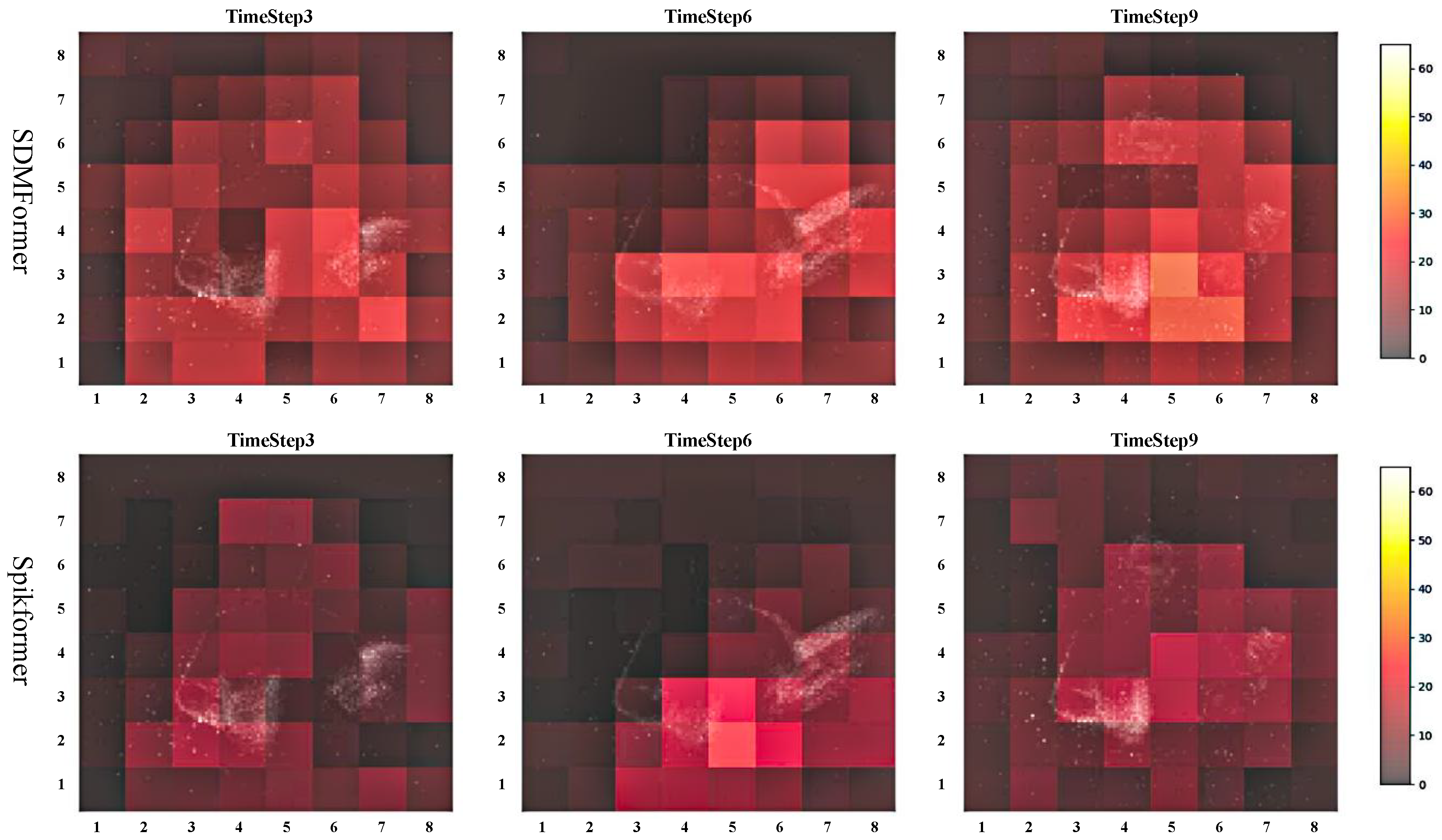
3.4. Lightweight Position Embedding

RPE is commonly employed in various visual Transformer architectures to capture long-range dependencies and local contextual information. Traditional relative position encoding employs a convolutional layer with the same number of output channels as the previous convolutional layer, and combines its output with that of the preceding layer through a residual connection. However, this encoding approach introduces additional computational overhead and increases the number of network parameters. According to our analysis in Spikformer, approximately 22% of the total parameters are attributed to the traditional relative position encoding module. To mitigate these drawbacks, we designed a Lightweight Position Embedding (LPE) module, a compact and efficient position encoding mechanism intended to replace the traditional relative position encoding used in the Spiking Patch Splitting (SPS) stage of Spikformer. Unlike methods that rely on large numbers of parameters or computationally expensive self-attention modules to capture positional information, LPE initializes a learnable position embedding using truncated normal distribution, significantly reducing model complexity while preserving essential spatiotemporal cues from the input frames.

At the core of LPE is a learnable position embedding tensor $P\in {\mathbb{R}}^{1\times 1\times D\times N}$, where D denotes the embedding dimension and N represents the number of patches obtained after multiple convolution and pooling operations. This embedding models the position of each patch, allowing the network to retain necessary positional information while discarding unnecessary complexity. Unlike conventional RPE implementations, which generate position embeddings separately for each spatial location, LPE consolidates parameters into a single learnable tensor to represent the positions of all patches. This parameter-sharing strategy drastically reduces the total number of learnable parameters. For SNNs or models processing event-based data, capturing spatiotemporal information hinges on effectively extracting event triggers, spike emissions, and contextual associations between local and global features. LPE introduces a concise learnable position embedding to uniformly incorporate spatiotemporal positional information into all patches after multiple convolution and downsampling processes. This enables the network’s primary components (e.g., multi-layer convolutions, spike-generating units) to focus on capturing critical spikes and feature activations. In contrast, traditional RPE modules may distribute attention across excessive parameters, complicating the model’s ability to understand local and global relationships. As shown in Figure 4, after applying the LPE in SDMFormer, the patches surrounding the waving person in the DVS128 dataset consistently exhibit higher activation values than the background across different time steps, helping the network concentrate on the most discriminative feature regions. In contrast, with the conventional RPE in Spikformer, the value contrast between the person-related patches and the background patches is much less pronounced.

4. Experiments

In this section, we conduct comprehensive experiments across multiple neuromorphic datasets to evaluate the effectiveness of our SDMFormer framework. Neuromorphic datasets preserve the native spatiotemporal dynamics and sparsity of real-world spike streams, allowing SNNs to be evaluated under the same asynchronous input statistics they are designed for—so latency and energy consumption become meaningful and comparable. We select the following three representative neuromorphic datasets:

• DVS128 Gesture [51]: Captured using Dynamic Vision Sensors (DVS), this dataset records pixel-change events rather than conventional image frames. It contains 11 hand gestures performed by 29 subjects under three illumination conditions, comprising 1342 event streams.
• CIFAR10-DVS [52]: As a neuromorphic adaptation of CIFAR-10, this dataset features 10 classes with 10,000 samples per class. Following Spikformer’s protocol, we use the first 9000 samples per class for training and the remaining 1000 for testing, ensuring fair comparison.
• N-Caltech101 [53]: This neuromorphic conversion of Caltech101 excludes duplicate “Faces” categories, resulting in 100 object classes plus background. Captured via ATIS sensor mounted on a pan-tilt unit observing LCD-displayed images, it preserves biological vision characteristics through active camera movements.

4.1. Implementation Details

Our model implementation utilizes PyTorch [54] (version 2.2.2) and SpikingJelly [55] (version 0.0.0.0.14) frameworks, and all experiments are implemented on a single NVIDIA GeForce RTX 2080 Ti GPU custom-modified to 22 GB VRAM. We use the notation M-L-D to denote a model configuration, where M indicates the network architectures (e.g., SDMFormer), L represents the number of Transformer encoder modules in the model, and D refers to the patch embedding dimension. All tested models are set with four SPS blocks, a patch size of 16, and 16 detection heads by default. To ensure a fair comparison, we keep the training hyperparameters fixed across all experiments: 16 batch size, 16 timesteps, 200 epochs, AdamW optimization, and an initial learning rate of $1\times {10}^{-3}$.

4.2. Mask Rate

As illustrated in Figure 5, we present the experimental results of the masking ratios for SDMFormer-2-256 on the DVS128 dataset. From the perspective of individual layers, the sparsities of the QConv, KConv, and VConv modules are relatively similar and remain at a comparatively low masking rate. This ensures that the attention mechanism effectively captures crucial features, thus providing necessary support for deeper feature representations. In contrast, the masking ratios of the multilayer perceptron (MLP) modules are significantly higher than those of the self-attention layers, especially for MLP2 in the second layer (L2), whose masking ratio approaches 80%, reflecting markedly enhanced dynamic channel sparsity. This outcome indicates that the dynamic masking mechanism contributes more prominently to the sparsification of MLPs, suggesting that the network substantially increases sparsity when processing deeper features. Higher sparsity can reduce activation of redundant channels and minimize information interference, thereby preserving the effective propagation of critical spike signals and ultimately boosting the likelihood of deep spike activation.

Overall, the second layer (L2) exhibits a substantially higher average masking ratio compared to the first layer (L1). Specifically, the masking ratios for components in L1 range from 0.30 to 0.71, while those for L2 vary from 0.39 to 0.79. This phenomenon can be explained by the deep-layer characteristics of spiking neural networks. Due to the discrete nature of spikes and their propagation properties, the firing of neurons in deeper layers often faces challenges such as “vanishing gradients” or “insufficient spikes,” which make deeper features difficult to fully represent. Consequently, deeper network structures require a stronger representational capacity and more robust sparsity-control mechanisms to prevent further reduction in deep spike excitation efficiency caused by redundant channels or non-essential features.

4.3. Comparison with Baseline

In this subsection, we provide a quantitative comparison between the proposed SDMFormer and the baseline Spikformer, aiming to verify the practical benefits of our architectural modifications in terms of both compactness and efficiency.

4.3.1. Number of Parameters

The reduction in the number of parameters for SDMFormer primarily stems from two aspects: the decrease in LPE parameters and the reduction in the number of convolution kernels within the Dynamic Mask Encoder Block. For the LPE, its parameter count is $D\times N$ (introduced in Section 3.4). In contrast, the original Spikformer employs an RPE (Relative Positional Encoding) with a single convolution layer. The FLOPs of this convolutional layer are calculated as follows:

$$F_{Conv}=K^2·H_{\mathrm{out}}·W_{\mathrm{out}}·C_{\mathrm{in}}·C_{\mathrm{out}}$$

(7)

For the Dynamic Mask Encoder Block, the FLOPs of the convolutional mask layer can be calculated as follows:

$$F_M=K^2·H_{\mathrm{out}}·W_{\mathrm{out}}·C_{\mathrm{in}}·C_{\mathrm{out}}·R_{\mathrm{mask}}$$

(8)

Among them, K represents the convolution kernel size, while $H_{\mathrm{out}}$ and $W_{\mathrm{out}}$ denote the height and width of the output feature map, respectively. $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ represent the input and output channel dimensions, respectively, and $R_{\mathrm{mask}}$ refers to the masking ratio of convolutional layer channels.

Table 1. Parameter ratio of SDMFormer compared to Spikformer.

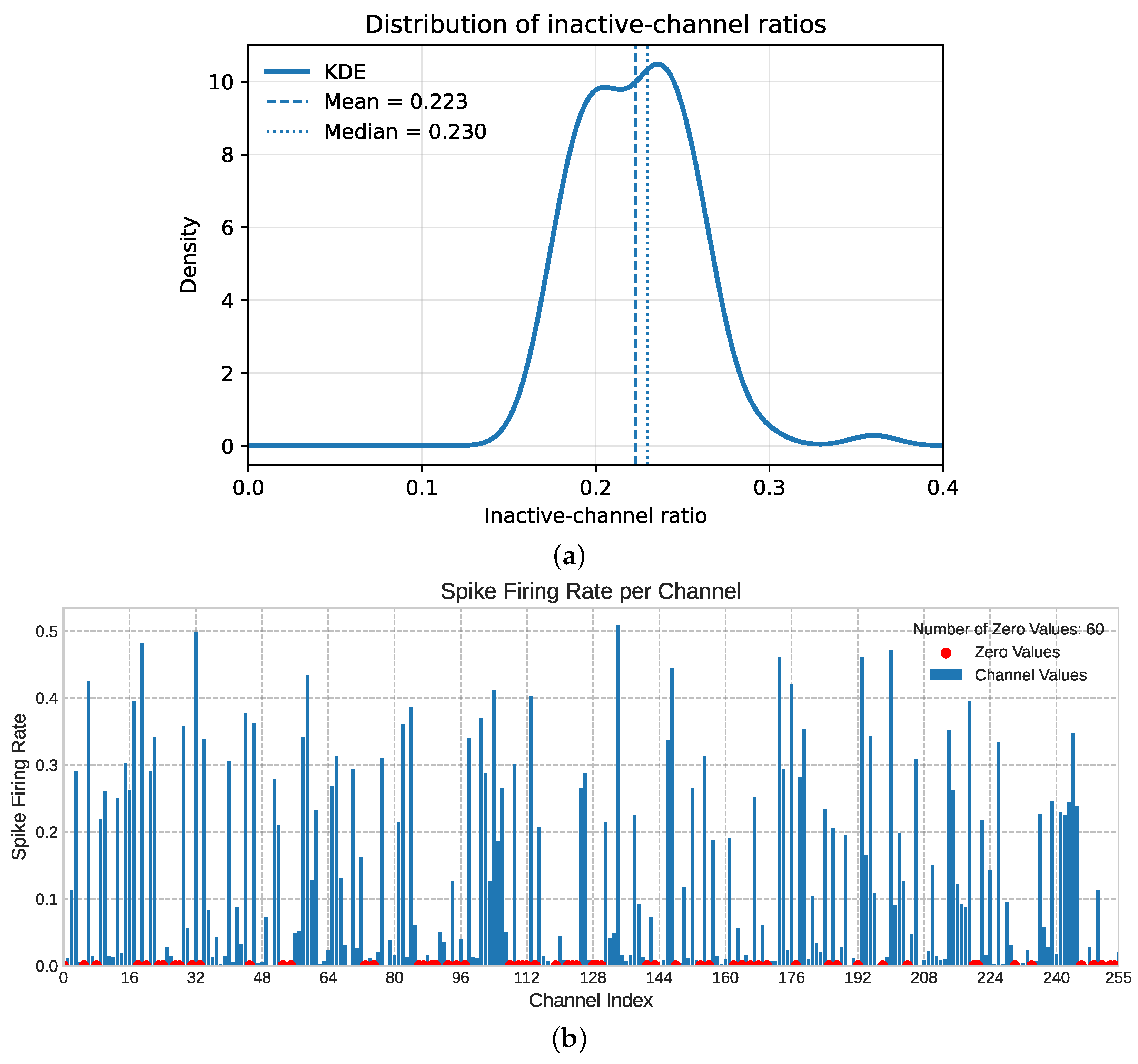
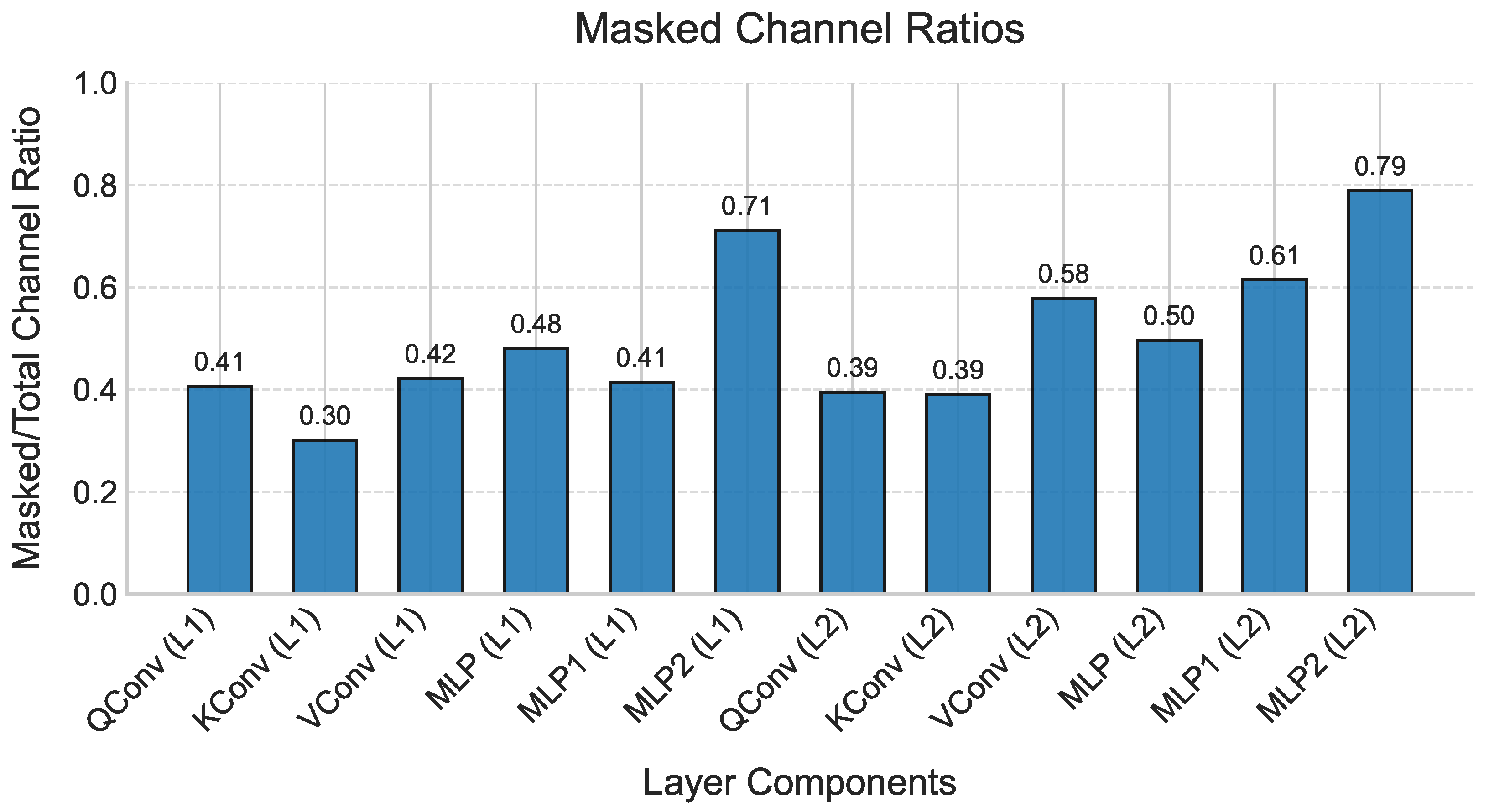
	DVS128	CIFAR10-DVS	N-Caltech101
SDMFormer-2-256/Spikformer-2-256	40.88%	42.69%	37.93%
SDMFormer-1-512/Spikformer-1-512	39.39%	39.72%	37.62%

presents the performance of the SDMFormer model in terms of parameter compression relative to the Spikformer model, where the data is expressed as a percentage of the parameter count ratio. To verify the reliability of our proposed method, we conducted experiments on three datasets with different network architectures. SDMFormer replaces certain modules based on the configurations of Spikformer-2-256 and Spikformer-1-512 and evaluates its parameter compression effectiveness on three event-driven datasets (DVS128, CIFAR10-DVS and N-Caltech101). Specifically, the parameter count of SDMFormer-2-256 is 40.88% of that of Spikformer-2-256 on the DVS128 dataset, 42.69% on the CIFAR10-DVS dataset, and 37.93% on the N-Caltech101 dataset. Similarly, SDMFormer-1-512 exhibits an even higher compression ratio, reducing the parameter count to 39.39%, 39.72%, and 37.62% of Spikformer-1-512 on the respective datasets.

From the results, it can be observed that despite the differences in dataset characteristics, the SDMFormer model consistently compresses the parameter count to approximately 40% of the original model across all scenarios, demonstrating the adaptability and generalizability of the proposed parameter pruning method.

4.3.2. Energy Consumption

Furthermore, we calculated the energy consumption of the SDMFormer model, with the energy consumption formulas for each module presented in

Table 2. Energy consumption formulas for different modules.

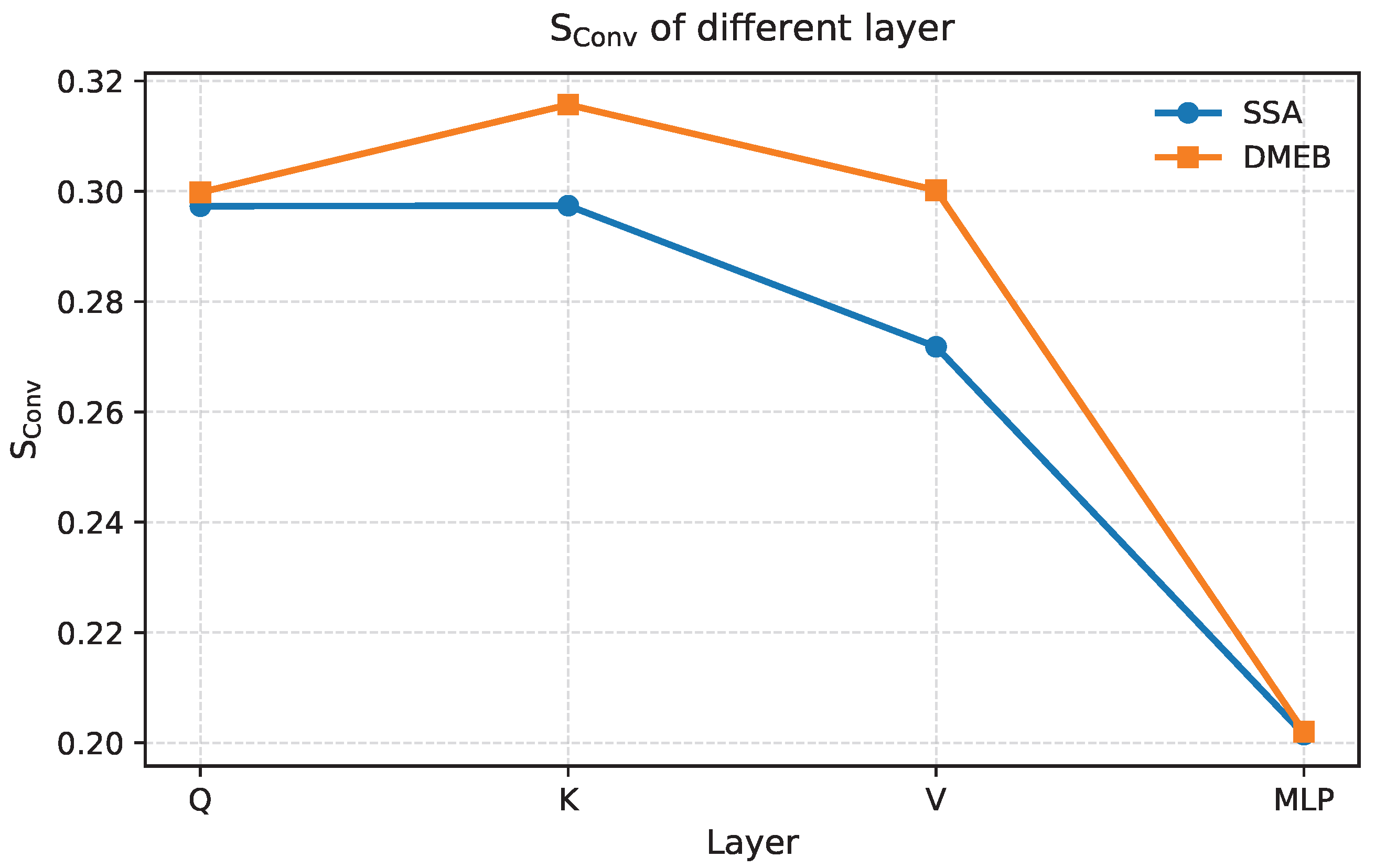
Model	Block	Layer	Energy Consumption
Spikformer	Embedding	First Conv	$E_{\mathrm{MAC}}·F_{\mathrm{Conv}}·T$
		Other Convs	$E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
	SSA	Q,K,V	$3·E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
		MLP	$E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
	MLP	MLP1	$E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
		MLP2	$E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
SDMFormer	Embedding	First Conv	$E_{\mathrm{MAC}}·F_{\mathrm{Conv}}·T$
		Other Convs	$E_{\mathrm{AC}}·F_{\mathrm{Conv}}·T·S_{\mathrm{Conv}}$
	DMEB	Q,K,V	$3·E_{\mathrm{AC}}·F_{\mathrm{M}}·T·S_{\mathrm{Conv}}$
		MLP	$E_{\mathrm{AC}}·F_{\mathrm{M}}·T·S_{\mathrm{Conv}}$
		MLP1	$E_{\mathrm{AC}}·F_{\mathrm{M}}·T·S_{\mathrm{Conv}}$
		MLP2	$E_{\mathrm{AC}}·F_{\mathrm{M}}·T·S_{\mathrm{Conv}}$

. Here, $E_{\mathrm{MAC}}$ represents the energy consumption of a MAC operation, $F_{\mathrm{Conv}}$ denotes the FLOPs of the convolutional layer defined in Equation (7), $F_{\mathrm{M}}$ denotes the FLOPs of the convolutional layer with the mask layer defined in Equation (8), T is the time step, and $S_{\mathrm{Conv}}$ represents the channel-averaged spike firing rate in the convolutional layer.

In the embedding block, for the first convolutional layer, energy consumption related to the emission rate does not need to be considered since we use direct encoding to convert floating-point pixel values into binary spikes. Consequently, $E_{\mathrm{MAC}}$ is used for floating-point pixel inputs. Following previous works, we compute energy consumption based on FLOP operations executed in a 45 nm CMOS process. For instance, $E_{\mathrm{MAC}}=4.6$ pJ, and $E_{\mathrm{AC}}=0.9$ pJ.

We compare the energy consumption of SDMFormer and Spikformer. Similarly, we conduct experiments with different model configurations on three datasets during dataset inference. The total energy consumption is obtained by summing the energy consumption values computed for every layer. The experimental results are illustrated in

Table 3. Energy consumption ratio of SDMFormer relative to Spikformer on different datasets.

	DVS128	CIFAR10-DVS	N-Caltech101
SDMFormer-2-256/Spikformer-2-256	45.38%	50.13%	42.79%
SDMFormer-1-512/Spikformer-1-512	47.56%	48.45%	44.17%

. To avoid ambiguity, we clarify that the reported energy values are algorithm-level estimates derived from operation counts and spike activity. We do not measure power on physical neuromorphic hardware in this work; therefore, the numbers should be interpreted as a relative proxy for energy efficiency rather than absolute hardware energy.

The experimental results demonstrate that SDMFormer exhibits significant energy efficiency advantages compared to the baseline model Spikformer across three benchmark datasets and two architectural configurations. Specifically, the energy consumption of SDMFormer-2-256 is reduced to 45.38%, 50.13%, and 42.79% of the original model on the DVS128, CIFAR10-DVS, and N-Caltech101 datasets, respectively. Similarly, SDMFormer-1-512 achieves reductions to 47.56%, 48.45%, and 44.17%.

It is noteworthy that the energy-consumption ratio is higher than the parameter ratio (37.93–40.88%). This mismatch is expected because, under the energy model in Table 2, the overall energy consumption is not determined by parameter count alone: the dominant terms are jointly modulated by (i) the effective operation count of each convolution ($F_{\mathrm{Conv}}$ vs. $F_{\mathrm{M}}$) and (ii) the channel-averaged spike firing rate $S_{\mathrm{Conv}}$. In SDMFormer, DMEB reduces the effective convolutional cost via channel-wise masking, so the operation count scales with the retained-channel ratio $F_{\mathrm{M}}$, which is the primary source of energy savings. Meanwhile, the gradient-learned masks also reallocate spike activity by suppressing uninformative channels and concentrating spiking on the remaining salient channels. As a result, the channel-averaged spike firing rate $S_{\mathrm{Conv}}$ can increase, as illustrated in Figure 6. This increase partially offsets the reduction in $F_{\mathrm{M}}$, leading to an energy consumption ratio that does not decrease as aggressively as the parameter ratio. Overall, SDMFormer achieves a favorable trade-off: it reduces effective compute through structured channel masking while improving channel-level feature selection, thereby delivering higher efficiency under a more compact model architecture.

These results indicate that combining dynamic channel masking with spatiotemporal sparsity can substantially reduce algorithmic operation costs, suggesting the potential of SDMFormer for energy-constrained deployment. Nevertheless, since our evaluation is based on an operation-level energy proxy rather than measurements on neuromorphic chips, absolute on-device energy will depend on hardware non-idealities and device transport characteristics [56]. We leave a direct hardware-level power evaluation as future work.

4.4. Comparison with Related Work

In this subsection, we compare SDMFormer with recent related work in terms of accuracy, parameter count, and computational efficiency. All experimental settings are kept consistent with those described in Section 4.1.

We provide a detailed analysis of the params and accuracy results in

Table 4. Comparison of parameter and accuracy.

Method	Architecture	Params	CIFAR10-DVS	DVS128	N-Caltech101
PLIF [57]	5Conv,2FC	17.22 M	74.8%	-	-
Dspike [58]	ResNet-18	11.21 M	75.4%	-	-
Spikformer [8]	Spikformer-2-256	2.59 M	80.9%	97.22%	84.59%
CML [59]	Spikformer-2-256	2.57 M	80.9%	98.6%	-
Spikingformer [60]	Spikingformer-2-256	2.55 M	81.3%	98.3%	-
Spike-driven Transformer [37]	Spike-driven Transformer-2-256	2.55 M	80.0%	99.3%	-
Auto-Spikformer [61]	Auto-Spikformer	2.48 M	81.2%	98.6%	-
STSA [62]	STSAFormer-2-256	1.99 M	79.93%	98.7%	-
TCJA-SNN [63]	MS-ResNet-18	1.73 M	80.7%	99.0%	82.5%
QKFormer [64]	HST-2-256	1.50 M	84.0%	98.6%	-
STBP-tdBN [9]	ResNet-17	1.40 M	67.8%	96.9%	-
SEW-ResNet [65]	Wide-7B-Net	1.20 M	74.4%	97.9%	-
SDMFormer-Cifar10dvs (ours)	SDMFormer-2-256	1.09 M	81.5 ± 0.1%	-	-
SDMFormer-DVS128 (ours)	SDMFormer-2-256	1.04 M	-	98.61 ± 0.03%	-
SDMFormer-N-Caltech101 (ours)	SDMFormer-2-256	0.98 M	-	-	83.54 ± 0.46%

. To assess the robustness of the reported accuracy of our model and avoid conclusions based on single-run fluctuations, we repeat each experiment with three independent random seeds for network initialization and data shuffling, which allows us to quantify the variance across runs and verify that the observed gains are not due to random noise. As the trainable parameters of our dynamic masking method are optimized differently across the three datasets, the learned masks vary accordingly; therefore, the resulting SDMFormer models have different parameter count. Our model stands out as a highly efficient architecture in terms of both parameter count and accuracy. The SDMFormer-Cifar10dvs achieves an accuracy of 81.5% on CIFAR-10 DVS with 1.09 M parameters, outperforming Auto-Spikformer by 0.3 percentage points and Spike-driven Transformer by 1.5 percentage points, while using substantially fewer parameters than both. The SDMFormer-DVS128 achieves a high accuracy of 98.61% with 1.04 M parameters. This accuracy is broadly comparable to that of other methods, while our model uses the fewest parameters among them. More impressively, the SDMFormer-N-Caltech101 achieves an accuracy of 83.54% with just 0.98 M parameters, achieving the lowest parameter count among all methods.

To further demonstrate the superior performance of our method, we report a comparison of the inference throughput between SDMFormer and other state-of-the-art SNN models on the CIFAR10-DVS dataset. The experimental settings are consistent with those described in Section 4.1. We use “images per second” (img/s) to characterize inference throughput, where each “image” corresponds to one sample processed with a time-step length of 16. The result is shown in

Table 5. Comparison of inference throughput across different methods.

Method	Architecture	Inference Throughput (img/s)
STSA	STSAFormer-2-256	105.78
QKFormer	HST-2-256	139.05
TCJA-SNN	MS-ResNet-18	144.46
SDMFormer	SDMFormer-2-256	196.20

. SDMFormer achieves the highest inference throughput of 196.20 img/s among all compared methods. Compared with STSA, QKFormer and TCJA-SNN, our method improves the throughput by 85.5%, 41.1% and 35.8% respectively, indicating that our method can process event streams with substantially higher throughput, highlighting its strong potential for low-latency deployment.

This speed advantage is consistent with our architectural design. On the one hand, the DMEB introduces a learnable channel-wise binary masking mechanism that suppresses redundant channels during forward propagation, so the effective computation of convolution scales down with the retained channel ratio, leading to direct inference acceleration. On the other hand, the LPE injects information of local-global relationship in a more lightweight manner, avoiding the additional convolutional overhead introduced by conventional RPE.

We also report comparisons of training throughput and training memory usage between SDMFormer and other methods, as shown in

Table 6. Comparisons of training throughput and training memory usage across different methods.

Method	Architecture	Training Throughput (img/s)	Training Memory Usage (MiB)
STSA	STSAFormer-2-256	43.49	10,328
QKFormer	HST-2-256	60.02	8409
TCJA-SNN	MS-ResNet-18	57.88	8776
SDMFormer	SDMFormer-2-256	57.37	8771

. Training throughput and memory usage are largely correlated with the number of model parameters during the training phase. In training, our model introduces an additional trainable parameter vector $m\in {\mathbb{R}}^C$ after every $1\times 1$ convolution layer in the DMEB module. However, its parameter count is negligible compared to that of convolutional layers. Moreover, since the proposed LPE module significantly reduces the number of trainable parameters, our method is still able to achieve competitive performance compared with other state-of-the-art models.

5. Discussion

To address the issues of computational redundancy and excessive parameter count in Spikformer, we propose SDMFormer, a novel efficient and lightweight architecture. By introducing the DMEB and the LPE module, SDMFormer substantially reduces model size while improving computational efficiency and feature representation.

Experimental results on multiple neuromorphic datasets (DVS128, CIFAR10-DVS, and N-Caltech101) demonstrate the effectiveness of the proposed design. Compared to Spikformer, SDMFormer improves accuracy by 1.39%, 0.7%, and 0.53%, respectively, while reducing parameter count to 37.93–42.69% of the baseline and lowering the energy consumption by 42.79–50.13%. Moreover, SDMFormer remains competitive against recent related works in terms of accuracy, parameter count, and inference throughput. Overall, these results support the benefit of jointly leveraging dynamic channel-wise pruning and spatiotemporal sparsity for efficient spike-based Transformers.

Beyond the neuromorphic evaluation, we clarify the scope and potential transferability of our approach. Our contributions are architecture-level modifications and are largely independent of the specific data modality. Therefore, in principle, SDMFormer can be extended to frame-based pipelines, for example by first converting static frames into spike sequences via spike encoding. However, since we do not report results on frame-based benchmarks in this work, our quantitative conclusions are scoped to neuromorphic datasets. A more systematic evaluation of SDMFormer on frame-based benchmarks will be conducted in future work.

Despite the encouraging results, several limitations remain. Although DMEB introduces learnable mask parameters for adaptive channel selection, we do not explicitly analyze the training stability of mask learning. In deeper spiking Transformer layers, the joint optimization of spiking dynamics and mask parameters may lead to gradient attenuation or unstable spike activity. A systematic investigation of convergence behavior, gradient flow characteristics, and spike statistics during training is an important direction for future research and may further improve the robustness of dynamic masking in deep spiking Transformers.