Network Splitting Techniques and Their Optimization for Lightweight Ternary Neural Networks
Abstract
1. Introduction
- We propose a co-design approach between neural network and hardware to achieve more efficient computation energy usage. The convolutional operations in the neural network are split into groups, where each group fits the hardware array for computation so that the output activation operations are performed in each array. Thus, the analog-to-digital converter (ADC) can be entirely removed from the PIM hardware design. In addition, this method is applicable to various architectures, including a large-scale neural network.
- We evaluate the proposed network splitting technique in TNN and compare its performance with XNOR-Net, a widely used BNN. Our experiments on CIFAR-10 and CIFAR-100 datasets show that the proposed scheme can maintain comparable inference accuracy to the original network, even in a large architecture such as ResNet-20. The proposed design offers a trade-off between memory, computational saving, and accuracy, achieving significant savings with minimal performance degradation.
2. Preliminary Works
2.1. Network Quantization
2.1.1. Ternary Neural Network
2.1.2. XNOR-Net
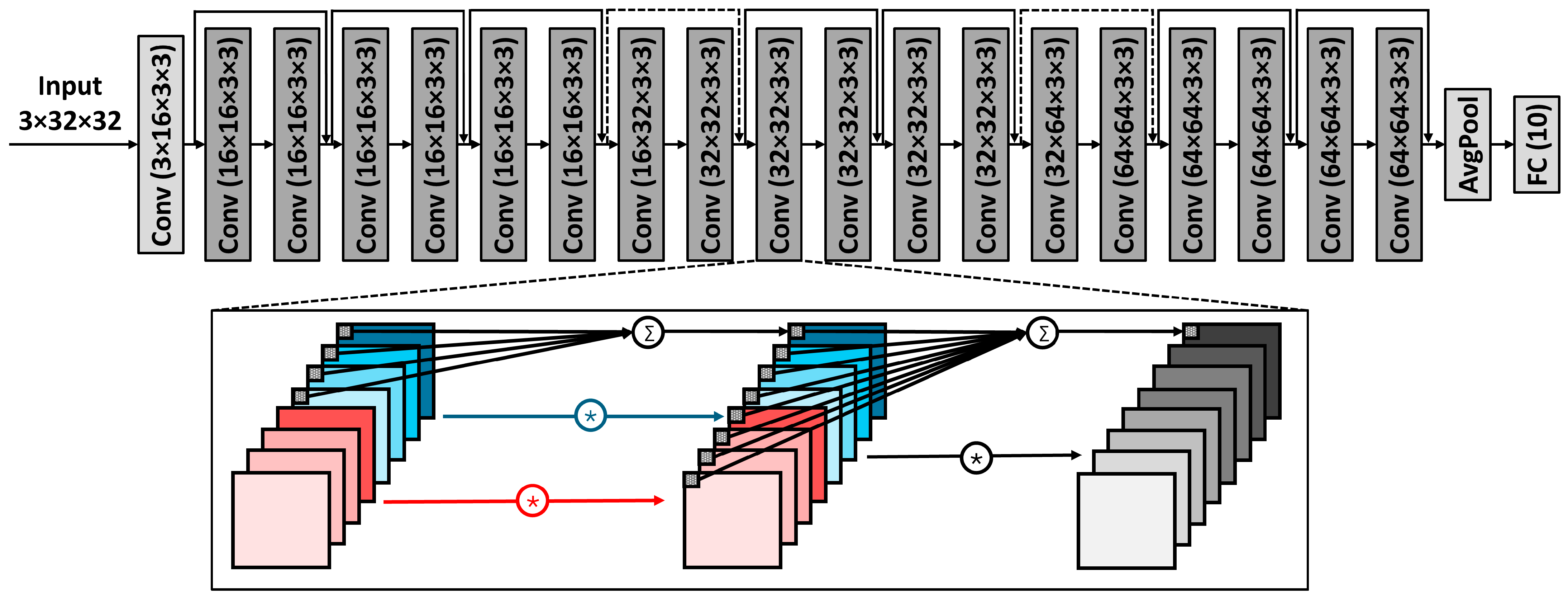
2.2. Residual Network
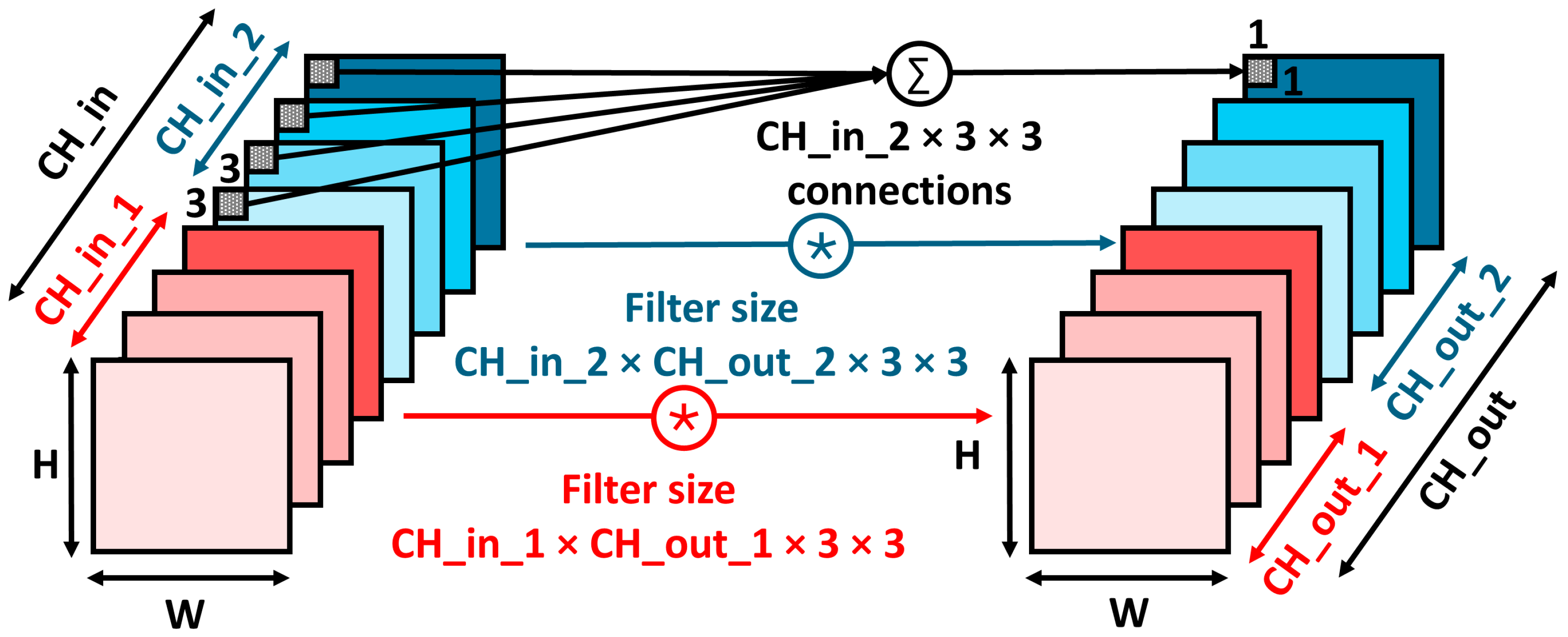
2.3. Grouped Convolution
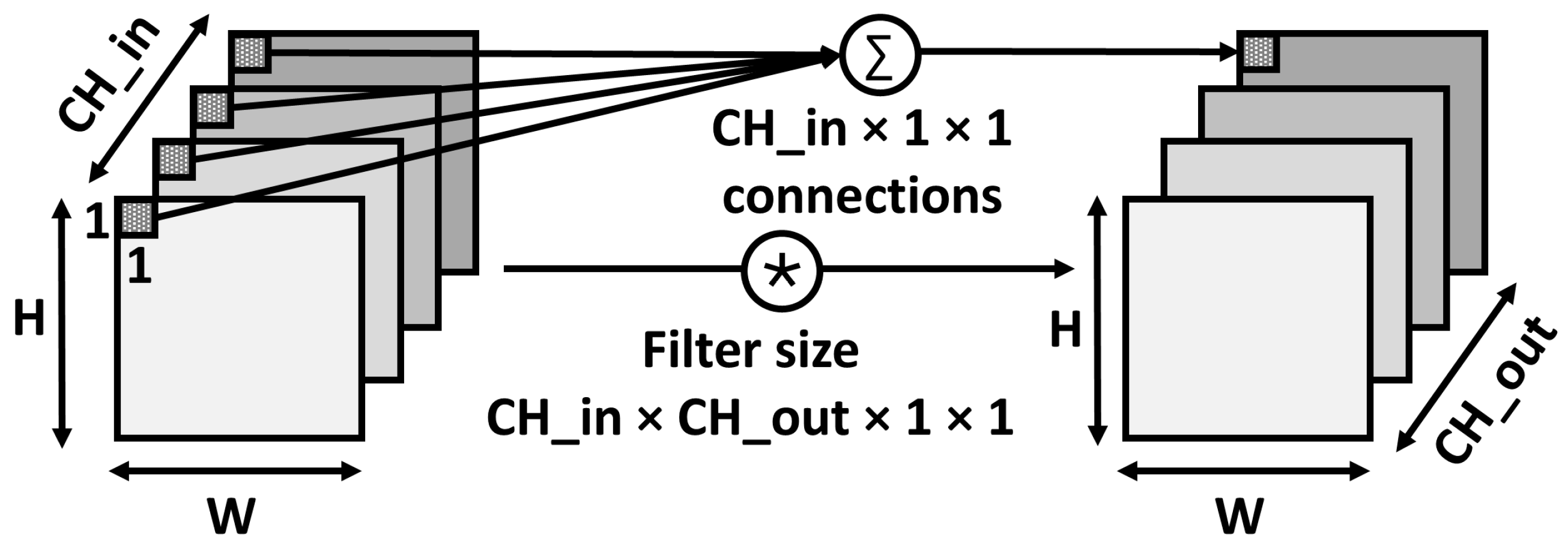
2.4. Pointwise Convolution
3. Proposed Method
3.1. Network Splitting Technique
| Algorithm 1: Network splitting technique on a convolution operation |
| Input: Hardware array size (), input channel size (), output channel size () 1: // number of connections to produce one output 2: // calculate number of groups 3: // grouped convolution 4: if then // no grouping, continue with identity 5: 6: else // pointwise convolution to share information across groups 7: |
3.2. TNN Training
| Algorithm 2: Neural network training with ternarized weight and input |
| Input: Batch of input and target output (), cost function , full-precision weight (), learning rate (), thresholding factor () Output: updated weight and learning rate 1: for to do 2: // find threshold for weight ternarization in this layer 3: 4: for in do // ternarize weight 5: 6: // find threshold for input ternarization in this layer 7: 8: for in do // ternarize input 9: 10: // forward propagation with convolution using network splitting technique and ternarized weight and input 11: // backward propagation using ternary weight 12: // parameter update using real-valued weight 13: |
4. Experimental Results
4.1. Experimental Setup
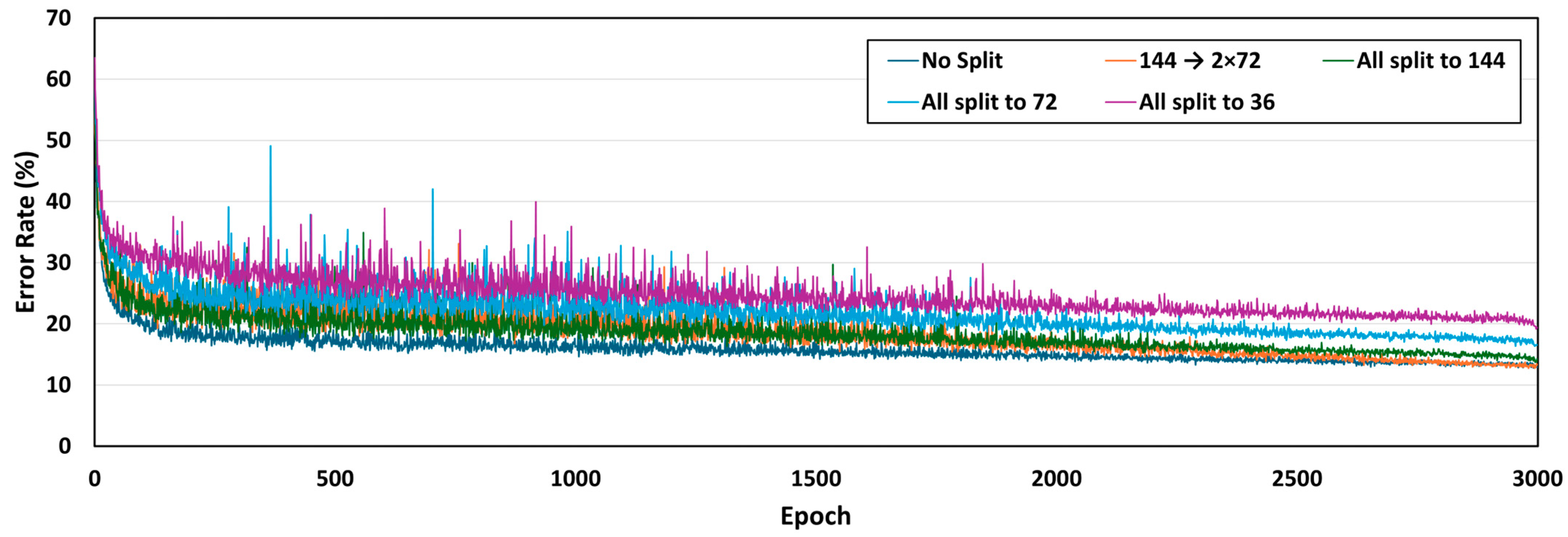
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, Z.; Soudry, D.; Mao, Z.; Lan, Z. Training Binary Multilayer Neural Networks for Image Classification Using Expectation Backpropagation. arXiv 2015, arXiv:1503.03562. [Google Scholar] [CrossRef]
- Soudry, D.; Hubara, I.; Meir, R. Expectation Backpropagation: Parameter-Free Training of Multilayer Neural Networks with Continuous or Discrete Weights. In Proceedings of the Advances in Neural Information Processing Systems 2 Conference: Neural Information Processing, Montreal, QC, Canada, 8 December 2014. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.-P. BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations. In Proceedings of the 29th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar] [CrossRef]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In Proceedings of the 14th European Conference: Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Lin, X.; Zhao, C.; Pan, W. Towards Accurate Binary Convolutional Neural Network. In Proceedings of the 31st International Conference on Neural Information Processing, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- He, Z.; Gong, B.; Fan, D. Optimize Deep Convolutional Neural Network with Ternarized Weights and High Accuracy. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019. [Google Scholar]
- Zhu, C.; Han, S.; Mao, H.; Dally, W.J. Trained Ternary Quantization. arXiv 2016, arXiv:1612.01064. [Google Scholar]
- Kim, J.; Hwang, K.; Sung, W. X1000 Real-Time Phoneme Recognition VLSI Using Feed-Forward Deep Neural Networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014. [Google Scholar]
- Hwang, K.; Sung, W. Fixed-Point Feedforward Deep Neural Network Design Using Weights +1, 0, and −1. In Proceedings of the IEEE Workshop on Signal Processing Systems (SiPS), Belfast, UK, 20–22 October 2014. [Google Scholar]
- Alemdar, H.; Leroy, V.; Prost-Boucle, A.; Pétrot, F. Ternary Neural Networks for Resource-Efficient AI Applications. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Li, Y.; Ding, W.; Liu, C.; Zhang, B.; Guo, G. TRQ: Ternary Neural Networks With Residual Quantization. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, Canada, 2–9 February 2021. [Google Scholar]
- Wan, D.; Shen, F.; Liu, L.; Zhu, F.; Qin, J.; Shao, L.; Shen, H.T. TBN: Convolutional Neural Network with Ternary Inputs and Binary Weights. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, P.; Zhuang, B.; Shen, C. FATNN: Fast and Accurate Ternary Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021. [Google Scholar]
- Rutishauser, G.; Mihali, J.; Scherer, M.; Benini, L. XTern: Energy-Efficient Ternary Neural Network Inference on RISC-V-Based Edge Systems. In Proceedings of the IEEE 35th International Conference on Application-specific Systems, Architectures and Processors (ASAP), Hong Kong, China, 24–26 July 2024. [Google Scholar]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars. In Proceedings of the 43rd International Symposium on Computer Architecture (ISCA), Seoul, Republic of Korea, 18–22 June 2016. [Google Scholar]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory. In Proceedings of the 43rd International Symposium on Computer Architecture (ISCA), Seoul, Republic of Korea, 18–22 June 2016. [Google Scholar]
- Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An Energy-Efficient Reconfigurable Accelerator for Deep Convolutional Neural Networks. IEEE J. Solid-State Circuits 2017, 52, 127–138. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, S.; Park, K.; Jung, J.; Lee, K.J. A Ternary Neural Network Computing-in-Memory Processor With 16T1C Bitcell Architecture. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1739–1743. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, H.; Kim, J.-J. Neural Network-Hardware Co-Design for Scalable RRAM-Based BNN Accelerators. arXiv 2019, arXiv:1811.02187. [Google Scholar]
- Li, F.; Liu, B.; Wang, X.; Zhang, B.; Yan, J. Ternary Weight Networks. arXiv 2016, arXiv:1605.04711. [Google Scholar] [CrossRef]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. arXiv 2013, arXiv:1308.3432. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv 2013, arXiv:1312.4400. [Google Scholar] [PubMed]
- Krizhevsky, A.; Geoffrey, H. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009; Volume 1, pp. 1–60. [Google Scholar]



| Configurations | Number of Groups × Connections | ||
|---|---|---|---|
| 16 Channels | 32 Channels | 64 Channels | |
| No Split | 1 × 144 | 1 × 288 | 1 × 576 |
| 144 → 2 × 72 | 2 × 72 | 1 × 288 | 1 × 576 |
| All split to 144 | 1 × 144 | 2 × 144 | 4 × 144 |
| All split to 72 | 2 × 72 | 4 × 72 | 8 × 72 |
| All split to 36 | 4 × 36 | 8 × 36 | 16 × 36 |
| Parameter | Value |
|---|---|
| Number of epochs | 3000 |
| Batch size | 128 |
| Learning rate | 0.06–0.3 |
| Weight decay | 4 × 10−6–9 × 10−4 |
| Thresholding factor | 0.02–0.04 |
| Split Size Configuration | TNN (This Work) | XNOR-Net [5] | ||
|---|---|---|---|---|
| Accuracy (%) | Drop (%) | Accuracy (%) | Drop (%) | |
| No Split | 88.38 (±0.20) | - | 83.23 (±0.05) | - |
| 144 → 2 × 72 | 87.14 (±0.12) | 1.24 | 82.68 (±0.07) | 0.55 |
| All split to 144 | 86.18 (±0.05) | 2.20 | 76.16 (±0.52) | 7.07 |
| All split to 72 | 83.51 (±0.09) | 4.87 | 70.43 (±2.51) | 12.80 |
| All split to 36 | 80.97 (±0.50) | 7.41 | 67.73 (±2.31) | 15.50 |
| Split Size Configuration | TNN (This Work) | XNOR-Net [5] | ||||
|---|---|---|---|---|---|---|
| Top-1 (%) | Top-5 (%) | Drop (%) | Top-1 (%) | Top-5 (%) | Drop (%) | |
| No Split | 61.33 (±0.28) | 87.10 (±0.29) | - | 53.56 (±0.06) | 81.58 (±0.14) | - |
| 144 → 2 × 72 | 59.35 (±0.15) | 86.00 (±0.23) | 1.98/1.10 | 53.25 (±0.27) | 81.25 (±0.22) | 0.31/0.33 |
| All split to 144 | 53.98 (±0.91) | 82.60 (±0.73) | 7.35/4.50 | 44.01 (±0.13) | 74.25 (±0.13) | 9.55/7.33 |
| All split to 72 | 49.64 (±1.09) | 79.46 (±0.99) | 11.69/7.64 | 34.79 (±1.41) | 64.71 (±1.39) | 18.77/16.87 |
| All split to 36 | 48.09 (±0.39) | 78.36 (±0.16) | 13.24/8.74 | 32.17 (±3.49) | 62.68 (±3.55) | 21.39/18.9 |
| Split Configuration | Number of Parameters | Memory Saving |
|---|---|---|
| No Split | 270,538 | 1.00× |
| 144 → 2 × 72 | 263,882 | 1.02× |
| All split to 144 | 129,738 | 2.08× |
| All split to 72 | 83,914 | 3.22× |
| All split to 36 | 59,722 | 4.53× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimah, H.N.; Prihatiningrum, N.; Gong, Y.-H.; Jin, J.; Seo, Y. Network Splitting Techniques and Their Optimization for Lightweight Ternary Neural Networks. Electronics 2025, 14, 3651. https://doi.org/10.3390/electronics14183651
Karimah HN, Prihatiningrum N, Gong Y-H, Jin J, Seo Y. Network Splitting Techniques and Their Optimization for Lightweight Ternary Neural Networks. Electronics. 2025; 14(18):3651. https://doi.org/10.3390/electronics14183651
Chicago/Turabian StyleKarimah, Hasna Nur, Novi Prihatiningrum, Young-Ho Gong, Jonghoon Jin, and Yeongkyo Seo. 2025. "Network Splitting Techniques and Their Optimization for Lightweight Ternary Neural Networks" Electronics 14, no. 18: 3651. https://doi.org/10.3390/electronics14183651
APA StyleKarimah, H. N., Prihatiningrum, N., Gong, Y.-H., Jin, J., & Seo, Y. (2025). Network Splitting Techniques and Their Optimization for Lightweight Ternary Neural Networks. Electronics, 14(18), 3651. https://doi.org/10.3390/electronics14183651





