Optimal Control for Networked Control Systems with Stochastic Transmission Delay and Packet Dropouts
Abstract
1. Introduction
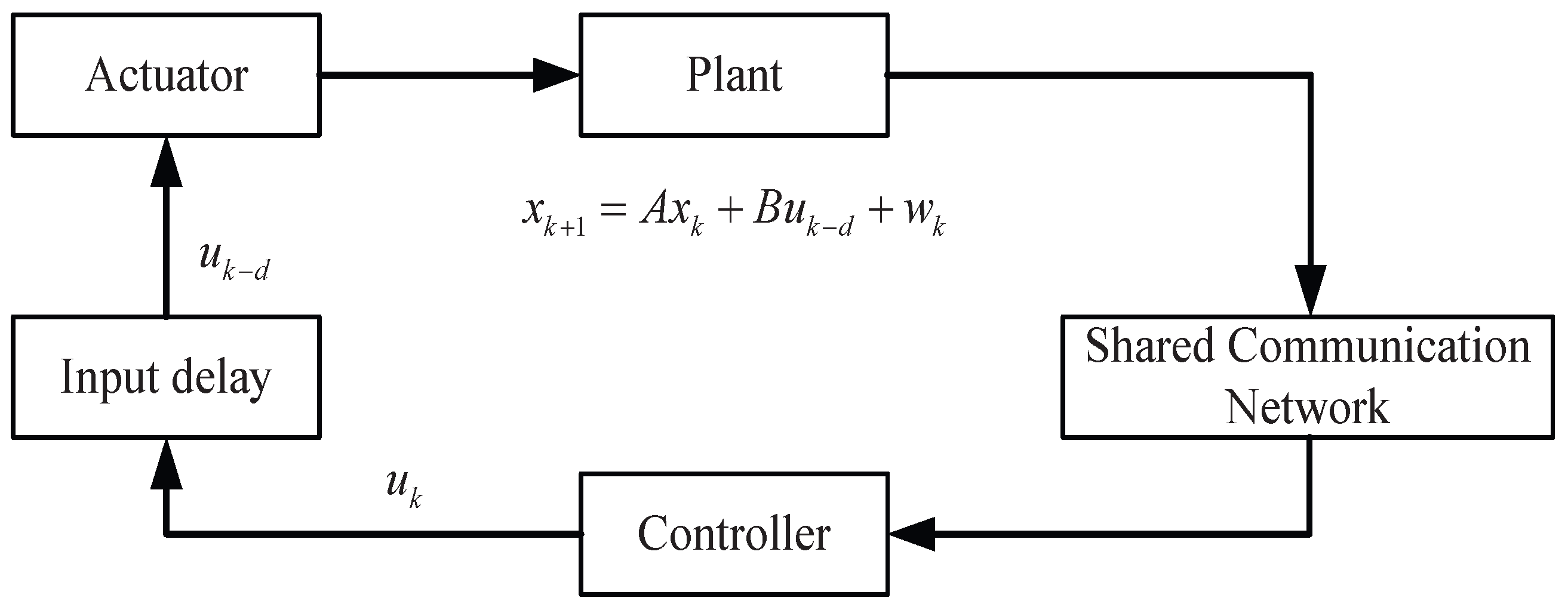
2. Traffic Networked Control Systems Model
2.1. System Model
2.2. Shared Communication Channel Model
3. Optimal Estimation and Control
3.1. Optimal Estimation
3.2. Optimal Control
3.3. Traffic Networked Control Systems: A Special Case
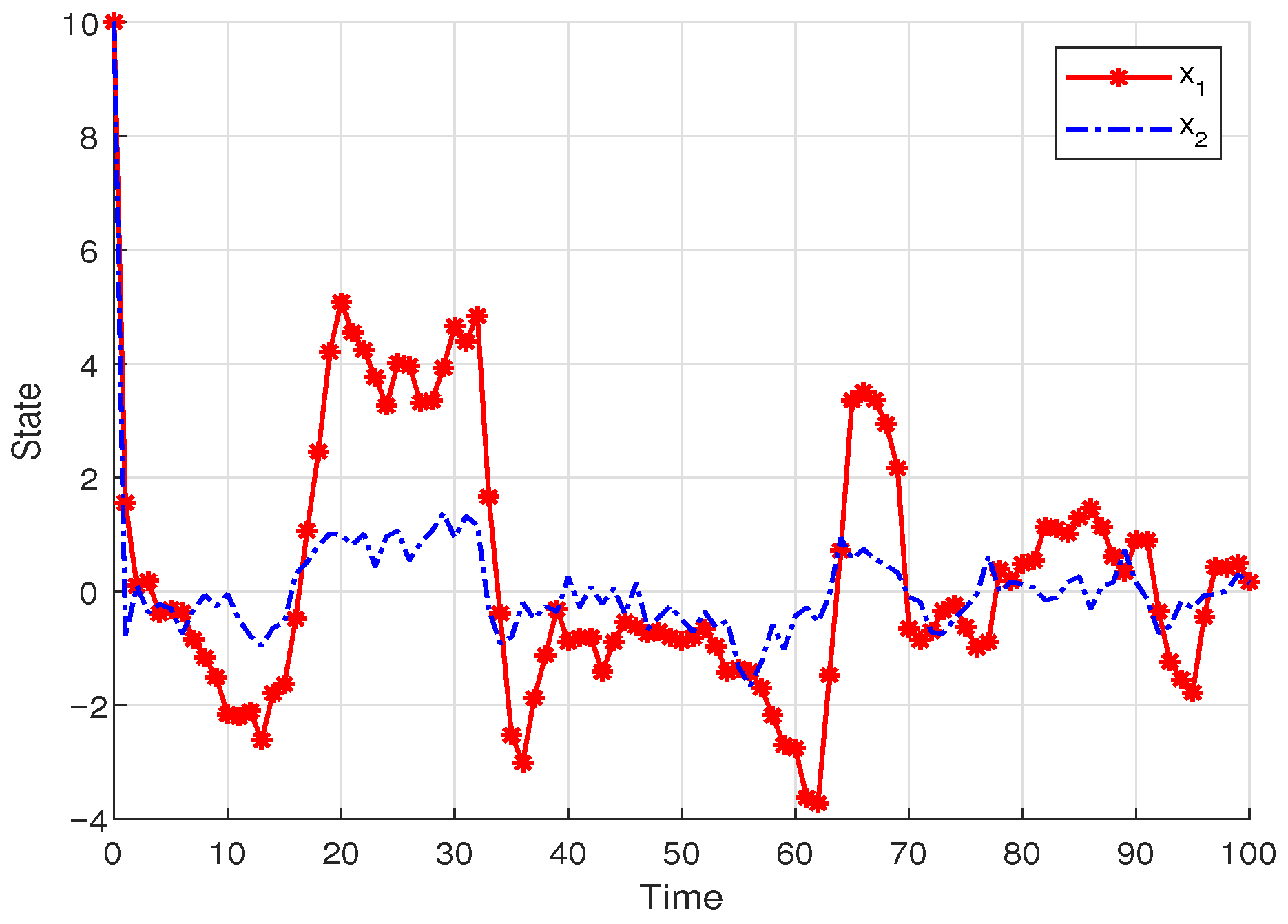
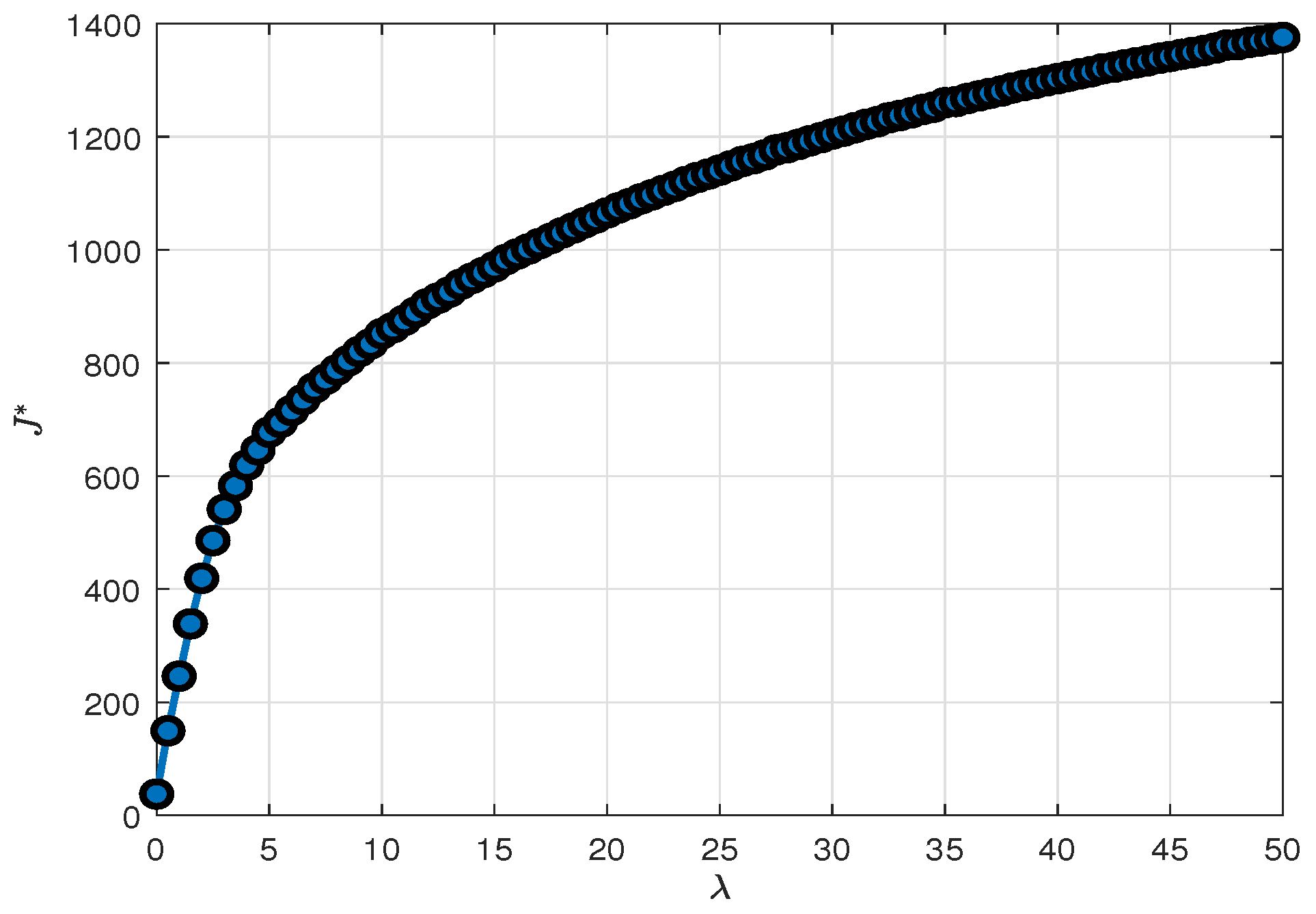
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, C.K.; Hui, S.Y. Reduction of energy storage requirements in future smart grid using electric springs. IEEE Trans. Smart Grid 2013, 4, 1282–1288. [Google Scholar] [CrossRef]
- Xu, J.; Sun, Q.; Han, Q.-L.; Tang, Y. When Embodied AI Meets Industry 5.0: Human-Centered Smart Manufacturing. IEEE/CAA J. Autom. Sin. 2025, 12, 485–501. [Google Scholar] [CrossRef]
- Li, W.; Ma, Y.; Zhang, Y.; Li, B.; Shi, Y.; Chu, L. A Multiangle Observation and Imaging Method for UAV Swarm SAR Based on Consensus Constraints. IEEE Sens. J. 2025, 25, 19776–19793. [Google Scholar] [CrossRef]
- Li, K.; Wang, J.; Zheng, Y. Cooperative Formation of Autonomous Vehicles in Mixed Traffic Flow: Beyond Platooning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15951–15966. [Google Scholar] [CrossRef]
- Zhang, M.; Raghunathan, A.; Jha, N.K. MedMon: Securing Medical Devices Through Wireless Monitoring and Anomaly Detection. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 871–881. [Google Scholar] [CrossRef]
- Li, M.; Lin, H.-J. Design and Implementation of Smart Home Control Systems Based on Wireless Sensor Networks and Power Line Communications. IEEE Trans. Ind. Electron. 2015, 62, 4430–4442. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked Control Systems: A Survey of Trends and Techniques. IEEE/CAA J. Autom. Sin. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Mu, T.; Pang, Z.-H.; Guo, H.; Liu, G.-P.; Han, Q.-L. Output Tracking Predictive Control of Uncertain Networked Control Systems. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3141–3145. [Google Scholar] [CrossRef]
- Sleiman, M.; Bouyekhf, R.; El Moudni, A. Urban transportation network analysis from a thermodynamic perspective. J. Frankl. Inst. 2019, 356, 351–381. [Google Scholar] [CrossRef]
- Gupta, R.A.; Chow, M.-Y. Networked Control System: Overview and Research Trends. IEEE Trans. Ind. Electron. 2010, 57, 2527–2535. [Google Scholar] [CrossRef]
- Sun, H.-Y.; Hou, S.; Du, S.; Han, H.-G.; Qiao, J.-F. Sampled-Data H∞ Dynamic Output-Feedback Control for NCSs With Successive Packet Losses and Stochastic Sampling. IEEE Trans. Cybern. 2024, 54, 6024–6034. [Google Scholar] [CrossRef]
- Zhu, X.L.; Zhang, X.; Wei, J.; Lin, H. Output-Based Dynamic Event-Triggered Control for Networked Control Systems with Delays and Packet Losses Without Acknowledgements. IEEE Trans. Autom. Control 2023, 68, 7120–7135. [Google Scholar] [CrossRef]
- Li, C.; Zhao, X.; Chen, M.; Xing, W.; Zhao, N.; Zong, G. Dynamic Periodic Event-Triggered Control for Networked Control Systems Under Packet Dropouts. IEEE Trans. Autom. Sci. Eng. 2024, 21, 906–920. [Google Scholar] [CrossRef]
- Sun, Y.; Qin, S. Stability and Stabilization of Networked Control Systems with Bounded Packet Dropout. Acta Autom. Sin. 2011, 37, 113–118. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, H.; Ding, S.X.; Wang, G.; Zhou, D. Residual generation and evaluation of networked control systems subject to random packet dropout. Automatica 2009, 45, 2427–2434. [Google Scholar] [CrossRef]
- Imer, O.C.; Yüksel, S.; Başar, T. Optimal control of LTI systems over unreliable communication links. Automatica 2006, 42, 1429–1439. [Google Scholar] [CrossRef]
- Liu, J.; Wu, L.; Wu, C.; Luo, W.; Franquelo, L.G. Event-triggering dissipative control of switched stochastic systems via sliding mode. Automatica 2019, 103, 261–273. [Google Scholar] [CrossRef]
- Nayyar, N.; Kalathil, D.; Jain, R. Optimal decentralized control with asymmetric one-step delayed information sharing. IEEE Trans. Control Netw. Syst. 2018, 5, 653–663. [Google Scholar] [CrossRef]
- Asghari, S.; Ouyang, Y.; Nayyar, A. Optimal local and remote controllers with unreliable uplink channels. IEEE Trans. Autom. Control 2019, 64, 1816–1831. [Google Scholar] [CrossRef]
- Liang, X.; Xu, J. Control for networked control systems with remote and local controllers over unreliable communication channel. Automatica 2018, 98, 86–94. [Google Scholar] [CrossRef]
- Liang, X.; Xu, J.; Zhang, H. Optimal control and stabilization for networked control systems with asymmetric information. IEEE Control Netw. Syst. 2020, 7, 1355–1365. [Google Scholar] [CrossRef]
- Liang, X.; Qi, Q.; Zhang, H.; Xie, L. Decentralized control for networked control systems with asymmetric information. IEEE Trans. Autom. Control 2022, 67, 2076–2083. [Google Scholar] [CrossRef]
- Lu, M.; Liu, S.; Luo, Y.; Qi, Q.; Sun, Y.; Li, J. Modeling and Output Feedback Tracking Control of Self-Developed Autonomous Underwater Vehicle. Unmanned Syst. 2025, 13, 1639–1660. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.P.; Wang, Y.; Qi, Q.; Wang, X. Adaptive Interval Observer-Based Fault-Tolerant Control for a 3-DOF Helicopter Without Angular Velocity Measurement. IEEE Trans. Control Syst. Technol. 2025, 33, 2476–2482. [Google Scholar] [CrossRef]
- Qi, Q.; Xie, L.; Zhang, H.; Liang, X. Jointly Optimal Local and Remote Controls for Networked Multiple Systems With Multiplicative Noises and Unreliable Uplink Channels. IEEE Trans. Autom. Control 2025, 70, 1054–1067. [Google Scholar] [CrossRef]
- Qi, Q.; Xie, L.; Zhang, H. Optimal Control for Stochastic Systems With Multiple Controllers of Different Information Structures. IEEE Trans. Autom. Control 2021, 66, 4160–4175. [Google Scholar] [CrossRef]
- Lai, C.L.; Hsu, P.-L. The Butterfly-Shaped Feedback Loop in Networked Control Systems for the Unknown Delay Compensation. IEEE Trans. Ind. Inform. 2014, 10, 1746–1754. [Google Scholar] [CrossRef]
- Qiu, L.; Dai, L.; Ahsan, U.; Fang, C.; Najariyan, M.; Pan, J. Model Predictive Control for Networked Multiple Linear Motors System Under DoS Attack and Time Delay. IEEE Trans. Ind. Inform. 2023, 19, 790–799. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, H.; Wong, W.S.; Zhang, Z. Feedback Stabilization of Uncertain Networked Control Systems Over Delayed and Fading Channels. IEEE Trans. Control Netw. Syst. 2021, 8, 260–268. [Google Scholar] [CrossRef]
- Zhang, W.-A.; Yu, L. Modelling and control of networked control systems with both network-induced delay and packet-dropout. Automatica 2008, 44, 3206–3210. [Google Scholar] [CrossRef]
- Tipsuwan, Y.; Chow, M.-Y. Control methodologies in networked control systems. Control Eng. Pract. 2003, 11, 1099–1111. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, B.; Chen, X.; Yan, H. Tracking performance limitations of MIMO discrete-time networked control systems with multiple constraints. Sci. China Inf. Sci. 2023, 66, 189203. [Google Scholar] [CrossRef]
- Du, X.; Zhan, X.; Wu, J.; Yan, H. Effects of Two-Channel Noise and Packet Loss on Performance of Information Time Delay Systems. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8549–8556. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Fu, J.; Duan, P.; Wen, G.; Huang, T. Distributed State Estimation Under Multistep Random Transmission Delay and Packet Loss. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 11875–11887. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, G.P.; Hu, W. Coordinated Distributed Predictive Control for Voltage Regulation of DC Microgrids With Communication Delays and Data Loss. IEEE Trans. Smart Grid 2023, 14, 1708–1722. [Google Scholar] [CrossRef]
- Zhao, J.; Li, B. Finite-Time H∞ Robust Controller Design for a Class of Singular Discrete-Time Markov Jump Delay Systems With Packet Loss Compensation and Input Saturation. IEEE Access 2022, 10, 101465–101473. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Shi, Y.; Li, C. Packet-loss-dependent stabilization of NCSs with network-induced delay and packet dropout. J. Syst. Eng. Electron. 2012, 23, 408–413. [Google Scholar] [CrossRef]
- Tan, C.; Li, L.; Zhang, H. Stabilization of networked control systems with both network-induced delay and packet dropout. Automatica 2015, 59, 194–199. [Google Scholar] [CrossRef]
- Liang, X.; Xu, J.; Zhang, H. Optimal Control and Stabilization for Networked Control Systems With Packet Dropout and Input Delay. IEEE Trans. Circuits Syst.-II Express Briefs 2017, 64, 1087–1091. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Shirmohammadi, S.; Altamimi, S. A Multimodal Deep Learning-Based Distributed Network Latency Measurement System. IEEE Trans. Instrum. Meas. 2020, 69, 2487–2494. [Google Scholar] [CrossRef]
- Ren, W.; Xiong, J. Tracking Control of Nonlinear Networked and Quantized Control Systems With Communication Delays. IEEE Trans. Autom. Control 2020, 65, 3685–3692. [Google Scholar] [CrossRef]
- Maity, D.; Mamduhi, M.H.; Hirche, S.; Johansson, K.H. Optimal LQG Control of Networked Systems Under Traffic-Correlated Delay and Dropout. IEEE Control Syst. Lett. 2022, 6, 1280–1285. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, A.; Liang, X. LQG control for networked control systems with packet dropouts and input delay: UDP case. Optim. Control Appl. Methods 2025, 41, 259–270. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liu, J.; Tan, B.; Mu, X. Optimal Control for Networked Control Systems with Stochastic Transmission Delay and Packet Dropouts. Electronics 2026, 15, 180. https://doi.org/10.3390/electronics15010180
Liu J, Tan B, Mu X. Optimal Control for Networked Control Systems with Stochastic Transmission Delay and Packet Dropouts. Electronics. 2026; 15(1):180. https://doi.org/10.3390/electronics15010180
Chicago/Turabian StyleLiu, Jingmei, Boqun Tan, and Xiaojian Mu. 2026. "Optimal Control for Networked Control Systems with Stochastic Transmission Delay and Packet Dropouts" Electronics 15, no. 1: 180. https://doi.org/10.3390/electronics15010180
APA StyleLiu, J., Tan, B., & Mu, X. (2026). Optimal Control for Networked Control Systems with Stochastic Transmission Delay and Packet Dropouts. Electronics, 15(1), 180. https://doi.org/10.3390/electronics15010180






