Optimization of Pumped Storage Capacity Configuration Considering Inertia Constraints and Duration Selection

Abstract

In response to the decline in the inertia level of the power system caused by the large-scale integration of new energy, this paper proposes a grid-side pumped storage configuration strategy considering inertia constraints. The general pumped storage configuration ignores the duration of pumped storage and selects only single-duration units for capacity and power configuration. A single unit cannot balance rapid frequency response and long-term energy transfer, forcing thermal power to operate at high costs continuously to provide inertia support, while also causing a sharp increase in wind and solar power curtailment. This paper breaks through the limitations of the traditional single-duration pumped storage configuration and proposes a configuration-operation collaborative optimization strategy that combines inertia constraints and pumped storage duration selection. Firstly, starting from the system’s inertia requirements, the minimum inertia required by the system is obtained, respectively, based on the constraints of the system’s frequency change rate and the lowest point of the frequency. Furthermore, the minimum inertia demand constraint of the power system is constructed, and a capacity configuration strategy for grid-side pumped storage is proposed with the goal of minimizing the total operating cost of the power system throughout its entire cycle, taking into account the penalty term of the peak-valley difference index of the load curve and the penalty of the inertia guarantee value of medium and long-term units, while considering the inertia constraint. Finally, the effectiveness and superiority of the proposed method were verified through simulation analysis.

1. Introduction

The traditional power system, based on synchronous units providing inertia support, can effectively deal with frequency offsets caused by power disturbances. In recent years, with the large-scale integration of new energy into the grid, the proportion of traditional synchronous units has declined. Furthermore, power electronic interfaces (e.g., inverters for renewable energy integration) inherently provide little or no inertia support. This leads to a significant drop in the overall inertia level of the power system, which poses greater risks to the frequency stability and anti-disturbance capacity of the power system [1,2,3,4]. To address the above-mentioned issues, the power system needs to take multiple measures to enhance its operational stability, among which the application of energy storage technology is particularly important. Pumped storage, as the most mature large-scale energy storage technology, features rapid start-up and flexible regulation, and has a lower cost compared to other energy storage methods. It has continuously dominated global energy storage applications [5,6]. Therefore, estimating the inertia of power systems containing new energy and rationally allocating a certain capacity of pumped storage is of great significance for ensuring the safe grid connection and operation of new energy.

The minimum inertia of the system can be evaluated by considering the constraints of Rate of Change of Frequency (RocoF) and the lowest point of frequency (Nadir) under large disturbances [7,8]. Ref. [9] considered the static load characteristics and the dynamic frequency spatial distribution characteristics when constructing the RocoF constraints. In the lowest frequency constraint, the system frequency response model of multiple types of frequency modulation resources was taken into account for the minimum inertia evaluation. Ref. [10] studied the interaction between the inertia response and primary frequency modulation under high-power disturbances. An evaluation model was established with Nadir as the dynamic frequency stability constraint, and the minimum primary frequency modulation capacity and the minimum inertia time constant of the system were estimated.

At present, with the continuous increase in the penetration rate of new energy, the optimal dis-patching considering the frequency security of the power system has become a hot research issue [11]. Refs. [12,13] conduct theoretical analysis on inertia support and frequency security in power system optimization problems, emphasizing the significance of considering frequency security and inertia support in enhancing the safety and stability of power systems and responding to power disturbances under the background of large-scale new energy grid connection. Ref. [14] explored an analytical method for aggregating the frequency response models of multi-machine systems into single-machine models, and analyzed the application potential of this method in aspects such as system frequency control, frequency stability, and dynamic model simplification. In the research of embedding frequency stability constraints into the operation of power systems, Reference [9] pro-posed a system minimum inertia demand assessment method that comprehensively considers RocoF and Nadir. Ref. [15] proposed an optimization operation method for high-proportion new energy power systems. By decomposing the optimization operation problem into two steps, namely “minimum inertia evaluation” and “optimization operation”, it decouples the embedded frequency stability constraints.

The aforementioned research has significant reference value, but it also faces the following two issues: (1) The nonlinear characteristics of frequency stability-related constraints lead to difficulties in solving the model. Existing studies typically use time-domain simulation or optimization algorithms to approximate Nadir, among other methods. However, these approaches often involve high complexity in theoretical derivation and model resolution processes and require substantial computational resources, limiting their widespread application in actual power systems; (2) Most of the literature focuses on solving frequency constraint issues from the perspective of scheduling thermal power units, neglecting the possibility of addressing frequency safety issues in high-proportion renewable energy power systems through coordination with various energy storage systems and thermal power units. Based on this, Ref. [16] proposed an optimal scheduling model for the combined wind-solar-thermal-energy storage system taking inertia constraints into account. The study evaluated the minimum inertia requirements of the system according to RoCoF and Nadir constraints and introduced this result into the scheduling framework. While taking into account the uncertainty of source-load, it coordinated the supporting role of the inertia of synchronous units and the virtual inertia of energy storage. Thus, the economic operation of the system has been optimized while ensuring the stability of the frequency. Ref. [17] investigated frequency issues in grids containing energy storage and low-inertia components, linearizing the nonlinear frequency constraints, and subsequently incorporating energy storage into traditional scheduling models using model predictive control, thus pro-posing a unit combination and economic scheduling model that considers frequency stability constraints with energy storage, ensuring the grid frequency remains within constraints after disturbances, effectively enhancing the frequency safety of the grid. Ref. [18] accounted for the uncertainty of wind power and energy storage battery models while integrating dynamic constraints of grid frequency, establishing a new optimal scheduling model, and finally, through case analysis, verified that the model can reduce operating costs while ensuring grid frequency safety.

While the aforementioned studies provide valuable insights into frequency security, a critical limitation lies in their primary focus on leveraging thermal power units for inertia support. A planning and dispatch strategy that does not explicitly incorporate inertia constraints carries significant risks for systems with high renewable energy penetration. It can lead to operational states where the system inertia is critically low, making the grid vulnerable to large disturbances. To maintain stability under such a paradigm, system operators are often forced to keep more thermal units online than economically optimal, leading to increased operational costs and curtailed renewable energy generation due to the minimum technical output limits of thermal plants. This creates a fundamental conflict between economic efficiency and frequency security, which is not adequately resolved by existing methods that neglect to embed inertia requirements directly into the optimization model.

Furthermore, in the domain of pumped storage planning, a prevalent simplification is the configuration of pumped storage with a single, fixed duration [19]. This conventional approach represents a significant technical gap. A uniform-duration pumped storage cannot simultaneously optimize for the diverse services required by modern power systems. Specifically, it fails to balance the need for rapid frequency response, best served by short-duration units with fast ramping capabilities, and long-term energy transfer for peak shaving and renewable energy absorption, requiring long-duration units with large energy capacity. This inadequacy forces a compromise, where a single-duration pumped storage is suboptimal for both functions. It can lead to insufficient frequency support during critical periods and an inability to fully utilize renewable energy, ultimately forcing thermal power units to operate continuously at high costs to provide the necessary stability, thereby undermining the economic.

To overcome the shortcomings of existing studies in pumped storage planning, such as not considering frequency safety constraints and adopting fixed durations, this paper proposes a new capacity configuration-operation collaborative optimization strategy that integrates inertia constraints and operating duration selection. Firstly, based on the analysis of the inertia support requirements of the power system, the minimum moment of inertia required by the system is derived, respectively, according to the frequency change rate limit of the system and the requirements of the frequency Nadir. Subsequently, a capacity optimization allocation model for grid-side pumped storage was constructed, which includes the minimum inertia demand constraint and aims to minimize the total operating cost of the power system throughout its entire cycle by taking into account the penalty term of the peak-valley difference index of the load curve and the penalty of the inertia guarantee value of medium and long-term units. Ultimately, the simulation experiments verified the significant advantages of this collaborative optimization strategy in enhancing the system’s inertia support capacity and economy.

2. Assessment of Minimum Inertia Requirement in Power System

The inertia of a power system is defined as the ability of the system to maintain its frequency within a safe and allowable fluctuation range when facing external disturbances or internal equipment failures [20]. The inertial resources in a power system play a significant role in reducing the variation in system frequency and maintaining frequency stability. Since the disturbance occurs, the frequency response of the power system usually includes inertia response, unit output characteristic adjustments of primary frequency regulation and secondary frequency regulation, and tertiary frequency regulation process [21]. Among them, the inertia response process is supported by synchronous inertia and virtual inertia, while the primary frequency regulation process is achieved through the output adjustment of the prime mover and the coordinated control of the speed regulation system. The frequency response mechanism studied in this paper mainly focuses on inertial response and the primary frequency modulation process.

Inertia response, as the core physical basis for system frequency stability, runs through the entire process of the system’s dynamic frequency response. During this period, any factor that can impede frequency variation can be included in the category of generalized system inertia, including the physical inertia of the synchronous generator set, the quasi-inertial response generated by the static frequency regulation effect of the load (${\displaystyle \frac{dP}{df}}$ characteristics), and the virtual inertia produced by the virtual synchronous machine, etc. The above-mentioned inertia collaboratively releases the kinetic energy of the rotor, jointly suppressing the frequency variation in the system.

When power disturbances occur in the power system, the frequency dynamic response characteristics can be characterized by the rotor motion equation, and the specific expression is:

$$2H_{sys}\frac{df(t)}{f_{N}dt} = P_m\left(t\right)-P_e\left(t\right)-D_s\Delta f(t),$$

(1)

where $f\left(t\right)$ represents the system frequency at time t, which is usually expressed by the frequency of the system’s inertial center; $f_N$ is the rated frequency of the system; $P_m\left(t\right)$ is the total mechanical power; $P_e\left(t\right)$ is the total electromagnetic power; $D_s$ is the damping coefficient in the system frequency response process; $\Delta f\left(t\right)$ represents the system frequency deviation.

RocoF and the lowest point of frequency are the key indicators for measuring frequency stability under disturbance. Under a certain disturbance power, the factors influencing the instantaneous frequency change rate of the disturbance are inertia and the load voltage characteristics. The factors influencing the lowest point of frequency include inertia, primary frequency regulation of the generator, load frequency regulation and load voltage characteristics [9]. The minimum inertia requirement of the system can be evaluated from the frequency constraints and influencing factors of these two aspects.

2.1. Minimum Inertia Based on the Constraint of RocoF

At the moment when the disturbance occurs, the rate of change in the system frequency reaches an extreme value, and the system inertia is at its lowest point. At this point, the system frequency has not deviated, the generator governor has not started, and the load frequency regulation effect has not been manifested. The frequency change at this time can be regarded as jointly determined by the system inertia and the disturbance power. If the RoCoF after disturbance does not exceed the maximum allowable value as a constraint condition, then the RoCoF at the moment of disturbance should be used as the evaluation criterion [12]. Therefore, based on the rotor motion equation, the expression of the maximum frequency change rate of the system can be calculated as:

$${RocoF}_M = {\left.{\displaystyle \frac{df\left(t\right)}{dt}}\right|}_{t=0^{+}}=-{\displaystyle \frac{f_N\Delta P_{max}}{2H_{sys}}},$$

(2)

where ${RocoF}_M$ represents the maximum frequency change rate of the system; $∆P_{max}$ represents the maximum disturbance power allowed to occur in the system.

The constraint expression of the maximum frequency change rate of the system is:

$$\left|{RocoF}_M\right|\le {RocoF}_{max},$$

(3)

where ${RocoF}_{max}$ represents the maximum allowable value of the system’s frequency change rate.

From this, the minimum moment of inertia based on RocoF constraints can be further obtained as:

$$H_{RocoF} = {\displaystyle \frac{f_N\Delta P_{max}}{2{RocoF}_{max}}},$$

(4)

2.2. Minimum Inertia Based on the Constraint of Nadir

In the power system, a complex interconnected network with strong nonlinear and time-varying characteristics, maintaining the dynamic balance of power generation and consumption is of vital importance. When the system is subjected to large disturbances such as sudden changes in power generation/load power, its transient energy balance state will be disrupted, causing fluctuations in system frequency. After the system is impacted by the imbalance between supply and demand, it reaches the frequency Nadir. If the frequency is too low, it may trigger some protection mechanisms such as low-frequency load reduction. In severe cases, it may cause power outages in some or all areas, causing great inconvenience to users’ lives and economic losses [22]. To prevent the low-frequency load shedding device from operating, it is necessary to maintain the lowest point above a certain predetermined threshold, that is:

$$f_{Nadir}\ge f_{min},$$

(5)

where $f_{min}$ is the preset lowest frequency point.

To quantitatively describe the relationship between inertia demand, the lowest point of frequency and frequency modulation rate, it is necessary to focus on the relationship between frequency dynamic characteristics and frequency modulation control parameters, as shown in Figure 1, in which, 0 represents the moment when the disturbance occurs; $-\Delta P_{max}$ is the power deficit; $f_{db}$ is the dead zone of primary frequency modulation control; $t_{db}$ is the time of one frequency modulation action; $t_{Nadir}$ is the lowest point of frequency; $R_s$ represents the primary frequency modulation rate.

Firstly, assume that the fault occurs at the initial 0 time and the system frequency reaches the extreme value at the $t_{Nadir}$ time. Integrate Equation (1) from 0 to the $t_{db}$ time, and we have:

$${\int }_0^{t_{db}}{\displaystyle \frac{df\left(t\right)}{dt}}dt = {\displaystyle \frac{f_N}{2H_{sys}}}{\int }_0^{t_{db}}(P_m\left(t\right)-P_e(t\left)\right)dt-{\displaystyle \frac{f_N{D}_s}{2H_{sys}}}{\int }_0^{t_{db}}\Delta f\left(t\right)dt,$$

(6)

From 0 to $t_{db}$ stage, since the system frequency control measures have not been initiated yet, the overall active power imbalance $-\Delta P_{max}$ does not change. At this stage, mechanical inertia responds to power imbalance by regulating the mechanical kinetic energy of the unit. The influence of the active power imbalance of the system on the frequency is continuous. Based on the current assumptions, solving Equation (6), the expression of $t_{db}$ can be obtained as:

$$t_{db} = {\displaystyle \frac{4H_{sys}{f}_{db}}{f_N(2\Delta P_{max}-D_s{f}_{db})}},$$

(7)

Integrating Equation (1) from 0 to $t_{Nadir}$, we have:

$$f_{min}-f_N = -{\displaystyle \frac{f_N}{2H_{sys}}}\Delta P_{max}{t}_{Nadir}-{\displaystyle \frac{f_N{D}_s}{2H_{sys}}}{\int }_0^{t_{Nadir}}\Delta f\left(t\right)dt,$$

(8)

According to the linearization idea shown in Figure 1, $\Delta f\left(t\right)$ can be expressed as:

$$\Delta f\left(t\right) = {\displaystyle \frac{f_{min}-f_N}{t_{Nadir}}}t,$$

(9)

Furthermore, by introducing the primary frequency modulation rate $R_s$ to quantitatively describe the time from the initiation of a primary frequency modulation measure until the system frequency reaches the transient extremum, the time expression for the system frequency to reach the minimum value can be obtained:

$$t_{Nadir} = t_{db}+{\displaystyle \frac{\Delta P_{max}}{R_s}},$$

(10)

Substituting Equations (9) and (10) into Equation (8) yields:

$$f_{min}-f_N=-{\displaystyle \frac{f_N}{4H_{sys}}}[2\Delta P_{max}{t}_{db}{R}_s+2\Delta P_{max}^2+D_s\left(f_{min}-f_N\right)t_{db}{R}_s+D_s(f_{min}-f_N)\Delta P_{max}]$$

(11)

Further sorting leads to:

$$H_{Nadir} = -{\displaystyle \frac{a_1+a_2+a_3+a_4}{b}},$$

(12)

$$a_1=2f_N\Delta P_{max}{t}_{db}{R}_s,$$

(13)

$$a_2=2f_N\Delta P_{max}^2,$$

(14)

$$a_3=f_N{D}_s(f_{min}-f_N)t_{db}{R}_s,$$

(15)

$$a_4={ f}_N{D}_s(f_{min}-f_N)\Delta P_{max},$$

(16)

$$b=4R_s(f_{min}-f_N),$$

(17)

2.3. Minimum Inertia Requirement of the System

The system inertia should be simultaneously higher than the inertia required under the constraints of RocoF and Nadir, that is, the minimum inertia requirement of the system is:

$$H_{min,t} = max\left\{H_{RocoF},H_{Nadir}\right\},$$

(18)

Equations (4) and (12) derive the minimum inertia requirements from the RocoF and Nadir constraints, respectively. We will add explanations noting that Equation (4) provides a conservative estimate to limit the initial RocoF after a disturbance, while Equation (12) incorporates the delayed effect of primary frequency regulation for comprehensive frequency stability. Their combination in Equation (18) ensures a complete inertia assessment.

With the continuous growth of the penetration rate of new energy power generation such as wind power and photovoltaic power, the inertia characteristics of the new power system are undergoing structural changes. The inertia of the traditional synchronous dominant power system is mainly provided by the synchronous machine. However, when new energy units are connected to the grid through power electronic devices, the overall inertia of the system drops significantly, greatly accelerating the frequency variation and seriously threatening the frequency stability of the system [23]. Against this backdrop, the analysis of the overall inertia of the power system based solely on the mechanical moment of inertia of synchronous generators is no longer applicable. The system studied in this paper covers various energy forms such as thermal power, nuclear power, wind power, photovoltaic power and pumped storage power. Therefore, it is necessary to comprehensively consider the contribution of each type of energy to the equivalent inertia of the system. The real-time inertia of the system obtained is:

$$H_{sys,t} = {\sum }_{i=1}^{N_g}{H}_{gen,i}{P}_{gen,i}{u}_{gen,i}^t+{\sum }_{i=1}^{N_{ps}}{H}_{ps,i}{P}_{ps,i}{u}_{ps,i}^t+{\sum }_{i=1}^{N_{he}}{H}_{he,i}{P}_{he,i}{u}_{he,i}^t,$$

(19)

where $N_g$, $N_{ps}$ and $N_{he}$ represent the number of thermal power units, pumped storage units, and nuclear power units, respectively; $H_{gen,i}$ and $P_{gen,i}$ are, respectively, the inertia time constant and rated power of the i-th conventional thermal power unit; $H_{ps,i}$ and $P_{ps,i}$ are the inertia time constants and rated power of the i-th pumped storage unit, respectively; $H_{he,i}$ and $P_{he,i}$ are, respectively, the inertia time constant and rated power of the i-th nuclear power unit; $u_{gen,i}^t$, $u_{ps,i}^t$, and $u_{he,i}^t$ are Boolean variables representing the start-up and shutdown states of the i-th thermal power plant and pumped storage unit at time t, respectively.

Although the virtual inertia control strategy can enable wind turbines to participate in the primary frequency regulation of the power grid, this strategy may lead to a significant increase in the wind power curtailment rate, resulting in a limit on the wind power consumption rate. Therefore, this paper does not consider using the virtual synchronous generator technology of wind turbines to provide virtual inertia.

3. Optimal Configuration of Pumped Storage Considering Inertia Constraints

3.1. Objective Function

On the basis of meeting the minimum inertia requirement of the power system, with the goal of minimizing the total operating cost of the power system throughout its entire cycle, penalties for the peak-valley difference index of the load curve and the guarantee value of the medium and long-term unit inertia are added:

$$minF = C_1+C_2+C_3+C_4+C_5,$$

(20)

$$C_1={\sum }_{t=1}^T{\sum }_{i=1}^{N_g}[f_i\left(P_{gen,i,t}\right)u_{gen,i}^t+C_{qt,i}],$$

(21)

$$C_2={\sum }_{t=1}^T\left[C_{cur}\right(P_{wind,t}^f-P_{wind,t}+P_{pv,t}^f-P_{pv,t}\left)\right],$$

(22)

$$C_3={\sum }_{t=1}^T{\sum }_{i=1}^{N_{ps}}\left[C_{ps}\right(P_{i,t}^{psG}+P_{i,t}^{psP}\left)\right],$$

(23)

$$C_4=\lambda ({pl}_{max}-{pl}_{min}),$$

(24)

$$C_5={\sum }_{t\in T_{risk}}{\lambda }_H{(H_{min,t}-{\sum }_{d\in \left\{6h,8h\right\}}{H}_{d,t})}^{+},$$

(25)

where $f_i$ is the fuel cost of the i-th thermal power unit; $P_{gen,i,t}$ represents the output power of the i-th thermal power unit at time t; $C_{qt,t}$ represents the start-up and shutdown costs of the i-th thermal power unit; $C_{cur}$ represents the unit cost of wind and solar power curtailment; $P_{wind,t}^f$ and $P_{pv,t}^f$ represent the available power of wind power and photovoltaic power at time t on that day, respectively; $P_{wind,t}$ and $P_{pv,t}$ represent the output power of wind power and photovoltaic power at time t, respectively; $C_{ps}$ represents the unit power usage cost of pumped storage; $P_{i,t}^{psG}$ and $P_{i,t}^{psP}$ represent the power generation and pumping power of the pumped storage power station at time t on that day, respectively. $\lambda$ is the peak-valley difference penalty coefficient, which is taken as 10⁶ in this paper; ${pl}_{max}$ represents the maximum load value of the power grid in a day, and ${pl}_{min}$ represents the minimum load value of the power grid in a day; $T_{risk}$ is the set of periods with high disturbance risk; $H_{d,t}$ represents the equivalent inertia provided by the 6 h and 8 h units at time t; ${\lambda }_H$ is the unit inertia missing penalty coefficient, which is taken as 10⁶ here; ${\left(x\right)}^{+}$ is a positive part function, taking x when x > 0 and 0 otherwise.

The peak-valley difference penalty $C_4$ incentivizes pumped storage to smooth the load curve, while the inertia guarantee penalty $C_5$ is a novel soft constraint to ensure inertia security, highlighting the trade-off between economy and stability. In view of the mathematical characteristics of the penalty function method, this paper selects a sufficiently large penalty coefficient to prioritize ensuring safety constraints such as frequency stability and load smoothing in the optimization.

Among them, the fuel cost expression of the thermal power unit is:

$$f_i\left(P_{gen,i,t}\right) = a{P}_{gen,i,t}^2+b{P}_{gen,i,t}+c,$$

(26)

where a, b, and c represent the fuel cost coefficients. This formula is a nonlinear constraint. In this paper, it is linearized through interval division [24].

3.2. Constraints

3.2.1. Constraints on Wind Power and Photovoltaic Units Output

$$0\le P_{wind,t}\le P_{wind,t}^f,$$

(27)

$$0\le P_{pv,t}\le P_{pv,t}^f,$$

(28)

3.2.2. Constraints on Thermal Power Units

• Constraint on upper and lower limit of output power;

  $$P_{gen,i}^{min}{u}_{gen,i}^t\le P_{gen,i,t}\le P_{gen,i}^{max}{u}_{gen,i}^t,$$

  (29)

  where $P_{gen,i}^{max}$ and $P_{gen,i}^{min}$ are, respectively, the upper and lower limits of the output of the i-th thermal power unit.

2.

Constraint on state;

$$u_{switch,i}^t=\left|u_{gen,i}^t-u_{gen,i}^{t-1}\right|,$$

(30)

where $u_{switch,i}^t$ is a Boolean variable representing the switching of the operating state of a thermal power unit during period t.

3.

Constraint on ramp;

$$\left\{\begin{array}{c}{P}_{gen,i,t}-P_{gen,i,t-1}\le r_i^{up}\Delta t+P_{gen,i}^{max}(1-u_{gen,i}^{t-1})\\ P_{gen,i,t-1}-P_{gen,i,t}\le r_i^{down}\Delta t+P_{gen,i}^{max}(1-u_{gen,i}^t)\end{array}\right.,$$

(31)

where $r_i^{up}$ and $r_i^{down}$ represent the uphill and downhill climbing rates of the i-th thermal power unit, respectively; $∆t$ represents the unit scheduling duration. The additional item relaxes the constraints during start-up and shutdown by introducing $P_{gen,i}^{max}$, allowing the unit to break through the conventional climbing rate limit at the moment of start-up and shutdown, and avoiding the optimization model being unsolver due to strict constraints.

4.

Constraint on minimum start-stop time;

$$\left\{\begin{array}{c}{t}_{i,on}\ge t_{i,on}^{min}\\ t_{i,off}\ge t_{i,off}^{min}\end{array}\right.,$$

(32)

where $t_{i,on}$ and $t_{i,off}$ represent the continuous operation and shutdown times of the i-th thermal power unit, respectively; $t_{i,on}^{min}$ and $t_{i,off}^{min}$ are, respectively, the minimum allowable continuous operation and shutdown times for the i-th thermal power unit.

3.2.3. Constraints on Pumped Storage Units

• Constraint on duration-and-capacity bounding;

The capacity of each type of unit is independently configured and is bound to its exclusive duration with the power capacity.

$$E_d=P_d·d,\forall d\in \left\{4\mathrm{h},6\mathrm{h},8\mathrm{h}\right\},$$

(33)

where $E_d$ represents the capacity of d-class units for duration; $P_d$ represents the power of d-class units for duration; d is the exclusive duration for the crew, with d = 4, 6, 8 h.

2.

Constraint on rapid adjustment time of short-term unit;

The 4 h unit needs to achieve an appropriate frequency of charge and discharge switching to match the load peak-valley tracking requirements.

$$K_{min}\le {\sum }_{t=1}^T(\left|u_{d=4\mathrm{h},t}^{psG}-u_{d=4\mathrm{h},t-1}^{psG}\right|+\left|u_{d=4\mathrm{h},t}^{psP}-u_{d=4\mathrm{h},t-1}^{psP}\right|)\le K_{max},$$

(34)

where $K_{min}$ and $K_{max}$ represent the minimum and maximum allowable state switching times of pumped storage within the optimization period, respectively. In this paper, $K_{min}$ = 3 and $K_{max}$ = 6. $\left|∆u\right|$ represents the state change in the Boolean variable and requires linearization processing.

Binary delta secondary variables ${\delta }_{G,t}^{+}\in \left\{\mathrm{0,1}\right\}$ said power status starting (switching from 0 to 1), and ${\delta }_{G,t}^{-}\in \left\{\mathrm{0,1}\right\}$ said state power stopping (switching from 1 to 0), and ${\delta }_{P,t}^{+}$, ${\delta }_{P,t}^{-}$ are defined by the same token, the state associated constraints can be obtained:

$$\left\{\begin{array}{c}{u}_{d=4\mathrm{h},t}^{psG}-u_{d=4\mathrm{h},t-1}^{psG}={\delta }_{G,t}^{+}-{\delta }_{G,t}^{-}\\ u_{d=4\mathrm{h},t}^{psP}-u_{d=4\mathrm{h},t-1}^{psP}={\delta }_{P,t}^{+}-{\delta }_{P,t}^{-}\end{array}\right.,$$

(35)

The switching action can be characterized as:

$$\Delta u_{d=4\mathrm{h},t} = {\delta }_{G,t}^{+}+{\delta }_{G,t}^{-}+{\delta }_{P,t}^{+}+{\delta }_{P,t}^{-},$$

(36)

From this, the constraint can be linearized as:

$$K_{min}\le {\sum }_{t=2}^T\Delta u_{d=4\mathrm{h},t}\le K_{max},$$

(37)

3.

Constraint on duration constraint of continuous support for medium and long-term units;

The 6 h and 8 h units need to continuously provide inertia support during high-risk periods.

$${\sum }_{k=t}^{t+{\tau }_d}(u_{d,k}^{psG}+u_{d,k}^{psP})\ge {\tau }_d,\forall t\in T_{risk},\forall d\in \left\{6\mathrm{h},8\mathrm{h}\right\},$$

(38)

where ${\tau }_d$ represents the minimum continuous running duration.

4.

Constraint on full-station power coupling;

The operation of the three types of units is decoupled, but the total power capacity is equal to the total installed capacity of the entire station.

$${\sum }_d{P}_d=P_{total}^{max},$$

(39)

where $P_{total}^{max}$ is the pumped storage total power boundary.

5.

Constraint on state;

$$0\le u_{d,t}^{psG}+u_{d,t}^{psP}\le 1,$$

(40)

where $u_{d,t}^{psG}$ represents the Boolean variable indicating whether the d-class pumped storage unit is in the power generation condition at time t; $u_{d,t}^{psP}$ is a Boolean variable indicating whether a d-class pumped storage unit is in the pumping condition at time t.

6.

Constraint on storage capacity;

$$V_{min}^{up}\le V_t^{up}\le V_{max}^{up},$$

(41)

$$V_{min}^{down}\le V_t^{down}\le V_{max}^{down},$$

(42)

$$V_t^{up}=V_{t-1}^{up}-{\sum }_{i=1}^{N_{ps}}{Q}_{i,t}^{psG}+{\sum }_{i=1}^{N_{ps}}{Q}_{i,t}^{psP},$$

(43)

$$V_t^{down}=V_{t-1}^{down}+{\sum }_{i=1}^{N_{ps}}{Q}_{i,t}^{psG}-{\sum }_{i=1}^{N_{ps}}{Q}_{i,t}^{psP},$$

(44)

$$V_T^{up}=V_{pre}^{up},$$

(45)

where $V_{min}^{up}$ and $V_{max}^{up}$ are the minimum and maximum values of the upper reservoir capacity of the pumped storage power station, respectively; $V_t^{up}$ represents the storage capacity of the upper reservoir at time t; $V_{min}^{down}$ and $V_{max}^{down}$ are, respectively, the minimum and maximum values of the lower reservoir capacity of the pumped storage power station; $V_t^{down}$ represents the reservoir capacity at time t; $Q_{i,t}^{psG}$ and $Q_{i,t}^{psP}$ represent the water consumption of the pumped storage unit at time t under power generation and pumping conditions, respectively; $V_T^{up}$ is to optimize the water level of the upper reservoir at the end of the cycle; $V_{pre}^{up}$ is the control target for optimizing the water level of the upper reservoir at the end of the cycle.

7.

Constraint on upper and lower limit of output power;

$$u_{d,t}^{psG}{P}_{d,min}^{psG}\le P_{d,t}^{psG}\le u_{d,t}^{psG}{P}_{d,max}^{psG},$$

(46)

$$u_{d,t}^{psG}{P}_{d,min}^{psG}\le P_{d,t}^{psG}\le u_{d,t}^{psG}{P}_{d,max}^{psG},$$

(47)

where $P_{d,min}^{psG}$ and $P_{d,max}^{psG}$ represent the minimum and maximum power values of d-class pumped storage units under power generation conditions, respectively; $P_{d,min}^{psP}$ and $P_{d,max}^{psP}$ are, respectively, the minimum and maximum power values of d-class pumped storage units under pumping conditions; $P_{d,t}^{psG}$ and $P_{d,t}^{psP}$ are respectively the power generation and pumping power of d-class pumped storage units at time t.

The configuration of pumped storage should comprehensively consider the technical limitations of the system, economic requirements, and the demands of the power grid to ensure that, under the premise of meeting the stability and cost-effectiveness of the power system supply, the maximum power output of pumped storage does not exceed the actual tolerable range, that is:

$$0\le P_{d,t}^{ps}\le P_d^{max},$$

(48)

$${\sum }_d{P}_d^{max}={ P}_{total}^{max},$$

(49)

Since the maximum power of pumped storage needs to be configured and the maximum power is multiplied by the 0–1 variables $u_{d,t}^{psG}$ and $u_{d,t}^{psP}$ in the operating state to form a nonlinear constraint, this paper converts the nonlinear constraint Equations (46) and (47) into linear constraint expressions based on the McCormick envelope.

$$\left\{\begin{array}{c}{m}_{1,d}\ge u_{d,t}^{psG}{P}_d^{min}\\ m_{1,d}\ge P_{d,t}^{ps}+u_{d,t}^{psG}{P}_d^{max}-P_d^{max}\\ \begin{array}{c}{m}_{1,d}\le P_{d,t}^{ps}+u_{d,t}^{psG}{P}_d^{min}-P_d^{min}\\ m_{1,d}\le u_{d,t}^{psG}{P}_d^{max}\\ 0\le P_{d,t}^{psG}\le m_{1,d}\end{array}\end{array}\right.,$$

(50)

$$\left\{\begin{array}{c}{m}_{2,d}\ge u_{d,t}^{psP}{P}_d^{min}\\ m_{2,d}\ge P_{d,t}^{ps}+u_{d,t}^{psP}{P}_d^{max}-P_d^{max}\\ \begin{array}{c}{m}_{2,d}\le P_{d,t}^{ps}+u_{d,t}^{psP}{P}_d^{min}-P_d^{min}\\ m_{2,d}\le u_{d,t}^{psP}{P}_d^{max}\\ 0\le P_{d,t}^{psP}\le m_{2,d}\end{array}\end{array}\right.,$$

(51)

where $m_{1,d}$ and $m_{2,d}$ are the transformed linear variables; $P_d^{max}$ and $P_d^{min}$ are, respectively, the upper and lower limits of the rated power of the allowable installed capacity of pumped storage.

3.2.4. Constraints on Minimum Inertia of the System

To ensure the stability of the system frequency, the real-time inertia of the system at each time period should not be less than the minimum inertia requirement of the system, and the expression is:

$$H_{sys,t}\ge H_{min,t},$$

(52)

where $H_{sys,t}$ represents the real-time inertia of the system at time t. In actual operating systems, this value can be measured by an online system inertia monitoring device. In the optimization model proposed in this paper, it can be estimated by Equation (19).

3.2.5. Constraints on Power Balance

$$P_{L,t}={\sum }_{i=1}^{N_g}{P}_{gen,i,t}+P_{wind,t}+P_{pv,t}+P_{he,t}+{\sum }_{i=1}^{N_{ps}}(P_{i,t}^{psG}-P_{i,t}^{psP}),$$

(53)

where $P_{he,t}$ represents the output power of the nuclear power unit at time t, which is directly given in this paper.

3.2.6. Peak-Valley Difference of the Load Curve

$$P_{net,t}=P_{L,t}-{\sum }_{i=1}^{N_{ps}}(P_{i,t}^{psG}-P_{i,t}^{psP}),$$

(54)

$${pl}_{min}\le P_{net,t}\le {pl}_{max},\forall t=\mathrm{1,2},\dots ,T,$$

(55)

where $P_{net,t}$ represents the equivalent load of the system after considering the influence of pumped storage.

3.3. Model Solving

In the high-proportion new energy power grid operation model considering the minimum inertia constraint, the joint dispatching of various power resources such as thermal power, nuclear power, wind power, photovoltaic power and pumped storage power is involved. Due to the complexity of the cost function of thermal power units and the fact that the system needs to meet a series of conditions such as inertia constraints, this problem is a mixed-integer nonlinear programming problem. In order to improve the efficiency of the solution, this paper adopts an appropriate linearization processing strategy to simplify the cost function of the thermal power unit and the system inertia requirement. Thus, this problem is transformed into a mixed integer linear programming (MILP) problem. This problem can be solved by invoking the Gurobi solver using the Yalmip toolbox.

4. Case Analysis

4.1. Case Data

To verify the rationality of the above strategies, this paper selects the data of a provincial power grid for case study analysis. The load curves are shown in Figure 2a, and the output curves of wind power and photovoltaic power are shown in Figure 2b. The deviation of the maximum frequency change rate of the system is set at 1 Hz, that is, the lower limit of the frequency during the dynamic process of the system is 49 Hz, and the maximum frequency change rate of the system is 0.3 Hz/s. The power deficit in each period is 5% of the total load of the corresponding period. Parameters of the thermal power unit are shown in the Appendix A.

Combined with the daily load curve of the system shown in Figure 2, the peak load and high-fluctuation periods are mainly concentrated from 8:00 to 11:00 and from 18:00 to 21:00. During these two periods, the system operates at a high power level and has the greatest demand for inertia support. Meanwhile, rapid changes in load, such as a sharp increase in load around 18:00, also mean that the risk of the system being disturbed significantly increases. Therefore, in this paper, the set of periods with high disturbance risk is defined as $T_{risk}=\left\{t|t\in \left[\mathrm{8,11}\right]\cup \left[\mathrm{18,21}\right]\right\}$, and the minimum continuous operation time ${\tau }_d=4$ for 6 h and 8 h units, to ensure that the optimally configured pumped storage capacity can provide sufficient inertia and frequency support for the system during this critical period.

The parameter Settings of the thermal power unit are shown in

Table A1. Parameters of thermal power units.

Generator Number	Minimum Output/MW	Maximum Output/MW	Inertial Time Constant/s	Start-Stop Cost/CNY
1	72	180	3.5	6000
2	222	556	5.0	6000
3	135	338	5.7	6000
4	320	799	3.5	6000
5	195	487	5.0	6000
6	287	717	3.5	6000
7	293	733	3.5	6000
8	197	492	5.0	10,000
9	63	158	5.8	6000
10	63	158	5.8	6000
11	193	483	5.0	6000
12	72	180	5.8	6000
13	95	237	5.8	6000
14	288	719	3.5	6000
15	288	719	3.5	6000
16	288	719	3.5	10,000
17	288	719	3.5	6000
18	288	719	3.5	6000

.

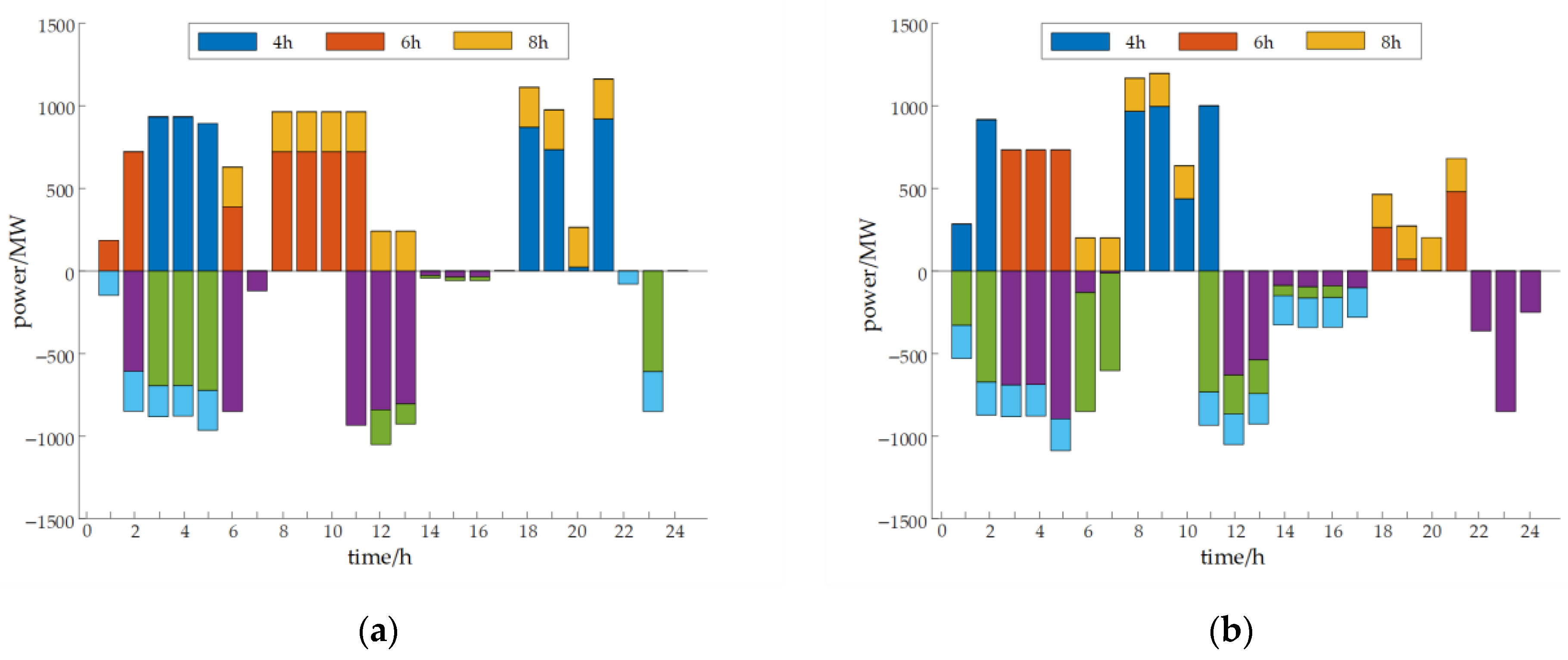
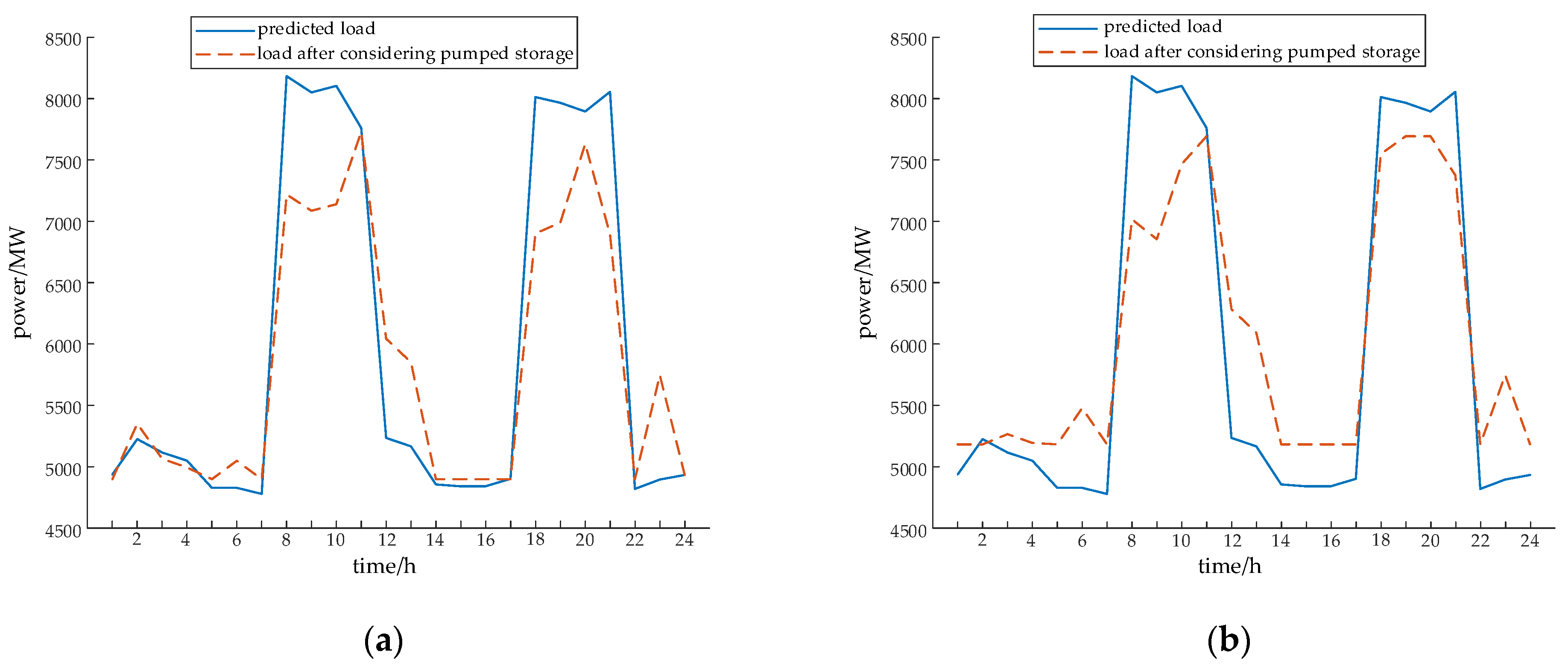
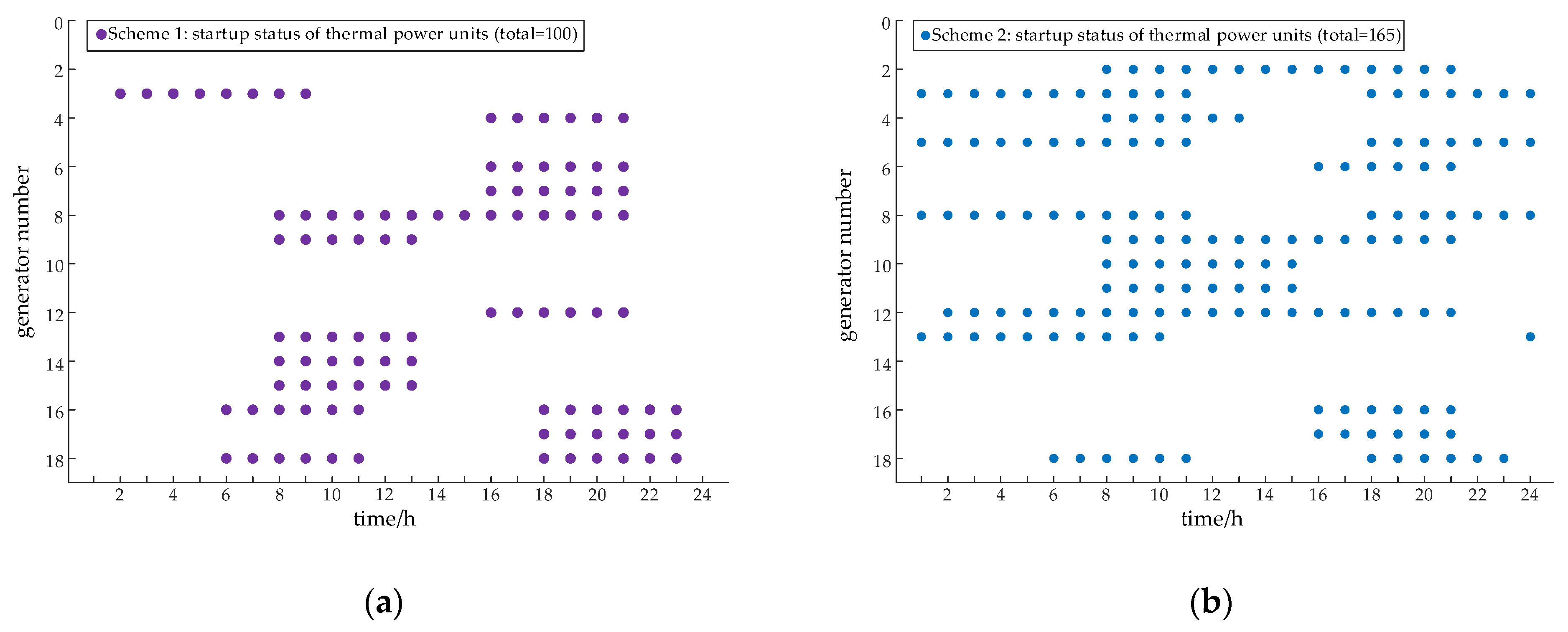
4.2. Results Presentation

To verify the necessity of considering inertia constraints in the dispatching process of power grids with a high proportion of new energy, as well as the superiority of considering the selection of pumped storage duration in the process of optimal configuration, the calculation examples compare the results of whether frequency safety constraints are considered and whether the selection of pumped storage duration is considered. At present, most of the literature in the planning stage selects 6 h units [19], so in this paper, all the schemes that do not consider the duration of pumped storage are 6 h units. The specific plan Settings are as follows:

Scheme 1: Without considering the selection of pumped storage duration, all units will be con-figured with 6 h units, and inertia safety constraints will not be taken into account during the dispatching process.

Scheme 2: Do not consider the selection of pumped storage duration. All units will be configured with 6 h units, and inertia safety constraints will be taken into account during the dispatching process.

Scheme 3: Consider the selection of pumped storage duration and configure 4 h, 6 h, and 8 h units, respectively, and do not take inertia safety constraints into account during the dis-patching process.

Scheme 4: Consider the selection of pumped storage duration and configure 4 h, 6 h, and 8 h units, respectively, and take inertia safety constraints into account during the dispatching process.

The optimization results of each scheme are shown in

Table 1. Optimization results of each scheme.

Scheme	Total Cost of Full-Cycle Operation (107 CNY)	Start-Up and Shutdown Costs of Thermal Power Plants (104 CNY)	Operating Costs of Thermal Power (107 CNY)	Cost of Wind and Photovoltaic Power Curtailment (106 CNY)
1	3.4414	22.0	2.4545	2.7816
2	3.8808	24.0	2.8920	4.9287
3	4.1352	20.8	1.9185	1.0156
4	4.3920	24.2	2.1701	1.3135

.

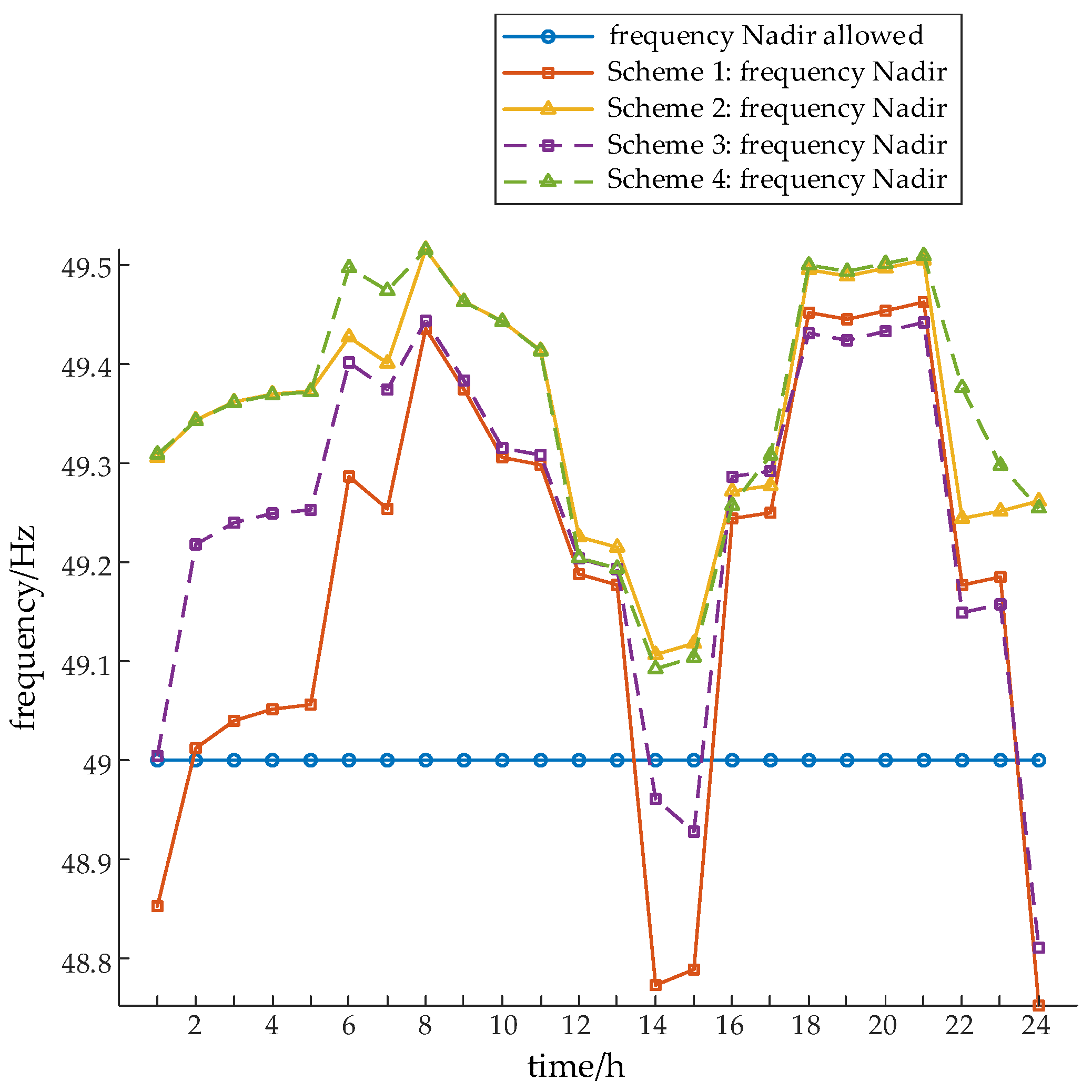
4.3. Influences on the Results Considering Inertia Constraints

By comparing the results of Schemes 1 and 2 as well as Schemes 3 and 4 in Table 1, respectively, the following conclusions can be drawn:

• The comprehensive operating cost of the system in Scheme 2 is 4.39 million yuan higher than that in Scheme 1, and the comprehensive operating cost in Scheme 4 is 2.57 million yuan higher than that in Scheme 3. It can be seen that when considering the inertia constraint, the comprehensive operating cost has increased. The main reason for the increase in cost lies in the fact that the synchronous inertia of the system can only be provided by thermal power units, nuclear power units and pumped storage units. Therefore, when the system inertia is low, more thermal power units will be online, which in turn leads to an increase in the start-up and shutdown costs as well as the operating costs of thermal power;
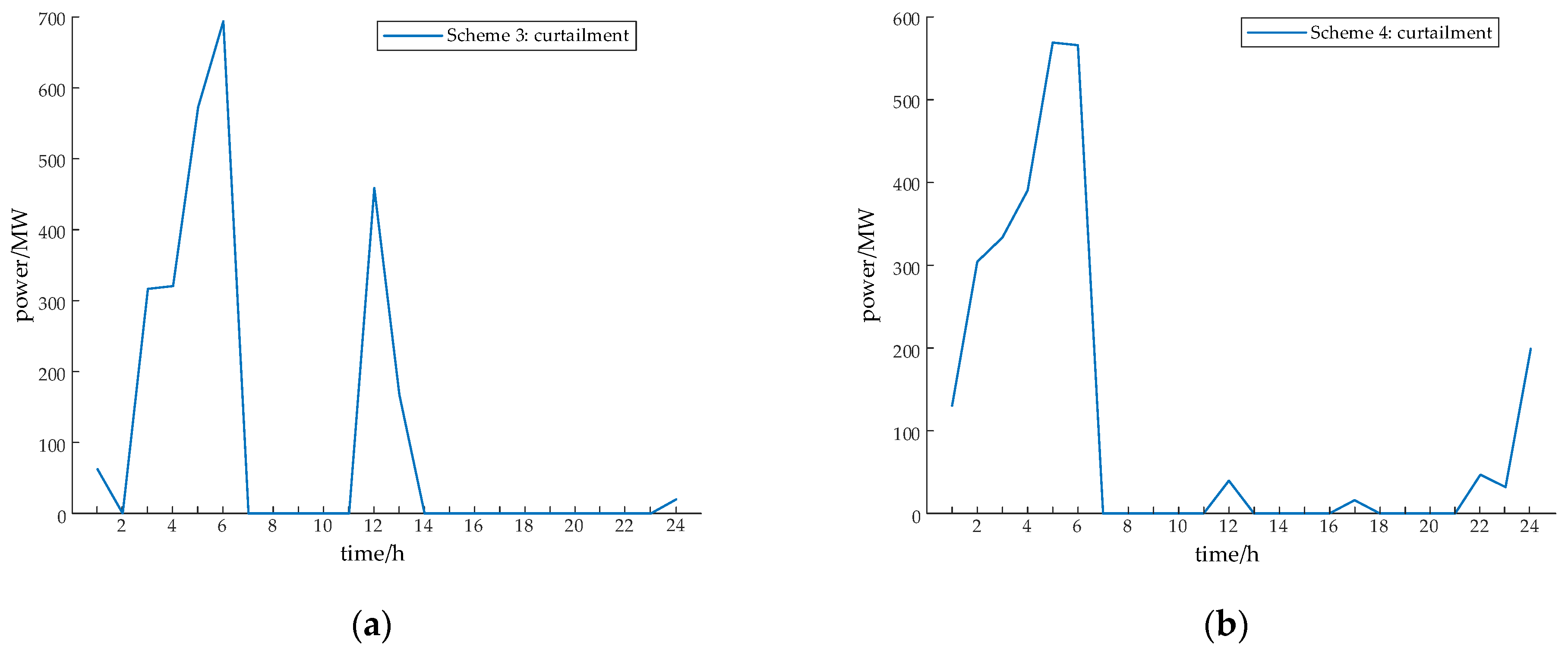
• The cost of wind and solar power curtailment in Scheme 2 is 2.15 million yuan higher than that in Scheme 1, and in Scheme 4, it is 300,000 yuan higher than that in Scheme 3. It can be seen that when considering the inertia constraint, the cost of wind and solar power curtailment has in-creased. This is because thermal power units usually have a minimum technical output. When the power grid selects to operate more thermal power units, due to the constant load at a certain moment in the power grid, some new energy sources that could have been consumed are abandoned. At the same time, pumped storage units may be more used for frequency regulation rather than consuming renewable energy, further exacerbating the curtailment of wind and solar power.

Next, take a typical day as an example to observe the start-up and shutdown conditions of the thermal power units, the abandoned electricity, the grid inertia, and the changes in the frequency Nadir when disturbances occur under Schemes 1 and 2. The comparative analysis of the operation results of Schemes 3 and 4 will be elaborated in detail in Section 4.5. The results are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.

Figure 3 shows the startup status of thermal power units in Scheme 1 and Scheme 2, and Figure 4 shows the minimum inertia requirement and actual inertia of the systems in Scheme 1 and Scheme 2.

By analyzing the start-stop conditions of thermal power units under different schemes and combining the changes in system inertia under different schemes, it can be found that when considering the inertia constraint, during the peak load period from 8 a.m. to 11 a.m., compared with when the inertia constraint is not considered, The system will select to activate the thermal power units 2, 3, 5, 10, 11, and 12 with larger inertial time constants, while shutting down the thermal power units 14, 15, and 16 with smaller inertial time constants, thereby ensuring that the real-time inertia meets the requirements. During the peak load period from 6 p.m. to 9 p.m., the system will choose to start the thermal power units 2, 3, 5 and 9 with larger inertia time constants and shut down the thermal power units 4 and 7 with smaller inertia time constants, thereby ensuring that the system’s inertia meets the minimum inertia requirement.

4.4. Influences on the Results Considering Duration Selection

By comparing the results of Schemes 1 and 3 as well as Schemes 2 and 4 in Table 1, respectively, the following conclusions can be drawn:

• In Scheme 3, the operating cost of thermal power is reduced by 5.36 million yuan compared to Scheme 1, and in Scheme, it is reduced by 7.22 million yuan compared to Scheme 2. It can be seen that after considering the selection of pumped storage duration, the operating cost of thermal power has been significantly reduced. The reason is that in the hybrid configuration considering the selection of pumped storage duration, the 4 h unit provides rapid frequency regulation capability, sharing the instantaneous regulation pressure of thermal power. The 8 h unit undertakes long-term energy transfer, such as absorbing wind and solar power across time periods, reducing the fluctuation of thermal power output. Thermal power units have been able to operate stably within an efficient and economic range, avoiding frequent starts and stops as well as inefficient peak shaving;
• In Scheme 3, the proportion of thermal power operation cost in the comprehensive system operation cost decreased by approximately 25% compared to Scheme 1. In Scheme 4, the pro-portion of thermal power operation cost in the comprehensive operation cost decreased by approximately 25% compared to Scheme 2. It can be seen that after considering the selection of pumped storage duration, the proportion of thermal power operation cost in the total long-term dispatching has decreased. The reason lies in that the hybrid units have a more obvious substitution effect on the functions of thermal power, the regulating value of pumped storage units has significantly increased, and the system’s dependence on thermal power units has decreased;
• In Scheme 3, the cost of wind and solar power curtailment is reduced by 1.77 million yuan compared to Scheme, and in Scheme 4, it is reduced by 3.62 million yuan compared to Scheme 2. It can be seen that after considering the selection of pumped storage duration, the cost of wind and solar power curtailment has decreased. The reason lies in the fact that the regulation capacity of a single 6 h unit is limited, while in a hybrid configuration, a 4 h unit can quickly respond to fluctuations in wind and solar power and reduce instantaneous power curtailment. The 8 h unit can charge a large amount of new energy during off-peak hours. The coordination of hybrid units can significantly enhance the capacity to consume renewable energy. In addition, in Section 3.3, the cost of wind and solar power cursory in Scheme 2 is 2.15 million yuan higher than that in Scheme 1, and in Scheme 4, it is 300,000 yuan higher than that in Scheme 3. It can be seen that under the inertia constraint, the regulation failure of the system under a single 6 h unit is due to the fact that the dispatching strategy forces pumped storage to prioritize frequency regulation, which cannot fully consume wind and solar power, and the regulation rate of a single 6 h unit is insufficient. The system is forced to rely on thermal power to provide instantaneous inertia support. As thermal power continues to operate, its technical output limit squeezes the space for new energy, further exacerbating power curtailment;
• The comprehensive operating cost of the system in Scheme 3 is 6.94 million yuan higher than that in Scheme 1, and in Scheme 4, it is 5.11 million yuan higher than that in Scheme 2. It can be seen that after considering the selection of pumped storage duration, the comprehensive operating cost of the system has increased. The reason lies in the increase in the cost-sharing ratio of pumped storage regulation. Although these incremental costs have pushed up the overall operating cost of the system, in essence, they are the necessary cost for the power system to transform from a fuel cost core to a regulation service core.

4.5. Influences on the Results Considering Inertia Constraints Under Mixed Durations

The following conclusion can be drawn from

Table 2. Influences on the configuration results considering inertia constraints under mixed durations.

Scheme	Configuration Power/MW				Configuration Capacity/MWh				Configuration Capacity Proportion/%
	4 h	6 h	8 h	total	4 h	6 h	8 h	total	4 h	6 h	8 h
3	933.2	722.9	241.2	1897.3	3732.8	4337.4	1929.6	9999.8	37.3	43.4	19.3
4	1000.0	732.9	200.4	1933.3	4000.0	4397.4	1603.2	10,000.6	40.0	44.0	16.0

:

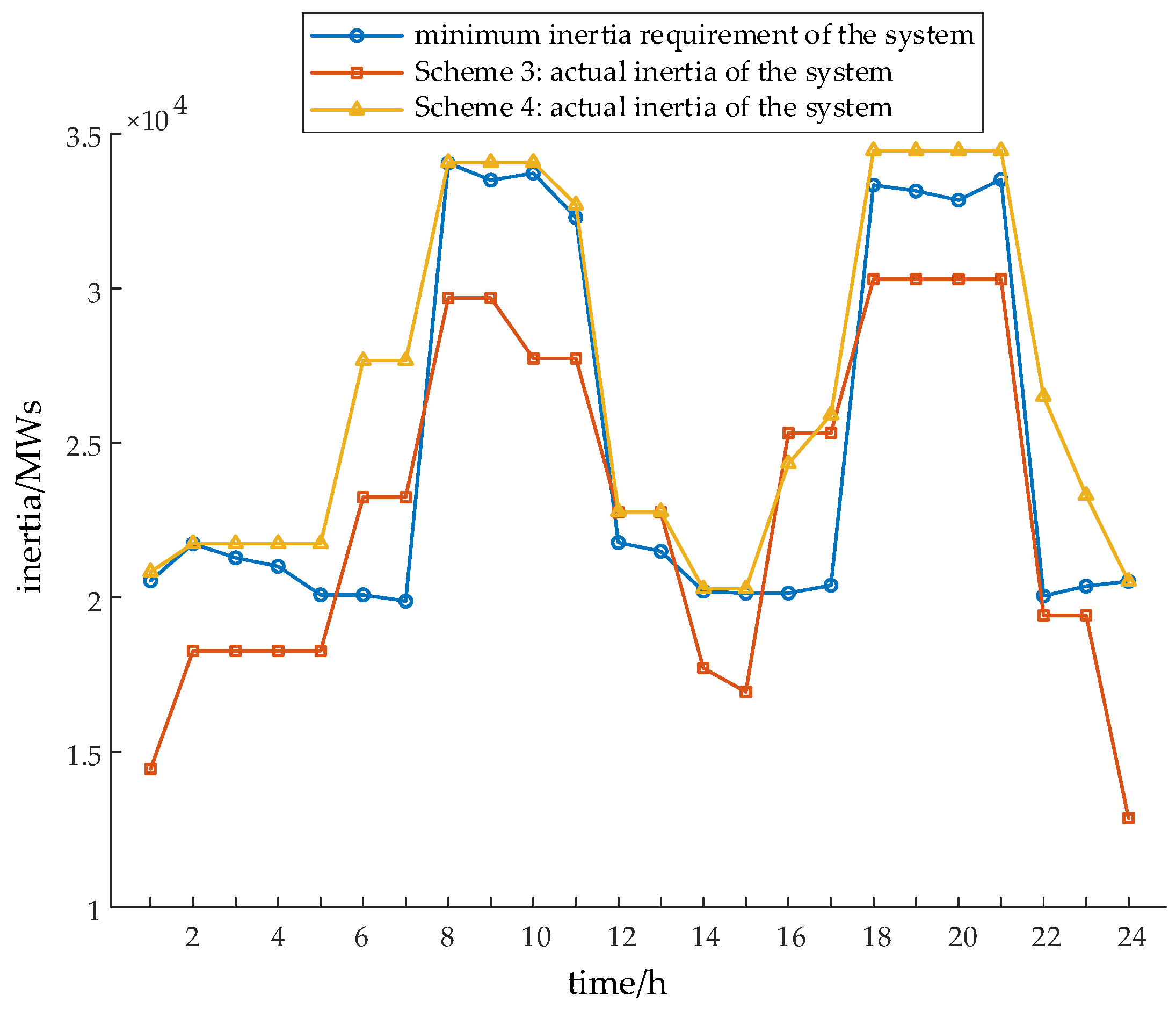
• When considering the inertia constraints, the total power rises from 1897.3 MW to 1933.3 MW. This is because the inertia constraint places higher demands on the system’s frequency regulation capability. The inertia provided by pumped storage is used in conjunction with thermal power and nuclear power units to jointly meet the inertia requirements of the power grid;
• When inertia constraints are taken into account, the proportion of configured power and con-figured capacity of the 4 h unit has both increased compared to when inertia constraints are not considered. This is because the 4 h unit has a faster response speed and is more suitable for providing inertia support;
• When inertia constraints are taken into account, the proportion of configured power and con-figured capacity of the 8 h unit is both lower compared to when inertia constraints are not considered. This indicates that the priority of dynamic stability requirements in the power system is higher than that of simple capacity scale.

Next, a typical day is selected as an example to observe the start-up and shutdown conditions of thermal power units, grid dispatching, pumped storage output, abandoned electricity, grid inertia, and the changes in the frequency Nadir when disturbances occur under Schemes 3 and 4.

Figure 5 shows the Startup status of thermal power units in Scheme 3 and Scheme 4.

Figure 5. Startup status of thermal power units in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 5. Startup status of thermal power units in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 6. Power grid dispatching results in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 6. Power grid dispatching results in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

As is shown in Figure 6, when the inertia constraint is not taken into account, the output of thermal power changes rapidly with the load and drops significantly during the low load period, reflecting the priority of economic dispatching. When considering the inertia constraint, the output fluctuation of thermal power de-creases, and even during low periods, a certain output is maintained. The reason is that inertia support needs to be provided, indicating that the system prioritizes frequency stability at the expense of some economic benefits. This corresponds to the increase in the start-stop cost and operating cost of thermal power as shown in Table 1.

Figure 7. Schematic diagram of pumped storage output in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 7. Schematic diagram of pumped storage output in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

As can be seen from Figure 7, when the inertia constraint is not taken into account, the charging and discharging amplitude of the 4 h unit is large, undertaking the main energy storage task. The output of the 6 h unit is relatively stable. The 8 h unit only operates during peak and off-peak hours. When considering the inertia constraint, the charging and discharging of the 4 h unit are more frequent, but the amplitude is reduced. The 6 h unit participates in frequency regulation, and the output fluctuation increases. The reason is that under the inertia constraint, the system requires more units to provide dynamic support. The 8 h unit almost participates in minor adjustments throughout the day, which is to ensure that the system always has the ability to respond to inertia.

Figure 8. Curtailment in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 8. Curtailment in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

As can be seen in Figure 8, when the inertia constraint is not taken into account, the abandoned power is basically concentrated during the off-peak period when the load demand is insufficient. At this time, thermal power needs to meet the minimum technical output, and the charging power of pumped storage is relatively high, approaching full charge, and cannot further consume wind and solar power. When considering the inertia constraint, the abandoned electricity is still distributed after 3 p.m. The underlying reason is that, under inertia constraints, the system needs to keep more thermal units online operating at their higher technical minimum output to ensure real-time inertia levels. Particularly during the afternoon load valley, this locked-in minimum thermal output occupies the transmission capacity and regulation space that could otherwise be used for integrating wind and solar power. This restricts the downward flexibility of the net load. Consequently, even with abundant wind and solar resources available, their generation output has to be forcibly curtailed, leading to the curtailment peak in the afternoon. Both peaks of abandoned electricity have decreased, which is because the inertia provided by pumped storage during discharge has also been taken into account.

Figure 9. Load curve in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 9. Load curve in Scheme 3 and Scheme 4. (a) Scheme 3; (b) Scheme 4.

Figure 9 shows that, when considering the inertia constraint, the effect of pumped storage in peak shaving and valley filling is obvious. This is because when there is no inertia constraint, the system prioritizes economic scheduling, pumped storage responds flexibly to market signals, and the correction amplitude of the load curve is relatively small. Under the constraint of inertia, the system requires a stronger power balance capability, and pumped storage is forced to be used for more aggressive peak shaving and valley filling.

Although the amount of wind and solar power curtailment has increased, through the regulation of pumped storage, better peak shaving and valley filling have been achieved instead, which reflects the complex trade-offs in high-proportion renewable energy systems.

Figure 10 shows the minimum inertia requirement and actual inertia of the systems in Scheme 3 and Scheme 4, and Figure 11 shows the frequency Nadir of each scheme.

Figure 10. The minimum inertia requirement and actual inertia of the systems in Scheme 3 and Scheme 4.

Figure 10. The minimum inertia requirement and actual inertia of the systems in Scheme 3 and Scheme 4.

Figure 11. Frequency Nadir of each scheme.

Figure 11. Frequency Nadir of each scheme.

By analyzing the changes in the lowest point of the system frequency when disturbances occur under different schemes, it can be known that without considering the inertia constraint, the system frequency fluctuation cannot be effectively controlled. When facing the same high-power disturbance, the over-limit situation will occur frequently. When considering the inertia constraint and configuring the pumped storage capacity, the power grid can rely on the coordination of thermal power, nuclear power units and pumped storage units to provide inertia support, thereby effectively controlling the frequency fluctuation of the system within the allowable range.

Furthermore, the frequency Nadir of Scheme 1 is lower than that of Scheme 3, indicating that the system frequency over-limit is more severe when the pumped storage duration is not considered in the selection. This fully demonstrates the practicality and effectiveness of the pumped storage capacity configuration model proposed in this paper, which considers inertia constraints and duration selection.

5. Conclusions

This paper designs a collaborative framework for capacity configuration and operation optimization in view of the limitation of traditional capacity configuration methods for pumped storage power stations that only consider a single operating duration, and takes into account the system inertia constraint. Specifically, first from the perspective of ensuring the frequency security of the system, two minimum inertia analytical conditions based on RocoF and Nadir constraints were derived. Based on this, a pumped storage configuration optimization model was constructed with the goal of minimizing the total operating cost of the system throughout its entire cycle. This model simultaneously takes into account the penalty term of the peak-valley difference index of the load curve and the penalty for the guarantee value of the medium and long-term unit inertia. The validity and advantages of the method proposed in this paper are verified through numerical examples, and the conclusions drawn are as follows:

• Inertia constraint is a key factor affecting the economic operation of the system and the consumption of new energy. To ensure the stability of the system frequency, it is necessary to maintain a sufficient level of synchronous inertia, which will force more thermal power units to be in an online state. The simulation results of this paper show that considering the inertia constraints will lead to a certain increase in the comprehensive operating cost of the system. Meanwhile, the minimum technical output of thermal power units limits their regulation flexibility, occupies the space for the consumption of new energy, and causes the cost of wind and solar power curtailment to rise;
• The duration selection strategy of pumped storage power stations has a significant impact on the system operation mode. The adoption of a mixed configuration mode of 4 h and 8 h units demonstrates significant synergistic advantages compared to a single 6 h configuration. In the hybrid configuration mode, the 4 h unit effectively shares the instantaneous frequency regulation pressure of the system with its rapid response capability, while the 8 h unit better undertakes the tasks of long-term energy transfer and new energy consumption. This division of labor enables thermal power units to operate under more efficient and stable conditions, significantly reducing the operating costs of thermal power and their proportion in the total cost. At the same time, it enhances the system’s capacity to absorb renewable energy and effectively lowers the costs of wind and solar power curtailment;
• The system optimization objective needs to strike a balance between stability and economy. Although the frequency safety of the system is guaranteed after considering the inertia constraint, and the configuration strategy that takes into account the duration selection brings about the optimization of the cost structure, its investment power cost is relatively high, resulting in an increase in the comprehensive operating cost of the system. This highlights a key challenge in the transition of power systems: the investment in flexibility and stability-enhancing resources such as pumped storage inevitably introduces additional costs. These costs can be viewed as necessary for shifting the system’s operational paradigm from being primarily fuel-cost-centric to one that values regulation services and security assurance. In this article, such costs can be regarded as the necessary cost for the system to shift from being centered on fuel costs to being centered on regulation services and security guarantees.

The proposed strategy exhibits broad applicability to power grids with diverse characteristics. The inertia constraints and mixed-duration storage configuration are derived from fundamental principles, allowing adaptation to systems with varying renewable integration levels, load patterns, and security standards. While parameters such as inertia thresholds and penalty coefficients may require localization, the core optimization framework ensures scalability and transferability.

At this stage, the impact of prediction errors such as load and the uncertainty of wind and solar energy has not been fully studied. In the future, based on the research progress, it will be continuously deepened. At the same time, a full life cycle cost–benefit framework that takes social and environ-mental indicators into consideration will be introduced to establish a more comprehensive pumped storage evaluation system.