A Clustering and Reinforcement Learning-Based Handover Strategy for LEO Satellite Networks in Power IoT Scenarios

Abstract

Communication infrastructure in remote areas struggles to deliver stable, high-quality services for power systems. Low Earth Orbit (LEO) satellite networks offer an effective solution through their low latency and extensive coverage. Nevertheless, the high orbital velocity of LEO satellites combined with massive user access frequently leads to signaling congestion and degradation of service quality. To address these challenges, this paper proposes a LEO satellite handover strategy based on Quality of Service (QoS)-constrained K-Means clustering and Deep Q-Network (DQN) learning. The proposed framework first partitions users into groups via the K-Means algorithm and then imposes an intra-group QoS fairness constraint to refine clustering and designate a cluster head for each group. These cluster heads act as proxies that execute unified DQN-driven handover decisions on behalf of all group members, thereby enabling coordinated multi-user handover. Simulation results demonstrate that, compared with conventional handover schemes, the proposed strategy achieves an optimal balance between performance and signaling overhead, significantly enhances system scalability while ensuring long-term QoS gains, and provides an efficient solution for mobility management in future large-scale LEO satellite networks.

1. Introduction

With the continuous advancement of China’s new-type power system, the demand for higher power supply reliability and greater intelligence has grown substantially. The ever-expanding scale of the power grid, increasing structural complexity, and rapid growth in the number of connected power terminals collectively impose stringent requirements on communication systems, particularly in terms of real-time performance, coverage, and resilience [1]. At present, optical fiber remains the primary wired communication medium in power systems and offers excellent transmission performance; however, its deployment is challenging and prone to damage in disaster-prone regions or areas with complex terrain [2]. Although wireless private networks and public cellular networks provide certain flexibility, their performance is fundamentally limited by base-station coverage and ground infrastructure conditions. As a result, effective communication cannot be ensured in remote mountainous regions, deserts, maritime areas, and other challenging environments, leaving some transmission corridors in long-term “communication blind zones” [3]. When terrestrial communication facilities fail due to extreme weather or geological disasters, the power system cannot transmit operational status information in a timely manner, posing severe risks to secure and stable grid operation. In the context of the emerging smart grid, all segments—generation, transmission, and distribution—rely heavily on highly reliable communication links. Thus, the limitations of traditional communication methods in special scenarios have become a critical bottleneck restricting full-domain situational awareness and real-time grid control [4].

Satellite communication technology, with its advantages of wide-area coverage, independence from geographical constraints, and strong disaster resilience, is rapidly becoming an indispensable component of the power communication architecture [5]. In remote areas where terrestrial communication cannot provide effective coverage, as well as in emergency scenarios, satellite communication can deliver stable and reliable channels for data, voice, and image transmission. It is the only means capable of providing connectivity in regions where both wired and wireless terrestrial networks are unavailable, effectively filling the coverage gaps left by optical fiber, public wireless networks, and private networks [6,7]. In critical operations such as emergency command and post-disaster restoration, satellite links enable real-time information exchange between frontline personnel and control centers, significantly enhancing the resilience and response efficiency of the power grid [8]. Moreover, during periods of heavy communication demand or terrestrial network congestion, satellite systems can offload traffic, alleviating ground-network pressure and improving overall load balancing [5]. As the development roadmap for sixth-generation (6G) mobile communications becomes clearer, integrated space–air–ground networks are emerging as a key direction for future information infrastructure. Satellite communication will integrate deeply with terrestrial systems to establish a comprehensive, intelligent, and highly reliable communication foundation for the power Internet of Things. Therefore, incorporating satellite communication systems into the power communication network is not only a practical necessity for operating under complex environments and extreme conditions, but also an essential path toward building future high-reliability smart grids.

LEO satellite communication systems, featuring global seamless coverage, low propagation latency, and high-bandwidth potential, have become a critical component of space–air–ground integrated networks. LEO satellites typically operate at altitudes below 2000 km and offer shorter transmission delays and lower energy consumption compared to Medium Earth Orbit (MEO) and Geostationary Earth Orbit (GEO) satellites. They support high-data-rate transmission and wide-area coverage, effectively compensating for the coverage limitations of terrestrial communication networks in remote regions, oceanic environments, and aerial platforms [9,10]. However, the rapid relative motion between LEO satellites and user terminals results in frequent link handovers. Coupled with time-varying network topology, uneven traffic distribution, multi-user resource contention, and diverse service requirements, these characteristics often lead to increasing handover failure rates and network load imbalance, severely degrading service continuity and overall system performance [11]. As a core component of mobility management, satellite handover decision-making must balance decision efficiency, resource utilization, and user experience, and its effectiveness directly determines the continuity and quality of communication services. With the continuous expansion of mega-constellation LEO networks, the complexity of network modelling grows exponentially, creating an urgent need for efficient handover algorithms suitable for large-scale dynamic scenarios. Existing research has evolved from simple clustering-based scheduling to multidimensional intelligent optimization, forming a technical system that encompasses user grouping, target-satellite selection, and handover-sequence scheduling. Nevertheless, significant challenges remain in terms of dynamic adaptability, multi-objective coordination, and robustness in complex environments.

Early satellite handover decision-making primarily relied on simple, single-attribute–driven algorithms in which decisions were based on a single performance metric to simplify the decision logic. Yue et al. [12] proposed the HM-LRT algorithm, which predicts the link remaining time (LRT) by exploiting deterministic satellite motion patterns. This approach effectively reduces data loss and rerouting overhead caused by handovers; however, it neglects satellite load conditions and channel resource availability, making it prone to handover failures due to channel congestion in high-traffic scenarios. Some studies have associated satellite topology with mathematical graph theory to better accommodate the characteristics of LEO satellite networks. Wu et al. [13] proposed a directed-graph-based handover framework that maps satellite coverage periods to nodes and potential handover relationships to directed edges. By applying Dijkstra’s algorithm to compute the shortest path and minimize the number of handovers, the framework flexibly adapts to multiple handover criteria. Nevertheless, the static topology assumption fails to account for the dynamic movements of satellites and users, leading to reduced handover accuracy in highly mobile environments. Hu et al. [14] addressed topology time-variation induced by terminal mobility by introducing a Time-Evolving Graph (TEG)-based handover prediction framework. Through dynamic time-slot partitioning and shortest-path updates, this method effectively lowers handover failure rates and the probability of unnecessary handovers; however, its reliance on predefined criterion weights limits adaptability to diverse multi-service demands.

To overcome the limitations of single-attribute decision-making, multi-attribute decision algorithms have increasingly become a research focus, enabling global optimization of handover decisions through the integration of multidimensional performance metrics. Zhang et al. [15] proposed a multi-attribute decision algorithm based on the entropy weight method, transforming the four metrics—weighted channel quality, remaining service time, number of satellite-served users, and power allocation—into a multi-objective optimization problem. Simulations demonstrated its superiority over the maximum remaining service time and optimal channel quality strategies in terms of handover frequency, user SNR, and system load balancing. To further enhance customisation and multi-factor coordination in handover decisions, improved methods based on multi-attribute weighting and time-dynamic graphs have emerged. Hozayen et al. [16] proposed a customizable graph-based handover framework that constructs a time-series satellite node graph and converts multiple criteria—such as data rate and latency—into edge weights. Using Dijkstra’s algorithm to derive the optimal handover sequence, their approach improves data rate and maintains stable QoS in Starlink constellation simulations. Zhang et al. [15] employed a weighted bipartite graph model and used entropy weighting to combine objectives such as channel quality and remaining service time into a single optimisation function, effectively balancing handover frequency with system load. However, entropy-weight computation depends on historical statistics, resulting in insufficient real-time responsiveness for highly dynamic scenarios. Dai et al. [17] presented the MADG-MADM dynamic handover scheme, which models satellite link elevation angle, coverage duration, and idle channel status via a Multi-Attribute Dynamic Graph (MADG) and selects optimal handover paths using Multi-Attribute Decision Making (MADM), significantly reducing handover delay and interruption probability. Liang et al. [18] proposed a multi-attribute path-selection algorithm based on the niche-based Pareto multi-objective genetic algorithm (NPGA). By jointly considering service duration, communication elevation angle, and idle channel status, their method identifies optimal handover paths and effectively reduces handover failure rates and new-call blocking rates. However, the iterative nature of the algorithm induces substantial on-board computational overhead.

Frequent group handover issues, triggered by high-speed satellite movement and massive user access, often lead to signaling congestion, increased handover failure rates, and degraded service quality, severely limiting network performance. Group handover technology, by grouping and scheduling users with similar characteristics, can significantly reduce signaling overhead and handover conflicts, becoming a key approach for managing large-scale user mobility. Group handover research centers on fundamental clustering and simple scheduling, focusing on reducing handover overhead and avoiding congestion. Zhu et al. [19] proposed an active group handover scheme based on spectral clustering, employing a non-cooperative game model to schedule handover timing and alleviate congestion. This effectively reduced handover delay and conflict probability. However, spectral clustering requires pre-specifying the number of groups, and the convergence speed of the game model is significantly affected by user scale. Yang et al. [20] proposed a group handover strategy combining hierarchical clustering with network flow analysis. This approach eliminates the need for predefined group sizes by dynamically aggregating users through hierarchical clustering. It employs a network flow model and Shortest Path First Algorithm (SPFA) for target satellite selection, significantly reducing signaling overhead and handover failure rates. To enhance resource adaptability and decision accuracy in group handover, multidimensional clustering and joint optimization algorithms have gradually emerged. Zhu et al. [21] proposed the Dual Grouping Handover scheme, employing beam-constrained hierarchical clustering for user grouping. It combines a greedy algorithm with dynamic programming for satellite grouping and utilizes a conditional handover (CHO) mechanism to optimize the handover process. While improving handover success rates and network throughput while reducing signaling redundancy, the satellite grouping process did not fully account for users’ differentiated QoS requirements. Xing et al. [22] proposed the Customized Handover Algorithm, based on greedy dynamic programming (DP) clustering and graph perfect matching, to achieve optimal matching between user groups and satellites. Supporting customized QoS services, it reduced handover frequency by 12.6% and increased success rate by 21.9%. However, the graph matching algorithm exhibits high computational complexity. Therefore, for large-scale complex network scenarios, advanced solutions integrating intelligent algorithms with multi-period scheduling are needed to further overcome performance bottlenecks. Yan et al. [23] proposed the Joint User Association and Handover (JUAH) strategy, which employs simulated annealing for user grouping and prioritizes co-directional rotating satellites via a biased handover mechanism. This approach reduced propagation delay jitter (PDJ) and handover counts by 39.83% and 63.25%, respectively. Yang et al. [24] proposed a cluster handover strategy based on Clustering Feature (CF) trees and Multi-Layer Graphs (MLGs). By dynamically clustering via CF trees to avoid invalid grouping and constructing MLG models to transform multi-period multi-cluster handover into dynamic network flow problems, they employed the SPFA algorithm to solve for minimum-cost maximum flow. This achieved synergistic optimization of handover overhead, success rate, and service quality in massive user scenarios. However, constructing and maintaining MLGs involves high computational complexity, and satellite deployment costs are constrained.

DQN algorithms in deep reinforcement learning have emerged as a key technical means for optimising satellite handover decisions due to their strong capability for adaptive learning in dynamic environments. Existing research has evolved from basic DQN applications in single-scenario settings to increasingly complex optimisation schemes involving multi-scenario and multi-objective coordination. This evolution has resulted in a comprehensive technical framework encompassing single-user decision-making, group handover optimization, and satellite–terrestrial integrated scheduling. Nevertheless, challenges remain with respect to controlling computational complexity, achieving high-precision multi-attribute coordination, and ensuring robustness in dynamic environments. Early DQN-based handover approaches focused primarily on optimizing fundamental network metrics to simplify the decision logic, thereby serving only single-user handover requirements. Kim et al. [25] proposed a DQN-based satellite scheduling algorithm that constructs the state space using user–satellite distance, elevation angle, received signal strength, and SNR, while introducing a handover-cost penalty term to reduce unnecessary handover. Their approach achieves rapid convergence of received signal strength and improves system throughput. Yu et al. [26] introduced a graph-enhanced DQN handover model that integrates Message Passing Neural Networks (MPNNs) to encode the dynamic satellite–user topology. By capturing spatial dependencies that conventional DQN cannot model, this approach improves handover accuracy, lowers handover frequency, and enhances service continuity in fast-varying LEO constellations. Liu et al. [11] proposed a distributed handover scheme based on Successive Deep Q-Learning (SDQL). By decomposing the state space according to satellite independence properties and modeling the link using a shadowed Rician channel, they designed a utility function combining user data rate and satellite channel resources, thereby reducing decision complexity while enabling effective inter-satellite load balancing.

To enhance multi-objective coordination in handover decisions, DQN optimization schemes integrating multi-attribute fusion and conditional handover mechanisms have gradually emerged. Zhang et al. [27] proposed a DQN-driven Conditional Handover (CHO) algorithm that uses a dual Q-network to improve decision stability, significantly reducing handover failure rates and interruption delays while extending link service time. However, the algorithm does not accommodate differentiated QoS requirements, limiting its applicability in heterogeneous service scenarios. Wan et al. [28] introduced a DQN-based load-balancing handover scheme for satellite–terrestrial integrated networks. By incorporating user service type and network load conditions into the reward function and adopting a centralised controller for adaptive access-point selection, their approach effectively reduces connection rejection rates and enhances resource utilisation. Nonetheless, the centralised architecture incurs high on-board computational overhead, which constrains real-time performance in large-scale user scenarios. For large-scale satellite–ground hybrid networks, more advanced DQN schemes combining clustering and multi-attribute decision-making have been proposed to overcome performance bottlenecks. Jia et al. [29] developed a multi-attribute handover strategy that integrates Fuzzy C-Means (FCM) clustering with reinforcement learning. Users are first clustered based on location, velocity, and bandwidth demand to reduce decision burdens; then a multi-attribute reward function—considering received signal strength, network bandwidth utilization, and handover cost—is constructed to jointly reduce handover demand and enhance resource utilization.

To address the increased algorithmic complexity brought by large-scale LEO satellite networks, the stringent requirement for dynamic adaptability under rapidly time-varying topologies, and the intensified competition for service resources resulting from massive multi-user access, this paper proposes a group-based handover decision framework built upon DQN. In power Internet of Things (IoT) scenarios, such as wide-area grid monitoring, status telemetry reporting, and emergency control signaling in remote or disaster-affected areas, these information flows must rely on LEO satellite backhaul to ensure connectivity and service continuity. The framework is designed to enhance the stability, scalability, and intelligence of handover strategies in complex dynamic environments, and extensive simulations have been conducted to validate its performance advantages.

The main contributions of this paper are summarised as follows:

-

Proposing a user clustering algorithm with QoS fairness constraints for power IoT services: Addressing the shortcoming of traditional clustering methods that overlook inter-user QoS variations within groups, which may degrade the transmission performance of critical power monitoring and control information, this paper incorporates a QoS variance constraint into the K-Means algorithm. Groups where the variance of the aggregate QoS scores among users exceeds a predetermined threshold are subsequently disaggregated. This prevents users with vastly differing QoS requirements from being grouped together, ensuring balanced QoS distribution within each cluster and thereby achieving fairer user grouping.

-

Establishing a Hierarchical DQN-based group handover decision framework tailored to power IoT access: To address the state space explosion in scenarios with a large number of power IoT terminals transmitting periodic telemetry data and occasional emergency signaling, this paper designs a hierarchical decision architecture combining user clustering with DQN. At the start of each DQN round, user clustering is performed to select a cluster leader for each group. Subsequently, the cluster leader represents the entire group for DQN training and decision-making. This approach significantly reduces computational complexity and signaling overhead, enhancing the algorithm’s computational efficiency and scalability when supporting long-term and large-scale power system communications over LEO satellite networks.

The remainder of this paper is organized as follows: Section 2 describes the system model and problem formulation. Section 3 details the proposed strategy. Section 4 presents simulation results and analysis. Finally, Section 5 concludes the paper.

2. Materials and Methods

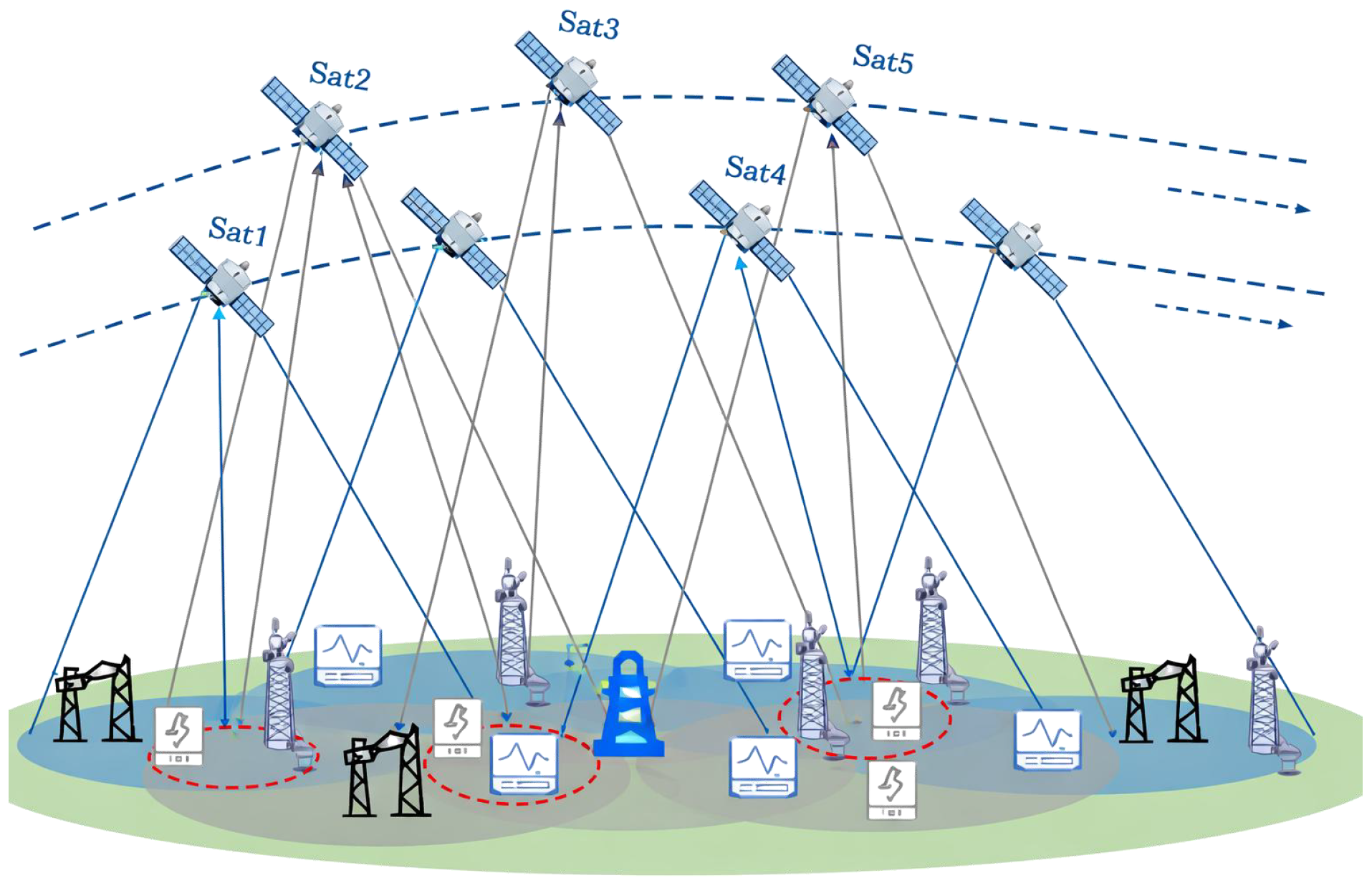
2.1. System Model

This paper considers a typical LEO satellite communication scenario for power Internet of Things applications, where multiple LEO satellites jointly serve densely deployed ground terminals within a coverage area. Each coverage area is assumed to be continuously covered by at least one satellite, consistent with the mobility management framework defined in 3GPP Release 17 for non-geostationary satellite systems.

The system consists of three components: a space segment composed of M LEO satellites, a ground relay station, and distributed power grid sensing devices. The relay station aggregates data from all terminals within its coverage area and maintains satellite connectivity on behalf of the user group. Due to the limited service duration of individual LEO satellites and the long communication cycles required by power services, group-based satellite handover is adopted: when the elevation angle of the serving satellite approaches a threshold, the entire user group switches simultaneously to a candidate satellite to ensure service continuity while reducing signaling overhead. Figure 1 illustrates the system model developed in this paper.

To accurately predict the serviceable time window for each satellite, we use the Global Positioning System to obtain location information for the user group and employ a simplified universal perturbation model based on TLE ephemeris data to calculate satellite orbits. Using the satellite ephemeris and terminal location, we can compute the service time window for each satellite over the target area.

$$T=\left\{\left(t_s^1,t_e^1\right),\left(t_s^2,t_e^2\right),\dots ,\left(t_s^i,t_e^i\right),\dots ,\left(t_s^n,t_e^n\right)\right\}$$

(1)

In this formula, $\left({\mathrm{t}}_{\mathrm{s}}^{\mathrm{i}},{\mathrm{t}}_{\mathrm{e}}^{\mathrm{i}}\right)$ denotes the start and end times at which satellite i provides service to this user group. Within a vast satellite network, each high-speed LEO satellite can only cover a specific area of the ground within a limited time window. Coverage cycles vary among satellites. When their service times overlap (as shown by the dashed box in Figure 2, where ${\mathrm{t}}_{\mathrm{s}}^1<{\mathrm{t}}_{\mathrm{s}}^2<{\mathrm{t}}_{\mathrm{e}}^1$ constitutes an overlap window between Satellites 1 and 2), this is a decision point for group handover.

At this point, the entire user group can handover concurrently from the satellite currently serving them (e.g., Sat1) to a candidate satellite within the overlap window (e.g., Sat2). Handover cannot be performed if there is no overlap in coverage time between satellites (e.g., Sat1 and Sat3).

A set of candidate satellites capable of providing service during the user’s communication duration can be identified based on the predicted overlap of satellite service cycles for terminals over a future period. This paper models the user’s decision-making process for satellite handover as a sequential problem and uses reinforcement learning methods to solve it. The key lies in the agent observing the environmental state at each decision point, comprising the remaining service time, communication rate and communication delay of the current serving satellite, and then selecting whether to maintain the current satellite or handover to a specific candidate satellite. Therefore, in order to solve this multi-objective optimisation problem, the aim of this paper is to maximise user service quality and identify the optimal handover decision.

Based on predictions of service time window overlaps between satellites and user groups over a future period, a set of available candidate satellites can be determined dynamically. This paper models the group satellite handover decision process as a sequential decision problem, employing the DQN method to solve it. At each decision time step, the agent observes an environmental state $s_t$ representing the communication status of the entire user group. This state comprises key variables: the remaining service time of the current serving satellite, the average communication rate of the user group and the average communication delay. Based on this state, the agent selects an action, either maintaining the current connection or handing over the entire group to one of the remaining candidate satellites.

Thus, the research objective becomes a multi-objective optimisation problem: the DQN agent learns an optimal policy, $\pi$, that maps states to actions in order to maximise the long-term aggregate service quality for the user group. This process involves finding the optimal handover decision sequence for the entire group.

2.2. Handover Decision Factor Analysis

For power grid communications in remote areas, satellite handover optimization must jointly consider transmission latency, data transmission rate, and remaining satellite service duration. These three factors directly determine the real-time responsiveness, transmission efficiency, and service continuity of power communication links.

2.2.1. Transmission Latency

During the design and development of satellite handover algorithms for power systems, transmission latency over satellite-to-ground links is a critical performance metric that must be carefully considered. Transmission latency directly affects the timeliness and accuracy of power data delivery, which is essential for the reliable operation of smart grids. Smart grid systems depend on the real-time acquisition and rapid processing of large volumes of operational data to enable dynamic situational awareness and precise control of grid conditions. Increased transmission latency introduces delays in information exchange, thereby degrading real-time monitoring performance and impairing the effectiveness of control actions. In particular, under abrupt operational changes, equipment failures, or emergency scenarios, low-latency satellite-to-ground communication is essential to ensure the timely transmission of emergency control commands and rapid feedback of fault information. Such capabilities are crucial for preventing fault escalation and maintaining the safe and stable operation of power systems. Consequently, satellite handover algorithms for power applications should prioritize the optimization of satellite-to-ground transmission latency. Through appropriate algorithmic architecture design and parameter tuning, low-latency and high-reliability communication links can be achieved, thereby meeting the stringent requirements of real-time interaction and precise control scheduling in power grid communications. The propagation distance between the satellite and the user is denoted by d, and it is calculated as follows:

$$d=\sqrt{h^2+{\left(x-o_x\right)}^2+{\left(y-o_y\right)}^2}$$

(2)

where ($o_x$, $o_y$) denotes the position directly beneath the satellite, (x, y) denotes the user’s coordinate position, and h denotes the vertical height between the satellite and the ground. The transmission delay $TD$ is defined by the following expression:

$$TD={\displaystyle \frac{d}{c}}$$

(3)

where c is the speed of light.

2.2.2. Data Transmission Rate

During the design of satellite handover algorithms for power systems, the data transmission rate for grid users is a core consideration that cannot be neglected. This is primarily due to the power system’s stringent requirements for rapid response to real-time monitoring and control commands, given that the user data rate directly dictates the overall efficiency of power information transmission. The development of satellite handover algorithms must prioritize guaranteeing the efficient transmission of monitoring data, metering information, and control signals. Only in this way can a rapid response to situations such as grid operational anomalies and equipment failures be realized. Consequently, incorporating the grid user data rate into the comprehensive design framework of satellite handover algorithms is a critical prerequisite for ensuring the performance of power system communication links and data transmission. Furthermore, owing to the long-distance transmission characteristics between satellites and ground terminals, signals are prone to interference from complex environmental factors during propagation. This gives rise to various loss and fading phenomena, ultimately leading to the attenuation of signal strength. From the perspective of channel modeling, the factors contributing to such losses and fading correspond to different types of channel losses. These include free-space propagation loss (FSPL), atmospheric loss, and shadow fading, among others. Among these, free-space propagation loss (FSPL) is the dominant loss type in wireless signal transmission.

Based on the satellite-to-ground link distance, the free-space propagation loss (FSPL) can be defined as follows:

$$FSPL=20lg\left({\displaystyle \frac{4\pi df}{\lambda }}\right)$$

(4)

where f denotes the carrier frequency, measured in gigahertz (GHz). Let $L_a$ denote signal losses induced by atmospheric conditions, precipitation, and other factors, and $L_{misc}$ denote other types of losses and fading. The total signal loss during transmission, denoted as $L_{total}$ can then be expressed as follows:

$$L_{total}=FSPL+L_a+L_{misc}$$

(5)

The received power (PR) is defined as

$$P_R=P_T-L_{total}+G_R+G_T$$

(6)

where $P_T$ denotes the transmit power, and $G_T$ and $G_R$ represent the antenna gains of the transmitter and receiver, respectively. According to Shannon’s capacity theorem, the achievable data rate R can be expressed as

$$R=Blog\left(1+{\displaystyle \frac{P_R}{N}}\right)$$

(7)

where B denotes the channel bandwidth, and N denotes the noise power.

2.2.3. Remaining Service Duration

Within the design framework of satellite handover algorithms for power systems, satellite service duration is a critical dimension that must be taken as a core consideration. The service duration that a satellite can provide to grid user terminals is a core metric for assessing the adaptability of satellite communication to power services. It exhibits a significant correlation with satellite handover frequency during communication: for grid user terminals in an active communication state, a longer service duration of candidate satellites results in a lower frequency of satellite handovers initiated by the terminal. Satellite service duration directly affects the reliability and stability of power system operations, and it acts as the fundamental guarantee for core grid functions, including real-time monitoring, remote control, and emergency operations. Excessively frequent satellite handovers that result in prolonged communication interruptions may readily lead to the loss of power operational data and delays in command transmission, thereby significantly compromising the power system’s capabilities for real-time monitoring and precise regulation. Thus, satellite service duration is identified as the core handover factor in satellite handover algorithms. When a grid user terminal needs to access the satellite communication system or handover from the current serving satellite to another satellite, the terminal can upload its location information to the ground station. Upon receiving this information, the ground station will return a feedback matrix T.

$$T=\left[\begin{array}{c}{t}_1^m{t}_2^m{t}_3^m\dots t_N^m\\ t_1^n{t}_2^n{t}_3^n\dots t_N^n\end{array}\right]$$

(8)

T is a 2 × N matrix, where the first row denotes the start time at which satellite j provides service, and the second row denotes the corresponding end time (1 ≤ j ≤ N, with N being the number of LEO satellites in the satellite network). Thus, the remaining service duration of satellite j for user i at time t can be expressed as follows:

$$T_{ij}\left(t\right)=t_j^n-t$$

(9)

2.3. Problem Description

This paper models the satellite handover problem for user groups as a multi-objective optimisation problem, with the aim of finding the optimal handover strategy for the entire group. The objective is to maximise the comprehensive utility, which is determined by the remaining service time, communication rate and latency over the entire service cycle T.

The comprehensive utility function for a group connected to satellite s at time t is defined as follows:

$$U(\mathrm{u},\mathrm{s},\mathrm{t})=\alpha {\displaystyle \frac{R(\mathrm{u},\mathrm{s},\mathrm{t})}{R_{\max }}}+\beta {\displaystyle \frac{T_{\mathrm{remain}}(\mathrm{u},\mathrm{s},\mathrm{t})}{T_{\max }}}-\gamma {\displaystyle \frac{D_{\mathrm{prop}}(\mathrm{u},\mathrm{s},\mathrm{t})}{D_{\max }}}$$

(10)

Our goal is to find an optimal handover strategy $\pi$ that maximizes long-term cumulative utility:

$$\underset{\pi }{max}\sum _{\mathrm{t}=0}^{\mathrm{T}}\mathbb{E}\left[\mathrm{U}(\mathrm{u},\pi \left({\mathrm{s}}_{\mathrm{t}}\right),\mathrm{t})\right]$$

(11)

This optimization problem is modeled as a Markov Decision Process (MDP) due to the highly dynamic nature of the environment and is solved using deep reinforcement learning methods.

3. Research on LEO Satellite Handover Strategies Based on Constrained K-Means Clustering and DQN

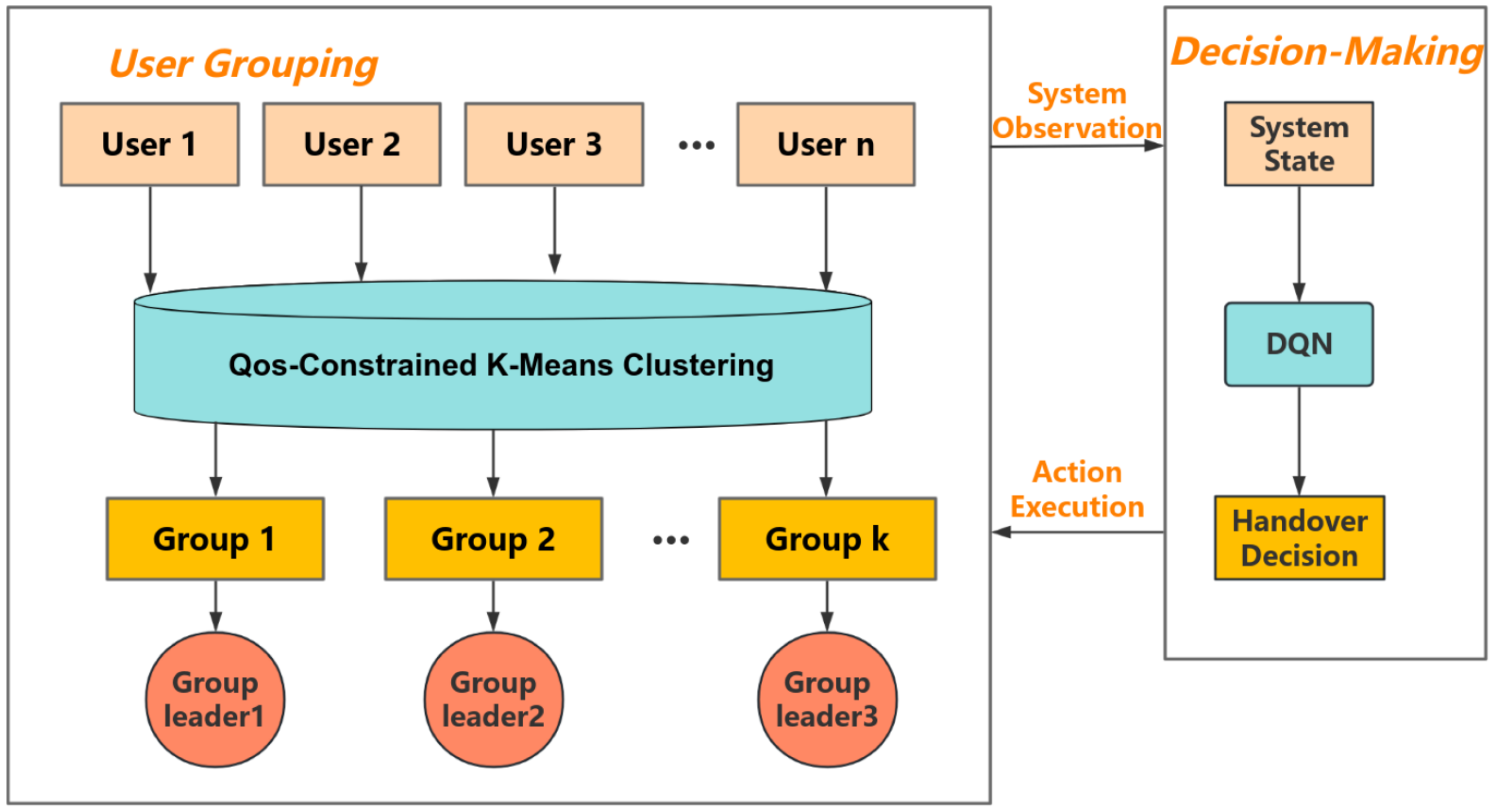
3.1. User Grouping

To reduce the computational load in large-scale user scenarios and ensure fairness, we propose a K-Means clustering method with QoS fairness constraints.

In order to ensure similarity among users within each group, five attributes are selected for grouping: user geographic location, current serving satellite, propagation delay, data rate, and remaining service time. Users are uniformly distributed within a circular region of radius 10 km centered on (−62°, 50°, 0 m), and their positions are obtained via GPS. Propagation delays, data rates, and remaining service times between users and satellites are computed from real satellite trajectory data. Consequently, for each user u, a multidimensional feature vector $f_u$ is constructed as

$${\mathrm{f}}_{\mathrm{u}}=[{\mathrm{Lat}}_{\mathrm{u}},{\mathrm{Lon}}_{\mathrm{u}},{\mathrm{SatID}}_{\mathrm{u}},{\mathrm{D}}_{\mathrm{u}},{\mathrm{R}}_{\mathrm{u}},{\mathrm{T}}_{\mathrm{u}}]$$

(12)

where $La{t}_u$ and $Lo{n}_u$ denote the user’s geographical coordinates; $SatI{D}_u$ denotes the ID of the current serving satellite; and $D_u$, $R_u$, and $T_u$ represent the propagation delay, data rate, and remaining service time, respectively.

K-Means is a classical unsupervised clustering algorithm that partitions the data set into K clusters by minimizing the sum of squared errors (SSEs) within the cluster. After constructing the user feature vectors, the similarity of the user is measured by the Euclidean distance between the feature vectors. Each feature dimension is normalized prior to distance computation to remove the impact of scale differences. For users u and v with feature vectors $f_u$ and $f_v$, the Euclidean distance is

$$dist(u,v)=\sqrt{\sum _{i=1}^n{(f_{u,i}-f_{v,i})}^2}$$

(13)

where n denotes the dimension of the feature vector.

The K-Means clustering is then applied to obtain an initial grouping. The algorithm randomly selects K initial centers. Each user computes the Euclidean distance between its feature vector and each centre and joins the group associated with the nearest centre. The mean of the user vectors in each group is then used to update the cluster centre. This assignment-and-update process repeats until group membership no longer changes. The objective function for the grouping process is

$$J=\sum _{j=1}^K\sum _{u\in C_j}\left|\right|{\mathbf{f}}_u-u_j{\left|\right|}^2$$

(14)

where $C_j$ denotes the jth cluster, and $u_j$ represents the cluster centre.

To prevent users with significantly different QoS conditions from being clustered together, we introduce a QoS fairness constraint. For each group, a composite QoS score is first calculated for each user, and the variance ${\sigma }_j^2$ of the QoS scores within group $C_j$ is computed. If ${\sigma }_j^2$ exceeds the threshold ${\sigma }_{max}^2$, group $C_j$ is split into two subgroups based on the median QoS score. This process is repeated until all groups satisfy the QoS variance constraint. The composite QoS score for each user is given by

$$S_{QoS}\left(u\right)=0.5·{\displaystyle \frac{R_u}{R_{max}}}-0.3·{\displaystyle \frac{D_u}{D_{max}}}+0.2·{\displaystyle \frac{T_u}{T_{max}}}$$

(15)

This score comprehensively reflects the user’s communication quality. The constraint on the variance of the comprehensive QoS scores among users within a group is as follows:

$${\sigma }_j^2={\displaystyle \frac{1}{|C_j|}}\sum _{u\in C_j}{(S_{QoS}\left(u\right)-S_j)}^2\le {\sigma }_{max}^2$$

(16)

Once all groups satisfy the QoS constraint, a cluster leader is selected for each group. Specifically, in each group $C_j$, the user with the highest QoS score is chosen as the leader $L_j$. The selected leader acts as the proxy decision-maker for the entire cluster in handover decisions. The formula for calculating the leader is

$$L_j=arg\underset{u\in C_j}{max}\left[S_{QoS}\left(u\right)\right]$$

(17)

The workflow of the user clustering algorithm is shown in Algorithm 1. First, using K-Means clustering based on the feature vectors, all users are divided into K groups. Next, the variance of the QoS within each group is calculated. Groups with variance exceeding the maximum threshold are split until all groups satisfy the constraint. Finally, the user with the highest QoS score in each group is selected as the group leader.

Algorithm 1: K-Means User Clustering Algorithm with QoS Constraints

Input: User set U, feature data F, variance threshold $max\_var$, initial number of clusters K

Output: Clustering result G, set of cluster leaders L

Initialization: Divide users U into K groups using K-Means based on their feature vectors F

1: For $g_1,g_2,\dots ,g_k$ in G

2:      Calculate the variance of QoS within the groups

3:      If var_g > max_var Then

4:         Split group g into $g_m$ and $g_n$ based on the median QoS

5:          Update the grouping set G

6:      End If

7:      All groups satisfy variance constraints

8: End For

9: For each group g, select argmax($QoS\_score$) as the group leader

10: Return G, L

3.2. DQN Algorithm

Deep Reinforcement Learning (DRL) combines the representational capacity of deep neural networks with the sequential decision-making mechanism of reinforcement learning, and has been widely applied to complex optimization and control problems arising in high-dimensional state spaces. Through continuous interaction with the environment, an agent repeatedly balances exploration and exploitation to learn a policy that maximizes the long-term cumulative reward. Within the MDP framework, DRL defines a state set S, an action set A, and a reward function, enabling the agent to dynamically update state–action pairs and progressively approximate an optimal policy. This learning paradigm allows agents to extract salient features directly from high-dimensional and unstructured observations, thereby achieving end-to-end policy optimization [30].

Among model-free reinforcement learning methods, Q-learning is a foundational approach that derives a policy $\pi :S\to A$ by estimating the action-value function $Q(s,a)$. The algorithm maintains a Q-table that stores the value of every state–action pair and updates these values according to the Bellman recurrence relation. Specifically, when the agent takes an action in a given state and receives an immediate reward, the corresponding Q-value is incrementally updated using a learning rate $r\left(s_t,{\alpha }_t\right)$, enabling the method to gradually converge to the optimal action-value function through repeated interactions. While Q-learning performs effectively in discrete and small-scale state–action spaces, it suffers from the curse of dimensionality and limited generalization capability when applied to high-dimensional environments.

To overcome the scalability limitations of traditional Q-learning in large state spaces, the DQN replaces the discrete Q-table with a deep neural network to approximate the action-value function. DQN was the first to demonstrate that deep networks can stably estimate Q-values from high-dimensional observational inputs, and its stability is enhanced through the use of experience replay and a target network. Given the current state as input, the network outputs the Q-values associated with all candidate actions, with an $\epsilon$-greedy strategy typically employed to balance exploration and exploitation. Compared with classical Q-learning, DQN generalizes better to unseen state–action pairs, enabling effective policy learning in complex tasks. This approach has been extensively validated in scenarios such as wireless resource scheduling and UAV network control. For instance, DQN has been employed to achieve adaptive learning of scheduling strategies at the 5G MAC layer, optimising throughput and fairness metrics from scratch [31]. Additionally, within UAV–ground networks, DQN has been utilized to optimize UAV positioning, reflection parameters, and power allocation, yielding faster convergence and more stable control performance [32].

Furthermore, as summarized by Majid et al. [30], DQN represents a prototypical value-based deep reinforcement learning method. Its core characteristics include approximating the Q-function using neural networks, mitigating sample correlation through experience replay, improving training stability via target networks, and achieving a fundamental exploration–exploitation trade-off through $\epsilon$-greedy behavior. This survey further indicates that DQN-based algorithms demonstrate good scalability when handling high-dimensional inputs, yet may still exhibit instability under long-term sequential decision-making and high discount factor scenarios. This provides a theoretical basis for subsequent algorithmic enhancements.

In the context of this study, three key elements define our proposed DQN algorithm: the state space, action space, and reward function. These are described as follows:

• State Space

We partition the communication session into K equal time steps and denote the environment state at step t by $S_t$. The state $S_t$ is constructed from the link characteristics of the $N_{sat}=5$ candidate satellites visible at time t, including propagation delay, user data rate, and remaining service duration. Therefore, the state space has dimension $3N_{sat}=15$. The state space is specifically represented as follows:

$${\mathrm{S}}_{\mathrm{t}}=[{\mathrm{D}}_1,\dots ,{\mathrm{D}}_5,{\mathrm{R}}_1,\dots ,{\mathrm{R}}_5,{\mathrm{T}}_1,\dots ,{\mathrm{T}}_5]$$

(18)

where $D_1,\dots ,D_5$ denote the propagation delays of the five candidate satellites, $R_1$,…, $R_5$ denote the user data rates of the five candidate satellites, and $T_1$,…, $T_5$ denote the remaining service duration of the five candidate satellites.

B.

Action Space

Action space $a_t$ defines the set of operations an agent may execute. In this scenario, action at denotes selecting one target satellite for connection from the currently visible $N_{sat}$ candidate satellites. We employ one-hot encoding to represent the action space:

$$a_t=\{a\in {\{0,1\}}^{N_{sat}}|\sum _{i=1}^{N_{sat}}{a}_i=1\}$$

(19)

For example, when the agent selects the second satellite, the one-hot action space is $a_t=[0,1,0,0,0]$.

C.

Reward Function

The system’s reward function should relate to the optimization objective. For the satellite handover decision problem studied herein, the reward function aims to maximize QoS while minimizing frequent handover. Consequently, the reward function is defined as a function of the user’s service quality, calculated as follows:

$$r_t={\omega }_1{\displaystyle \frac{R}{R_{max}}}+{\omega }_2{\displaystyle \frac{T}{T_{max}}}-{\omega }_3{\displaystyle \frac{D}{D_{max}}}+P_{handover}$$

(20)

where the weights are ${\omega }_1=5/9$, ${\omega }_2=3/9$, and ${\omega }_3=1/9$. $P_{handover}$ denotes the handover penalty or reward term: +5.0 for maintaining connection, −5.0 for handover to an invalid satellite.

3.3. LEO Satellite Handover Strategy Based on QoS-Constrained K-Means Clustering and DQN

To address the optimization of satellite handover decisions in multi-user scenarios, this paper proposes a LEO satellite handover strategy based on QoS-constrained K-Means clustering and DQN. This approach transforms the LEO satellite handover problem into maximizing the cumulative expected value of a multi-attribute reward function over the entire service cycle.

During each iteration of the DQN algorithm, user clustering is performed once at the beginning of the episode. First, feature vectors are constructed for all users based on geographic location, current serving satellite, propagation delay, data rate, and remaining service time. The Euclidean distance between feature vectors is then used to measure similarity, and K-Means clustering is applied to obtain an initial grouping. Subsequently, each cluster is checked against the QoS fairness constraint. Clusters whose QoS score variance exceeds the threshold are split, preventing users with significantly different QoS conditions from being grouped together. Within each group, the user with the highest QoS score is selected as the leader. The DQN observes the state of each leader and chooses a satellite handover action for that leader. Once a handover decision is made, all users in the group follow the leader’s action and handover simultaneously. The leader’s handover experience is recorded in a shared replay buffer for DQN training and parameter updates. The overall framework of the satellite handover optimization strategy designed in this paper is illustrated in Figure 3.

The specific workflow of the handover algorithm is detailed in Algorithm 2. First, we initialize the satellite environment, the DQN, and the clustering module. In each episode, we perform QoS-constrained K-Means clustering over all users to obtain K clusters and their corresponding leaders. For each leader, we construct the state space using the propagation delay, data rate, and remaining service duration of its five candidate satellites, and the leader then executes the selected action on behalf of all users in the cluster. The DQN selects a handover action based on the current state. The leader then executes this action with all members of its group and calculates the group’s average reward. Subsequently, the experience from this handover is stored in the shared experience pool. Sampling from this pool updates the DQN’s parameters $\theta$.

Algorithm 2: Cluster-Based DQN Satellite Handover Algorithm

Initialization: satellite environment, DQN network, and clustering algorithm

Training:

1: For episode = 1 to M Do

2:      Perform user clustering once per episode (Algorithm 1)

3:      For each cluster leader $u\_leader$:

4:         Obtain state $S_t$

5:         DQN selects action $a_t=argmaxQ(S_t,a;\theta )$

6:         All members within the group execute action $a_t$

7:         Calculate group average reward $r\_group$

8:         Store experience $(S_t,a_t,r\_group,S_{t+1})$

9:      Sampling from the experience pool and updating DQN parameters $\theta$

10: End For

4. Results

4.1. Simulation Setup

This section presents the simulation environment and DQN parameter configurations. The experiment considers multiple satellites jointly serving a fixed tracking region centred at (−62°, 50°, 0 m), with users distributed within a 10 km radius. Starting from 09:30 UTC on 1 May 2023, a 30 min communication session is divided into 60 equal time slots.

Table 1. Summary of LEO satellite mobility environment parameters.

Parameter	Value
User centre position (Latitude, Longitude, Altitude)	(−62°, 50°, 0 m)
Simulation time (minutes)	30
Number of total time slots	60
Satellite altitude (km)	550
Simulation commencement time	05-01-2023 09:30 a.m. (UTC)

summarizes the LEO mobility environment settings, and

Table 2. Summary of DQN framework parameters.

Parameter	Value
Discount factor $\gamma$	0.6
Learning rate	0.001
Initial exploration rate	1.0
Termination exploration rate	0.005
Training batch size	32
Q-target network parameter update step (episodes)	100
DQN iteration count	1000
Loss Function	MSE Loss
Optimizer	Adam

lists the DQN hyperparameters used during training.

4.2. Learning Convergence Analysis

Within the reinforcement learning framework, the learning process achieves convergence when the agent’s policy or value function stabilizes and ceases to exhibit significant temporal variation, indicating the agent has acquired the optimal strategy for the given task. We set 60 users distributed within a range centred at (−62°, 50°, 0 m) with a radius of 10 km, simulating 1000 episodes. The learning convergence diagram for the QoS-constrained K-Means clustering and DQN-based LEO satellite handover strategy is shown in Figure 4. We observe that the mean reward gradually increases from approximately 0.5 as training progresses. After roughly 550 episodes, the mean reward stabilizes around 3.6, signifying that the learning process has converged upon the optimal handover scheme.

4.3. Comparison of Algorithm Performance

After approximately 550 episodes, the mean reward stabilizes around 3.6, indicating that the learning process converges towards the optimal handover scheme.

To comprehensively evaluate the performance of the proposed method, two additional comparison strategies were selected: (1) Maximum Elevation Angle Method: This traditional geometric handover strategy always selects the satellite with the highest elevation angle. As the elevation angle strongly correlates with distance, this method typically provides good signal strength. However, due to the rapid movement of LEO satellites, it may result in frequent handovers. This method represents a greedy strategy that disregards network load and handover costs. (2) Maximum Remaining Service Time: Maintains the current satellite connection as long as its remaining service time meets a minimum threshold requirement. Handover is only triggered when the current satellite is about to become unavailable, selecting the satellite with the longest remaining service time. This strategy aims to minimize handover frequency and ensure connection stability.

To quantitatively evaluate each method’s performance, we selected two key metrics:

• Handover Frequency:

Handover frequency reflects network connection stability. Frequent handover not only increases the risk of communication interruption but also consumes significant network resources. The calculation formula is as follows:

$$F_{ho}={\displaystyle \frac{{\sum }_{u=1}^U{N}_{ho}\left(u\right)}{U\times T_{sim}}}$$

(21)

where $N_{ho}\left(u\right)$ denotes the total number of handovers experienced by user u during the simulation period, U represents the total number of users, and $T_{sim}$ is the simulation duration (in minutes).

• Signaling overhead:

Signaling overhead measures the volume of control messages required to maintain network operation. We calculated this based on the 3GPP standard model, encompassing periodic measurement reports and RRC reconfiguration messages during handover execution. The formula is as follows:

$$S_{overhead}={\displaystyle \frac{N_{msg}^{monitor}+N_{msg}^{ho}}{U\times T_{sim}}}$$

(22)

where $N_{msg}^{monitor}$ denotes the total number of monitoring messages, and $N_{msg}^{ho}$ denotes the total number of handover execution messages.

Simulation experiments were conducted over 1000 rounds with user counts of 60, 70, 80, 90, and 100. Evaluation results from the final 100 rounds were plotted for comparison. The comparison results for handover frequency and signaling overhead are shown in Figure 5 and Figure 6, respectively.

As depicted in Figure 5, the maximum elevation angle method exhibits the highest handover frequency at approximately 0.7 times per minute. This stems from its complete tracking of satellite geometric motion, where the high-speed characteristics of LEO satellites inherently induce elevated natural handover rates. The maximum remaining time method exhibits the lowest handover frequency, approximately 0.38–0.40 times per minute. This stems from its stringent latency mechanism, which only initiates handover when the current satellite is absolutely unavailable, thereby reducing handover frequency to its physical limit. The proposed method’s handover frequency is marginally higher than the maximum remaining time method, at approximately 0.40–0.44 times per minute, yet remains significantly lower than the maximum elevation angle method. This arises because the DQN agent, in pursuing long-term rewards, considers not only handover costs but also comprehensively evaluates QoS metrics such as data rate and latency. To achieve superior communication quality, the agent may proactively initiate handover when necessary, rather than persisting with the current connection until disconnection as the Maximum Residual Time method does. This moderate handover is undertaken to secure higher QoS benefits.

As illustrated in Figure 6, our approach demonstrates overwhelming superiority in signaling overhead. Despite the maximum remaining time method exhibiting the lowest handover frequency, its signaling overhead remains high at approximately 4.7 times per minute, comparable to the maximum elevation angle method (around 5.3 times per minute). This stems from traditional handover strategies requiring each user to independently and periodically report measurement data to the network for handover decisions. This high-volume monitoring signaling constitutes a substantial portion of the signaling overhead as the number of users increases. In contrast, the signaling overhead of the proposed method is only 3.0–3.2 times per minute, representing a reduction of approximately 35–40% compared to the other two methods. The core reason for this significant advantage lies in the proposed cluster head proxy mechanism. Under the clustering mode, only the cluster leader reports status information on behalf of the entire group, eliminating the need for frequent measurement reports from other members. This substantially reduces uplink monitoring signaling volume, achieving signaling compression during the monitoring phase. In summary, while the maximum residual time method achieves the ultimate reduction in handover frequency, it fails to address signaling costs in large-scale user scenarios. The proposed method not only better accommodates user QoS but also achieves substantial signaling cost reduction by sacrificing only a minimal increase in handover frequency. This demonstrates the immense potential of user-clustered hierarchical architectures for enhancing resource efficiency and system scalability in LEO satellite networks.

5. Discussion and Future Directions

This study postulates that, in LEO satellite networks, users located in close geographical proximity typically experience highly correlated channel conditions. Exploiting this property, clustering users with similar features and employing a cooperative handover mechanism can substantially reduce the overall signaling overhead, while only moderately increasing the handover frequency. Although the maximum remaining service time strategy attains the physically minimal handover rate through a stringent decision rule, its signaling cost grows approximately linearly with the number of users in highly concurrent multi-user scenarios, rendering it unsuitable for large-scale access. By contrast, the method proposed in this paper exhibits a slightly higher handover frequency, but this moderate increase in handover is traded for significantly improved long-term QoS gains and more efficient utilization of system resources. Under a 100-user configuration, the signaling overhead is reduced by approximately 35% relative to conventional schemes, indicating that the learning agent successfully acquires an optimal policy that balances individual communication quality against system-level cost control. These results further corroborate the effectiveness and scalability of the hierarchical decision architecture in large-scale user access scenarios.

With the deployment of large-scale LEO constellations, user access density is expected to grow rapidly, and traditional strategies in which each user independently executes handover decisions are likely to encounter severe control-plane signaling congestion. Migrating computational and signaling burdens from the individual-user level to the group level enables the network to support a larger number of users without incurring substantial additional resource consumption, thereby improving overall resource efficiency and reducing operational costs. Despite the demonstrated advantages of the proposed method, several aspects remain open for further refinement. Firstly, in terms of clustering, the periodic clustering mechanism adopted in this study is structurally simple and easy to implement, but may fail to update clusters in a timely manner under highly dynamic conditions such as high user mobility. Future work may investigate clustering schemes with stronger adaptability to rapidly varying network topologies. Secondly, more advanced DRL methods, such as DDPG, can be used when making satellite handover decisions. Finally, the differentiation of service types is not yet explicitly modeled. The current framework assesses QoS scores based solely on users’ state-space features, whereas in practical networks, users are characterized by heterogeneous service requirements. How to appropriately group users carrying different service types and, at the same time, adequately satisfy their diverse QoS demands during the clustering and decision-making process constitutes an important and interesting research problem.

6. Conclusions

This work proposes a QoS-aware, cluster-based handover strategy for large-scale LEO satellite networks in power communication scenarios, leveraging the spatial correlation among geographically proximate users. By combining QoS-constrained K-Means clustering with a hierarchical DQN framework in which cluster leaders make group-wise decisions, the scheme shifts computation and signaling from individual users to user groups. In multi-user scenarios, compared with the traditional independent or maximum remaining service time strategies, it can reduce certain signaling overhead. These results demonstrate that the hierarchical decision structure can effectively balance individual communication quality and system-wide cost, and offers good scalability for dense mega-constellation deployments. The proposed strategy provides a practical and scalable solution for future power grid communications that rely on large-scale LEO constellations, ensuring service quality while significantly reducing control-plane overhead. Future work will focus on more adaptive clustering mechanisms for highly dynamic topologies and explicit modeling of heterogeneous service types to further enhance QoS differentiation and multi-service coordination.