Abstract
This paper proposes a method for recommending parent–child travel destinations and planning travel routes tailored to children of different ages. The method inputs basic information about the attractions (such as ticket prices, geographical locations, opening hours, etc.) into the system database and intelligently recommends suitable attractions based on user-provided data, including the children’s age, travel time, and trip theme. The paper transforms the route planning problem into a Traveling Salesman Problem (TSP) to optimize the travel route further. It presents an improved single-parent genetic algorithm based on sine chaos mapping (SCM-SPGA) to solve and optimize the shortest path for parent–child trips. Experimental results demonstrate that this algorithm has significant advantages in path planning accuracy and efficiency. The method is applied to a tourism dataset of Hainan, providing more personalized and age-appropriate attraction recommendations for tourists planning a parent–child trip to Hainan and optimizing the travel route. The research shows that the proposed method can effectively meet the personalized needs of parent–child travelers, significantly improving the overall travel experience by offering more tailored, efficient, and enjoyable trip-planning solutions.
1. Introduction
In recent years, changes in family education concepts and living standards have led parents to emphasize parent–child interaction and family education. An increasing number of families are choosing parent–child tourism to enhance emotional interaction and communication between parents and children, thus driving the development of the parent–child tourism market. However, despite leveraging big data and artificial intelligence for personalized recommendations, existing travel recommendation systems fail to meet the specific needs of parent–child tourism fully. Additionally, traditional travel path planning algorithms (such as Dijkstra’s and A* algorithms) [1] become trapped in local optima. They suffer from path intersection issues when dealing with complex scenarios and large-scale data. Heuristic and intelligent algorithms (such as genetic algorithms and particle swarm optimization) can alleviate local optimization problems, but they still have limitations in global optimization.
This paper proposes a method for attraction recommendation and path planning designed for parent–child tourism to address these challenges. The method combines children’s age and personality traits with attraction data and utilizes a sine chaotic mapping-based single-parent genetic algorithm (SCM-SPGA) for path optimization. By comprehensively considering user preferences, children’s age and temperament, and dynamic attraction data, the proposed method enhances recommendation accuracy, optimizes path planning, simplifies itineraries, reduces information search and decision-making time, and improves the overall travel experience.
The innovation of this paper lies in the proposal of a multi-factor attraction recommendation model based on children’s age, tailored for the parent–child tourism scenario, and the design of the SCM-SPGA algorithm for path planning. This approach improves the accuracy and applicability of route recommendations. By applying the method to a dataset of Hainan tourist attractions, personalized, age-appropriate attraction recommendations and optimized routes are provided for parent–child tourists in Hainan, meeting diverse needs and enhancing the travel experience.
2. Related Work
Tourist attraction path planning is an essential component of innovative tourism services. It aims to plan the optimal travel route for visitors to maximize their attraction experience or minimize time and cost investment. Researchers have proposed various path-planning algorithms in this field, including classic graph theory algorithms, heuristic algorithms, and AI-based methods.
Classic graph theory algorithms have been widely used in travel path planning. For example, the Dijkstra and A* algorithms are commonly used to find the shortest path and have been successfully applied to route planning for attraction maps [1]. However, with the increasing personalization and complexity of travel demands, traditional path-planning algorithms struggle to meet the diverse needs of tourists. As a result, heuristic and intelligent algorithms have been introduced to optimize path planning. Yu K.M. [2] proposed using ant colony algorithms to address dynamic path planning issues in tourist attractions, with results showing that this method has good adaptability in global path optimization.
In recent years, intelligent optimization algorithms such as genetic algorithms and particle swarm optimization (PSO) have also received widespread attention in tourist attraction path planning. Şehab et al. [3] proposed a genetic algorithm-based path-planning method, which can provide efficient touring paths for visitors under multiple constraints. At the same time, Lu [4] explored the application of PSO in complex attraction path planning, with results indicating that this method has significant advantages in search efficiency and convergence. Additionally, deep learning technologies have made path planning more intelligent. For example, Wang [5] proposed a dynamic path planning model based on deep reinforcement learning, which can adaptively adjust paths according to real-time behaviors and preferences of visitors, thus improving visitor satisfaction.
Path planning cannot always consider only a single factor; it must consider multiple factors. Researchers have applied Multi-Criteria Decision-Making (MCDM) methods to address this issue in path planning, especially in dynamic and complex environments. MCDM methods can simultaneously consider multiple decision criteria such as time, cost, distance, traffic conditions, and weather, thus making more reasonable path choices in complex decision environments. For instance, Wang P. et al. [6] proposed a method based on Complex Intuitionistic Fuzzy information and the Dombi operational law, which considers the priority relationships among multiple decision criteria and integrates optimization in supplier selection in resilient supply chain management. Garg et al. [7] proposed a weighted geometric aggregation operator based on complex intuitionistic fuzzy sets used to solve MCDM problems. This operator handles uncertainty and multi-dimensional data, enhancing multi-decision support systems in complex environments. Zhu et al. [8]. proposed an improved genetic algorithm for robot path planning. The algorithm overcomes the limitations of traditional methods by utilizing population initialization with directional guidance, non-common point crossover, and range mutation operators. It enhances both local and global search capabilities. The algorithm also introduces a simplification operator to remove redundant nodes. It employs a multi-constraint fitness function for path optimization, balancing path length and smoothness to ensure improved energy efficiency for the robot. Such methods also apply to tourist path planning problems, effectively handling the influence of multiple factors in complex environments.
Planning for tourism scenarios. In response to user preferences, Mou [9] proposed a path planning model that combines personalized visitor preferences, significantly improving the accuracy of path recommendations by modeling visitors’ attraction interests based on historical behavior data. Wang Z. et al. [10] combined collaborative filtering algorithms with geographic location data to construct a path-planning model based on user preferences. This model can provide personalized recommendations based on different visitors’ interests and behaviors, significantly improving the accuracy of recommended paths and user satisfaction. For real-time dynamic path updates, Li J. et al. [11] pointed out that the application of the Internet of Things (IoT) and big data provides new possibilities for real-time path planning. By collecting real-time data on factors such as crowd flow and attraction weather conditions, paths can be dynamically adjusted to avoid overcrowding and improve visitor comfort. Ding et al. [12] proposed a real-time path planning system based on IoT mobile devices, which integrates GPS positioning and user preference analysis to provide real-time path optimization suggestions.
In the context of parent–child travel, recent studies have also been increasing. For example, Wei Y. et al. [13] suggested that the recommendations for parent–child travel destinations should emphasize diversity, including natural landscapes, museums, science museums, and theme parks. These attractions can stimulate children’s curiosity and enhance their exploratory abilities. Zhao et al. [14] further pointed out that when selecting parent–child travel attractions, considerations should also include the safety and comfort of children, such as whether there are child-friendly activities and safety measures. Li et al. [15] emphasized that visiting cultural or historical attractions through parent–child travel allows children to receive education in a relaxed and enjoyable atmosphere, thus strengthening their cultural identity and understanding of history.
3. Methods
3.1. Overall Framework for Parent–Child Travel Attraction Recommendation and Path Planning
This paper proposes a systematic framework for parent–child travel attraction recommendation and path planning, which includes modules for user information collection, classification, demand matching, and path recommendation. First, the system collects users’ basic information, such as age group, residence area, travel time, and specific travel preferences, to conduct precise user demand analysis and classification. Next, the system refines the classification based on users’ age groups to provide targeted travel plans for families of different age ranges. Based on this, the system combines attraction information and considers multiple factors to recommend suitable attractions for users. Finally, the paper proposes a single-parent genetic algorithm based on sine chaotic mapping to plan paths for the recommended attractions, aiming to provide the best travel route for users. The effectiveness and efficiency of this algorithm are validated through experiments. The overall framework of this paper is shown in Figure 1.
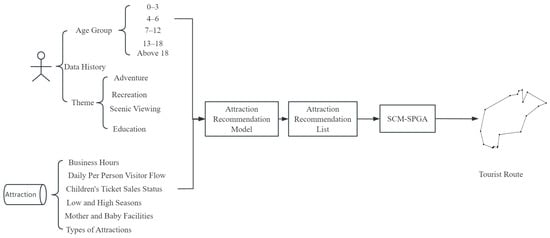
Figure 1.
Overall Framework Diagram.
3.2. Process of Parent–Child Travel Attraction Recommendation
Parent–child tourism, as a special form of tourism, has unique characteristics in terms of both the travel context and the target audience. Therefore, when recommending tourist attractions, it is essential to fully consider the attractions’ attributes and the diverse needs of different users. For the attractions, it is necessary to systematically collect and store key information such as the attraction’s name, theme, facilities, opening hours, and daily visitor flow. At the same time, to address user needs, it is essential to analyze the data provided by users and their historical data within the system to understand their travel habits and preferences. This includes analyzing their past travel experiences, the children’s age groups, and preferences for the trip’s theme. Doing so can create a detailed user profile, providing more personalized and accurate recommendations.
3.2.1. Collecting Attraction Information
In building a parent–child travel recommendation system, collecting attraction information is key to ensuring the system’s effectiveness. To achieve accurate and personalized attraction recommendations, it is necessary to systematically gather and organize detailed data on various tourist attractions.
Firstly, the attraction name is basic information for identifying and searching attractions. An accurate attraction name ensures that users obtain precise search results. Secondly, the theme of the attraction is an important data dimension. Classifying attractions into themes (such as natural landscapes, historical culture, entertainment, and leisure) makes it easier to match user preferences, enhancing the recommendations’ accuracy.
In addition, collecting information related to parent–child travel facilities, such as nursing rooms, children’s play areas, parent–child interactive zones, dining services, and sanitary facilities, is essential. This facility information helps parents assess the suitability of the attraction and, in turn, improves the overall parent–child travel experience.
Opening hours are crucial information, including regular operating hours and special holiday arrangements. Accurate opening hours help users plan their trips efficiently and avoid inconvenience due to missing information. Moreover, daily visitor flow data are critical to optimizing the user experience. By obtaining and analyzing the daily visitor flow at attractions, the system can help users choose less crowded times, thus improving travel comfort.
This information will be collected from various channels, including the official websites of attractions, user review platforms, and cooperating travel operators. The collected data will be systematically stored in a database and regularly updated to ensure the timeliness and accuracy of the recommendation results. Comprehensive collection and maintenance of this information lays the data foundation for the subsequent development and optimization of the recommendation model, ensuring that the system effectively meets the diverse needs of parent–child travelers.
3.2.2. Constructing User Profiles
In constructing user profiles for parent–child travel and considering users’ historical data, we focus on analyzing the impact of children’s age on parent–child travel needs. Based on the personality traits and developmental needs of children in different age groups, we categorize children into several stages and provide detailed analyses for each stage.
For children in the infant stage (0–3 years old) and their families, the primary considerations for travel are safety and convenience. It is recommended that attractions be chosen that are close by and easily accessible, with well-equipped maternal and child facilities such as nursing rooms and stroller rentals. Additionally, the environment should be calm and quiet, avoiding stimulating factors. Suitable attractions include large city parks or family friendly museums that are flat, barrier-free, and meet good hygiene standards.
For children in the early childhood stage (4–6 years old) [16], who are in a key phase of social and emotional development, there is a strong interest in interactive experiences. Families in this stage should prioritize attractions with rich entertainment facilities, such as amusement parks or children’s theme parks. These attractions usually provide age-appropriate play facilities and safe, hygienic, child-friendly services like children’s meals and restrooms.
For children aged 7–12 [17] who are in the cognitive development stage and eager to deepen their understanding of the world through firsthand experience, it is recommended to choose educational attractions such as science museums, planetariums, and botanical gardens, or engage in suitable outdoor activities like easy hiking or beach activities. These activities can satisfy their curiosity while enriching their knowledge in a safe environment.
For teenagers aged 13–18 [18] developing independent thinking and a spirit of adventure, suitable attractions include places that offer exciting activities, such as surfing and skiing, or cultural sites like historical landmarks and museums. These activities help expand their horizons and provide opportunities for self-challenge.
As children enter adulthood, parent–child travel transforms into family interaction and emotional bonding, with travel being more about companionship and sharing quality time. At this stage, it is recommended to choose scenic and tranquil natural attractions, such as lakes or forests, and engage in mild outdoor activities suitable for the whole family, such as hiking or boating, to strengthen emotional connections among family members.
By combining users’ historical information with the characteristics of children’s age groups, the system can offer more personalized recommendations for parent–child travelers, enhancing the family travel experience and satisfaction.
3.2.3. Attraction Recommendation Modeling
In the attraction recommendation modeling section, to ensure that users receive the most suitable parent–child travel experience based on their needs, this article designs a comprehensive recommendation algorithm that selects the most appropriate attractions from the database based on the personal and travel preferences entered by the user.
Users input information such as the child’s age, travel region, travel dates, and preferred travel theme (optional) through the front-end interface. Based on this input, the system recommends attractions through the following steps:
- Suppose the user selects a specific travel theme. In that case, the system will analyze the attraction’s core features, activity types, and facilities, among other dimensions, to assess how well the attraction aligns with the chosen theme. Based on this analysis, the system will calculate a matching score for each attraction concerning the selected theme.
- Based on the user’s input regarding the child’s age and historical data and using the user profiling method described in Section 3.2.2, the system will generate a user profile. The system will then score each attraction according to this profile, rating each attraction based on how well it matches the user’s preferences and needs.
- The system combines ticket sales information, analyzing each attraction’s daily active user count and children’s ticket sales to assess its appeal to family visitors. The daily active user count reflects the overall popularity of the attraction, while the sale of children’s tickets directly indicates its attractiveness to family tourists. The system calculates an attraction’s appeal score by comprehensively analyzing these factors. Additionally, the daily active user count also considers the issue of overcrowding. To avoid recommending attractions with excessive crowds, the system pays special attention to the suitability of visitor flow and provides a comfort score for the visitor flow at each attraction. Through these scores, the system ensures that the recommended attractions offer a rich travel experience while providing a comfortable environment for visitors.
- The system will precisely match the user’s travel time with the opening hours of each attraction to ensure that the recommended attractions are open during the user’s planned visit. Additionally, the system will consider the impact of peak and off-peak seasons on the opening hours of attractions. For example, some attractions may experience high visitor numbers and increased popularity during the peak season, with more activities and entertainment facilities available. In contrast, during the off-peak season, reduced visitor flow may result in limited activities or facilities, and some attractions may adjust their opening hours based on the season. Therefore, the system will calculate a “time suitability” score for each attraction based on its opening hours and seasonal information, helping users filter out attractions where the opening times or the best viewing times fall outside their travel schedule.
- The total score for each attraction t, where t [0, m], and m is the total number of attractions, is calculated using the following formula:where is the weight of the th is the weight of the , and is the th score of the influencing factor, with , , and is the number of influencing factors considered.
- Based on the user’s preset travel time and combining the scores of each attraction with their average visit duration, the system will recommend a suitable list of attractions for the user. To enhance the user’s autonomy, they can also add attractions they are personally interested in or remove those they do not wish to visit from the recommended list, ultimately generating a personalized travel attraction recommendation list.
3.3. Sine Chaos Mapping Improved Path Planning Algorithm for Parent–Child Travel
In path planning, abstracting the problem of attraction route planning as a Traveling Salesman Problem (TSP) model is aimed at solving the complexity of planning routes between attractions using mathematical optimization methods. This approach begins by extracting each attraction’s location information (latitude and longitude) from the database and organizing it into standard (longitude, latitude) coordinates. Then, the Sine Chaos Mapping Single-Parent Genetic Algorithm (SCM-SPGA) proposed in this paper is used to optimize the paths of these attractions, generating the optimal travel route.
3.3.1. Traveling Salesman Problem (TSP) Model
In the TSP model [19,20,21,22], each tourist attraction can be viewed as a node (city). The user wishes to visit multiple attractions in one trip, each being visited exactly once. The routes (paths) between attractions are considered edges connecting the nodes in the TSP model. The weight of each edge represents the distance from one attraction to another. The TSP model aims to find the shortest path that allows the tourist to start from a given starting point, visit all the selected attractions, and return to the starting point. The optimal path must cover all the attractions and minimize the total distance cost. The mathematical model for finding the optimal path among the given attractions is as follows:
where represents the total distance of the path, is the city number, is the distance from the city to city , n is the total number of cities, and the range of i is: 1 ≤ i ≤ n.
3.3.2. Sine Chaotic Mapping Improved Circle Operator
In solving the Traveling Salesman Problem (TSP), a common optimization approach is to reduce the occurrences of crossings in the path and avoid intersections in the cycle except between the starting and ending points. When unnecessary crossings appear, a route can always be found to eliminate them and improve the solution. Eliminating crossings involves continuously removing intersecting edges from a given initial Hamiltonian cycle [23] until no further improvement can be made. However, when solving larger instances of TSP, this method can lead to high computational complexity and significantly reduce solving efficiency. Therefore, a chaotic mapping operator with randomness and diversity must be introduced to determine the improvement region in each iteration. This chaotic operator can cover the solution space as broadly as possible while generating nonlinear and non-periodic sequences to prevent the algorithm from becoming trapped in local optima, thereby enhancing its search capability. Previous studies have explored solutions to such problems, for example, Kou et al. [24] used Logistic–Tent chaotic mapping to demonstrate its randomness and dynamic behavior, thereby increasing the diversity of initial solutions when initializing the population and improving the genetic algorithm’s searchability. However, the output of the Logistic mapping fluctuates dramatically with changes in the control parameter r, especially near boundary values, which can cause instability in the sequence. The Tent mapping, being piecewise linear, exhibits abrupt changes and can lead to large jumps near specific values, potentially interfering with the algorithm.
In contrast, the sine chaotic mapping operator proposed in this paper generates chaotic sequences through the nonlinear behavior of the sine function, offering smoother and more adjustable characteristics. The oscillatory nature of the sine function allows it to generate more complex, non-periodic, stable, and highly random sequences. By combining the sine chaotic mapping operator with the previously mentioned crossing elimination operator, we form the sine chaotic mapping crossing elimination operator, which is applied to the mutation strategy of the single-parent genetic algorithm to optimize the mutated solutions. The specific solving steps of this operator are as follows.
The improvement interval is randomly generated based on the sine chaotic mapping. The improvement interval refers to the gene segment length of each individual in the population during one round of improvement operation. It is taken from the range [1, ]. where is randomly generated according to the following sine chaotic mapping formula:
where t is the current iteration number; Represents the random value generated through the sine chaotic mapping in the th iteration; is the total number of iterations; is the total number of cities; is an initial random number in the range of (0, 1); is a control parameter, usually between 0 and 1.
For the selected improvement interval [1, ], one round of improvement operation is executed. Two adjacent gene loci and are selected, and it is determined whether there exist gene loci and in the subsequent section of the interval that forms a crossover loop with them. The formula for determining this is as follows:
represents the distance between the city and the city. If the above condition is satisfied, it means that these four points form a crossed loop. In this case, the sequence between and will be reversed; otherwise, it remains unchanged.
The above concept indicates that after applying the sine chaotic mapping improvement operator, the new path will not be worse than the original path. Therefore, the sine chaotic mapping improvement operator can theoretically optimize the current individual, playing a role in deep search optimization.
3.3.3. Basic Steps of the Algorithm
The sine mapping operator can improve the mutation operation and enhance the algorithm’s deep optimization ability. This study combines the sine mapping operator with the single-parent genetic algorithm [25,26] (SPGA) to fully leverage its advantages. It eliminates the crossover strategy typically used in traditional genetic algorithms, maximizing the benefits of the mutation operator. In addition, traditional operators such as greedy initialization [27], tabu search [28], and shift-reversal-swap combination operators [29] are incorporated. The final result is the proposed Single-Parent Genetic Algorithm based on Sine Chaotic Mapping (SCM-SPGA). The basic steps of the algorithm are as follows:
- Set the algorithm parameters, including population size NP, number of iterations G, chromosome gene length N, gene encoding method, initialization of the tabu list, and other basic parameters. In the TSP problem in this paper, the gene encoding method is natural number encoding, and the chromosome length is the number of cities in the actual problem.
- Calculate the distance matrix D between the cities in the problem and use the greedy initialization operator to obtain the initial population .
- Enter the iteration loop, checking if the current iteration count exceeds the preset total number of iterations. If it does, exit the loop; if not, continue the loop. Calculate the path length L(V) for each individual in the population according to the formula in Section 3.3.1, where V represents the current individual. The normalized population fitness is then calculated using the following formula:where and represent the fitness and path length of the ith individual, respectively, and maxlen and minlen represent the longest and shortest paths among all individuals in the current population, where , represents a tiny non-negative constant, typically taken as .
The formula calculates the fitness value of each individual in the population. , evaluating the quality of each individual. Normalizing the path length maps the path length to a fitness value between 0 and 1. According to the formula, when approaches , the fitness value approaches 1, indicating that the path quality is better; when approaches , the fitness value approaches 0, indicating that the path quality is poorer. The non-negative small constant is used to prevent division by zero anomalies. Through this fitness function, the individuals in the population can be effectively evaluated and compared, progressively allowing the optimization process to approach the shortest path solution.
- 4.
- According to the fitness values, record the individual with the highest fitness in this iteration, update the optimal solution sequence and path length, and then use the tournament selection [30] strategy to choose high-fitness individuals to form a new population .
- 5.
- Place the population into the mutation genetic loop, apply the shift-reversal-swap combination operator to each individual, and apply the sine chaotic mapping operator after each operation.
- 6.
- After completing one round of the mutation strategy, select the top NP individuals to form a new offspring population . Apply the tabu search strategy to population to obtain the new .
- 7.
- Check whether the current iteration count is less than the maximum iteration count, G. If it is, execute Step 3; otherwise, exit the genetic mutation loop, output the individual with the shortest path in the current population, and plot the curves of the shortest path and fitness changes concerning the number of iterations.
3.3.4. Basic Flow of the Algorithm
The flowchart of the algorithm is shown in Figure 2 below.
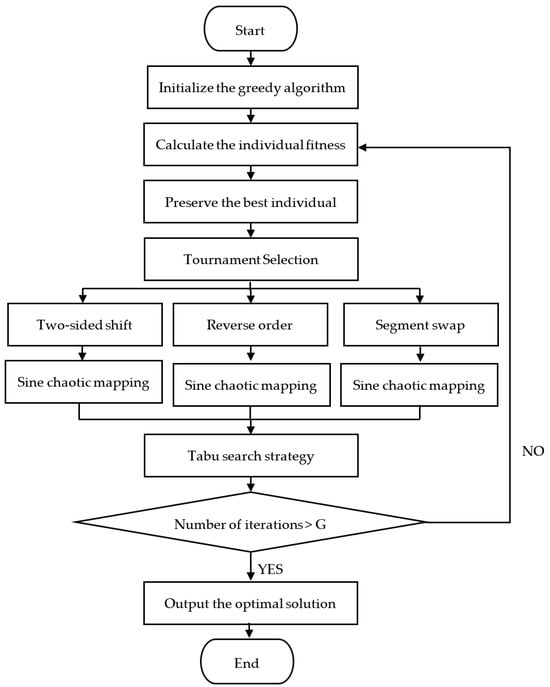
Figure 2.
Algorithm flowchart.
4. Results and Discussion
4.1. Datasets
This study uses the TSPLIB (Traveling Salesman Problem Library) and the Hainan Tourist Attractions Dataset.
TSPLIB is a dataset for the TSP, which is a widely used and publicly available dataset containing multiple TSP instances of various sizes and types. It provides standard test cases for researchers to validate and compare algorithms that solve the TSP. The TSPLIB dataset includes TSP instances ranging from dozens to thousands of cities, offering city coordinates or distance matrices and known optimal solutions as benchmarks. In this paper, the TSPLIB dataset is used to evaluate the performance of the SCM-SPGA.
Additionally, we have obtained the Hainan Tourist Attractions Dataset from the Hainan Provincial Government Data Open Platform. This dataset contains detailed information about 98.
Tourist attractions in Hainan Province. The data includes attraction names, addresses, geographic coordinates (latitude and longitude), attraction ratings, opening and closing hours, peak and off-peak seasons, maximum capacity, and other relevant information. The Hainan Tourist Attractions Dataset provides a specific application scenario for the parent–child attraction recommendation model and the SCM-SPGA proposed in this paper, aiming to help achieve personalized parent–child travel recommendations and route optimization.
4.2. Experiments and Results Analysis
To test the performance of this algorithm, the TSPLIB standard public dataset was selected, and experiments were conducted on a Windows system platform using MATLAB 2023a.
4.2.1. Performance Analysis of the Sine Chaos Mapping Operator
To verify the improvement effect of the sine chaotic mapping operation and explore its role in enhancing the convergence speed and global search capability of the genetic algorithm, this experiment selected four standard datasets from the TSPLIB library (Tsp225, Lin318, U159, and Rat783) for testing. The experiment followed the steps described in Section 3.2.3, with parameters set to G = 200 iterations and NP = 300 population size. Through comparative experiments, the performance of the sine chaotic mapping operator (SCM-SPGA), Logistic–Tent chaotic mapping operator (LTCM-SPGA), and the traditional single-parent genetic algorithm (SPGA) were compared, with the experimental results shown in Figure 3.
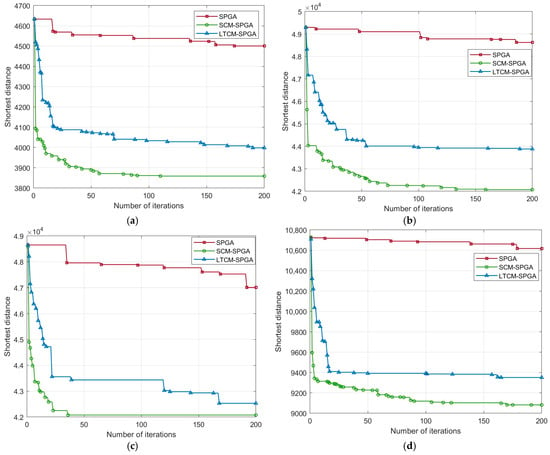
Figure 3.
Comparison of the solving capability of SCM-SPGA, LTCM-SPGA, and SPGA on datasets TSP225, Lin318, U159, and Rat783: Variation of the optimal solution over iterations (the “☐”, “△” and “○” in the figure represent the points where the data changes, including the starting and ending points). (a) Tsp225, (b) Lin318, (c) U159, and (d) Rat783.
From the Figure 3, it can be seen that SCM-SPGA shows significant optimization advantages over SPGA when solving the TSP problem. In comparative experiments on four standard datasets (TSP225, Lin318, U159, and Rat783), SCM-SPGA exhibited faster convergence speed and stronger global search capability. Compared to SPGA, the optimization curve of SCM-SPGA started to descend rapidly from the first iteration, indicating its ability to quickly optimize known optimal solutions, with a significantly faster convergence rate. In the U159 dataset, SCM-SPGA converged after approximately the 36th iteration; in the TSP225 dataset, convergence occurred around the 110th iteration; and in the Lin318 and Rat783 datasets, convergence occurred around the 150th iteration. In contrast, SPGA did not converge in any of the four datasets even after 200 iterations, and the quality of the solutions remained poor. Meanwhile, LTCM-SPGA showed a noticeable improvement in convergence speed and solution ability compared to SPGA in the four datasets, but its convergence and deep solution capabilities were still weaker than those of SCM-SPGA. By comparing the data points indicating changes in the curves, it is evident that SCM-SPGA has significantly more data points than SPGA, indicating that the sine chaotic mapping operator effectively improves the ability of SPGA to escape local optima. The experimental results validate that the sine chaotic mapping-modified circular operator significantly enhances the convergence speed and global optimal solution search capability of the single-parent genetic algorithm.
4.2.2. Analysis of SCM-SPGA’s Solving Ability
To explore the solving ability of the sine chaotic mapping improved loop algorithm, 21 standard TSP test instances were selected for testing. The algorithm parameters were set as follows: NP = 300. When the gene size N < 200, the number of iterations G was set to 200, and when N ≥ 200, the number of iterations G was set to 500. To better assess the performance of the algorithm, each dataset was independently run 10 times, and the following evaluation metrics were selected: the best solution (best), the average value (ave), the best solution error rate (BER), and the mean solution error rate (MER). The formulas for BER and FER are as follows:
where represents the best solution obtained from running the algorithm 10 times, represents the known optimal solution and represents the average solution obtained from running the algorithm 10 times. The experimental results are shown in Table 1 below.

Table 1.
Performance of SCM-SPGA on different datasets.
The results above show that the optimal solutions obtained for the datasets are close to the known optimal solutions. Among them, the results for the datasets Dantzig42, Pr136, Pr144, U159, and Tsp225 are better than the known optimal solutions. The dataset with the maximum BER is Rat783, with an error rate of 1.28%, while the mean BER in the table is −0.01%. The dataset with the maximum MER is Rat783, with an error rate of 1.75%, and the mean MER in the table is 0.18%. The optimal solutions obtained are mostly close to the officially published optimal solutions. This is true for both small datasets, such as Att48, Berlin52, and St70, as well as for medium to large datasets like Kroa100, Lin105, Ch150, Kroa200, Pr299, and P654, where the BER is small and very close to the officially published optimal solutions. The experiment confirms that this paper’s sine chaotic mapping algorithm has a strong global search capability for optimal solutions to the TSP problem. It also demonstrates that the algorithm, which integrates three main operators, effectively solves issues such as slow convergence and becoming trapped in local optima, thus enabling the algorithm to achieve relatively ideal optimal solutions. The solution results for six instances using the sine chaotic mapping improved single-parent genetic algorithm are shown in the following Figure 4.
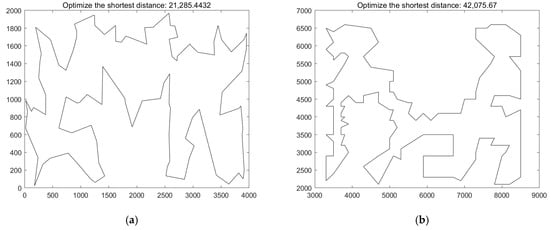
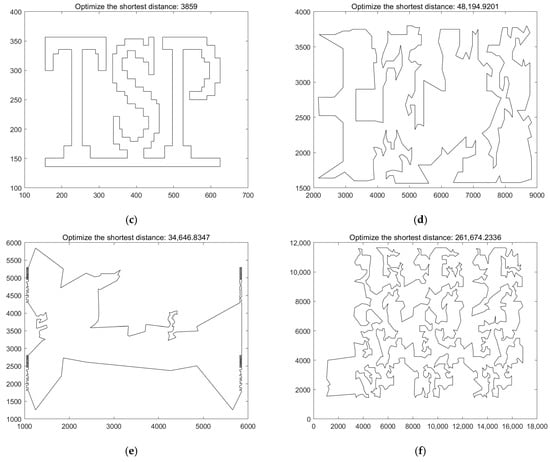
Figure 4.
Solution results of 6 instances solved by SCM-SPGA. (a) Kroa100, (b) U159, (c) Tsp 225, (d) Pr299, (e) p654, and (f) pr1002.
4.2.3. Comparison of SCM-SPGA with Other Algorithms
To further investigate the efficiency of the sine chaotic mapping single-parent genetic algorithm (SCM-SPGA) proposed in this paper, it is compared with the Exploration-Development-Jumping Strategy Single-Parent Genetic Algorithm (EDJS-PGA) [29], the Genetic Algorithm and Multi-Agent Reinforcement Learning (GA + MARL) [31], the Iterative Local Search Algorithm (ILSA) [32], and the Improved Genetic Algorithm (IGA) [33]. The same number of iterations, population size, and identical runtime environment are set, as specified in the parameters in Section 4.2.2. The comparison results are shown in Table 2 below.

Table 2.
Comparison of SCM-SPGA with other algorithms.
The Table 2 shows that the SCM-SPGA proposed in this paper performs excellently on the Tsp225, Pr299, and Lin318 datasets, with the best and average solutions being the best among the five algorithms. In the Kroa100 dataset, although the best solution is slightly worse than the GA + MARL, ILSA, and IGA algorithms, the difference is minimal, only 3.4432, and the average solution is better than ILSA and GA + MARL. In the Rd400 dataset, SCM-SPGA outperforms EDJS-PGA, GA + MARL, and ILSA in both the best and average solutions, although it is slightly worse than IGA. However, while there is a larger gap in the best solution, the difference in the average solution is relatively slight. Overall, through the comparison experiments, it is further verified that the SCM-SPGA proposed in this paper demonstrates good solving ability and robustness.
4.3. Application Case Analysis
The data from 98 tourist attractions in Hainan Province were selected to construct user profiles based on different age groups of children. Combining the recommended attraction methods from Section 3.2, suitable attractions for each age group of family travelers were recommended, ultimately designing an ideal travel route.
To facilitate the description of the tourist attractions, the 98 attractions in Hainan Province were numbered. A partial list of the numbering results is shown in Table 3 below. The complete table is shown in Appendix A.

Table 3.
Partial attraction numbers and attraction names.
Based on the attraction recommendation model and path planning algorithm described in this paper, the iteration parameter for the path planning algorithm was set to G = 100. The resulting travel route map for family trips across different age groups in Hainan Province is shown in Figure 5 below.
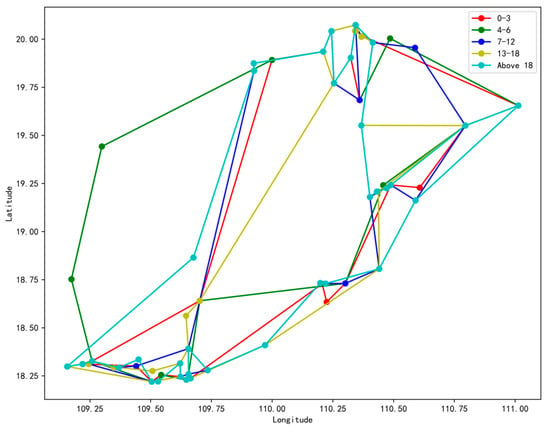
Figure 5.
Travel route planning map for family trips in Hainan Island by age group.
The routes and total travel distances for each age group are shown in Table 4 below. The calculation method for path length is provided in Appendix B.

Table 4.
Travel routes for each age group.
From the attraction numbers corresponding to different age groups in the travel route table and the attraction names in Appendix A, we can see that the recommended list generated by the model generally aligns with the developmental needs of children and family members at various stages.
Most 26 attractions recommended for infants aged 0–3 are well-equipped indoor venues or tranquil, mild outdoor environments. For example, attractions like Haikou Baishamen Park (S29), Wugong Ancestral Temple (S26), and Qionghai South China Sea Museum (S94) typically offer good infrastructure, providing a safe and comfortable environment for parents to care for their children. Attractions such as Qixianling Hot Spring National Forest Park (S25) and Nanshan Cultural Tourism Area (S5) offer peaceful natural landscapes, avoiding excessive noise stimulation, which helps infants emotionally regulate and rest.
For the 19 attractions recommended for children aged 4–6, the provided rich interactive experiences and entertainment facilities fully meet the developmental needs of this age group. For instance, attractions like Yalong Bay Love Fun Beach Resort (S16) and Holiday Beach Tourism Area (S13) offer children’s play areas, swimming pools, and cycling projects that stimulate curiosity and enhance social interaction skills. Attractions such as Rufli Mangrove Bay Wetland Park (S80) and Wanquan River Water Village (S65) offer interactive experiences in natural environments, helping children develop a closer connection with nature.
For the 30 attractions recommended for children aged 7–12, the attractions excel in education and interactivity, effectively promoting children’s cognitive development. Cultural sites like Hainan Provincial Museum (S3) and Haikou Jingrun Pearl Museum (S53) help broaden children’s horizons and spark curiosity through exhibits and interactive projects. Attractions such as Hainan Tropical Wildlife Park (S11) and Xinglong Tropical Botanical Garden (S21) offer children opportunities to learn about natural ecosystems and enhance their awareness of plant and environmental protection. At the same time, attractions like Wuzhizhou Island (S10) and Yalong Bay Tropical Paradise Forest (S19) offer outdoor activities, such as easy hikes and beach activities, fulfilling children’s interest in exploring nature while promoting physical exercise and teamwork.
For the 30 attractions recommended for teenagers aged 13–18, the selected attractions offer a wealth of cultural and adventure activities that effectively foster teenagers’ independent thinking and adventurous spirit. Cultural attractions like the Hainan Provincial Museum (S3) and Binglang Valley Li-Miao Cultural Tourism Area (S9) spark their desire for self-exploration and knowledge through rich historical and cultural displays. Natural attractions such as Hainan Tropical Wildlife Park (S11) and China Leiqiong Haikou Volcanic Cluster World Geopark (S12) allow teenagers to engage with nature, cultivating their scientific interest and observational skills. For adventurous teenagers, attractions like Yalong Bay Love Fun Beach Resort (S16) and Sanya West Island Ocean Cultural Tourism Area (S18) provide water sports and surfing activities to satisfy their need for challenge and excitement.
As teenagers gradually transition into adulthood, family travel shifts toward family companionship and emotional bonding. In the 35 attractions recommended for adults, locations like Nanshan Cultural Tourism Area (S5), Wuzhishan Tropical Rainforest Scenic Area (Wuman Area) (S48), and Hainan Tropical Wildlife Park (S11) offer expansive natural landscapes and easy outdoor activities, suitable for family participation, such as hiking and boating. These activities help enhance communication and emotional connection among family members. Attractions like Wuzhizhou Island (S10) and Yalong Bay Tropical Paradise Forest (S19) provide an ideal environment for family members to enjoy peaceful nature while sharing pleasant moments. These attractions strengthen the bond between family members and provide an ideal environment to enhance emotional connections and create valuable shared memories.
From the above analysis, it can be concluded that the attraction recommendation model proposed in this paper effectively combines the characteristics of different age groups to recommend suitable travel destinations. In practical applications, users can filter or add attractions based on their personal itinerary and travel preferences, optimizing the range of attractions to better meet individualized needs.
The travel route planning map in Figure 5 shows that the SCM-SPGA proposed in this paper effectively generates travel route maps for each age group, with no unnecessary loops or intersections in the routes. This further validates the effectiveness of the chaotic mapping improved circle operator.
5. Managerial Applications
This research and the proposed parent–child travel attraction recommendation and route planning algorithm have significant potential for application in the business sector, particularly in parent–child travel and trip planning. In the parent–child travel domain, by effectively integrating the characteristics of different age groups, the attraction recommendation model can assist travel companies and platforms in offering more personalized travel itineraries. This can enhance customer satisfaction by providing tailor-made travel experiences based on user preferences. The SCM-SPGA route planning algorithm can also be applied to other businesses in the tourism industry to optimize travel routes. Relevant travel companies can adopt this algorithm to reduce unnecessary loops or intersections in travel itineraries, thus improving the customer experience and lowering operational costs.
Moreover, the adaptability of this model and algorithm can extend to other industries requiring personalized services or route optimization, such as logistics and transportation. Businesses can leverage this model to increase customer engagement, streamline service processes, and drive customer-centric decision-making, enhancing overall business efficiency and competitiveness.
6. Conclusions
This paper focuses on the issue of travel route planning for family trips, proposing a family travel route planning algorithm based on sine chaotic mapping improvement. The effectiveness of the various operators within the algorithm and its overall efficiency have been validated from multiple perspectives. Additionally, a family trip-oriented travel route recommendation model has been constructed to assist in optimizing travel route planning. To verify the algorithm’s effectiveness and model in practical applications, they were applied to family trip route planning in Hainan Island, with personalized travel routes designed for families of different age groups.
7. Limitations
Although this paper provides an effective parent–child tourism route planning solution, certain limitations remain. The proposed parent–child tourism route planning method focuses on attraction recommendations based on age-specific characteristics and determining the shortest path without fully considering real-time factors such as weather changes, visitor flow, and traffic conditions. These factors often significantly influence the choice of travel routes in practical applications. For instance, weather changes may lead to adjustments in attraction opening hours, excessive visitor flow may degrade the quality of the attraction experience, and traffic conditions directly affect travel efficiency. The method presented in this paper follows a strategy of first recommending attractions and then planning the route. However, this approach separates attraction recommendation from route planning, failing to effectively integrate the synergistic effects, which may limit the optimization outcomes. Additionally, since we only obtained a dataset of attractions from Hainan Province, and there are specific difficulties in acquiring attraction datasets from other regions, this method has not been extensively validated in other provinces or regions of China.
8. Future Research
Future research could integrate the proposed parent–child tourism route planning method with weather forecasts, IoT devices, and traffic management systems to incorporate real-time data, thereby comprehensively considering the impact of dynamic factors on travel routes. Furthermore, introducing Multi-Criteria Decision Making (MCDM) models and Multi-Objective Optimization algorithms [34] could facilitate the dynamic adjustment of tourism routes based on multiple factors, better addressing the complex needs of parent–child tourism. Additionally, future studies should expand the scope of data collection to include attraction data from other provinces in China and regions worldwide to validate the applicability and effectiveness of the proposed method in broader contexts.
Author Contributions
Conceptualization, Z.-H.W.; Data curation, Z.-H.W.; Funding acquisition, X.-W.L.; Methodology, Z.-H.W.; Resources, X.-W.L.; Supervision, X.-W.L.; Writing—original draft, Z.-H.W.; Writing—review and editing, X.-W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (nos. 71762010) and the Hainan Provincial Natural Science Foundation of China (nos. 621RC1059, 721RC553).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SCM-SPGA | Single-Parent Genetic Algorithm based on Sine Chaos Mapping |
| TSP | Traveling Salesman Problem |
| EDJS-PGA | Exploration-Development-Jumping Strategy Single-Parent Genetic Algorithm |
| GA + MARL | Genetic Algorithm and Multi-Agent Reinforcement Learning |
| ILSA | Iterative Local Search Algorithm |
| IGA | Improved genetic algorithm |
| NA | Not applicable |
| BER | Best solution error rate |
| MER | Mean solution error rate |
| TSPLIB | Traveling Salesman Problem Library |
| MCDM | Multi-Criteria Decision-Making |
| LTCM-SPGA | Logistic–Tent Chaotic Mapping Single-Parent Genetic Algorithm |
| GA | Genetic Algorithm |
Appendix A
The 98 tourist attractions in Hainan Province and their corresponding numbers are shown in the table below:
| Attraction Number | Attraction Names |
| S1 | Hainan Province, Wenchang City, Hainan Tonggu Ridge Scenic Area |
| S2 | Qiongzhong Li and Miao Autonomous County, Baisha Uprising Memorial Park |
| S3 | Hainan Province, Haikou City, Qiongshan District, Hainan Provincial Museum |
| S4 | Hainan Province, Qionghai City, Chunhui Coconut Culture Tourism Park |
| S5 | Nanshan Cultural Tourism Zone |
| S6 | Dadonghai Cave Scenic Area |
| S7 | Hainan Yanoda Rainforest Cultural Tourism Zone |
| S8 | Hainan Fenjiezhou Island Tourist Area |
| S9 | Binglang Valley Li and Miao Culture Tourism Zone |
| S10 | Wuzhizhou Island Tourist Area |
| S11 | Hainan Tropical Wildlife and Botanical Garden |
| S12 | China Leiqiong Haikou Volcano Group Global Geopark |
| S13 | Holiday Beach Tourist Area |
| S14 | Haikou Mission Hills Resort and Tourist Area |
| S15 | Tianya Haijiao Scenic Area |
| S16 | Yalong Bay Aiyuan Beach Resort |
| S17 | Sanya Dadonghai Tourist Area |
| S18 | Sanya West Island Marine Culture Tourist Area |
| S19 | Yalong Bay Tropical Paradise Forest Tourism Area |
| S20 | Bo’ao Asia Forum Permanent Venue Scenic Area |
| S21 | Xinglong Tropical Botanical Garden |
| S22 | Dongshanling Cultural Tourism Zone |
| S23 | Nanwan Monkey Island Ecological Tourism Area |
| S24 | Hainan Wenbi Peak Pangu Culture Tourism Area |
| S25 | Qixianling Hot Springs National Forest Park |
| S26 | Wugong Ancestral Hall |
| S27 | Haikou Qiongzhou Cultural Style Street |
| S28 | Haikou Qilou Snack Style Street |
| S29 | Haikou Baishamen Park |
| S30 | Haikou Qilou Architecture Historical and Cultural Street |
| S31 | Luhuitou Park |
| S32 | Nantian Tropical Botanical Garden |
| S33 | Sanya Phoenix Hill Love and Mountain Oath Scenic Area |
| S34 | Yalong Bay Underwater World |
| S35 | Yalong Bay International Rose Valley |
| S36 | Conch Girl Creative Cultural Park |
| S37 | Sanya Orchid World Cultural Tourism Area |
| S38 | Yetian Ancient Village Scenic Area |
| S39 | Coconut Grand View Garden |
| S40 | Red Detachment of Women Memorial Park |
| S41 | Bo’ao Water City Tourist Area |
| S42 | Bo’ao Oriental Cultural Park |
| S43 | Hainan Baishiling Tourist Scenic Area |
| S44 | Xinglong Tropical Medicinal Plant Garden |
| S45 | Wanning Outlets Cultural Tourism Area |
| S46 | Hainan Danzhou Shihua Water Cave Geological Park |
| S47 | Dongpo Academy |
| S48 | Wuzhishan Tropical Rainforest Scenic Area (Shui Man Area) |
| S49 | Wanjia Fruit Tropical Botanical Garden |
| S50 | Fushan Coffee Culture Style Town Center Area |
| S51 | Hainan Yongqing Cultural Tourism Scenic Area |
| S52 | Hai Rui Tomb |
| S53 | Haikou Jinrun Pearl Museum |
| S54 | Wanquan Lake Tourist Area |
| S55 | Qionghai Duohai Cultural Valley Tourist Area |
| S56 | Hainan Tropical Birds World |
| S57 | Haikou Mangrove Rural Tourism Area |
| S58 | Sanya International Duty-Free City |
| S59 | Sanya Little Fish Hot Springs |
| S60 | Sanya Eternal Love Scenic Area |
| S61 | Wenchang Confucian Temple |
| S62 | Wenchang Aerospace Science and Technology Center |
| S63 | Hainan Tonggu Ridge International Ecological Tourism Area |
| S64 | Song Family Ancestral Home |
| S65 | Wanquan River Water Village |
| S66 | Wanquan River Canyon Drift |
| S67 | Riyue Bay South China Sea Fishing Village Cultural Tourism Area |
| S68 | South National Tropical Rainforest Tour Area |
| S69 | Wuzhishan Red Canyon Scenic Area |
| S70 | Wuzhishan Grand Canyon Scenic Area |
| S71 | Wuzhishan Nature Reserve |
| S72 | Baisha Luoshuai Tianya Post Station |
| S73 | Baisha Lao Zhou San Wellness Resort |
| S74 | Hainan Tropical Botanical Garden |
| S75 | Dalong Scenic Tourism Area |
| S76 | Exiangling Forest Tourism Area |
| S77 | March 3rd Cultural Tourism Area |
| S78 | Yalong Small Guilin Tourism Area |
| S79 | Jinshan Temple |
| S80 | Fuli Red Tree Bay Wetland Park |
| S81 | Jianfengling National Forest Park |
| S82 | Maogong Mountain Scenic Area |
| S83 | Muwei Mountain Red Scenic Area |
| S84 | Nanli Lake |
| S85 | Hainan Changying Global 100 Fantasy Theme Park Scenic Area |
| S86 | Qingshui Bay Tourist Area |
| S87 | Guilinyang National Tropical Agricultural Park Scenic Area |
| S88 | Baisha Uprising Memorial Park |
| S89 | Tunchen Dream Fragrant Mountain Aromatic Culture Park |
| S90 | Ding’an County Yamen Museum |
| S91 | Bawangling |
| S92 | Hainan Province Ding’an County Wanjia Fruit Tropical Botanical Garden |
| S93 | Hainan Province Qionghai City Red Detachment of Women Memorial Park |
| S94 | Hainan Province Qionghai City China (Hainan) South China Sea Museum |
| S95 | Hainan Dongfang Beach Park Tourist Area |
| S96 | Hainan Province Wenchang City Chunguang Coconut Kingdom |
| S97 | Hainan Province Ledong Li Autonomous County Maogong Mountain Ecological Tourism Scenic Area |
| S98 | Bamen Bay Mangrove Scenic Area |
Appendix B
The commonly used formula to calculate the actual distance between two points on Earth is the Haversine Formula. It calculates the spherical distance between two points given their latitude and longitude. The formula is as follows:
The latitudes of the two points are denoted as and , (in radians), while the longitudes are represented by and (in radians). The differences in latitude and longitude are given by and , respectively. R represents the Earth’s radius, typically 6371 km, and d is the distance between the two points.
References
- Sano, V.D.; Sianipar, P.M. Algorithm to find tourism place shortest route: A systematic literature review. J. Theor. Appl. Inf. Technol. 2021, 99, 787–794. [Google Scholar]
- Yu, K.M.; Lee, M.G.; Chi, S.S. Dynamic path planning based on adaptable Ant colony optimization algorithm. In Proceedings of the 2017 Sixth International Conference on Future Generation Communication Technologies (FGCT), Dublin, Ireland, 21–23 August 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Şehab, M.; Turan, M. An enhanced genetic algorithm solution for itinerary recommendation considering various constraints. PeerJ Comput. Sci. 2024, 10, e2340. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Zhou, C. Particle swarm algorithm and its application in tourism route design and optimization. Comput. Intell. Neurosci. 2022, 2022, 6467086. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hu, P. Deep Reinforcement Learning-Based Multi-Object Adaptive Route Planning for Traveling Recommender Systems. IEEE Access 2023, 11, 120258–120269. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, B.; Yu, Y.; Ali, Z.; Almohsen, B. Complex intuitionistic fuzzy DOMBI prioritized aggregation operators and their application for resilient green supplier selection. Facta Univ. Ser. Mech. Eng. 2023, 21, 339–357. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Robust Averaging–Geometric Aggregation Operators for Complex Intuitionistic Fuzzy Sets and Their Applications to MCDM Process. Arab. J. Sci. Eng. 2019, 44, 1–23. [Google Scholar] [CrossRef]
- Zhu, J.; Pan, D. Improved Genetic Algorithm for Solving Robot Path Planning Based on Grid Maps. Mathematics 2024, 12, 4017. [Google Scholar] [CrossRef]
- Mou, N.; Jiang, Q.; Zhang, L.; Niu, J.; Zheng, Y.; Wang, Y.; Yang, T. Personalized tourist route recommendation model with a trajectory understanding via neural networks. Int. J. Digit. Earth 2022, 15, 1738–1759. [Google Scholar] [CrossRef]
- Li, J.; Wang, R.Y. Analysis of spatial-temporal accessibility in Huizhou West Lake scenic spot using big data for smart city. Glob. J. Arts Humanit. Soc. Sci. 2023, 2583, 2034. [Google Scholar]
- Wang, T.Z. Intelligent recommendation model of tourist places based on collaborative filtering and user preferences. Appl. Artif. Intell. 2023, 37, 2203574. [Google Scholar] [CrossRef]
- Ding, M.; Xu, Y. Real-Time Wireless Sensor Network-Assisted Smart Tourism Environment Suitability Assessment for Tourism IoT. J. Sens. 2021, 2021, 8123014. [Google Scholar] [CrossRef]
- Wei, Y.; Park, K.; Liu, H.; Zhao, Y. Influence of Parent-child Travel Push-pull Motivation, Experience on Behavioral Intention. J. Korea Contents Assoc. 2021, 21, 462–473. [Google Scholar] [CrossRef]
- Zhao, Q.; Thongma, W. Current Analysis of Parent-Child Tourism Market for Preschool Children in Nanning City of China. Master’s Thesis, Maejo University, Chiang Mai, Thailand, 2022. [Google Scholar]
- Li, Z.Z.; Yang, Y.; Zhang, X. Family travel as an educational experience: Revealing multi-level Parents’ perceived value through a family systems approach. Tour. Manag. Perspect. 2024, 53, 101301. [Google Scholar] [CrossRef]
- Rojas-de-Gracia, M.-M. Who Influences Family Tourism Decisions? Incorporating Children’s Perceptions. Serv. Bus. 2025, 19, 8. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Okumus, F.; Zhang, J.Z.; Liu, D.Y.; Qi, J. Understanding the Antecedents of Adolescent Family Tourism Motivation: The Role of Adolescents’ Self-Differentiation and Parent-Child Relationships. J. Travel Res. 2024; in press. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, L. Traveling Food Tourism with Children Industry: Motivation, Involvement, Experience Value and Visit Intention. Int. Food Agribus. Manag. Rev. 2024, 1, 1–19. [Google Scholar] [CrossRef]
- Pop, P.C.; Cosma, O.; Sabo, C.; Sitar, C.P. A Comprehensive Survey on the Generalized Traveling Salesman Problem. Eur. J. Oper. Res. 2024, 314, 819–835. [Google Scholar] [CrossRef]
- Traub, V.; Vygen, J.; Zenklusen, R. Reducing Path TSP to TSP. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing 2020, Chicago, IL, USA, 22–26 June 2020; pp. 14–27. [Google Scholar] [CrossRef]
- Cheng, H.; Zheng, H.; Cong, Y.; Jiang, W.; Pu, S. Select and Optimize: Learning to Solve Large-Scale TSP Instances. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 25–27 April 2023; pp. 1219–1231. [Google Scholar] [CrossRef]
- Gomes, D.E.; Iglésias, M.I.D.; Proença, A.P.; Lima, T.M.; Gaspar, P.D. Applying a Genetic Algorithm to a m-TSP: Case Study of a Decision Support System for Optimizing a Beverage Logistics Vehicles Routing Problem. Electronics 2021, 10, 2298. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A. Traffic Improvement in Manhattan Road Networks With the Use of Parallel Hybrid Biobjective Genetic Algorithm. IEEE Veh. Technol. Soc. Sect. 2024, 12, 19532–19547. [Google Scholar] [CrossRef]
- Kou, L.; Wang, Y.; Zhang, F.; Yuan, Q.; Wang, Z.; Wen, J.; Ke, W. A Chaotic Simulated Annealing Genetic Algorithm with Asymmetric Time for Offshore Wind Farm Inspection Path Planning. Int. J. Bio-Inspired Comput. 2025, 25, 69–78. [Google Scholar] [CrossRef]
- Zainuddin, F.A.; Abd Samad, M.F.; Jamaluddin, H.; Azad, A.K.M. A Novel Single Parent Mating Technique in Genetic Algorithm for Discrete-Time System Identification. J. Adv. Res. Appl. Sci. Eng. Technol. 2024, 42, 49–57. [Google Scholar] [CrossRef]
- Kralev, V.; Kraleva, R. Combining Genetic Algorithm with Local Search Method in Solving Optimization Problems. Electronics 2024, 13, 4126. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, T. Travel route planning based on genetic algorithm and greedy algorithm. Sci. J. Technol. 2025, 7, 125–134. [Google Scholar] [CrossRef]
- Ban, H.; Pham, H.-D. A Multi-Population Multi-Tasking Tabu Search with Variable Neighborhood Search Algorithm to Solve Post-Disaster Clustered Repairman Problem with Priorities. Appl. Soft Comput. 2024, 170, 112655. [Google Scholar] [CrossRef]
- Chen, J.; Tan, D. Partheno-genetic algorithm based on explore-develop-jump strategy for solving traveling salesman problem. Comput. Appl. Res. 2023, 40, 1375–1384. [Google Scholar] [CrossRef]
- Xia, D.; Wu, X.; Yan, M.; Xiong, C. An Adaptive Stochastic Ranking-Based Tournament Selection Method for Differential Evolution. J. Supercomput. 2024, 80, 20–49. [Google Scholar] [CrossRef]
- Alipour, M.M.; Razavi, S.N.; Feizi Derakhshi, M.R.; Balafar, M.A. A hybrid algorithm using a genetic algorithm and multiagent reinforcement learning heuristic to solve the traveling salesman problem. Neural Comput. Appl. 2017, 28, 3273–3286. [Google Scholar] [CrossRef]
- Ruoyu, W.; Yongquan, C. Solution construction methods based on reinforcement learning for the traveling salesman problem. Comput. Eng. 2020, 46, 293–300. [Google Scholar] [CrossRef]
- Xu, W.; Wei, C.; Zhang, G.; Zhao, C.; Xiong, J. Solving the traveling salesman problem using a genetic algorithm based on K-nearest neighborhood search. J. Kunming Univ. Sci. Technol. 2022, 47, 139–144. [Google Scholar] [CrossRef]
- Chen, G.; Gao, J.; Chen, D. Research on Vehicle Routing Problem with Time Windows Based on Improved Genetic Algorithm and Ant Colony Algorithm. Electronics 2025, 14, 647. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).