Abstract
Multi-signature applications allow multiple signers to collaboratively generate a single signature on the same message, which is widely applied in blockchain to reduce the percentage of signatures in blocks and improve the throughput of transactions. The k-sum attacks are one of the major challenges in designing secure multi-signature schemes. In this work, we address k-sum attacks from a novel angle by defining a Public Third Party (PTP), which is an automatic process that can be verifiable by the public and restricts the signing phase from continuing until receiving commitments from all signers. Further, a two-round multi-signature scheme HEMS with PTP is proposed, which is secure based on the discrete logarithm assumption in the random oracle model. As each signer communicates directly with the PTP instead of other co-signers, the total amount of communication is significantly reduced. In addition, as PTP participates in the computation of the aggregation and signing algorithms, the computation cost left for each signer and verifier remains the same as the basis Schnorr signature. To the best of our knowledge, this is the high efficiency that a Schnorr-based multi-signature scheme can achieve. Further, HEMS is applied in a blockchain platform, e.g., Fabric, to improve transaction efficiency.
1. Introduction
Digital signature is used extensively in blockchain to guarantee the integrity and non-repudiation of transactions. However, when multiple parties are involved in an approval process, verifying and storing individual signatures from each party is costly. Multi-signature schemes, which can jointly produce a single signature on the same message among a group of signers, can play an important role in shrinking the size of blocks and extending blockchain ability. For instance, Maxwell et al. [1] suggested using multi-signatures to shrink the transaction data associated with Bitcoin Multisig addresses. Xiao et al. [2] deployed a multi-signature scheme in Fabric to reduce the size of transactions and improve the efficiency of endorsement and ledger updates. Drijvers et al. [3] proposed a forward-secure multi-signature scheme, which is applied to Proof-of-Stake Consensus in blockchain and yields notable savings in storage, bandwidth, and block verification time.
Based on the different difficulty assumptions and basis signature schemes, there are three major categories of multi-signature schemes, such as RSA-based, BLS-based, and Schnorr-based multi-signature schemes. When one uses a 2048-bit modulus, the corresponding signature lengths for RSA, BLS, and Schnorr-based schemes are 2048 bits, 224 bits, and 448 bits, respectively. Although the BLS-based scheme achieves the smallest signature length, its high computational cost can not be overlooked. Due to their advantages in balancing the computational complexity and required storage space, Schnorr-based multi-signature schemes have attracted extensive research attention recently.
However, the earlier Schnorr-based multi-signature schemes [4] are vulnerable to rogue-key attacks [5]. In such attacks, an adversary chooses its public key as a function of that of honest users, and forges multi-signatures easily. To resist rogue-key attacks, Bellare et al. [5] first presented a multi-signature scheme BN in the plain public-key model. After that, Maxwell et al. [1] proposed another multi-signature scheme Musig, where the joint signature could be verified exactly as a standard Schnorr signature due to key aggregation. The shortage of BN and MuSig is that three-round interactions are needed during the signing phase, increasing the communication overhead. Bagherzandi et al. [6] proposed an improved scheme BCJ and reduced the signing protocol rounds to two by using homomorphic trapdoor commitments, and Maxwell et al. [1] proposed another two-round MuSig. However, in 2019, Drijvers et al. [7] showed that none of the existing two-round multi-signature schemes, including BCJ [6] and MuSig [1], can be proved secure under standard assumptions for the k-sum problem. Based on the k-sum problem, if a signer can choose their commitment according to the other co-signers commitments, they can forge a signature, passing the verification successfully.
Therefore, how to resist k-sum attacks has recently become one focus of Schnorr-based multi-signature schemes. Up to now, there are several schemes to resist k-sum attacks, including the three-round schemes, BN [5] and MuSig [1], and two-round schemes, mBCJ [7] and MuSig2 [8]. Their major working mechanisms are briefly described as follows.
- 1.
- An additional preliminary round interaction with commitment hash. This mechanism is adopted by BN and MuSig, where three-round interactions are required in the signing protocol. Compared with the later two-round schemes, a preliminary round is needed to prevent a signer from changing their commitment based on the others’ commitments. Specifically, signer i submits a hash value of their commitment (i.e., ), before they transmit this commitment to other co-signers. In this case, the commitment of each signer is independent.
- 2.
- Random commitment parameters. Adopted by mBCJ, this mechanism has its commitment parameters determined by the output of a random oracle applied to the message, thus parameters in sign query phase and sign forge phase are different. In this case, the forged signature based on the k-sum problem cannot pass the verification.
- 3.
- Commitment vector. This method was first used in MuSig2, where a signer i uses a commitment vector instead of a single commitment , and defines a linear combination as their commitment, where coefficients are the hash of vector . As the commitment of each signer is related to the commitment vector of all signers, it is impossible to generate commitment according to other co-signers’ commitment vectors.
In general, in order to resist k-sum attacks, there are additional communication or computation costs involved, preventing any signer from choosing their commitment based on that of other cosigners. In fact, as long as the last signer, who is the last one to submit the commitment, is always honest, k-sum attacks can be prevented. But this assumption that the last signer is honest is unreasonable. If we could find an honest party or program, which takes the final step of generating the commitment, the security issue of k-sum attacks would be solved without additional communication or computation cost. However, we need to assume PTP is honest in both theoretical and practical applications. In the fields of cryptology and its applications, we often assume that there is a Trusted Third Party (TTP). But the assumption that everyone can trust the same party is too strong and typically leads to a centralized solution. Inspired by smart contracts on blockchains, which can be distributed on peer-to-peer networks, are publicly verifiable, and executed automatically, we define a new concept, Public Third Party (PTP), as follows.
Definition 1
(Public Third Party). A Public Third Party (PTP) is an honest party or a piece of program whose actions or execution steps can be (1) fully open and verified by the public and (2) automatically run without external interruptions.
In this paper, we proposed to leverage a smart contract as a PTP to complete the last step of generating the joint commitment. Please note that, different from a TTP, which relies on a strong assumption of everyone’s trust, a PTP earns its trust through its transparency, publicly verifiability, and automatic execution. Furthermore, the contribution of PTP in reducing communication overhead and simplifying the signature process is difficult to achieve with traditional TTP solutions.
In summary, we propose a new Schnorr-based multi-signature scheme, by introducing PTP instead of additional communication or computation consumption to defend against k-sum attacks. The proposed scheme can be completed in two rounds, and achieves almost the same computational complexity as the basis Schnorr signature. Therefore, we name it a High Efficient Multi-Signature (HEMS). Our major contributions are listed as follows.
- Smart contracts are leveraged as a Public Third Party (PTP) program that contributes to resisting k-sum attacks in the proposed scheme HEMS. After all signers send their own commitment to PTP, PTP generates a timestamp t. As PTP is public, the timestamp t is difficult to manipulate or estimate by an adversary. As joint commitment is generated based on and t, a malicious signer cannot generate a valid commitment with the k-sum problem.
- Security reduction of the proposed scheme HEMS is proved. Let the timestamp generated by PTP be t. By programming the random oracle and computing , the challenger can know the joint commitment before the adversary. Thus, our scheme HEMS is proved secure under the discrete logarithm assumption in the random oracle model.
- HEMS reduces the number of communication connections required. Although mBCJ and MuSig2 are also two-round, each signer needs to communicate with the other signers during the signing process involving n signers. Therefore, they require a total of communication connections per semi-round. While, HEMS introduces a PTP, signers only need to establish communication with the PTP, which only requires n communication connections per semi-round, significantly less than that of other schemes.
- The proposed HEMS scheme can achieve a low computation cost. Because each signer only needs to know the group element corresponding to the timestamp, the computation cost of the signing process can be reduced to 1exp. For the computational cost of the verification, like most schemes, HEMS only needs two exponentiation operations. For each signer and verifier, the computation cost of HEMS is consistent with that of the basis Schnorr signature scheme.
- We apply the proposed HEMS scheme in Fabric, one of the most popular blockchain platforms, for endorsement, and propose a modified Fabric transaction protocol mFabric, which can significantly improve the transaction efficiency. As HEMS aggregates multiple signatures into one joint signature, the proportion of signatures in a transaction gradually decreases. Meanwhile, the verification time for a block is shortened significantly.
2. Related Work
2.1. Schemes Against Rogue Key Attacks
Many existing studies consider the threat of rogue key attacks when proposing multi-signature schemes. Since this kind of attack is feasible both in theory and in practice, existing multi-signature schemes take on different measures to deal with this kind of attack.
Typically, there are two models to prevent rogue key attacks. One is the Key Verification (KV) model used in [6,7,9], where each public key is accompanied by a self-signed proof, which is essentially a Schnorr signature. The other is the Plain Public-Key (PPK) model proposed in BN [5], where the only requirement is that each signer must have a public key. This solution is to make each signer use a distinct challenge when computing the partial signature . Ref. [10] also adopted this idea, except that the challenge is obtained by a double hash. Later, Refs. [1,8,11] made a further improvement. They split challenge into and c, so that the verification overhead is constant and independent of the number of signers.
Both methods have their pros and cons. For schemes adopting the KV model, the aggregation of public keys is a simple product of all public keys. However, each public key has a certificate, which is equivalent to increasing the length of the public key. For schemes adopting the PPK model, the overhead to compute an aggregated public key is still linear to the number of signers.
2.2. Schemes Against k-Sum Attacks
In 2019, Drijvers et al. [7] introduced sub-exponential attacks that apply to several multi-signature schemes [6,9,10]. In such attacks, adversary performing concurrent signing queries can create a forgery in time and space, where p is the order of the group. In each signing query, the adversary chooses their commitment after the other co-signers. This results in the hash on the product of commitments in queries being equal to the sum of hashes on the commitments in query based on the k-sum problem. Therefore, it is possible to forge a multi-signature on any message.
As mentioned earlier, how to defend against this kind of attack has become a focus recently. MuSig [1] is immune to these attacks because it has three-round interactions in the signing phase. In the first preliminary round, each signer has to submit the hash on their chosen commitment, which forces each signer to determine their own commitment before learning other commitments.
Next, Drijvers et al. [7] proved that none of the existing two-round multi-signature schemes could be proved secure under standard assumptions and presented a variant of the BCJ scheme called mBCJ. In mBCJ, commitment parameters rely on the message and, thus, can be different in the sign query phase and the sign forge phase. Hence, mBCJ is the first two-round multi-signature scheme, which is proved to be secure based on the Discrete Logarithm (DL) assumption.
Nick et al. [12] proposed a special multi-signature scheme MuSig-DN to resist this attack, which uses a pseudo-random function to generate random numbers deterministically. The adversary needs to select a suitable random number from a huge random number space to successfully carry out the attack. Therefore, MuSig-DN, which is the first Schnorr multi-signature scheme with deterministic signing, is immune to attacks.
Recently, based on a stronger One-More Discrete Logarithm (OMDL) assumption, Nick et al. [8] presented a variant of the MuSig scheme called MuSig2, which is another secure two-round scheme. It uses commitment vectors instead of a single commitment, and each signer generates the commitment related to all other signer commitment vectors, which can effectively prevent k-sum attacks. Applying a similar idea as MuSig2, a two-round multi-signature scheme via delinearized witness DWMS [11] was proposed, which is secure in the Algebraic Group Model (AGM) and the Random Oracle Model (ROM) under the assumption of the difficulty of the one-more discrete logarithm problem and the 2-entwined sum problem. Lee et al. [13] used a similar method of commitment vector to resist k-sum attacks and propose an efficient two-round scheme based on Okamoto signatures. As analyzed in Ref. [13], it is less efficient compared with most Schnorr-based schemes in terms of both communications and computations.
2.3. Other Multi-Signature Schemes
In addition to Schnorr-based multi-signature schemes, there are BLS-based and lattice-based multi-signature schemes. BLS-based multi-signature schemes only require a designated signer to collect the signatures of all signing participants and do not require multiple interactions, which is very suitable for distributed application scenarios. Boneh et al. [14] construct a pairing-based multi-signature scheme by replacing the Schnorr signature in [1] with a BLS signature, which is also suitable for Bitcoin. Drijvers et al. [3] proposes a forward-secure BLS-based multi-signature, which is designed to deal with the problem of posterior corruptions in PoS Blockchain. Recently, Pan et al. [15] provided the first multi-signature scheme for ECDSA.
Considering attacks based on quantum computing, some lattice-based multi-signature schemes are proposed. Kansal et al. [16] proposed a lattice-based multi-signature scheme that supports public key aggregation. In [17], simultaneous multi-signature and sequential multi-signature schemes based on lattices are proposed to resist quantum attacks using the difficulty of average-case Short Integer Solution (SIS) problem.
3. Preliminaries
3.1. Notation and Difficulty Problem
Notation 1.
For a non-empty set S, means to select an element uniformly and randomly from the set and assign it to s. We let denote the group description, where is a cyclic group of order p, and g is the generator of . Let λ be the security parameter and bit length of p. For a signer i, assume the pair of public key and private key are denoted by , where . Assume there are n signers participating in the multi-signatures. We define three cryptographic hash functions , , .
Definition 2
(Discrete Log Problem). For a group description , we define of an adversary as
where the probability is taken over the random draw of X and random coins of . -breaks the discrete log problem if it runs in time at most t with at least ε. The discrete log is -hard if no such adversary exists.
3.2. Generalized Forking Lemma
Our security proof requires the Generalized Forking Lemma [5], which extends Pointcheval and Stern’s Forking Lemma [18]. The proof of this lemma can be seen in [5].
Lemma 1.
Fix an integer . Let be an algorithm which takes as input inp and randomness , where ρ is ’s random coins and are random values from , and returns the failure symbol or a pair (i,out), where and out is the side output. The accepting probability of , denoted as acc (), is defined as the probability, over the random selection of inp, , and the random coins ρ of , that returns a non-⊥ output. The forking algorithm associated to is a randomized algorithm that takes input inp, as described in Algorithm 1. Let frk be the probability that returns a non-⊥ output. Then,
| Algorithm 1 (inp) |
|
3.3. Rogue Key Attacks
In rogue key attacks, the adversary is one of the involved signers denoted by n who, for the vulnerability in the key setup phase, chooses and uses a function of the honest signer’s public key as its public key, i.e.,
With this specially chosen public key, the adversary can arbitrarily forge the signature, since the aggregated secret key corresponding to the aggregated public key is known to the adversary.
3.4. k-Sum Attacks
We further elaborate the attack to the multi-signature situation based on the k-sum problem [7]. For simplicity, we consider the case where only two signers participate. The honest signer owns the keys , and the adversary owns the keys . The adversary concurrently opens signing oracle queries with the honest signer on arbitrary message m. Let j denote an index of the signing oracle query. According to [7], the adversary will perform the following steps:
- 1.
- For each query , the adversary retrieves the public key and a commitment from the honest signer. Then, it creates k empty lists of equal size , which will be filled with random elements next.
- 2.
- For each list , the adversary picks and computes as its commitment against . It continues to compute and add to list . The adversary repeats this process times for each list .
- 3.
- For list , the adversary picks messages randomly, and adds to list . It repeats this process until has elements.
- 4.
- The adversary can obtain specific from list to solve the k-sum problem in terms of Wagner’s algorithm [19], namelyNext, it finds the as its commitment for all corresponding to . Then, it responds to the honest signer, which are exactly corresponding to signing oracle queries.
- 5.
- The adversary receives partial signatures from the honest signer, where . Now, all signing oracle queries come to an end. The adversary obtains the message corresponding to (also called ) for which a forgery will be generated.
- 6.
- Finally, the adversary produces a forgery , where .
Therefore, based on the k-sum problem, the adversary performing concurrent signing queries can create a forgery in time and space, where p is the order of the group.
An important premise for this attack to be effective is that the adversary knows the of all other co-signers before submitting its own R. Therefore, in the proposed scheme, we address this attack by allowing the adversary to compute c only if it submits its R, which deters the adversary’s behavior from step (2).
4. A Multi-Signature Scheme with Public Third Party
In order to defend against k-sum attacks, different from the existing schemes involving extra communication or computation costs, we propose to introduce a Public Third Party (PTP) (see Definition 1) to take the final step of generating commitment, which is the least costly way. The definition and construction of the proposed multi-signature with PTP are presented in this section.
4.1. The Definition
The multi-signature scheme with the security parameter consists of the following algorithms.
- ParamGen() : It generates the parameters of the signature scheme with respect to the security parameter .
- KeyGen: For any signer i, it generates a public/private key pair with the input .
- Agg: Input the public keys of n signers, and output the aggregated public key .
- Sign: It is an interactive algorithm that runs between n signers with private keys and a PTP in order to sign a common message , where is the message space. is the signature output.
- Verify: It verifies whether the signature is signed by the parties with the aggregated public key for the message m.
4.2. The Proposed Scheme
The specific multi-signature scheme is as follows:
- Parameter Generation (ParamGen()). Given security parameter , ParamGen generates a group with prime p order and a generator . In the end, it outputs .
- Key Generation (KeyGen). Each signer i randomly generates a secret private key and calculates the corresponding public key .
- Aggregation (Agg): Suppose are the public keys of n signers. For , calculatewhere . Then, compute the aggregated public key : , which is open to the public.
- Signing (Sign). As shown in Figure 1, the signers will interact with a PTP in two rounds.
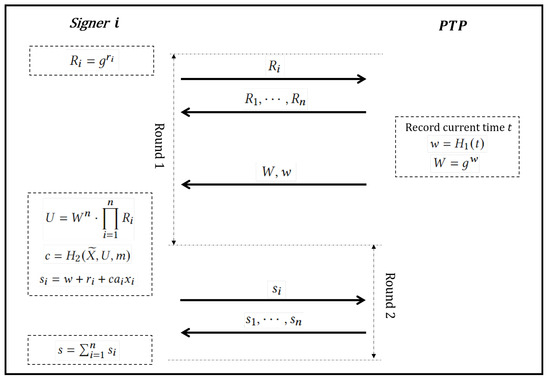 Figure 1. The signing process.
Figure 1. The signing process.
- Round 1:First, signer i generates a random number , computes their commitment , and sends to PTP.Next, PTP waits to receive all commitments from signers, and forwards them to all signers.Last, PTP records the timestamp t of the current time, makes a hash , and computes . PTP returns w and W to all signers.As PTP is automatic and public, the commitments and timestamp t are public and immutable.
- Round 2:Upon reception of , w and W from PTP, any signer i continues to compute the joint commitmentand the partial signaturewhere , and sends to PTP.After collecting all partial signatures , PTP sends them to all signers.Finally, every signer can compute as the joint signature. The output of this algorithm is .
- Verification (Verify). Given the aggregated public key , a message m and a signature , the verifier calculatesand outputs 1 if
5. Security Proof
Proof Sketch With reference to [1], we also use the forking lemma twice to prove security. Concretely, we first construct an algorithm , which runs the forger, simulating and uniformly at random, and the signature oracle by programming , and returns a forgery together with extra information about the forger execution. Later, we construct an algorithm , which runs the forking algorithm , obtaining two forgeries, from which the discrete algorithm of the aggregated public key can be extracted. Then, we construct an algorithm , which runs the forking algorithm , solving the DL problem.
5.1. Security Definition
As there is a PTP that accepts signers and verifiers in multi-signature models, this security model has made some modifications on the basis of [5].
The security model requires the multi-signature to be unforgeable with the participation of at least one honest signer and a PTP, which cannot be corrupted by the adversary. It is important to note that we assume that the PTP is publicly verifiable, which is different from the assumption that there is a trusted third party. Without loss of generality, we assume that there is only one honest signer, and that the adversary corrupts all other signers (excluding PTP) and can choose their public keys arbitrarily. The adversary can concurrently participate in any number of signature processes with an honest signer before returning a forged signature.
Next, we formally define the security game involving an adversary (forger) :
- Randomly generate a pair containing a public key and secret key , for the honest signer, using the public key as the input for the forger .
- The adversary can participate in any number of signing processes with the honest signer. Formally, the adversary can take as input a set of public keys , where occurs at least once and a message m to access a signing oracle. This oracle implements the signature algorithm corresponding to the honest signer’s , while the adversary plays the roles of the other corrupted signers in .
- At the end, the adversary has to output a set of public keys , a message m, and a signature .
The adversary wins the game if , the forged signature is valid, and never engages signature protocol for the public key set and the message m.
5.2. Security Analysis
Our general idea is that assuming that there is a forger who can forge signatures for the above multi-signature scheme, by applying the forking lemma twice, the discrete logarithm problem can be solved with non-negligible probability. We use to denote that the forger runs in time for up to t, makes at most signature queries, and at most hash queries, with a probability of success of at least , and has at most N signers in the query process.
Theorem 1.
Assume that there exists a ()-forger against the multi-signature scheme with group parameter and hash functions modeled as random oracles. is the cyclic group generated by the base point G on the secp256k1 elliptic curve. The functions and all denote the SHA-256 hash function. Then, there exists an algorithm that -solves the DL problem for , with , where is the time of an exponentiation in and
Proof of Theorem 1.
We construct an algorithm , which simulates random oracles , , and using three empty tables , , and , respectively, and initializes three counters ctr0, ctr1, and ctr2 as zero. Then, algorithm picks random coins and runs the forger to input the public key , replying to hash queries and signing queries from the forger as follows.
- Hash query : (Assume and .) If has not been defined, then increments ctr0 by one, randomly assigns for all and assigns . Then, it returns .
- Hash query : If is undefined, then increases ctr1 and assigns . Then, it returns .
- Hash query : If has not been defined, then increments ctr2 by one and assigns . Then, it returns .
- Signature query : If , then returns ⊥ to the forger . Otherwise, it parses as . If is undefined, it makes an “internal” query to , which will define for each , , sets , and computes . Then, increments ctr2, lets , , draws , and computes where will be assigned to the value of the next undefined query to later. sends to PTP. Next, waits for sent by PTP. After collects , it computes . If has already been defined, sets = true and returns ⊥. Otherwise, it sets . Note that PTP has made query to but not yet sent t and forger does not know t at this time. Then, waits to receive t from PTP and compares w with . If w is not equal to , sets = true and returns ⊥. Otherwise, sends to PTP, completing the signature query.
If gives a forged signature for a public keys multiset , where and a message m, verifies that this is a valid forgery, and stops if it is invalid. If the forgery is valid, takes extra steps. Let be the value of ctr0 when is assigned and be the value of ctr2 when is assigned. If the assignment occurs before the assignment , sets BadOrder = true and returns ⊥. If there exists another multiset of public keys such that the aggregated public key (corresponding to ) is equal to (corresponding to ), sets PKColl = true and returns ⊥. Otherwise, it outputs , where vector a = (). By construction, for each i such that , and the validity of the forgery implies
After analysis, the following conclusions can be drawn.
Lemma 2.
Assume that there exists a ()-forger in the random oracle model against our multi-signature scheme with group parameter () and let . Then, there exists an algorithm that takes as input a uniformly random group element from and uniformly random scalars , and , and with successful probability at least
outputs where , is a multiset of public keys such that ,a= is a tuple of scalars such that for any i such that .
Next, we use to construct an algorithm , which will rewind . Algorithm runs with , as defined in Lemma 2. At this time, inp refers to , and . () play the role of (). plays the role of i. play the role of out.
Here, we use the forking lemma for the first time to draw the following conclusions.
Lemma 3.
Assume that there exists a ()-forger in the random oracle model against the multi-signature scheme with group parameters , and let . Then, there exists an algorithm that takes as input a uniformly random group element and uniformly random scalars , and, accepting probability, at least
outputs a tuple () where , = is a multiset of public keys such that , a = () is a tuple of scalars such that for any i such that , and is the discrete logarithm of in base g.
We proceed to construct an algorithm that rewinds algorithm . We let . Algorithm runs with , as defined in Lemma 3. At this time, and play the role of inp. () play the role of (). plays the role of i. plays the role of out.
Finally, we use the forking lemma for the second time, leading to Theorem 1. □
ROM idealizes hash functions as a publicly accessible random oracle for all parties. This significantly simplifies the modular reduction for the Fiat–Shamir [20] transformation and concurrent security, enabling a compact and efficient security proof for a two-round communication Schnorr multi-signature construction. However, there remains a gap between the ROM and the instantiation with any concrete hash function.
5.3. Security Analysis of PTP
In our experiments, the PTP fully leverages Fabric’s decentralized features—multi-organization endorsement, immutable ledger, atomic chaincode execution, and event-driven architecture—to ensure end-to-end integrity and security of the commit–aggregate workflow.
The PTP smart contract itself is designed with several intrinsic security guarantees. It operates as a publicly verifiable and transparent component, whose execution is deterministic, tamper-proof, and fully traceable on-chain. Below, we analyze the security properties of PTP from multiple dimensions.
Network Attack Resistance. All interactions with the PTP—including the submission of commitments , the computation of the hash challenge based on a recorded timestamp t, and the collection of partial signatures —are conducted on-chain. This prevents network-level threats such as message forgery, man-in-the-middle attacks, or replay attacks. In particular, the inclusion of a fresh timestamp ensures that w is non-repeatable and unpredictable, which strengthens the resilience of the protocol under adversarial conditions.
Transparency and Public Verifiability. The PTP ensures full transparency by recording all key data—commitments, timestamp, computed values (w, ), and partial signatures—on the ledger. Since all messages are publicly observable, any external auditor or verifier can reproduce the state transitions and validate that the signing protocol follows its intended logic.
Robustness in Adversarial and Unreliable Environments. The smart contract is resilient to partial signer failure or delays. Threshold signing ensures that the protocol can proceed as long as a sufficient subset of valid signers participate. Timeout mechanisms can be incorporated to advance the process if some participants become unresponsive. These safeguards maintain reliability even under network latency, participant crash, or adversarial behavior.
Smart Contract–Level Security. The PTP contract is implemented in Go and deployed as a chaincode on Hyperledger Fabric. It follows secure development principles specific to the Fabric chaincode model, avoiding common pitfalls such as improper access control, unchecked parameter validation, and unsafe state transitions.
While real-world smart contracts may still face external risks such as DoS attacks or platform-level congestion, these are orthogonal to our scope and have been addressed in prior work [21,22]. Our focus remains on ensuring that the internal logic of PTP, as deployed on a permissioned blockchain environment, maintains security, correctness, and auditability by design.
6. Performance Analysis and Application
6.1. Theorectical Analysis
We compared the communication and computation cost of current two-round Schnorr-based multi-signature schemes, including mBCJ, MuSig2, DWMS, and our HEMS. As shown in Table 1, we analyze the size of the joint signatures, public key and secret key of a single signer, communication round, and the total number of communications in the signing phase. The proposed HEMS has the same and optimal signature size , public key size , and key size with MuSig2 and DWMS, and outperforms mBCJ. Although two-round interactions are needed, the total number of communications for HEMS is the lowest when due to the introduction of PTP.

Table 1.
Communication cost comparisons among two-round multi-signature schemes. Here, is the prime p order group that these schemes work in. and denote the size of a group element and a scalar, respectively.
In terms of computational cost, as shown in Table 2, we analyze the consumption of Sign, Verify, and Agg algorithms compared with mBCJ, MuSig2, and DWMS. Although public key aggregation happens in sign and verify algorithms for some schemes, we list it separately in Table 2 without loss of generality. As the PPK model is used in MuSig2, DWMS, and HEMS to resist rogue key attacks, the Agg algorithm consumes n exponentiation operations. Meanwhile, mBCJ uses the KV model, and its Agg algorithm is implemented by multiplications, so the time consumption is negligible. This is also the reason why the size of pubic keys of mBCJ is the largest. The Sign algorithm only consumes 1 exponentiation operation, which is one of the major advantages of the proposed HEMS scheme when compared with other multi-signature schemes. For the computational cost of verification, like most schemes, we only need two exponentiation operations. In terms of security, our scheme is resistant to the k-sum attacks, and a security proof is given in the ROM model based on the DL problem.

Table 2.
Computation cost and security comparisons among two-round multi-signature schemes with n signers. kexp shows k-exponentiation in . Compared to exponential operations, the cost of addition, multiplication, and hash is considered negligible. v and m represent the number of randomness in MuSig2 and DWMS, respectively. Typically, and .
6.2. Experiment Analysis
Prototype: We implemented mBCJ, Musig2, DWMS, and our HEMS in the Go Programming language. This experiment compares the time cost of Sign and Verify algorithms for each signer, not including aggregating public keys. Note that the implementation of DWMS does not organize signers into a spanning tree.
Physical configuration: The experiments were performed on CentOS Linux release 7.9.2009, with an Intel(R) Core(TM) i5-9500 CPU @ 3.00 GHz processor and 4 GB of RAM. In our experimental setup, all signers’ operations were carried out sequentially in a local environment (i.e., simulating multiple participants on the same machine). The experimental tests of the four schemes were all carried out in the same experimental environment. In order to accurately measure the computational cost of the Sign algorithm, the round-trip delay of the network was ignored during the experiments.
Experiments: We simulated the signing and verification process of the four schemes to evaluate their computational overhead. Every experiment was repeated 10 times, and the average of all the runs was compared.
Results: Figure 2 depicts the result of signing time, showing that one signer’s signing time is no more than 10 milliseconds even if it scales to 4000 signers. Although the cost of an addition, multiplication, and hash is negligible compared to the exponent, a large number of these operations result in fluctuant running time. Here, the signing time only includes cryptographic operations. Out of the four schemes, HEMS takes the least amount of time. On the contrary, DWMS increases the signing time rapidly as the number of signers increases. This is because the exponential operation required to calculate the joint commitment is linearly increasing when the number of signers increases. Figure 3 shows that in our scheme, the verification time is consistent with most of the other schemes. Overall, the proposed scheme achieves higher efficiency in the signature process, while maintaining the same verification efficiency as most of the other schemes.
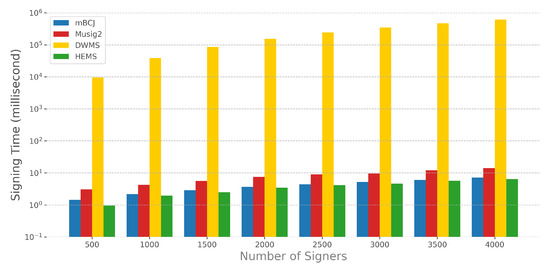
Figure 2.
The time consumption for Sign algorithm (y-axis has logarithmic scale).
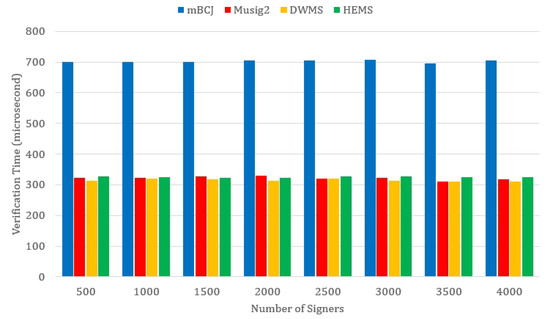
Figure 3.
The time consumption for the Verify algorithm.
7. Application in Blockchain Transactions
Fabric is a permissioned blockchain platform with Certificate Authority (CA). Whenever a client wants to create a new transaction or query the ledger, it needs to first connect to a peer node. Peer nodes are the fundamental elements of Fabric, responsible for managing ledgers and smart contracts. Some peer nodes are called endorsers, which are responsible for simulating the execution of transactions and generating signature endorsements. One or more orderers provide the ordering service, and their main function is to pack transactions into a block and distribute it to peer nodes. Each peer node on the blockchain network, also called the committing node, validates or invalidates the transactions in the blocks and commits valid blocks to its copy of the ledger.
In order to ensure that the ledger remains consistent and up-to-date on all peer nodes in a channel, before a new transaction is committed to the ledger from a client, it must be endorsed by the peer nodes specified by the endorsement policy. Endorsement is the process where some endorsers simulate executing a transaction and return a proposal response to the client. The proposal response is the execution result of the smart contract on the peer nodes and contains a signature to prove that the node executed the smart contract. In most cases, the state update of the ledger requires the endorsement of the vast majority of peer nodes, which means that multiple signatures will be generated during the endorsement process, and the validity of the signatures needs to be verified multiple times. We apply our multi-signature scheme HEMS in the endorsement process to replace the original ECDSA signature, and optimize the endorsement process.
PTP, as a Fabric smart contract, does not introduce any new root certificates or trust anchors. All participants (signers, peers, orderers) must first obtain identity certificates from the Fabric CA, which are then managed and validated by the MSP. Only clients holding identities issued by a trusted CA can invoke the smart contract and submit signatures.
Before a transaction process begins, there are some preparations. First, the orderer needs to deploy a smart contract approved by the members in the network as the PTP. Second, Fabric CA uses ParamGen to generate signature-related parameters . After obtaining the public parameter from the CA, each peer node generates its own public and private key with KeyGen(). At this point, the preparation work has been completed. Next, we will introduce the revised transaction process, as shown in Figure 4.
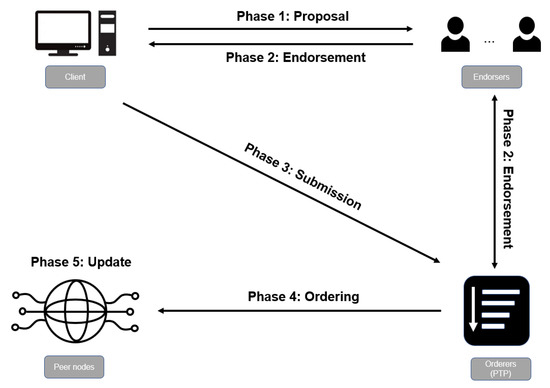
Figure 4.
Our revised transaction process on Blockchain Fabric.
Phase 1 (Proposal): The client generates a transaction proposal, signs the transaction proposal, and sends it to all endorsers specified by the endorsement policy.
Phase 2 (Endorsement): After the endorsers receive the transaction proposal, they first check whether the transaction proposal is accompanied by a valid signature of the client. Then, the endorsers execute the smart contract with the transaction proposal, generate a transaction proposal response, and call Sign() to sign the proposal response. In this process, the endorsers will interact with the smart contract on the orderer: the endorsers send the random number and the public key to the smart contract, and the smart contract sends , and W to the endorsers. After that, all endorsers use to obtain , proceed to the Round 2 of Sign. After an interaction with the orderer, each endorser obtains all partial signatures . Eventually, the endorser computes , appends it to the proposal response, and sends the proposal response to the client.
Phase 3 (Submission): After the client collects sufficient proposal responses from endorsers, it generates a transaction that contains the proposal and responses, and submits the transaction to the orderer.
Phase 4 (Ordering): The orderer receives transactions from different clients simultaneously, sorts these transactions in a predefined order, and packs the transactions into blocks, which are then distributed to the nodes in the network.
Phase 5 (Update): After the committing node receives a block, it first uses Agg to obtain the aggregated public key of endorsers, and then calls the Verify to verify the endorsement of each transaction in the block. If the signature is valid, the transaction satisfies the endorsement policy.
Next, we choose Fabric v2.2.8 (https://github.com/hyperledger/fabric/tree/v2.2.8 (accessed on 1 December 2024)) to conduct experiments. For the convenience of description, the transaction process on Fabric v2.2.8 is named Fabric, and the modified transaction process is referred to as mFabric. The computer configuration used in the experiment is the same as before.
First, we compare the proportion of signatures in each transaction of Fabric and mFabric. In Fabric v2.2.8, the structure of a transaction includes five parts, namely, header, signature, proposal, response, and endorsement. The endorsement part contains the signatures of all endorsers generated during the endorsement process, and the number of signatures is the same as the number of endorsers. In mFabric, we modified the endorsement part to have only one signature no matter how many endorsers there are. The experimental results are shown in Figure 5. It can be seen from the figure that as the number of endorsers continues to increase, the proportion of signatures in a transaction in Faric gradually increases, but the proportion of signatures in a transaction in mFaric gradually decreases, even approaching .
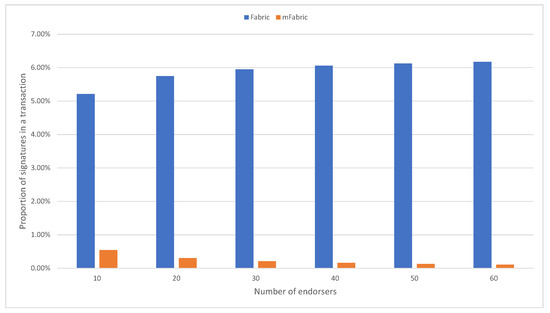
Figure 5.
Proportion of signature in a transaction in Fabric and mFabric.
Second, we compare the verification time on a single submitting node for a block containing only one transaction in Faric and mFabric. The experimental results are shown in Figure 6. In both Faric and mFabric, as the number of endorsers gradually increases, the time for committing nodes to verify a single block will continue to increase. However, with the same number of endorsers, the verification time of a block in mFaric is always less than that in Fabric. This is because it is necessary to verify as many signatures as the number of endorsers in Fabric, while only one signature needs to be verified in mFabric.
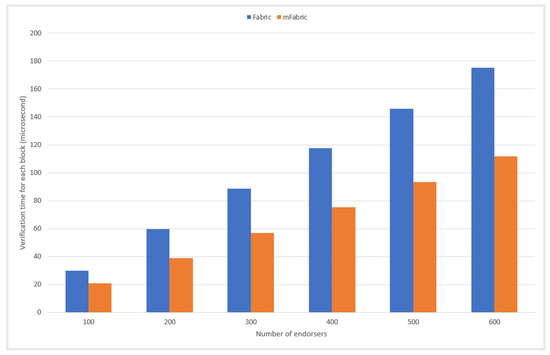
Figure 6.
Time for a block containing only one transaction to be verified by a single node in Faric and mFaric.
Under the premise of keeping the signature time basically consistent, the comparison of the above two aspects shows that our multi-signature scheme cannot only reduce the space occupied by the signature in the block, but also improve the verification efficiency of the block. In fact, the modification of the network configuration in Fabric, including member changes, also requires the consent of multiple organizations, and it can also be improved with a multi-signature scheme. Therefore, the multi-signature scheme has a wide range of application scenarios in Fabric.
8. Conclusions
Inspired by Blockchain and the smart contract, a new method to resist k-sum attacks in the Schnorr-based multi-signature scheme is advanced through a Public Third Party (PTP) program, which executes codes publicly and automatically in a decentralized way. By requiring the recipient of all commitments as one execution condition of the smart contract, the proposed scheme can effectively prevent k-sum attacks. Based on this idea, a two-round multi-signature scheme with high efficiency (HEMS) is proposed, which is proven secure based on discrete logarithm assumptions in the random oracle model. Performance analysis shows that the proposed HEMS scheme achieves the lowest communication and computation costs compared to the other two-round Schnorr-based multi-signature schemes, including mBCJ, MuSig2, and DWMS. As HEMS keeps the same efficiency as the basis Schnorr signature, we confirm that HEMS achieves high efficiency. Its applications in the blockchain platform Fabric show that HEMS can reduce the space occupied by the signatures and improve the verification efficiency of the block.
Author Contributions
Conceptualization, P.Z. and F.G.; methodology, P.Z. and F.G.; software, F.G. and Z.T.; validation, P.Z., F.G., Z.T. and W.X.; formal analysis, P.Z. and F.G.; investigation, F.G. and Z.T.; data curation, F.G.; writing—original draft preparation, P.Z., F.G. and Z.T.; writing—review and editing, P.Z., W.X. and F.G.; visualization, F.G. and Z.T.; supervision, P.Z. and W.X.; project administration, P.Z. and W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maxwell, G.; Poelstra, A.; Seurin, Y.; Wuille, P. Simple Schnorr multi-signatures with applications to Bitcoin. Des. Codes Cryptogr. 2019, 87, 2139–2164. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, P.; Liu, Y. Secure and efficient multi-signature schemes for fabric: An enterprise blockchain platform. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1782–1794. [Google Scholar] [CrossRef]
- Drijvers, M.; Gorbunov, S.; Neven, G.; Wee, H. Pixel: Multi-signatures for Consensus. In Proceedings of the USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 2093–2110. [Google Scholar]
- Horster, P.; Michels, M.; Petersen, H. Meta-Multisignature schemes based on the discrete logarithm problem. In Information Security—The Next Decade: Proceedings of the IFIP TC11 Eleventh International Conference on Information Security, IFIP/Sec ’95; Eloff, J.H.P., von Solms, S.H., Eds.; Springer: Boston, MA, USA, 1995; pp. 128–142. [Google Scholar] [CrossRef]
- Bellare, M.; Neven, G. Multi-signatures in the plain public-key model and a general forking lemma. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 390–399. [Google Scholar]
- Bagherzandi, A.; Cheon, J.H.; Jarecki, S. Multisignatures secure under the discrete logarithm assumption and a generalized forking lemma. In Proceedings of the 15th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 27–31 October 2008; pp. 449–458. [Google Scholar]
- Drijvers, M.; Edalatnejad, K.; Ford, B.; Kiltz, E.; Loss, J.; Neven, G.; Stepanovs, I. On the security of two-round multi-signatures. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 1084–1101. [Google Scholar]
- Nick, J.; Ruffing, T.; Seurin, Y. MuSig2: Simple two-round Schnorr multi-signatures. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2021; pp. 189–221. [Google Scholar]
- Syta, E.; Tamas, I.; Visher, D.; Wolinsky, D.I.; Jovanovic, P.; Gasser, L.; Gailly, N.; Khoffi, I.; Ford, B. Keeping authorities “honest or bust” with decentralized witness cosigning. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 526–545. [Google Scholar]
- Ma, C.; Weng, J.; Li, Y.; Deng, R. Efficient discrete logarithm based multi-signature scheme in the plain public key model. Des. Codes Cryptogr. 2010, 54, 121–133. [Google Scholar] [CrossRef]
- Kılınç Alper, H.; Burdges, J. Two-round trip schnorr multi-signatures via delinearized witnesses. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2021; pp. 157–188. [Google Scholar]
- Nick, J.; Ruffing, T.; Seurin, Y.; Wuille, P. MuSig-DN: Schnorr Multi-Signatures with Verifiably Deterministic Nonces. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 9–13 November 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1717–1731. [Google Scholar]
- Lee, K.; Kim, H. Two-Round Multi-Signatures from Okamoto Signatures. Mathematics 2023, 11, 3223. [Google Scholar] [CrossRef]
- Boneh, D.; Drijvers, M.; Neven, G. Compact multi-signatures for smaller blockchains. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2018; pp. 435–464. [Google Scholar]
- Pan, S.; Chan, K.Y.; Cui, H.; Yuen, T.H. Multi-signatures for ECDSA and Its Applications in Blockchain. In Information Security and Privacy—27th Australasian Conference, ACISP 2022, Wollongong, NSW, Australia, 28–30 November 2022; Lecture Notes in Computer Science; Nguyen, K., Yang, G., Guo, F., Susilo, W., Eds.; Springer: Cham, Switzerland, 2022; Volume 13494, pp. 265–285. [Google Scholar]
- Kansal, M.; Singh, A.K.; Dutta, R. Efficient multi-signature scheme using lattice. Comput. J. 2021, 65, 2421–2429. [Google Scholar] [CrossRef]
- Peng, C.; Du, X. New lattice-based digital multi-signature scheme. In International Conference of Pioneering Computer Scientists, Engineers and Educators; Springer: Singapore, 2020; pp. 129–137. [Google Scholar]
- Pointcheval, D.; Stern, J. Security arguments for digital signatures and blind signatures. J. Cryptol. 2000, 13, 361–396. [Google Scholar] [CrossRef]
- Wagner, D. A Generalized Birthday Problem. In Advances in Cryptology—CRYPTO 2002; Yung, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 288–304. [Google Scholar]
- Fiat, A.; Shamir, A. How to prove yourself: Practical solutions to identification and signature problems. In Conference on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1986; pp. 186–194. [Google Scholar]
- Zhu, H.; Yang, L.; Wang, L.; Sheng, V.S. A Survey on Security Analysis Methods of Smart Contracts. IEEE Trans. Serv. Comput. 2024, 17, 4522–4539. [Google Scholar] [CrossRef]
- Wei, Z.; Sun, J.; Zhang, Z.; Zhang, X.; Yang, X.; Zhu, L. Survey on Quality Assurance of Smart Contracts. ACM Comput. Surv. 2024, 57, 1–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).