Design of a New Busbar for VFTO Suppression and Analysis of the Suppression Effect
Abstract
1. Introduction
2. Analysis of Damping Busbar Design and Suppression Mechanism
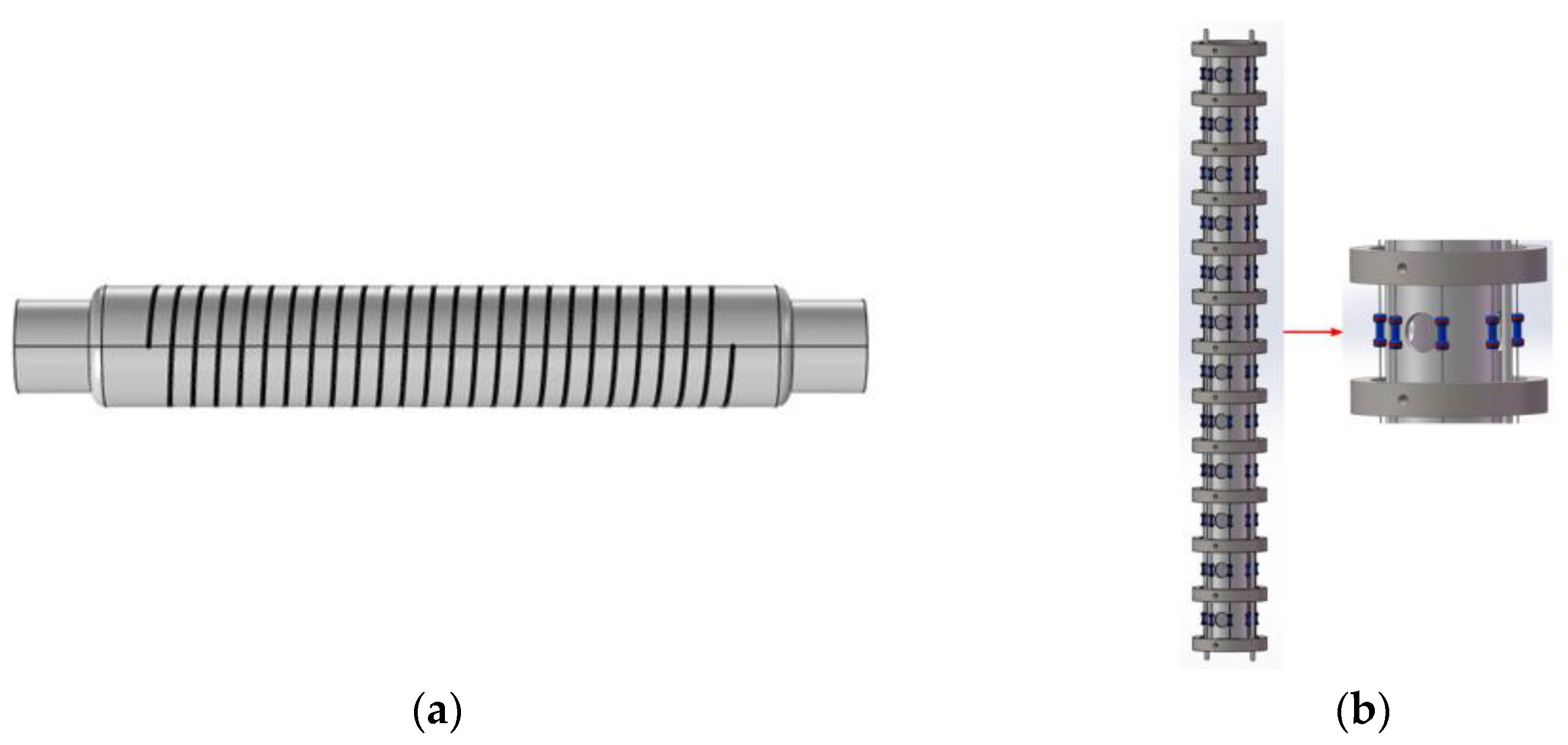
2.1. Structure Design
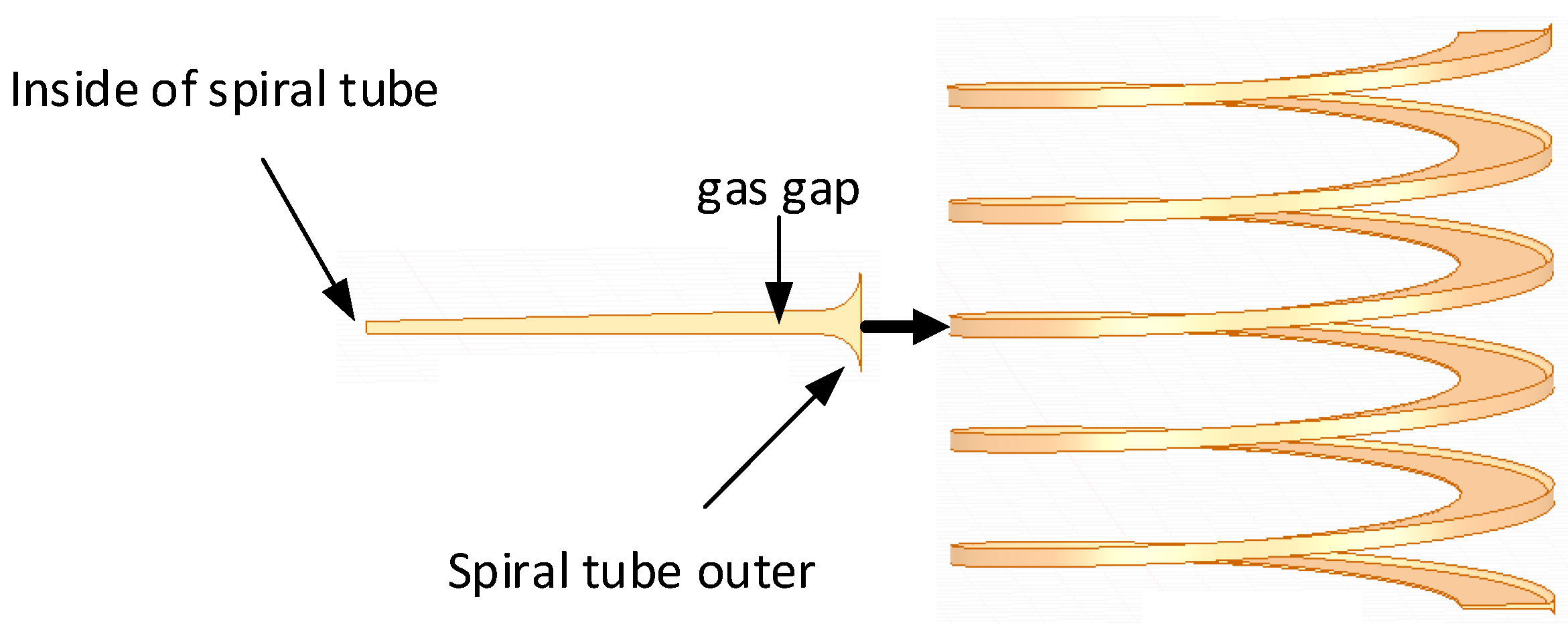
2.2. Suppression Mechanism
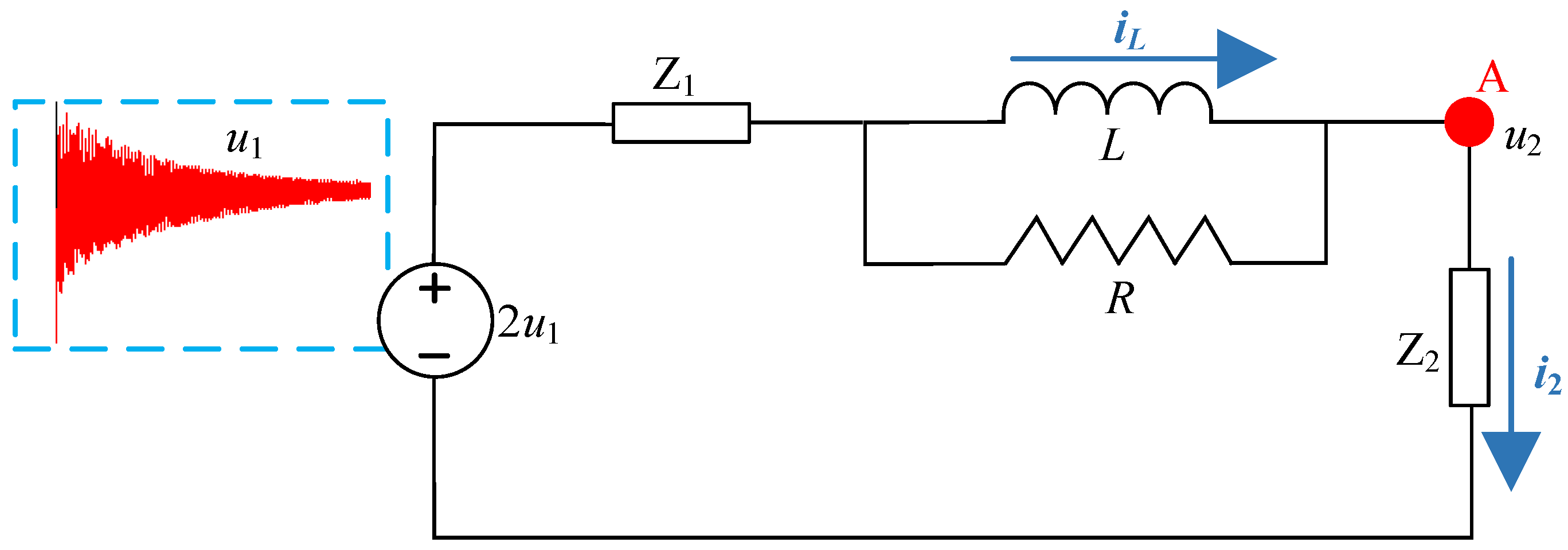
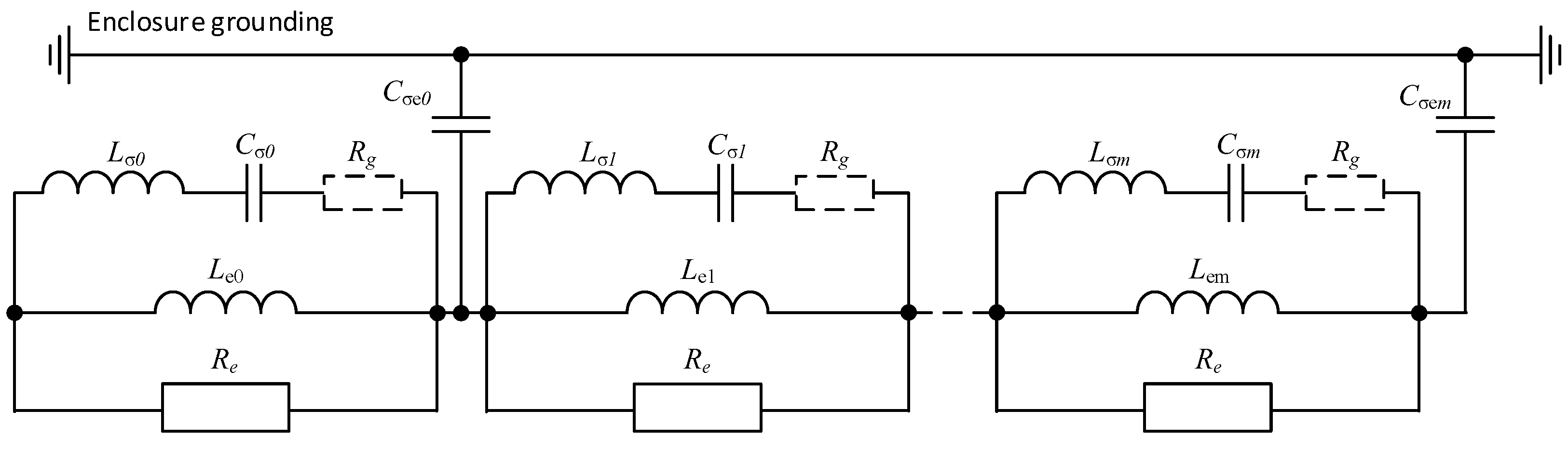
2.3. Equivalent Circuit Parameter Analysis
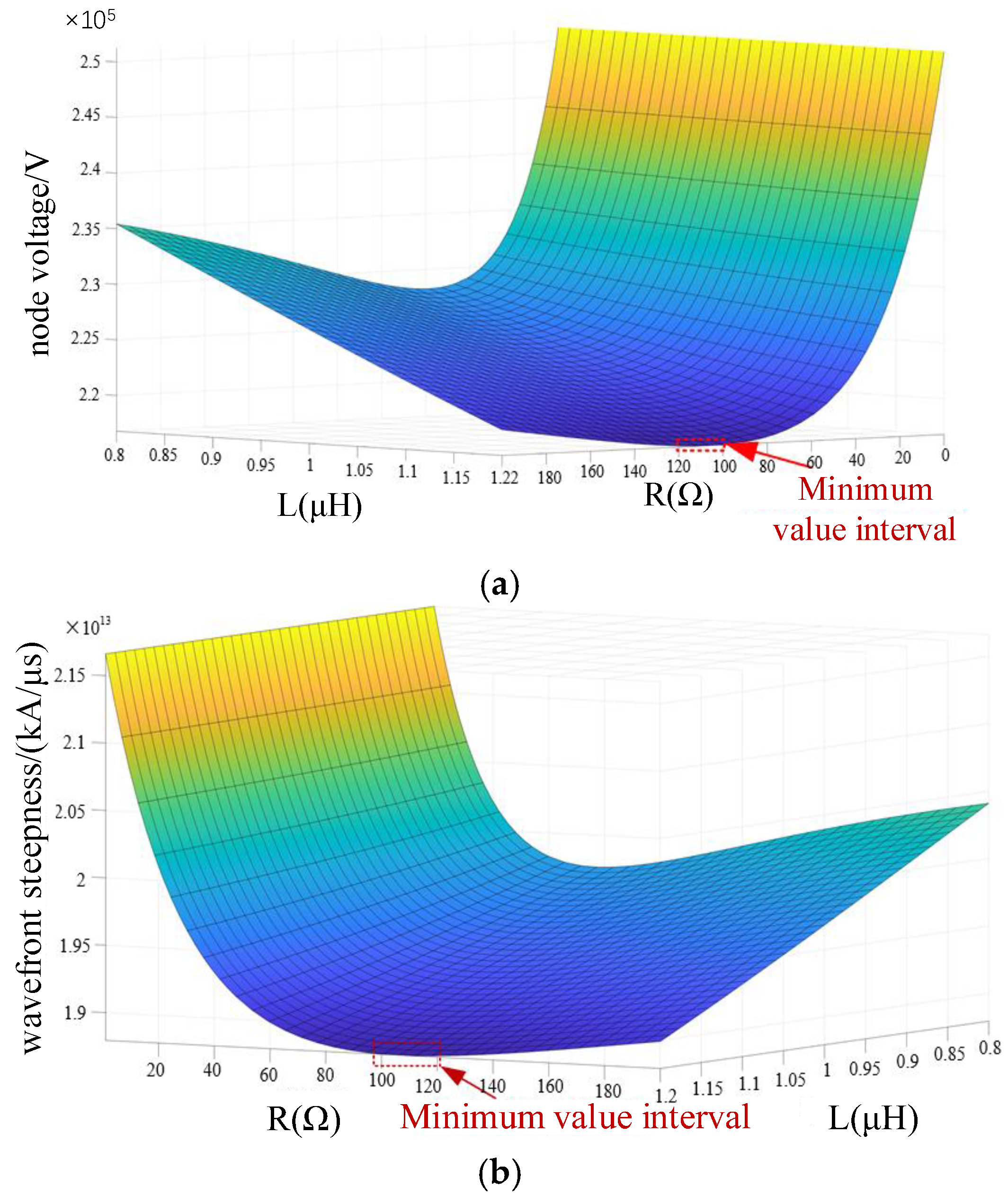
3. Structural Optimization Design of Damping Busbar
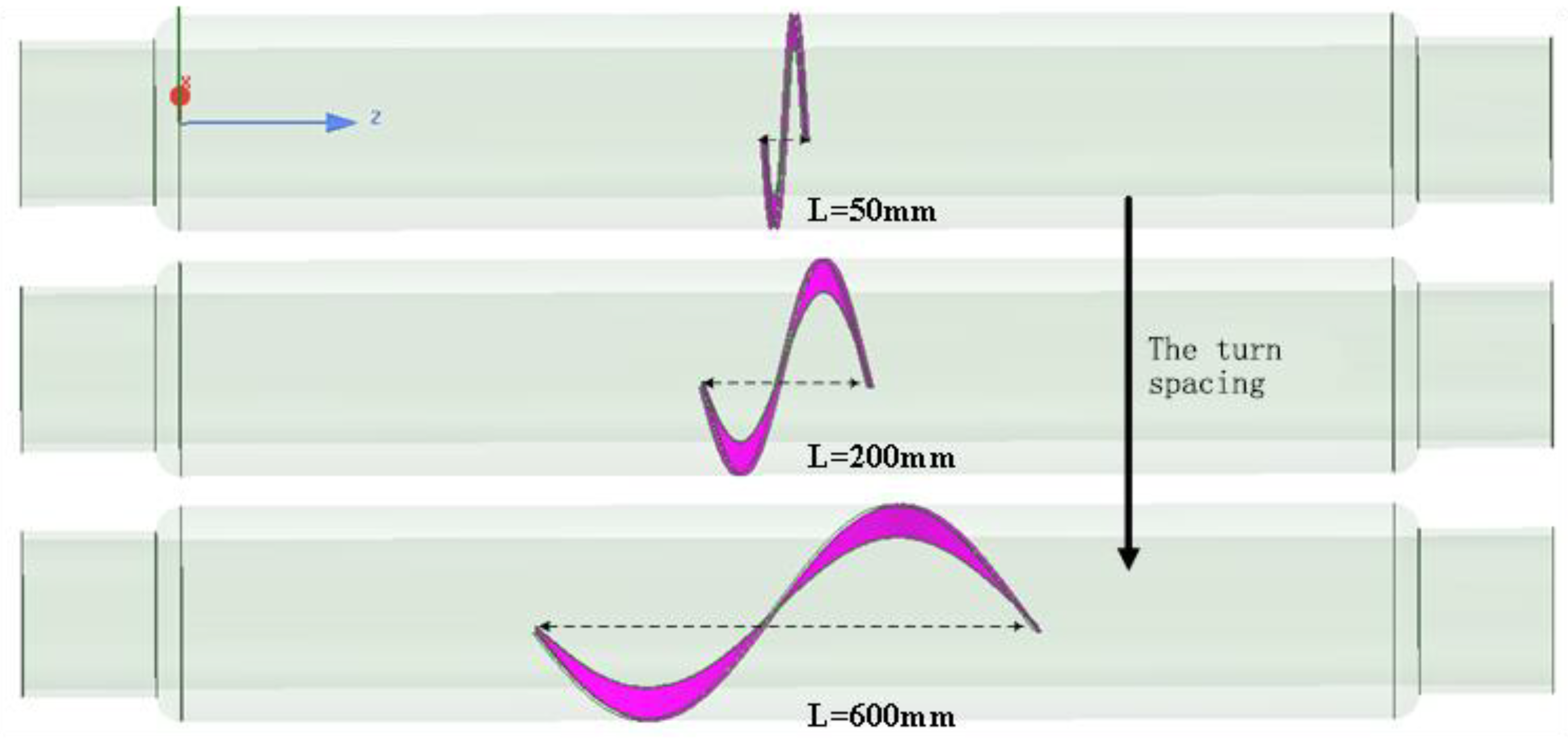
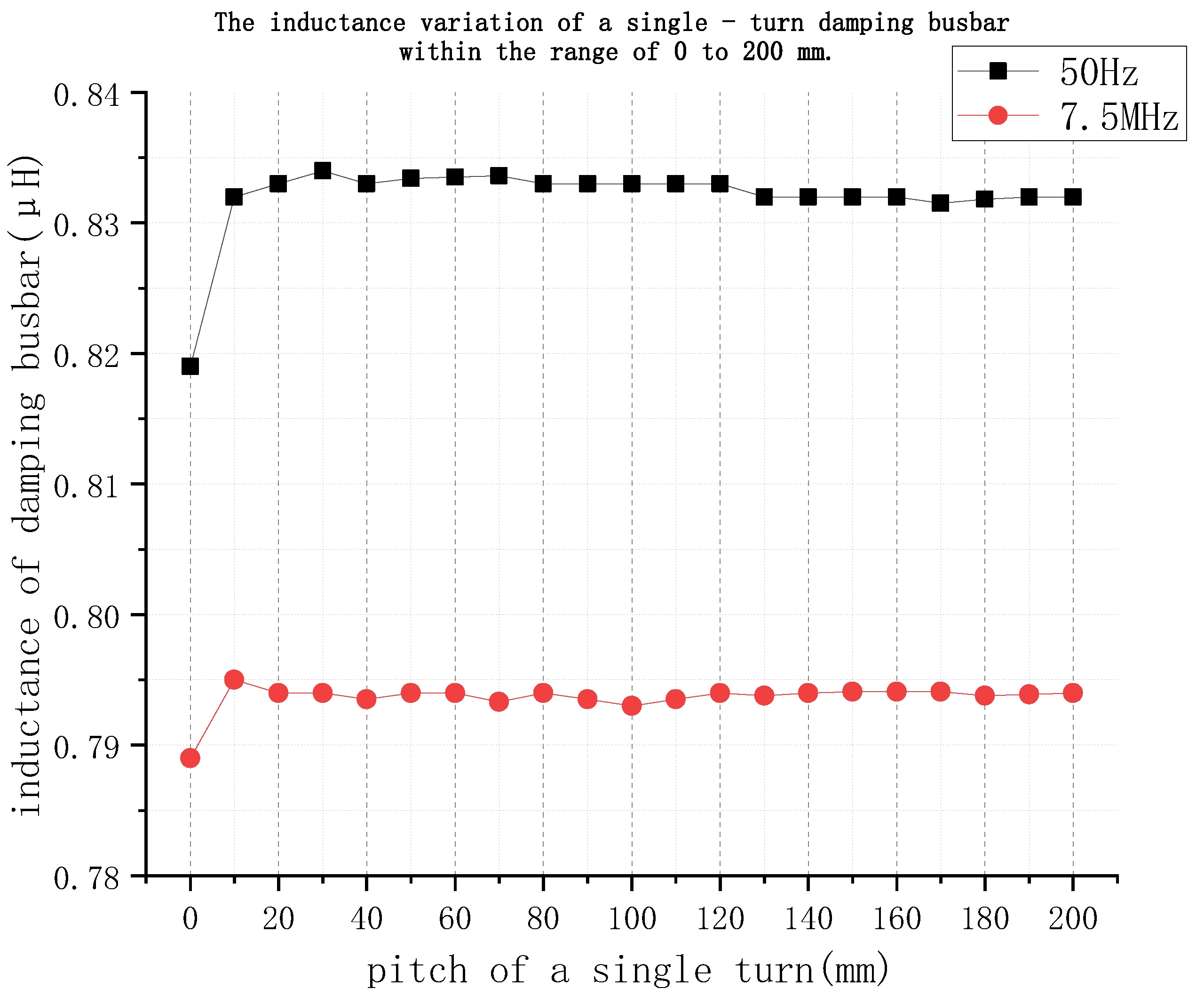
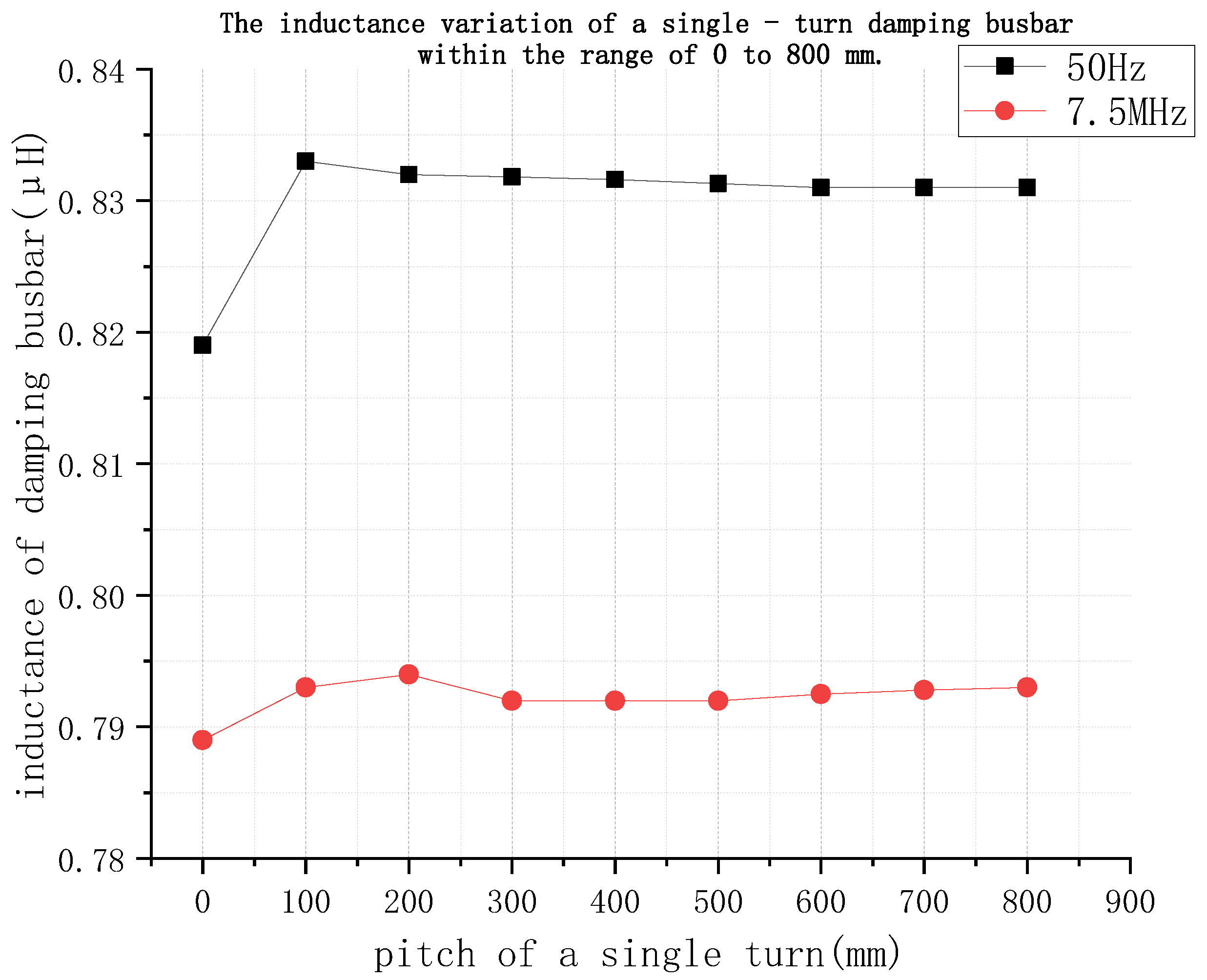
3.1. Analysis of the Effect of Turn Spacing on Inductance
- Small increase in turn spacing between 0 and 200 mm.
- Wide range of turn spacing between 200 and 800 mm.
- (1)
- Inductance variation within 0~200 mm turns spacing
- (2)
- Inductance Variation within 0~800 mm Turn Pitch
3.2. Analysis of the Effect of the Number of Turns on Inductance
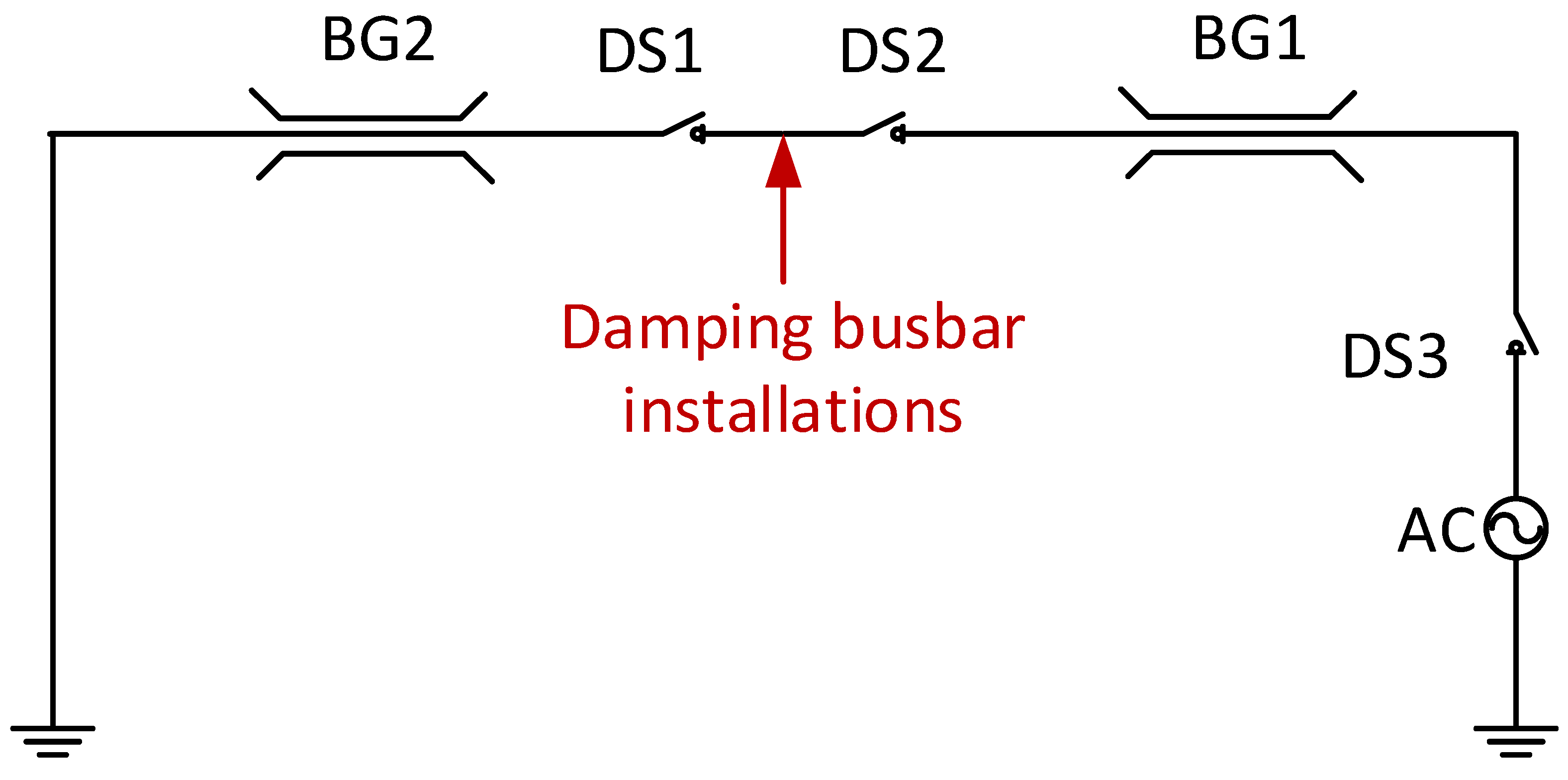
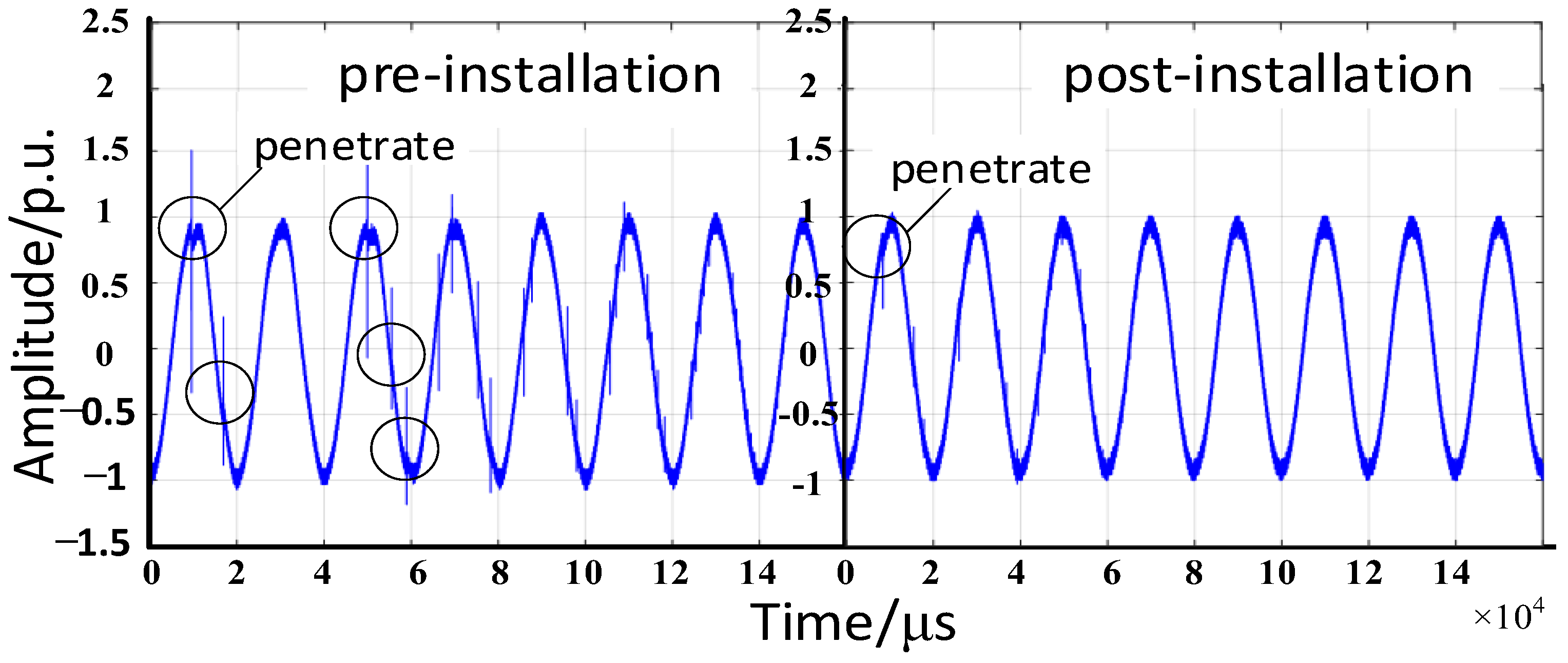
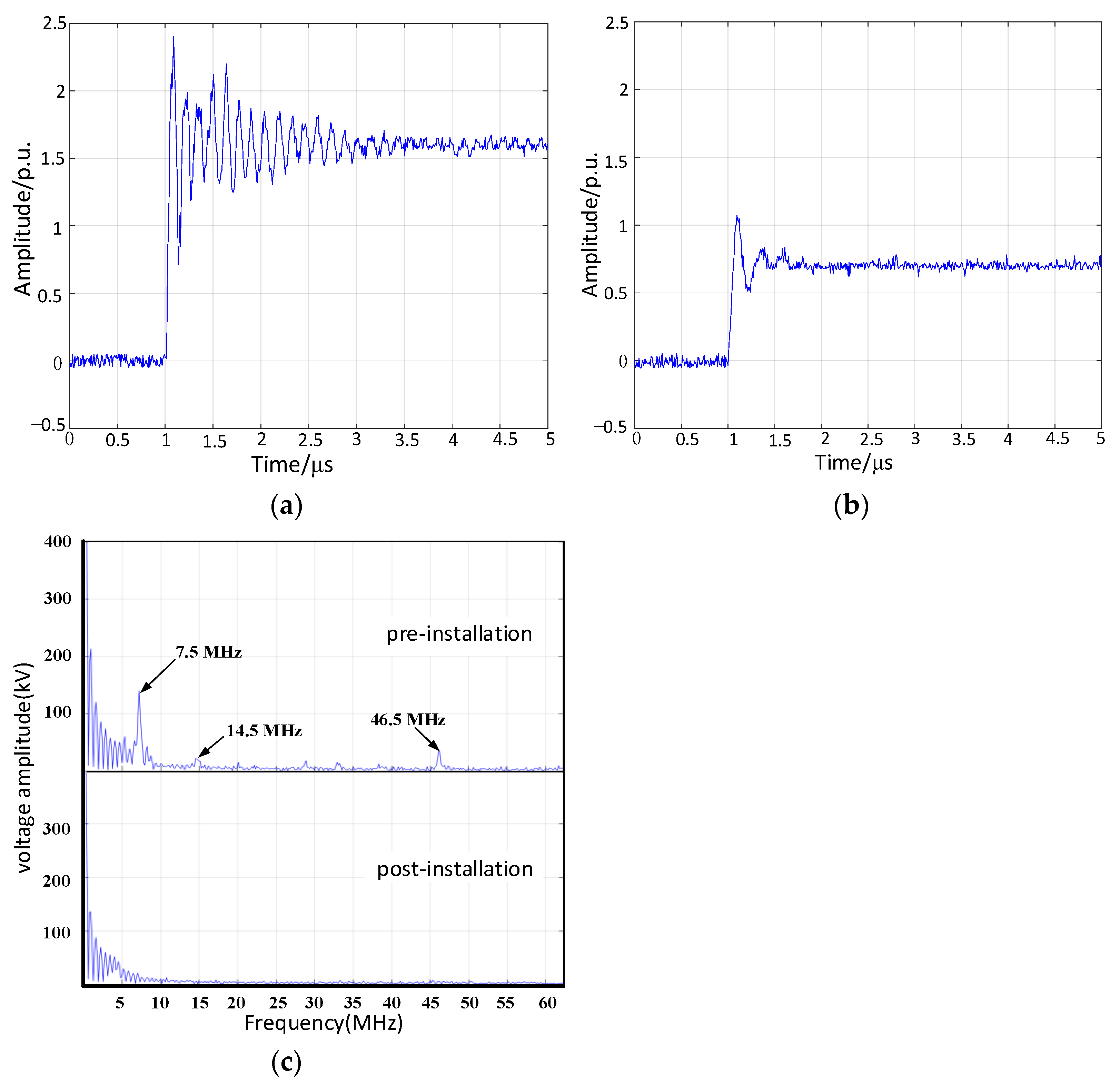
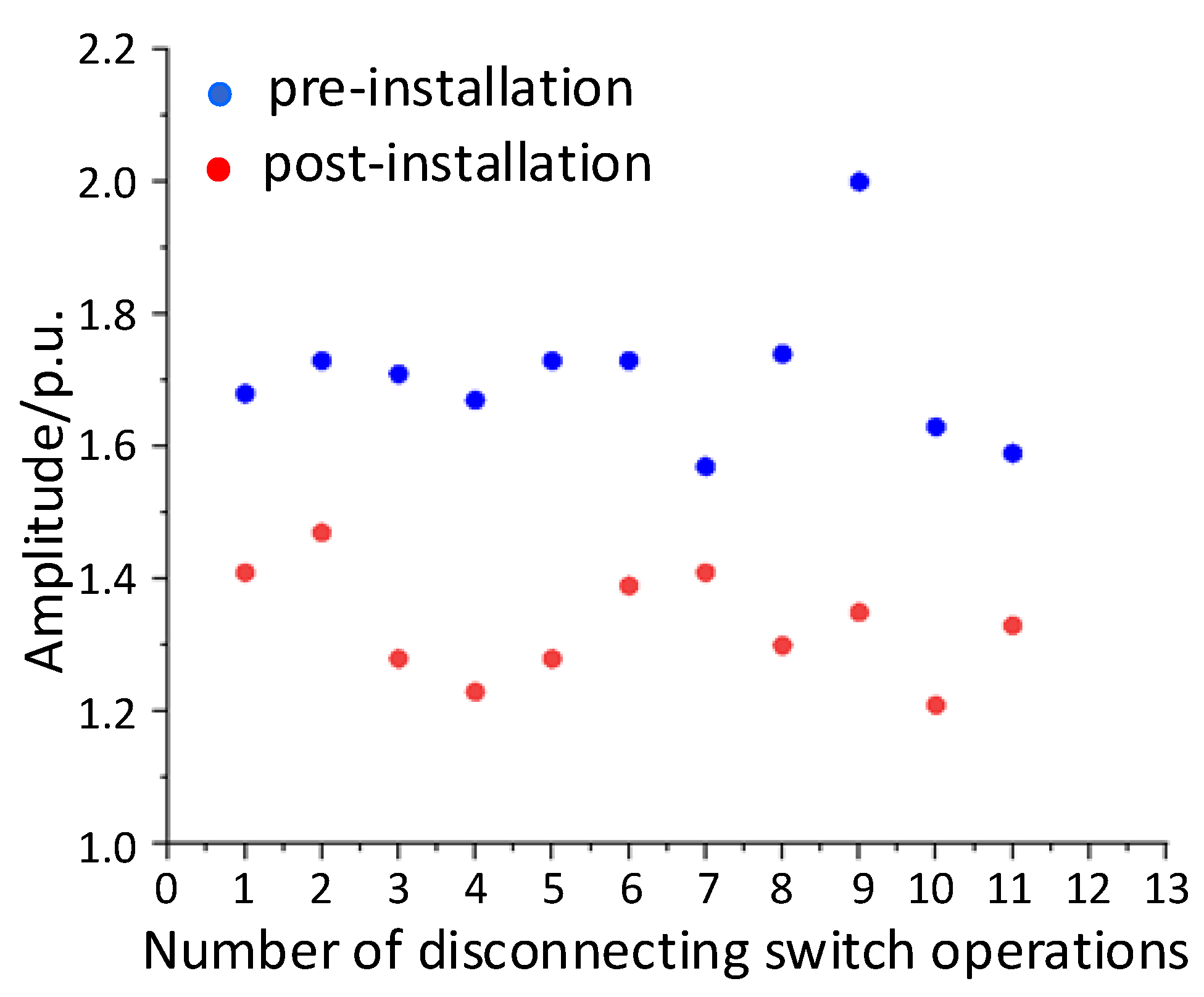
4. Analysis of Damping Busbar Effect on VFTO Suppression
5. Conclusions
- As ordinary busbar using 550 kV GIS platform was processed into a spiral damping busbar. After processing, its stray inductance was about 0.4 μH and its stray capacitance was about 0.18 nF.
- The structural parameter that plays a decisive role in the inductance of the damping busbar is the number of turns. Whether under industrial-frequency or high-frequency excitation, when the length of the damping bus is certain, the higher the number of turns, the greater the bus inductance. The value of inductance under industrial-frequency excitation is greater than that under high-frequency excitation. Damping bus inductance increases approximately linearly with the number of turns, similar to the linear increase in inductance with the number of turns of a conventional helical coil.
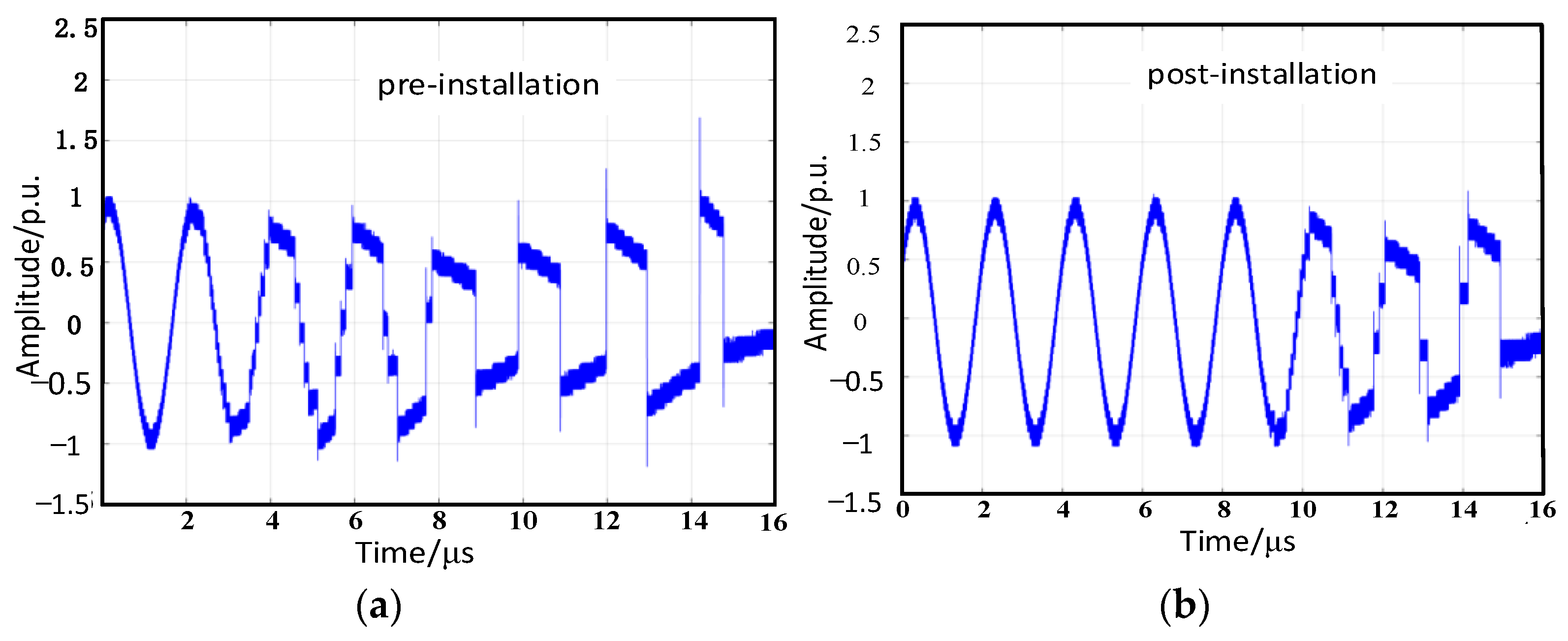
- The VFTO suppression effect of the damping busbar was systematically verified using a combination of simulation calculation and experimental verification. The test data showed that the average amplitude of VFTO decreased by 20.36% after addition of the damping busbar, the number of breakdowns decreased by about 66.7%, and there was no obvious high frequency after the installation of the damping busbar. These data show that the damping busbar has a good suppression effect on the amplitude and frequency of VFTO, and reduces the number of breakdowns.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.J.; Yan, Q.L.; Li, Z.B.; Dai, M.; Li, C.R.; Liu, W.D.; Chen, H.B.; Zhang, Q.G.; Wei, G.L.; Zhang, M. New Advances in Research on Very Fast Transient overvoltage in Gas-Insulated Switchgear. Proc. CSEE 2011, 31, 1–11. [Google Scholar]
- Chen, W.J.; Li, Z.B.; Sun, G.; Dai, M.; Liu, W.D.; Li, C.R.; Wang, L.; Wang, H.; Chen, G.Q.; Yao, T.; et al. Experimental research on the characteristics of very fast Transient overvoltage in ultra-high voltage gas insulated switchgear. Proc. CSEE 2011, 31, 38–47. [Google Scholar]
- Liu, W.D.; Wang, L.S.; Chen, W.J.; Dai, M.; Li, Z.B.; Yve, G.C. Study on the Repeated Breakdown Process During Very Fast Transient Overvoltage Tests in UHV GIS. High Volt. Eng. 2011, 37, 644–650. [Google Scholar]
- Huang, H.M. Research on Electromagnetic Disturbance of Secondary Equipment Caused by UHV VFTO. Master‘s Thesis, North China Electric Power University, Beijing, China, 2012. [Google Scholar]
- Li, Y.; Shang, Y.; Shi, R.; Zhang, L. Analysis of On-site Measured Waveforms of VFTO in 750kV GIS. Power Syst. Clean Energy 2011, 27, 25–29. [Google Scholar]
- Nie, H.Y.; Zhang, C.H.; Yao, Y.H.; Gu, Z.Y.; Liu, X.S. Partial discharge characteristics of interturn insulation of dry-type air core reactor under the accumulative effect of switching overvoltage. Electr. Mach. Control 2018, 22, 15–23. [Google Scholar]
- Jiang, X.B.; Liang, L.; Chen, G.; Wan, Y.R.; Zhou, H. Simulation Study on Very Fast Transient Overvoltage and Its Protective Measures in 500kV GIS Substation. Energy Eng. 2010, 3, 19–22, 27. [Google Scholar]
- Wang, S.C.; Zhang, X.L. Study on Algorithms for Optimal Operation of Transformers. Electr. Power 2007, 36–40. [Google Scholar]
- Zou, Z.Y.; Xia, Y.; Zhou, H.L.; Miu, J.S.; Xv, Z. Research on suppression measures of disturbance to secondary equipment by GIS switch operation. Highlights Sci. Pap. Online 2023, 16, 21–28. [Google Scholar]
- Riechert, U.; Krusi, U.; Sologuren-Sanchez, D. Very fast transient overvoltage during switching of bus-charging currents by 1100 kv disconnector. Water Energy Int. 2011, 68, 67–68. [Google Scholar]
- Shu, Y.B.; Han, B.; Lin, J.M.; Chen, W.J.; Ban, L.G.; Xiang, Z.T. Influence of the switching speed of the disconnector on very fast transient overvoltage. IEEE Trans. Power Del. 2013, 28, 2080–2084. [Google Scholar]
- Zhang, H.W. Simulation Study on VFTO Caused by Isolating Switchgear Operation in 750 kV HGIS Station. Electr. Saf. Technol. 2025, 27, 28–33. [Google Scholar]
- He, J.Y.; Yang, Z.B. Study on Limiting Very Fase Transient Overvoltage of Transformer Winding by MOV. Jilin Electric Power 2023, 51, 35–39. [Google Scholar]
- Pathak, N.; Bhatti, T.S.; Ibraheem, I. Study of very fast transient overvoltage and mitigation techniques of a gas insulated substation. In Proceedings of the International Conference on Circuit, Nagercoil, India, 19–20 March 2015. [Google Scholar]
- Yamagata, Y.; Tanaka, K.; Nishiwaki, S.; Takahashi, N.; Kokumai, T.; Miwa, I.; Komukai, T.; Imai, K. Suppression of VFT in 1100kV GIS by adopting resistor-fitted disconnector. IEEE Trans. Power Deliv. 1996, 11, 872–880. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, S.P.; Wu, X.X.; Wang, H.; Wang, L.; Gong, R.L.; Zhou, Y.W. New Method of Restraining VFTO-the High Frequence Overvoltage Restraining Busbar. High Volt. Appar. 2018, 54, 90–96. [Google Scholar]
- Gao, F.F.; Tan, X.Y.; Liang, C.; Zhang, J.P.; Wang, J.J.; Liang, Z.R. Experimental Study on Suppression of VFTO in GIS by Installing Large Magnetic Rings with Small Magnetic Rings. High Volt. Appar. 2019, 55, 56–61+69. [Google Scholar]
- Smajic, J.; Shoory, A.; Burow, S.; Holaus, W.; Riechert, U.; Tenbohlen, S. Simulation-Based Design of HF Resonators for Damping Very Fast Transients in GIS. IEEE Trans. Power Deliv. 2014, 29, 2528–2533. [Google Scholar] [CrossRef]
- Guan, Y.G.; Guo, P.Q.; Chen, W.J.; Liu, W.D.; Duan, S.F.; Yve, G.C. Experimental Study on Suppression of VFTO in 252 kV GIS Using Ferrite Magnetic Rings. High Volt. Eng. 2014, 40, 1977–1985. [Google Scholar]
- Zhou, L.J.; Hu, C.; Huang, L.; Wang, D.Y.; Wu, T.S.; Zhang, D.; Chen, S.X. Lightning overvoltage suppression method based on magnetic ring for transmission line. Electr. Power Autom. Equip. 2022, 42, 186–191+198. [Google Scholar]
- Zhang, J.; Peng, X.; Wang, L.; Liang, S.; Tang, Y.; Zhang, Q. Simulation Study on Lightning-Induced Overvoltage Characteristics of Overhead Lines in Complex Terrain. High Volt. Eng. 2019, 45, 3708–3714. [Google Scholar]
- Zhou, H.; Li, Y.; Shen, Y.; Wan, Y.R.; Chen, G.; Sun, K. Limitation of the Front Steepness of Very Fast Transient Overvoltage Invading Extra-High-Voltage Transformers by Overhead Lines. High Volt. Eng. 2013, 39, 943–950. [Google Scholar]
- Zhou, L.H.; Liu, J.J.; Zhong, X.Q.; Liu, B.W.; Fan, B.; Zhu, L.F. Analysis of the Suppression Effect of Overhead Lines on VFTO in GIS Substations. J. Electr. Power Sci. Technol. 2015, 30, 41–46. [Google Scholar]
- Zhao, L.; Ye, L.; Yang, Y.; Jiang, P. Simulation Study on Very Fast Transient Overvoltage Caused by the Operation of 550kV GIS Disconnector. Zhejiang Electr. Power 2018, 37, 86–92. [Google Scholar]
- Wu, X.X.; Feng, X.T.; Hu, Y.F. Inductor Characteristics of Spiral Tube Damping Busbar Based on Optimal VFTO Suppression Effects. Power Syst. Technol. 2022, 46, 2812–2826. [Google Scholar]
- Wang, H.; Wu, X.; Feng, X.; Li, C.; Yang, X.; Wu, S.; Hou, H.; Li, H. Calculation and analysis the dynamic breakdown characteristic of SF6 discharge caused by GIS disconnector operation. Phys. Scr. 2023, 98, 1–15. [Google Scholar]
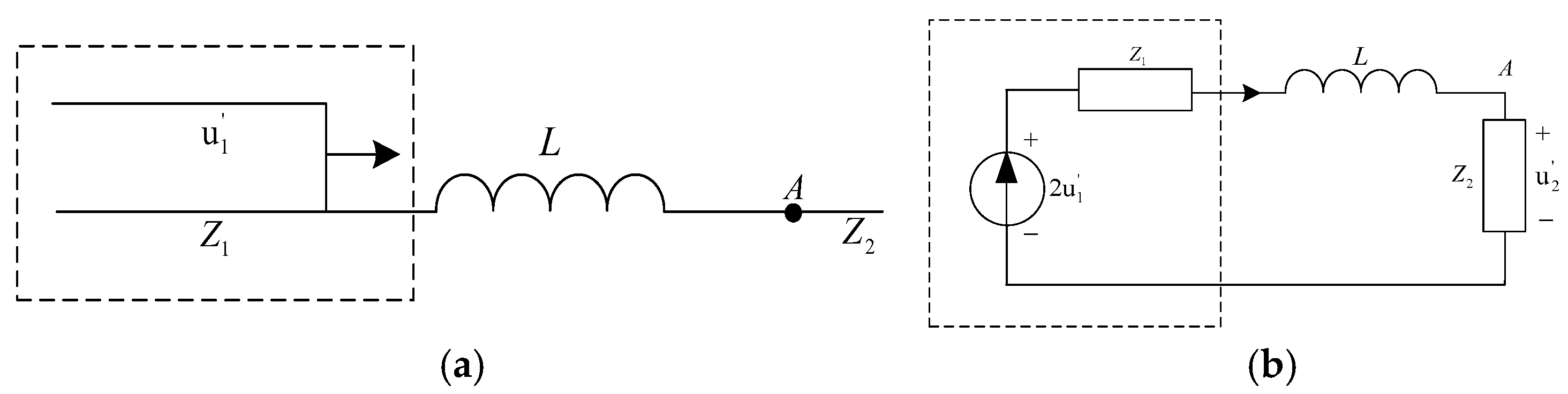


| Method | Advantage | Disadvantage |
|---|---|---|
| Damping resistance Method | Principle is simple and the inhibitory effect is good | Increases the complexity of the isolation switch structure and makes it expensive |
| Magnetic ring schemes | Good inhibitory effect | Easy to saturate |
| Lightning arrester method | Low cost, no need to change the GIS structure | The amplitude suppression effect is significant, but the wavefront steepness suppression effect is not significant, and the protection range is limited |
| Parameter | Lσ0 | Le0 (μH) | Lσ1 = ……Lσ24 | Cσ0 | Cσe0 | Cσ1 = ……Cσ24 | Re | Rg |
|---|---|---|---|---|---|---|---|---|
| Amplitude | 18.46 | 40.28 | 0.432 | 0.18 | 0.187 | 5.2 | 4 | 0.5 |
| Piral Processed Turns | Inductance (μH) 50 Hz | Inductance (μH) 50 Hz | Spiral Processed Turns | Inductance (μH) 50 Hz | Inductance (μH) 50 Hz |
|---|---|---|---|---|---|
| 1 | 0.83906 | 0.79384 | 15 | 9.1246 | 6.5351 |
| 3 | 1.2405 | 0.91169 | 17 | 10.567 | 7.4277 |
| 5 | 2.1894 | 1.2157 | 19 | 11.912 | 8.6756 |
| 7 | 3.4927 | 2.0156 | 21 | 13.445 | 10.069 |
| 9 | 4.785 | 2.7401 | 23 | 15.234 | 11.583 |
| 11 | 6.2028 | 3.6758 | 25 | 16.347 | 12.888 |
| 13 | 7.3524 | 4.9515 |
| Installation Status | Amplitude | Number of Breakdowns |
|---|---|---|
| Before installation | 1.57 p.u. | 18 |
| After installation | 1.19 p.u. | 6 |
| Main Frequency (MHz) | |
|---|---|
| Before Adding Damping Busbar | After Adding Damping Busbar |
| 0–7.5, 46.5 | 0–5 |
| Installed State | Average Amplitude of VFTO (p.u.) | Standard Deviation | F-Value for t-Test | Degree of Reduction in the Average Value of the Amplitude (%) |
|---|---|---|---|---|
| Before installation | 1.67 | 0.135 | 4.207 ** | 20.36% |
| After installation | 1.33 | 0.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, X.; Diao, Y.; Chen, X.; Du, B. Design of a New Busbar for VFTO Suppression and Analysis of the Suppression Effect. Electronics 2025, 14, 1815. https://doi.org/10.3390/electronics14091815
Wang H, Wu X, Diao Y, Chen X, Du B. Design of a New Busbar for VFTO Suppression and Analysis of the Suppression Effect. Electronics. 2025; 14(9):1815. https://doi.org/10.3390/electronics14091815
Chicago/Turabian StyleWang, Huan, Xixiu Wu, Yinglong Diao, Xiwen Chen, and Bolun Du. 2025. "Design of a New Busbar for VFTO Suppression and Analysis of the Suppression Effect" Electronics 14, no. 9: 1815. https://doi.org/10.3390/electronics14091815
APA StyleWang, H., Wu, X., Diao, Y., Chen, X., & Du, B. (2025). Design of a New Busbar for VFTO Suppression and Analysis of the Suppression Effect. Electronics, 14(9), 1815. https://doi.org/10.3390/electronics14091815




