Ultra-Lightweight and Highly Efficient Pruned Binarised Neural Networks for Intrusion Detection in In-Vehicle Networks
Abstract
1. Introduction
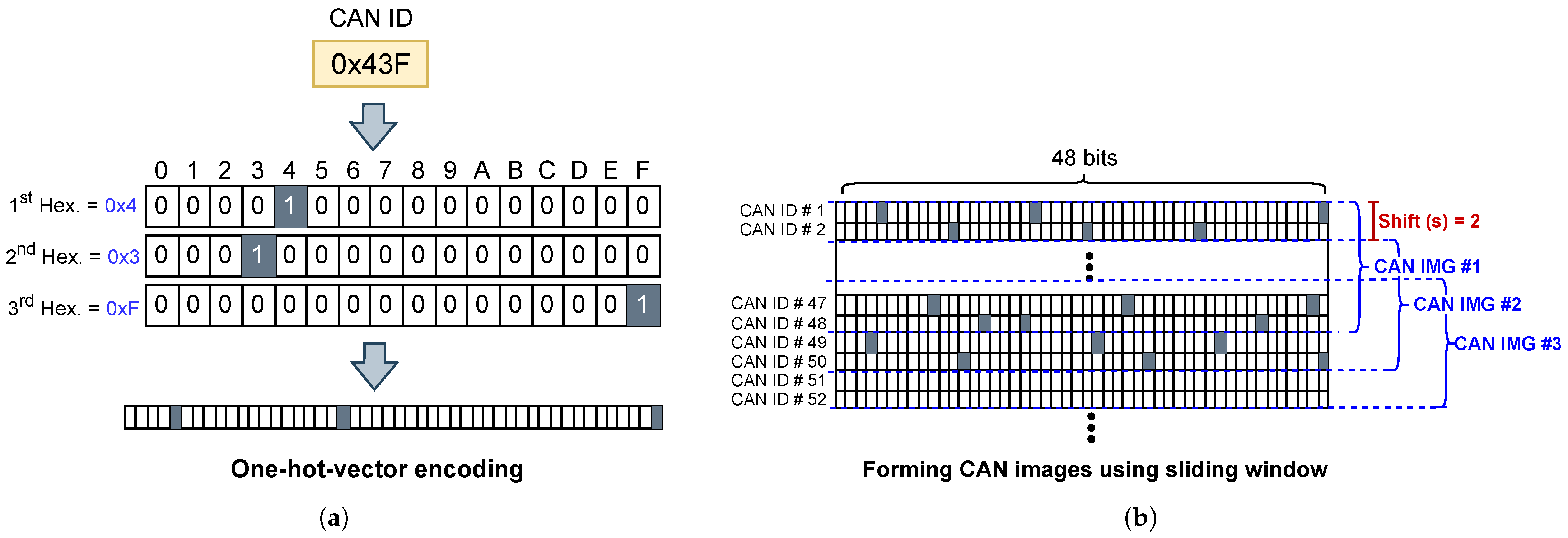
- A sliding-window technique is implemented during CAN message encoding to increase the amount of data. This technique improves detection accuracy by up to 0.66%, as demonstrated through experiments on three datasets extracted from different vehicles.
- A proposed network pruning process is applied to BNN-based IDS models trained on these three datasets. The pruned models achieve up to 91.07% parameter reduction while maintaining near-identical accuracy, with only a 0.01% drop.
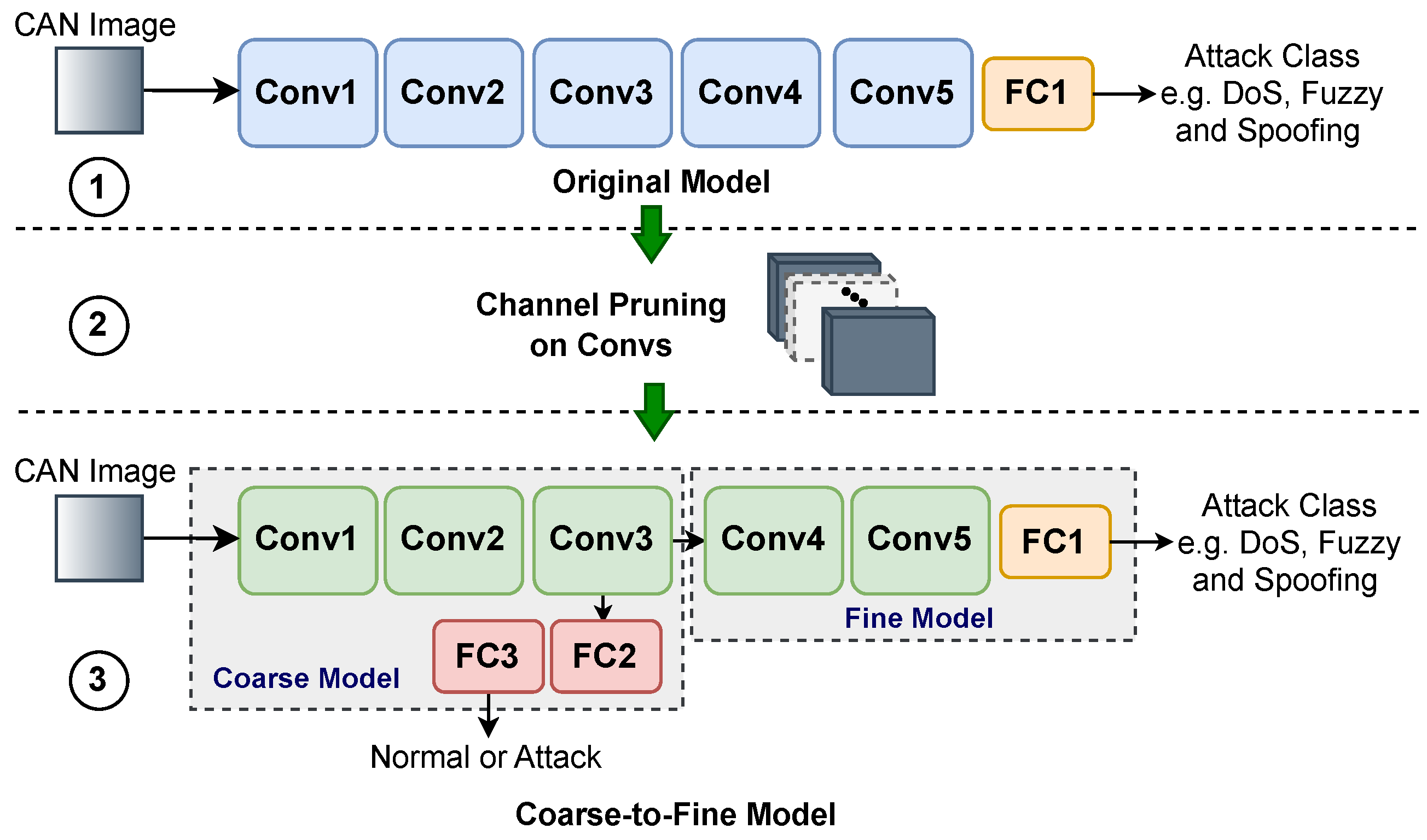
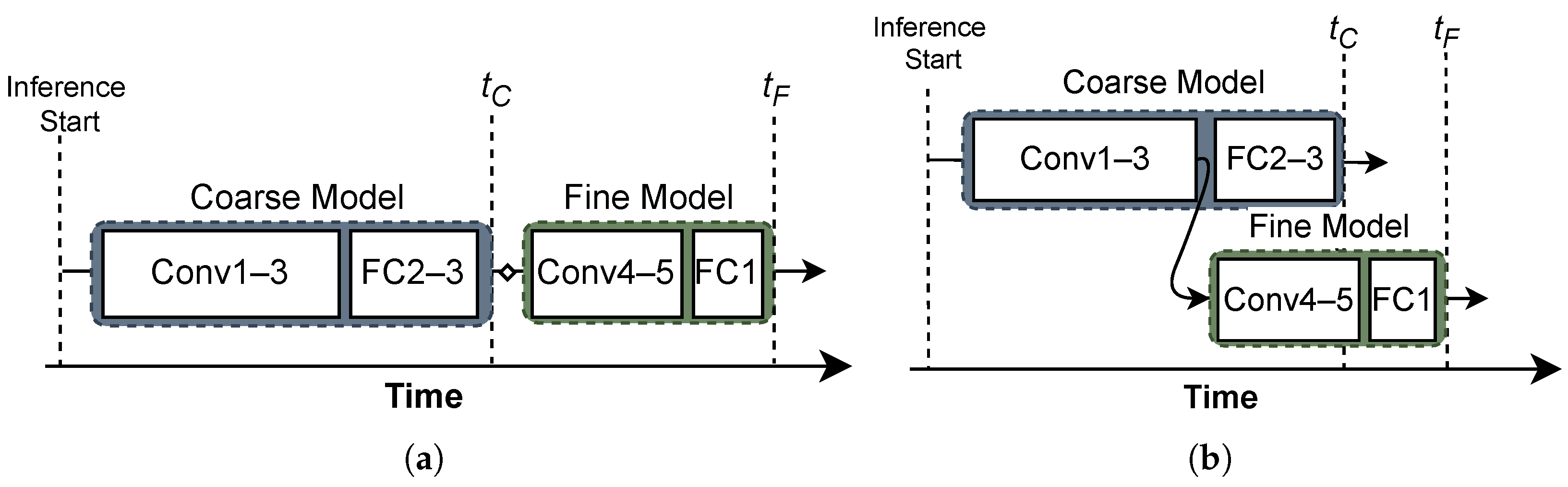
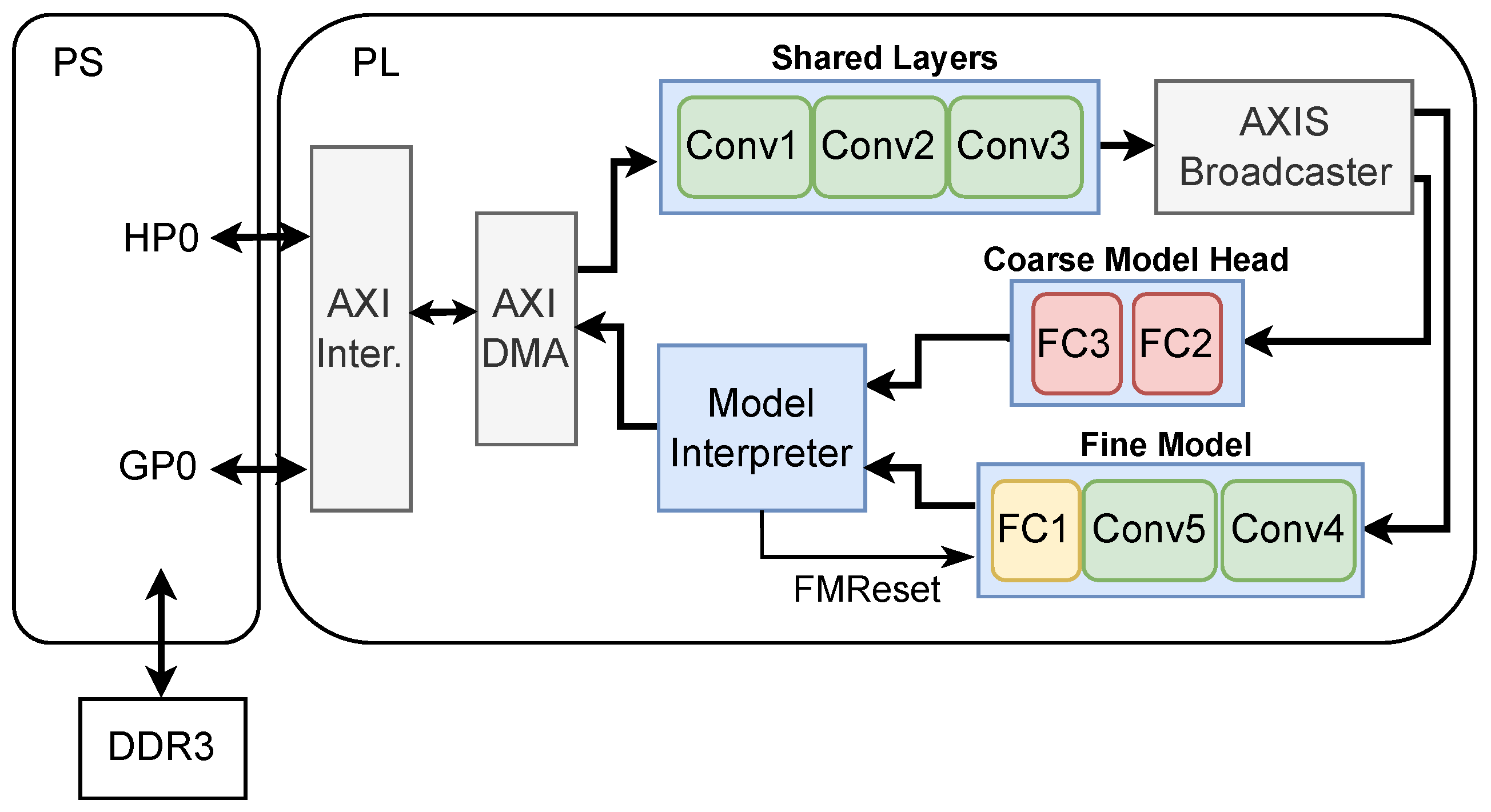
- The developed models are then structured using the Coarse-to-Fine (C2F) approach, which further reduces inference time by allowing the Coarse model to perform initial attack detection, while the Fine model is executed only when an attack is detected for classification. This approach saves inference time by up to 19.3% on GPU and 33% on FPGA when no attack is detected.
- The developed BNN-based IDSs are implemented on CPU, GPU, and FPGA platforms using state-of-the-art frameworks to fully exploit their computational efficiencies. The FPGA implementation demonstrates superior performance, outperforming GPU and CPU implementations by up to 3.7× and 2.4× in speed, while achieving up to 7.4× and 3.8× greater energy efficiency, respectively.
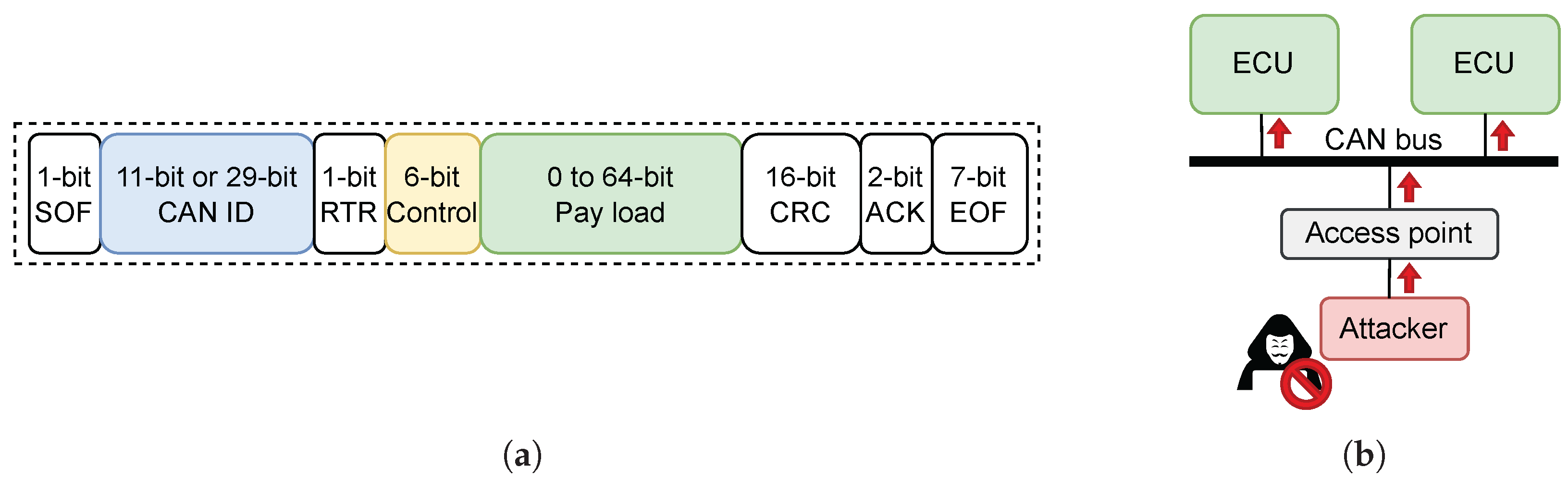
2. Background and Related Work
2.1. CAN Message and Injection Attack Datasets
- The first dataset, known as the Car-Hacking dataset (CH) [18], collected from a Hyundai FY Sonata, includes four attack types: DoS, Fuzzy, Gear Spoofing, and RPM Spoofing. During a DoS attack, messages with CAN ID 0x000 were injected every 0.3 ms to flood the network. For the Fuzzy attack, both CAN IDs and payloads were randomly generated, with messages injected at an interval of 0.5 ms. As the names of attacks imply, for Gear Spoofing and RPM Spoofing, messages with CAN IDs responsible for displaying gear position and speed gauge in RPM (revolutions per minute) were injected every 1 ms to manipulate these vehicle functions.
- The second dataset, part of the Survival Analysis Dataset (SA) [19], was extracted from a Chevrolet Spark, and comprises three attack types: DoS, Fuzzy, and Spoofing. Again, during DoS attack, messages with CAN ID 0x000 were injected to overload the network. During Fuzzy attack, messages with random CAN IDs ranging from 0x000 to 0x7FF were injected every 0.3 ms. Messages with a specific CAN ID (0x18E) were injected to deceive the vehicle’s systems during the Spoofing attack.
- The third dataset, collected from a Hyundai Avante CN7 in the Attack & Defense Challenge (ATK&DEF) [20], contains four attack types: DoS, Fuzzy, Spoofing, and Replay. The CAN messages were captured in both driving and stationary states, with preliminary round data used in this study. The DoS and Fuzzy attacks involve sending messages with the highest priority CAN ID (0x000) and random CAN IDs, respectively. Various Spoofing attacks were performed, including factory-mode warning, RPM gauge manipulation, engine-off warning, blind-spot collision warning, and rear-camera activation. During the Replay attack, previously captured CAN messages were re-injected into the network at a later time to mimic legitimate activity.
2.2. Related Work on BNN-Based IDSs
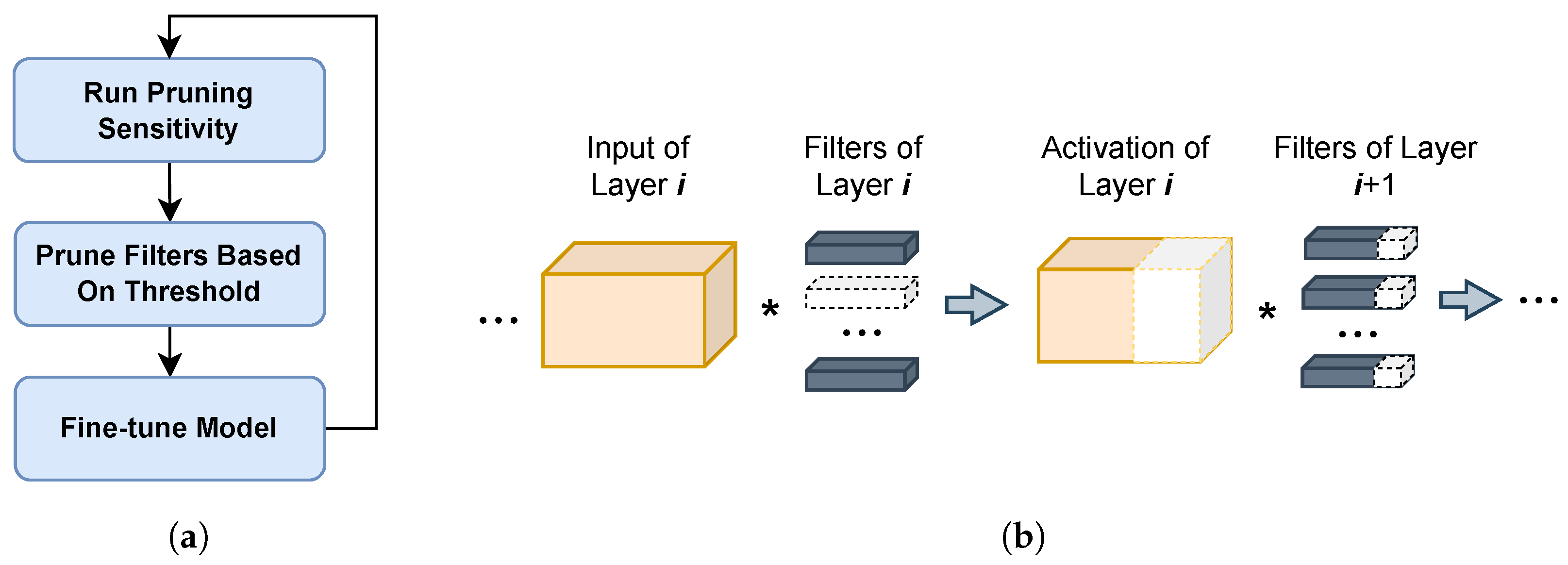
3. Proposed Pruned BNN-Based IDSs
3.1. Network Pruning for BNNs
3.2. Developing BNN-Based IDSs
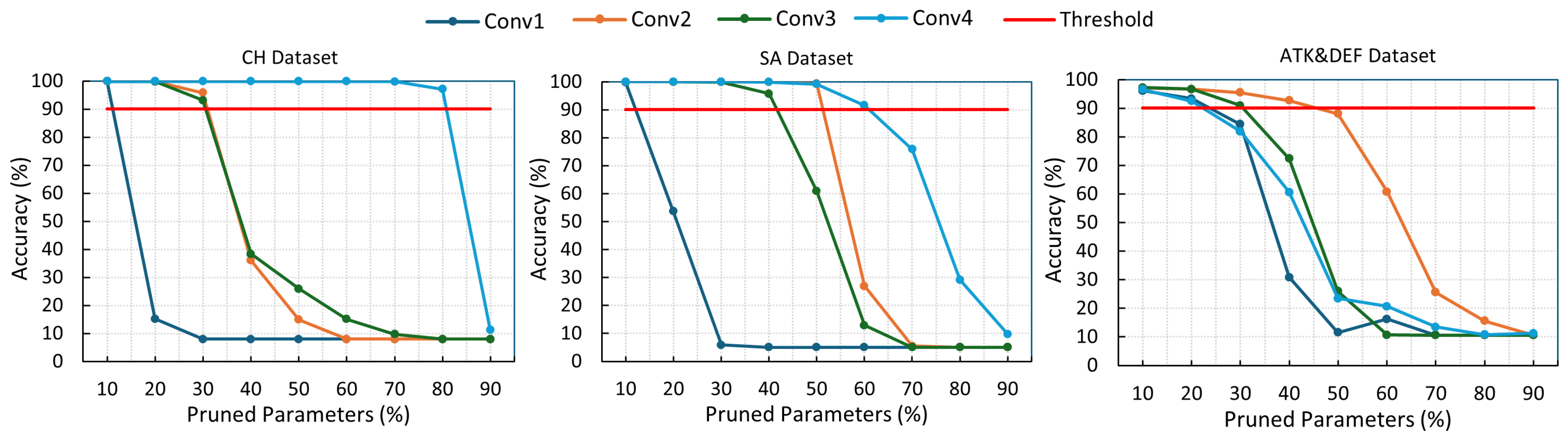
3.3. Pruning Models
3.4. Hardware Implementation Frameworks
3.4.1. CPU-Based BNN with Larq Compute Engine
3.4.2. GPU-Based BNN with Bit-Tensor Cores
3.4.3. FPGA-Based BNN with FINN
4. Validation and Experimental Results
4.1. Experimental Setup
- CPU—Raspberry Pi 5 [47]: A 64-bit quad-core Arm Cortex-A76 processor, using Larq Compute Engine (LCE) version 0.13.0.
- GPU—Jetson Orin Nano [48]: 1024-core NVIDIA Ampere architecture GPU with 32 Tensor Cores, using Bit-Tensor Core (BTC).
- FPGA—Zedboard [49]: Xilinx Zynq 7000 System-On-Chip (SoC), using FINN version 0.10 and Xilinx Vivado 2022.2.
4.2. Pruned Model Accuracy
4.3. CPU-Based Implementation
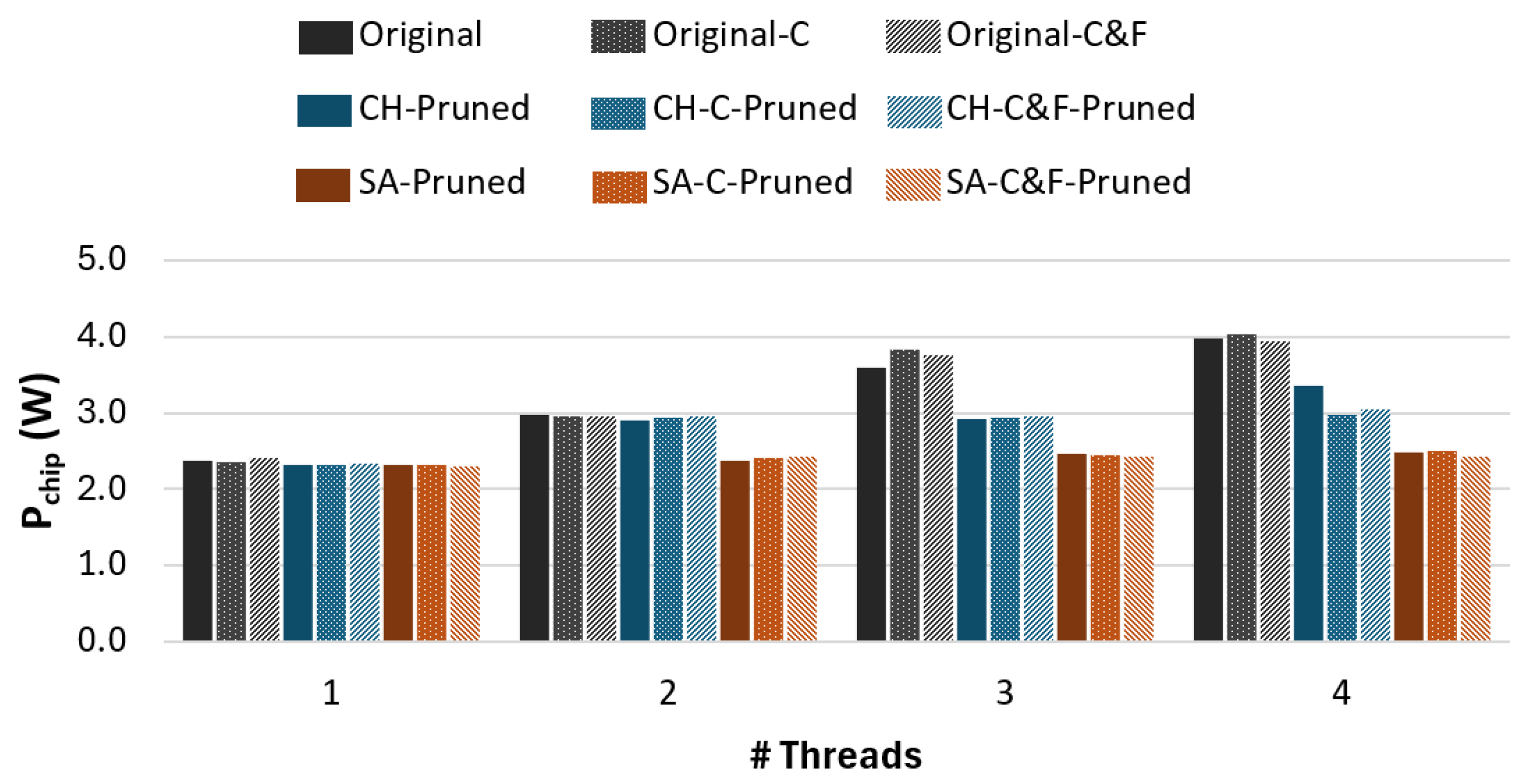
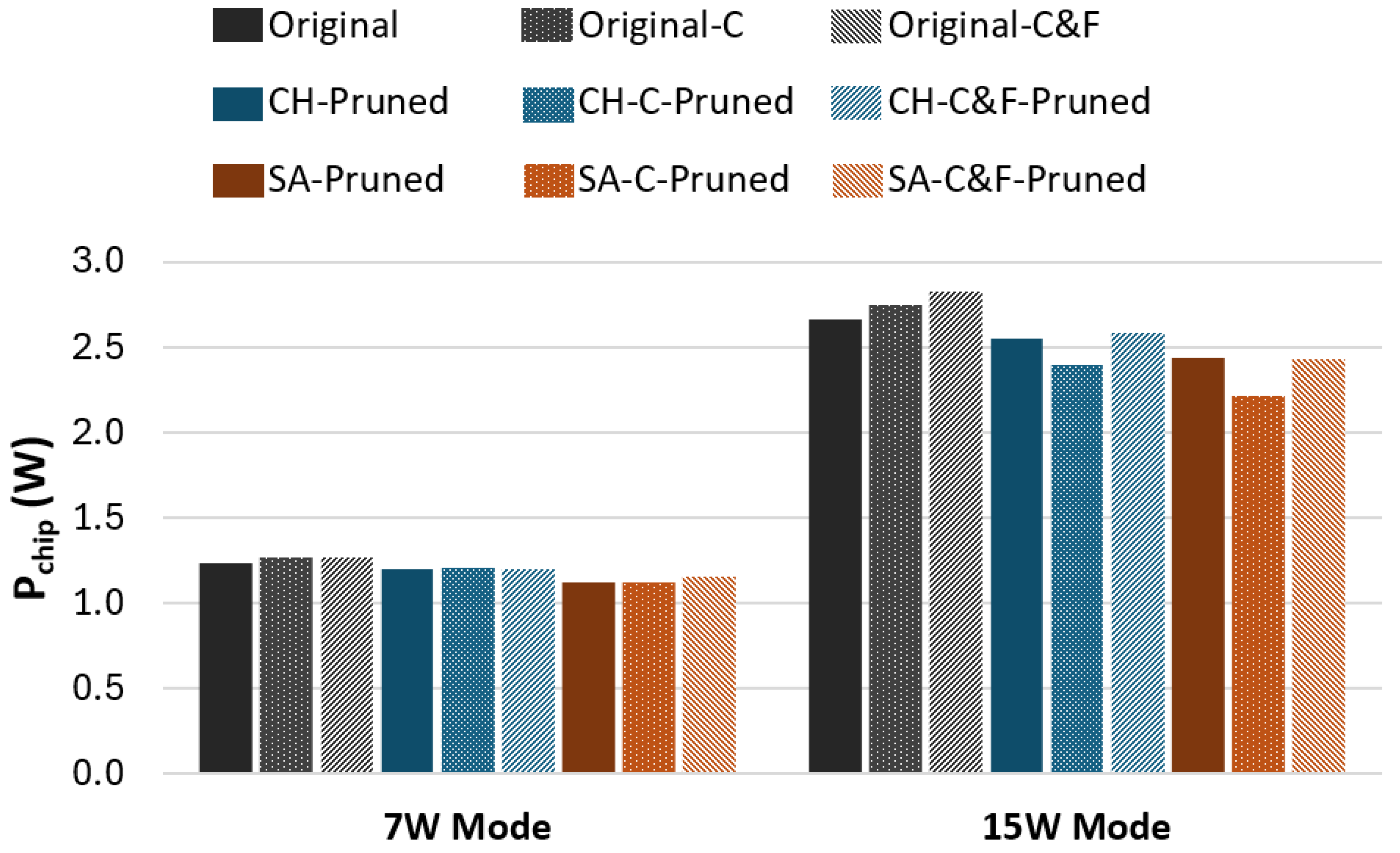
4.4. GPU-Based Implementation
4.5. FPGA-Based Implementation
4.6. Performance and Energy Efficiency Comparison
4.7. A Comparative Performance Analysis of the Proposed FPGA-Based IDS Against Other BNN-Based Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, T.U.; Song, H.M.; Jeong, S.; Kim, H.K. Automated reverse engineering and attack for CAN using OBD-II. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; IEEE: Piscatway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Miller, C. Remote exploitation of an unaltered passenger vehicle. In Proceedings of the Black Hat USA, Las Vegas, NV, USA, 1–6 August 2015. [Google Scholar]
- Jafarnejad, S.; Codeca, L.; Bronzi, W.; Frank, R.; Engel, T. A car hacking experiment: When connectivity meets vulnerability. In Proceedings of the 2015 IEEE globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; IEEE: Piscatway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Aliwa, E.; Rana, O.; Perera, C.; Burnap, P. Cyberattacks and countermeasures for in-vehicle networks. ACM Comput. Surv. (CSUR) 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Van Herrewege, A.; Singelee, D.; Verbauwhede, I. CANAuth-a simple, backward compatible broadcast authentication protocol for CAN bus. In Proceedings of the ECRYPT Workshop on Lightweight Cryptography, Louvain-la-Neuve, Belgium, 28 November 2011; Volume 2011, p. 20. [Google Scholar]
- Hazem, A.; Fahmy, H. Lcap-a lightweight can authentication protocol for securing in-vehicle networks. In Proceedings of the 10th Escar Embedded Security in Cars Conference, Berlin, Germany, 28–29 November 2012; Volume 6, p. 172. [Google Scholar]
- Farag, W.A. CANTrack: Enhancing automotive CAN bus security using intuitive encryption algorithms. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, 4–6 April 2017; IEEE: Piscatway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Lokman, S.F.; Othman, A.T.; Abu-Bakar, M.H. Intrusion detection system for automotive Controller Area Network (CAN) bus system: A review. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Rajapaksha, S.; Kalutarage, H.; Al-Kadri, M.O.; Petrovski, A.; Madzudzo, G.; Cheah, M. AI-based intrusion detection systems for in-vehicle networks: A survey. ACM Comput. Surv. 2023, 55, 1–40. [Google Scholar] [CrossRef]
- Khandelwal, S.; Shreejith, S. A lightweight FPGA-based IDS-ECU architecture for automotive CAN. In Proceedings of the 2022 International Conference on Field-Programmable Technology (ICFPT), Hong Kong, China, 5–9 December 2022; IEEE: Piscatway, NJ, USA, 2022; pp. 1–9. [Google Scholar]
- Khandelwal, S.; Walsh, A.; Shreejith, S. Quantised Neural Network Accelerators for Low-Power IDS in Automotive Networks. In Proceedings of the 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 17–19 April 2023; IEEE: Piscatway, NJ, USA, 2023; pp. 1–2. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks: Training deep neural networks with weights and activations constrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Zhang, L.; Yan, X.; Ma, D. A binarized neural network approach to accelerate in-vehicle network intrusion detection. IEEE Access 2022, 10, 123505–123520. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; Ma, D. Efficient and Effective In-Vehicle Intrusion Detection System using Binarized Convolutional Neural Network. In Proceedings of the IEEE INFOCOM 2024-IEEE Conference on Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; IEEE: Piscatway, NJ, USA, 2024; pp. 2299–2307. [Google Scholar]
- Rangsikunpum, A.; Amiri, S.; Ost, L. An FPGA-Based Intrusion Detection System Using Binarised Neural Network for CAN Bus Systems. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024; IEEE: Piscatway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Rangsikunpum, A.; Amiri, S.; Ost, L. BIDS: An efficient Intrusion Detection System for in-vehicle networks using a two-stage Binarised Neural Network on low-cost FPGA. J. Syst. Archit. 2024, 156, 103285. [Google Scholar] [CrossRef]
- Rangsikunpum, A.; Amiri, S.; Ost, L. A Reconfigurable Coarse-to-Fine Approach for the Execution of CNN Inference Models in Low-Power Edge Devices. IET Comput. Digit. Tech. 2024, 2024, 6214436. [Google Scholar] [CrossRef]
- Seo, E.; Song, H.M.; Kim, H.K. GIDS: GAN based intrusion detection system for in-vehicle network. In Proceedings of the 2018 16th Annual Conference on Privacy, Security and Trust (PST), Belfast, UK, 28–30 August 2018; IEEE: Piscatway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Han, M.L.; Kwak, B.I.; Kim, H.K. Anomaly intrusion detection method for vehicular networks based on survival analysis. Veh. Commun. 2018, 14, 52–63. [Google Scholar] [CrossRef]
- Kang, H.; Kwak, B.I.; Lee, Y.H.; Lee, H.; Lee, H.; Kim, H.K. Car hacking and defense competition on in-vehicle network. In Proceedings of the Workshop on Automotive and Autonomous Vehicle Security (AutoSec), Online, 25 February 2021; Volume 2021, p. 25. [Google Scholar]
- Ioffe, S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Hinton, G. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Sharma, A.; Vans, E.; Shigemizu, D.; Boroevich, K.A.; Tsunoda, T. DeepInsight: A methodology to transform a non-image data to an image for convolution neural network architecture. Sci. Rep. 2019, 9, 11399. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Chen, M.; Gu, Z.; Luan, S.; Zeng, H.; Chakrabory, S. CAN bus intrusion detection based on auxiliary classifier GAN and out-of-distribution detection. ACM Trans. Embed. Comput. Syst. (TECS) 2022, 21, 45. [Google Scholar] [CrossRef]
- Mao, H.; Han, S.; Pool, J.; Li, W.; Liu, X.; Wang, Y.; Dally, W.J. Exploring the granularity of sparsity in convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 13–20. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Hu, H. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient inference engine on compressed deep neural network. ACM SIGARCH Comput. Archit. News 2016, 44, 243–254. [Google Scholar] [CrossRef]
- Luo, J.H.; Wu, J. An entropy-based pruning method for cnn compression. arXiv 2017, arXiv:1706.05791. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel pruning for accelerating very deep neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1389–1397. [Google Scholar]
- Li, Y.; Ren, F. Bnn pruning: Pruning binary neural network guided by weight flipping frequency. In Proceedings of the 2020 21st International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 25–26 March 2020; IEEE: Piscatway, NJ, USA, 2020; pp. 306–311. [Google Scholar]
- Guerra, L.; Drummond, T. Automatic pruning for quantized neural networks. In Proceedings of the 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia, 29 November–1 December 2021; IEEE: Piscatway, NJ, USA, 2021; pp. 01–08. [Google Scholar]
- Bannink, T.; Hillier, A.; Geiger, L.; de Bruin, T.; Overweel, L.; Neeven, J.; Helwegen, K. Larq compute engine: Design, benchmark and deploy state-of-the-art binarized neural networks. Proc. Mach. Learn. Syst. 2021, 3, 680–695. [Google Scholar]
- Chen, T.; Moreau, T.; Jiang, Z.; Zheng, L.; Yan, E.; Shen, H.; Cowan, M.; Wang, L.; Hu, Y.; Ceze, L.; et al. {TVM}: An automated {End-to-End} optimizing compiler for deep learning. In Proceedings of the 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), Carlsbad, CA, USA, 10–12 July 2018; pp. 578–594. [Google Scholar]
- Zhang, J.; Pan, Y.; Yao, T.; Zhao, H.; Mei, T. dabnn: A super fast inference framework for binary neural networks on arm devices. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2272–2275. [Google Scholar]
- Google. LiteRT. Available online: https://ai.google.dev/edge/litert (accessed on 27 February 2025).
- Geiger, L.; Team, P. Larq: An open-source library for training binarized neural networks. J. Open Source Softw. 2020, 5, 1746. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Available online: https://www.tensorflow.org/ (accessed on 27 February 2025).
- Larq. Optimizing Models for Larq Compute Engine. Available online: https://docs.larq.dev/compute-engine/model_optimization_guide/ (accessed on 27 February 2025).
- Li, A.; Su, S. Accelerating binarized neural networks via bit-tensor-cores in turing gpus. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1878–1891. [Google Scholar] [CrossRef]
- NVIDIA. NVIDIA Tensor Cores. Available online: https://www.nvidia.com/en-eu/data-center/tensorcore/ (accessed on 27 February 2025).
- Umuroglu, Y.; Fraser, N.J.; Gambardella, G.; Blott, M.; Leong, P.; Jahre, M.; Vissers, K. Finn: A framework for fast, scalable binarized neural network inference. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; pp. 65–74. [Google Scholar]
- Blott, M.; Preußer, T.B.; Fraser, N.J.; Gambardella, G.; O’brien, K.; Umuroglu, Y.; Leeser, M.; Vissers, K. FINN-R: An end-to-end deep-learning framework for fast exploration of quantized neural networks. ACM Trans. Reconfigurable Technol. Syst. (TRETS) 2018, 11, 1–23. [Google Scholar] [CrossRef]
- Pappalardo, A. Xilinx/brevitas; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- ARM. AMBA AXI-Stream Protocol Specification; ARM: Cambridge, UK, 2021. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. In Proceedings of the 2017 Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Raspberry Pi. Raspberry Pi 5. Available online: https://www.raspberrypi.com/products/raspberry-pi-5/ (accessed on 27 February 2025).
- NVIDIA. Jetson Orin Nano Super Developer Kit. Available online: https://www.nvidia.com/en-gb/autonomous-machines/embedded-systems/jetson-orin/nano-super-developer-kit/ (accessed on 27 February 2025).
- Avnet. Zedboard—Avnet Boards. Available online: https://www.avnet.com/wps/portal/us/products/avnet-boards/avnet-board-families/zedboard/ (accessed on 27 February 2025).
- AMD. AXI DMA LogiCORE IP Product Guide (PG021). Available online: https://docs.amd.com/r/en-US/pg021_axi_dma (accessed on 27 February 2025).
- AMD. AXI4-Stream Infrastructure IP Suite (PG085). Available online: https://docs.amd.com/r/en-US/pg085-axi4stream-infrastructure/AXI4-Stream-Broadcaster (accessed on 27 February 2025).

| Dataset | Year | Vehicle | # Messages | # Attacks |
|---|---|---|---|---|
| Car Hacking (CH) [18] | 2018 | Hyundai YF Sonata | 17,558,462 | 4 |
| Survial Analysis (SA) [19] | 2018 | Chevrolet Spark | 402,956 | 3 |
| Attack & Defense Challenge (ATK&DEF) [20] | 2021 | Hyundai Avante CN7 | 7,424,197 | 4 |
| Model | Input | Classifier | Key Techniques |
|---|---|---|---|
| BNN-FCs, 2022 [13] | ID, Payload | Binary | Evaluation on CPU, GPU, and FPGA |
| BCNN, 2024 [14] | ID, Payload | Binary | DeepInsight [23] for image formation |
| BNN-C2F, 2024 [15] | ID | Multiclass | Coarse-to-Fine (C2F) model |
| BIDS, 2024 [16] | ID | Multiclass | GAN for unknown attack detection |
| This work | ID | Multiclass | Pruning with CPU, GPU, and FPGA evaluation |
| Dataset | Shift (s) | # CAN Images w/o SW | # CAN Images with SW | Acc. (%) w/o SW | Acc. (%) with SW | ||
|---|---|---|---|---|---|---|---|
| Normal | Attack | Normal | Attack | ||||
| CH—Hyundai YF Sonata | 24 | 232,838 | 132,539 | 450,914 | 265,026 | 99.91 | 99.94 |
| ATK&DEF— Hyundai Avante CN7 | 12 | 47,693 | 28,807 | 189,083 | 115,114 | 96.98 | 97.64 |
| SA—Chevrolet Spark | 1 | 6181 | 2212 | 257,648 | 104,346 | 99.76 | 99.99 |
| Dataset | # Iterations | Acc. (%) | ΔAcc. (%) | Reduced Params (%) |
|---|---|---|---|---|
| CH | 3 | 99.93 | −0.01 | 91.07 |
| SA | 3 | 99.98 | −0.01 | 87.51 |
| ATK&DEF | 1 | 96.51 | −1.13 | 33.39 |
| Layer | # Original Params | Params Pruned | # Original Activations | Acts Pruned | ||
|---|---|---|---|---|---|---|
| CH | SA | CH | SA | |||
| Conv1 | 0.4 k | 18.8% | 27.1% | 27.6 k | 18.8% | 27.1% |
| Conv2 | 41.5 k | 54.3% | 81.8% | 13.8 k | 43.8% | 75.0% |
| Conv3 | 82.9 k | 80.7% | 92.5% | 3.4 k | 65.6% | 69.8% |
| Conv4 | 165.9 k | 98.2% | 94.9% | 1.7 k | 94.8% | 83.3% |
| Conv5 | 331.8 k | 94.8% | 83.2% | 0.2 k | 0% | 0% |
| Total | 622.5 k | 91.1% | 87.5% | 46.8 k | 32.3% | 46.3% |
| Dataset | Attack | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) |
|---|---|---|---|---|---|
| CH (Pruned) | DoS | 99.92 | 99.98 | 99.88 | 99.93 |
| Fuzzy | 99.99 | 99.65 | 99.82 | ||
| Spoofing RPM | 99.97 | 99.81 | 99.89 | ||
| Spoofing Gear | 99.98 | 100 | 99.99 | ||
| SA (Pruned) | DoS | 99.96 | 100 | 99.95 | 99.98 |
| Fuzzy | 99.97 | 99.70 | 99.84 | ||
| Spoofing | 100 | 99.80 | 99.90 | ||
| ATK&DEF (Original) | DoS | 96.96 | 100 | 99.66 | 99.83 |
| Fuzzy | 97.94 | 95.18 | 96.54 | ||
| Spoofing | 92.26 | 85.71 | 88.86 | ||
| Replay | 97.46 | 86.40 | 91.60 |
| Dataset | Attack | TP | TN | FP | FN |
|---|---|---|---|---|---|
| CH (Pruned) | DoS | 9165 | 125,827 | 2 | 11 |
| Fuzzy | 10,732 | 124,235 | 1 | 37 | |
| Spoof RPM | 15,944 | 119,026 | 5 | 30 | |
| Spoof Gear | 17,252 | 117,731 | 3 | 19 | |
| SA (Pruned) | DoS | 11,064 | 61,330 | 0 | 5 |
| Fuzzy | 3633 | 68,754 | 1 | 11 | |
| Spoofing | 6080 | 66,307 | 0 | 12 | |
| ATK&DEF (Original) | DoS | 7337 | 53,478 | 0 | 25 |
| Fuzzy | 6125 | 54,276 | 129 | 310 | |
| Spoofing | 3208 | 56,828 | 269 | 535 | |
| Replay | 4760 | 55,207 | 124 | 749 |
| Model | Average Inference Time (µs) | |||
|---|---|---|---|---|
| 1 Thread | 2 Threads | 3 Threads | 4 Threads | |
| Original | 204 | 181 | 159 | 225 |
| Original-C | 197 | 177 | 154 | 222 |
| Original-C&F | 222 | 200 | 182 | 254 |
| CH-Pruned | 160 | 130 | 125 | 127 |
| CH-C-Pruned | 153 | 127 | 131 | 127 |
| CH-C&F-Pruned | 163 | 137 | 141 | 138 |
| SA-Pruned | 129 | 114 | 109 | 107 |
| SA-C-Pruned | 124 | 112 | 107 | 112 |
| SA-C&F-Pruned | 136 | 122 | 117 | 129 |
| Model | Average Inference Time (µs) | |
|---|---|---|
| 7 W Mode | 15 W Mode | |
| Original | 512 | 243 |
| Original-C | 413 | 178 |
| Original-C&F | 529 | 254 |
| CH-Pruned | 424 | 212 |
| CH-C-Pruned | 357 | 170 |
| CH-C&F-Pruned | 458 | 235 |
| SA-Pruned | 369 | 183 |
| SA-C-Pruned | 305 | 140 |
| SA-C&F-Pruned | 405 | 205 |
| Model | LUTs | BRAM | Pchip (W) | Inf. Time (µs) |
|---|---|---|---|---|
| Original | 24,463 | 3.29 Mb | 2.41 | 65 |
| Original-C2F | 26,793 | 4.52 Mb | 2.51 | 53 (Coarse) 65 (C&F) |
| CH-Pruned | 13,613 | 1.35 Mb | 2.13 | 63 |
| CH-C2F-Pruned | 14,557 | 1.48 Mb | 2.13 | 42 (Coarse) 63 (C&F) |
| SA-Pruned | 10,067 | 0.67 Mb | 1.89 | 60 |
| SA-C2F-Pruned | 10,909 | 0.74 Mb | 1.89 | 40 (Coarse) 60 (C&F) |
| Model | FPGA | GPU (Max Performance) | CPU (Max Performance) | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
Inf. Time
(µs) |
Pboard (W) | Efficiency (# Inf./J) |
Inf. Time
(µs) |
Pboard (W) | Efficiency (# Inf./J) |
Inf. Time
(µs) |
Pboard (W) | Efficiency (# Inf./J) | |
| Original | 65 | 4.6 | 3344 | 243 | 9.1 | 452 | 159 | 7.2 | 873 |
| Original-C | 53 | 4.7 | 4014 | 178 | 9.1 | 617 | 154 | 7.2 | 902 |
| Original-C&F | 65 | 4.7 | 3273 | 254 | 9.2 | 428 | 182 | 7.2 | 763 |
| CH-Pruned | 63 | 4.5 | 3527 | 212 | 9.0 | 524 | 125 | 6.3 | 1270 |
| CH-C-Pruned | 42 | 4.4 | 5291 | 175 | 8.9 | 642 | 127 | 6.3 | 1250 |
| CH-C&F-Pruned | 63 | 4.5 | 3527 | 240 | 9.0 | 463 | 137 | 6.3 | 1159 |
| SA-Pruned | 60 | 4.5 | 3788 | 183 | 8.8 | 621 | 107 | 5.8 | 1611 |
| SA-C-Pruned | 40 | 4.4 | 5682 | 145 | 8.7 | 793 | 107 | 5.7 | 1640 |
| SA-C&F-Pruned | 60 | 4.4 | 3788 | 210 | 8.9 | 535 | 117 | 5.6 | 1526 |
| Model | Dataset | Accuracy (%) | F1 (%) | Avg. Inf. Time (µs) | Device |
|---|---|---|---|---|---|
| BNN-FC [13] | 4 Cars | 93.15 | - | 400 | Xilinx PYNQ Artix-7 |
| BCNN [14] | 95.51 | 96.93 | 600 | Nvidia RTX 2070 Super | |
| BNN-C2F [15] | CH | 99.83 | 99.75 | 364 | Zedboard |
| BIDS [16] | 99.72 | 99.52 | 169 | ||
| Proposed IDS | 99.92 | 99.91 | 50 | ||
| BIDS [16] | SA | 98.87 | 95.54 | 162 | |
| Proposed IDS | 99.96 | 99.91 | 48 | ||
| Proposed IDS | ATK&DEF | 96.96 | 94.21 | 56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rangsikunpum, A.; Amiri, S.; Ost, L. Ultra-Lightweight and Highly Efficient Pruned Binarised Neural Networks for Intrusion Detection in In-Vehicle Networks. Electronics 2025, 14, 1710. https://doi.org/10.3390/electronics14091710
Rangsikunpum A, Amiri S, Ost L. Ultra-Lightweight and Highly Efficient Pruned Binarised Neural Networks for Intrusion Detection in In-Vehicle Networks. Electronics. 2025; 14(9):1710. https://doi.org/10.3390/electronics14091710
Chicago/Turabian StyleRangsikunpum, Auangkun, Sam Amiri, and Luciano Ost. 2025. "Ultra-Lightweight and Highly Efficient Pruned Binarised Neural Networks for Intrusion Detection in In-Vehicle Networks" Electronics 14, no. 9: 1710. https://doi.org/10.3390/electronics14091710
APA StyleRangsikunpum, A., Amiri, S., & Ost, L. (2025). Ultra-Lightweight and Highly Efficient Pruned Binarised Neural Networks for Intrusion Detection in In-Vehicle Networks. Electronics, 14(9), 1710. https://doi.org/10.3390/electronics14091710







