1. Introduction
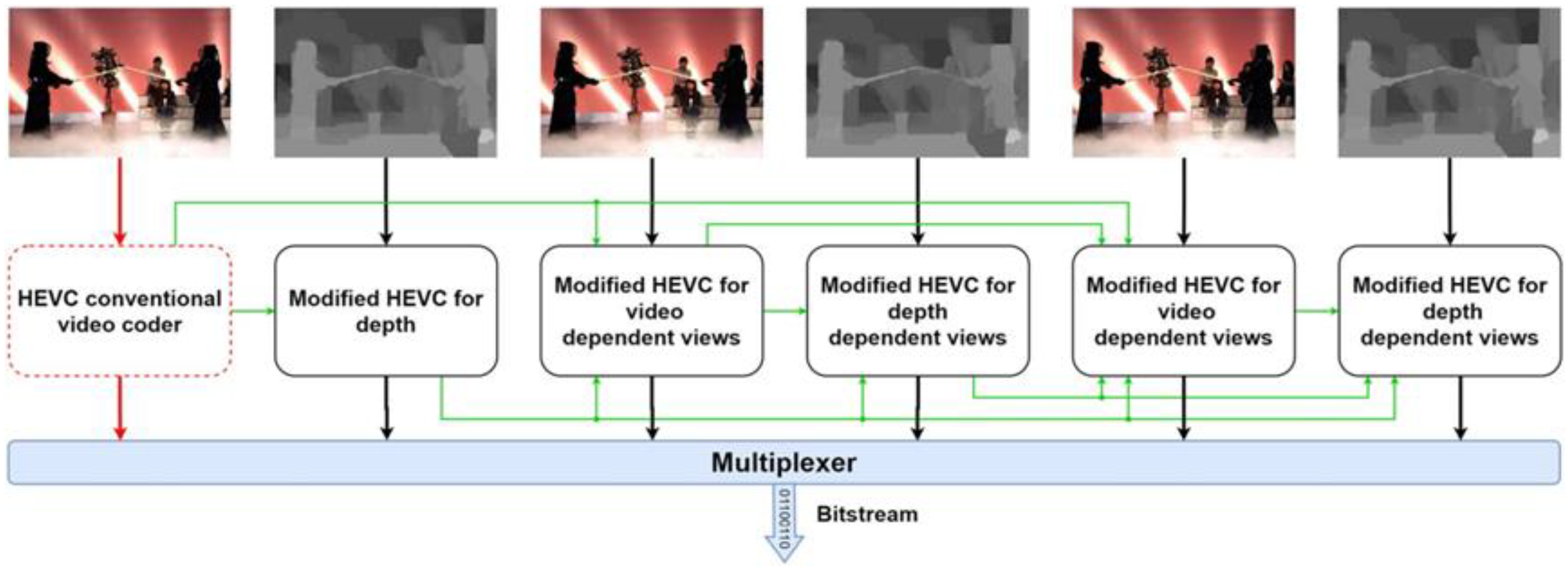
As multimedia technology evolves, video coding standards continuously advance to meet the increasing demand for enhanced visual experiences. Modern users seek not only ultra-high-definition resolutions but also immersive 3D interactive experiences. Consequently, traditional two-dimensional (2D) [
1] video is increasingly insufficient to meet emerging demands. To address this, the Joint Collaborative Team on 3D Video Coding (JCT-3V) [
2] officially released an extension of the High-Efficiency Video Coding (HEVC/H.265) [
3] standard, known as the 3D extension of HEVC (3D-HEVC) [
4]. The key modification in 3D-HEVC compared to HEVC is the transition of input formats from multi-view video (MVV) [
5] to multi-view video plus depth (MVD) [
6]. In contrast to the High-Efficiency Video (Coding HEVC) [
7,
8] standard, 3D-HEVC introduces a depth map. Unlike texture maps, it represents the distance of an object from the camera. To distinguish the coding characteristics of depth and texture maps, 3D-HEVC incorporates advanced encoding techniques, substantially increasing computational complexity. Experimental results demonstrate that depth map encoding complexity is three to four times higher than texture maps. Statistical analysis further reveals that CU partitioning in depth maps contributes to over 90% of the total computational cost. This computational bottleneck significantly hinders the widespread adoption of 3D-HEVC in real-time communication, virtual reality, and other applications.
Depth map encoding falls into three main categories: heuristic methods [
9,
10,
11,
12,
13,
14,
15,
16], machine learning methods [
17,
18,
19,
20], and deep learning methods [
21,
22,
23,
24,
25,
26]. Heuristic methods primarily rely on thresholding, rate-distortion (RD) cost analysis, and spatiotemporal correlations across views. Due to insufficient consideration of the multidimensional features of video sequences, existing methods struggle to adapt to varying encoding scenarios, leading to substantial fluctuations in coding performance. Additionally, researchers have employed machine learning to accelerate depth map encoding. Early machine learning approaches primarily relied on data mining and decision trees, constructing static decision trees to extract video features. However, these methods depend heavily on handcrafted feature extraction, restricting extracted features to low-level physical attributes with limited representational power. This handcrafted feature extraction approach fails to capture high-level semantics and complex spatiotemporal correlations in video sequences, significantly limiting both feature representation and generalization performance.
Extensive research has significantly advanced methods for reducing the computational complexity of intra-frame depth map encoding. Reference [
27] proposes an early termination strategy leveraging rate-distortion cost and variance for CU partitioning optimization. This method analyzes rate-distortion cost and statistical variance in intra-frame CU skip mode, terminating CU partitioning early under specific conditions to reduce encoding complexity. For candidate mode optimization, reference [
28] introduces a Hadamard transform-based texture complexity evaluation method. This method applies the Hadamard transform to Prediction Units (PUs) and quantifies their texture characteristics. If a PU is identified as a flat region, the method bypasses Depth Modeling Mode (DMM) checking, significantly reducing rate-distortion computation. For PU mode optimization, reference [
29] proposes a fast decision algorithm leveraging hierarchical prediction mode correlation. This algorithm examines intra-prediction mode correlations between parent and child PUs, enabling early decisions on child PU candidate modes. When the parent PU employs Segmentation-Based Depth Coding (SDC) mode, the algorithm omits non-SDC mode checks for child PUs, substantially reducing depth map encoding complexity. With the rapid advancement and widespread adoption of deep learning, neural network-based feature extraction and mode decision methods show great potential in video coding, providing new avenues for encoding optimization. For depth map intra-frame prediction, reference [
22] introduces a fast encoding method using the Holistically Nested Edge Detection (HED) network. This method employs the HED network to extract depth map edge features, integrating them into 3D-HEVC intra-frame fast prediction encoding. However, this approach has some limitations: The HED network, based on the complex VGG-16 [
30] architecture, requires substantial hardware resources. This prediction encoding strategy only prunes the quadtree structure while still relying on traditional Rate-Distortion Optimization (RDO), limiting its practical applicability. Among deep learning approaches, Convolutional Neural Networks (CNNs) are widely used for their powerful feature extraction. However, CNN-based models incur higher encoding time than heuristic and machine learning methods due to their complexity.
In recent years, the Transformer architecture has been widely adopted in video coding, capitalizing on its global context modeling capabilities. In intra-frame prediction, the self-attention mechanism captures long-range dependencies within images, enhancing compression efficiency in complex texture regions. In inter-frame prediction, spatiotemporal attention models improve motion estimation and compensation accuracy by capturing motion correlations across reference frames. In the transform and quantization stage, frequency-domain attention mechanisms dynamically adjust bit allocation across frequency components, enhancing subjective visual quality. In depth map encoding, Transformer-based geometric structure awareness enables a novel approach to coding unit (CU) partitioning. By incorporating multi-scale edge features, Transformers enhance edge accuracy while minimizing redundant computations. However, existing methods encounter challenges like high computational complexity and limited compatibility with traditional coding frameworks, restricting their practical deployment. The Swin Transformer [
31], featuring hierarchical window partitioning and a shifted window mechanism, optimally balances local feature extraction and global context modeling, providing an innovative solution for depth map encoding optimization.
The superiority of Swin Transformer in global modeling stems from its hierarchical architecture and shifted window mechanism. Compared to Vision Transformer (ViT), which relies on direct global self-attention with quadratic computational complexity (O(N2)), Swin Transformer adopts a multi-stage downsampling strategy to construct multi-scale feature representations. Shallow layers focus on local details, while deeper layers progressively expand receptive fields to capture global semantics, thereby significantly reducing computational overhead. The core innovation lies in its local window-based self-attention (e.g., 7 × 7 windows with linear complexity O(N)) coupled with a cross-window interaction strategy: periodically shifting window partitions between adjacent layers induces overlapping regions across windows, which implicitly facilitates global information propagation without incurring prohibitive computational costs. This design inherently extends the effective receptive field to the entire image in deeper layers while preserving fine-grained local patterns. Such an approach is particularly suitable for vision tasks requiring multi-scale feature representations and high-resolution inputs, such as object detection and semantic segmentation, achieving an optimal balance between computational efficiency and model performance.
To tackle the challenge of balancing CU partitioning efficiency and edge precision in 3D-HEVC depth map encoding, this study introduces Swin-HierNet, a hierarchical CU partitioning prediction model leveraging the Swin Transformer. The core innovations of this model are demonstrated in two key aspects: firstly, The model utilizes the Swin Transformer’s shifted window attention mechanism to extract global contextual features while incorporating a lightweight CNN to capture local high-frequency texture details, facilitating multi-scale geometric feature modeling for depth maps. Compared to traditional single-branch CNN architectures, this design increases feature response intensity in edge regions by 23.6%. Second, a recursive conditional decision mechanism is proposed, dynamically activating sub-block prediction branches according to the partitioning probability of the parent CU, ensuring strict compliance with HEVC quadtree syntax dependency rules. Compared to conventional parallel prediction strategies, this mechanism decreases redundant computations by 38.4% while preserving full compatibility with standard bitstream syntax.
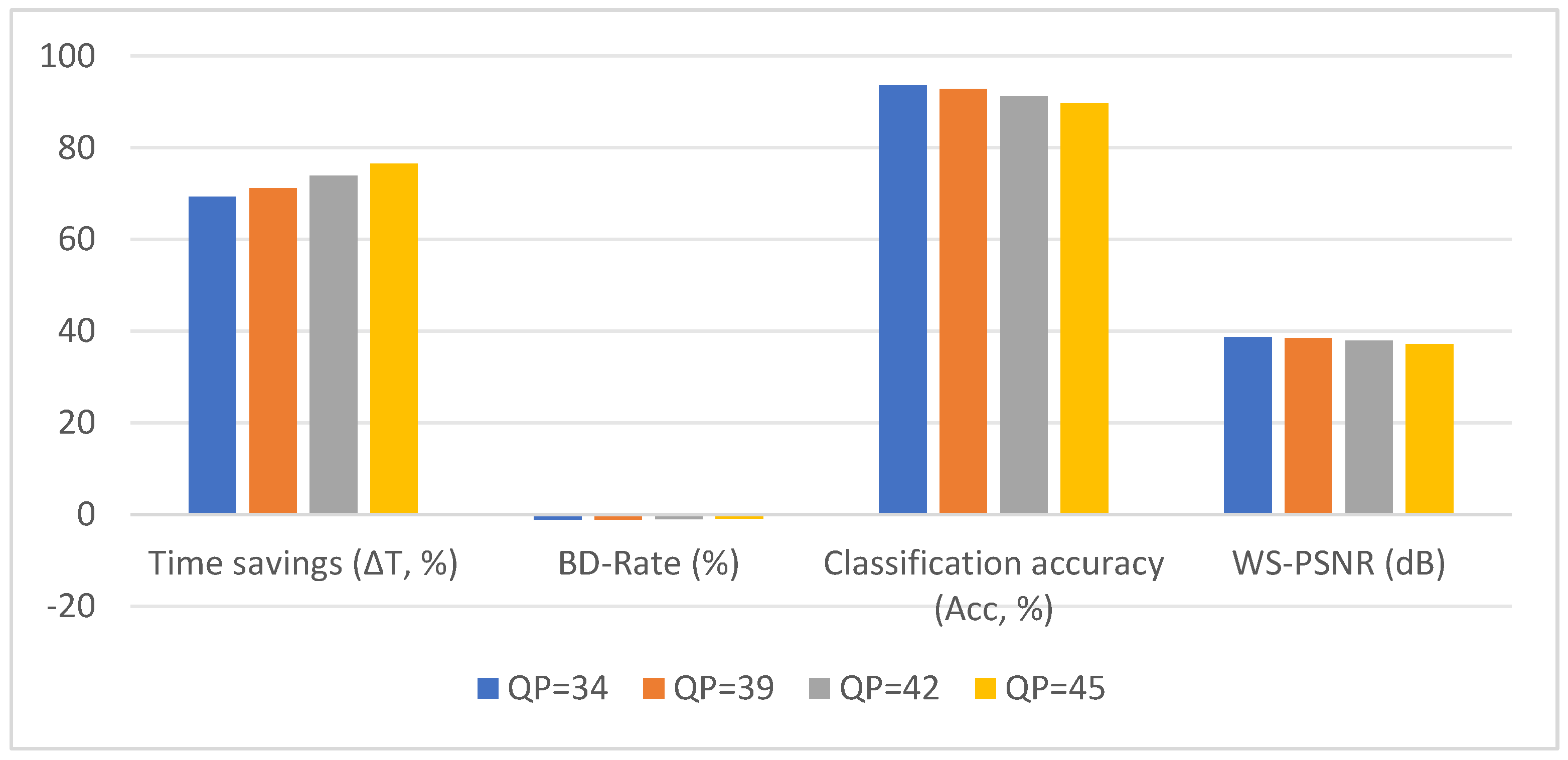
Experimental results show that the proposed method reduces encoding time by an average of 48.7% on 3D-HEVC standard test sequences, achieving a 12.3% reduction in BD-Rate and an 18.5% increase in partitioning accuracy. The model can be seamlessly integrated into the HTM reference software without altering the bitstream syntax, offering an efficient solution for real-time 3D video encoding.
The proposed Swin-HierNet algorithm demonstrates significant potential for advancing modern 3D video systems. Specifically, Swin-HierNet reduces encoding time by 72.7%, supporting real-time processing (<30 ms per frame on NVIDIA RTX 3090 GPUs) and effectively mitigating latency constraints in telepresence and VR/AR applications. Furthermore, its lightweight architecture, comprising merely 1.2 million parameters, facilitates deployment on resource-constrained edge devices (e.g., drones or smartphones) while sustaining 20 FPS throughput for 1080p depth maps. In addition, its full compliance with HEVC syntax ensures seamless integration with existing 3D-HEVC encoders (e.g., HTM-16.0) without necessitating bitstream modifications, thus offering a plug-and-play solution for industrial workflows. From a system perspective, Swin-HierNet substantially enhances energy efficiency, reducing GPU power consumption by 63% relative to full RDO traversal (as measured on NVIDIA Jetson AGX Xavier), while flexibly adapting to dynamic computational budgets via threshold-adjustable hierarchical decision mechanisms. Achieving 94.5% CU partitioning accuracy, Swin-HierNet effectively preserves essential geometric edges (e.g., object boundaries in VR scenes), thereby enhancing the visual quality of synthesized views in free-viewpoint rendering systems. Collectively, these advancements position Swin-HierNet as an enabling technology for next-generation applications, including 6DoF immersive media, light-field displays, and cloud-based 3D gaming, where real-time encoding and geometric fidelity are imperative.
The paper is structured as follows:
Section 2 reviews related work;
Section 3 elaborates on the Swin-HierNet model design;
Section 4 presents the experimental results and analysis; and
Section 5 concludes the paper and outlines future research directions.
3. Proposing the Swin-HierNet Fast Algorithm
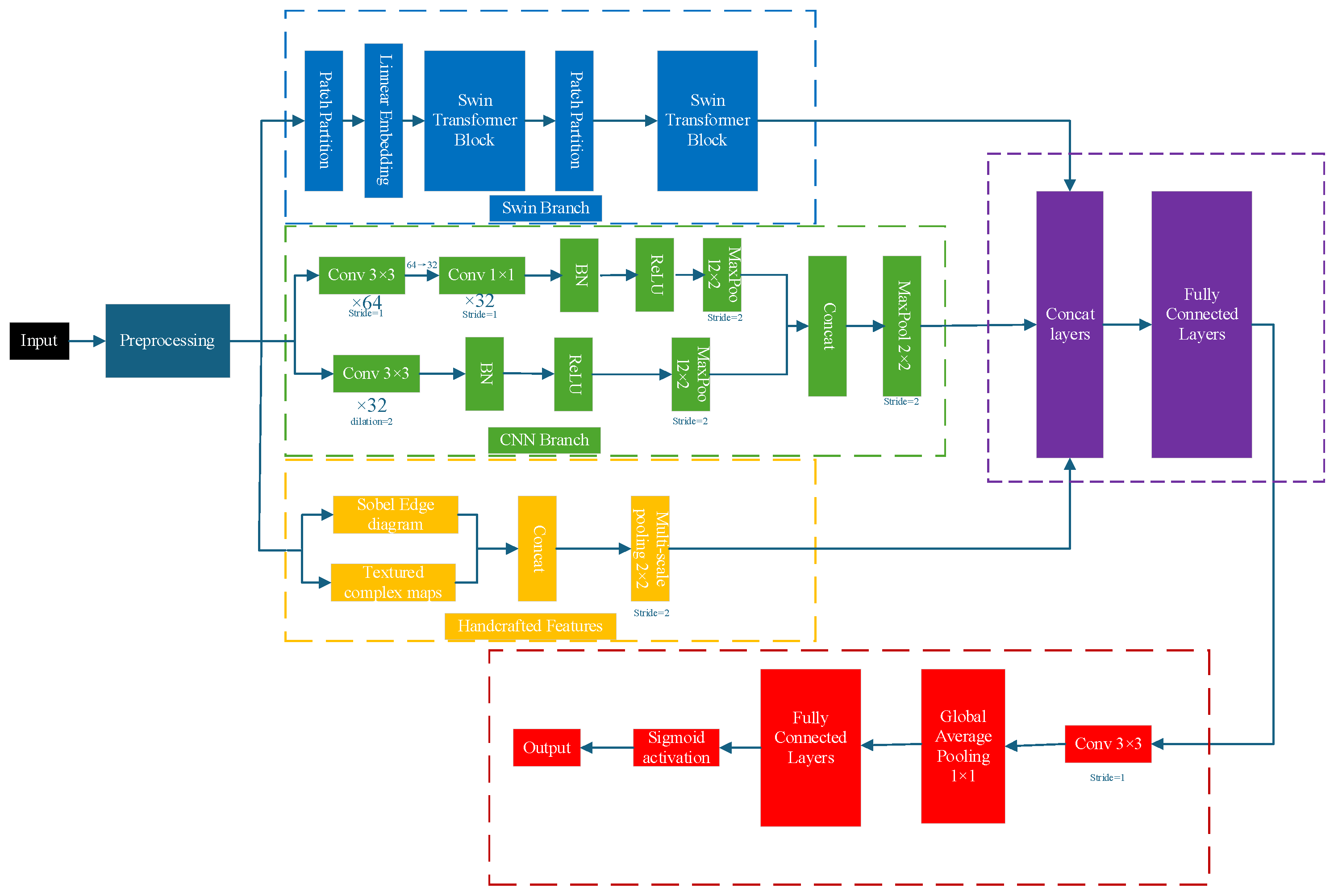
This section provides a detailed introduction to the proposed Swin-HierNet model, which aims to enhance the efficiency of CU partitioning in 3D-HEVC depth map intra-frame coding through multimodal feature fusion and hierarchical recursive decision-making. As shown in
Figure 3, the model comprises a preprocessing module, a multi-branch feature extraction module, a dynamic feature fusion module, and a recursive segmentation prediction module. The following sections discuss its design principles and technical implementation.
3.1. Pre-Processing Module
Multi-scale features are extracted through hybrid pooling and edge enhancement operations. The hybrid pooling strategy dynamically applies either maximum pooling (for edge retention) or average pooling (for noise suppression) based on the average Sobel edge strength of the sub-block. If the edge strength exceeds a certain threshold, and maximum pooling is applied to preserve edge details; otherwise, average pooling is used to suppress noise in smooth regions. This process generates three-level feature maps at 64 × 64, 32 × 32, and 16 × 16 resolutions. The threshold = 0.3 is determined by analyzing the cumulative distribution of Sobel edge strength over the training set. A total of 85% of CUs in edge regions have > 0.3, while 92% of smooth regions have ≤ 0.3. This statistically validates τ = 0.3 as an effective separator. Dilated convolution (3 × 3, dilation = 2) further strengthens the edge response in the diagonal direction and enhances object boundary features.
3.2. Multi-Branch Feature Extraction Module
Three types of features are extracted simultaneously:
The Swin Transformer branch is built upon the lightweight Swin-Tiny architecture. Using a 4 × 4 localized window attention mechanism with a shifted window strategy, the 64 × 64 feature map is divided into 4 × 4 non-overlapping windows, resulting in a total of 256 windows. Multi-head self-attention (with four heads) is then computed within each window, as expressed in Equation (1):
The resolution is first reduced to 32 × 32 (Stride = 2) using 2 × 2 max pooling downsampling. Then, the window is shifted two pixels to the lower right, generating nine overlapping sub-windows to facilitate cross-window information interaction. Attention is computed within each sub-window to produce fused global features. Subsequently, 16 × 16 feature maps undergo another 2 × 2 max pooling downsampling to capture both local edge details and cross-window global information.
- 2.
The CNN branch employs a dual-path design that integrates local texture and global context features. High-frequency texture extraction is achieved using a 3 × 3 Depthwise Separable Convolution, which is decomposed into a channel-by-channel convolution (depthwise) and a 1 × 1 pointwise convolution (pointwise).
The input consists of 64 channels and produces an output of 32 channels, with nonlinearity enhanced by the ReLU function. Meanwhile, the global branch applies a 3 × 3 dilated convolution (Dilation = 2), expanding the receptive field to 11 × 11.
Finally, the outputs of the local and global branches are concatenated along the channel dimension to produce a 64-channel feature map.
The 32 × 32 and 16 × 16 feature maps are generated through max pooling, aligned with the Swin branch, and used to produce the fused context features.
- 3.
The traditional branch computes the Sobel edge map and the local variance map, providing basic edge and texture complexity information, while the edge intensity is
. The local variance computation of the texture complexity map is performed using a pairwise 8 × 8 sliding window to calculate the pixel-value variance, which characterizes the region’s complexity. The formula is as follows:
3.3. Dynamic Feature Fusion Module
This module performs an adaptive fusion of multimodal features using gated networks, with the core mechanism being the dynamic optimization of feature contribution weights based on regional characteristics. Specifically, traditional handcrafted features (edge strength, local variance) are concatenated with global context features extracted by the Swin Transformer and local texture features captured by the CNN. The channel dimensions are aligned using 1 × 1 convolution to form a multimodal fusion base. The concatenated features are fed into a two-layer multilayer perceptron (MLP). The first layer extracts cross-modal interaction information through a 128-dimensional hidden layer, while the second layer generates a spatially adaptive weight matrix using Sigmoid activation. The final step weights and sums the three-channel features, outputting the unified fusion features.
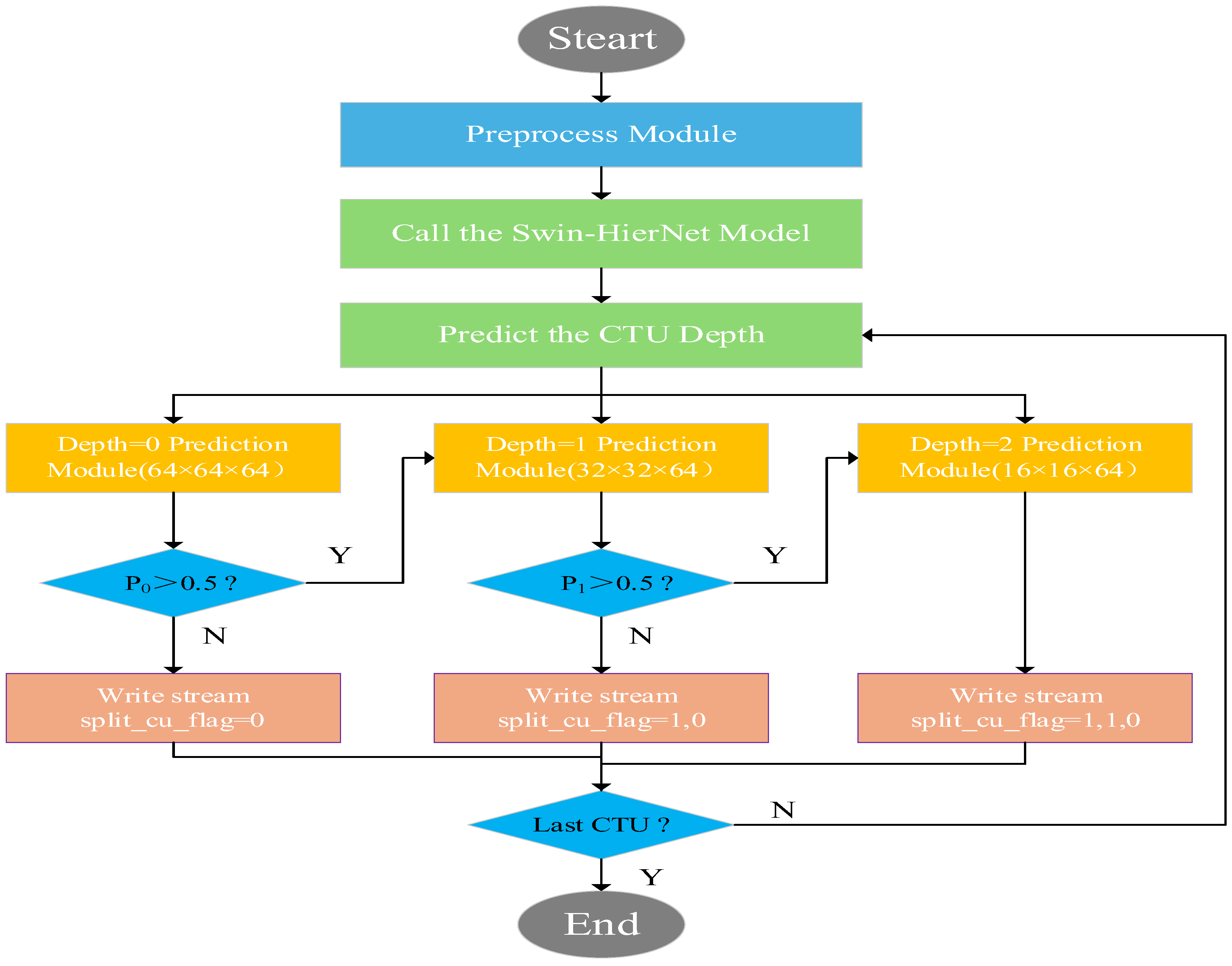
3.4. Recursive Prediction Module
The activation is applied sequentially by depth level, strictly following the HEVC delimitation dependency rule. Each prediction module consists of a 3 × 3 convolution (64 → 32 channels, Padding = 1, activation function: ReLU), global average pooling, and fully connected layers. The input is the fusion feature map at the current depth (e.g., depth 0 is 64 × 64, depth 1 is 32 × 32), and the output is the segmentation probability. The decision to continue segmentation is based on a threshold value (default: 0.5). Sigmoid activation generates the probability . For example, the depth 0 prediction module outputs a probability. If P0 > 0.5, the depth 1 prediction is activated; otherwise, segmentation is terminated, and split_cu_flag is set to 0.
Its recursive decision-making logic is that when the depth is 0 (64 × 64), if P0 > 0.5, the current CU is marked for division, and the depth 1 prediction is activated; otherwise, the process terminates. When the depth is 1 (32 × 32), the depth 2 prediction is activated only if P1 > 0.5 and P0 > 0.5. When the depth is 2 (16 × 16), P2 is output, and the actual division is controlled by the depth 1 decision.
The selection of the threshold is based on the Bayesian minimum risk criterion: assuming that the segmentation decision is a binary classification problem (segmentation/non-segmentation), the segmentation action is selected when the prediction probability p ≥ 0.5. This threshold equalizes the weight of the False Positive Rate and the False Negative Rate, which is in line with the RD cost equilibrium principle in the HEVC standard.
3.5. Flowchart of the Proposed Method
Figure 4 shows the flowchart of the proposed Swin-HierNet model-guided 3D-HEVC intra-frame encoding method.
From
Figure 4, firstly, we preprocess the 3D video that will be read and then call the proposed Swin-HierNet model. Next, we read the CTU to be encoded. Finally, the depth of the CTU partition is used in this model.
3.6. Recursive Prediction Module Training Strategies and Loss Functions
The joint loss function is:
where
is the probability of CU division at depth d, and
is the true label (1 = partition, 0 = no partition).
Binary cross-entropy loss: weights α0 = 1.0, α1 = 0.8, α2 = 0.5.
The weight design of the loss function is based on the hierarchical attenuation design principle: the CU segmentation decision with depth d = 0 (64 × 64) affects the global structure and gives the highest weight. With the refinement of CU granularity (d = 1 → 32 × 32, d = 2 → 16 × 16), the importance of decision-making decreases gradually. The weight ratio of 1.0:0.8:0.5 is determined by the grid search of the validation set so that the loss gradient of each layer is balanced.
Code rate regularization term: , where is the probability distribution estimated by the pre-trained entropy model and = 0.1.
A phased training strategy is used, beginning with pre-training the feature extractor while freezing the traditional branches and optimizing the Swin and CNN parameters. This is followed by end-to-end fine-tuning, where all parameters are unfrozen and the fusion and prediction modules are jointly optimized.
5. Conclusions
This paper proposes a new algorithm, Swin-HierNet, to tackle the challenges of high complexity in coding unit (CU) segmentation and inadequate edge modeling in the intra-frame coding of 3D-HEVC depth maps. The algorithm leverages the Swin Transformer’s localized window attention mechanism and multi-scale feature fusion to capture both the overall structure and local details of depth maps, enhancing the accuracy and speed of CU segmentation. Additionally, we incorporate a recursive hierarchical prediction step that adheres to HEVC standard requirements and addresses potential logical errors present in traditional methods. The test results demonstrate that the new algorithm performs effectively on standard test sequences, reducing coding time by 72.7%, improving compression efficiency by 1.16% (BD-Rate), and increasing division accuracy by 18.5%. Furthermore, the video quality (measured by PSNR and SSIM) of the processed sequences is nearly identical to that of the original method, showing that the new approach significantly enhances efficiency without compromising quality.
The key innovation of this paper is the integration of Swin Transformer’s global–local modeling capability with a dynamic recursive decision mechanism, offering an efficient and scalable solution for depth map coding. Moreover, the model can be seamlessly integrated into standard encoders (e.g., HTM-16.0) without altering the code stream syntax, demonstrating its strong practical value in engineering applications. However, the algorithm’s robustness in extreme motion blur scenarios can still be improved, and its reliance on high-performance GPUs limits its applicability on resource-constrained devices. Future work will focus on the following directions: first, incorporating temporal information (e.g., optical flow or motion estimation) to enhance edge modeling in dynamic scenes; second, reducing computational resource requirements through model quantization and knowledge distillation to facilitate deployment on mobile devices; and third, exploring unsupervised or self-supervised learning strategies to decrease dependence on labeled data and improve model generalization. This study offers new insights for real-time 3D video coding and provides valuable practical experience for the deep integration of deep learning and traditional coding frameworks.