A Secure Bank Loan Prediction System by Bridging Differential Privacy and Explainable Machine Learning
Abstract
1. Introduction
- Analysis of the effectiveness of different DP techniques under various PBs to gain a secure DP-based framework for recognizing bank loan statuses while preserving the confidentiality of individual financial details.
- Performance analysis for various ML models for both DP-based secure and non-DP-based general designs of the BLP system.
- Exploring explanations of how ML models reach certain conclusions for bank loan status from randomized and normal financial information.
2. Literature Review
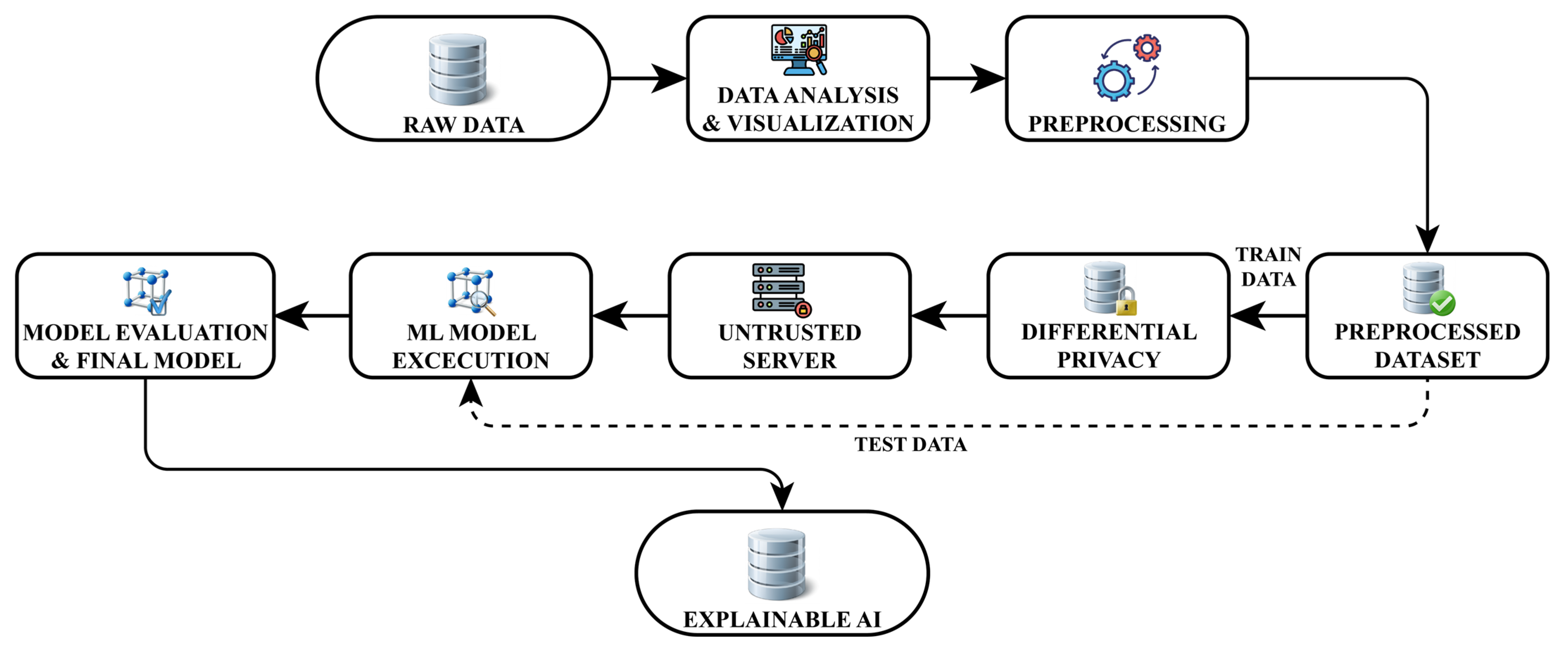
3. Materials and Methods
3.1. Raw Data
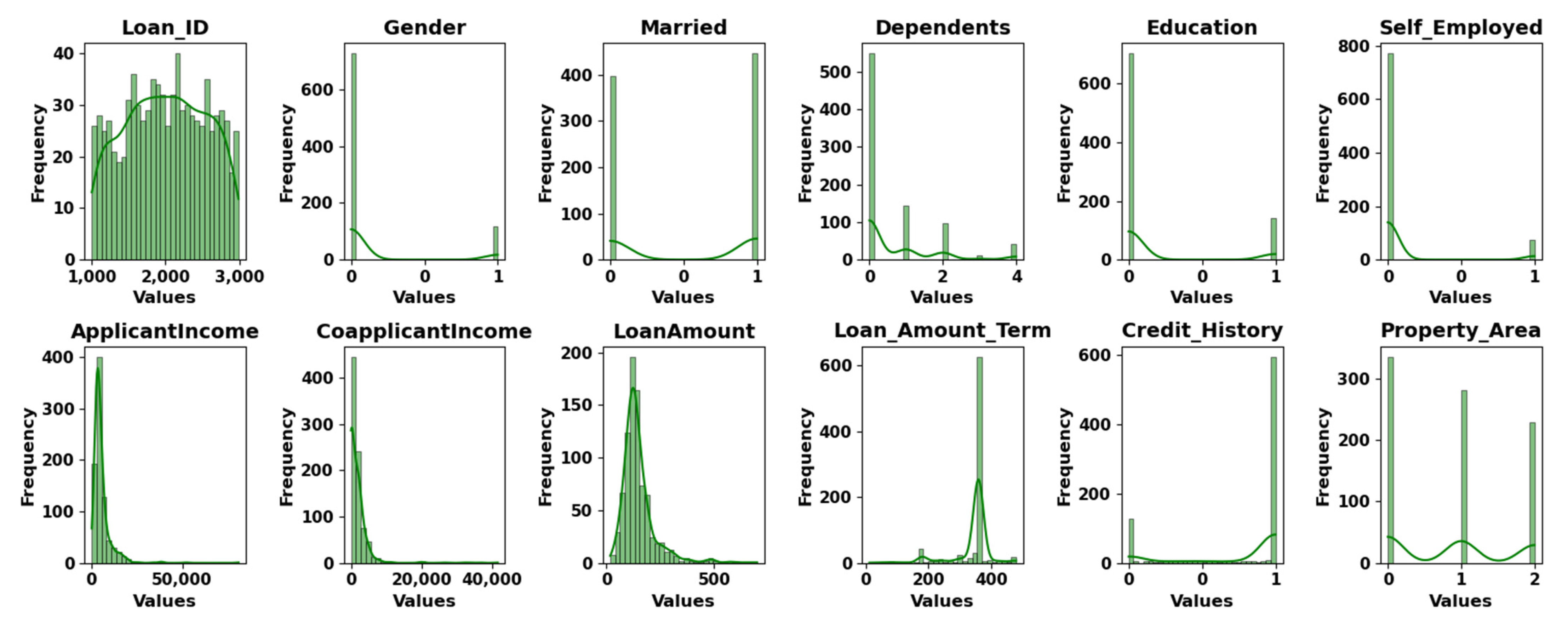
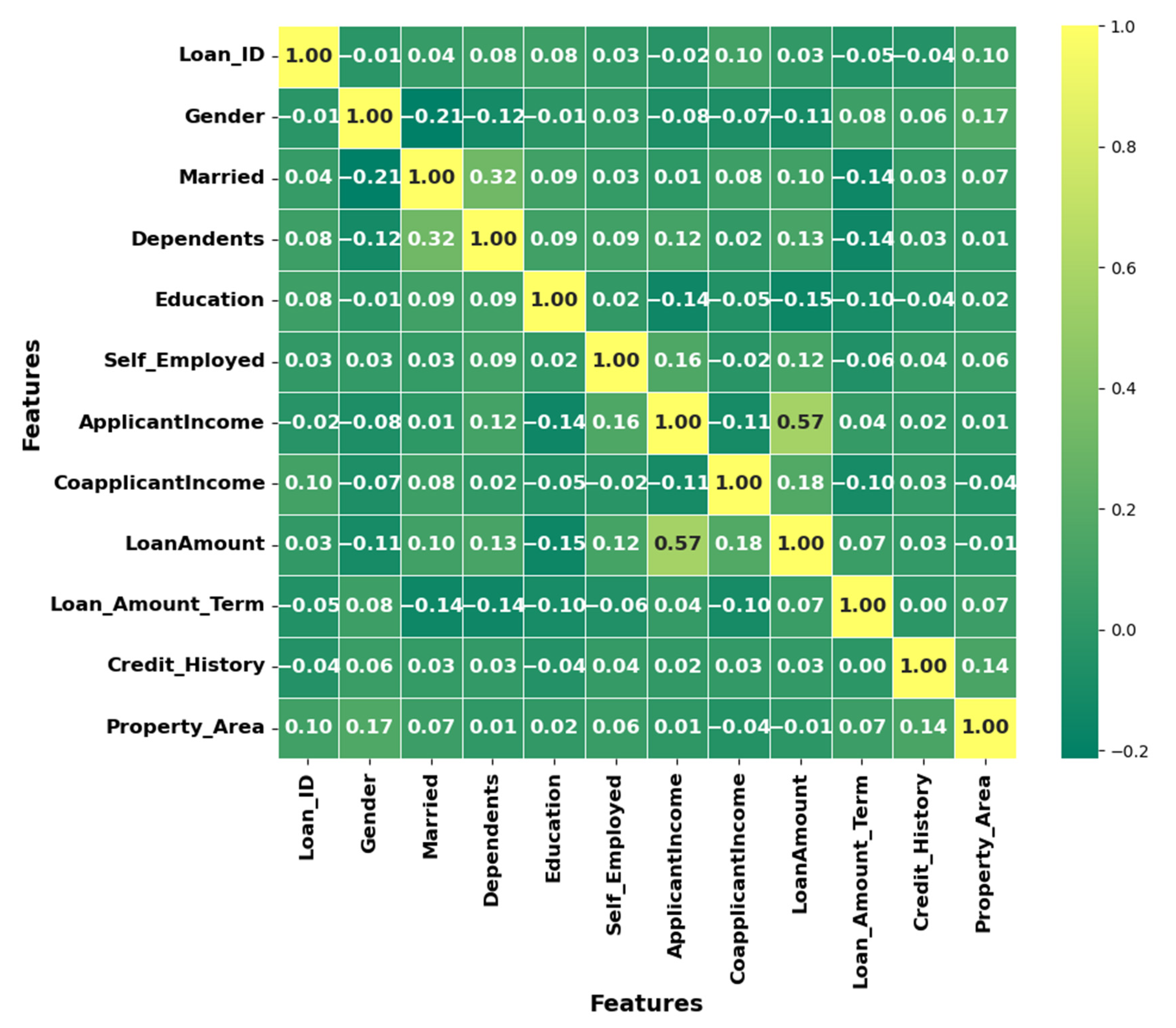
3.2. Data Analysis and Visualization
3.3. Preprocessing
3.4. Preprocessed Dataset
3.5. Differential Privacy
3.6. Untrusted Server
3.7. ML Model Execution
3.8. Model Evaluation and Final Model
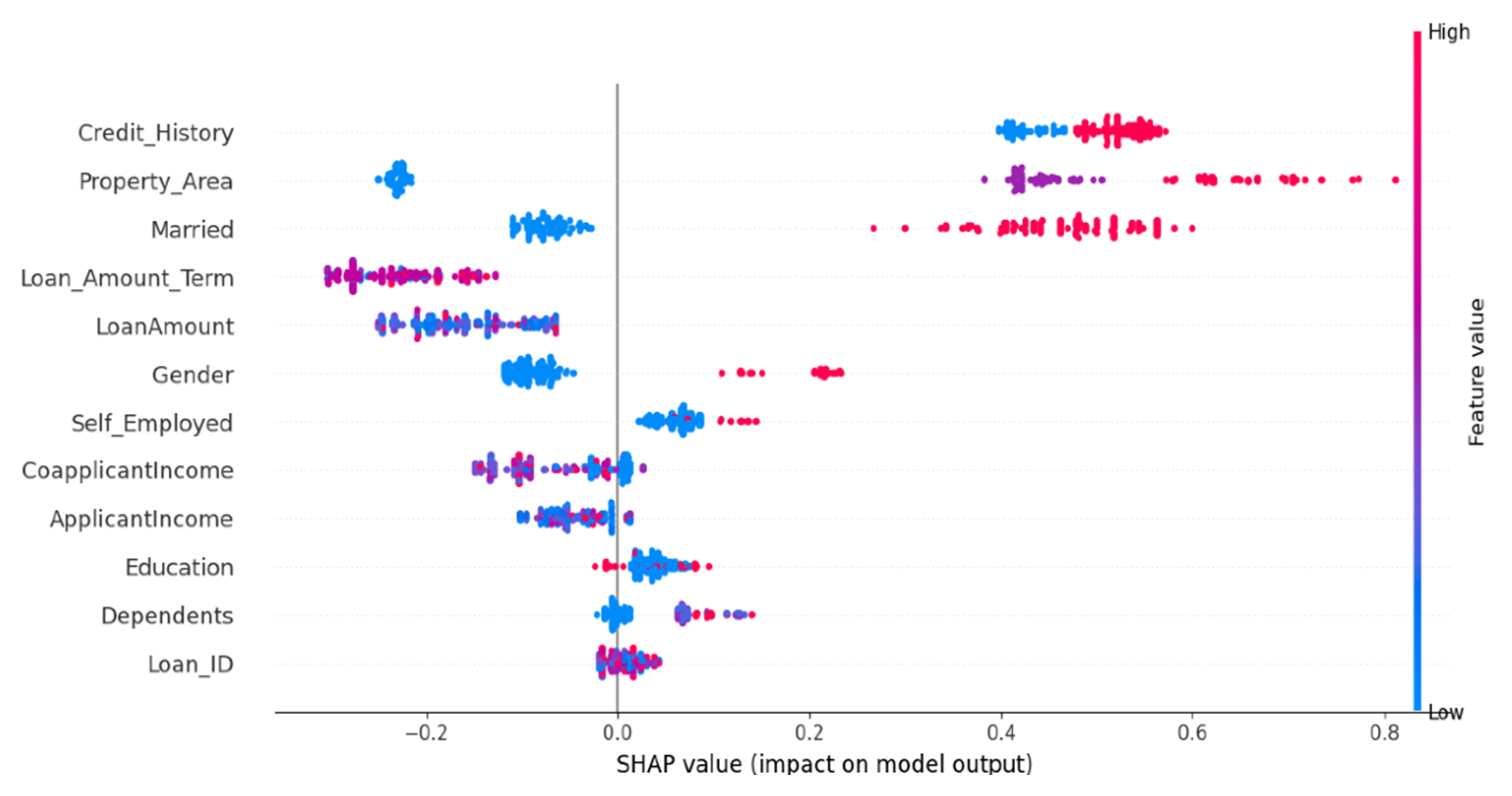
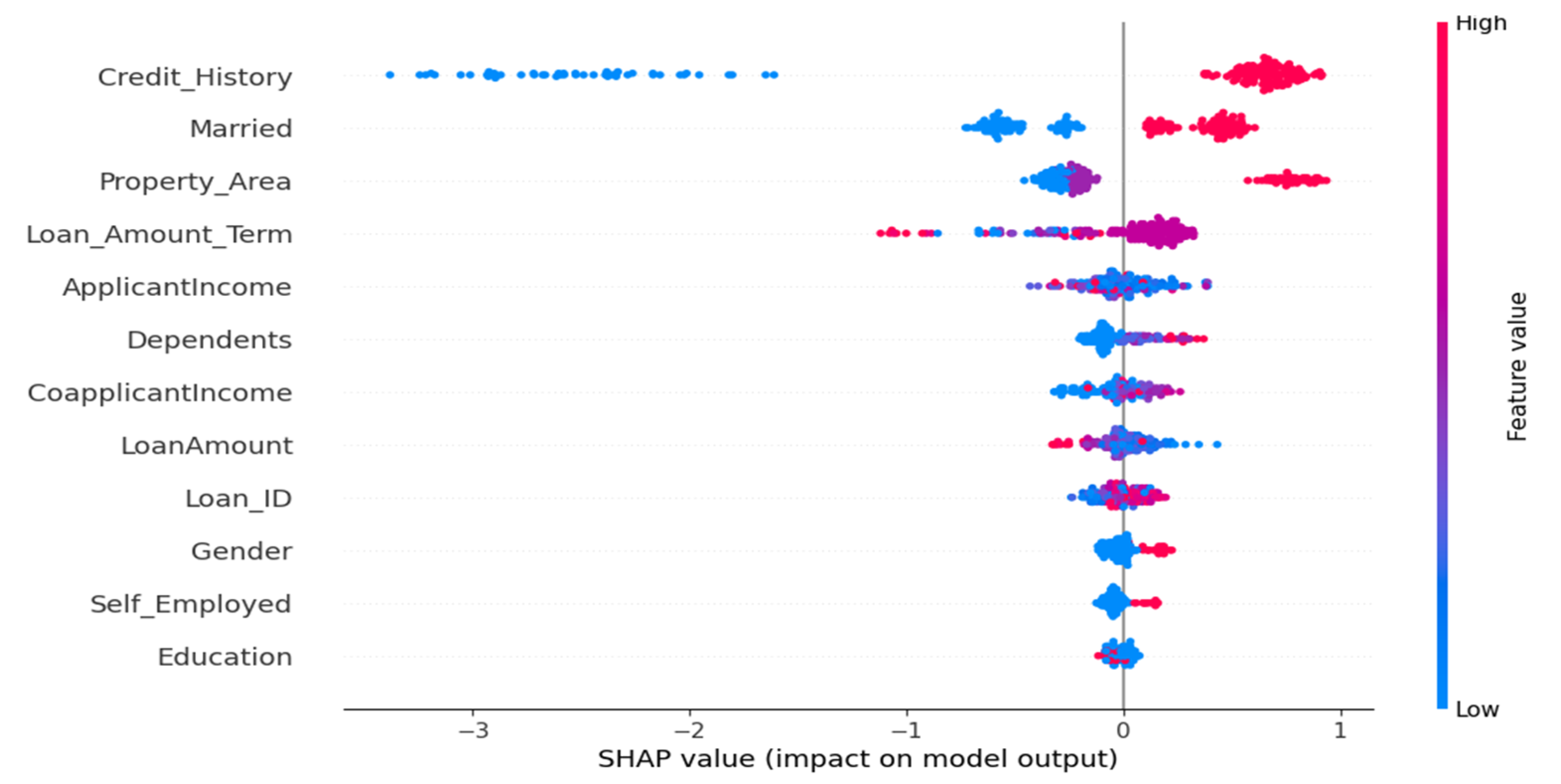
3.9. Explainable AI
4. Result and Discussion
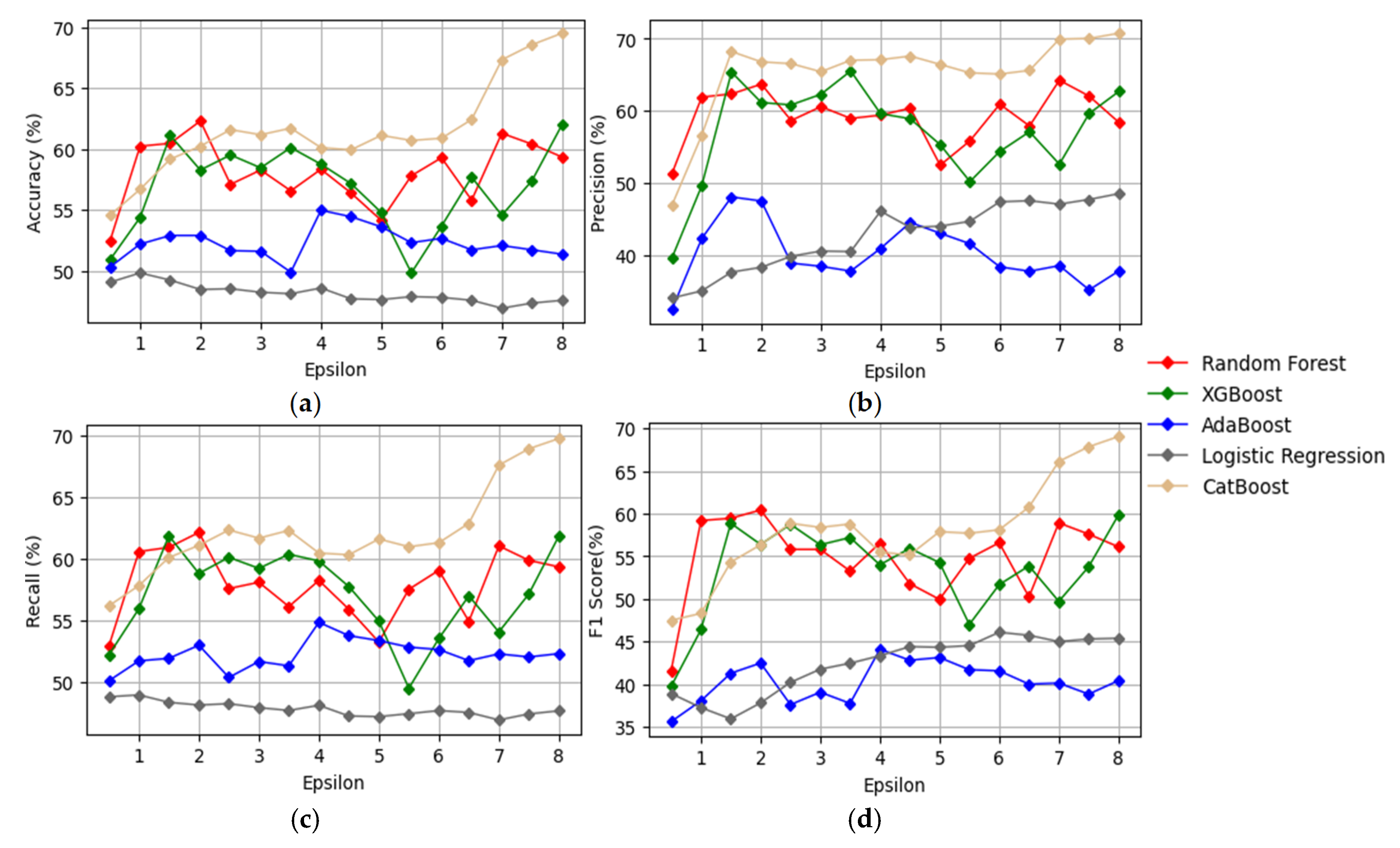
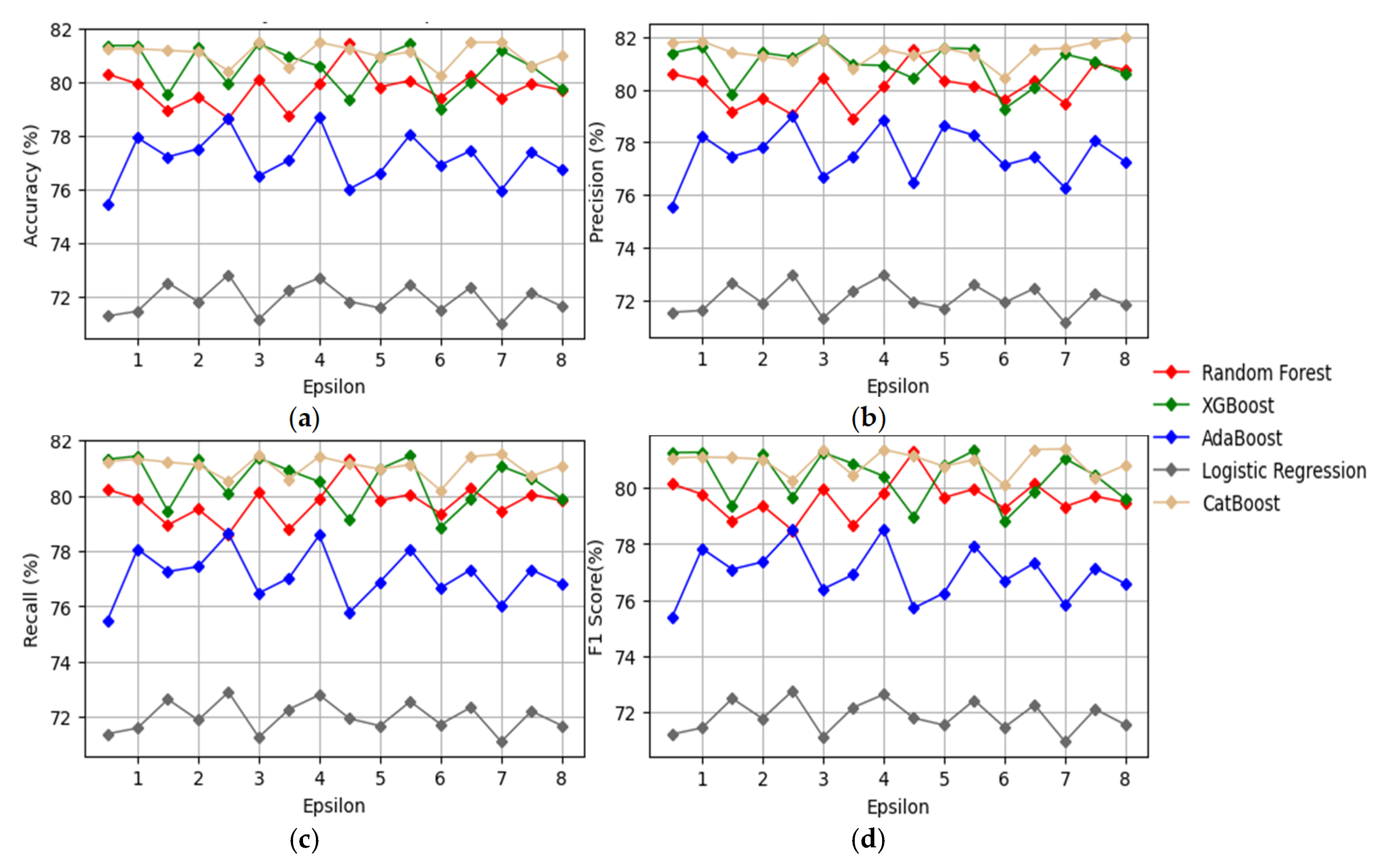
4.1. Results Using Laplacian Differential Privacy
4.2. Results Using Gaussian Differential Privacy with δ = 10−5
4.3. Results Using Gaussian Differential Privacy with δ = 10−6
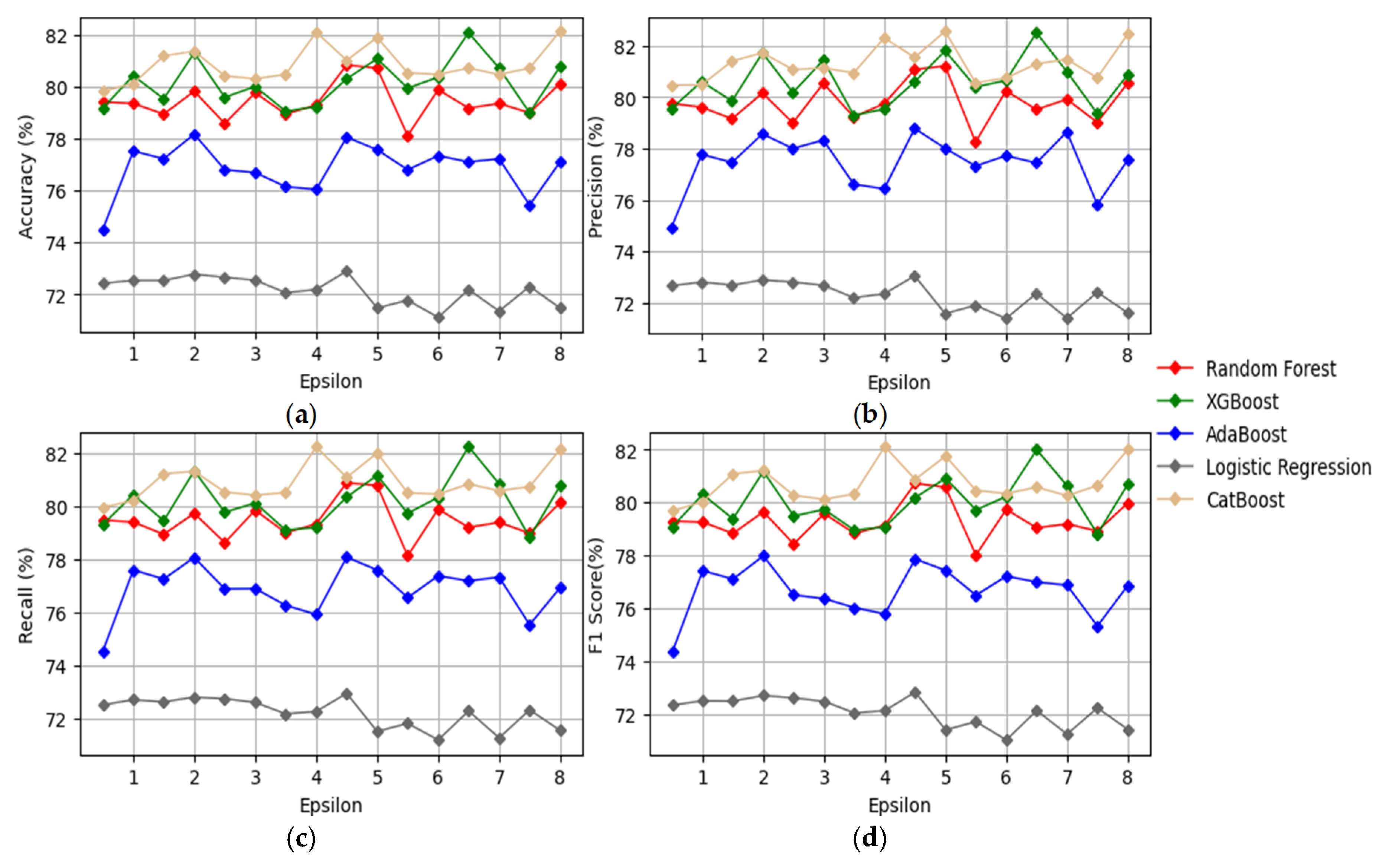
4.4. Results Using Conventional ML Models
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112, p. 18. [Google Scholar]
- Musdholifah, M.; Hartono, U.; Wulandari, Y. Banking crisis prediction: Emerging crisis determinants in Indonesian banks. Int. J. Econ. Financ. Issue 2020, 10, 124. [Google Scholar] [CrossRef]
- Money and Credit. Retrieved from Bank of England. July 2019. Available online: https://www.bankofengland.co.uk/statistics/money-and-credit/2019/july-2019 (accessed on 20 March 2025).
- Gaur, M. Statistical Tables relating to Banks in India: 2021–22’—Web Publication Released by RBI. Retrieved from Current Affairs. December 2022. Available online: https://currentaffairs.adda247.com/statistical-tables-relating-to-banks-in-india-2021-22-web-publication-released-by-rbi/ (accessed on 20 March 2025).
- Milojević, N.; Redzepagic, S. Prospects of artificial intelligence and machine learning application in banking risk management. J. Cent. Bank. Theory Pract. 2021, 10, 41–57. [Google Scholar] [CrossRef]
- Identity Theft Resource Center. Identity Theft Resource Center’s 2021 Annual Data Breach Report Sets New Record for Number of Compromises. 2022. Available online: https://www.idtheftcenter.org/post/identity-theft-resource-center-2021-annual-data-breach-report-sets-new-record-for-number-of-compromises/ (accessed on 6 April 2025).
- Elgan, M. Cost of a Data Breach: The Healthcare Industry. IBM. 6 August 2024. Available online: https://www.ibm.com/think/insights/cost-of-a-data-breach-healthcare-industry (accessed on 6 April 2025).
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography: Third Theory of Cryptography Conference, Proceedings of the TCC 2006, New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Mamun, M.A.; Farjana, A.; Mamun, M. Predicting Bank Loan Eligibility Using Machine Learning Models and Comparison Analysis. In Proceedings of the 7th North American International Conference on Industrial Engineering and Operations Management, Orlando, FL, USA, 11–14 June 2022; pp. 12–14. [Google Scholar]
- Viswanatha, V.; Ramachandra, A.C.; Vishwas, K.N.; Adithya, G. Prediction of Loan Approval in Banks using Machine Learning Approach. Int. J. Eng. Manag. Res. 2023, 13, 7–19. [Google Scholar]
- Spoorthi, B.; Kumar, S.S.; Rodrigues, A.P.; Fernandes, R.; Balaji, N. Comparative Analysis of Bank Loan Defaulter Prediction Using Machine Learning Techniques. In Proceedings of the 2021 IEEE International Conference on Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Nitte, India, 19–20 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 24–29. [Google Scholar]
- Shinde, A.; Patil, Y.; Kotian, I.; Shinde, A.; Gulwani, R. Loan prediction system using machine learning. In ITM Web of Conferences; EDP Sciences: Les Ulis, France, 2022; Volume 44, p. 03019. [Google Scholar]
- Bhargav, P.; Sashirekha, K. A Machine Learning Method for Predicting Loan Approval by Comparing the Random Forest and Decision Tree Algorithms. J. Surv. Fish. Sci. 2023, 10, 1803–1813. [Google Scholar]
- Uddin, N.; Ahamed, M.K.U.; Uddin, M.A.; Islam, M.M.; Talukder, M.A.; Aryal, S. An ensemble machine learning based bank loan approval predictions system with a smart application. Int. J. Cogn. Comput. Eng. 2023, 4, 327–339. [Google Scholar] [CrossRef]
- Maniar, T.; Akkinepally, A.; Sharma, A. Differential Privacy for Credit Risk Model. arXiv 2021, arXiv:2106.15343. [Google Scholar]
- Ratadiya, P.; Asawa, K.; Nikhal, O. A decentralized aggregation mechanism for training deep learning models using smart contract system for bank loan prediction. arXiv 2020, arXiv:2011.10981. [Google Scholar]
- Zheng, Y.; Wu, Z.; Yuan, Y.; Chen, T.; Wang, Z. PCAL: A privacy-preserving intelligent credit risk modeling framework based on adversarial learning. arXiv 2020, arXiv:2010.02529. [Google Scholar]
- Alagic, A.; Zivic, N.; Kadusic, E.; Hamzic, D.; Hadzajlic, N.; Dizdarevic, M.; Selmanovic, E. Machine learning for an enhanced credit risk analysis: A comparative study of loan approval prediction models integrating mental health data. Mach. Learn. Knowl. Extr. 2024, 6, 53–77. [Google Scholar] [CrossRef]
- Chang, V.; Xu, Q.A.; Akinloye, S.H.; Benson, V.; Hall, K. Prediction of bank credit worthiness through credit risk analysis: An explainable machine learning study. Ann. Oper. Res. 2024, 1–25. [Google Scholar] [CrossRef]
- Nguyen, L.; Ahsan, M.; Haider, J. Reimagining peer-to-peer lending sustainability: Unveiling predictive insights with innovative machine learning approaches for loan default anticipation. FinTech 2024, 3, 184–215. [Google Scholar] [CrossRef]
- Yang, C. Research on loan approval and credit risk based on the comparison of Machine learning models. In SHS Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 181, p. 02003. [Google Scholar]
- Juyal, A.; Sethi, N.; Pandey, C.; Negi, D.; Joshi, A.; Verma, R. A comparative study of machine learning models in loan approval prediction. In Challenges in Information, Communication and Computing Technology; CRC Press: Boca Raton, FL, USA, 2025; pp. 453–458. [Google Scholar]
- Zhu, X.; Chu, Q.; Song, X.; Hu, P.; Peng, L. Explainable prediction of loan default based on machine learning models. Data Sci. Manag. 2023, 6, 123–133. [Google Scholar] [CrossRef]
- Lu, Z.; Li, H.; Wu, J. Exploring the impact of financial literacy on predicting credit default among farmers: An analysis using a hybrid machine learning model. Borsa Istanb. Rev. 2024, 24, 352–362. [Google Scholar] [CrossRef]
- Chatterjee, D. Loan Prediction Problem Dataset. 2021. Available online: https://www.kaggle.com/altruistdelhite04/loan-prediction-problem-dataset (accessed on 20 March 2025).
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Mendenhall, W.; Beaver, R.J.; Beaver, B.M. Introduction to Probability and Statistics; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar] [CrossRef]
- Secrest, B.R.; Lamont, G.B. Visualizing particle swarm optimization-Gaussian particle swarm optimization. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 198–204. [Google Scholar]
- Wilkinson, L.; Friendly, M. The history of the cluster heat map. Am. Stat. 2009, 63, 179–184. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Phan, N.; Wu, X.; Hu, H.; Dou, D. Adaptive Laplace mechanism: Differential privacy preservation in deep learning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 385–394. [Google Scholar]
- Dong, J.; Roth, A.; Su, W.J. Gaussian differential privacy. arXiv 2019, arXiv:1905.02383. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, F.; Cheng, Y.; Gu, X.; Liu, W.; Peng, J. XGBoost classifier for DDoS attack detection and analysis in SDN-based cloud. In Proceedings of the 2018 IEEE International Conference on Big Data and Smart Computing (BigComp), Shanghai, China, 15–17 January 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 251–256. [Google Scholar]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class AdaBoost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- LaValley, M.P. Logistic regression. Circulation 2008, 117, 2395–2399. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Samek, W.; Montavon, G.; Vedaldi, A.; Hansen, L.K.; Müller, K.R. (Eds.) Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer Nature: Cham, Switzerland, 2019; Volume 11700. [Google Scholar]






| Existing Work | Method | Accuracy | Limitation | Future Work |
|---|---|---|---|---|
| Mamun et al. [9] | LR | 92% | Earlier data reliance; lack of privacy and outcome explanation | Designing software adaptable system to evolve with new data |
| Viswanatha et al. [10] | NB | 83.73% | Data imbalance; lack of privacy and outcome explanation | Utilizing advanced-ensemble approaches, feature engineering, models optimization, etc. |
| Spoorthi B et al. [11] | RF | 85% | Lack of privacy and model interpretability | Utilizing a user-friendly interface to input consumer details |
| Shinde et al. [12] | RF with grid search | 79% | Insufficient outcome analysis and lack of privacy | -- |
| Bhargav and Sashirekha [13] | RF | 79.44% | Limited model utilization, insufficient outcome analysis, and absence of privacy | Expanding by more advanced mechanisms |
| Uddin et al. [14] | Voting ensemble | 87.26% | Neglecting the utilization of diverse- balancing techniques, unsupervised models, and ensemble methods | Improving models by incorporating diverse data balancing techniques, unsupervised models, and advanced ensemble methods |
| Maniar et al. [15] | GB + DP | -- | Absence of model explanation | Employing outcome explanation tools |
| Ratadiya et al. [16] | ANN + Blockchain | 98.13% | Scalability issues and computational overhead challenges | Employing time series and image data, integrating the secure encryption method, and using the method to share multiple data sources without accessing actual information |
| Zheng et al. [17] | PCAL | 95.29% | High computational complexity by adversarial learning | -- |
| Alagic et al. [18] | XGBoost | 84% | Imbalanced datasets | Incorporating additional mental health variables and addressing ethical concerns |
| Chang et al. [19] | GB | 82% | Insufficient feature availability | Improving data balancing techniques like SMOTE |
| Nguyen et al. [20] | LR | 83% | Challenge of relying less on personal data | Gathering new features, exploring advanced feature selection methods |
| Chunyu Yang [21] | LR | 76% | Need for careful parameter selection in logistic regression | Applying the methodology to different loan approval datasets |
| Juyal et al. [22] | RF | 84.37% | -- | -- |
| Zhu et al. [23] | LightGBM | 81.04% | -- | Applying XAI to estimate the overall influence of the features used |
| Lu et al. [24] | k-Means + AdaBoost | 84% | Data from a single bank limits generalizability | Using data from diverse institutions |
| Feature | Description | Type | Value |
|---|---|---|---|
| Loan_ID | Unique identifier for individual loan records | Nominal | No |
| Gender | Categorization of individuals into male or female groups | Nominal | Male/Female |
| Married | Distinguishing between those who are married and those who are not. | Nominal | Yes/No |
| Dependents | Providing insights into familial responsibilities | Nominal | No. of Dependents |
| Education | Educational background, those with graduate and non-graduate status | Nominal | Graduate/Not Graduate |
| Self_Employed | Insights into their occupational status | Nominal | Yes/No |
| ApplicantIncome | Financial earnings of loan applicants | Numeric | USD |
| CoapplicantIncome | Financial earnings of co-applicants associated with loan applicants | Numeric | USD |
| Loan_Amount | Signifies the monetary value requested by loan applicants | Numeric | USD |
| Name | Equation | Meaning |
|---|---|---|
| Accuracy | The overall prediction accuracy | |
| Precision | Ability to correctly detect approved loan cases from all predicted approved cases | |
| Recall | Ability to correctly detect approved loan cases | |
| F1 Score | Explains how robust and precise a model is |
| Specification | Details |
|---|---|
| Programming Language | Python (via Anaconda3—Spyder IDE) |
| Operating System | Windows |
| CPU | Intel Processor @ 3.60 GHz (base)/4.00 GHz (boost) |
| GPU | Nvidia RTX 2070 Super (8 GB GDDR6 VRAM) |
| RAM | 16 GB DDR4 (3200 MHz) |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| RF | 85.33 | 85.56 | 85.34 | 85.25 |
| XGBoost | 85.33 | 85.41 | 85.34 | 85.27 |
| AdaBoost | 78.34 | 78.52 | 78.37 | 78.24 |
| LR | 71.95 | 71.96 | 71.97 | 71.88 |
| CatBoost | 85.56 | 85.83 | 85.57 | 85.48 |
| Research Objective | How the Experimental Setup Achieves This |
|---|---|
| Analyze the effectiveness of different DP techniques under various PBs | Laplacian and Gaussian DP mechanisms are applied to the dataset. PBs (ε) range from 0.5 to 8 with 0.5 increments. Each combination is evaluated using 10-fold cross-validation. |
| Compare the performance of multiple ML models in DP-based and non-DP-based BLP systems | Five ML models, namely Rf, XGBoost, AdaBoost, LR, and CatBoost, are trained and tested on both original and DP-processed data to observe trade-offs in performance. |
| Provide interpretation of how models conclude predictions on private and regular data | XAI techniques are used to interpret feature importance and decision-making paths in both DP and non-DP settings, enhancing transparency in loan status predictions. |
| Ensure reproducibility and support practical deployment | The experiments are implemented using Python in the Spyder environment. The system runs on Windows 10 with an Intel CPU, 16 GB RAM, and an Nvidia RTX 2070 Super. This setup allows for reproducible testing and deployment. |
| Existing Work | DP | Privacy Concern | XAI |
|---|---|---|---|
| Mamun et al. [9] | ✖ | ✖ | ✖ |
| Viswanatha et al. [10] | ✖ | ✖ | ✖ |
| Spoorthi B et al. [11] | ✖ | ✖ | ✖ |
| Shinde et al. [12] | ✖ | ✖ | ✖ |
| Bhargav and Sashirekha [13] | ✖ | ✖ | ✖ |
| Uddin et al. [14] | ✖ | ✖ | ✖ |
| Maniar et al. [15] | ✔ | ✔ | ✖ |
| Ratadiya et al. [16] | ✖ | ✔ | ✖ |
| Zheng et al. [17] | ✖ | ✔ | ✖ |
| Alagic et al. [18] | ✖ | ✖ | ✖ |
| Chang et al. [19] | ✖ | ✖ | ✔ |
| Nguyen et al. [20] | ✖ | ✖ | ✖ |
| Chunyu Yang [21] | ✖ | ✖ | ✖ |
| Juyal et al. [22] | ✖ | ✖ | ✖ |
| Zhu et al. [23] | ✖ | ✖ | ✔ |
| Lu et al. [24] | ✖ | ✖ | ✖ |
| Proposed Method | ✔ | ✔ | ✔ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.M.; Mamun, M.; Munir, A.; Rahman, M.M.; Chowdhury, S.H. A Secure Bank Loan Prediction System by Bridging Differential Privacy and Explainable Machine Learning. Electronics 2025, 14, 1691. https://doi.org/10.3390/electronics14081691
Hossain MM, Mamun M, Munir A, Rahman MM, Chowdhury SH. A Secure Bank Loan Prediction System by Bridging Differential Privacy and Explainable Machine Learning. Electronics. 2025; 14(8):1691. https://doi.org/10.3390/electronics14081691
Chicago/Turabian StyleHossain, Muhammad Minoar, Mohammad Mamun, Arslan Munir, Mohammad Motiur Rahman, and Safiul Haque Chowdhury. 2025. "A Secure Bank Loan Prediction System by Bridging Differential Privacy and Explainable Machine Learning" Electronics 14, no. 8: 1691. https://doi.org/10.3390/electronics14081691
APA StyleHossain, M. M., Mamun, M., Munir, A., Rahman, M. M., & Chowdhury, S. H. (2025). A Secure Bank Loan Prediction System by Bridging Differential Privacy and Explainable Machine Learning. Electronics, 14(8), 1691. https://doi.org/10.3390/electronics14081691









