Network Function Placement in Virtualized Radio Access Network with Reinforcement Learning Based on Graph Neural Network
Abstract
1. Introduction
- (1)
- We formulate an optimization model using mixed integer nonlinear programming to integrate the functional split and network function placement problems. The objective of the model is to minimize the number of active computing resources while maximizing the centralization level of vRAN. Details can be found in Section 3;
- (2)
- We propose an efficient GPPO-based DRL algorithm. In this framework, GNNs incorporating both node and edge feature embeddings are integrated into the actor and critic networks, providing a more comprehensive view of the network state. This enables the actor network to make more precise policy decisions and the critic network to deliver more accurate evaluations. The improvement is mainly due to the GNN’s ability to effectively leverage topological structure information, enhancing the embedded representation of both node and edge features. Refer to Section 4 for more information;
- (3)
- Simulation experiments across different RAN scenarios with varying node configurations demonstrate that our approach achieves a superior network centralization level and outperforms several existing methods. An in-depth analysis can be found in Section 5.
2. Related Work
- -
- -
- -
- -
- -
- Maximizing throughput [25];
- -
3. System Model and Problem Formulation
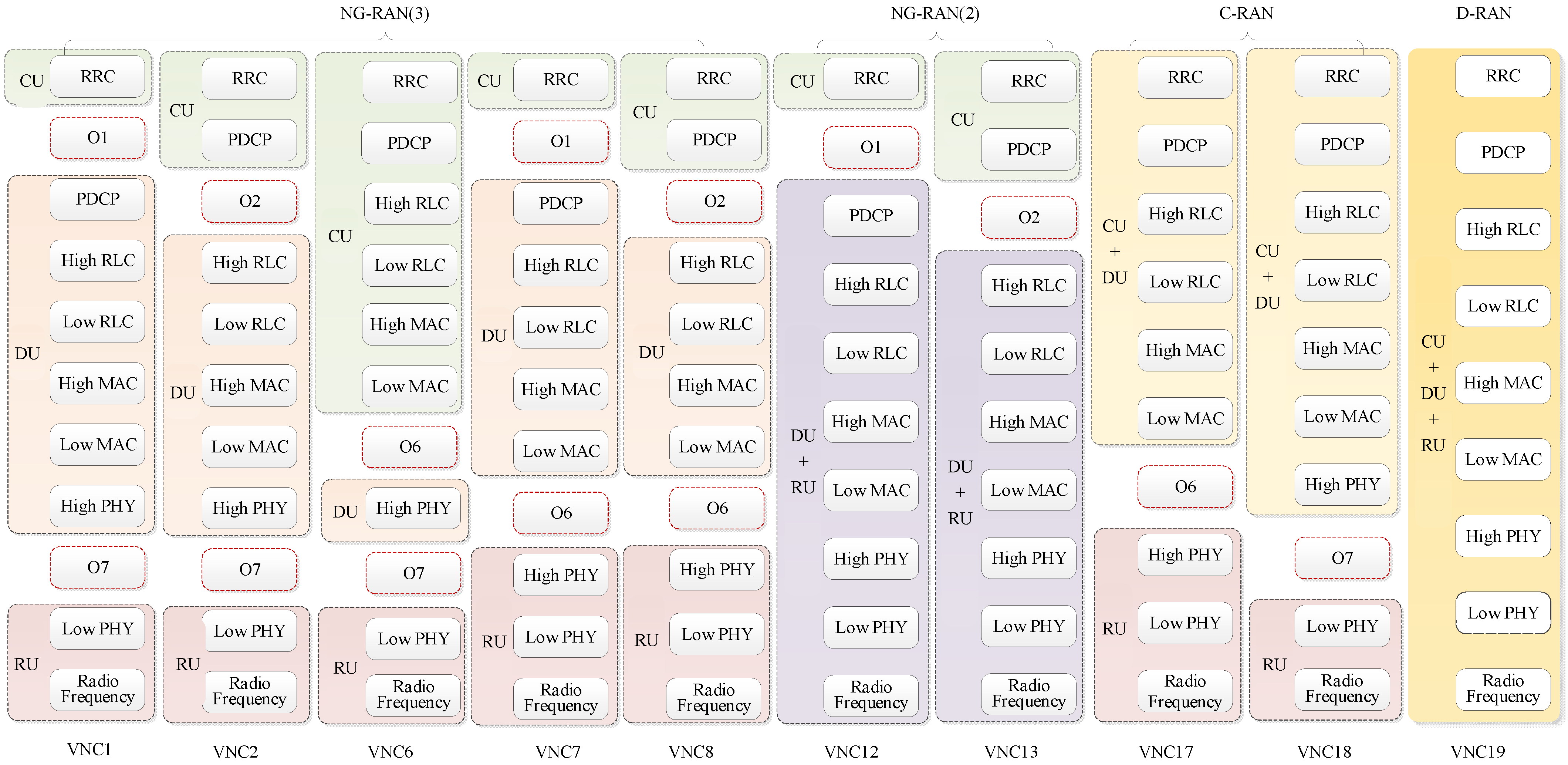
3.1. System Model
3.2. Function Placement Problem Formulation
- A.
- Combinational constraints
- B.
- Link capacity constraints
- C.
- Tolerable latency constraints
- D.
- Processing capacity constraint
4. DRL Method Based on GNN for Function Placement Problems
4.1. Three Essential Elements of DRL
4.1.1. State Representation
4.1.2. Action Space
4.1.3. Reward Design
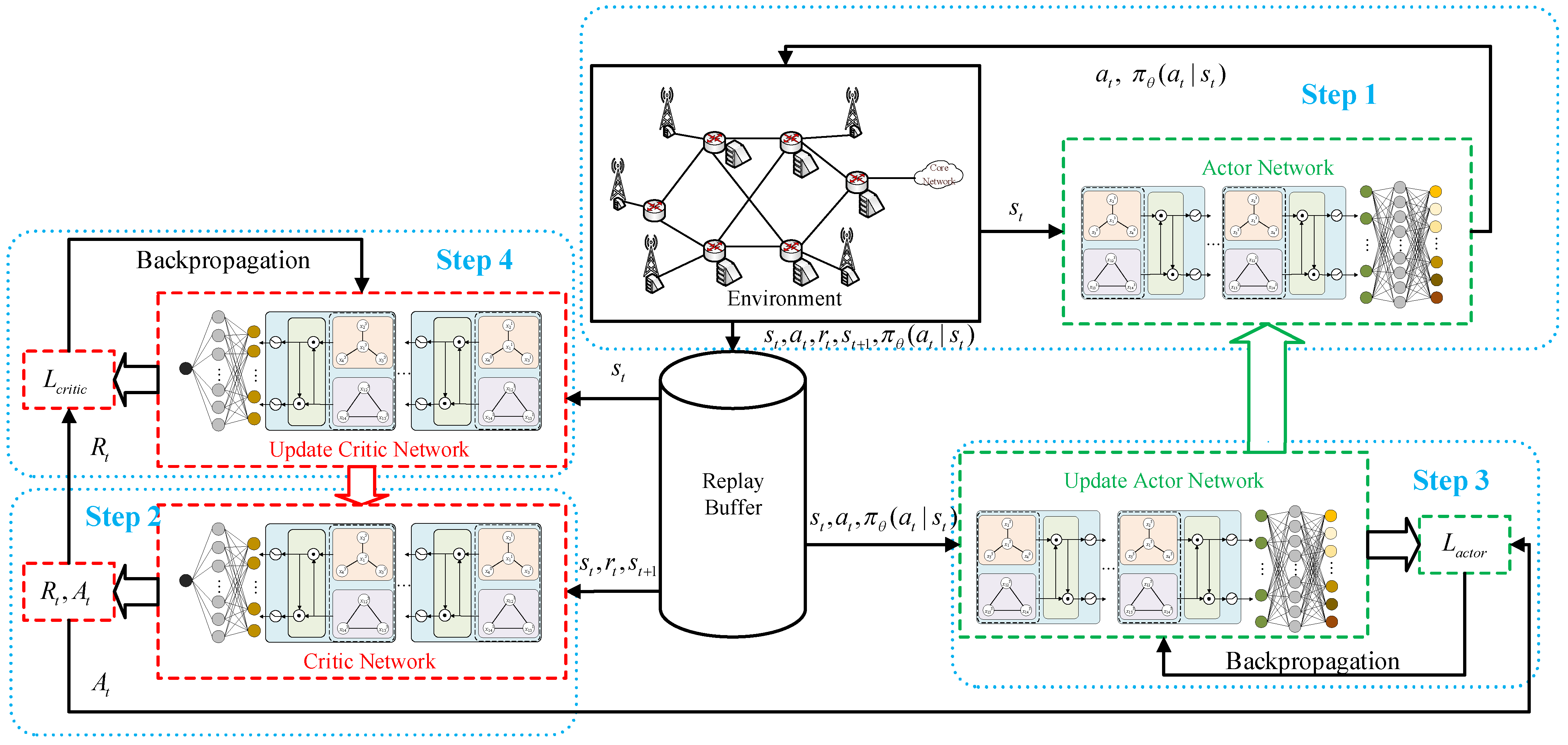
4.2. Graph Proximal Policy Optimization
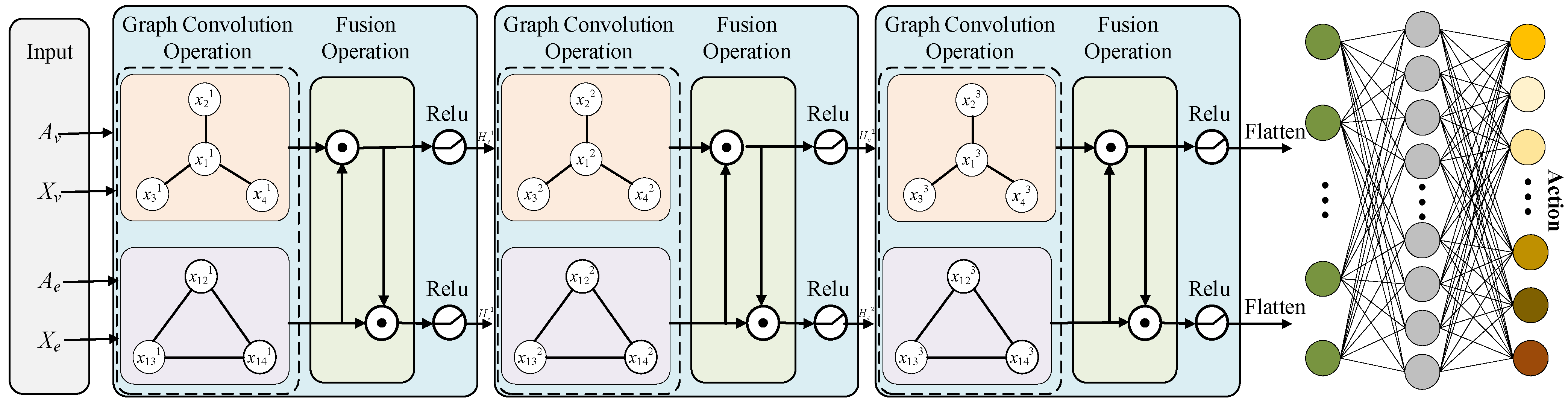
4.2.1. Actor Network
4.2.2. Critic Network
4.2.3. GPPO Algorithm
| Algorithm 1. GPPO Algorithm | ||
| Input: ,, , discount, learning rate, Clipping parameter | ||
| Output: final actor parameters , final critic parameters | ||
| 1: | Initialize: the parameter of the actor network ; | |
| the parameter of the critic network ; | ||
| iteration epochs , updating times of every epoch. | ||
| 2: | for do | |
| 3: | Empty replay buffer B and reset the environment; | |
| 4: | ; | |
| 5: | for do | |
| 6: | Sample action based on ; | |
| 7: | Execute action and obtain next state ; | |
| 8: | Compute reward according to Equation (12); | |
| 9: | Store experience in replay buffer B; | |
| 10: | Compute the return according to Equation (17); | |
| 11: | Estimate the advantage from according to Equation (18); | |
| 12: | end for | |
| 13: | for do | |
| 14: | Sample a batch of experiences from replay buffer B; | |
| 15: | according to Equation (19); | |
| 16: | according to Equation (22); | |
| 17: | end for | |
| 18: | , and ; | |
| 19: | end for | |
- (1)
- Interaction with the environment (lines 6–9): the actor network interacts with the environment of the network functional placement problem, then samples an action from the action distribution given state , executes the action in the environment and receives a reward at the next state , and stores the experience in the buffer. The above operations are repeated to collect training data. These data are generated through interaction with a simulated vRAN environment.
- (2)
- Compute advantages (lines 10–11): compute the value function for every state using the critic network and compute the return and the advantage based on the current critic network.
- (3)
- Update the actor network (line 15): based on the sample data in the reply buffer and the advantage , the actor network is updated by maximizing the PPO-Clip objective.
- (4)
- Update the critic network (line 16): similarly, the critic network is updated using the Mean Squared Error (MSE) between the estimated values and the computed returns.
5. Performance Evaluation
5.1. Baseline Methods and Simulation Setup
- (1)
- The first case does not consider routing, where a single path is assigned for functional split for each RU, corresponding to the system model proposed by Mutri [10];
- (2)
- The second case considers routing, where functional split and function placement must be decided from multiple paths for each RU, reflecting the system model proposed in this paper. Therefore, Table 4 presents the parameters and information about the network resources employed in these experiments.
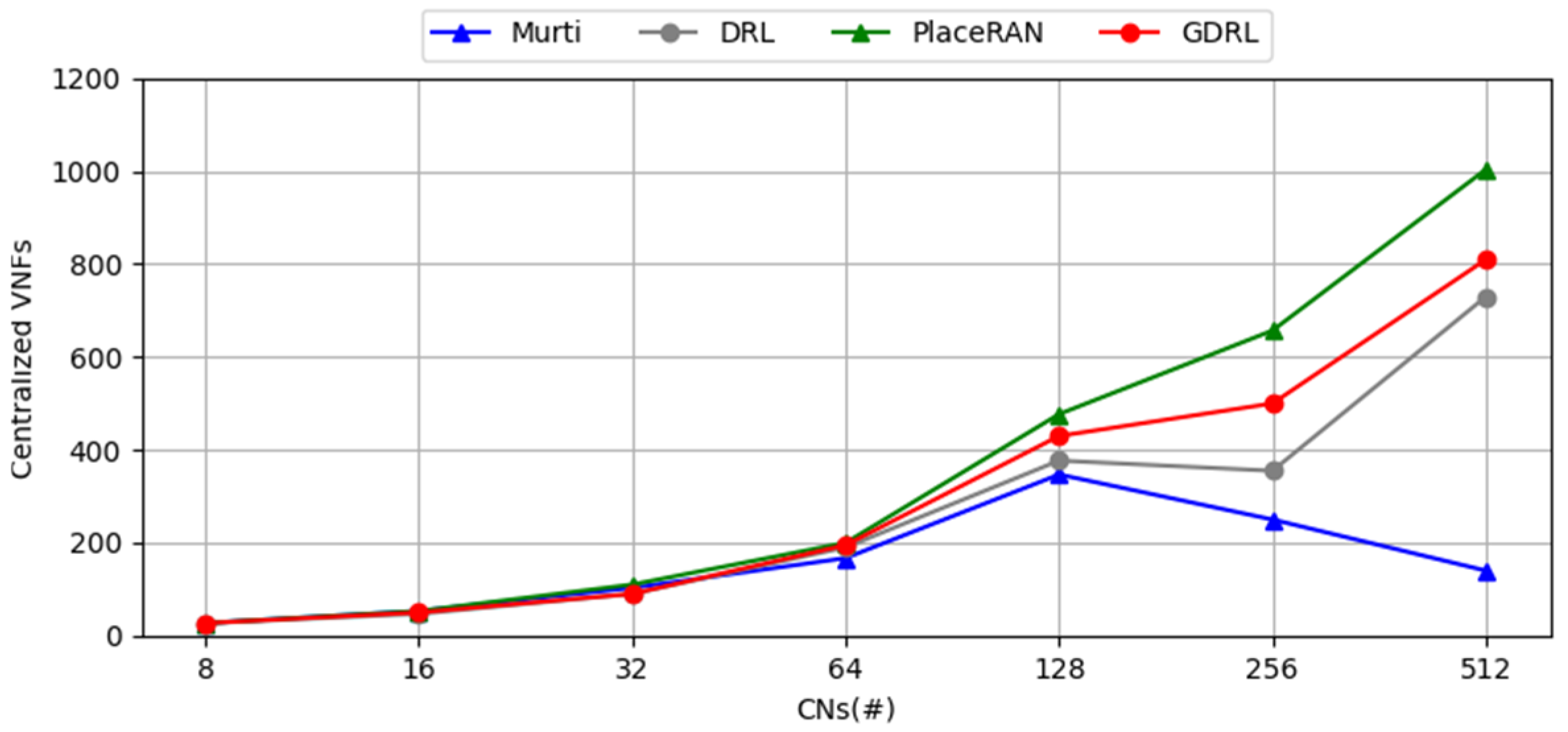
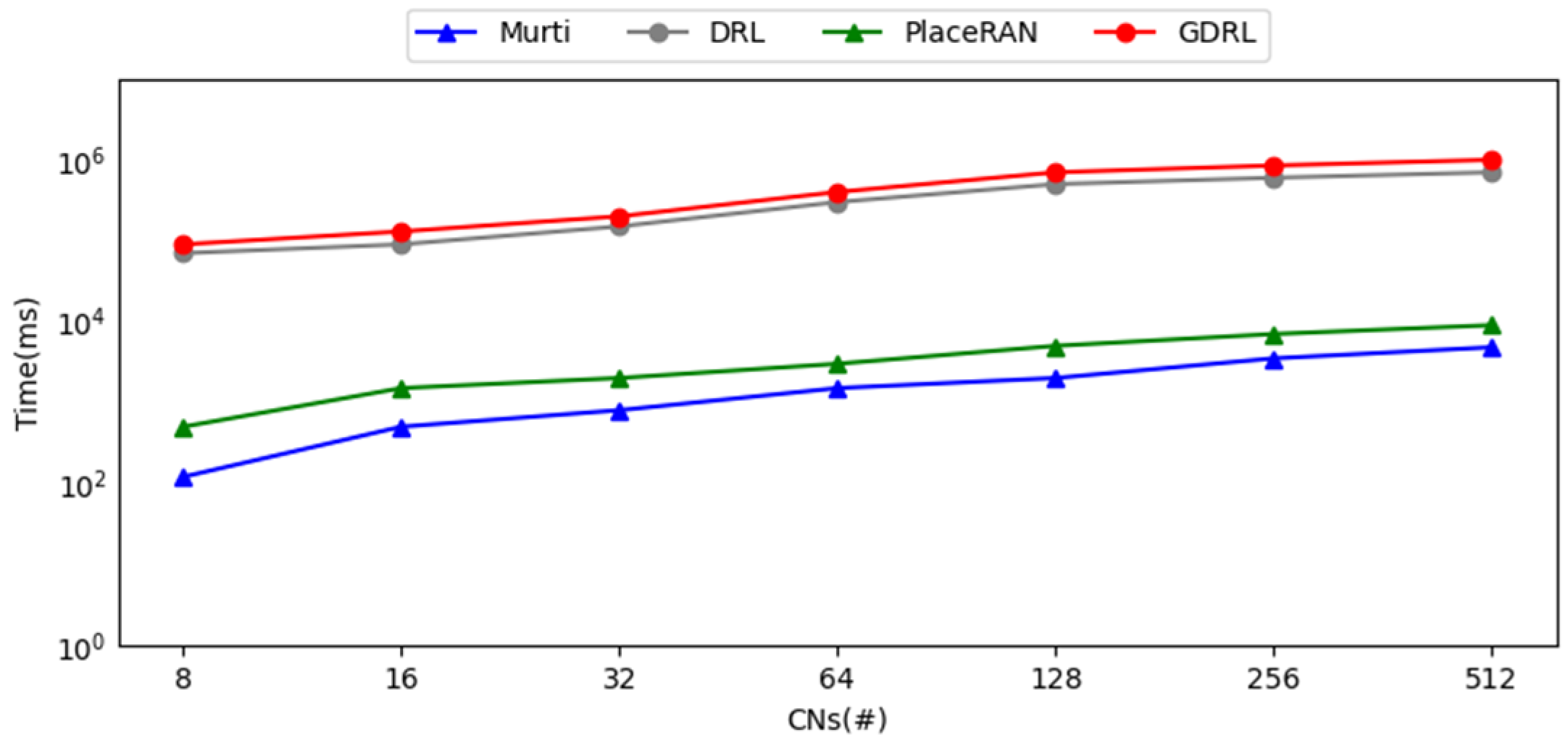
5.2. Evaluation Without Routing Decisions
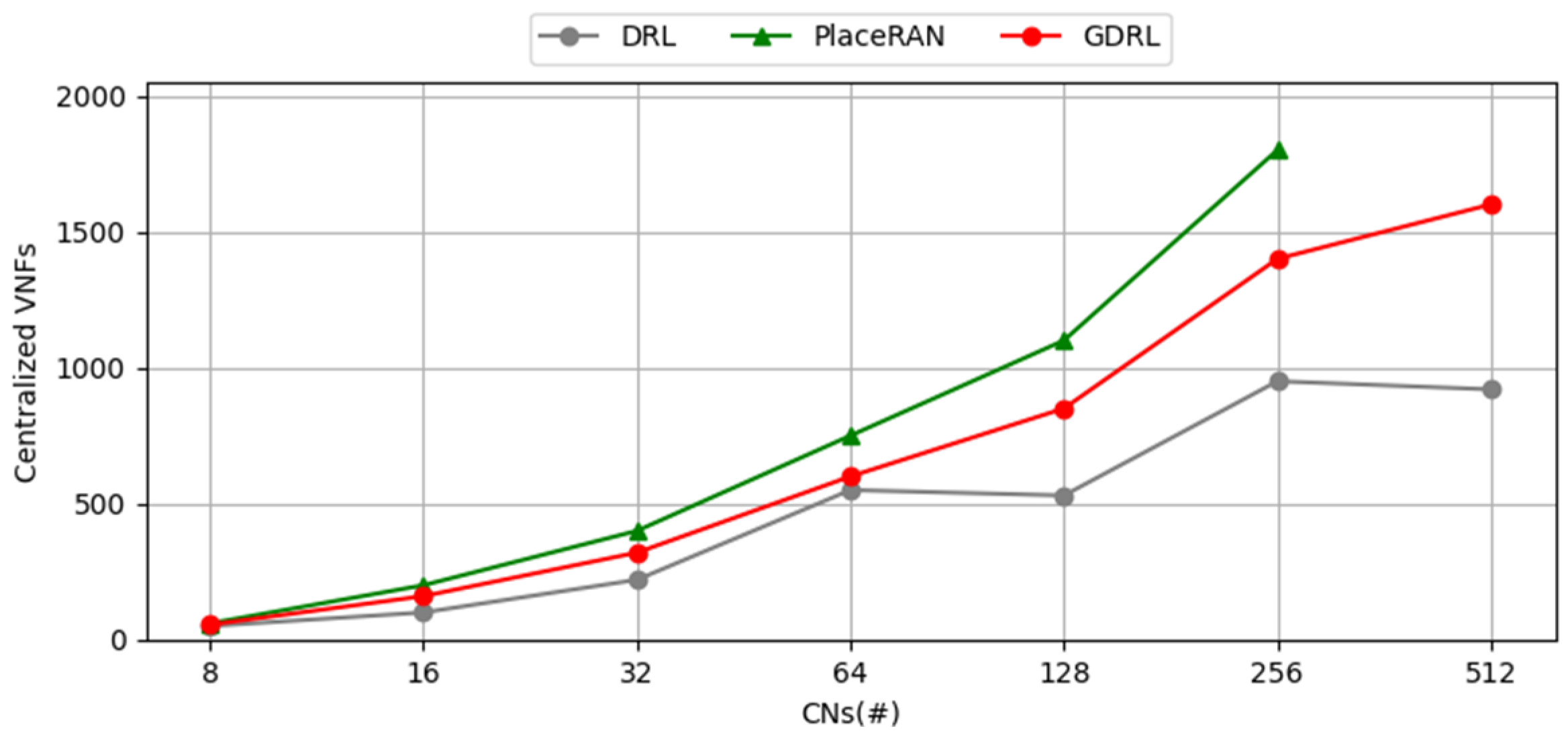
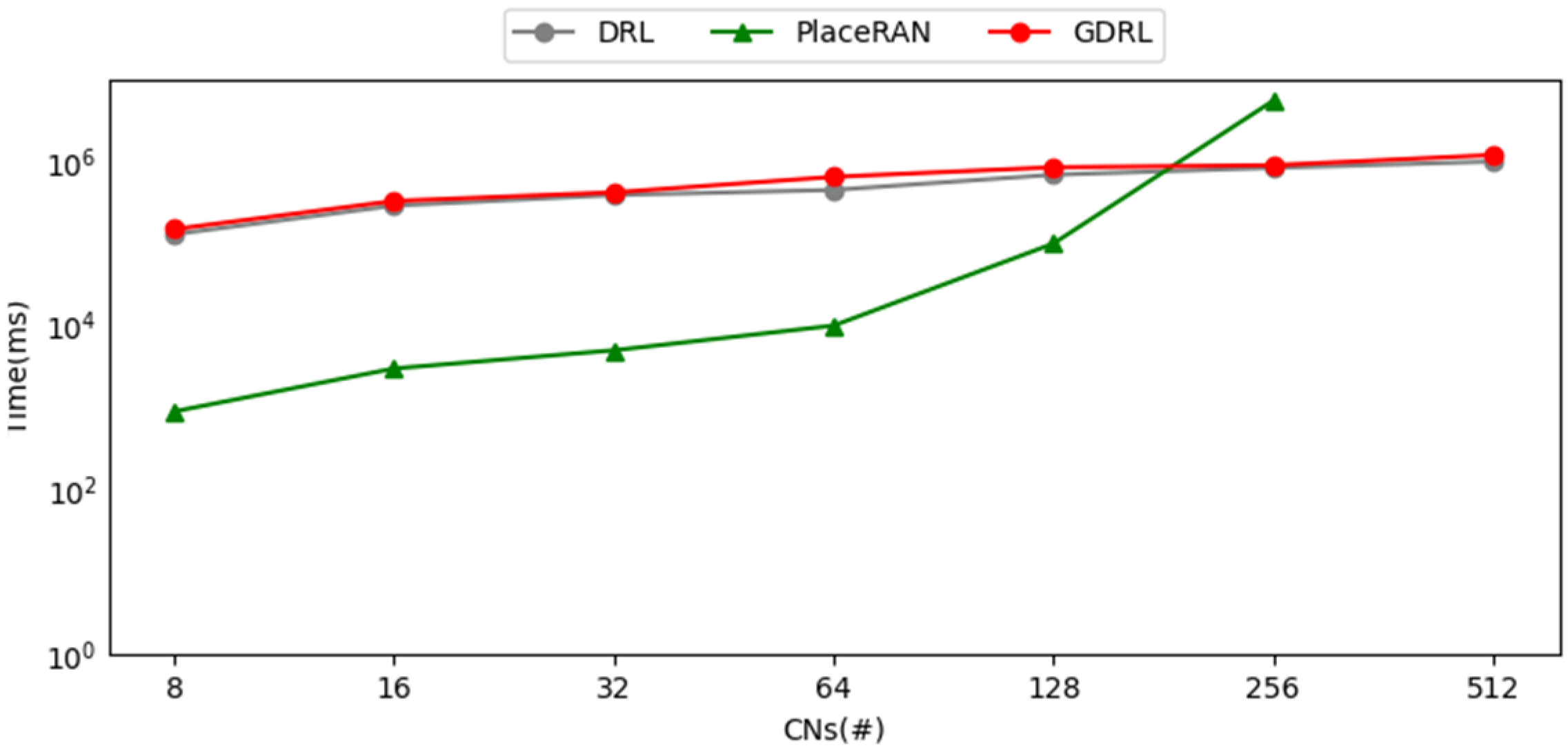
5.3. Evaluation with Routing Decisions
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RAN | Radio Access Network |
| DRL | Deep Reinforcement Learning |
| GNNs | Graph Neural Networks |
| GPPO | Graph Proximal Policy Optimization |
| vRAN | Virtualized RAN |
| BS | Base Station |
| RRU | Remote Radio Unit |
| BBU | Baseband Unit |
| C-RAN | Cloud RAN |
| NG-RAN | Next-Generation RAN |
| RU | Radio Unit |
| DU | Distributed Unit |
| CU | Central Unit |
| NFV | Network Functions Virtualization |
| VNF | Virtualized Network Function |
| MILP | Mixed-Integer Linear Programming |
| RL | Reinforcement Learning |
| ILP | Integer Linear Programming |
| O-RAN | Open RAN |
| ML | Machine Learning |
| LSTM | Long Short-Term Memory |
| DQN | Deep Q-Network |
| VNC | Viable NG-RAN Configuration |
| CN | Computing Node |
| PPO | Proximal Policy Optimization |
| MLP | Multi-Layer Perceptron |
| MSE | Mean Squared Error |
References
- Larsen, L.M.; Checko, A.; Christiansen, H.L. A survey of the functional splits proposed for 5G mobile crosshaul networks. IEEE Commun. Surv. Tuts. 2018, 21, 146–172. [Google Scholar] [CrossRef]
- 3GPP. Study on New Radio Access Technology: Radio Access Architecture and Interfaces, version 14.0.0; Technical Specification (TS) 38.801; 3rd Generation Partnership Project (3GPP): Antibes, France, 2017. [Google Scholar]
- 3GPP. Architecture Description (Release 16), version 16.1.0; Technical Specification Group Radio Access Network (NG-RAN) 38.401; 3rd Generation Partnership Project (3GPP): Antibes, France, 2020. [Google Scholar]
- Chang, C.Y.; Nikaein, N.; Knopp, R.; Spyropoulos, T.; Kumar, S.S. FlexCRAN: A flexible functional split framework over ethernet fronthaul in Cloud-RAN. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–7. [Google Scholar]
- Marsch, P.; Bulakci, Ö.; Queseth, O.; Boldi, M. (Eds.) 5g System Design: Architectural and Functional Considerations and Long Term Research; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Laghrissi, A.; Tarik, T. A survey on the placement of virtual resources and virtual network functions. IEEE Commun. Surv. Tutor. 2018, 21, 1409–1434. [Google Scholar] [CrossRef]
- Bhamare, D.; Erbad, A.; Jain, R.; Zolanvari, M.; Samaka, M. Efficient virtual network function placement strategies for cloud radio access networks. Comput. Commun. 2018, 127, 50–60. [Google Scholar] [CrossRef]
- Yu, H.; Musumeci, F.; Zhang, J.; Xiao, Y.; Tornatore, M.; Ji, Y. DU/CU placement for C-RAN over optical metro-aggregation networks. In Optical Network Design and Modeling: 23rd IFIP WG 6.10 International Conference (ONDM 2019); Springer International Publishing: Cham, Switzerland, 2019; pp. 82–93. [Google Scholar]
- Rodriguez, V.Q.; Guillemin, F.; Ferrieux, A.; Thomas, L. Cloud-RAN functional split for an efficient fronthaul network. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 245–250. [Google Scholar]
- Murti, F.W.; Ayala-Romero, J.A.; Garcia-Saavedra, A.; Costa-Pérez, X.; Iosifidis, G. An optimal deployment framework for multi-cloud virtualized radio access networks. IEEE Trans. Wirel. Commun. 2020, 20, 2251–2265. [Google Scholar] [CrossRef]
- Mushtaq, M.; Golkarifard, M.; Shahriar, N.; Boutaba, R.; Saleh, A. Optimal functional splitting, placement and routing for isolation-aware network slicing in NG-RAN. In Proceedings of the 19th International Conference on Network and Service Management (CNSM), Niagara Falls, ON, Canada, 30 October–2 November 2023; pp. 1–5. [Google Scholar]
- Morais, F.Z.; de Almeida, G.M.F.; Pinto, L. PlaceRAN: Optimal placement of virtualized network functions in beyond 5G radio access networks. IEEE Trans. Mob. Comput. 2023, 22, 5434–5448. [Google Scholar] [CrossRef]
- Almeida, G.M.; Pinto, L.L.; Both, C.B.; Cardoso, K.V. Optimal joint functional split and network function placement in virtualized RAN with splittable flows. IEEE Wirel. Commun. Lett. 2022, 11, 1684–1688. [Google Scholar] [CrossRef]
- Pires, W.T.; Almeida, G.; Correa, S.; Both, C.; Pinto, L.; Cardoso, K. Optimizing Energy Consumption for vRAN Placement in O-RAN Systems with Flexible Transport Networks. TechRxiv 2025. TechRxiv:173611601.16245000. [Google Scholar]
- Ahsan, M.; Ahmed, A.; Al-Dweik, A.; Ahmad, A. Functional split-aware optimal BBU placement for 5G cloud-RAN over WDM access/aggregation network. IEEE Syst. Syst. J. 2022, 17, 122–133. [Google Scholar] [CrossRef]
- Amiri, E.; Wang, N.; Shojafar, M.; Tafazolli, R. Optimizing virtual network function splitting in open-RAN environments. In Proceedings of the IEEE 47th Conference on Local Computer Networks (LCN), Edmonton, AB, Canada, 26–29 September 2022; pp. 422–429. [Google Scholar]
- Almeida, G.M.; Camilo-Junior, C.; Correa, S.; Cardoso, K. A genetic algorithm for efficiently solving the virtualized radio access network placement problem. In Proceedings of the IEEE International Conference on Communications (ICC 2023), Rome, Italy, 28 May–1 June 2023; pp. 1874–1879. [Google Scholar]
- Zhu, Z.; Li, H.; Chen, Y.; Lu, Z.; Wen, X. Joint Optimization of Functional Split, Base Station Sleeping, and User Association in Crosshaul Based V-RAN. IEEE Internet Things J. 2024, 11, 32598–32616. [Google Scholar] [CrossRef]
- Sen, N.; Antony Franklin, A. Towards energy efficient functional split and baseband function placement for 5g ran. In Proceedings of the IEEE 9th International Conference on Network Softwarization (NetSoft), Madrid, Spain, 19–23 June 2023; pp. 237–241. [Google Scholar]
- Sen, N.; Antony Franklin, A. Slice aware baseband function placement in 5g ran using functional and traffic split. IEEE Access 2023, 11, 35556–35566. [Google Scholar] [CrossRef]
- Sen, N.; Antony Franklin, A. Slice aware baseband function splitting and placement in disaggregated 5G Radio Access Network. Comput. Netw. 2025, 257, 110908. [Google Scholar] [CrossRef]
- Klinkowski, M. Optimized planning of DU/CU placement and flow routing in 5G packet Xhaul networks. IEEE Trans. Netw. Serv. Manag. 2023, 21, 232–248. [Google Scholar] [CrossRef]
- Almeida, G.M.; Lopes, V.H.; Klautau, A.; Cardoso, K.V. Deep reinforcement learning for joint functional split and network function placement in vRAN. In Proceedings of the 2022 IEEE Global Communications Conference (GLOBECOM 2022), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1229–1234. [Google Scholar]
- Murti, F.W.; Ali, S.; Latva-Aho, M. Constrained deep reinforcement based functional split optimization in virtualized RANs. IEEE Trans. Wirel. Commun. 2022, 21, 9850–9864. [Google Scholar] [CrossRef]
- Mollahasani, S.; Erol-Kantarci, M.; Wilson, R. Dynamic CU-DU selection for resource allocation in O-RAN using actor-critic learning. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM 2021), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Joda, R.; Pamuklu, T.; Iturria-Rivera, P.E.; Erol-Kantarci, M. Deep reinforcement learning-based joint user association and CU–DU placement in O-RAN. IEEE Trans. Netw. Serv. Manag. 2022, 19, 4097–4110. [Google Scholar] [CrossRef]
- Gao, Z.; Yan, S.; Zhang, J.; Han, B.; Wang, Y.; Xiao, Y.; Simeonidou, D.; Ji, Y. Deep reinforcement learning-based policy for baseband function placement and routing of RAN in 5G and beyond. J. Light. Technol. 2022, 40, 470–480. [Google Scholar] [CrossRef]
- Li, H.; Li, P.; Assis, K.D.; Aijaz, A.; Shen, S.; Yan, S.; Nejabati, R.; Simeonidou, D. NetMind: Adaptive RAN Baseband Function Placement by GCN Encoding and Maze-solving DRL. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Li, H.; Emami, A.; Assis, K.D.; Vafeas, A.; Yang, R.; Nejabati, R.; Yan, S.; Simeonidou, D. DRL-based energy-efficient baseband function deployments for service-oriented open RAN. IEEE Trans. Green. Commun. Netw. 2023, 8, 224–237. [Google Scholar] [CrossRef]
- Sun, P.; Lan, J.; Li, J.; Guo, Z.; Hu, Y. Combining deep reinforcement learning with graph neural networks for optimal VNF placement. IEEE Commun. Lett. 2020, 25, 176–180. [Google Scholar] [CrossRef]
- Qiu, R.; Bao, J.; Li, Y.; Zhou, X.; Liang, L.; Tian, H.; Zeng, Y.; Shi, J. Virtual network function deployment algorithm based on graph convolution deep reinforcement learning. J. Supercomput. 2023, 79, 6849–6870. [Google Scholar] [CrossRef]
- Jiao, L.; Shao, Y.; Sun, L.; Liu, F.; Yang, S.; Ma, W.; Li, L.; Liu, X.; Hou, B.; Zhang, X. Advanced deep learning models for 6G: Overview, opportunities and challenges. IEEE Access 2024, 12, 133245–133314. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Al-qaness, M.A.A.; Dahou, A.; Alsamhi, S.H.; Abualigah, L.; Ibrahim, R.A.; Ewees, A.A. Evolution toward intelligent communications: Impact of deep learning applications on the future of 6G technology. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2024, 14, e1521. [Google Scholar] [CrossRef]
- Morais, F.Z.; Bruno, G.Z.; Renner, J.; de Almeida, G.M.F.; Contreras, L.M.; Righi, R.D.R.; Cardoso, K.V.; Both, C.B. OPlaceRAN—A Placement Orchestrator for Virtualized Next-Generation of Radio Access Network. IEEE Trans. Netw. Serv. Manag. 2022, 20, 3274–3288. [Google Scholar] [CrossRef]
- Fraga, L.d.S.; Almeida, G.M.; Correa, S.; Both, C.; Pinto, L.; Cardoso, K. Efficient allocation of disaggregated ran functions and multi-access edge computing services. In Proceedings of the GLOBECOM 2022–2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022. [Google Scholar]
- Jiang, X.; Zhu, R.; Ji, P.; Li, S. Co-embedding of nodes and edges with graph neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 45, 7075–7086. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Vecchietti, L.F.; Choi, K.; Lee, S.; Har, D. Machine learning for advanced wireless sensor networks: A review. IEEE Sens. J. 2020, 21, 12379–12397. [Google Scholar] [CrossRef]
- Hojeij, H.; Sharara, M.; Hoteit, S.; Vèque, V. Dynamic placement of O-CU and O-DU functionalities in open-ran architecture. In Proceedings of the 2023 20th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Madrid, Spain, 11–14 September 2023. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Ardjmand, E.; Fallahtafti, A.; Yazdani, E.; Mahmoodi, A.; Young II, W.A. A guided twin delayed deep deterministic reinforcement learning for vaccine allocation in human contact networks. Appl. Soft Comput. 2024, 167, 112322. [Google Scholar] [CrossRef]
- Yang, Y.; Zou, D.; He, X. Graph neural network-based node deployment for throughput enhancement. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 14810–14824. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, P.; Liu, C.; Gao, H.; Wang, X. MACNS: A generic graph neural network integrated deep reinforcement learning based multi-agent collaborative navigation system for dynamic trajectory planning. Inf. Fusion. 2024, 105, 102250. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, J.; Wen, G. Graph soft actor–critic reinforcement learning for large-scale distributed multirobot coordination. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 665–676. [Google Scholar] [CrossRef]
- Sun, Q.; He, Y.; Li, Y.; Petrosian, O. Edge Feature Empowered Graph Attention Network for Sum Rate Maximization in Heterogeneous D2D Communication System. Neurocomputing 2025, 616, 128883. [Google Scholar] [CrossRef]
- Peng, Y.; Guo, J.; Yang, C. Learning resource allocation policy: Vertex-GNN or edge-GNN? IEEE Trans. Mach. Learn. Commun. Netw. 2024, 2, 190–209. [Google Scholar] [CrossRef]


| Works | Objectives | Methods |
|---|---|---|
| Murti et al. [10] | Minimize the network costs and the number of functions placed at CUs | Cutting planes |
| Mushtaq et al. [11] | Maximize the profit of Infrastructure Providers considering computation, virtual machine instantiation and routing costs | Gurobi Solver |
| Morais et al. [12] | Maximize the centralization level of vRAN functions and minimize the active computing resources number | MILP Solver |
| Almeida et al. [13] | Maximize the centralization level of vRAN functions and minimize the active computing resources number | MILP Solver |
| Pires et al. [14] | Minimize the energy consumption of O-RAN systems | MILP Solver |
| Almeida et al. [17] | Maximize the centralization level of vRAN functions and minimize the active computing resources number | Genetic algorithm |
| Zhu et al. [18] | Minimize RAN total expenditure | Blenders decomposition, Heuristic algorithm, |
| Sen et al. [19] | Minimize energy consumption in the network | Heuristic algorithm |
| Sen et al. [20] | Maximize the centralization level of the network | Heuristic algorithm |
| Sen et al. [21] | Minimize overall cost of active nodes | Heuristic algorithm |
| Klinkowski [22] | Minimize the number of active computing resources and the sum of latencies of all FH flows | Heuristic algorithm |
| Almeida et al. [23] | Maximize the centralization level of vRAN functions and minimize the active computing resources number | DRL |
| Murti et al. [24] | Minimize network cost, integrating computational cost and routing cost | DRL based on LSTM |
| Mollahasani et al. [25] | Minimize Latency and Maximize throughput | RL based on Artor-Critic learning |
| Joda et al. [26] | Minimize delay and cost | DRL based on deep Q-network |
| Gao et al. [27] | Minimize the number of active computing resources, the cost of bandwidth on all links, and latency | DRL based on deep double Q-learning |
| Li et al. [28] | Minimize the power consumption | DRL based on GNN |
| Notations | Descriptions |
|---|---|
| Topology of the vRAN | |
| Set of nodes of | |
| Core network nodes | |
| Set of BSs (RUs) | |
| Set of transport nodes | |
| Set of CNs | |
| Transmitting capacity of link | |
| Estimated latency | |
| Node of graph G | |
| Neighborhood of | |
| Set of the k-shortest routes for RU | |
| Set of disaggregated RAN VNFs | |
| Set of VNCs | |
| Indicates if belongs to | |
| Indicates if runs from | |
| , , | Indicates if is part of the backhaul, midhaul, and fronthaul |
| , , | Bitrate demands in the backhaul, midhaul, and fronthaul for |
| , , | Maximum tolerated latency in the backhaul, midhaul, and fronthaul for |
| Computing demand of | |
| Processing capacity of |
| Split Option | Functional Split | One-Way Maximum Latency | Minimum Bitrate (Gbps) | |
|---|---|---|---|---|
| Down Link | Up Link | |||
| O1 | RRC–PDCP | 10 ms | 4 | 3 |
| O2 | PDCP–High RLC | 10 ms | 4 | 3 |
| O3 | High RLC–Low RLC | 10 ms | 4 | 3 |
| O4 | Low RLC–High MAC | 1 ms | 4 | 3 |
| O5 | High MAC–Low MAC | <1 ms | 4 | 3 |
| O6 | Low MAC–High PHY | 250 μs | 4.13 | 5.64 |
| O7 | High PHY–Low PHY | 250 μs | 86.1 * | 86.1 * |
| O8 | Low PHY–Radio Frequency | 250 μs | 157.3 | 157.3 |
| Parameters | Values |
|---|---|
| || | {5, 10, 19, 35, 80, 122, 213} |
| || | {8, 16, 32, 64, 128, 256, 512} |
| || | {4, 9} |
| (Gpbs) | {200, 400, 800, 1000} |
| (ms) | {0.163, 0.22, 0.29} |
| (cores) | {8, 16, 32, 64} |
| epochs | 5000 |
| Timestep | 5000 |
| Batch size | 50 |
| discount | 0.99 |
| learning rate | 0.001 |
| Clipping parameter | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, M.; Lin, M.; Chen, W. Network Function Placement in Virtualized Radio Access Network with Reinforcement Learning Based on Graph Neural Network. Electronics 2025, 14, 1686. https://doi.org/10.3390/electronics14081686
Yi M, Lin M, Chen W. Network Function Placement in Virtualized Radio Access Network with Reinforcement Learning Based on Graph Neural Network. Electronics. 2025; 14(8):1686. https://doi.org/10.3390/electronics14081686
Chicago/Turabian StyleYi, Mengting, Mugang Lin, and Wenhui Chen. 2025. "Network Function Placement in Virtualized Radio Access Network with Reinforcement Learning Based on Graph Neural Network" Electronics 14, no. 8: 1686. https://doi.org/10.3390/electronics14081686
APA StyleYi, M., Lin, M., & Chen, W. (2025). Network Function Placement in Virtualized Radio Access Network with Reinforcement Learning Based on Graph Neural Network. Electronics, 14(8), 1686. https://doi.org/10.3390/electronics14081686





