Abstract
To address the needs of enhancing adaptive control and reducing emissions at intersections within intelligent traffic signal systems, this study innovatively proposes a deep reinforcement learning signal control model tailored for mixed traffic flows. Addressing shortcomings in existing models that overlook mixed traffic scenarios, neglect optimization of CO2 emissions, and overly rely on high-performance algorithms, our model utilizes vehicle queue length, average speed, numbers of gasoline and electric vehicles, and signal phases as state information. It employs a fixed-phase strategy to decide between maintaining or switching signal states and incorporates a reward function that balances vehicle CO2 emissions and waiting times, significantly lowering intersection carbon emissions. Following training with reinforcement learning algorithms, the model consistently demonstrates effective control outcomes. Simulation results using the SUMO platform reveal that our designed reward mechanism facilitates the rapid and stable convergence of intelligent agents. Compared with Fixed Time Control (FTC), Actuated Traffic Signal Control (ATSC), and Fuel-ECO TSC (FECO-TSC) methods, our model achieves superior performance in average waiting times and CO2 emissions. Even across scenarios with gasoline–electric vehicle ratios of 25–75%, 50–50%, and 75–25%, the model exhibits significant advantages. These simulations validate the model’s rationality and effectiveness in promoting low-carbon travel and efficient signal control.
1. Introduction
The transportation sector, as a major contributor to carbon emissions, consistently accounts for a significant portion of global emissions. Optimizing traffic flow through intelligent technologies to enhance traffic signal control efficiency and effectively reduce CO2 emissions from motor vehicles has become a crucial research topic. Traffic signal control, as a core measure in urban traffic management, exerts a significant influence on traffic flow and vehicle carbon emissions. At the end of the last century, Hoglund [1] proposed reducing vehicle pollutant emissions by optimizing the design scheme of transportation infrastructure, which provides a reference perspective for this study. However, traditional signal control methods lack flexibility and global optimization capabilities, making them ill-suited for adapting to complex and dynamic traffic conditions. This inadequacy often exacerbates traffic congestion and increases vehicle carbon emissions.
With the rapid development of artificial intelligence technology, machine learning [2,3] technology is gradually applied in the field of transportation, such as using historical traffic data for traffic flow prediction [4,5]. For the field of traffic signal control, adaptive traffic signal control based on reinforcement learning has become the mainstream direction. Boukerche et al. [6], using the Deep Q-Network (DQN) algorithm, minimized average waiting time, queue length, and delays as reward functions to jointly minimize fuel consumption and vehicle travel time. Liu et al. [7] proposed an improved model based on the Double DQN algorithm, enhancing learning efficiency and stability compared with traditional reinforcement learning methods, thereby reducing vehicle travel delays. Bouktif et al. [8], building upon the Double DQN algorithm with a prioritized experience replay mechanism, defined the agent’s state and reward in a consistent manner. Liang et al. [9] integrated dueling networks, target networks, and PER mechanisms into the Double DQN algorithm to form the Dueling Double Deep Q-Network (D3QN) algorithm, effectively reducing vehicle waiting times. Lu Liping et al. [10] introduced the 3DRQN algorithm, which effectively reduces vehicle stopping times in various traffic flows and special traffic scenarios. Li et al. [11], using the Proximal Policy Optimization (PPO) algorithm, proposed a reinforcement learning signal control model based on fairness in vehicle driver waiting times, offering a new research perspective in existing studies. Mao et al. [12] applied the Soft Actor-Critic (SAC) algorithm to traffic signal control and compared it with other types of reinforcement learning algorithms. Jiang et al. [13] proposed a reinforcement learning traffic signal control framework under generic unknown scenarios to enhance model generalization. Tan et al. [14] introduced a new timed control method from a data-driven perspective. Vlachogiannis et al. [15] presented a novel decentralized adaptive traffic signal control algorithm aimed at optimizing pedestrian throughput at intersections. Gu et al. [16] proposed a regional signal control framework that efficiently searches for optimal actions by intelligent agents. Tan et al. [17], focusing on privacy protection for networked vehicle passengers, proposed an adaptive traffic signal control method with privacy protection features.
Existing studies have made certain progress in adaptive traffic signal control. However, there remain significant gaps. First, most models focus exclusively on fuel-powered vehicles and overlook the simultaneous presence of electric vehicles (EVs) in urban traffic. As EV adoption accelerates, such models cannot accommodate the distinct acceleration profiles, energy consumption patterns, and emission characteristics of EVs, leading to signal plans that are suboptimal for increasingly heterogeneous traffic flows. Second, existing approaches typically optimize using a single reinforcement learning (RL) algorithm, and when alternative RL methods are applied, control performance degrades markedly. This lack of algorithmic adaptability undermines model robustness, restricts generalizability across diverse traffic scenarios, and complicates deployment in real world, dynamically changing environments. Finally, current adaptive signal control models tend to focus solely on reducing vehicle waiting times or improving intersection throughput, without simultaneously considering the effective control of CO2 emissions, leading to compromises in balancing environmental benefits and traffic efficiency. In summary, this study addresses the aforementioned research gaps by proposing an adaptive signal control model based on deep reinforcement learning, which demonstrates superior algorithm adaptability in mixed traffic environments of fuel-powered and electric vehicles, achieving dual optimization in traffic efficiency and carbon emission reduction. This approach provides a new perspective and an effective solution for current signal control research.
The main contributions of this study are focused on targeted improvements addressing the existing deficiencies in adaptive traffic signal control:
- (1)
- Aiming at the limitation that existing models only consider fuel-powered vehicle scenarios, an adaptive signal control model suitable for mixed traffic flows of fuel-powered and electric vehicles is proposed, thereby more authentically reflecting the complexity of modern urban traffic.
- (2)
- The constructed model exhibits high algorithm adaptability, achieving excellent control performance under various common deep reinforcement learning frameworks, which overcomes the current models’ heavy dependence on specific algorithms.
- (3)
- A novel reward function integrating vehicle waiting times with CO2 emission control is designed, thereby achieving synchronous optimization of both traffic efficiency and environmental benefits and compensating for the shortcomings of existing models that only focus on single-metric optimization.
These contributions not only address the identified deficiencies but also offer a practical, scalable solution for modern urban signal control.
2. Methodology
2.1. D3QN
The D3QN algorithm enhances the conventional DQN framework by incorporating the Double Q-Learning and dueling network architectures. These modifications are designed to mitigate the overestimation of Q-values and improve the stability of the learning process. The Q-value update equation for the D3QN algorithm is presented in Equation (1):
In Equation (1), represents the estimated Q-value of the current Q-network for the state and action , where α denotes the learning rate and γ denotes the discount factor. The term corresponds to the immediate reward obtained by executing action in state at time step t. Furthermore, represents the Q-value estimate from the target Q-network in the subsequent state for the optimal action, , selected by the current Q-network.
The corresponding loss function for the D3QN algorithm is defined as shown in Equation (2):
In Equation (2), parameter θ denotes the parameters of the current Q-network, whereas parameter represents the parameters of the target Q-network.
2.2. PPO
PPO is a widely adopted policy gradient method in the field of reinforcement learning. It is designed to optimize policies while ensuring that updates do not deviate excessively from the previous policy, thereby striking a balance between learning efficiency and stability. The loss function of PPO is defined as shown in Equation (3):
In Equation (3), represents the advantage of a specific action at time t relative to the average action, and ε is the clipping coefficient. In order to ensure stable policy updates, PPO’s core formula incorporates a clipping mechanism. This mechanism constrains the probability ratio between the new and the old policies to a predetermined range close to 1, fostering consistent updates.
Another critical component of PPO is the value loss function, which minimizes the discrepancy between the predicted value function and the actual return. This helps to improve the accuracy of state value predictions. Its typical form is expressed in Equation (4):
Finally, the overall objective function for PPO is given in Equation (5):
In Equation (5), and serve as weight coefficients, with indicating the entropy of the policy at state .
2.3. SAC
SAC is an entropy maximization-based reinforcement learning algorithm that combines soft Q-learning and Actor-Critic methods. By maximizing the expected return of the policy and entropy, it encourages the agent to explore more of the action space, thereby improving the robustness and stability of the algorithm. The objective of SAC is to maximize the weighted sum of the expected return and the policy entropy, as shown in Equation (6):
The SAC update process consists of three main steps: updating the critic, updating the actor, and updating the entropy weight. The critic network is updated by minimizing the following loss function:
The computation of the target value function is described in Equation (8):
The actor network is updated by maximizing the following objective function:
The entropy weight can be adaptively adjusted by minimizing the following loss function:
3. Modeling
3.1. State Space
For deep reinforcement learning agents, various state spaces provide the necessary informational support for training. Therefore, the reasonableness of the state space design directly affects the overall training effectiveness of the model. In the context of an intersection environment, if the state information acquired by the agent is overly simplistic, it will fail to effectively capture the characteristics of the traffic environment. Conversely, if it is overly complex, it will impose additional computational burdens on the training process.
Considering the application scenario of this study, the state space is designed as a one-dimensional matrix comprising five types of traffic information: queue length of vehicles, average vehicle speed, the number of fuel-powered vehicles, the number of electric vehicles, and the traffic signal phase information from the previous time step. The queue length and speed information help the agent understand the overall traffic flow status at the intersection. The information on the number of fuel-powered and electric vehicles allows the agent to make intelligent decisions based on vehicle types. Finally, the inclusion of signal phase information aids the agent in better learning the relationships between traffic signal phases, thereby improving the effectiveness of action transitions. Combining the above traffic information, the state space of the model is defined as shown in Equation (11):
In Equation (11), L represents all incoming lanes at the intersection, l denotes one specific incoming lane, St refers to the state space at time t, and is the vehicle queue length on lane l at time t; similarly, is the average vehicle speed, is the number of fuel-powered vehicles, is the number of electric vehicles, and represents the traffic signal phase information at the intersection. These vehicle data can be obtained through SUMO simulation. The design of the state space outlined above provides the agent with reasonable state information, thereby improving the ability of the deep neural network to extract relevant features from the state information, which in turn facilitates better learning and training for the agent.
3.2. Action Space
In research on adaptive traffic signal control based on reinforcement learning, action modes can be categorized into two main types: fixed phase sequences and non-fixed phase sequences. Non-fixed phase sequence modes primarily allow the agent to randomly select actions from a predefined phase set, offering higher flexibility. In contrast, fixed phase sequence modes switch actions according to a fixed order of phases, aligning more closely with established traffic behavior norms. From the perspective of real-world traffic signal applications, the release order of vehicles at road intersections follows a fixed sequence. Arbitrarily changing the phase sequence within a signal cycle could cause discomfort for traffic participants and even lead to traffic accidents. Therefore, fixed phase sequence modes better meet the practical requirements of traffic development, and this study adopts such a mode for modeling.
For a typical four-phase single intersection, there are three types of lanes: left-turn lanes, through lanes, and through-right lanes. Vehicles in left-turn and through lanes can only proceed during green lights, while right-turn vehicles can pass if road conditions are safe. The phase information includes east–west green (EWG), east–west left green (EWLG), south–north green (SNG), and south–north left green (SNLG). Considering the waiting tolerance of drivers during red lights and the need for pedestrian crossings, all phases are assigned both maximum and minimum green light durations. Additionally, yellow light phases are implemented during each phase transition to ensure safety. In the control model proposed in this study, the phase sequence set is defined as {EWG, EWLG, SNG, SNLG}, and the action set is defined as action = {0,1}. Executing an action of 0 means maintaining the current phase, while action 1 indicates switching to the next phase. Maintaining a phase extends the green light duration by 3 s for each action.
3.3. Reward
The reward function is a critical component of reinforcement learning as it directly defines the optimization objectives of the control task and fundamentally influences the agent’s training process. Therefore, it is essential to design the reward function based on the specific requirements of the control scenario. In conventional traffic signal control problems, commonly used reward metrics include lane queue length and vehicle waiting time.
For different vehicle types, it is essential to calculate carbon dioxide emissions separately. In the case of fuel-powered vehicles, CO2 emissions can be determined by acquiring their fuel consumption emissions and subsequently converting these values into carbon dioxide emissions. Conversely, electric vehicles do not produce exhaust emissions during operation. Instead, their carbon dioxide emissions are associated with the electricity generation methods. Therefore, by measuring the energy consumption during operation, one can compute the corresponding carbon dioxide emissions.
In this study, the reward function is designed to prioritize road traffic efficiency while promoting low-carbon transportation as a secondary objective. To achieve this, the reward function is defined as the sum of the CO2 emissions from vehicles and their stopping delays. Because the traffic flow environment in this study comprises both fuel-powered vehicles and electric vehicles, the CO2 emissions are computed separately based on vehicle type, as shown in Equation (12):
In Equation (12), and represent the CO2 emission factors for fuel consumption in conventional vehicles and electricity consumption in electric vehicles, respectively. represents the fuel consumption of conventional vehicle i and represents the electricity consumption of electric vehicle j. These emission factors, 2.31 kg CO2/liter and 0.531 kg CO2/kWh, are determined based on internationally accepted standards for carbon emissions from fuels and electricity. The former is widely employed to quantify CO2 emissions from fossil fuel vehicles, whereas the latter reflects the average carbon intensity of electricity grids and is commonly utilized in global greenhouse gas emission assessments.
In addition to emissions, vehicle waiting time is incorporated into the reward function. The complete reward function is mathematically defined as follows in Equation (13):
In Equation (13), denotes the waiting time of all vehicles. The reward function defined in Equation (13) was chosen based on its ability to balance environmental and operational objectives. A preliminary analysis indicated that using only the CO2 emission metric did not yield satisfactory convergence due to the non-uniqueness of solutions within the system. By incorporating vehicle waiting time as an additional metric, the solution quality was improved, enabling the model to achieve better overall performance. The weight coefficients m allow for flexible tuning of the reward function to prioritize different objectives based on specific application scenarios.
4. Results and Discussion
4.1. Basic Setup
The simulation environment in this study is a standard four-phase intersection, with four entry and exit approaches. Each entry approach consists of three lanes, corresponding to left-turn, straight-through, and straight-right movements. The intersection was modeled using the traffic simulation software SUMO v1.19.0, which served as the simulation platform for all simulations. The deep learning framework employed was PyTorch v2.1, and the model training was conducted on an NVIDIA RTX 3070Ti GPU which came from the Alienware brand computer under Dell and was made in the United States. For vehicle parameters, all simulated vehicles were set to have a length of 5 m, and the minimum safe distance between vehicles was set to 2 m. The Krauss car-following model was used to simulate vehicle dynamics, with a maximum speed of 13.89 m/s, a maximum acceleration of 1 m/s2, and a maximum deceleration of 4.5 m/s2. In the reward function, the weight coefficient m was set to 0.7, reflecting the study’s primary objective of minimizing vehicle CO2 emissions. As for the value of m, we find through repeated verification that when m is set to 0.7, vehicle carbon dioxide emissions and vehicle waiting time can be simultaneously optimized, which is consistent with the purpose pursued in this study. In this study, two traffic scenarios were considered: a simulated scenario and a real-world scenario (specifically, the intersection of Dayu North Road and Jianshe Road in Jining City). Both scenarios exhibit dynamically varying traffic flow characteristics. In the simulated scenario, vehicles are generated randomly on each lane at intervals ranging from 1.25 to 8 s, ensuring that the traffic arrival rate follows a Poisson distribution. The real-world scenario, primarily used for comprehensive comparative simulations, was based on field-collected data, with the detailed traffic flow data being presented in Table 1. In this study, the input layer size of the neural network structure is 28, the output layer size is 2, the middle contains two hidden layers, each hidden layer has 128 neurons, and the hidden layer uses an ReLU activation function.

Table 1.
The traffic flow of real-world (Jining) scenario.
To maintain consistency and fairness across all comparative simulations, the hyperparameters of the reinforcement learning algorithms were configured as summarized in Table 2. The setting of each hyperparameter in this study is mainly based on simulation tuning, and its values have been verified by many simulations to show good robustness on different tasks, thus proving the rationality of the selected hyperparameter values. During the agent training phase, each simulation episode lasted 3600 s, and each control algorithm was trained for 1000 episodes. Model parameters were periodically saved throughout the training process for subsequent evaluation. To evaluate the performance of the proposed model, six control methods were selected for comparison:

Table 2.
Hyperparameter settings.
- (a)
- Fixed time control (FTC): a static control strategy with pre-set signal timings.
- (b)
- Actuated traffic signal control (ATSC): a fully actuated control method based on real-time vehicle detection.
- (c)
- FECO-TSC: we use the simulation results of [2] for comparison named Fuel-ECO TSC (FECO-TSC). Because its simulation results cannot be directly compared with this study, we have converted the data.
- (d)
- D3QN: an adaptive traffic signal control model using Double Deep Q-Networks.
- (e)
- PPO: an adaptive model based on the Proximal Policy Optimization algorithm.
- (f)
- SAC: the Soft Actor-Critic algorithm proposed in this study.
These methods were chosen to represent a range of traditional and reinforcement-learning-based approaches, providing a comprehensive evaluation of the proposed model’s performance under various traffic control scenarios.
4.2. Validation of the Reward Function
To validate the effectiveness of the reward function proposed in this study, which is defined as the sum of vehicle CO2 emissions and waiting time, three reward functions were designed for comparison: R1, which represents the proposed reward function; R2, which is based on the cumulative CO2 emissions of vehicles; and R3, which is based on the cumulative waiting time of vehicles. Because the primary purpose of this simulation is to verify the effectiveness of the reward function, only the training and comparison of three reinforcement learning control strategies are involved here, while comparisons with other classical signal control methods will be presented in the next section.
Figure 1a,b illustrate the training process of the PPO control strategy under the three reward functions, showing the cumulative waiting time and cumulative CO2 emissions, respectively. From the figures, it can be observed that PPO, when using cumulative CO2 emissions as the reward function (PPO_R2), achieved convergence only after 800 episodes, with significant fluctuations during the training process. When using cumulative waiting time as the reward function (PPO_R3), the convergence speed improved compared with PPO_R2, but the training curve still exhibited relatively large fluctuations. In contrast, when using the proposed reward function (PPO_R1), the convergence speed was the fastest, and the training curve showed the smallest fluctuations, achieving the best convergence performance among the three cases.
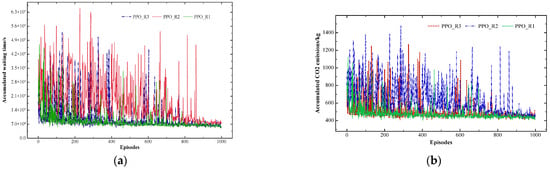
Figure 1.
(a) Comparison of cumulative waiting time under different rewards of PPO. (b) Comparison of cumulative CO2 emissions under different rewards of PPO.
Figure 2a,b illustrate the training comparison of the D3QN control strategy under different reward functions. From the figures, it can be observed that when using cumulative CO2 emissions as the reward (D3QN_R2), significant fluctuations occurred in the early stages of training, and the curve continued to oscillate during the convergence phase. In contrast, when using cumulative waiting time as the reward (D3QN_R3), the convergence performance of D3QN showed significant improvement. However, overall, when using the proposed reward function (D3QN_R1), D3QN achieved the fastest convergence speed and the highest stability.
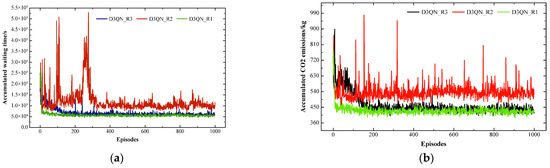
Figure 2.
(a) Comparison of cumulative waiting time under different rewards of D3QN. (b) Comparison of cumulative CO2 emissions under different rewards of D3QN.
Figure 3a,b illustrate the training comparison of the SAC control strategy under different reward functions. Unlike PPO and D3QN, SAC achieved relatively good convergence performance under all three reward functions. However, when using cumulative CO2 emissions as the reward function (SAC_R2), SAC exhibited significant fluctuations during the early training stages, which were not observed when using the other reward functions. Additionally, when using cumulative waiting time as the reward function (SAC_R3), the time required to achieve convergence was longer compared with using the proposed reward function (SAC_R1). From these comparisons, it can be concluded that the proposed reward function helps the agent improve convergence performance.
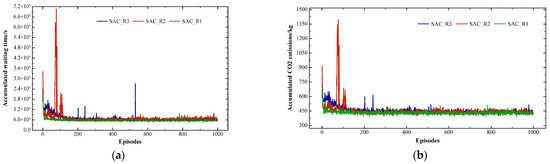
Figure 3.
(a) Comparison of cumulative waiting time under different rewards of SAC. (b) Comparison of cumulative CO2 emissions under different rewards of SAC.
In summary, from the perspective of traffic flow and reinforcement learning analysis, all of the reinforcement learning algorithms are able to achieve a better level of control because the reward function designed in this paper is able to meet the needs of intersection traffic efficiency as the main focus and low-carbon traffic as the secondary focus, and they help the agent to better learn and grasp the relationship between the overall control of the intersection and the carbon emissions of the vehicles so that it can better play out the reinforcement learning technology’s advantages. While a better system solution cannot be obtained when carbon emission is chosen as the reward function alone, the addition of waiting time can further improve the efficiency of the intelligent body in solving the existing control problems. Therefore, the effectiveness of the reward function designed in this paper is verified, and the reward function will be used in subsequent simulations to demonstrate and evaluate other aspects.
4.3. Comparison of Model Control Performance
After verifying the rationality of the reward function, it is necessary to compare the proposed model with other signal control methods to validate its effectiveness. Therefore, the subsequent simulations focus on testing and comparing various traffic signal control methods, including FTC, ATSC, PPO, D3QN, and SAC. For PPO, D3QN, and SAC, the model parameters saved during the 900th training episode were loaded into the testing environment for comparison. All signal control methods were tested over 100 episodes.
Figure 4 and Figure 5 illustrate the performance comparison of the five signal control methods in terms of average CO2 emissions and average waiting time, respectively. From the figures, it can be observed that the FTC method performs the worst on both metrics, while ATSC performs better than FTC. However, these two classical signal control methods still lag behind the PPO, D3QN, and SAC reinforcement learning methods. Among the latter three methods, D3QN and SAC achieve better control performance, while PPO performs relatively worse. In terms of control stability, FTC exhibits the largest fluctuations and the poorest stability. The ATSC method maintains a relatively stable control level. Among the three reinforcement learning strategies, PPO’s stability is inferior to ATSC, while D3QN and SAC demonstrate stability comparable with ATSC.
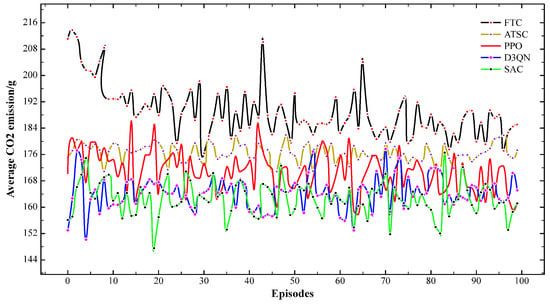
Figure 4.
Comparison of average vehicle CO2 emissions.
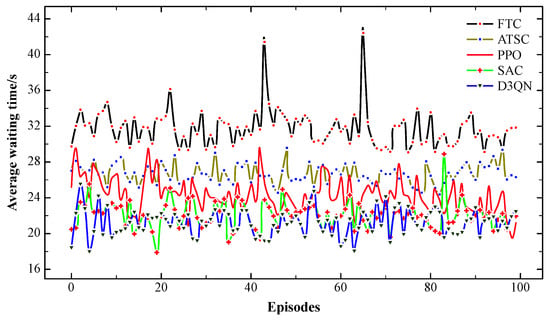
Figure 5.
Comparison of average vehicle waiting time.
In addition, the detailed analysis of the performance data for all control methods across different metrics is presented in Table 3. Considering the relatively strong control performance and stability of the ATSC method, it was selected as the baseline for comparison. From the table, in terms of average CO2 emissions, FTC, ATSC, PPO, D3QN, and SAC achieve 189.16 g, 176.49 g, 171.49 g, 164.34 g, and 162.46 g, respectively. In comparison, ATSC, PPO, D3QN, and SAC reduce CO2 emissions by 3.27%, 6.88%, and 7.95%, respectively. For the average waiting time, FTC, ATSC, PPO, D3QN, and SAC achieve 31.76 s, 26.71 s, 24.27 s, 21.24 s, and 22.09 s, respectively. In comparison, ATSC, PPO, D3QN, and SAC reduce the average waiting time by 9.14%, 20.48%, and 17.30%, respectively.

Table 3.
Comparison of different indicators for all methods.
Adaptive signal control methods based on DRL outperform traditional methods such as FTC and ATSC. By combining the traffic signal control model proposed in this study, reinforcement learning methods achieve excellent results. This is because traffic signals, acting as agents, are able to learn how to dynamically adjust signal timing plans by leveraging effective traffic state information during training, thereby further enhancing the control efficiency of intersection signals.
Furthermore, the traffic signal control model proposed in this study is designed to address the problem of minimizing vehicle CO2 emissions in a mixed scenario of fuel-powered and electric vehicles. Considering that the proportion of fuel-powered and electric vehicles varies across different urban road systems, the performance of the proposed model needs to be further validated under varying vehicle type ratios. The subsequent simulations evaluate the control performance under three vehicle type ratio scenarios: Scenario (i): 25% fuel-powered vehicles and 75% electric vehicles; Scenario (ii): 50% fuel-powered vehicles and 50% electric vehicles; Scenario (iii): 75% fuel-powered vehicles and 25% electric vehicles.
Figure 6 and Figure 7 illustrate the performance comparison of FTC, ATSC, SAC, and D3QN under different vehicle type ratio scenarios. Figure 6 shows the comparison of average CO2 emissions per vehicle across different scenarios. In Scenario (i), the average CO2 emissions for the four methods are 155.4 g, 129.4 g, 119.6 g, and 119.3 g, respectively. SAC achieves reductions of 23.1% and 7.6% compared with FTC and ATSC, while D3QN achieves reductions of 23.2% and 7.8%. In Scenario (ii), the average CO2 emissions for the four methods are 189.2 g, 176.5 g, 162.5 g, and 164.3 g, respectively. SAC achieves reductions of 14.1% and 7.9% compared with FTC and ATSC, while D3QN achieves reductions of 13.2% and 6.9%. Finally, in Scenario (iii), the average CO2 emissions for the four methods are 242.3 g, 220.3 g, 205.1 g, and 203.9 g, respectively. SAC achieves reductions of 15.38% and 6.93% compared with FTC and ATSC, while D3QN achieves reductions of 15.8% and 7.4%.
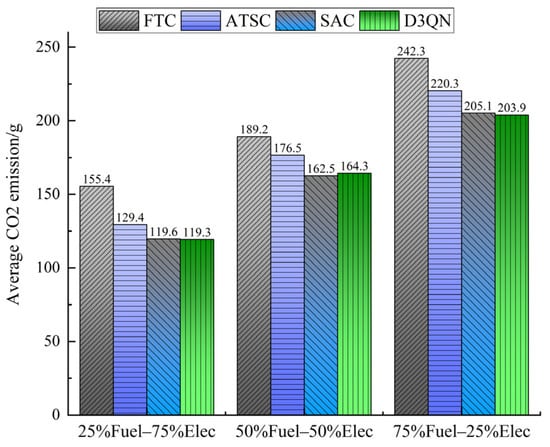
Figure 6.
Comparison of average CO2 emissions under different proportions of vehicle types.
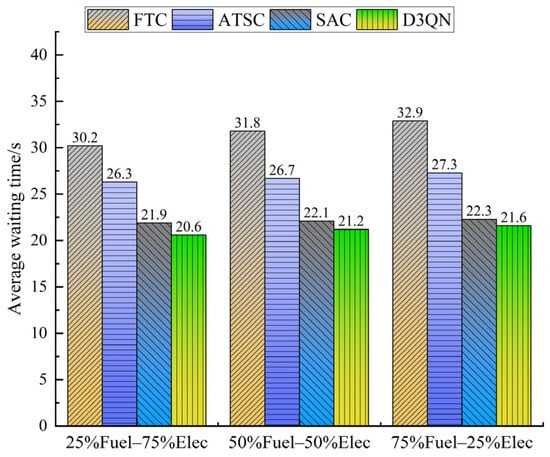
Figure 7.
Comparison of average waiting time under different proportions of vehicle types.
Figure 7 illustrates the comparison of average waiting time across the four methods. From the figure, it can be observed that the average waiting time of D3QN stabilizes at around 21 s, SAC stabilizes at around 22 s, and ATSC stabilizes at around 26 s, while FTC exhibits large fluctuations.
5. Conclusions
This study introduces an innovative adaptive signal control model designed specifically for mixed traffic scenarios involving gasoline and electric vehicles, with the dual objectives of reducing both average waiting times and CO2 emissions. By developing a comprehensive signal control framework that incorporates a range of reinforcement learning algorithms for training and evaluation, we conducted a series of extensive simulations to test the model’s performance. The results of these simulations reveal several key innovations. Notably, in response to the increasing penetration of electric vehicles in the traffic flow, the reward function proposed in this study effectively guides intelligent agents to learn optimal control strategies, balancing the needs of both gasoline and electric vehicles. Through detailed comparisons with traditional traffic signal control methods, such as FTC and ATSC, our model consistently outperforms these approaches in terms of both reducing average vehicle waiting times and lowering CO2 emissions per vehicle. This demonstrates the superior efficiency of our model, particularly in real-world scenarios where dynamic traffic flow patterns are common. Additionally, the model’s robustness is further validated across different traffic scenarios, including varying proportions of gasoline and electric vehicles, where it continues to achieve impressive results in both key performance metrics. This reinforces the versatility and adaptability of our approach, even in the face of shifting traffic compositions.
Furthermore, while the study focuses on standard single-point intersections with four phases—a common intersection type—real-world traffic networks feature a variety of intersection configurations, including complex multi-phase and multi-lane intersections. In future work, the current single-intersection model can be extended to a multi-intersection cooperative control framework. In this framework, multiple intersections would share traffic flow information to achieve coordinated optimization of vehicle movement across the road network, thereby alleviating traffic congestion and high carbon dioxide emissions in certain urban areas. In addition, because of its good driving mode and high level of intelligent control effect, autonomous vehicles will have a significant impact on the intersection and air pollution adaptive signal control model, which will also become an important research direction in the future [18]. The model proposed in this paper incorporates only conventional fuel vehicles and electric vehicles, with a primary focus on small passenger cars, which limits its scope in terms of vehicle type diversity. Future research could expand the model by including a broader range of vehicle types, such as new energy construction vehicles, freight trucks, and specialized emergency vehicles, thereby enhancing the model’s practical feasibility. Moreover, the carbon emission calculation model presented here considers only fuel and electricity consumption. Given the more complex energy composition of hybrid vehicles, it is necessary to further refine the carbon emission model in future studies to more accurately reflect the energy consumption structures of most common vehicle types.
Author Contributions
L.D.: Conceptualization; methodology; supervision; formal analysis; investigation; visualization; writing—original draft; writing—review and editing. H.Z.: writing—review and editing; project administration; resources; validation. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the Natural Science Foundation of Gansu Province (Grant: 24JRRA255) and the Lanzhou Youth Science and Technology Talent Innovation Program (Grant: 2023-QN-125).
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Höglund, P.G. Alternative intersection design—A possible way of reducing air pollutant emissions from road and street traffic? Sci. Total Environ. 1994, 146, 35–44. [Google Scholar] [CrossRef]
- Liu, L.Y.; Zhang, J.; Qian, K.; Min, F. Semi-supervised regression via embedding space mapping and pseudo-label smearing. Appl. Intell. 2024, 54, 9622–9640. [Google Scholar] [CrossRef]
- Liu, L.Y.; Zuo, H.M.; Min, F. BSRU: Boosting semi-supervised regressor through ramp-up unsupervised loss. Knowl. Inf. Syst. 2024, 66, 2769–2797. [Google Scholar] [CrossRef]
- He, S.F. Traffic flow prediction using an AttCLX hybrid model. World J. Inf. Technol. 2025, 3, 84–88. [Google Scholar]
- Chang, A.; Li, D.; Cao, G.F.; Liu, W.; Wang, L.; Zhou, N. Research on traffic object tracking and trajectory prediction technology based on deep learning. World J. Inf. Technol. 2024, 2, 40–47. [Google Scholar]
- Boukerche, A.; Zhong, D.H.; Sun, P. FECO: An Efficient Deep Reinforcement Learning-Based Fuel-Economic Traffic Signal Control Scheme. IEEE Trans. Sustain. Comput. 2022, 7, 144–156. [Google Scholar] [CrossRef]
- Liu, J.X.; Qin, S.; Su, M.; Luo, Y.; Zhang, S.; Wang, Y.; Yang, S. Traffic Signal Control Using Reinforcement Learning Based on the Teacher-Student Framework. Expert Syst. Appl. 2023, 228, 120458. [Google Scholar] [CrossRef]
- Bouktif, S.; Cheniki, A.; Ouin, A.; El-Sayed, H. Deep Reinforcement Learning for Traffic Signal Control with Consistent State and Reward Design Approach. Knowl.-Based Syst. 2023, 267, 110440. [Google Scholar] [CrossRef]
- Liang, X.Y.; Du, X.S.; Wang, G.L.; Han, Z. A deep reinforcement learning network for traffic light cycle control. IEEE Trans. Veh. Technol. 2019, 68, 1243–1253. [Google Scholar] [CrossRef]
- Lu, L.-P.; Cheng, K.; Chu, D.; Wu, C.; Qiu, Y. Adaptive Traffic Signal Control Based on Dueling Recurrent Double Q Network. China J. Highw. Transp. 2022, 35, 267–277. [Google Scholar]
- Li, C.H.; Ma, X.T.; Xia, L.; Zhao, Q.; Yang, J. Fairness Control of Traffic Light via Deep Reinforcement Learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering, Hong Kong, China, 20–21 August 2020. [Google Scholar]
- Mao, F.; Li, Z.H.; Li, L. A Comparison of Deep Reinforcement Learning Models for Isolated Traffic Signal Control. IEEE Intell. Transp. Syst. Mag. 2023, 15, 160–180. [Google Scholar] [CrossRef]
- Jiang, H.Y.; Li, Z.Y.; Li, Z.S.; Bai, L.; Mao, H.; Ketter, W.; Zhao, R. A General Scenario-Agnostic Reinforcement Learning for Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11330–11344. [Google Scholar] [CrossRef]
- Tan, C.P.; Cao, Y.M.; Ban, X.G.; Tang, K. Connected Vehicle Data-Driven Fixed-Time Traffic Signal Control Considering Cyclic Time-Dependent Vehicle Arrivals Based on Cumulative Flow Diagram. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8881–8897. [Google Scholar] [CrossRef]
- Vlachogiannis, D.M.; Wei, H.; Moura, S.; Macfarlane, J. HumanLight: Incentivizing Ridesharing via Human-centric Deep Reinforcement Learning in Traffic Signal Control. Transp. Res. Part C Emerg. Technol. 2024, 162, 104593. [Google Scholar] [CrossRef]
- Gu, H.K.; Wang, S.B.; Ma, X.G.; Jia, D.; Mao, G.; Lim, E.G.; Wong, C.P.R. Large-Scale Traffic Signal Control Using Constrained Network Partition and Adaptive Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7619–7632. [Google Scholar] [CrossRef]
- Tan, C.P.; Yang, K.D. Privacy-preserving Adaptive Traffic Signal Control in A Connected Vehicle Environment. Transp. Res. Part C: Emerg. Technol. 2024, 158, 104453. [Google Scholar] [CrossRef]
- Wiseman, Y. Autonomous Vehicles. In Research Anthology on Cross-Disciplinary Designs and Applications of Automation; Information Resources Management Association: Alexandria, VA, USA, 2022; Volume 2, pp. 878–889. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).