Eco-Cooperative Planning and Control of Connected Autonomous Vehicles Considering Energy Consumption Characteristics
Abstract
1. Introduction
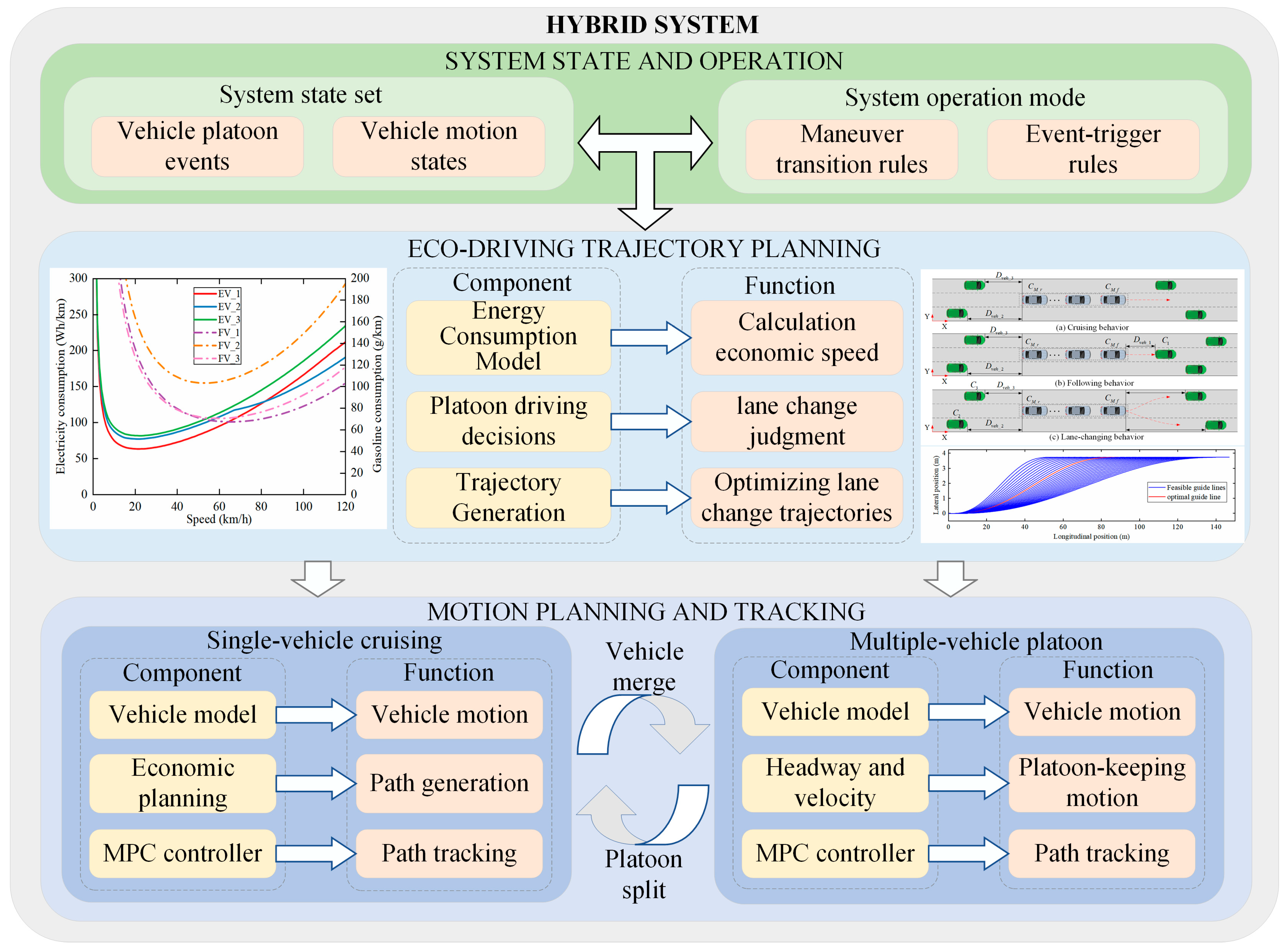
2. System Architecture
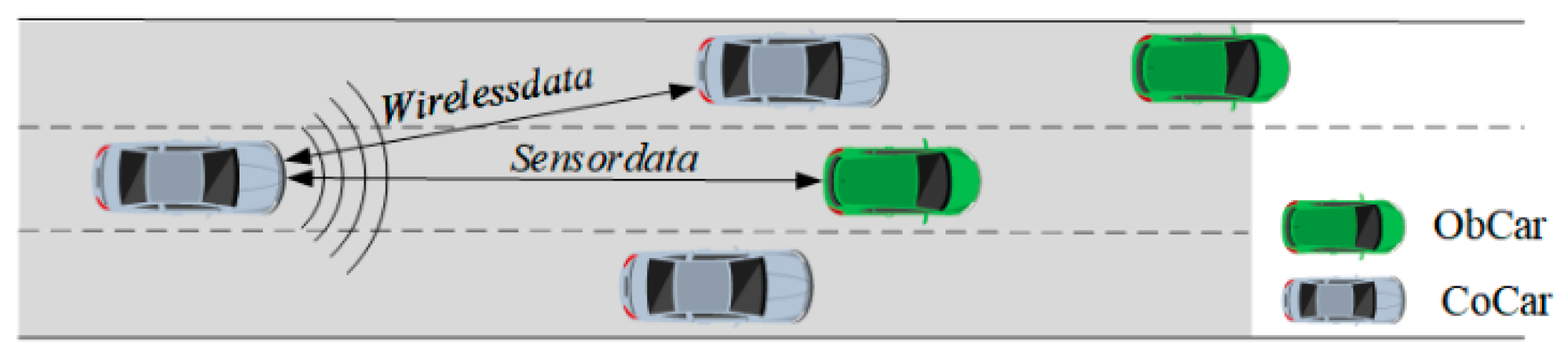
2.1. System Operating Environment
- (1)
- Road system: CAVs driving on roads provided with communication infrastructure. The road system communications infrastructure enables functions related to information sense, transmission, computation, storage, and control.
- (2)
- Information communication: CAVs can sense, transmit, and receive information about the driving environment and vehicle control in real-time with negligible delay in information communication.
- (3)
- Vehicle control: CAVs can accurately control the state of the CAV’s movement and are equipped with a formation system that allows them to drive in adaptive cruise control and formation with other CAVs. Vehicle platoon control is based on a distributed control framework, where each vehicle can autonomously regulate its driving behavior according to dynamic conditions.
2.2. Overall Framework
- (1)
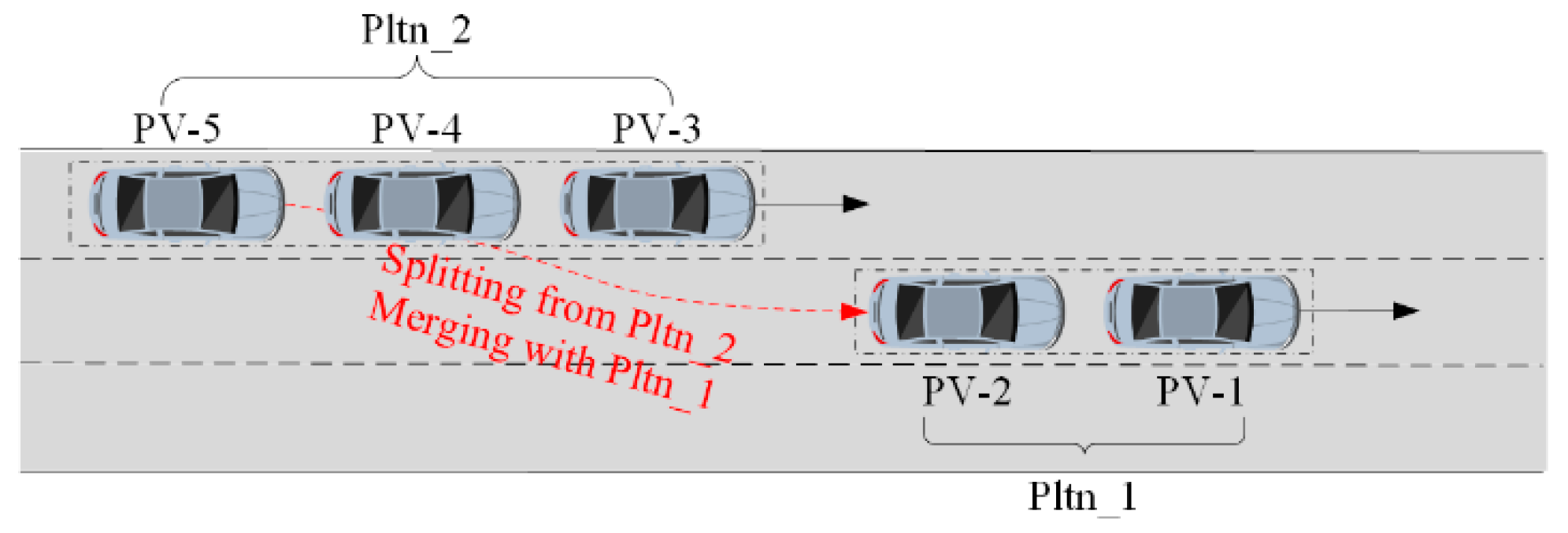
- As the core of coordinating various functional modules, the cooperative driving system’s collaborative operation includes a control architecture that encompasses two key components: the state set and the operation mode. The state set characterizes the motion status and attributes of both the controlled vehicles and the surrounding environment. The operation mode outlines the transition rules for maneuvers between individual vehicle cruising and platooning, specifies the triggering mechanisms for platoon splitting and merging, and manages the formation and dissolution of vehicle groups.
- (2)
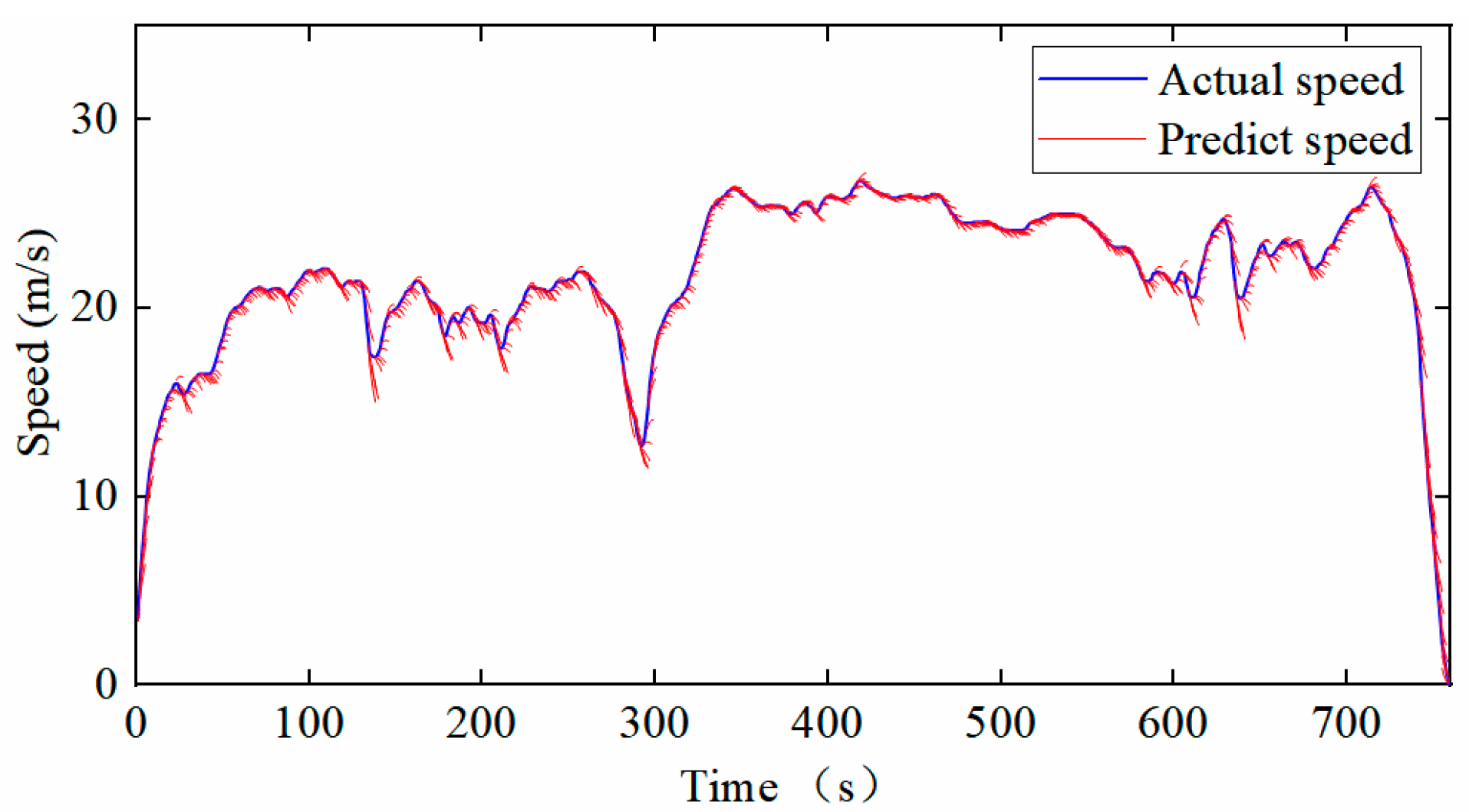
- Vehicle cooperative speed planning is the core content of the cooperative eco-driving system, mainly containing two key aspects. First, the driving system plans the economic speed for cooperative driving according to the energy consumption characteristics of all vehicles in the vehicle platoon. It optimally adjusts it globally to minimize the overall energy consumption. Second, when encountering the vehicle ahead, the system will forecast the future speed of the vehicle via the RBF neural network while ensuring safety. It will then make intelligent energy-saving lane-changing decisions and optimize the lane-changing path to ensure both the efficiency of lane-changing and passenger comfort.
- (3)
- The aim of trajectory tracking is to ensure vehicles adhere to a pre-planned path accurately and swiftly. Within a vehicle platoon, the lead vehicle’s control goal is to track the planned reference trajectory, whereas the follower vehicle’s control goal is to track the lead vehicle’s path and maintain proper platoon spacing. In this paper, distinct controllers for the lead and follower vehicles are constructed using the MPC method to achieve vehicle following and formation maintenance based on their respective control objectives.
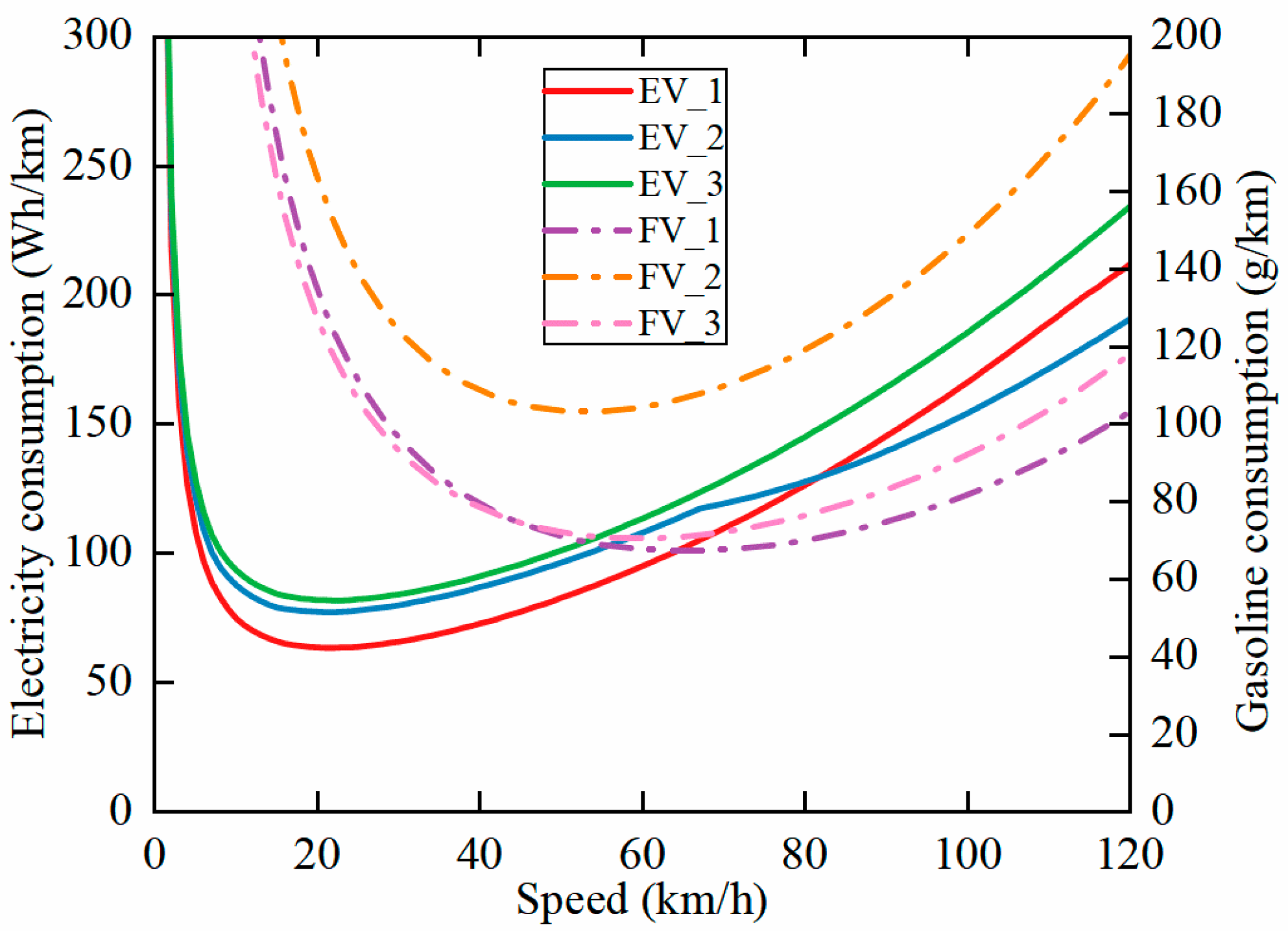
3. Calculation of Economic Cruising Speed Considering Energy Consumption Characteristics
3.1. Fuel Vehicle Energy Consumption Model
3.2. Electric Vehicle Energy Consumption Model
3.3. Calculation of Optimum Cruising Speed
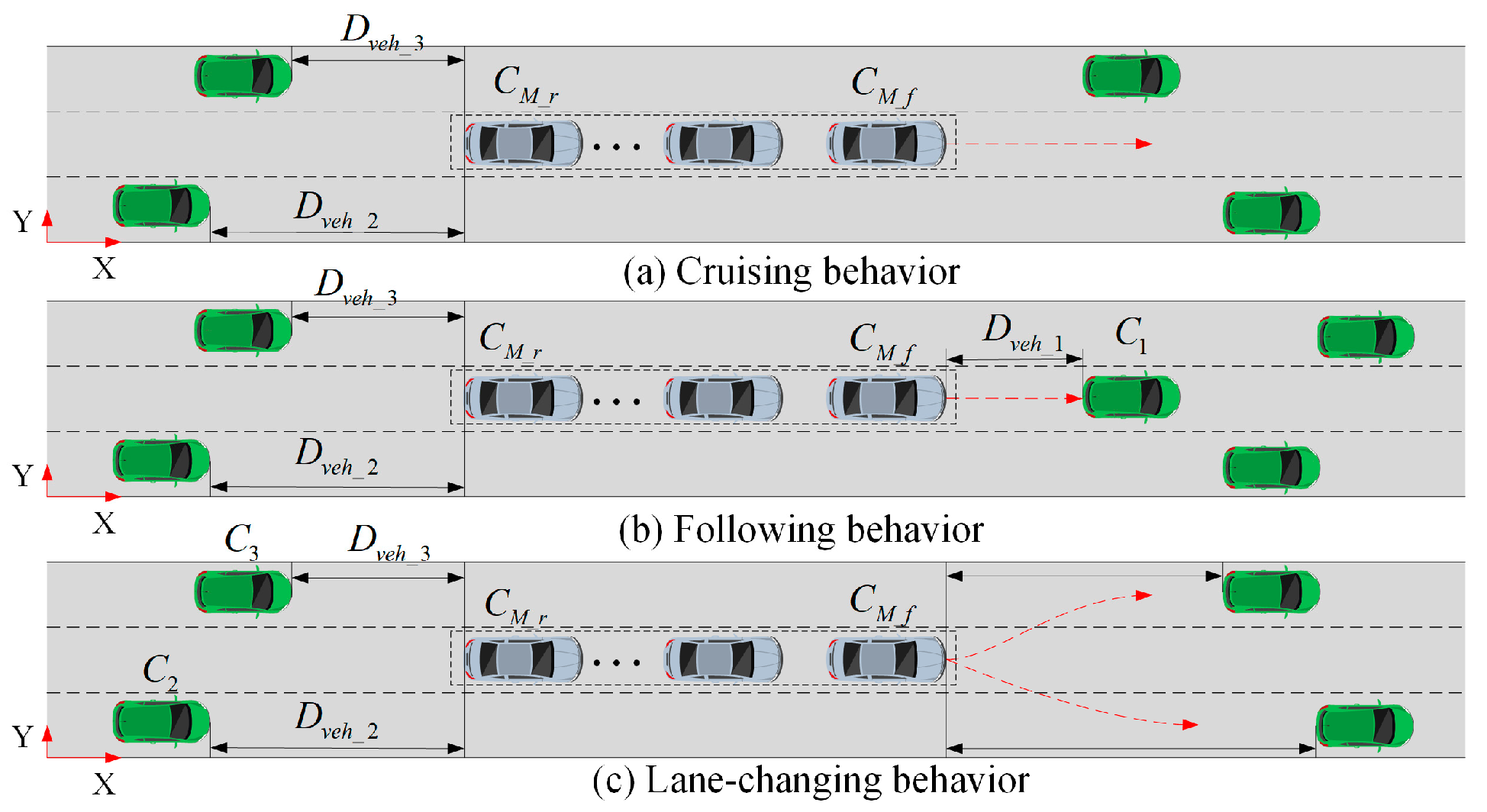
4. Vehicle Platoon Driving Planning Based on Economic Cruise Speed
4.1. Vehicle Platoon Driving Decisions
4.1.1. Safety Decision-Making
4.1.2. Economic Decision-Making
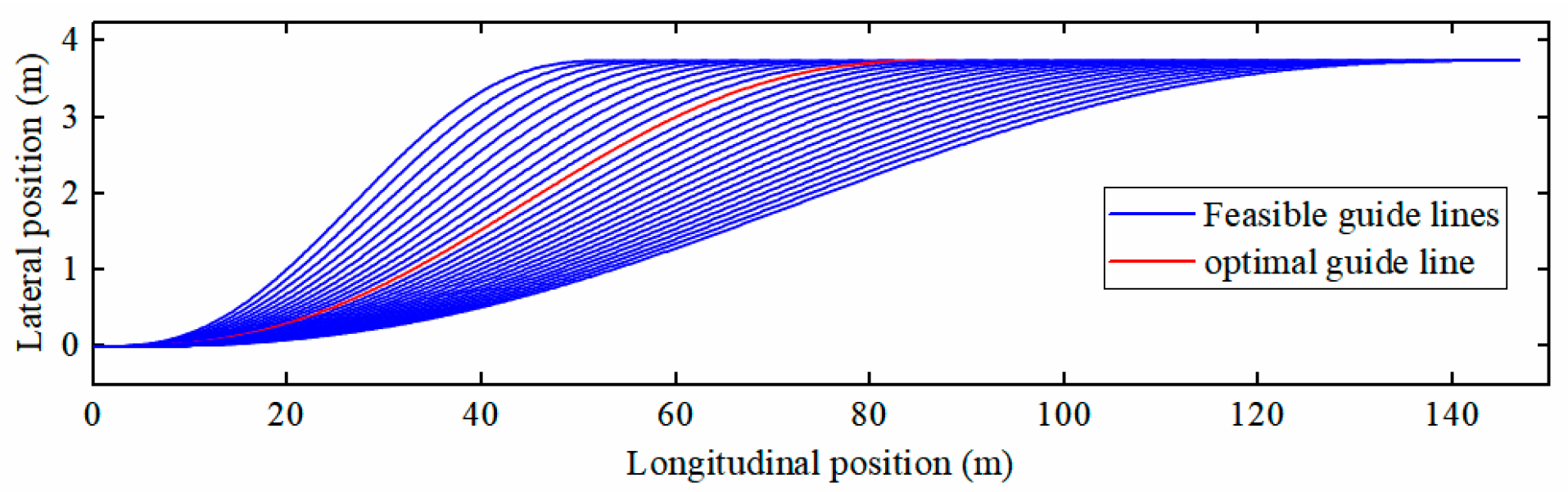
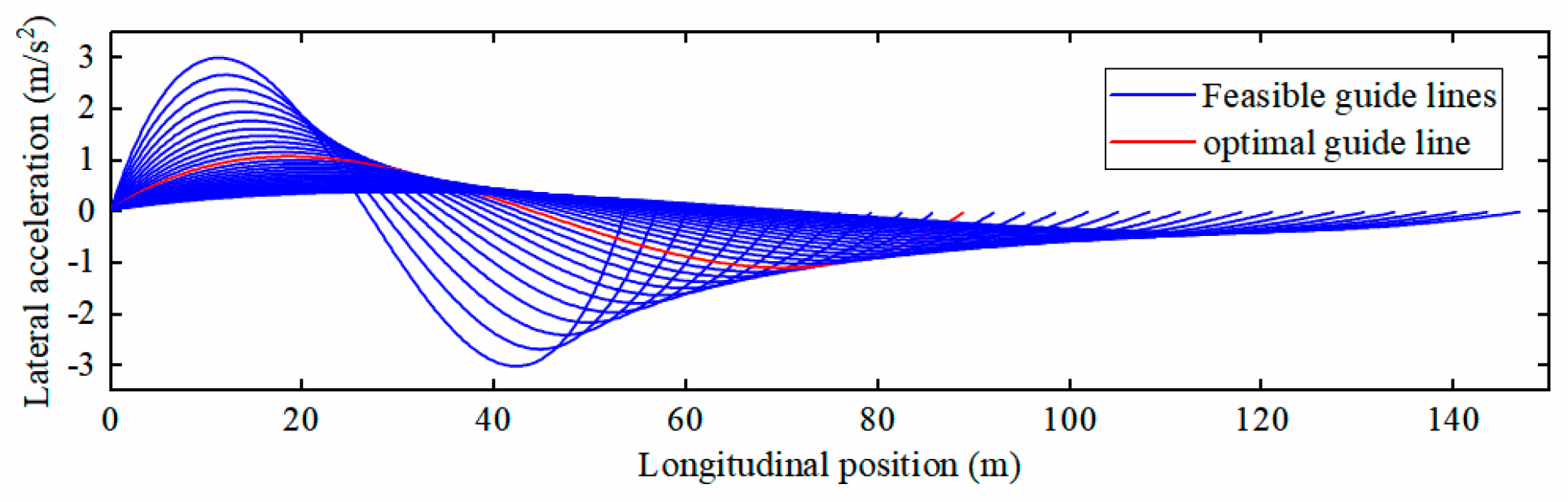
4.2. Vehicle Platoon Trajectory Generation
5. Trajectory Tracking Control Based on MPC
5.1. Construction of Vehicle Kinematics Model
5.2. Objective Function and Constraint Setting for MPC
6. Vehicle Cooperative System Modeling Based on Hybrid Automata
6.1. Vehicle and Environmental Status Definitions
6.2. Event Triggering Rules
7. Simulation Test
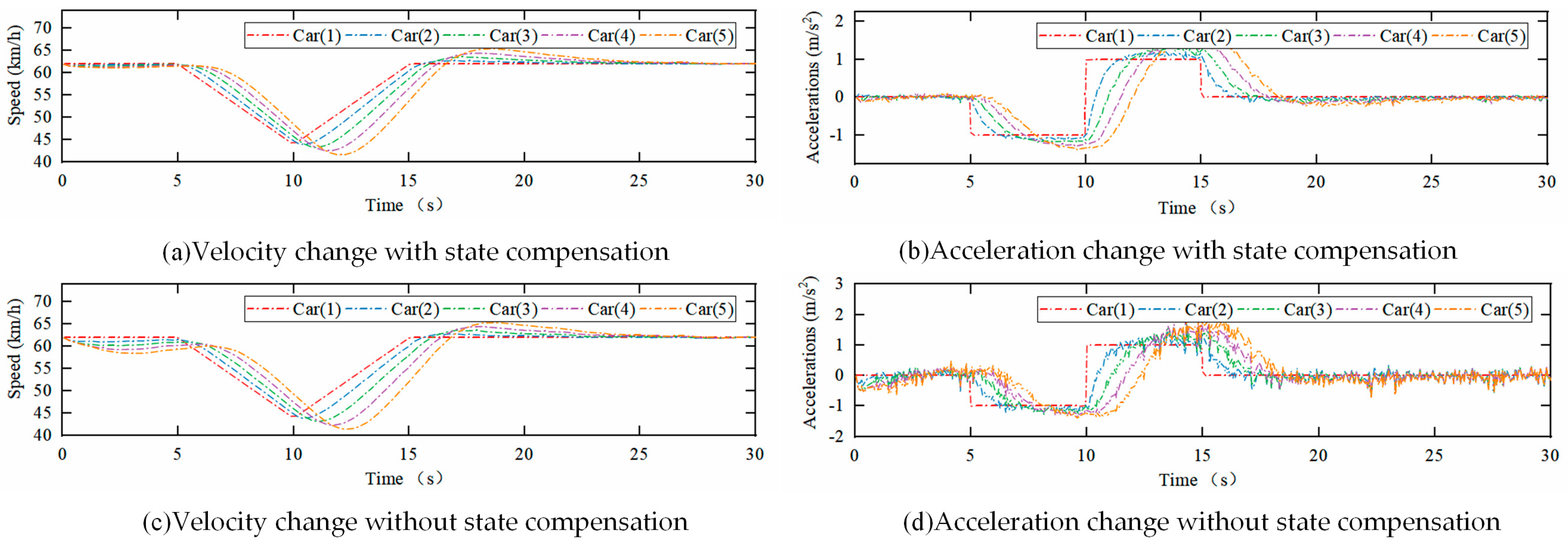
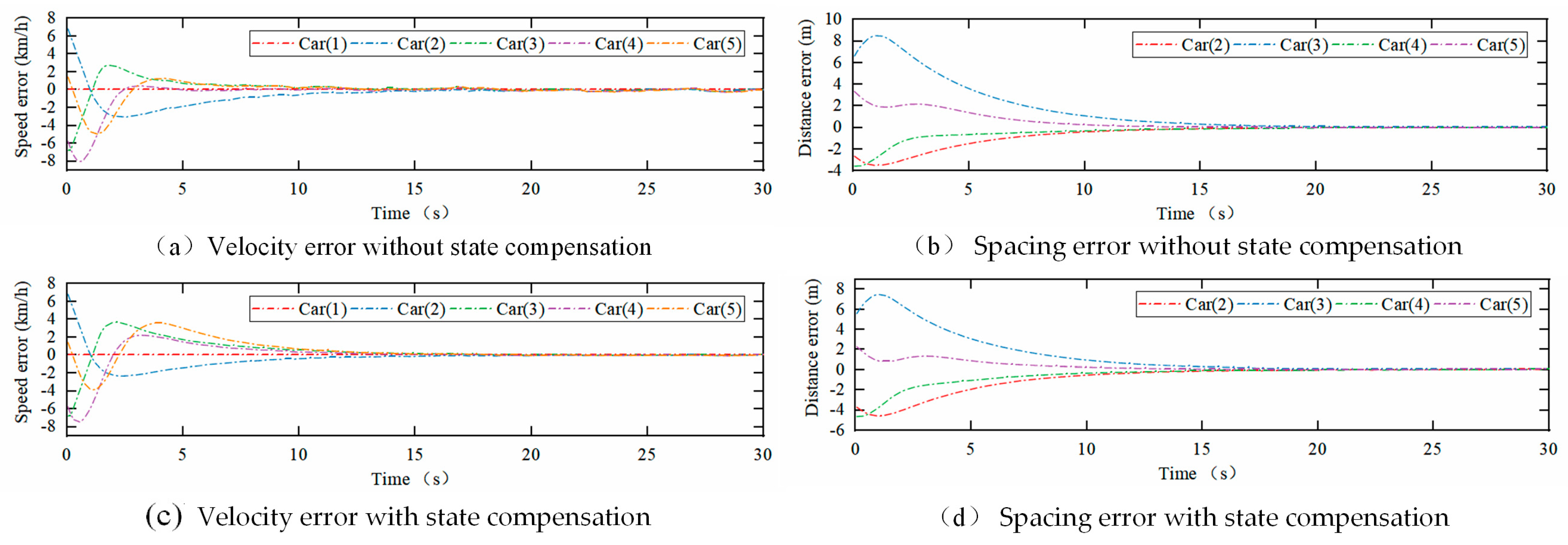
7.1. Platoon Stability Verification
7.1.1. String Stability
7.1.2. Internal Stability
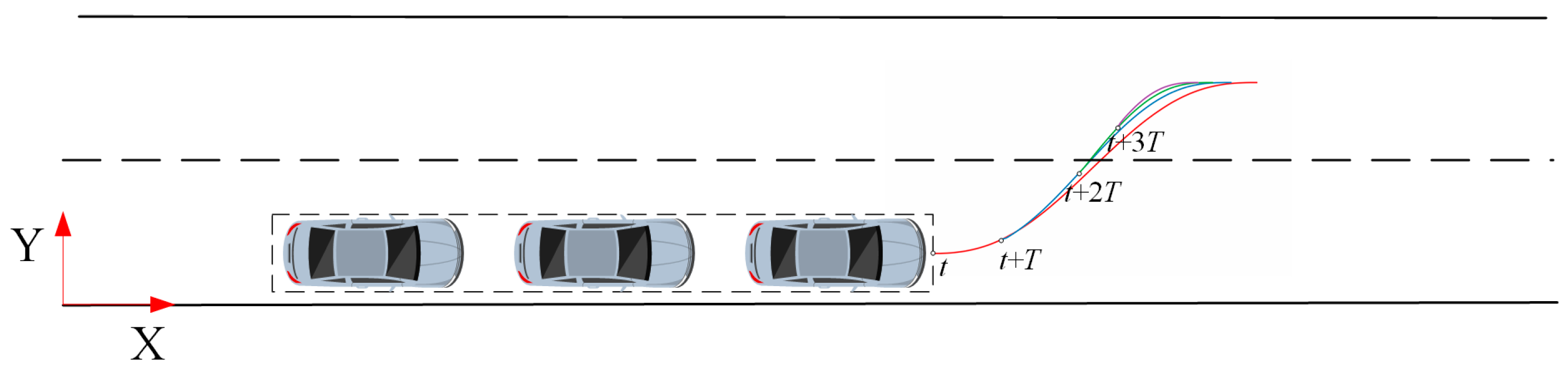
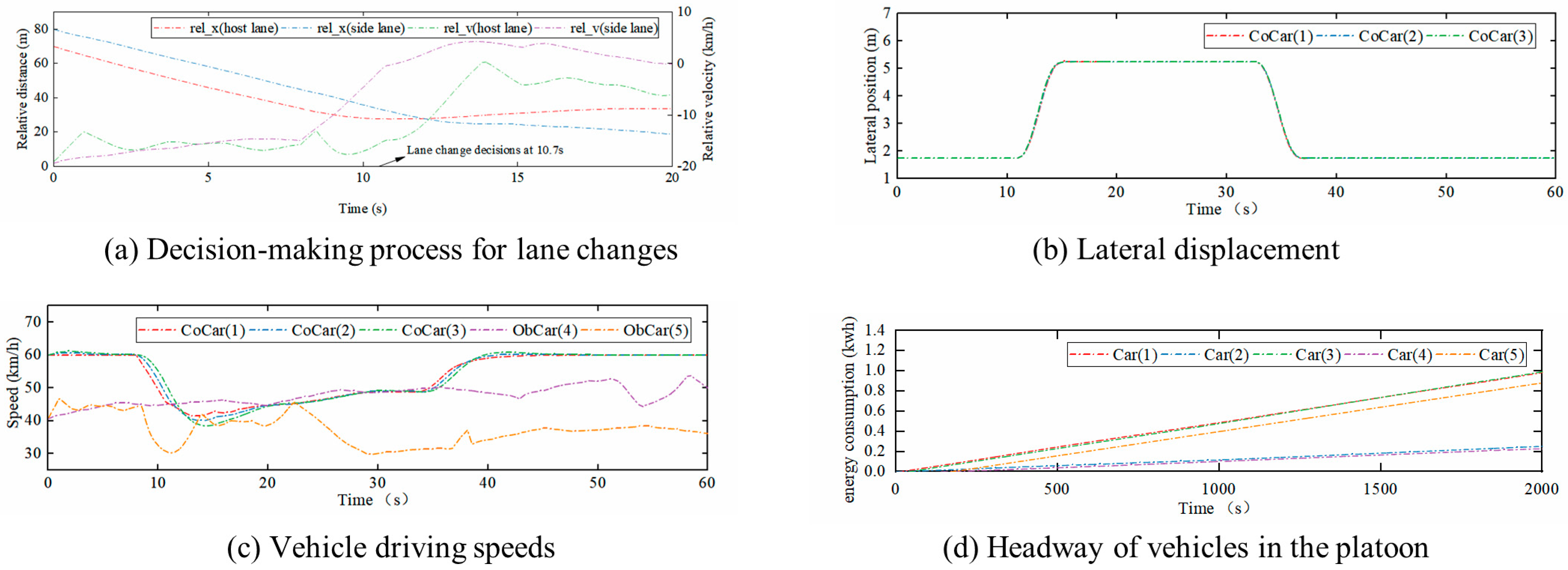
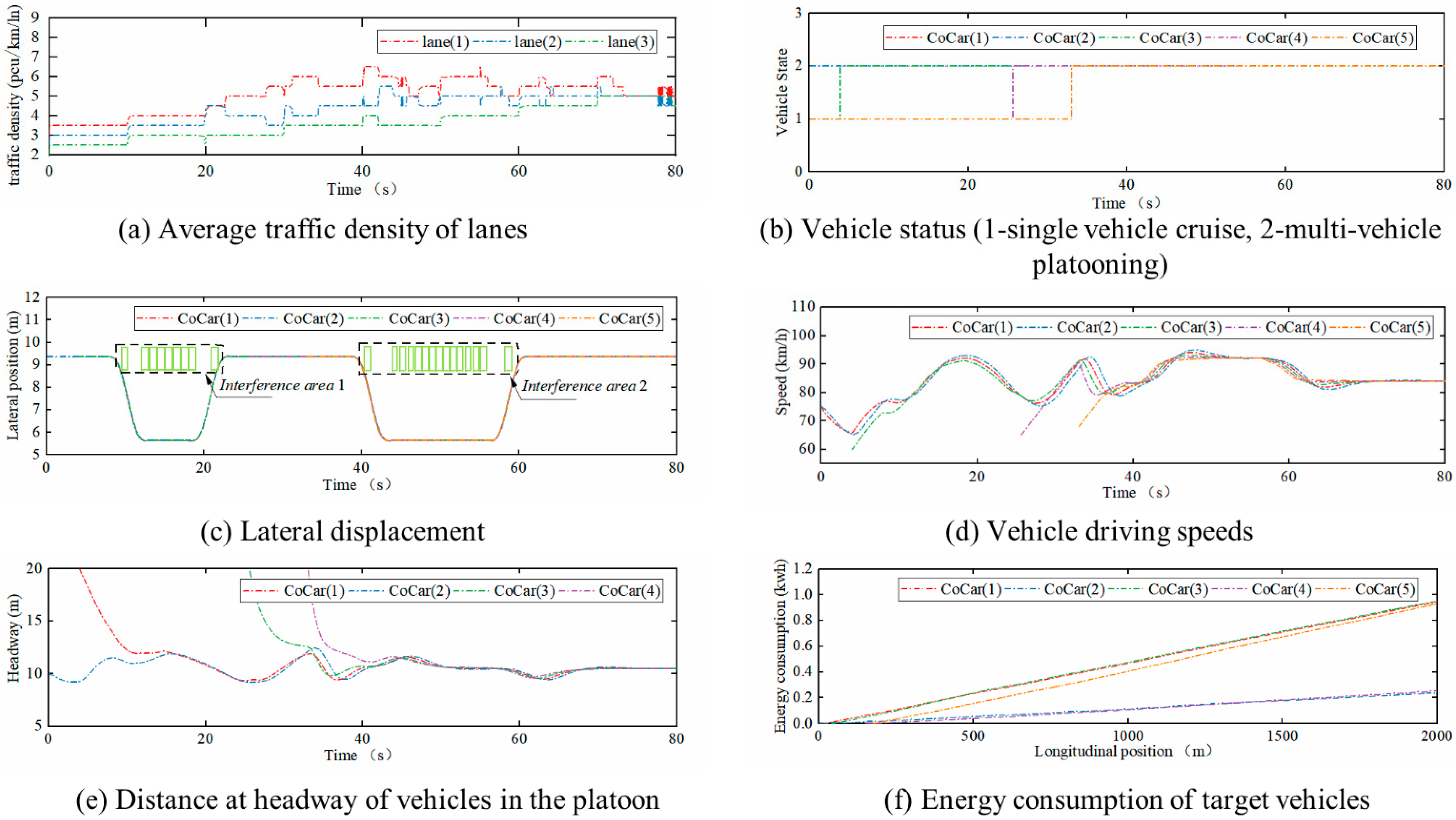
7.2. Vehicle Platoon Lane Change Verification
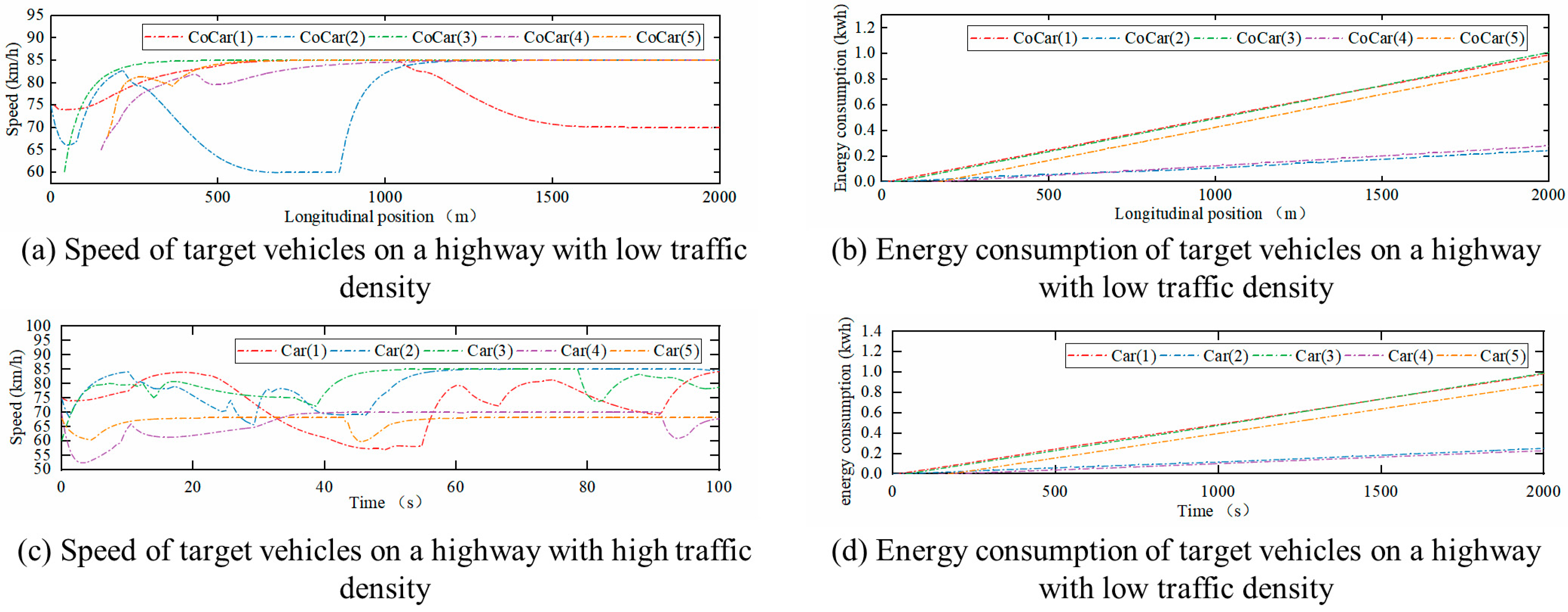
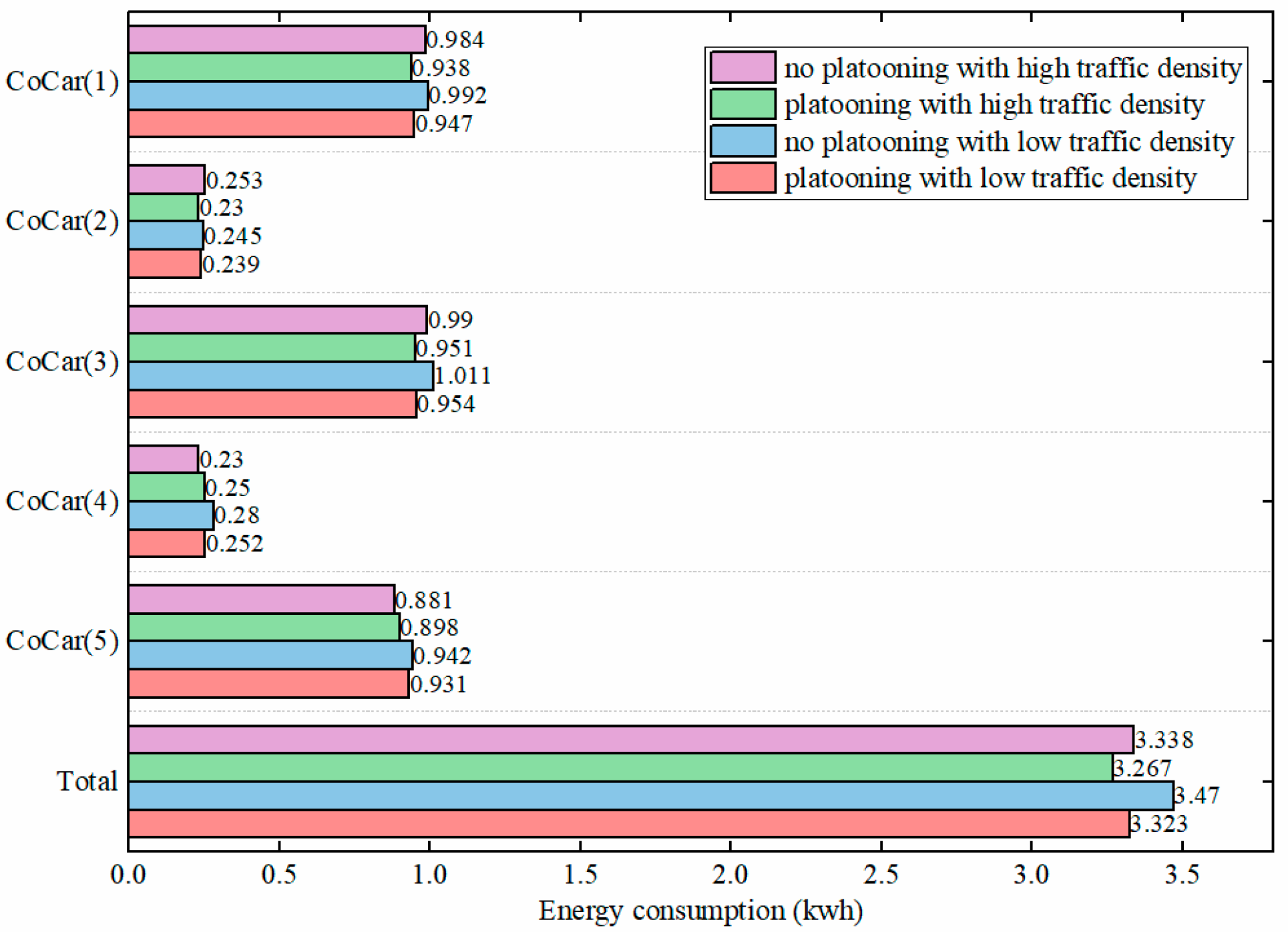
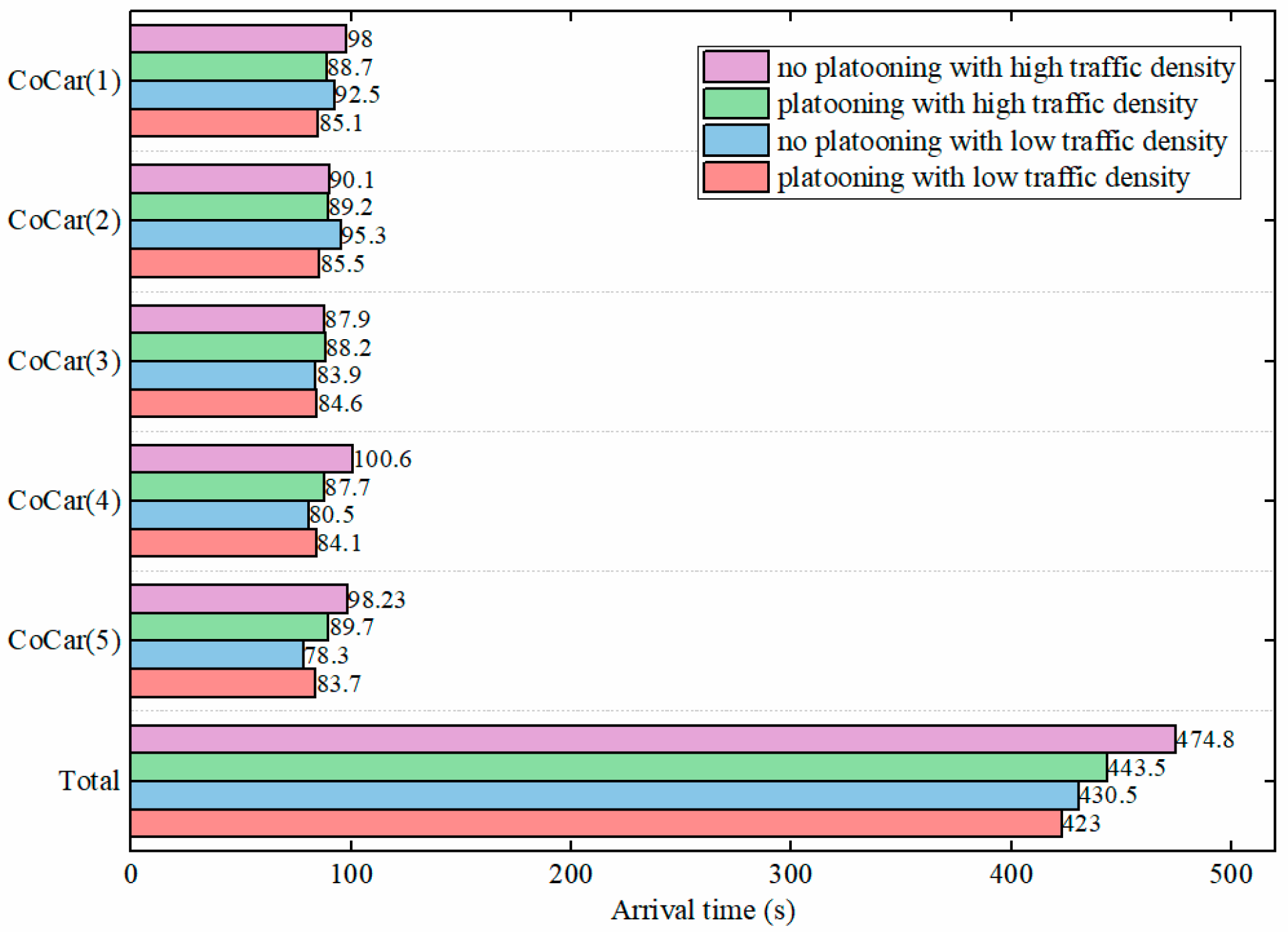
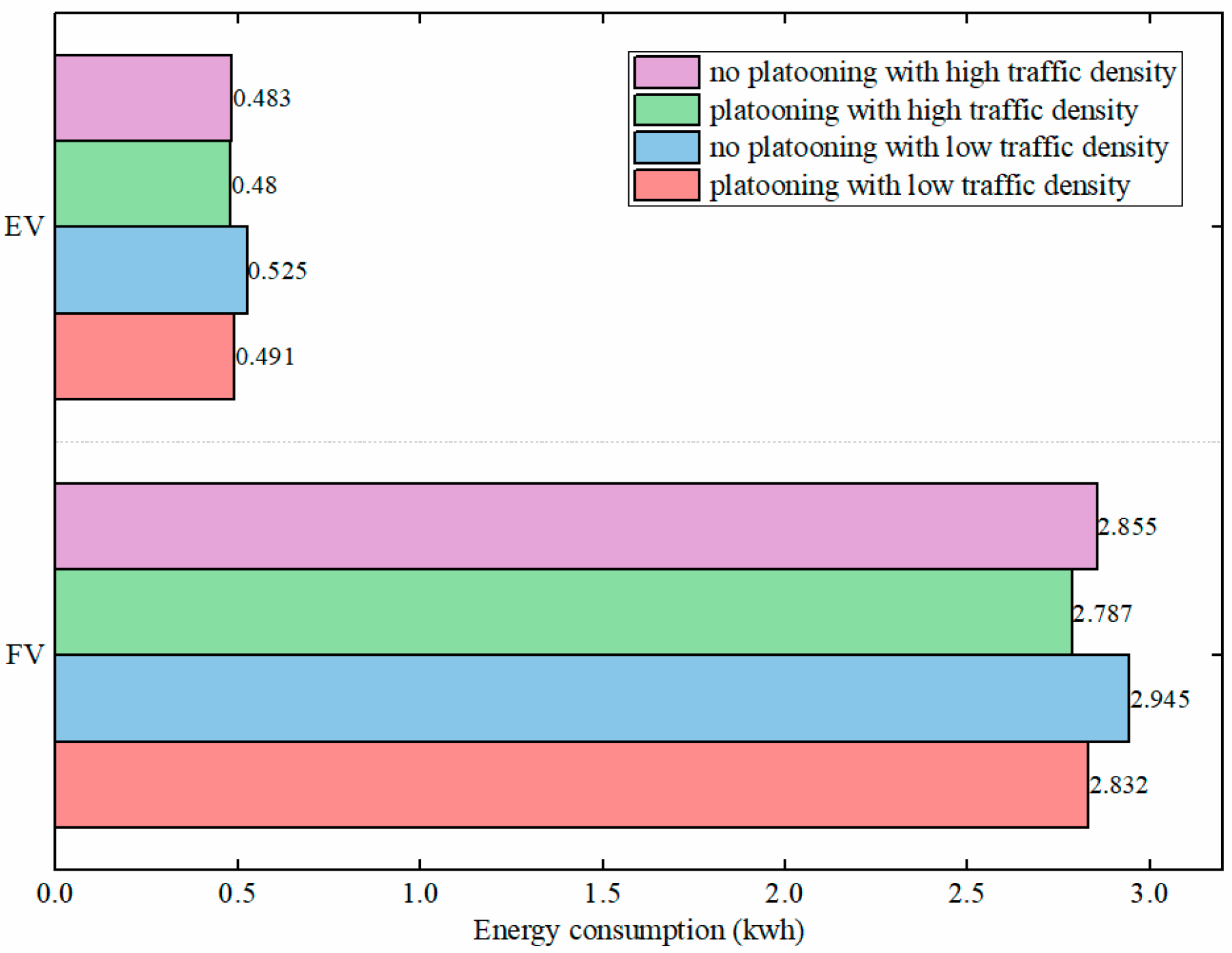
7.3. Energy Efficiency Verification
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zahoor, A.; Mehr, F.; Mao, G.; Yu, Y.; Sápi, A. The carbon neutrality feasibility of worldwide and in China’s transportation sector by E-car and renewable energy sources before 2060. J. Energy Storage 2023, 61, 106696. [Google Scholar] [CrossRef]
- Rehman, F.U.; Islam, M.; Miao, Q. Environmental sustainability via green transportation: A case of the top 10 energy transition nations. Transp. Policy 2023, 137, 32–44. [Google Scholar] [CrossRef]
- Matin, A.; Dia, H. Impacts of Connected and Automated Vehicles on Road Safety and Efficiency: A Systematic Literature Review. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2705–2736. [Google Scholar] [CrossRef]
- Wang, B.; Su, R. A Distributed Platoon Control Framework for Connected Automated Vehicles in an Urban Traffic Network. IEEE Trans. Control Netw. Syst. 2022, 9, 1717–1730. [Google Scholar] [CrossRef]
- Pi, D.; Xue, P.; Wang, W.; Xie, B.; Wang, H.; Wang, X.; Yin, G. Automotive platoon energy-saving: A review. Renew. Sustain. Energy Rev. 2023, 179, 113268. [Google Scholar] [CrossRef]
- Hussein, A.A.; Rakha, H.A. Vehicle Platooning Impact on Drag Coefficients and Energy/Fuel Saving Implications. IEEE Trans. Veh. Technol. 2022, 71, 1199–1208. [Google Scholar] [CrossRef]
- Stegner, E.; Ward, J.; Siefert, J.; Hoffman, M.; Bevly, D.M. Experimental Fuel Consumption Results from a Heterogeneous Four-Truck Platoon; SAE Technical Paper: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Zhai, C.; Luo, F.; Liu, Y.; Chen, Z. Ecological Cooperative Look-Ahead Control for Automated Vehicles Travelling on Freeways with Varying Slopes. IEEE Trans. Veh. Technol. 2019, 68, 1208–1221. [Google Scholar] [CrossRef]
- Jia, Y.; Nie, Z.; Wang, W.; Lian, Y.; Guerrero, J.M.; Outbib, R. Eco-driving policy for connected and automated fuel cell hybrid vehicles platoon in dynamic traffic scenarios. Int. J. Hydrogen Energy 2023, 48, 18816–18834. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Li, X.; Wu, G.; Zhao, Y.; Wu, L.; Aksun-Guvenc, B.; Guvenc, L. Eco-driving-based cooperative adaptive cruise control of connected vehicles platoon at signalized intersections. Transp. Res. Part D Transp. Environ. 2021, 92, 102746. [Google Scholar] [CrossRef]
- Wu, S.; Chen, Z.; Shen, S.; Shen, J.; Guo, F.; Liu, Y.; Zhang, Y. Hierarchical cooperative eco-driving control for connected autonomous vehicle platoon at signalized intersections. IET Intell. Transp. Syst. 2023, 17, 1560–1574. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Su, Z.; Chen, P. Cooperative Eco-driving Controller for Battery Electric Vehicle Platooning. IFAC-Pap. 2022, 55, 205–210. [Google Scholar] [CrossRef]
- Lacombe, R.; Gros, S.; Murgovski, N.; Kulcsár, B. Distributed Eco-Driving Control of a Platoon of Electric Vehicles Through Riccati Recursion. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3048–3063. [Google Scholar] [CrossRef]
- Hu, M.; Li, C.; Bian, Y.; Zhang, H.; Qin, Z.; Xu, B. Fuel Economy-Oriented Vehicle Platoon Control Using Economic Model Predictive Control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20836–20849. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy Adaptive Energy Management Strategy for a Hybrid Agricultural Tractor Equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, Y.; Wang, D.; Cai, Y.; Lai, L. Energy Saving Performance of Agricultural Tractor Equipped with Mechanic-Electronic-Hydraulic Powertrain System. Agriculture 2022, 12, 436. [Google Scholar] [CrossRef]
- Li, A.; Xu, Z.; Li, W.; Chen, Y.; Pan, Y. Urban signalized intersection traffic state prediction: A spatial–temporal graph model integrating the cell transmission model and transformer. Appl. Sci. 2025, 15, 2377. [Google Scholar] [CrossRef]
- Ala, M.V.; Yang, H.; Rakha, H. Modeling Evaluation of Eco–Cooperative Adaptive Cruise Control in Vicinity of Signalized Intersections. Transp. Res. Rec. J. Transp. Res. Board 2016, 2559, 108–119. [Google Scholar] [CrossRef]
- Zhai, C.; Luo, F.; Liu, Y. Cooperative Power Split Optimization for a Group of Intelligent Electric Vehicles Travelling on a Highway with Varying Slopes. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4993–5005. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K. Deep reinforcement learning-based energy management strategy for fuel cell buses integrating future road information and cabin comfort control. Energy Convers. Manag. 2024, 321, 119032. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K. Health-conscious deep reinforcement learning energy management for fuel cell buses integrating environmental and look-ahead road information. Energy 2024, 290, 130146. [Google Scholar] [CrossRef]
- Li, K.; Zhou, J.; Jia, C.; Yi, F.; Zhang, C. Energy sources durability energy management for fuel cell hybrid electric bus based on deep reinforcement learning considering future terrain information. Int. J. Hydrogen Energy 2024, 52, 821–833. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Zhu, C.; Zhang, H. Deep Learning-Based Energy-Efficient Spacing Policy and Platooning Control Co-Design for Connected and Automated Vehicles on Inclined Roads. IEEE Trans. Veh. Technol. 2024, 73, 14486–14498. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Ye, R.; Sun, Y.; Liu, C.; Zhang, J. Eco-driving-based mixed vehicular platoon control model for successive signalized intersections. Phys. A Stat. Mech. Its Appl. 2024, 639, 129641. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, J.; Shi, X.; Cheng, J. Learning the Policy for Mixed Electric Platoon Control of Automated and Human-Driven Vehicles at Signalized Intersection: A Random Search Approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5131–5143. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Z.; Malekian, R.; Zheng, S.; Sotelo, M.A. A Novel Multimode Hybrid Control Method for Cooperative Driving of an Automated Vehicle Platoon. IEEE Internet Things J. 2021, 8, 5822–5838. [Google Scholar] [CrossRef]
- He, X.; Wu, X. Eco-driving advisory strategies for a platoon of mixed gasoline and electric vehicles in a connected vehicle system. Transp. Res. Part D Transp. Environ. 2018, 63, 907–922. [Google Scholar] [CrossRef]
- Bichiou, Y.; Rakha, H. Vehicle Platooning: An Energy Consumption Perspective. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, D.; Lan, J.; Xue, S.; Zhao, W.; Tian, D.; Zhou, Q.; Song, K. Eco-Driving of General Mixed Platoons with CAVs and HDVs. IEEE Trans. Intell. Veh. 2023, 8, 1190–1203. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Wang, B.; Li, M. Collision Avoidance Motion Planning for Connected and Automated Vehicle Platoon Merging and Splitting with a Hybrid Automaton Architecture. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1445–1464. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Guo, J.; Papamichail, I.; Papageorgiou, M.; Wang, F.-Y.; Bertini, R.; Hua, W.; Yang, Q. Ego-efficient lane changes of connected and automated vehicles with impacts on traffic flow. Transp. Res. Part C Emerg. Technol. 2022, 138, 103478. [Google Scholar] [CrossRef]
- Yao, J.; Chen, G.; Gao, Z. Target Vehicle Selection Algorithm for Adaptive Cruise Control Based on Lane-changing Intention of Preceding Vehicle. Chin. J. Mech. Eng. 2021, 34, 135. [Google Scholar] [CrossRef]
- Huang, C.; Li, L.; Fang, S.; Cheng, S.; Chen, Z. Energy saving performance improvement of intelligent connected PHEVs via NN-based lane change decision. Sci. China Technol. Sci. 2021, 64, 1203–1211. [Google Scholar] [CrossRef]
- Kou, Y.; Ma, C. Dual-objective intelligent vehicle lane changing trajectory planning based on polynomial optimization. Phys. A Stat. Mech. Appl. 2023, 617, 128665. [Google Scholar] [CrossRef]
- Huang, Z.; Chu, D.; Wu, C.; He, Y. Path Planning and Cooperative Control for Automated Vehicle Platoon Using Hybrid Automata. IEEE Trans. Intell. Transp. Syst. 2019, 20, 959–974. [Google Scholar] [CrossRef]
- Scholte, W.J.; Zegelaar, P.W.; Nijmeijer, H. Gap Opening Controller Design to Accommodate Merges in Cooperative Autonomous Platoons. IFAC-Pap. 2020, 53, 15294–15299. [Google Scholar] [CrossRef]
- Rakha, H.A.; Ahn, K.; Moran, K.; Saerens, B.; Van Den Bulck, E. Virginia Tech Comprehensive Power-Based Fuel Consumption Model: Model development and testing. Transp. Res. Part D Transp. Environ. 2011, 16, 492–503. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Dai, Q.; Chen, H.; Wang, Y.; Zhao, W. A Distributed Adaptive Triple-Step Nonlinear Control for a Connected Automated Vehicle Platoon with Dynamic Uncertainty. IEEE Internet Things J. 2020, 7, 3861–3871. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Chen, Z.; Li, X. A dynamic cooperative lane-changing model for connected and autonomous vehicles with possible accelerations of a preceding vehicle. Expert Syst. Appl. 2021, 173, 114675. [Google Scholar] [CrossRef]
- Xu, M.; Luo, Y.; Yang, G.; Kong, W.; Li, K. Dynamic Cooperative Automated Lane-Change Maneuver Based on Minimum Safety Spacing Model. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar] [CrossRef]
- Pan, C.; Li, Y.; Wang, J.; Liang, J.; Jinyama, H. Research on multi-lane energy-saving driving strategy of connected electric vehicle based on vehicle speed prediction. Green Energy Intell. Transp. 2023, 2, 100127. [Google Scholar] [CrossRef]
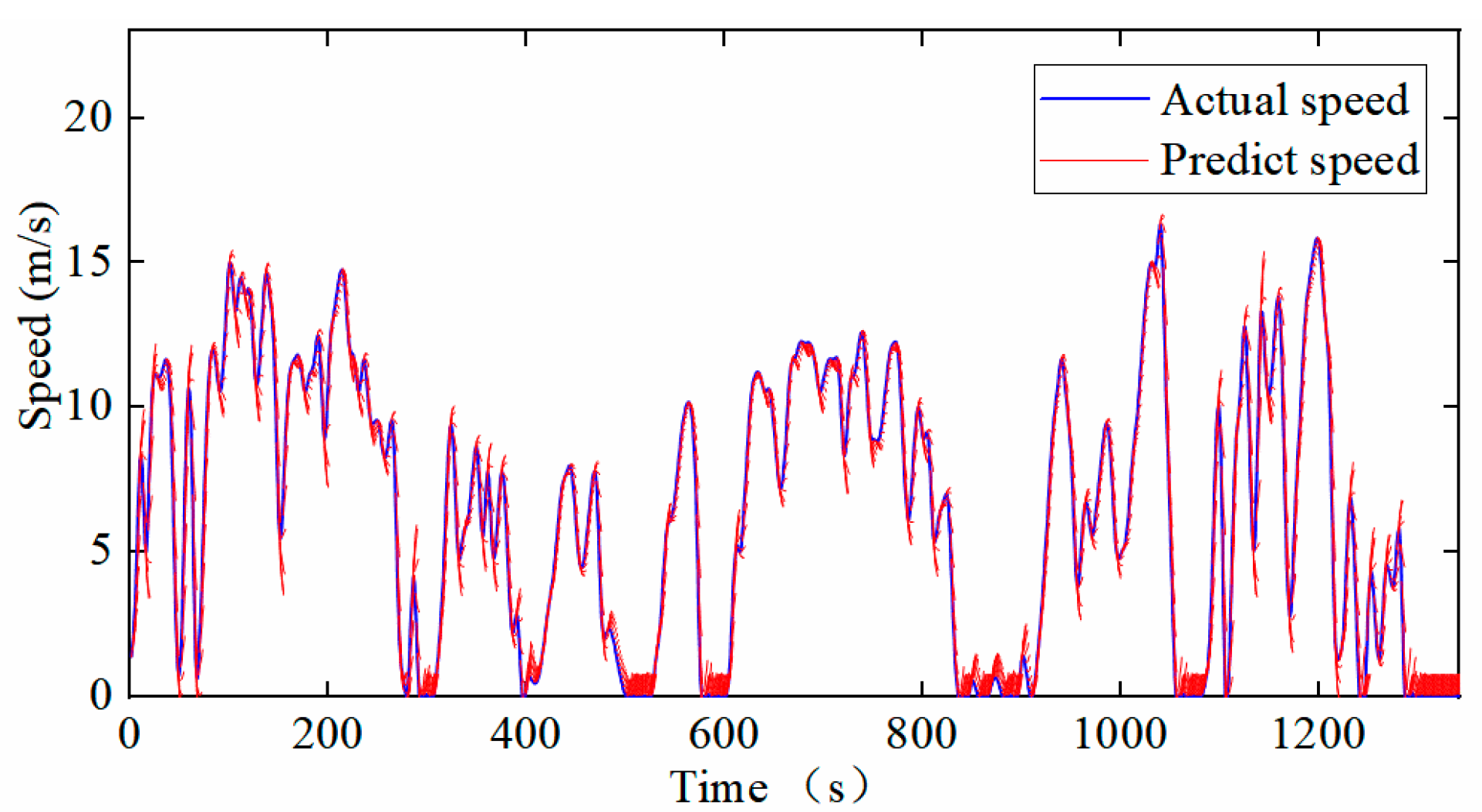
- Hou, J.; Yao, D.; Wu, F.; Shen, J.; Chao, X. Online Vehicle Velocity Prediction Using an Adaptive Radial Basis Function Neural Network. IEEE Trans. Veh. Technol. 2021, 70, 3113–3122. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, C.; Zheng, X.; Han, Z.; Gao, Y.; Yan, C.; Luo, F.; Xu, J. Ecological Cooperative Adaptive Cruise Control for Heterogenous Vehicle Platoons Subject to Time Delays and Input Saturations. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2862–2873. [Google Scholar] [CrossRef]
- Won, M. L-platooning: A protocol for managing a long platoon with DSRC. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5777–5790. [Google Scholar] [CrossRef]
- Liu, S.; Yu, B.; Tang, J.; Zhu, Y.; Liu, X. Communication challenges in infrastructure-vehicle cooperative autonomous driving: A field deployment perspective. IEEE Wirel. Commun. 2022, 29, 126–131. [Google Scholar] [CrossRef]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD Dataset: A Drone Dataset of Naturalistic Vehicle Trajectories on German Highways for Validation of Highly Automated Driving Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, X.; Ma, X. Evaluation of Automatic Lane-Change Model Based on Vehicle Cluster Generalized Dynamic System. Automot. Innov. 2022, 5, 91–104. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Pedersen, K.; Stroe, D.-I. Lithium-ion battery operation, degradation, and aging mechanism in electric vehicles: An overview. Energies 2021, 14, 5220. [Google Scholar] [CrossRef]





| Type | Mass (kg) | Drag Coefficient | Frontal Area (m2) |
|---|---|---|---|
| EV_1 | 1417 | 0.29 | 2.38 |
| EV_2 | 1794 | 0.26 | 2.36 |
| EV_3 | 2124 | 0.28 | 2.54 |
| FV_1 | 1500 | 0.28 | 2.424 |
| FV_2 | 2190 | 0.31 | 2.911 |
| FV_3 | 1453 | 0.30 | 2.32 |
| VehID | Transition | PltnEn | PlatoonID | PrecedID | PltnNum | PltnLength | Manv |
|---|---|---|---|---|---|---|---|
| PV-1 | Before | 1 | Pltn-1 | 0 | 1 | 2 | Cruising |
| After | 1 | Pltn-1 | 0 | 1 | 3 | Cruising | |
| PV-2 | Before | 1 | Pltn-1 | PV-1 | 2 | 2 | Platooning |
| After | 1 | Pltn-1 | PV-1 | 2 | 3 | Platooning | |
| PV-3 | Before | 1 | Pltn-3 | 0 | 1 | 3 | Cruising |
| After | 1 | Pltn-3 | 0 | 1 | 2 | Cruising | |
| PV-4 | Before | 1 | Pltn-3 | PV-3 | 2 | 3 | Platooning |
| After | 1 | Pltn-3 | PV-3 | 2 | 2 | Platooning | |
| PV-5 | Before | 1 | Pltn-3 | PV-3 | 3 | 3 | Platooning |
| After | 1 | Pltn-1 | PV-1 | 3 | 3 | Platooning |
| Initial Number of Vehicles | Vehicle Generation Time | Speed Range | |
|---|---|---|---|
| Low traffic density | 20 | 10 s | 60–90 km/h |
| High traffic density | 60 | 3 s | 60–90 km/h |
| Average Energy Efficiency Rate | Standards Deviation | |
|---|---|---|
| Low traffic density | 2.86% | 0.39% |
| High traffic density | 3.25% | 0.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Pi, J.; Wang, J. Eco-Cooperative Planning and Control of Connected Autonomous Vehicles Considering Energy Consumption Characteristics. Electronics 2025, 14, 1646. https://doi.org/10.3390/electronics14081646
Pan C, Pi J, Wang J. Eco-Cooperative Planning and Control of Connected Autonomous Vehicles Considering Energy Consumption Characteristics. Electronics. 2025; 14(8):1646. https://doi.org/10.3390/electronics14081646
Chicago/Turabian StylePan, Chaofeng, Jintao Pi, and Jian Wang. 2025. "Eco-Cooperative Planning and Control of Connected Autonomous Vehicles Considering Energy Consumption Characteristics" Electronics 14, no. 8: 1646. https://doi.org/10.3390/electronics14081646
APA StylePan, C., Pi, J., & Wang, J. (2025). Eco-Cooperative Planning and Control of Connected Autonomous Vehicles Considering Energy Consumption Characteristics. Electronics, 14(8), 1646. https://doi.org/10.3390/electronics14081646






