High-Fidelity Modeling and Stability Analysis of Microgrids by Considering Time Delay
Abstract
1. Introduction
Novelty of This Study
2. Control of Island Microgrids
2.1. Power Sharing Based on Conventional Droop Control and Virtual Impedance
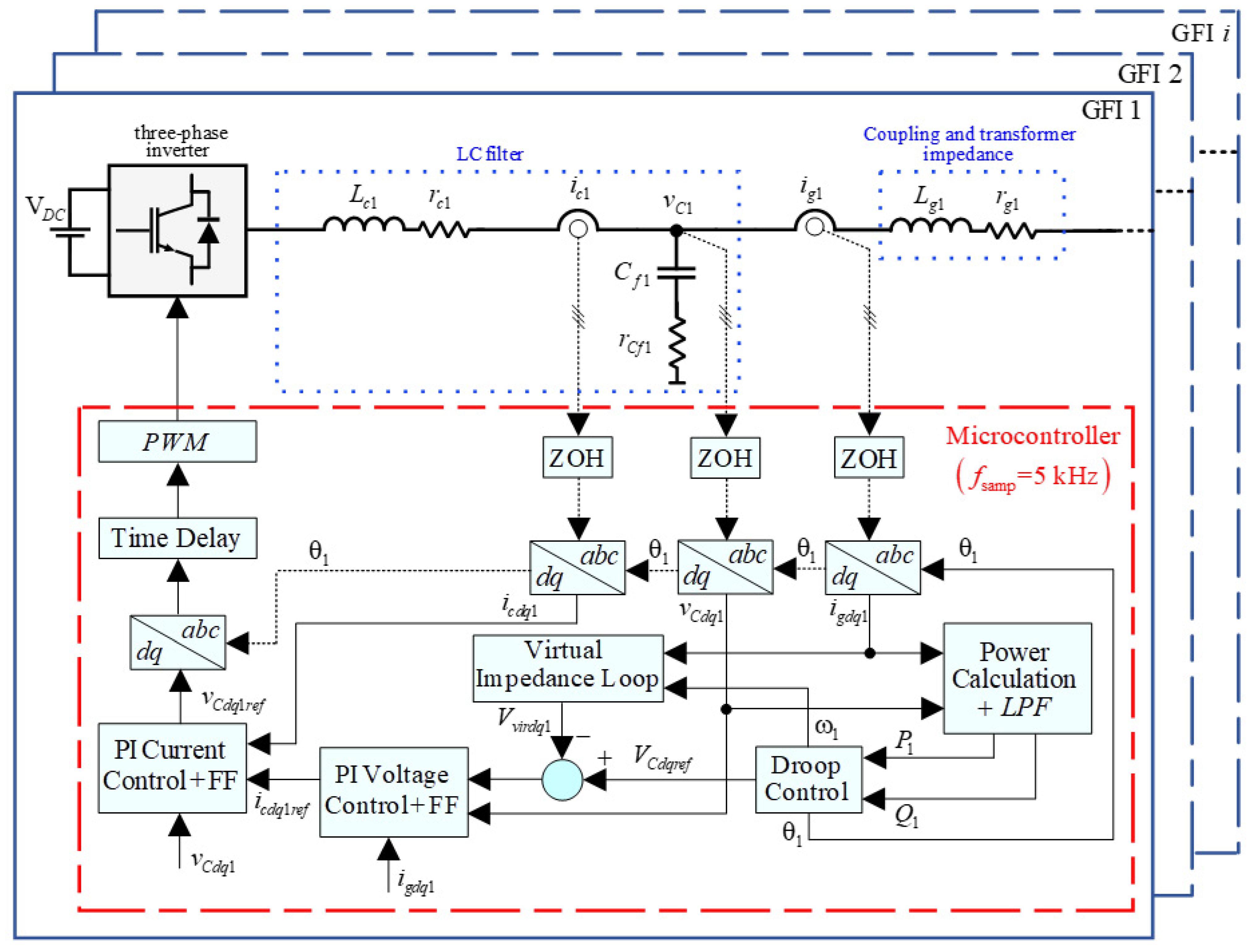
2.2. Cascaded Outer Voltage and Inner Current Control of Island Microgrid
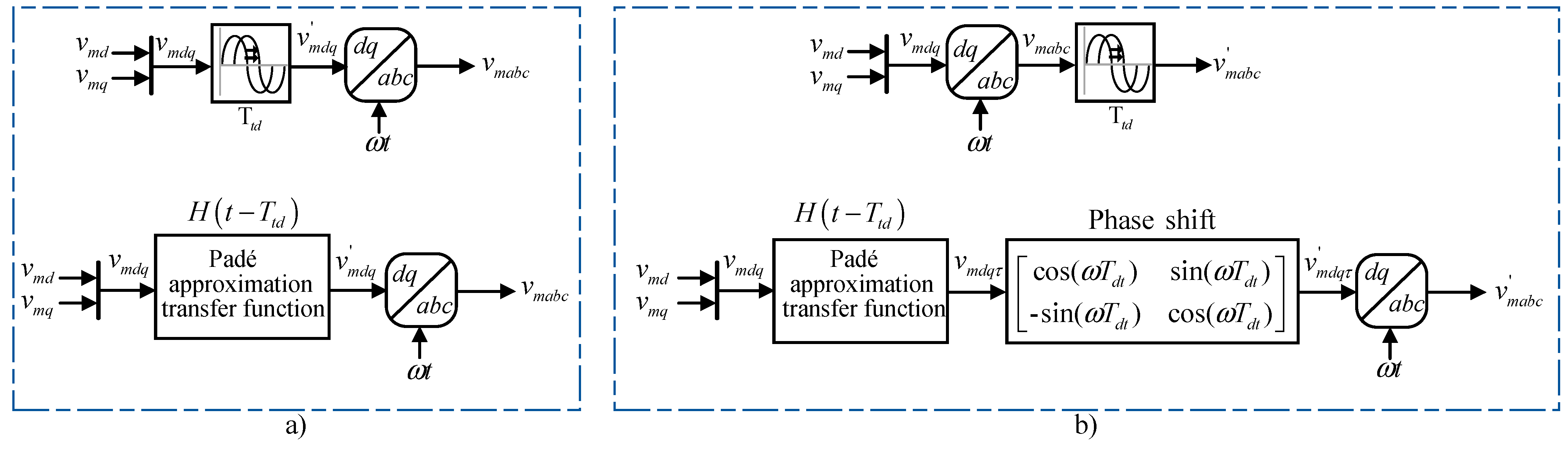
3. Time Delay Representation in Regard to the dq-Axis for Use in Small-Signal Stability Analysis [46,47]
3.1. Necessity of Modeling the Time Delay
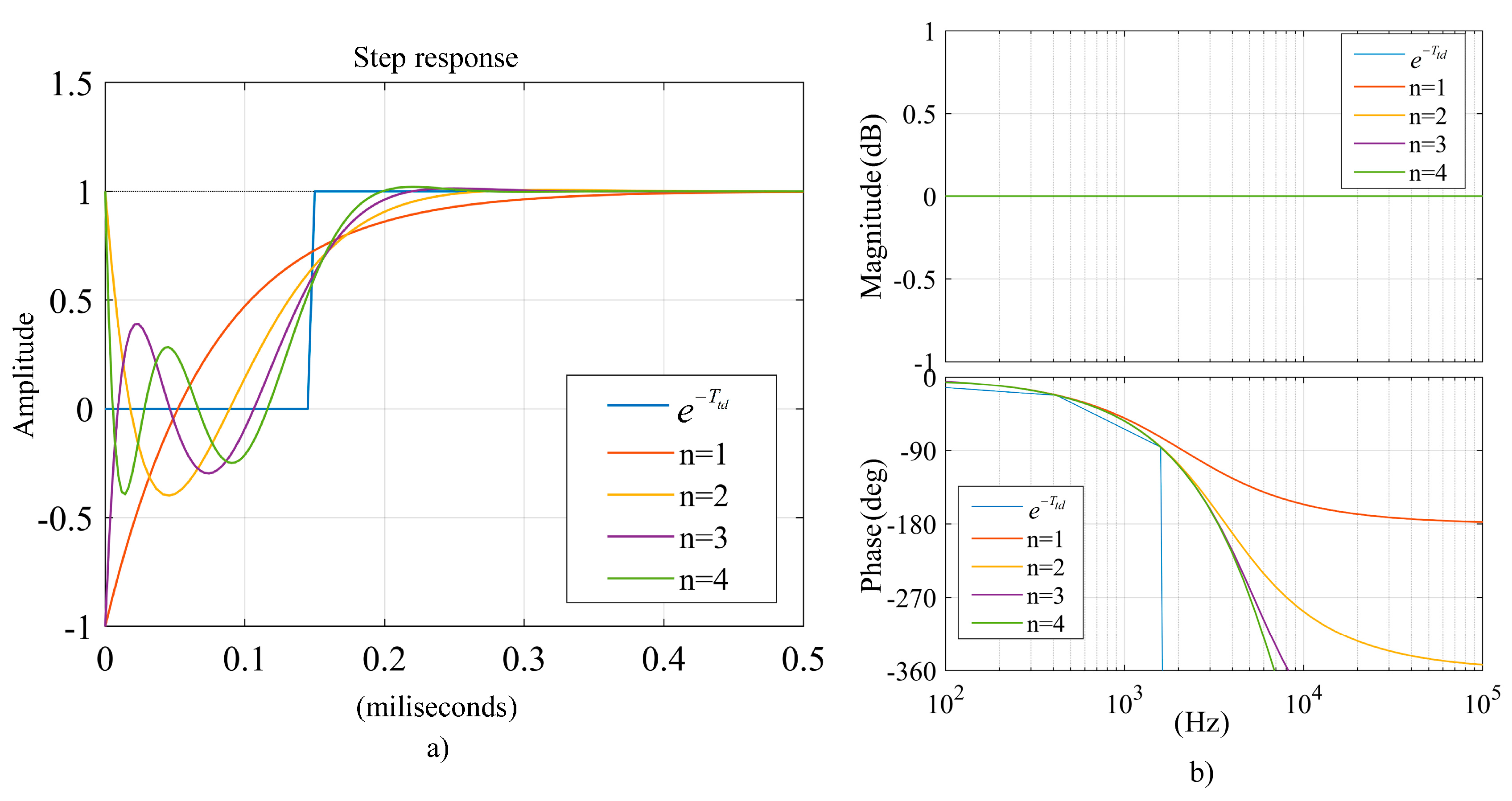
3.2. Conventional Time Delay Modeling Approach
3.3. Proposed Accurate Time Delay Representation in Regard to the dq-Axis
3.3.1. Time Delay in Regard to the abc-Axis Stationary Reference Frame
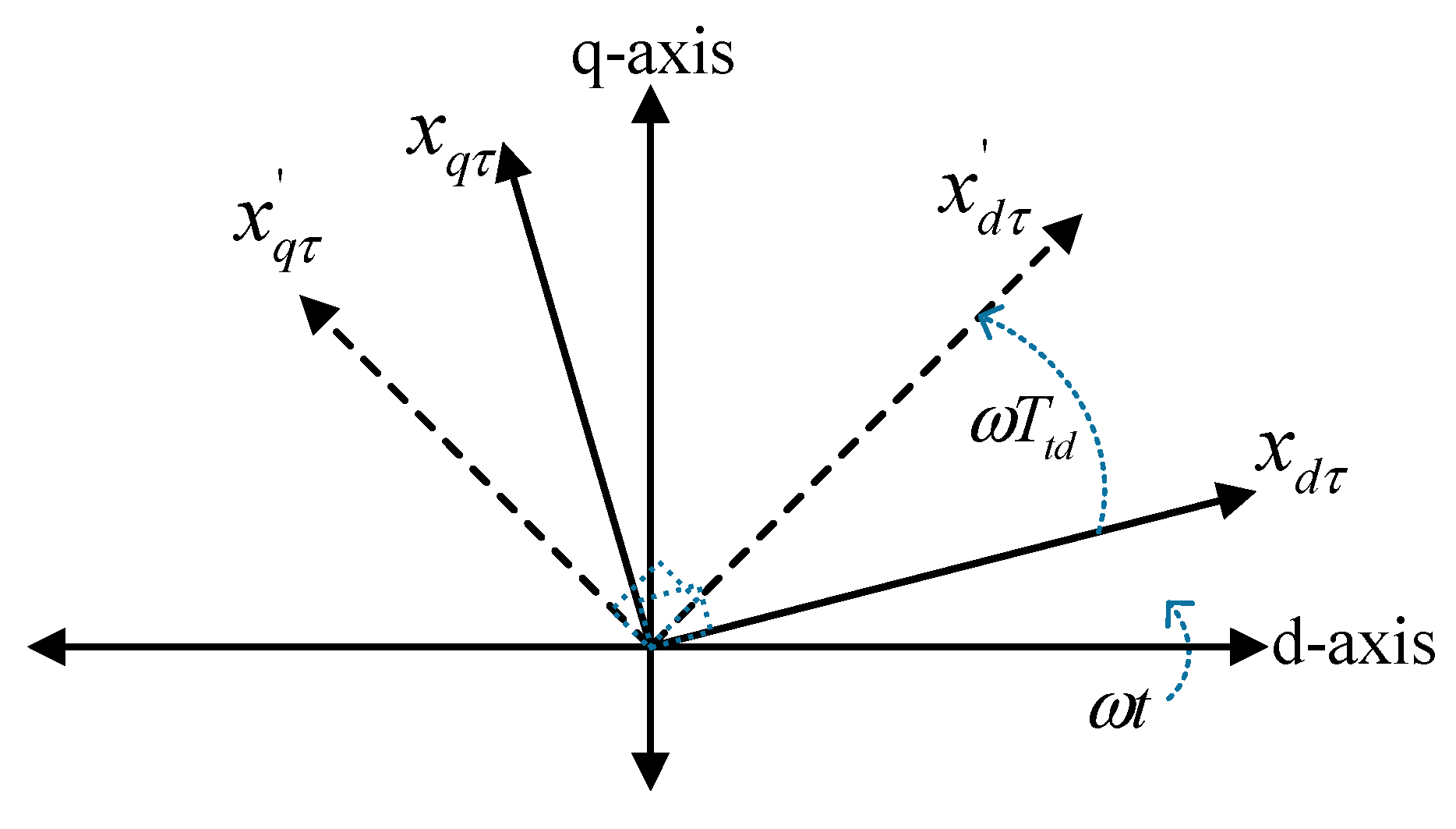
3.3.2. Accurate Time Delay Representation in Regard to the dq-Axis
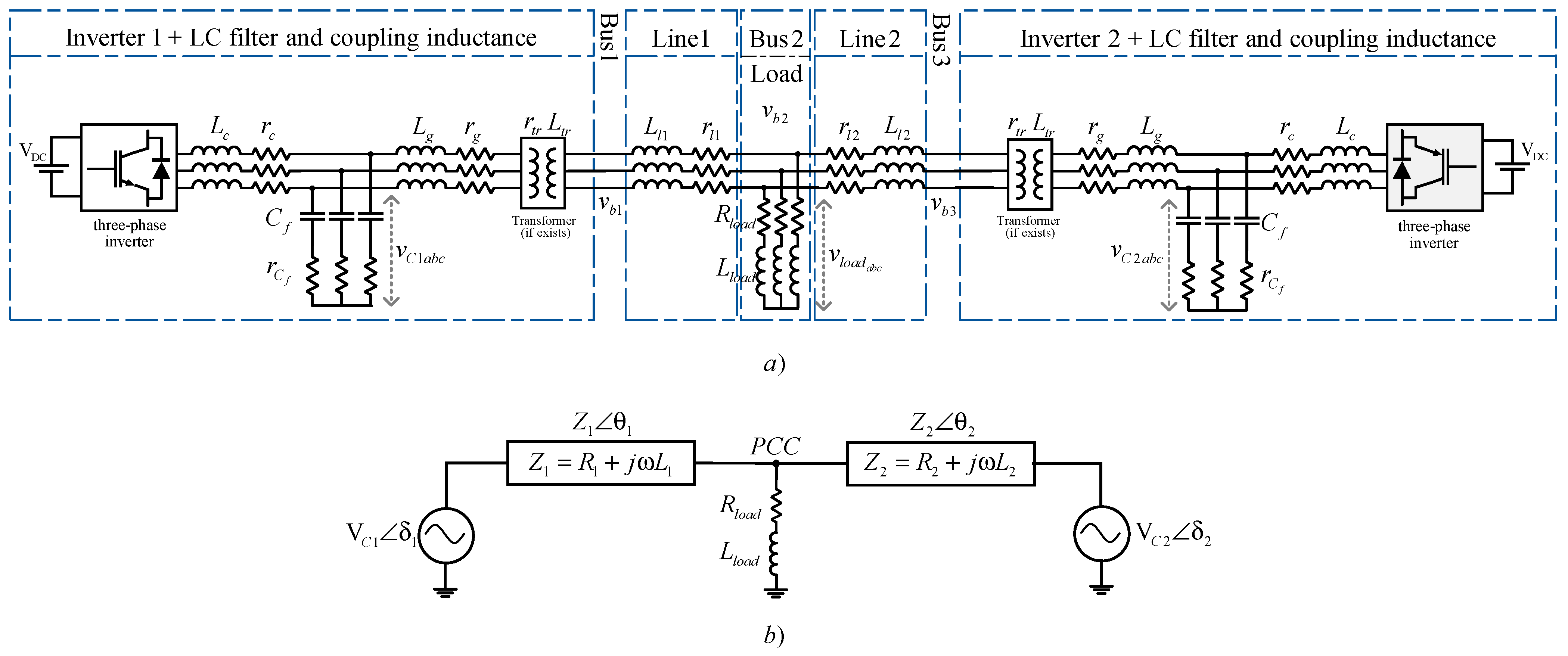
4. Small-Signal Modeling of an Island Microgrid
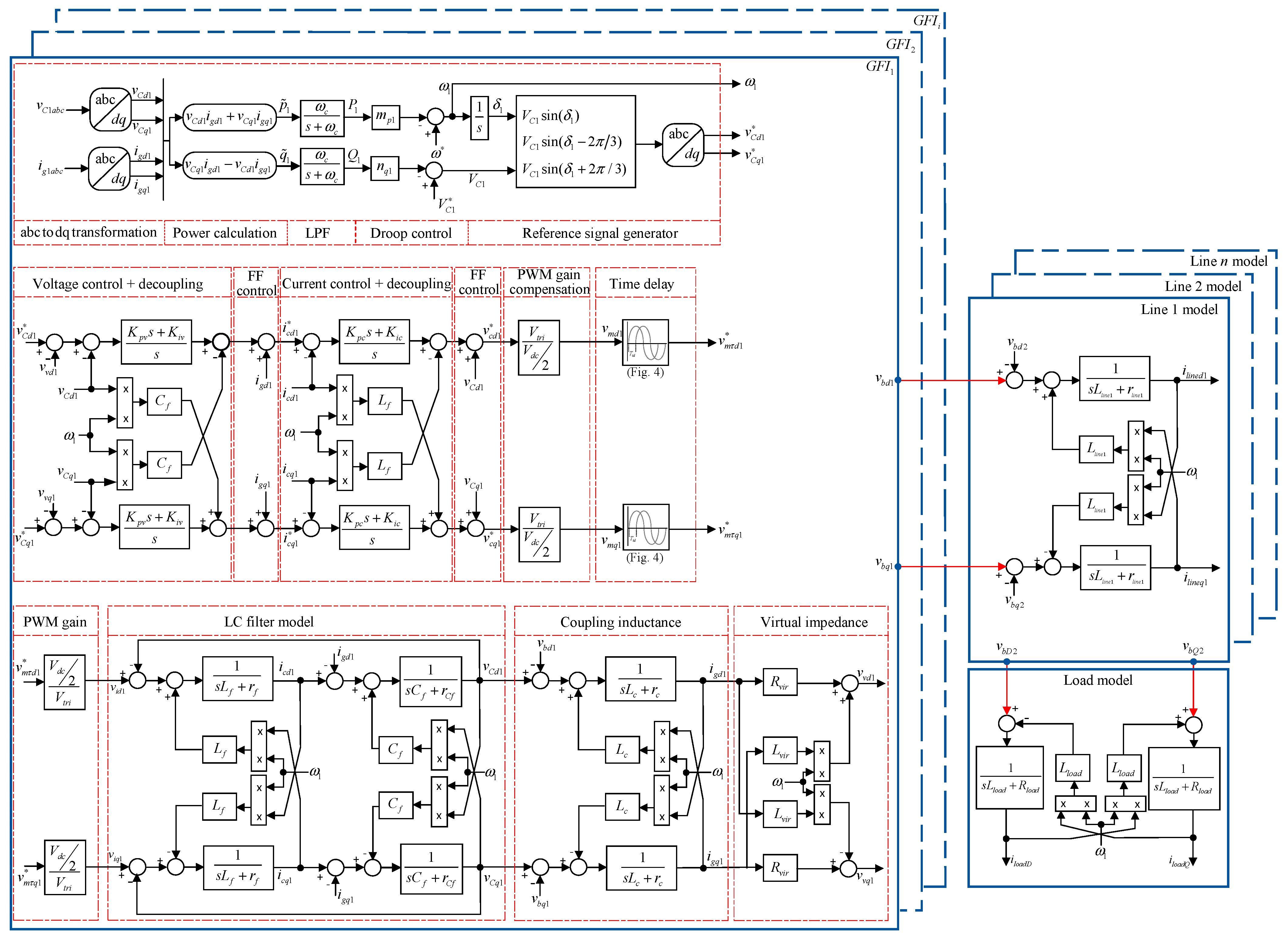
4.1. Small-Signal Model of Parallel-Connected GFIs
4.1.1. Power Controller Small-Signal Model
4.1.2. Voltage Controller Small-Signal Model
4.1.3. Current Controller Small-Signal Model
4.1.4. Virtual Impedance Small-Signal Model
4.1.5. LC Filter and Coupling Inductance Small-Signal Model
4.1.6. Small-Signal Model of a GFI
4.2. Transmission Line Small-Signal Model
4.3. Load Small-Signal Model
4.4. Complete Small-Signal Model of an Island Microgrid
5. Results and Validation
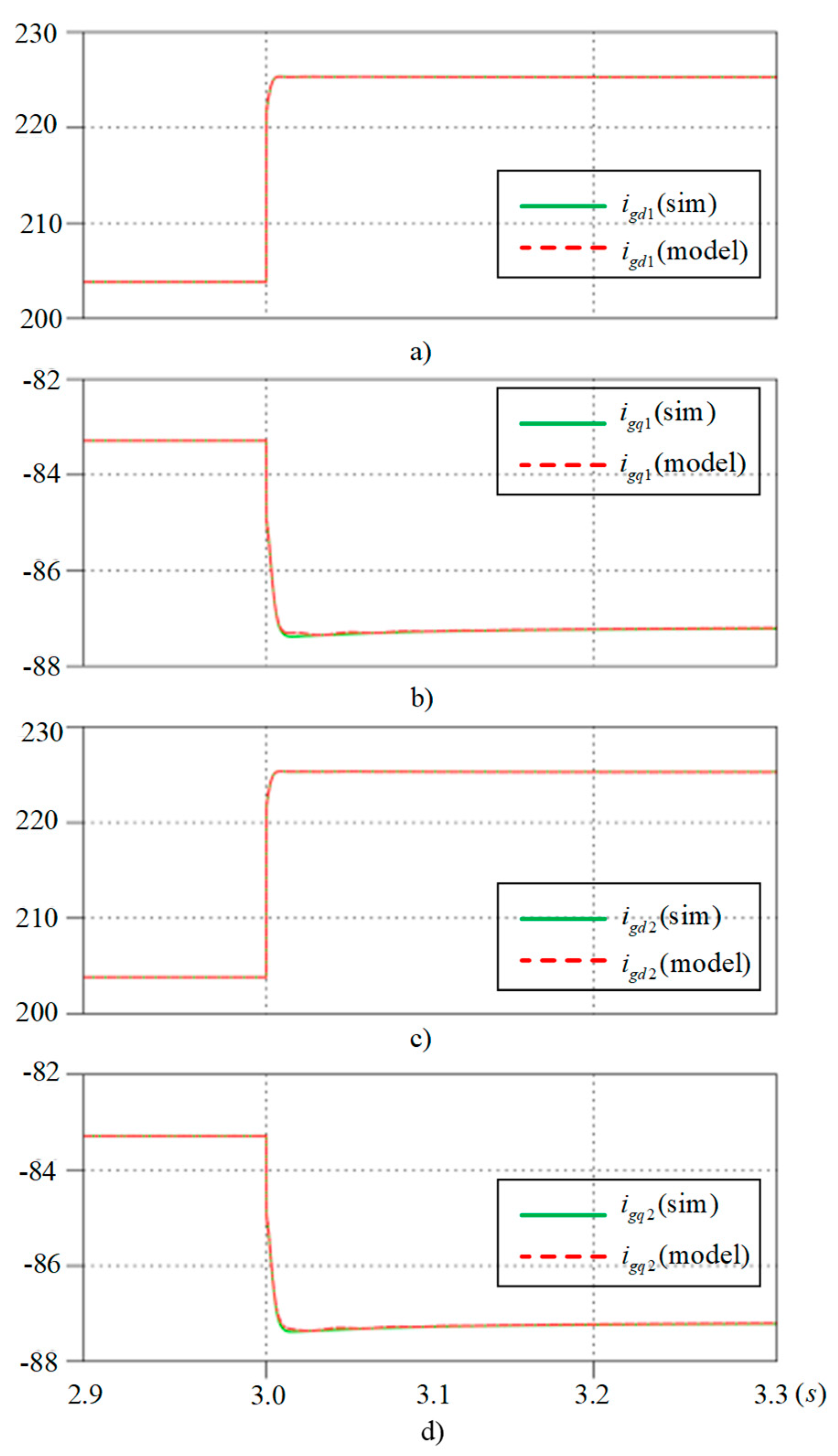
5.1. Validation of Small-Signal Model for GFIs with Proposed Accurate Time Delay Representation in Regard to the dq-Axis
5.2. Comparison of Conventional Time Delay Modeling and Proposed Accurate Time Delay Representation in Regard to the dq-Axis Accuracy with the Real-Time Simulation Results
5.2.1. Case 1: Validation Based on Active Power Droop Coefficient
5.2.2. Case 2: Validation Based on Reactive Power Droop Coefficient
5.3. Virtual Impedance Effect Validation on Small-Signal Stability
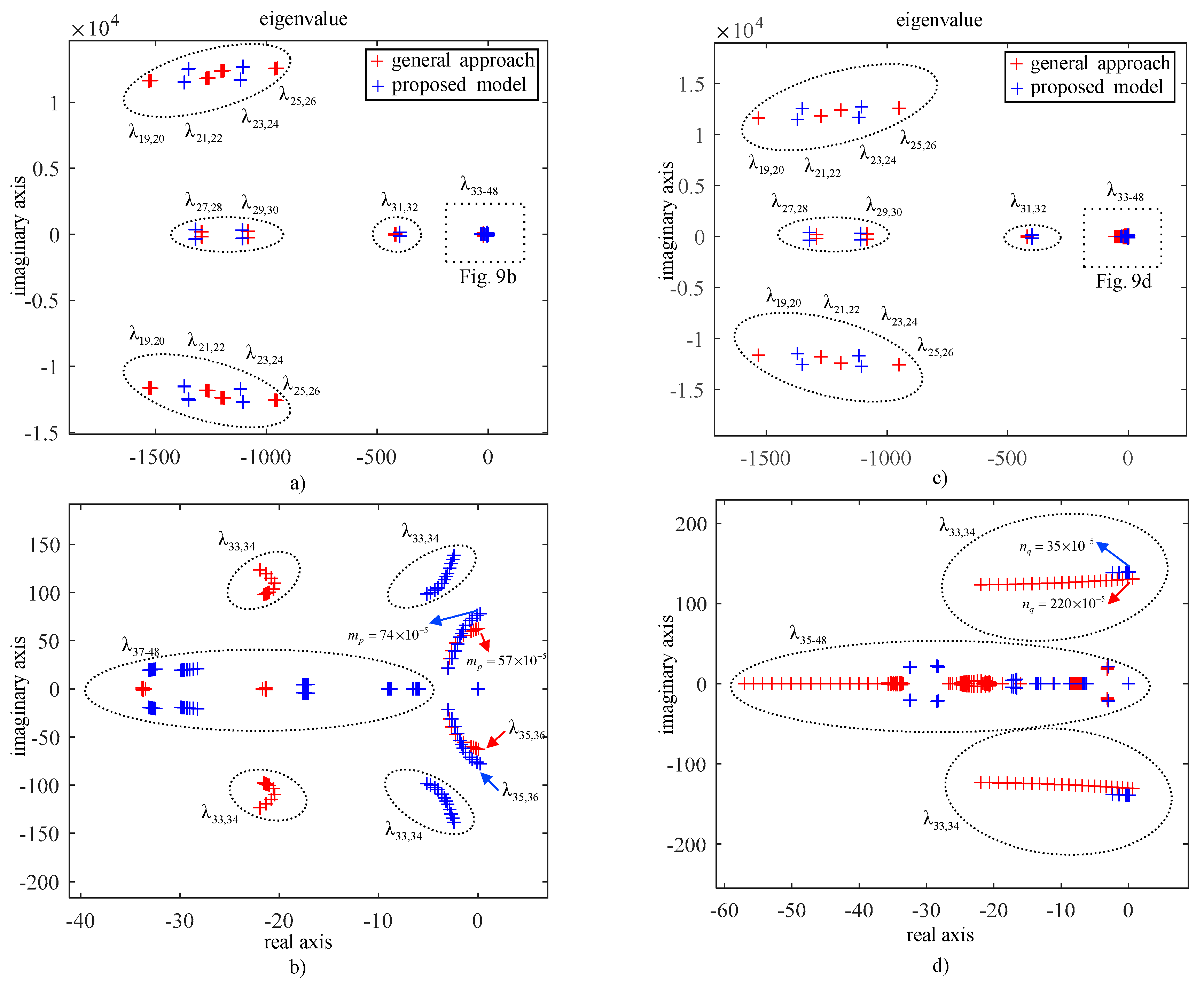
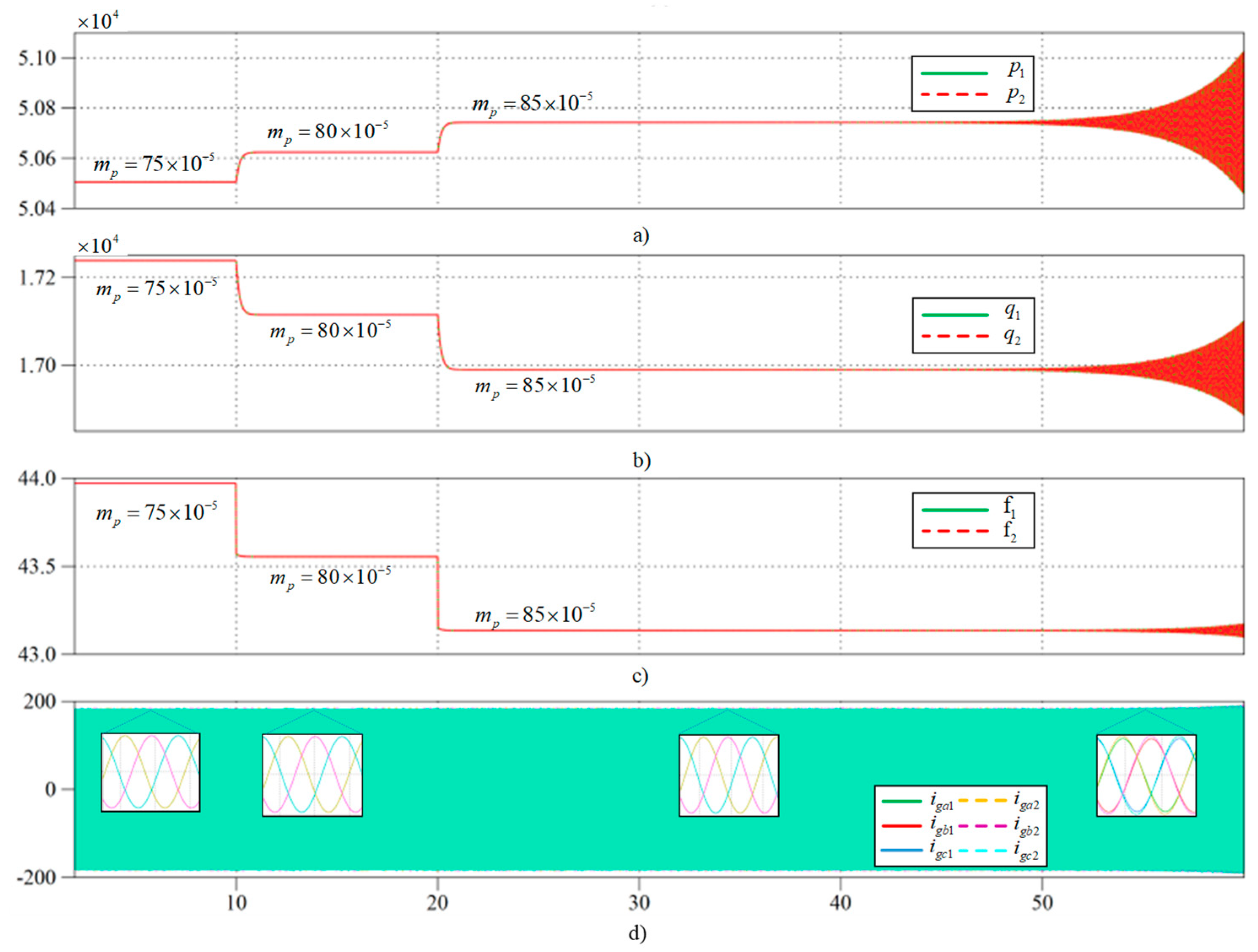
5.3.1. Case 3: Comparison of Virtual Impedance Effect on Stability Based on Eigenvalue Trajectory for Active Power Droop Coefficient
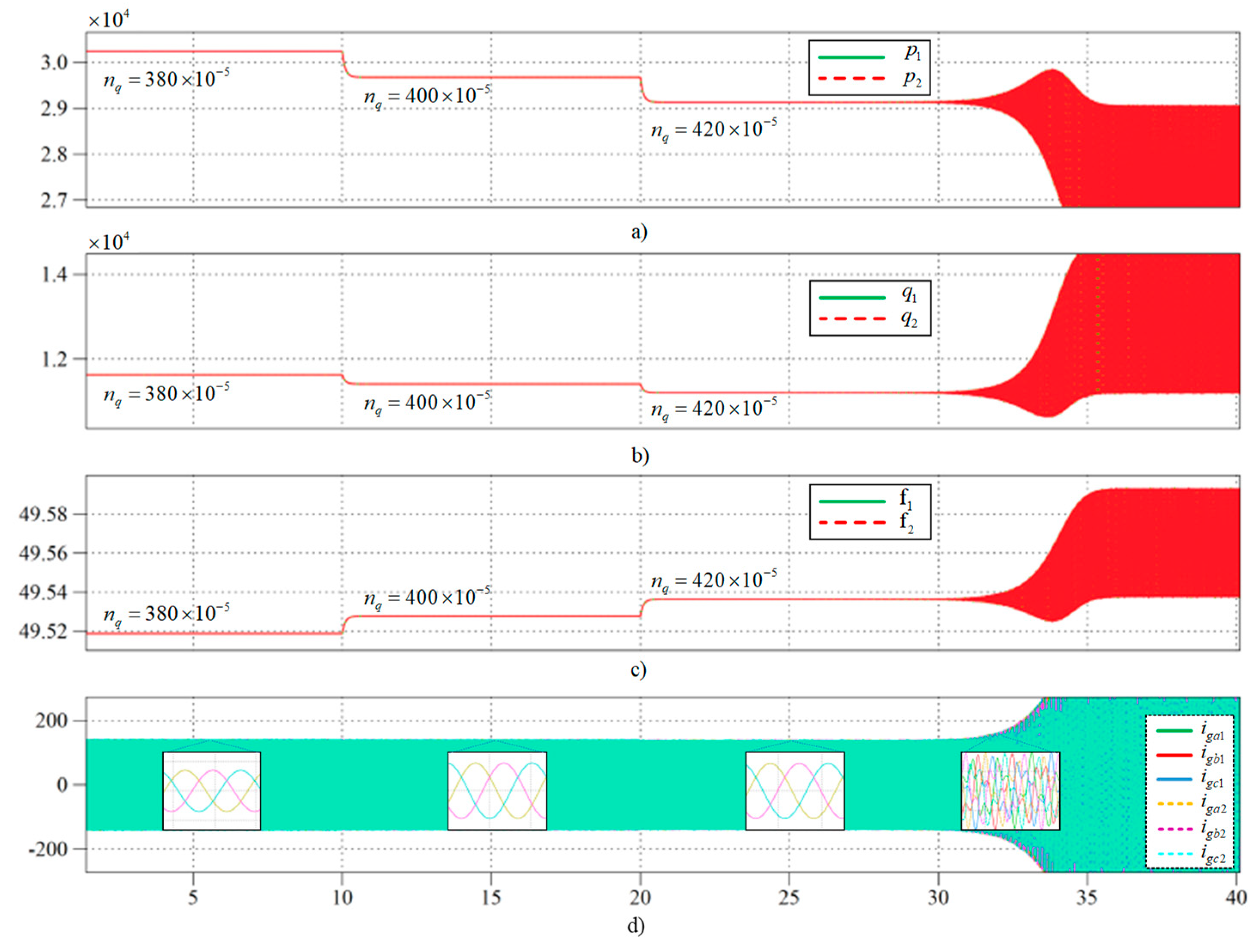
5.3.2. Case 4: Comparison of Virtual Impedance Effect on Stability Based on Eigenvalue Trajectory for Reactive Power Droop Coefficient
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| MG | Microgrid |
| DER | Distributed energy resources |
| DG | Distributed generation |
| GFI | Grid-forming inverter |
| PCC | Point of common coupling |
| VSI | Voltage source inverter |
| AC | Alternating current |
| DC | Direct current |
| SISO | Single input–single output |
| PI | Proportional–integral |
| PR | Proportional–resonant |
| FF | Feed forward |
| PM | Phase margin |
| ZOH | Zero-order hold |
| abc-axis | Stationary ref. frame in regard to abc-coordinate |
| αβ-axis | Stationary ref. frame in regard to αβ-coordinate |
| dq-axis | Synchronous ref. frame in regard to dq-coordinate |
| DQ-axis | Common reference frame in regard to dq-axis |
| Indices | |
| ∆ | Linearization of state variables |
| A dot above: derivative of variables | |
| i | The number of GFIs |
| j, k | Indices for line bus number |
| n | The number of lines |
| m | The number of buses |
| * and ref | Reference value of the variables |
| com | Common variables for the MG |
| dq | Variables in regard to the dq-axis |
| d | Variables in regard to the d-axis |
| q | Variables in regard to the q-axis |
| m | Modulation |
| v | Virtual |
| Parameters | |
| Ref. grid frequency (rad/s) | |
| δ | Angular velocity (rad) |
| Kin | Input gain |
| Switching frequency (Hz) | |
| Sampling frequency (Hz) | |
| Time delay (seconds) | |
| mp | Active power droop coefficient |
| nq | Reactive power droop coefficient |
| Droop cut-off frequency (rad/s) | |
| Voltage control bandwidth (Hz) | |
| Voltage control P gain | |
| Voltage control I gain | |
| Current control bandwidth (Hz) | |
| Current control P gain | |
| Current control I gain | |
| Filter inductance (H) | |
| Parasitic resistance of Lf (Ω) | |
| Filter capacitance (F) | |
| Parasitic resis. of Cf (Ω) | |
| Coupling inductance (F) | |
| Parasitic resis. of Lc (Ω) | |
| Virtual resistance (Ω) | |
| Virtual inductance (F) | |
| Line resistance (Ω) | |
| Line inductance (F) | |
| Line resistance (Ω) | |
| Line inductance (F) | |
| Load resistance (Ω) | |
| Load inductance (F) | |
| Bus virtual resistance (Ω) | |
| State Variables | |
| DC bus voltage (V) | |
| Instantaneous active power (W) | |
| Instantaneous reactive power (VAr) | |
| P | Filtered active power (W) |
| Q | Filtered reactive power (VAr) |
| LCL filter input voltage (V) | |
| ic | Converter-side current (A) |
| Filter capacitor voltage (V) | |
| ig | Grid-side current (A) |
| vm | Modulation signal (V) |
| Bus voltage (V) | |
| ϕ | State variables of voltage contr. |
| γ | State variables of current contr. |
| τ | State variables of time delay |
| Output of Padé app. transfer func. (V) | |
| Output of phase shift model (V) |
References
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanović, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Atmaca, O.; Karabacak, M. Frequency, Phase, and Magnitude Difference Locked-Loop Based Linear Synchronization Scheme for Islanded Inverters and Microgrids. IEEE Access 2023, 11, 61748–61772. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Stability and Control Aspects of Microgrid Architectures-A Comprehensive Review. IEEE Access 2020, 8, 144730–144766. [Google Scholar] [CrossRef]
- Alkahtani, A.A.; Alfalahi, S.T.Y.; Athamneh, A.A.; Al-Shetwi, A.Q.; Mansor, M.B.; Hannan, M.A.; Agelidis, V.G. Power Quality in Microgrids including Supraharmonics: Issues, Standards, and Mitigations. IEEE Access 2020, 8, 127104–127122. [Google Scholar] [CrossRef]
- Kamel, R.M. New inverter control for balancing standalone micro-grid phase voltages: A review on MG power quality improvement. Renew. Sustain. Energy Rev. 2016, 63, 520–532. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Memon, A.A.A.; Karimi, M.; Kauhaniemi, K. Evaluation of New Grid Codes for Converter-Based DERs From the Perspective of AC Microgrid Protection. IEEE Access 2022, 10, 127005–127030. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.R. Different control schemes of entire microgrid: A brief overview. In Proceedings of the 2016 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 22–24 September 2016; pp. 1–6. [Google Scholar]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Timbus, A.; Member, S.; Liserre, M.; Member, S.; Teodorescu, R.; Member, S.; Rodriguez, P.; Blaabjerg, F. Evaluation of Current Controllers for Distributed Power Generation Systems. IEEE Trans. Power Electron. 2009, 24, 654–664. [Google Scholar] [CrossRef]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, J.M. Review of Active and Reactive Power Sharing Strategies in Hierarchical Controlled Microgrids. IEEE Trans. Power Electron. 2017, 32, 2427–2451. [Google Scholar] [CrossRef]
- Tayab, U.B.; Roslan, M.A.B.; Hwai, L.J.; Kashif, M. A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Issa, W.; Hossain, M.J. Overview of AC microgrid controls with inverter-interfaced generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Begum, M.; Li, L.; Zhu, J. Distributed control techniques for autonomous AC Microgrid-A brief review. In Proceedings of the 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 21–23 December 2017; pp. 357–362. [Google Scholar]
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New Perspectives on Droop Control in AC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5741–5745. [Google Scholar] [CrossRef]
- Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Angle droop versus frequency droop in a voltage source converter based autonomous microgrid. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Zhong, Q.C. Robust droop controller for accurate proportional load sharing among inverters operated in parallel. IEEE Trans. Ind. Electron. 2013, 60, 1281–1290. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Zeng, Y. Universal Droop Control of Inverters with Different Types of Output Impedance. IEEE Access 2016, 4, 702–712. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Accurate reactive power sharing in an islanded microgrid using adaptive virtual impedances. IEEE Trans. Power Electron. 2015, 30, 1605–1617. [Google Scholar] [CrossRef]
- Yao, W.; Chen, M.; Matas, J.; Guerrero, J.M.; Qian, Z.M. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing. IEEE Trans. Ind. Electron. 2011, 58, 576–588. [Google Scholar] [CrossRef]
- Zheng, Y. Virtual Inertia Emulation in Islanded Microgrids with Energy Storage System; Delft University of Technology: Delft, The Netherlands, 2016. [Google Scholar]
- Kundur, P. Power System Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small-signal stability for parallel-connected inverters in stand-alone ac supply systems. IEEE Trans. Ind. Appl. 2002, 38, 533–542. [Google Scholar] [CrossRef]
- Mohamed, Y.A.I.; El-saadany, E.F.; Member, S. Adaptive Decentralized Droop Controller to Preserve Power Sharing Stability of Paralleled Inverters in Distributed Generation Microgrids. IEEE Trans. Power Electron. 2008, 23, 2806–2816. [Google Scholar] [CrossRef]
- Wei, Z.; Jie, C.; Gong, C. Small signal modeling and analysis of synchronverters. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015. [Google Scholar]
- Vemula, N.K.; Parida, S.K. Small Signal Stability Assessment of an Inverter-Based Microgrid with Universal Droop and Internal Model-Based Controllers. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018. [Google Scholar]
- Dheer, D.K.; Vijay, A.S.; Kulkarni, O.V.; Doolla, S. Improvement of stability margin of droop-based islanded microgrids by cascading of lead compensators. IEEE Trans. Ind. Appl. 2019, 55, 3241–3251. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Liu, J.; Boroyevich, D.; Burgos, R. Small-signal modeling and stability prediction of parallel droop-controlled inverters based on terminal characteristics of individual inverters. IEEE Trans. Power Electron. 2020, 35, 1045–1063. [Google Scholar] [CrossRef]
- Naderi, M.; Shafiee, Q.; Bevrani, H.; Blaabjerg, F. Low-Frequency Small-Signal Modeling of Interconnected AC Microgrids. IEEE Trans. Power Syst. 2021, 36, 2786–2797. [Google Scholar] [CrossRef]
- Rasheduzzaman, M.; Mueller, J.A.; Kimball, J.W. Reduced-order small-signal model of microgrid systems. IEEE Trans. Sustain. Energy 2015, 6, 1292–1305. [Google Scholar] [CrossRef]
- Leitner, S.; Yazdanian, M.; Mehrizi-Sani, A.; Muetze, A. Small-Signal Stability Analysis of an Inverter-Based Microgrid with Internal Model-Based Controllers. IEEE Trans. Smart Grid 2018, 9, 5393–5402. [Google Scholar] [CrossRef]
- Moon, H.-J.; Kim, Y.-J.; Moon, S.-I. Frequency-Based Decentralized Conservation Voltage Reduction Incorporated Into Voltage-Current Droop Control for an Inverter-Based Islanded Microgrid. IEEE Access 2019, 7, 140542–140552. [Google Scholar] [CrossRef]
- Pournazarian, B.; Sangrody, R.; Saeedian, M.; Gomis-Bellmunt, O.; Pouresmaeil, E. Enhancing Microgrid Small-Signal Stability and Reactive Power Sharing Using ANFIS-Tuned Virtual Inductances. IEEE Access 2021, 9, 104915–104926. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. Voltage Stabilization in Microgrids via Quadratic Droop Control. IEEE Trans. Automat. Control 2017, 62, 1239–1253. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.R.I. Modeling, analysis, and stabilization of converter-fed AC microgrids with high penetration of converter-interfaced loads. IEEE Trans. Smart Grid 2012, 3, 1213–1225. [Google Scholar] [CrossRef]
- Eberlein, S.; Rudion, K. Small-signal stability modelling, sensitivity analysis and optimization of droop controlled inverters in LV microgrids. Int. J. Electr. Power Energy Syst. 2021, 125, 106404. [Google Scholar] [CrossRef]
- Abdelgabir, H.; Shaheed, M.N.B.; Elrayyah, A.; Sozer, Y. A Complete Small-Signal Modelling and Adaptive Stability Analysis of Nonlinear Droop-Controlled Microgrids. IEEE Trans. Ind. Appl. 2022, 58, 7620–7633. [Google Scholar] [CrossRef]
- Dağ, B.; Aydemir, M.T. A simplified stability analysis method for LV inverter-based microgrids. J. Mod. Power Syst. Clean Energy 2019, 7, 612–620. [Google Scholar] [CrossRef]
- Malik, S.M.; Sun, Y.; Ai, X.; Chen, Z.; Wang, K. Small-Signal Analysis of a Hybrid Microgrid with High PV Penetration. IEEE Access 2019, 7, 119631–119643. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. Impact of Virtual Admittance on Small-Signal Stability of Grid-Forming Inverters. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orleans, LA, USA, 8–10 November 2021. [Google Scholar]
- Liu, R.; Ding, L.; Xue, C.; Li, Y. Small-signal modelling and analysis of microgrids with synchronous and virtual synchronous generators. IET Energy Syst. Integr. 2023, 6, 45–61. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Small-Signal Stability Analysis of Inverter-Fed Power Systems Using Component Connection Method. IEEE Trans. Smart Grid 2018, 9, 5301–5310. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic instability assessment using state-space modeling and participation analysis in inverter-fed power systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Liu, F.; Liu, W.; Wang, H.; Xie, Z.; Yang, S.; Wang, J. Small Signal Modeling and Discontinuous Stable Regions of Grid-connected Inverter Based on Pade Approximation. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1076–1081. [Google Scholar]
- Vemula, N.K.; Parida, S.K. Impact of time delay on performance and stability of inverter-fed islanded MG utilizing internal model controller. Int. J. Electr. Power Energy Syst. 2023, 146, 108713. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L. Review of primary control strategies for islanded microgrids with power-electronic interfaces. Renew. Sustain. Energy Rev. 2013, 19, 613–628. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Hornik, T. Control of Power Inverters in Renewable Energy and Smart Grid Integration; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ramezani, M.; Li, S.; Sun, Y. DQ-reference-frame based impedance and power control design of islanded parallel voltage source converters for integration of distributed energy resources. Electr. Power Syst. Res. 2019, 168, 67–80. [Google Scholar] [CrossRef]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Zou, C.; Liu, B.; Duan, S.; Li, R. Stationary frame equivalent model of proportional-integral controller in dq synchronous frame. IEEE Trans. Power Electron. 2014, 29, 4461–4465. [Google Scholar] [CrossRef]
- Freijedo, F.D.; Vidal, A.; Yepes, A.G.; Guerrero, J.M.; Lopez, O.; Malvar, J.; Doval-Gandoy, J. Tuning of Synchronous-Frame PI Current Controllers in Grid-Connected Converters Operating at a Low Sampling Rate by MIMO Root Locus. IEEE Trans. Ind. Electron. 2015, 62, 5006–5017. [Google Scholar] [CrossRef]
- De Bosio, F.; Pastorelli, M.; De Souza Ribeiro, L.A.; Freijedo, F.D.; Guerrero, J.M. Effect of state feedback coupling on the transient performance of voltage source inverters with LC filter. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016. [Google Scholar]
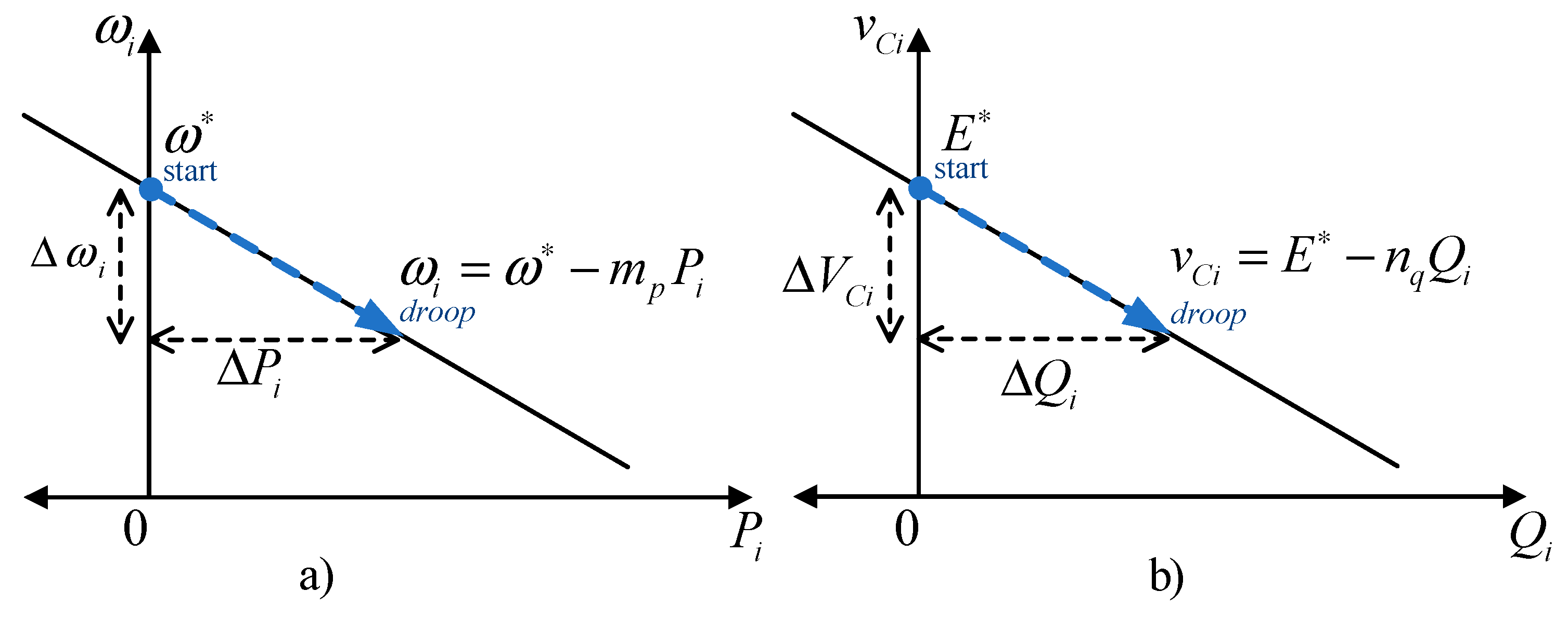



| Related Papers | Primary Control (Low-Frequency Dynamics) | Zero Level Control (High-Frequency Dynamics) | Time Delay Consideration |
|---|---|---|---|
| [27,28,29,31,33] | Yes | No | No |
| [4,30,32,34,35,36,37,38,39,40,41,42,44,45] | Yes | Yes | No |
| [46,47,48,49] | Yes | Yes | Yes (Padé approx. directly in regard to dq-axis) |
| Order | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| mp | |||
| nq | |||
| 175 kHz | |||
| 0.4948 | |||
| 10.9956 | |||
| 1 kHz | |||
| 0.3393 | |||
| 10.2102 | 0.5 mH | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| [] | |||
| General Approach Time Delay Modeling | Proposed Accurate Time Delay Modeling | ||
|---|---|---|---|
| Eigenvalues | )i | Eigenvalues | )i |
| −30 × 109 ± 309.1i | −30 × 109 ± 309.1i | ||
| −33.6 × 106 ± 309.1i | −33.6 × 106 ± 309.1i | ||
| −10 × 109 ± 309.1i | −10 × 109 ± 309.1i | ||
| −96,471.3 ± 1131.8i | −96,431.95 ± 2364.5i | ||
| −96,459.7 ± 1132.6i | −96,420.4 ± 2365.4i | ||
| −20,037.2 ± 49,022.93i | −20,307.34 ± 49,274.8i | ||
| −19,705.8 ± 48,359.2i | −19,454.7 ± 48,106i | ||
| −20,018.2 ± 49,027i | −20,288.53 ± 49,279i | ||
| −19,687.4 ± 48,364.7i | −19,436.19 ± 48,111.4i | ||
| −1191.3 ± 12,398.1i | −1350.86 ± 12,539i | ||
| −1532.3 ± 11,620.1i | −1370.8 ± 11,483.3i | ||
| −950.3 ± 12,580.7i | −1105.8 ± 12,711.8i | ||
| −1273.7 ± 11,812.3i | −1116.88 ± 11,686.8i | ||
| −1082 ± 249.9i | −1109.28 ± 322.6i | ||
| −1291.6 ± 189i | −1321.25 ± 374.8i | ||
| −420.2 ± 49.6i | −399.22 ± 159.3i | ||
| −21.9 ± 123.6i | −2.41 ± 138.5i | ||
| −3 ± 21.6i | −32.44 ± 20.5i | ||
| −6.2 + 0.0i | −2.98 ± 21.6i | ||
| −6.45 + 0.0i | −28.23 ± 20.9i | ||
| −8.8 + 0.0i | −6.2 + 0.0i | ||
| −33.7 ± 1.32i | −6.45 + 0.0i | ||
| −33.48 ± 0.024i | −17.38 ± 4.29i | ||
| −21.68 ± 0.04i | −17.05 ± 4.47i | ||
| −21.34 ± 0.99i | −8.75 + 0.0i | ||
| 0.0 + 0.0i | 0.0 + 0.0i | ||
| Conventional Approach | Proposed Model | Real-Time Simulation Result | Deviation % | |
| Case 1 | mp = 57 × 10−5 | mp = 74 × 10−5 | mp = 74 × 10−5 | 22% |
| Case 2 | nq = 220 × 10−5 | nq = 35 × 10−5 | nq = 35 × 10−5 | 530% |
| Without Virtual Impedance | With Virtual Impedance | Real-Time Simulation Result | Deviation % | |
| Case 3 | mp = 74 × 10−5 | mp = 80 × 10−5 | mp = 80 × 10−5 | 6% |
| Case 4 | nq = 35 × 10−5 | nq = 400 × 10−5 | nq = 400 × 10−5 | 1000% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuyumcu, A.; Karabacak, M.; Boz, A.F. High-Fidelity Modeling and Stability Analysis of Microgrids by Considering Time Delay. Electronics 2025, 14, 1625. https://doi.org/10.3390/electronics14081625
Kuyumcu A, Karabacak M, Boz AF. High-Fidelity Modeling and Stability Analysis of Microgrids by Considering Time Delay. Electronics. 2025; 14(8):1625. https://doi.org/10.3390/electronics14081625
Chicago/Turabian StyleKuyumcu, Ali, Murat Karabacak, and Ali Fuat Boz. 2025. "High-Fidelity Modeling and Stability Analysis of Microgrids by Considering Time Delay" Electronics 14, no. 8: 1625. https://doi.org/10.3390/electronics14081625
APA StyleKuyumcu, A., Karabacak, M., & Boz, A. F. (2025). High-Fidelity Modeling and Stability Analysis of Microgrids by Considering Time Delay. Electronics, 14(8), 1625. https://doi.org/10.3390/electronics14081625








