A Study on the Electromagnetic Characteristics of Very-Low-Frequency Waves in the Ionosphere Based on FDTD
Abstract
1. Introduction
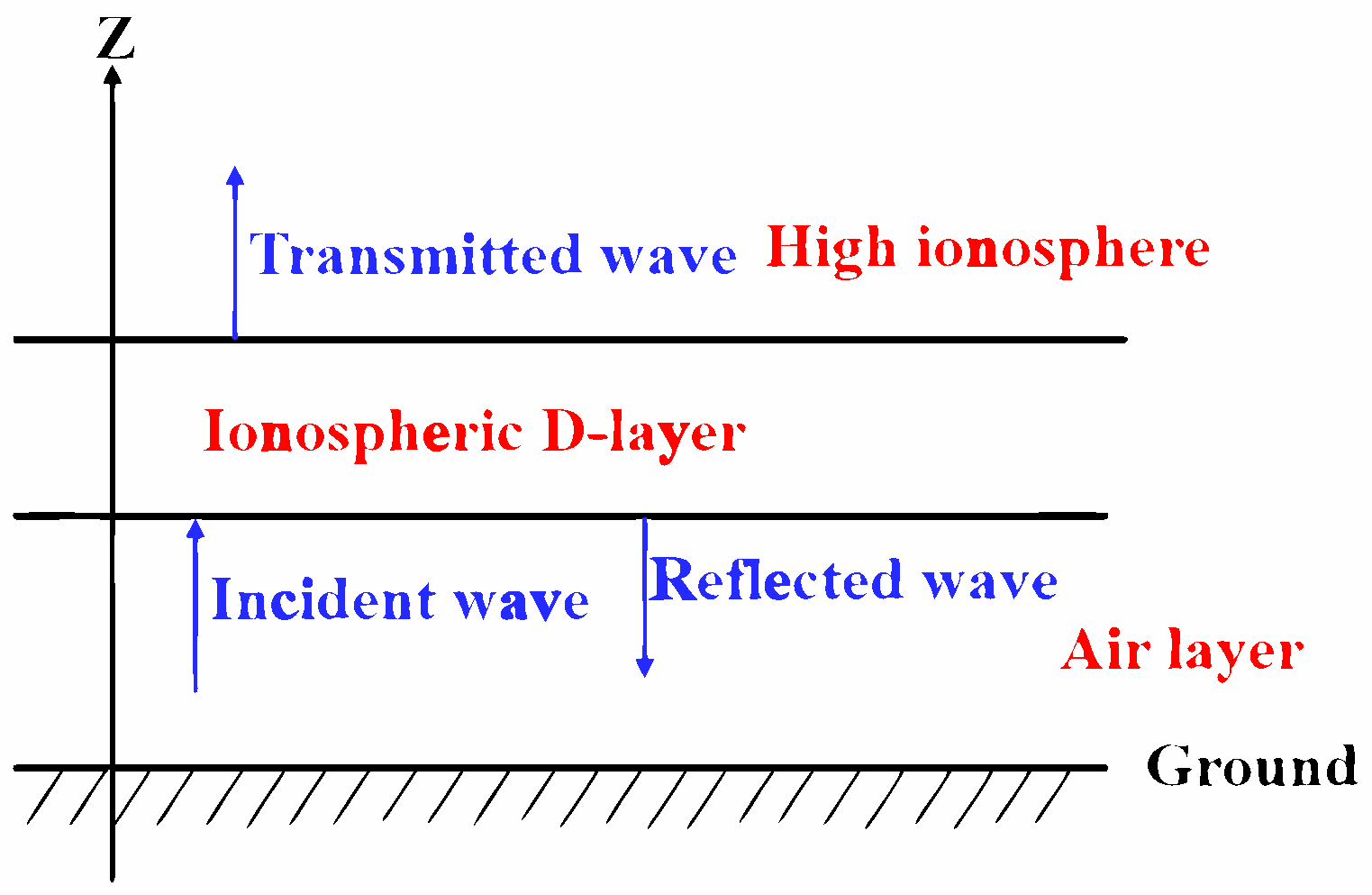
2. Formulation
2.1. Ionospheric Parameter Model
2.2. Equivalent Ionospheric Current-Density Model
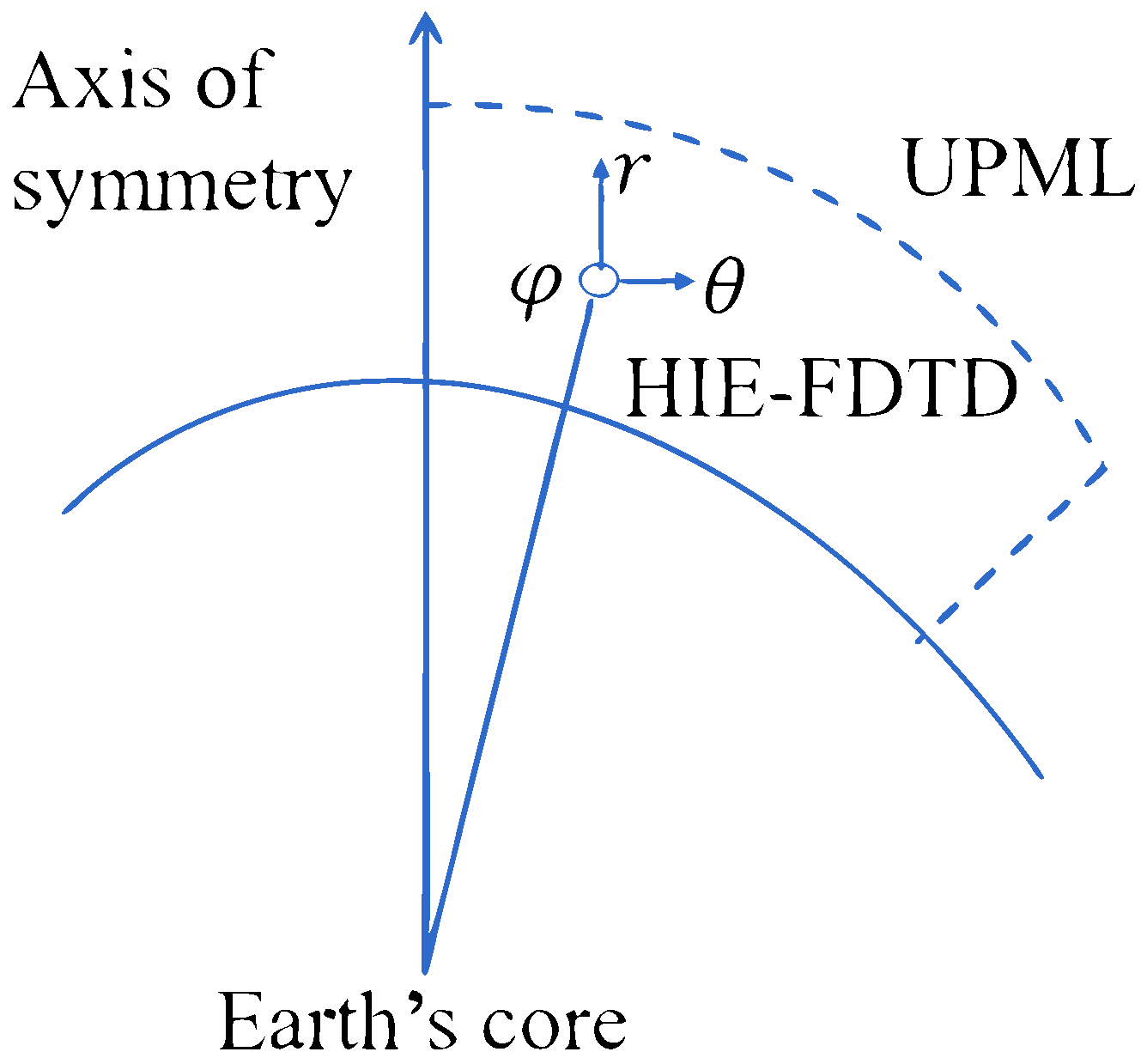
2.3. Algorithm and Its Optimization
3. Analysis of Accuracy and Performance
3.1. Analysis of Accuracy
3.2. Analysis of VLF Amplitude and Phase Characteristics
3.2.1. Signal-Source Modeling
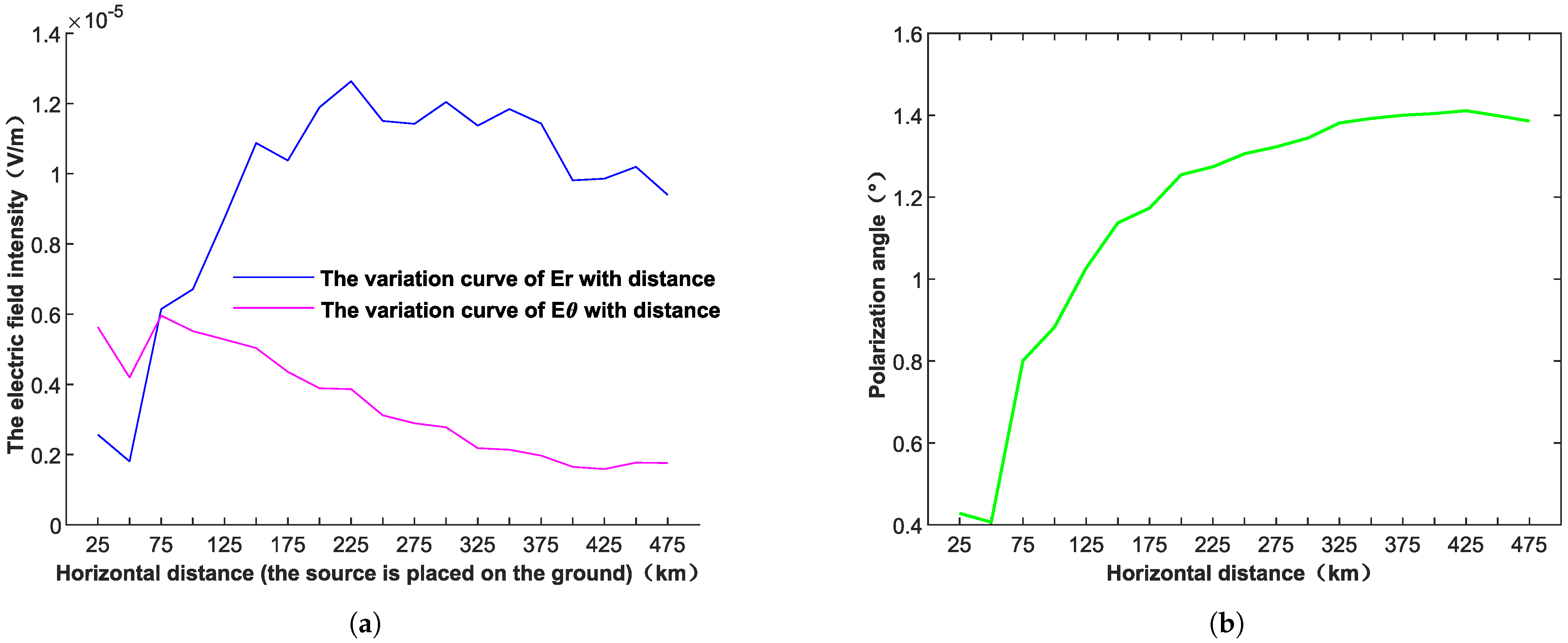
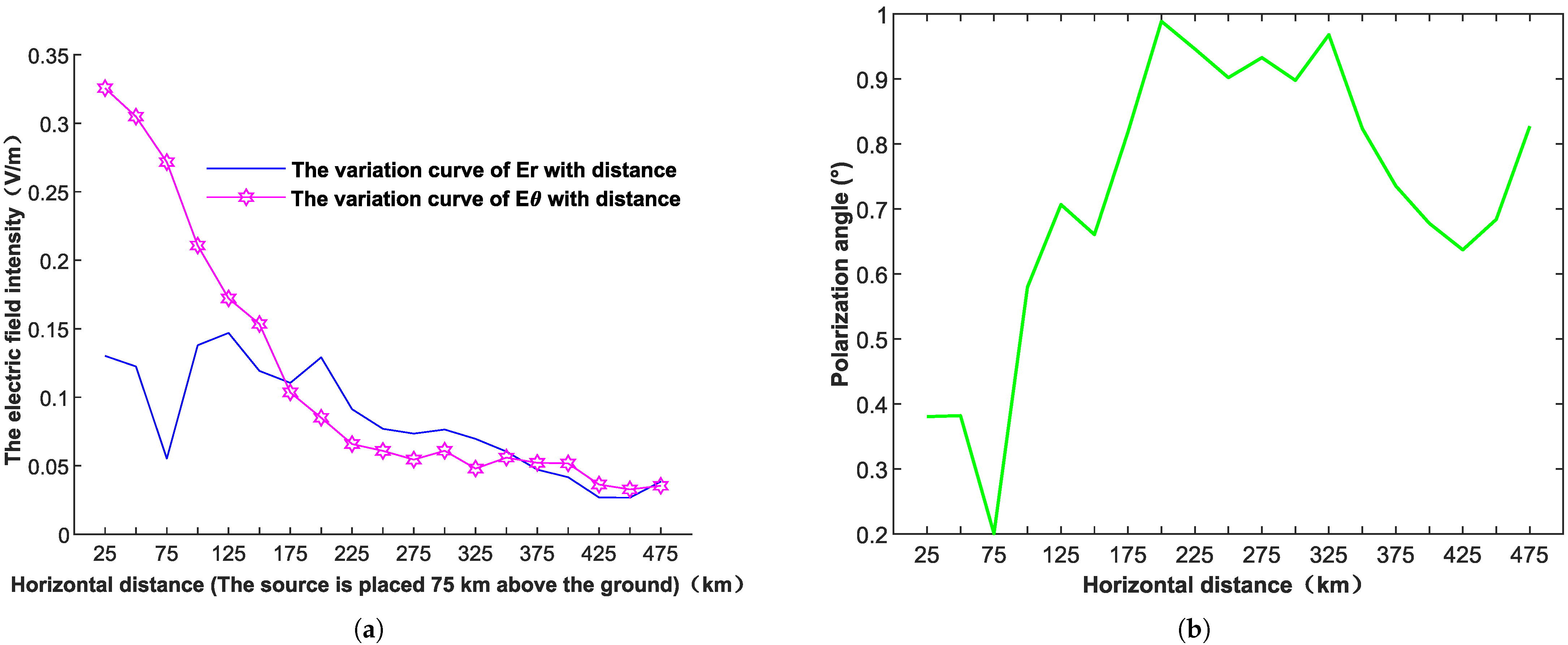
3.2.2. An Analysis of the Amplitude Attenuation, Phase-Distribution, and Polarization Characteristics of VLF Electromagnetic Waves in the Horizontal Propagation Direction of the Ionosphere
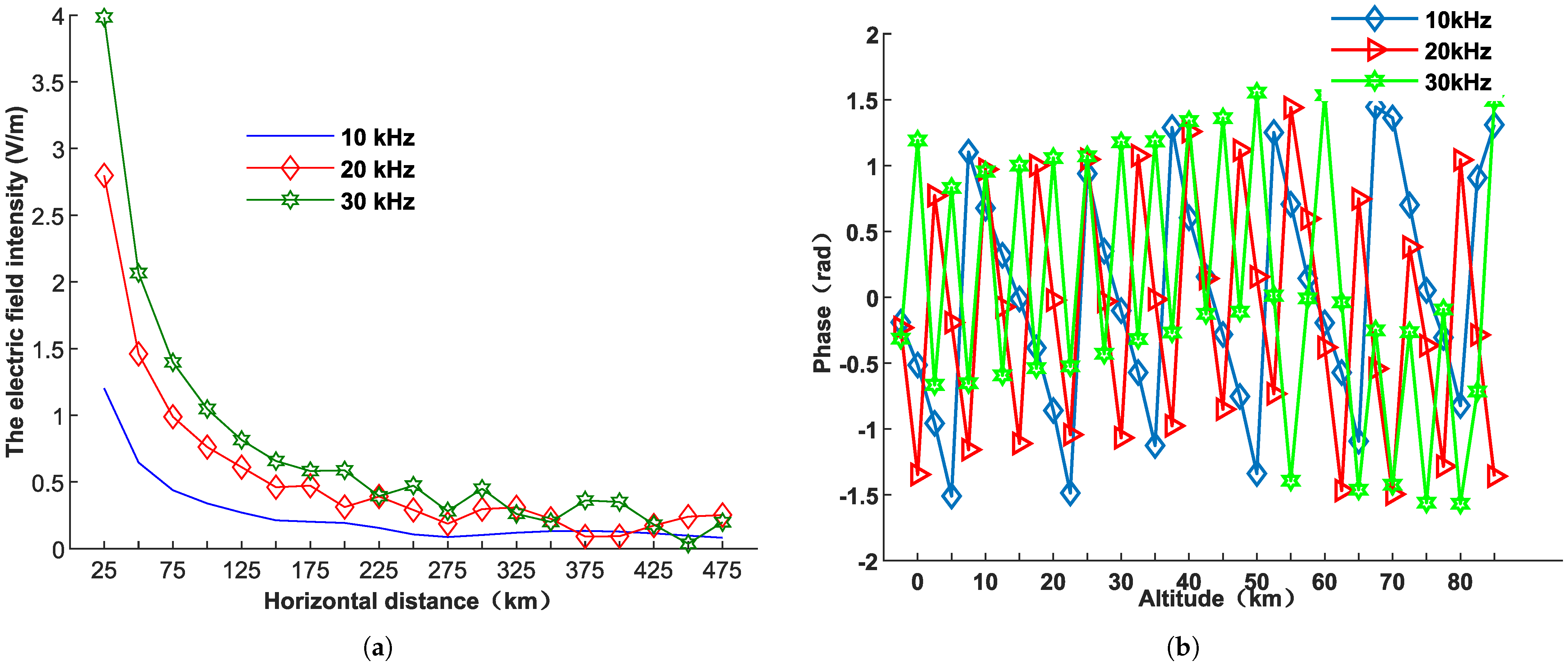
3.2.3. The Amplitude Attenuation and Phase-Distribution Characteristics of VLF Electromagnetic Waves with Different Frequencies When Propagating in the Ionosphere
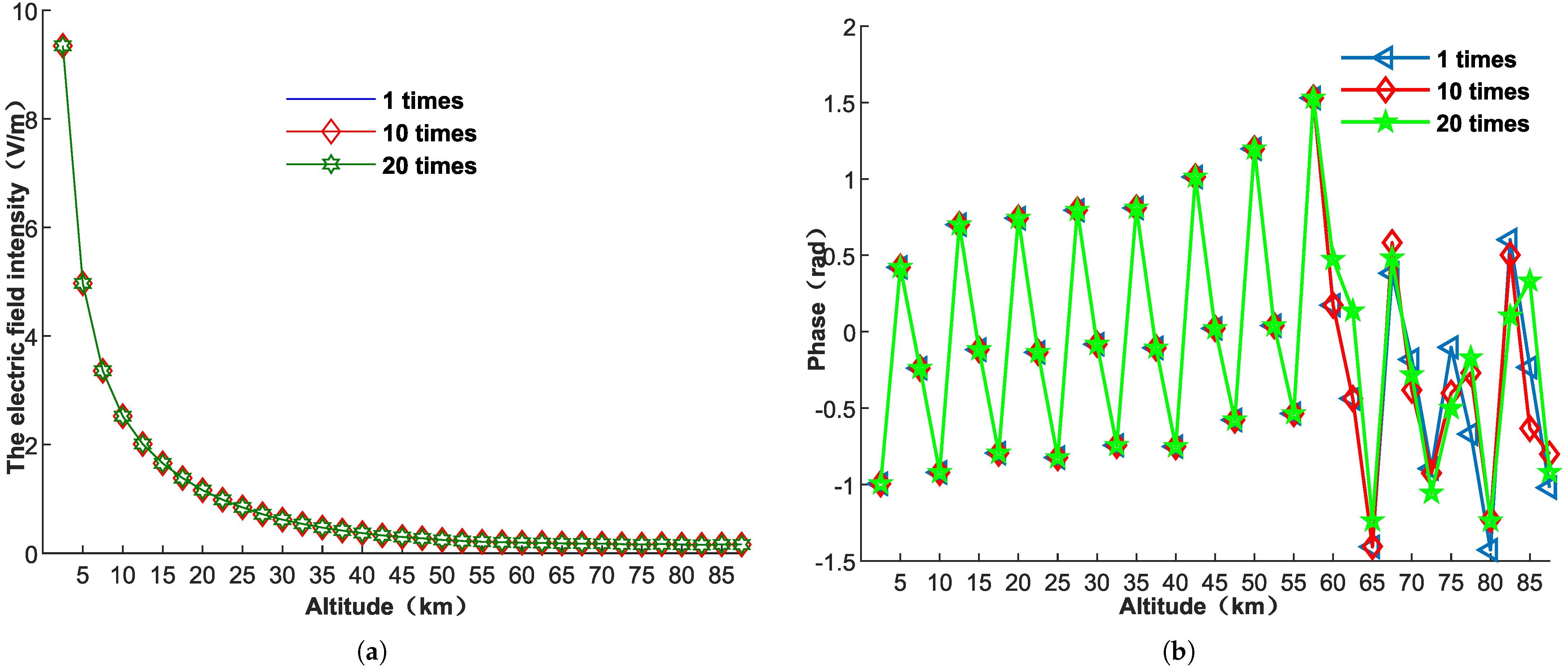
3.2.4. The Influence of Electron Density Variation on Amplitude and Phase
3.2.5. The Influence of the Change in Collision Frequency on the Phase
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, H.J. Latest development progress and trends of foreign data relay satellite systems. Telecommun. Eng. 2016, 56, 109–116. [Google Scholar]
- Tamagnone, M.; Gomez-Diaz, J.S.; Mosig, J.R.; Perruisseau-Carrier, J. Reconfigurable teraherz plasmonic antenna concept using a graphene stack. Appl. Phys. Lett. 2012, 101, 836–842. [Google Scholar] [CrossRef]
- Qu, Z.H.; Lai, M.Q. A review on electromagnetic, acoustic, and new emerging technologies for submarine communication. IEEE Access 2024, 12, 12110–12125. [Google Scholar] [CrossRef]
- Lehtinen, N.G.; Inan, U.S. Full-wave modeling of transionospheric propagation of VLF waves. Geophys. Res. Lett. 2009, 36, 151–157. [Google Scholar] [CrossRef]
- Su, Y.; Xu, Z.W. Numerical calculation of hierarchical transmission model of electromagnetic wave communication through formation based on FDTD. IEEE Access 2016, 35, 123–126. [Google Scholar]
- Liu, H.C.; Liang, H. Design of an anti-interference digital receiver for satellite mobile communication systems in low SNR application. Telecommun. Eng. 2014, 54, 1418–1423. [Google Scholar]
- Zhao, S.F.; Shen, X.H. Full wave calculation of VLF wave penetrated into satellite altitude ionosphere. IEEE Access 2015, 35, 178–184. [Google Scholar] [CrossRef]
- Alexeff, I.; Anderson, T.; Parameswaran, S.; Pradeep, E.P.; Hulloli, J.; Hulloli, P. Experimental and theoretical results with plasma antennas. IEEE Trans. Plasma Sci. 2006, 34, 166–172. [Google Scholar] [CrossRef]
- Bilitza, D. International reference ionosphere 200. Radio Sci. 2001, 36, 261–275. [Google Scholar] [CrossRef]
- Yang, H.W.; Liu, Y. Numerical analysis of the reflection and absorption of electromagnetic wave in nonuniform magnetized plasma slab. Int. J. Light Electron Opt. 2012, 123, 371–375. [Google Scholar] [CrossRef]
- Hu, X.W.; Liu, M.H. Propagation of an electromagnetic wave in a mixing of plasma-dense neutral gas. Plasma Sci. Technol. 2004, 6, 2564–2566. [Google Scholar]
- Li, H.J.; Liu, D.C. Propagation of strong electroma-genetic pulse in space. In Proceedings of the Tenth National Antiradiation Electronics and Electromagnetic Pulse Annual Academic Conference, Sanya, China, 1 July 2009. [Google Scholar]
- Shang, J.N.; Li, L.; Liu, C.J. Exploration and experiment of low information rate satellite communicationsystem in S-band. Telecommun. Eng. 2016, 56, 54–59. [Google Scholar]
- Ye, Z.H.; Liao, C. Analysis of electromagnetic pulse propagation in the ionosphere. Sci. Technol. Eng. 2011, 11, 4449–4452. [Google Scholar]
- Wu, Y.L.; Ge, D.B. Analysis of electromagnetic wave propagation in ionosphere by using FDTD combined with Z transform method. J. Hangzhou Inst. Electron. Eng. 2002, 22, 57–60. [Google Scholar]
- Mur, G. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Trans. Electromagn. Compat. 1981, 23, 377–382. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, B.; Shi, L.; Gao, C.; Chen, B. A Novel 3-D HIE-FDTD Method With One-Step Leapfrog Scheme. IEEE Trans. Microw. Theory Tech. 2014, 62, 1275–1283. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, B. A Novel HIE-FDTD Method with Large Time-Step Size [Programmer’s Notebook]. IEEE Antennas Propag. Mag. 2015, 57, 24–28. [Google Scholar] [CrossRef]
- Dong, M.; Chen, J.; Zhang, A. Fourth-order hybrid implicit and explicit-FDTD method. Int. J. Numer. Model. Electron. Netw. Devices Fields 2006, 29, 181–191. [Google Scholar] [CrossRef]
- Sounas, D.L.; Caloz, C. Gyrotropy and nonreciprocity of graphene for microwave applications. IEEE Trans. Microw. Theory Tech. 2008, 60, 901–904. [Google Scholar] [CrossRef]
- Chen, Z. A finite-difference time-domain method without the Courant stability conditions. IEEE Microw. Guid. Wave Lett. 1999, 9, 441–443. [Google Scholar]
- Moore, R.C.; Agrawal, D. ELF/VLF wave generation using simultaneous CW and modulated HF heating of the ionosphere. J. Geophys. Res. Space Phys. 2011, 116, A04217. [Google Scholar] [CrossRef]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. JIEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Cho, M.; Rycroft, M.J. Computer simulation of the electric field structure and optical emission from cloud-top to the iono-sphere. J. Atmos. Sol. Terr. Phys. 1988, 60, 871–888. [Google Scholar] [CrossRef]
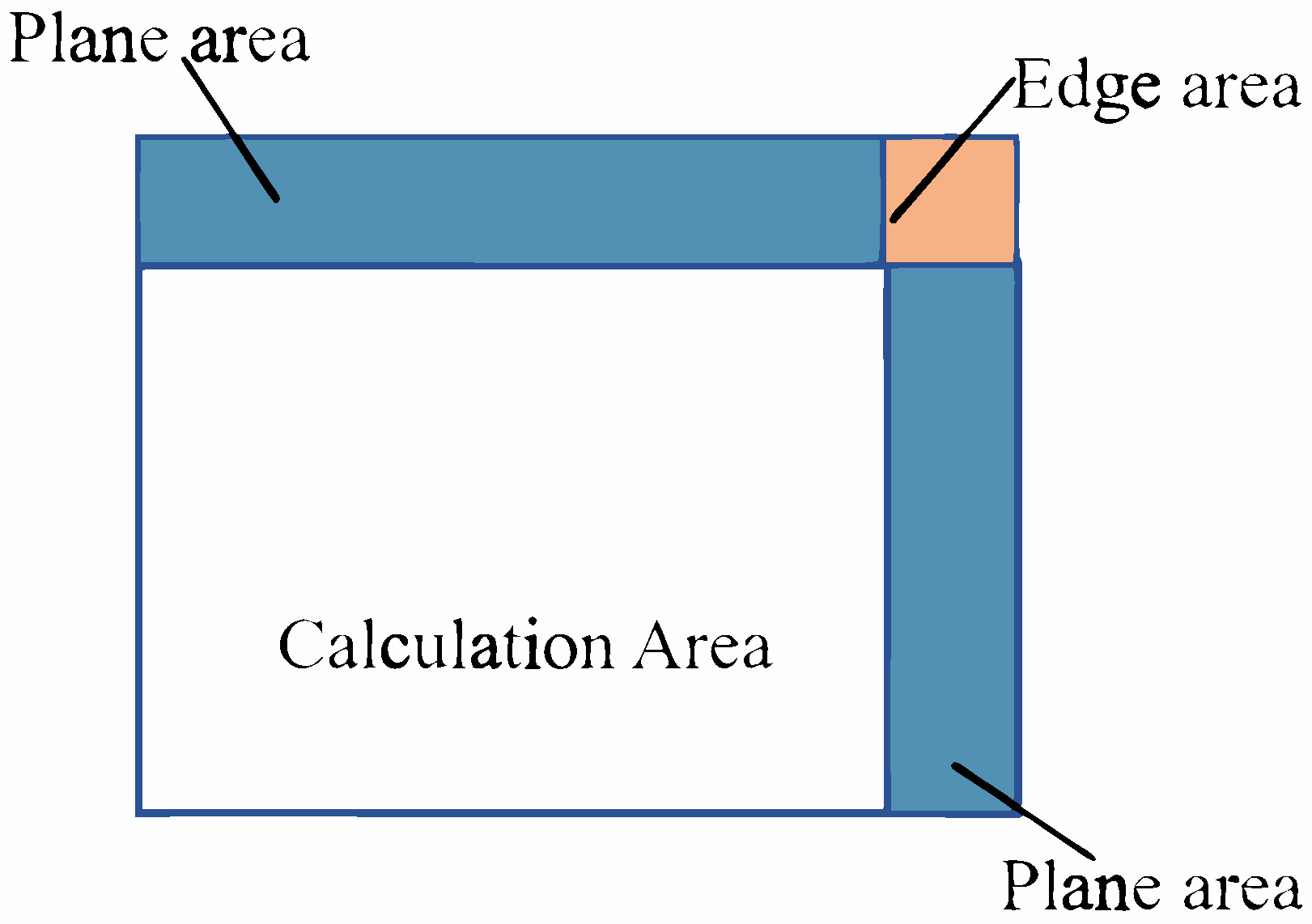





| UPML Region | Parameter |
|---|---|
| Edge area | |
| Plane area |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Xiao, Q.; Chen, J.; Dong, M. A Study on the Electromagnetic Characteristics of Very-Low-Frequency Waves in the Ionosphere Based on FDTD. Electronics 2025, 14, 1545. https://doi.org/10.3390/electronics14081545
Huang K, Xiao Q, Chen J, Dong M. A Study on the Electromagnetic Characteristics of Very-Low-Frequency Waves in the Ionosphere Based on FDTD. Electronics. 2025; 14(8):1545. https://doi.org/10.3390/electronics14081545
Chicago/Turabian StyleHuang, Kui, Qi Xiao, Juan Chen, and Mian Dong. 2025. "A Study on the Electromagnetic Characteristics of Very-Low-Frequency Waves in the Ionosphere Based on FDTD" Electronics 14, no. 8: 1545. https://doi.org/10.3390/electronics14081545
APA StyleHuang, K., Xiao, Q., Chen, J., & Dong, M. (2025). A Study on the Electromagnetic Characteristics of Very-Low-Frequency Waves in the Ionosphere Based on FDTD. Electronics, 14(8), 1545. https://doi.org/10.3390/electronics14081545




