Design and Modeling Guidelines for Auxiliary Voltage Sensing Windings in High-Voltage Transformers and Isolated Converters
Abstract
1. Introduction
- In comparison to standard auxiliary voltage sensing methods, the proposed method simplifies the design by bypassing the need for current zero-crossing detection.
- In comparison to other advanced methods such as knee point detectors, voltage slope tracking, and zero slope detector, the proposed approach offers reduced computational complexity and improved accuracy, mitigating errors caused by rapid voltage and current fluctuations.
2. Main Result
2.1. Background: Basic Design Procedures
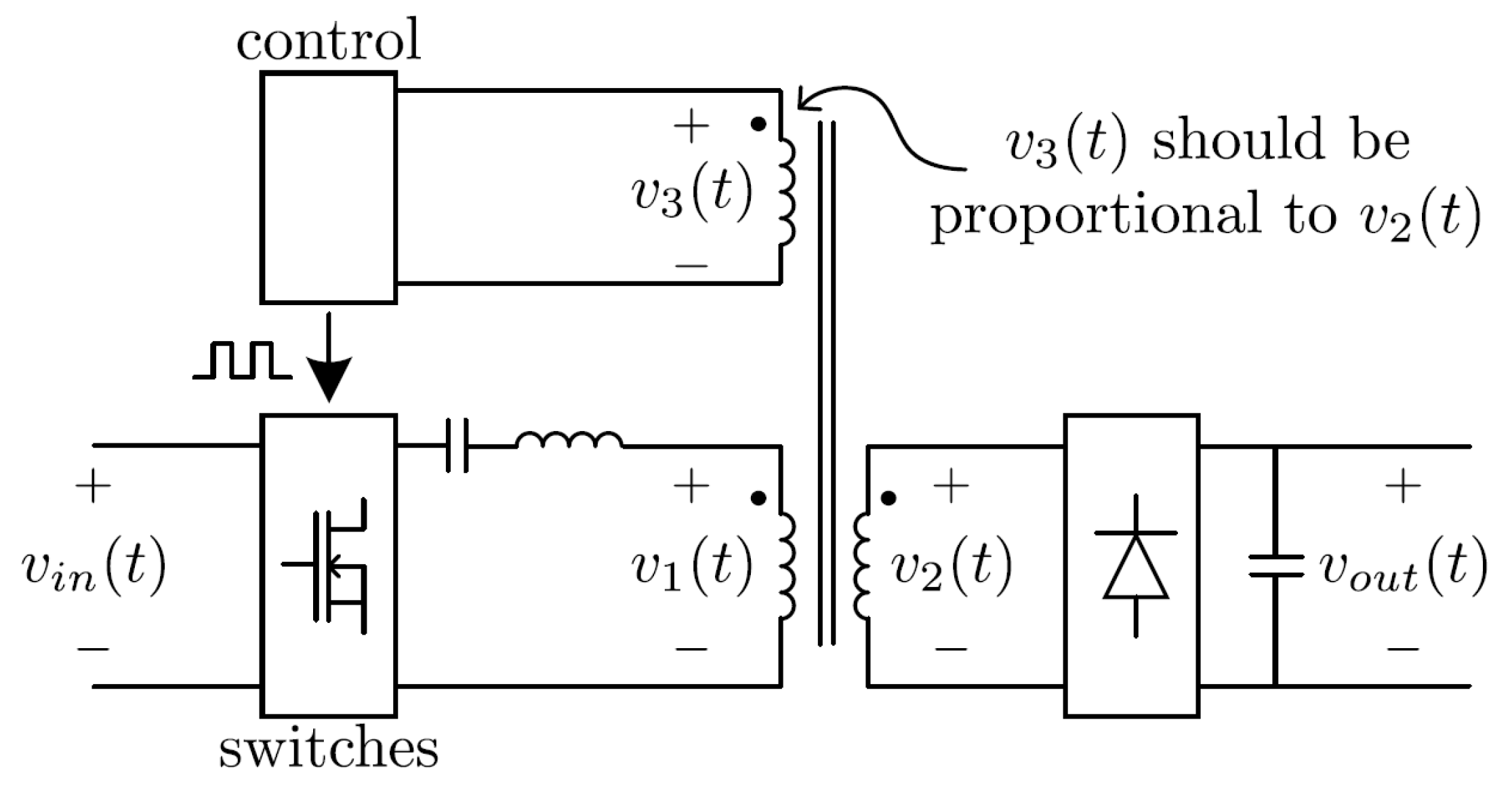
2.2. The Proposed Method for Sensing the Voltage on the Secondary Winding
3. Simulation and Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, S.; Kou, X.; Wang, C.; Sun, W.; Shi, L. New digital control method for improving dynamic response of synchronous rectified PSR flyback converter with CCM and DCM modes. IEEE Trans. Power Electron. 2020, 35, 12347–12358. [Google Scholar] [CrossRef]
- Kang, S.H.; Maksimović, D.; Cohen, I. Efficiency optimization in digitally controlled flyback DC–DC converters over wide ranges of operating conditions. IEEE Trans. Power Electron. 2012, 27, 3734–3748. [Google Scholar] [CrossRef]
- Chang, C.W.; Tzou, Y.Y. Primary-side sensing error analysis for flyback converters. In Proceedings of the International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 524–528. [Google Scholar] [CrossRef]
- Dong, H.; Xie, X.; Mao, F.; Zhang, L.; He, Y. A novel primary-side regulation control scheme for CCM and DCM LLC LED driver based on “Magnetizing Current Cancellation Method”. IEEE Trans. Power Electron. 2020, 35, 12223–12237. [Google Scholar] [CrossRef]
- Cho, J.G.; Baek, J.W.; Jeong, C.Y.; Yoo, D.W.; Joe, K.Y. Novel zero-voltage and zero-current-switching full bridge PWM converter using transformer auxiliary winding. IEEE Trans. Power Electron. 2000, 15, 250–257. [Google Scholar] [CrossRef]
- Burkard, J.; Biela, J. Design of a protection concept for a 100-kVA hybrid transformer. IEEE Trans. Power Electron. 2019, 35, 3543–3557. [Google Scholar] [CrossRef]
- Wang, C.; Xu, S.; Lu, S.; Sun, W. A low-cost constant current control method for DCM and CCM in digitally controlled primary-side regulation flyback converter. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 1483–1494. [Google Scholar] [CrossRef]
- Laboratories, S.N. Performance Model for Grid-Connected Photovoltaic Inverters. 2025. Available online: https://www.esig.energy/wiki-main-page/performance-model-for-grid-connected-photovoltaic-inverters/ (accessed on 18 March 2025).
- Dong, R.; Ruan, X.; Xu, Y.; Yu, J. A Two-Stage DC-DC Converter with Wide Input Voltage Range Based on Magnetic Isolation Feedback Control. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Vancouver, BC, Canada, 10–14 October 2021; pp. 2184–2188. [Google Scholar] [CrossRef]
- Yang, G.; Dubus, P.; Sadarnac, D. Design of a high efficiency, wide input range 500 kHz 25 W LLC resonant converter. J. Low Power Electron. 2012, 8, 498–508. [Google Scholar] [CrossRef]
- Lin, Y.T.; Liang, T.J.; Chen, K.H. IC design of primary-side control for flyback converter. In Proceedings of the International Future Energy Electronics Conference, Tainan, Taiwan, 3–6 November 2013; pp. 449–453. [Google Scholar] [CrossRef]
- Hsieh, P.C.; Chang, C.J.; Chen, C.L. A primary-side-control quasi-resonant flyback converter with tight output voltage regulation and self-calibrated valley switching. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 3406–3412. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, W.; Yang, X.; Yang, X.; Sun, J. A novel constant current and constant voltage adaptive blanking regulation scheme for primary-side controlled flyback converter. In Proceedings of the International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016; pp. 1652–1659. [Google Scholar] [CrossRef]
- Chiu, C.C.; Lin, M.; Chang, C.W.; Meng, C.H.; Yang, H.A.; Chen, K.H. Self-Calibrated Knee Voltage Detector With 99.65% High Accuracy for AC Charger System in 0.5 μm 500 V UHV Process. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 61, 2786–2795. [Google Scholar] [CrossRef]
- Nalepa, R.; Barry, N.; Meaney, P. Primary side control circuit of a flyback converter. In Proceedings of the APEC 2001, Sixteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.01CH37181), Anaheim, CA, USA, 4–8 March 2001; Volume 1, pp. 542–547. [Google Scholar] [CrossRef]
- Tzelepis, D.; Psaras, V.; Tsotsopoulou, E.; Mirsaeidi, S.; Dyśko, A.; Hong, Q.; Dong, X.; Blair, S.M.; Nikolaidis, V.C.; Papaspiliotopoulos, V.; et al. Voltage and Current Measuring Technologies for High Voltage Direct Current Supergrids: A Technology Review Identifying the Options for Protection, Fault Location and Automation Applications. IEEE Access 2020, 8, 203398–203428. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, T.; Zhao, S.; Zeng, H.; Zhang, J. Evaluation of primary side control schemes for flyback converter with constant current output. In Proceedings of the Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 17–21 March 2013; pp. 1859–1863. [Google Scholar] [CrossRef]
- Yao, M.; Liao, S.; Lin, F.; Long, Z.; Liu, R.; Liu, Y. Overview of Broadband Measurement Characteristics of Voltage Sensing Devices. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024; pp. 3238–3245. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ker, P.J.; Lipu, M.S.H.; Choi, Z.H.; Rahman, M.S.A.; Muttaqi, K.M.; Blaabjerg, F. State of the Art of Solid-State Transformers: Advanced Topologies, Implementation Issues, Recent Progress and Improvements. IEEE Access 2020, 8, 19113–19132. [Google Scholar] [CrossRef]
- Malik, A.; Haque, A.; Kurukuru, V.B.; Khan, M.A.; Blaabjerg, F. Overview of fault detection approaches for grid connected photovoltaic inverters. e-Prime Adv. Electr. Eng. Electron. Energy 2022, 2, 100035. [Google Scholar] [CrossRef]
- Zentani, A.; Almaktoof, A.; Kahn, M.T. A Comprehensive Review of Developments in Electric Vehicles Fast Charging Technology. Appl. Sci. 2024, 14, 4728. [Google Scholar] [CrossRef]
- Sayani, M.; White, R.; Nason, D.; Taylor, W. Isolated feedback for off-line switching power supplies with primary-side control. In Proceedings of the APEC ’88 Third Annual IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 1–5 February 1988; pp. 203–211. [Google Scholar] [CrossRef]
- Irving, B.T.; Jovanovic, M.M. Design considerations for magnetic feedback using amplitude modulation. In Proceedings of the 2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 71–77. [Google Scholar] [CrossRef]
- O’Loughlin, M. A hidden limitation in compensating the control loop of an isolated switching power supply. Micro-Electron. China Taiwan 2004, 1, 449–453. [Google Scholar]
- Dassault Systemes. The CST Studio Suite. 2025. Available online: https://www.3ds.com/products/simulia/cst-studio-suite/electromagnetic-design-environment (accessed on 8 April 2025).
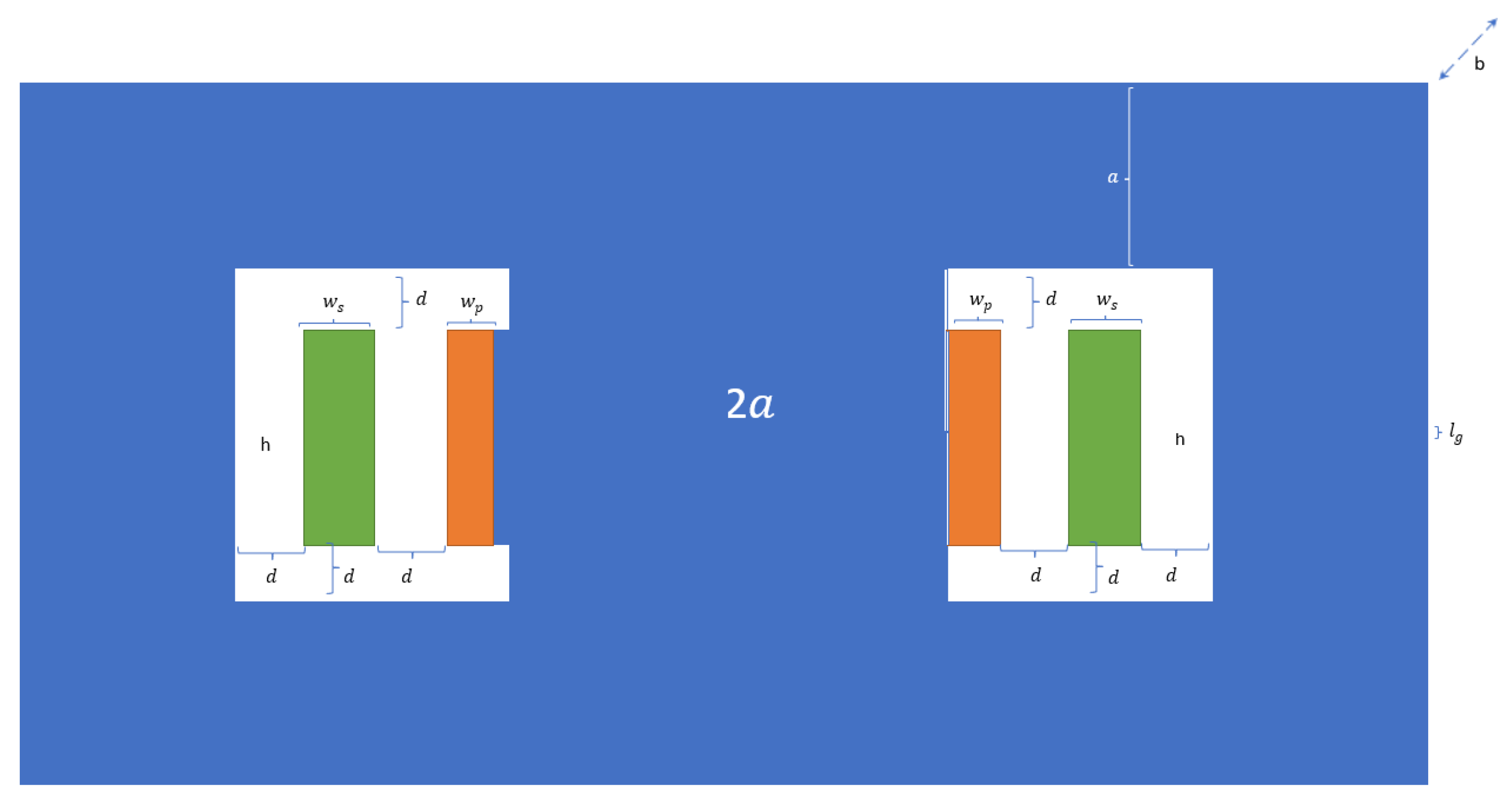
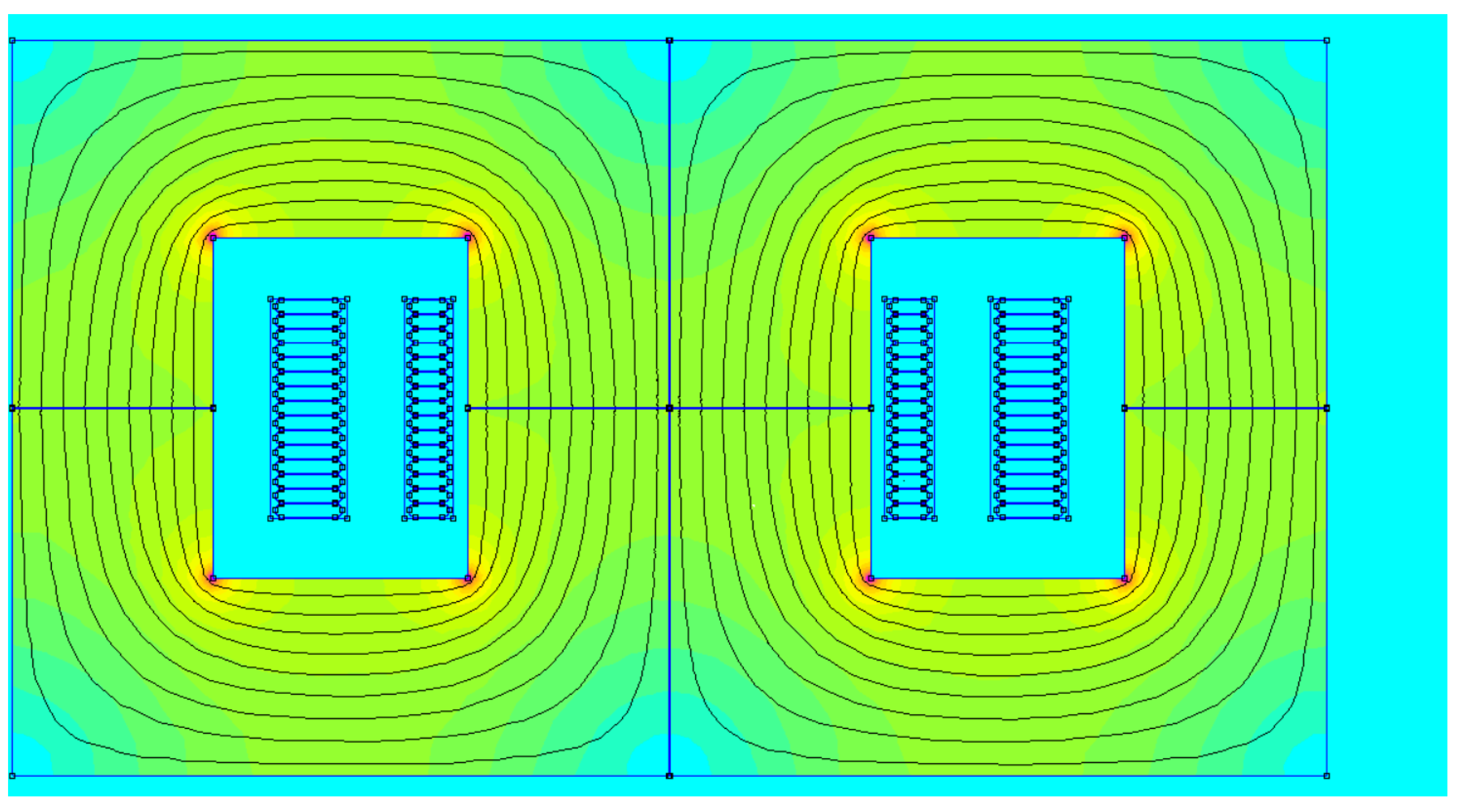
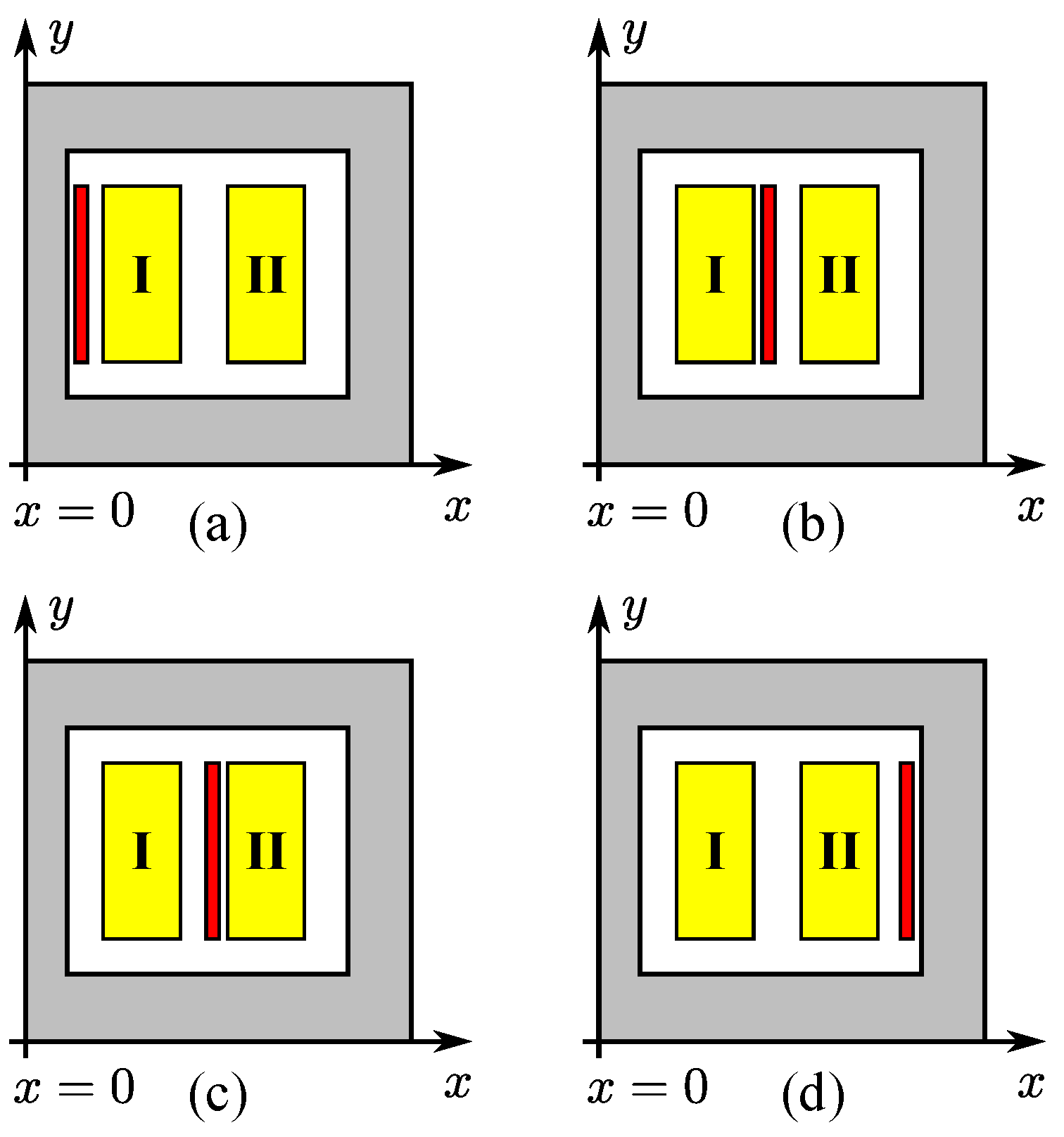
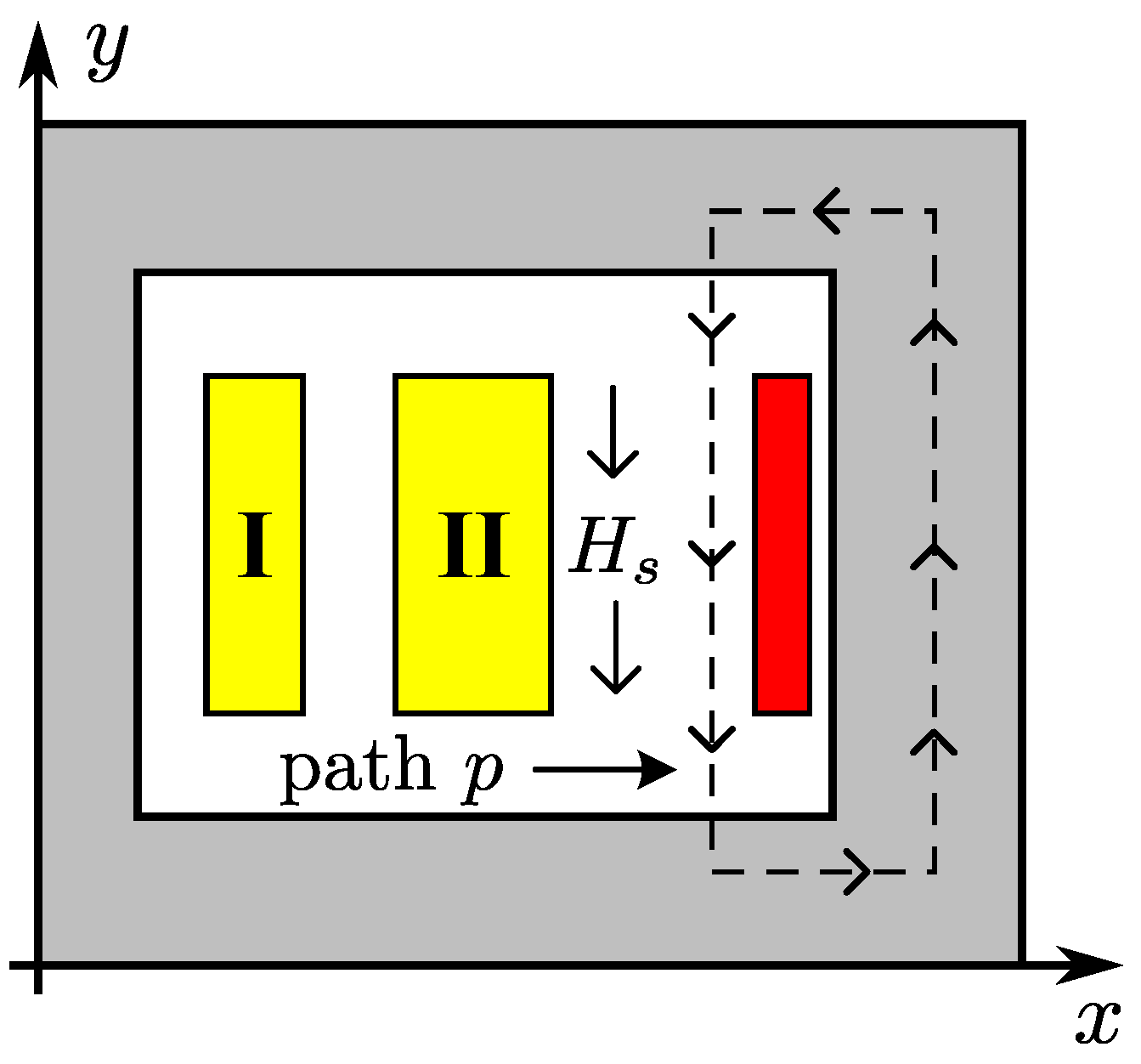
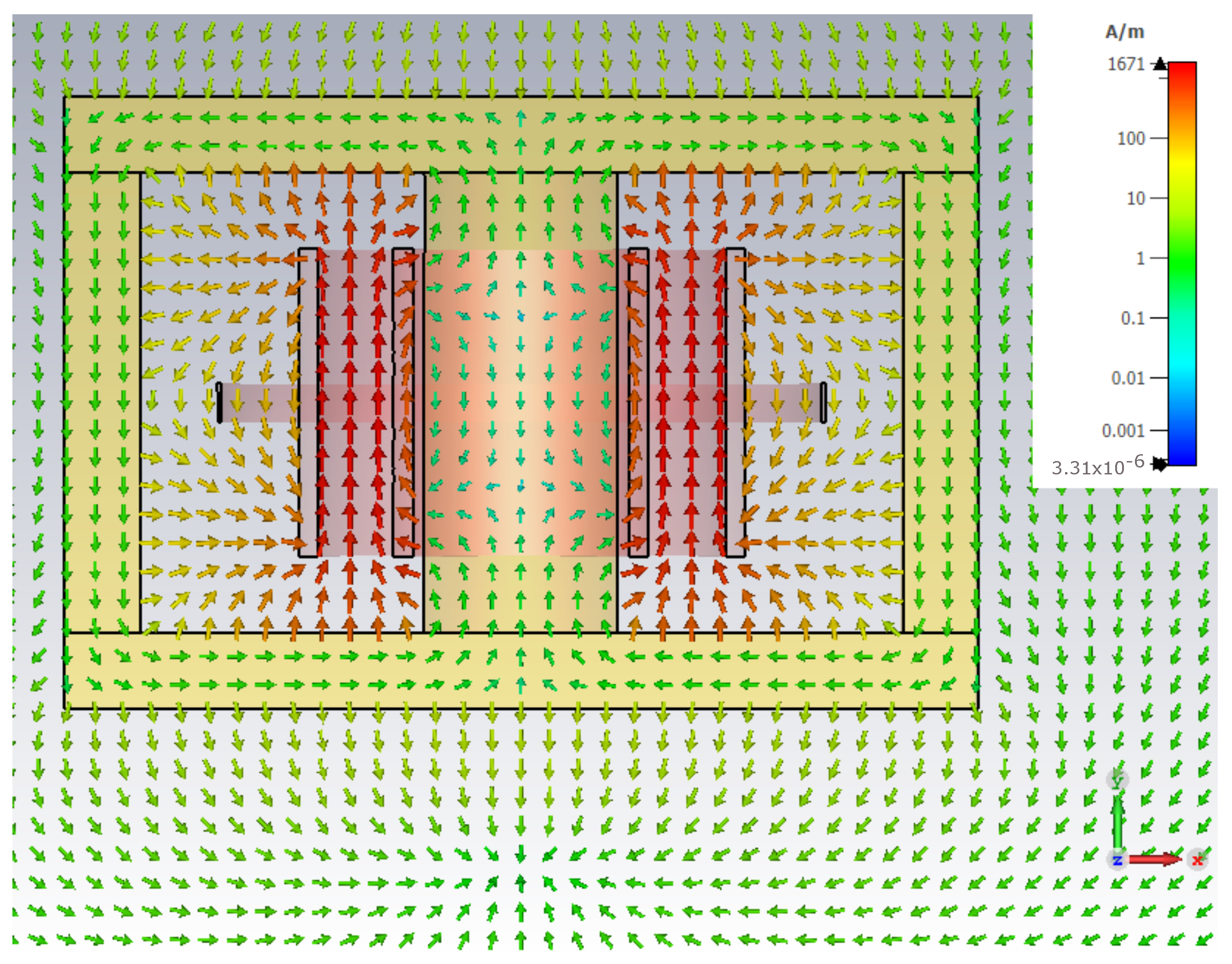



| Parameter | Value [Units] | Parameter | Value [Units] |
|---|---|---|---|
| f | 48 [kHz] | 0.2 [mm] | |
| n | 15 | x | 182 [mm] |
| a | 28.5 [mm] | y | 104 [mm] |
| b | 30 [mm] | z | 82 [mm] |
| d | 8 [mm] | h | 31 [mm] |
| 7 [mm] | 11 [mm] |
| Parameter | Value | Unit |
|---|---|---|
| Relative core permeability | 2000 | – |
| Central limb diameter | 50 | mm |
| Window breadth (y-axis) | 120 | mm |
| Window width (x-axis) | 74 | mm |
| Spacing between core and primary (inner) winding | 3 | mm |
| Primary winding width (x-axis) | 5 | mm |
| Primary winding breadth (y-axis) | 80 | mm |
| Primary winding number of turns | 10 | – |
| Spacing between primary and secondary (mid) windings | 20 | mm |
| Secondary winding width (x-axis) | 5 | mm |
| Secondary winding breadth (y-axis) | 80 | mm |
| Secondary winding number of turns | 10 | – |
| Spacing between secondary and tertiary (outer) windings | 20 | mm |
| Tertiary winding width (x-axis) | 1 | mm |
| Tertiary winding breadth (y-axis) | 10 | mm |
| Tertiary winding number of turns | 1 | – |
| Parameter | Value |
|---|---|
| Parameter | Value | Unit |
|---|---|---|
| Nominal power | 10 | kW |
| Nominal primary voltage | 500 | V |
| Nominal secondary voltage | 500 | V |
| Primary to secondary isolation | 60 | kV |
| Nominal switching frequency | 50 | kHz |
| Number of turns on primary | 12 | – |
| Number of turns on secondary | 12 | – |
| Number of turns on sensing winding | 1 | |
| 2007, 2071.7, 15.86 | H | |
| 0.9963, 0.9857, 0.9893 | – | |
| Magnetic core | 2 · Ferroxcube U93/52/30-3C94 | – |
| Gap between primary and secondary | 7 | mm |
| Isolation material | Polyurethane compound | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginzburg-Ganz, E.; Baimel, D.; Belikov, J.; Levron, Y. Design and Modeling Guidelines for Auxiliary Voltage Sensing Windings in High-Voltage Transformers and Isolated Converters. Electronics 2025, 14, 1519. https://doi.org/10.3390/electronics14081519
Ginzburg-Ganz E, Baimel D, Belikov J, Levron Y. Design and Modeling Guidelines for Auxiliary Voltage Sensing Windings in High-Voltage Transformers and Isolated Converters. Electronics. 2025; 14(8):1519. https://doi.org/10.3390/electronics14081519
Chicago/Turabian StyleGinzburg-Ganz, Elinor, Dmitry Baimel, Juri Belikov, and Yoash Levron. 2025. "Design and Modeling Guidelines for Auxiliary Voltage Sensing Windings in High-Voltage Transformers and Isolated Converters" Electronics 14, no. 8: 1519. https://doi.org/10.3390/electronics14081519
APA StyleGinzburg-Ganz, E., Baimel, D., Belikov, J., & Levron, Y. (2025). Design and Modeling Guidelines for Auxiliary Voltage Sensing Windings in High-Voltage Transformers and Isolated Converters. Electronics, 14(8), 1519. https://doi.org/10.3390/electronics14081519








