Abstract
This study proposes DtMin, a novel protocol for implementing data minimization principles in medical information sharing between healthcare providers (HCPs) and electronic health record providers (EHRPs). DtMin utilizes a multi-type encryption approach, combining attribute-based encryption (ABE) and hybrid encryption techniques. The protocol classifies patient data attributes into six categories based on sensitivity, consent status, and sharing requests. It then applies differential encryption methods to ensure only the intersection of patient-consented and EHRP-requested attributes is shared in decipherable form. DtMin’s security is formally analyzed and proven under the ICR-DB and ICR-IS security games. Performance analysis demonstrates efficiency across various data volumes and patient numbers. This study explores the integration of DtMin with advanced cryptographic techniques such as lattice-based ABE and lightweight ABE variants, which can potentially enhance its performance and security in complex healthcare environments. Furthermore, it proposes strategies for integrating DtMin with existing healthcare information systems and adapting it to future big data environments processing over 100,000 records. These enhancements and integration strategies position DtMin as a scalable and practical solution for implementing data minimization in diverse healthcare settings, from small clinics to large-scale health information exchanges.
1. Introduction
Medical data contain some of the most sensitive personal information, and improper sharing or breaches of these data can lead to severe consequences, such as privacy violations and identity theft. The issue here is that while medical information is sensitive data that must be protected, it is also information that needs to be shared among various entities for the public good, such as for statistical purposes, research, or to provide medical services. Healthcare providers (HCPs) are regularly required to exchange patient information with electronic health record providers (EHRPs), insurance companies, and research institutions.
This exchange of data poses significant privacy risks. In today’s healthcare ecosystem, sharing medical information faces considerable challenges. For example, in 2023, Change Healthcare, the largest medical claims processor in the United States, suffered a ransomware attack that exposed the medical records of approximately 300 million people, causing severe disruption across the healthcare system. In 2021, Scripps Health, a major healthcare system in California, experienced a cyberattack that leaked personal information of more than 150,000 patients and staff, resulting in a month-long disruption of medical services. Similarly, in the same year, the Health Service Executive (HSE) of Ireland was hit by a ransomware attack that led to thousands of patient appointments being canceled and emergency services being halted, causing a national healthcare crisis.
To prevent such medical data breaches, extensive research has been conducted from various perspectives. In particular, numerous studies have focused on addressing privacy concerns that arise when multiple healthcare institutions share medical information. Despite these efforts, challenges still remain [1,2,3,4,5,6,7,8,9,10].
1.1. Problem Identification
A very recent paper by Kim et al. [1] proposed a Diffie–Hellman-based private set intersection (DH-PSI) protocol to identify common patients between hospitals and insurance companies. It indicates that the information of these identical patients can be shared between the two entities. However, this approach does not comply with the principle of data minimization, which is a cornerstone of data protection regulations such as Europe’s GDPR [11] and the US’s HIPAA [12].
Globally, strengthening privacy regulations requires healthcare institutions to collect, store, and share patient data in ways that collect and process only the minimum necessary data, according to the ’data minimization’ principle. However, previous papers have only suggested methods or algorithms to enhance privacy protection and efficiency in sharing medical information. These approaches lack a data minimization process and lead to the retention and processing of unnecessary information, which can provide additional attack routes or result in systems that are inefficient and less secure. This study aims to identify the limitations in existing studies on medical information sharing and propose a protocol that adheres to the data minimization principle.
1.2. Objectives and Methods
We propose a protocol to achieve the principle of data minimization for information security and privacy protection during sharing medical information between EMR (electronic medical record) and EHR (electronic health record) systems. This is not about developing a new algorithm to improve the performance of the latest encryption algorithms. Instead, we propose the DtMin protocol to enhance efficiency and security by implementing the fundamental principles of information security through minimal collection, retention, and processing of resources.
The DtMin protocol utilizes a multi-type encryption approach using attribute-based encryption (ABE) and hybrid encryption techniques. The key mechanisms are as follows:
- Data Classification System: Attributes are classified into six categories based on sensitivity (ciphertext/plaintext), patient consent/non-consent, and EHR request/non-request, applying different encryption methods to each level.
- Multiple Encryption: Different encryption methods are used according to the type of attribute.
- Hybrid Encryption: Shared key generation is performed via a key exchange method.
- Multi-Layer Encryption Process:
- First Encryption: Encrypts using the doctor’s private key/public key based on the patient’s consent/non-consent.
- Second Encryption: Further encrypts with the HCP’s secret key.
- Decryption: Decrypts with HCP’s secret key only for the attributes which EHRP requested to be shared.
- Re-Encryption: Re-encrypts with a sharing key for the sensitive attributes in ciphertext.
Unlike existing approaches, which focus solely on secure transmission or access control, DtMin implements a selective sharing mechanism to ensure that only the intersection of attributes consented to by the patient and specifically requested attributes is shared.
1.3. Contributions
- Attributes are classified based on six criteria: sensitivity (ciphertext/plaintext), patient consent/non-consent, and EHR request/non-request, using different encryption methods for each. This forms the basis for implementing a selective sharing mechanism, achieving fine cryptographic access control (Fine CAC) that enables fine-grained access control.
- This protocol is designed to practically implement the data minimization principle emphasized in modern privacy regulations such as GDPR, meeting the regulatory requirements and privacy principles that must be adhered to during information sharing in healthcare.
- By integrating attribute-based encryption (ABE) with the data minimization principle, an encryption infrastructure is established that inherently enforces minimal data disclosure. Traditional healthcare information sharing systems handle data in an “All-or-Nothing” manner. In contrast, DtMin selectively shares only the intersection of attributes consented to by the patient and requested by the EHRP.
- Quantitative performance evaluation and theoretical security analysis are provided; the performance of the proposed protocol is actually measured and analyzed based on varying data sizes and numbers of patients (see Section 6), and formal security proofs are used to rigorously analyze the security of the protocol (see Section 5).
- As a result, efficiency is improved: (1) the amount of data to be processed is reduced, lowering computational costs; (2) system efficiency is enhanced due to reduced storage and transmission requirements; and (3) the security overhead is reduced by limiting the range of data requiring security management.
- Consequently, DtMin ensures minimal information sharing based on patient consent and data sensitivity, drastically reducing unnecessary data exposure.
- This approach becomes a practical solution that can significantly reduce the risk of privacy breaches and regulatory non-compliance in real healthcare environments.
- As future enhancements, we explore strategies to apply advanced cryptographic techniques to DtMin in complex, diverse, and large-scale healthcare environments to adhere to the principle of data minimization.
The following sections detail DtMin’s design, security analysis, and performance evaluation. Section 2 reviews related works in medical information sharing and data minimization. Section 3 introduces the preliminaries, including the application scenario, notation, and security building blocks. Section 4 describes the construction of the DtMin protocol. Section 5 provides a comprehensive security analysis, while Section 6 evaluates the protocol’s efficiency. Section 7 compares DtMin to existing systems, highlighting its strengths and potential limitations. Finally, Section 8 explores future enhancements, including integration strategies with advanced cryptographic techniques and existing healthcare systems, before concluding in Section 9.
2. Related Works
This study proposes a protocol that adheres to the principle of data minimization, a fundamental aspect of information security and privacy, in the process of sharing medical information. It also explores related research and regulations.
2.1. Characteristics of Medical Information
To develop such a protocol, it is necessary to first understand the characteristics of medical information. In [13], Park emphasizes the unique characteristics of medical information compared to general data, pointing out that medical information is sensitive personal information and, at the same time, it should be provided as data for public interest and academic development. Park also highlights the distinctions between the data subject, data generator, and data manager. Additionally, Park criticizes existing studies for applying general data security techniques without considering the unique characteristics of medical information and proposed solutions to protect personal data’s self-determination. In this study, we propose a protocol that adheres to the principles of data self-determination (or self-regulation) and minimization in the process of sharing medical information, based on Park’s concept of medical information outlined in reference [13].
2.2. Sharing of Medical Information
Next, we review studies on sharing medical information. In reference [4], the author proposes a Secure Information Sharing System (SISS) for online patient networks. SISS utilizes a group key cryptosystem to securely share sensitive health information while preserving privacy. It solves the problem of rekeying and redistribution for membership changes and utilizes 3D Stereoscopic Image Mobile Security Technology to prevent conspiracy among group members. In [5], Heng Pan et al. propose a scheme named MDS2-C3PF, which addresses the imbalance of access control and data processing in medical data sharing by using cloud-chain cooperation and policy fusion. It introduces a conflict resolution algorithm to create balanced access control policies between doctors and patients and a cloud-chain cooperation ciphertext retrieval method to ensure secure and efficient data retrieval while mitigating malicious feedback from cloud servers. Reference [6] presents a secure and privacy-preserving health data sharing framework using homomorphic encryption, allowing for AI-driven analysis while complying with GDPR regulations. The authors demonstrate the effectiveness of their framework through real-world application and evaluation. This study’s [7] privacy-preserving medical data sharing system utilizes symmetric encryption and blockchain to address the challenges of data interoperability and unauthorized data sharing. The system utilizes a chameleon signature algorithm to prevent visitors from sharing the obtained data with unauthorized parties, and it also allows for revoking the permissions of data managers to prevent data misuse. In reference [8], there is a comparison among three popular attribute-based encryption schemes—CP-ABE, KP-ABE, and MA-ABE—for securing electronic health records in a cloud environment. The authors built EHR systems using knowledge graphs and the MIMIC-III dataset to evaluate the performance and usability of these ABE schemes. The authors suggest that healthcare organizations should carefully consider the specific requirements and constraints of their EHR system before choosing a particular ABE scheme. Jihyeon Oh et al. propose a secure and privacy-preserving medical data sharing scheme that uses key aggregation encryption and private set intersection (PSI) to ensure data confidentiality and prevent sensitive information exposure in [9]. The authors conducted formal and informal security analyses, as well as performance evaluations, to demonstrate the effectiveness and efficiency of their scheme compared to other existing approaches. Mao et al. discuss the efficient and secure management of medical data sharing using blockchain technology, addressing challenges such as data privacy and trust in multi-party environments. It proposes a blockchain-based framework that enhances data provenance and security in [10] and accessibility, ultimately facilitating trusted sharing of medical information among various organizations. Another use of blockchain was proposed by Xu et al. in [14]. This study proposes a healthcare data sharing scheme called 2DCM-DS, which uses two-dimensional chaotic mapping and blockchain. It integrates biometric audio information for identity verification and employs smart contracts for data integrity and authentication. The paper focuses on secure data sharing but does not explicitly address data minimization principles, because it involves reducing the amount of data shared to only what is necessary for a specific purpose. Bai et al. explore healthcare data sharing within digital platforms, focusing on the risks of data breaches in [15]. It uses evolutionary game theory to model interactions among medical institutions, data platforms, and insurance companies. The study examines strategies for anonymous information sharing, platform regulation, and insurance company auditing. It finds that when breaches occur, medical institutions tend to seek shared responsibility, promoting stricter platform regulation and encouraging insurance audits. While the paper discusses anonymous information sharing, it does not also explicitly address data minimization principles, which are crucial for reducing unnecessary data exposure. Reference [16] is about amendments to South Korea’s health and medical data utilization guidelines, focusing on the safe use of genomic data. It introduces pseudonymization methods for genomic sequences and metadata, aiming to balance data utilization with privacy protection. The process of pseudonymizing genomic data can be complex and may not fully eliminate the risk of re-identification, especially when combined with other data sources. Barker et al. examined the evolution of health information technology (health IT) in the United States, highlighting significant advancements in electronic health records (EHRs), interoperable data exchange, e-prescribing, and patient access to health information [17]. These developments have improved healthcare outcomes and patient engagement, but challenges persist, including interoperability hurdles and inequitable access. The authors of reference [1], which motivated our research, suggested a new Diffie–Hellman-based private set intersection (PSI) protocol for securely sharing medical data between institutions. This protocol allows institutions to identify common patients without revealing sensitive data and is efficient in terms of communication costs. It also avoids the need for a third-party trusted authority.
2.3. Data Minimization Principle
Lastly, we examine research and regulations regarding data minimization principles.
2.3.1. Regulation
In the fields of privacy and information security, the data minimization principle is a key concept, and its importance is emphasized in various research papers and regulatory frameworks. The EU’s General Data Protection Regulation (GDPR) is one of the most influential international regulations explicitly stipulating the data minimization principle. Article 5(1)(c) of the GDPR states that “personal data shall be adequate, relevant, and limited to what is necessary in relation to the purposes for which they are processed (data minimization).” It defines data minimization as a core principle of data processing, requiring organizations to collect, process, and store only the minimum data necessary for specific purposes [11]. Additionally, Article 3 of the Personal Information Protection Act of South Korea specifies the principle of “collecting only the minimum necessary personal information lawfully and appropriately within the scope required for processing purposes,” emphasizing the minimization principle in relation to the data subject’s right to self-regulation [18].
2.3.2. Research Papers Emphasizing the Importance of the Principle of Minimization
There are papers on data minimization related to this study. In reference [19] by Mukta et al., it is said that data minimization is the practice of limiting the collection and use of personal information to what is necessary, which can enhance trust in blockchain-based healthcare systems. They define data minimization as “the practice of limiting the collection and use of personal information to what is necessary” and emphasize that this can enhance trust in blockchain-based healthcare systems. However, systematic research on this topic is lacking. Mukta et al. investigate data minimization techniques, classify and compare methods based on different data processing stages, and propose research directions to improve privacy protection. In reference [20], Conte et al. detail “Health360, a SaaS platform” prioritizing data minimization in healthcare. SaaS platforms often store and process large volumes of sensitive data, including personal health information. Minimizing the amount of data collected reduces the exposure risk in case of a data breach. It uses role-based access control, modular architecture, and pseudonymization to limit data exposure, balancing research needs with stringent privacy regulations. The authors highlight the platform’s design choices in achieving data minimization while addressing legal and ethical considerations. However, the Health360 platform is a case study focused on a specific type of data (e.g., neuromuscular disease-related data) for a small healthcare organization and lacks validation of its applicability in a large healthcare system, which may limit the applicability of data minimization principles to a wider range of healthcare data types. While there is discussion of compliance with regulations such as GDPR, there is a lack of specificity in how it actually meets the complex legal and technical requirements to comply with such regulation and a lack of substantive validation of the effectiveness of security and privacy mechanisms. In [21], Bargh et al. address the challenge of implementing data minimization techniques, specifically Statistical Disclosure Control (SDC), within organizations. It presents a framework for embedding SDC, emphasizing a phased approach that gradually empowers local data stewards with the necessary knowledge and tools. They highlight the development of several artifacts—reports, guidelines, and a user interface—to support this process, thereby promoting practical data minimization while addressing legal and technical complexities. The authors of [22] present a methodology to help software developers understand and minimize data usage in system design, addressing the challenges of balancing privacy with functionality. It uses a three-pronged approach focusing on data sensitivity, visibility, and relevance to inform design decisions, ultimately aiming to improve the practical application of data minimization principles in software development. The methodology was evaluated through three studies, demonstrating its potential for enhancing privacy-conscious design practices. These studies on data minimization [19,20,21,22] provide important foundations for our work, though none have specifically applied these principles to medical information sharing with the granularity offered by DtMin.
Although these related works suggest various approaches to protect personal information in sharing medical information, they do not directly address the topic that this study intends to propose. In particular, there is a still lack of research on how to systematically implement the data minimization principle in a medical information sharing environment. Encryption-based approaches ensure data confidentiality, but most of them treat all attributes with the same level of security, which does not effectively implement the ‘data minimization’ principle. Specifically, existing studies do not provide a mechanism to selectively share information according to patient consent, request for sharing, and data sensitivity. DtMin, proposed in this study, attempts to overcome these limitations by combining multi-type attribute classification and attribute-based encryption.
3. Preliminaries
3.1. Application Scenario and Participants
3.1.1. Participants
- HCP (HealthCare Provider): This is an institution that provides medical services, such as hospitals, clinics, and public health centers. HCPs use an electronic medical record (EMR) system.
- EHRP (EHR Provider): This is an entity that uses an electronic health record (EHR) system, such as insurance companies and government health agencies.
- Patients and Doctor: These are individuals registered with the HCP. The doctor makes the final decision on whether to share only the information the patient has consented to share.
- Server Administrator: This is the HCP’s server manager responsible for managing patient data.
3.1.2. Application Scenario
For patients common to both the EHRP and HCP, the EHRP securely shares patient information from the HCP’s EMR database, respecting patient-defined limits. Because patients may not wish to disclose all their information, they decide in advance which information to share publicly and inform their doctor. The doctor separately encrypts non-shareable and shareable information with different keys, and then HCP’s server manager encrypts it again with the server’s secret key so that no one can access the patient’s information without the server administrator’s permission. When the EHRP requests information sharing with the HCP, the HCP generates a sharing mechanism after mutual authentication. The EHRP then requests the desired attributes from the HCP with this sharing key. The HCP server administrator decrypts the requested attributes using its secret key. The HCP server administrator re-encrypts all attributes in ciphertext with the sharing key and sends the result to the EHRP. The EHRP decrypts this, obtaining only the intersection of the requested and permitted attributes. Figure 1 shows the system architecture of the DtMin protocol.
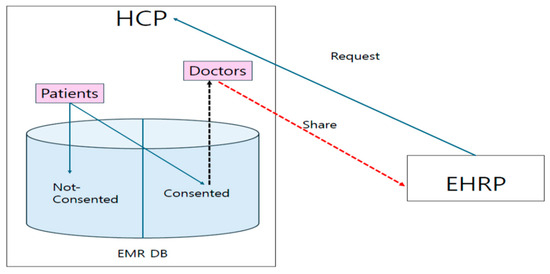
Figure 1.
System architecture of DtMin.
3.2. Notation
- : pseudorandom function for symmetric encryption
- : reverse function of , in other words, decryption function of
- : asymmetric encryption/decryption function
- : encryption functions f and E for message M with the encryption key K
- : re-encryption with a sharing key for all attributes
- : doctor’s private/public key
- : ID and password of EHRP
- sk: HCP server’s secret key for symmetric encryption
- : random number generated for every session j
- : sharing key between HCP and EHRP
- : consented/non-consented attributes
- : authentication polynomial
- : share-requested attributes of user i
- At_t: t-th attributes
- : requested sharing attributes in the consented/non-consented attributes of user i
- : non-requested sharing attributes in the consented/non-consented attributes of user i
3.3. Security Building Blocks
Definition 1.
Discrete logarithm problem (DLP): It is a hard problem to find the integer x ) such that (mod p), given a prime p, a generator α of , and an element [23].
Definition 2.
Decisional Diffie–Hellman (DDH): Let G be a group of prime order q and g a generator of G. The DDH problem is to distinguish between triplets of the form (, , ) and (, , ), where a, b, c are random elements of {1,…,q − 1}.
The following experiment with a polynomial time adversary A: Flip a coin δ to get 0 or 1, if δ = 1, set c = ab, else choose c at random. The DDH problem is said to be hard if for any polynomial time adversary A, |Pr(A(G, , , ) = δ) − 1/2| is negligible [23].
Definition 3.
Pseudorandom Function (PRF): We say that ‘F: is (t,q,e)—secure pseudorandom function’ if every oracle algorithm A making at most q oracle queries and with running time at most t has advantage AdvA < e. The advantage is defined as AdvA = |Pr[AFk = 1] − Pr[AR = 1], where R represents a random function selected uniformly from he set of all maps from X to Y, in which the probabilities are taken over the choice of k and R [24].
Definition 4.
Pseudorandom Generator (PRG): We say that ‘Gr: KGr → S is a (t,e)—secure pseudorandom generator’ if every algorithm A with running time at most t has advantage AdvA < e. The advantage is defined as AdvA = |Pr[A(Gr(UKGr)) = 1] − Pr[A(US) = 1]|. Where UKGr, US are random variables distributed uniformly on KGr and S [24].
Definition 5.
Public-key (Asymmetric) Cryptography: It is a cryptographic system that employs a pair of keys: a public key () and a private key (). The public key is widely distributed, while the private key is kept secret [25].
- -
- Encryption: A message (M) is encrypted using the public key () to produce a ciphertext (C). This process can be mathematically represented as C = E(, M), where (E) denotes the encryption function.
- -
- Decryption: The ciphertext (C) is decrypted using the private key () to retrieve the original message (M). Mathematically, this is represented as M = D(, C), where (D) denotes the decryption function [9].
- -
- In this study, we use RSA as a public key cryptography:
- such that Where, e is a public key, and d is a private key.
- Encryption: Decryption: (M is a message).
- RSA’s security is based on the intractability of the Integer Factorization Problem (IFP) for sufficiently large integers. RSA operates within the multiplicative group of integers modulo n, denoted as , [23].
In the following, we present two security games that are variants of the CPA (chosen plaintext attack) model.
Definition 6.
Security Game ICR-DB (Indistinguishability of Ciphertexts from Random Bit Strings in DB).
This game is a modification of CPA (chosen plaintext attack) model.
Setup. The challenger C creates a ciphertext set B of mmessages and gives this to the adversary A. A chooses a polynomial numberof subsets from B. This collection of subsets is called B*; C runs algorithm SysPrm, KGenRg and encrypts each subset running algorithm EnCDB. Finally, C sends A all ciphertexts with their associated subsets.
Queries. A may request the encryption EnCDB(B*) of any B
Challenge. A chooses a B0 and its subsets such that none of the algorithm EnCDB given in the step Queries distinguishes B0 from B1 = rand(B0). The challenger C chooses a random bit b and gives EnCDB(Bb) to A. A again asks for encrypted messages with the restriction that A may not ask for the algorithm that distinguishes B0 from B1. The total number of ciphertexts verifications is in s.
Response. A outputs . If , A is successful. In security game ICR-DB, adversary’s advantage is defined as .
Here, refers to the attacker’s advantage in an environment where the system parameter is given as s. Let b ∈ {0, 1} denote the challenge bit selected by the challenger in the ICR-DB game, and let ∈ {0, 1} represent the adversary A’s guess of the bit b. This guess is made after A interacts with the oracle and obtains the information needed to attempt to distinguish between the encryption of a real message and a random bit string. The adversary’s advantage in the security game is defined as: AdvA = |Pr[] − 1/2|. For a more detailed explanation of the proof of the CPA model, please refer to [26,27,28].
This equation calculates the difference between the probability of the adversary successfully guessing the bit b and the probability of guessing correctly by chance (1/2). A significant advantage implies that the adversary can distinguish the real message from the random string with a non-negligible probability, undermining the security of the ICR-DB game. Through the following steps, it demonstrates that this advantage is negligible under the assumed cryptographic hardness assumptions.
Definition 7.
Security Game ICR-IS (Indistinguishability of Ciphertexts from Random Bit Strings in Information Sharing)
Setup. The challenger C creates a ciphertext set B of m messages and gives this to the adversary A. A chooses a polynomial number of subsets from B. This collection of subsets is called B*; C runs algorithm SysPrm, KGenRg, EnCDB, MuAuth, ShKGen, ShRq and ReEnC re-encrypts each subset running algorithm ReEnC. Finally, C sends A all re-encryptions with their associated subsets.
Queries. A may request the re-encryption ReEnC (B*) of any B
Challenge. A chooses a B0 and its subsets such that none of the algorithm ReEnC given in the step Queries distinguishes B0 from B1 = rand(B0). The challenger C chooses a random bit b and gives ReEnC (Bb) to A. A again asks for re-encrypted messages with the restriction that A may not ask for the algorithm that distinguishes B0 from B1. The total number of ciphertexts verifications is in s.
Response. A outputs . If A is successful. In security game ICR-IS, adversary’s advantage is defined as .
3.4. Algorithms
- SysPrm () → λ: The parameter-generating algorithm SysPrm takes a security parameter s as input and generates a set of system parameters λ.
- KGenRg () → Pr, Pu, sk, ID, PW: Given λ as input, the key generation and registration algorithm KGenRg generates a public key Pu and a private key Pr for each participant and a secret key for HCP, and ID/PW for each participant.
- EnCDB (Pr, Pu, sk, ) → 1st and 2nd Enc.: The inputs for DB Encryption algorithm EnCDB are {Pr, Pu, sk, The outputs are 1st and 2nd Encryptions. The first one is that and are encrypted with different keys. The second one on top of that is encrypted with the HCP’s secret key.
- MuAuth (vrfinf, ) → Verified or Fail: Given verifiable information vrfinf and random number , the mutual authentication algorithm MuAuth outputs Verified or Fail.
- ShKGen (Verified, , Pr, ) → ShKey: If the verification is successful, the sharing key generation algorithm ShKGen produces the sharing key ShKey between HCP and EHRP.
- ShRq ( This sharing request algorithm ShRq takes as an input and HCP decrypts the requested attributes.
- ReEnC (ShKey The re-encryption algorithm ReEnC encrypts for all attributes again with the sharing key.
- Dec (ShKey, Pu): The decryption algorithm Dec decrypts all attributes with the shaing key ShKey first, then secondly decrypts with the public key. The result is the requested attributes in plaintext and others in ciphertext.
3.5. Attribute Types of Database
The attributes of patients’ DB are largely classified into two types: non-sensitive and sensitive. Sensitive attributes are encrypted, and non-sensitive ones are in plaintext.
Sensitive attributes are classified again into shareable (consented) and unshareable (non-consented) attributes. Shareable attributes are encrypted with the Dr’s private key, and unshareable attributes are encrypted with the Dr’s public key. It means that shareable attributes can be decrypted with the Dr’s public key by anyone, and unshareable attributes can be decrypted with the Dr’s private key only by the doctor.
When a sharing request is received from the EHRP, the encrypted data are re-encrypted with a sharing key. Figure 2 illustrates all of the attribute types, categorized by sensitivity(Sensitive/Non-Sensitive), consent for sharing(Consented(C)/Non-Consented(NC)), and whether they are requested(Requested(R)/Non-Requested(NR)). This simplified representation of Figure 2 is for clarity; the actual order of attributes in the database may vary.

Figure 2.
Attribute types of DB.
3.6. Authentication Polynomial (AP)
A polynomial for authentication is generated. .
Here, ID and PW are the identity and password of EHRP; n is the total number of the registered EHRPs.
4. Construction of DtMin Encryption Protocol
We construct a cryptographic protocol, DtMin (data minimization), according to the eight algorithms in Section 3.4.
4.1. System Setting and Registration
4.1.1. SysPrm ()
- 1.
- Input: s (security parameter)
- 2.
- Output: λ (system parameters’ set) = {}
The basis of the data minimization encryption protocol system is established. is a pseudorandom function and is a pseudorandom generator. is a randomly generated number through for every session j. G is a cyclic group G of finite field with order q, which is a large prime, and g is a generator of a cyclic group G. i is each participant of group G. E and D are encryption and decryption functions. is an authentication polynomial, is a database, and a is an attribute of .
4.1.2. KGenRg ()
- 3.
- Input:
- 4.
- Output: Pr (private key), Pu (public key), sk (symmetric key), ID, PW
Key materials and other secret values for registration are generated. Pr and Pu are the private key and public key for the public key cryptosystem. sk is a secret key for the symmetric key cryptosystem. ID and PW are identity and password for log-in. Each EHRP’s ID and PW are generated. Doctor’s private/public keys, HCP’s private/public keys, and HCP’s secret key are generated.
4.1.3. EnCDB (Pr, Pu, sk, )
- 5.
- Input: Pr, Pu, sk,
- 6.
- Output: 1st and 2nd Enc.
- ○
- 1st Encryption:
- ○
- 2nd Encryption:
Using this algorithm, the database of HCP is encrypted in two stages. The first one is that and are encrypted with different keys: doctor’s private key and doctor’s public key . The second one on top of that is encrypted with the HCP’s secret key. Figure 3 shows that patient information is encrypted and stored in the HCP’s EMR DB.

Figure 3.
Stored encrypted in HCP’s DB.
4.2. Log-In by Authentication
MuAuth (vrfinf, )
- 7.
- Input: vrfinf (verifiable information),
- 8.
- Output: Verified or Fail
- The process for mutual authentication is as follows:
- ○
- EHRP sends its verifiable information:
- -
- , where is a randomly generated number for this session. The encryption key is HCP’s public key and the message is encrypted by RSA.
- ○
- HCP deceypts: Here, the decryption key is HCP’s private key and the above ciphertext is decrypted by RSA.
- ○
- HCP authenticates the subject of the received information using polynomials
- -
- If 1 (Successful)
- -
- (first, compute and then compute:
4.3. Key Sharing
ShKGen (1, , Pr, )
- 9.
- Input: 1, , ,
- 10.
- Output: ShKey =
- ○
- HCP generates the sharing key with EHRP:
- ○
- HCP sends EHRP the encryption of the shaing key:
- ○
- EHRP decrypts the received ciphertext with the random number : . The resulte is HCP’s public key and the sharing key .
- ○
- EHRP decrypts again for the result() with HCP’s public key: ) = .
- ○
- Then, EHRP checks whether the result is the same as , which was sent from EHRP to HCP for authentication.
4.4. Information Shring
4.4.1. ShRq (
- 11.
- Input:
- 12.
- Output: All attributes for 2nd Decryption
- ○
- EHRP requests the attributes of user i they wish to share from HCP:
- -
- . The attributes EHRP wants to share are encrypted with their sharing key and sent to HCP.
- ○
- HCP decrypts:
- -
- 1st Decryption with Sharing Key: . With the decryption key , the received ciphertext is decrypted. The result is the attributes which EHRP wants to share
- -
- 2nd Decryption (only for the requested attributes): . The only requested ciphertexts are decrypted with the HCP’s symmetric secret key sk
In results, HCP decrypts the only requested attributes with its secret key as Figure 4.

Figure 4.
Encryption status of DB after EHRP sharing request.
4.4.2. ReEnC (ShKey
- 13.
- Input: ShKey, all attributes
- 14.
- Output: ReE
- ○
- HCP re-encrypts the encrypted attributes of user i with sharing key:
- ○
- HCP sends EHRP the re-encrypted attributes including .
Figure 5 shows the re-encrypted DB state with their sharing key.

Figure 5.
Re-encrypted attributes, which are requested from EHRP, with shared key.
4.4.3. Dec (ShKey, Pu):
- 15.
- Input: , ReE
- 16.
- Output: Final 2nd Decryption
- ○
- 1st Decryption: EHRP decrypts the received encryption with their sharing key:
- Here, is the RSA encryption, which encrypts the with the Dr’s private key . is encrypted twice. The first is encrypted with RSA using the doctor’s private key as the encryption key for , and the second is encrypted with PRF f using sk_s as the encryption key, for the first encryption. is the RSA encrypted with the doctor’s public key for . is also encrypted twice. For , it is first RSA encrypted with and, second, encrypted with PRF f using sk_s. The result is the same as in Section 4.4.1.
- ○
- 2nd Decryption: EHRP decrypts the first decryption with doctor’s public key
Figure 6 shows the 2nd decyption state with public key .

Figure 6.
Final decryption of request results by EHRP.
Finally, EHRP obtains and } as in Figure 7. These are the intersection of the attributes that the HCP allowed to be shared and the attributes that the EHRP requested to be shared.

Figure 7.
Final acquisition of request result {At_C_R_i} by EHRP.
4.5. The Whole Flow of Protocol Data
Table 1 shows the whole flow of protocol data.

Table 1.
The whole flow of protocol data.
5. Security Analysis
5.1. Proof of Security
This protocol’s data encryption employs different encryption keys at each stage, resulting in two main encryption states. The first state involves differentially encrypting attributes based on patient consent; attributes with consent are encrypted differently than those without, and all are stored in the database. The second state involves differentially encrypting attributes based on whether a request has been received; requested attributes are encrypted differently than unrequested attributes, and all of the attributes in ciphertext and the requested attributes in plaintext are transmitted to the EHRP. In the first state, the final encryption uses the HCP’s secret key, sks. In the second state, the final encryption uses a sharing key, , based on the decisional Diffie–Hellman (DDH) assumption. These differing encryption methods require different security analyses, which are presented in the following theorems. Only sensitive data are considered in these security analyses; non-sensitive data (stored in plaintext) are excluded.
Theorem 1.
If f is PRF and the key material is chosen as described above, then data minimization protocol DtMin is secure according to the security game ICR-DB.
Proof of Theorem 1.
We prove it with contraposition. A is assumed as an attack algorithm (adversary) that wins the security game ICR-DB with advantage ε. We construct an algorithm β, which can solve the problem that f is PRF or random bit strings. □
β can access an oracle for the unknown function f. β substitutes the values of f through the queries to the oracle . β uses an algorithm A as a subroutine and simulates algorithm A using Security Game ICR-DB.
Setup. The attack algorithm β creates a set M of m messages and gives this to the adversary A. A chooses a polynomial number of subsets from M. This collection of subsets is called M*. A sends them to β again. β invokes algorithm SysPrm, KGenRg and EnCDB, which encrypts each subset. Finally, β sends A all ciphertexts with their associated subsets. Each ciphertext can belong to one of the following two forms: .
Queries. A may request β the encryption EnCDB (M*) of any M. If A queries for the message m of At_t, β outputs the form of encryption . Regardless of whether the message attribute is At_C or , the key that is ultimately used for encryption is sk_s.
Challenge. After making some queries, A chooses a M0 and its subsets such that none of the algorithm EnCDB given in the step queries distinguishes M0 from M1 = rand(M0). β chooses a random bit b and gives EnCDB (Mb) to A. A again asks for encrypted messages with the restriction that A may not ask for the algorithm that distinguishes M0 from M1. The total number of ciphertext verifications is in s.
Response. Finally, A outputs . If , β outputs 0 (PRF instance). In security game ICR-DB, adversary’s advantage is defined as . Otherwise, it outputs 1 (not a PRF instance), because the encryption will be random for EnCDB if and only if the challenge is not a PRF instance, β solves the problem about PRF or random bit strings with the same advantage as A as follows.
Theorem 2.
Data minimization protocol DtMin is secure according to the ICR-IS game, if DDH is hard.
Proof of Theorem 2.
It is also proved by contraposition. The process is similar to Theorem 1. Here, we will mainly explain the differences. A is assumed as an attack algorithm (adversary) that wins the security game ICR-IS with advantage ε. We construct an algorithm , which can solve the DDH problem with a non-negligible advantage □.
uses an algorithm A as a subroutine and simulates algorithm A using security game ICR-IS.
Setup. The process of generating M* is the same as Theorem 1. A sends them to again. invokes algorithm SysPrm, KGenRg, EnCDB, MuAuth, ShKGen, ShRq and ReEnC re-encrypts each subset running algorithm ReEnC. Finally, sends A all re-encryptions with their associated subsets. Each ciphertext can belong to one of the following four forms:
Here, we assume that , , are a Diffie–Hellman triplet. The challenge is to determine δ = τ γ. guesses a value for the message that A will choose in the game ICR-IS, by selecting uniformly at random in {} (). simulates the algorithm ReEnC on {} to a random value {}. For M = {}, selects random number and outputs:
Here, is made by EHRP, is HCP’s value.
Queries. A may request the re-encryption ReEnC (M*) of any M. If A queries for the message m of At_t, outputs the form of encryption . Regardless of whether the message attribute is or , or , or the key that is ultimately used for encryption is .
Challenge. After making some queries, A chooses M0 and its subsets, such that none of the algorithm ReEnC given in the step queries distinguishes M0 from M1 = rand(M0). The following process is the same as Theorem 1.
Response. Finally, A outputs . If , β outputs 0 (DDH triplet). Otherwise, it outputs 1 (not a DDH triplet), because the encryption will be random for ReEnC if and only if the challenge is not a DDH triplet, β breaks the DDH hard problem with the same advantage as A, as follows.
The next process is the same as Theorem 1.
5.2. Discussion About Security
Section 5.2.1, Section 5.2.2, Section 5.2.3, Section 5.2.4, Section 5.2.5 and Section 5.2.6 discuss the security aspects of this protocol, focusing on the following:
5.2.1. Confidentiality
This section analyzes the protocol’s effectiveness in protecting data confidentiality. Data confidentiality mandates restricted access to authorized individuals only [29]. This is fundamental to data protection, fostering trust and integrity in systems handling sensitive information. Our proposed protocol encrypts all sensitive attributes using multi-type encryption and session-specific random keys (). This ensures that even repeated encryptions of the same data produce unique ciphertexts, effectively preventing attackers from inferring the original data. The sharing key, incorporating , thus functions as a one-time session key.
5.2.2. Mutual Authentication
Secure communication requires mutual authentication, a process where both parties verify each other’s identities before exchanging data. This prevents unauthorized access and establishes trust [30]. In our system, the HCP uses its private key to encrypt the data requested by the EHRP. The HCP then uses the EHRP’s session key () to encrypt a subsequent message. The EHRP’s successful decryption of this message using the same , and subsequent verification of the HCP’s public key validates the mutual authentication process.
5.2.3. Intractability of Replay or Reflection
Replay attacks, in which an attacker intercepts and reuses legitimate data (e.g., log-in credentials) to gain unauthorized access, pose a significant security threat [31]. Our system mitigates this risk by using session-specific random numbers (). Because is unique to each session, any attempt to replay previously intercepted data will fail due to the mismatch in session keys. This protection extends to various forms of session hijacking and similar attacks.
5.2.4. Self-Regulation for Privacy
Individuals have the right to control how their personal information is collected, used, and shared, a principle known as informational self-determination [18]. Our system reflects this by employing a tiered approach to data handling. Attributes are classified into six categories based on sensitivity and consent status: non-sensitive (unencrypted), sensitive and consented (requested or not), and sensitive and non-consented (requested or not). All attributes except non-sensitive data (plaintext) are stored in encrypted form. The important thing is that ′Sensitive and Consented Data′ are encrypted with the doctor’s private key, while ′Sensitive and Non-Consented Data′ are encrypted with the doctor’s public key. Consequently, ’Sensitive and Consented Data’ can be decrypted by anyone with the doctor’s public key, but ’Sensitive and Non-Consented Data’ cannot be decrypted by anyone other than the doctor who has the doctor’s private key. It means that only consented data by the patient (user) can be collected, used, and shared.
5.2.5. Limited Access Control
To summarize again, our DB has six total types of attributes:}, All data, except for plaintext data, are encrypted using different keys. As a measure for self-regulation, non-consented data and consented data were encrypted with separate keys. For this reason, even server administrators cannot decrypt non-consented data . After a share request from EHRP, HCP decrypts the only requested attributes so that EHRP can obtain } and .
5.2.6. Data Minimization
Limiting data collection, storage, and processing—a core principle of data minimization—significantly enhances security. As we mentioned before, our system means that only data consented by the patient (user) can be collected, used, and shared. This approach reduces the impact of data breaches by minimizing the amount of sensitive information accessible to attackers. Ransomware attacks are similarly less effective with reduced data volume. The risk of successful phishing and social engineering attacks is also lessened, as is the potential for data exfiltration. Finally, data minimization facilitates regulatory compliance with data protection regulations, reducing the risk of legal actions and fines from data mishandling.
6. Efficiency Analysis
6.1. Time Complexity
After analyzing the time complexity for each algorithm construction, we finally represent the time complexity for the entire protocol using Big-O notation.
- SysPrm: O(m + n)
- The generation of system parameters is a constant-time operation, denoted as O(1). In this, the classification of attributes in the database takes time proportional to the number of attributes (m), resulting in a time complexity of O(m). Generating the authentication polynomial takes time proportional to the number of registered EHRPs (n), leading to a time complexity of O(n). Therefore, the final time complexity for this algorithm becomes O(1 + m + n). We can simplify this to O(m + n). The dominant factors in determining the runtime are the number of attributes (m) and the number of registered EHRPs (n).
- KGenRg: O(1)
- This step involves generating various cryptographic keys (for EHRP, doctor, HCP). The number of keys is fixed and does not scale with the input data size. Therefore, the time taken is considered constant, represented by O(1).
- EnCDB: O(m)
- This stage encrypts the database. The encryption process iterates through each of the ‘m’ attributes in the database, performing encryption operations on each one. The time taken is directly proportional to the number of attributes; hence, the time complexity is O(m).
- MuAuth and ShKGen: O(1)
- Mutual authentication involves verifying identities and generating a sharing key. These operations are assumed to have a constant-time complexity, independent of the database size or the number of attributes. Thus, the time complexity is O(1).
- ShRq: O(1)
- The EHRP requests specific attributes. This involves a single encryption operation using the sharing key. Since it is a fixed number of operations, regardless of the database size, the time complexity is O(1).
- ReEnC: O(r)
- This step re-encrypts the selected attributes. The number of attributes being re-encrypted is represented by ’r’. The time taken is directly proportional to ’r’, giving us a time complexity of O(r).
- Dec: O(r)
- The final decryption step decrypts the re-encrypted attributes. Similar to re-encryption, the time complexity is directly proportional to the number of attributes being decrypted (‘r’), resulting in O(r).
The overall time complexity is O(m + n + r). So, the runtime of the entire process grows linearly with the number of attributes (m), the number of registered EHRPs (n), and the number of attributes involved in re-encryption and decryption (r).
6.2. Performance Analysis
Our protocol uses different encryption keys based on attribute sensitivity levels, ensuring that only data the user has consented to share are released upon request. As shown in Section 6.1, the protocol’s performance depends on several factors: the number of attributes (m), the number of registered EHRPs (n), and the number of attributes requested by EHRP (r) and the network conditions. Since the entire protocol is significantly influenced by network conditions and various event scenarios, we focused solely on evaluating the key components of the proposed protocol.
6.2.1. Implementation and Experimental Setup
The measurement method involves timing the execution of the algorithm set up according to the scenario in Section 3.1.2. When there are two or more EHRPs, concurrent control processing of the database will take place; therefore, in this study, n is set to 1. Although the size and number of attributes will have a substantial impact on performance, as the number of attributes permitted and requested for sharing varies based on the situation, we set 20 attributes arbitrarily for each of the six types of attributes shown in Figure 2. Their sizes are set differently to 1 KB, 10 KB, 100 KB, 1 MB, and 10 MB, and the performance is measured accordingly. The experimental setups are detailed in Table 2.

Table 2.
Experimental setup.
The details of the cryptographic parameters and libraries are provided in Table 3.

Table 3.
Cryptographic parameters and libraries.
6.2.2. Performance Measurement of Key Algorithms
(1) MuAuth (vrfinf, ): By varying the total number of polynomial terms, that is, the total number of patients, performance is measured. Table 4 shows the results. Figure 8 is a graphical representation of Table 4.

Table 4.
Running time of MuAuth algorithm.
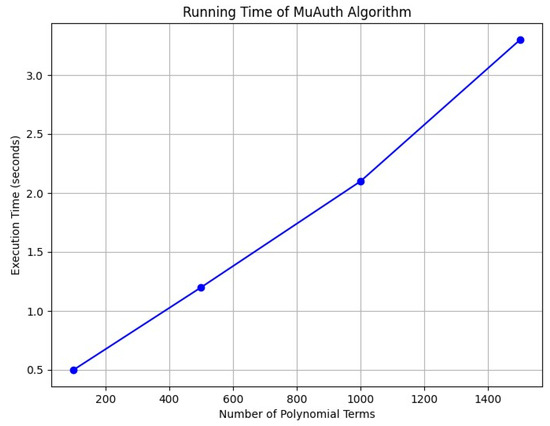
Figure 8.
Running time of MuAuth algorithm.
When the number of polynomial terms exceeds 1000, it is observed that the authentication time exceeds 2 s, indicating a significant delay. Therefore, if the number of patients exceeds 1000, we need to devise a strategy to create additional polynomials. In other words, the number of polynomial terms should be limited to less than 1000, and the number of polynomials should be determined based on the number of patients.
(2) ShKGen (1, , Pr, ): The execution time of ShKGen, shared key generation algorithm, is measured as 0.539055 s.
(3) ShRq (: Table 5 and Figure 9 show the results of measuring the execution time of the algorithm by setting the size of attributes differently.

Table 5.
Running time of ShRq algorithm.
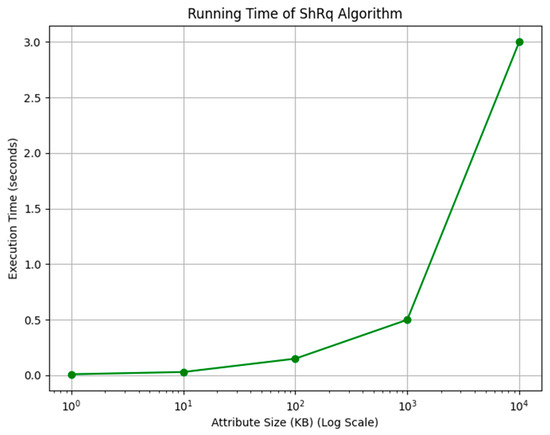
Figure 9.
Running time of ShRq algorithm.
When the size of an attribute exceeds 10 MB, the execution time surpasses 3 s, and at 100 MB, it takes a significant 44 s. Therefore, if the amount of data exceeds 10 MB, we should adopt a method of splitting the data and distributing them across different attributes. In other words, the size of an attribute should be limited to less than 10 MB, and large volumes of data should be divided and stored separately.
(4) ReEnC (ShKey and Dec (ShKey, Pu): The execution time of these two algorithms was measured by setting the size of attributes to 1 KB, 10 KB, 100 KB, 1 MB, and 10 MB based on the result analysis of Table 5. The results for ReEnC and Dec are shown in Table 6 and Figure 10.

Table 6.
Running time of ShRq and Dec algorithm.
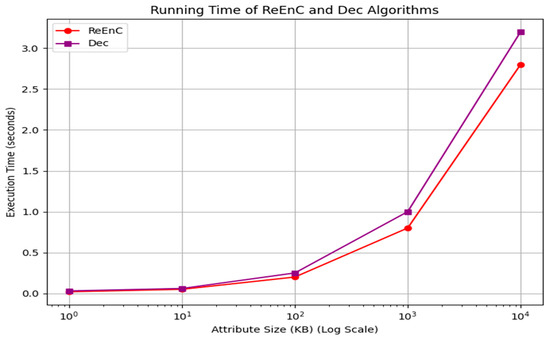
Figure 10.
Running time of ShRq and Dec algorithm.
6.3. Data Minimization as a Key Efficiency Metric
This study’s efficiency analysis goes beyond simply computational time complexity and performance; a crucial aspect lies in its efficiency from a data minimization perspective.
The core idea of data minimization is to collect, process, and store only the minimum necessary personal data for specified, explicit, and legitimate purposes. This principle is central to data privacy and security regulations like GDPR. This study achieves data minimization efficiency in several ways:
- Intersection of Consented and Requested Attributes: The protocol cleverly ensures that only the intersection of the patient’s consented attributes and the EHRP’s requested attributes are shared, in other words, selective sharing. This minimizes data exposure, enhances security, and directly implements data minimization. Only absolutely necessary information is exchanged, reducing storage, processing, and transmission overheads.
- Reduced Storage and Processing Requirements: By only sharing the minimal necessary data, the system reduces storage requirements for both the HCP and the EHRP. Having fewer data also means less processing overhead for tasks like queries, analysis, and reporting.
- Improved Data Quality: Data minimization often leads to improved data quality as well. Focusing on essential data simplifies data management, reducing the chance of errors or inconsistencies. This indirectly improves efficiency by avoiding the need for extensive data cleaning or correction.
- Enhanced Compliance: Data minimization aligns with data protection regulations and reduces the risk of non-compliance. This indirect efficiency is vital; it avoids potential penalties, legal issues, and reputational damage that could significantly hamper the system’s operational efficiency.
- Streamlined Security Measures: Protecting fewer data inherently simplifies security measures. Fewer data points to secure make monitoring, auditing, and responding to potential security threats more manageable and efficient.
7. Analysis Comparing DtMin to Existing Systems
This section provides a detailed comparison of the DtMin protocol with existing health information systems, highlighting its strengths and weaknesses in terms of security, privacy, and efficiency. To conduct a comprehensive review of existing systems for medical information sharing, we considered a variety of sources, including academic papers, regulatory frameworks, and industry reports [5,10,11,12,13,18,19,20,21,22,26,32,33]. The existing health information systems include electronic health records (EHRs), health information exchange (HIE), and Clinical Trial Management Systems. Below is a detailed overview of the materials used for this comparison.
7.1. Comparative Analysis Framework
To ensure a comprehensive comparison, we will evaluate DtMin against several key criteria:
- Security and Privacy: How well does the system protect sensitive medical data?
- Data Minimization: Does the system adhere to the principle of collecting, processing, and storing only the minimum necessary data?
- Efficiency: What are the computational and operational efficiencies of the system?
- Scalability: How does the system perform with increasing data volumes and user numbers?
- Interoperability: Can the system integrate with other healthcare systems?
- User Control: To what extent does the system empower users with control over their data?
7.2. Comparison with Existing Systems
7.2.1. Security and Privacy
- DtMin:
- -
- Utilizes a multi-layered encryption approach, leveraging attribute-based encryption (ABE) and a hybrid encryption technique that incorporates decisional Diffie–Hellman (DDH) assumption, pseudorandom generators (PRGs), and pseudorandom functions (PRFs).
- -
- Formal security analysis under ICR-DB and ICR-IS security games, proving security based on the hardness of established cryptographic assumptions.
- -
- Provides granular control over data access based on attribute sensitivity levels and user consent, minimizing data exposure.
- Existing Systems:
- -
- EHRs, HIEs, and Clinical Trial Management Systems often rely on simpler access control mechanisms, which might not offer the same level of granular control or formal security analysis.
- -
- Some systems use blockchain technology for security, but they might not prioritize data minimization or provide the same level of user control over data sharing.
7.2.2. Data Minimization
- DtMin:
- -
- Explicitly designed to minimize the amount of data shared, ensuring only the necessary information is released based on user consent and data sensitivity.
- -
- Implements selective sharing, where only the intersection of consented and requested attributes is shared, reducing data exposure and enhancing security.
- Existing Systems:
- -
- Many systems do not prioritize data minimization, leading to the collection and storage of more data than necessary, increasing the risk of data breaches and non-compliance with privacy regulations.
7.2.3. Efficiency
- DtMin:
- -
- Performance analysis demonstrates efficiency across various data volumes and patient numbers, with a time complexity of O(m + n + r), where m is the number of attributes, n is the number of registered EHRPs, and r is the number of attributes being shared.
- -
- Reduces storage and processing requirements by minimizing data sharing, leading to improved data quality and streamlined security measures.
- Existing Systems:
- -
- Systems like EHRs and HIEs might face scalability issues due to the volume of data they handle, potentially leading to higher computational costs and slower performance.
7.2.4. Scalability
- DtMin:
- -
- While the multi-layered encryption and ABE mechanisms might present scalability challenges, the strategies like distributed computing, efficient data sharding, and optimized database design can mitigate these issues.
- Existing Systems:
- -
- Scalability is often a concern, especially with large datasets and numerous users. Systems like blockchain-based HIEs might struggle with scalability due to the inherent limitations of blockchain technology.
7.2.5. Interoperability
- DtMin:
- -
- Designed with interoperability in mind, DtMin can integrate with existing healthcare systems through standardized data formats and protocols.
- Existing Systems:
- -
- Interoperability remains a significant challenge due to the lack of standardization in data formats and communication protocols across different healthcare systems.
7.2.6. User Control
- DtMin:
- -
- Empowers users with control over their data through a tiered approach to data handling, allowing patients to decide which information to share publicly.
- Existing Systems:
- -
- User control is often limited, with systems primarily managed by healthcare providers or third parties, reducing patient autonomy over their data.
Table 7 shows the summary for the comparison with DtMin Protocol and other existing systems.

Table 7.
Comparison of security and privacy technologies.
7.3. Strengths and Weaknesses
DtMin represents a significant advancement in implementing data minimization principles within medical information sharing systems.
7.3.1. Strenghths
DtMin offers significantly more granular control over data access than existing systems, enhancing security and privacy. It uses a multi-type encryption approach, leveraging attribute-based encryption (ABE) and hybrid encryption.
DtMin is explicitly designed to minimize the amount of data shared, ensuring only necessary information is released based on user consent and data sensitivity. It implements selective sharing, where only the intersection of consented and requested attributes is shared, reducing data exposure and enhancing security. DtMin improves security, efficiency, and regulatory compliance through its rigorous data minimization approach, aligning with data protection regulations like GDPR.
The protocol’s security is formally analyzed and proven to be secure under the ICR-DB and ICR-IS security games, contingent upon the hardness of established cryptographic assumptions.
Performance analysis demonstrates efficiency across various data volumes and patient numbers, with a time complexity of O(m + n + r), where m is the number of attributes, n is the number of registered EHRPs, and r is the number of attributes being shared.
7.3.2. Weaknesses
While strategies can mitigate scalability issues, the current design might face challenges with extremely large datasets and user numbers.
Additionally, although designed for interoperability, DtMin may require additional adaptation layers to integrate with existing healthcare systems.
In conclusion, its strengths in granular control, data minimization, and formal security analysis make it a promising solution for enhancing privacy and efficiency in healthcare data sharing. However, its potential scalability and interoperability issues require careful consideration and optimization for real-world implementation
Future work should focus on addressing these weaknesses while leveraging DtMin’s strengths to further improve security, performance, and scalability in healthcare information sharing environments.
8. Future Enhancements: Integration with Advanced Cryptographic Techniques for Data Sizes of over 100,000 in Real Environments
8.1. Integration with Advanced Cryptographic Techniques
The essence of DtMin is not to develop efficient encryption algorithms but to propose a methodological protocol that implements the principle of data minimization. This study is not about proposing specific public key encryption functions or symmetric key encryption functions. In fact, it does not matter which public key or symmetric key encryption function is used in the DtMin protocol. It merely employed RSA 2048-bit, which is commonly used by public institutions in South Korea, and AES in the purpose of practical performance measurement.
If more secure and efficient advanced encryption functions than these commercial versions are utilized, the performance of the proposed protocol could be further enhanced. Furthermore, it is clear that the healthcare information environment will become increasingly complex and diverse in the future, so we explore strategic responses accordingly.
8.1.1. Applying Lattice-Based ABE
Lattice-based encryption is a leading candidate for post-quantum cryptography and can be more efficient than traditional attribute-based encryption (ABE). The following factors will further improve the performance of DtMin:
- RLWE (Ring Learning With Errors)-based KP-ABE: RLWE-based KP-ABE is more efficient than LWE-based variants. It has a complexity that depends only on the depth of the policy circuit, rather than its size [34].
- GPU acceleration: According to implementation research [34], encryption operations can be accelerated using Graphics Processing Units (GPUs). This demonstrates that public key and ciphertext evaluation tasks can be performed within a reasonably short time.
- Use of Small Secret Keys: Lattice-based ABE has the advantage that the secret key is much smaller than those in similar constructions, which are proportional to the size of the policy circuit [34].
8.1.2. Adoption of Lightweight ABE Variants
- Utilization of Optimized Data Structures: As proposed in the ABE Squared benchmarking framework, ABE implementations can be optimized using efficient data structures [35].
- ABE Library for Android Devices: As mentioned in [36], the ABE library for the Android operating system, AndrABEn, can be implemented with satisfactory performance using ABE on Android smartphones and similar devices.
- Minimization of Input Data Size: Medical data, such as ECG (electrocardiogram) signals, can be significantly reduced in size using DTW (Dynamic Time Warping) compression, which can help lower encryption costs [36].
8.2. Analysis of Integration Strategies with Existing Medical Information Systems
First, we examine the current standards for medical information and explore how to integrate DtMin into the system based on the standards.
8.2.1. Analysis of the Current Medical Information Standards Environment
The most widely used standards for electronic health record (EHR) systems today are as follows:
- -
- HL7 FHIR (Fast Healthcare Interoperability Resources): A framework for standardized representation and exchange of healthcare data. FHIR focuses on increasing the interoperability of healthcare information by facilitating data sharing between various healthcare systems [37].
- -
- HL7 v2.x: A set of standards for exchanging health information electronically. It is widely used in healthcare for messaging between different systems, such as hospitals, laboratories, and pharmacies. HL7 v2.x supports various types of messages, including patient demographics, orders, results, and billing information [38].
- -
- DICOM (Digital Imaging and Communications in Medicine): A standard for handling, storing, printing, and transmitting medical imaging information. It includes a file format definition and a network communications protocol, ensuring interoperability among different medical imaging devices and systems [39].
- -
- IHE (Integrating the Healthcare Enterprise): A framework that integrates various healthcare systems to ensure interoperability. It provides a set of standards and guidelines to facilitate the sharing of patient information across different healthcare systems [40].
8.2.2. Adaptation Strategy to Integrate DtMin into Current Healthcare Information Systems
1. API-based Integration Layer: Build a RESTful API (A RESTful API is an interface based on the principles of REST (Representational State Transfer) that allows for communication between systems using standard HTTP methods and enables accessing and manipulating resources with stateless interactions, typically using JSON or XML for data exchange [41]) layer on top of the DtMin protocol to ensure compatibility with standard healthcare data exchange protocols like FHIR. The components and processes are as follows:
- FHIR Resource Mapping: Map DtMin’s attribute-based classification to FHIR resources and extensions.
- API Gateway: Mediate requests between DtMin and EHR systems while handling authentication and authorization.
- Transformation Service: Handle data transformation between the DtMin protocol and standard healthcare data formats.
2. Middleware Integration Pattern: Establish a middleware layer between existing EHR systems and the DtMin protocol to manage data transformation and protocol adaptation.
3. Plugin Architecture: Design DtMin as a standalone module to be implemented as a plugin or extension for existing EHR systems.
8.2.3. Case-by-Case Integration Patterns
DtMin integration patterns tailored to various medical environments are as follows:
1. Large Healthcare Organization Integration Pattern: Typically have complex IT infrastructure and in-house development capabilities:
- ESB (Enterprise Service Bus) Integration: Utilize existing ESB to integrate DtMin services into the organization’s service mesh.
- API Management Platform: Manage DtMin APIs via existing API gateways.
- Phased Implementation: Gradually expand, starting from specific departments or data types.
2. Small to Medium Healthcare Organization Integration Pattern: Require a simplified approach due to limited IT resources:
- Cloud-Based Integration: Minimize integration complexity with DtMin services offered as a SaaS model.
- Standard Connectors: Provide pre-built connectors for common EHR systems.
- Simplified Configuration: Interfaces configurable with minimal technical knowledge
3. Health Information Exchange (HIE) Integration Pattern: Facilitates data exchange among various healthcare institutions:
- IHE Profile Compliance: Extend IHE XDS (Cross-Enterprise Document Sharing) profiles to integrate DtMin capabilities.
- Common Data Model: Map HIE’s common data model with DtMin’s attribute classification.
- Interoperability Gateway: Integrate DtMin capabilities into HIE gateways to apply data minimization principles to all exchanged data.
8.3. Integrated Strategy Analysis for Large-Scale Environments Processing More than 100,000 Big Data
8.3.1. Data Partitioning and Parallel Processing
Medical big data are continually increasing, and distributed data processing techniques are essential for efficient handling. By partitioning large EHR data into small chunks and processing them in parallel across multiple nodes, the efficiency of encryption and decryption operations can be significantly improved. Large data exceeding 10 MB should especially be divided and processed across multiple attributes.
8.3.2. Improved Authentication Polynomial
When the number of patients exceeds 1000, the authentication time increases to over 2 s, necessitating a scalable authentication mechanism for large patient groups. Developing a strategy to generate and manage multiple authentication polynomials hierarchically can efficiently handle a large user base.
8.3.3. Multi-Level Architecture
Implementing a multi-level architecture using fog (fog computing is a distributed computing paradigm that extends cloud computing to the edge of the network, bringing computation, storage, and networking closer to the end-users [42]) computing can distribute computational loads and reduce latency. This approach helps minimize delays that may occur during the multi-layer encryption process of the DtMin protocol.
8.3.4. Incremental Updates
Introducing an incremental approach, which updates only changed records instead of re-encrypting the entire database in environments with over 100,000 EHRs, can greatly enhance the performance of large-scale systems.
9. Conclusions
The DtMin protocol is a novel method in implementing data minimization principles for medical information sharing. By classifying attributes and employing multi-type encryption, DtMin ensures that only necessary and consented data are shared, addressing critical privacy and security concerns in healthcare data exchange.
The security analysis proves DtMin’s robustness against potential attacks, while performance evaluations demonstrate its efficiency. The protocol’s design aligns with key regulatory requirements like GDPR, offering a practical solution for healthcare providers to enhance data protection and comply with privacy regulations.
DtMin’s approach of selective sharing based on patient consent and EHRP requests represents a paradigm shift from traditional “all-or-nothing” data sharing models in healthcare. This not only improves privacy and security but also enhances operational efficiency by reducing data processing and storage requirements.
Future work should focus on addressing potential scalability challenges in extremely large datasets and exploring integration strategies with existing healthcare information systems. Additionally, investigating the application of advanced cryptographic techniques like lattice-based ABE could further enhance DtMin’s performance and security in complex, large-scale healthcare environments.
In conclusion, DtMin offers a promising solution for balancing the need for data sharing in healthcare with stringent privacy and security requirements, paving the way for more secure and efficient medical information sharing systems.
Funding
This study was supported by research funds from Honam University, 2025.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Kim, K.; Kim, S.; Lee, I. A Study on Diffie Hellman-Private Set Intersection Protocol for Sharing of Medical Data. In Proceedings of the Korea Multimedia Society Spring Conference, Seoul, Republic of Korea, 16–18 May 2024; p. 27. [Google Scholar]
- Zhou, X.; Liu, J.; Wu, Q.; Zhang, Z. Privacy Preservation for Outsourced Medical Data with Flexible Access Control. IEEE Access 2018, 6, 14827–14841. [Google Scholar] [CrossRef]
- Miyaji, A.; Nakasho, K.; Nishida, S. Privacy-Preserving Integration of Medical Data. Trans. Process. Syst. 2017, 41, 37. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-A. Secure Information Sharing System for Online Patient Networks. J. Secur. Commun. Netw. 2019, 2019, 7541269. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, Y.; Si, X.; Yao, Z.; Zhao, L. MDS2-C3PF: A Medical Data Sharing Scheme with Cloud-Chain Cooperation and Policy Fusion in IoT. Symmetry 2022, 14, 2479. [Google Scholar] [CrossRef]
- Elvas, L.B.; Ferreira, J.C.; Dias, M.S.; Rosário, L.B. Health Data Sharing towards Knowledge Creation. Systems 2023, 11, 435. [Google Scholar] [CrossRef]
- Hu, M.; Ren, Y.; Chen, C. Privacy-Preserving Medical Data-Sharing System with Symmetric Encryption Based on Blockchain. Symmetry 2023, 15, 1010. [Google Scholar] [CrossRef]
- Walid, R.; Joshi, K.P.; Choi, S.G. Comparison of attribute-based encryption schemes in securing healthcare systems. Sci. Rep. 2024, 14, 7147. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Son, S.; Kwon, D.; Kim, M.; Park, Y.; Park, Y. Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System. Mathematics 2024, 12, 1717. [Google Scholar] [CrossRef]
- Mao, X.; Li, C.; Zhang, Y.; Zhang, G.; Xing, C. Efficient and Secure Management of Medical Data Sharing Based on Blockchain Technology. Appl. Sci. 2024, 14, 6816. [Google Scholar] [CrossRef]
- Official EU GDPR. Article 5—Principles Relating to Processing of Personal Data. Available online: https://gdpr.eu/ (accessed on 12 February 2025).
- U.S. Department of Health & Human Services HIPAA Page. Available online: https://www.hhs.gov/programs/hipaa/index.html (accessed on 12 February 2025).
- Park, H. Security and privacy model of electronic medical record systems. Int. J. Healthc. Technol. Manag. 2022, 19, 303–323. [Google Scholar]
- Xu, Z.; Zheng, E.; Han, H.; Dong, X.; Dang, X.; Wang, Z. A secure healthcare data sharing scheme based on two-dimensional chaotic mapping and blockchain. Sci. Rep. 2024, 14, 23470. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Zheng, J.; Wu, W.; Gao, D.; Gu, X. Research on healthcare data sharing in the context of digital platforms considering the risks of data breaches. Front. Public Health 2024, 12, 1438579. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Park, J.; Woo, H.; Yun, H.; Lee, M.; Hong, D. Safe Utilization and Sharing of Genomic Data: Amendment to the Health and Medical Data Utilization Guidelines of South Korea. Cancer Res. Treat. 2024, 7, 1027–1039. [Google Scholar]
- Barker, W.; Chang, W.; Everson, J.; Gabriel, M.; Patel, V.; Richwine, C.; Strawley, C. The Evolution of Health Information Technology for Enhanced Patient-Centric Care in the United States: Data-Driven Descriptive Study. J. Med. Internet Res. 2024, 26, e59791. [Google Scholar] [PubMed]
- Personal Information Protection Act, Amendment in 2022; Legislature of Republic of Korea: Seoul, Republic of Korea, 2022.
- Mukta, R.; Paik, H.; Lu, Q.; Kanhere, S. A survey of data minimisation techniques in blockchain-based healthcare. Comput. Netw. 2022, 205, 108766. [Google Scholar] [CrossRef]
- Conte, R.; Sansone, F.; Tonacci, A.; Pala, A. Privacy-by-Design and Minimization within a Small Electronic Health Record: The Health360 Case Study. Appl. Sci. 2022, 12, 8441. [Google Scholar] [CrossRef]
- Bargh, M.; Meijer, R.; Braak, S.; Latenko, A.; Vink, M.; Sunil, C. Embedding Personal Data Minimization Technologies in Organizations: Needs, Vision and Artifacts. In Proceedings of the 14th International Conference on Theory and Practice of Electronic Governance, Athens, Greece, 6–8 October 2021. [Google Scholar]
- Senarath, A.; Arachchilage, N. A Data Minimization Model for Embedding Privacy into Software Systems. Comput. Secur. 2019, 87, 101605. [Google Scholar]
- Menezes, A.J.; Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography, 1st ed.; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar]
- Schneier, B. Applied Cryptography, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Goldreich, O. Foundations of Cryptography, Volume 1, Basic Tools; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Bellare, M.; Rogaway, P. The Security of Triple Encryption and a Framework for Code-Based Game-Playing Proofs. In Proceedings of the 2005 International Conference on the Theory and Application of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005. [Google Scholar]
- Stallings, W.; Brown, L. Computer Security: Principles and Practice, 4th ed.; Pearson: London, UK, 2018. [Google Scholar]
- Stallings, W. Cryptography and Network Security: Principles and Practice, 7th ed.; Pearson: London, UK, 2016. [Google Scholar]
- Stallings, W. Network Security Essentials: Applications and Standards, 6th ed.; Pearson: London, UK, 2016. [Google Scholar]
- IBM Security Website. Cost of a Data Breach Report 2022. Available online: https://www.ibm.com/security/data-breach (accessed on 12 February 2025).
- Accenture’s Healthcare Industry Insights Page. Health/Digital-Health-Technology-Vision-2022. Available online: https://www.accenture.com/us-en/insights (accessed on 12 February 2025).
- Dai, W.; Doroz, Y.; Polyakov, Y.; Rohloff, K.; Sajjadpour, H.; Savas, E.; Sunar, B. Implementation and Evaluation of a Lattice-Based Key-Policy ABE Scheme. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1169–1184. [Google Scholar]
- Piedra1, A.; Venema, M.; Alpár, G. ABE Squared: Accurately Benchmarking Efficiency of Attribute-Based Encryption. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022, 2022, 192–239. [Google Scholar]
- Krinah, A.; Challal, Y.; Omar, M.; Nouali, O. Using ABE for Medical Data Protection in Fog Computing. In Proceedings of the 21st International Conference on Enterprise Information Systems, Heraklion, Greece, 3–5 May 2019; pp. 155–161. [Google Scholar]
- HL7 FHIR Documentation. Exchanging Resources. Available online: https://www.hl7.org/fhir/documentation.html (accessed on 12 February 2025).
- HL7 Official Website. HL7 v2.x. Available online: https://www.hl7.org/ (accessed on 12 February 2025).
- DICOM Official Website. Standard, DICOM Part 7: Message Exchange. Available online: https://www.dicomstandard.org/ (accessed on 12 February 2025).
- IHE Official Website. IHE Technical Framework Documents for Public Comment. Available online: https://www.ihe.net/ (accessed on 12 February 2025).
- Kim, S.; Chung, M.; Lee, T.; Won, J. Implementation of Medical Data-Based Big Data Analytics Service. In Proceedings of the Korean Institute of Information Scientists and Engineers 2015, Busan, Republic of Korea, 20–22 September 2015; pp. 157–159. [Google Scholar]
- What-Is-Distributed-Data-Processing. Available online: https://www.purestorage.com/kr/knowledge (accessed on 12 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).