Abstract
The budgeted influence maximization (BIM) problem aims to select an optimal subset of nodes, each with a unique selection cost, to maximize the influence in a network under a fixed budget. Most existing methods address static networks with constant node infection states, but usually dismiss the dynamic interaction of competing emotions within the network. This work extends the BIM problem to account for dynamic emotional competitions. Specifically, we first formally formulate the BIM problem in a competitive environment where emotions dynamically influence and transform each other over time. Then, we introduce a local structure-sensitive heuristic function designed to evaluate a node’s influence potential in a competitive environment. Furthermore, we propose a heuristic mutation particle swarm optimization (HMPSO) algorithm to identify a set of high-impact nodes, thereby maximizing desirable information spread. Experimental results conducted on two real-world networks demonstrate that the HMPSO algorithm outperforms existing advanced methods for the BIM problem.
1. Introduction
The influence maximization (IM) problem [1] aims to identify a subset of the most influential nodes within a network (graph) to maximize the spread of the information intended for promotion. The IM is a fundamental optimization problem in network science with broad applications across various networks. In social networks, this problem focuses on strategically selecting key nodes to enable a broader information diffusion of behaviors or emotions [2]. In sensor networks, this problem pertains to coverage optimization [3], which deploys critical monitoring nodes to maximize network coverage while minimizing consumption. With the rapid development of wireless sensor networks, the integration of 5G networks and big data connects people to the Internet, which has become a crucial platform for emotional expression and the formation of public opinion [4]. The perception and utilization of these data contribute to the support of key decision making, such as viral marketing [5], product recommendation [6], and cybersecurity [7].
Expanding upon the IM problem, the budgeted influence maximization (BIM) problem [8] considers the unique selection cost associated with each node, and imposes a given budget as a constraint. In addition, node states in networks are highly dynamic, often shifting over time. However, most IM and BIM studies focus on optimizing the diffusion mechanism under a single state, typically overlooking the interplay of competing states. Bharathi et al. [9] extend the IM problem to consider competitive environments, where conflicts may occur between node states. Yet, this competitive scenario, particularly with varying costs associated with distinct deploying strategies, remains underexplored.
Social media can be a non-intrusive sensor that captures a person’s behaviors through smart devices such as smartphones. Data collected from social sensors [10] typically cover various themes and convey different emotions. Currently, most existing work addressing the IM problem relies on static propagation models, such as the linear threshold model [11] or independent cascade model [12], to simulate influence spread. These models have two primary limitations. First, they overlook that more influential nodes are often associated with higher costs. Second, they do not consider the dynamic nature of the emotional competition. The “rich-get-richer” phenomenon [13] suggests that emotional leaders, located at the source of information diffusion, possess significant influence over subsequent emotional states. Engaging these emotional leaders typically incurs higher costs. Nevertheless, the traditional BIM problem, which assigns node costs randomly using a uniform distribution, fails to capture these cost differentials. For instance, as shown in Figure 1, although node A reaches the most subsequent nodes (4 positive nodes {A,b,c,d}, its high cost directly depletes the budget, thereby limiting its influence potential.
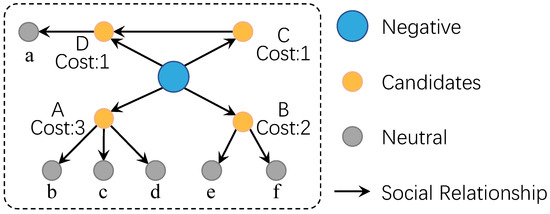
Figure 1.
A motivating example of the BIMEC problem. The purpose is to choose a set of positive seeds from candidates {A, B, C, D} within the budget, which could maximize the number of positive nodes. A node’s selection cost is simply assumed as its out-degree so that the costs of A, B, C, and D are 3, 2, 1, and 1, respectively. If the given budget is 3, there are three ways to deploy seeds: {A}, {B, C}, and {B, D}. And the {B, C} obtains the highest influence range {B, C, D, a, e, f} in the BIMEC problem.
In the context of prevailing propagation models [14], the emotional state is considered to be fixed once affected, even though emotions would be expected to fluctuate and change over time due to unfolding events [15]. For example, in Figure 1, the seed set {B, D} leads to 5 positive nodes {B, D, a, e, f}. If node D could be influenced only once and has been activated by a negative node, further positive influence from node C would be blocked, resulting in only 4 positive nodes {B, C, e, f}. However, allowing information from node C to counteract the negative influence could raise the positive nodes to 6, reflecting the real-world scenario where competing influences are constantly at play.
This paper focuses on the BIM problem with emotional competition (BIMEC), extending IM to incorporate both selection costs and a dynamic emotional propagation model. Although the greedy algorithm is commonly used for IM problems, its shortsightedness on local optimums may lead to suboptimal global solutions within budget constraints. Therefore, we propose a heuristic mutation particle swarm optimization (HMPSO) algorithm to solve the BIMEC problem. A dynamic emotional propagation model simulates the competitive environment, where activated nodes continually update their emotions over time based on the influence of emotional leaders. Then, a local structure-sensitive heuristic fitness function is proposed to estimate the selection advantage of a node, which takes comprehensive consideration of the ability to spread influence across various emotional states. Finally, a mutation particle swarm optimization algorithm is employed to search for optimal solutions. Experiments on synthetic and real-world networks validate the effectiveness of the proposed method.
The contributions of this paper can be summarized as:
- We define the budgeted influence maximization problem with emotional competition mathematically based on a dynamic emotional propagation model over time.
- We design a local structure-sensitive heuristic function to evaluate the potential benefits of individuals, and select ones that promote the spread of positive emotions and inhibit negative emotions.
- We propose a mutation particle swarm optimization method to solve the problem. Experimental results on two real-world networks demonstrate the superiority of our proposed model compared to baseline methods.
The paper is organized as follows. Section 2 introduces related work on influence maximization and emotional propagation. Section 3 defines the emotional propagation model and the budgeted influence maximization problem. Section 4 describes a vanilla greedy algorithm and our proposed heuristic mutation particle swarm optimization algorithm for the BIM problem. Section 5 presents the experimental environments and results. Section 6 discusses the theoretical and practical implications of the paper. Section 7 concludes the main findings and future work.
2. Related Work
Domingos and Richardson [16] formulate influence maximization as an optimization problem. An emotional propagation model in traditional information diffusion provides foundational conditions to portray competitive environments. This section reviews previous work on influence maximization and emotional propagation models and summarizes them in Table 1.

Table 1.
Summary of related work.
2.1. Influence Maximization
Kempe et al. [1] mathematically defined the IM problem, proving it to be NP-hard and proposing an approximation with a guarantee of the optimal solution. Chen et al. [30] reduced the problem size by two presolving methods, assembling nodes with similar structures to realize graph simplification. Building on the IM problem, scholars have conducted research on various behavior patterns [31]. Bharathi et al. [9] formulated the competitive influence maximization problem and proved that a greedy algorithm could approximate solutions effectively. Building upon a time-delayed independent cascade model [17], Li et al. [18] introduced dominated competitive influence maximization, aiming to maximize differences between opposing emotions. Cao et al. [19] examined the influence based on topic preferences of an interaction model in competitive settings, while Liang and Duan [20] proposed a three-party framework to analyze large-scale group competitive behavior. He et al. [21] proposed a competitive influence maximization strategy under an unknown competitor scenario. In addition, Nguyen and Zheng [8] proposed the BIM problem, where each node is assigned a selection cost. Shi et al. [22] further considered the varying costs associated with competitive behaviors, such as the lower costs for retweets versus original content creation. Banerjee et al. [23] examined network community structures to identify nodes with similar influence reach, aiming to minimize seed selection costs. Lozano-Osorio et al. [14] proposed a novel heuristic algorithm and verified its effectiveness.
In summary, existing methods mainly focus on discovering factors that affect the information process and optimizing algorithm performance. However, few studies took into account the impact of newly generated information through competitive interactions on historic nodes in real-life diffusion processes. In this paper, we study the budgeted influence maximization problem by considering the potential transformation between opposing emotions.
2.2. Emotional Propagation
The linear threshold model [11] and the independent cascade model [12] are the most commonly used propagation models in the IM problem. Subsequent models have largely built upon them, refining and incorporating additional factors that may impact the information diffusion process. Saito et al. [32] achieved asynchronous activation of nodes at non-equal intervals in the information diffusion process with a delay parameter. Zhang et al. [33] proposed an influence probability calculation method to take into account the decay of influence as the cascade depth grows over time. In addition, some research considers the change in emotions during propagation [34], which can be divided into the discrete model and the continuous model. The Voter model [24] is the simplest discrete model, which regards emotions as different discrete categories. Individuals will follow one of their neighbors to obtain positive, negative, or some other emotions. Wang et al. [25] expanded the diversity of emotions by categorizing them into fine-grained classes. Different from the discrete emotional propagation model, Deffuant et al. [26] used continuous values from 0 to 1 to represent emotions. When the difference between emotional values is less than the trust threshold, emotional propagation will occur and update the corresponding emotional values. Xiong et al. [2] proposed an emotional independent cascade model that constantly updated emotions within a time window. Du et al. [27] identified an individual’s emotional role to further explore the influence of different nodes in the emotional propagation process. Mohammadi et al. [28] proposed a fuzzy-based method to simulate the influence propagation for different edges. Yin et al. [29] proposed a dynamic propagation method that couples macro-information diffusion with micro-emotional influences, revealing the individual emotional evolution trends.
In summary, though discrete emotional propagation models incorporate more fine-grained emotions to broaden the spectrum of emotional expression, continuous emotional propagation models are more proficient in representing the potential transformation process between different emotional states. However, in most studies, nodes are afforded only a single opportunity to determine their state. This approach inadequately captures the potential emotional fluctuations that may arise in competitive environments.
3. Problem Definition
Given a directed network where U is the node set and V is the relationship edges, a set of initially positive (and negative) nodes (), and a budget K, the goal of the BIM problem is to find a subset of nodes S (referred to as the seed set) with at most K total selection cost (referred to as the budget), such that the final number of positive nodes is maximized. The diffusion process will be simulated by an emotional propagation model M, and we adopt a dynamic emotional propagation model based on an independent cascade (DepIC) [30] to describe a competitive environment. The main symbols are shown in the Table 2.

Table 2.
Definition of symbols.
3.1. Emotional Propagation Model
The DepIC model is a continuous propagation model in which information diffuses from a set of initially activated nodes. The DepIC model consists of three key factors. (1) Attractiveness—representing a node’s susceptibility to being influenced by others. A node will be activated when others impact it successfully. (2) Time decay effect—denoting the decline in a node’s influence over time, reflecting how topic popularity in a network wanes as time passes. (3) Exciting mechanism—complementing the time decay effect, it assumes that previously disseminated information continues to impact future diffusion.
Attractiveness. A node that sends messages that motivate others to engage possesses significant influence, while a node that frequently forwards messages is more susceptible to influence [35]. The attractiveness from node to node , denoted by , depends on node ’s influence and ’s susceptibility. The influence probability from node to node is defined based on attractiveness as follows:
where and represent the numbers of messages posted and received by node , respectively. is the total degree of node , and a larger indicates a higher propagation probability.
Time decay effect. Emotions usually evolve as events unfold. To capture the dynamic process, the DepIC model adopts the Rayleigh distribution to describe the “rise and fall” propagation pattern, which is modeled by the temporal relaxation function :
where t is the current time, is the activation time of node , and is a decay parameter. A higher accelerates the decline in topic popularity, thus shortening the diffusion process.
Exciting mechanism. The “rich-get-richer” effect implies that emotional leaders would continually exert influence over time. The exciting mechanism records each activation path to update emotional values dynamically. Unlike the traditional independent cascade model, where nodes have a single chance to affect others when activated, the exciting mechanism allows a node to influence others repeatedly if it generates different emotional states. The emotional value updated iteratively over time is:
where is the influence strength of emotion e, is the emotional value of node at time t, and is the set of upstream nodes that have activated node with emotion e by time t.
3.2. Budgeted Influence Maximization
In a network , is a set of N nodes, and is an adjacency matrix where 1 indicates a link between nodes and 0 otherwise. Let denote the selection cost of node , and denote the total selection cost of node set I. The matrix denotes the emotions of nodes over time, where indicates positive, neutral, and negative emotions of node at time t, respectively. Initially activated nodes include the positive node set and the negative node set . Let be the emotional value of node at time t. The mapping from to is as follows:
The goal of the BIMEC problem is to select a seed set whose total selection cost is less than the given budget K, thereby maximizing the difference between the final numbers of positive nodes and negative nodes . Since the initial state is given and supposed to be unchanged, we omit and in the conditions, and abbreviate the final numbers of positive and negative nodes as and , respectively. Formally, the objective of the BIMEC problem is:
where is the final number of negative nodes in the absence of intervention, and is the change in the number of negative nodes with intervention. Additionally, we define the function to facilitate the calculation of relative influence values [36].
Theorem 1.
The budgeted influence maximization problem with emotional competition is NP-hard.
Proof.
Considering the special case where the time decay effect is deactivated, i.e., , and each node has only one upstream activated neighbor, i.e., , the nodes’ emotional values remain static and are no longer influenced dynamically by others over time. This simplification reduces the dynamic emotional propagation model to the independent cascade model. Besides, if the selection cost for each node , the budget constraint transforms into . Consequently, the BIMEC problem degenerates to the influence maximization (IM) problem, which has been proven to be NP-hard [1]. Therefore, the BIMEC problem is also NP-hard. □
Theorem 2.
The budgeted influence maximization problem with emotional competition is monotone and sub-modular. Specifically, if , then the following holds. (1) Monotonicity: ; (2) Submodularity: .
Proof.
Bharathi et al. [9] and Nguyen et al. [8] respectively prove that the competitive influence maximization problem and the BIM problem are monotone and sub-modular. The proof concerning monotonicity and submodularity of the BIMEC problem could be derived analogously to the proof in [8,9]. □
Theorem 3.
Under budget constraints, a greedy algorithm may not achieve the optimal approximate solution.
Proof.
Figure 1 presents an example of the greedy algorithm that traps in the local optimum. Given the budget , the candidate seed {A,B,D} and their corresponding cost {3, 2, 1.1}, the incremental influence per unit cost for three candidates are . The greedy algorithm selects node D, leading to 2 incremental influences. In contrast, node A, the global optimum, results in 4 incremental influences. □
4. Methodology
Theorem 1 indicates that the BIMEC problem is NP-hard and is not easier than the BIM problem. Furthermore, Theorem 3 indicates that the BIMEC problem cannot be solved effectively by the greedy algorithm, necessitating the exploration of alternative approaches. In this section, we first introduce a vanilla greedy algorithm as a benchmark, and then propose a heuristic mutation particle swarm optimization algorithm to efficiently and effectively solve the BIMEC problem.
4.1. Vanilla Greedy Algorithm
The vanilla greedy algorithm adds the node with the highest “value” to the seed set at every step until the specific requirements are met. An intuitive definition of a node’s value is its incremental influence per unit cost, i.e., , where is the increase in influence gained by selecting node as a seed. As shown in Algorithm 1, the greedy algorithm includes three key steps: (1) We sample a sub-graph set by Monte Carlo simulations to account for variability in influence spread. (2) We evaluate each node by aggregating its influence in each sub-graph . Specifically, each node is temporarily added to the initially activated positive set to assess its potential incremental influence, or “value”. Formally,
where represents the cardinality of the set, and denotes the shortest distance from node to any node in the set I. A shorter distance to a specific emotional group implies that the node is more susceptible to being influenced by that emotion. (3) The node with the highest average values across all sub-graphs will be added to the seed set S. The selection process continues iteratively until the total selection cost reaches or exceeds a given budget constraint K.
| Algorithm 1 The vanilla greedy algorithm |
| Input: G: The social graph. : The initial positive and negative node set. : The size of sub-graph set . K: The budget. Output: S: The seed set.
|
4.2. Heuristic Mutation Particle Swarm Optimization
Theorem 3 suggests that the greedy algorithm cannot achieve a theoretically optimal solution to the BIMEC problem. The vanilla greedy algorithm, on behalf of the family of greedy algorithms, will be used as a baseline in experiments in Section 5. In contrast, the particle swarm optimization (PSO) algorithm [37] allows for a broader exploration of the solution space through random placement of particles, avoiding premature convergence to local optima. This multi-particle approach, inspired by the foraging behavior of bird flocks, leverages collective intelligence to navigate complex, nonlinear optimization problems. Each particle seeks to reach a more favorable position with higher benefit each time, balancing its exploratory moves with information from others in the swarm. The PSO algorithm requires only a few parameter adjustments, making it easier to implement than other optimization algorithms like genetic algorithms [38]. Additionally, the information sharing among particles makes it naturally suitable for parallel computing and generally converges faster. Therefore, with its ease of implementation and low computational cost, the PSO algorithm can effectively balance performance and efficiency in complex network optimization problems.
Formally, we define , and as the n-dimensional position vector, and the velocity vector of a particle r, respectively. At time t, the PSO algorithm updates the position and velocity of each particle by:
where and are the learning factors, and are sampled from a uniform distribution, e.g., . is the position that a particle r achieved the historic best benefit, and the is the global best position of all the swarms.
The original PSO algorithm is designed for continuous search spaces, making it challenging to apply directly to the discrete structure of graphs in the BIMEC problem. Therefore, we propose a heuristic mutation particle swarm optimization (HMPSO) algorithm, which integrates a heuristic fitness function and a discrete search strategy.
The local structure-sensitive heuristic fitness function assesses a seed node’s capacity to spread positive emotions and counteract negative ones, and prioritizes influential nodes within their local structure. Specifically, it consists of three metrics: betweenness centrality , effective coverage , and distance from the negative set for node . Formally,
, the betweenness centrality of node , quantifies the number of the shortest paths passing through node relative to all possible node pairs :
where is the number of the shortest paths from the node to .
represents the effective coverage of node . To avoid overlap in influence among highly connected emotional leaders, we calculate effective neighbors by excluding the neighbors of nodes that are already in the positive set and the current seed set S:
where includes the set of neighbors.
In the competition model, greater distances from the negative set weaken a node’s susceptibility to negative influence. Thus, is defined as the product of influence probabilities along the shortest path to :
The search strategy introduces a mutation operation to facilitate a particle’s position update. The position vector is a set of possible seeds that meets , and means a candidate seed, where n means the current number of seeds selected in the set . The velocity element determines whether a node will undergo mutation, so the size of is consistent with n of . It determines the seed where the mutation will occur by comparing the differences between and . The updating rules of every and are as follows:
Compared to Equation (9), Equation (15) includes an extra negative sign for . The inertia weight represents a particle’s ability to maintain its original status, and a negative implies that a particle attempting to reset particle’s position and resist mutation [39]. The in Equation (15) is an indicator function, which indicates the candidate seeds where mutations may occur. Formally,
These marked candidate seeds, i.e., , may be mutated into other nodes, driving the particle to seek a better solution. The rule of the mutation operation is:
where means randomly select a node that follows with the uniform distribution from the set as a seed to replace . As described in Algorithm 2, the proposed HMPSO algorithm has the following two key steps:
| Algorithm 2 The HMPSO algorithm |
| Input: N: The number of nodes. E: The adjacency matrix. : The initial positive and negative node set. K: The budget. : The number of particle numbers : The number of iterations. Output: S: The seed set.
|
- Initialization. Lines 3–10 initialize all particles. Half of them are selected based on the highest degree-to-cost ratio, and the other half are selected randomly. Lines 11–13 obtain the initial and of the particle swarm.
- Optimization. Lines 14–23 try to seek a better solution during the iteration cycle. Lines 16–17 update the position vector and velocity vector of the particle to obtain a potentially superior seed. Lines 18–22 determine and record the effectiveness of the current particle swarm.
Computational complexity: for the heuristic fitness function, its value is primarily derived from the local features of the network. The betweenness centrality is the most time-consuming part of the computation, whose worst computational complexity is based on Brandes algorithm [40]. For the search strategy, the updating of velocity and position for each particle costs . The update process, including an evaluation of fitness for the particles, will be repeated times. Thus, the computational complexity of the HMPSO algorithm is .
5. Experiments
This section introduces the datasets and the evaluation metric. Then the experimental settings of different parameters are given. To verify the effectiveness of the proposed HMPSO algorithm, we choose several baselines and analyze the performance of the fitness function. Finally, a case study is used to illustrate how the seed set works.
5.1. Datasets
We construct a Barabasi–Albert scale-free network to initially validate the basic performance of various IM algorithms using the Python package NetworkX with version 2.8.7, provided on the website https://networkx.org (accessed on 31 March 2025). Then, two public real-world datasets, Wiki and Bitcoin-OTC, are used to analyze the application effect. They are directed networks that contain three kinds of emotional labels, which meet the basic competitive diffusion conditions. Table 3 shows the statistics of datasets. The average degree represents the mean degree of all nodes in a graph, i.e., . Notice that both real-world datasets are built by previous work [41,42,43,44], and relative information is collected from social media sites.

Table 3.
Statistics of datasets.
BA Network [45] is generated by linking new nodes in sequence from initial nodes. Each new node is more likely to choose a node with higher degrees. This means a small number of hubs that have a large number of connections. Due to the lack of emotion labels, the emotional values of nodes would be assigned randomly. This dataset is utilized to evaluate the intervention effects of the algorithm on a simple network.
Wiki [41,42], provided on the website http://snap.stanford.edu/data/wiki-Elec.html (accessed on 31 March 2025), records the process of electing administrator through public voting. The voting record shows who supported which candidates and the election results for each. It is a directed network consisting of data from September, 2004 to January, 2008.
Bitcoin-OTC [43,44], provided on the website http://snap.stanford.edu/data/soc-sign-bitcoin-otc.html (accessed on 31 March 2025), is a directed network representing who-trusts-whom derived from a platform using Bitcoin transactions. The link demonstrates the reputation between nodes in increments of 1 from −10 (total distrust) to +10 (total trust). The data are from November, 2010 to January, 2016.
5.2. Evaluation Metric
Since the number of positive nodes is higher than the number of negative nodes in the real-world dataset, this paper defines the party with fewer nodes as the competition target , i.e., positive emotion, and the party with more nodes as the intervention target , i.e., negative emotion. The metrics for influence maximization effect include the relative influence R-Inf = , and the influence-time area under curve (IT-AUC). The IT-AUC considers the algorithm’s performance across different periods throughout the competitive process. It can be calculated using the following formula:
where and represent the numbers of positive and negative nodes at time t.
5.3. Experimental Settings
The programming language used in this paper is Python. We set the particle number , the number of iterations for HMPSO , and the budget . The emotional propagation process will end when the R-Inf remains unchanged for 7 consecutive time steps. The nodal costs setting follows the previous work [22]. The cost , where refers to a beta distribution, and is the out-degree of node . Furthermore, by applying the linear transformation , the value range is adjusted to fall within [1.0,3.0], which is consistent with [8]. The emotion label of a node u is calculated by Equation (20), where , , and represent performing a positive, neutral, and negative action, respectively. The initial emotional values of nodes in the positive set and the negative set are set to 1 and 0, respectively. In the BA network, other nodes’ initial emotional values are sampled from , where refers to a uniform distribution. In the real-world networks, their emotional values are determined by the emotion labels, i.e., the emotional values are set to 0.9, 0.5, and 0.1 for positive, neutral, and negative emotions, respectively. The Table 4 shows the settings of some parameters.

Table 4.
The settings of parameters.
5.4. Baselines
We select the following methods as baselines to validate the performance of our proposed HMPSO algorithm.
- Classical algorithms: Random is the simplest method. It selects seeds randomly from all nodes; Greedy has been introduced in Section 4.1, i.e., the vanilla greedy algorithm. It selects the seed that brings the highest incremental influence per unit cost within the budget. Degree is an intuitive measurement for choosing the seed. It selects several nodes with the highest degree without exceeding the given budget K as the seed set.
- DPSO [46] is a discrete particle swarm optimization algorithm. It constructs a local influence evaluation function to incorporate the PSO algorithm into the influence maximization problem. The key distinction between the DPSO algorithm and ours is that the DPSO algorithm is designed for the IM problem and does not take into account the budget or emotions.
- GRASP [14] means the greedy randomized adaptive search procedure methodology, which is a multi-start meta-heuristic algorithm. The randomly constructed initial solutions, along with an enhanced local search method, enable the algorithm to mitigate the impact of local optima. It is one of the most effective methods for the BIM problem.
5.5. Comparison Experiments
This section first conducts a simulation experiment based on the BA network to verify the performance of different methods for the BIMEC problem on a simple network. The experimental results are shown in Figure 2.
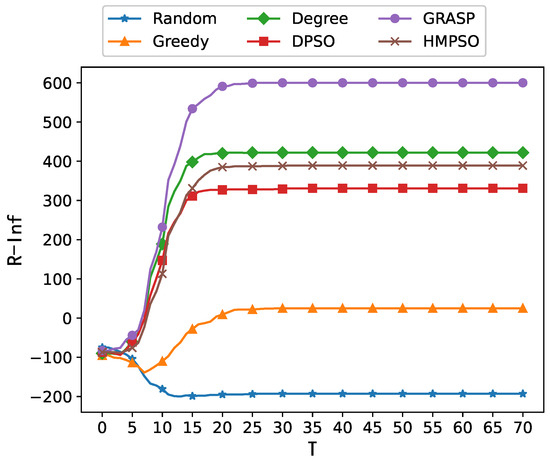
Figure 2.
The comparison of R-Inf across different methods on the BA network.
The experimental results on the BA network show that the GRASP algorithm achieved the best performance. The Degree, HMPSO, and DPSO algorithms followed in descending order of effectiveness. The greedy and random algorithms had the poorest performance, barely enhancing the spread of positive emotions. This is primarily because the BA network follows a power-law distribution, where a small number of hub nodes make static features such as nodes’ degrees more prominent. They can easily be used to identify emotional leaders through corresponding heuristics algorithms. The poor performance of the greedy algorithm indicates that the BIMEC problem is significantly different from the traditional IM problem, so solutions for the IM problem cannot be directly applied. Further experiments on two real-world complex networks will serve to analyze the specific reasons behind the differences in algorithmic performance. The complete experimental results are presented in Table 5 and Figure 3.

Table 5.
Performance comparison between our proposed model and baselines on the BA Network, Wiki, and Bitcoin-OTC datasets. The higher the metric IT-AUC, the better. The bold font marks the best.
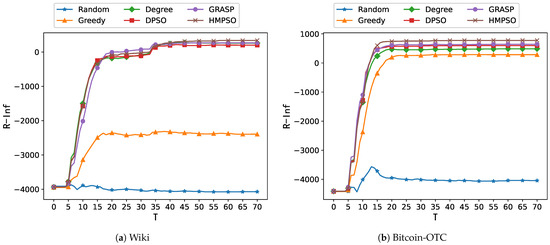
Figure 3.
The comparison of R-Inf across different methods on the real-world datasets.
The experimental results on the real-world networks show that the proposed HMPSO algorithm outperforms other methods. The HMPSO algorithm in R-Inf exceeded the runner-up, GRASP, by 26.59% and 20.50% in the Wiki and the Bitcoin-OTC, respectively. Moreover, the ratio of R-inf in the total node number improved by 0.99%, and 2.24%, respectively.
The HMPSO algorithm exhibits advanced performance due to its comprehensive consideration of different emotions: on the one hand, the algorithm filters out hub nodes in the network based on their betweenness centrality. The effective neighbors facilitate the evaluation of the potential propagation coverage. On the other hand, the algorithm identifies the nodes who can intervene in negative emotions through the distance to the negative set. Besides, the PSO algorithm is utilized to allocate the budget appropriately. Overall, the above considerations enable the HMPSO algorithm proposed in this paper to achieve better performance and provide a new perspective for exploring the emotion propagation mechanism in a network.
5.6. Analysis of the Budget
We analyzed the algorithms’ performance under different budgets in the Wiki. We follow the same budget setting used in [8], i.e., . The result is shown in Figure 4.
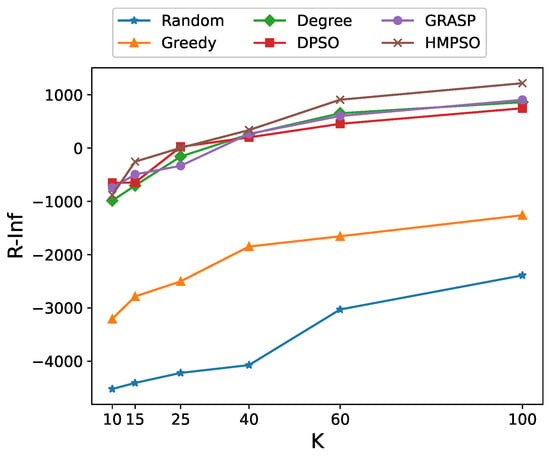
Figure 4.
The comparison of R-Inf among different budgets.
In most cases, the HMPSO algorithm achieves a better R-Inf compared to other algorithms. The results show that the growth rate of R-inf gradually slows down as the budget K increases. This is mainly because as the number of positive emotions in the network increases, the number of negative emotions that each positive emotion leader may influence will gradually decrease. In other words, the influence that positive emotion leaders can exert will weaken, which conforms to the law of diminishing marginal effect. This phenomenon indicates that the algorithm possesses a certain level of environmental adaptability. It can effectively allocate budget resources to select suitable positive emotion leaders from candidate nodes, thereby expanding relative influence in a competitive environment.
5.7. Ablation Study
The fitness function of the HMPSO algorithm is constructed by expanding positive emotions and intervening negative emotions. We designed an ablation experiment on the Wiki to verify their effects by removing the betweenness centrality and the effective neighbors number, the distance to the negative set, respectively. The two versions are recorded as w/o positive and w/o negative, respectively. The experimental results are shown in Figure 5.
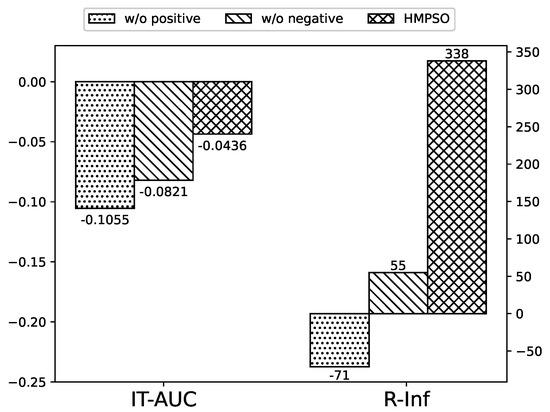
Figure 5.
The experimental results of the ablation study.
The experimental results show that the IT-AUC and R-Inf decreased by 6.19% and 3.85% in the w/o positive version, respectively. The IT-AUC and the ratio of R-inf in the total node number decreased by 5.69% and 3.93% in the w/o negative version, respectively. It indicates that both components are effective in expanding relative influence. Moreover, the performance degradation caused by the version w/o positive is more significant than that of the version w/o negative. This shows that the improvement of competitive influence mainly depends on finding influential positive emotion leaders. If some positive nodes are supplemented around the negative set, it helps to intervene in the spread of negative emotions and achieve better competitive effects.
5.8. Case Study
We visualize the emotional propagation process on the Bitcoin-OTC dataset by the network analysis software Gephi with version 0.10, provided on the website https://gephi.org (accessed on 31 March 2025). The nodes, whose out-degrees are more than 30 (approximately 3% of the total number of nodes and edges), are selected to draw Figure 6. We can see that the size of the red nodes is not uniform both in Figure 6a,b. This means that nodes with a high out-degree are not always suitable for selection as seeds. Although nodes with higher degrees usually tend to exhibit higher local influence, their associated high costs and overlapping impact with other nodes may limit their suitability as seed nodes.
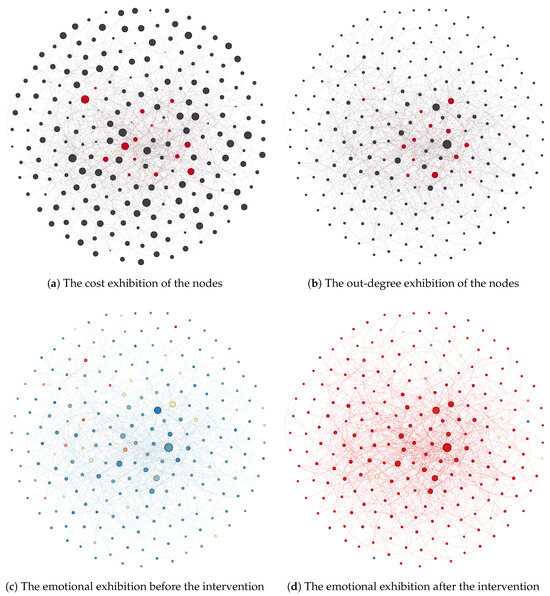
Figure 6.
The exhibition of emotional propagation process in the Bitcoin-OTC dataset. In the subgraphs (a,b), the red and gray colors indicate whether a node is selected as a seed or not. In the subgraphs (c,d), the red, yellow, and blue colors represent positive, neutral, and negative emotions, respectively. The size of nodes represents the selection cost in the subgraph (a). And a larger node in the other subgraphs means a greater out-degree.
Figure 6c shows that negative emotions (blue) will dominate after the emotional propagation process without intervention (among all nodes, negative emotions account for approximately 87%; among the visualized nodes, negative emotions account for approximately 85%). However, in Figure 6d, we can observe that after the intervention, the initially small amount of positive emotions (red) has captured the entire graph (among all nodes, positive emotions account for approximately 55%; among the visualized nodes, positive emotions account for approximately 95%). It means that emotions have reversed under the influence of selected positive nodes. Therefore, we can summarize two patterns that align with the assumptions of the BIMEC problem. (1) Emotional leaders can drive emotional change. Although only a few positive emotion leaders were added relative to the total number of nodes during the experiment, in the end, almost all key nodes were transformed into positive emotions. It shows the strong control of emotional leaders over time. (2) A seemingly high-impact node is not always the better choice. Due to the selection cost, a higher impact node may waste too much of the budget. The overlapping influence of emotional leaders who are close to each other will also indirectly weaken the intervention effect. On the other hand, sometimes low-cost nodes with low impact but the ability to block the spread of negative emotions may be a better choice.
6. Discussion
In this section, we discuss the theoretical and practical implications of this paper.
6.1. Theoretical Implication
This study contributes to extending the BIM problem to a competitive environment with emotional conflicts. Specifically, the varying costs associated with node selection and the volatility of emotions make this problem both more realistic and challenging to address. We propose a novel HMPSO algorithm to solve the problem. First, the node value fitness function, designed around the three interpretable factors, node centrality, effective coverage, and distance from the negative set, demonstrates that promoting the spread of positive emotions while inhibiting negative emotions could enhance the influence of information dissemination. Second, an improved particle swarm optimization algorithm is helpful in preventing the solution space from converging to a local optimum. However, a noteworthy limitation is that the performance of the HMPSO algorithm is sensitive to the selection of parameters, which are determined by prior experience rather than rigorous theoretical foundations in this paper. This dependence on empirical values introduces uncertainty in the optimization outcomes, making an adaptive or self-tuning mechanism a future study.
Our work discovers that seemingly influential nodes are not always the best choices through a case study. The reason is the existence of selection costs, where nodes with high influence may waste too much budget. The overlap in coverage of the influence of emotional leaders is also a reason for indirectly weakening the effect of the intervention.
6.2. Practical Implication
This paper can help in decision-making processes such as harmful information control [47] and advertising recommendations [48] on social media. The effectiveness of the proposed HMPSO algorithm was validated on real-world datasets by outperforming benchmarks in various metrics. Integrating the algorithm with sensor networks further expands its potential applications. Specifically, the nodes of interest could be users in social networks and sensors in sensor networks. Our research problem is identifying key nodes within the network to maximize a specific propagation effect, highly relevant to the internode collaboration in sensor networks. For example, the influence maximization problem studied in this paper shares conceptual similarities with the coverage optimization in sensor networks. Both problems aim to maximize coverage using limited resources by analyzing the network structure to pinpoint key nodes or deployment strategies that produce the greatest impact.
By integrating sensor-captured data in the real world, particularly the measurement of actual costs, this work can demonstrate greater practical value. In public health, it helps optimize the use of limited resources to spread awareness of diseases or vaccines to minimize intervention costs. In digital marketing, companies can identify influential individuals within a constrained advertising budget to maximize brand visibility.
7. Conclusions
In this paper, we suggested a heuristic mutation particle swarm optimization algorithm for the budgeted influence maximization problem with emotional competition and provided a formal definition of the BIMEC problem. The primary creative idea is the design of a heuristic fitness function that comprehensively considers different emotions. Then an improved particle swarm optimization algorithm is proposed to solve the problem. Experiments on real-world datasets provided performance analyses and verified the usefulness of our algorithm. Compared to baselines, the HMPSO algorithm in R-Inf achieved an improvement of 26.59% and 20.50% in Wiki and Bitcoin-OTC, respectively. In the future, accurately measuring the selection cost will be an important research direction for this problem. It is also worth further exploring an information propagation model that aligns more closely with actual competitive scenarios from real-world data.
Author Contributions
Conceptualization, Z.C. and C.C.; methodology, Z.C.; software, Z.C.; validation, T.C.; formal analysis, Z.C.; investigation, Z.C.; resources, X.L.; data curation, Z.C.; writing—original draft preparation, Z.C.; writing—review and editing, C.C., J.W. and X.L.; visualization, Z.C.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China OF FUNDER grant number 62476060.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available at http://snap.stanford.edu/data/wiki-Elec.html (Wiki, accessed on 21 January 2025) and http://snap.stanford.edu/data/soc-sign-bitcoin-otc.html (Bitcoin-OTC, accessed on 21 January 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kempe, D.; Kleinberg, J.; Tardos, E. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2003; KDD’03. pp. 137–146. [Google Scholar] [CrossRef]
- Xiong, X.; Li, Y.; Qiao, S.; Han, N.; Wu, Y.; Peng, J.; Li, B. An emotional contagion model for heterogeneous social media with multiple behaviors. Phys. Stat. Mech. Appl. 2018, 490, 185–202. [Google Scholar] [CrossRef]
- Yu, X.; Duan, Y.; Cai, Z.; Luo, W. An adaptive learning grey wolf optimizer for coverage optimization in WSNs. Expert Syst. Appl. 2024, 238, 121917. [Google Scholar] [CrossRef]
- Jusup, M.; Holme, P.; Kanazawa, K.; Takayasu, M.; Romić, I.; Wang, Z.; Geček, S.; Lipić, T.; Podobnik, B.; Wang, L.; et al. Social physics. Phys. Rep. 2022, 948, 1–148. [Google Scholar] [CrossRef]
- Tu, S.; Neumann, S. A Viral Marketing-Based Model For Opinion Dynamics in Online Social Networks. In Proceedings of the ACM Web Conference 2022, New York, NY, USA, 25–29 April 2022; WWW ’22. pp. 1570–1578. [Google Scholar] [CrossRef]
- Huang, L.; Ma, Y.; Liu, Y.; Danny Du, B.; Wang, S.; Li, D. Position-Enhanced and Time-aware Graph Convolutional Network for Sequential Recommendations. ACM Trans. Inf. Syst. 2023, 41, 1–32. [Google Scholar] [CrossRef]
- Li, Y.; Ma, S.; Zhang, Y.; Huang, R.; Kinshuk. An improved mix framework for opinion leader identification in online learning communities. Knowl.-Based Syst. 2013, 43, 43–51. [Google Scholar] [CrossRef]
- Nguyen, H.; Zheng, R. On Budgeted Influence Maximization in Social Networks. IEEE J. Sel. Areas Commun. 2013, 31, 1084–1094. [Google Scholar] [CrossRef]
- Bharathi, S.; Kempe, D.; Salek, M. Competitive Influence Maximization in Social Networks. In Proceedings of the 3rd International Conference on Internet and Network Economics, WINE’07, San Diego, CA, USA, 12–14 December 2007; Deng, X., Graham, F.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 306–311. [Google Scholar]
- Hernandez-Suarez, A.; Sanchez-Perez, G.; Toscano-Medina, K.; Martinez-Hernandez, V.; Perez-Meana, H.; Olivares-Mercado, J.; Sanchez, V. Social Sentiment Sensor in Twitter for Predicting Cyber-Attacks Using l1 Regularization. Sensors 2018, 18, 1380. [Google Scholar] [CrossRef]
- Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Goldenberg, J.; Libai, B.; Muller, E. Talk of the network: A complex systems look at the underlying process of word-of-mouth. Mark. Lett. 2001, 12, 211–223. [Google Scholar] [CrossRef]
- Shen, H.; Wang, D.; Song, C.; Barabási, A.L. Modeling and predicting popularity dynamics via reinforced Poisson processes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 17–31 July 2014; AAAI Press: Washington, DC, USA, 2014. AAAI’14. pp. 291–297. [Google Scholar]
- Lozano-Osorio, I.; Sánchez-Oro, J.; Duarte, A. An efficient and effective GRASP algorithm for the Budget Influence Maximization Problem. J. Ambient Intell. Humaniz. Comput. 2024, 15, 2023–2034. [Google Scholar] [CrossRef]
- Wu, F.; Huberman, B.A. Novelty and collective attention. Proc. Natl. Acad. Sci. USA 2007, 104, 17599–17601. [Google Scholar] [CrossRef] [PubMed]
- Domingos, P.; Richardson, M. Mining the network value of customers. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; KDD ’01. pp. 57–66. [Google Scholar] [CrossRef]
- Chen, W.; Lu, W.; Zhang, N. Time-critical influence maximization in social networks with time-delayed diffusion process. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; AAAI Press: Washington, DC, USA, 2012. AAAI’12. pp. 592–598. [Google Scholar]
- Li, H.; Pan, L.; Wu, P. Dominated competitive influence maximization with time-critical and time-delayed diffusion in social networks. J. Comput. Sci. 2018, 28, 318–327. [Google Scholar] [CrossRef]
- Cao, J.; Min, H.; Wang, H.; Ma, Z.; Liu, b. Self-Interest Influence Maximization Algorithm Based on Subject Preference in Competitive Environment. Chin. J. Comput. 2019, 42, 1495–1510. [Google Scholar]
- Liang, D.; Duan, W. Large-scale three-way group consensus decision considering individual competition behavior in social networks. Inf. Sci. 2023, 641, 119077. [Google Scholar] [CrossRef]
- He, Q.; Zhang, L.; Fang, H.; Wang, X.; Ma, L.; Yu, K.; Zhang, J. Multistage Competitive Opinion Maximization With Q-Learning-Based Method in Social Networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–11. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, C.; Chen, J.; Feng, Y.; Chen, C. Post and repost: A holistic view of budgeted influence maximization. Neurocomputing 2019, 338, 92–100. [Google Scholar] [CrossRef]
- Banerjee, S.; Jenamani, M.; Pratihar, D.K. ComBIM: A community-based solution approach for the Budgeted Influence Maximization Problem. Expert Syst. Appl. 2019, 125, 1–13. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, Z.; Jin, Y.; Cheng, S.; Yang, T. ESIS: Emotion-based spreader-ignorant-stifler model for information diffusion. Knowl. Based Syst. 2015, 81, 46–55. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Y.; Hu, J.; Li, X.; Chen, X. An emotion role mining approach based on multiview ensemble learning in social networks. Inf. Fusion 2022, 88, 100–114. [Google Scholar] [CrossRef]
- Mohammadi, S.; Nadimi-Shahraki, M.H.; Beheshti, Z.; Zamanifar, K. Fuzzy sign-aware diffusion models for influence maximization in signed social networks. Inf. Sci. 2023, 645, 119174. [Google Scholar] [CrossRef]
- Yin, F.; Tang, X.; Liang, T.; Kuang, Q.; Wang, J.; Ma, R.; Miao, F.; Wu, J. Coupled dynamics of information propagation and emotion influence: Emerging emotion clusters for public health emergency messages on the Chinese Sina Microblog. Phys. Stat. Mech. Appl. 2024, 639, 129630. [Google Scholar] [CrossRef]
- Chen, S.; Chen, W.; Dai, Y.; Yuan, J.; Zhang, H. Efficient presolving methods for the influence maximization problem. Networks 2023, 82, 229–253. [Google Scholar] [CrossRef]
- Li, Y.; Fan, J.; Wang, Y.; Tan, K.L. Influence Maximization on Social Graphs: A Survey. IEEE Trans. Knowl. Data Eng. 2018, 30, 1852–1872. [Google Scholar] [CrossRef]
- Saito, K.; Ohara, K.; Yamagishi, Y.; Kimura, M.; Motoda, H. Learning Diffusion Probability Based on Node Attributes in Social Networks. In Proceedings of the Foundations of Intelligent Systems, ISMIS, Warsaw, Poland, 28–30 June 2011; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6804, pp. 153–162. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Yang, J.; Paris, C.; Nepal, S. Learning Influence Probabilities and Modelling Influence Diffusion in Twitter. In Proceedings of the Companion of The 2019 World Wide Web Conference, WWW 2019, San Francisco, CA, USA, 13–17 May 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1087–1094. [Google Scholar] [CrossRef]
- Dong, Y.; Zhan, M.; Kou, G.; Ding, Z.; Liang, H. A survey on the fusion process in opinion dynamics. Inf. Fusion 2018, 43, 57–65. [Google Scholar] [CrossRef]
- Aral, S.; Walker, D. Identifying Influential and Susceptible Members of Social Networks. Science 2012, 337, 337–341. [Google Scholar] [CrossRef]
- Yang, D.; Liao, X.; Shen, H.; Cheng, X.; Chen, G. Relative influence maximization in competitive social networks. Sci. China Inf. Sci. 2017, 60, 108101:1–108101:3. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies 2023, 16, 1152. [Google Scholar] [CrossRef]
- Tian, D.; Zhao, X.; Shi, Z. DMPSO: Diversity-Guided Multi-Mutation Particle Swarm Optimizer. IEEE Access 2019, 7, 124008–124025. [Google Scholar] [CrossRef]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Leskovec, J.; Huttenlocher, D.P.; Kleinberg, J.M. Signed networks in social media. In Proceedings of the 28th International Conference on Human Factors in Computing Systems. Association for Computing Machinery, Atlanta, GA, USA, 10–15 April 2010; pp. 1361–1370. [Google Scholar] [CrossRef]
- Leskovec, J.; Huttenlocher, D.P.; Kleinberg, J.M. Predicting positive and negative links in online social networks. In Proceedings of the 19th International Conference on World Wide Web, WWW 2010, Raleigh, NC, USA, 26–30 April 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 641–650. [Google Scholar] [CrossRef]
- Kumar, S.; Spezzano, F.; Subrahmanian, V.S.; Faloutsos, C. Edge Weight Prediction in Weighted Signed Networks. In Proceedings of the IEEE 16th International Conference on Data Mining, ICDM, Barcelona, Spain, 12–15 December 2016; IEEE Computer Society: Los Alamitos, CA, USA, 2016; pp. 221–230. [Google Scholar] [CrossRef]
- Kumar, S.; Hooi, B.; Makhija, D.; Kumar, M.; Faloutsos, C.; Subrahmanian, V.S. REV2: Fraudulent User Prediction in Rating Platforms. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, WSDM 2018, Marina Del Rey, CA, USA, 5–9 February 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 333–341. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Yan, J.; Shen, B.; Ma, L.; Cai, Q. Influence maximization in social networks based on discrete particle swarm optimization. Inf. Sci. 2016, 367-368, 600–614. [Google Scholar] [CrossRef]
- Peng, S.; Wang, G.; Zhou, Y.; Wan, C.; Wang, C.; Yu, S.; Niu, J. An Immunization Framework for Social Networks Through Big Data Based Influence Modeling. IEEE Trans. Dependable Secur. Comput. 2019, 16, 984–995. [Google Scholar] [CrossRef]
- Sun, Y.; Cautis, B.; Maniu, S. Social Influence-Maximizing Group Recommendation. In Proceedings of the Seventeenth International AAAI Conference on Web and Social Media, ICWSM 2023, Limassol, Cyprus, 5–8 June 2023; Lin, Y., Cha, M., Quercia, D., Eds.; AAAI Press: Washington, DC, USA, 2023; pp. 820–831. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).