Improved Maneuver Detection-Based Multiple Hypothesis Bearing-Only Target Tracking Algorithm

Abstract

In ground-based bearing-only tracking of multiple maneuvering targets, there are difficulties in data association due to the reliance solely on azimuth information, making it challenging to distinguish and identify multiple targets. This problem is particularly pronounced when targets are close or overlapping, leading to disassociation or target loss. Moreover, bearing-only information struggles to accurately capture the dynamic changes in maneuvering targets, significantly affecting tracking accuracy. To address these issues, this paper proposes an Improved Maneuver Detection-Based Multiple Hypothesis Bearing-Only Target Tracking (IMD-MHRPCKF) algorithm. To begin with, the observation range is segmented into multiple sub-intervals through a distance parameterization technique, and within each sub-interval, a Cubature Kalman Filter (CKF) is applied. The Multiple Hypothesis Tracking (MHT) algorithm is then used for data association, solving the measurement ambiguity problem. To detect target maneuvers, the sliding window average of the innovation sequence is calculated. When a target maneuver is detected, the sub-filter parameters are reinitialized to ensure filter stability. In contrast, if no maneuver is detected, the filter parameters remain unchanged. Finally, simulations are used to compare this algorithm with various other algorithms. The results show that the proposed algorithm significantly improves system robustness, reduces tracking errors, and effectively tracks bearing-only multiple maneuvering targets.

1. Introduction

With the rapid advancement of modern science and technology, ground target tracking technology has increasingly become a focal point of research [1]. Ground target tracking systems are primarily categorized into active and passive tracking systems. In current land warfare where anti-radiation missiles and electronic jamming are extensively employed, active tracking systems are prone to exposing their locations and have poor anti-surveillance and anti-jamming capabilities. Conversely, passive tracking systems, which do not emit signals but rather receive signals emitted from the targets, offer advantages in survivability, detection range, and stealth. Bearing-only tracking is a significant branch of passive tracking, using only angular information to estimate target states. This tracking method is valued for its high concealment but faces complexities due to the nonlinear nature of its measurement equations and the absence of distance information, complicating the association of measurements with targets [2,3,4]. These challenges underscore the need for advanced nonlinear filtering algorithms and innovative approaches to estimate distances and improve system tracking performance, underscoring the critical importance of continued research and development in this area [5,6,7].

Pure angle tracking systems exhibit significant nonlinearity in their measurement equations, which prevents the direct application of traditional Kalman filter algorithms [8]. The Extended Kalman Filter (EKF) algorithm addresses this issue using a linearization truncation approach; however, when the equation’s nonlinearity is too strong, the filter’s performance may diverge [9]. Although the Modified Gain Extended Kalman Filter (MGEKF) improves stability and accuracy by enhancing the calculation of Kalman gain, it is still limited in handling highly nonlinear systems under certain conditions [10]. The Unscented Kalman Filter (UKF) algorithm employs Sigma points to approximate the system’s posterior probability density function, avoiding the expansion of Taylor terms and reducing linearization errors [11]. Both the Cubature Kalman Filter (CKF) algorithm and the Particle Filter (PF) algorithm approximate the posterior probability distribution of the target state through cubature points and particle sets, respectively, offering higher precision but also increasing computational complexity, which makes them less practical for real-time tracking in large-scale scenarios [12,13,14]. The Cubature Quadrature Kalman Filter (CQKF) combines the cubature criterion with the Gauss–Laguerre integration rule to enhance estimation accuracy from a numerical approximation perspective. The Gauss–Helmert Quadrature Filter (GHQF) employs the Gauss–Hermite integration rule for numerical approximation, offering higher estimation accuracy, though this method has higher computational complexity, making it unsuitable for real-time applications. K. Zhang et al. [15] integrated the maximum entropy criterion with the Unscented Gauss–Helmert Filter (UGHF) to achieve pure angle target tracking under non-Gaussian measurement noise. Wang et al. [16] combined the backward smoothing algorithm with a pure angle tracking algorithm, improving algorithm stability and accuracy. Zhang et al. [17] proposed a two-stage high-dimensional cubature information filtering algorithm within the extended information filtering framework, utilizing the equivalence between the inverse of the covariance and the information matrix to participate in the filtering recursion process, thereby reducing computational load while enhancing algorithm accuracy. M. Sun et al. [18] proposed an Adaptive Kernel Kalman Filter (AKKF) algorithm that uses kernel mean embedding to approximate the posterior probability density, significantly reducing the number of particles while enhancing tracking performance. However, these methods still struggle with computational efficiency when applied to large-scale systems.

Traditional constant velocity and constant acceleration models exhibit poor performance in maneuvering target tracking, with severe cases even leading to filter divergence [19]. To address this issue, R. Singer [20] modeled acceleration as zero-mean random noise and introduced the Singer model. Zhou Hongren proposed the CS model, which assumes that the probability density of target acceleration follows a modified Rayleigh distribution, applicable to a broader range of scenarios than the Singer model. K. Mehrotra and others proposed the Jerk model, which models the rate of change in acceleration. The Jerk model requires manually presetting the jerk variance. Zhang et al. [21] improved on the Jerk model by adaptively calculating the jerk variance using one-step-ahead position predictions, thus achieving adaptive adjustment of model parameters. However, real-world target motion models are often uncertain in mixed systems, and a single motion model cannot adequately describe the target’s motion state. In response to this, Bar-Shalom introduced the Interacting Multiple Model (IMM) algorithm, which uses a collaborative merging strategy to achieve interaction and matching between different motion models. Although the IMM algorithm has been widely used, it still has some drawbacks, such as excessive models leading to reduced tracking performance due to competition. To address this issue, Zeng et al. [22] proposed a Variable Structure-Interacting Multiple Model (VSIMM) algorithm with an adaptively tuned transition probability matrix, adjusting the state noise of the model set based on changes in the system’s innovation to achieve adaptive updates of the model set. Feng et al. [23] introduced a strong tracking particle filter and adaptive interacting multiple model algorithm based on fuzzy inference, improving the severe model probability switching jitter or over-switching issues encountered by the IMM algorithm in tracking highly maneuverable targets. Chen et al. [24] proposed a maneuvering target tracking method based on the minimum fuzzy error entropy unscented filtering, solving the single-weight issue in ordinary error entropy and providing effective tracking of maneuvering targets under non-Gaussian noise. With the rise of machine learning and deep learning algorithms, new methods for maneuvering target tracking continue to be developed [25].

The main issues in multi-target tracking include the uncertainty of measurements, such as false alarms, missed detections, and clutter, as well as the uncertainty of the target states, namely the variable number of targets [26,27,28,29]. Common multi-target tracking algorithms are primarily based on data association. The Nearest Neighbor (NN) algorithm is one of the most common data association algorithms, which selects the measurement closest to the target’s predicted position as the current measurement for the target. It is relatively simple to implement but performs poorly in high clutter density or when the number of targets is large. The Joint Probabilistic Data Association (JPDA) algorithm calculates feasible joint event sets and assigns weights to the association probabilities between each measurement and potential targets to obtain an equivalent measurement. The JPDA algorithm is a more refined method among data association algorithms, but the association events between targets and measurements grow exponentially with the number of targets, which does not meet real-time requirements well. To address this issue, Sheng et al. [30] proposed a new simplified JPDA algorithm that introduces a common measurement influence factor to adjust association probabilities, enhancing the algorithm’s real-time performance. The Multiple Hypothesis Tracking (MHT) algorithm establishes a potential tracking hypothesis tree for each candidate target and achieves multi-target tracking by managing these hypotheses. The MHT algorithm typically assumes that the clutter intensity is known a priori, and when the clutter in the observation scene is unknown, this assumption can lead to a dramatic decrease in tracking performance. In response to this, Li et al. [31] proposed an improved MHT algorithm based on an adaptive Gaussian Mixture Model (GMM) for clutter estimation, which uses an adaptive GMM to fit the unknown clutter spatial distribution and adaptively estimates the clutter intensity within the gate, achieving stable tracking in cluttered environments. Han et al. [32] proposed a Doppler blind zone target point-track association method based on MDA, which enhances the accuracy of data association by constructing a cost function and using optimization algorithms.

To address the problem of bearing-only tracking of multiple maneuvering targets, this paper proposes a Improved Maneuver Detection-Based Multiple Hypothesis Bearing-Only Target Tracking (IMD-MHRPCKF) (Maneuver Detection Multiple Hypothesis Range-Parameterized Cubature Kalman Filter) algorithm, which combines the advantages of cubature Kalman filtering, maneuver detection, and MHT. The key innovative contributions of the proposed algorithm are as follows:

• The proposed algorithm introduces the use of a range-parameterized method for dividing the observation range into sub-intervals, each employing Cubature Kalman Filtering (CKF) to address the challenges posed by bearing-only measurements. This innovative step reduces the dependency on linearization and mitigates the nonlinearity of measurement equations, offering an improvement over traditional methods like EKF. The application of CKF in each sub-interval effectively handles the known initial position problem and enhances tracking accuracy by reducing errors in filter performance.
• Maneuver detection is integrated using the innovation sequence, which helps in identifying target maneuvers. When a maneuver is detected, the sub-filter parameters are dynamically reset. This method enhances the robustness of the system by addressing filter divergence issues that arise during maneuvers, which is particularly crucial for tracking targets in complex dynamic environments.
• By incorporating the MHT algorithm, the proposed method excels in addressing the measurement ambiguity problem typical of multi-target tracking scenarios. This hybrid approach improves the robustness of the tracking system in the presence of clutter and measurement noise, ensuring accurate data association even when multiple targets are close together. The use of MHT for simultaneous hypothesis generation and pruning based on measurement likelihood further optimizes the performance of the system, particularly when handling uncertain and incomplete data.

2. Materials and Methods

2.1. Bearing-Only Tracking Modeling

2.1.1. Target Motion Model

Three commonly used motion models for targets are the Constant Velocity (CV) model, the Constant Acceleration (CA) model, and the Coordinated Turn (CT) model. Considering motion in a two-dimensional plane, when a target moves with constant velocity, its state equation is as follows:

$$X_{k+1}=F_{CV}{X}_k+W_k,$$

(1)

where the state transition matrix is denoted as $F_{CV}$:

$$F_{CV}=\left[\begin{array}{cccc}1& T& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& T\\ 0& 0& 0& 1\end{array}\right],$$

(2)

The target’s motion state at time k is represented as $X_k={\left[\begin{array}{cccc}{x}_k& v_{x,k}& y_k& v_{y,k}\end{array}\right]}^T$, T represents the system sampling period, and $W_k$ denotes the state noise.

When the target is undergoing constant accelerated motion, its state equation is as follows:

$$X_{k+1}=F_{CA}{X}_k+W_k,$$

(3)

where the state transition matrix is denoted as $F_{CA}$: $F_{CA}=\left[\begin{array}{cccccc}1& T& T^2/2& 0& 0& 0\\ 0& 1& T& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& T& T^2/2\\ 0& 0& 0& 0& 1& T\\ 0& 0& 0& 0& 0& 1\end{array}\right]$, the target’s motion state at time k is represented as $X_k={\left[\begin{array}{cccccc}{x}_k& v_{x,k}& y_k& v_{y,k}& a_k& j_k\end{array}\right]}^T$. When the target is undergoing constant turn motion, its state equation is as follows:

$$X_{k+1}=F_{CT}{X}_k+W_k,$$

(4)

where the state transition matrix is denoted as $F_{CT}$:

$$F_{CT}=\left[\begin{array}{cccccc}1& sin\left(\omega T\right)/\omega & 0& -(1-cos(\omega T\left)\right)/\omega & 0& 0\\ 0& cos\left(\omega T\right)& 0& -sin\left(\omega T\right)& 0& 0\\ 0& (1-cos(\omega T\left)\right)/\omega & 1& sin\left(\omega T\right)/\omega & 0& 0\\ 0& sin\left(\omega T\right)& 0& cos\left(\omega T\right)& 0& 0\end{array}\right],$$

(5)

And the target’s motion state at time k is represented as $X_k={\left[\begin{array}{cccc}{x}_k& v_{x,k}& y_k& v_{y,k}\end{array}\right]}^T$.

2.1.2. Measurement Model and System Observability Analysis

In the geographic rectangular coordinate system, the X-axis points due east, and the Y-axis points due north. The target is moving in the XOY plane. The motion state of the target at time k is represented as $X_k={\left[\begin{array}{cccc}{x}_k& v_{x,k}& y_k& v_{y,k}\end{array}\right]}^T$, and the position of the observation station at time k is represented as $s_k={\left[\begin{array}{cc}{s}_{x,k}& s_{y,k}\end{array}\right]}^T$. The observation station and the target trajectory are shown in Figure 1.

In Figure 1, the azimuth angle represents the angle between the target and the observation station. The azimuth angle is the horizontal angle measured clockwise from the true north direction of the observation station to the direction of the target, with a range of between 0 and 360 degrees. In a two-dimensional pure angle tracking model, the observation station can only obtain the target’s azimuth angle, and its measurement model is as follows:

$$Z_k={\hat{\beta }}_k=h\left(X_k\right)+V_k=arctan\left({\displaystyle \frac{x_k-s_{x,k}}{y_k-s_{y,k}}}\right)+V_k,$$

(6)

where $V_k$ represents the measurement noise, $Z_k$ is the measurement at time k, $h\left(X_k\right)$ is the nonlinear measurement function, and ${\hat{\beta }}_k$ denotes the relative bearing angle of the target as observed by the station.

Different relative motion patterns between the observation station and the target influence the system’s observability. To ensure that a single-station angle-only tracking system is observable, the order of motion of the observation station must be higher than that of the target.

Figure 2 illustrates the different relative motion patterns between the observation station and the target: (a) the target remains stationary while the observation station moves at a constant velocity; (b) the target moves at a constant velocity, and the observation station maneuvers once; (c) the target maneuvers once, while the observation station maneuvers twice. In all three scenarios, the order of motion of the observation station is greater than that of the target, allowing for relatively accurate estimation of the target state with the appropriate filtering algorithm; (d) both the observation station and the target move at a constant velocity, with their orders of motion being equal, rendering the target state unobservable and leading to significant estimation errors.

2.2. Multiple Hypothesis Bearing-Only Target Tracking Based on Maneuver Detection

2.2.1. Range-Parameterized Cubature Kalman Filter

The two typical problems in bearing-only tracking are the unknown initial position of the target and the nonlinearity of the measurement equation. To address these, a distance-parameterized cubature Kalman filter algorithm is designed. The RP algorithm is used to reduce the sensitivity of bearing-only tracking to initial state errors of the target, and the CKF algorithm is utilized to solve the nonlinearity issues of the measurement equation. In this method, the CKF is introduced into each subinterval to handle the nonlinearity separately within each range segment, ensuring that the nonlinearity of the bearing-only measurements is effectively addressed. By applying CKF to each subinterval, the algorithm can more precisely model the target’s movement within different range segments, thus improving tracking accuracy and stability compared to traditional methods that apply a single filter across the entire range.

The specific steps of the RP algorithm are as follows:

(1)

Distance interval partitioning

If the observation station is able to acquire measurement data from the target, it indicates that the target is within the station’s detection range. As a result, the detection range can be used as prior information, defining the initial relative distance interval between the target and the observation station.

The segmentation of the resolution interval in N-dimensional space is critical, where the interval $(r_{\min },r_{\max })$ is divided into N segments. Each segment spans from $(r_{\min }{\rho }^{n-1},r_{\min }{\rho }^n)$, and is determined by the ratio $\rho$.

$$\rho ={\left({\displaystyle \frac{r_{\max }}{r_{\min }}}\right)}^{{\displaystyle \frac{1}{N}}}$$

(7)

For instance, with N = 4, the initial subintervals into which the relative distance between the target and the observation station is divided are shown in Figure 3.

The RP algorithm refines the traditional approach to statistical estimation by introducing a new method of interval determination that calculates the average and standard deviation for each interval, denoted as ${\overline{r}}_n$ and ${\sigma }_{r_n}$, respectively.

$${\overline{r}}_n={\displaystyle \frac{r_{\min }{\rho }^{n-1}+r_{\min }{\rho }^n}{2}}$$

(8)

$${\sigma }_{r_n}={\displaystyle \frac{r_{\min }{\rho }^n-r_{\min }{\rho }^{n-1}}{\sqrt{12}}}$$

(9)

The covariance coefficient for the distance estimation in the subintervals is defined as follows:

$$C_r={\displaystyle \frac{{\sigma }_{r_n}}{{\overline{r}}_n}}={\displaystyle \frac{2(\rho -1)}{\sqrt{12(\rho +1)}}}$$

(10)

The covariance coefficient for distance estimation in subintervals impacts the tracking performance of the algorithm. A smaller $C_r$ results in higher tracking accuracy, but it also leads to a greater number of subintervals, affecting the real-time capability of the algorithm. When $C_r$ is reduced below a certain threshold, further decreases in $C_r$ have a limited impact on improving the accuracy.

For each subinterval, the RP algorithm assigns an independent sub-filter. Combining the angle information obtained at the initial moment, the initial state value $X_0|0^n$ and the initial state covariance $P_{0|0}^n$ for the n th sub-filter are computed as follows:

$${\hat{X}}_{0|0}^n={({\overline{r}}_{n}cos{\beta }_0,0,{\overline{r}}_{n}sin{\beta }_0,0)}^T$$

(11)

$$P_{0|0}^n=diag({\sigma }_{r_n}^2{cos}^2{\beta }_0,{\sigma }_{\nu }^2{cos}^2{\beta }_0,{\sigma }_{r_n}^2{sin}^2{\beta }_0,{\sigma }_{\nu }^2{sin}^2{\beta }_0)$$

(12)

where ${\beta }_0$ is the angle measured at the initial moment, ${\sigma }_{r_n}$ is the standard deviation of the distance in the n-th subinterval, representing the uncertainty in the relative distance between the target and the observation station, and ${\sigma }_{\nu }$ is the standard deviation of the target’s velocity at the initial moment, indicating the uncertainty in the target’s velocity. The covariance matrix $P_{0|0}^n$ accounts for the uncertainties in both position and velocity, with the position uncertainties weighted by ${cos}^2{\beta }_0$ and ${sin}^2{\beta }_0$, and the velocity uncertainties similarly weighted, reflecting the direction of the initial angle,

(2)

Sub-interval filter weight initialization and update

The RP algorithm assigns an initial weight to each sub-filter at the initial moment. The weight of the nth sub-filter, ${\omega }_0^n$ is given as follows:

$${\omega }_0^n={\displaystyle \frac{({\rho }^n-{\rho }^{n-1})r_{min}}{r_{max}-r_{min}}}$$

(13)

Sub-filters run in parallel across intervals to obtain the target state estimate ${\hat{X}}_{k+1|k+1}^n$, the measurement covariance $P_{zz,k+1|k}^n$, and the measurement residual ${\gamma }_{k+1}^n$. The likelihood function $L_{k+1,n}$ for the n-th sub-filter is calculated as follows:

$$L_{k+1,n}={\displaystyle \frac{1}{\sqrt{2\pi P_{zz,k+1|k}^n}}}exp(-0.5{\left({\gamma }_{k+1}^n\right)}^T{\left(P_{zz,k+1|k}^n\right)}^{-1}\left({\gamma }_{k+1}^n\right))$$

(14)

Next, CKF filters operate independently in each interval. The CKF algorithm is a Bayesian filtering method that progresses based on a numerical integration criterion involving volume. This algorithm does not require the calculation of the Jacobian matrix, nor does it require predefined parameters, resulting in good filtering performance. The processing steps of the CKF algorithm are as follows:

(1)

Compute the cubature points $X_{i,k|k}$

$$X_{i,k|k}=S_k{\xi }_i+{\hat{X}}_{k|k}$$

(15)

where $S_k=chol\left\{P_{k|k}\right\},chol\left\{\right\}$ denotes the Cholesky decomposition, i.e., $P_{k|k}=S_k{S}_k^T,{\zeta }_i$ denotes the i th volumetric point, ${\xi }_i=\sqrt{J/2}{\left[\delta \right]}_i,J$ denotes the number of volumetric points, and ${\left[\delta \right]}_i$ denotes the number of volumetric points. The ith column element of the matrix $[{\mathrm{I}}^{n^{*}n},-{\mathrm{I}}^{n^{*}n}]$ denotes the n-dimensional unit array, and n denotes the state dimension.

(2)

Calculate state predictions using volume points ${\hat{X}}_{k+1|k}$ and covariance predictions $P_{k+1|k}$:

$$X_{i,k+1|k}^{*}=F{X}_{i,k|k}$$

(16)

$${\hat{X}}_{k+1|k}=\sum _{i=1}^{2n}{w}_i{X}_{i,k+1|k}^{*}$$

(17)

$$w_i={\displaystyle \frac{1}{2n}}$$

(18)

$$P_{k+1|k}=\sum _{i=1}^{2n}{w}_i{X}_{i,k+1|k}^{*}{X}_{i,k+1|k}^{*}-{\hat{X}}_{k+1|k}+Q_k$$

(19)

where $w_i$ denotes the volume point weight.

(3)

Calculate the volumetric point $X_{i,k+1|k}$:

$$X_{i,k+1|k}=S_{k+1|k}{\xi }_i+{\hat{X}}_{k+1|k}$$

(20)

where $S_{k+1|k}=chol\left\{P_{k+1|k}\right\}$.

(4)

Calculate the quantile prediction $Z_{k+1|k}$ and quantile covariance $P_{zz,k+1|k}$ using volumetric points:

$$Z_{i,k+1|k}=h\left(X_{i,k+1|k}\right)$$

(21)

$$Z_{k+1|k}=\sum _{i=1}^{2n}{w}_i{Z}_{i,k+1|k}$$

(22)

$$P_{zz,k+1|k}=\sum _{i=1}^{2\mathrm{n}}{w}_i{Z}_{i,k+1|k}{Z}_{i,k+1|k}^T-Z_{k+1|k}{Z}_{k+1|k}^T+R_{k+1}$$

(23)

(5)

Calculate mutual covariance $P_{xz,k+1|k}$:

$$P_{xz,k+1|k}=\sum _{i=1}^{2\mathrm{n}}{w}_i{X}_{i,k+1|k}{Z}_{i,k+1|k}^T-{\hat{X}}_{k+1|k}{Z}_{k+1|k}^T$$

(24)

(6)

Calculate the Kalman filter gain $K_{k+1}$:

$$K_{k+1}=P_{xz,k+1|k}{P}_{zz,k+1|k}^{-1}$$

(25)

(7)

Calculate the state estimates ${\hat{X}}_{k+1|k+1}$ and the state covariance $P_{k+1|k+1}$:

$${\hat{X}}_{k+1|k+1}={\hat{X}}_{k+1|k}+K_{k+1}(Z_{k+1}-Z_{k+1|k})$$

(26)

$$P_{k+1|k+1}=P_{k+1|k}-K_{k+1}{P}_{zz,k+1|k}{K}_{k+1}^T$$

(27)

According to the processing flow of the above algorithm, it can be seen that the CKF algorithm works by selecting the approximate probability density function of the volume point through the volume rule, which helps avoid complex matrix operations typically involved in the filtering process. This feature makes the CKF easier to implement than the EKF algorithm, which relies on calculating Jacobians for linearizing the nonlinear models. Additionally, the method used by the CKF to select known volume points results in smaller errors and higher precision compared to the EKF. The CKF’s approach ensures that the filter remains more stable and accurate, especially in scenarios where nonlinearities are present.

When comparing the CKF with the UKF, the two algorithms share key similarities, such as both avoiding the linearization of the nonlinear model by selecting sampling points to perform the filtering process. However, there are significant differences between them. The CKF algorithm typically uses fewer sampling points than the UKF, which improves computational efficiency. Moreover, the CKF’s derivation process is more rigorous, lacking the approximations that are inherent in the UKF. For example, the UKF employs a Taylor series expansion to approximate the function, introducing certain assumptions and errors in the process. In contrast, the CKF’s approach is more precise, as it avoids these approximations, making it more accurate in certain situations where the UKF might incur higher error due to its assumptions.

The weight of each sub-filter is updated based on its likelihood function, the weight of the nth sub-filter at time $k+1$ is calculated, and weighted fusion of the filtering results from each sub-filter is performed to obtain the target state estimate ${\hat{X}}_{k+1|k+1}$.

$${\omega }_{k+1}^n={\displaystyle \frac{{\omega }_k^n{L}_{k+1,n}}{{\sum }_{i=1}^N{\omega }_k^i{L}_{k+1,i}}}$$

(28)

$${\hat{X}}_{k+1|k+1}=\sum _{n=1}^N{\omega }_{k+1}^n{\hat{X}}_{k+1|k+1}^n$$

(29)

The specific steps of the RPCKF algorithm are as follows, which are detailed in Algorithm 1.

Step 1: Based on the detection range of the observatory, divide the sub-intervals according to the principle of equal ratio, assign a sub-filter to each sub-interval, and set the initial state ${\hat{X}}_{0|0}^n$, covariance $P_{0|0}^n$, and weight ${\omega }_0^n$ of each interval sub-filter according to Equations (7)–(14).

Step 2: Run the CKF filter independently for each interval, calculate the sub-filter state estimates ${\hat{X}}_{k+1|k+1}^n$ and state covariance $P_{k+1|k+1}^n$ according to Equations (15)–(27), and update the sub-filter weights ${\omega }_{k+1}^n$ according to Equation (28) based on the measured likelihood function obtained in the filtering process.

Step 3: Weight the state estimates of the sub-filters and integrate them to obtain the state estimate of the target ${\hat{X}}_{k+1|k+1}$ according to Equation (29).

2.2.2. Modified Maneuver Detection

This results in the RPCKF (Range-Parameterized Cubature Kalman Filter), but the tracking accuracy of this algorithm decreases in the case of target maneuvers. In this paper, a maneuver detection algorithm is designed and combined with RPCKF, resulting in the IMD-RPCKF (Improved Modified Range-Parameterized Cubature Kalman Filter) algorithm.

Initially, we use the RPCKF to track the target and assume that the target is moving in a straight line with a constant velocity. As the subinterval weights stabilize, the weight of the subfilter corresponding to the initial relative distance of the target approaches 1, while the weights of the other subfilters decrease to 0. Once a target maneuver is detected, we reinitialize the filter based on the target information stored before the maneuver was detected. When reinitializing the filter, we also initialize the covariance matrix and account for changes in the target’s velocity or heading.

Algorithm 1 Range-Parameterized Cubature Kalman Filter (RPCKF)

1: Input: Detection range $(r_{\min },r_{\max })$, number of subintervals N, initial angle ${\beta }_0$ 2: Output: Estimated state ${\hat{X}}_{k+1|k+1}$

3: procedure Initialize Subintervals 4:     $\rho \leftarrow {\left({\displaystyle \frac{r_{\max }}{r_{\min }}}\right)}^{{\displaystyle \frac{1}{N}}}$ 5:     for $n=1$ to N do 6:         ${\overline{r}}_n\leftarrow {\displaystyle \frac{r_{\min }{\rho }^{n-1}+r_{\min }{\rho }^n}{2}}$ 7:         ${\sigma }_{r_n}\leftarrow {\displaystyle \frac{r_{\min }{\rho }^n-r_{\min }{\rho }^{n-1}}{\sqrt{12}}}$ 8:         Initialize $X_0|0^n$ and $P_{0|0}^n$ 9:     end for 10: end procedure

11: procedure Cubature Kalman Filter 12:     for $k=0$ to final time step do 13:         for each subinterval n do 14:            Compute cubature points and propagate 15:            Calculate predicted state and covariance 16:            Update measurements and compute Kalman gain 17:            Update state estimates and covariance matrices 18:         end for 19:         Fuse sub-filter estimates 20:     end for 21: end procedure

22: procedure Fuse Sub-filter Estimates 23:     for $n=1$ to N do 24:         Update weight ${\omega }_{k+1}^n$ based on likelihood 25:     end for 26:     ${\hat{X}}_{k+1|k+1}\leftarrow {\sum }_{n=1}^N{\omega }_{k+1}^n{\hat{X}}_{k+1|k+1}^n$ 27: end procedure

Various methods have been developed to detect target maneuvers in real time. Since we use multiple CKFs, we utilize all CKF modules to detect target maneuvers by calculating the innovation change to determine whether the target is maneuvering. We define the maneuver detection factor as follows:

$$I_k=\sum _{t=k-W_1+1}^k{\gamma }_t^T{P}_{zz,t}^{-1}{\gamma }_t$$

(30)

where ${\gamma }_t$ represents the difference between the measurement and the filter’s predicted output, i.e., the innovation, and $P_{zz}$ represents the innovation covariance. If ${\gamma }_t$ has zero mean and covariance $P_{zz}$, then ${\gamma }_t$ follows a chi-squared distribution with $W_1$ degrees of freedom. Based on this distribution, we can select a threshold U to detect a maneuver. However, in practical applications, sensor measurement noise and process noise are not always Gaussian distributed. To handle the impact of non-Gaussian noise, we adopt the time-averaging sliding window method introduced in Equation (25). By using the sliding window method, random errors in the innovation signal are reduced.

We set the maneuver detection threshold as U, which is determined based on the statistical properties of the innovation sequence. Specifically, U was chosen based on a series of experimental tests to ensure that the threshold effectively distinguishes between maneuvering and non-maneuvering targets. The threshold is set to a value that minimizes false positives while ensuring that real maneuvers are detected with high confidence. This value was fine-tuned through simulations and cross-validation on the dataset to optimize tracking performance and robustness against noise and clutter. At this point, the original covariance matrix is no longer sufficient to describe the new motion state, leading to increased tracking errors. To quickly adapt to the target’s maneuver behavior and re-estimate the target’s motion state, reducing tracking errors, we reinitialize the state estimates and covariance matrices of the subfilters. The method for reinitializing the sub-filter covariance is as follows:

$$P_{k+1|k+1}^{\prime }=\left[\begin{array}{cccc}{\left(I_{k+1}\cos {\beta }_{k+1}\right)}^2& 0& 0& 0\\ 0& {\hat{\nu }}_{max}^2& 0& 0\\ 0& 0& {(I_{k+1}sin{\beta }_{k+1})}^2& 0\\ 0& 0& 0& {\hat{\nu }}_{max}^2\end{array}\right]$$

(31)

where ${\beta }_{k+1}$ represents the measurement at time $k+1$, and ${\hat{\nu }}_{\max }$ is the maximum velocity of the target. By utilizing the latest measurement information, the covariance matrix becomes more representative and accurate, which better reflects the actual motion state of the target and improves tracking accuracy. ${\hat{\nu }}_{\max }$ is determined based on the target type. When the target type cannot be determined, the maximum value of the velocity estimates from historical filtering data is used as a substitute.

The calculation method for resetting the state estimate of the sub-filter is as follows: the state estimate ${\hat{X}}_{k|k}$ is updated by considering both the position and velocity components of the target. The updated state estimate is represented as follows:

$${\hat{X}}_{k|k}=\left[\begin{array}{c}{\hat{X}}_{k|k}\left(1\right)\\ {\hat{X}}_{k|k}\left(2\right)\\ cos\left({\varphi }_j\right){\hat{X}}_{k|k}\left(3\right)+sin\left({\varphi }_j\right){\hat{X}}_{k|k}\left(4\right)\\ -sin\left({\varphi }_j\right){\hat{X}}_{k|k}\left(3\right)+cos\left({\varphi }_j\right){\hat{X}}_{k|k}\left(4\right)\end{array}\right]$$

(32)

where ${\hat{X}}_{k|k}\left(1\right)$ and ${\hat{X}}_{k|k}\left(2\right)$ represent the position estimates, and ${\hat{X}}_{k|k}\left(3\right)$ and ${\hat{X}}_{k|k}\left(4\right)$ represent the velocity components in the x and y directions, respectively. The angle ${\varphi }_j$ represents the target’s heading rotation angle after the maneuver,

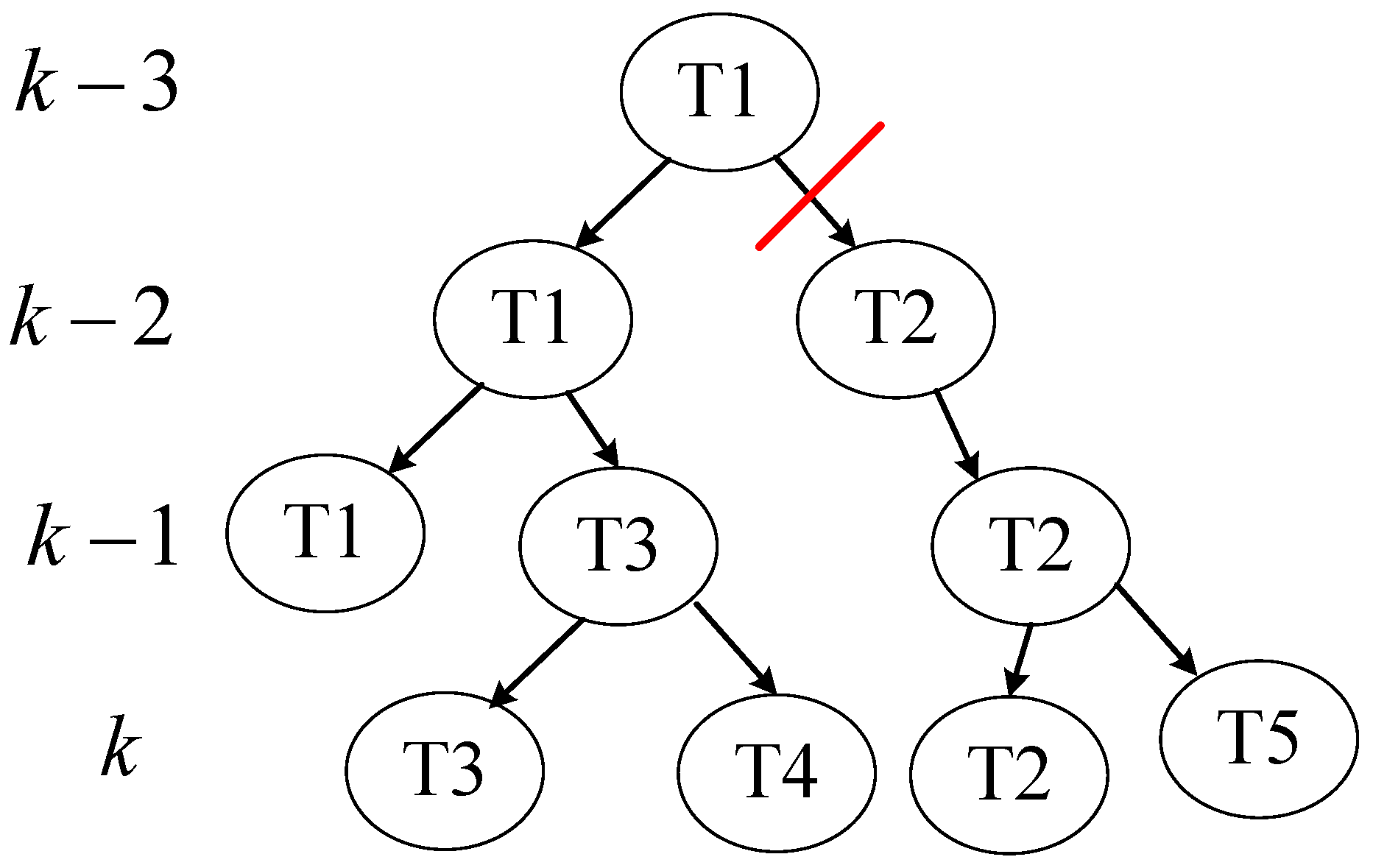
2.2.3. Integration of MHT and IMD-RPCKF for Bearing-Only Multi-Target Tracking

To address the issues of measurement ambiguity and uncertainty in model parameters in cluttered environments for multi-maneuvering target tracking, this paper proposes an MHT algorithm with maneuver detection. This approach combines MHT technology with maneuver detection methods and reinitializes the covariance matrix upon detecting target maneuvers to achieve precise tracking of maneuvering targets. The specific steps of the MHT algorithm are as follows:

• Hypothesis generation

Let $Z^{k+1}=\left\{Z_{k+1,1},\cdots ,Z_{k+1,i},i=1,2,\dots ,m_{k+1}\right\}$ represent the measurements at time $k+1$, where $m_{k+1}$ represent the number of measurements at time $k+1$, and ${\mathrm{\Omega }}^{k+1}$ represent the set of hypotheses at time $k+1$, while $Z(k+1)$ represent the cumulative measurement value at time $k+1$. The set ${\mathrm{\Omega }}^{k+1}$ is obtained from the association hypothesis set at time k and the current measurement set. The measurement $Z_{k+1,i}$ could correspond to an existing target track, a new target track, clutter, or false alarms. To find the optimal hypothesis for the set of hypotheses, the Murty algorithm is used. The Murty algorithm starts with the initial optimal match and iteratively generates suboptimal solutions by dividing the problem into multiple subproblems and solving them sequentially. Through sorting and selection, it generates multiple optimal and suboptimal matching combinations, thereby updating the hypothesis set.

Let ${\mathrm{\Omega }}_l^{k+1}$ represent the l th hypothesis in the hypothesis set ${\mathrm{\Omega }}^{k+1}$, obtained from the prior hypothesis ${\mathrm{\Omega }}_s^k$ and the association event ${\theta }_{k+1}$. Using Bayes’ theorem, the posterior probability of ${\mathrm{\Omega }}_l^{k+1}$ can be obtained as follows:

$$\begin{array}{c}\hfill P({\mathrm{\Omega }}_l^{k+1}\mid Z(k+1))=P({\theta }_{k+1},{\mathrm{\Omega }}_s^k\mid Z^{k+1},Z\left(k\right))\\ \hfill ={\displaystyle \frac{1}{c}}P(Z^{k+1}\mid {\theta }_{k+1},{\mathrm{\Omega }}_s^k,Z\left(k\right))P({\theta }_{k+1}\mid {\mathrm{\Omega }}_s^k,Z\left(k\right))P({\mathrm{\Omega }}_s^k\mid Z\left(k\right))\end{array}$$

(33)

$$c=P(Z^{k+1}\mid Z\left(k\right))$$

(34)

If the measurement $Z_{k+1,i}$ originates from an existing target track, it follows a Gaussian distribution. If $Z_{k+1,j}$ originates from a new target track, clutter, or a false alarm, it is assumed to follow a uniform distribution within the tracking gate. Thus, the first term in Equation (30) can be calculated as follows:

$$P(Z^{k+1}\mid {\theta }_{k+1},{\mathrm{\Omega }}^k,Z\left(k\right))=V^{-\mathrm{\Psi }-\eta }\prod _{i=1}^{m_{k+1}}{\left({\mathrm{\Lambda }}_{k+1,i}\right)}^{{\tau }_i}$$

(35)

$${\tau }_i=\left\{\begin{array}{cc}1,\hfill & If\mathrm{measurement}\mathrm{from}\mathrm{am}\mathrm{established}\mathrm{target}\mathrm{track}\hfill \\ 0,\hfill & \mathrm{others}\hfill \end{array}\right.i=1,2,\dots ,m_{k+1}$$

(36)

where $\mathrm{\Psi },\eta$ represent the number of false alarms and new targets in event ${\theta }_{k+1}$, respectively, and ${\mathrm{\Lambda }}_{k+1,i}$ represents the likelihood function of the innovation.

The first term in Equation (30) has already been calculated using Equation (32), and the second term can be computed as follows:

$$P({\theta }_{k+1}\mid {\mathrm{\Omega }}_s^k,Z\left(k\right))={\displaystyle \frac{\mathrm{\Psi }!\eta !}{m_{k+1}!}}{\mu }_n\left[\eta \left({\theta }_{k+1}\right)\right]{\mu }_f\left[\mathrm{\Psi }\left({\theta }_{k+1}\right)\right]\prod _t{\left(P_D\right)}^{{\delta }_i\left({\theta }_{k+1}\right)}{(1-P_D)}^{1-{\delta }_i\left({\theta }_{k+1}\right)}$$

(37)

where ${\mu }_n\left[\eta \left({\theta }_{k+1}\right)\right]$, ${\mu }_f\left[\mathrm{\Psi }\left({\theta }_{k+1}\right)\right]$ represent the prior probability distribution functions for the number of false alarms and new targets, respectively. ${\delta }_t\left({\theta }_{k+1}\right)$ denotes the target detection indicator, reflecting whether the target t in the hypothesis set is detected at time $k+1$, and $P_D$ is the detection probability. Substituting Equations (32) and (34) into Equation (30) gives the hypothesis probability for the lth hypothesis in the association hypothesis set ${\mathrm{\Omega }}^{k+1}$ as follows:

$$P({\mathrm{\Omega }}_l^{k+1}\mid Z(k+1))={\displaystyle \frac{1}{c}}{\displaystyle \frac{\mathrm{\Psi }!\eta !}{m_{k+1}!}}{\mu }_n\left[\eta \left({\theta }_{k+1}\right)\right]{\mu }_f\left[\mathrm{\Psi }\left({\theta }_{k+1}\right)\right]\prod _t{\left(P_D\right)}^{{\sigma }_i\left({\theta }_{k+1}\right)}{(1-P_D)}^{1-{\sigma }_i\left({\theta }_{k+1}\right)}\times V^{-\mathrm{\Psi }-\eta }\prod _{i=1}^{m_{k+1}}{\left({\mathrm{\Lambda }}_{k+1,i}\right)}^{{\tau }_i}P({\mathrm{\Omega }}_s^k\mid Z\left(k\right))$$

(38)

Using the N-scan pruning method, hypotheses with small weights are discarded, while those with large weights are retained, reducing the computational load during the filtering process. When the depth of the hypothesis tree reaches the threshold, the branch with the highest weight at the current moment is kept, and the rest are deleted. The principle of the N-scan pruning algorithm is shown in Figure 4.

As shown in Figure 4, pruning operations are performed at time k, where T1 to T5 represent the leaf nodes on the hypothesis trajectory tree. If at time k, T4 has the highest weight, only the branch containing T1, T3, and T4 is retained, and the other branches are deleted. The red line in the figure indicates the hypothesis branches that are discarded during the pruning process. These low-weight branches are removed to reduce computational complexity and focus on the most relevant hypotheses, which helps optimize the tracking process. T1 at time k-2 becomes the new root node.

Combining the IMD-RPCKF and MHT algorithms, the IMD-MHRPCKF algorithm was designed to solve the tracking problem of multi-target pure angle measurement in maneuvering scenarios. This algorithm improves the robustness of the algorithm to model uncertainty and reduces tracking errors for maneuvering targets.

The specific implementation steps of the algorithm can be summarized as follows:

Step 1: Parameterization of distance

The detection range of the observation station is divided into several intervals based on the proportionality principle. A sub-CKF filter is assigned to each target in each interval. The mean and standard deviation of the initial distance between the target and the observation station are calculated in each subinterval using Equations (7)–(14) and the initial angle measurement at the initial time. This allows for the determination of the initial state and covariance for each sub-CKF filter, and the initial weight for each sub-CKF filter is set accordingly.

Step 2: State prediction

Based on Equationa (15)–(19), perform state prediction and calculate the sub-filter state prediction values and covariance prediction values for each target in each sub-interval time.

Step 3: Hypothesis generation and calculation of hypothesis probability

Construct an allocation matrix, use the Murty algorithm to find the optimal allocation scheme for various measurements and targets, calculate the hypothesis probability based on Equations (30)–(35), and update the hypothesis tree using the current hypothesis.

Step 4: Status update

The state estimation values and measurement covariance of each sub-filter are updated based on Equations (20)–(27) from step three. Additionally, the weights of each sub-filter are updated according to Equation (28).

Step 5: Maneuver detection and initialization of covariance matrix

Calculate the innovation and innovation covariance matrix based on Equations (22) and (23), then calculate the detection factor of the sub-filter based on Equation (36), comparing it with the detection threshold. If the detection factor is greater than the threshold, reinitialize the covariance matrix of the sub-filter based on Equation (37).

Step 6: Assuming management

Delete hypothesis branches with lower weights and retain hypothesis branches with higher weights using the N-scan pruning method.

Step 7: Obtaining target state estimation

The state estimation values and weights of the sub-filters are extracted from the root nodes of the hypothesis tree. Multi-objective state estimates are then obtained by performing weighted fusion, as described in Equation (29).

3. Simulation Results and Analysis

The simulations presented in this paper were conducted using MATLAB 2024b with the MATLAB Optimization Toolbox and other necessary toolboxes for data processing and analysis. The experiments were executed on a system with an Intel(R) Core(TM) i9-14900KF CPU (Intel Corporation, Santa Clara, CA, USA) at 3.20 GHz, paired with an NVIDIA GeForce RTX 4090 GPU (NVIDIA Corporation, Santa Clara, CA, USA) with 24 GB of memory. Both the CPU and GPU were purchased from a local distributor in China. This platform setup provided the necessary computational power for efficiently running the experiments, ensuring robust validation of the proposed algorithm under various conditions, including different detection probabilities, clutter densities, and sensor noise levels.

3.1. Simulation Validation of Tracking Performance of the RP-MHTCKF

In this section, the tracking performance of the RP-MHTCKF algorithm is simulated and verified, and the comparison algorithms are the Reweighted Pseudo-Nearest Neighbor-based Constrained Kalman Filter (RP-NNCKF) algorithm and the Reweighted Pseudo-Nearest Neighbor-based Joint Probabilistic Data Association Constrained Kalman Filter (RP-JPDACKF) algorithm. These algorithms were chosen for comparison because they represent well-established methods in multi-target tracking and are known for their effectiveness in scenarios with varying detection probabilities and clutter. The RP-NNCKF algorithm, similar to our proposed method, also focuses on reweighted pseudo-nearest neighbor strategies, while the RP-JPDACKF algorithm integrates joint probabilistic data association, making them relevant benchmarks for evaluating the performance of our approach in handling measurement ambiguity and multi-target tracking in complex environments.

The simulation conditions are set to a sampling time of 0.1 s, the detection range of the observation station is between (500 m, 4000 m), and the number of sub-intervals is set to 4. The number of Monte Carlo simulations is set to 100. The initial position of the observation station is the origin. The amount of clutter obeys the Poisson distribution, the mean value is 5, the position obeys the uniform distribution, and different detection probabilities are set, which are $P_D=0.01$, hence $P_D=0.99$, respectively.

Tracking is conducted on three targets, each moving at a constant velocity in a straight line. The initial states for each target were set based on realistic assumptions about their positions and velocities at the beginning of the simulation. The initial states are as follows: [2500 m, 1900 m, −5.9 m/s, −7.9 m/s], [2500 m, 1600 m, −9.6 m/s, −4.8 m/s], and [2500 m, 2300 m, −8.3 m/s, 0 m/s], representing the initial positions and velocities of the targets in the x and y directions. The targets’ motion continues for 100 s, simulating the movement of real-world targets under constant velocity. The motion state of the observation station is as described in

Table 1. Resolution test results for different ranges.

Time/s	Motion Model	Radial Velocity
1–10	Uniform accelerated motion	Acceleration (0.8 m/s2, −0.8 m/s2)
10–25	Uniform turning motion	Angular velocity $\pi /15$ rad/s
25–100	Uniform linear motion	Velocity (−8 m/s, 8 m/s)

.

The target and observation station trajectories are displayed in Figure 5a, while the measurement and clutter distribution are depicted in Figure 5b.

Figure 5 and Figure 6 lead to the following conclusions:

(1)

At PD = 1, the error curves of the Reweighted Pseudo-Nearest Neighbor-based Constrained Kalman Filter (RP-NNCKF) algorithm are similar to those of the RP-JPDACKF algorithm, indicating comparable tracking performance between the two algorithms when no detection omissions occur. The RP-MHTCKF algorithm’s error rapidly decreases at the initial moment, showing overall superior tracking performance compared to the other two algorithms. The RP-MHTCKF algorithm, utilizing the multiple hypothesis framework of the MHT algorithm, initially simulates the target’s position through multiple hypotheses and efficiently eliminates sub-filters generated in incorrect intervals by evaluating the measurement likelihood function and residuals. This process retains only the filters within the correct interval, rapidly minimizing the initial tracking error.

(2)

At PD = 0.99, the errors of the RP-JPDACKF and RP-MHTCKF algorithms are similar to those when PD is 1, whereas the RP-NNCKF algorithm is more sensitive to changes in detection probability. When the detection probability is not 1, the error of this algorithm rapidly increases, and the final tracking error never converges. This is because the NN algorithm takes the nearest measurement to the target in relative statistical distance as the true measurement. If the true measurement is missed and no clutter is nearby, the system will take a more distant measurement as the true one, significantly impacting the tracking accuracy of the NN algorithm. In contrast, both of the other algorithms consider detection probability in their state estimation formulas, enhancing system robustness against missed detections. In summary, the RP-MHTCKF algorithm demonstrates superior tracking performance across different simulation scenarios compared to the RP-NNCKF and RP-JPDACKF algorithms.

3.2. Simulation Validation of Tracking Performance of the IMD-MHRPCKF

In this section, the tracking performance of the IMD-MHRPCKF algorithm is verified through simulation, comparing it with the Maneuver Detection Reweighted Pseudo-Nearest Neighbor-based Radial Parameterized Constrained Kalman Filter (MD-NNRPCKF), Maneuver Detection Cardinalized Probability Hypothesis Density Radial Parameterized Constrained Kalman Filter (MD-CPHDRPCKF), and Maneuver Detection Joint Probabilistic Data Association Radial Parameterized Constrained Kalman Filter (MD-JPDARPCKF) algorithms.

The simulation conditions are set as follows: the sampling time is 0.1 s, and the observation station’s detection range is between 500 m and 4000 m. The number of sub-regions is set to 4, and the Monte Carlo simulation runs 100 times. The initial position of the observation station is set to the origin. Noise data follow a Gaussian distribution with a mean of 5, and position errors follow a uniform distribution. The detection probability is set to $P_d=0.99.$ The model set is configured as follows: Model l is a CV model, and Model 2 is a CT model.

Three targets are tracked, with two targets performing constant-velocity linear motion. The initial states of these two targets are [2500 m, 1900 m, −5.9 m/s, −7.9 m/s], [2500 m, 1600 m, −9.6 m/s, −4.8 m/s], respectively. The third target’s motion trajectory is as follows: from 1 to 70 s, it performs constant-velocity linear motion; from 70 to 80 s, it performs constant-velocity circular motion at a speed of $\pi /30$ rad/s; and from 80 to 150 s, it resumes constant-velocity linear motion. The total movement time is 150 s. The motion state of the observation station is shown in

Table 2. Motion state of the observation station.

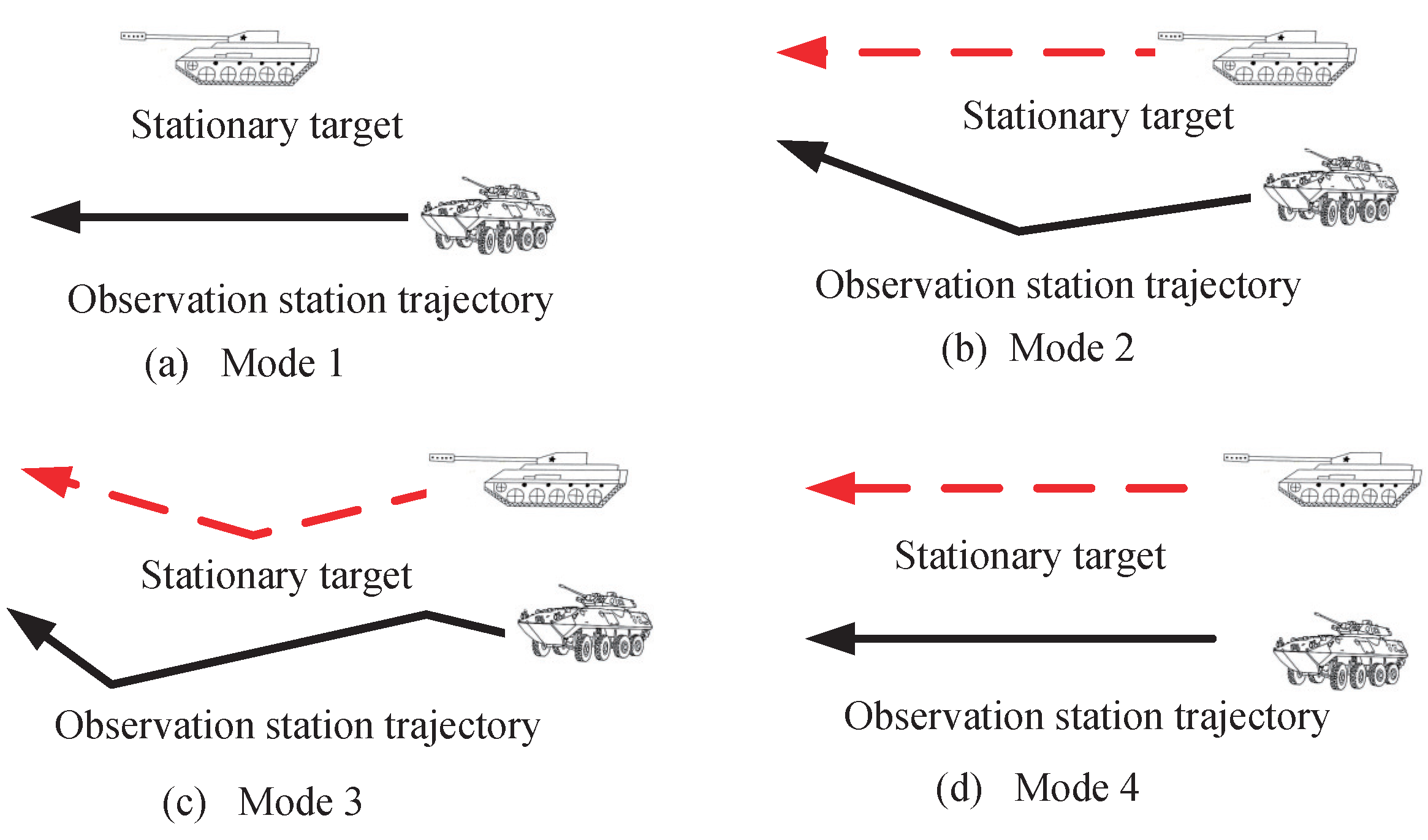
Time (s)	Motion Model	Motion Parameters
1–10	Constant acceleration motion	Acceleration (0.8 m/s2,−0.8 m/s2)
10–25	Constant turn motion	Angular velocity ($\pi /15$ rad/s)
25–80	Constant velocity linear motion	Velocity (−8 m/s, −8 m/s)
80–95	Constant turn motion	Angular velocity ($-\pi /15$ rad/s)
95–150	Constant velocity linear motion	Velocity (8 m/s, −8 m/s)

.

The trajectories of the targets and the observation station are illustrated in Figure 7a, while the distribution of measurements and noise is depicted in Figure 7b. The position root mean square errors (RMSEs) for each target using the MHRPCKF algorithm are presented in Figure 8a, while the position RMSEs for each target using the IMD-MHRPCKF algorithm are shown in Figure 8b. Additionally, the estimated trajectory points are displayed in Figure 9.

From Figure 8b, it can be seen that when Target 3 maneuvers, the estimated points of the IMD-MHRPCKF algorithm deviate from the true trajectory first and are then corrected, eventually aligning closely with the true trajectory. The algorithm’s estimates for Target l and Target 2 remain stable throughout. In comparison with Figure 8b and Figure 9, it is evident that partial false maneuvers do not affect the tracking accuracy of non-maneuvering targets under the MHT algorithm. However, for maneuvering targets, the tracking performance is reduced. The filter’s error in tracking maneuvering targets rises rapidly, and the observation station’s tracking error decreases slowly, but the rate of convergence slows down, and the overall error is large.

The IMD-MHRPCKF algorithm, which combines maneuver detection and MHT, effectively improves the system’s robustness to model uncertainty by resetting the covariance matrix and using different tracking models. This enables good tracking performance for both maneuvering and non-maneuvering targets. The tracking error for Targets 1 and 2 decreases rapidly and remains stable, while the post-maneuver tracking error for Target 3 rises and then falls, eventually converging with the target’s trajectory before the maneuver.

The Optimal Sub-Pattern Assignment (OSPA) metric evaluates multi-target tracking performance by measuring the difference between the estimated and true target states. It is sensitive to several factors, including detection probability ($P_D$) and clutter distribution. Two detection probabilities are considered: $P_D=1$ (perfect detection) and $P_D=0.99$ (slightly missed detections). When $P_D=1$, tracking accuracy is high, but as $P_D$ decreases, the **OSPA** distance increases, indicating reduced robustness due to missed detections. Clutter, modeled by a Poisson distribution with a mean of 5, also impacts the OSPA distance. Higher clutter density introduces more measurement uncertainty, increasing the OSPA distance. Finally, the IMD-MHRPCKF algorithm is compared with other algorithms, calculating the OSPA distance, as shown in Figure 10.

The average OSPA distance for each algorithm is also calculated, and the results are presented in the

Table 3. Average OSPA distance for different algorithms.

Algorithm	IMD- MHRPCKF	MD- CPHDRPCKF	MD- JDPARCKF	MD- NNRPCKF
OSPA (m)	58.10	81.67	132.23	554.69

.

From Figure 10, it can be seen that in the initial phase, the IMD-MHRPCKF and MD-JPDARPCKF algorithms converge quickly, with the error decreasing rapidly. Although the MD-CPHDRPCKF algorithm can also gradually converge, it consistently maintains a relatively large error. The MD-NNRPCKF algorithm fails to converge and exhibits the largest error. After the target maneuvers, the tracking errors for all algorithms increase, but the IMD-MHRPCKF algorithm experiences a smaller tracking error, converges more quickly, and maintains stable tracking.

4. Discussion

As shown in Table 3, the algorithm proposed in this paper achieves the smallest average OSPA distance and the highest tracking accuracy. This is mainly due to the powerful multi-hypothesis generation and evaluation mechanism of the MHT algorithm. It can simultaneously generate multiple possible target trajectory hypotheses, using each hypothesis to handle the potential uncertainty in sensor observation data. By processing and evaluating these hypotheses in parallel, MHT effectively resolves issues such as target crossover, noise interference, and data association.

Especially in complex dynamic environments, MHT demonstrates high flexibility. It can capture multiple target trajectories through various hypotheses and gradually eliminate less likely hypotheses based on new observation data, quickly converging to the correct trajectory. Furthermore, MHT can combine historical data with current observations to ensure that, even in the presence of noise, temporary target loss, or significant observation errors, it can still use hypotheses to predict the possible position of the target, thereby reducing tracking errors.

The multi-hypothesis target tracking algorithm solves the measurement ambiguity problem by establishing a set of hypotheses and updating this set using data association techniques. The downside is its high computational cost, as the increase in the number of targets and clutter will affect the algorithm’s real-time performance. However, the advantage is that it can establish a target library, making it easier to track specific targets. Additionally, since historical data are considered during data association, the tracking accuracy is relatively higher under the same conditions. In practical applications, a suitable multi-target tracking algorithm can be selected based on engineering requirements.

5. Conclusions

This paper proposes a multi-hypothesis pure bearing-only target tracking algorithm based on maneuver detection to address the problem of multi-target tracking in maneuvering scenarios using only angle measurements. First, the observation station’s detection range is divided into several sub-intervals using a range parameterization method, and a CKF is introduced in each interval to solve the problems of unknown initial position and the nonlinearity of the measurement equation. Then, the MHT algorithm is employed to address measurement ambiguity in multi-target tracking under complex environments. Furthermore, the sliding window average of the innovation sequence is calculated to detect whether a target is maneuvering, and a sub-filter parameter reset strategy is used to solve the problem of filter divergence caused by target maneuvers. Finally, simulation results show that the proposed algorithm achieves high tracking accuracy and effectively performs pure bearing-only multi-target tracking in maneuvering scenarios.

Future research could focus on extending the algorithm to incorporate additional sensor data, such as range or velocity measurements, to improve tracking accuracy. Investigating real-time applications in autonomous systems, handling larger numbers of targets, and exploring the integration of deep learning for state estimation and maneuver detection are promising areas. Additionally, practical deployment in real-world scenarios, such as surveillance or autonomous navigation, will be crucial for further validating the proposed algorithm.