Novel Multiple-Input Single-Output Shadow Filter with Improved Passband Gain Using Multiple-Input Multiple-Output DDTAs
Abstract
1. Introduction
- Operational Transresistance Amplifier (OTRA) [11];
- Operational Floating Current Conveyor (OFCC) [16];
- Current Backwards Transconductance Amplifier (CBTA) [21];
- Voltage Differencing Differential Difference Amplifier (VDDDA) [22];
- Voltage Differencing Gain Amplifier (VDGA) [23];
- Current Controlled Current Differencing Cascaded Transconductance Amplifier (CC-CDCTA) [24];
- Differential Current Conveyor Cascaded Transconductance Amplifier (DCCCTA) [27].
2. Circuit Description
2.1. Multiple-Input Multiple-Output DDTA
2.2. Proposed Shadow Filter
- Case 1
- BPF
- HPF
- LPF
- BSF
- APF
- Case 2
- HPF
- LPF
- BPF
- BSF
- APF
2.3. Non-Ideal Analysis
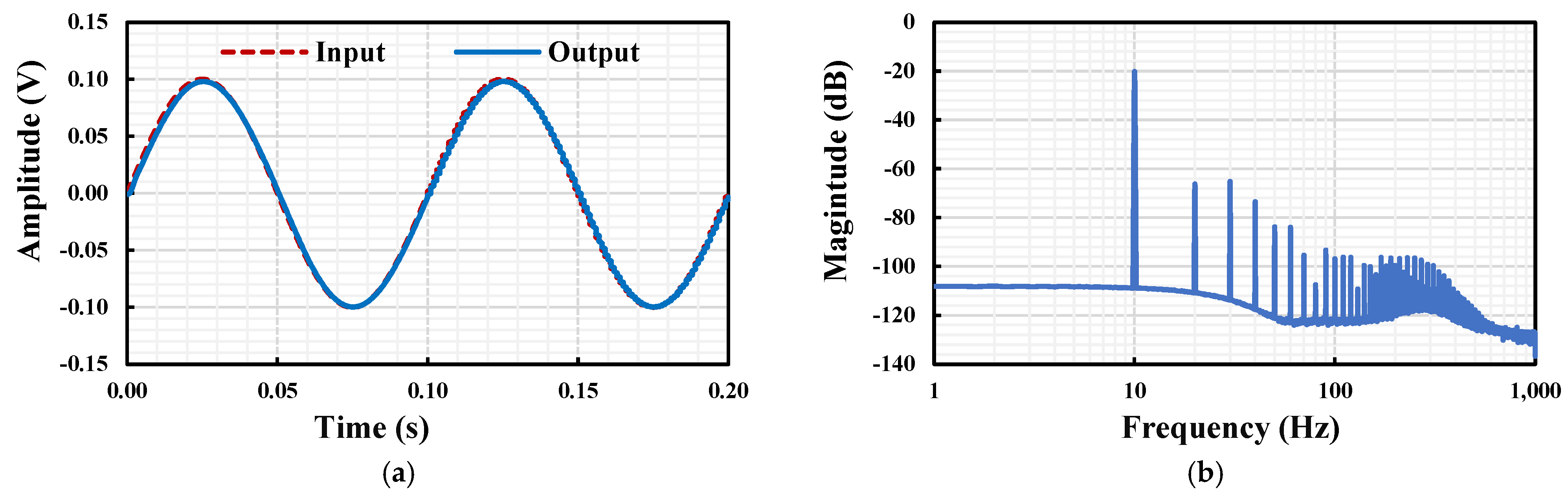
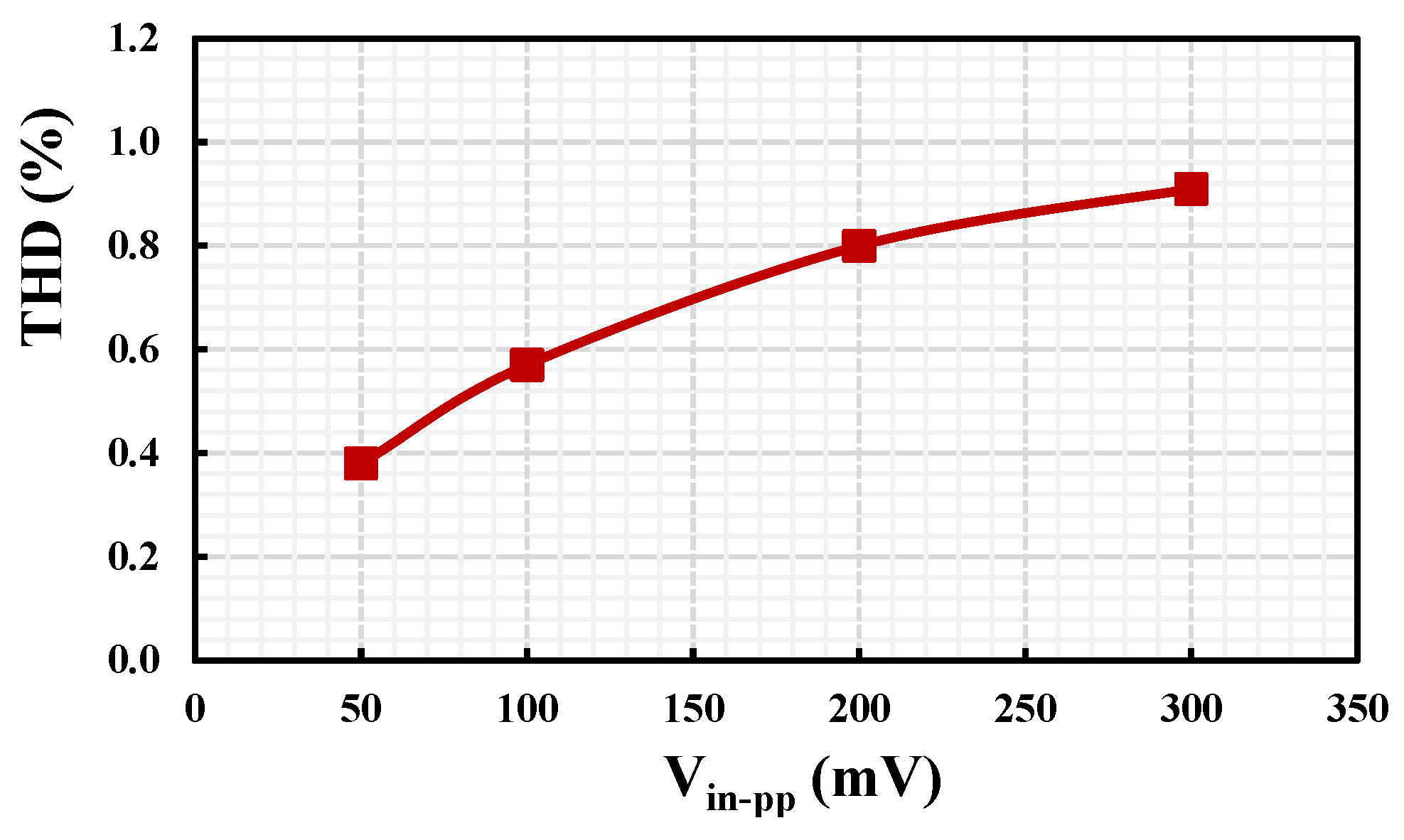
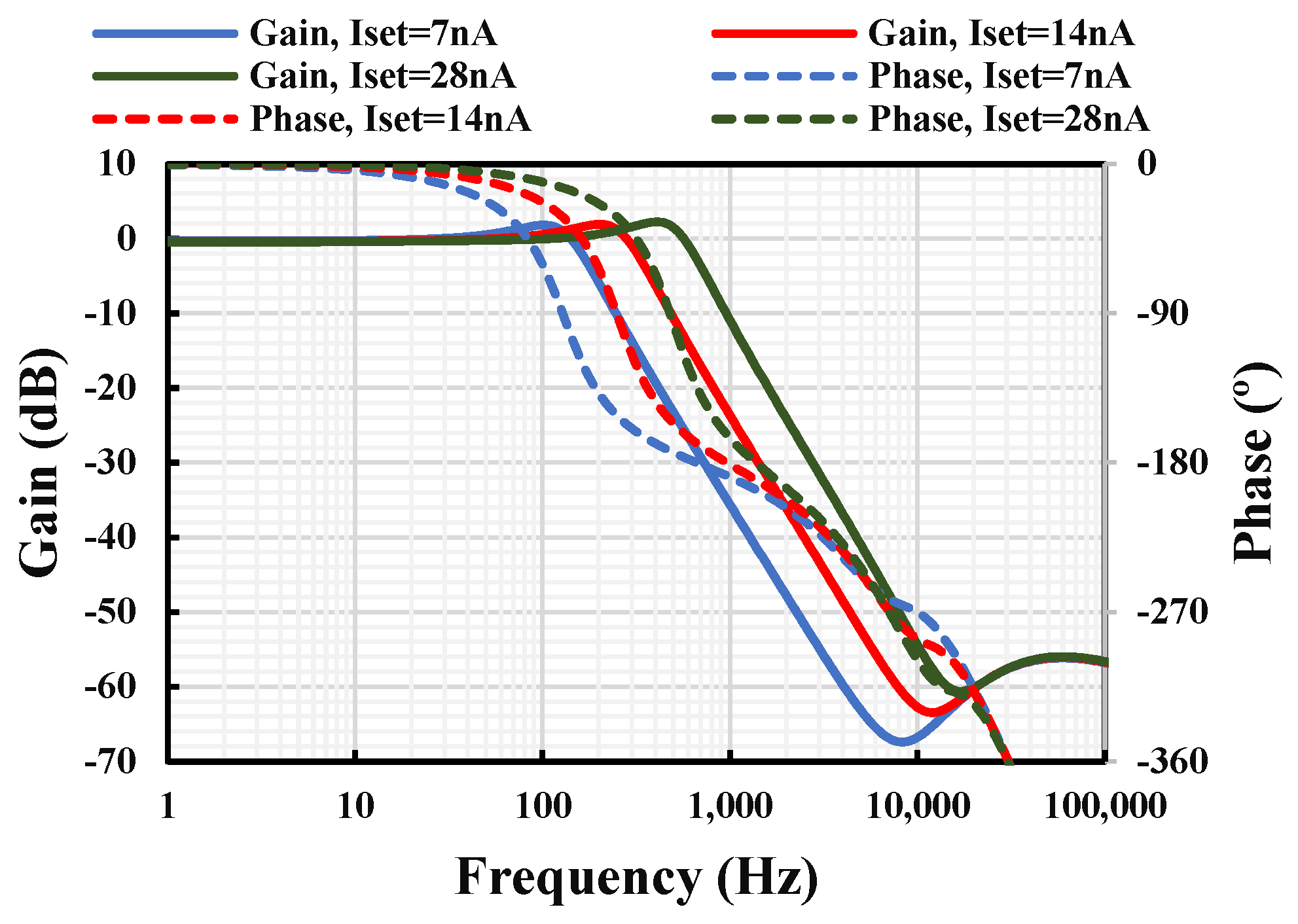
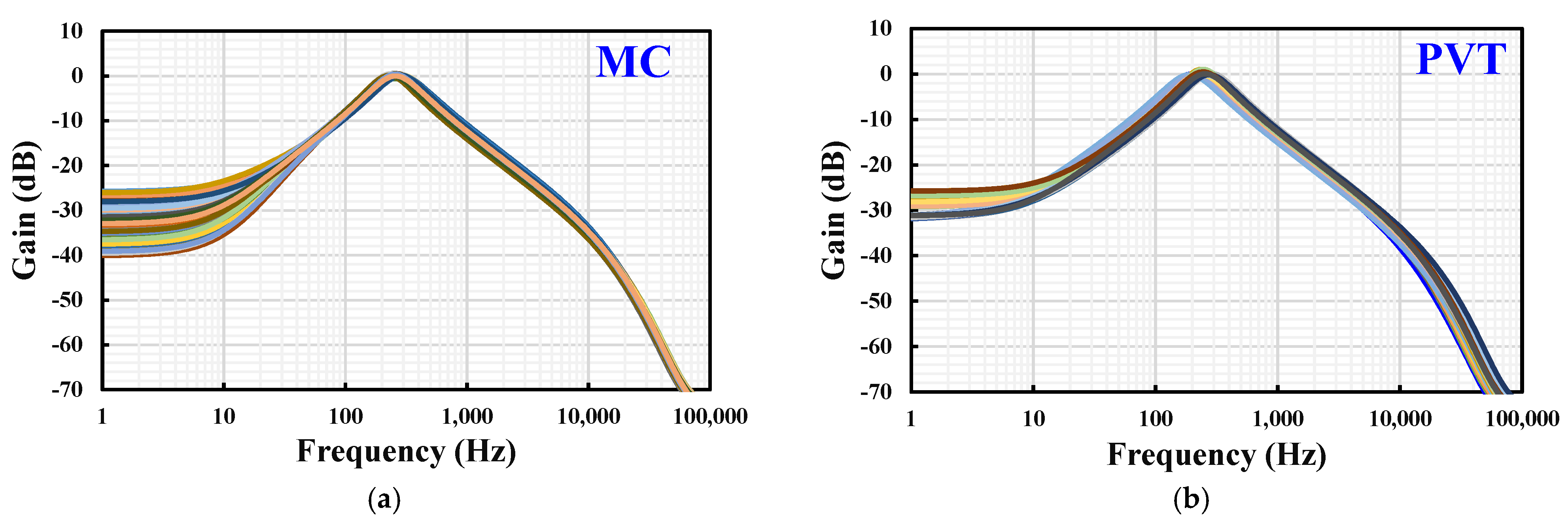
3. Results
- -
- Process corner: MOS transistor variations including fast–fast, slow–fast, fast–slow, and slow–slow, along with MIM capacitor variations of fast–fast and slow–slow.
- -
- Voltage corners: ±10% variation in supply voltage.
- -
- Temperature corners: A range from −10 °C to 60 °C.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lakys, Y.; Fabre, A. Shadow filters-new family of second-order filters. Electron. Lett. 2010, 46, 276–277. [Google Scholar] [CrossRef]
- Lakys, Y.; Fabre, A. Shadow filters generalisation to nth-class. Electron. Lett. 2010, 46, 985–986. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Almutairi, N.R. New current-feedback operational-amplifier based shadow filters. Analog. Integr. Circuits Signal Process. 2016, 86, 471–480. [Google Scholar] [CrossRef]
- Buakaew, S.; Wongtaychatham, C. Boosting the Quality Factor of the Shadow Bandpass Filter. J. Circuits Syst. Comput. 2022, 31, 2250248. [Google Scholar] [CrossRef]
- Varshney, G.; Pandey, N.; Pandey, R. Multi-Functional Fractional-Order Shadow Filter using OTA. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Khateb, F.; Jaikla, W.; Kulej, T.; Kumngern, M.; Kubanek, D. Shadow filters based on DDCC. IET Circuits Devices Syst. 2017, 11, 631–637. [Google Scholar] [CrossRef]
- Serdar, H. MOSFET-C Shadow Filters Based on FDCCII for Cognitive Communications. J. Circuits Syst. Comput. 2023, 32, 2350137. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. A Novel Multiple-Input Single-Output Current-Mode Shadow Filter and Shadow Oscillator Using Current-Controlled Current Conveyors. Circuits Syst. Signal Process. 2024, 43, 5438–5462. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Almutairi, N. New voltage-mode bandpass shadow filter. In Proceedings of the 2016 13th International Multi-Conference on Systems, Signals & Devices (SSD), Leipzig, Germany, 21–24 March 2016; pp. 412–415. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Almutairi, N.R. New CFOA-based shadow bandpass filter. In Proceedings of the 2016 International Conference on Electronics, Information, and Communications (ICEIC), Danang, Vietnam, 27–30 January 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Anurag, R.; Pandey, R.; Pandey, N.; Singh, M.; Jain, M. OTRA based shadow filters. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Alaybeyoglu, E.; Guney, A.; Altun, M.; Mustafa, M.; Kuntman, H. Design of positive feedback driven current-mode amplifiers Z-Copy CDBA and CDTA, and filter applications. Analog. Integr. Circuits Signal Process. 2014, 81, 109–120. [Google Scholar] [CrossRef]
- Pandey, N.; Sayal, A.; Choudhary, R.; Pandey, R. Design of CDTA and VDTA based frequency agile filters. Adv. Electron. 2014, 2014, 176243. [Google Scholar] [CrossRef]
- Atasoyu, M.; Kuntman, H.; Metin, B.; Herencsar, N.; Cicekoglu, O. Design of current-mode class 1 frequency-agile filter employing CDTAs. In Proceedings of the 2015 European Conference on Circuit Theory and Design (ECCTD), Trondheim, Norway, 24–26 August 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Alaybeyoglu, E.; Kuntman, H. A new frequency agile filter structure employing CDTA for positioning systems and secure communications. Analog. Integr. Circuits Signal Process. 2016, 89, 693–703. [Google Scholar] [CrossRef]
- Nand, D.; Pandey, N. New configuration for OFCC-based CM SIMO filter and its application as shadow filter. Arab. J. Sci. Eng. 2018, 43, 3011–3022. [Google Scholar] [CrossRef]
- Alaybeyoglu, E.; Kuntman, H. CMOS implementations of VDTA based frequency agile filters for encrypted communications. Analog. Integr. Circuits Signal Process. 2016, 89, 675–684. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. Fully active and minimal shadow bandpass filter. In Proceedings of the 2018 International Conference on Engineering, Applied Sciences, and Technology (ICEAST), Phuket, Thailand, 4–7 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. Shadow bandpass filter with Q-improvement. In Proceedings of the 2019 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Luang Prabang, Laos, 2–5 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. High quality-factor shadow bandpass filters with orthogonality to the characteristic frequency. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 372–375. [Google Scholar] [CrossRef]
- Chhabra, K.; Singhal, S.; Pandey, N. Realisation of CBTA based current mode frequency agile filter. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 1076–1081. [Google Scholar] [CrossRef]
- Huaihongthong, P.; Chaichana, A.; Suwanjan, P.; Siripongdee, S.; Sunthonkanokpong, W.; Supavarasuwat, P.; Jaikla, W.; Khateb, F. Single-input multiple-output voltage-mode shadow filter based on VDDDAs. AEU-Int. J. Electron. Commun. 2019, 103, 13–23. [Google Scholar] [CrossRef]
- Moonmuang, P.; Pukkalanun, T.; Tangsrirat, W. Voltage differencing gain amplifier-based shadow filter: A comparison study. In Proceedings of the 2020 6th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Chiang Mai, Thailand, 1–4 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Realization of current mode universal shadow filter. AEU-Int. J. Electron. Commun. 2020, 117, 153088. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Improved current mode biquadratic shadow universal filter. Inf. MIDEM 2022, 52, 51–66. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Mixed-mode universal filter using FD-CCCTA and its extension as shadow filter. Inf. MIDEM 2022, 52, 239–262. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Realization of multi-mode universal shadow filter and its application as a frequency-hopping filter. Mem.-Mater. Devices Circuits Syst. 2023, 4, 100049. [Google Scholar] [CrossRef]
- Khateb, F.; Kumngern, M.; Kulej, T.; Ranjan, R.K. 0.5 V multiple-input multiple-output differential difference transconductance amplifier and its applications to shadow filter and oscillator. IEEE Access 2023, 11, 31212–31227. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. Shadow filters using multiple-input differential difference transconductance amplifiers. Sensors 2023, 23, 1526. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. 0.5 V Universal Filter and Quadrature Oscillator Based on Multiple-Input DDTA. IEEE Access 2023, 11, 9957–9966. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Tang, K.-T. A 0.5-V multiple-input bulk-driven OTA in 0.18-μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1739–1747. [Google Scholar] [CrossRef]
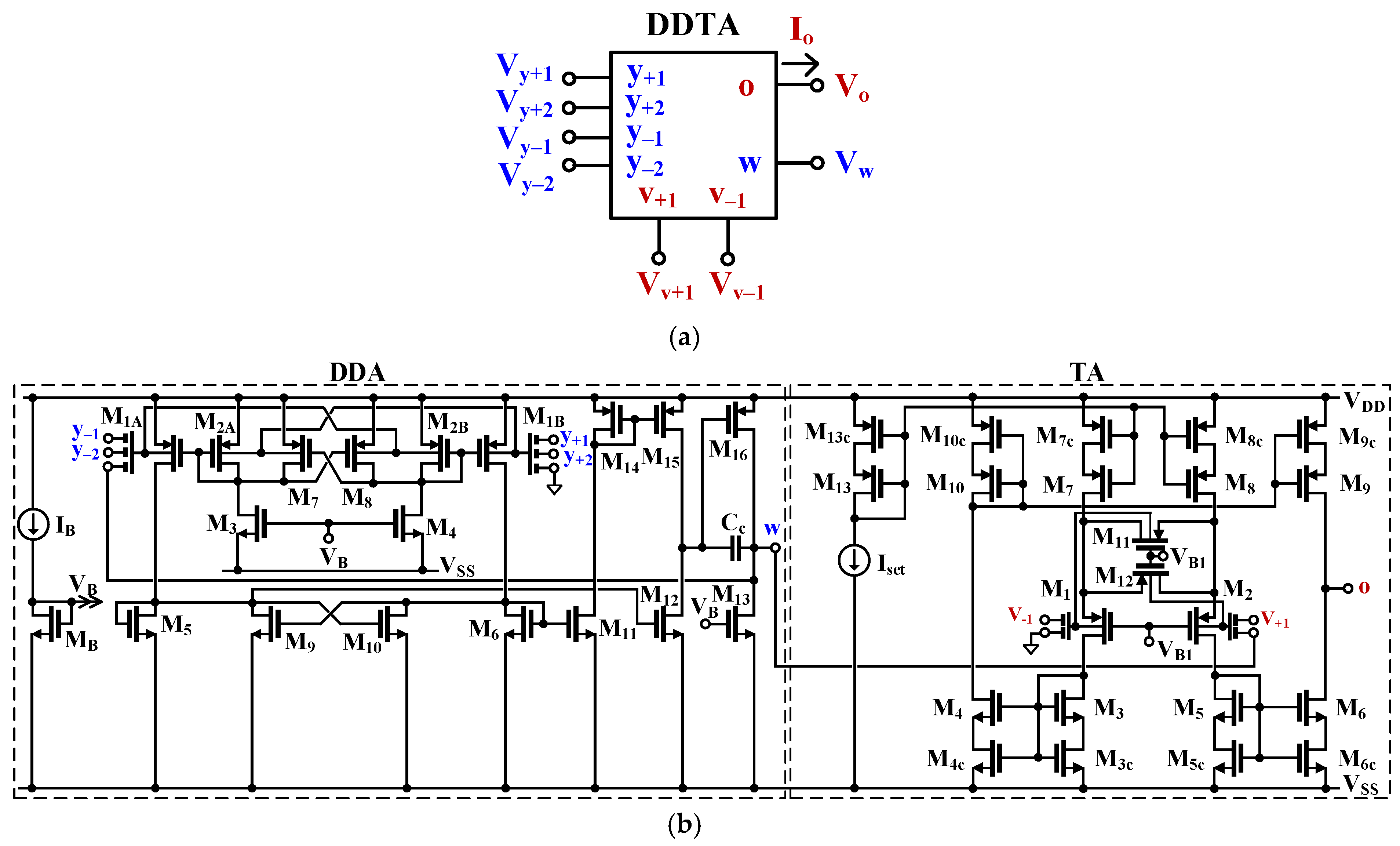
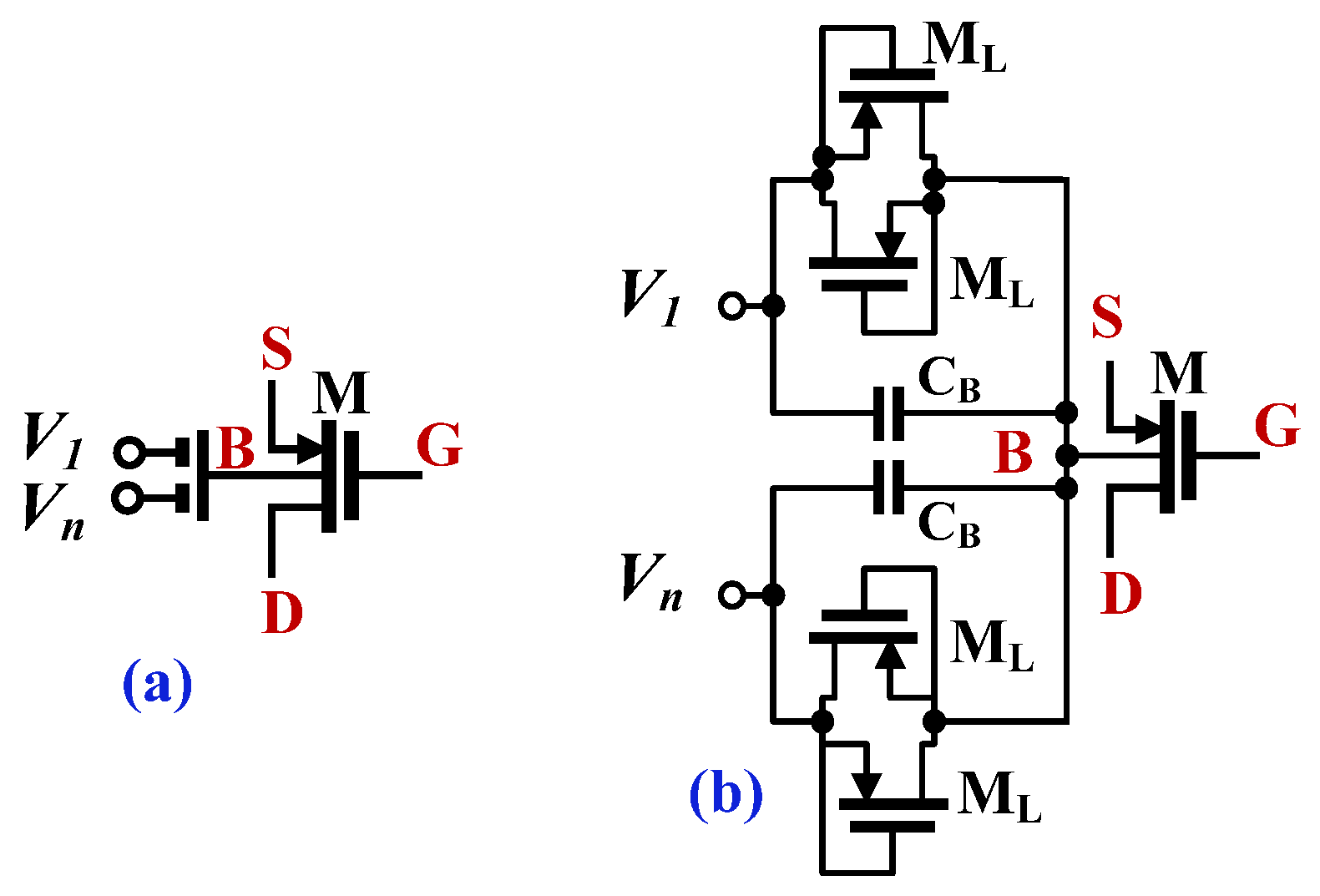




| DDA | W/L (µm/µm) | TA | W/L (µm/µm) |
|---|---|---|---|
| M1A, M2A, M1B, M2B M14, M15 | 16/3 | M1, M2 | 2 × 15/1 |
| M3–M8, M11–M12, MB | 8/3 | M3–M6 | 2 × 10/1 |
| M9, M10 | 4/3 | M3c–M6c | 10/1 |
| M16 | 6 × 16/3 | M7–M10, M13 | 2 × 15/1 |
| M13 | 6 × 8/3 | M7c–M10c, M13c, M11, M12 | 15/1 |
| ML | 5/4 | ML | 5/4 |
| MIM capacitor: CB = 0.5 pF, Cc = 6 pF | VB = −50 mV | ||
| Factor | Proposed | [22] 2019 | [24] 2020 | [25] 2022 | [27] 2023 | [28] 2023 |
|---|---|---|---|---|---|---|
| Number of devices | 4-DDTA, 2-C, 2-R | 3-VDDDA, 2-C, 1-R | 3-CDCTA, 1-CCII, 2-C | 2-CCCTA, 2-C | 2-DCCCTA, 2-C, 2-R | 4-DDTA, 2-C, 3-R |
| Realization | CMOS structure | CMOS structure & commercial IC | CMOS structure & commercial IC | CMOS structure | CMOS structure & commercial IC | CMOS structure |
| Type of filter | MISO | SIMO | MIMO | SIMO | SIMO | MISO |
| Operation mode | VM | VM | CM | CM | CM/TAM | VM |
| Number of offered responses | 10 | 5 | 5 | 5 | 5/5 | 4 |
| All grounded capacitor | Yes | Yes | No | Yes | Yes | Yes |
| Ideal input and output impedances for VM or CM circuit | Yes | No | No 1 | Yes | Yes | Yes |
| Adjusting and without altering the passband gain | Yes | No | No | No | No | No |
| Simulated power supply (V) | 0.5 | ±0.9 | ±1.25 | ±1.25 | ±1.7 | 0.5 |
| Natural frequency (Hz) | 251.18 | 1 × 106 | 81.2 × 106 | 20.02 × 106 | 6.57 × 106 | 214.3 |
| Power dissipation (mW) | 1.543 × 10−3 | - | 2.23 | 4.1 | 2.5 | 0.873 × 10−3 |
| Total harmonic distortion (%) | 0.8@0.2 Vpp | 1@200 mVpp | <1@600 μA | <1@400 μA | <2@400 μA | 2%@60 mVpp |
| Verification of result | Sim | Sim/Exp | Sim/Exp | Sim | Sim/Exp | Sim |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumngern, M.; Khateb, F.; Kulej, T. Novel Multiple-Input Single-Output Shadow Filter with Improved Passband Gain Using Multiple-Input Multiple-Output DDTAs. Electronics 2025, 14, 1417. https://doi.org/10.3390/electronics14071417
Kumngern M, Khateb F, Kulej T. Novel Multiple-Input Single-Output Shadow Filter with Improved Passband Gain Using Multiple-Input Multiple-Output DDTAs. Electronics. 2025; 14(7):1417. https://doi.org/10.3390/electronics14071417
Chicago/Turabian StyleKumngern, Montree, Fabian Khateb, and Tomasz Kulej. 2025. "Novel Multiple-Input Single-Output Shadow Filter with Improved Passband Gain Using Multiple-Input Multiple-Output DDTAs" Electronics 14, no. 7: 1417. https://doi.org/10.3390/electronics14071417
APA StyleKumngern, M., Khateb, F., & Kulej, T. (2025). Novel Multiple-Input Single-Output Shadow Filter with Improved Passband Gain Using Multiple-Input Multiple-Output DDTAs. Electronics, 14(7), 1417. https://doi.org/10.3390/electronics14071417








