Next Article in Journal
Influence of Environmental Factors on the Accuracy of the Ultrasonic Rangefinder in a Mobile Robotic Technical Vision System
Previous Article in Journal
DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection
Previous Article in Special Issue
Calibration-Enhanced Multi-Awareness Network for Joint Classification of Hyperspectral and LiDAR Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 14
Issue 7
10.3390/electronics14071392
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Feasibility Research on the Auxiliary Variables in Scaling of Soil Moisture Based on the SiB2 Model: A Case Study in Daman

by
Zebin Zhao
1 and
Rui Jin
1,2,*
1
Heihe Remote Sensing Experimental Research Station, Key Laboratory of Remote Sensing of Gansu Province, State Key Laboratory of Cryospheric Science and Frozen Soil Engineering, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China
2
University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Electronics 2025, 14(7), 1392; https://doi.org/10.3390/electronics14071392
Submission received: 17 February 2025 / Revised: 25 March 2025 / Accepted: 28 March 2025 / Published: 30 March 2025
(This article belongs to the Special Issue Advances in AI Technology for Remote Sensing Image Processing)
Browse Figures
Versions Notes

Abstract

:
Soil moisture is a core climate variable in land surface processes and has a strong influence on the energy balance and water exchange between the land surface–vegetation–atmosphere columns. However, the low spatial resolution of soil moisture remote sensing products cannot satisfy the requirements of research and applications based on hydro-meteorological and eco-hydrological simulations and the management of water resources at the watershed scale. A feasible solution is to downscale soil moisture products derived from microwave remote sensing, which often requires the support of auxiliary variables. Meanwhile, during the validation process of remote sensing products, the spatial scales between in situ observations and remote sensing pixel retrievals are inconsistent; thus, in situ observations should be translated to ground truths at a pixel scale via reasonable upscaling methods. Many auxiliary variables can serve as proxies in the scaling of soil moisture, although few studies have analyzed their feasibility and application conditions. In this paper, a SiB2 (Simple Biosphere Model-II) simulation for the Daman superstation from 1 May to 30 September 2013, was employed to calculate seven auxiliary variables related to soil moisture: ATIs and ATIc (Apparent Thermal Inertias based on surface soil temperature and canopy temperature), E (Evaporation), E/ETa (Ratio of Evaporation and Actual Evapotranspiration), E/ETp (Ratio of Evaporation and Potential Evapotranspiration), EF (Evaporative Fraction) and AEF (Actual Evaporative Fraction). The applicability of these variables was then evaluated via a correlation analysis between the variables and soil moisture. The results indicated that E is highly sensitive to soil moisture at Phase I (R2 ≥ 0.67), whereas ATIs is the greatest indicator of soil moisture at Phase II (R2 ≥ 0.51). Considering both the correlation and computability of these auxiliary variables, the EF (R2 ≥ 0.56) and AEF (R2 ≥ 0.54) are recommended as proxies for Phase I, while ATIs (R2 ≥ 0.51) is also recommended for Phase II.

1. Introduction

Soil moisture plays an important role in terrestrial water cycles and land–atmosphere interactions [1,2,3,4], which control the process of hydrothermal dynamics [1,2,5] and the vitality of ecosystems [2,6,7]. Thus, precise soil moisture information holds paramount importance for various applications, including drought monitoring [8], water resource management [9,10], and numerical weather prediction [11,12].
With the development of microwave remote sensing in recent years, research and applications related to soil moisture observed via active and passive microwave sensors have increased [13,14]. Microwave remote sensing has become the main technique used to measure soil moisture distribution at regional and global scales [15]. Recently, the L band has been considered optimal for monitoring soil moisture because of its high dielectric constant of liquid water and deeper penetration depth. The Soil Moisture and Salinity Mission (SMOS) [16] and Soil Moisture Active Passive Mission (SMAP) [17,18] were launched in 2009 and 2015, respectively, aimed to map global soil moisture with an accuracy of 0.04 cm3/cm3. However, soil moisture remote sensing products from passive radiometers and active scatterometers generally have a coarse spatial resolution (25~40 km), which does not provide detailed distribution data for soil moisture used in hydrological data assimilation systems, evapotranspiration estimations, and agricultural irrigation management at a watershed scale [19,20]. In practice, soil moisture maps with spatial resolutions of more than 10 km are urgently required at the watershed scale because vegetation coverage, soil texture, and topography lead to high spatial variations in soil moisture. Thus, downscaled microwave remote sensing soil moisture products have been rapidly developed in recent decades and are receiving more attention [21,22]. Advances in deep learning and artificial intelligence have opened new avenues for soil moisture downscaling. For instance, convolutional neural networks and other AI-based methods can effectively capture complex spatiotemporal patterns, often outperforming traditional methods in terms of spatial resolution and prediction accuracy [23,24,25]. Additionally, to achieve a more detailed soil moisture map, it is essential to acquire auxiliary variables at higher spatial resolutions. These high-resolution inputs are crucial for accurately capturing the spatial heterogeneity of soil moisture within microwave remote-sensing pixels. The footprint of microwave remote sensing pixels is substantially larger than the small-scale area (52 cm2) of in situ soil moisture measurement [26], a scale discrepancy arises during the validation of soil moisture products, especially when the spatial variability of soil moisture is much stronger because of the compound influence of soil, vegetation, topography, and precipitation [27,28,29]. At present, the use of multi-point wireless sensor networks [30] and systems such as the COSMOS (Cosmic-ray Soil Moisture Observing System), which performs at the footprint scale, are recommended for the validation of soil moisture products. Multi-point observations should be ground truthed at a pixel scale via reasonable upscaling [26,31], and this process also requires the support of auxiliary variables.
Multispectral remote sensing data from visible and near-infrared, to thermal infrared and microwave bands, constitute the primary source of auxiliary variables for soil moisture estimation [32]. Due to the distinct sensing principles across these bands, each auxiliary variable captures different aspects of soil moisture, reflecting conditions at various depths and under varying vegetation coverages. Optical remote sensing leverages the strong absorption in the red band and high reflection in the near-infrared band of vegetation to indirectly infer the soil moisture. During the entire vegetation growing season, a robust positive correlation occurs between the Normalized Difference Vegetation Index (NDVI) and soil moisture [33,34]. In addition, variables such as the Anomaly Vegetation Index (AVI), Vegetation Condition Index (VCI), and Temperature Vegetation Index (TVI) are effective in delineating interannual variations in soil water deficits. However, since these indexes are fundamentally derived from the NDVI, their application is largely confined to areas with significant vegetation cover. Thermal infrared remote sensing uses surface radiation to retrieve land surface temperatures. The correlation between Land Surface Temperature (LST) and soil moisture was initially presented by Carlson [33], who indicated that LST can reflect soil moisture when the underlying surface is bare and the weather is cloudless. However, accurate calculations of LST are often limited by cloudy skies. Furthermore, LST is sensitive to the vegetation water content and reflects the canopy temperature when the vegetation coverage fraction is high. Under conditions of bare soil and low vegetation cover, the Apparent Thermal Inertia (ATI) [35], which is a function of the LST and broadband albedo, proves more effective in capturing the spatial variability of soil moisture, although its correlation diminishes as vegetation cover increases. MODIS-derived ATI values have been successfully employed to upscale in situ soil moisture measurements on the Tibetan Plateau, where the predominant land cover alpine meadow [26,36]. Additionally, microwave remote sensing, which utilizes radiative and scattering signals to monitor the hydrological and geometrical characteristics on the land surface, is an essential method for monitoring soil moisture based on the dielectric sensitivity of the microwave brightness temperature to the soil moisture. Knipper [37] evaluated the contributions of albedo and brightness temperature in enhancing the spatial resolution of soil moisture products (at a 1 km scale) and found that brightness temperature offers superior precision in representing the spatial variability of soil moisture.
A series of auxiliary variables for estimating soil moisture has been developed in recent years by combining the advantages of optical and thermal infrared remote sensing. A combination of NDVI, albedo, and LST data have proven effective in downscaling soil moisture from a coarse resolution of 25 km to a finer resolution of 1 km, and the spatial distribution of the downscaled 1 km soil moisture remains relatively consistent with that of coarse measurements [38]. A Soil Moisture Agricultural Drought Index (SMADI) [39] developed in 2016 can capture the duration and intensity of drought events during the vegetation growing season. A new Temperature–Vegetation–soil Moisture Dryness Index (TVMDI) [40] was recently developed based on the LST, Vegetation Index (VI), and soil moisture, and it is regarded as a potential index for mapping dryness over different regions. The Temperature Vegetation Dryness Index (TVDI) [41] can efficiently estimate soil moisture in the vegetation root zone, although building the feature space requires a large number of samples and the scalability is weaker. Kang [42] used three auxiliary remote sensing data types (Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) TVDI data, airborne microwave brightness temperature, and MODIS TVDI data) to upscale soil moisture observed by a wireless sensor network, and they found that the ASTER TVDI is an optimal index for describing the heterogeneity of soil moisture within the microwave pixels compared with other types of remote sensing information. Based on the fractal interpolation theory, Kim [43] used the spatial and temporal distribution information of vegetation water content and soil texture to downscale 10 km soil moisture to a spatial resolution of 1 km. The results demonstrate that this method can obtain higher resolution soil moisture products and capture extremely high and low soil moisture distributions. A combination of optical, thermal infrared, and microwave bands can retrieve soil moisture with high accuracy, and this method has also recently become widely used. Soil Evaporative Efficiency (SEE), defined as the ratio of actual to potential evaporation [44], is particularly sensitive to the surface soil moisture; however, accurately estimating soil evaporation from remote sensing remains challenging, with uncertainties further compounded by factors such as precipitation and irrigation. Merlin [44] derived the SEE from the vegetation fraction and land surface temperature data and then employed the MODIS-derived SEE to downscale SMOS soil moisture from a 40 km resolution to finer scales of 10 km/4 km resolutions. Both the Evaporative Fraction (EF) and the Actual EF are sensitive to soil moisture. Merlin [45] effectively utilized these auxiliary information types to downscale soil moisture, and the results accurately captured the pattern of soil moisture in microwave pixels. Furthermore, integrating both active and passive L-band microwave remote sensing has emerged as a promising strategy for enhancing the spatial resolution of soil moisture. Researchers have combined Sentinel-1 backscatter data and SMOS or SMAP brightness temperatures to retrieve soil moisture data with a spatial resolution of 100 m [46]. By leveraging high-resolution active microwave backscatter, it becomes possible to decompose the L-band passive microwave brightness temperature, yielding brightness temperature data at finer resolutions. This, in turn, enables the retrieval of soil moisture at a higher spatial resolution [47].
In soil moisture simulation and land surface process studies, commonly used land surface models include the Simple Biosphere Model-II (SiB2) [48,49], the Noah Land Surface Model (Noah LSM) [50], and the Community Land Model (CLM) [51]. Each of these models has distinct characteristics in terms of complexity, computational requirements, input demands, and applicability. Selecting an appropriate model is crucial for ensuring the accuracy and feasibility of research on soil moisture-related auxiliary variables. SiB2 is a well-established biosphere model capable of simulating land–atmosphere interactions, including energy fluxes and water exchanges between the soil, vegetation, and atmosphere [49]. It provides key hydrological and biophysical variables, such as evaporation, potential evapotranspiration, actual evapotranspiration, and surface energy fluxes. Compared to Noah LSM, SiB2 offers a more comprehensive representation of plant physiological processes, making it particularly suitable for studying the influence of vegetation on soil moisture dynamics. In contrast to CLM, SiB2 maintains a high level of simulation accuracy while requiring lower computational costs, making it well-suited for regional-scale soil moisture studies. Furthermore, SiB2 has strong scalability and can directly generate multiple auxiliary variables closely related to soil moisture. These outputs facilitate direct applications in soil moisture estimation and scaling, eliminating the need for additional complex parameterizations. Additionally, SiB2 has been widely applied in hydrological and eco-hydrological studies across various regions [52], demonstrating its reliability and robustness in different environmental conditions. Considering model complexity, computational efficiency, the ability to capture vegetation-soil moisture interactions, and overall suitability for the objectives of this study, SiB2 is the most appropriate choice. It provides a balance between accuracy and efficiency while offering direct outputs of key auxiliary variables, supporting soil moisture scaling and mapping applications.
In the above studies, numerous auxiliary variables have been employed to facilitate soil moisture scaling, yet comprehensive evaluations of their applicability remain scarce. Therefore, this study aims to analyze the applicable conditions for each auxiliary variable through SiB2 simulations in Daman station. By performing so, the study aims to provide robust pattern information that can enhance the accuracy of soil moisture scale conversion, ultimately supporting the development of more reliable remote sensing products.

2. Materials

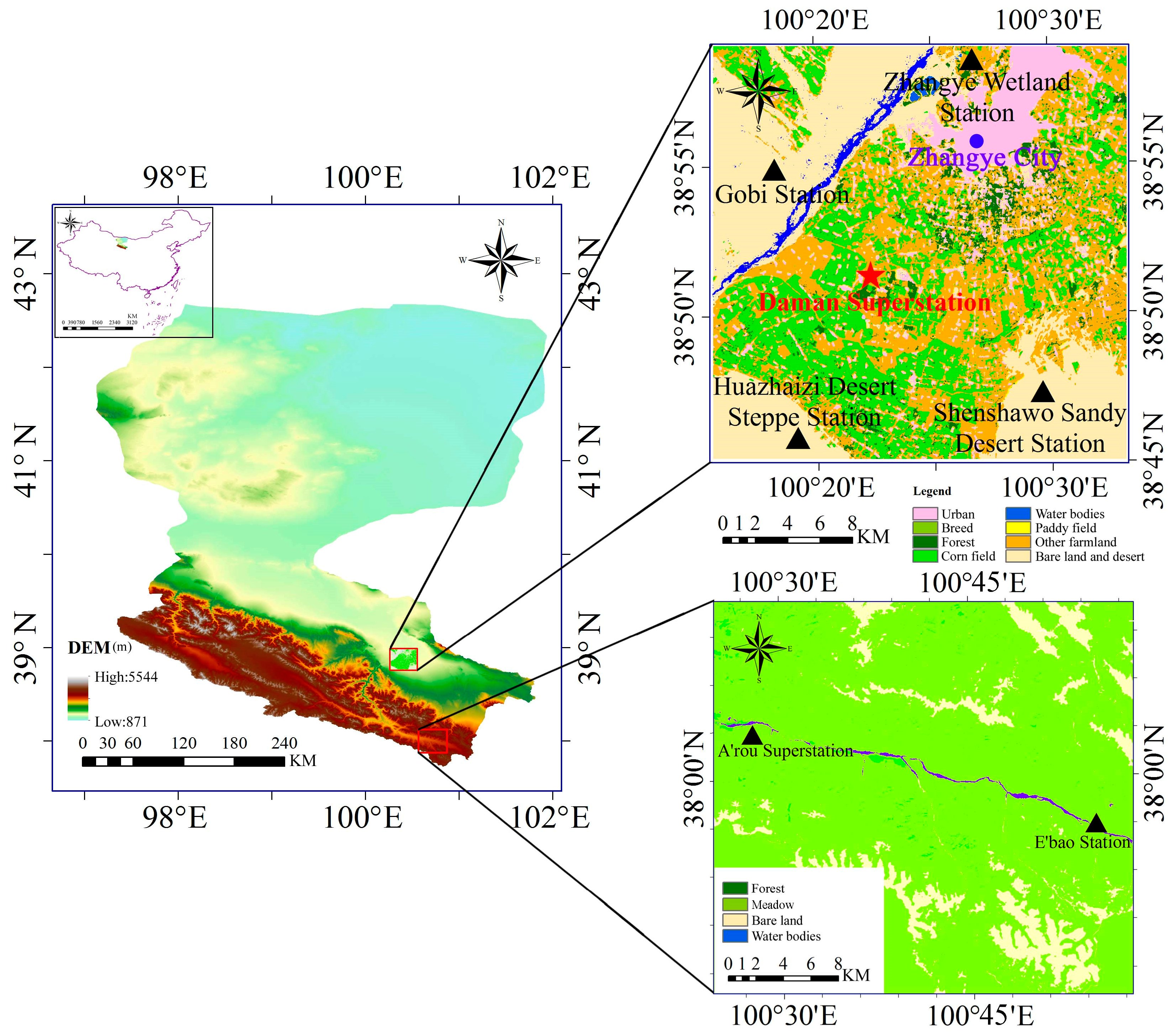
2.1. Study Area

The study area is situated in the Daman irrigation region of Zhangye City, Gansu Province, in northwestern China. The Daman superstation (100.37223° E, 38.85551° N, 1556 m), equipped with a 40 m boundary layer tower, is located southwest of the Zhangye Oasis in the middle reach of the Heihe River Basin (Figure 1). This station is centrally positioned within a seed corn field, reflecting the region’s predominant agricultural activity. The region’s soils are predominantly classified as gray desert soils, characterized by a coarse texture with sandy loam and loamy sand compositions. Climatically, the area experiences a typical continental steppe desert climate, primarily influenced by high-altitude westerly winds, circulation patterns, and cold air masses. The annual average air temperature is 6 °C, with the highest and lowest air temperature occurring in July and January, respectively. The average annual rainfall is 114.9 mm, and 70% of the precipitation appears from June to September. In spring, sandstorms occasionally happen. Crops are irrigated approximately once per month during the growing season [53,54]. The fractured landscape and rotational irrigation system are the two main factors resulting in the heterogeneity of soil moisture and evapotranspiration.

2.2. Data

All of the data in this study were provided freely by the Heihe Watershed Allied Telemetry Experimental Research (HiWATER) project (https://www.ncdc.ac.cn/portal/, accessed on 1 May 2022). The Daman Superstation observations were performed between Julian days 121 to 273 of 2013 (1 May to 30 September 2013), and they were used to force the SiB2 model [53,54,55], which includes four components of radiation, air pressure, air relative humidity, horizontal wind speed, air temperature, and precipitation with 10 min observation steps (Table 1). Artificial irrigation was converted to precipitation (mm) by the unit area average. The soil parameters are mainly extracted from “HiWATER: Dataset of soil parameters in the middle reaches of the Heihe River Basin” [56], which includes soil texture, soil porosity, soil bulk density, saturated hydraulic conductivity, and organic matter content information (Table 2). For instance, at the 0–5 cm depth, clay accounted for 5.27%, silt for 66.01%, and sand for 28.72%; at the 10 cm depth, clay comprised 4.78%, silt 65.03%, and sand 30.19%.

3. Methods

The SiB2 is a process-based land surface model that simulates the exchanges of energy, water, and carbon between the land surface and the atmosphere. It incorporates key biophysical and hydrological processes, including surface energy balance, soil moisture dynamics, evapotranspiration, and canopy interactions. SiB2 parameterizes land cover, soil properties, and meteorological forcing data to estimate critical variables such as surface and canopy temperature, latent and sensible heat fluxes, and soil moisture content. These outputs provide a comprehensive representation of land–atmosphere interactions, making SiB2 well-suited for soil moisture studies. In this study, we utilize the SiB2 model [48,49] to simulate the soil moisture, soil surface/canopy temperature, evaporation, and evapotranspiration of the study area; whereas the Penman–Monteith formula was used to calculate the potential evapotranspiration (Appendix A, Table A1). Then, seven auxiliary indices were estimated based on the SiB2 simulation: ATIs and ATIc (Apparent Thermal Inertia based on the soil surface temperature and canopy temperature, respectively), E (Evaporation), E/ETa (Ratio of Evaporation and Actual Evapotranspiration), E/ETp (Ratio of Evaporation and Potential Evapotranspiration), EF (Evaporative Fraction) and AEF (Actual Evaporative Fraction). Eventually, the correlations between these auxiliary variables and soil moisture at 2 cm and 10 cm simulated by SiB2 were analyzed during the growing season in Phase I (from 1 May to 1 July) and Phase II (from 2 July to 30 September) to quantitatively determine the feasibility of the variables. The definition and calculation of these variables are described below.

3.1. Auxiliary Information

3.1.1. Apparent Thermal Inertia (ATI)

The soil thermal inertia is a variable used to describe the impedance of soil to temperature variation, which is closely dependent on the soil moisture. For calculation simplicity, the ATI was proposed by Price [35] to represent the relative value of thermal inertia, which is a function of the difference between the LSTs in the daytime and at nighttime. Here, ATI (K−1) is calculated according to Price’s method [35]:
A T I = 1 − A L S T m a x − L S T m i n
where A is the broadband albedo, which can be calculated from the ratio of reflected radiation to total incident radiation; and LSTmax and LSTmin are the daily maximum and minimum land surface temperatures (K), respectively. In this paper, the ATI will be calculated by two different methods to test the effects of two components of LST: one is based on the vegetation canopy temperature (Tc) and the other is based on the soil surface temperature (Ts). The vegetation canopy temperature and the soil surface temperature are all derived from the SiB2 simulation.

3.1.2. Evaporation (E)

Evaporation from the soil surface is one of the key components of land surface energy and water balance and influences the partitioning of available energy into sensible and latent heat fluxes [57]. Moreover, evaporation regulates climate through a series of feedback acting on air temperature, humidity, and precipitation [4,58]. Evaporation is highly sensitive to the availability of surface soil moisture. Evaporation in the SiB2 is parameterized as follows:
E = ∆ · R n − G + ρ a · C p · D / r a ∆ + γ · 1 + r s / r a
where E represents evaporation (mm), refers exclusively to soil evaporation—the water loss directly from the soil surface, Δ is the slope of saturated vapor pressure with temperature (Pa/K), Rn is the surface net radiation (W/m2), G is the surface ground heat flux (W/m2), D is the vapor pressure (Pa), rs is the surface soil resistance (s/m), ra is the aerodynamic resistance between ground and canopy air space (s/m), ρa is the air density (kg/m3), CP is the specific heat of air (J/(kg·K)), and γ is the psychrometric constant (Pa/K).

3.1.3. Ratio of Evaporation and Actual Evapotranspiration (E/ETa)

Actual evapotranspiration contains both soil evaporation and vegetation transpiration, reflecting the constraints imposed by the available soil moisture. Therefore, E/ETa represents the fraction of soil evaporation among the total evapotranspiration. Here, E and ETa are outputted directly from the SiB2 simulation.

3.1.4. Ratio of Evaporation and Potential Evapotranspiration (E/ETp)

ETp refers to the theoretical maximum evaporation and transpiration rate that would occur under conditions of unlimited water supply. E/ETp represents the ratio of soil evaporation to potential evapotranspiration. Evaporation is obtained from the SiB2 simulation, and potential evapotranspiration is calculated by the Penman–Monteith formula.
E T p = 0.408 × ∆ · R n − G + γ · 37 T · u 2 · D ∆ + γ · 1 + 0.34 · u 2
where ETp is the potential evapotranspiration (mm) computed by the Penman–Monteith formula, Δ is the slope of the saturation vapor pressure versus temperature relationship, Rn is the surface net radiation (W/m2), G is the surface ground heat flux (W/m2), T is the average temperature (K) at 2 m, D represents the vapor pressure deficit of the air, γ is the psychrometric constant (Pa/K), and u2 is the wind speed (m/s) at 2 m.

3.1.5. Evaporative Fraction (EF)

Because of the stability of the EF on sunny days [59], it is usually used in temporal extrapolation methods to convert the instantaneous evapotranspiration to daily evapotranspiration. Shuttleworth [59] presented an EF formula that assumes constancy during the daytime, and EF is calculated as the ratio of latent heat flux to the total energy available at the soil surface, thus representing the proportion of energy that contributes to evaporation:
E F = λ · E R n − G
where λE is the latent heat flux (W/m2), Rn is the surface net radiation (W/m2), and G is the surface ground heat flux (W/m2). All of these parameters can be provided by the SiB2 simulation.

3.1.6. Actual Evaporative Fraction (AEF)

The AEF is a fundamental driver of plant growth and can be used to describe regional climate characteristics [60] and dynamic changes in soil moisture [61]. This index is defined as the ratio of actual to potential evapotranspiration and can be written as follows:
A E F = E T a E T p
where ETa represents actual evapotranspiration and is obtained from the SiB2 simulation and ETp represents potential evapotranspiration and is derived from the Penman–Monteith formula. AEF directly reflects the water availability and the efficiency of water use in terms of evaporation and transpiration. By emphasizing that EF is primarily driven by energy balance while AEF is more closely tied to surface moisture conditions.

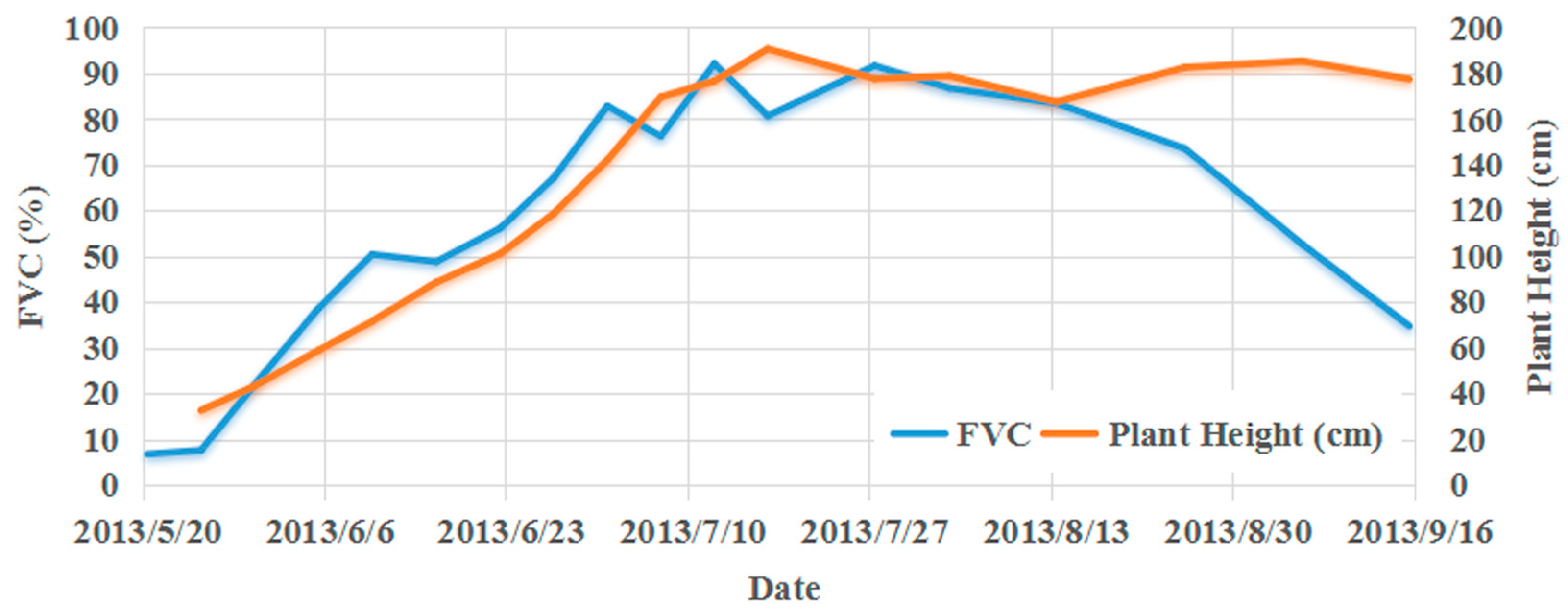
3.2. Vegetation Growth Seasons

Soil moisture is significantly affected by the vegetation type and coverage. In bare soil, the water content dynamics have strong absorption in the near-infrared wave band. However, the dynamics are weakened under middle-to-high vegetation canopy coverage. Previous studies have also shown that the correlations between the soil moisture and auxiliary information vary at different stages of vegetation growth, e.g., ATI is only applied to bare soils and lower vegetation coverage surfaces [62,63]. Therefore, the applicability of these indices in different growth seasons should be analyzed. Based on observations of vegetation growth and surveys of local farmers, vegetation experiences rapid growth and a significant increase in coverage from mid-to-late June to early-to-mid July. Therefore, we define two stages within the growing season: Phase I (incomplete vegetation coverage) and Phase II (complete vegetation coverage) (Figure 2). And set 1 July as the tipping point.

4. Results and Discussion

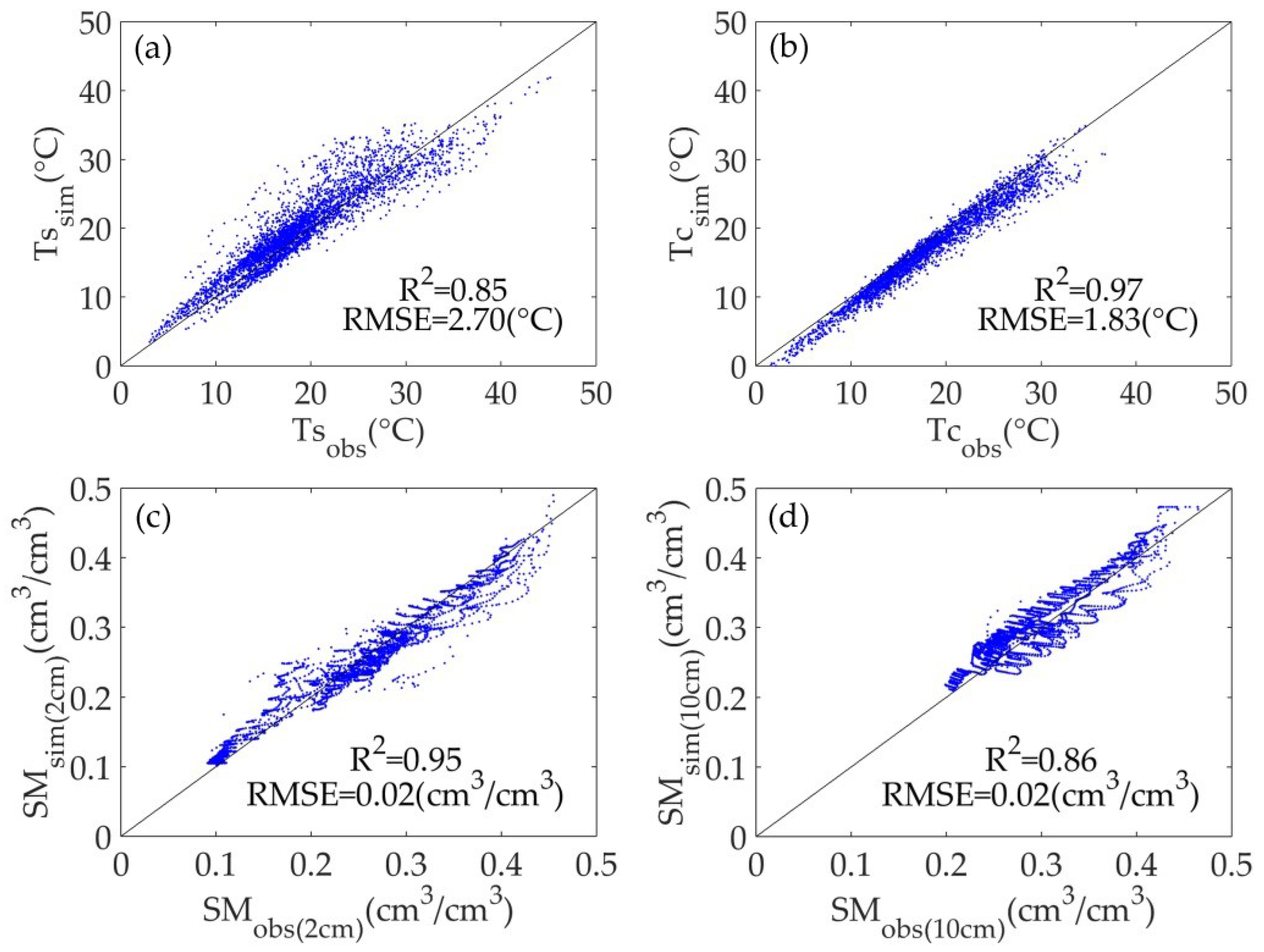
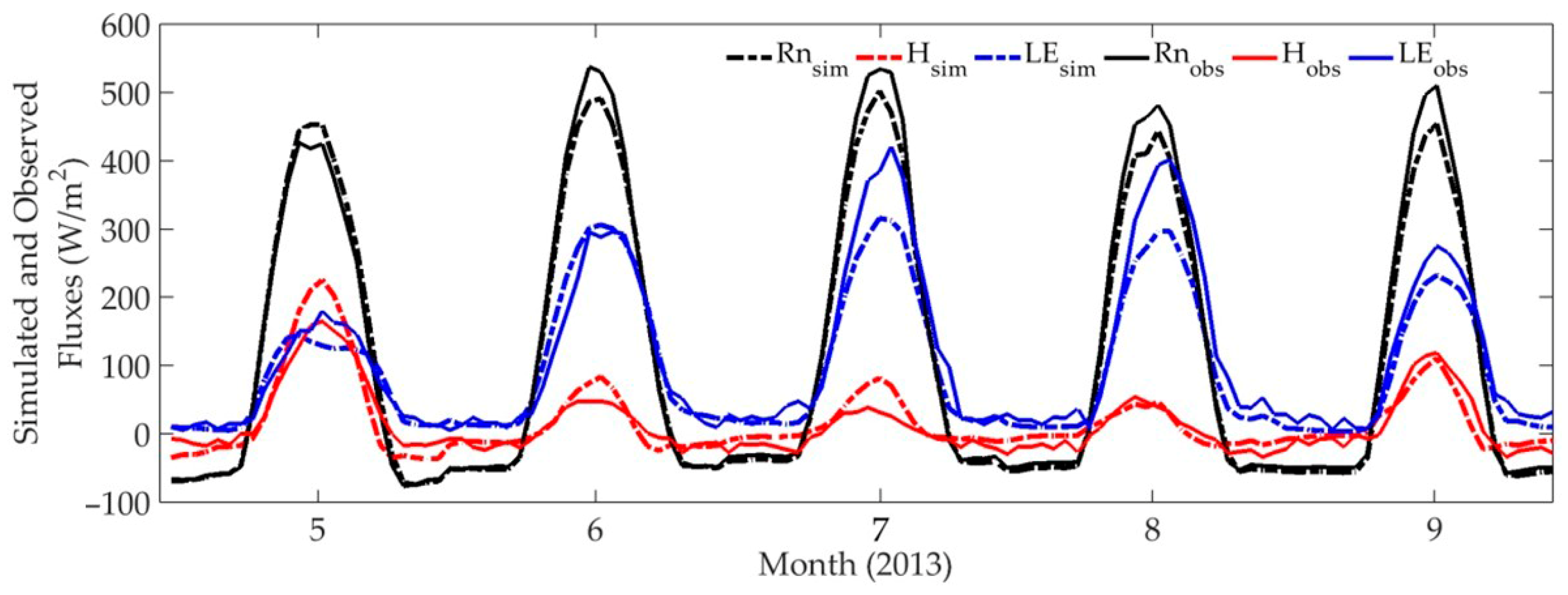
4.1. Validation of SiB2 Simulation

The SiB2 simulation was validated against the observations from the Daman superstation. The soil surface temperature (Ts) and canopy temperature (Tc) outputted from the SiB2 simulation were verified by ground surface temperature observations (0 cm) and canopy temperature (calculated according to the four radiation observation components), respectively. The verification indicated that for Ts or Tc, the linear correlation was significant (R2 ≥ 0.85), and the simulation error was less than 2.70 °C. The soil moisture was verified by the soil moisture observations at 2 cm and 10 cm. The correlation between the simulated and observed soil moisture was also high (R2 ≥ 0.86), and the root mean square error was small (RMSE = 0.02 cm3/cm3). All these values were closely distributed around line 1:1 (Figure 3).
Figure 4 presents a comparison of the simulated and observed surface fluxes. These curves show that there is good consistency between the simulations and observations. The latent heat flux decreases in July and August because of irrigation and vegetation water retention. Net radiation and the latent heat flux are underestimated by 6.3% and 10.34%, respectively, and the sensible heat flux is overestimated by 10.97% compared with the observations because of systematic errors. These results are similar to that of Randall [64]. Net radiation presents a stronger correlation to the observations than the latent or sensible heat fluxes, and R2 is 0.97 for net radiation, 0.69 for sensible heat flux, and 0.80 for latent heat flux. These simulations present higher accuracy compared with the results of previous studies, such as Li [65]. Based on the above validation, the SiB2 simulation accuracy is considered satisfactory and can be used for index calculations and statistical analyses.

4.2. Correlation Analysis Between the Auxiliary Variables and Soil Moisture

The correlation analysis between the seven auxiliary variables and soil moisture is described in this section. All the statistical data are summarized in Table 3 and Figure 5.
The ATIs were calculated based on the soil surface temperature, and the ATIc was calculated using the vegetation canopy temperature. The correlations between the ATIs/ATIc and the simulated soil moisture at 2 cm and 10 cm were compared (Figure 5a,b) during Phase I and Phase II of the growing season. The results (Table 3) show that in Phase I and Phase II, the ATIc was insensitive (R2 ≤ 0.29) to soil moisture while the ATIs showed a stronger correlation (R2 ≥ 0.45) with soil moisture, which is inconsistent with previous results indicating that the ATI-based on LST retrieved from the thermal infrared bands is only suitable for bare soil and lower vegetation cover conditions. Considering the definition of the ATI as a function of surface temperature, this index should be more effective in dry environments [66]. LST represents an aggregation of the soil surface temperature and canopy temperature and depends on their areal fractions. When the surface is bare soil, the LST is similar to the soil surface temperature. However, when the vegetation coverage increases, the LST deviates from the soil surface temperature and is closer to the vegetation canopy temperature when the vegetation coverage is full. In Phase II, the land surface coverage was relatively homogeneous and a precise decomposition of the LST mainly considers the vegetation canopy as a large leaf rather than a combination of bare soil and vegetation, which results in a high correlation between the ATIs and soil moisture. Thus, the ATIs can directly reflect soil moisture information. Therefore, to improve the sensitivity of the ATI to soil moisture, a temperature component decomposition of LSTs is necessary. The ATI estimated that utilizing the soil surface temperature can reflect the thermal inertia of soil rather than that of the land surface and better reflect the soil moisture conditions.
E accounts for approximately 20~40% of global evapotranspiration [67], which is mainly controlled by atmospheric conditions, surface soil moisture, vegetation coverage, and soil texture. The water supply for E is directly obtained from the surface soil and it approaches evapotranspiration from the free water surface under a sufficient soil moisture content and forcing energy. In most cases in arid regions, E is limited by the water supply and can reflect changes in soil moisture. The correlation (Table 3) between E and soil moisture is better (R2 ≥ 0.67) in Phase I when the vegetation coverage fraction is relatively lower than 75%, and E represents the main factor controlling the water vapor cycle; therefore, the correlation between E and soil moisture is stronger. However, because evapotranspiration and water retention gradually increase with the growth of vegetation, a weak correlation (R2 ≤ 0.34) was observed between E and soil moisture in Phase II. Because the deep soil layer directly contributes little water to E, the correlations are weak at a depth of 10 cm.
E is highly sensitive to surface soil moisture; hence, the ratio of E in ETa often has a high correlation with soil moisture. From the perspective of two phases of vegetation growth, the correlation (Table 3) between E/ETa and soil moisture in Phase I (R2 ≥ 0.56) is slightly better than that in Phase II (R2 ≤ 0.56) because E is the main factor controlling the water vapor cycle on the land surface under sparse vegetation coverage and transpiration is assumed to be constant. With the growth of crops, E is insensitive to soil moisture because E decreases as transpiration increases. The change in E is insufficient to detect changes in soil moisture while transpiration is sensitive to changes in soil moisture. Compared with the ETa, the ETp refers to evapotranspiration from the free water surface, and E/ETp reflects the ratio of E and ETp. According to the scatter plot shown in Figure 5d, the correlation (Table 3) between E/ETp and soil moisture is like that between E/ETa and soil moisture. This index is also controlled by E assuming that the change in ETp is slight. These results are consistent with previous research [68] and indicate that the correlations between an E-based index and soil moisture are higher during the vegetation growing season and decrease with the depth of soil.
The EF is a sensitive index that can reflect soil moisture based on the energy balance. Statistical analyses showed that a logarithmic fitting relationship (Table 3) occurs between the EF and soil moisture, and the correlation between these parameters is significant (R2 ≥ 0.56) in Phase I. The EF depends on the latent heat flux when the total energy available at the soil surface is not considered. The available soil moisture has a strong influence on the EF because it is the main limiting factor of latent heat flux in arid regions. The latent heat flux increases with increased water content. Because the soil water content is higher at a depth of 10 cm than 2 cm, the correlation (R2) between the EF and soil moisture is higher (R2 = 0.68) at a depth of 10 cm and lower (R2 = 0.56) at a depth of 2 cm in Phase I. With vegetation growth, the coverage fraction gradually increases, and the canopy hinders the net radiation from reaching the land surface. Therefore, the available energy decreases with vegetation growth, which leads to a stronger correlation between the EF and soil moisture in Phase I than in Phase II. The correlations between the EF and soil moisture are 0.34 and 0.23 at a depth of 2 cm and 10 cm in Phase II, respectively. Compared with E, EF is directly controlled by the energy balance, whereas E is primarily influenced by soil moisture; therefore, E is more suitable for indicating a change in soil moisture.
The AEF was successfully used to downscale the SMOS soil moisture product from a resolution of 40 km to 1 km [45]. According to the definition of the AEF, it relates to the ETa and ETp and is dependent on the air temperature, relative humidity, wind speed, flux, vapor pressure, and surface soil moisture. Because the ETp is close to the free water evapotranspiration, the AEF mainly depends on the ETa. In essence, the EF is related to the surface at the “thermal equilibrium”, which is directly controlled by net radiation and sensible and latent heat fluxes, whereas the AEF is intrinsically directly linked to the surface moisture status because it is related to a “wet surface” [45]. In the case of bare soil, various analyses have shown that the AEF can be expressed as a function of the land surface soil moisture alone. For vegetated surfaces, the AEF also depends on the vegetation types and water potential in the root zone [45]. Because soil evaporation and vegetation transpiration change with vegetation growth, the ETa gradually approaches a summit and the fluctuations are small, which leads to a stable AEF in Phase II. Accordingly, the correlation between the AEF and soil moisture is stronger (Table 3) in Phase I (R2 ≥ 0.54) than in Phase II (R2 ≤ 0.35). In addition, the relevance between the AEF and soil moisture is consistent at a soil depth of 2 cm or 10 cm in each phase because of the ETa, which remains constant within a depth of 10 cm at the same time. Overall, a stronger correlation is observed between the AEF and soil moisture in Phase I, and the AEF can be used as an auxiliary index for the scale conversion of soil moisture before the sealing ridge.

4.3. Validation of Auxiliary Variables Applicability in Different Areas

A’rou Superstation (100.4643° E, 38.0473° N, 3033 m) and E’bao Automatic Meteorological Station (100.9151° E, 37.9492° N, 3294 m) have been selected to validate the applicability of auxiliary variables. Both stations are situated in the upper reaches of the Heihe River Basin (Figure 1). The predominant land cover at both sites is alpine meadow, characterized by cold grassland typical of the Qilian Mountains. Due to the availability of soil moisture data, the depths of 2 cm and 10 cm at A’rou and the depth of 4 cm at E’bao were analyzed (Table 4). The results reveal that, at both stations, the EF, AEF, and ATIs are the most optimal auxiliary variables, and the others are relatively poorer. The AEF consistently exhibits the strongest correlation with soil moisture across both sites and soil depths in most cases (R2 value reaches 0.68). The EF also demonstrates relatively high correlations (R2 value reaches 0.58), making these two evaporation-based indices generally more robust indicators of soil moisture compared to the other variables. This result underscores the importance of latent heat flux-related variables in capturing soil moisture dynamics, particularly in semi-arid or alpine meadow environments. Furthermore, the results indicate that the correlations between ATIs and soil moisture consistently outperform those between ATIc and soil moisture at both A’rou and E’bao. This finding underscores the advantage of decomposing the LST into its constituent components, as the soil surface temperature-based ATI more accurately reflects soil moisture conditions. However, it is noteworthy that at both A’rou and E’bao, the differences between the correlations of ATIs and ATIc with soil moisture are minimal. This outcome likely results from the fact that, in these regions, the soil surface and canopy temperatures are relatively similar, and thus both closely approximate the overall LST.
In summary, these findings emphasize that, particularly in areas with sparse vegetation cover and limited water availability, evaporation-driven indices (such as AEF) and soil surface temperature-derived metrics (such as ATIs) provide a more reliable indication of soil moisture. This enhanced understanding is critical for improving the scaling of soil moisture remote sensing products in heterogeneous environments.

4.4. Discussion

In this study, the selection of seven auxiliary variables (ATIs, ATIc, E, E/ETa, E/ETp, EF, and AEF) was guided by their relevance to soil moisture dynamics and their feasibility within the SiB2 modeling framework. These variables exhibit direct or indirect associations with soil moisture. For instance, evaporation plays a crucial role in soil moisture variation as it directly governs water loss from the soil. Similarly, EF and AEF are integral to the energy balance processes that influence soil moisture conditions. Moreover, these auxiliary indicators can be directly or indirectly derived from the SiB2 model, ensuring their applicability in this study. By incorporating these variables, this study aims to comprehensively assess their effectiveness in soil moisture scaling and contribute valuable insights for future research. However, the SiB2 model itself contains certain assumptions and simplifications, and these assumptions may introduce some deviations in practical applications, which could in turn affect the accuracy of the auxiliary variables. Therefore, improving the simplifications within the SiB2 model and exploring the use of other more advanced hydrological models to achieve more accurate calculations of auxiliary variables are necessary. Meanwhile, additional auxiliary variables (e.g., SMDI and VWC) or alternative methodologies (e.g., machine learning approaches) could further enhance the analysis. Exploring these aspects remains an important direction for future work.
Due to data limitations, no extreme climate events, such as heavy rainfall or drought, occurred during the study period. As a result, this study did not consider the potential impact of such events on the auxiliary variables. Furthermore, this study was conducted at a watershed scale over one growing season, which may constrain the generalizability of the findings. The results in this study are more likely to be applicable under specific climatic conditions, such as irrigated systems or semi-arid steppe climates, rather than across a broader range of environmental settings. Given the spatial and temporal variability of soil moisture dynamics, validation across multiple locations and different climatic conditions will be essential in future research. Expanding the study scope will not only improve the robustness of the findings but also provide a more comprehensive understanding of the factors influencing soil moisture variability under diverse environmental conditions.
Model parameterization plays a fundamental role in determining the accuracy of auxiliary variables, as different parameter settings can lead to variations in key outputs such as surface albedo and roughness length. These variations, in turn, influence the precision of soil moisture estimation. A systematic sensitivity analysis of the model parameters could help quantify their impact on the auxiliary variables, providing a more rigorous basis for optimizing parameter selection and improving model performance. In addition to parameterization, uncertainties in input data, particularly meteorological forcing data, may introduce biases that affect the reliability of soil moisture simulations. For instance, inaccuracies in precipitation data can propagate through the model and result in deviations in soil moisture estimates. To address this issue, advanced error analysis techniques, such as Monte Carlo simulations, could be employed to assess how uncertainties in input data influence model outputs. Furthermore, integrating multi-source observational data for cross-validation can serve as an effective strategy for reducing the uncertainties associated with a single data source. By incorporating measurements from multiple sensors or monitoring stations, the robustness of model simulations can be further enhanced. Overall, improving the accuracy and reliability of soil moisture estimation using the SiB2 model requires a careful assessment of both parameterization processes and input data quality. Addressing these factors in future studies will be crucial for refining model performance and ensuring more reliable applications in soil moisture research.
Our study suggests that among the auxiliary variables analyzed, ATIs, EF, and AEF are effective indicators for soil moisture estimation. However, from a computational perspective, ATI stands out as a more practical choice, as it requires relatively fewer input parameters and can be derived directly from satellite-based LST products. This makes ATI particularly advantageous for large-scale applications, where data availability and computational efficiency are critical factors. Regarding computational costs, the primary challenge lies in obtaining actual and potential evapotranspiration (ETa and ETp) for AEF and EF calculations, as these variables often require complex modeling approaches. In contrast, ATI’s dependency on LST makes it a computationally efficient option. With the increasing availability of high-resolution LST products from satellite missions (e.g., MODIS, Landsat, Sentinel-3), large-scale soil moisture mapping using ATI is feasible with reasonable computational resources.

5. Conclusions

To satisfy the requirements for producing mid- to high-resolution soil moisture products and validate soil moisture remote sensing products, this study quantitatively evaluated the applicability of seven auxiliary variables (ATIs, ATIc, E, E/ETa, E/ETp, EF, and AEF) from SiB2 model.
The findings indicate that the E, E/ETa, and E/ETp variables are highly sensitive to changes in the surface soil water content in bare soil and low vegetation coverage conditions when the water supply is adequate, and these responses decrease with vegetation growth. Furthermore, these E-based variables are suitable for areas under soil water stress. Compared with these E-based indices, the ATIs, EF, and AEF can be calculated from surface fluxes and meteorological observations. In addition, these indices can also be estimated by the satellite-based LST products and vegetation coverage fraction based on remote sensing images. Considering both the correlation and computability of remote sensing, the ATIs, EF, and AEF are recommended as auxiliary variables for the scaling of surface soil moisture, the EF (R2 ≥ 0.56) and AEF (R2 ≥ 0.54) are recommended when scaling the soil moisture during the early phase of the growing season when vegetation cover is sparse, whereas the ATIs (R2 ≥ 0.51) is recommended in Phase II. Additionally, the ATI-based soil surface temperature (ATIs) consistently outperformed its canopy-based counterpart (ATIc), suggesting that soil surface temperature provides a more reliable representation of moisture dynamics. Future research will focus on expanding the study across diverse climatic conditions and multiple locations will ensure the generalizability of our findings, ultimately supporting robust, large-scale eco-hydrological applications.

Author Contributions

Conceptualization, Z.Z. and R.J.; methodology, Z.Z.; software, Z.Z.; validation, Z.Z. and R.J.; formal analysis, R.J.; investigation, Z.Z.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, R.J.; visualization, Z.Z.; supervision, R.J.; project administration, R.J.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Program of the State Key Laboratory of Cryospheric Science and Frozen Soil Engineering, CAS (grant no. CSFSE-ZZ-2409), the National Natural Science Foundation of China (grant no. 42201441), the China Postdoctoral Science Foundation (grant no. 2022M723359), and the Chinese Academy of Sciences “Special Research Assistant Program” (grant no. 2024000284).

Data Availability Statement

The data presented in this study are available upon request from the first author.

Acknowledgments

The authors would like to thank all of the scientists, engineers, and students who participated in the HiWATER comprehensive experiment.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. The definition of the variables used in the study.
Table A1. The definition of the variables used in the study.
VariablesDefinitionRequired InputsData Source
Apparent Thermal Inertia (ATI)A function of the difference between the LSTs in the daytime and at nighttimeBroadband albedo, daily maximum and minimum temperaturesSiB2 simulation outputs
Evaporation (E)Water loss directly from the soil surfaceNet radiation, ground heat flux, meteorological dataSiB2 simulation outputs
Actual Evapotranspiration (ETa)Combined water loss from soil evaporation and vegetation transpirationEnergy fluxes; meteorological dataSiB2 simulation outputs
Potential Evapotranspiration (ETp)Theoretical maximum evapotranspiration assuming unlimited water supplyMeteorological data; inputs for the Penman–Monteith formulaCalculated from meteorological data using the Penman–Monteith formula
E/ETaThe ratio of soil evaporation to actual evapotranspirationE, ETaSiB2 simulation outputs
E/ETpThe ratio of soil evaporation to potential evapotranspirationE, ETpSiB2 simulation outputs and the Penman–Monteith formula
Evaporative Fraction (EF)The ratio of latent heat flux to the net available energy at the soil surfaceLatent heat flux, net radiation, ground heat fluxSiB2 simulation outputs
Actual Evaporative Fraction (AEF)The ratio of actual to potential evapotranspiration, reflecting water availabilityActual and potential evapotranspiration (ETa and ETp)SiB2 simulation outputs and the Penman–Monteith formula

References

  1. Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R. The ESA climate change initiative: Satellite data records for essential climate variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
  2. Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Small, E.E.; Zreda, M. State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar]
  3. Wagner, W.; Bloschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Water Policy 2007, 38, 1–20. [Google Scholar] [CrossRef]
  4. Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
  5. Western, A.W.; Grayson, R.B.; Blöschl, G. Scaling of Soil Moisture: A Hydrologic Perspective. Annu. Rev. Earth Planet. Sci. 2003, 8, 149–180. [Google Scholar] [CrossRef]
  6. Kim, J.; Hogue, T.S. Improving Spatial Soil Moisture Representation Through Integration of AMSR-E and MODIS Products. IEEE Trans. Geosci. Remote Sens. 2012, 50, 446–460. [Google Scholar] [CrossRef]
  7. Vereecken, H.; Amelung, W.; Bauke, S.L.; Bogena, H.; Brüggemann, N.; Montzka, C.; Vanderborght, J.; Bechtold, M.; Blöschl, G.; Carminati, A. Soil hydrology in the Earth system. Nat. Rev. Earth Environ. 2022, 3, 573–587. [Google Scholar]
  8. Zhang, J.; Zhou, Z.; Yao, F.; Yang, L.; Hao, C. Validating the modified perpendicular drought index in the North China region using in situ soil moisture measurement. IEEE Geosci. Remote Sens. Lett. 2014, 12, 542–546. [Google Scholar] [CrossRef]
  9. Smith, K.A.; Barker, L.J.; Tanguy, M.; Parry, S.; Harrigan, S.; Legg, T.P.; Prudhomme, C.; Hannaford, J. A multi-objective ensemble approach to hydrological modelling in the UK: An application to historic drought reconstruction. Hydrol. Earth Syst. Sci. 2019, 23, 3247–3268. [Google Scholar] [CrossRef]
  10. Ghasemloo, N.; Matkan, A.A.; Alimohammadi, A.; Aghighi, H.; Mirbagheri, B. Estimating the agricultural farm soil moisture using spectral indices of Landsat 8, and Sentinel-1, and artificial neural networks. J. Geovisualization Spat. Anal. 2022, 6, 19. [Google Scholar] [CrossRef]
  11. Hunt, K.M.; Turner, A.G. The effect of soil moisture perturbations on Indian monsoon depressions in a numerical weather prediction model. J. Clim. 2017, 30, 8811–8823. [Google Scholar] [CrossRef]
  12. Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
  13. Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar]
  14. Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; Juglea, S.E. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar]
  15. Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.-C.; Shang, G.-F. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar]
  16. Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2002, 39, 1729–1735. [Google Scholar]
  17. Entekhabi, D.; Njoku, E.G.; Neill, P.E.O.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
  18. Chen, Y.; Yang, K.; Qin, J.; Cui, Q.; Lu, H.; Zhu, L.; Han, M.; Tang, W. Evaluation of SMAP, SMOS, and AMSR2 soil moisture retrievals against observations from two networks on the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 5780–5792. [Google Scholar]
  19. Entekhabi, D.; Asrar, G.R.; Betts, A.K.; Beven, K.J.; Bras, R.L.; Duffy, C.J.; Dunne, T.; Koster, R.D.; Lettenmaier, D.P.; McLaughlin, D.B. An agenda for land surface hydrology research and a call for the second international hydrological decade. Bull. Am. Meteorol. Soc. 1999, 80, 2043–2058. [Google Scholar]
  20. Merlin, O.; Chehbouni, A.; Boulet, G.; Kerr, Y. Assimilation of disaggregated microwave soil moisture into a hydrologic model using coarse-scale meteorological data. J. Hydrometeorol. 2006, 7, 1308–1322. [Google Scholar]
  21. Song, C.; Hu, G.; Wang, Y.; Qu, X. Downscaling ESA CCI Soil Moisture Based on Soil and Vegetation Component Temperatures Derived From MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2175–2184. [Google Scholar]
  22. Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar]
  23. Senanayake, I.P.; Pathira Arachchilage, K.R.; Yeo, I.-Y.; Khaki, M.; Han, S.-C.; Dahlhaus, P.G. Spatial downscaling of satellite-based soil moisture products using machine learning techniques: A review. Remote Sens. 2024, 16, 2067. [Google Scholar] [CrossRef]
  24. Liu, J.; Rahmani, F.; Lawson, K.; Shen, C. A multiscale deep learning model for soil moisture integrating satellite and in situ data. Geophys. Res. Lett. 2022, 49, e2021GL096847. [Google Scholar]
  25. Poehls, J.; Alonso, L.; Koirala, S.; Reichstein, M.; Carvalhais, N. Downscaling soil moisture to sub-km resolutions with simple machine learning ensembles. J. Hydrol. 2025, 652, 132624. [Google Scholar] [CrossRef]
  26. Qin, J.; Yang, K.; Lu, N.; Chen, Y.; Zhao, L.; Han, M. Spatial upscaling of in-situ soil moisture measurements based on MODIS-derived apparent thermal inertia. Remote Sens. Environ. 2013, 138, 1–9. [Google Scholar]
  27. Al Bitar, A.; Leroux, D.; Kerr, Y.H.; Merlin, O. Evaluation of SMOS Soil Moisture Products Over Continental U.S. Using the SCAN/SNOTEL Network. Geosci. Remote Sens. IEEE Trans. 2012, 50, 1572–1586. [Google Scholar]
  28. Jackson, T.J.; Bindlish, R.; Cosh, M.H.; Zhao, T. Validation of Soil Moisture and Ocean Salinity (SMOS) Soil Moisture Over Watershed Networks in the U.S. Geosci. Remote Sens. IEEE Trans. 2012, 50, 1530–1543. [Google Scholar]
  29. Sanchez, N.; Martinez-Fernandez, J.; Scaini, A.; Perez-Gutierrez, C. Validation of the SMOS L2 Soil Moisture Data in the REMEDHUS Network (Spain). IEEE Trans. Geosci. Remote Sens. 2012, 50, 1602–1611. [Google Scholar]
  30. Jin, R.; Li, X.; Yan, B.; Li, X.; Luo, W.; Ma, M.; Guo, J.; Kang, J.; Zhu, Z.; Zhao, S. A Nested Ecohydrological Wireless Sensor Network for Capturing the Surface Heterogeneity in the Midstream Areas of the Heihe River Basin, China. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2015–2019. [Google Scholar]
  31. Qin, J.; Zhao, L.; Chen, Y.; Yang, K.; Yang, Y.; Chen, Z.; Lu, H. Inter-comparison of spatial upscaling methods for evaluation of satellite-based soil moisture. J. Hydrol. 2015, 523, 170–178. [Google Scholar] [CrossRef]
  32. Bai, X.; Wang, Z.; Wu, J.; Zhang, Z.; Zhang, P. A novel multivariate multiscale index for drought-flood abrupt alternations: Considering precipitation, evapotranspiration, and soil moisture. J. Hydrol. 2024, 643, 132039. [Google Scholar] [CrossRef]
  33. Carlson, T.N.; Gillies, R.R.; Perry, E.M. A Method to Make Use of Thermal Infrared Temperature and NDVI measurements to Infer Surface Soil Water Content and Fractional Vegetation Cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar] [CrossRef]
  34. Zhao, Z.; Jin, R.; Kang, J.; Ma, C.; Wang, W. Using of Remote Sensing-Based Auxiliary Variables for Soil Moisture Scaling and Mapping. Remote Sens. 2022, 14, 3373. [Google Scholar] [CrossRef]
  35. Price, J.C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia. Remote Sens. Environ. 1985, 18, 59–73. [Google Scholar] [CrossRef]
  36. Gao, S.; Zhu, Z.; Weng, H.; Zhang, J. Upscaling of sparse in situ soil moisture observations by integrating auxiliary information from remote sensing. Int. J. Remote Sens. 2017, 38, 4782–4803. [Google Scholar] [CrossRef]
  37. Knipper, K.R.; Hogue, T.S.; Franz, K.J.; Scott, R.L. Downscaling SMAP and SMOS soil moisture with moderate-resolution imaging spectroradiometer visible and infrared products over southern Arizona. J. Appl. Remote Sens. 2017, 11, 026021. [Google Scholar] [CrossRef]
  38. Chauhan, N.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
  39. Sánchez, N.; Gonzálezzamora, Á.; Piles, M.; Martínezfernández, J. A New Soil Moisture Agricultural Drought Index (SMADI) Integrating MODIS and SMOS Products: A Case of Study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar] [CrossRef]
  40. Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-Vegetation-soil Moisture Dryness Index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
  41. Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
  42. Kang, J.; Jin, R.; Li, X. Regression Kriging-Based Upscaling of Soil Moisture Measurements From a Wireless Sensor Network and Multiresource Remote Sensing Information Over Heterogeneous Cropland. IEEE Geosci. Remote Sens. Lett. 2015, 12, 92–96. [Google Scholar] [CrossRef]
  43. Kim, G.; Barros, A.P. Downscaling of remotely sensed soil moisture with a modified fractal interpolation method using contraction mapping and ancillary data. Remote Sens. Environ. 2002, 83, 400–413. [Google Scholar] [CrossRef]
  44. Merlin, O.; Walker, J.P.; Chehbouni, A.; Kerr, Y. Towards deterministic downscaling of SMOS soil moisture using MODIS derived soil evaporative efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef]
  45. Merlin, O.; Chehbouni, A.; Walker, J.P.; Panciera, R. A Simple Method to Disaggregate Passive Microwave-Based Soil Moisture. Geosci. Remote Sens. IEEE Trans. 2008, 46, 786–796. [Google Scholar] [CrossRef]
  46. Gao, Q.; Zribi, M.; Escorihuela, M.; Baghdadi, N. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at 100 m Resolution. Sensors 2017, 17, 1966. [Google Scholar] [CrossRef]
  47. Bindlish, R.; Barros, A.P. Subpixel variability of remotely sensed soil moisture: An inter-comparison study of SAR and ESTAR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 326–337. [Google Scholar] [CrossRef]
  48. Sellers, P.J. A revised land surface parameterization (SiB2) for atmospheric GCMs, Part II: The generation of global fields of terrestrial biophysical parameters from satellite data. J. Clim. 1996, 9, 706–737. [Google Scholar] [CrossRef]
  49. Sellers, P.J.; Randall, D.A.; Collatz, G.J.; Berry, J.A.; Field, C.B.; Dazlich, D.A.; Zhang, C.; Collelo, G.D.; Bounoua, L. A Revised Land Surface Parameterization (SiB2) for Atmospheric GCMS. Part I: Model Formulation. J. Clim. 1996, 9, 676–705. [Google Scholar] [CrossRef]
  50. Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12. [Google Scholar] [CrossRef]
  51. Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G. The common land model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1024. [Google Scholar]
  52. Zhou, J.; Yang, K.; Dong, J.; Crow, W.T.; Lu, H.; Zhao, L.; Feng, H.; Tian, J.; Ma, X.; Tian, X. Mapping global soil moisture and evapotranspiration coupling strength based on a two-system method and multiple data sources. Water Resour. Res. 2025, 61, e2023WR036847. [Google Scholar] [CrossRef]
  53. Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
  54. Li, X.; Liu, S.; Ma, M.; Xiao, Q.; Liu, Q.; Jin, R.; Che, T.; Wang, W.; Qi, Y.; Li, H. HiWATER:An Integrated Remote Sensing Experiment on Hydrological and Ecological Processes in the Heihe River Basin. Adv. Earth Sci. 2012, 27, 481–498. [Google Scholar]
  55. Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
  56. Ma, M.; Wang, X.; Wang, H.; Yu, W. HiWATER: Dataset of soil parameters in the midstream of the Heihe River Basin (2012). National Tibetan Plateau/Third Pole Environment Data Center. 2017. Available online: https://cstr.cn/18406.11.hiwater.147.2013.db (accessed on 16 February 2025). [CrossRef]
  57. Nishida, K.; Nemani, R.R.; Glassy, J.M.; Running, S.W. Development of an evapotranspiration index from Aqua/MODIS for monitoring surface moisture status. IEEE Trans. Geosci. Remote Sens. 2003, 41, 493–501. [Google Scholar] [CrossRef]
  58. Koster, R.D.; Sud, Y.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Davies, H. GLACE: The global land–atmosphere coupling experiment. Part I: Overview. J. Hydrometeorol. 2006, 7, 590–610. [Google Scholar]
  59. Shuttleworth, W.; Gurney, R.; Hsu, A.; Ormsby, J. FIFE: The variation in energy partition at surface flux sites. IAHS Publ. 1989, 186, 523–534. [Google Scholar]
  60. Licker, R.; Johnston, M.; Foley, J.A.; Barford, C.; Kucharik, C.J.; Monfreda, C.; Ramankutty, N. Mind the gap: How do climate and agricultural management explain the ‘yield gap’of croplands around the world? Glob. Ecol. Biogeogr. 2010, 19, 769–782. [Google Scholar]
  61. McVicar, T.R.; Jupp, D.L. Using covariates to spatially interpolate moisture availability in the Murray–Darling Basin: A novel use of remotely sensed data. Remote Sens. Environ. 2002, 79, 199–212. [Google Scholar]
  62. Van de Griend, A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar]
  63. Verhoef, A. Remote estimation of thermal inertia and soil heat flux for bare soil. Agric. For. Meteorol. 2004, 123, 221–236. [Google Scholar]
  64. Randall, D.A.; Dazlich, D.A.; Zhang, C.; Denning, A.S.; Sellers, P.J.; Tucker, C.J.; Bounoua, L.; Berry, J.A.; Collatz, G.J.; Field, C.B. A Revised Land Surface Parameterization (SiB2) for GCMS. Part III: The Greening of the Colorado State University General Circulation Model. J. Clim. 1996, 9, 738–763. [Google Scholar] [CrossRef]
  65. Li, Y.; Sun, R.; Liu, S. Vegetation physiological parameter setting in the Simple Biosphere model 2 (SiB2) for alpine meadows in the upper reaches of Heihe river. Sci. China Earth Sci. 2015, 58, 755–769. [Google Scholar]
  66. Watson, K. Regional thermal-inertia mapping from an experimental satellite. Geophysics 1982, 47, 1681–1687. [Google Scholar]
  67. Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189, 115–117. [Google Scholar]
  68. Zhao, Z.; Jin, R.; Tian, W.; Kang, J.; Su, Y. Applicability Research of Indices in Soil Moisture Downscaling based on SiB2 Simulation. Remote Sens. Technol. Appl. 2017, 32, 195–205. [Google Scholar]
Electronics 14 01392 g001
Figure 1. Location of the study area.
Figure 1. Location of the study area.
Electronics 14 01392 g001
Electronics 14 01392 g002
Figure 2. Fraction of vegetation coverage (FVC, %) and plant height (cm) during the growth season.
Figure 2. Fraction of vegetation coverage (FVC, %) and plant height (cm) during the growth season.
Electronics 14 01392 g002
Electronics 14 01392 g003
Figure 3. Validation of the soil surface temperature (a), canopy temperature (b), and soil moisture (SM) at 2 cm (c) and 10 cm (d) based on the SiB2 simulation.
Figure 3. Validation of the soil surface temperature (a), canopy temperature (b), and soil moisture (SM) at 2 cm (c) and 10 cm (d) based on the SiB2 simulation.
Electronics 14 01392 g003
Electronics 14 01392 g004
Figure 4. Diurnal composite showing a comparison of the SiB2-simulated and observed net radiation (Rn), sensible heat flux (H), and latent heat flux (LE).
Figure 4. Diurnal composite showing a comparison of the SiB2-simulated and observed net radiation (Rn), sensible heat flux (H), and latent heat flux (LE).
Electronics 14 01392 g004
Electronics 14 01392 g005
Figure 5. Scatter plot of the seven auxiliary variables (a) ATIs, (b) ATIc, (c) E, (d) E/ETa, (e) E/ETp, (f) EF, (g) AEF, and soil moisture during the two phases of the vegetation growing season.
Figure 5. Scatter plot of the seven auxiliary variables (a) ATIs, (b) ATIc, (c) E, (d) E/ETa, (e) E/ETp, (f) EF, (g) AEF, and soil moisture during the two phases of the vegetation growing season.
Electronics 14 01392 g005
Table 1. Observation measurements at the Daman superstation.
Table 1. Observation measurements at the Daman superstation.
Observation ItemsInstrument Installation Height (m)Observation Instrument
Four components of radiation (W/m2)12PIR&PSP (Campbell)
Air pressure (hPa)2CS100 (Campbell)
Relative humidity (%)3, 5, 10, 15, 20, 30, 40AV-14TH (Avalon)
Horizontal wind speed (m/s)3, 5, 10, 15, 20, 30, 40Windsonic (Gill)
Air temperature (°C)3, 5, 10, 15, 20, 30, 40AV-14TH (Avalon)
Precipitation (mm)8, instrument height is 2.5 mTE525MM (Texas Electronics)
Table 2. Layered soil parameters at the Daman superstation.
Table 2. Layered soil parameters at the Daman superstation.
Soil
Para		Saturated Hydraulic Conductivity (mm/min)Porosity (%)Bulk Density (g/cm3)Soil Texture (%)
Depth Clay (<2 µm)Silt (2–50 µm)Sand (50–2000 µm)
0–5 cm0.3000.511.3125.2766.0128.72
10 cm0.0880.501.3734.7865.0330.19
20 cm0.1130.491.4714.4667.8127.73
40 cm0.2920.421.4635.471.9422.66
60 cm0.1350.401.5305.4163.5731.02
80 cm0.2140.421.5669.9374.915.17
100 cm0.0560.411.5248.4873.8817.64
Table 3. Correlation and fitting equations of the seven auxiliary indices and soil moisture (θ) at depths of 2 cm and 10 cm.
Table 3. Correlation and fitting equations of the seven auxiliary indices and soil moisture (θ) at depths of 2 cm and 10 cm.
DepthIndexFitting Equation at Phase IR2 at Phase IFitting Equation at Phase IIR2 at Phase II
2 cmATIsATIs = 0.0788θ0.5770.45ATIs = 0.0822θ0.65970.59
ATIcATIc = 0.054θ0.38390.20ATIc = 0.0513θ0.40540.29
EE = 0.0997ln(θ) + 0.21840.73E = 0.0563ln(θ) + 0.13940.34
E/ETaE/ETa = 19.016ln(θ) + 45.6730.71E/ETa = 14.636ln(θ) + 36.7810.56
E/ETpE/ETp = 21.372ln(θ) + 49.2430.70E/ETp = 16.801ln(θ) + 40.6440.54
EFEF = 48.485ln(θ) + 143.980.56EF = 26.175ln(θ) + 114.450.34
AEFAEF = 60.708ln(θ) + 184.210.54AEF = 22.236ln(θ) + 132.850.35
10 cmATIsATIs = 0.1155θ0.92380.50ATIs = 0.1213θ1.09370.51
ATIcATIc = 0.0744θ0.66030.26ATIc = 0.0604θ0.6090.21
EE = 0.1443ln(θ) + 0.26160.67E = 0.0817ln(θ) + 0.1590.22
E/ETaE/ETa = 25.432ln(θ) + 50.8760.56E/ETa = 23.042ln(θ) + 43.9790.43
E/ETpE/ETp = 29.805ln(θ) + 56.8740.60E/ETp = 26.533ln(θ) + 49.0040.41
EFEF = 81.519ln(θ) + 181.720.68EF = 38.562ln(θ) + 124.180.23
AEFAEF = 95.746ln(θ) + 222.250.58AEF = 32.407ln(θ) + 140.70.23
Note: The fitting equations presented in Table 3 were derived using a data-driven approach, where the functional form for each relationship was chosen based on its ability to best represent the underlying data trends. For some auxiliary variables, a logarithmic relationship provided a superior fit, reflecting a saturating effect in the response of soil moisture, while for others, a power law or linear relationship was more appropriate. These diverse forms are not arbitrary; rather, they reflect the inherent differences in the physical processes governing each variable’s relationship with soil moisture. Goodness-of-fit metrics (such as R2 values) guided our selection of the most appropriate models, ensuring that the chosen equations accurately capture the observed variability.
Table 4. Correlation of the seven auxiliary indices and soil moisture (θ) at A’rou and E’bao.
Table 4. Correlation of the seven auxiliary indices and soil moisture (θ) at A’rou and E’bao.
Depth IndexATIsATIcEE/ETaE/ETpEFAEF
R2
2 cm
(A’rou)		R2 at Phase I0.430.290.410.240.530.580.68
R2 at Phase II0.500.310.300.510.560.280.60
10 cm
(A’rou)		R2 at Phase I0.410.290.220.200.120.550.45
R2 at Phase II0.390.250.340.180.170.100.19
4 cm
(E’bao)		R2 at Phase I0.450.230.280.180.310.220.37
R2 at Phase II0.310.180.300.340.330.120.26
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhao, Z.; Jin, R. Feasibility Research on the Auxiliary Variables in Scaling of Soil Moisture Based on the SiB2 Model: A Case Study in Daman. Electronics 2025, 14, 1392. https://doi.org/10.3390/electronics14071392

AMA Style

Zhao Z, Jin R. Feasibility Research on the Auxiliary Variables in Scaling of Soil Moisture Based on the SiB2 Model: A Case Study in Daman. Electronics. 2025; 14(7):1392. https://doi.org/10.3390/electronics14071392

Chicago/Turabian Style

Zhao, Zebin, and Rui Jin. 2025. "Feasibility Research on the Auxiliary Variables in Scaling of Soil Moisture Based on the SiB2 Model: A Case Study in Daman" Electronics 14, no. 7: 1392. https://doi.org/10.3390/electronics14071392

APA Style

Zhao, Z., & Jin, R. (2025). Feasibility Research on the Auxiliary Variables in Scaling of Soil Moisture Based on the SiB2 Model: A Case Study in Daman. Electronics, 14(7), 1392. https://doi.org/10.3390/electronics14071392

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop