A Noise-Shaping SAR-Based Capacitance-to-Digital Converter for Sensing Applications
Abstract
1. Introduction
2. The Proposed CDC Architecture
3. The Impact of Nonidealities
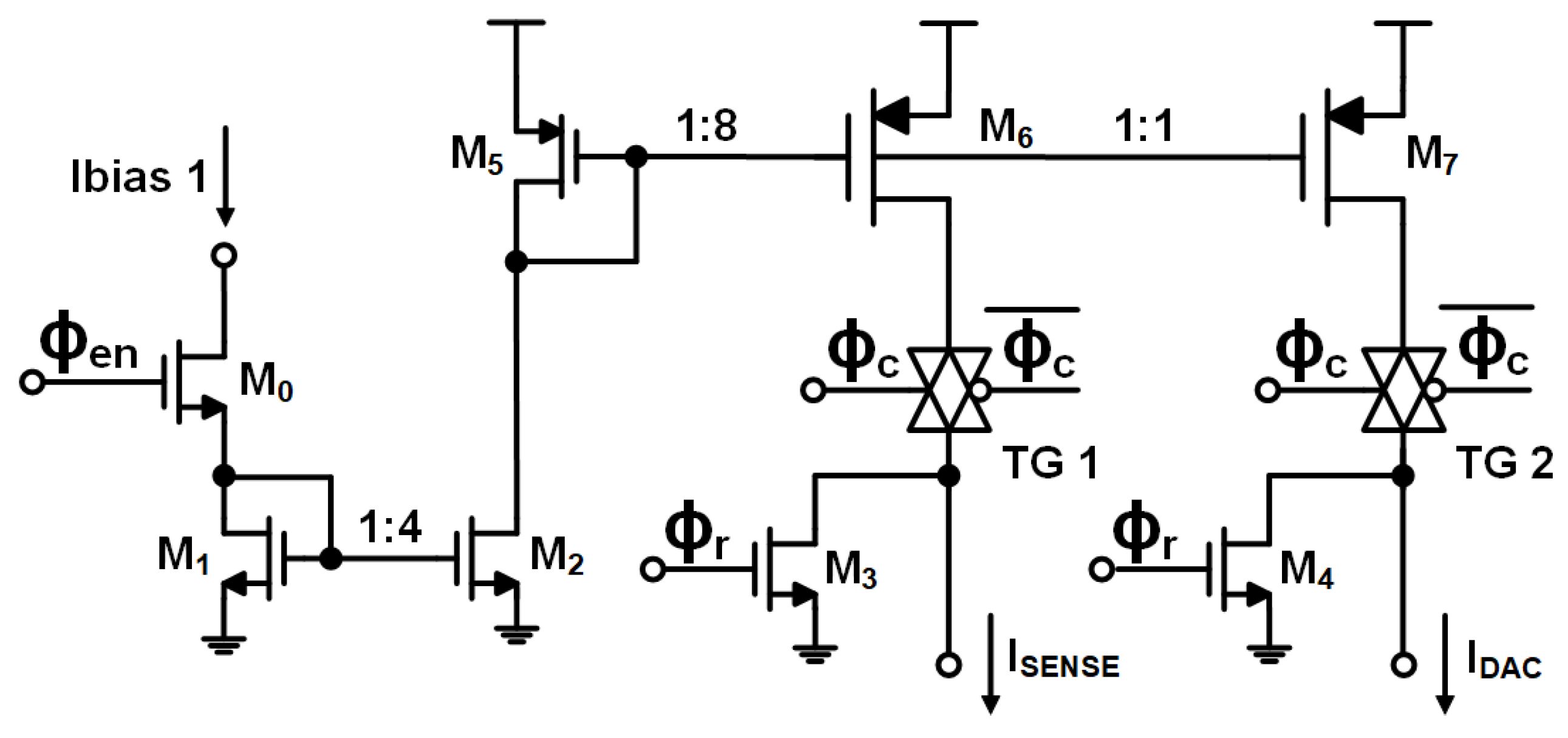
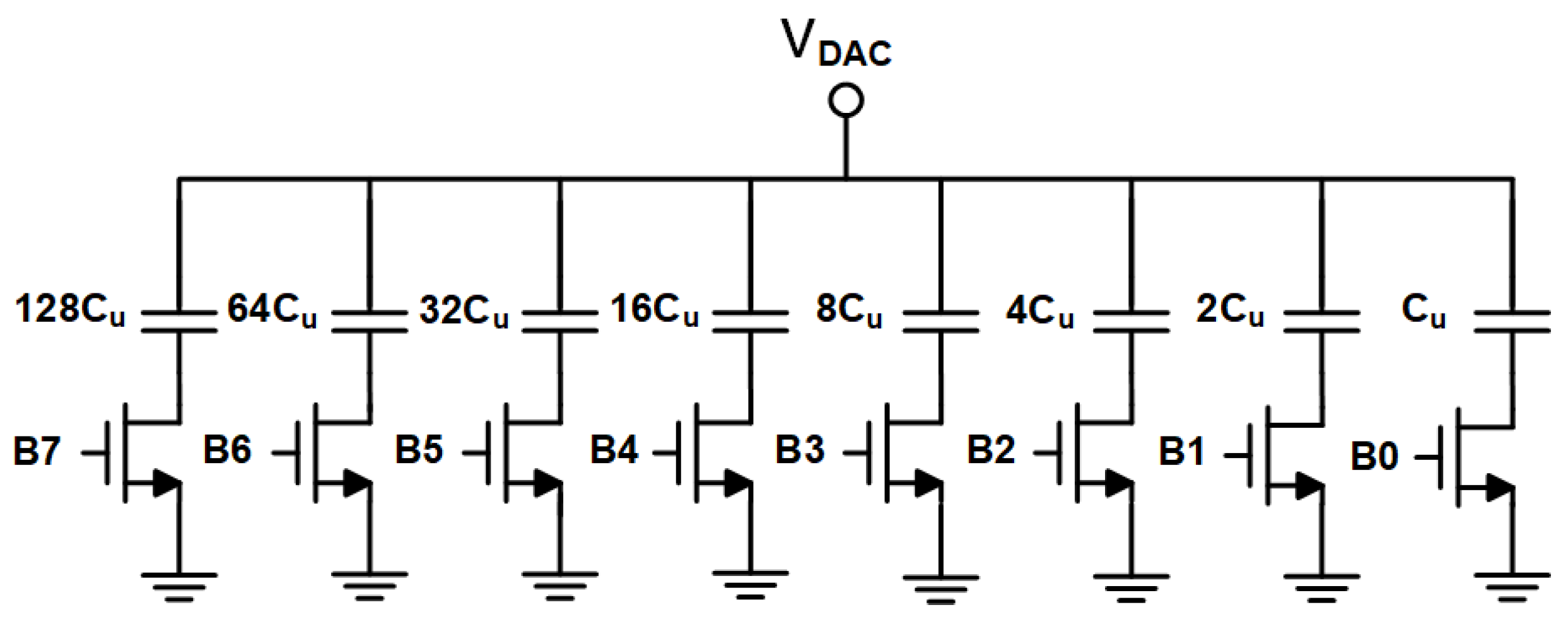
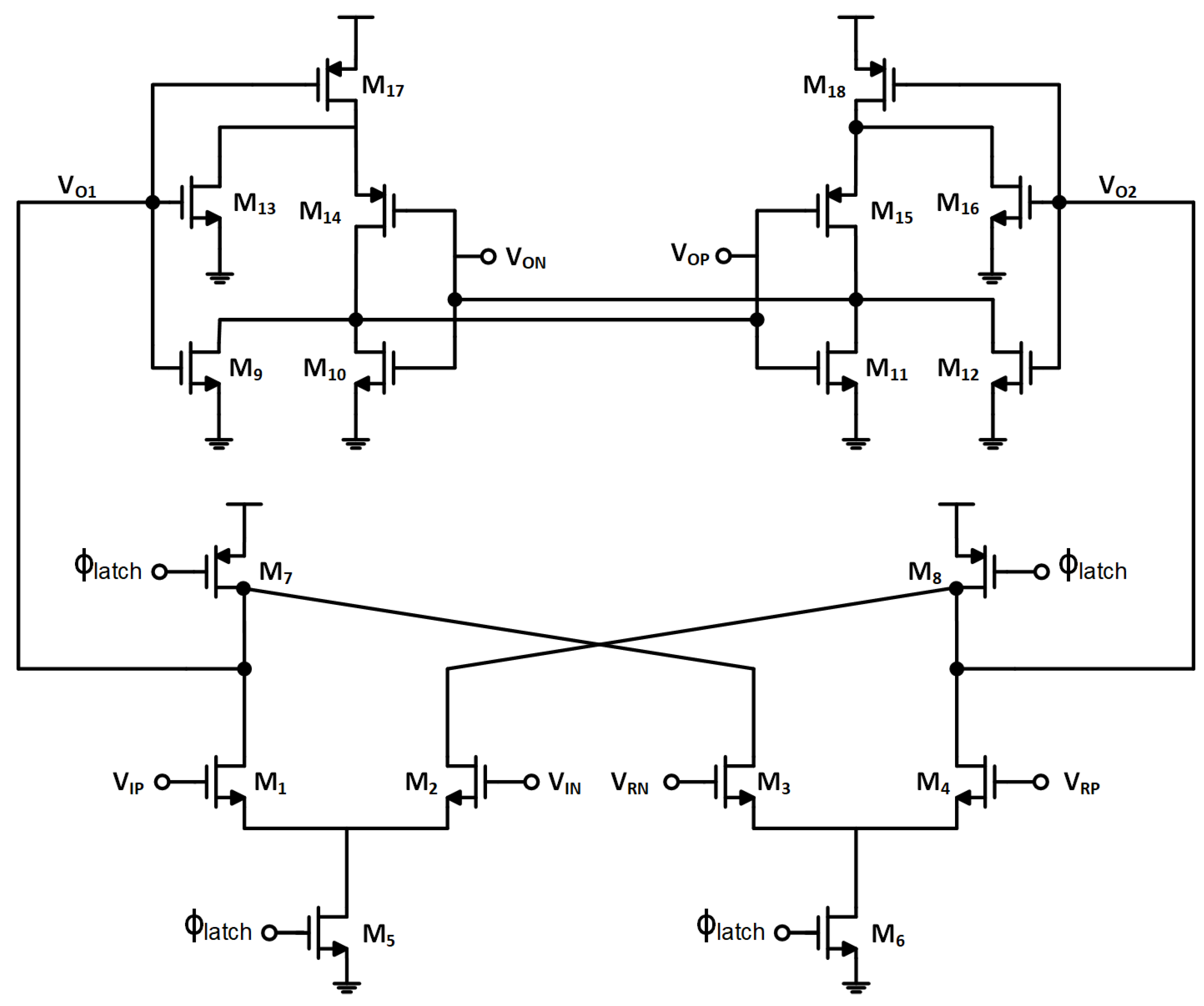
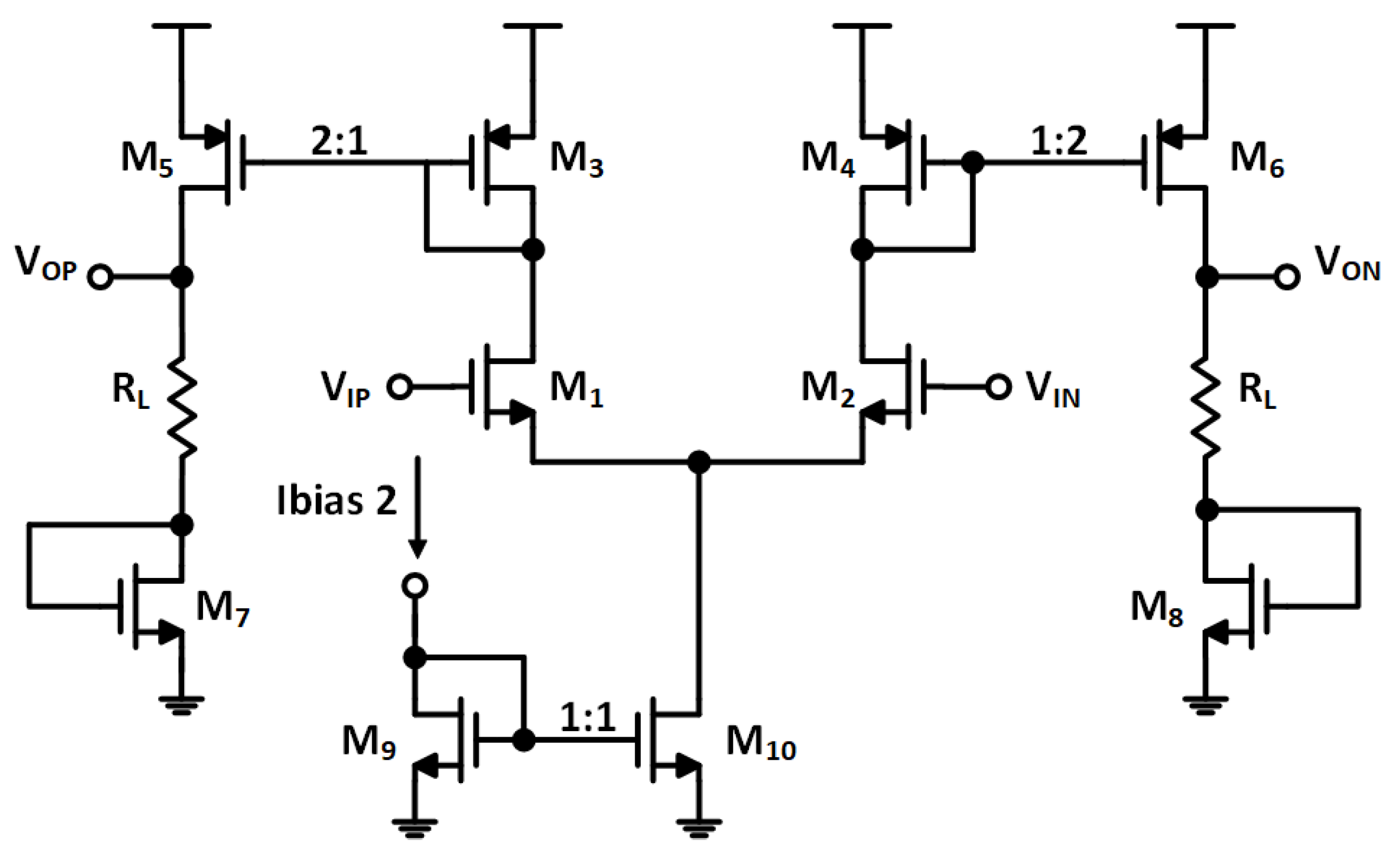
4. Circuit-Level Implementation
4.1. The Charging Current Sources
4.2. The Capacitive DAC
4.3. The Multi-Input Comparator and Digital Processing
4.4. The Loop Filter
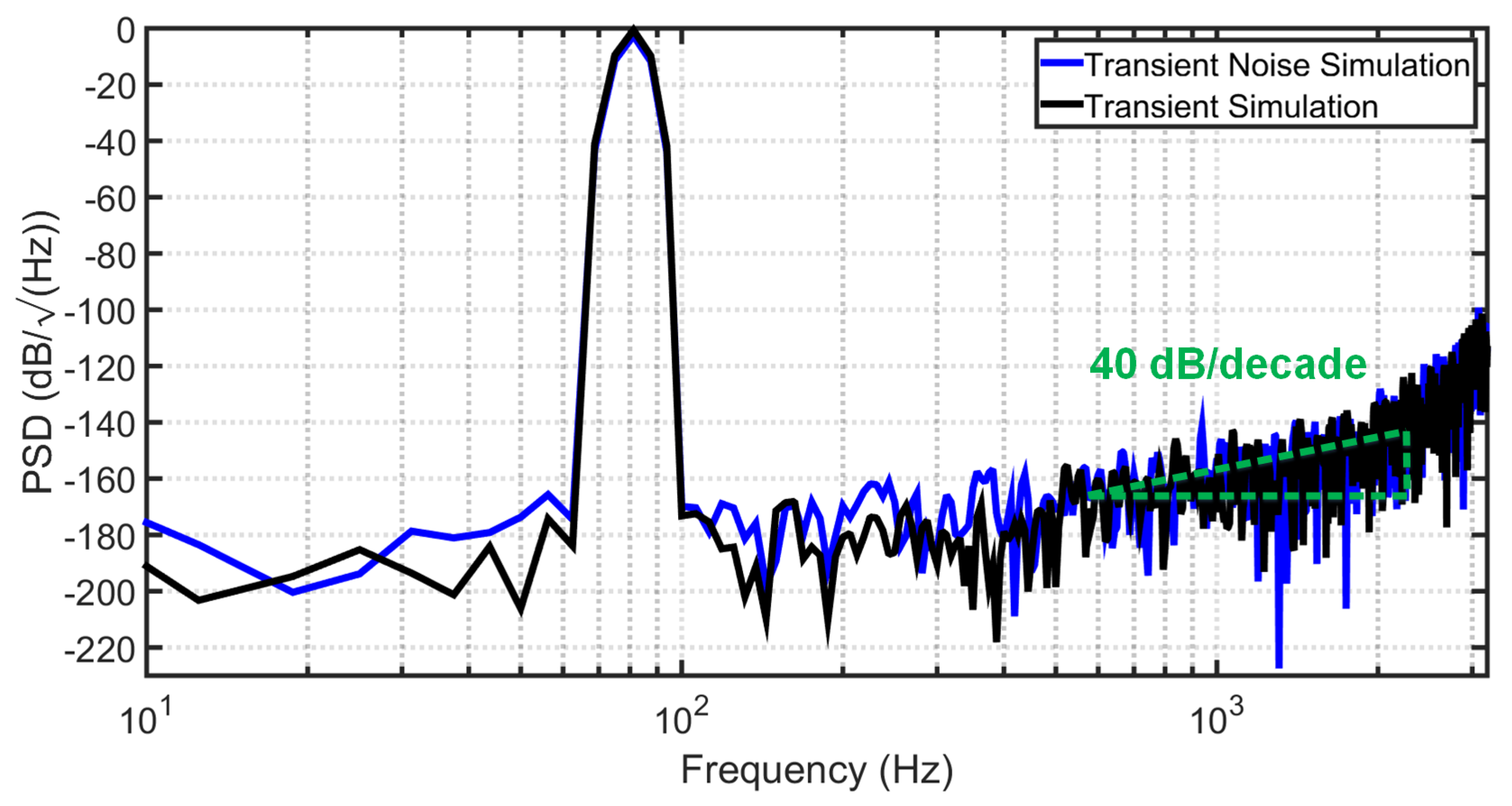
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NS | Noise shaping |
| ADC | Analog-to-Digital converter |
| DAC | Digital-to-Analog converter |
| SAR | Successive-approximation register |
| CDC | Capacitance-to-Digital converter |
| TDC | Time-to-Digital converter |
| FIR | Finite impulse response |
| IIR | Infinite impulse response |
| OSR | Oversampling ratio |
| FoM | Figure of Merit |
| NTF | Noise transfer function |
| CIFF | Cascaded-integrator feed-forward |
| EF | Error-feedback |
| SQNR | Signal-to-quantization-noise ratio |
| SNDR | Signal-to-noise and distortion ratio |
| CAPDAC | Capacitive DAC |
| INL | Integral non-linearity |
| DNL | Differential non-linearity |
| LSB | Least significant bit |
| ENOB | Effective number of bits |
References
- Pan, S.; Zhang, X.; Zheng, B.; Cheng, Y.; Jiang, H.; Wu, H. 28.4 A 143dB-Dynamic-Range 119dB-CMRR Capacitance-to-Digital Converter for High-Resolution Floating-Target Displacement Sensing. In Proceedings of the 2025 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2025; Volume 68, pp. 1–3. [Google Scholar] [CrossRef]
- Kim, M.; Han, S.; Kim, S.; Rhee, J. A 105 dB Effective Dynamic Range Self- Capacitance Proximity Sensing System with Consecutive Double-Sided Conversion Technique. IEEE Sens. J. 2023, 23, 18325–18337. [Google Scholar] [CrossRef]
- Jiang, H.; Amani, S.; Vogel, J.G.; Shalmany, S.H.; Nihtianov, S. A 117-dB In-Band CMRR 98.5-dB SNR Capacitance-to-Digital Converter for Sub-nm Displacement Sensing with an Electrically Floating Target. IEEE Solid-State Circuits Lett. 2020, 3, 9–12. [Google Scholar] [CrossRef]
- Xia, S.; Makinwa, K.; Nihtianov, S. A capacitance-to-digital converter for displacement sensing with 17b resolution and 20μs conversion time. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 198–200. [Google Scholar] [CrossRef]
- Xia, Q.; Zhou, F.; Niu, Y.; He, M.; Lu, W.; Zhang, Y.; Chen, Z. An Energy-Efficient Capacitance-to-Digital Converter with Top and Bottom Plate Sampling for Pressure Sensors. IEEE Trans. Circuits Syst. II Express Briefs 2025. early access. [Google Scholar] [CrossRef]
- Keshyagol, K.; Hiremath, S.; H. M., V.; Kini U., A.; Naik, N.; Hiremath, P. Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model. Sensors 2024, 24, 3504. [Google Scholar] [CrossRef]
- Xia, Q.J.; Zhang, Y.C.; You, Y.; Zhou, F.; Lu, W.g. A 9.1μW Capacitance-to-Digital Converter for Pressure Sensor Systems. In Proceedings of the 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Nangjing, China, 25–28 October 2022; pp. 1–3. [Google Scholar] [CrossRef]
- Park, S.; Lee, G.H.; Cho, S. A 2.92-μW Capacitance-to-Digital Converter With Differential Bondwire Accelerometer, On-Chip Air Pressure, and Humidity Sensor in 0.18-μm CMOS. IEEE J. Solid-State Circuits 2019, 54, 2845–2856. [Google Scholar] [CrossRef]
- Kar, S.; Leon-Salas, W.D. A low-power 12-bit capacitance-to-digital converter for capacitive MEMS pressure sensor. In Proceedings of the SENSORS, Limerick, Ireland, 28–31 October 2011; pp. 1855–1858. [Google Scholar] [CrossRef]
- Ismail, A.; El-Nafarawi, M. Energy-efficient successive-approximation-register based capacitive interface for pressure sensors. Electron. Lett. 2015, 51, 2007–2009. [Google Scholar] [CrossRef]
- Ismail, A.H.; El-Nafarawi, M. A low-energy SAR-based capacitance-to-digital converter for pressure sensors: System analysis, design and calibration. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, H.; Liu, X. A wide dynamic range, high-resolution multi-step SAR CDC for implanted humidity sensors. In Proceedings of the 2024 IEEE Biomedical Circuits and Systems Conference (BioCAS), Xi’an, China, 24–26 October 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Li, H.; Tan, Z.; Bao, Y.; Xiao, H.; Zhang, H.; Du, K.; Shen, L.; Ru, J.; Zhang, Y.; Ye, L.; et al. Energy-Efficient CMOS Humidity Sensors Using Adaptive Range-Shift Zoom CDC and Power-Aware Floating Inverter Amplifier Array. IEEE J. Solid-State Circuits 2021, 56, 3560–3572. [Google Scholar] [CrossRef]
- Wen, Y.; Demosthenous, A.; Donaldson, N.; Liu, X. A Capacitance-to-Digits Readout Circuit for Integrated Humidity Sensors for Monitoring the In-Package Humidity of Ultra-Small Medical Implants. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Lai, K.Y.T.; Yang, Y.T.; Chen, B.J.; Shen, C.J.; Shiu, M.F.; He, Z.C.; Chang, H.C.; Lee, C.Y. A 3.3V 15.6b 6.1pJ/0.02%RH with 10ms response humidity sensor for respiratory monitoring. In Proceedings of the 2014 IEEE Asian Solid-State Circuits Conference (A-SSCC), KaoHsiung, Taiwa, 10–12 November 2014; pp. 293–296. [Google Scholar] [CrossRef]
- Tan, Z.; Daamen, R.; Humbert, A.; Ponomarev, Y.V.; Chae, Y.; Pertijs, M.A.P. A 1.2-V 8.3-nJ CMOS Humidity Sensor for RFID Applications. IEEE J. Solid-State Circuits 2013, 48, 2469–2477. [Google Scholar] [CrossRef]
- Long, S.; Ma, S.; Fan, X.; Wu, C.; Tong, Z.; He, K.; Tang, X. An ASIC Interface for MEMS Vibratory Gyroscopes with a 110 dB DR and 0.001 s/Hz Noise Floor over a 100 Hz. In Proceedings of the 2023 8th International Conference on Integrated Circuits and Microsystems (ICICM), Nanjing, China, 20–23 October 2023; pp. 55–60. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Y.; Middelburg, L.; Mansouri, B.E.; Nihtianov, S. A Continuous-Time Readout IC with 0.12 aF/Hz for Capacitive Inertial Sensors. In Proceedings of the 2021 IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Zhuhai, China, 24–26 November 2021; pp. 14–15. [Google Scholar] [CrossRef]
- Rombach, S.; Marx, M.; Nessler, S.; De Dorigo, D.; Maurer, M.; Manoli, Y. An Interface ASIC for MEMS Vibratory Gyroscopes with a Power of 1.6 mW, 92 dB DR and 0.007°/s/Hz Noise Floor over a 40 Hz Band. IEEE J. Solid-State Circuits 2016, 51, 1915–1927. [Google Scholar] [CrossRef]
- Tan, Z.; Nguyen, K.; Yan, J.; Samuels, H.; Keating, S.; Crocker, P.; Clark, B. A dual-axis MEMS vibratory gyroscope ASIC with 0.0061°/s/VHz noise floor over 480 Hz bandwidth. In Proceedings of the 2017 IEEE Asian Solid-State Circuits Conference (A-SSCC), Seoul, Republic of Korea, 6–8 November 2017; pp. 21–24. [Google Scholar] [CrossRef]
- Ezekwe, C.D.; Boser, B.E. A Mode-Matching ΣΔ Closed-Loop Vibratory Gyroscope Readout Interface With a 0.004°/s/Hz Noise Floor Over a 50 Hz Band. IEEE J. Solid-State Circuits 2008, 43, 3039–3048. [Google Scholar] [CrossRef]
- Ghanbari, M.M.; Tsai, J.M.; Gambini, S. An energy-efficient heterogeneously-integrated capacitive pressure sensing system. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Trung, N.T.; Häfliger, P. A Submicrowatt Implantable Capacitive Sensor System for Biomedical Applications. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 209–213. [Google Scholar] [CrossRef]
- Shin, D.Y.; Lee, H.; Kim, S. A Delta–Sigma Interface Circuit for Capacitive Sensors with an Automatically Calibrated Zero Point. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 90–94. [Google Scholar] [CrossRef]
- Jung, Y.; Duan, Q.; Roh, J. A 17.4-b Delta-Sigma Capacitance-to-Digital Converter for One-Terminal Capacitive Sensors. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 1122–1126. [Google Scholar] [CrossRef]
- Omran, H.; Alhoshany, A.; Alahmadi, H.; Salama, K.N. A 33fJ/Step SAR Capacitance-to-Digital Converter Using a Chain of Inverter-Based Amplifiers. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 310–321. [Google Scholar] [CrossRef]
- Alhoshany, A.; Omran, H.; Salama, K.N. A 45.8fJ/Step, energy-efficient, differential SAR capacitance-to-digital converter for capacitive pressure sensing. Sens. Actuators A Phys. 2016, 245, 10–18. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Z.; Liu, L.; Zhang, C.; Wang, Z. A combined low power SAR capacitance-to-digital / analog-to-digital converter for multisensory system. In Proceedings of the 2012 IEEE 55th International Midwest Symposium on Circuits and Systems (MWSCAS), Boise, ID, USA, 5–8 August 2012; pp. 1000–1003. [Google Scholar] [CrossRef]
- Oh, S.; Lee, Y.; Wang, J.; Foo, Z.; Kim, Y.; Jung, W.; Li, Z.; Blaauw, D.; Sylvester, D. A Dual-Slope Capacitance-to-Digital Converter Integrated in an Implantable Pressure-Sensing System. IEEE J. Solid-State Circuits 2015, 50, 1581–1591. [Google Scholar] [CrossRef]
- Sanjurjo, J.; Prefasi, E.; Buffa, C.; Gaggl, R. An energy-efficient 17-bit noise-shaping Dual-Slope Capacitance-to-Digital Converter for MEMS sensors. In Proceedings of the ESSCIRC Conference 2016: 42nd European Solid-State Circuits Conference, Lausanne, Switzerland, 12–15 September 2016; pp. 389–392. [Google Scholar] [CrossRef]
- Rogi, C.; Buffa, C.; De Milleri, N.; Gaggl, R.; Prefasi, E. A Fully-Differential Switched-Capacitor Dual-Slope Capacitance-To-Digital Converter (CDC) for a Capacitive Pressure Sensor. Sensors 2019, 19, 3673. [Google Scholar] [CrossRef]
- He, Y.; Chang, Z.y.; Pakula, L.; Shalmany, S.H.; Pertijs, M. 27.7 A 0.05 mm2 1V capacitance-to-digital converter based on period modulation. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference - (ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Hassan, A.H.; Fouad, A.; Mostafa, H.; Salama, K.N.; Soliman, A.M. A New Design Methodology for Time-Based Capacitance-to-Digital Converters (T-CDCs). AEU Int. J. Electron. Commun. 2018, 96, 238–245. [Google Scholar] [CrossRef]
- Jung, W.; Jeong, S.; Oh, S.; Sylvester, D.; Blaauw, D. 27.6 A 0.7pF-to-10nF fully digital capacitance-to-digital converter using iterative delay-chain discharge. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference - (ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Alhoshany, A.; Salama, K.N. A Precision, Energy-Efficient, Oversampling, Noise-Shaping Differential SAR Capacitance-to-Digital Converter. IEEE Trans. Instrum. Meas. 2019, 68, 392–401. [Google Scholar] [CrossRef]
- Lim, C.; Choi, Y.; Song, J.; Ahn, S.; Jang, S.; Kim, C. An 88.9-dB SNR Fully-Dynamic Noise-Shaping SAR Capacitance-to-Digital Converter. IEEE J. Solid-State Circuits 2022, 57, 2778–2790. [Google Scholar] [CrossRef]
- Jie, L.; Tang, X.; Liu, J.; Shen, L.; Li, S.; Sun, N.; Flynn, M.P. An Overview of Noise-Shaping SAR ADC: From Fundamentals to the Frontier. IEEE Open J. Solid-State Circuits Soc. 2021, 1, 149–161. [Google Scholar] [CrossRef]
- Fredenburg, J.A.; Flynn, M.P. A 90-MS/s 11-MHz-Bandwidth 62-dB SNDR Noise-Shaping SAR ADC. IEEE J. Solid-State Circuits 2012, 47, 2898–2904. [Google Scholar] [CrossRef]
- Fredenburg, J.; Flynn, M. A 90MS/s 11MHz bandwidth 62dB SNDR noise-shaping SAR ADC. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 468–470. [Google Scholar]
- Luo, Y.; Jain, A.; Wagner, J.; Ortmanns, M. Input Referred Comparator Noise in SAR ADCs. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 718–722. [Google Scholar] [CrossRef]
- Yip, M.; Chandrakasan, A.P. A resolution-reconfigurable 5-to-10b 0.4-to-1V power scalable SAR ADC. In Proceedings of the 2011 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 190–192. [Google Scholar] [CrossRef]
- Ismail, A.H. On the System-Level Design of Noise-Shaping SAR Analog-to-Digital Converters. Electronics 2024, 13, 4128. [Google Scholar] [CrossRef]



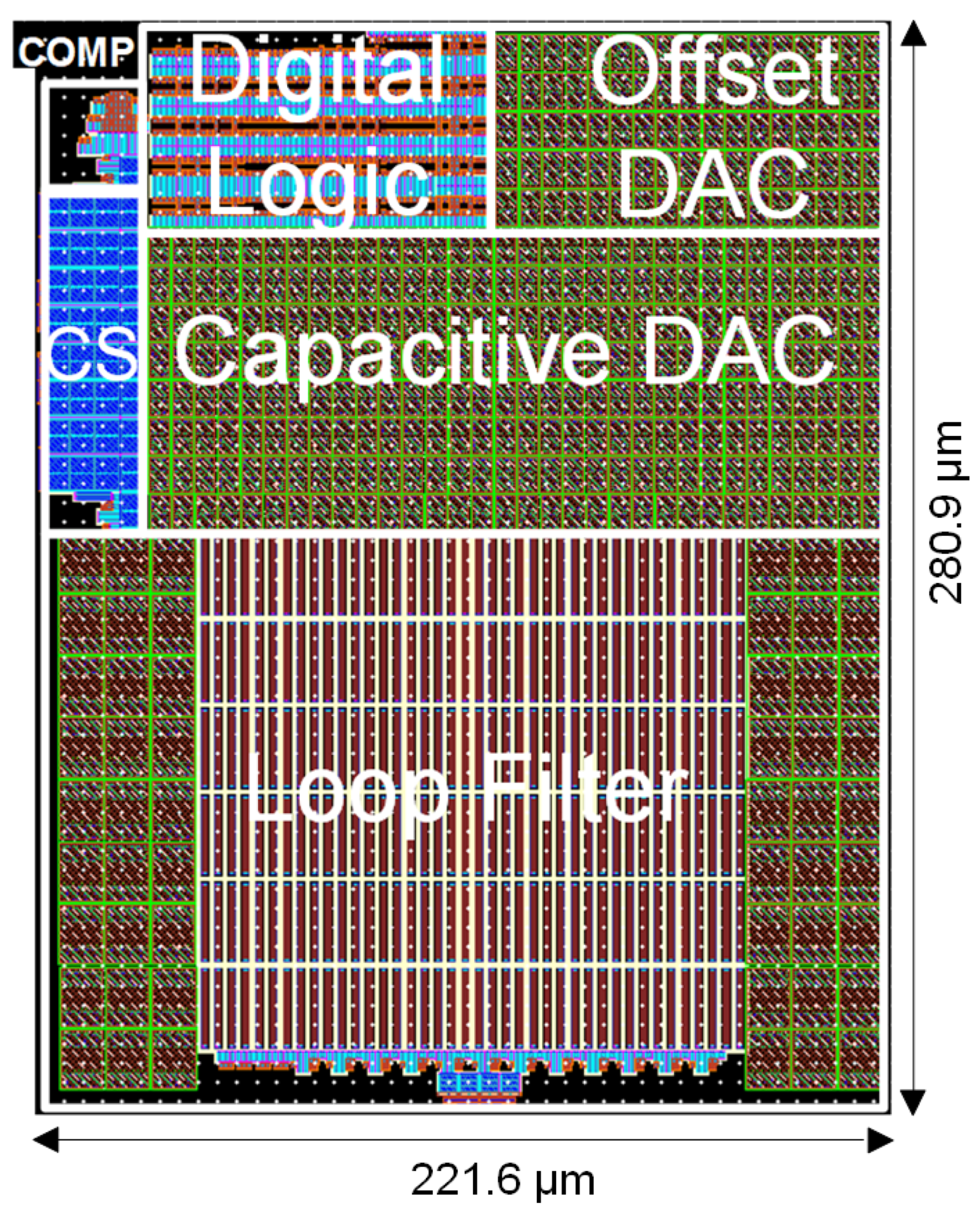
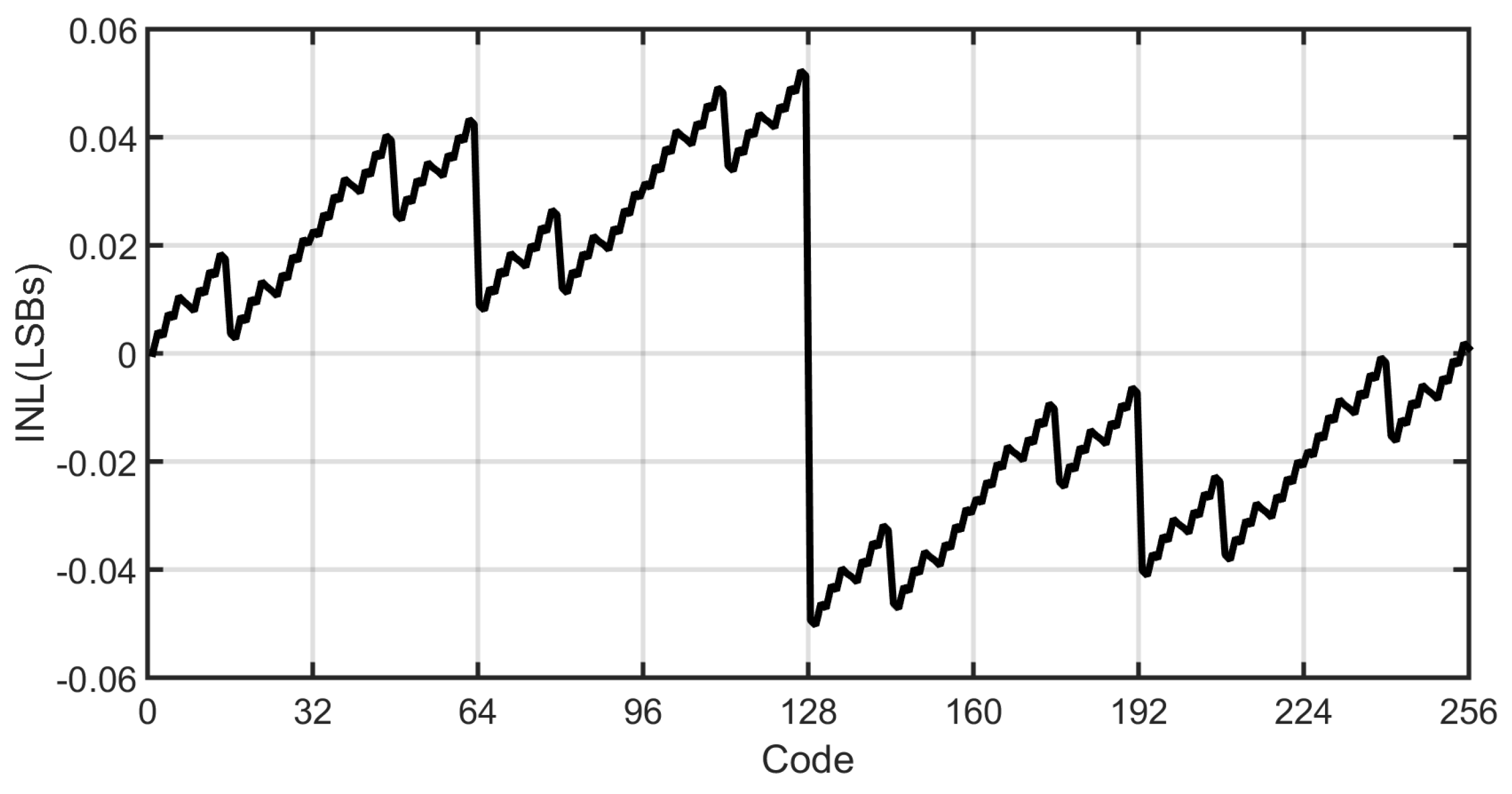
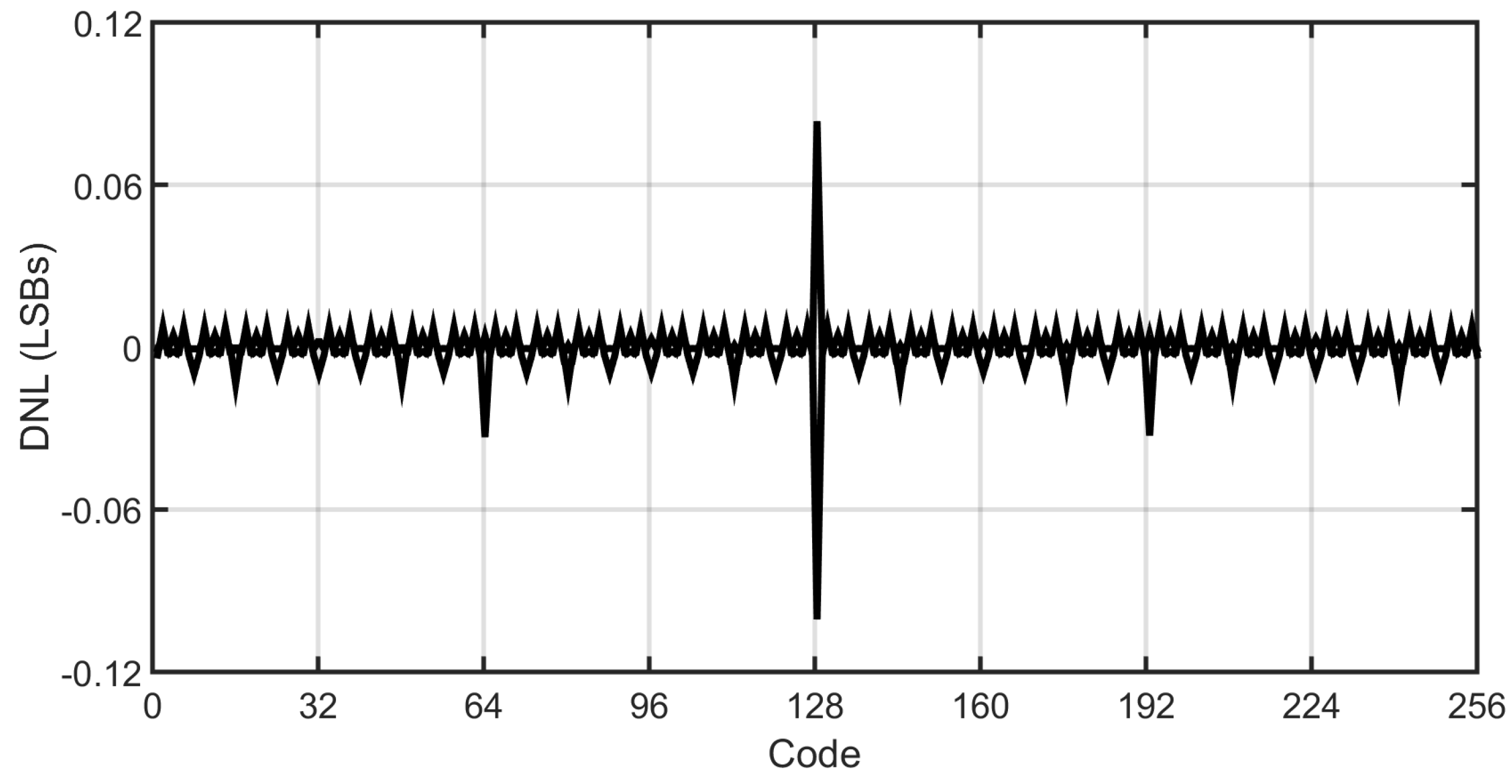
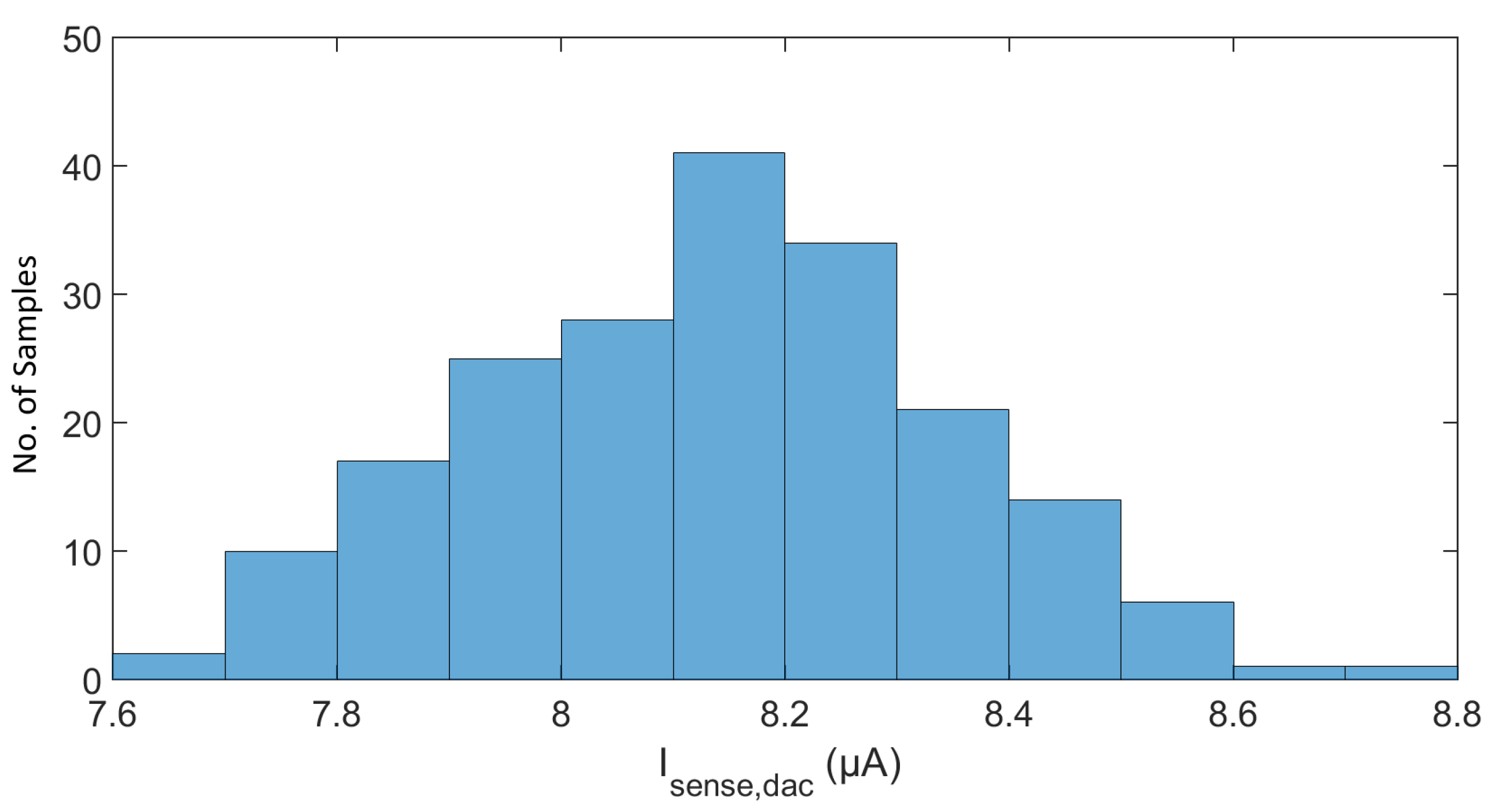
| Block | Current Consumption (nA) | Percentage % |
|---|---|---|
| Charging current sources | 334 | 33.1 |
| Multi-input comparator | 50 | 5 |
| Noise-shaping Filter | 225 | 22.3 |
| Digital and switching | 400 | 39.6 |
| Specification | TIM’ 2019 | JSSC’ 2022 | ISSCC’ 2012 | JSNA’ 2016 | TCAS-I’ 2017 | This |
|---|---|---|---|---|---|---|
| [35] | [36] | [4] | [27] | [26] | Work * | |
| Technology (nm) | 180 | 180 | 350 | 180 | 180 | 130 |
| Architecture | NS SAR | NS SAR | SAR | SAR | NS SAR | |
| Noise-Shaping Order | 1st | 2nd | 3rd | - | - | 2nd |
| Dynamic Range | Fixed | Fixed | Fixed | Fixed | Fixed | Scalable |
| Offset Cap. Cancel. | N/A | N/A | Yes | N/A | N/A | Yes |
| Supply Voltage (V) | 0.8/1 | 1.8 | 3.3 | 0.9/1 | 0.8/1.2 | 0.8 |
| Input Range (pF) | 3.6 | 13.6 | 3.2 | 16.14 | 12.66 | 4 |
| Meas. Time (S) | 810 | 50 | 20 | 42.5 | 16 | 2500 |
| Cap. Resolution () | 150 | 172 | 65 | 1300 | 1200 | 282 |
| Power Consump. (W) | 1.59 | 63.28 | 15,000 | 3.84 | 6.44 | 0.8 |
| Resolution (bits) | 11 | 12 | 6 | 12 | 12 | 8 |
| ENOB (bits) | 12.74 | 14.5 | 13.8 | 11.8 | 11.6 | 12.0 |
| SNDR (dB) | 78.5 | 88.9 | 84.8 | 72.8 | 71.6 | 74.0 |
| Area (mm2) | 0.3 | 0.25 | 2.6 | 0.1 | 0.2 | 0.062 |
| FoM (fJ/conv.-step) | 187 | 139 | 20,823 | 45.8 | 33 | 488 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allam, A.F.; Omran, H.A.; Ismail, A.H. A Noise-Shaping SAR-Based Capacitance-to-Digital Converter for Sensing Applications. Electronics 2025, 14, 1386. https://doi.org/10.3390/electronics14071386
Allam AF, Omran HA, Ismail AH. A Noise-Shaping SAR-Based Capacitance-to-Digital Converter for Sensing Applications. Electronics. 2025; 14(7):1386. https://doi.org/10.3390/electronics14071386
Chicago/Turabian StyleAllam, Ahmad F., Hesham A. Omran, and Ayman H. Ismail. 2025. "A Noise-Shaping SAR-Based Capacitance-to-Digital Converter for Sensing Applications" Electronics 14, no. 7: 1386. https://doi.org/10.3390/electronics14071386
APA StyleAllam, A. F., Omran, H. A., & Ismail, A. H. (2025). A Noise-Shaping SAR-Based Capacitance-to-Digital Converter for Sensing Applications. Electronics, 14(7), 1386. https://doi.org/10.3390/electronics14071386






