Abstract
In this paper, we introduce a robust framework for linear regression–based channel estimation (CE) designed for multipath channel environments within a new radio (NR) sounding reference signal (SRS) system. The main contribution of this study is to show that integrating channel impulse response (CIR) refinement with existing CE schemes significantly improves CE performance in terms of normalized mean squared error (NMSE). Specifically, our approach employs thresholding-based CIR refinement to eliminate noise tap components effectively, discern the lengths of dominant tap elements, and augment linear regression–based CE’s efficacy. Specifically, it is shown that increasing the number of channel taps for threshold setting further enhances the performance of regression–based CE by leveraging CIR refinement. By utilizing an optimized threshold design, our results reveal close performance compared to both ideal tap information-based regression and the theoretical performance of linear minimum mean square error (LMMSE) estimation, whose findings are substantiated by numerical analyses employing our proposed polynomial regression–based channel estimation (PRCE) and DFT regression–based channel estimation (DRCE) schemes.
1. Introduction
In recent years, the exponential growth in applications requiring high data rates, such as video streaming and cloud-based services, has significantly driven the demand for increased channel capacity. To address these needs, advanced communication technologies such as the long-term evolution standard and new radio (NR) are being extensively utilized. These standards are designed to support an expanded volume of users and devices, ensuring faster and more reliable connectivity. In addition, the role of the physical layer is becoming increasingly important with the shift to a 6G approach, where much more accurate and rigorous performance requirements are expected. In this context, enhancing the performance of channel estimation (CE) in the physical layer is crucial, as it optimizes the overall performance of this layer [1,2,3].
The enhancement in CE performance in orthogonal frequency division multiple access (OFDMA) systems is crucial for improving system performance by promoting efficient equalization, resource allocation, and interference reduction. This process not only enhances the capacity of OFDMA systems by reducing the bit error rate but also facilitates beamforming and adaptive modulation. For this purpose, pilot symbols placed between data symbols enable CE implementation of data symbols through interpolation. In the NR uplink system presented in the third-generation partnership project specification, various pilot types are used for the CE, including sounding reference signal (SRS), phase-tracking reference signals, and demodulation reference signals [4,5]. Numerous studies on CE utilizing reference signals have been conducted within the NR system [6,7,8]. This paper specifically focuses on CE in the NR-SRS framework.
Various channel estimation schemes, including machine learning [9,10], message passing, and sparse Bayesian learning schemes [11], have been studied to improve estimation performance in complex environments. However, this study focuses on linear regression–based channel estimation and CIR refinement schemes to achieve robust performance with low computational complexity. For this purpose, this paper provides a detailed analysis of computationally efficient channel estimation schemes that enhance the performance of least squares (LS)-based linear regression methods. In [12,13,14,15], an improved bit error rate performance was achieved with low computational complexity by employing polynomial regression–based channel estimation (PRCE). In the PRCE, the channel frequency response (CFR) curve is fitted utilizing a design matrix characterized by a specified polynomial order. The channel impulse response (CIR), when analyzed through the Fourier transform, is equivalent to CFR, a scheme for CE based on the discrete Fourier transform (DFT) which is proposed in [16,17] to mitigate estimation errors associated with multipath channels. In the context of DFT regression–based channel estimation (DRCE), the residual estimation error decreases significantly while projecting into a low-dimensional space. Furthermore, there is an absence of modeling error, as the CIR is equivalent to the CFR. This approach effectively minimizes the estimation error of LS and aligns with maximum likelihood estimation, provided that accurate channel tap information is available [16].
Various thresholding schemes for CIR refinement have been proposed, including the maximum power thresholding-based CIR refinement (MTCR) [18], the sub-optimal thresholding for CIR refinement (STCR) [19,20], the noise-standard-deviation thresholding for CIR refinement (NTCR) [21], and the weighted noise thresholding-based CIR refinement (WTCR) [22,23]. MTCR determines the threshold based on the strongest tap component’s power, offering reliable performance in specific scenarios. However, its reliance on a single tap limits its flexibility and effectiveness in channels with complex multipath characteristics. STCR focuses on frequency-domain optimization, leveraging power delay profiles and impulse response decimation to refine CIR, while NTCR adopts time-domain thresholding based on noise statistics to handle sparse channels. The WTCR scheme, recognized as a state-of-the-art approach in CIR refinement [23], employs a noise-weight parameter to dynamically adjust thresholds, achieving high accuracy across varying channel conditions. Despite their strengths, these schemes exhibit limitations in addressing diverse channel scenarios and integrating effectively with linear regression frameworks.
In this study, we refine the MTCR scheme to enhance its adaptability and performance under varying channel conditions, assuming a channel environment where the delay spread remains nearly constant over time. Additionally, we propose the average power threshold-based CIR refinement (ATCR), which leverages multiple dominant taps for threshold determination, improving robustness and accuracy in multipath environments. Through comprehensive analysis, we compare our proposed optimized ATCR and MTCR approaches with the state-of-the-art WTCR model following the guidelines in [23].
Building on this foundation, this paper presents a framework for a linear regression–based CE with CIR refinement, in the NR-SRS system. Since traditional PRCE schemes did not utilize channel tap length, we present an enhanced polynomial regression model with channel tap length, based on the polynomial characteristics of the CFR in the multipath channel. Thresholding-based CIR refinement effectively removes noise tap components to obtain the length of dominant tap elements and improves the performance of CE based on the linear regression method. Utilizing an optimized threshold based on the number of channel taps and signal-to-noise ratio (SNR), the performance of the regression–based CE with threshold is compared to that of regression–based CE with ideal tap information and linear minimum mean square error (LMMSE) employing perfect statistical data. Furthermore, the proposed schemes are rigorously validated through simulations against the state-of-the-art WTCR model, which is identified as such among the STCR, NTCR, and WTCR schemes presented in [23], as well as a CIR refinement model that relies exclusively on the maximum delay spread. A concise comparison of CIR refinement schemes for linear regression–based CE is summarized in Table 1.

Table 1.
A concise comparison about CIR refinement schemes for linear regression–based channel estimations.
This paper is organized as follows: in Section 2, we describe a multipath-based OFDMA system model in the NR-SRS system. Section 3 focuses on explicating the linear regression methods for CE and their theoretical analysis. Section 4 details CIR refinement using linear regression methods. Numerical results are presented in Section 5, offering empirical insights into the performance of the discussed schemes. Finally, conclusions are drawn in Section 6, which summarizes the key finding of our research.
2. System Model
2.1. Channel Model
We analyze a single-input single-output (SISO) OFDMA system, assuming perfect synchronization in time and frequency. SRS sequence is generated for insertion into the uplink transmission signal in the frequency domain. The sequence generation equation is represented as
where and is a root sequence generated from a Zadoff–Chu sequence [25]. This sequence has constant amplitude and zero autocorrelation, allowing for orthogonal code multiplexing with a cyclic shift offset, . The indicates the SRS sequence length, with both and are determined by higher-layer parameters. After generating the sequence, it is normalized by the number of antennas and the amplitude scaling factor , then mapped to length subcarriers:
where , is the number of transmission comb and is the frequency domain starting position. After that, zero padding (ZP) is performed and then processed through the N-point inverse fast Fourier transform (IFFT). The output vector is represented as
where is a N-length ZP output vector and is the N-point IFFT matrix.
After adding a cyclic prefix (CP) of length that exceeds the maximum channel delay spread , signal is transmitted through the additive white Gaussian noise (AWGN) and multipath channel. Since we assume that the channel variations are negligible over a one-symbol block, the CIR vector is constant within a single-symbol block. To simplify the channel model, we define the CIR vector for the dominant L channel paths ..., where the superscript indicates the vector transpose. The received signal vector is represented as
where is a Toeplitz matrix constructed using the CIR vector and is the noise vector composed of independent and identically distributed Gaussian entries with a mean of zero and variance of .
After the fast Fourier transform (FFT) block, the output signal vector of length in the pilot position is represented as
where is a diagonal matrix of the SRS pilot sequence, and is length frequency domain AWGN vector having the same statistical property with . The vector represents the CFR, with each component denoted as
where is the pilot index of the OFDMA block for and . Therefore, using the CIR vector , (5) is expressed as [16]
where is a matrix with entries of
where and .
2.2. Conventional Channel Estimation Schemes
Decoding transmission data requires an equalization process that relies on channel state information; however, since accurate channel state information is typically unavailable in real-world scenarios, the estimated CFR is generally used for decoding. The LS CE [26,27] is a widely used CE scheme. This scheme multiplies the received pilot data by the inverse of the pilot matrix . If each pilot symbol is generated from a unit power sequence, is an unitary matrix. Therefore, multiplying the matrix (the conjugate transpose of ) by (7) produces
where and it has equal statistical property with . The LS estimator is popular for its low computational complexity. However, the feature that residual noise has the same statistical properties as the received signal makes it vulnerable to low SNR environments. The LMMSE estimator [28,29,30] has robust performance for SNR by leveraging statistical information such as noise distribution and channel correlation. The LMMSE estimator formula is represented as
where is a correlation matrix of CFR and is a size identity matrix. The Fourier transform does not affect the statistical properties of AWGN, so the noise variance in the frequency domain is . The LMMSE estimator typically performs better than the LS estimator because it takes into account both the noise levels and the specific characteristics of the channel, leading to more reliable results. Under the assumption of infinite noise variance, the LMMSE estimator is equivalent to the LS estimator. Numerous methodologies based on LS estimation have been proposed to achieve effective performance while minimizing computational complexity. Our study concentrates on noise reduction in LS estimation through regression. Specifically, we explore tap length estimation schemes for multipath channels to enhance the effectiveness of regression–based estimators.
3. Preliminaries on Linear Regression–Based Channel Estimation
Several linear regression schemes have been proposed for CE [12,13,14,15,16,17]. Linear regression [31,32] effectively handles data using a simple linear model, represented as a linear combination of input features. This approach simplifies parameter estimation and minimizes errors. In addition, assuming that the residual noise in regression or the prediction error follows a normal distribution, the LS solution for linear regression is the maximum likelihood estimate. The performance of linear regression is strongly influenced by whether the features of the data are accurately modeled. As an example, polynomial basis functions effectively capture nonlinear relationships and are suitable for scenarios generated by polynomial input features. On the other hand, regression methods that utilize DFT basis functions are based on the concept that CFR is the DFT of CIR in multipath channel modeling. This approach can further improve the accuracy of curve fitting for CFR. This scheme corresponds to the maximum likelihood estimation, particularly in environments with Gaussian noise and multipath channels, where the exact channel tap length is known. In this section, we will describe the linear regression–based CE. Subsequently, we theoretically analyze the linear regression model to investigate approaches for performance enhancement.
3.1. Polynomial Regression–Based Channel Estimation
Polynomial regression is one of the most commonly used regression methods. It uses the coefficients of polynomial terms to represent the CFR curve in CE scenarios. The PRCE scheme [12,13,14] for a CFR was obtained by fixed window size and the basis function is expressed as a quadratic function. To optimize estimation performance, we utilize a total pilot sample, which requires a larger fitting matrix for aligning high-dimensional curves, increasing computational complexity and the cost associated with inverse matrix computation.
In the PRCE model, each element in the LS CE can be considered as a standard extension of the linear regression, with a polynomial function
where is the polynomial coefficient to be estimated, p is the dimension of the PRCE model (or polynomial order), and denotes a residual noise. The derivation of this polynomial model and its application in linear regression–based channel estimation can be found in [31,32]. As mentioned in [13], is complex Gaussian distributed in a Rician or Rayleigh fading channel. We utilize scaling and centering for polynomial basis functions to avoid ill-conditioned matrices and overflow problems [33], which is represented as
where and is the average of index n. The polynomial model (11) can be written as
where is a design matrix in PRCE with its nth row being defined as , and . The maximum likelihood estimate of the coefficient vector is derived as [32]
where is estimated coefficient vector. The regression estimation can be expressed through the model expressed in (13), the fitted CFR curve of the PRCE is given by
For theoretical analysis, in [12], the mean square error (MSE) was separated by modeling error and error from residual noise. In the LS CE (9), the MSE is represented as
The modeling error and residual noise are given by [12]
and
respectively, where is the projection matrix of PRCE. To reduce the modeling error in PRCE, the projection matrix needs to minimize the loss of information regarding the DFT matrix in its role in converting CIR to CFR, as indicated in (9). However, the inherent structural limitations of the polynomial series lead to unavoidable information loss in the CFR vector , which results in persistent modeling errors. To mitigate these errors, the projection matrix should be carefully optimized to minimize distortion of while preserving as much information as possible.
In addition, in terms of reducing residual noise, by confining the noise CFR vector to a polynomial subspace, the projection matrix filters the noise from polynomial components unnecessary for CFR modeling (11) and reduces MSE. Since the number of polynomial subspaces is proportional to the polynomial order, the CFR vector should be regressed onto a projection matrix based on a lower polynomial order to reduce residual noise. Therefore, to minimize errors in the PRCE model, the projection matrix preserves CFR data while keeping the polynomial order at least low.
3.2. DFT Regression–Based Channel Estimation
The DRCE is a linear regression scheme designed based on multipath channels, offering better computational efficiency and estimation accuracy than conventional channel estimation schemes. In (6), the CFR vector is formulated as a linear regression model using CIR coefficients. Therefore, the linear regression solution based on the multipath channel model (6) does not encounter issues related to structural defects and is consequently robust to model inaccuracies. In this approach, the regression feature vector corresponds to the CIR vector , so increasing the data length does not affect the design matrix’s order, unlike in PRCE. In [24], it has been demonstrated that increasing the number of data points in the DFT regression model effectively reduces residual noise.
The DRCE model is identical to (6), except for the estimated channel tap length and noise elements, and is given by a linear combination of DFT series
where is the coefficient of the DRCE model to be estimated, the dimension of the DRCE model is equivalent to the estimated tap length , denotes a residual error in the DRCE and, based on (8), is represented as
The coefficients are equivalent to the CIR element, which is represented in (6). Similar to PRCE model as in (13), the DRCE model (19) can be written as
where is a design matrix of DRCE model with its nth row being defined as , corresponds to the CIR vector and . In the same way as the PRCE model, the maximum likelihood estimate of the coefficient vector is derived as
where is estimated coefficient vector. Since the regression estimate can be expressed through the regression model based on (6), the fitted CFR curve of the DRCE can be obtained as
In the same manner as the method in PRCE, the MSE is divided into modeling error and error from residual noise as
Following the same principle as PRCE, the modeling error and the error from residual noise are denoted by
and
respectively, where is the projection matrix of DRCE. As mentioned previously in the context of the PRCE, to reduce modeling errors in the DRCE, it is essential to minimize the information loss regarding the DFT matrix in the transformation by the projection matrix . Unlike PRCE, DRCE is free from modeling errors caused by structural defects. It guarantees no modeling errors if the order of the DFT series is greater than or equal to the actual number of channel taps.
The residual noise term decreases when using with a low or when using a large amount of pilot data . However, if the actual channel model is unknown and an estimated degree of DFT series is shorter than the dominant channel tap length L, modeling errors occur significantly in of (23). In practical cases, accurate channel information is usually unknown, so it is necessary to estimate the channel tap information. A common practice in OFDMA systems, as described in [28], is to ensure that the CP length is longer than the maximum delay spread, thus removing tap elements other than the CP length. On the other hand, we set the estimated tap length to the degree of DFT series in order to obtain more performance improvement than CP length in terms of noise reduction. If the estimated tap length is shorter, the residual noise is reduced by projecting to a smaller DFT subspace. Considering modeling errors and residual noise reduction, better performance is achieved when the estimated tap length is minimized to include only the dominant tap elements. Therefore, the DFT regression method ensures enhanced performance when accurate channel tap information is provided along with sufficient pilot data.
4. Design of Effective NR-SRS Based Channel Estimation
In the previous section, we found that accurate information about dominant taps significantly improves the estimation performance of DRCE. However, in practical cases, the dominant tap information is not provided. To address this challenge, we effectively extract dominant tap elements through the CIR refinement scheme. In this section, we consider the effectiveness of CIR refinement and propose a framework for linear regression–based CE with the CIR refinement. Additionally, we introduce an approach to enhance PRCE by leveraging channel tap information.
4.1. Thresholding-Based CIR Refinement
4.1.1. Maximum Power Thresholding-Based CIR Refinement
In [18,24], thresholding-based CIR refinement schemes efficiently enhance the accuracy of channel estimators. This scheme minimizes noise and other interference by removing CIR components below a dynamically adjusted threshold or those not included in specific dominant taps. In [24], predetermined refinement parameters are used, which do not guarantee robustness when the channel tap length changes. In contrast, ref. [18] introduces a more flexible approach by adapting to changing channel conditions by optimizing thresholds based on the tap component with the highest power, which is the MTCR. This adaptive method enhances robustness by accommodating variations more effectively. The CIR used in the MTCR is obtained by inserting LS channel estimates at the pilot locations and extracting dominant tap components via IFFT applied to a zero-padded vector adjusted to match the FFT size, as shown in (3)
where is the result of inserting LS channel estimates into pilot locations and zero padding to match the FFT size.
The maximum power-based threshold, , is defined by the highest tap power with the parameter as
The effective tap length to be estimated is defined as
based on MTCR, where .
4.1.2. Average Power Thresholding-Based CIR Refinement
The MTCR scheme relies on the element with the highest power, as the threshold is determined based on this element. Therefore, we execute a scheme that considers all channel elements based on their average data, which is the ATCR. In this case, since the delay of channel tap components is smaller than , we only consider elements from 1 to . The average power-based threshold is represented as
The effective tap length to be estimated is given by
based on ATCR, where .
4.2. Regression–Based Channel Estimation with CIR Refinement
In the previously utilized PRCE approach [12,13,14,15], the polynomial order was determined based on numerical results. We propose a method to determine a reasonable polynomial order by utilizing the channel tap information. We noted that the curve of CFR is generated from a Fourier series consisting of CIR-based cosine and sine functions. The polynomial order of a trigonometric function over a specific interval is estimated by considering the approximate length of elements corresponding to the pilot symbols. Considering the above, in our paper, we optimize the polynomial order through simulation. We assumed a specific NR-SRS system and performed optimization. The polynomial design matrix is determined by estimated channel tap length with thresholding-based CIR refinement. The CE for the polynomial regression is then obtained according to (15). Table 2 displays the results of optimized polynomial order for SNR from −10 to 30 in 10 intervals, in a multipath scenario with channel tap length varying from 1 to 20, which is represented as
where is the PRCE order parameter related to the dominant tap length L. A comparison of normalized mean squared error (NMSE) performance between PRCE and DRCE was conducted for channel taps ranging from 1 to 20, based on regression model order. As an example, the optimization of the regression order for a four-tap channel is illustrated in Figure 1. When expressing discrete Fourier series as a polynomial series, the polynomial series cannot accurately represent the Fourier series with a fixed order. Therefore, in PRCE, the optimized regression order exhibits a pattern that varies with SNR, whereas in DRCE, it remains constant with respect to SNR.

Table 2.
optimization.
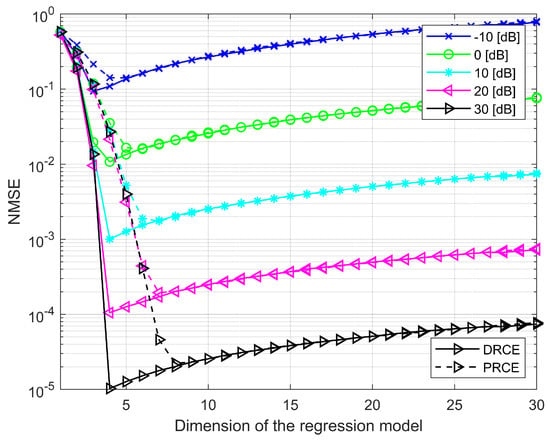
Figure 1.
Regression–based CE NMSE comparison by dimension of the regression model (4–tap channel).
We define the design matrix for PRCE and DRCE based on the estimated dominant tap length using ATCR and MTCR. The PRCE with MTCR is a scheme for performing PRCE with estimated dominant tap length based on MTCR. When CIR refinement is performed using thresholds determined by the tap element with the highest power, it effectively reduces modeling and residual errors caused by noise taps in channels where the tap distribution is concentrated in one tap element. Specifically, if the channel power is concentrated in one tap, the subspace of the PRCE is the same as the CIR. Therefore, when PRCE is applied with CIR information that is refined based on maximum tap power, errors by the regression model are reduced. However, in multipath channels with long delay spreads, the threshold is based only on information from one tap, which can lead to poor performance due to the inability to distinguish noisy taps.
On the other hand, PRCE with ATCR is the scheme of performing PRCE based on the length of dominant taps estimated based on ATCR. Since ATCR utilizes more channel tap components than MTCR, it is expected to demonstrate relatively strong performance in scenarios with long delay spreads. However, accounting for the numerous tap elements of ATCR in a single-tap channel can interfere with the dominant single path and increase complexity.
DRCE with MTCR can expect significant performance in a one-tap channel with the same principle as PRCE with MTCR. In addition, when the tap length is overestimated, the residual error is reduced by using a relatively low-dimensional design matrix compared to the PRCE, so DRCE with MTCR can expect robust performance against errors caused by tap length and estimation. Nevertheless, threshold schemes utilizing a single tap element, such as MTCR with PRCE, face challenges in optimizing the dimension of the DRCE model when channel power is distributed across multiple CIRs.
DRCE with the ATCR scheme performs DRCE using the dominant tap length estimated by ATCR, so it uses the accurately estimated tap information of MTCR when the CIR distribution is spread. Therefore, from a regression perspective, the modeling error due to the exclusion of dominant tap elements and the increase in the residual error due to the overestimated tap length are mitigated.
4.3. Computational Complexity
A comparison of the computational complexities of each CE scheme is presented in Table 3. In this analysis, the SNR was fixed at 10 dB, and the complexity of each scheme was evaluated under this condition. The inverse matrix was calculated using the Gauss–Jordan elimination method. Figure 1 and Section 3 show that the regression method is more negatively affected by modeling errors due to the loss of tap information than by residual noise due to an excessive number of estimation taps. Therefore, the estimated number of taps based on the threshold is at least equal to the actual number, resulting in greater complexity for the estimated tap-based regression scheme compared to the scheme using actual tap information. This leads to higher complexity in polynomial regression compared to DFT regression, as shown in Table 3.

Table 3.
Computational complexity comparison.
The computational complexity of existing channel estimation was presented for comparison with the regression–based CE scheme. Although the LMMSE scheme demonstrates strong performance, it encounters the challenge of exponentially increasing computational complexity as the sequence length grows, due to the necessity of computing inverse matrices. In contrast, the LS approach offers lower complexity but is highly susceptible to noise. In regression–based schemes, the complexity of calculating inverse matrices is determined by the estimated number of taps. In general, since the estimated number of taps is smaller than the length of the CFR sequence, the complexity of inverse matrices based on taps is much lower than that based on sequence length.
4.4. Discussion
The block diagram of regression–based CE by leveraging CIR refinement is presented in Figure 2. The CIR estimated before CIR refinement is obtained as IFFT for CFR estimated by LS. At this stage, the non-pilot position is set to zero, causing interference in the estimated CIR. This problem indicates that it is reasonable to use CIR information as DRCE, rather than using the estimated CIR as LS. The channel tap length estimated by the two CIR refinement schemes MTCR or ATCR determines the parameter for the dimension of each regression model. PRCE and DRCE are linear regression schemes that project LS estimates into polynomial space and multipath channel model-based space, respectively. In terms of modeling and residual error, DRCE is better than PRCE, and even computational complexity is found to be low.
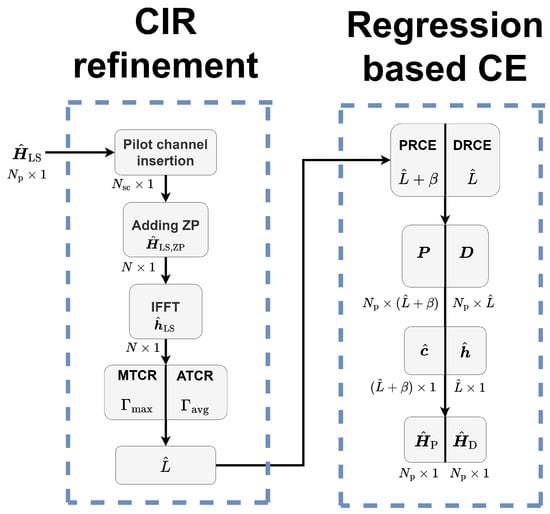
Figure 2.
Block diagram of regression–based CE by leveraging CIR refinement.
The CIR refinement scheme effectively improves the performance of regression–based channel estimation. Specifically, MTCR effectively reduces modeling errors and residual noise by setting thresholds based on the highest power tap elements. Since this scheme relies on single-tap information, performance is degraded in environments with long delay spreads. Conversely, ATCR containing more channel tap components is more robust in long-delay spread conditions, due to enhanced tap estimation performance from multiple tap information. However, when the power is concentrated in the dominant tap, ATCR shows no performance advantages over MTCR, leading to the drawback of excessive computational complexity.
5. Numerical Results
For experimental validation of the theoretical analysis in the previous sections, we present numerical results of channel estimation in the NR-SRS system.
5.1. Simulation Environment
The SRS system parameters are in Table 4 (see [4,5]). Based on that, the mapping of SRS pilot symbols is shown in Figure 3. We assume that each tap of the multipath channel [34] is statistically independent, the average power is of the same magnitude, and that there are no time or frequency offsets, focusing on the CE performance concerning multipath effects. The number of taps in the CIR is set to or , which takes into account a short delay spread where power is concentrated in one tap, and a long delay spread condition where power is spread in multiple taps. The performance of the proposed scheme was validated under a specific SRS configuration environment based on the 3GPP NR standard, demonstrating its applicability to practical communication systems. Note that the applicability of the proposed scheme does not limited to the specific SRS configuration. The proposed scheme can be applied to multiple-input multiple-output (MIMO) and multi-user cases since the NR-SRS pilot patterns over antenna and user are usually not overlapped.

Table 4.
The parameters for the numerical results.
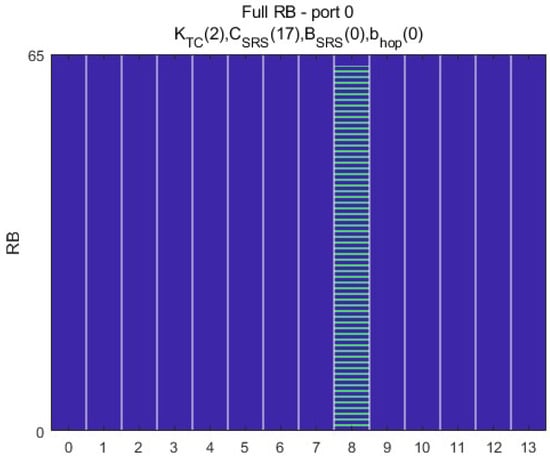
Figure 3.
SRS pilot assignment.
Each simulation was run a total of 100,000 times for SNR levels at 10 dB intervals from −10 dB to 30 dB. To determine the experimental marginal performance, LMMSE calculated the performance using the correlation matrix . This result is referred to as the ideal LMMSE because it cannot be achieved in real-world scenarios. We assumed that the maximum delay spread () is approximately 20 and that the delay spread remains relatively constant over time. For the WTCR, the total non-zero channel taps and channel length were set using the maximum delay spread. The noise-weight parameter was optimized for each SNR level and channel condition, selecting the best value from a range of 0 to 300 in steps of 10. In addition to WTCR, our scheme optimizes the threshold scaling parameter through Monte Carlo simulations conducted within the range of 0.05–7.0, using intervals of 0.05 for each multipath and SNR environment. All the simulations performed in this paper present the outcomes achieved by running 10,000 times. The NMSE is expressed by
The optimized gamma values are specified in Table 5.

Table 5.
Scaling factor optimization.
The analysis in this paper is conducted under a standardized NR-SRS environment with a static multipath channel model. Although the consideration of various Doppler spreads and time-varying fading conditions is an important research topic, this paper focuses on establishing baseline performance and verifying the theoretical validity of the proposed CE framework under static channel conditions.
5.2. Performance Evaluation
Figure 4, Figure 5, Figure 6 and Figure 7 present a comparative analysis of linear regression schemes used for CE in one-tap and four-tap channels. To evaluate the effectiveness of regression–based CE, performance comparisons of regression models designed based on the respective channel tap lengths are presented in Figure 4 and Figure 6. Furthermore, to analyze the impact of applying CIR refinement on the regression model, the performance results of a regression model with CIR information limited to the maximum delay spread and a regression model with CIR refinement applied are presented in Figure 5 and Figure 7. The regression model utilizing only the maximum delay spread, without applying CIR refinement, is labeled as “DRCE” and “PRCE”, while the regression model that knows the actual channel tap length is labeled as “Ideal DRCE” and “Ideal PRCE”.
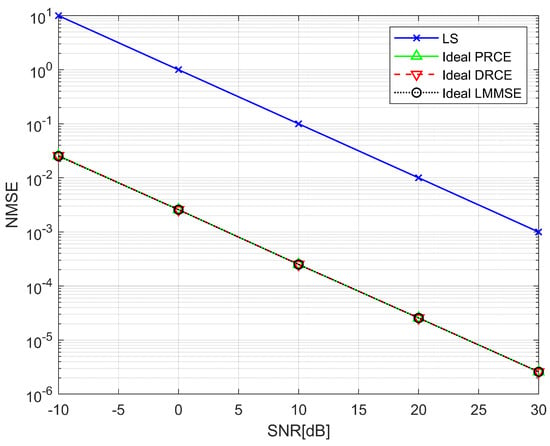
Figure 4.
NMSE performance comparison based on accurate channel information (1–tap channel).
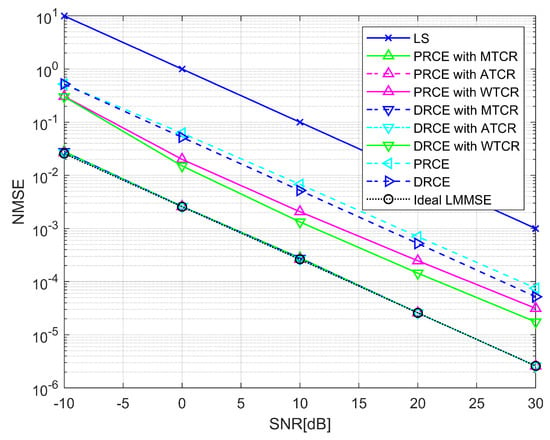
Figure 5.
NMSE performance comparison based on estimated channel information (1–tap channel).
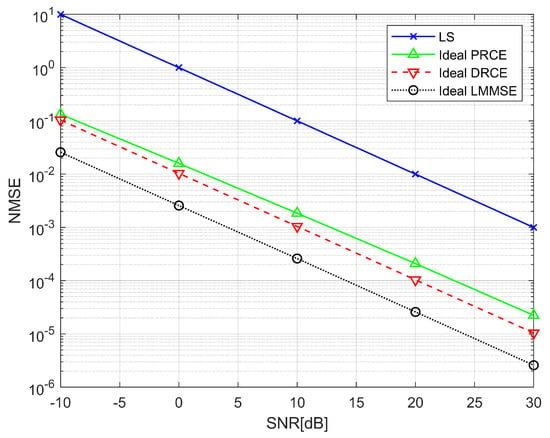
Figure 6.
NMSE performance comparison based on accurate channel information (4–tap channel).
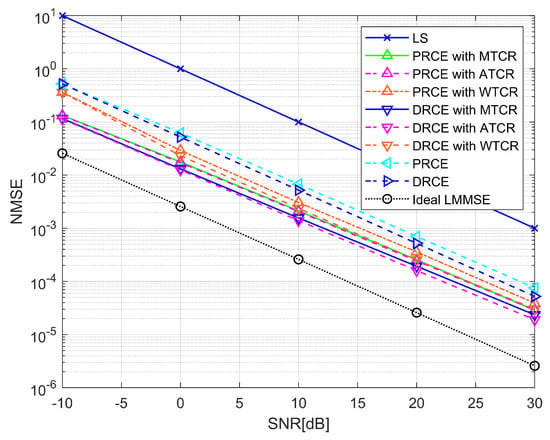
Figure 7.
NMSE performance comparison based on estimated channel information (4–tap channel).
5.2.1. The Effectiveness of the CIR Refinement on Regression Based CE
According to Figure 4 and Figure 6, DRCE improved the performance of regression–based CE by 26 dB in one tap channel and by 20 dB in four tap channels. Both regression–based CE schemes even showed the same performance as the ideal LMMSE on the one-tap channel. In contrast, PRCE demonstrated performance gains of 19 dB at low SNR (−10 dB) and 16.5 dB at high SNR (30 dB). In the four-tap channel, PRCE performs worse than DRCE due to inherent structural limitations, which result in the optimized regression dimension exceeding the number of channel taps by the amount shown in Table 2. Additionally, the reason PRCE’s performance towards that of DRCE at low SNR is that the reduction in residual noise is greater than the modeling error caused by the reduced dimension. These results demonstrate that the regression model effectively enhances CE performance and that the performance of each regression model varies depending on the specific channel condition.
Figure 5 and Figure 7 demonstrate the performance gain of the CIR refinement scheme compared to a regression model designed based on CIR information using only the maximum delay spread. Additionally, there is a performance difference depending on the CIR refinement scheme. In four tap channels, ATCR outperforms MTCR, with the difference being more apparent in DRCE. This effect becomes more significant at high SNR, as the reduction in noise components increases the proportion of modeling errors caused by inaccurate tap information. The performance gains of ATCR are more evident in DRCE than in PRCE due to smaller structural differences from the actual channels and the greater impact of more precise CIR refinements. For one tap channel, it can be seen that the regression–based CE with optimized CIR definition is the same as when the channel tap length is known. Therefore, when the channel power is concentrated in a particular tap, it is sufficient to perform CIR refinement with the maximum power tap component. Furthermore, our proposed CIR refinement schemes demonstrate a clear performance advantage over the state-of-the-art WTCR scheme in linear regression–based CE. This improvement is evident in terms of both accuracy and robustness across varying channel conditions.
5.2.2. Execution Time
In Table 6, the average execution time is presented for each simulation in SNR of 10 dB. Since the execution time is not affected by the channel tap length, LMMSE and LS were presented as the average of the results in each scenario. According to Table 3, the regression–based scheme shows longer processing time compared to LS but shows lower computational complexity compared to LMMSE, which is the same as the aspect of the Table 6. Between regression schemes, the DRCE scheme exhibits a shorter duration than the PRCE due to the small size of the required inverse matrix. It is clear that the time required for DRCE and PRCE schemes is shortened because the size of the inverse matrix involved is reduced when the tap length information is known accurately. Our comprehensive evaluation demonstrates that linear regression CE schemes, particularly the DRCE model, effectively reduce NMSE across varying channel conditions and tap-length complexities. These findings underline the importance of model selection and optimization of threshold parameters in enhancing the efficiency and accuracy of CEs in wireless communications.

Table 6.
Execution time in the SNR of 10 dB.
5.3. Discussion
Through this simulation, the performance of the regression–based CE models showed a significant improvement over LS and close to LMMSE. The reason for this performance gain is that regression–based CE schemes such as PRCE and DRCE effectively reduce residual noise while projecting CFR into the subspace of each regression model. As mentioned in Section 3, reducing modeling error is also crucial for enhancing the performance of regression–based CE. Given accurate channel information, DRCE has a modeling error of zero and at the same time shows less residual noise than PRCE. On the other hand, PRCE does not guarantee zero modeling error, which results in a lower performance than DRCE. While the CIR refinement scheme improved the performance of regression–based CE, the performance aspect of each CIR refinement scheme was different depending on the channel scenario. It has been confirmed that this difference in performance depends on the ratio of modeling errors compared to the noise of the LS.
6. Conclusions
In this paper, we proposed a regression–based CE framework that utilizes CIR refinement to enhance the performance of both DRCE and PRCE. By leveraging channel tap information derived from CIR refinement, we dynamically determine the dimension of the regression model, thereby optimizing CE performance. Unlike traditional PRCE, which employs fixed polynomial orders, our approach adapts the polynomial structure based on channel tap information, allowing for a more flexible model despite a fixed number of data points used for regression. Moreover, while conventional DRCE relies solely on maximum tap power for threshold setting, our scheme introduces a threshold-based regression that utilizes multiple tap information via an average threshold scheme, demonstrating superior performance in multipath channel environments. Our framework significantly enhances CE performance, outperforming regression schemes without CIR refinement and achieving performance nearly equivalent to the ideal LMMSE in single-tap channel scenarios. From a performance comparison perspective, the ATCR scheme outperformed the MTCR in environments characterized by long delay spreads. Additionally, our proposed CIR refinement schemes outperformed the state-of-the-art WTCR scheme, demonstrating improved accuracy and robustness across various channel conditions. In conclusion, our findings underscored the critical role of channel tap information obtained through CIR refinement in enhancing the efficacy of existing linear regression–based CE schemes. The variability in the performance of CIR refinement schemes based on channel conditions suggested potential areas for future research, including the exploration of advanced machine learning-based CIR refinement schemes for handling diverse and unexpected CIR distributions.
Author Contributions
Conceptualization, Y.-S.C. and S.-W.C.; methodology, Y.-S.C., J.-Y.H. and S.-W.C.; software, Y.-S.C.; validation, Y.-S.C. and J.-Y.H.; formal analysis, Y.-S.C. and S.-W.C.; investigation, Y.-S.C.; resources, Y.-S.C.; data curation, Y.-S.C.; writing—original draft preparation, Y.-S.C.; writing—review and editing, S.-W.C.; visualization, Y.-S.C.; supervision, S.-W.C.; project administration, S.-W.C.; funding acquisition, S.-W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Kyonggi University Research Grant 2024.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATCR | Average power Thresholding-based Channel impulse response Refinement |
| AWGN | Additive White Gaussian Noise |
| CFR | Channel Frequency Response |
| CIR | Channel Impulse Response |
| CP | Cylic Prefix |
| DFT | Discrete Fourier Transform |
| DRCE | DFT regression–based Channel Estimation |
| FFT | Fast Fourier Transform |
| IFFT | Inverse FFT |
| LMMSE | Linear Minimum Mean Square Error |
| LS | Least Squares |
| MIMO | Multiple-Input Multiple-Output |
| MSE | Mean Square Error |
| MTCR | Maximum power Thresholding-based CR |
| NMSE | Normalized MSE |
| NR | New Radio |
| NTCR | Noise-standard-deviation Thresholding for CR |
| OFDMA | Orthogonal Frequency Division Multiple Access |
| PRCE | Polynomial regression–based Channel Estimation |
| SISO | Single-Input Single-Output |
| SNR | Signal-to-Noise Ratio |
| SRS | Sounding Reference Signal |
| STCR | Sub-optimal Thresholding for CR |
| WTCR | Weighted noise Thresholding based CR |
| ZP | Zero Padding |
References
- Matthaiou, M.; Yurduseven, O.; Ngo, H.Q.; Morales-Jimenez, D.; Cotton, S.L.; Fusco, V.F. The Road to 6G: Ten Physical Layer Challenges for Communications Engineers. IEEE Commun. Mag. 2021, 59, 64–69. [Google Scholar]
- Chen, Z.; Han, C.; Wu, Y.; Li, L.; Huang, C.; Zhang, Z.; Wang, G.; Tong, W. Terahertz Wireless Communications for 2030 and Beyond: A Cutting-Edge Frontier. IEEE Commun. Mag. 2021, 59, 66–72. [Google Scholar]
- Chataut, R.; Akl, R. Massive MIMO Systems for 5G and beyond Networks—Overview, Recent Trends, Challenges, and Future Research Direction. Sensors 2020, 20, 2753. [Google Scholar] [CrossRef] [PubMed]
- 3GPP TS 36.211. Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation. Available online: https://www.3gpp.org/ftp/Specs/archive/36_series/36.211/36211-h40.zip (accessed on 15 January 2024).
- 3GPP TR 38.211. Nr; Physical Channels and Modulation. Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.211/38211-h70.zip (accessed on 24 March 2024).
- Kalachikov, A.; Stenin, A. Performance Evaluation of the SRS Based MIMO Channel Estimation on 5G NR Open Source Channel Model. In Proceedings of the 2021 IEEE 22nd International Conference of Young Professionals in Electron Devices and Materials (EDM), Souzga, Russia, 16 August 2021; pp. 124–127. [Google Scholar]
- Sun, B.; Tan, B.; Ashraf, M.; Valkama, M.; Lohan, E.S. Embedding the Localization and Imaging Functions in Mobile Systems: An Airport Surveillance Use Case. IEEE Open J. Commun. Soc. 2022, 3, 1656–1671. [Google Scholar] [CrossRef]
- Sengupta, A.; Davydov, A.; Wang, G.; Pawar, S.; Morozov, G. Low PAPR DM-RS Design for 5G Systems Operating in High Frequency Bands. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Liu, F.; Zhang, J.; Jiang, P.; Wen, C.-K.; Jin, S. CE-ViT: A Robust Channel Estimator Based on Vision Transformer for OFDM Systems. In Proceedings of the GLOBECOM 2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 4798–4803. [Google Scholar]
- Soltani, M.; Pourahmadi, V.; Mirzaei, A.; Sheikhzadeh, H. Deep Learning-Based Channel Estimation. IEEE Commun. Lett. 2019, 23, 652–655. [Google Scholar]
- Li, M.; Zhang, S.; Ge, Y.; Gao, F.; Fan, P. Joint Channel Estimation and Data Detection for Hybrid RIS Aided Millimeter Wave OTFS Systems. IEEE Trans. Commun. 2022, 70, 6832–6848. [Google Scholar] [CrossRef]
- Wang, X.; Liu, K.J.R. Channel estimation for multicarrier modulation systems using a time-frequency polynomial model. IEEE Trans. Commun. 2002, 50, 1045–1048. [Google Scholar] [CrossRef]
- Chang, M.X.; Su, Y.T. Model-based channel estimation for OFDM signals in Rayleigh fading. IEEE Trans. Commun. 2002, 50, 540–544. [Google Scholar] [CrossRef]
- Chang, M.X.; Su, Y.T. 2D regression channel estimation for equalizing OFDM signals. In Proceedings of the IEEE Vehicular Technology, Tokyo, Japan, 15–18 May 2000; pp. 240–244. [Google Scholar]
- Hijazi, H.; Ros, L. Polynomial Estimation of Time-Varying Multipath Gains with Intercarrier Interference Mitigation in OFDM Systems. IEEE Trans. Veh. Technol. 2009, 58, 140–151. [Google Scholar]
- Morelli, M.; Mengali, U. A comparison of pilot-aided channel estimation methods for OFDM systems. IEEE Trans. Signal Process. 2001, 49, 3065–3073. [Google Scholar] [CrossRef]
- Ancora, A.; Bona, C.; Slock, D.T.M. Down-Sampled Impulse Response Least-Squares Channel Estimation for LTE OFDMA. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; pp. III–293–III–296. [Google Scholar]
- Minn, H.; Bhargava, V.K. An investigation into time-domain approach for OFDM channel estimation. IEEE Trans. Broadcast. 2000, 46, 240–248. [Google Scholar] [CrossRef]
- Rosati, S.; Corazza, G.E.; Vanelli-Coralli, A. OFDM Channel Estimation with Optimal Threshold-Based Selection of CIR Samples. In Proceedings of the 2009 IEEE Global Telecommunications Conference (GLOBECOM 2009), Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–7. [Google Scholar]
- Rosati, S.; Corazza, G.E.; Vanelli-Coralli, A. OFDM Channel Estimation Based on Impulse Response Decimation: Analysis and Novel Algorithms. IEEE Trans. Commun. 2012, 60, 1996–2008. [Google Scholar] [CrossRef]
- Xie, H.; Andrieux, G.; Wang, Y.; Diouris, J.F.; Feng, S. Efficient Time Domain Threshold for Sparse Channel Estimation in OFDM System. AEU-Int. J. Electron. Commun. 2014, 68, 277–281. [Google Scholar]
- Sure, P.; Bhuma, C.M. Weighted-noise threshold based channel estimation for OFDM systems. Sādhanā 2015, 40, 2111–2128. [Google Scholar]
- Samah, A.; Alrababah, A.; Alfandi, O. A survey on OFDM channel estimation techniques based on denoising strategies. Eng. Sci. Technol. Int. J. 2020, 23, 897–909. [Google Scholar]
- Xie, H.; Andrieux, G.; Wang, Y.; Diouris, J.F.; Feng, S. Threshold based most significant taps detection for sparse channel estimation in OFDM system. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC 2013), Kunming, China, 5–8 August 2013; pp. 1–5. [Google Scholar]
- Chu, D. Polyphase codes with good periodic correlation properties (Corresp.). IEEE Trans. Inf. Theory 1972, 18, 531–532. [Google Scholar]
- Colieri, S.; Ergen, M.; Puri, A.; Bahai, A. A study of channel estimation in OFDM systems. In Proceedings of the IEEE 56th Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002; pp. 894–898. [Google Scholar]
- Wei, C.; Liu, H.; Zhang, Z.; Dang, J.; Wu, L. Near-Optimum Sparse Channel Estimation Based on Least Squares and Approximate Message Passing. IEEE Wireless Commun. Lett. 2017, 6, 754–757. [Google Scholar] [CrossRef]
- Van de Beek, J.; Edfors, O.; Sandell, M.; Wilson, S.K.; Borjesson, P.O. On channel estimation in OFDM systems. In Proceedings of the 1995 IEEE 45th Vehicular Technology Conference, Chicago, IL, USA, 25–28 July 1995; pp. 815–819. [Google Scholar]
- Edfors, O.; Sandell, M.; van de Beek, J.; Wilson, S.K.; Borjesson P., O. OFDM channel estimation by singular value decomposition. IEEE Trans. Commun. 1996, 46, 931–939. [Google Scholar] [CrossRef]
- Savaux, V.; Louët, Y. LMMSE channel estimation in OFDM context: A review. IET Signal Process. 2017, 11, 123–134. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Machine Learning Basics. In Deep Learning (Adaptive Computation and Machine Learning Series); The MIT Press: Cambridge, MA, USA, 2017; pp. 107–110. [Google Scholar]
- Bishop, C. Linear Models for Regression. In Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; pp. 137–146. [Google Scholar]
- Trefethen, N.; Bau, D., III. Linear Systems. In Numerical Linear Algebra, 1st ed.; SIAM: Philadelphia, PA, USA, 1997; pp. 82–84. [Google Scholar]
- 3GPP TR 38.901. Study on Channel Model for Frequencies from 0.5 to 100 GHz. Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.901/38901-h10.zip (accessed on 24 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).