Generative Adversarial Networks in Imbalanced Gas Samples
Abstract
1. Introduction
- We propose a novel sample equalization method for sensor arrays. This method utilizes an SSGAN to generate synthetic minority class samples along with their corresponding labels, thereby improving the accuracy of the target model;
- We develop a specialized generator loss function that encourages the generated data to closely resemble real sensor data while preventing exact duplication;
- Extensive experiments are conducted on an open-access air quality dataset from the UC Irvine Machine Learning Repository. The dataset includes sensor readings from five metal oxide chemical sensors used for gas concentration estimation. We analyze the impact of imbalanced data on target models and demonstrate that SSGANs significantly enhance model performance when trained with the generated data;
- We design an attention-based model for gas concentration estimation, utilizing the steady-state value of the sensor as input. This model achieves comparable accuracy to the CNN model while requiring fewer parameters.
2. Proposed Method
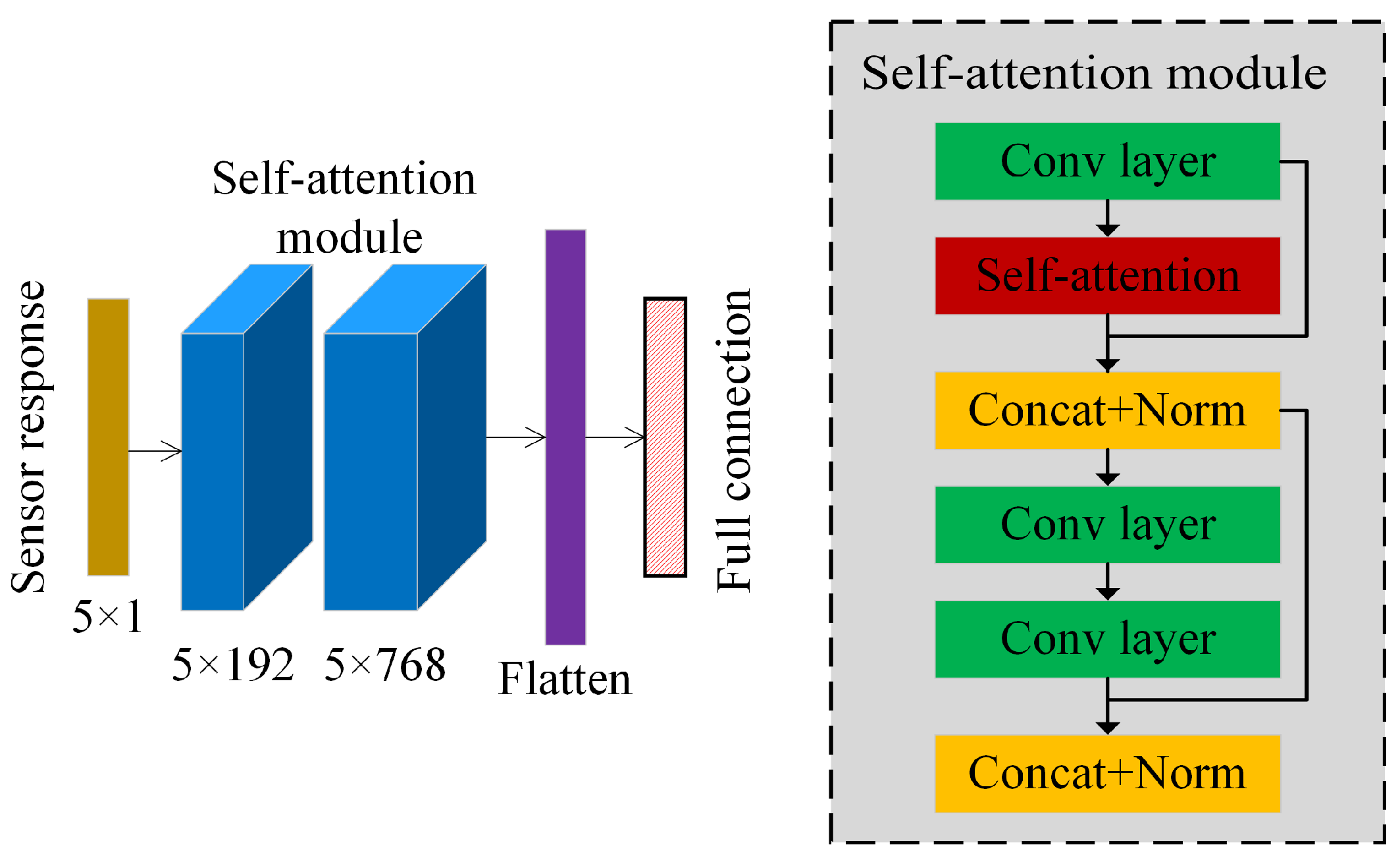
2.1. Generator
2.2. Discriminator
2.3. Target Model
2.4. Model Training with Outcome Assessment Strategy
3. Experiments
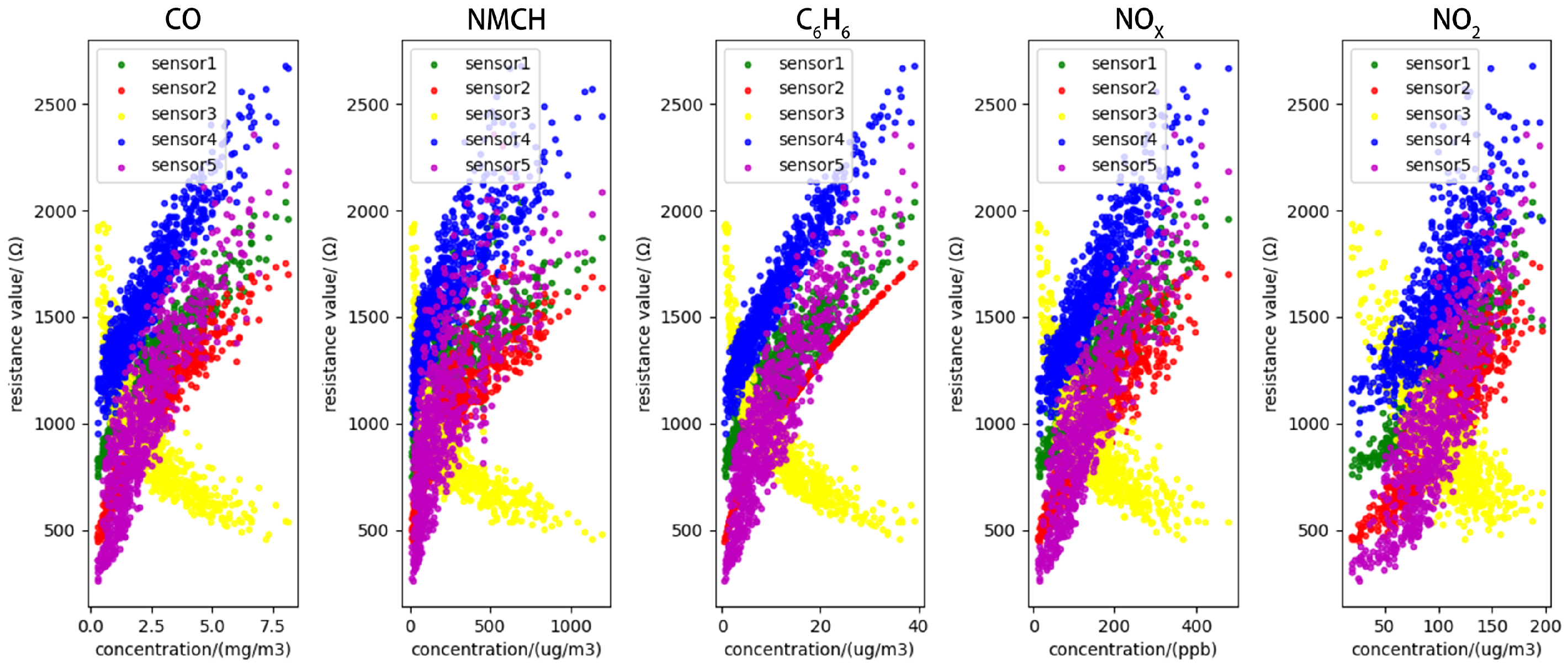
3.1. Dataset Description
3.2. Experimental Setting
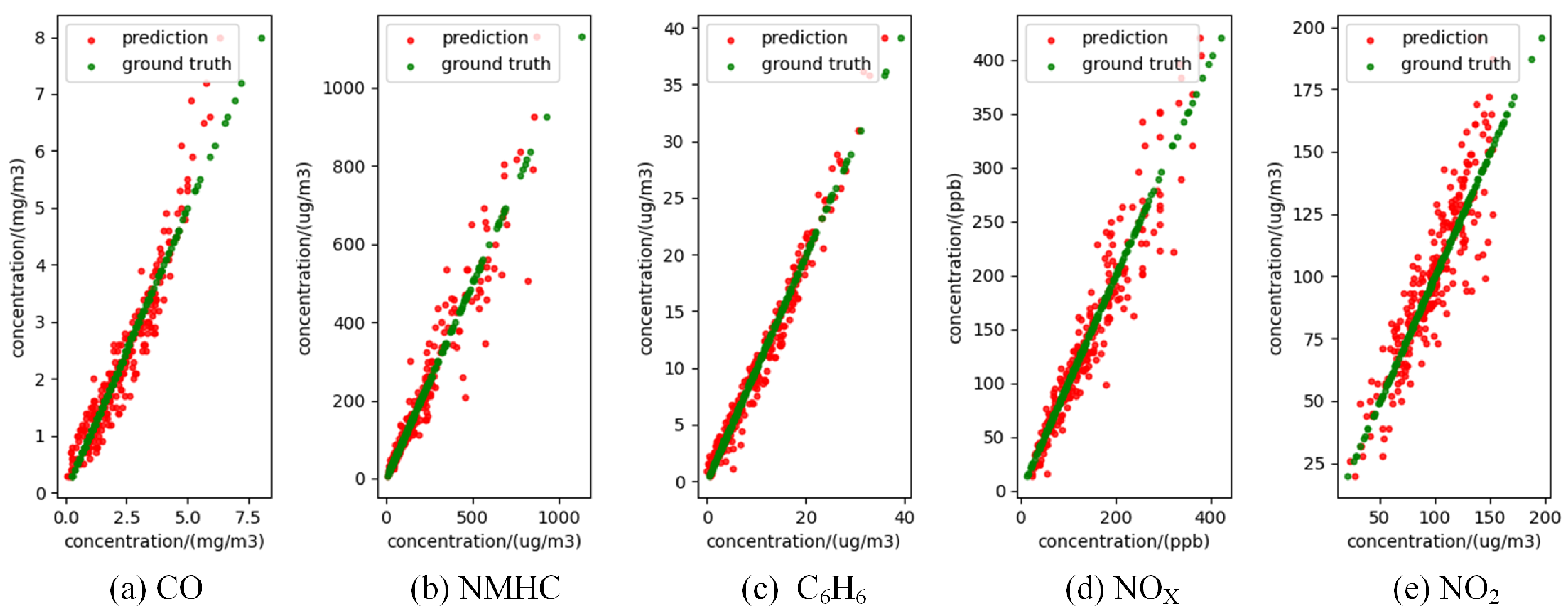
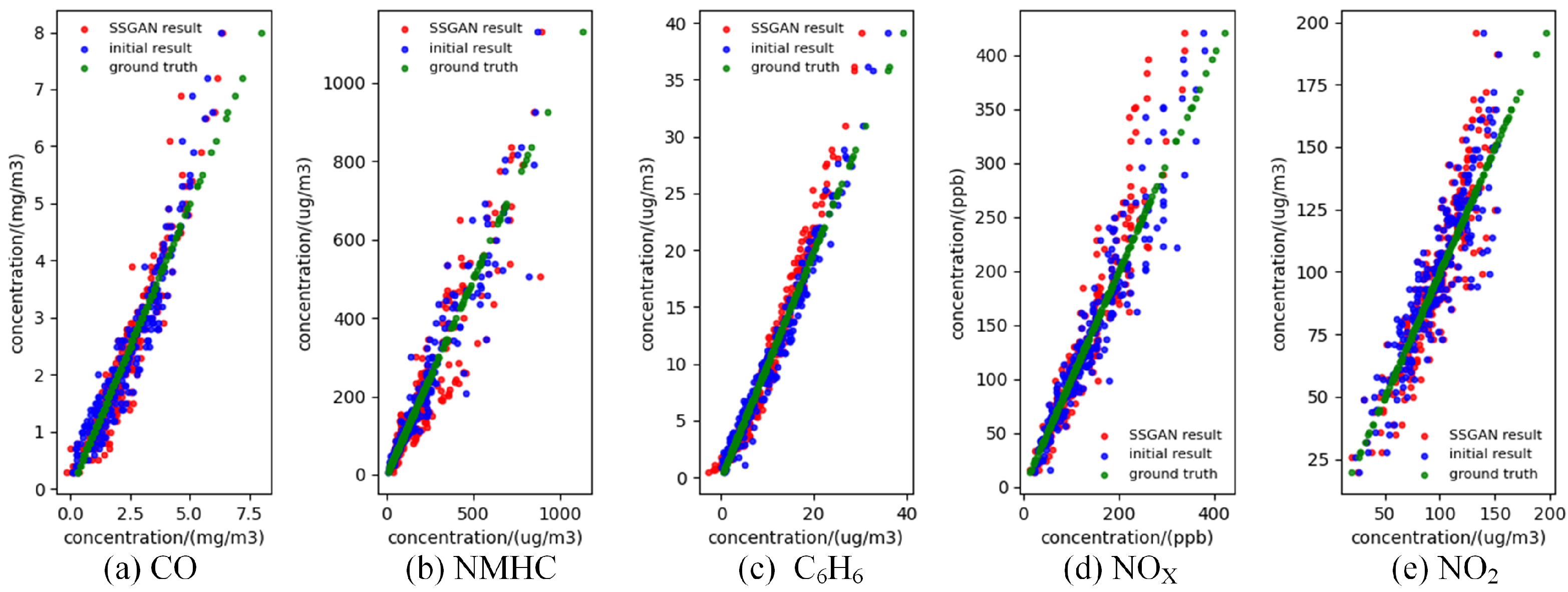
3.3. Experimental Results
3.3.1. BPNN Results
3.3.2. CNN Results
3.3.3. Attention Model Results
4. Discussion
4.1. Imbalanced Samples Analysis
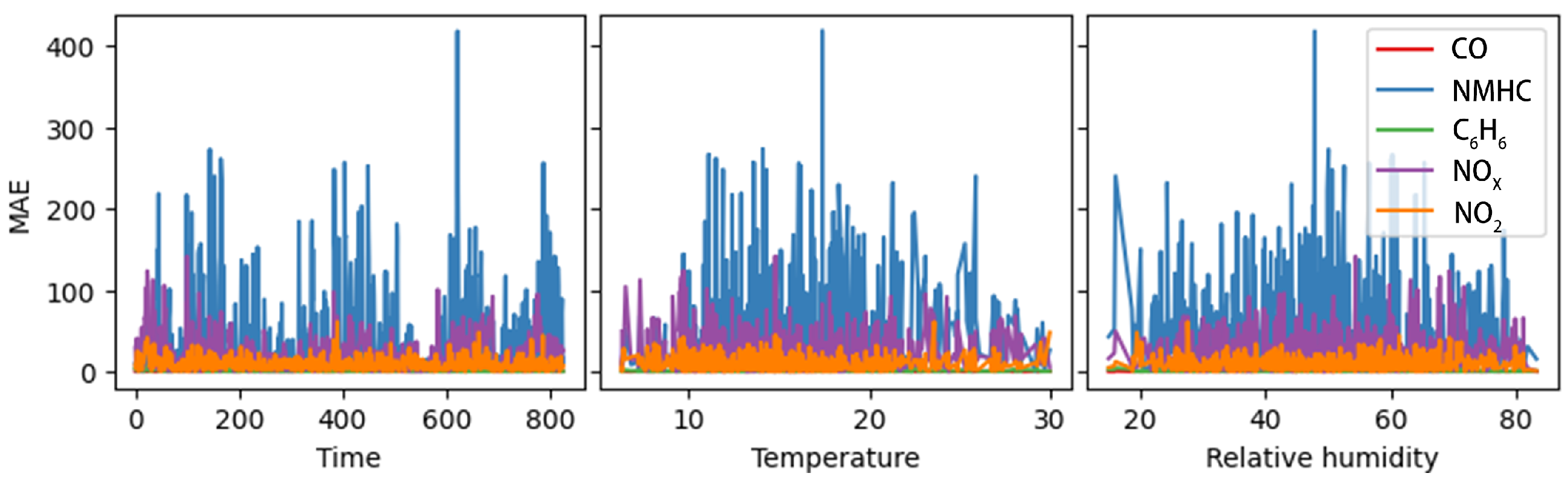
- Sensor drift: Sensors experience drift in sensitivity due to environmental factors such as time, temperature, and humidity, resulting in inconsistent sensor responses. This could contribute to degraded model performance. Figure 16 illustrates the relationship between gas identification accuracy and time, temperature, and humidity in the target model. We observe that model accuracy does not significantly change under varying sensor drifts caused by time, temperature, and humidity. Therefore, when sensor drift data are included in the training set, the target model shows a degree of localized robustness against these interferences. As a result, the error in gas concentration identification exhibits a low correlation with sensor drift;
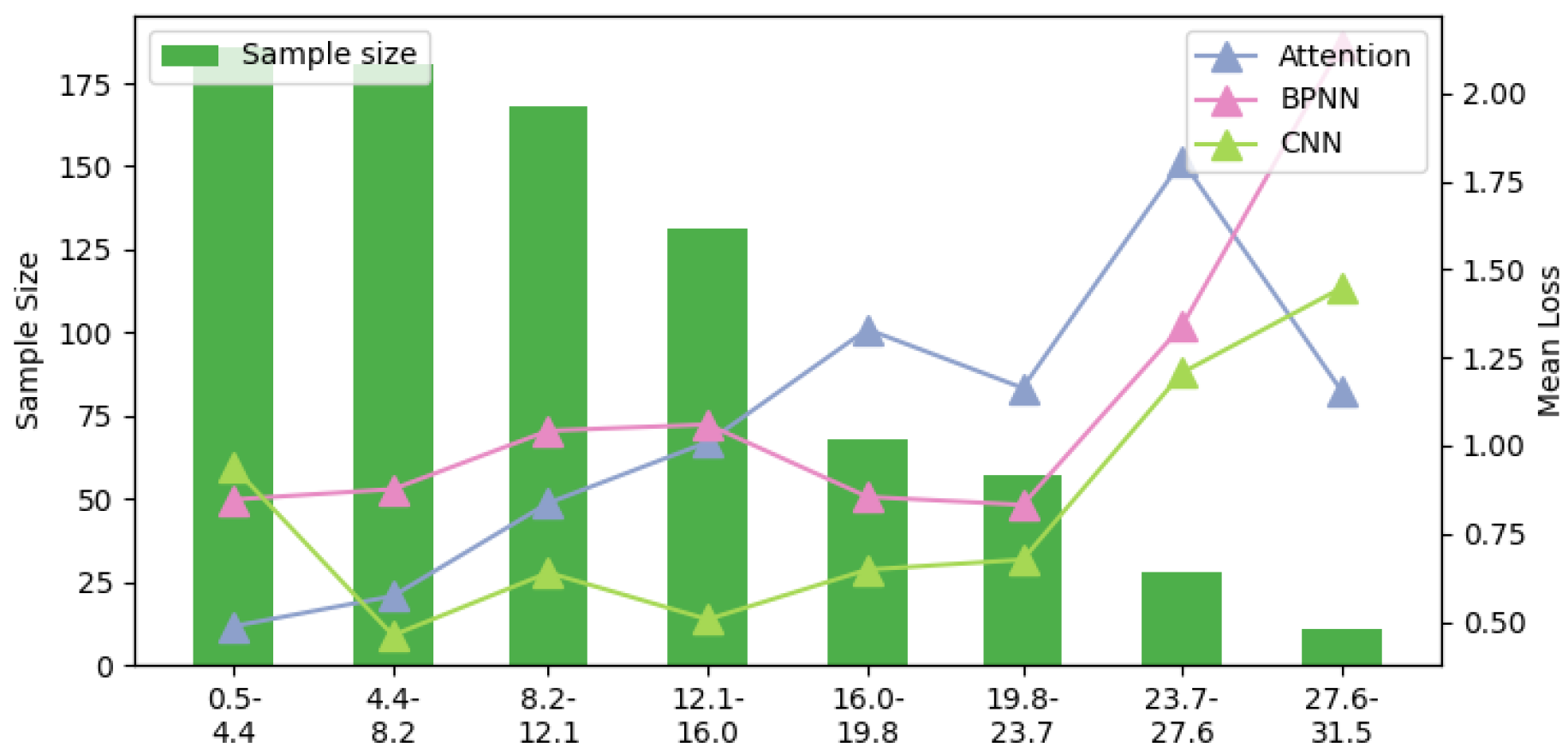
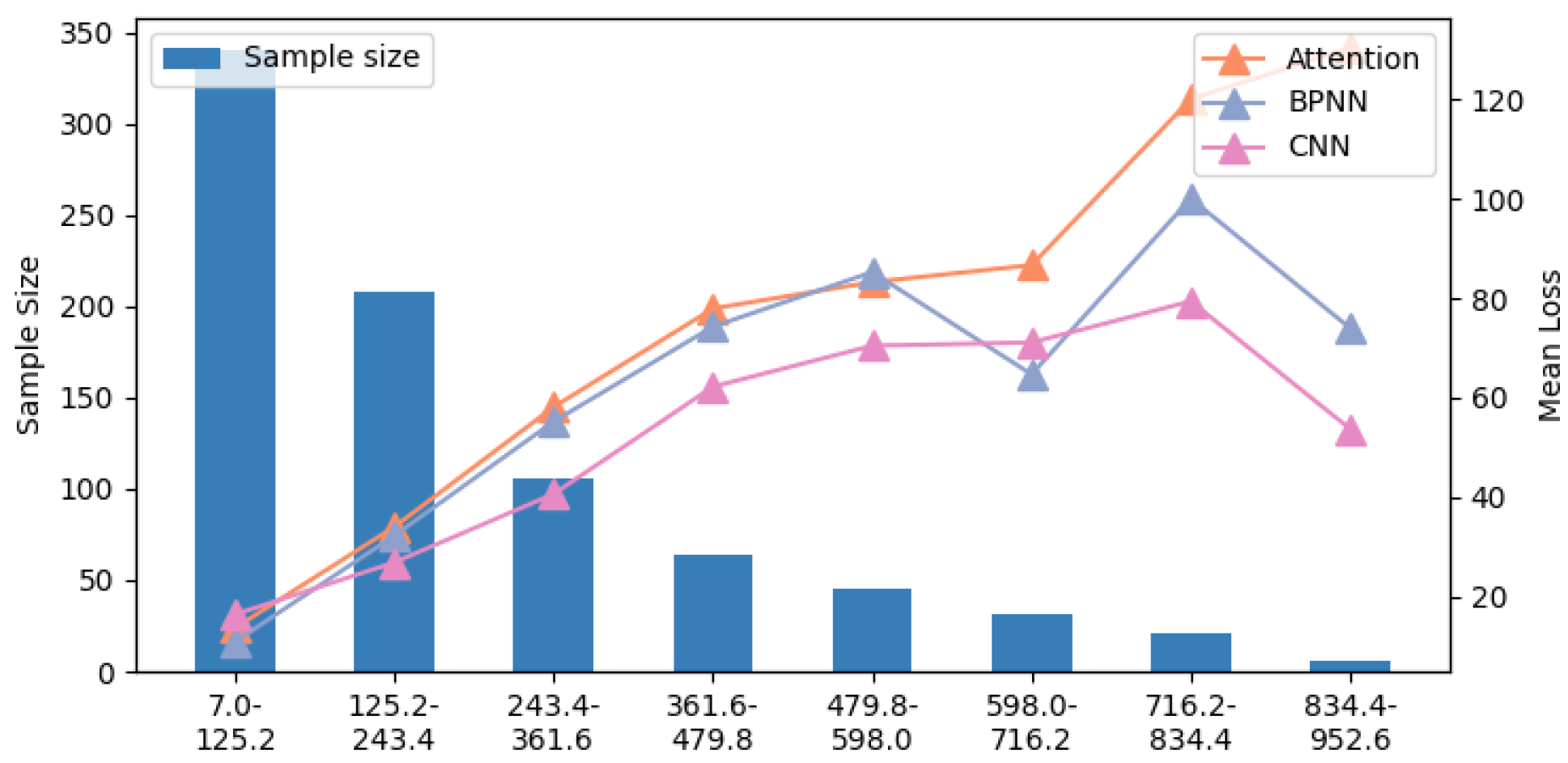
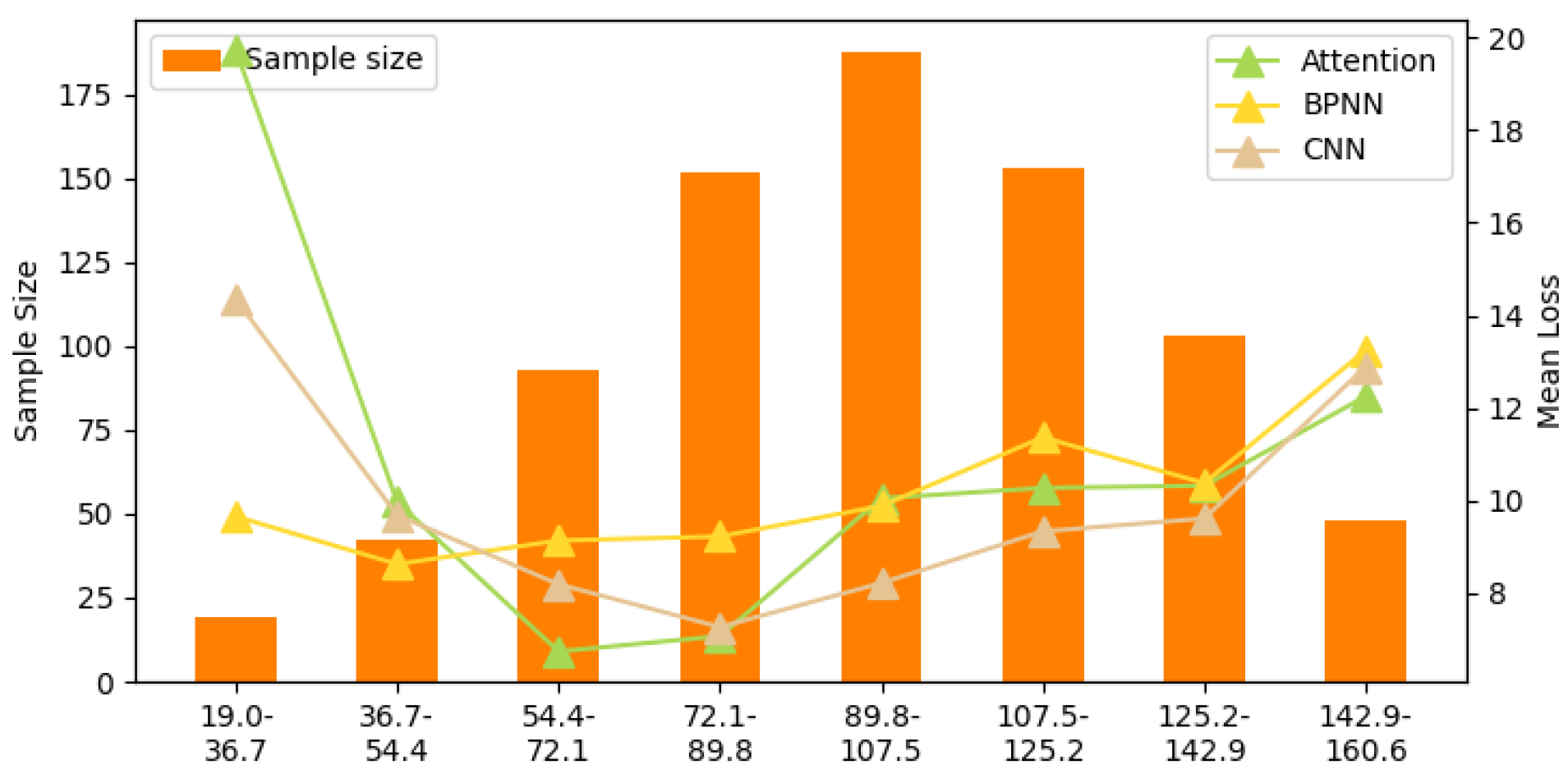
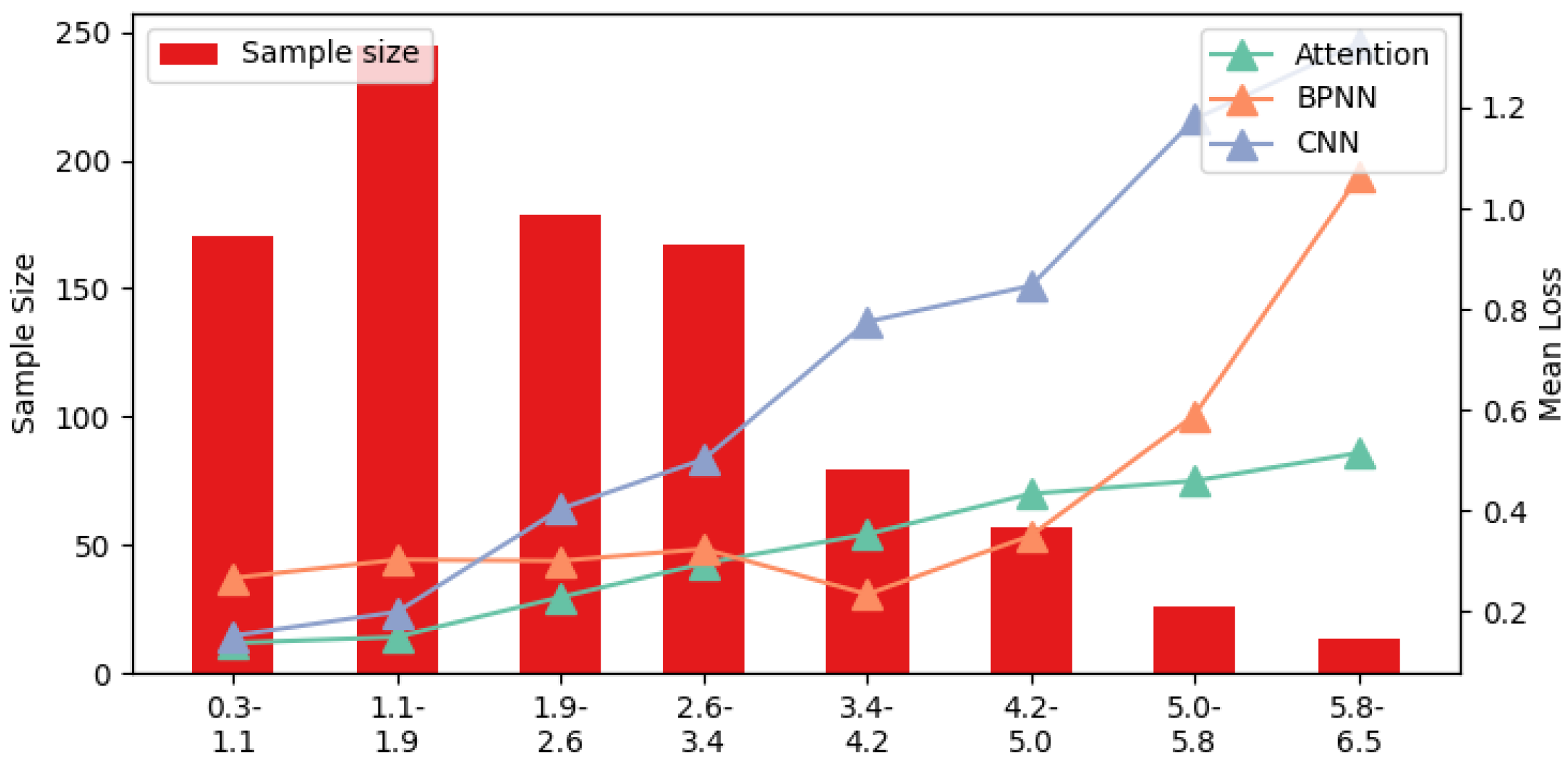
- Imbalanced samples: In long-term gas detection, the gas concentration tends to remain stable, with minimal fluctuations. This results in imbalanced gas concentration data, which can lead to bias in the gas concentration estimation model. Figure 17 shows the accuracy of the target model under different CO gas concentrations (relationships for other gases are provided in Appendix A, Figure A1, Figure A2, Figure A3 and Figure A4). In Figure 17, a significant negative correlation between gas concentration and accuracy is observed, confirming that sample imbalance negatively impacts the accuracy of the target model.
4.2. Study of Specific Generative Loss
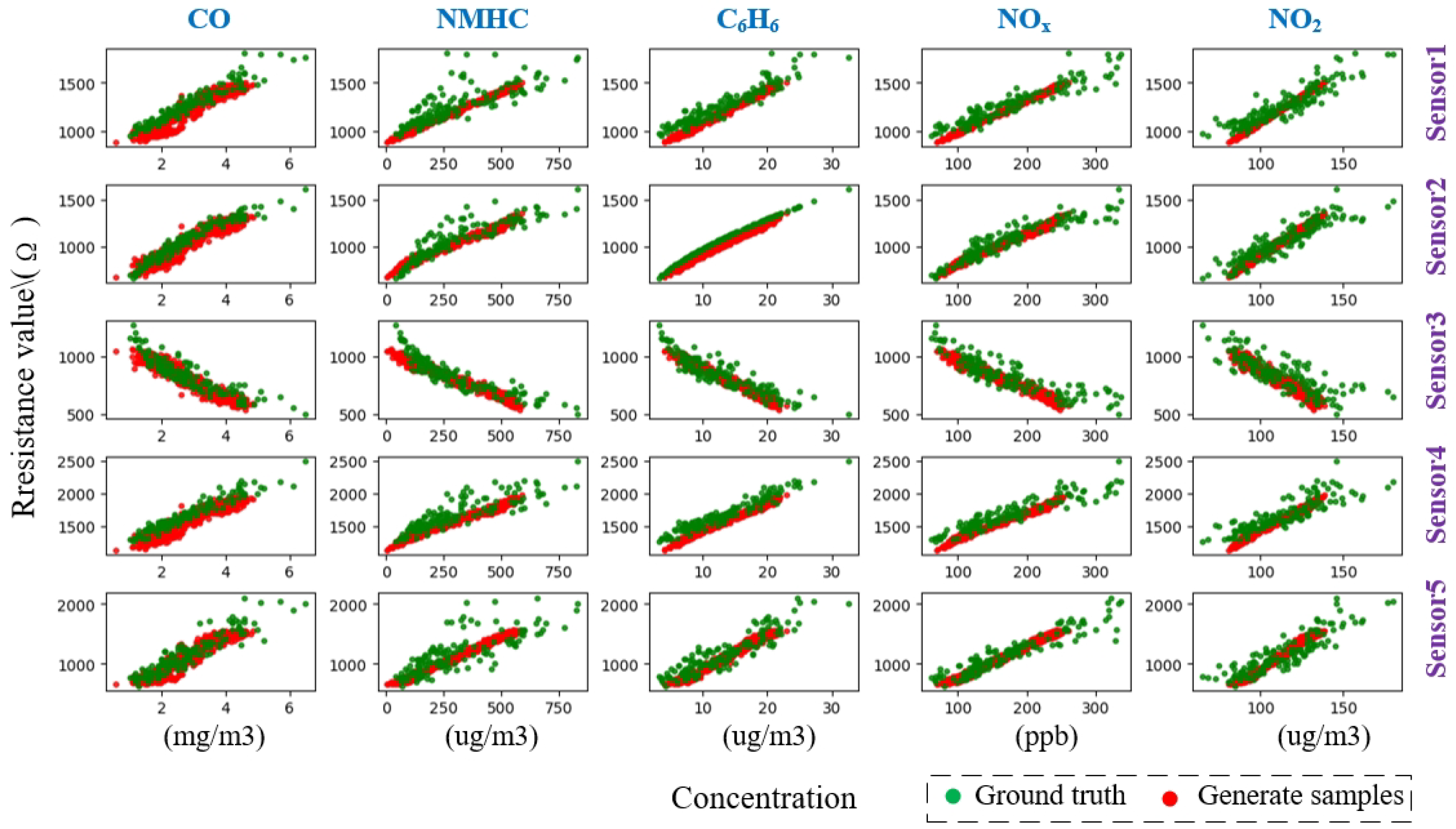
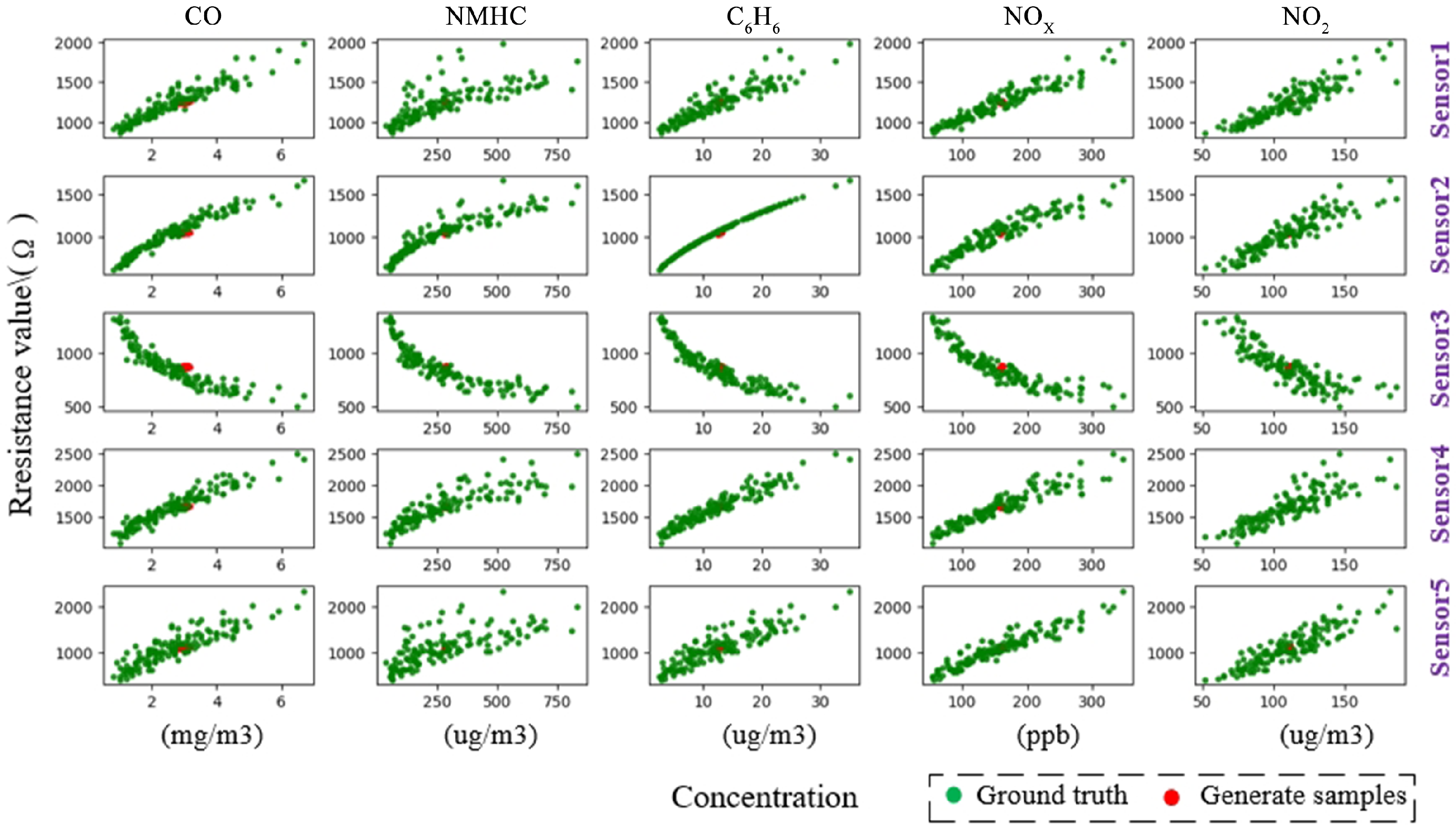
- Within-class scatter loss : Figure 18 shows the study of within-class scatter loss. The colors represent the samples generated by the SSGAN model. In Figure 18, the color on all subfigures has a similar trend. The generator without can only generate the central sample in the training set. Although the generated sample is similar to the instant, the variance in sensor response and gas concentration is different. This results in an absence of abnormally high-concentration gas samples, which was expected in this study. During the training of the target model, this could lead to overfitting and performance degradation. Therefore, the generative loss function requires an additional constraint on inter-class separability;
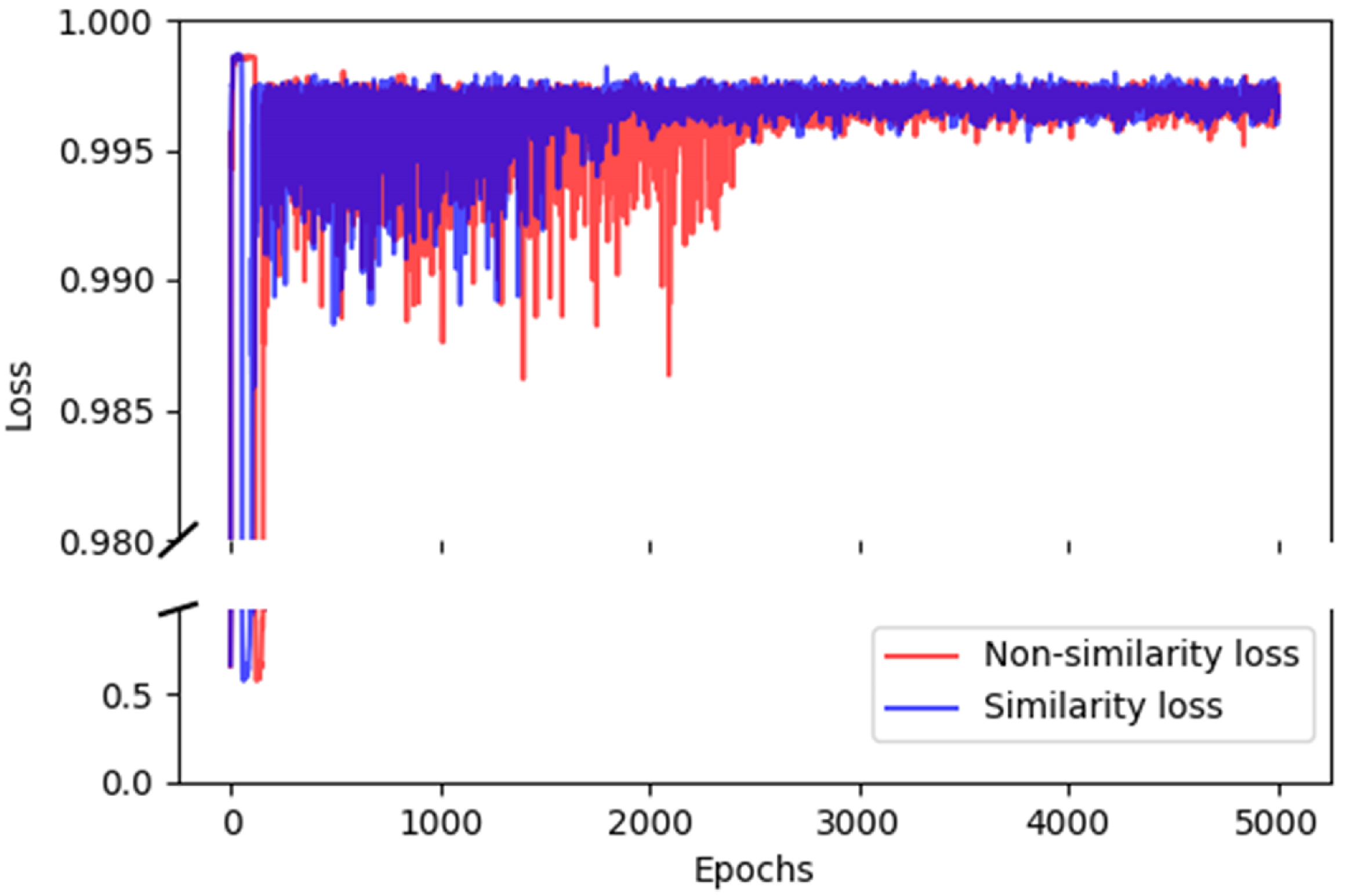
- Similarity loss : Figure 19 contrasts the effect of the similarity loss on the cosine similarity of the generated samples. We can see that the cosine similarity results of the specific generative loss and none are generally the same, but their decline rates are different. The specific generative loss achieved the lowest cosine similarity after 1700 epochs, which is reduced by 500 epochs compared to no . This observation illustrates the similarity loss function can better guide the model training. Additionally, we observe that the cosine similarity of is slightly higher than the loss function without , possibly because the makes the model focus more on the direction of vector similarity;
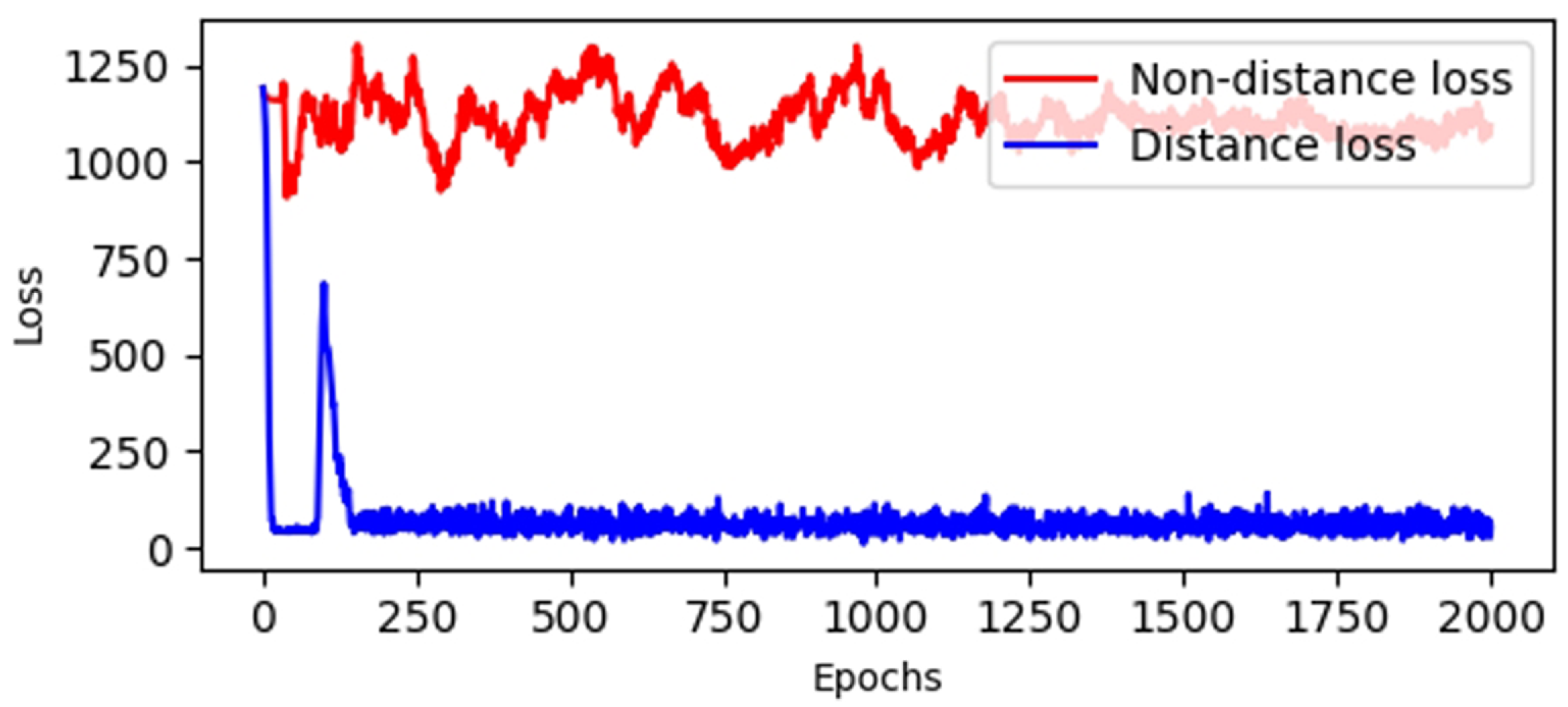
- Distance loss : Distance loss constrains the generated data to stay within the range of real sensor responses and gas concentrations. To illustrate the influence of the distance loss term on generated samples, we analyzed the distance between the generated samples and real instances, both with and without the distance loss term. Figure 20 shows the change curve of distance loss for each epoch. We observe that the generated samples without have an average Euclidean distance of 1200 from the real instances, placing the results outside the expected range of the sensor response. In contrast, when the specific generative loss includes , the distance is significantly reduced to 150, ensuring that the generated samples adhere more closely to the real data distribution. Therefore, the distance loss improves the generator’s ability to constrain the desired range of generated data;
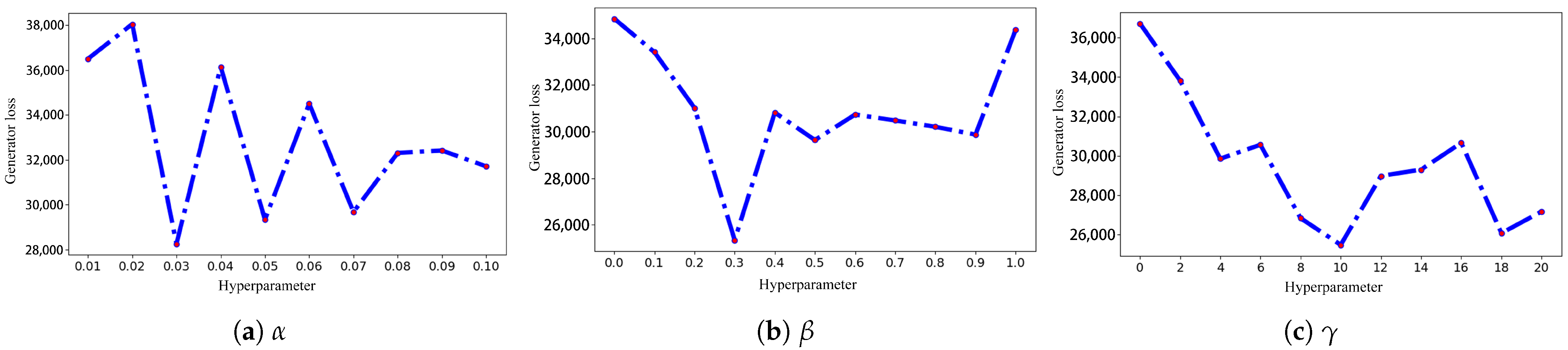
- Hyperparameter study: Figure 21 presents the study of the three hyperparameters in Equation (5): , , and . In Figure 21, , , and range from 0.01 to 0.1, 0 to 1, and 0 to 20, respectively. When the value of hyperparameters is 0, the specific generative loss is not utilized, as discussed in the previous section. We can clearly see that the curve between hyperparameters and generator loss on the three subfigures has a similar trend. The generator loss decreases gradually as the hyperparameter increases. Upon reaching an optimal value, the generator loss begins to increase and ultimately stabilizes. Therefore, values of 0.03, 0.3, and 10 for , , and yield better-generated samples.
4.3. Study of Existing Data Augmentation Methods
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three-letter acronym |
| LD | Linear dichroism |
| SSGAN | Simulated sensor generative adversarial network |
| CNN | Convolutional neural network |
| BPNN | Backpropagation neural network |
| GAN | Generative adversarial network |
| SVM | Support vector machine |
| PCA | Principal component analysis |
| ANN | Artificial neural networks |
| T | Target model |
| G | Generator |
| D | Discriminator |
| b | Batch size |
| d | Dimensions |
| x | Minority sample |
| l | Label |
| Generative loss | |
| Within-class scatter loss | |
| Similarity loss | |
| Distance loss | |
| Specific generative loss | |
| Discriminator loss | |
| MAPE | Mean absolute percentage error |
| Total nitrogen oxide | |
| Nitrogen dioxide | |
| CO | Carbon monoxide |
| MAE | Mean absolute error |
| MRE | Mean relative error |
Appendix A

Appendix B
| Model | Metrics | Formaldehyde | Ethanol | Mean |
|---|---|---|---|---|
| Attention model | MAE | 0.0048 | 0.0203 | 0.0126 |
| MRE | 0.7300 | 1.5978 | 1.1639 | |
| MSE | 0.00004 | 0.0006 | 0.0003 | |
| Attention model + SSGAN | MAE | 0.0046 | 0.0124 | 0.0085 |
| MRE | 0.7153 | 1.02952 | 0.8724 | |
| MSE | 0.00003 | 0.0002 | 0.0001 | |
| Enhancement (%) | MAE | 4.62 | 39.08 | 32.47 |
| MRE | 2.01 | 35.57 | 25.05 | |
| MSE | 31.92 | 64.65 | 62.50 |

References
- Tan, J.; Xu, J. Applications of electronic nose (e-nose) and electronic tongue (e-tongue) in food quality-related properties determination: A review. Artif. Intell. Agric. 2020, 4, 104–115. [Google Scholar]
- Di Natale, C.; Macagnano, A.; Davide, F.; D’amico, A.; Paolesse, R.; Boschi, T.; Faccio, M.; Ferri, G. An electronic nose for food analysis. Sens. Actuators B Chem. 1997, 44, 521–526. [Google Scholar]
- Dragonieri, S.; Annema, J.T.; Schot, R.; van der Schee, M.P.; Spanevello, A.; Carratú, P.; Resta, O.; Rabe, K.F.; Sterk, P.J. An electronic nose in the discrimination of patients with non-small cell lung cancer and COPD. Lung Cancer 2009, 64, 166–170. [Google Scholar]
- Montuschi, P.; Mores, N.; Trové, A.; Mondino, C.; Barnes, P.J. The electronic nose in respiratory medicine. Respiration 2012, 85, 72–84. [Google Scholar] [PubMed]
- Baldwin, E.A.; Bai, J.; Plotto, A.; Dea, S. Electronic noses and tongues: Applications for the food and pharmaceutical industries. Sensors 2011, 11, 4744–4766. [Google Scholar] [CrossRef]
- Robin, Y.; Amann, J.; Baur, T.; Goodarzi, P.; Schultealbert, C.; Schneider, T.; Schütze, A. High-performance VOC quantification for IAQ monitoring using advanced sensor systems and deep learning. Atmosphere 2021, 12, 1487. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Yu, D.; Gu, Y. Air quality index and air pollutant concentration prediction based on machine learning algorithms. Appl. Sci. 2019, 9, 4069. [Google Scholar] [CrossRef]
- Furizal, F.; Ma’arif, A.; Firdaus, A.A.; Rahmaniar, W. Future Potential of E-Nose Technology: A Review. Int. J. Robot. Control. Syst. 2023, 3, 449–469. [Google Scholar]
- Chen, Z.; Zheng, Y.; Chen, K.; Li, H.; Jian, J. Concentration estimator of mixed VOC gases using sensor array with neural networks and decision tree learning. IEEE Sens. J. 2017, 17, 1884–1892. [Google Scholar]
- Fan, S.; Li, Z.; Xia, K.; Hao, D. Quantitative and qualitative analysis of multicomponent gas using sensor array. Sensors 2019, 19, 3917. [Google Scholar] [CrossRef]
- Zimmerman, N.; Presto, A.A.; Kumar, S.P.; Gu, J.; Hauryliuk, A.; Robinson, E.S.; Robinson, A.L.; Subramanian, R. A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring. Atmos. Meas. Tech. 2018, 11, 291–313. [Google Scholar] [CrossRef]
- Liu, M.; Wang, M.; Wang, J.; Li, D. Comparison of random forest, support vector machine and back propagation neural network for electronic tongue data classification: Application to the recognition of orange beverage and Chinese vinegar. Sens. Actuators B Chem. 2013, 177, 970–980. [Google Scholar] [CrossRef]
- Li, Q.; Gu, Y.; Jia, J. Classification of multiple Chinese liquors by means of a QCM-based e-nose and MDS-SVM classifier. Sensors 2017, 17, 272. [Google Scholar] [CrossRef]
- Shi, Y.; Yuan, H.; Zhang, Q.; Sun, A.; Liu, J.; Men, H. Lightweight interleaved residual dense network for gas identification of industrial polypropylene coupled with an electronic nose. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
- Bauder, R.A.; Khoshgoftaar, T.M.; Hasanin, T. An empirical study on class rarity in big data. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 785–790. [Google Scholar]
- Bauder, R.A.; Khoshgoftaar, T.M. The effects of varying class distribution on learner behavior for medicare fraud detection with imbalanced big data. Health Inf. Sci. Syst. 2018, 6, 1–14. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, Y. Early-stage gas identification using convolutional long short-term neural network with sensor array time series data. Sensors 2021, 21, 4826. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Gao, J.; Zhang, Z.; Zhao, H. Gas recognition method based on the deep learning model of sensor array response map. Sens. Actuators B Chem. 2021, 330, 129349. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, T.; Zou, Z.; Chen, Y.; Zhang, H. Imbalanced data fault diagnosis of hydrogen sensors using deep convolutional generative adversarial network with convolutional neural network. Rev. Sci. Instruments 2021, 92, 095007. [Google Scholar] [CrossRef]
- Jana, D.; Patil, J.; Herkal, S.; Nagarajaiah, S.; Duenas-Osorio, L. CNN and Convolutional Autoencoder (CAE) based real-time sensor fault detection, localization, and correction. Mech. Syst. Signal Process. 2022, 169, 108723. [Google Scholar] [CrossRef]
- Van Hulse, J.; Khoshgoftaar, T.M.; Napolitano, A. Experimental perspectives on learning from imbalanced data. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 935–942. [Google Scholar]
- Mani, I.; Zhang, I. kNN approach to unbalanced data distributions: A case study involving information extraction. In Proceedings of the ICML Workshop on Learning from Imbalanced Datasets, Washington, DC, USA, 21 August 2003; Volume 126, pp. 1–7. [Google Scholar]
- Nitesh, V.C. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321. [Google Scholar]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. Safe-level-smote: Safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. In Proceedings of the Advances in Knowledge Discovery and Data Mining: 13th Pacific-Asia Conference, PAKDD 2009, Bangkok, Thailand, 27–30 April 2009; proceedings 13. pp. 475–482. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Li, X.; Luo, J.; Younes, R. ActivityGAN: Generative adversarial networks for data augmentation in sensor-based human activity recognition. In Proceedings of the Adjunct Proceedings of the 2020 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2020 ACM International Symposium on Wearable Computers, Virtual, 12–17 September 2020; pp. 249–254. [Google Scholar]
- Zhao, P.; Ding, Z.; Li, Y.; Zhang, X.; Zhao, Y.; Wang, H.; Yang, Y. SGAD-GAN: Simultaneous generation and anomaly detection for time-series sensor data with generative adversarial networks. Mech. Syst. Signal Process. 2024, 210, 111141. [Google Scholar] [CrossRef]
- Mahinnezhad, S.; Mahinnezhad, S.; Kaur, K.; Shih, A. Data augmentation and class imbalance compensation using CTGAN to improve gas detection systems. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 20–23 May 2024; pp. 1–6. [Google Scholar]
- Son, J.; Byun, H.J.; Park, M.; Ha, J.; Nam, H. Spectral Data Augmentation Using Deep Generative Model for Remote Chemical Sensing. IEEE Access 2024, 12, 98326–98337. [Google Scholar] [CrossRef]
- Qi, P.F.; Meng, Q.H.; Zeng, M. A CNN-based simplified data processing method for electronic noses. In Proceedings of the 2017 ISOCS/IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Montreal, QC, Canada, 28–31 May 2017; pp. 1–3. [Google Scholar]
- Xiong, L.; He, M.; Hu, C.; Hou, Y.; Han, S.; Tang, X. Image presentation and effective classification of odor intensity levels using multi-channel electronic nose technology combined with GASF and CNN. Sens. Actuators B Chem. 2023, 395, 134492. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Gu, Y. A model transfer learning framework with back-propagation neural network for wine and Chinese liquor detection by electronic nose. IEEE Access 2020, 8, 105278–105285. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Dong, D.; Yao, G.; Wei, G.; He, A.; Wu, H.; Zhu, H.; Huang, Z.; Tang, Z. E-nose based on a high-integrated and low-power metal oxide gas sensor array. Sens. Actuators B Chem. 2023, 380, 133289. [Google Scholar]
- De Vito, S.; Massera, E.; Piga, M.; Martinotto, L.; Di Francia, G. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008, 129, 750–757. [Google Scholar]
- Zhang, W.; Zheng, Y.; Lin, Z. Real-time gas composition identification and concentration estimation model for artificial olfaction. IEEE Trans. Ind. Electron. 2023, 71, 8055–8065. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Frank, A. UCI Machine Learning Repository. 2010. Available online: http://archive.ics.uci.edu/ml (accessed on 20 February 2025).
- Mead, M.; Popoola, O.; Stewart, G.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.; McLeod, M.; Hodgson, T.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atmos. Environ. 2013, 70, 186–203. [Google Scholar] [CrossRef]
- Bond-Taylor, S.; Leach, A.; Long, Y.; Willcocks, C.G. Deep generative modelling: A comparative review of vaes, gans, normalizing flows, energy-based and autoregressive models. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7327–7347. [Google Scholar]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 IEEE 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; pp. 243–248. [Google Scholar]





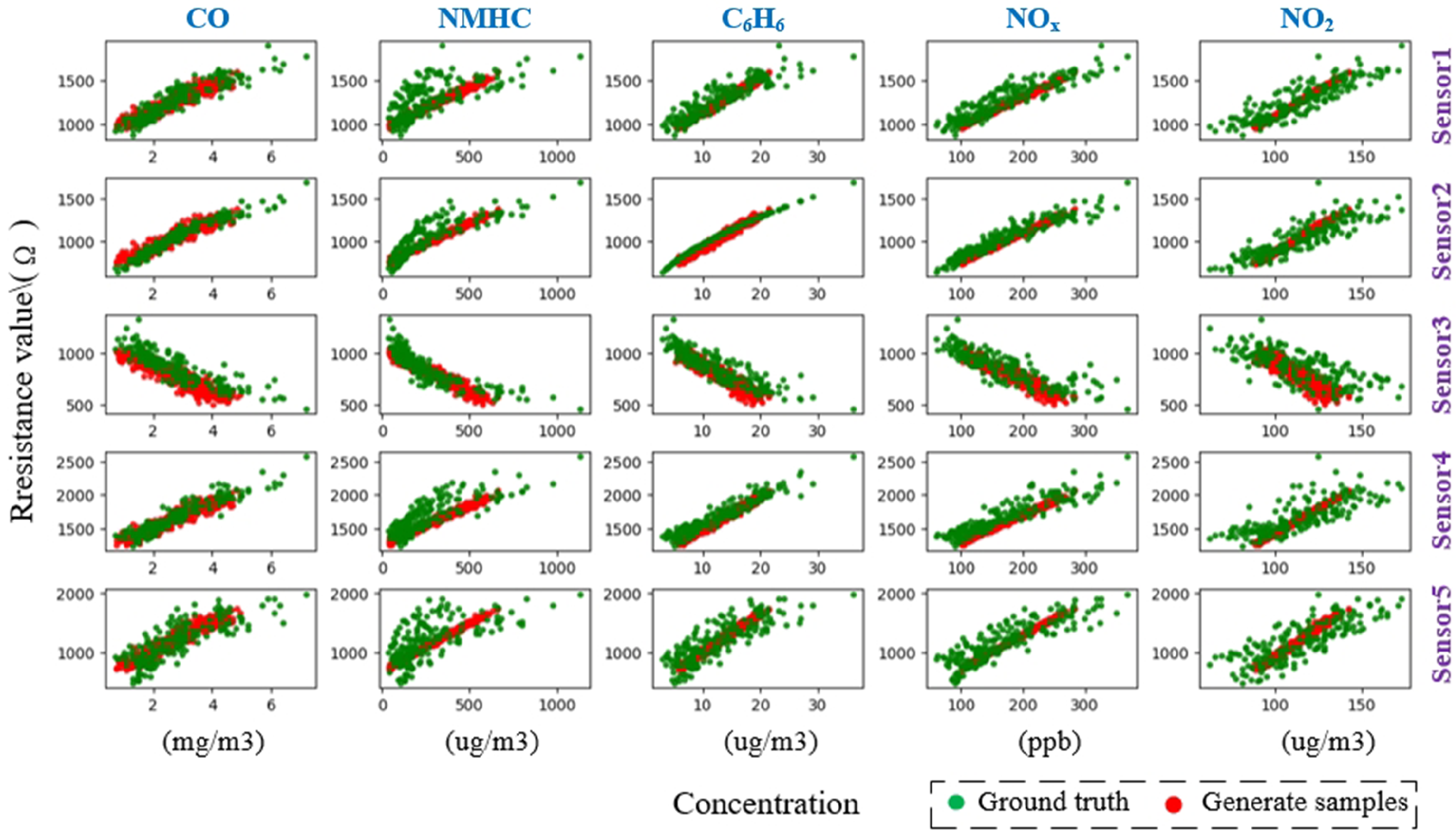
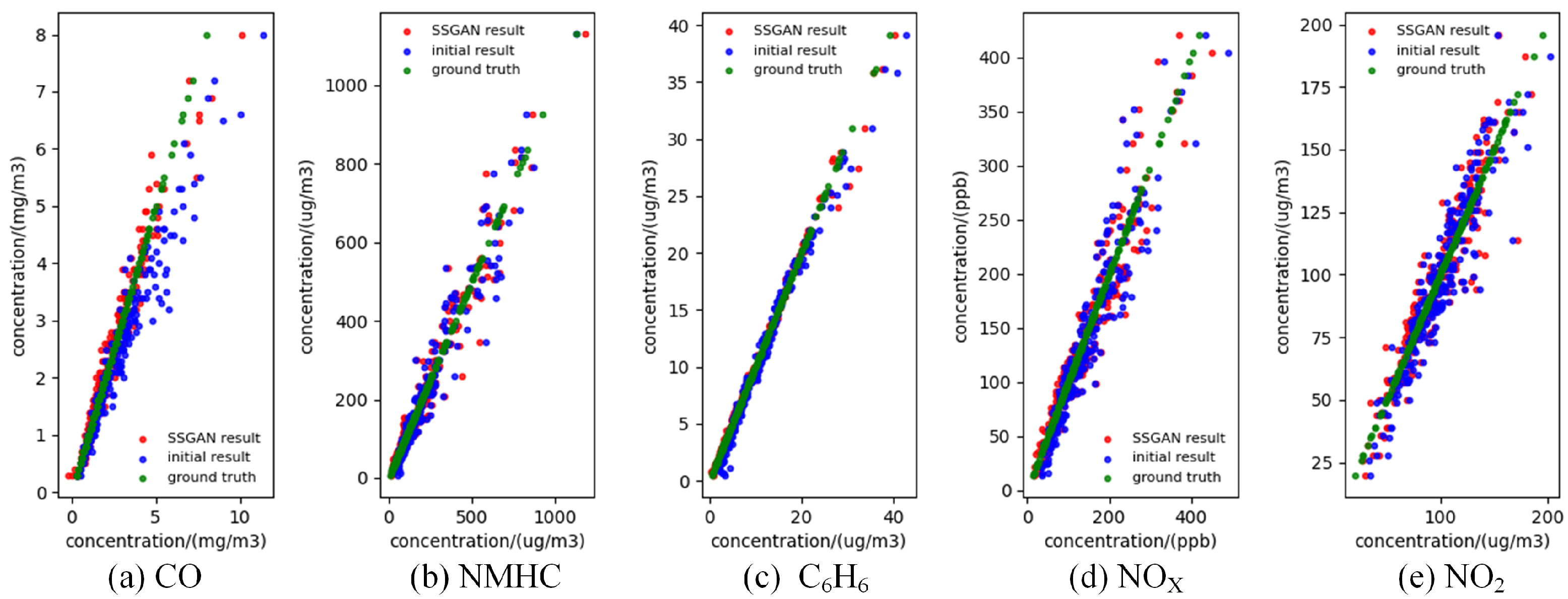
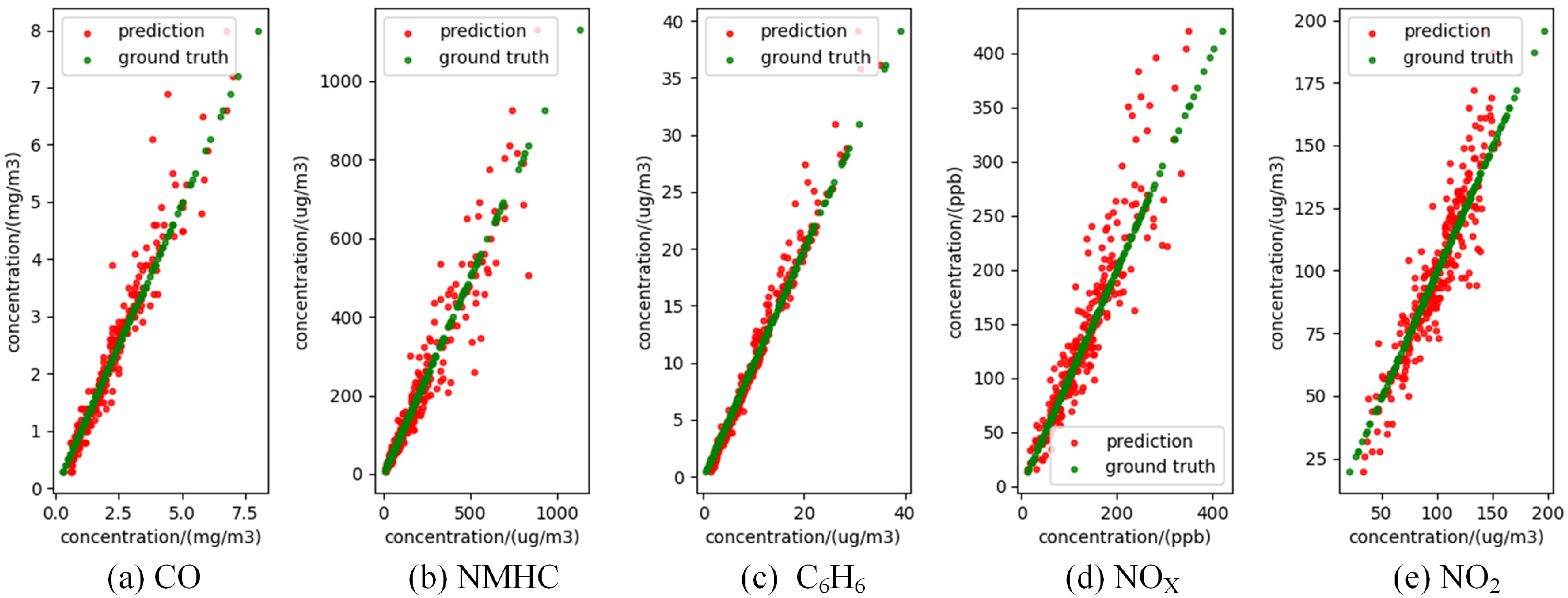
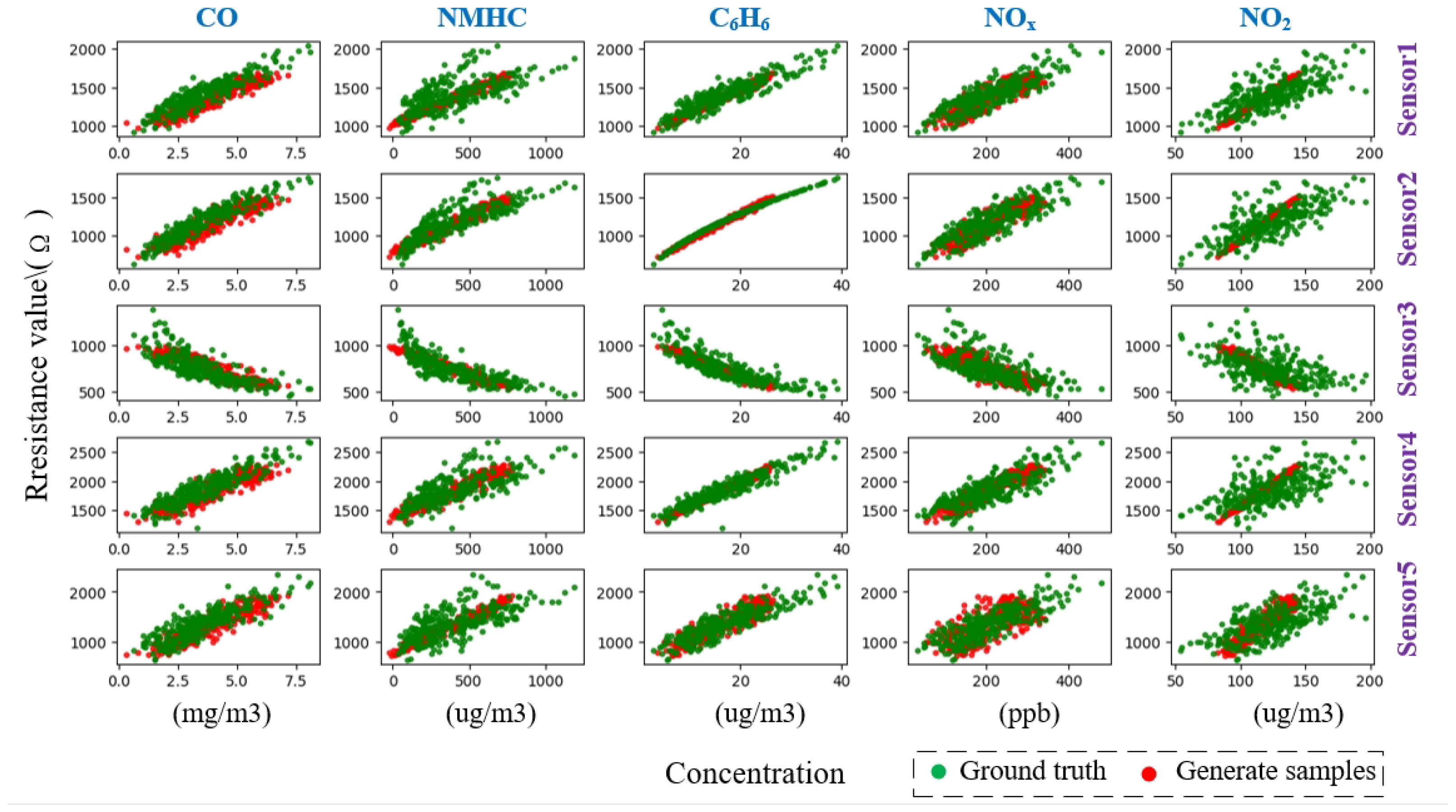

| Model | Metrics | CO | NMHC | C6H6 | Mean | ||
|---|---|---|---|---|---|---|---|
| BPNN | MAE | 1.5081 | 203.1564 | 8.1824 | 88.3552 | 34.8352 | 67.2075 |
| MRE | 99.2208 | 192.5111 | 157.1520 | 97.8494 | 42.9541 | 117.9375 | |
| MSE | 3.7009 | 78,250.9600 | 109.6785 | 12,875.4700 | 1880.6373 | 18,624.09 | |
| BPNN + SSGAN | MAE | 1.4495 | 203.6666 | 7.6831 | 81.7475 | 32.9960 | 65.5085 |
| MRE | 96.5658 | 196.6645 | 148.7511 | 89.4066 | 41.1859 | 114.5148 | |
| MSE | 3.4834 | 77,245.9300 | 96.0657 | 10,965.9370 | 1701.6248 | 18,002.6074 | |
| Enhancement (%) | MAE | 3.89 | −0.25 | 6.10 | 7.48 | 5.28 | 4.45 |
| MRE | 2.68 | −2.15 | 5.34 | 8.63 | 4.12 | 3.72 | |
| MSE | 5.88 | 1.28 | 12.41 | 14.83 | 9.2 | 8.76 |
| Model | Metrics | CO | NMHC | C6H6 | Mean | ||
|---|---|---|---|---|---|---|---|
| CNN | MAE | 0.4417 | 32.0820 | 0.7760 | 20.0776 | 9.0806 | 12.4896 |
| MRE | 17.2745 | 24.9271 | 19.0617 | 18.3452 | 10.4591 | 18.0207 | |
| MSE | 0.5121 | 2384.297 | 1.0802 | 772.6922 | 138.3014 | 659.3767 | |
| CNN + SSGAN | MAE | 0.2526 | 27.9720 | 0.4084 | 17.7480 | 8.5353 | 10.9832 |
| MRE | 12.7600 | 15.5680 | 5.7231 | 14.3212 | 9.3658 | 11.5476 | |
| MSE | 0.1337 | 1933.2006 | 0.4955 | 588.1096 | 131.8301 | 530.754 | |
| Enhancement (%) | MAE | 42.82 | 12.81 | 69.98 | 11.60 | 6.00 | 12.06 |
| MRE | 26.14 | 37.55 | 46.68 | 21.93 | 10.76 | 35.92 | |
| MSE | 73.86 | 18.92 | 54.13 | 23.89 | 4.68 | 19.51 |
| Model | Metrics | CO | NMHC | C6H6 | Mean | ||
|---|---|---|---|---|---|---|---|
| Attention model | MAE | 0.2234 | 37.0816 | 0.8511 | 22.3352 | 9.9708 | 14.0924 |
| MRE | 11.3531 | 19.0948 | 12.2931 | 19.3524 | 11.5774 | 14.7342 | |
| MSE | 0.1298 | 3695.0596 | 1.4793 | 994.2543 | 171.1836 | 972.4214 | |
| Attention model + SSGAN | MAE | 0.2307 | 36.2352 | 0.8492 | 20.9190 | 9.8505 | 13.6169 |
| MRE | 11.6757 | 18.6365 | 15.1697 | 16.2638 | 11.1091 | 14.5708 | |
| MSE | 0.1279 | 3529.2622 | 1.3503 | 922.4245 | 174.0809 | 925.4491 | |
| Enhancement (%) | MAE | −3.35 | 2.28 | 0.22 | 6.34 | 1.21 | 3.38 |
| MRE | −2.84 | 2.40 | −23.4 | 15.96 | 4.04 | 1.11 | |
| MSE | 1.47 | 4.49 | 8.71 | 7.22 | −1.69 | 1.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shi, Y.; Niu, H.; Zhao, K. Generative Adversarial Networks in Imbalanced Gas Samples. Electronics 2025, 14, 1346. https://doi.org/10.3390/electronics14071346
Liu J, Shi Y, Niu H, Zhao K. Generative Adversarial Networks in Imbalanced Gas Samples. Electronics. 2025; 14(7):1346. https://doi.org/10.3390/electronics14071346
Chicago/Turabian StyleLiu, Jinzhou, Yunbo Shi, Haodong Niu, and Kuo Zhao. 2025. "Generative Adversarial Networks in Imbalanced Gas Samples" Electronics 14, no. 7: 1346. https://doi.org/10.3390/electronics14071346
APA StyleLiu, J., Shi, Y., Niu, H., & Zhao, K. (2025). Generative Adversarial Networks in Imbalanced Gas Samples. Electronics, 14(7), 1346. https://doi.org/10.3390/electronics14071346






