1. Introduction
As industrial systems advance toward higher levels of automation, complexity, and interconnectivity, ensuring system reliability has become paramount [
1]. Fault Detection and Diagnosis (FDD) technologies play a crucial role in maintaining continuous system operation by identifying and localizing faults, thereby supporting maintenance decisions [
2]. Over the past decade, FDD technologies have made significant strides across various sectors, including manufacturing [
3], energy systems [
4], and transportation [
5].
Maritime transport, as a cost-effective mode of global trade, has become increasingly vital and demonstrates promising growth potential [
6]. Ships powered by marine diesel engines form the backbone of this industry. Failure to detect engine faults promptly can result in substantial economic losses and severe safety risks [
7]. Diesel engine faults account for the majority of marine power system failures. Recently, with advancements in artificial intelligence and industrial big data, data-driven FDD methods have been widely adopted for marine diesel engine maintenance, becoming crucial tools for ensuring safe navigation [
8]. While this study validates our unsupervised fault detection approach using marine diesel engine data, its reliance on general principles of anomaly detection and time series analysis—independent of domain-specific features—suggests potential applicability to other engineering fields, such as aerospace or manufacturing, pending validation with diverse datasets. This study implements an unsupervised FDD approach for marine diesel engines using tanker data; however, it does not involve dataset-specific feature optimization or tailored preprocessing efforts. While rooted in general anomaly detection and time series analysis principles, its applicability to other domains—such as aerospace or manufacturing—remains to be validated with diverse datasets.
In the domains of ship fault detection, traditional approaches have primarily relied on models and expert knowledge. However, as ship systems grow increasingly complex and certain vessels require unique and confidential handling, model-based methods have become progressively infeasible. The complexity and uncertainty of marine engine systems make constructing precise models nearly impossible, significantly undermining the reliability of traditional fault detection methods. Moreover, relying solely on expert knowledge poses challenges, particularly in addressing the diverse and complex nature of ship operations [
9].
With the rapid advancement of artificial intelligence, these methods have shifted away from reliance on prior knowledge, instead leveraging large-scale real-world data and experience to achieve higher accuracy in fault diagnosis and detection [
10]. Data-driven techniques can integrate multi-source data, overcoming traditional methods’ limitations, and have increasingly become the dominant approach in this field [
11]. However, in practical applications, the high cost of acquiring and labeling fault data, coupled with the complexity and variability of fault patterns, makes supervised learning methods difficult to implement widely [
12]. Unsupervised learning, which identifies anomalous states by learning system behavior patterns during normal operation, offers a new approach to addressing data scarcity [
13].
Unsupervised anomaly detection approaches that establish predictive patterns from normal operation data provide an effective mechanism for identifying potential anomalies without invasive interventions. Unlike many supervised frameworks that employ physics-informed models or depend on labeled fault data, our method integrates UMAP for nonlinear dimensionality reduction and transition state extraction with TimeMixer-FI for unsupervised time series prediction. By comparing UMAP-reduced features from six correlated metrics against a seventh un-reduced metric, anomalies are detected via mode transitions without requiring fault labels. By defining a baseline of typical behavior using sensor data, deviations from this norm can be flagged as early indicators of faults, eliminating the need for labeled fault data or destructive testing. However, in high-dimensional time series data, the complexity of analysis escalates, making dimensionality reduction techniques indispensable. These methods extract critical features while reducing computational overhead, enabling proactive maintenance without compromising system integrity. Traditional approaches like Principal Component Analysis (PCA) generate orthogonal components but struggle to preserve the intrinsic structure of nonlinear data. In contrast, Uniform Manifold Approximation and Projection (UMAP) has emerged as a powerful alternative, excelling in maintaining both local and global data structures, as highlighted in [
14]. This topology-preserving characteristic makes UMAP particularly suitable for fault detection in a nondestructive maintenance context, as it effectively captures system state transitions in a reduced dimensional space using only noninvasive sensor readings, a strength further emphasized in [
15]. By enabling early anomaly detection without physical disruption, UMAP supports the goals of nondestructive maintenance, such as preserving equipment functionality and minimizing operational risks.
The selection of UMAP for dimensionality reduction in high-dimensional marine engine data is driven by its demonstrated superiority in handling nonlinear data structures, making it an optimal choice for fault detection in complex systems. Studies such as Altin and Cakir (2024) [
16] have shown that UMAP enhances anomaly detection accuracy in multivariate time series datasets like MSL, SMAP, and SWaT, while significantly reducing training times by approximately 300–650%, owing to its ability to preserve both local and global structures. Similarly, research on structural health monitoring of damaged wind turbine blades underscores UMAP’s superior performance over PCA and t-SNE in feature extraction and classification of vibration signals, adeptly managing high-dimensional nonlinear data despite a modest increase in computational demand [
17]. Furthermore, a recent study on dimensionality reduction in structural health monitoring reinforces these findings, demonstrating UMAP’s effectiveness in processing complex datasets under varied conditions, thus supporting its application in marine diesel engine fault detection, where nonlinear relationships and high dimensionality are prevalent [
18].
With UMAP’s topology-preserving properties simplifying high-dimensional data, effective time series analysis becomes essential for processing the resulting reduced-dimensional features. In time series prediction, Transformer models excel at capturing long-term dependencies through self-attention mechanisms, as introduced in [
19]. Notable variants enhance this capability further: Informer [
20] incorporates sparse attention mechanisms and multi-scale modeling for greater efficiency; Autoformer [
21] integrates adaptive seasonal-trend decomposition to better handle periodic patterns; and Iformer [
22] combines the multi-scale feature extraction of Inception modules with Transformer’s global context modeling. Together, these advancements enable precise anomaly detection in reduced-dimensional time series, seamlessly leveraging UMAP’s structural insights to facilitate robust fault identification in intricate systems like marine engines.
However, these attention-based methods have inherent limitations: attention mechanisms’ permutation invariance leads to temporal information loss, preservable only through positional encoding, while quadratic computational complexity with sequence length severely restricts large-scale data processing efficiency [
23].
Recently, MLP-based methods have gained attention for their structural simplicity and computational efficiency. Wu et al.’s TimeMixer [
24] achieved significant progress in this direction, but limitations remain in handling complex feature interactions. Addressing this, we enhance feature interaction modeling by introducing MLP-Mixer layers, providing more effective solutions for UMAP-reduced feature processing.
Based on this analysis, the main innovations include:
(1) UMAP was employed for dimensionality reduction of high-dimensional marine engine data, facilitating early fault warning by establishing a reference baseline from UMAP-reduced features under normal conditions to detect anomalies through significant deviations in real-time data.
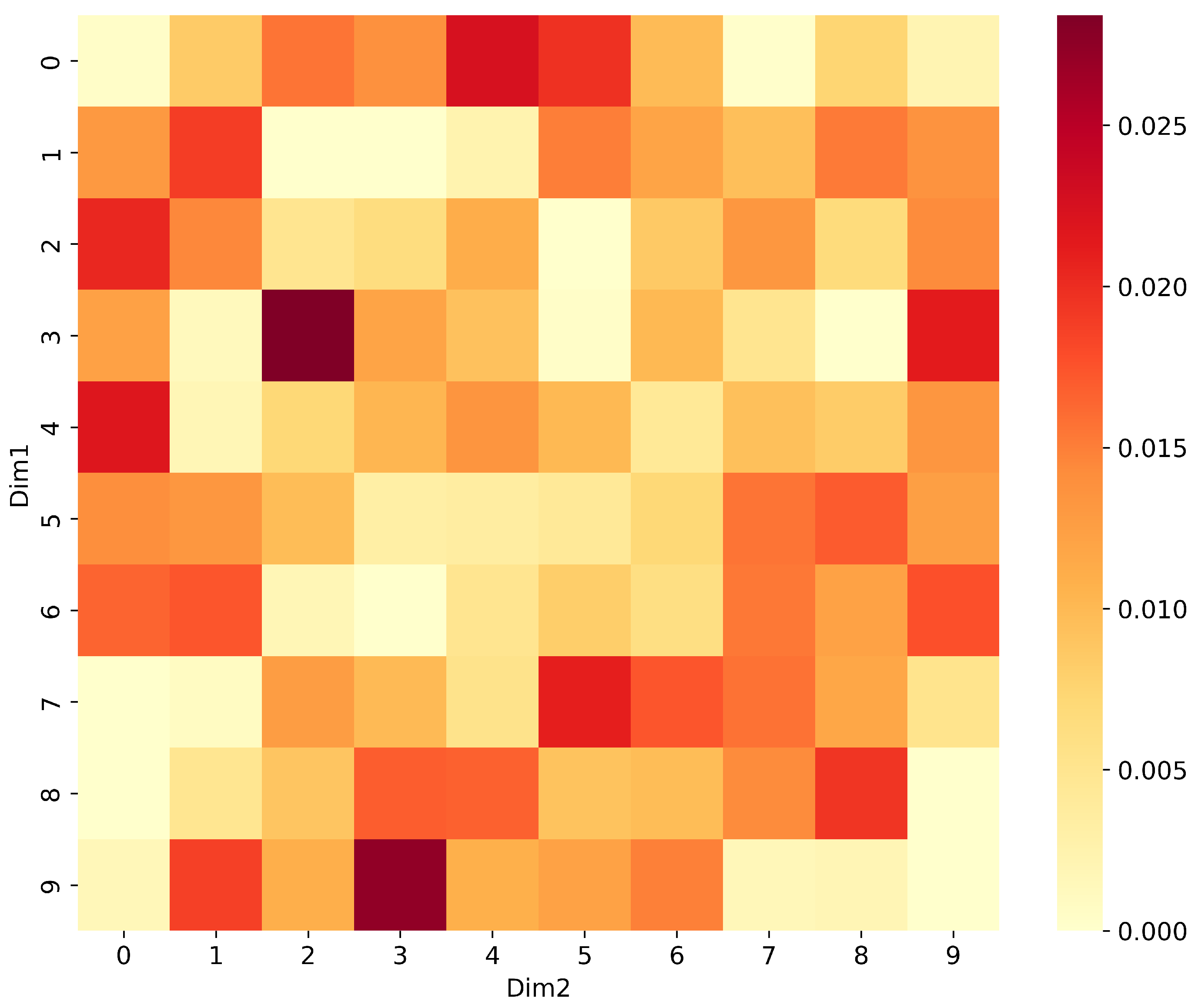
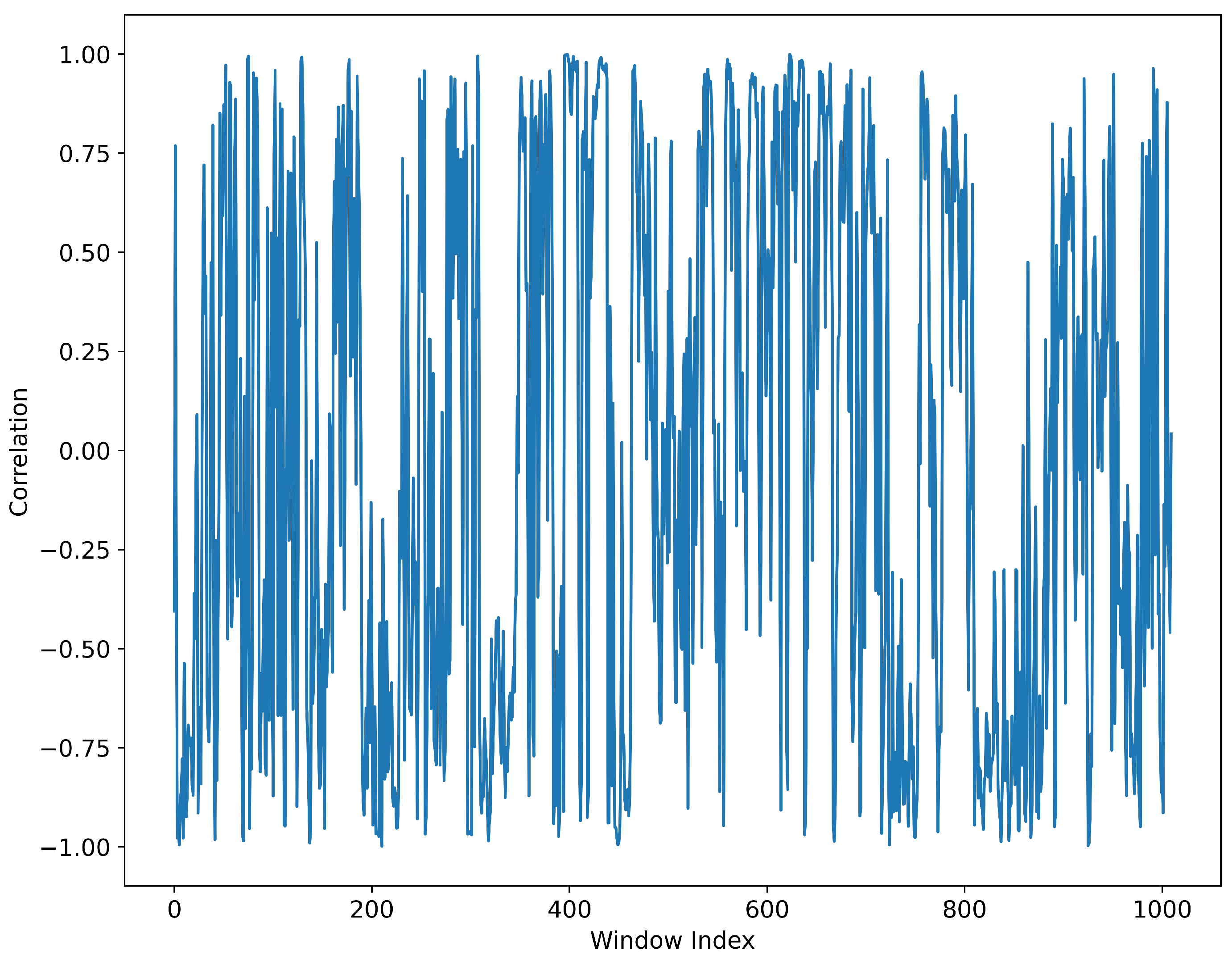
(2) Analysis of feature distributions revealed nonlinear relationships among UMAP-reduced features, with metrics such as Pearson and Spearman correlation coefficients indicating weak linear ties, while nonlinear metrics like mutual information highlighted significant dependencies, laying the groundwork for advanced feature interaction modeling.
(3) The TimeMixer-FI model was developed by integrating MLP-Mixer layers into the TimeMixer architecture, enhancing feature interaction capabilities and demonstrating consistent superior performance over the baseline TimeMixer and traditional methods across multiple test scenarios.
2. Materials and Methods
2.1. UMAP
UMAP serves as a sophisticated dimensionality reduction and visualization framework, uniquely designed to maintain both local and global data structures when mapping high-dimensional information into lower-dimensional spaces, facilitating deeper insights into data patterns. The algorithm constructs a topological representation by modeling data points as vertices and their relationships as edges. This process initiates by analyzing local neighborhoods in the high-dimensional space, establishing their structural characteristics, and generating a corresponding graph representation. The method then creates a parallel graph in low-dimensional space, optimizing the embedding by minimizing structural disparities between dimensions. The UMAP implementation encompasses several key phases:
1. Neighborhood Analysis: For each point
, k-nearest neighbors are determined using k-NN methodology [
25], with high-dimensional proximity calculated via a Gaussian kernel:
where
functions as a locally adaptive scaling parameter derived from neighborhood distances.
2. High-dimensional Network Formation: The proximity metrics establish a weighted graph structure that captures the dataset’s inherent organization.
3. Dimensional Transformation: Points are mapped into lower dimensions, with inter-point relationships modeled through a Student’s
t-distribution:
where
and
denote the transformed coordinates in the reduced space.
The process concludes by optimizing the cross-entropy between dimensional representations to maximize topological preservation. UMAP distinguishes itself through computational efficiency and visualization quality, particularly excelling in processing large-scale datasets. Its capacity to preserve multi-scale structural relationships enables effective dimensionality reduction across diverse machine learning applications.
In fault detection scenarios, UMAP exhibits two crucial properties:
(1) Structural Preservation: Through optimization of graph structures between high- and low-dimensional spaces, UMAP maps system state transitions into continuous trajectories in reduced dimensions. As systems gradually deteriorate from normal conditions, these trajectories display predictable deviation patterns.
(2) Local Sensitivity: UMAP demonstrates high sensitivity to subtle data variations through local distance metrics () and global optimization objectives. This capability amplifies early fault signatures, transforming potentially overlooked system degradation signals into detectable feature variations. Leveraging these properties, UMAP is integrated with time series prediction for fault detection. By monitoring prediction deviations in UMAP-reduced space, early detection of system state transitions becomes feasible. This approach not only inherits UMAP’s dimensional reduction advantages but also utilizes its anomaly pattern amplification effect, establishing a novel technical pathway for fault warning systems. This methodology offers three distinct advantages:
(1) Enhanced sensitivity to incipient faults through UMAP’s local structure preservation.
(2) Computational efficiency via dimensionality reduction.
(3) Early warning capability through combined anomaly amplification and prediction deviation analysis.
The integration creates a robust framework that bridges the gap between traditional dimensionality reduction and proactive fault detection, offering a more nuanced approach to system health monitoring.
2.2. TimeMixer-FI (Feature Interaction)
Time series at different scales inherently exhibit distinct characteristics, with finer scales capturing detailed patterns, while coarser scales emphasize broader, macro-level changes. This multi-scale perspective intrinsically facilitates the interpretation of complex variations across multiple components, offering advantages in modeling temporal dynamics. In predictive tasks, multi-scale time series demonstrate varying levels of predictive capability, as they are governed by different dominant temporal patterns. To effectively harness these multi-scale sequences, Wu et al. introduced TimeMixer [
24], which employs a pure MLP architecture, utilizing a combination of a Temporal Mixing Layer and a Feature Mixing Layer to capture temporal features at different scales. However, TimeMixer exhibits limitations in processing complex feature interactions. To address this challenge, we propose enhancing the TimeMixer framework by incorporating MLP-Mixer layers, thereby improving the model’s capability to capture feature interactions.
TimeMixer-FI(Feature Interaction) extends the original TimeMixer framework by incorporating the MLPMixer architecture to facilitate sophisticated feature interactions. Overview of the proposed framework as show in
Figure 1. The process includes three main steps: (a) Multivariate Time Series Multiscale Decomposition, (b) Past Decompose Mixing, and (c) Future Multipredictor Mixing. On the left, batches corresponding to the signals are shown, with different colors representing distinct signals or channels. Arrows indicate the data flow through the three main steps, where step (a) decomposes the signals into multiscale components, step (b) mixes the decomposed components, and step (c) performs future prediction.
Unlike PCA [
26], which produces independent principal components, UMAP’s dimensionality reduction preserves intricate topological relationships among features, resulting in a graph-like structure of interconnected components. Traditional linear layers are insufficient to capture these complex, nonlinear relationships between reduced dimensions.
The MLP-Mixer mechanism is introduced to facilitate comprehensive feature interaction learning through its dual-path mixing strategy. This enhancement enables the model to effectively capture both local and global feature dependencies, resulting in more nuanced representation learning. The combination of token-mixing and channel-mixing operations in MLPMixer provides an elegant solution for modeling the inherent graph-like relationships present in UMAP-reduced features, thereby improving the model’s ability to leverage the rich structural information preserved by UMAP transformation.
2.2.1. Multilayer Perceptron
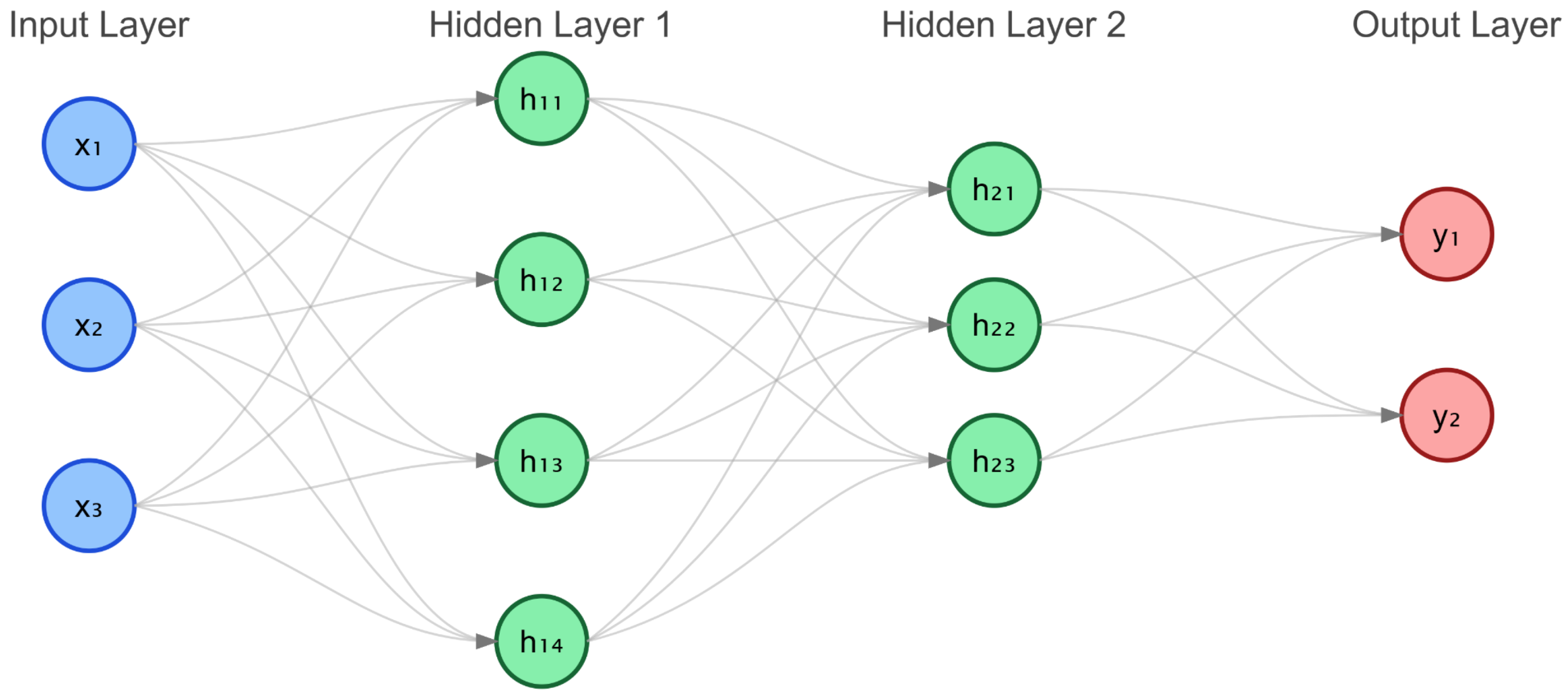
As a fundamental neural architecture, MLP enables effective handling of classification and regression tasks through its adaptive feedforward structure. This network comprises an input layer, multiple hidden layers, and an output layer, distinguished by its adaptability in modeling complex nonlinear relationships. The structural design is illustrated in
Figure 2.
1. Architecture Design: The framework incorporates interconnected layers where information flows from input through hidden transformations to generate output predictions. Hidden layers utilize ReLU activation to introduce nonlinearity, defined by:
2. Signal Propagation: Information traverses the network through sequential layer transformations. Each layer processes its input through linear operations followed by nonlinear activation:
where
and
denote the weight matrix and bias vector at layer
l,
represents the previous layer output, and
f indicates the activation function.
3. Optimization Framework: The network parameters are refined by minimizing objective functions—typically, MSE for regression or cross-entropy for classification tasks. Parameter updates utilize gradient computation through backpropagation, implementing optimization strategies like Adam [
27] or SGD [
28].
MLP’s effectiveness stems from its architectural simplicity combined with modeling versatility. The integration of hidden transformations and nonlinear activations enables capture of intricate data patterns, establishing MLP as a cornerstone component in deep learning applications. As shown in
Figure 2, to disentangle complex variations, we first apply average pooling to the observation
, resulting in
M low-dimensional sequences
, where
and
. The lower-level sequence
is the input sequence containing the finest scale variations, while the higher-level sequence captures more macro-level trends. We then embed these multi-scale sequences into a deeper feature representation
, which encodes the multi-scale properties of the sequence.
Next, we propose to decompose the past sequences and extract multi-scale historical information through a Progressive Decomposition Module (PDM) across layers. The output at layer
l can be formalized as follows:
where
L is the total number of layers, and
, where each sequence
represents a progressively refined representation of the input. The detailed operations of the PDM are described in the next section.
For the forecasting stage, we employ a Future Multiscale Mixer (FMM) module to aggregate the multi-scale information
and generate the future prediction:
where
denotes the final predicted sequence. Through this design, the TiMixer architecture effectively captures essential past information and utilizes the strengths of multi-scale representations to forecast the future.
2.2.2. Construction of Multi-Scale Temporal Representations
To disentangle complex variations, the past observations
are first downsampled into
M scales through average pooling, ultimately obtaining a set of multiscale time series
, where
,
, and
C denotes the variate number. The lowest-level series
represents the input series containing the finest temporal variations, while the highest-level series
captures macroscopic variations. Subsequently, these multiscale series are projected into deep features
through the embedding layer, which can be formalized as
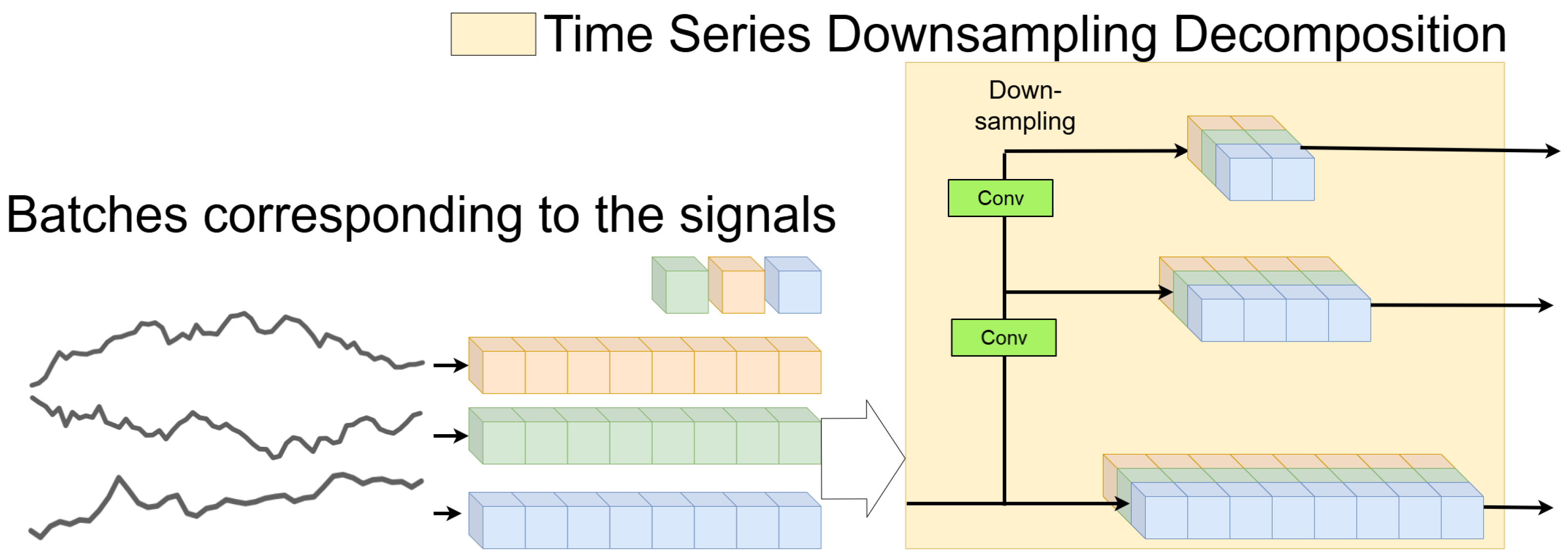
. Through the above designs, multiscale representations of the input series are obtained. Illustration of the Time Series Downsampling Decomposition process as show in
Figure 3. The input signals (batches on the left) are processed through multiple Conv and Downsampling layers to decompose the time series into multiscale components. Different colors represent distinct signals or channels, with the output components at varying scales shown on the right. Arrows indicate the data flow through the Conv and Downsampling layers, where each layer reduces the temporal resolution to capture multiscale patterns.
2.2.3. Seasonal Component Mixing
In seasonal analysis, cyclical patterns can be detected over time, such as daily peaks in traffic volume. With time, sharp seasonal shifts occur, necessitating finer adjustments in future predictions. To this end, we employ a bottom-up approach to integrate the information across time scales, progressively refining the seasonal patterns from the coarse to finer scales.
For a set of seasonal components
we recursively compute the seasonal interaction at layer
l as follows:
where
Bottom-Up-Mixing(·) is linear and operates across temporal dimensions using GELU activations, with input dimension
, and
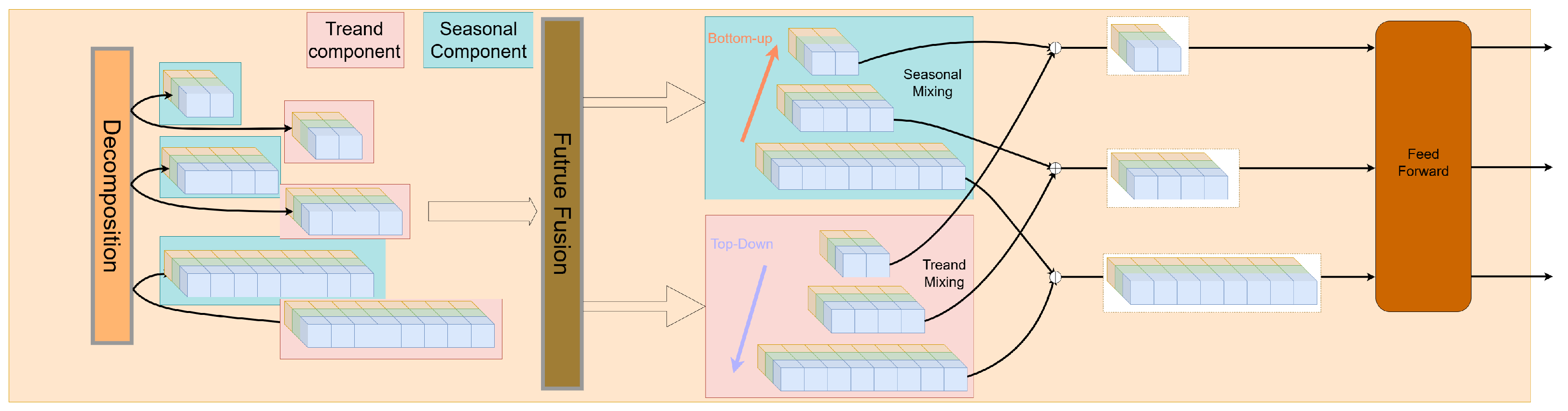
Feature Fusion(·) applies a LayerNorm followed by GELU. The structure of this module is shown in the
Figure 4. Pink represents the trend component, blue represents the seasonal component, and orange indicates the decomposition process. The brown section on the right denotes the feed-forward process. Arrows (bottom-up in red and top-down in purple) denote the seasonal and trend mixing directions.
2.2.4. Trend Component Mixing
In contrast to the seasonal part, trend components often exhibit smoother, macro-level changes. Upper layers tend to contain coarse information, while lower layers reveal more refined variations. Thus, we apply a top-down mixing approach, using coarse scales to guide the refinement of the trend patterns across finer scales.
For a set of trend components
we recursively compute the trend interaction as follows:
where
Top-Down-Mixing(·) uses GELU activations and progressively refines the trends with input dimension
Feature Fusion(·) is similar to the seasonal fusion process, involving two linear layers followed by GELU activations and LayerNorm.
2.2.5. Feature Fusion
Given input feature
, the Feature Fusion operation is defined as:
where
denotes the patch operation,
represents the channel processing operation,
indicates Layer Normalization, and
is the Multi-Layer Perceptron.
represents the final transformation. For each channel
, the operation can be formulated as follows:
where
represents the channel-processed feature. Through this Feature Fusion module, we can effectively integrate multi-scale features while preserving the original information through skip connections. The structure of the Future Fusion module (highlighted in brown in
Figure 4) as show in
Figure 5. The module processes input data through LayerNorm, Patch, and multiple MLP layers with skip-connections. Different colors represent distinct channels of the input data, which are processed and fused across layers. The ‘T’ denotes a transpose operation to adjust the dimensions of the data, and arrows indicate the data flow with skip-connections enabling information transfer across layers.
2.2.6. Future Multiscale Forecasting Mixer
After processing through the PDM block, we acquire the multi-scale past information
, where
. Since different scales of the sequence exhibit distinct primary variations, they also demonstrate different forecasting capabilities. To fully exploit this multi-scale information, we propose a future multiscale forecasting mixer (FMM), which generates predictions by combining predictions from various scales:
where
represents the future prediction at scale
m, and the final output
represents the predicted future sequence.
(·) refers to the predictor for the
m-th scale sequence, which applies a linear layer to the final deepest feature representation from the previous layers, mapping it to the future sequence of length
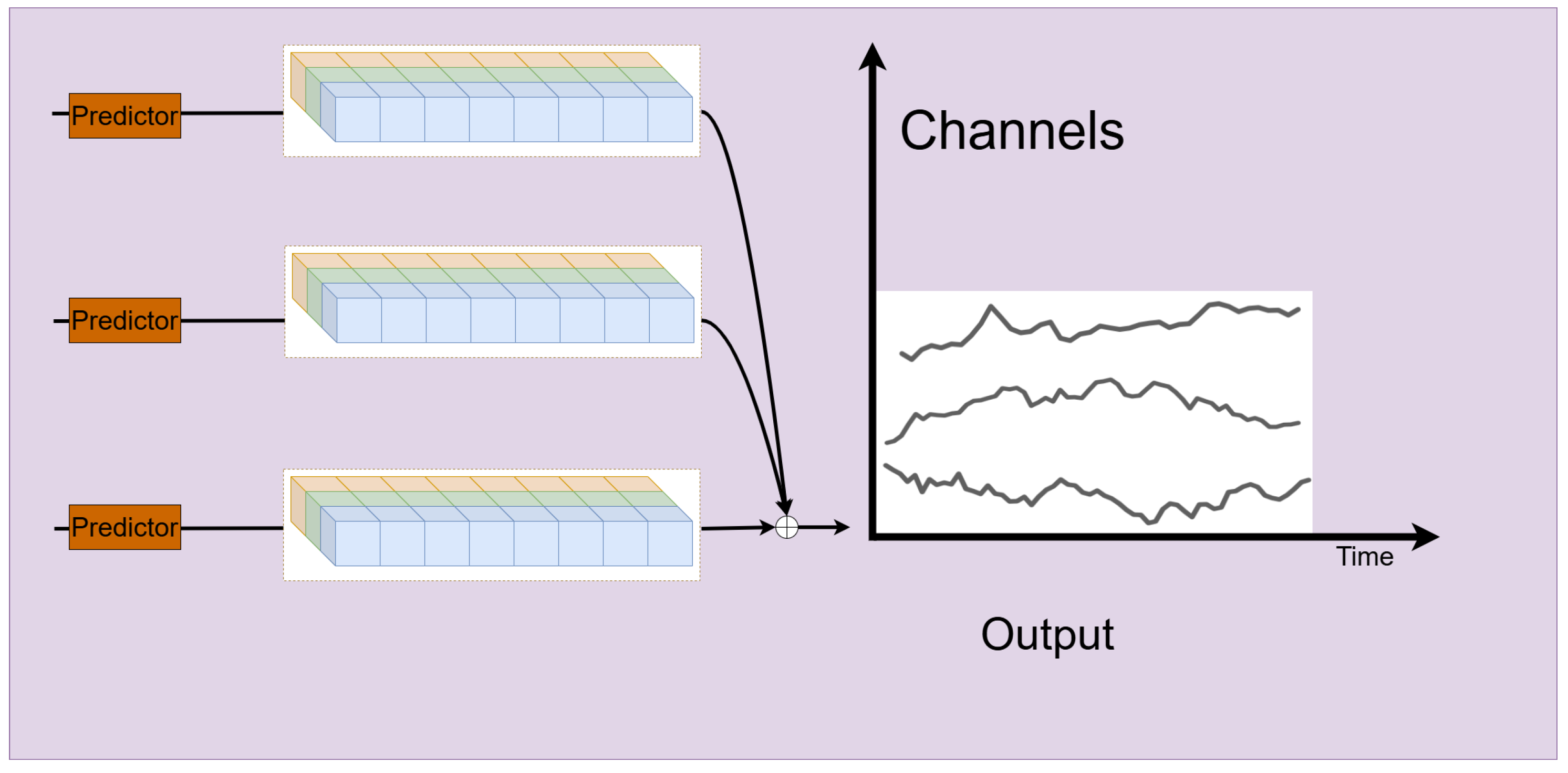
F. Notably, FMM aggregates multiple predictors, each utilizing the historical information from different scales. This aggregation enhances the predictive capabilities, especially in forecasting complex, multi-scale sequences. The structure of the Predictor module as show in
Figure 6. The module processes multi-channel input data (represented by different colors) and generates the output time series. The vertical axis represents channels, and the horizontal axis represents time. Each predictor block processes a subset of channels to produce the final prediction. Arrows indicate the data flow from input to output through the Predictor blocks, and the output on the right shows the predicted time series for each channel.
5. Conclusions
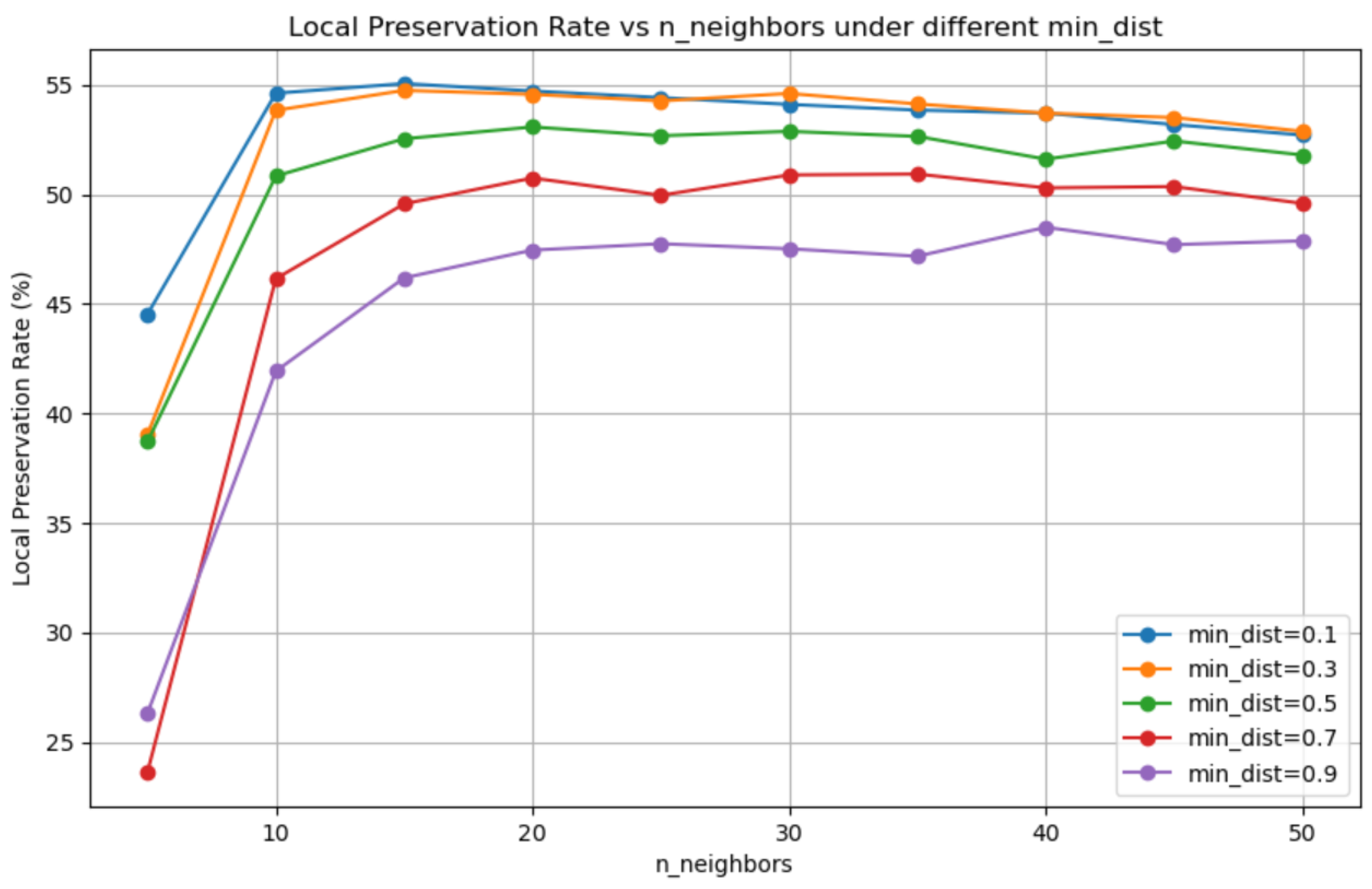
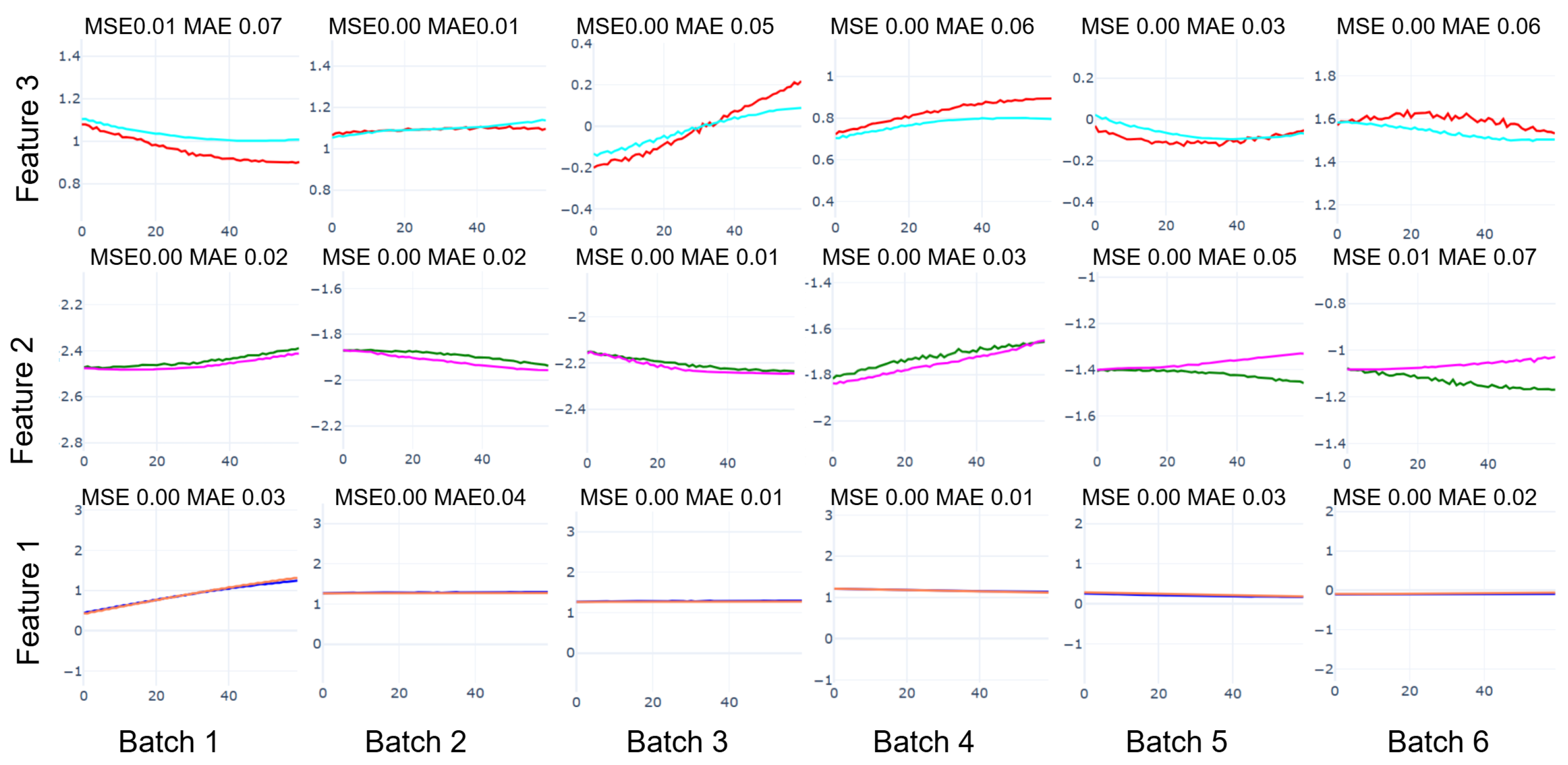
An unsupervised approach is introduced for early fault signals in marine diesel engines, combining UMAP dimensionality reduction with time series prediction to tackle the challenges of high-dimensional data and scarce fault labels in marine diesel engine fault diagnosis. UMAP effectively preserves topological structures and amplifies local differences, making subtle early fault signatures more detectable in the reduced dimensional space. To address the complex nonlinear relationships in UMAP-reduced features, the TimeMixer-FI model integrates MLP-Mixer layers, enhancing feature interaction modeling. The study concludes that this approach significantly improves fault detection, as validated by experiments: UMAP preserves topological structures with a local preservation rate of approximately 55% using default hyperparameters (
Section 4.2,
Figure 11), amplifying subtle anomalies, while TimeMixer-FI achieves a 69.1% MSE reduction (0.0544 to 0.0168) and 46.3% MAE reduction (0.1023 to 0.0549) at 60 time steps, enabling detection in Batch 2 (e.g., MSE 0.03, MAE 0.16 for Feature 2) versus Batch 4 for raw power output (MSE 0.17, MAE 0.35), two batches earlier, per
Figure 16 (
Section 4.3). Experiments demonstrate that TimeMixer-FI surpasses several baseline models in both steady-state and fault transition scenarios. By learning normal operating patterns as a baseline and monitoring deviations in the UMAP space, this approach detects anomalies before they significantly impact standard performance metrics, thereby improving the precision and efficiency of predictive maintenance in marine systems.
However, the current evaluation is limited to a single dataset from the YUAN FU YANG tanker, reflecting specific operational conditions (steady-state and rapid speed reduction), which may not fully represent diverse engine types or operating modes. Despite these advancements, practical deployment faces challenges, including: (1) model interpretability, as the complexity of UMAP and TimeMixer-FI may hinder engineers’ understanding of fault detection decisions; (2) generalization across diverse conditions, as varying marine environments or engine types may affect consistent fault detection; and (3) computational scalability, as the combined framework may demand substantial resources for real-time use on resource-limited shipboard systems. Future work will address these limitations by: (1) improving interpretability through feature importance analysis or UMAP embedding visualizations to clarify fault detection outcomes for engineers; (2) enhancing generalization with adaptive learning techniques to accommodate diverse marine conditions and engine variations, alongside testing on additional datasets; and (3) optimizing computational efficiency via model compression or lightweight architectures to ensure scalability for real-time shipboard applications. Future work could explore compatibility with optimization techniques like Bayesian Optimization to refine hyper-parameter tuning, enhancing model performance across diverse conditions.