Machine Learning-Assisted Design and Optimization of a Broadband, Low-Loss Adiabatic Optical Switch
Abstract
:1. Introduction
2. Materials and Methods
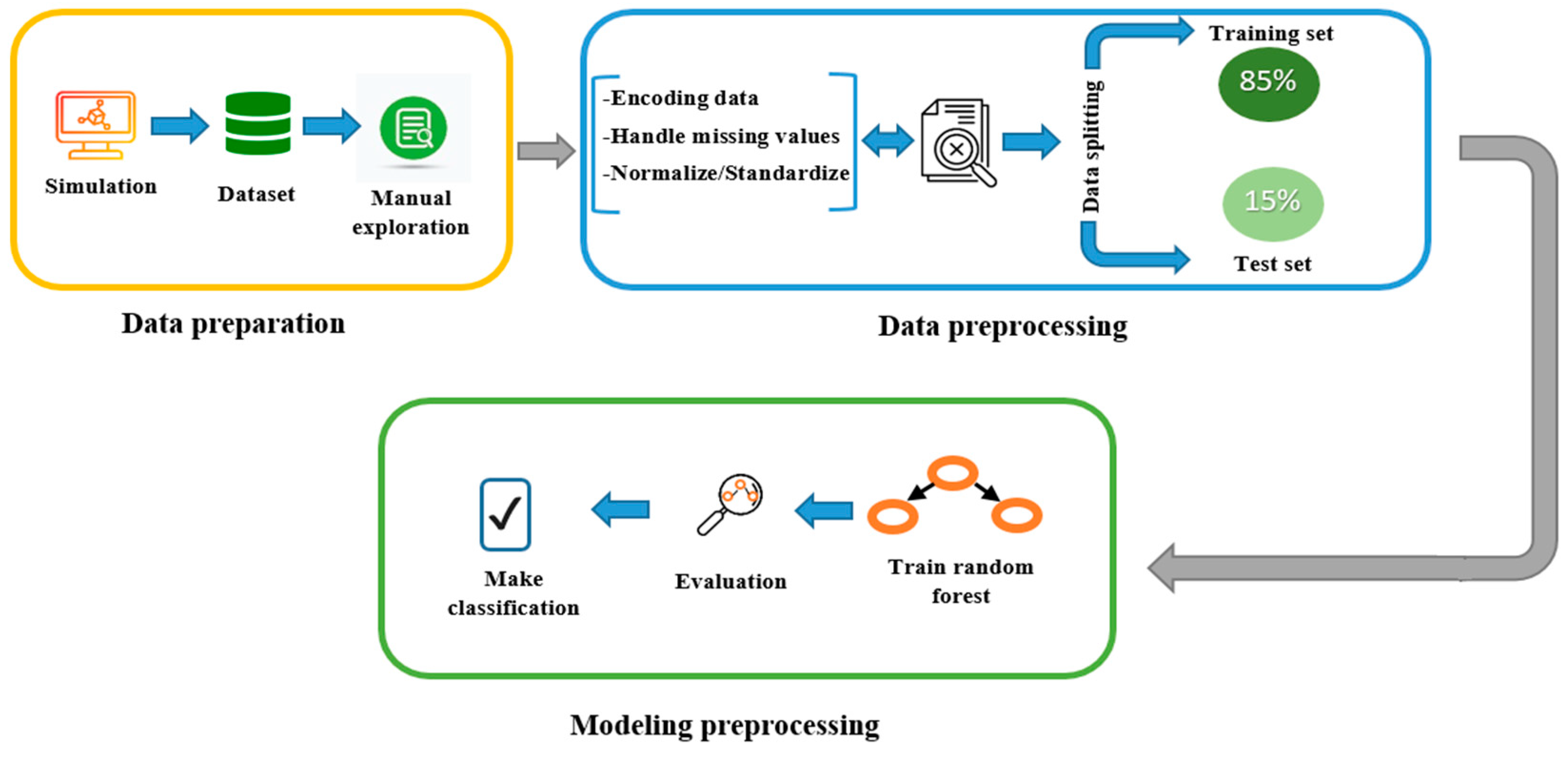
2.1. Machine Learning Technique Application
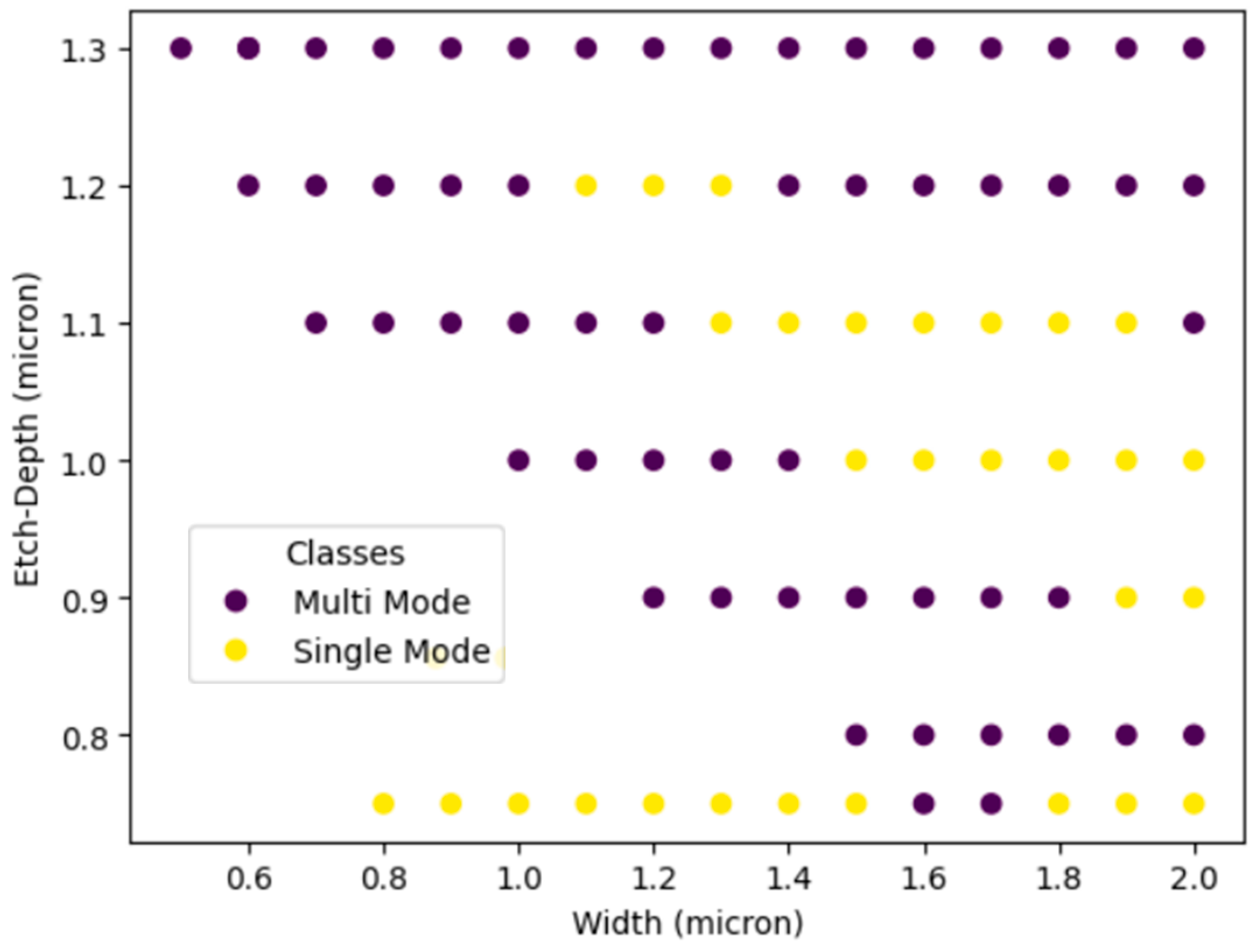
2.2. Dataset Construction
2.3. Machine Learning Model Building
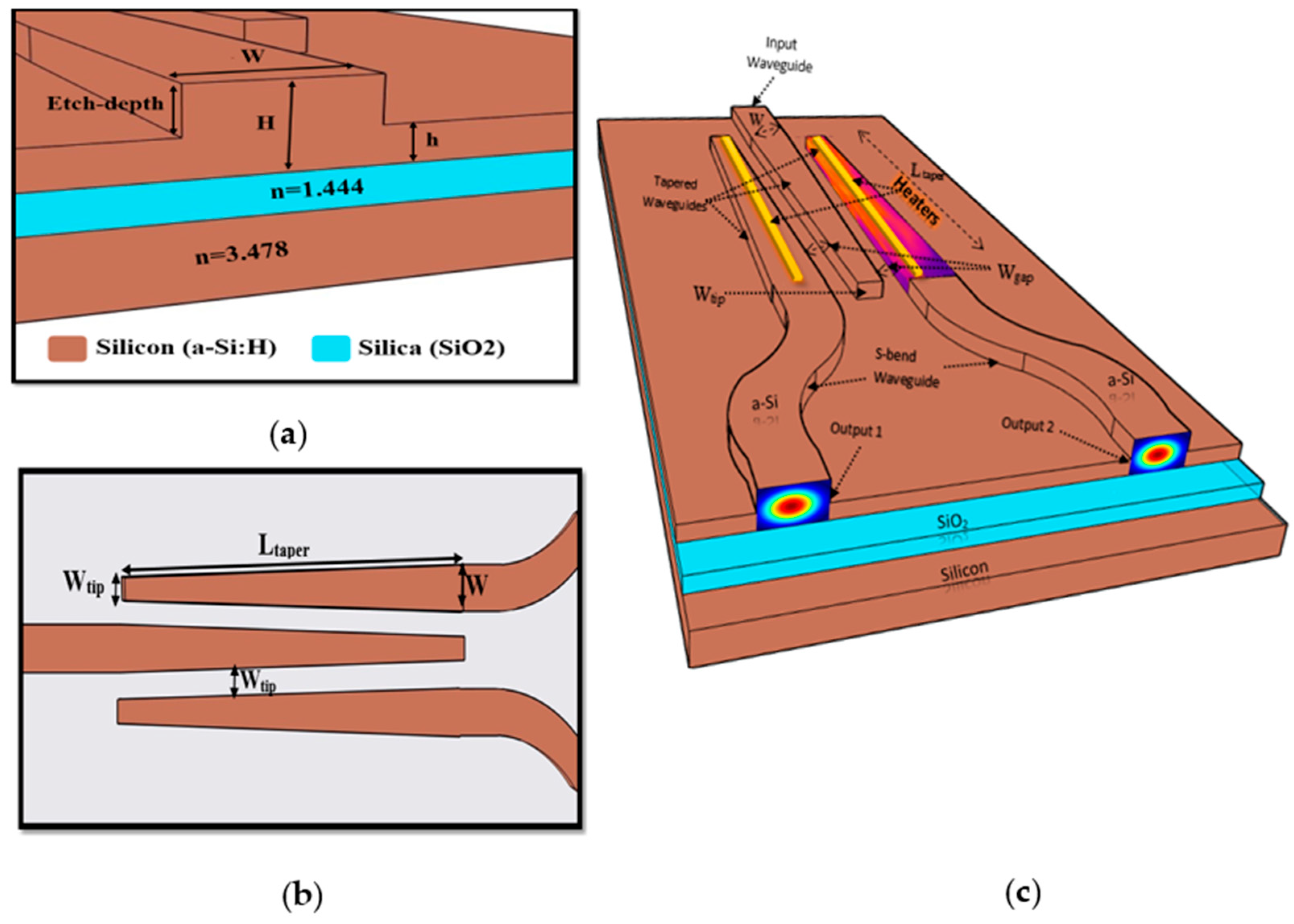
2.4. 1 × 2 Y-Junction Adiabatic Optical Power Splitter Design
2.5. Setup of Thermo-Optic Effect Simulation for the Adiabatic Switch
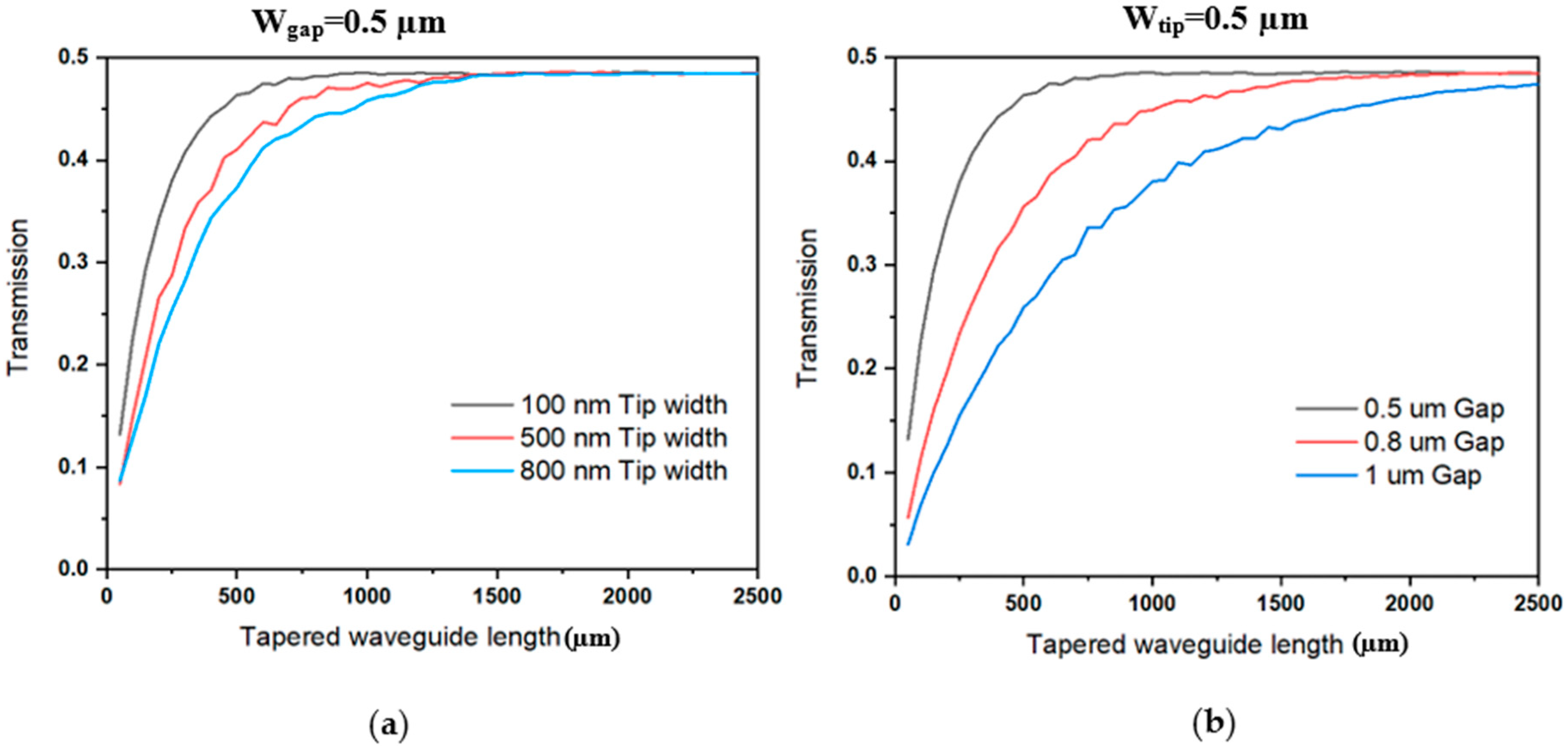
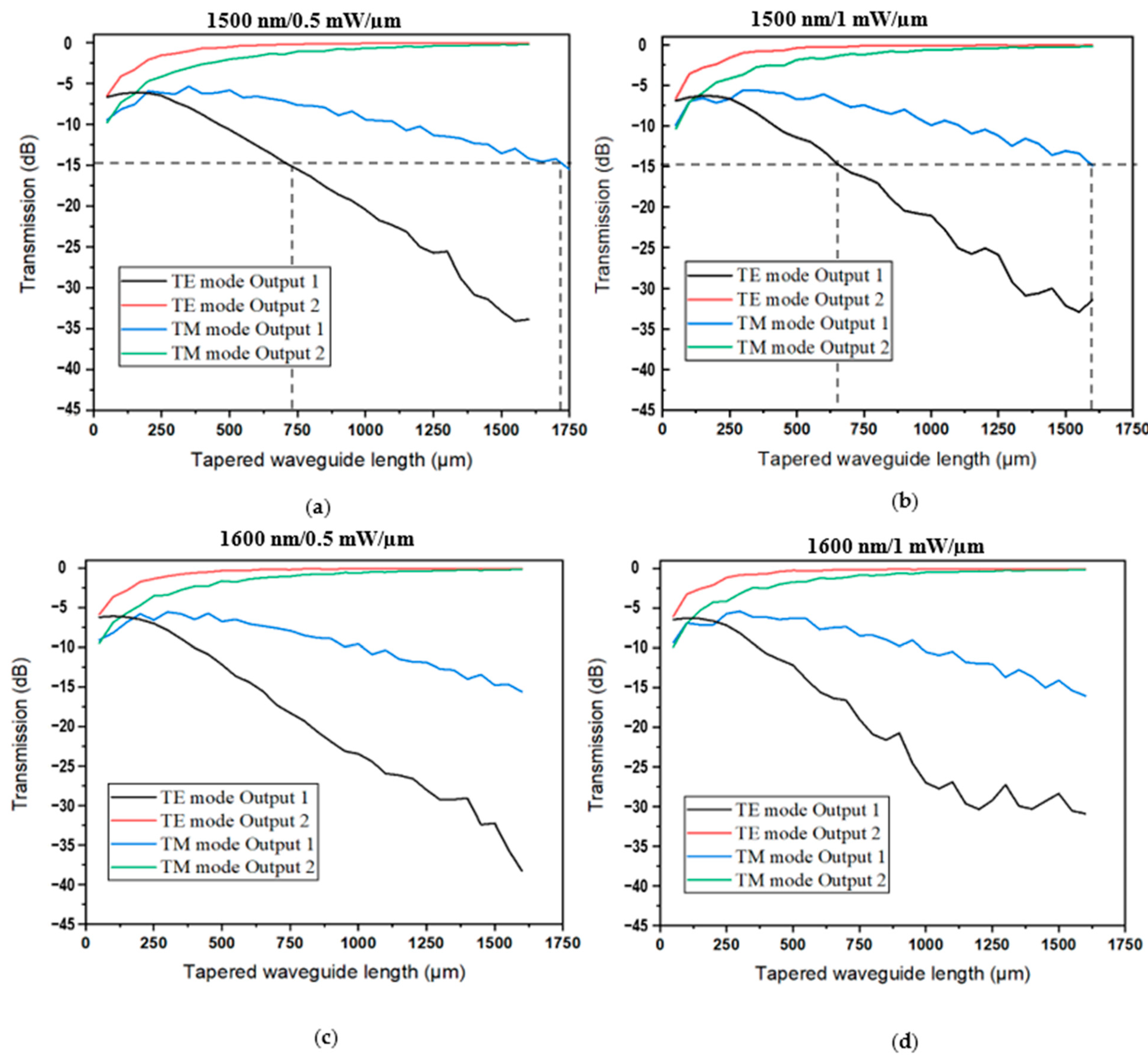
3. Y-Adiabatic Switch Optical Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gostimirovic, D.; Soref, R. An Integrated Optical Circuit Architecture for Inverse-Designed Silicon Photonic Components. Sensors 2023, 23, 626. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Riemensberger, J.; Lihachev, G.; Churaev, M.; Kao, W.; Ji, X.; Zhang, J.; Blesin, T.; Davydova, A.; et al. Lithium tantalate photonic integrated circuits for volume manufacturing. Nature 2024, 629, 784–790. [Google Scholar] [CrossRef]
- Cheng, Q.; Bahadori, M.; Glick, M.; Rumley, S.; Bergman, K. Recent advances in optical technologies for data centers: A review. Optica 2018, 5, 1354–1370. [Google Scholar] [CrossRef]
- Farmakidis, N.; Youngblood, N.; Lee, J.S.; Feldmann, J.; Lodi, A.; Li, X.; Aggarwal, S.; Zhou, W.; Bogani, L.; Pernice, W.H.; et al. Electronically Reconfigurable Photonic Switches Incorporating Plasmonic Structures and Phase Change Materials. Adv. Sci. 2022, 9, e2200383. [Google Scholar] [CrossRef]
- Chen, X.; Lin, J.; Wang, K. A Review of Silicon-Based Integrated Optical Switches. Laser Photon Rev. 2023, 17, 2200571. [Google Scholar] [CrossRef]
- Yue, W.; Cai, Y.; Yu, M. Review of 2 × 2 Silicon Photonic Switches. Photonics 2023, 10, 564. [Google Scholar] [CrossRef]
- Kondo, Y.; Murai, T.; Shoji, Y.; Mizumoto, T. All-Optical Switch by Light-to-Heat Conversion in Metal Deposited Si Ring Resonator. IEEE Photon. Technol. Lett. 2020, 32, 807–810. [Google Scholar] [CrossRef]
- Soref, R. Tutorial: Integrated-photonic switching structures. APL Photonics 2018, 3, 021101. [Google Scholar] [CrossRef]
- Tu, X.; Song, C.; Huang, T.; Chen, Z.; Fu, H. State of the Art and Perspectives on Silicon Photonic Switches. Micromachines 2019, 10, 51. [Google Scholar] [CrossRef]
- Ironside, C.N.; Aitchison, J.S.; Arnold, J.M. An all-optical switch employing the cascaded second-order nonlinear effect. IEEE J. Quantum Electron. 1993, 29, 2650–2654. [Google Scholar] [CrossRef]
- Kim, S.-H.; You, J.-B.; Rhee, H.-W.; Yoo, D.E.; Lee, D.-W.; Yu, K.; Park, H.-H. High-Performance Silicon MMI Switch Based on Thermo-Optic Control of Interference Modes. IEEE Photon. Technol. Lett. 2018, 30, 1427–1430. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Zhao, J.; Li, C. Ultrafast, low power, and highly stable all-optical switch in MZI with two-arm-sharing nonlinear ring resonator. Opt. Commun. 2005, 256, 319–325. [Google Scholar] [CrossRef]
- Mecozzi, A.; Shtaif, M. Polarization dependent loss and its impact in optical communications systems. In Proceedings of the Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 23–27 February 2004; p. 648. [Google Scholar]
- Ozcan, C.; Aitchison, J.S.; Mojahedi, M. Foundry-Processed Compact and Broadband Adiabatic Optical Power Splitters with Strong Fabrication Tolerance. Photonics 2023, 10, 1310. [Google Scholar] [CrossRef]
- Queraltó, G.; Ahufinger, V.; Mompart, J. Integrated photonic devices based on adiabatic transitions between supersymmetric structures. Opt. Express 2018, 26, 33797–33806. [Google Scholar] [CrossRef]
- Paschotta, R. Single-Mode Fibers, Single-Mode Fibers—Launching Light, Monomode Fiber, Cut-Off Wavelength. Available online: https://www.rp-photonics.com/single_mode_fibers.html (accessed on 5 February 2025).
- Kimerling, L.; Baets, R.; Jacob, A.; Rahim, A.E.A. Silicon photonics. In Integrated Photonic Systems Roadmap-International (IPSR-I); PhotonDelta: Eindhoven, The Netherlands, 2020. [Google Scholar]
- Fahrenkopf, N.M.; McDonough, C.; Leake, G.L.; Su, Z.; Timurdogan, E.; Coolbaugh, D.D. The AIM Photonics MPW: A Highly Accessible Cutting Edge Technology for Rapid Prototyping of Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–6. [Google Scholar] [CrossRef]
- Guerrero, A.B.G.; Pozo, J. The Merits of Single-Mode vs. Multimode Fiber Optics. Photonics Spectra. 2018. Available online: https://www.photonics.com/Articles/The_Merits_of_Single-Mode_vs_Multimode_Fiber/a63723 (accessed on 16 January 2025).
- Xu, D.-X.; Schmid, J.H.; Reed, G.T.; Mashanovich, G.Z.; Thomson, D.J.; Nedeljkovic, M.; Chen, X.; Van Thourhout, D.; Keyvaninia, S.; Selvaraja, S.K. Silicon Photonic Integration Platform—Have We Found the Sweet Spot? IEEE J. Sel. Top. Quantum Electron. 2014, 20, 189–205. [Google Scholar] [CrossRef]
- Okamoto, K. Progress and technical challenge for planar waveguide devices: Silica and silicon waveguides. Laser Photon. Rev. 2011, 6, 14–23. [Google Scholar] [CrossRef]
- Vivien, L.; Rouvière, M.; Fédéli, J.-M.; Marris-Morini, D.; Damlencourt, J.F.; Mangeney, J.; Crozat, P.; El Melhaoui, L.; Cassan, E.; Le Roux, X.; et al. High speed and high responsivity germanium photodetector integrated in a Silicon-On-Insulator microwaveguide. Opt. Express 2007, 15, 9843–9848. [Google Scholar] [CrossRef]
- Headley, W.R.I. Optical Ring Resonators in Silicon-On-Insulator. Ph.D. Thesis, University of Surrey, Guildford, UK, 2005. [Google Scholar]
- Petermann, K. Properties of optical rib-guides with large cross-section. Arch. Elektr. Uebertragung 1976, 30, 139–140. [Google Scholar]
- Soref, R.A.; Schmidtchen, J.; Petermann, K. Large single-mode rib waveguides in GeSi-Si and Si-on-SiO/sub 2/. IEEE J. Quantum Electron. 1991, 27, 1971–1974. [Google Scholar] [CrossRef]
- Pogossian, S.P.; Vescan, L.; Vonsovici, A. The single-mode condition for semiconductor rib waveguides with large cross section. J. Light. Technol. 1998, 16, 1851–1853. [Google Scholar] [CrossRef]
- Ansys Lumerical. Available online: https://www.lumerical.com (accessed on 18 March 2025).
- Mammeri, M.; Dehimi, L.; Bencherif, H.; Pezzimenti, F. Paths towards high perovskite solar cells stability using machine learning techniques. Sol. Energy 2023, 249, 651–660. [Google Scholar] [CrossRef]
- LaValle, S.M.; Branicky, M.S. On the relationship between classical grid search and probabilistic roadmaps. In Algorithmic Foundations of Robotics V; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 59–75. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 2001; Volume 45, pp. 5–32. [Google Scholar]
- Weninger, D.M.; Serna, S.; Jain, A.; Kimerling, L.; Agarwal, A. High density vertical optical interconnects for passive assembly. In Proceedings of the Optical Interconnects XXIII, San Francisco, CA, USA, 1 February 2023; p. 15. [Google Scholar] [CrossRef]
- Liang, T.-L.; Tu, Y.; Chen, X.; Huang, Y.; Bai, Q.; Zhao, Y.; Zhang, J.; Yuan, Y.; Li, J.; Yi, F.; et al. A Fully Numerical Method for Designing Efficient Adiabatic Mode Evolution Structures (Adiabatic Taper, Coupler, Splitter, Mode Converter) Applicable to Complex Geometries. J. Light. Technol. 2021, 39, 5531–5547. [Google Scholar] [CrossRef]
- Hashemi, B.; Casalino, M.; Crisci, T.; Mammeri, M.; DellaCorte, F.G. Broadband Thermo-Optic Photonic Switch for TE and TM Modes with Adiabatic Design. Photonics 2024, 11, 1177. [Google Scholar] [CrossRef]
- Hauffe, R.; Petermann, K. Thermo-Optic Switching. In Optical Switching; El-Bawab, T.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Cocorullo, G.; Della Corte, F.; Iodice, M.; Rendina, I.; Sarro, P. Silicon-on-silicon rib waveguides with a high-confining ion-implanted lower cladding. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 983–989. [Google Scholar] [CrossRef]
- Kawamata, Y.; Ito, H.; Nikkuni, H.; Ito, M. Deposition Temperature Dependence of Optical Properties of a-Si:H for Short-wave Near-infrared Filter by DC Sputtering. Vac. Surf. Sci. 2021, 64, 375–381. [Google Scholar] [CrossRef]
- Kawamata, Y.; Ono, D.; Ito, H.; Nikkuni, H.; Ito, M. Film structure and optical characteristics of a-Si:H prepared with a rotary table type layer-by-layer sputtering method for application in short-wave near-infrared filters. Opt. Mater. Express 2022, 12, 4223–4234. [Google Scholar] [CrossRef]
- Palik, E. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1997; Volume 5, pp. 116–117. [Google Scholar]
- Della Corte, F.G.; Montefusco, M.E.; Moretti, L.; Rendina, I.; Rubino, A. Study of the thermo-optic effect in hydrogenated amorphous silicon and hydrogenated amorphous silicon carbide between 300 and 500 K at 1.55 μm. Appl. Phys. Lett. 2001, 79, 168–170. [Google Scholar] [CrossRef]
- Palik, E.D.; Ghosh, G. Handbook of Optical Constants of Solids; Elsevier Science: Burlington, MA, USA, 2014. [Google Scholar]
- Gao, H.; Jiang, Y.; Cui, Y.; Zhang, L.; Jia, J.; Jiang, L. Investigation on the Thermo-Optic Coefficient of Silica Fiber Within a Wide Temperature Range. J. Light. Technol. 2018, 36, 5881–5886. [Google Scholar] [CrossRef]
- Kyocera Solide Carbide Tools. Titanium Properties. Available online: https://kyocera-sgstool.co.uk/titanium-resources/titanium-information-everything-you-need-to-know/titanium-properties/#:~:text=Titanium%20has%20low%20thermal%20conductivity,the%20performance%20of%20the%20metal. (accessed on 5 February 2025).
- Cocorullo, G.; Minarini, C.; Rubino, A.; Della Corte, F.G.; Rendina, I.; Terzini, E. Amorphous silicon waveguides and light modulators for integrated photonics realized by low-temperature plasma-enhanced chemical-vapor deposition. Opt. Lett. 1996, 21, 2002–2004. [Google Scholar] [CrossRef]
- Morishita, K. Wavelength-selective optical-fiber directional couplers using dispersive materials. Opt. Lett. 1998, 13, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Thottoli, A.; Biagi, G.; Vorobev, A.S.; Giglio, M.; Magno, G.; O’faolain, L.; Grande, M. Highly efficient and selective integrated directional couplers for multigas sensing applications. Sci. Rep. 2023, 13, 22720. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics Non-Relativistic Theory; Pergamon: London, UK, 1958; pp. 304–313. [Google Scholar]
- Xing, J.; Li, Z.; Yu, Y.; Yu, J. Design of polarization-independent adiabatic splitters fabricated on silicon-on-insulator substrates. Opt. Express 2013, 21, 26729–26734. [Google Scholar] [CrossRef] [PubMed]
- Solehmainen, K.; Kapulainen, M.; Harjanne, M.; Aalto, T. Adiabatic and Multimode Interference Couplers on Silicon-on-Insulator. IEEE Photon. Technol. Lett. 2006, 18, 2287–2289. [Google Scholar] [CrossRef]
- Cao, L.; Elshaari, A.; Aboketaf, A.; Preble, S. Adiabatic couplers in SOI waveguides. In Proceedings of the CLEO/QELS: 2010 Laser Science to Photonic Applications, San Jose, CA, USA, 16–21 May 2010; pp. 1–2. [Google Scholar]
- Tran, M.A.; Zhang, C.; Bowers, J.E. A broadband optical switch based on adiabatic couplers. In Proceedings of the 2016 IEEE Photonics Conference (IPC), Waikoloa, HI, USA, 2–6 October 2016; pp. 755–756. [Google Scholar] [CrossRef]
- Wang, S.; Dai, D. Polarization-insensitive 2 × 2 thermo-optic Mach–Zehnder switch on silicon. Opt. Lett. 2018, 43, 2531–2534. [Google Scholar] [CrossRef] [PubMed]
- Yue, J.; Wang, M.; Zou, J.; Liu, T.; Fang, J.; Sun, X.; Wu, Y.; Zhang, D. Low-loss silica waveguide 1×8 thermo-optic switch based on large-scale multimode interference couplers. Opt. Commun. 2024, 573, 131014. [Google Scholar] [CrossRef]
- Li, W.; Xu, L.; Zhang, J.; Mao, D.; D’Mello, Y.; Wei, Z.; Plant, D.V. Broadband Polarization-Insensitive Thermo-Optic Switches on a 220-nm Silicon-on-Insulator Platform. IEEE Photon. J. 2022, 14, 6658807. [Google Scholar] [CrossRef]


| Width (µm) | Height (µm) | Etch-Depth (µm) | Polarization | Single Mode | Polarization Independent |
|---|---|---|---|---|---|
| 2.00 | 1.20 | 1.00 | TE | True | False |
| 0.85 | 0.70 | 0.50 | TE | False | False |
| 1.00 | 1.40 | 0.65 | TE | False | False |
| 1.50 | 0.90 | 0.35 | TM | False | False |
| Parameters | Symbols | Value (µm) |
|---|---|---|
| Waveguide rib width | W | 1.40 |
| Tip width of the tapered waveguide | Wtip | 0.50 |
| Gap between external and middle waveguides | Wgap | 0.50 |
| Input and output waveguide length | L | 15.0 |
| Tapered waveguides length | Ltaper | variable |
| Distance between the heater and the waveguides | h | 0.50 |
| Width of heater | Wh | 0.50 |
| Heat Capacity (J/kg.K) | Thermal Conductivity (W/m.K) | Thermo-Optic Coefficient (K−1) | |
|---|---|---|---|
| Hydrogenated amorphous Silicon (a-Si: H) | 703 [38] | 1.5 [29] | 2.3 × 10−4 [39] |
| Silicon oxide (SiO2) | 709 [38] | 1.38 [40] | 8.4 × 10−6 [41] |
| Titanium (Ti) | 522.3 [42] | 11.4 [42] | / |
| Ref. | Scale | Structure | Material | Footprint (µm2) | Power (mW) | IL (dB) | BW (nm) | ER (dB) | Year |
|---|---|---|---|---|---|---|---|---|---|
| This work | 1 × 2 | Y-adiabatic | Hydrogenated amorphous silicon | 1600 × 8 | 800 | 0.1 | 100 | TE and TM | 2025 |
| [50] | 1 × 8 | MZIS | Silicon | 1100 × 5.7 | 315.8 | 3.4~3.6 | 120 | TE and TM | 2016 |
| [51] | 2 × 2 | MZIS | Lithium niobate | 5400 × 140 | 7.3 | <2 | 75 | TE | 2018 |
| [52] | 1 × 2 | MMI | Silica | 1754 × 19 | 1830 | ~3 | / | TE | 2024 |
| [53] | 1 × 2 | MMI | Silicon nitride | 2335 × 30 | 57.4 | 13.1 | 120 | TE and TM | 2023 |
| [33] | 1 × 2 | Adiabatic | Silicon | 280 × 8 | 250 | 0.52 | 100 | TE and TM | 2024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mammeri, M.; Casalino, M.; Crisci, T.; Hashemi, B.; Vergari, S.; Dehimi, L.; Dellacorte, F.G. Machine Learning-Assisted Design and Optimization of a Broadband, Low-Loss Adiabatic Optical Switch. Electronics 2025, 14, 1276. https://doi.org/10.3390/electronics14071276
Mammeri M, Casalino M, Crisci T, Hashemi B, Vergari S, Dehimi L, Dellacorte FG. Machine Learning-Assisted Design and Optimization of a Broadband, Low-Loss Adiabatic Optical Switch. Electronics. 2025; 14(7):1276. https://doi.org/10.3390/electronics14071276
Chicago/Turabian StyleMammeri, Mohamed, Maurizio Casalino, Teresa Crisci, Babak Hashemi, Stefano Vergari, Lakhdar Dehimi, and Francesco Giuseppe Dellacorte. 2025. "Machine Learning-Assisted Design and Optimization of a Broadband, Low-Loss Adiabatic Optical Switch" Electronics 14, no. 7: 1276. https://doi.org/10.3390/electronics14071276
APA StyleMammeri, M., Casalino, M., Crisci, T., Hashemi, B., Vergari, S., Dehimi, L., & Dellacorte, F. G. (2025). Machine Learning-Assisted Design and Optimization of a Broadband, Low-Loss Adiabatic Optical Switch. Electronics, 14(7), 1276. https://doi.org/10.3390/electronics14071276









