Research on Prediction of Dissolved Gas Concentration in a Transformer Based on Dempster–Shafer Evidence Theory-Optimized Ensemble Learning
Abstract
1. Introduction
- This paper establishes a Bagging model using decision trees as the base learner for predicting dissolved gas concentrations in transformers, and applies D-S evidence theory to the aggregation layer of the Bagging model, optimizing the flexibility and stability of the existing Bagging model’s predictions. It is noteworthy that both Bagging models and D-S evidence theory have been extensively researched, but this paper is the first to combine them to construct an optimized Bagging model.
- The fusion effect of D-S evidence theory depends on the values of the basic probability assignment, but few studies have optimized the basic probability assignment. Therefore, this paper considers using the sequential least squares programming algorithm to optimize the basic probability assignment values in D-S evidence theory, with the goal of minimizing the mean square error as the optimal solution for the objective function. The results show that this optimization operation for D-S evidence theory also improves the prediction accuracy of the entire prediction model.
2. Related Work
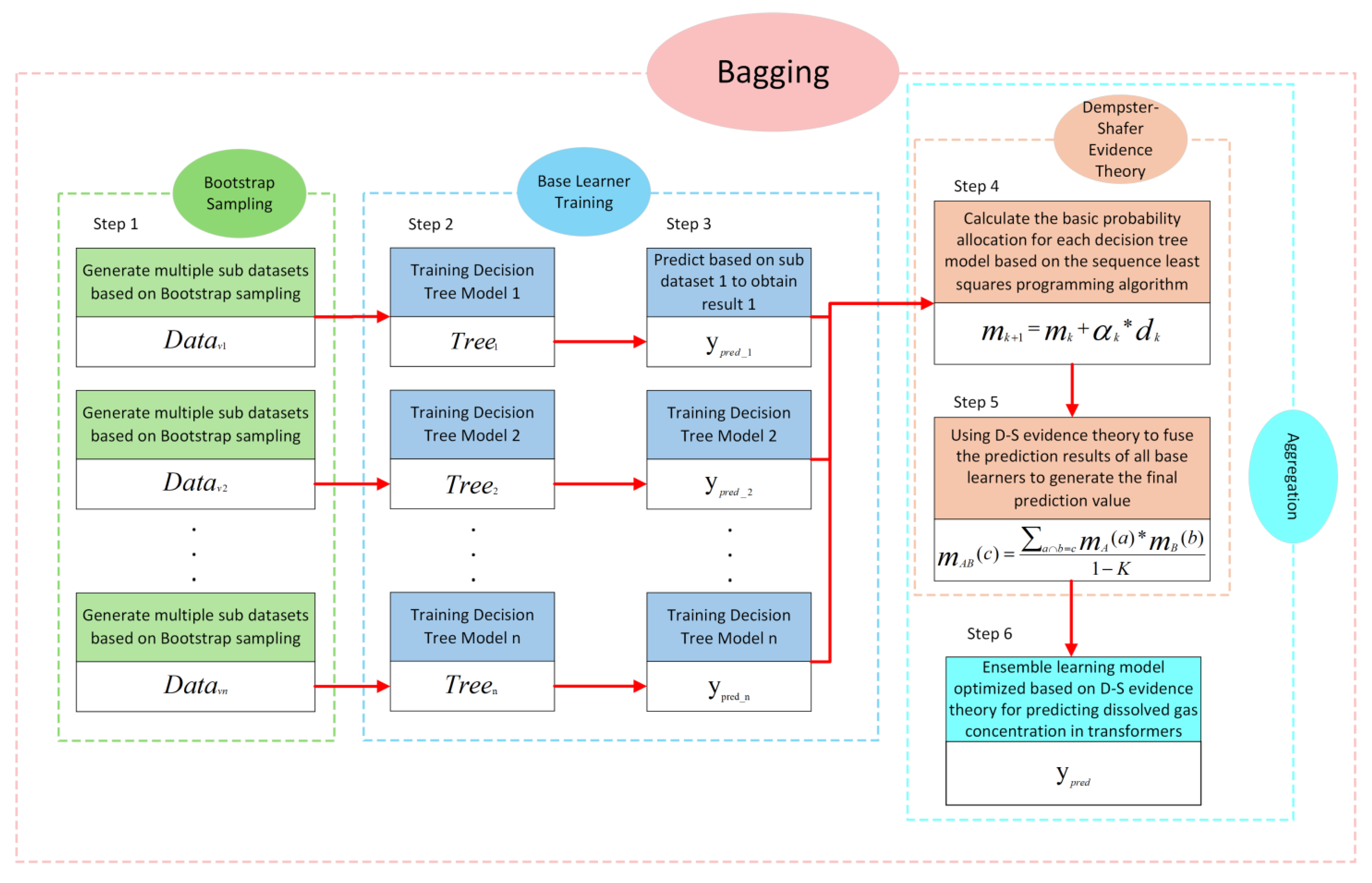
3. Bagging Model Based on D-S Evidence Theory
3.1. D-S Evidence Theory Based on Sequential Least Squares Programming Algorithm Optimization
3.2. Prediction Model of Transformer Dissolved Gas Concentration Based on Bagging
4. Results of Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Youssef, M.M.; Ibrahim, R.A.; Desouki, H.; Moustafa, M.M.Z. An overview on condition monitoring & health assessment techniques for distribution transformers. In Proceedings of the 2022 6th International Conference on Green Energy and Applications (ICGEA), Singapore, 4–6 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 187–192. [Google Scholar]
- Xian, R.; Wang, L.; Zhang, B.; Li, J.; Xian, R.; Li, J. Identification method of interturn short circuit fault for distribution transformer based on power loss variation. IEEE Trans. Ind. Inform. 2023, 20, 2444–2454. [Google Scholar] [CrossRef]
- Shiravand, V.; Faiz, J.; Samimi, M.H.; Djamali, M. Improving the transformer thermal modeling by considering additional thermal points. Int. J. Electr. Power Energy Syst. 2021, 128, 106748. [Google Scholar] [CrossRef]
- Saroja, S.; Haseena, S.; Madavan, R. Dissolved gas analysis of transformer: An approach based on ML and MCDM. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2429–2438. [Google Scholar]
- Ramesh, J.; Shahriar, S.; Al-Ali, A.R.; Osman, A.; Shaaban, M.F. Machine learning approach for smart distribution transformers load monitoring and management system. Energies 2022, 15, 7981. [Google Scholar] [CrossRef]
- Wani, S.A.; Rana, A.S.; Sohail, S.; Rahman, O.; Parveen, S.; Khan, S.A. Advances in DGA based condition monitoring of transformers: A review. Renew. Sustain. Energy Rev. 2021, 149, 111347. [Google Scholar] [CrossRef]
- Odongo, G.; Musabe, R.; Hanyurwimfura, D. A multinomial DGA classifier for incipient fault detection in oil-impregnated power transformers. Algorithms 2021, 14, 128. [Google Scholar] [CrossRef]
- Thango, B.A. Dissolved gas analysis and application of artificial intelligence technique for fault diagnosis in power transformers: A South African case study. Energies 2022, 15, 9030. [Google Scholar] [CrossRef]
- Xing, Z.; He, Y.; Wang, X.; Shao, K.; Duan, J. VMD-IARIMA-Based Time-Series Forecasting Model and its Application in Dissolved Gas Analysis. IEEE Trans. Dielectr. Electr. Insul. 2022, 30, 802–811. [Google Scholar] [CrossRef]
- Patil, M.; Paramane, A.; Das, S.; Rao, U.M.; Rozga, P. Hybrid Algorithm for Dynamic Fault Prediction of HVDC Converter Transformer Using DGA Data. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2128–2135. [Google Scholar]
- Wang, T.L.; Yang, J.G.; Li, J.S.; Li, Y.; Wu, P.; Lin, J.S.; Liang, J.B. Time Series Prediction of Dissolved Gas Concentrations in Transformer Oil using ARIMA-NKDE Method. In Proceedings of the 2022 2nd International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 16–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 129–133. [Google Scholar]
- Mahamdi, Y.; Boubakeur, A.; Mekhaldi, A.; Benmahamed, Y. Power transformer fault prediction using naive Bayes and decision tree based on dissolved gas analysis. ENP Eng. Sci. J. 2022, 2, 1–5. [Google Scholar]
- Ekojono; Prasojo, R.A.; Apriyani, M.E.; Rahmanto, A.N. Investigation on machine learning algorithms to support transformer dissolved gas analysis fault identification. Electr. Eng. 2022, 104, 3037–3047. [Google Scholar]
- Al-Sakini, S.R.; Bilal, G.A.; Sadiq, A.T.; Al-Maliki, W.A.K. Dissolved Gas Analysis for Fault Prediction in Power Transformers Using Machine Learning Techniques. Appl. Sci. 2024, 15, 118. [Google Scholar] [CrossRef]
- Zeng, B.; Guo, J.; Zhang, F.; Zhu, W.; Xiao, Z.; Huang, S.; Fan, P. Prediction model for dissolved gas concentration in transformer oil based on modified grey wolf optimizer and LSSVM with grey relational analysis and empirical mode decomposition. Energies 2020, 13, 422. [Google Scholar] [CrossRef]
- Zhou, X.; Tian, T.; He, N.; Ma, Y.; Liu, W.; Yan, Z.; Luo, Y.; Li, X.; Ni, H. Prediction Method of Dissolved Gas in Transformer Oil Based on Firefly Algorithm-Random Forest. In Proceedings of the 2022 Asia Power and Electrical Technology Conference (APET), Shanghai, China, 11–13 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 51–55. [Google Scholar]
- Wang, N.; Li, W.; Li, J.; Li, X.; Gong, X. Prediction of Dissolved Gas Content in Transformer Oil Using the Improved SVR Model. IEEE Trans. Appl. Supercond. 2024, 34, 9002804. [Google Scholar]
- Elânio Bezerra, F.; Zemuner Garcia, F.A.; Ikuyo Nabeta, S.; Martha de Souza, G.F.; Chabu, I.E.; Santos, J.C.; Junior, S.N.; Pereira, F.H. Wavelet-like transform to optimize the order of an autoregressive neural network model to predict the dissolved gas concentration in power transformer oil from sensor data. Sensors 2020, 20, 2730. [Google Scholar] [CrossRef]
- Wang, L.; Littler, T.; Liu, X. Dynamic incipient fault forecasting for power transformers using an LSTM model. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1353–1361. [Google Scholar]
- Xing, M.; Ding, W.; Li, H.; Zhang, T. A power transformer fault prediction method through temporal convolutional network on dissolved gas chromatography data. Secur. Commun. Netw. 2022, 2022, 5357412. [Google Scholar]
- Das, S.; Paramane, A.; Rao, U.M.; Chatterjee, S.; Kumar, K.S. Corrosive dibenzyl disulfide concentration prediction in transformer oil using deep neural network. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1608–1615. [Google Scholar]
- Shao, J.; Wang, J.; Pan, X.; Wang, R.; Liu, S.; Jin, Z.; Wang, Z. Probabilistic Modeling of Dissolved Gas Concentration for Predicting Operating Status of Oil-Immersed Transformers. IEEE Trans. Ind. Inform. 2024, 21, 1339–1348. [Google Scholar]
- Luo, D.; Fang, J.; He, H.; Lee, W.J.; Zhang, Z.; Zai, H.; Chen, W.; Zhang, K. Prediction for dissolved gas in power transformer oil based on TCN and GCN. IEEE Trans. Ind. Appl. 2022, 58, 7818–7826. [Google Scholar]
- Hu, C.; Zhong, Y.; Lu, Y.; Luo, X.; Wang, S. A prediction model for time series of dissolved gas content in transformer oil based on LSTM. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Xi’an, China, 20–22 August, 2020; Volume 1659, p. 012030. [Google Scholar]
- Zhang, Y.; Liu, D.; Liu, H.; Wang, Y.; Wang, Y.; Zhu, Q. Prediction of dissolved gas in transformer oil based on SSA-LSTM model. In Proceedings of the 2022 9th International Conference on Condition Monitoring and Diagnosis (CMD), Kitakyushu, Japan, 13–18 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 177–182. [Google Scholar]
- Zhang, X.; Wang, S.; Jiang, Y.; Wu, F.; Sun, C. Prediction of dissolved gas in power transformer oil based on LSTM-GA. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 675, p. 012099. [Google Scholar]
- Mahrukh, A.W.; Lian, G.X.; Bin, S.S. Prediction of power transformer oil chromatography based on LSTM and RF model. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Zhang, W.; Zeng, Y.; Li, Y.; Zhang, Z. Prediction of dissolved gas concentration in transformer oil considering data loss scenarios in power system. Energy Rep. 2023, 9, 186–193. [Google Scholar]
- Yang, T.; Fang, Y.; Zhang, C.; Tang, C.; Hu, D. Prediction of dissolved gas content in transformer oil based on multi-information fusion. High Volt. 2024, 9, 685–699. [Google Scholar]
- Oprea, S.V.; Bâra, A. A stacked ensemble forecast for photovoltaic power plants combining deterministic and stochastic methods. Appl. Soft Comput. 2023, 147, 110781. [Google Scholar]
- Zeng, T.; Wu, L.; Peduto, D.; Glade, T.; Hayakawa, Y.S.; Yin, K. Ensemble learning framework for landslide susceptibility mapping: Different basic classifier and ensemble strategy. Geosci. Front. 2023, 14, 101645. [Google Scholar]
- Shahriar, M.S.; Shafiullah, M.; Pathan, M.I.H.; Sha’aban, Y.A.; Bouchekara, H.R.; Ramli, M.A.; Rahman, M.M. Stability improvement of the PSS-connected power system network with ensemble machine learning tool. Energy Rep. 2022, 8, 11122–11138. [Google Scholar]
- Bhusal, N.; Shukla, R.M.; Gautam, M.; Benidris, M.; Sengupta, S. Deep ensemble learning-based approach to real-time power system state estimation. Int. J. Electr. Power Energy Syst. 2021, 129, 106806. [Google Scholar]
- Liu, J.; Zhao, Z.; Zhong, Y.; Zhao, C.; Zhang, G. Prediction of the dissolved gas concentration in power transformer oil based on SARIMA model. Energy Rep. 2022, 8, 1360–1367. [Google Scholar]

| H2 | C2H6 | C2H4 | CH4 | Overall Deviation | |
|---|---|---|---|---|---|
| Actual value | 20.600 | 112.500 | 64.200 | 31.200 | 0 |
| Bagging | 20.333 | 110.362 | 64.433 | 31.905 | 3.343 |
| SARIMA | 19.198 | 111.890 | 64.638 | 31.890 | 3.140 |
| Optimized Bagging based on D-S evidence theory | 20.400 | 112.182 | 64.115 | 32.196 | 1.599 |
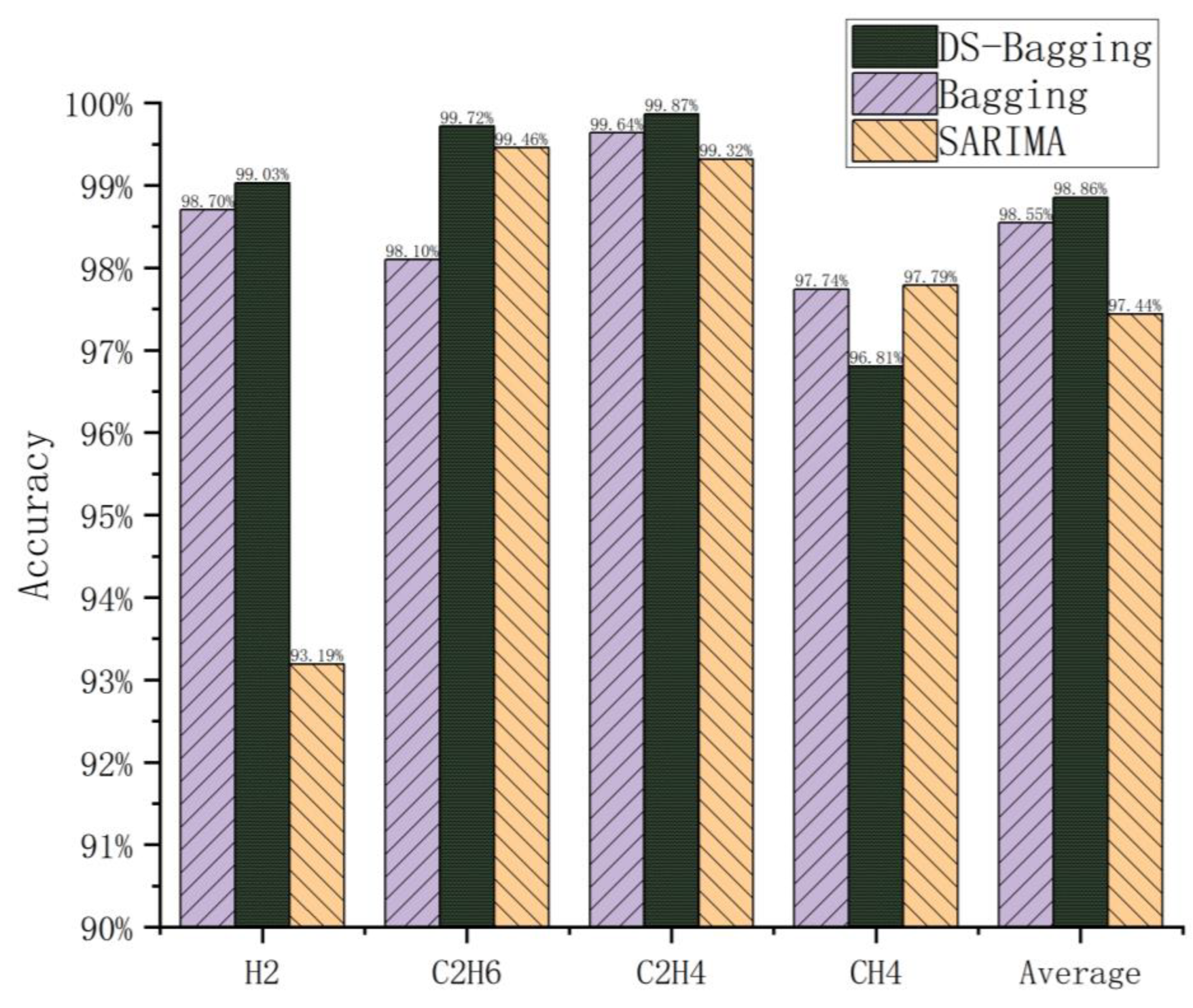
| H2 | C2H6 | C2H4 | CH4 | Overall Accuracy | |
|---|---|---|---|---|---|
| SARIMA | 0.932 | 0.995 | 0.993 | 0.978 | 0.974 |
| Bagging | 0.987 | 0.981 | 0.996 | 0.977 | 0.985 |
| Optimized Bagging based on D-S evidence theory | 0.990 | 0.997 | 0.999 | 0.968 | 0.989 |
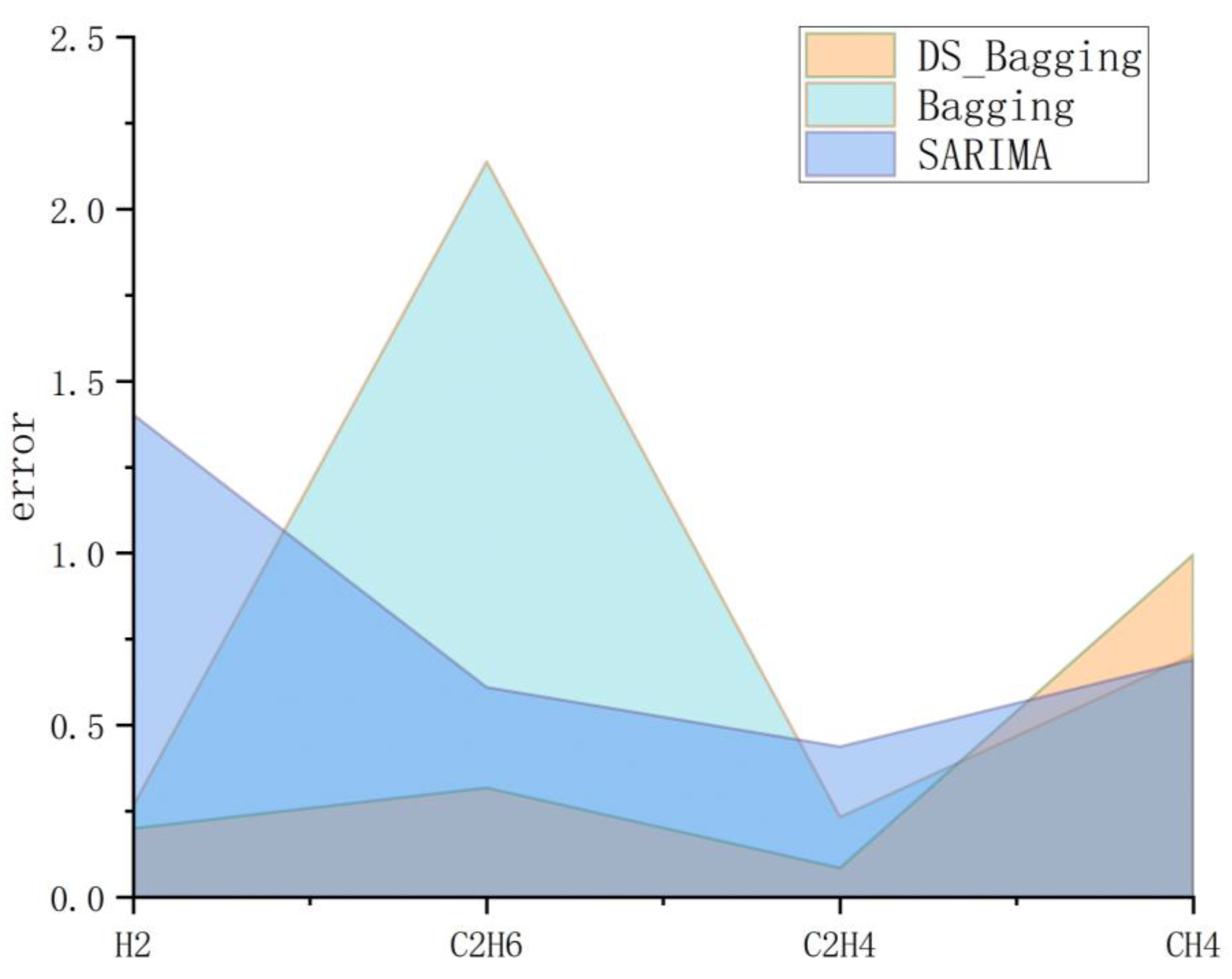
| H2 | C2H6 | C2H4 | CH4 | Overall Mean Square Error | |
|---|---|---|---|---|---|
| Bagging | 0.071 | 4.571 | 0.054 | 0.497 | 5.194 |
| SARIMA | 1.966 | 0.373 | 0.192 | 0.476 | 3.006 |
| Optimized Bagging based on D-S evidence theory | 0.040 | 0.101 | 0.007 | 0.992 | 1.140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Hu, K.; Yang, Y.; Yi, G.; Zhang, X.; Peng, R.; Liu, J. Research on Prediction of Dissolved Gas Concentration in a Transformer Based on Dempster–Shafer Evidence Theory-Optimized Ensemble Learning. Electronics 2025, 14, 1266. https://doi.org/10.3390/electronics14071266
Zhang P, Hu K, Yang Y, Yi G, Zhang X, Peng R, Liu J. Research on Prediction of Dissolved Gas Concentration in a Transformer Based on Dempster–Shafer Evidence Theory-Optimized Ensemble Learning. Electronics. 2025; 14(7):1266. https://doi.org/10.3390/electronics14071266
Chicago/Turabian StyleZhang, Pan, Kang Hu, Yuting Yang, Guowei Yi, Xianya Zhang, Runze Peng, and Jiaqi Liu. 2025. "Research on Prediction of Dissolved Gas Concentration in a Transformer Based on Dempster–Shafer Evidence Theory-Optimized Ensemble Learning" Electronics 14, no. 7: 1266. https://doi.org/10.3390/electronics14071266
APA StyleZhang, P., Hu, K., Yang, Y., Yi, G., Zhang, X., Peng, R., & Liu, J. (2025). Research on Prediction of Dissolved Gas Concentration in a Transformer Based on Dempster–Shafer Evidence Theory-Optimized Ensemble Learning. Electronics, 14(7), 1266. https://doi.org/10.3390/electronics14071266






