Three-Dimensional Hybrid Finite Element–Boundary Element Analysis of Linear Induction Machines
Abstract
1. Introduction
- (1)
- It considers the real shape of the machine and takes into consideration the end effects both in the longitudinal and transverse directions.
- (2)
- The actual stator slots housing the three-phase coils are represented in the models rather than the familiarly used infinitesimally current sheet to simulate the stator current excitation.
- (3)
- Iron parts can be simulated either as constant permeability regions or represented by their actual nonlinear B-H curve.
- (4)
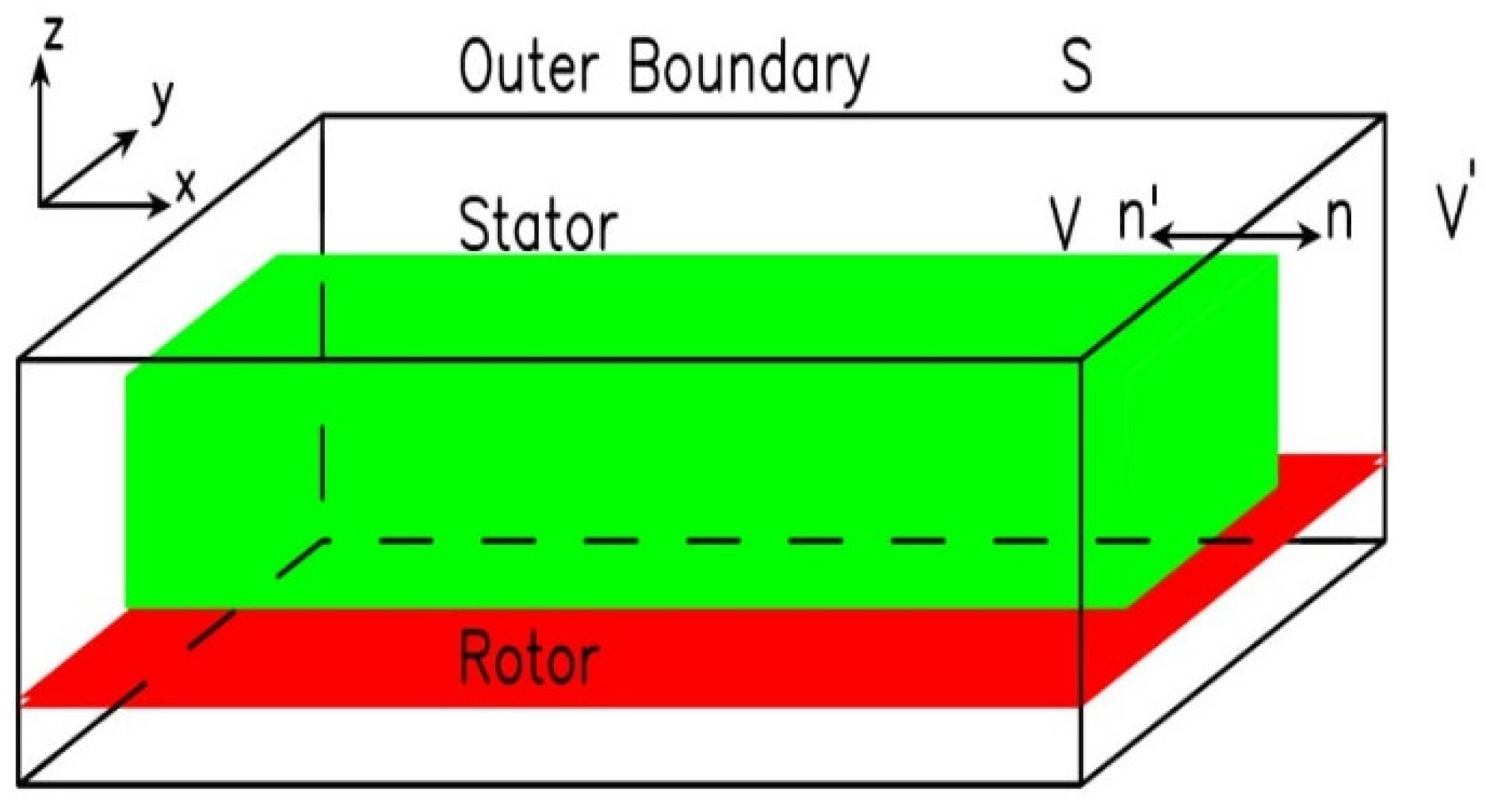
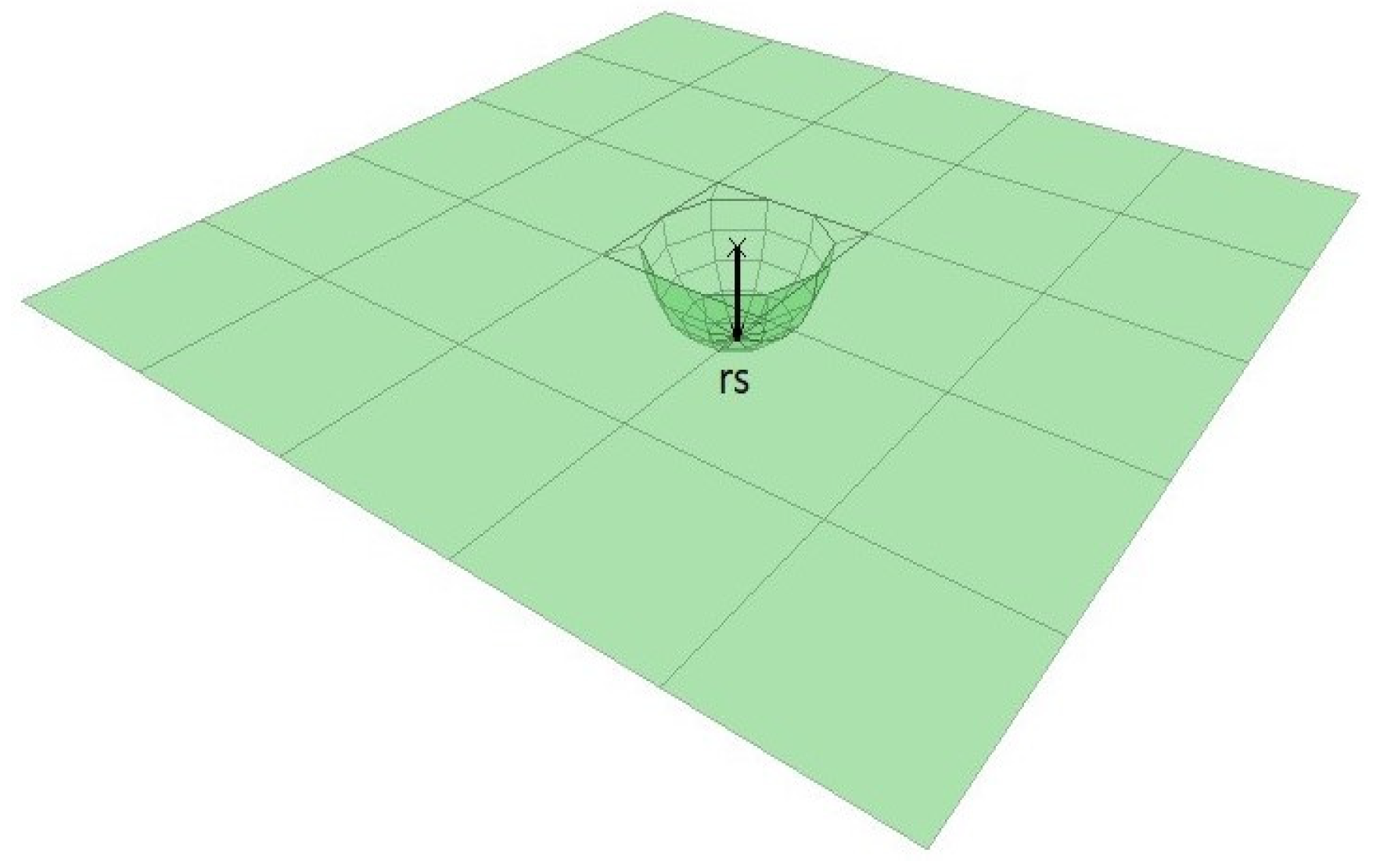
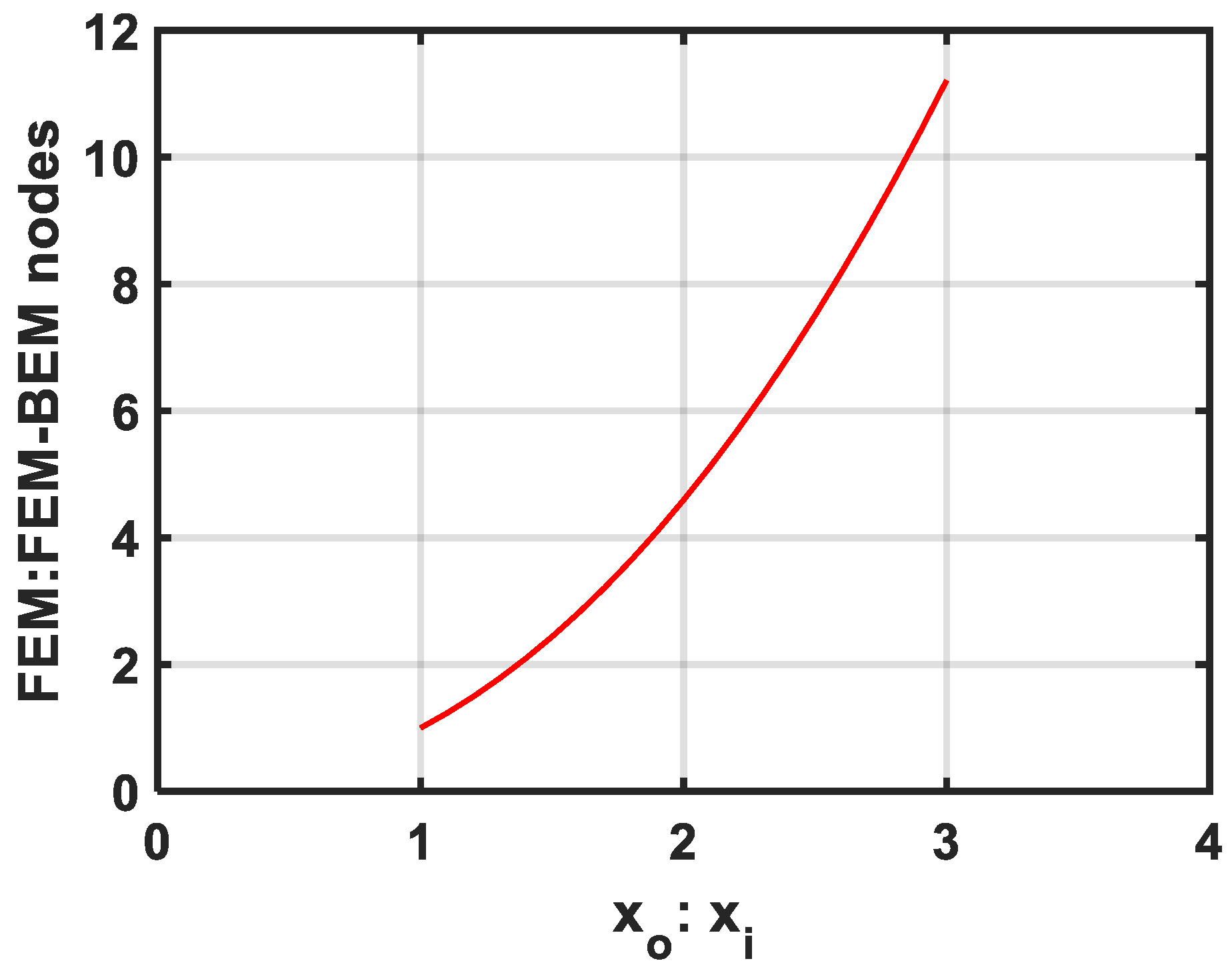
- It is not necessary to have a far boundary as in the conventional FEM. Instead of that, an arbitrary boundary is chosen at any distance close to the machine ends, which leads to minimization of the dimensions of the problem domain and the associated computer storage and computation time, while in the FEM, the same accuracy can be obtained by choosing a farther outer boundary from the machine ends.
- i.
- The effect of changing the frequency or slip.
- ii.
- The effect of changing the coils’ distribution and the magnetic poles’ configuration.
- iii.
- Evaluation of the effect of using back iron in comparison with the case of using sheet rotor only.
2. Mathematical Model
3. FEM Formulation
4. BEM Formulation
5. Coupling of the BEM with the FEM
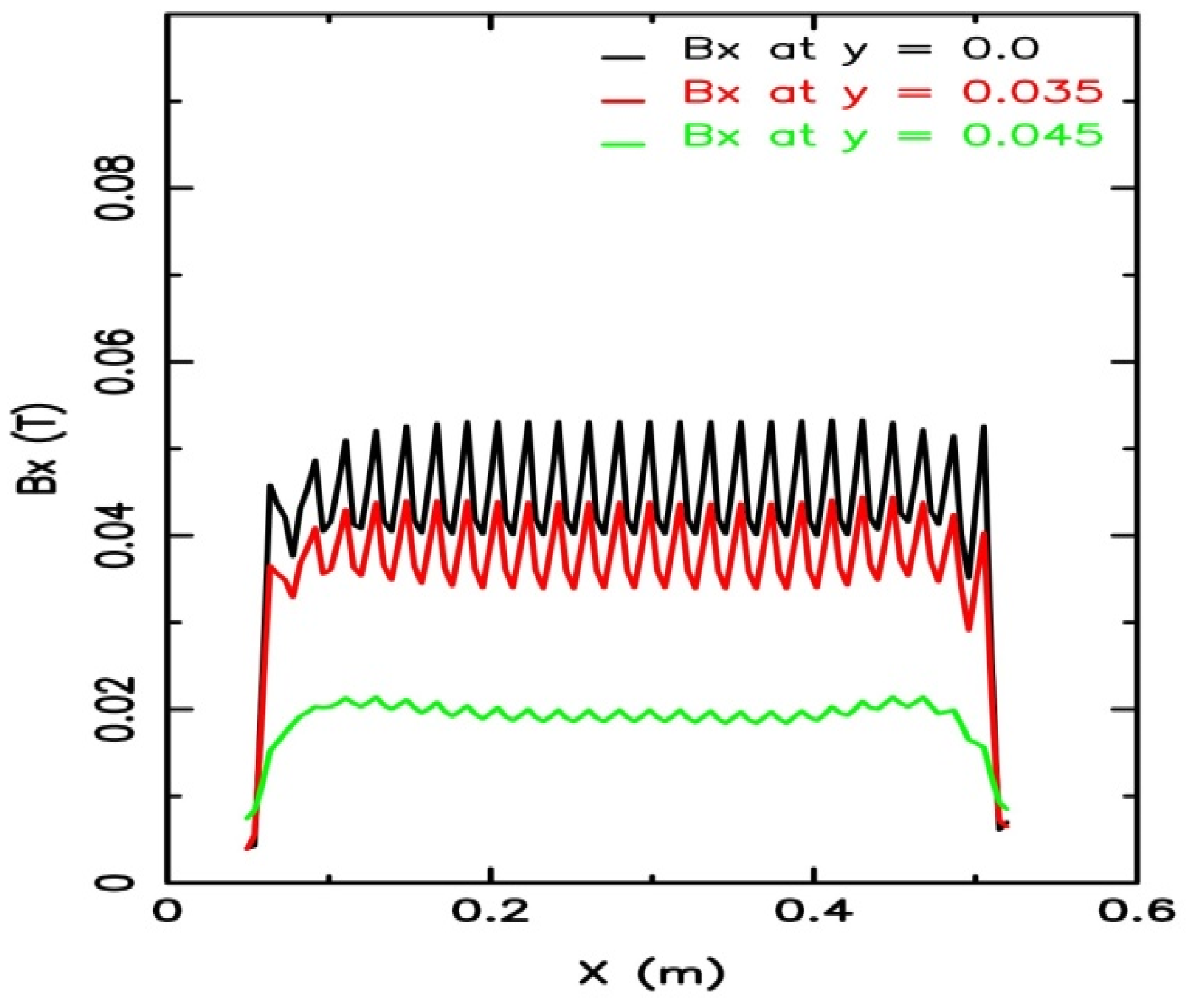
6. Results
6.1. Model-A Results
6.2. Model-B Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yamaguchi, T.; Kawase, Y.; Yoshida, M.; Saito, Y.; Ohdachi, Y. 3-D Finite element analysis of a linear induction motor. IEEE Trans. Magn. 2001, 37, 3668–3671. [Google Scholar] [CrossRef]
- Ravanji, M.; Gheidari, Z. Design optimization of a ladder secondary single-sided linear induction motor for improved performance. IEEE Trans. Energy Convers. 2015, 30, 1595–1603. [Google Scholar] [CrossRef]
- Qaseer, L.; Marzouk, R. Hybrid finite element-boundary element analysis of a single-sided sheet rotor linear induction motor. IEEE Trans. Energy Convers. 2014, 29, 188–195. [Google Scholar] [CrossRef]
- Di, J.; Fletcher, J.E.; Fan, Y.; Liu, Y.; Sun, Z. Design and performance investigation of the double-sided linear induction motor with a ladder slot secondary. IEEE Trans. Energy Convers. 2019, 34, 1603–1612. [Google Scholar] [CrossRef]
- Lv, G.; Zhou, T.; Zeng, D.; Liu, Z. Influence of secondary constructions on transverse forces of linear induction motors in curve rails for urban rail transit. IEEE Trans. Ind. Electron. 2019, 66, 4231–4239. [Google Scholar] [CrossRef]
- Xu, W.; Sun, G.; Wen, G.; Wu, Z.; Chu, P.K. Equivalent circuit derivation and performance analysis of a single sided linear induction motor based on the winding function theory. IEEE Trans. Veh. Tech. 2012, 61, 1515–1525. [Google Scholar] [CrossRef]
- Li, D.; Li, W.; Zhang, X.; Fang, J.; Qiu, H.; Shen, J.; Wang, L. A New approach to evaluate influence of transverse edge effect of a single-sided HTS linear induction motor used for linear metro. IEEE Trans. Magn. 2015, 51, 8200404. [Google Scholar]
- Zeng, D.; Lv, G.; Zhou, T. Equivalent circuits for single-sided linear induction motors with asymmetric cap secondary for linear transit. IEEE Trans. Energy Convers. 2018, 33, 1729–1738. [Google Scholar] [CrossRef]
- Lv, G.; Zeng, D.; Zhou, T.; Degano, M. A complete equivalent circuit for linear induction motors with laterally asymmetric secondary for urban railway transit. IEEE Trans. Energy Convers. 2020, 36, 1014–1022. [Google Scholar] [CrossRef]
- Zeng, D.; Lv, G.; Zhou, T. Analysis of secondary losses and efficiency in linear induction motors with composite secondary based on space harmonic method. IEEE Trans. Energy Convers. 2017, 32, 1583–1591. [Google Scholar]
- Lv, G.; Zeng, D.; Zhou, T. Influence of ladder-slit secondary on reducing the edge effect and transverse forces in the linear induction motor. IEEE Trans. Ind. Electron. 2018, 65, 7516–7525. [Google Scholar] [CrossRef]
- Xu, W.; Elmorshedy, M.F.; Liu, Y.; Islam, R.; Allam, S.M. Finite-set model predictive control based thrust maximization of linear induction motors used in linear metros. IEEE Trans. Veh. Tech. 2012, 68, 5443–5458. [Google Scholar] [CrossRef]
- Tiunov, V. Linear induction motors tractive force components analysis with regard to the motors’ electromagnetic no-symmetry. In Proceedings of the 2019 International Multi-Conference on Industrial Engineering and Modern Technologies, Vladivostok, Russia, 1–4 October 2019; p. 19229138. [Google Scholar]
- Lu, Q.; Li, L.; Zhan, J.; Huang, X.; Cai, J. Design optimization and performance investigation of novel linear induction motors with two kinds of secondaries. IEEE Trans. Ind. Appl. 2019, 55, 5830–5842. [Google Scholar] [CrossRef]
- Xu, W.; Xiao, X.; Du, G.; Hu, D.; Zou, J. Comprehensive efficiency optimization of linear induction motors for urban transit. IEEE Trans. Veh. Technol. 2020, 69, 131–139. [Google Scholar] [CrossRef]
- Williamson, S.; Chan, E. Three-dimensional finite-element for problems involving time-varying fields, relative motion, and magnetic saturation. Proc. IEE A 1993, 140, 121–130. [Google Scholar]
- Nath, S. Finite Element and Boundary Element Analysis of Electromagnetic NDE Phenomena. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1992. [Google Scholar]
- Becker, A.A. The Boundary Element Method in Engineering A Complete Course; Mc-Graw-Hill: New York, NY, USA, 1992; Section 3.1. [Google Scholar]
- Beer, G.; Smith, I.; Duenser, C. The Boundary Element Method with Programming for Engineers and Scientists; Springer: New York, NY, USA, 2008. [Google Scholar]
- Fetzer, J.; Kurz, S.; Lehner, G. The Coupling of boundary elements and finite elements for nondestructive testing applications. IEEE Trans. Magn. 1997, 33, 677–681. [Google Scholar] [CrossRef]
- Chandrupatla, T.; Chandrupatla, T.R.; Belegundu, A. Introduction to Finite Elements in Engineering, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; Section 7.3. [Google Scholar]
- Al-Maayouf, M.A. A Study of a Linear Induction Motor Using Alternative Models. Ph.D. Dissertation, Department of Electrical Engineering, The City University, London, UK, 1981. [Google Scholar]
- Say, M.G. The Performance and Design of Alternating Current Machines, 3rd ed.; Isaac Pitman & Sons: London, UK, 1965; p. 201. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill Book Co.: New York, NY, USA,, 1941; Section 1.9. [Google Scholar]

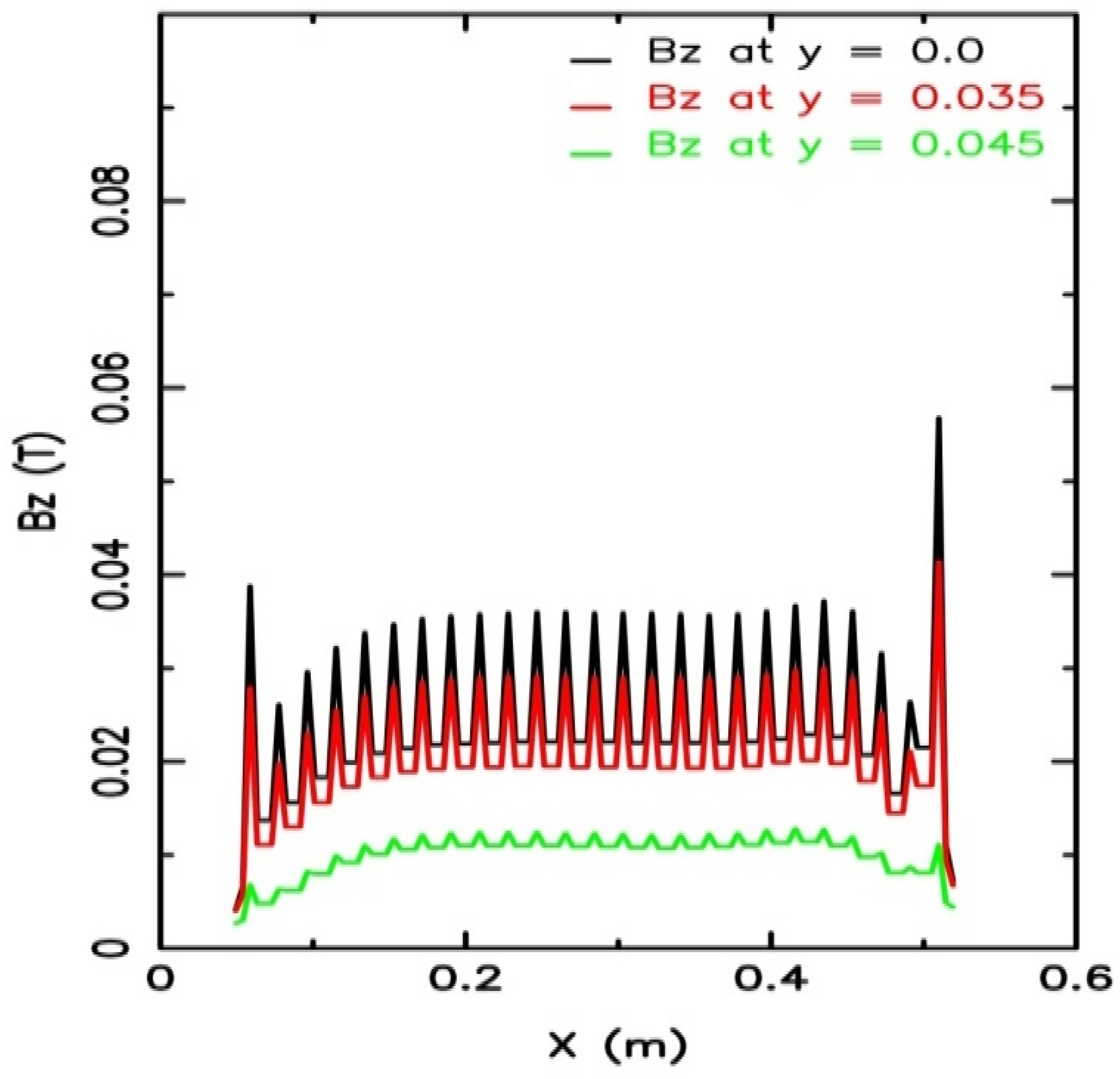
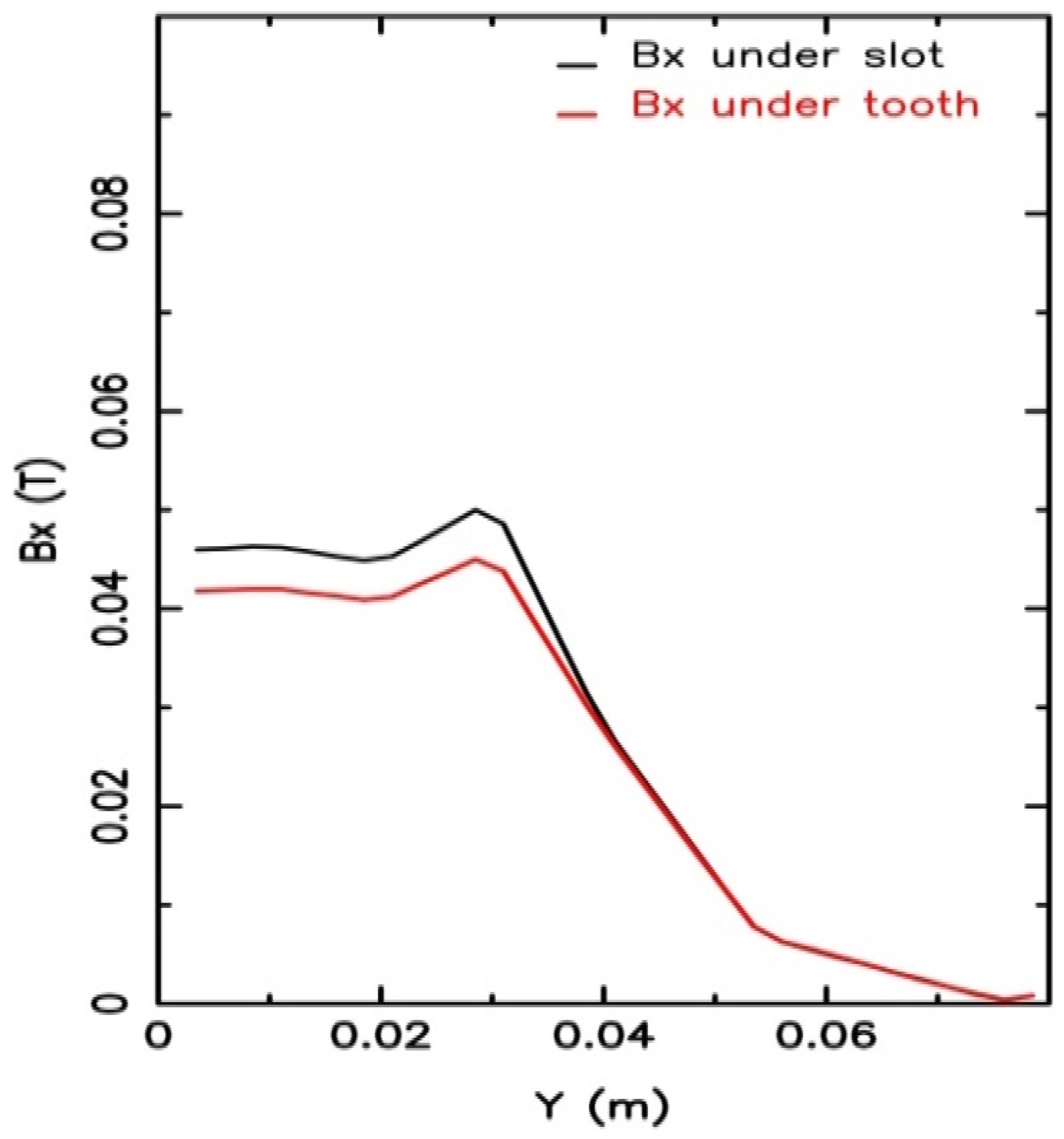
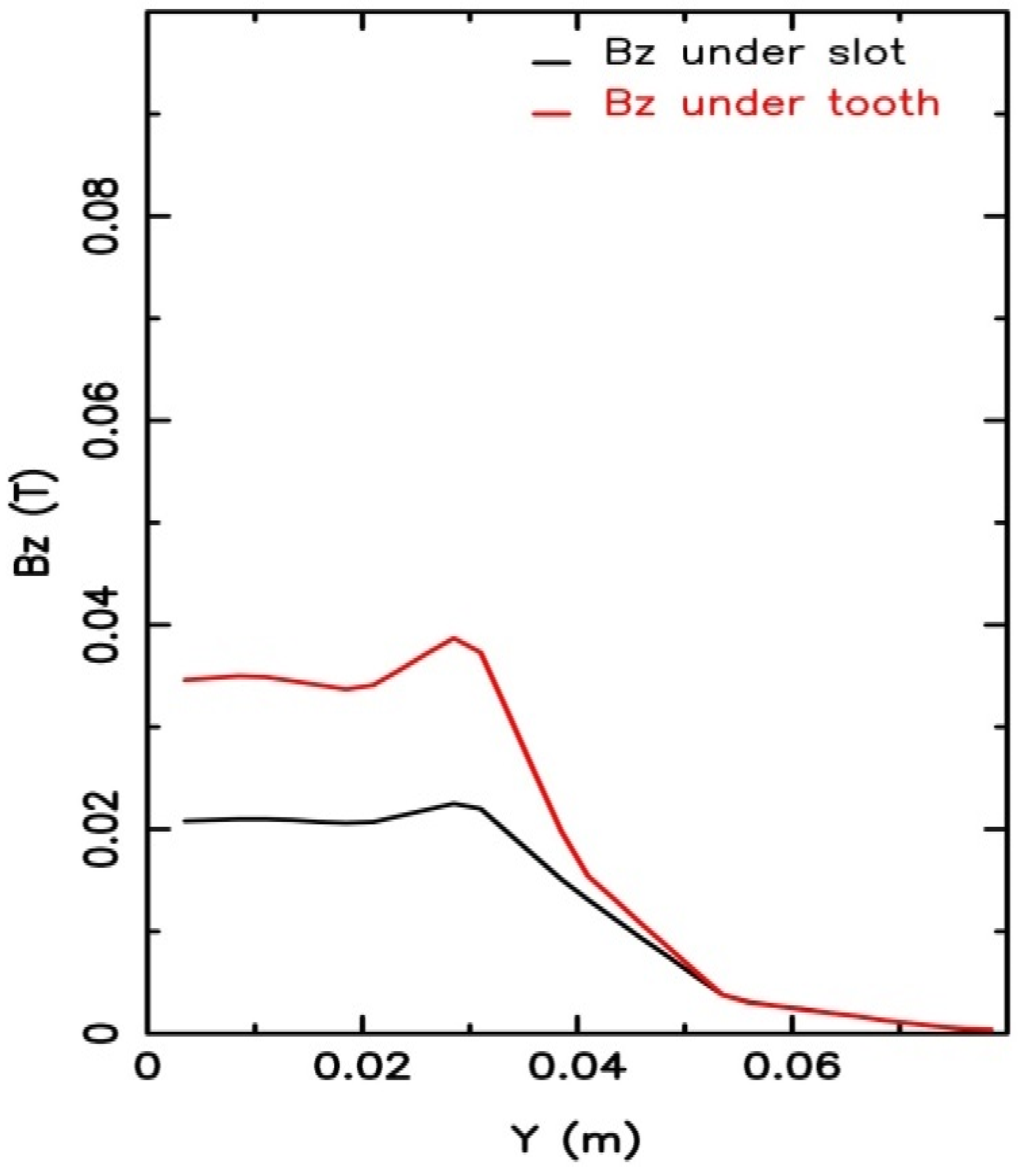






| Quantity | Model A | Model B |
|---|---|---|
| Number of poles | 4 | 6 |
| Number of phases | 3 | 3 |
| Frequency (Hz) | 50 | 50 |
| Stator length (mm) | 448 | 798 |
| Stator height (mm) | 76 | 99 |
| Stator width (mm) | 80 | 100 |
| Pole pitch (mm) | 112 | 117 |
| Slot pitch (mm) | 18.667 | 19.5 |
| Slot width (mm) | 13 | 11.7 |
| Slot depth (mm) | 38 | 30 |
| Air gap length (mm) | 9.5 | 10 |
| Number of turns per slot | 100 | 36 |
| Slot per pole per phase | 2 | 2 |
| Phase current r.m.s (A) | 5 | 11 |
| Type of rotor | Aluminum | Aluminum |
| Thickness of rotor (mm) | 3.175 | 5 |
| Rotor width (mm) | 240 | 160 |
| Conductivity of rotor (S/m) | 3.54 × 107 | 3.54 × 107 |
| Back iron width (mm) | --- | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzouk, R.; Qaseer, L. Three-Dimensional Hybrid Finite Element–Boundary Element Analysis of Linear Induction Machines. Electronics 2025, 14, 1261. https://doi.org/10.3390/electronics14071261
Marzouk R, Qaseer L. Three-Dimensional Hybrid Finite Element–Boundary Element Analysis of Linear Induction Machines. Electronics. 2025; 14(7):1261. https://doi.org/10.3390/electronics14071261
Chicago/Turabian StyleMarzouk, Razzak, and Layth Qaseer. 2025. "Three-Dimensional Hybrid Finite Element–Boundary Element Analysis of Linear Induction Machines" Electronics 14, no. 7: 1261. https://doi.org/10.3390/electronics14071261
APA StyleMarzouk, R., & Qaseer, L. (2025). Three-Dimensional Hybrid Finite Element–Boundary Element Analysis of Linear Induction Machines. Electronics, 14(7), 1261. https://doi.org/10.3390/electronics14071261





