An Optimized Hybrid Approach to Denoising of EEG Signals Using CNN and LMS Filtering
Abstract
1. Introduction
- A combination of CNN with LMS filtering to denoise EEG signals is introduced in this study.
- Several optimizations such as the Strassen–Winograd algorithm, is used to simplify matrix multiplication in CNN.
- The LMS filter is refined using two’s complement distributed arithmetic (DA)algorithm, Offset Binary Coding (OBC)-based DA and CORDIC.
- The improvement strategies mentioned above enable a more area- and power-efficient system for FPGA implementation.
2. Materials and Methods
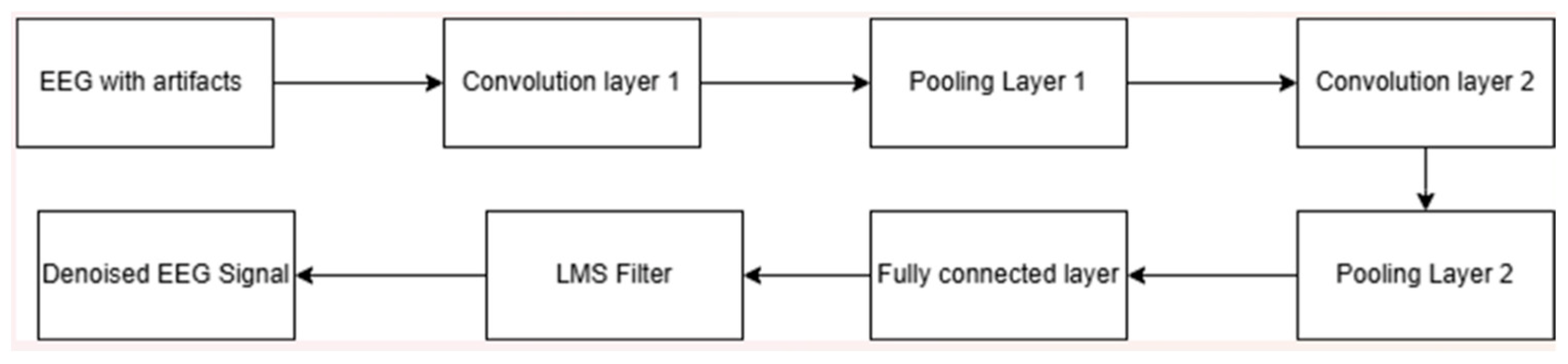
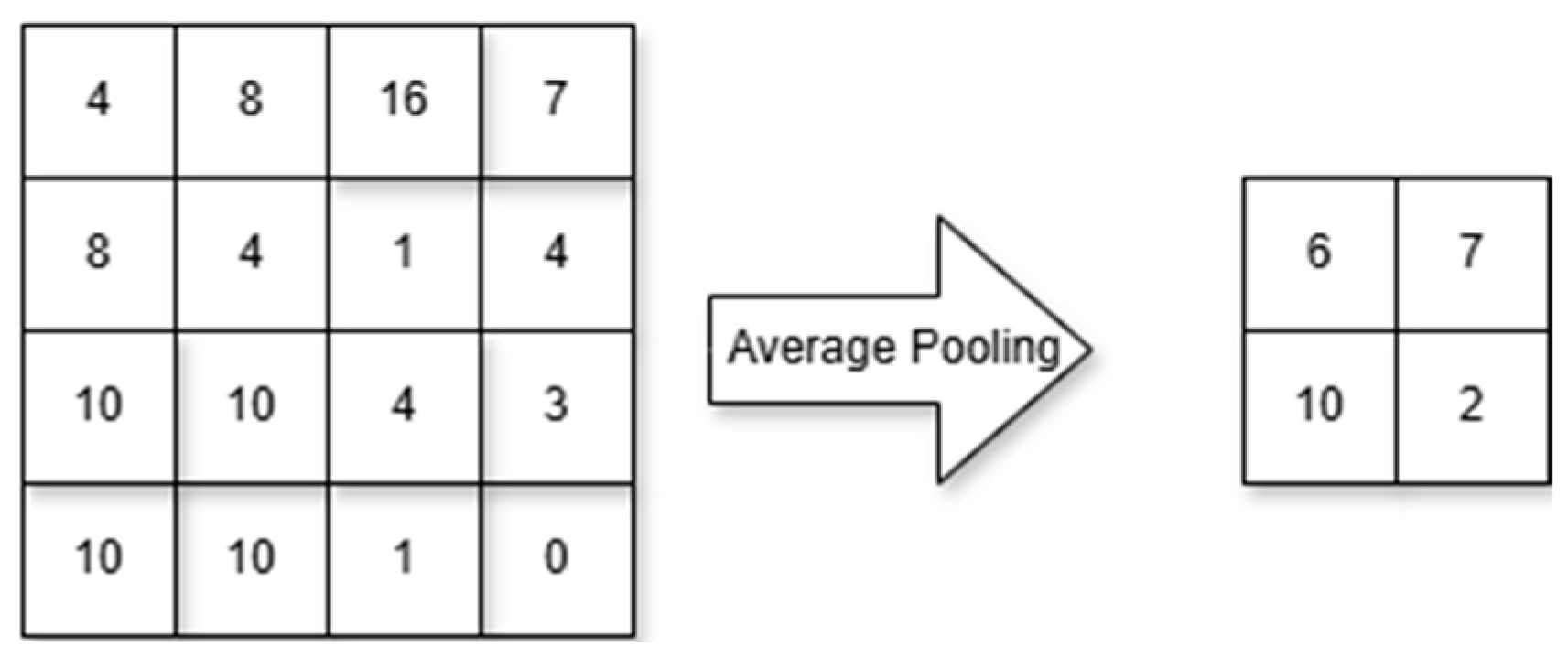
2.1. Hardware Optimized CNN
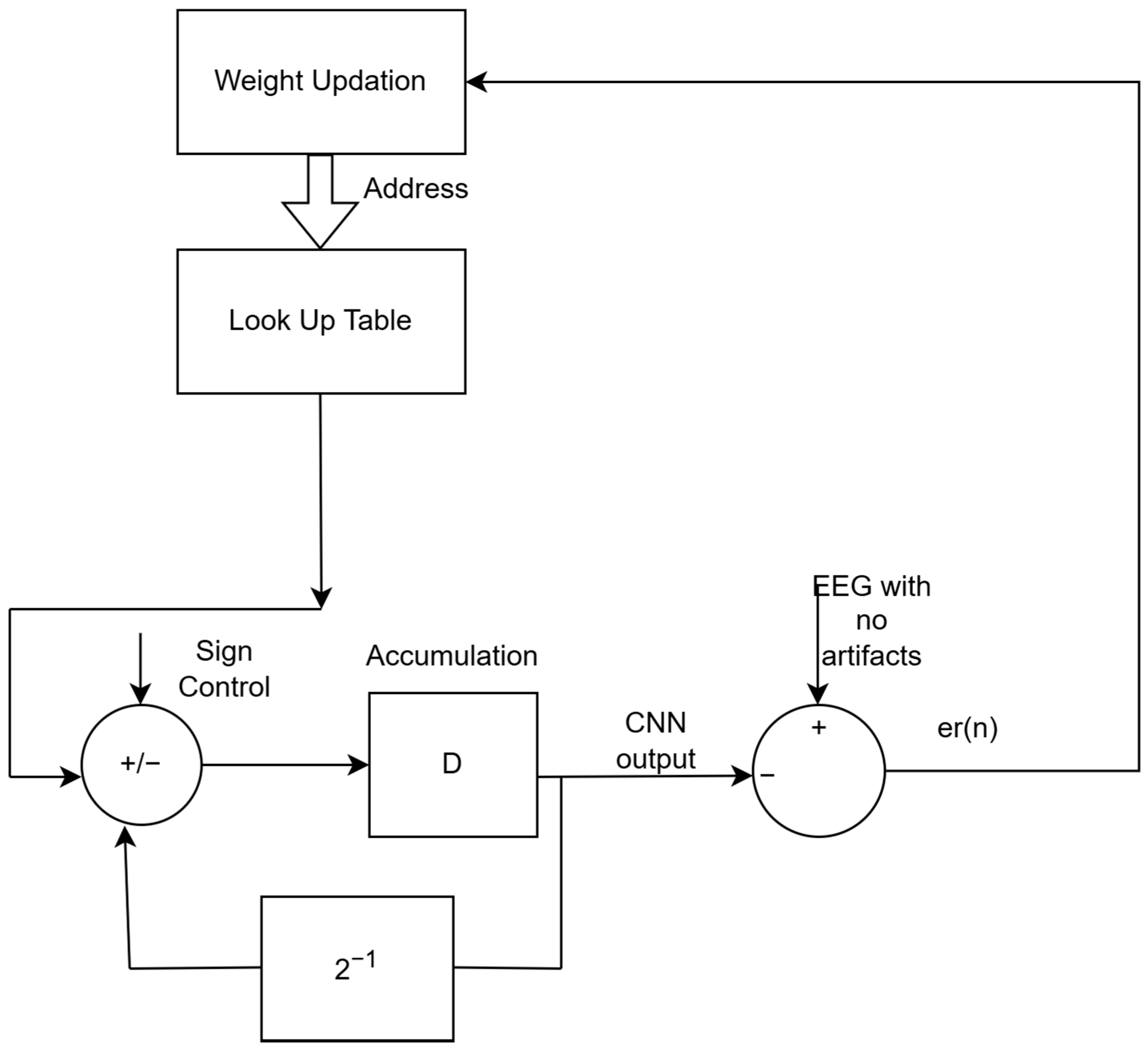
2.2. LMS Filtering
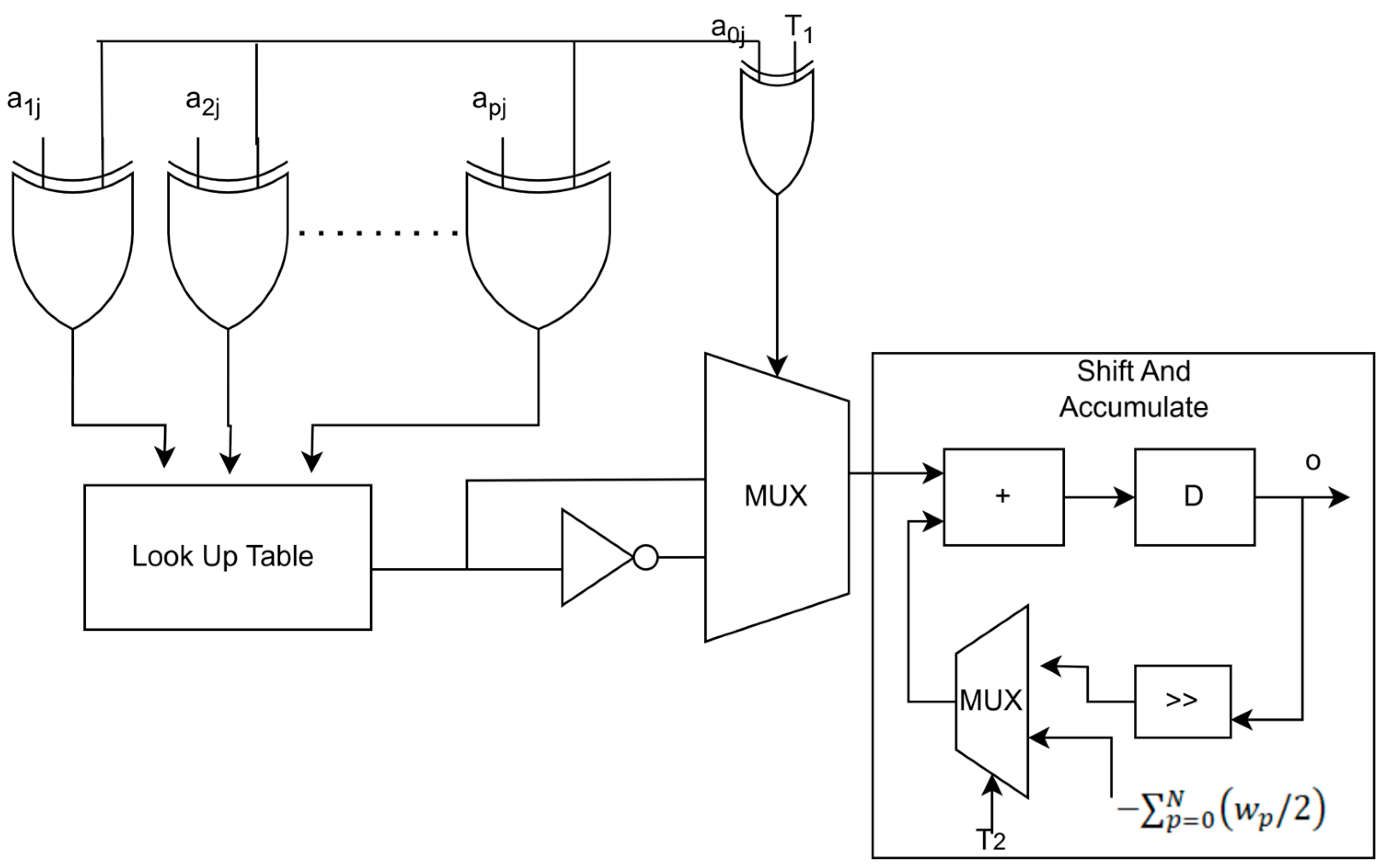
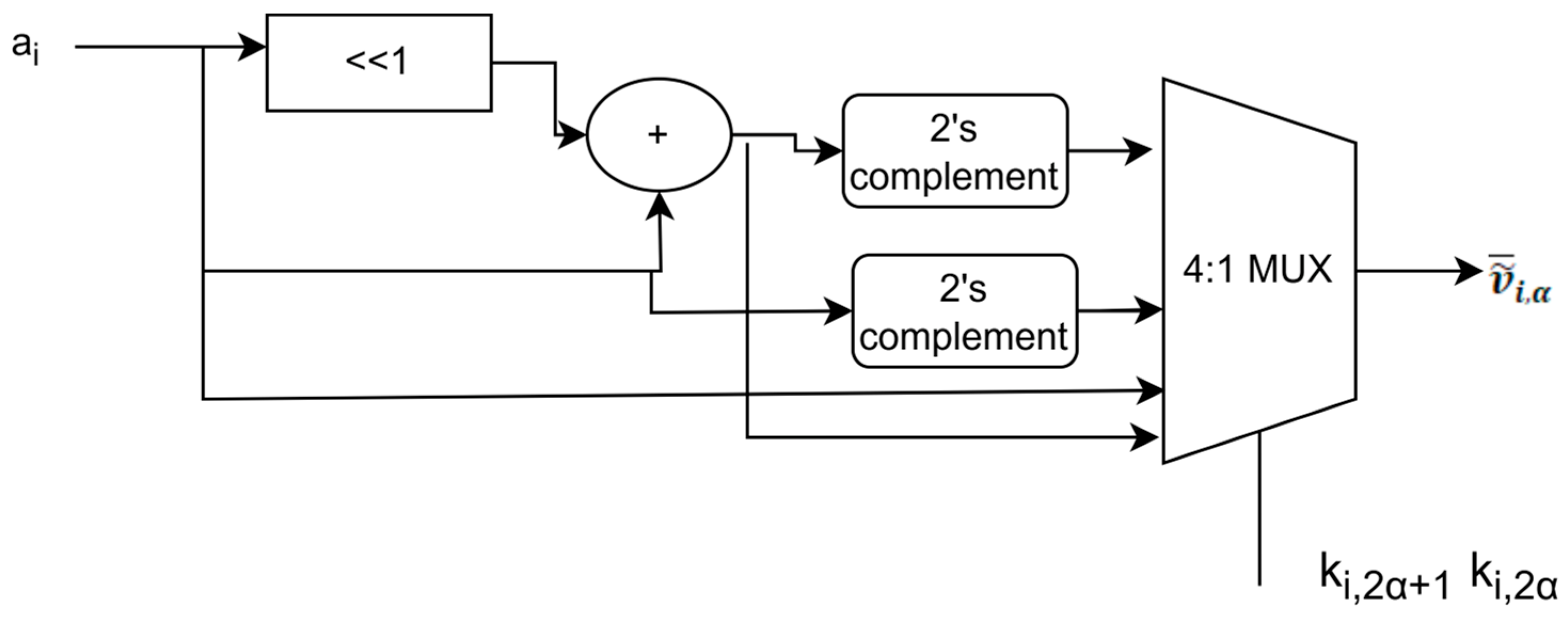
2.2.1. Two Complement Distributed Arithmetic
2.2.2. Offset Binary Coding-Based Distributed Arithmetic
2.2.3. Offset Binary Coding Radix 4-Based Distributed Arithmetic
2.2.4. Coordinate Rotational Digital Computer (CORDIC)-Based TLMS Filter
2.2.5. Comparison Between Various LMS Filters
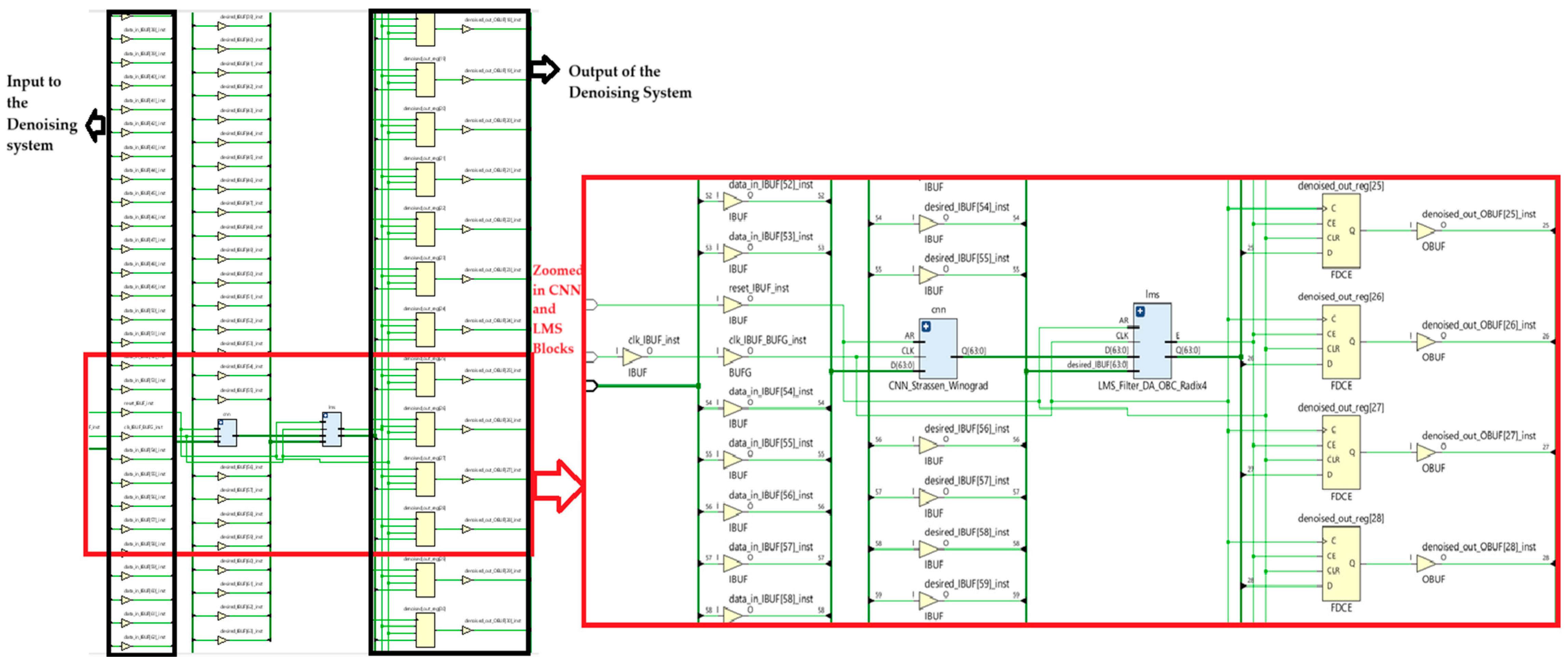
3. Results
Synthesis Results of the Overall Design
4. Discussion
4.1. Signal Analysis
4.2. Power Comparison
4.3. Area Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paris, A.; Atia, G.K.; Vosoughi, A.; Berman, S.A. A new statistical model of electroencephalogram noise spectra for real-time brain–computer interfaces. IEEE Trans. Biomed. Eng. 2016, 64, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Astolfi, L.; Valdés-Sosa, P.A.; Marinazzo, D.; Palva, S.O.; Bénar, C.G.; Michel, C.M.; Koenig, T. Electrophysiological brain connectivity: Theory and implementation. IEEE Trans. Biomed. Eng. 2019, 66, 2115–2137. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.B.; Kim, H.; Kim, Y.T.; Zeiler, F.A.; Smielewski, P.; Czosnyka, M.; Kim, D.J. Artifact removal from neurophysiological signals: Impact on intracranial and arterial pressure monitoring in traumatic brain injury. J. Neurosurg. 2019, 132, 1952–1960. [Google Scholar] [CrossRef]
- Lee, S.; McKeown, M.J.; Wang, Z.J.; Chen, X. Removal of high-voltage brain stimulation artifacts from simultaneous EEG recordings. IEEE Trans. Biomed. Eng. 2018, 66, 50–60. [Google Scholar] [CrossRef] [PubMed]
- Ranjan, R.; Sahana, B.C.; Bhandari, A.K. Cardiac artifact noise removal from sleep EEG signals using hybrid denoising model. IEEE Trans. Instrum. Meas. 2022, 71, 4007810. [Google Scholar] [CrossRef]
- Gandhi, T.K.; Chakraborty, P.; Roy, G.G.; Panigrahi, B.K. Discrete harmony search based expert model for epileptic seizure detection in electroencephalography. Expert Syst. Appl. 2012, 39, 4055–4062. [Google Scholar] [CrossRef]
- Shoeb, A.H. Application of Machine Learning to Epileptic Seizure Onset Detection and Treatment. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Jiang, X.; Bian, G.B.; Tian, Z. Removal of artifacts from EEG signals: A review. Sensors 2019, 19, 987. [Google Scholar] [CrossRef]
- Waser, M.; Garn, H.; Jennum, P.J.; Sorensen, H.B. A blind source-based method for automated artifact-correction in standard sleep EEG. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; IEEE: Toulouse, France; pp. 6010–6013. [Google Scholar]
- Yadav, S.; Saha, S.K.; Kar, R.; Mandal, D. Optimized adaptive noise canceller for denoising cardiovascular signal using SOS algorithm. Biomed. Signal Process. Control. 2021, 69, 102830. [Google Scholar] [CrossRef]
- Albin, P.; Cardoso, J.F.; Gramfort, A. Spectral independent component analysis with noise modeling for M/EEG source separation. J. Neurosci. Methods 2021, 356, 109144. [Google Scholar]
- Polat, C.; Özerdem, M.S. Introduction to Wavelets and their applications in signal denoising. Bitlis Eren Univ. J. Sci. Technol. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Jur czak, M.; Kołodziej, M.; Majkowski, A. Implementation of a convolutional neural network for eye blink artifacts removal from the electroencephalography signal. Front. Neurosci. 2022, 16, 782367. [Google Scholar]
- James, B.P.; Leung, M.F.; Vaithiyanathan, D.; Mariammal, K. Optimal Realization of Distributed Arithmetic-Based MAC Adaptive FIR Filter Architecture Incorporating Radix-4 and Radix-8 Computation. Electronics 2024, 13, 3551. [Google Scholar] [CrossRef]
- Arivalagan, S.; James, B.P.; Leung, M.F. Reconfigurable Frequency Response Masking Multi-MAC Filters for Software Defined Radio Channelization. Electronics 2024, 13, 4211. [Google Scholar] [CrossRef]
- Yergaliyev, S.; Akhtar, M.T. A Systematic Review on Distributed Arithmetic-Based Hardware Implementation of Adaptive Digital Filters. IEEE Access 2023, 11, 85165–85183. [Google Scholar] [CrossRef]
- Guo, R.; DeBrunner, L.S. Two high-performance adaptive filter implementation schemes using distributed arithmetic. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 600–604. [Google Scholar] [CrossRef]
- Khan, M.T.; Shaik, R.A. Optimal complexity architectures for pipelined distributed arithmetic-based LMS adaptive filter. IEEE Trans. Circuits Syst. I Regul. Papers 2018, 66, 630–642. [Google Scholar] [CrossRef]
- Akhter, N.; Fatema, K.; Ferdouse, L.; Khandaker, F. Implementation of the Trigonometric LMS Algorithm using Original Cordic Rotation. arXiv 2010, arXiv:1008.3328. [Google Scholar] [CrossRef]
- Kemp, B.; Zwinderman, A.H.; Tuk, B.; Kamphuisen, H.A.; Oberye, J.J. Analysis of a sleep-dependent neuronal feedback loop: The slow-wave microcontinuity of the EEG. IEEE Trans. Biomed. Eng. 2000, 47, 1185–1194. [Google Scholar] [CrossRef]
- Gold berger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.C.; Mark, R.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar]
- Habib, G.; Qureshi, S. Optimization and acceleration of convolutional neural networks: A survey. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 4244–4268. [Google Scholar] [CrossRef]
- Murthy, C.S.; Sridevi, K. Design and implementation of hybrid techniques and DA-based reconfigurable FIR filter design for noise removal in EEG signals on FPGA. WSEAS Trans. Syst. Cont. 2022, 17, 324. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Wu, Z.; Su, Y.; Yan, F. Design and FPGA implementation of an adaptive narrowband interference suppression filter. IEEE Trans. Instrum. Meas. 2024, 73, 8002215. [Google Scholar] [CrossRef]
- Wu, B.; Wu, X.; Li, P.; Gao, Y.; Si, J.; Al-Dhahir, N. Efficient FPGA Implementation of Convolutional Neural Networks and Long Short-Term Memory for Radar Emitter Signal Recognition. Sensors 2024, 24, 889. [Google Scholar] [CrossRef] [PubMed]







| Address | LUT Data [TC] |
|---|---|
| 0000 | 0 |
| 0001 | w0 |
| 0010 | w1 |
| 0011 | w0 + w1 |
| 0100 | w2 |
| 0101 | w0 + w2 |
| 0110 | w1 + w2 |
| 0111 | w0 + w1+ w2 |
| 1000 | w3 |
| 1001 | w3 + w0 |
| 1010 | w3 + w1 |
| 1011 | w3 + w1 + w0 |
| 1100 | w3 + w2 |
| 1101 | w3 + w2 + w0 |
| 1110 | w3 + w2 + w1 |
| 1111 | w3 + w1 + w2 + w0 |
| Address {a0j,a1j,a2j,a3j} | DA_LUT |
|---|---|
| 0000 | −1/2 × (w0 + w1 + w2 + w3) |
| 0001 | −1/2 × (w0 + w1 + w2 − w3) |
| 0010 | −1/2 × (w0 + w1 − w2 + w3) |
| 0011 | −1/2 × (w0 + w1 − w2 − w3) |
| 0100 | −1/2 × (w0 − w1 + w2 + w3) |
| 0101 | −1/2 × (w0 − w1 + w2 − w3) |
| 0110 | −1/2 × (w0 − w1 − w2 + w3) |
| 0111 | −1/2 × (w0 − w1 − w2 − w3) |
| 1000 | 1/2 × (w0 − w1 − w2 − w3) |
| 1001 | 1/2 × (w0 − w1 − w2 + w3) |
| 1010 | 1/2 × (w0 − w1 + w2 − w3) |
| 1011 | 1/2 × (w0 − w1 + w2 + w3) |
| 1100 | 1/2 × (w0 + w1 − w2 − w3) |
| 1101 | 1/2 × (w0 + w1 − w2 + w3) |
| 1110 | 1/2 × (w0 + w1 + w2 − w3) |
| 1111 | 1/2 × (w0 + w1 + w2 + w3) |
| Method | Computational Complexity | LUT Usage | Operations Required |
|---|---|---|---|
| Conventional Multiplication | O(n2) | No LUTs used | n × n bit multiplications |
| Shift-and-Add Multiplication | O(n) | No LUTs used | Sequential shift and add operations |
| Two’s Complement DA (TCDA) | O(n) | 2n | Precomputed LUT-based operations |
| OBC DA | O(n) | 2n−1 | LUT-based DA with OBC encoding |
| OBC Radix-4 DA | O(log n) | 2n/2 | Reduced LUT size, fewer iterations |
| CORDIC | O(log n) | No LUTs used | Iterative rotation & scaling, no multiplications |
| Methods | RMSE (µV) | SNR (dB) | CC |
|---|---|---|---|
| CNN Only | 3.3 ± 0.8 | 19 ± 1.5 | 0.90 ± 0.02 |
| LMS Filtering | 3.9 ± 0.5 | 18 ± 0.5 | 0.88 ± 0.02 |
| CNN + LMS Filtering(2’s complement DA) | 3.0 ± 0.5 | 21.5 ± 1.3 | 0.93 ± 0.02 |
| CNN + LMS Filtering(OBC DA) | 2.7 ± 0.4 | 24.5 ± 1.2 | 0.95 ± 0.02 |
| CNN + LMS Filtering(OBC Radix 4 DA) | 3.0 ± 0.5 | 22.5 ± 1.2 | 0.93 ± 0.02 |
| CNN + LMS Filtering(CORDIC) | 3.3 ± 0.9 | 20 ± 1.5 | 0.90 ± 0.03 |
| Parameters | Available | DA-Based FIR with Machine Learning. Srinivas A Murthy, et al. [23] | CNN with CORDIC-Based LMS Filter | CNN with DA-Based LMS Filter | CNN with OBC-Based LMS Filter | CNN with OBC Radix 4-Based LMS Filter |
|---|---|---|---|---|---|---|
| Filtering Approach | - | DA-based FIR(fixed) | CORDIC-based LMS | 2’s complement DA-based LMS | OBC-based DA-based LMS | OBC with Radix 4-based DA LMS |
| Machine Learning | - | Support Vector Machine | CNN(optimized) | CNN(optimized) | CNN(optimized) | CNN(optimized) |
| FPGA Device | Artix-7 | Artix-7 | Artix-7 | Artix-7 | Artix-7 | |
| Slice Registers | 41,600 | 2872 | 960 | 800 | 656 | 637 |
| Slice LUTs | 20,800 | 2871 | 940 | 730 | 646 | 623 |
| Bonded IO | 300 | - | 120 | 111 | 102 | 99 |
| BUFGCTRL | 24 | - | 2 | 2 | 2 | 2 |
| Resource Utilization | Available | IMLMS, Zhang Y, et al. [24] | CORDIC-Based LMS Filter | DA-Based LMS Filter | OBC-Based LMS Filter | OBC Radix 4-Based LMS Filter |
|---|---|---|---|---|---|---|
| FPGA Device | Xilinx UltraScale KU115 | |||||
| LUT | 663,360 | 5643 | 228 | 211 | 184 | 160 |
| DSP | 5520 | 669 | 32 | 20 | 19 | 17 |
| Bonded IO | 520 | - | 28 | 19 | 15 | 12 |
| BUFGCTRL | 96 | - | 1 | 1 | 1 | 1 |
| Resource Utilization | Available | Wu B., et al. [25] | CNN with CORDIC-Based LMS Filter | CNN with DA-Based LMS Filter | CNN with OBC-Based LMS Filter | CNN with OBC Radix 4-Based LMS Filter |
|---|---|---|---|---|---|---|
| LUT | 242,000 | 171,497 | 960 | 800 | 646 | 623 |
| FF | 484,000 | 188,405 | 1220 | 976 | 636 | 612 |
| DSP | 1920 | 1920 | 32 | 20 | 19 | 17 |
| Bonded IO | 520 | - | 28 | 19 | 15 | 12 |
| BUFGCTRL | 96 | - | 1 | 1 | 1 | 1 |
| Parameters | DAAFA-Radix-8 James, B.P. et al. [14] | DAAFA- Radix-4 James, B.P. et al. [14] | CORDIC-Based LMS Filter | OBC-Based LMS Filter | DA-Based LMS Filter | OBC Radix 4-Based LMS Filter |
|---|---|---|---|---|---|---|
| Device | Xilinx Virtex-5 XC5VLX30 FF324-3 FPGA (Xilinx Inc. (San Jose, CA, USA)) | |||||
| Slices | 202 | 210 | 230 | 188 | 217 | 162 |
| Four-input LUTs | 197 | 208 | 228 | 184 | 211 | 160 |
| Bonded IO | - | - | 28 | 19 | 15 | 12 |
| BUFGCTRL | - | - | 1 | 1 | 1 | 1 |
| MSP (ns) | 3.1 | 2.9 | 4.8 | 3.5 | 2.7 | 3.6 |
| MSF(MHz) | 322.58 | 344.82 | 208.33 | 285.71 | 370.37 | 277.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nair, S.; James, B.P.; Leung, M.-F. An Optimized Hybrid Approach to Denoising of EEG Signals Using CNN and LMS Filtering. Electronics 2025, 14, 1193. https://doi.org/10.3390/electronics14061193
Nair S, James BP, Leung M-F. An Optimized Hybrid Approach to Denoising of EEG Signals Using CNN and LMS Filtering. Electronics. 2025; 14(6):1193. https://doi.org/10.3390/electronics14061193
Chicago/Turabian StyleNair, Suma, Britto Pari James, and Man-Fai Leung. 2025. "An Optimized Hybrid Approach to Denoising of EEG Signals Using CNN and LMS Filtering" Electronics 14, no. 6: 1193. https://doi.org/10.3390/electronics14061193
APA StyleNair, S., James, B. P., & Leung, M.-F. (2025). An Optimized Hybrid Approach to Denoising of EEG Signals Using CNN and LMS Filtering. Electronics, 14(6), 1193. https://doi.org/10.3390/electronics14061193






