Proximal Policy-Guided Hyperparameter Optimization for Mitigating Model Decay in Cryptocurrency Scam Detection

Abstract

As cryptocurrency transactions continue to grow, detecting scams within transaction records remains a critical challenge. These transactions can be represented as dynamic graphs, where Neural Network Convolution (NNConv) models are widely used for detection. However, NNConv models suffer from model decay due to evolving transaction patterns, the introduction of new users, and the emergence of adversarial techniques designed to evade detection. To address this issue, we propose an automated, periodic hyperparameter optimization method based on proximal policy optimization (PPO), a reinforcement learning algorithm designed for dynamic environments. By leveraging PPO’s stable policy updates and efficient exploration strategies, our approach continuously refines hyperparameters to sustain model performance without frequent retraining. We evaluate the proposed method on a large-scale cryptocurrency transaction dataset containing 2,973,489 nodes and 13,551,303 edges. The results demonstrate that our method achieves an F1 score of 0.9478, outperforming existing graph-based approaches. These findings validate the effectiveness of PPO-based optimization in mitigating model decay and ensuring robust cryptocurrency scam detection.

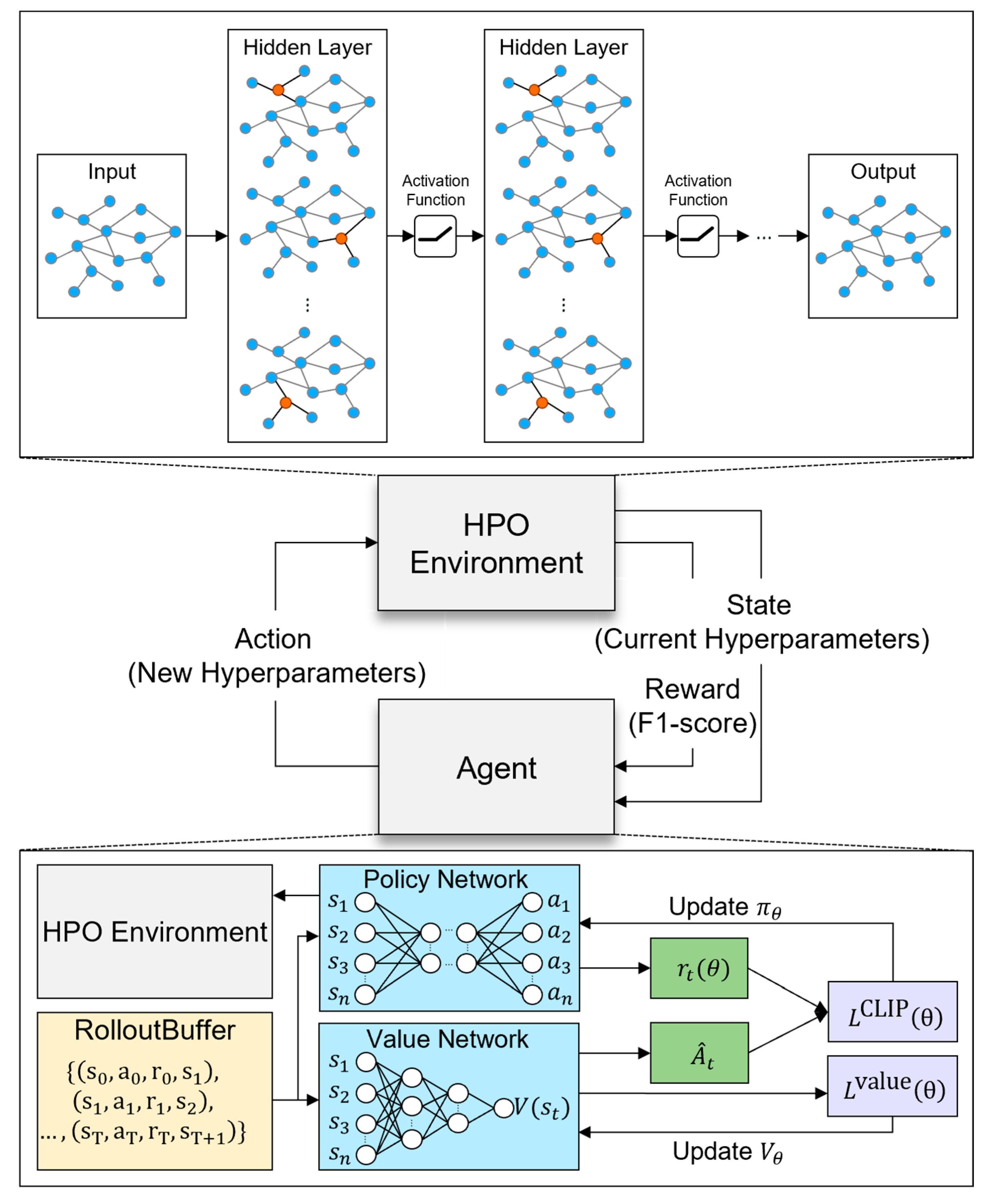
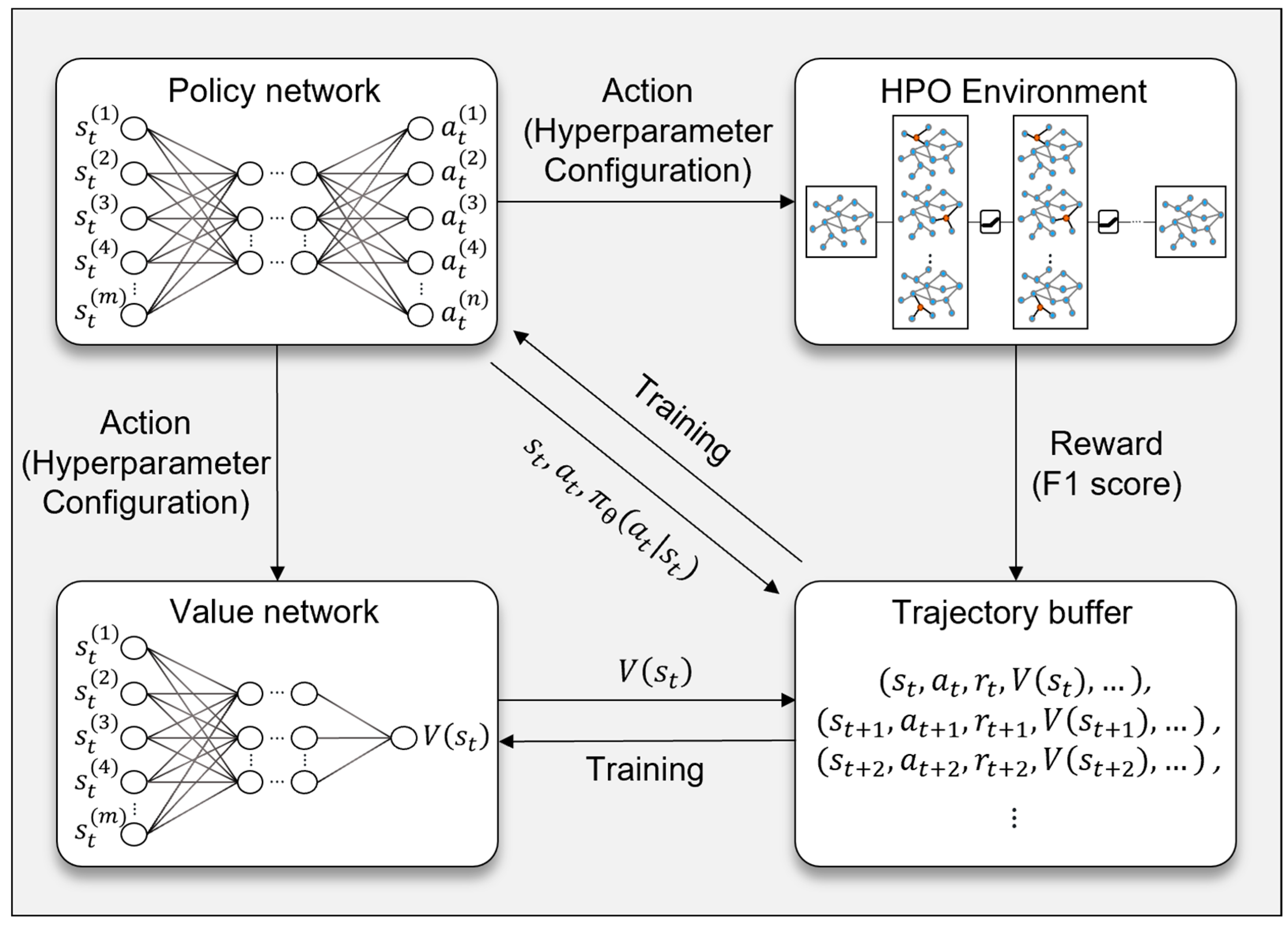
1. Introduction

The growing popularity of cryptocurrencies has not only presented substantial economic opportunities but has also led to an increase in fraudulent activities, including scams. As the adoption of cryptocurrencies like Ethereum expands, so do the methods used by malicious actors to exploit blockchain-based transactions. The decentralized and programmable nature of Ethereum has enabled the development of smart contracts and decentralized applications (DApps), among other things, resulting in a complex transaction network, with Ethereum recording a transaction volume of USD 15 billion as of December 2023 [1]. However, the same attributes that make Ethereum a powerful platform also pose significant security challenges. The ability of users to create pseudonymous accounts and the dynamic nature of transaction flows make fraudulent activities more difficult to track and detect. In addition, the rapid evolution of transaction patterns and the continued emergence of sophisticated fraud techniques further complicate the detection process, often surpassing traditional security measures.

In addition, while governments, financial institutions, and security researchers are actively working to mitigate these threats, there are still significant gaps in cybersecurity methodologies, particularly in addressing the problem of concept drift [2], a phenomenon where model performance degrades as the statistical properties of data change over time.

Concept drift [2] is when the statistical properties of the target variable a model is trying to predict change in unexpected ways over time. Figure 1 shows an example of concept drift. Concept drift is particularly problematic in cryptocurrency scam detection because fraudsters continuously develop new schemes to bypass detection mechanisms. As transaction patterns shift and new fraud techniques emerge, models trained on historical data become less effective. This issue, known as model decay, necessitates continuous model monitoring and periodic retraining to maintain effectiveness. Traditional scam detection models, particularly those based on deep learning, often struggle to keep up with this rapidly evolving landscape due to their reliance on static training datasets. This calls for a more adaptive and automated approach to fraud detection, one that can efficiently adapt to new fraud patterns without excessive human intervention.

A key challenge in improving scam detection models lies in the optimization of hyperparameters. Deep learning models for graph-based transaction analysis often require extensive tuning of hyperparameters, such as learning rates, weight decay, loss functions, and class imbalance handling mechanisms. Manually selecting and fine-tuning these hyperparameters is a labor-intensive process that demands substantial domain expertise and computational resources. Furthermore, the complexity of cryptocurrency transaction networks, with their dense interconnections and evolving fraud patterns, makes it even more difficult to determine an optimal set of hyperparameters that can generalize well across different time periods and fraud types.

To address these challenges, we propose a novel methodology that leverages proximal policy optimization (PPO) [3], a reinforcement learning (RL) algorithm, for automated hyperparameter optimization (HPO) in Ethereum scam detection models. PPO is an on-policy RL algorithm that enables dynamic hyperparameter tuning by continuously adapting to changes in transaction data distribution. Unlike traditional grid search or Bayesian optimization methods, PPO explores the hyperparameter space more efficiently by learning an optimal policy for selecting hyperparameters in response to real-time transaction data. This approach significantly reduces the need for manual tuning while improving model adaptability to evolving fraud trends.

To enhance the clarity of our research goals, we now explicitly state that the primary objective of this work is to develop a dynamic hyperparameter optimization method using PPO that continuously adapts NNConv-based scam detection models to evolving data distributions. This goal is driven by the need to mitigate the model decay phenomenon resulting from concept drift in rapidly changing Ethereum transaction networks.

By integrating PPO-based HPO into Neural Network Convolution (NNConv) [4]-based scam detection models, we enhance their ability to detect fraudulent transactions despite the presence of concept drift. Our approach includes the following:

• State and action space modeling: We encode discrete and continuous hyperparameters using one-hot encoding and normalization techniques to facilitate learning in the PPO environment;
• Reward function design: We consider the inherent class imbalance in scam detection and formulate a reward function that optimizes both F1 score and scam recall, ensuring that fraud instances are accurately identified;
• Dynamic class weighting and focal loss tuning: To mitigate the negative effects of data imbalance, we enable the dynamic adjustment of class weights and focal loss parameters, enhancing the model’s sensitivity to fraudulent transactions;
• Efficient graph data processing: Our method integrates NeighborLoader [5] and chunk-based evaluation to optimize GPU memory usage, allowing scalability to large transaction graphs.

The significance of our proposed approach lies in its ability to address the limitations of existing scam detection models in the face of evolving fraud patterns. Our research contributes to the field of blockchain security in three keyways:

• A novel reinforcement learning-based optimization approach: By introducing PPO-guided HPO, we enhance the security and robustness of cryptocurrency transaction monitoring, reducing the impact of concept drift and model decay;
• Improved efficiency in deep graph traversal and classification: Our PPO-based method optimizes hyperparameters for NNConv models, improving their ability to analyze large-scale Ethereum transaction graphs and classify complex fraud patterns more effectively;
• Empirical validation on real-world Ethereum transaction data: We rigorously evaluate our methodology against real Ethereum transaction datasets, demonstrating superior performance over existing optimization techniques in maintaining model effectiveness over time.

The rest of this white paper is organized as follows. Section 2 reviews existing human-driven hyperparameter tuning, traditional HPO, and AutoML [6] (Automated Machine Learning)-based approaches in cryptocurrency fraud detection and discusses their strengths, weaknesses, and limitations. Section 3 details the overall structure and algorithm of our proposed PPO-based HPO method, including the graph construction, NNConv model design, and dynamic optimization process via PPO, through formulas and pseudocode. In Section 4, we present the experimental design and evaluation results using a large-scale Ethereum transaction dataset, including performance comparison with other models, reward function design, and model decay mitigation effects. Finally, in Section 5, we synthesize our findings, summarize the contributions and limitations of our method, and discuss future research directions.

2. Related Works

In this section, we review various papers that apply optimization algorithms to cryptocurrency fraud detection models. Table 1 provides an overview of these methodologies, categorized into human-guided optimization, traditional HPO, and AutoML [6].

First, human optimization involves using prior knowledge of the model to manually tune hyperparameters to achieve fast optimization. Ref. [7] adopts this method to optimize an ATD-SGAN (anomaly detection using semi-supervised generative adversarial networks) model that uses SGANs to detect anomalous transactions in the Ethereum network. In this approach, the SGAN hyperparameters of the model (e.g., loss function, activation function, learning rate) are manually tuned. In ATD-SGAN, feature selection is performed using two biologically inspired algorithms, Manta Ray Foraging Optimization (MRFO) [8] and Particle Swarm Optimization (PSO) [9]. MRFO leverages a biological optimization algorithm to select features. PSO uses a particle swarm optimization technique to select the best features. In [10], the model is optimized by human hyperparameter optimization. The optimization target is a model called Self-supervised IncrEmental deep Graph lEarning (SIEGE). It is designed for detecting Ethereum phishing scams based on a Graph Neural Network (GNN) and utilizes GraphSage [5] as the underlying GNN encoder. The Self-Supervised Learning (SSL) technique is used to solve the problem of lack of labels, and an incremental learning technique is used to solve the problem of constantly changing graph data. For the SIEGE model, they optimized GraphSage’s hyperparameters, SSL pretext task, incremental learning, optimizer, and learning rate. For each hyperparameter, they conducted experiments with various candidates to find the optimal combination of hyperparameters. In this process, they demonstrated that relatively fast HPO is possible by fine-tuning each hyperparameter to reflect the researcher’s domain knowledge.

Traditional HPO methods are computationally expensive because they explore independently without utilizing previous results, but they can be parallelized to test multiple hyperparameter combinations simultaneously. In [11], K-Nearest Neighbors, Decision Tree, naïve Bayes, Random Forest [12], and stacking models were proposed and optimized, and the performance of all classifiers was improved when random search was applied, with the best performance coming from models that applied ADASYN-TL [13] and SMOTE-ENN [14] techniques in combination with stacking models. This shows that random search is the most effective HPO method for large-scale data. On the other hand, Bayesian optimization performs a more precise optimization but may require longer training time, and grid search performs the most exhaustive search but is impractical due to its high computational cost. Ref. [15] classified ransomware-related Bitcoin transactions using three models: Logistic Regression, Random Forest, and Extreme Gradient Boosting (XGBoost) [16]. HPO using random search was performed on these models to evaluate the different models and select the best-performing hyperparameter combinations. XGBoost performed the best in ransomware detection, proving to be a robust model for detecting ransomware in Bitcoin transactions. In [17], they leveraged an optimized Genetic Algorithm-Cuckoo Search (GA-CS) to optimize the performance of deep learning models. Genetic algorithms were utilized to improve global search capabilities during the exploration and optimization process. A genetic algorithm (GA) [18] explores various solutions by randomly generating initial solutions and evaluates the performance of an object through a fitness function. Selection, crossover, and mutation operations are applied to evolve an optimal solution. In this paper, GA is combined with Cuckoo Search (CS) [19] to improve optimization performance. GA-CS is an optimization technique that mimics the habit of cuckoos in nature to lay eggs in other birds’ nests. It is designed to combine with GA to solve the problem of falling into a local optimum during the search process. They used CS to effectively expand the search space, while performing the function of finding the optimal solution in a random walk fashion. Finally, they leveraged GA’s global search capabilities to generate the initial solution and CS’s local search capabilities to perform the refinement optimization. They used GA to generate multiple candidate solutions and then used CS to select and tune the optimal solution from among them, which helped speed up the model’s convergence and solve the problem of local optima escaping.

AutoML [6] automatically adjusts the hyperparameter search space and iteratively finds the optimal settings. It automatically explores models that perform relatively well even if the user does not specify the exploration space exactly. Ref. [20] used XGBoost as the main model to solve the problem of cryptocurrency scam detection. In this paper, the optimization was performed using Optuna [21]. Optuna is an efficient hyperparameter search library based on Bayesian optimization and the Tree-structured Parzen Estimator (TPE) [22] algorithm. In the paper, they optimized the following XGBoost hyperparameters: XGBoost’s max_depth (maximum depth of the tree; larger values make the model more complex and increase the risk of overfitting), subsample (proportion of training samples; smaller values reduce overfitting, but too small makes learning difficult), gamma (minimum loss reduction value required to further divide the leaf nodes of the tree; larger values make the model simpler and prevent overfitting), and lambda (L2 normalization factor (like ridge regression); larger values constrain the weights more, preventing overfitting). These hyperparameters were set dynamically via Optuna’s trial object, and a hyperparameter search based on random walk and TPE was performed to find the best combination. The paper validated the HPO results by applying five-fold cross-validation, which included avoiding overfitting and checking the model’s generalization performance. Stratified cross-validation was used to ensure that each fold contained the same proportion of malicious and non-malicious tokens. HPO was performed separately for each fold and the optimized model was used to evaluate test data from that fold. In [23], they leveraged the PyCaret [24] library to perform automated hyperparameter tuning and model selection. PyCaret is an AutoML library that provides the ability to automatically train and compare multiple models and select the best model and hyperparameters. PyCaret was used to tune hyperparameters, compare model performance, and automatically select the best model. They utilized PyCaret’s tune_model function to perform HPO. The hyperparameters that were optimized were the following: learning rate, number of trees, depth tuning for LGBM, L2 normalization factor, boosting iteration count tuning for CatBoost [25], max depth, learning rate, gamma tuning for XGBoost, and number of trees and max depth tuning for Random Forest. They demonstrated that automated hyperparameter tuning and model selection using PyCaret is effective in Ethereum scam detection.

Table 1. Research trends in the application of optimization methodologies to cryptocurrency fraud detection models.

Citation	Optimized Method		Purpose of Optimization	Domain or Dataset	Year
[7]	Human-guided optimization		Improving performance	Benchmark Labeled Transactions Ethereum (BLTE)	2023
[10]			Improving performance	Ethereum transaction dataset	2023
[11]	Traditional HPO methods	Random search, grid search, and Bayesian optimization	Optimizing model	Ethereum transaction dataset (self-production)	2023
[15]		Random search	Optimizing performance	Bitcoin heist dataset	2024
[17]		Genetic algorithm	Improving performance	Bitcoin heist ransomware dataset	2023
[20]	AutoML	Optuna framework	Optimizing performance	Uniswap scam token dataset	2022
[23]		Pycaret library	Enabling efficient model selection and hyperparameter tuning	Ethereum transaction dataset using various collection methods	2023

Table 1. Research trends in the application of optimization methodologies to cryptocurrency fraud detection models.

Citation	Optimized Method		Purpose of Optimization	Domain or Dataset	Year
[7]	Human-guided optimization		Improving performance	Benchmark Labeled Transactions Ethereum (BLTE)	2023
[10]			Improving performance	Ethereum transaction dataset	2023
[11]	Traditional HPO methods	Random search, grid search, and Bayesian optimization	Optimizing model	Ethereum transaction dataset (self-production)	2023
[15]		Random search	Optimizing performance	Bitcoin heist dataset	2024
[17]		Genetic algorithm	Improving performance	Bitcoin heist ransomware dataset	2023
[20]	AutoML	Optuna framework	Optimizing performance	Uniswap scam token dataset	2022
[23]		Pycaret library	Enabling efficient model selection and hyperparameter tuning	Ethereum transaction dataset using various collection methods	2023

In previous studies, human-guided optimization approaches have been able to achieve rapid initial performance improvements by fine-tuning model components and hyperparameters based on domain expert knowledge, but they rely on a manual tuning process, which is time-consuming and subjective. Traditional HPO techniques have the advantage of evaluating multiple candidate combinations through automated exploration, but computational costs can skyrocket when the exploration space is large, and the model is susceptible to model decay because it is difficult for the model to adapt in real time to changes in data distribution. AutoML-based approaches are efficient in that they search for the optimal model without user intervention, but they suffer from the limitation that the initial optimization results are difficult to maintain in the long term with respect to changes in data characteristics over time.

In contrast, HPO based on PPO leverages reinforcement learning to adapt to changes in data distribution in real time. While traditional HPO methods require periodic re-optimization of hyperparameters to respond to changes in the data, PPO can automatically adjust the optimal hyperparameters based on dynamic data changes. Specifically, the following obtain:

• PPO can perform continuous optimization over time by transforming hyperparameter exploration into a policy learning problem;
• Traditional HPO techniques provide optimization results based on historical data and are not responsive to changes in future data;
• PPO reflects the changing dataset over time and rewards F1 scores to maintain model performance continuously.

In this work, we propose a dynamic HPO technique based on proximal policy optimization (PPO). The proposed method is designed to allow a reinforcement learning agent to receive quantitative reward signals from the environment, such as F1 scores, to continuously update its policy and explore optimal combinations within a hyperparameter space. This allows the model to quickly adapt to changes in data characteristics over time, effectively mitigating the phenomenon of model decay. PPO-based optimization overcomes the computational cost and static setup limitations of traditional HPO techniques and contributes to maintaining long-term model performance by rebalancing hyperparameter combinations in real time to match the latest data distribution.

3. Proposed Method

In this paper, we propose an algorithm to dynamically optimize hyperparameters based on PPO to mitigate the model decay of Graph Neural Networks (GNNs) that classify benign and scam nodes in Ethereum transaction graphs. The main objective of our method is to maintain robust model performance over time by continuously adapting the NNConv model’s hyperparameters to changes in the underlying data distribution. The proposed method consists of graph construction and feature extraction, NNConv-based classification model construction, and HPO via PPO. Figure 2 provides an overview of the proposed model. Algorithm 1 shows the pseudo code of the proposed model.

Algorithm 1: Hyperparameter optimization for scam detection in Ethereum Phishing Transaction Networks using PPO.

Description: Optimizes a Graph Transformer model for detecting scam nodes in the Ethereum Phishing Transaction Network (EPTN) by utilizing proximal policy optimization (PPO). This includes graph traversal via weighted random walks based on transaction time and amount, and hyperparameter tuning through PPO to maximize the model’s performance. Input: EPTN: Ethereum Phishing Transaction Network num_episodes: Number of optimization episodes for hyperparameter tuning training_hyperparams: Initial hyperparameters for model training Output: optimized_model: Scam detection model optimized for detecting scam nodes best_hyperparams: Optimized hyperparameters Process: Data Loading and Preprocessing 1.1: Load EPTN data from pickle files: Load sampled graph (G_sampled) and nodes (sampled_nodes); 1.2: Convert the graph to a simple undirected graph to remove duplicate and self-loop edges; 1.3: Extract node features, including degree, degree centrality, clustering coefficient, and PageRank. Normalize these features using mean and standard deviation; 1.4: Map node indices and create edge indices for NNConv input; 1.5: Compute edge features from transaction metadata (amount and timestamp), applying logarithmic transformation and normalization; 1.6: Generate labels for nodes and calculate class distribution. 2. Environment Setup 2.1: Define the hyperparameter space: - Discrete hyperparameters include hidden channels, number of layers, optimizers, aggregation methods, edge neural network configurations, class weight options, and batch size; - Continuous hyperparameters include learning rate, dropout rate, loss parameters (gamma, alpha), weight decay, and the number of neighbors. 2.2: Encode hyperparameters as states and decode actions into hyperparameters for interaction with PPO. 3. PPO-Based HPO 3.1: Define the optimization environment: - Set up observation and action spaces based on hyperparameter spaces; - Calculate rewards using F1 score as the primary metric and modify the reward function as needed. 3.2: Train and evaluate the model: - Sample hyperparameters using PPO; - Train the NNConv model using a focal loss with class weights; - Evaluate the model on test data, tracking F1 score, recall, and confusion matrix; - Update the PPO agent’s policy based on rewards derived from evaluation metrics. 4. Model Training and Evaluation 4.1: Train the NNConv model using NeighborLoader for efficient data batching; 4.2: Evaluate the model performance in chunks to manage memory constraints; 4.3: Log the best hyperparameters and metrics, ensuring performance improvements 5. Visualization and Results 5.1: lot F1 score progression across episodes; 5.2: Visualize episode-wise rewards to assess PPO convergence; 5.3: Record and display hyperparameters yielding high F1 scores (e.g., F1 ≥ 0.88). 6. Return Optimized Model and Hyperparameters 6.1: Finalize the optimized NNConv model; 6.2: Return the best hyperparameters discovered during the optimization process.

3.1. Graph Construction and Feature Extraction

First, construct a graph $G=\left(V,\epsilon \right)$ that represents the relationships between nodes based on Ethereum transaction data. Each element of the node set $V$ represents an account and the edge $E$ represents transaction information. To find accounts that are directly related to the scam account (node), we use a “bidirectional breadth-first search” (BFS). This finds all accounts associated with the fraudulent account and expands to any additional accounts associated with them, and finally computes the features (degree [26], clustering coefficient [27], degree centrality [28], PageRank [29]) of each node for the sampled graph $G_s\subset G$. First, the ‘degree of connectedness’ of each account (node) is measured by the number of transactions it has participated in, i.e., how many transactions one account has sent to or from another account. Expressed in a formula, this looks like the following:

$$d\left(v\right)=\left|\{u\in V∣\left(v,u\right)\in \epsilon \mathrm{or}\left(u,v\right)\in \epsilon \}\right|$$

(1)

Degree centrality is defined as follows:

$$C_D\left(v\right)={\displaystyle \frac{d\left(v\right)}{\left|V\right|-1}}$$

(2)

Next is the clustering coefficient. The clustering coefficient of node $v$ is defined as follows:

$$C\left(v\right)={\displaystyle \frac{2T\left(v\right)}{d\left(v\right)\left(d\left(v\right)-1\right)}}$$

(3)

where $T\left(v\right)$ is the number of triangles containing node $v$. The PageRank value is calculated by the following ignition formula:

$$\pi \left(v\right)=\alpha \sum _{u\in \mathcal{N}\left(v\right)}{\displaystyle \frac{\pi \left(u\right)}{d\left(u\right)}}+{\displaystyle \frac{1-\alpha }{\left|V\right|}}$$

(4)

where $\alpha$ is the attenuation factor, and $\mathcal{N}\left(v\right)$ is the set of neighbors of $v$. These features are normalized and assigned as model inputs $\mathit{x}\in R^{N\times F}$, where $N=\left|V\right|$ and $F$ is the feature dimension.

3.2. Construction of NNConv-Based Classification Model

The model we propose for node classification in graphs is based on NNConv. The NNConv layer is designed to reflect the characteristics of each connection (transaction) in the process of exchanging information between nodes (message passing). In other words, it is not just about exchanging information between connected nodes but also about reflecting the characteristics of the transaction in the learning, which is represented as follows:

$$f_{\mathit{edge}}\left(\mathit{e}\right)=W_2\left(\mathit{ReLU}\left(W_1\mathit{e}\right)\right)$$

(5)

where $W_1$ amd $W_2$ are the weight matrices. The $\left(l+1\right)$-layer hidden representation ${\mathit{h}}_{\mathit{v}}^{\left(\mathit{l}+1\right)}$ of node $v$ is updated as follows:

$${\mathit{h}}_{\mathit{v}}^{\left(\mathit{l}+\mathbf{1}\right)}=\sigma \left(\mathit{BN}\left(\sum _{u\in \mathcal{N}\left(v\right)}{f}_{\mathit{edge}}\left({\mathit{e}}_{\mathit{u}\mathit{v}}\right){\mathit{h}}_{\mathit{u}}^{\left(\mathit{l}\right)}\right)\right)$$

(6)

where $\sigma \left(\cdot \right)$ is the activation function and BN is the batch normalization. The activation function depends on which hyperparameters are chosen during HPO. For the last hidden state ${\mathit{h}}_{\mathit{v}}^{\left(\mathit{L}\right)}$, the classifier computes the class probability of a node by performing the following linear transformation:

$${\mathit{y}}_{\mathit{v}}=\mathit{softmax}\left(W_{\mathit{out}}{\mathit{h}}_{\mathit{v}}^{\left(\mathit{L}\right)}\right)$$

(7)

To mitigate class imbalance during training, we use focal loss, which is defined as follows:

$${\mathcal{L}}_F\left(p_t\right)=-\alpha {\left(1-p_t\right)}^{\gamma }\mathit{log}\left(p_t\right)$$

(8)

where $p_t$ is the predicted probability for the correct answer class, and $\alpha$ and $\gamma$ are hyperparameters.

3.3. Proximal Policy-Guided Hyperparameter Optimization with Proximal Policy Optimization

To optimize the model’s performance and generalization ability, we leverage proximal policy optimization (PPO), a reinforcement learning technique, to automatically tune the hyperparameters of the NNConv model. This component directly addresses our research goal of mitigating model decay by adapting hyperparameters in response to changing data patterns. While traditional hyperparameter optimization methods require humans to try different combinations, PPO allows a reinforcement learning agent to experiment and find the optimal combination. The process of performing HPO using the PPO algorithm is visualized in Figure 3.

The set of hyperparameters to be optimized consists of two groups: discrete hyperparameters ${\mathcal{H}}_d$ and continuous hyperparameters ${\mathcal{H}}_c$:

$$\begin{gathered} {\mathcal{H}}_d=\{\mathit{hidden}\_\mathit{channels}, \mathit{num}\_\mathit{layers}, \mathit{optimizer}, \dots \}, \\ {\mathcal{H}}_c=\{\mathit{learning}\_\mathit{rate}, \mathit{dropout}\_\mathit{rate}, \mathit{loss}\_\mathit{gamma},\dots \} \end{gathered}$$

(9)

Each entry in ${\mathcal{H}}_d$ is chosen from a predetermined set of options, and each entry in ${\mathcal{H}}_c$ has a value in the interval $\left[\min , \max \right]$. The size of the final state vector is computed as follows:

$$\mathit{state}\_\mathit{size}=\sum _{h\in {\mathcal{H}}_d}\left|{\mathcal{H}}_d\left(h\right)\right|+\left|{\mathcal{H}}_c\right|$$

(10)

The RL agent observes the current hyperparameter setting encoded as a state $\mathit{s}\in R^d$, where an action $a$ represents a change in the selected hyperparameter. The decoding process for continuous and discrete arguments, respectively, follows the following formulae:

$${\theta }_k=\mathit{decode}\left(a_k\right)=a_k\cdot \left({\mathit{max}}_k-{\mathit{min}}_k\right)+{\mathit{min}}_k,\hspace{1em}{a}_k\in \left[\mathrm{0,\; 1}\right]$$

(11)

$${\theta }_k={\mathit{option}}_{a_k},\hspace{1em}{a}_k\in \{\mathrm{0,\; 1}, \dots , \left|{\mathcal{H}}_d\left(h\right)\right|-1\}$$

(12)

The behavior $a_k$ denotes its index within the corresponding hyperparameter option set.

In the PPO algorithm, the agent chooses behavior $a_t$ in each state $s_t$, trains an NNConv model with the corresponding hyperparameter ${\theta }_t$, and is rewarded with F1 score $r_t=f1\left({\theta }_t\right)$. The PPO algorithm maximizes a clipped surrogate objective to update the parameter $\theta$ of the policy ${\pi }_{\theta }\left(a_t|s_t\right)$. First, the behavioral ratio $r_t\left(\theta \right)$ is defined as follows:

$$r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t|s_t\right)}}$$

(13)

The PPO’s objective function for this is defined as follows:

$$L^{\mathit{CLIP}}\left(\theta \right)=\widehat{E_t}\left[\mathit{min}\left(r_t\left(\theta \right)\widehat{A_t},\mathit{clip}\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right)\widehat{A_t}\right)\right]$$

(14)

where $\widehat{A_t}$ is the advantage estimate and $ϵ$ is the clipping parameter. The policy parameters are updated in the following gradient ascent method:

$${\theta }_{k+1}={\theta }_k+\alpha {𝛻}_{\theta }{L}^{\mathit{CLIP}}\left(\theta \right)$$

(15)

$\alpha$ is the learning rate, which allows the agent to find the optimal ${\theta }^{\ast }$ in the hyperparameter space with an exploration–exploitation tradeoff.

The RL environment trains the NNConv model according to the hyperparameters chosen by the agent, then computes the F1 score on the validation data and uses it as the reward $r_t$, i.e., $r_t=f1\left({\theta }_t\right)$. This reward function can be varied depending on performance. As we will see in Section 4.2, the performance with $r_t=f1\left({\theta }_t\right)$ yielded the highest F1 score. The model evaluation process involves the following training–evaluation loop:

• Train a model: Train a model with hyperparameter ${\theta }_t$ for E epochs ${\theta }_t\to {\mathit{h}}^{\left(\mathit{L}\right)}$;
• Evaluate the model: Make predictions on test nodes, yield F1 score $f1\left({\theta }_t\right)$.

For each episode, the agent records the F1 score based on the latest hyperparameter settings and stores the hyperparameter combinations that perform above a certain threshold separately to derive the final optimal hyperparameter set ${\theta }^{\ast }$.

4. Experiments

4.1. Datasets

In this study, we utilized a graphical Ethereum transaction history dataset. We followed the methodology presented in our previous work [30]. We crawled the Ethereum label cloud of phishing accounts reported by Etherscan (https://etherscan.io/apis, accessed on 8 February 2025), categorized as “fake phishing”, and then leverage the API provided by Etherscan to obtain a large transaction network with edges directed and weighted by two layers of BFS. We obtained a large graph with 2,973,489 nodes and 13,551,303 edges. A node represents an Ethereum trading account, and an edge represents a transaction history between accounts. Each edge contains transaction date and transaction volume information. If a node’s label value is 0, it is a benign node, and if it is 1, it is a scam node. Out of 2,973,489 nodes, the number of scam nodes is 1165. This indicates that the number of benign nodes is approximately 2500 times greater than that of scam nodes, highlighting a significant class imbalance.

To extract subgraphs from the original Ethereum transaction graph, we first loaded the entire graph object from a pickle file and then performed bidirectional BFS-based sampling centered on scam accounts (labeled 1). Specifically, we first select the nodes corresponding to scam accounts among all nodes and then proceed with BFS within the maximum exploration depth (max_depth = 5) using those nodes as the starting point. During this process, we sorted each node’s neighbors (trailing and leading nodes) in a fixed order and then varied the exploration order by random shuffle to reflect different paths. The sampling depth (max_depth) was determined based on a balance between capturing sufficient transaction history while avoiding excessive graph expansion, which could introduce irrelevant benign nodes. The target number of sampled nodes was determined to ensure that the extracted subgraph maintained meaningful structural characteristics of the original graph while being computationally manageable for training.

One of the main challenges in preprocessing the Ethereum transaction dataset was handling missing and noisy data. To address missing transaction records, we supplemented incomplete subgraphs by selecting additional nodes in descending order of their degree in the original graph. This ensured that sampled subgraphs preserved the essential connectivity structure of the Ethereum network. Additionally, since transaction volumes can have extreme variations, we applied a logarithmic transformation to the ‘amount’ attribute to mitigate the impact of outliers. To standardize node and edge features, we normalized all attributes using the mean and standard deviation, ensuring consistent feature scales across different subgraphs. Furthermore, edges without transaction timestamps were discarded, and scam nodes with no recorded transactions were removed to maintain the integrity of the dataset.

If the target number of sample nodes was not reached, we supplemented the remaining nodes by selecting them in the order of their high connectivity (node degree) in the original graph to form a subgraph of sufficient size. Additionally, to further address the significant class imbalance in the dataset, we considered various oversampling techniques such as SMOTE (Synthetic Minority Over-sampling Technique) [31] and GAN-based [32] synthetic data generation. However, due to the graph-based nature of the dataset and the need to preserve structural relationships between nodes, these traditional oversampling methods were not directly applicable. Instead, we adopted a graph-aware sampling approach that selectively expands the neighborhood around scam nodes while maintaining realistic transaction patterns. Future work may explore the integration of advanced graph-based oversampling techniques or distributed sampling approaches to enhance fraud detection performance while reducing computational costs.

Finally, we generated subgraphs of the original graph based on the selected nodes and characterized the data by checking the number of nodes with no transaction records among scam accounts. These preprocessed subgraphs were used in the experiments in Section 2 and Section 3. Information about the subgraphs is shown in

Table 2. Analysis of statistical characteristics by graph size of the Ethereum transaction network.

Number of Nodes	Number of Edges	Average Degree	The Number of Connected Components	Class Imbalance Rate (%)	Density (%)
2,973,489	13,551,302	9.11	22	0.039	0.00015
30,000	1,250,628 ± 5793.44	83.38 ± 0.39	16	4.04	0.14 ± 0.0006
40,000	1,315,068 ± 7373.78	65.75 ± 0.37	16	3.0	0.082 ± 0.0005
50,000	1,393,497 ± 37,335.54	55.74 ± 1.49	16	2.38	0.056 ± 0.0015

. Table 2 shows details for different graph sizes (original graph and graphs with 30,000 to 50,000 nodes), including number of edges, average degree, number of connected components, class imbalance, and density.

To analyze the impact of computational constraints, we measured the GPU/CPU resources and time required to process subgraphs of different sizes. When performing PPO-based hyperparameter optimization on a subgraph with about 50,000 nodes, we perform a total of 100 epochs and train the fraud detection model on the subgraph for a total of 8 epochs, with 8 steps per episode. Each time you train the model, you train for a total of 100 epochs. The training time of the model varies depending on the combination of hyperparameters. On average, the overall training process required an NVIDIA RTX A6000 GPU with 48GB VRAM, and model training took approximately 20 h per experiment. The model training used 20 CPU cores out of 128, based on an Intel(R) Xeon(R) Platinum 8362 CPU. This is expected to be significantly reduced depending on the implementation. On average, about 2 GB of RAM was used. The scalability of the method to larger datasets is feasible but requires distributed computing or memory-efficient training strategies, as processing the full Ethereum transaction graph would be computationally expensive. Further optimization techniques, such as mini-batch processing using NeighborLoader and model parallelism, could improve scalability for handling even larger transaction networks.

In Section 4 and Section 5, we need a slightly different format of data for experiments related to the model decay phenomenon. In the preprocessing, we split the graph into multiple time bins based on the timestamp recorded on each edge of the original graph. The given Python 3.9.20 code first extracted all timestamp values in the graph and then calculated the oldest time (min_ts) and the latest time (max_ts). It then sets up six equally spaced bins (intervals), which are further subdivided (intervals_renew), resulting in a total of 31 time bins. Each bin always starts with the earliest timestamp (min_ts) and only extracts the edge up to the end of the bin (end_ts) to create a subgraph. In this process, the subgraph corresponding to each time window reflects the transaction history up to that point in the original graph, allowing us to precisely analyze the evolution of the network and changes in transaction patterns over time.

The dataset of 31 subgraphs finally generated in this way is utilized for HPO experiments to evaluate the performance of cryptocurrency fraud detection models, mitigates the model decay problem in Section 4 and Section 5, and plays an important role in model evaluation and improvement considering the changes in network characteristics over time and the class imbalance problem. A detailed description of the experiments is given in those sections.

To train the final fraud detection model, the subgraphs preprocessed according to the above process are further preprocessed as follows. It is converted to a simple undirected graph to remove redundant edges and simplify the structure. For each node, various attributes such as connectivity, degree centrality, clustering coefficient, and PageRank are calculated and stored in a list, which is then converted to a tensor and normalized using the mean and standard deviation. We organize edge information by mapping node identifiers to indices, extract ‘amount’ and ‘timestamp’ values from each edge, apply a logarithmic transformation to ‘amount’, and normalize the overall edge characteristics. Finally, node labels are extracted, and the data object contains node attributes, edge indices, edge characteristics, and labels to complete the dataset for model training, while StratifiedShuffleSplit 1.2.2 is used to create training and test masks to facilitate hyperparameter optimization and model evaluation. The training and test sets are split in a 7:3 ratio.

4.2. Implementation

In this paper, we implement the HPO algorithm for an Ethereum scam detection model by implementing three main components (scam detection model, HPO environment, and PPO algorithm). First, the fraud detection model is designed to simultaneously utilize statistical characteristics of nodes in the graph and edge information representing transaction history, and it is given normalized node characteristics (node degree, degree centrality, clustering coefficient, PageRank) and edge attributes (transaction amount and timestamp) that characterize each transaction as input. To utilize the edge attributes, the first NNConv layer applies a multilayer perception (MLP) to transform the original edge attribute dimensions into node characteristics and hidden dimensions through two linear layers and an intermediate ReLU activation function and collects messages from each node’s neighbors based on the transformed edge information, applying batch normalization, ReLU activation, and dropout in turn to achieve stable learning and overfitting prevention. The additional layers of the NNConv take the output of the first layer as input and perform message forwarding after converting edge attributes at each layer in the same way, and each layer is designed to update node embedding within the hidden_channels dimension to learn gradually more complex transaction patterns and structural characteristics as the depth of the network increases.

The conversion of edge information is scaled according to the user-selected edge_nn option (32, 64, 128, 256), and the aggregation method (mean, add, max, min) is also applied at the same time. Finally, the extracted hidden representation after the multi-layer NNConv layer is mapped into two classes via a linear layer and the final output is converted into probability distributions for each class (benign/scam) by applying the log_softmax function. To efficiently explore the vast hyperparameter space (over 1.4 trillion combinations), the PPO-based HPO process employs several key techniques. First, the discrete and continuous hyperparameter spaces are encoded as structured state vectors, ensuring that the PPO agent can effectively navigate the search space. The PPO algorithm balances exploration and exploitation by leveraging an entropy coefficient (ent_coef) to prevent premature convergence to suboptimal hyperparameters. However, a key trade-off exists in terms of computational complexity: while PPO dynamically adjusts hyperparameters based on continuous feedback, the optimization process remains expensive due to the necessity of training multiple models per episode. To mitigate this, we introduce structured constraints by tuning n_steps and max_steps, setting n_steps = 4 to ensure two PPO updates per episode while limiting max_steps = 8 to manage the computational cost of evaluating each hyperparameter configuration. This structured approach enables an efficient balance between hyperparameter exploration and resource consumption.

In the PPO-based HPO process, the components of the NNConv model (hidden_channels, num_layers, dropout_rate, aggregation method, edge_nn structure, etc.) are dynamically adjusted according to the hyperparameter values selected by the PPO agent in the environment, and the NNConv model is built, trained, and evaluated with each hyperparameter combination generated by the agent’s behavior to derive the optimal model configuration. The structure of the NNConv model and the information about the hyperparameters to be optimized are summarized in

Table 3. Structure and number of parameters in an NNConv model.

Layer (Type: Depth-idx)	Shape (Dynamic)	Number of Parameters
NNConv	[batch_size, num_node_features]	-
NNConv (1–1)	[batch_size, hidden_channels]	(edge_dim × num_node_features × hidden_channels) + (edge_dim × hidden_channels)
BatchNorm (1–2)	[batch_size, hidden_channels]	2 × hidden_channels
Dropout (1–3)	[batch_size, hidden_channels]	0
(The same structure is repeated for the number of layers.)
NNConv (2–1)	[batch_size, hidden_channels]	(edge_dim × hidden_channels × hidden_channels) + (edge_dim × hidden_channels)
BatchNorm (2–2)	[batch_size, hidden_channels]	2 × hidden_channels
Dropout (2–3)	[batch_size, hidden_channels]	0
NNConv (3–1)	[batch_size, hidden_channels]	(edge_dim × hidden_channels × hidden_channels) + (edge_dim × hidden_channels)
BatchNorm (3–2)	[batch_size, hidden_channels]	2 × hidden_channels
Dropout (3–3)	[batch_size, hidden_channels]	0
(The above structure is repeated based on the value of num_layers. For example, if num_layers = 4, there are 4 NNConv–BatchNorm–Dropout blocks.)
Linear (output layer)	[batch_size, num_classes]	(hidden_channels × num_classes) + num_classes

and

Table 4. Hyperparameters to be optimized and used to train scam detection model.

Type		Hyperparameter	Description	Value
Graph convolution network	Discrete	hidden_channels	Number of hidden channels in the NNConv layers	[8, 16, 32, 64]
		num_layers	Number of layers in the NNConv model	[1, 2, 3, 4, 5, 6]
		aggr	Aggregation method for NNConv layers	[‘mean’, ‘add’, ‘max’, ‘min’]
		edge_nn	Defines the edge neural network size for processing edge attributes	[32, 64, 128, 256]
	Continuous	dropout_rate	Dropout rate applied to NNConv layers to prevent overfitting	(0.0, 0.9)
Training hyperparameters	Discrete	optimizer	Optimization algorithm used for training	[‘adam’, ‘sgd’, ‘adamw’, ‘rmsprop’]
		class_weights_choice	Determines the strategy for balancing class weights	[‘none’, ‘balanced’, ‘inverse_frequency’]
		batch_size	Batch size for the training loader	[256, 512, 1024, 2048, 4096]
	Continuous	learning_rate	Learning rate for the optimizer	(1 × 10−6, 1 × 10−1)
		loss_gamma	Gamma parameter for focal loss to focus on harder examples	(0.5, 5.0)
		loss_alpha	Alpha parameter for focal loss to adjust class balance	(0.1, 5.0)
		weight_decay	Weight decay parameter to control L2 regularization	(1 × 10−8, 1 × 10−1)
		num_neighbors	Number of neighbors sampled per layer in the graph during training	(1, 51)
Total hyperparameter combination: 4 × 6 × 4 × 4 × 4 × 3 × 5 × 206 = 1,474,560,000,000

, respectively.

The environment for HPO is implemented as a custom class extending the OpenAI Gym interface, which takes both types of parameters as arguments to effectively represent the joint space of discrete and continuous hyperparameters. Discrete parameters are represented in the form of a one-hot encoding state vector for each option, while continuous parameters are encoded as normalized values within their range to form the dimension of the overall state (state_size). This organized state is defined by the environment’s observation_space, which is set to be a box with all values between 0 and 1. The environment’s action_space is defined as a MultiDiscrete space, initially reflecting the number of possible options for each discrete hyperparameter, and later the number of discretizations (bins) of continuous actions specified by the user to represent continuous parameters. The action selected by the agent is converted to the actual hyperparameter value via the decode_action function within the step function, where the continuous action is divided by a predetermined number of bins and restored to its original range. The environment creates an initial state by randomly sampling hyperparameter values on the initial reset function call, and the state is then updated based on the agent’s actions. The environment’s action_space is defined as a MultiDiscrete space, initially reflecting the number of possible options for each discrete hyperparameter, and then the number of discretizations (bins) of continuous actions specified by the user to represent continuous parameters. The action selected by the agent is converted to the actual hyperparameter value by the decode_action function within the step function, where the continuous action is divided by a predetermined number of bins and restored to its original range. In this paper, we set the bin to be relatively large, 20, to maximize the difference between subtle changes in hyperparameters. The environment creates an initial state by randomly sampling hyperparameter values on the initial reset function call, and the state is then updated based on the agent’s actions. At each step, the environment generates a Neural Network Convolution (NNConv) model composed of the hyperparameter combinations based on the decoded hyperparameters and trains and evaluates it. The model uses graph degree, degree centrality, clustering coefficient, and PageRank as node features and has a multi-layer structure that includes layers from the NNConv family, batch normalization, and dropout. It also applies focal loss to mitigate the class imbalance problem and uses NeighborLoader to efficiently process large graph data in batches. The model is trained for a fixed number of epochs, and during evaluation, the data are partitioned into chunks to compute the macro F1 score and recall values for scam nodes in a memory-efficient manner.

The PPO algorithm was implemented utilizing the Stable-Baselines3 framework and was integrated with a custom HPO environment by importing previously trained PPO models from a saved directory and wrapping them in a DummyVecEnv. In each episode, the agent selects a hyperparameter for a given timestep, trains and evaluates the model with that configuration, and receives the F1 score as a reward signal, as it effectively balances precision and recall, making it well suited for imbalanced classification problems like scam detection. However, alternative reward functions such as weighted recall or precision might be more effective in scenarios where a higher recall is preferred (e.g., reducing false negatives in fraud detection systems) or where precision is more critical (e.g., minimizing false positives in legal investigations). Additionally, the PPO reward function could be adjusted dynamically based on specific business requirements, such as incorporating cost-sensitive learning strategies where false positives and false negatives have different penalties. A custom callback, F1LoggingCallback, is used to log the change in reward (i.e., F1 score) within an episode, and the entropy coefficient (ent_coef) of the PPO is adjusted to optimize the exploration–exploitation tradeoff. This is an important setting to control the cost of evaluation for individual hyperparameter configurations and to manage the time and resource usage of the entire HPO process.

In the PPO algorithm, there are two hyperparameters, n_steps and max_steps, that control the learning cycle. max_steps refers to the maximum number of steps to advance during an episode within a user-defined HPO environment. This is an important setting to control the cost of evaluation for individual hyperparameter configurations and to manage the time and resource usage of the overall HPO process. n_steps is a hyperparameter used by the PPO algorithm itself and refers to the length of timesteps (rollout) that the agent gathers from the environment before proceeding with a policy update. PPO collects experience (rollout) for a certain period (n_steps) before updating the policy and value function based on it. A large n_steps means that you can expect stable updates using longer sequences of data, but conversely, it can lead to longer intervals between updates, which can affect the exploration–exploitation tradeoff. We set max_steps to 8, which considers the computational cost of training and evaluates the NNConv model for each individual hyperparameter configuration. We set n_steps to 4 so that two PPO updates are made in one epoch. By limiting the number of steps per episode in this way, we can reduce the cost of evaluating each hyperparameter combination and reduce the overall exploration time. In each episode, the hyperparameter configuration selected by the agent leads to the learning and evaluation of the NNConv model, and the resulting F1 score is used as a reward to update the policy. As such, the hyperparameters and preferences in PPO are strategic choices to efficiently find reliable hyperparameter configurations within the exploration space, with a focus on minimizing computational cost while maintaining the exploration–exploitation tradeoff.

4.3. Comparison of PPO-NNConv to Other Models

A comparative analysis of our proposed model further clarifies the effectiveness of this methodology. In

Table 5. Comparison of PPO-NNConv with other models.

Algorithm	Graph Size = 30,000			Graph Size = 40,000			Graph Size = 50,000
	Precision	Recall	F1 Score	Precision	Recall	F1 Score	Precision	Recall	F1 Score
Node2Vec [33]	0.4984	0.4917	0.4507	0.5093	0.5073	0.5080	0.5118	0.5145	0.5129
LINE [34]	0.5074	0.5064	0.5067	0.5075	0.5064	0.5068	0.5146	0.5113	0.5126
SDNE [35]	0.6081	0.8048	0.6448	0.6268	0.7998	0.6717	0.6374	0.8034	0.6850
LSTM [36]	0.5039	0.5232	0.5134	0.5058	0.5215	0.5135	0.5099	0.5790	0.5423
DGTSD [37]	0.6520	0.8400	0.7018	0.6604	0.8407	0.7132	0.6489	0.8672	0.7059
PPO-NNConv (ours)	0.9374	0.9218	0.9294	0.9497	0.8970	0.9216	0.9699	0.9278	0.9478

, the comparison with Node2Vec, Large-scale Information Network Embedding (LINE), Structural Deep Network Embedding (SDNE), Long Short-Term Memory (LSTM), and Deep Graph traversal based on Transformer for Scam Detection (DGTSD) demonstrates that PPO-NNConv outperforms these traditional and state-of-the-art graph analysis techniques. Our method achieves a good F1 score to effectively identify scam nodes despite high-dimensional data and class imbalance issues. Below is a description of other methods compared to our method:

Node2Vec [33] is an effective method for embedding complex connections between nodes in a network, capturing structural and neighborhood information based on random walks.

LINE [34], an algorithm designed for embedding large-scale information networks, adopts an approach that considers relationships in both one and two dimensions.

SDNE [35] is a graph embedding technique that utilizes neural networks to effectively learn the structural information of a graph. It is known to be particularly strong at learning the high-dimensional structure of graphs nonlinearly.

LSTM [36] is a form of RNN suitable for sequential data processing and is widely used in time series data and natural language processing, with strengths in modeling long dependencies.

DGTSD [37] is a model that specializes in detecting fraudulent transactions in the Ethereum network, focusing on effectively analyzing large transaction graphs. The model utilizes DeepWalk [36] to explore the graph structure and applies a Transformer-based classifier to learn complex relationships between nodes. It uses multi-head attentions to identify sophisticated patterns in the Ethereum transaction graph.

PPO-NNConv significantly outperformed existing methods such as Node2Vec, LINE, SDNE, LSTM, and DGTSD for different graph sizes (30,000, 40,000, and 50,000 nodes). As shown in the table, for the 30,000-node graph, PPO-NNConv achieved a precision of 0.9374, recall of 0.9218, and F1 score of 0.9294, which is significantly higher than other methods such as DGTSD’s F1 score of 0.7018. The 40,000-node and 50,000-node graphs also show consistently good results, indicating that performance remains stable as the model size increases. This performance improvement can be attributed to the effective application of HPO over PPO to the simple NNConv model.

From the results in Table 5, the main reason why PPO-NNConv outperforms the existing models is due to the efficient edge information processing capability of the NNConv structure and its optimization through reinforcement learning-based HPO (PPO). Node2Vec and LINE mainly capture local structural information of the graph and do not fully reflect the complex nature of the overall graph structure, resulting in relatively low F1 scores. SDNE learns deep structural information nonlinearly, but higher dimensionality makes it prone to overfitting, especially with high recall but relatively low precision, limiting overall performance. LSTMs were optimized for sequential data processing and could not cope well with non-sequential and complex graph structures. DGTSD, on the other hand, utilized Transformer’s multi-headed attention to capture complex patterns in the graph, but it still did not reflect edge-level information as closely as NNConv, which resulted in lower performance than PPO-NNConv. PPO-NNConv showed stable performance even when the graph size increased from 30,000 to 50,000, with precision and recall improving together, because the reinforcement learning-based HPO effectively adapted to changes in graph size and data distribution while minimizing model decay.

In terms of scalability, Node2Vec, SDNE, and LSTM, which rely on deep network structures, face scalability issues due to their computational complexity. PPO-NNConv, on the other hand, achieves both high F1 scores and excellent scalability by performing various types of hyperparameter optimization tasks due to the low computational amount of NNConv by default. It is also more transparent in terms of functional contribution and decision-making process compared to other models by maintaining structural information by analyzing edge information together through the NNConv layer.

To further validate whether the observed performance differences in Table 5 are statistically significant, we conducted the Hassani–Silva KS test [38], a non-parametric statistical test designed to compare the distributions of model residuals. This test assesses whether the differences in F1 scores between PPO-NNConv and other models are due to random variations or indicate a meaningful performance improvement.

Table 6. Hassani–Silva KS test results for model comparison.

Model Pair	KS Statistic (D)	p-Value	$\mathbf{Significance} (\mathit{\alpha }$ = 0.05)
PPO-NNConv vs. Node2Vec	0.592	0.002	Significant
PPO-NNConv vs. LINE	0.576	0.003	Significant
PPO-NNConv vs. SDNE	0.438	0.017	Significant
PPO-NNConv vs. LSTM	0.552	0.004	Significant
PPO-NNConv vs. DGTSD	0.321	0.048	Significant

presents the results of the Hassani–Silva KS test applied to compare the residual distributions of PPO-NNConv and the competing models. The KS statistic (D) measures the maximum divergence between two cumulative distributions, while the p-value determines whether this divergence is statistically significant. The results indicate that the differences in F1 scores between PPO-NNConv and other models are statistically significant (p < 0.05 for all comparisons). This confirms that PPO-NNConv’s improved performance is unlikely to be due to random variations and is instead attributed to the reinforcement learning-based hyperparameter optimization strategy.

While our approach was specifically designed for Ethereum transaction networks, its methodology—leveraging graph-based representation learning and reinforcement learning-driven hyperparameter optimization—could potentially be applied to other types of large-scale networked data, such as social networks or financial transaction networks. In practice, there are many examples of using NNConv to analyze graph-structured data [39,40,41]. The key advantage of our framework lies in its ability to optimize hyperparameters dynamically based on structural and transactional features, which are common in various graph-based domains.

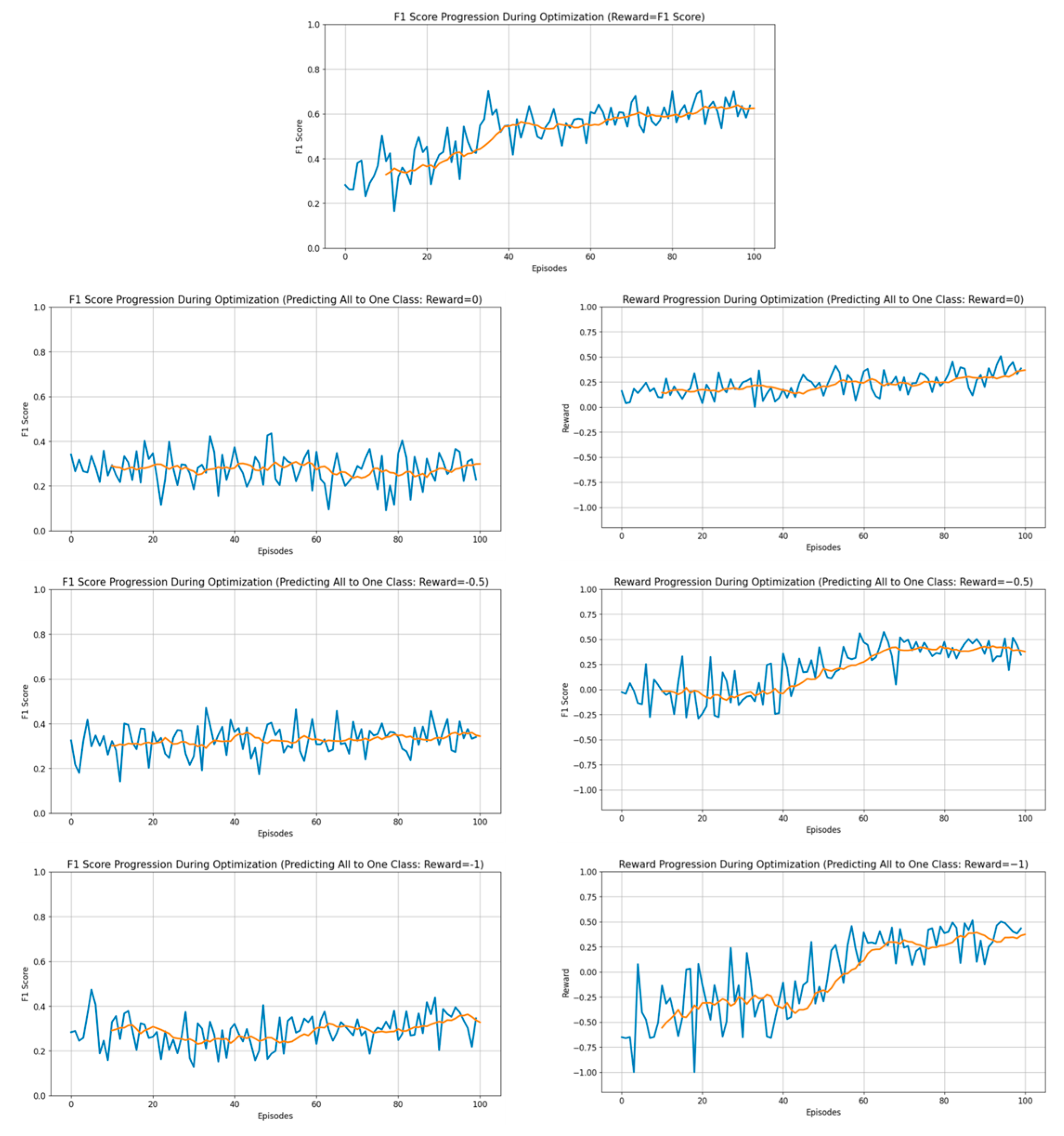
4.4. Optimization Performance Based on PPO-NNConv’s Reward Function

In this section, we analyze the impact of the design of the reward function on the optimization performance while optimizing the hyperparameters of the NNConv model using PPO. As described in Section 4.1, we extracted a subgraph of 50,000 nodes from the original Ethereum transaction graph and used PPO to optimize the hyperparameters of the NNConv model. In total, we compared four reward functions, with the following configurations:

• Reward 1: Reward proportional to the simple F1 score;
• Reward 2: 0 reward if the model predicts a single class;
• Reward 3: Reward of −0.5 if the model predicts that the model clusters into one class;
• Reward 4: Reward of −1 if the model clusters into one class and makes a prediction.

We visualized the performance per episode for each reward function as shown in Figure 4. The graph at the top of the figure has only one visualization because we set a reward equal to F1 score. Starting from the second row, the results are visualized according to F1 score on the left and reward on the right. In our experiments, we found that as the episodes progressed, the model performance improved most effectively when using a simple F1 score-based reward function, while other reward functions performed relatively poorly regardless of the size of the reward value (0, −0.5, −1) given for predicting to a class.

The reward function proportional to F1 score provided stable and fine-grained feedback to the PPO agent by continuously reflecting even small changes in F1 score, which is a combination of precision and recall. This continuous feedback helped the agent navigate the hyperparameter space and update its policy more effectively. In contrast, the reward function for lumping into a class showed discontinuous and rapidly changing reward signals. In extreme class imbalance situations, the model may inevitably make predictions that are biased towards one class, where strong negative rewards or fixed reward values limited the agent’s ability to perceive small performance improvements and caused it to choose inefficient exploration paths during the initial exploration phase. As a result, these reward schemes skewed the exploration–exploitation tradeoff, negatively impacted the derivation of optimal hyperparameter combinations, and contributed to the poor performance of PPO-based optimization.

4.5. Hyperparameter Optimization Performance of PPO-NNConv

In this section, we evaluate how the PPO-based HPO technique responds to data changes over time and, as a result, mitigates model decay. The dataset used in the experiments in this section was partitioned into 31 subgraphs using the timestamp information recorded on each edge of the Ethereum transaction graph, as described in Section 4.1, and then six representative time bins were selected to train PPO agents to optimize the hyperparameters of the NNConv model in each bin in two ways. We trained the PPO agents in two ways: first, by independently training a new agent for each time bin, and second, by sequentially updating the agent trained on the first graph as a starting point. Each subgraph reflects the transaction history up to that time, and the NNConv model performance was evaluated by the macro F1 score.

Figure 5 provides a visualization of the experimental results. The graph at the top of the figure visualizes only one newly trained result, as no PPO model was trained at the previous time point. Starting from the second row, the left side is the result of defining and training the PPO agent independently, and the right side is the result of training sequentially, starting with the PPO agent trained in the previous graph, and fetching the updated model from the previous bin in the subsequent graphs. The experimental results show that the PPO agents trained sequentially over time achieve higher F1 scores overall than those trained independently in each bin. In the last 6 graphs, the sequential training method significantly outperforms the independent training method. These results suggest that in the early time bins, the PPO agent was able to effectively learn the interrelationships between hyperparameters and quickly adapt to small changes in the data distribution as it moved into later bins. The initial learning results served as a starting point for subsequent episodes, increasing the probability of finding the optimal hyperparameter combinations, which we interpret as contributing to mitigating model decay. In contrast, the independently trained PPO agent had to start with an initial state each time, which limited its ability to adapt to changes in the data distribution.

A key advantage of PPO-based HPO in handling vast search spaces is its ability to iteratively refine hyperparameters through continuous feedback. Unlike traditional grid search or random search methods, which scale exponentially with the number of parameters, PPO efficiently prunes the search space by dynamically updating the policy network based on F1 score rewards. This enables the model to focus on promising hyperparameter regions while gradually discarding suboptimal configurations. Furthermore, by maintaining a historical memory of previously explored configurations, PPO avoids redundant evaluations, significantly improving computational efficiency. This strategy is particularly beneficial given that the hyperparameter space in this study consists of more than 1.4 trillion possible combinations.

In addition, the PPO agent learns and evaluates an NNConv model with a selected hyperparameter configuration in each episode and uses the results as a reward signal to update its policy. In a sequential learning approach, these reward-based updates are stabilized by the accumulated experience from previous episodes, resulting in a more effective balance between exploration and exploitation. As a result, we observed a gradual improvement in HPO performance over time and ultimately found that sequentially trained PPO agents were able to find optimal hyperparameter combinations that were more persistent and stable than if they were trained independently.

The experiments demonstrate that the trained PPO agent leverages its previous experience to incrementally adjust hyperparameters to fit new data. They also demonstrate that model performance does not degrade rapidly in response to changes in the data distribution, and that it is easy to maintain over the long term. In the experiments, the model with PPO-based HPO maintained a more stable F1 score than the traditional HPO method. These results show that PPO is more effective at mitigating model decay than traditional static HPO techniques.

4.6. Whether to Mitigate Model Decay

In this section, we partition the original Ethereum transaction data into time bins to quantitatively analyze the model decay phenomenon due to changes in data distribution and demonstrate the effectiveness of the PPO-based HPO technique in mitigating it. In this experiment, we preprocessed the entire data into 31-time bins by utilizing the timestamp information recorded on each edge in the original transaction graph as described in Section 4.1 and selected six representative bins (Graphs 1–6) to train the model by applying the optimal hyperparameter combinations derived from the previous training process to each bin. The trained model was saved as a weight file with the best-performing weights, which were then used to make predictions on all graph data after that bin.

Evaluation was performed in two ways: one by keeping the same order of nodes as the subgraph used for training, and the other by randomly selecting neighboring nodes to extract five different subgraphs. Both approaches showed model decay over time, with relatively high performance when the same node configuration was maintained and greater performance degradation with random subgraphs. This suggests that the stored optimal hyperparameters and model weights are optimized for the data distribution in a particular time window, and that model performance degrades as the data structure and trading patterns change. To further illustrate the extent of model decay, we analyzed the F1 score drop rate over time. This metric was computed as follows:

$$F1 \mathit{Drop} \mathit{Rate}={\displaystyle \frac{\mathit{F}{1}_{\mathit{initial}}-F{1}_{\mathit{final}}}{F{1}_{\mathit{initial}}}}\times 100$$

(16)

Figure 6 visualizes the F1 score drop rate over time. When the same nodes were used, this indicates that concept drift primarily affects new nodes entering the transaction network. However, when subgraphs were randomly sampled, the performance degradation was more severe, with an average F1 drop rate of 25–40%, demonstrating the challenges of adapting to evolving network structures. Compared to traditional models, which exhibited an F1 drop rate of up to 50% over the experiment period, PPO-NNConv showed a significantly lower rate of decline, maintaining higher stability over time.

To address the robustness of the model against concept drift, we incorporate sequential PPO updates to allow hyperparameters to dynamically adjust as data evolve. Instead of relying solely on static hyperparameter tuning, our approach enables the agent to leverage prior knowledge accumulated across different time bins, improving adaptability to gradual changes in transaction patterns. By training the PPO agent sequentially over multiple time intervals, the system effectively tracks shifts in data distribution and mitigates model degradation over time.

However, limitations remain in handling abrupt concept drift, where sudden shifts in fraudulent transaction behaviors may require more proactive adjustments. In such cases, additional mechanisms such as adaptive learning rate strategies, online hyperparameter updates, and real-time data augmentation techniques could further enhance model robustness. Future research will explore integrating these strategies to maintain consistent performance across evolving transaction networks.

Figure 7 presents a comparative analysis of model decay under two different node sampling strategies. The left plot illustrates the F1 score trends when models are trained and evaluated using subgraphs sampled with the same nodes, whereas the right plot shows the results when subgraphs are randomly sampled at each evaluation step. The x-axis represents the graph index over time, while the y-axis measures the F1 score. In the left plot, PPO-NNConv maintains an F1 score above 0.78 even in later stages, whereas other models show a gradual decline. In contrast, in the right plot, where subgraphs are randomly sampled, PPO-NNConv initially achieves a high F1 score but exhibits a sharper decline over time, stabilizing around 0.58. Other baseline models suffer even greater performance degradation, with some models dropping below 0.3.

The experimental results from the HPO perspective clearly show the sensitivity to changes in the data distribution. The results of high performance immediately after model refresh and rapid performance degradation over time indicate the need for periodic hy-perparameter re-optimization and model updates to respond to changes in data distribu-tion. The PPO-based HPO technique offers the potential to quickly adapt to these data changes and shows that re-tuning hyperparameters to the latest data can help maintain model performance over the long term.

4.7. Case Analysis

In this experiment, we evaluate how the transaction history and prediction performance of each node has been improved by the optimization process by precisely analyzing the difference in prediction results between the fraud detection model with PPO-based HPO and the existing model. To achieve this, we saved the parameters of the 20 best-performing models and aggregated the number of prediction successes (success_count) for each node. We then treated the cases with 19 or more successful predictions as the best case and the cases with 5 or fewer successful predictions as the worst case. We divided them into four types as shown in

Table 7. The table summarizes which types of nodes are present in each case.

Case		Type	Visualization	Node Address
The existing model does not fit but the optimized model does	Benign predicted to be benign	Small transaction history Existing transaction history with scam accounts	(a)	0x646ed8a07d8a70b9c63121… 0x0f38daecb3fb7b87a8d3ed… 0x883506829ca0554f1086126… 0x4bf6a7faff3278fdfd203d50…
	Scam predicted to be a scam	Large transaction history Few transactions with scam accounts Relatively high number of 0 ETH transactions	(b)	0x3b5744c7f340e0d2dcf7a07… 0x33ed22f4b6b05f8a5faac47… 0x87b4eed5a781d8b8476450… 0x56238ccf73f97ad6ed170d1…
Neither model predicts	Benign predicted to be a scam	Small transaction history History of transactions with scam accounts Buying in small increments and then dumping it all at once or not selling at all	(c)	0x2dd2da464cb85850754d64… 0x008f8b5749963946c205b29… 0x4ea8b50fc927b093edf7657… 0xf77f4810e7521298a6e2a04…
	Scam predicted to be benign	Small transaction history Very few transactions with scam accounts	(d)	0x205906790a597972f97fccd… 0x456f6042c81651d234cc13c… 0x4f1872383be22878af5d479… 0x13f674c399a868feeca37cc…

. A visualization of the representative accounts in each case is shown in Figure 8.

The first type is the case where a normal node is predicted as normal. In the cases predicted as normal nodes, we found a pattern of low transaction history or some connections to scam accounts in the existing transaction history. While the original model did not clearly classify nodes with few transactions, the optimized model exhibited better generalization performance. This suggests that the optimized model learned the connectivity and structural features of specific nodes more effectively. The second type of nodes predicted as scams were characterized by having many transactions and a history of transacting with some scam accounts. Zero ETH transactions often appeared at a high frequency. In some cases, the existing model misidentified benign nodes, but the optimized model detected them more accurately. This suggests that PPO-based optimization has been trained to more accurately reflect the correlation between nodes by adjusting the sensitivity of the model.

The third case is when a benign node is predicted to be fraud. In this case, the transaction history was sparse, but there were often connections to some scam accounts, and there was a pattern of buying assets in small increments and then selling them all at once or holding them for long periods of time. These nodes are considered ambiguous in practice, and there is a possibility that the model could mistake them for fraud. These results suggest that transaction history alone may be limited in determining fraud and may need to be combined with additional static analysis techniques. Scam nodes that were predicted to be benign often had low transaction histories and few direct transactions with scam accounts. These nodes are likely to be low-activity accounts or cases where early-stage fraudulent behavior has not been detected. If the model was trained based on transaction patterns during training, it may have difficulty detecting these nodes. These results are somewhat related to class imbalance issues in the data and may require additional feature engineering to improve detection performance in the future.

The results above illustrate the impact of HPO on the performance of the model. As seen in the first type, the optimized model learned clearer patterns than the original model and helped to effectively detect scam nodes. For the third and fourth types, HPO alone may not be able to fully resolve nodes with low transaction histories or unusual transaction patterns. This suggests that additional data enrichment and feature engineering may be required.

One of the critical concerns in fraud detection is the ethical implications of false positives. Misclassifying benign users as fraudulent can lead to serious consequences, such as unwarranted financial restrictions, reputational damage, and loss of access to essential services. In regulatory and compliance-driven environments, falsely flagging transactions can also result in increased scrutiny from financial institutions and potential legal implications for the affected parties. To mitigate the risks associated with false positives, our proposed PPO-based HPO approach incorporates dynamic class weighting and focal loss tuning, which allows the model to adjust its sensitivity to different classes. By fine-tuning hyperparameters dynamically, the model avoids excessive bias towards over-detecting fraud, ensuring that legitimate users are not unduly penalized. Furthermore, in real-world deployment, additional mechanisms such as manual review processes, confidence score thresholds, and anomaly re-evaluation strategies can be integrated to further reduce the likelihood of false-positive decisions affecting genuine users.

4.8. Explainable AI (XAI) Analysis Using LIME

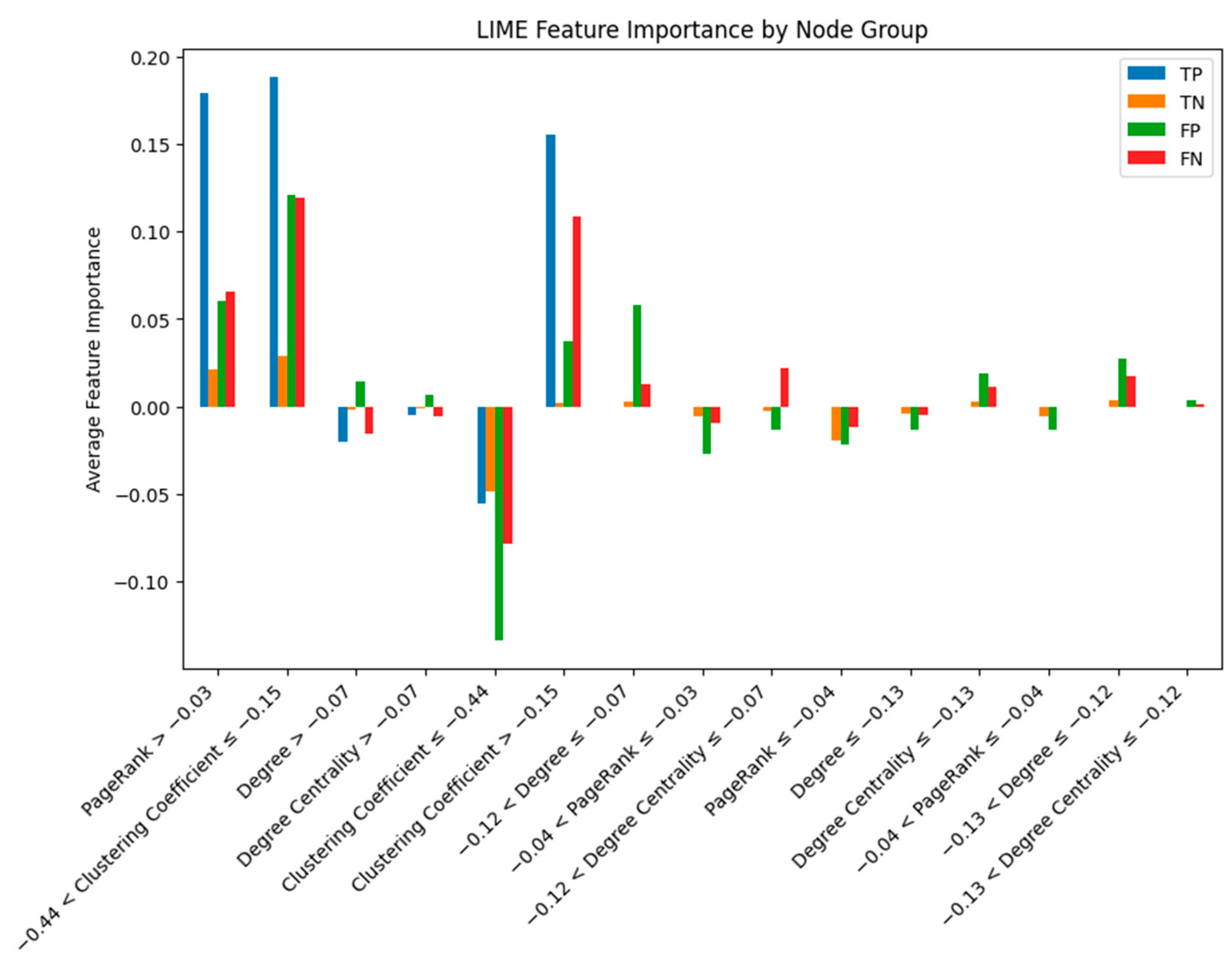
In this study, we applied LIME (Local Interpretable Model-Agnostic Explanations) [42], a local model interpretation technique, to clearly understand why the NNConv model classifies certain nodes as fraudulent transactions. Specifically, we divided the nodes into four groups: TP (true positive), TN (true negative), FP (false positive), and FN (false negative), and analyzed the important characteristics of each group. As shown in Figure 9, in the TP group, attributes with a low clustering coefficient (−0.44 < clustering coefficient ≤ −0.15) and a high PageRank (PageRank > −0.03) had the greatest impact on predicting fraudulent transactions, indicating that fraudulent accounts tend to be connected to accounts with high importance with relatively low connection density in the network.

In the FN group, the low clustering coefficient attribute (−0.44 < clustering coefficient ≤ −0.15) was also a key variable, but it had a lower average impact than the TP group. The FP group had characteristics with high PageRank and degree centrality, reflecting cases that were misclassified due to their high centrality in the network despite being legitimate transactions. The TN group had a low and uniform influence across attributes, indicating a stable attribute distribution of legitimate accounts.

These LIME-based analyses clearly demonstrate which network characteristics the NNConv model in this study emphasizes in detecting fraudulent transactions, suggesting that it can improve the reliability and transparency of the model and support more accurate decision-making in practical applications.

5. Conclusions

This paper presented a dynamic hyperparameter optimization technique using PPO applied to NNConv-based models for cryptocurrency scam detection. Our primary research goal is to mitigate model decay by continuously adapting hyperparameters in response to evolving data distributions. The experimental results on a large-scale Ethereum transaction dataset demonstrate that our approach significantly improves model performance and stability over time. We also visualize the collapse of classification models dealing with graph data with the method presented in Figure 6. In Section 4.5, we demonstrate that sequential PPO updates allow models to utilize previous experience, resulting in higher F1 scores and better adaptation to concept drift compared to traditional static HPO methods.

Despite the effectiveness of the proposed methodology, several limitations remain. One notable challenge is the high computational cost associated with the PPO-based optimization process. This method demands significant resources to maintain the balance between exploration and exploitation, and the reward function design, which primarily relies on F1 score, may not fully capture subtle performance improvements. Additionally, extreme class imbalance in the dataset was partially addressed through hyperparameter optimization but was not fundamentally resolved through direct data manipulation.

Another limitation stems from the reliance on reward signals derived solely from F1 scores. While this approach provides a useful evaluation metric, it may overlook finer-grained improvements or long-term effects of hyperparameter configurations, ultimately affecting the stability and consistency of the learned policy. Addressing this issue by incorporating multi-objective reinforcement learning or more adaptive reward functions could enhance the reliability of hyperparameter tuning. Furthermore, the generalizability of the proposed method to other blockchain networks remains an open challenge. The Ethereum-based approach may require structural adaptations to be effectively applied to networks such as Bitcoin or Binance Smart Chain, given the fundamental differences between Ethereum’s account-based model and Bitcoin’s UTXO-based model.

Future research will focus on enhancing the generality and efficiency of the proposed method. This will involve integrating multi-objective-based optimization techniques that incorporate diverse reward signals, experimenting with alternative Graph Neural Network models, and exploring more effective hyperparameter search strategies. Expanding the current approach to diverse blockchain datasets will also be a priority, considering the unique transaction dynamics and graph structures of different networks. To improve sample efficiency, alternative reinforcement learning algorithms such as Soft Actor-Critic (SAC) or Deep Deterministic Policy Gradient (DDPG) may be explored. Additionally, the computational overhead could be mitigated by leveraging Bayesian optimization or surrogate modeling to reduce the number of hyperparameter evaluations per training episode.

Another promising direction is the implementation of real-time adaptive hyperparameter tuning through online learning frameworks. This approach would enable the model to dynamically adjust to concept drift in scam detection, ensuring that detection strategies remain effective as new scam patterns emerge. Scalability improvements through distributed computing and model parallelism will also be explored to extend the methodology to even larger transaction datasets. Finally, hybrid detection approaches that combine rule-based heuristics with machine learning models will be considered. By incorporating domain expertise into the detection framework, the system can reduce false positives while maintaining high fraud detection performance. Future work will focus on integrating additional safeguards to ensure that legitimate users are not unfairly flagged as fraudulent, further enhancing the robustness and fairness of the detection system.

The significance of this research is that it presents a new approach to solve the model decay problem in the field of cryptocurrency fraud detection, which overcomes the existing static hyperparameter tuning limitations and confirms the possibility of developing models that adapt to dynamic environments. The proposed method can make practical contributions to the fields of blockchain security and financial crime prevention and can be extended to real-time monitoring and response schemes in various industries in the future.