Generator-Level Transient Stability Assessment in Power System Based on Graph Deep Learning with Sparse Hybrid Pooling
Abstract
1. Introduction
1.1. Literature Review and Motivation
1.2. Contribution in This Paper
2. The Motivation for the Data-Driven GTSA Scheme
2.1. The Underlying Design Philosophy of GTSA
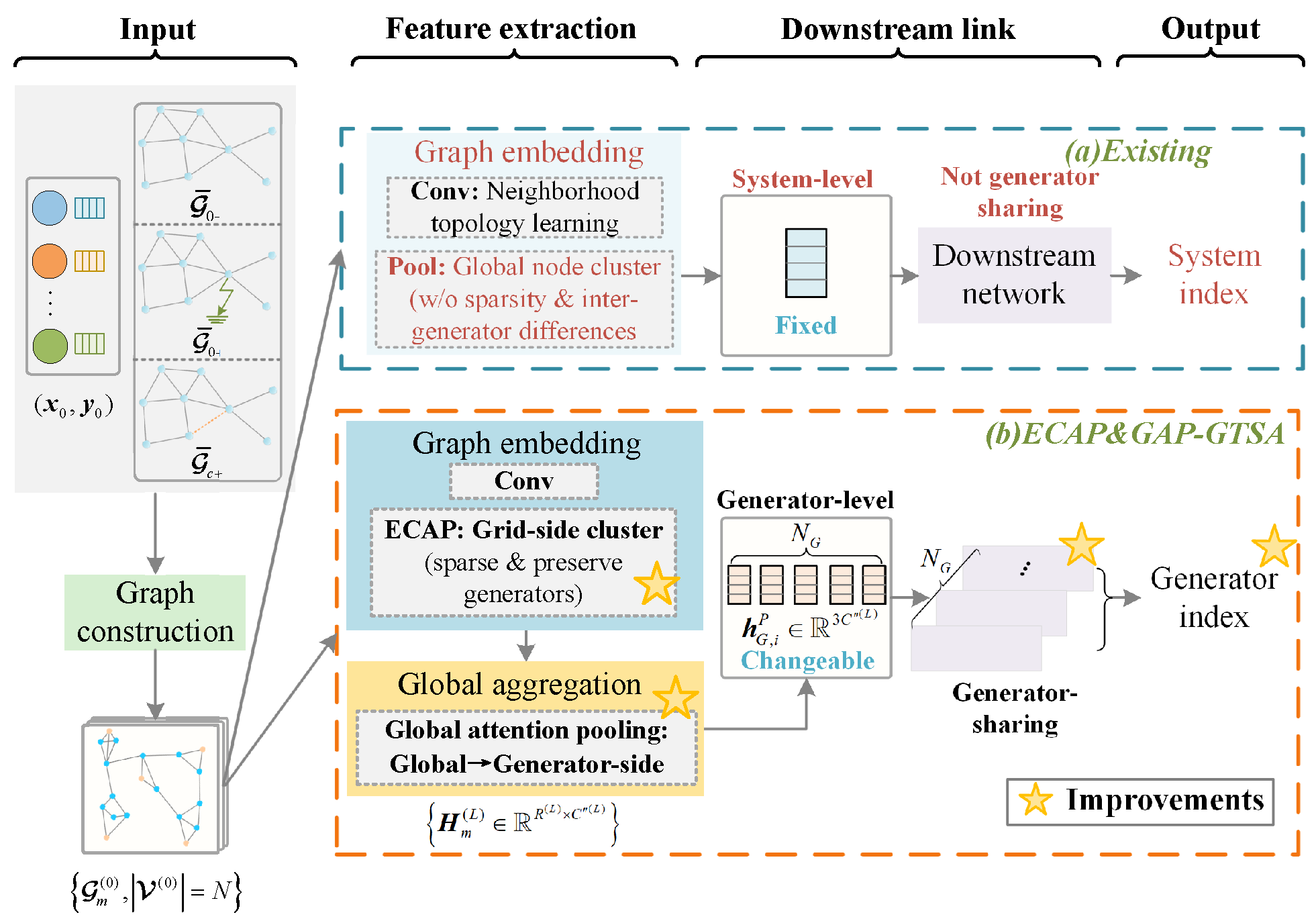
2.2. Related Works and the Proposed Improvements
3. The Scheme Overview of ECAP &GAP-GTSA
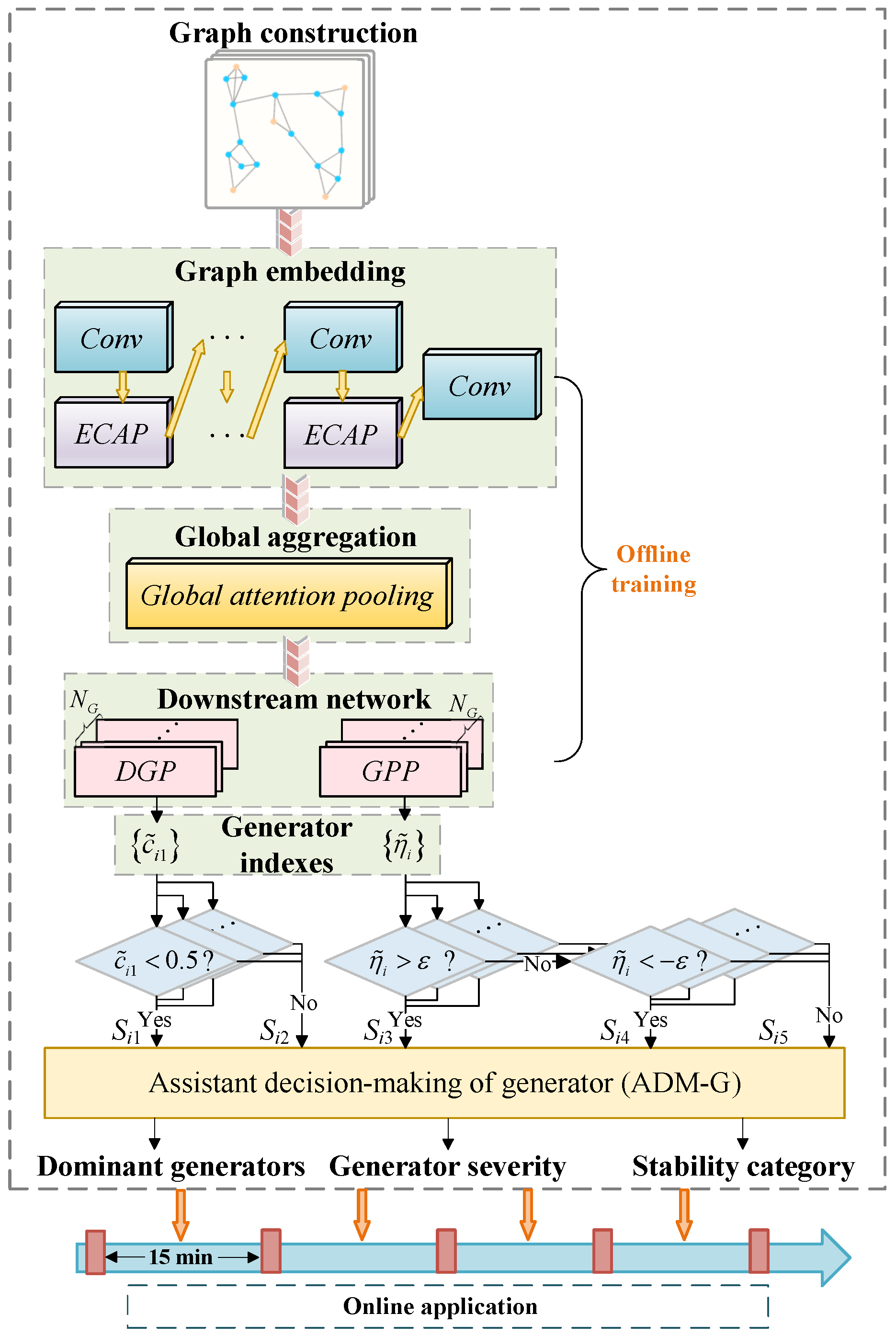
4. Detailed Designs of the ECAP &GAP-GTSA
4.1. The Generator-Level Stability Indexes
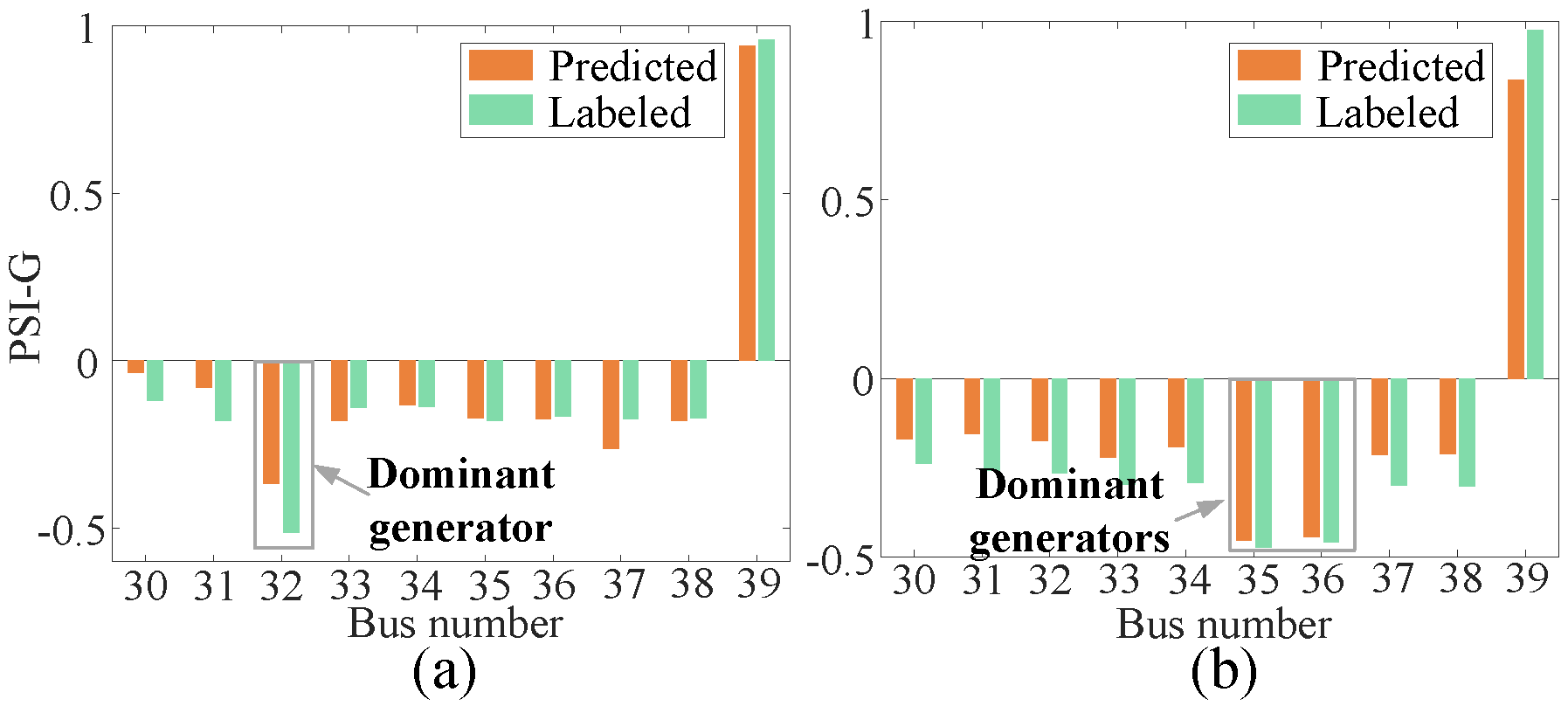
4.1.1. Dominant Generators
4.1.2. Generator Severity
4.2. Construction of Feature Extraction in Feed-Forward Propagation
4.3. ECAP
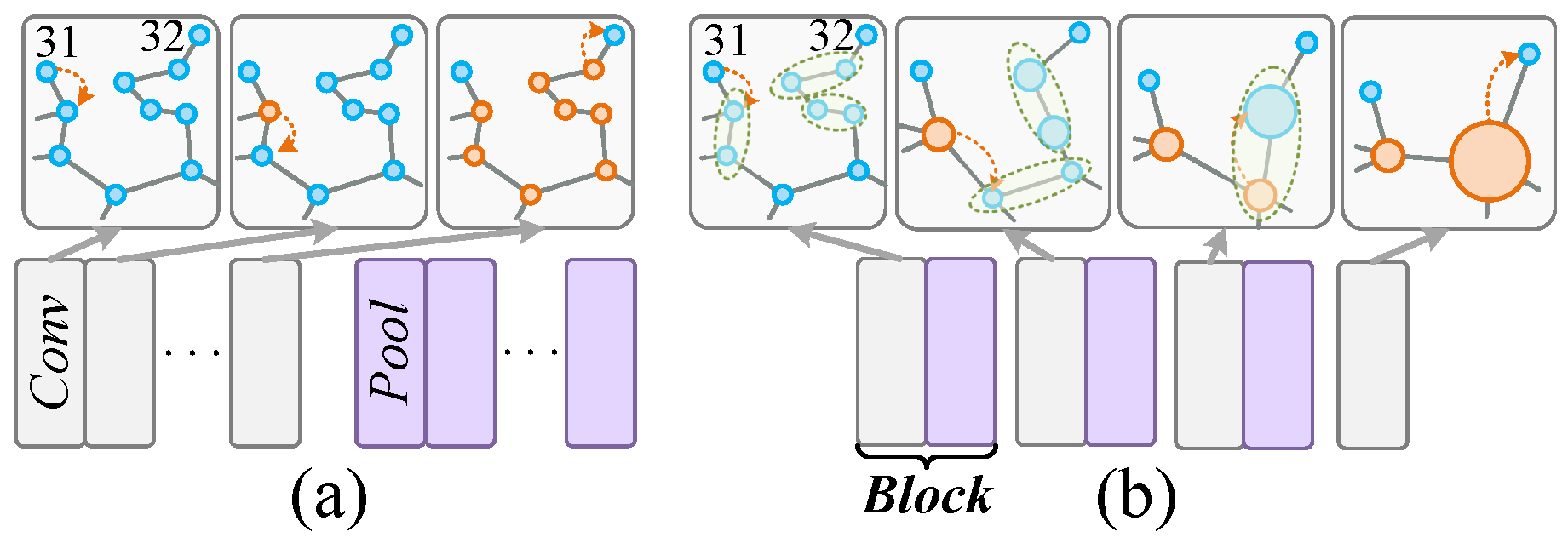
4.3.1. The Pooling Template
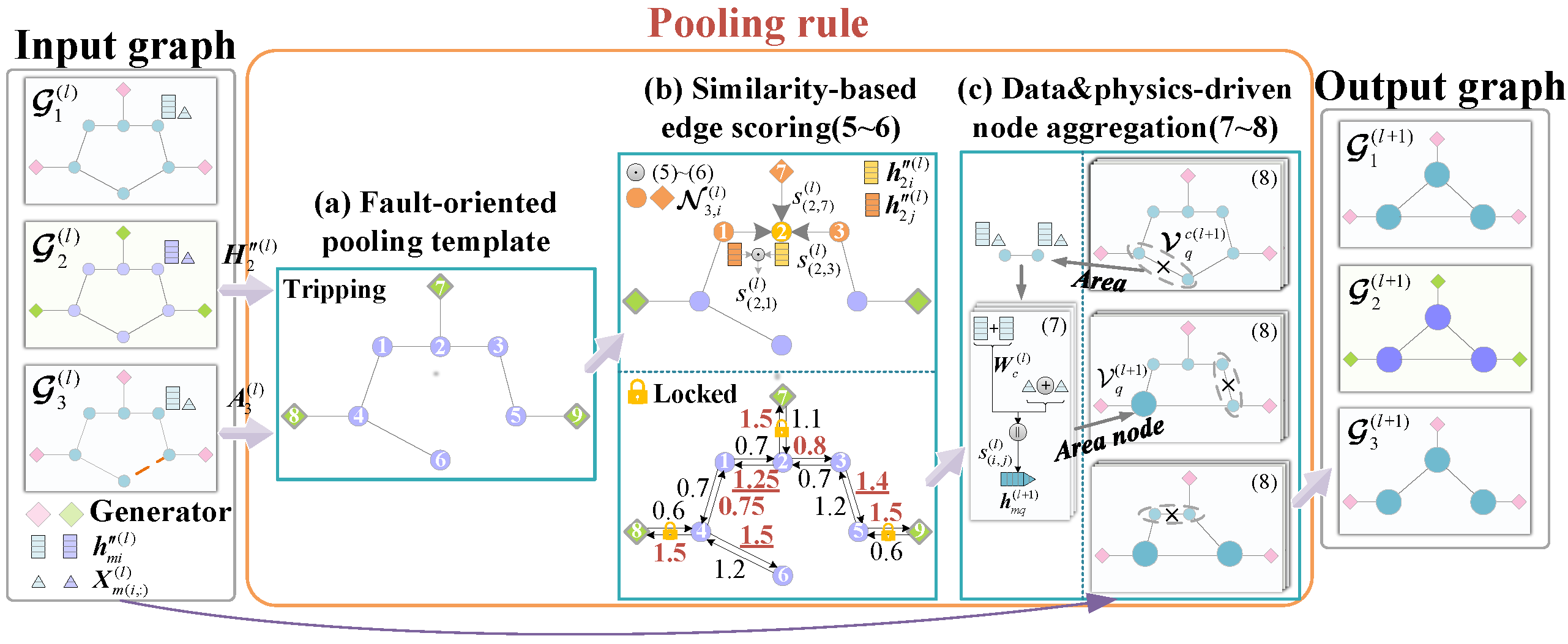
4.3.2. The Pooling Operation
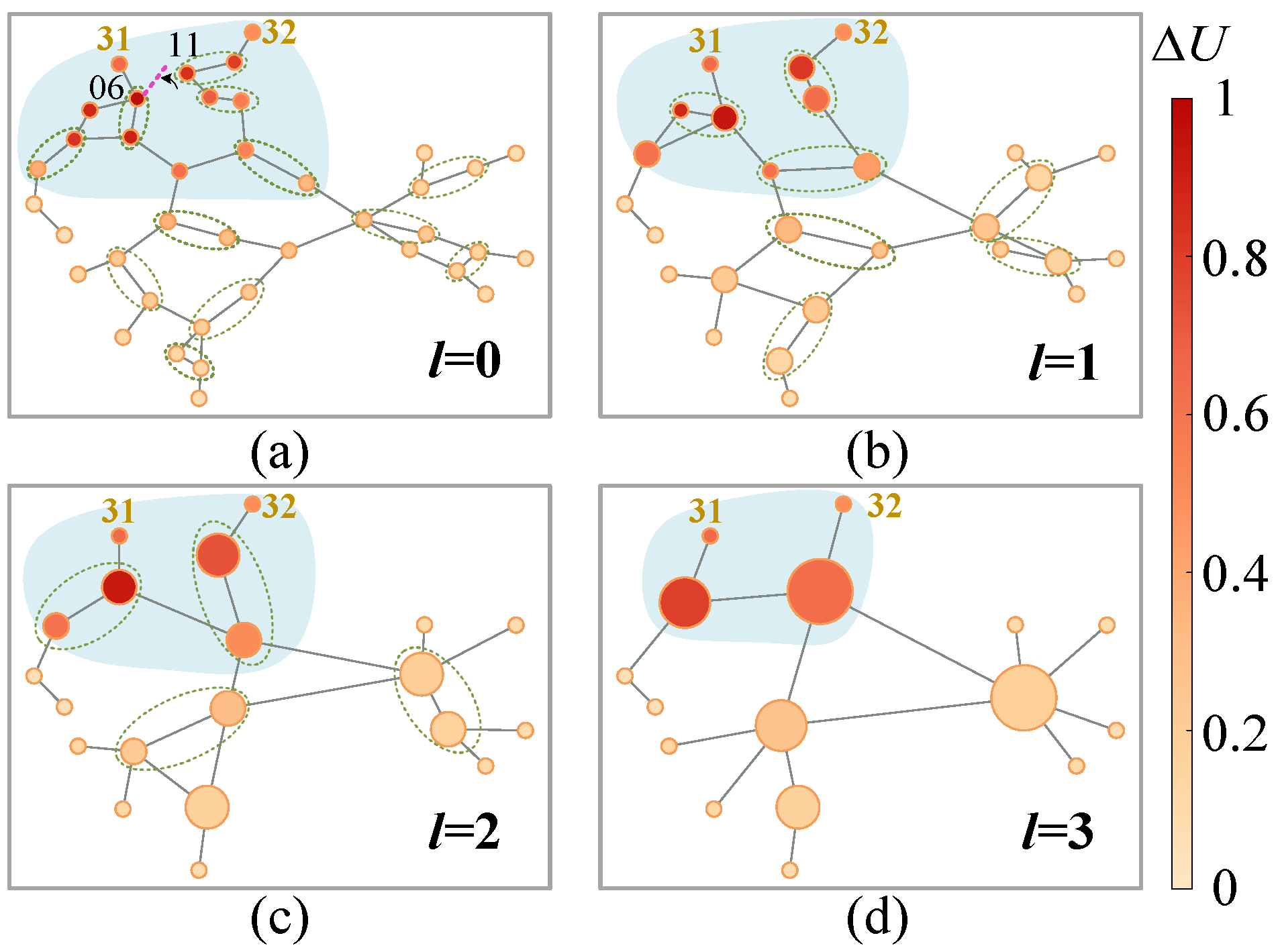
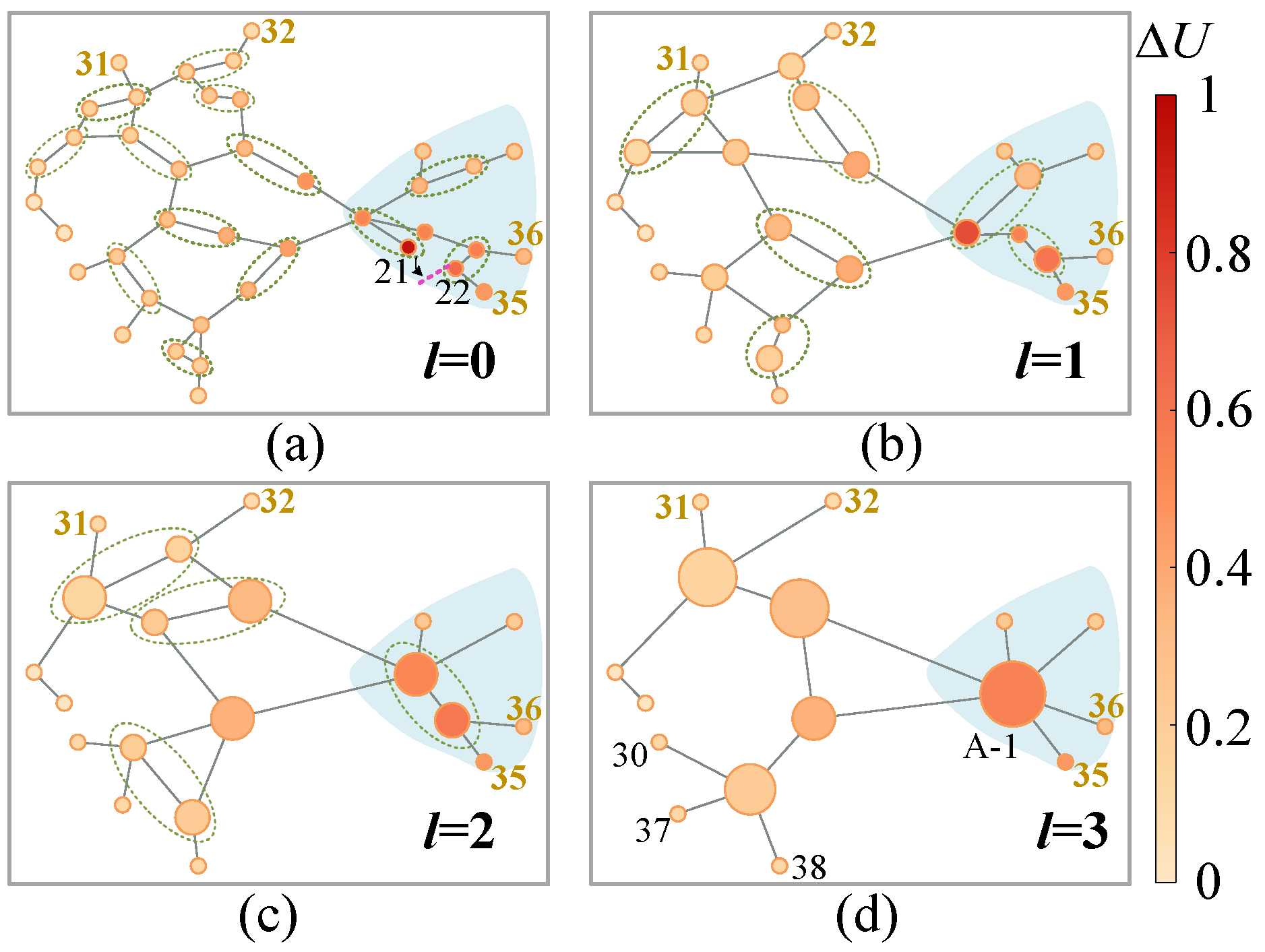
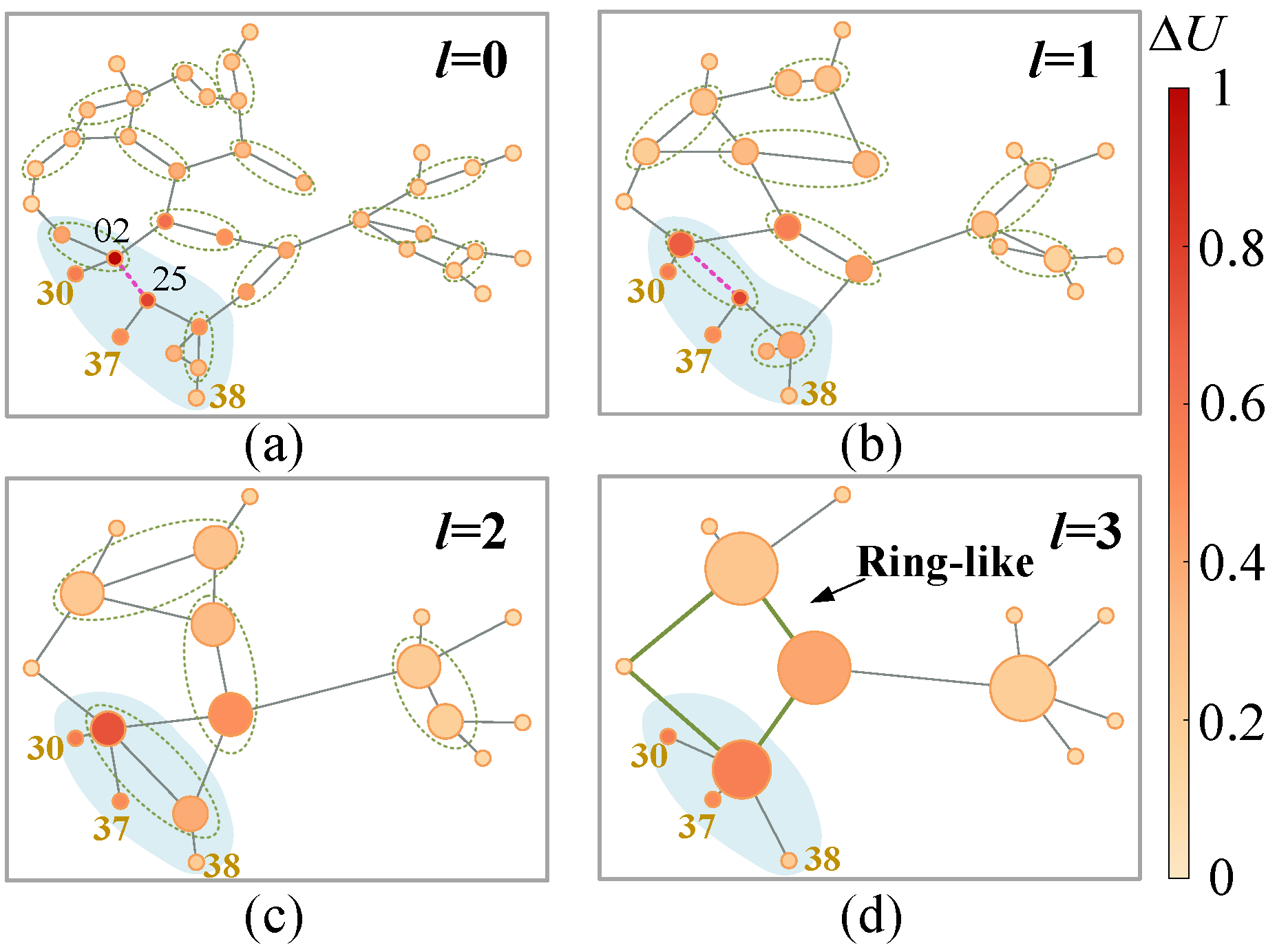
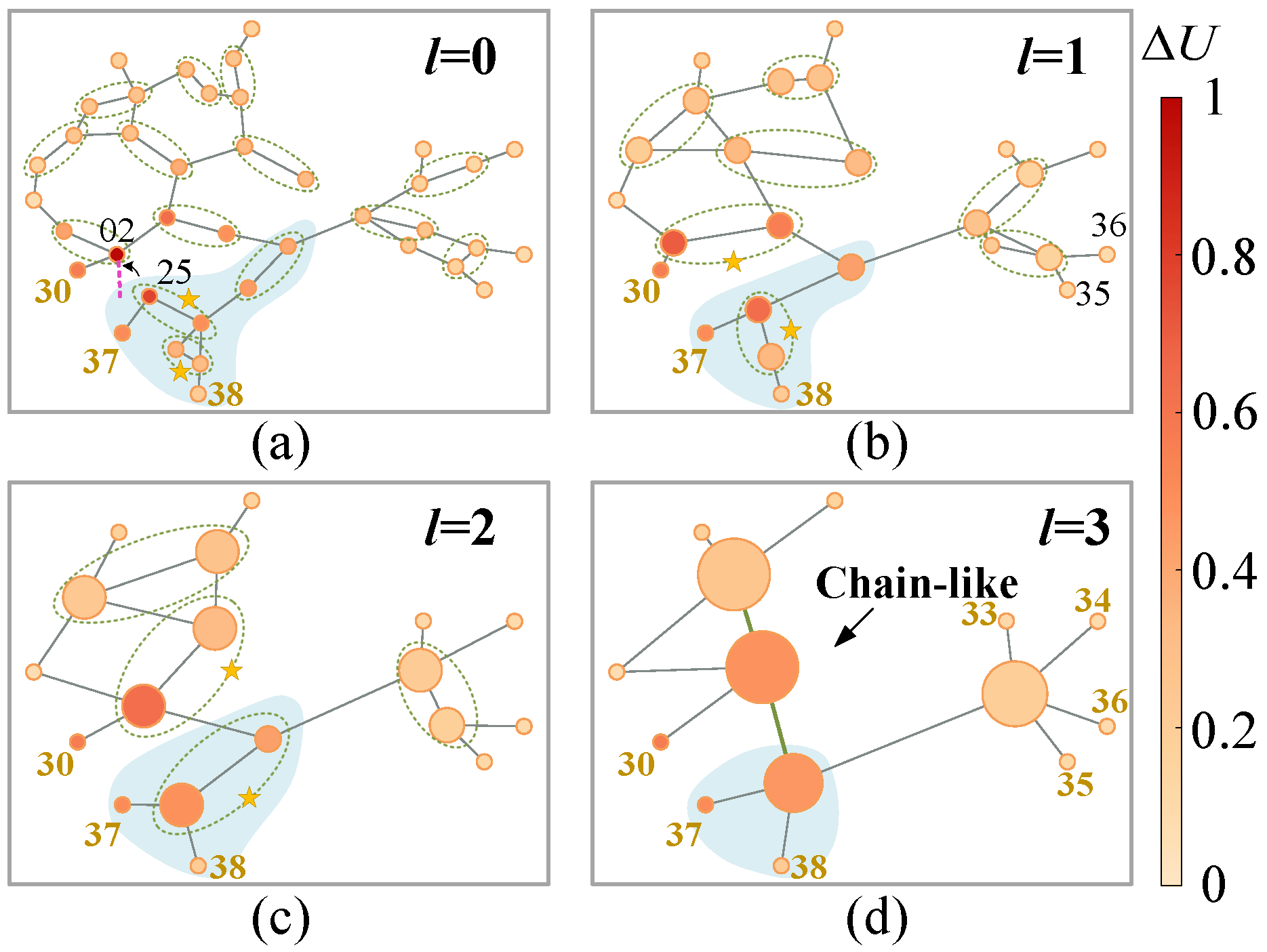
- The edge contraction criterionTo preserve the inter-node difference as much as possible, node similarity is preferred as the edge contraction criterion. The first-order neighborhood representations involving continuous attributes and discrete topologies are available from convolutions. An attention mechanism is required [23]:where denotes the row of and the first-order neighborhood set comes from . Hence, the attention coefficients vary as the pooling template changes, which meets the principle I. refers to the LeakyReLu function. refers to the parameter matrix of attention head. Diehl et al. [23] indicate that the mean of edge scores should be close to 1 considering the numerical stability of model training. Specifically, the node similarity is quantified by the edge scoreHere, edge attention coefficients are averaged. Note that is common after the softmax operation and the mergence is actually directional. Define as the edge score from node to node . Only consider unidirectional mergence along the one of larger value is considered, i.e, if , the smaller is ignored during mergence. It means the is combined to along the edge . In Figure 6b, obtains its neighborhood edge scores through (7)∼(8) and the scores highlighted in red are left.Generally, the areas are produced according to from high to low. Extra limits are also required considering the nature of the power system. On the one hand, generators are usually connected to the main network through substation branches. Edges derived from such branches rank the highest after (7)∼(8), which might cause all the key generators to be merged during the first pooling. This violates the requirement in principle I. Hence, generators and relevant edges are “locked”, i.e., independent from the pooling. On the other, an area node should share the same physical meaning with the area. It means a node can only be assigned to an area during an ECAP. Two areas or an area and a node are not allowed to be merged since (7) does not define their similarity. An ECAP ends only when no node meets the above limits. In this way, the flexibility is enhanced since no extra hyper-parameters is required for such scale reduction.
- Generation rule for a new graphLet an area and its area node be , . The features of are described as follows.where represents the transformation matrix for the data-driven features (left). The physical features (right) promote inter-node distinction in the new graphs and enhance the feature-level interpretability. As Figure 6c, weights the features after calculating in each graph such that ECAP pay less attention to those areas including nodes with low similarity.In addition, the new graphs are expected to reflect the sparsity in the original topologies. Hence, the edges in the old graphs are all preserved. Take an area node in the graph as an example. Its first-order neighborhood is expressed asWhen the number of edges is greater than one, the areas are connected with multiple tie-lines. In this sense, the edge weights are summed in light of the aggregation of parallel transmission lines in the power system. Such topology generation ensures path simplification among nodes as well as network sparsity. This meets principle II and enables topology-level interpretability.
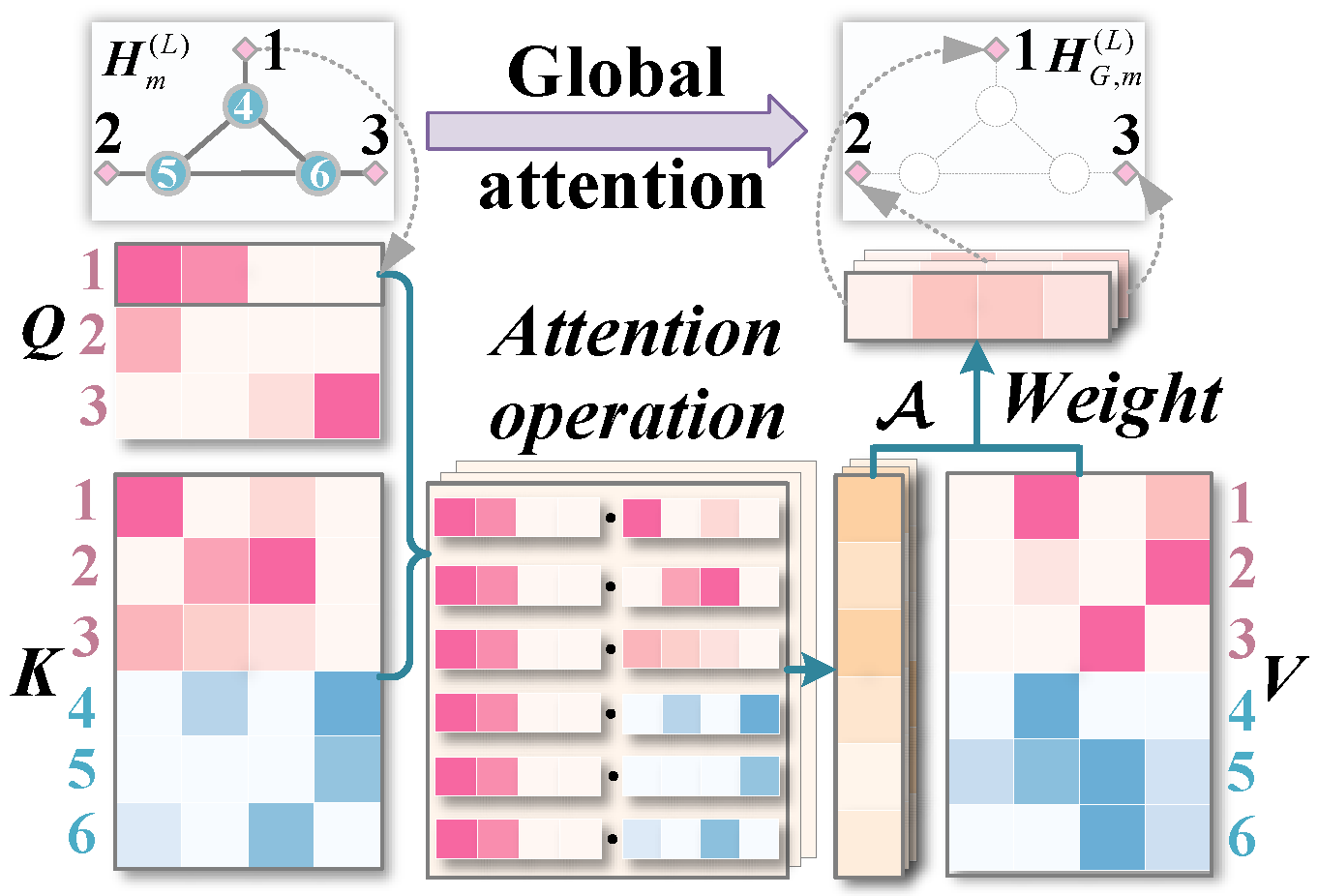
4.4. Global Attention Pooling
4.5. Downstream Link
5. Training and Evaluation of ECAP&GAP-GTSA Scheme
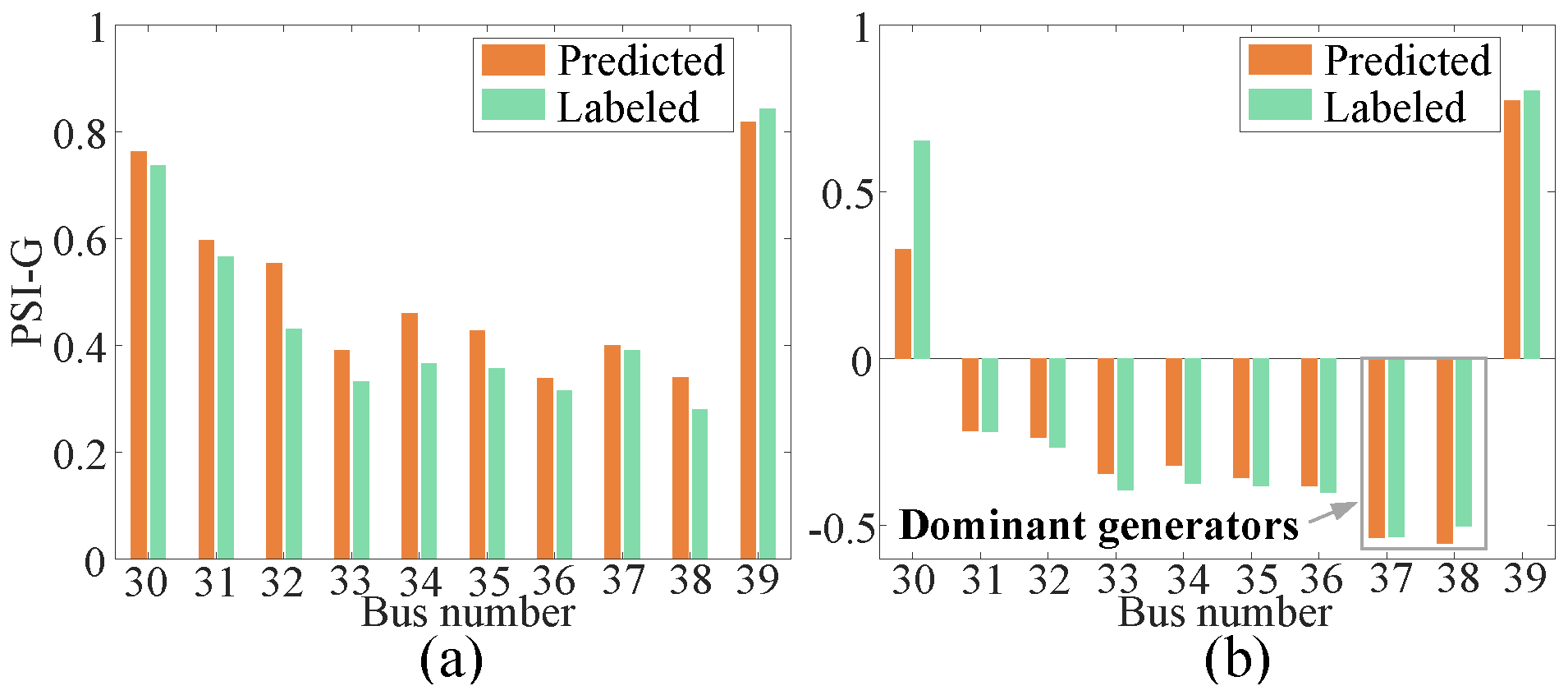
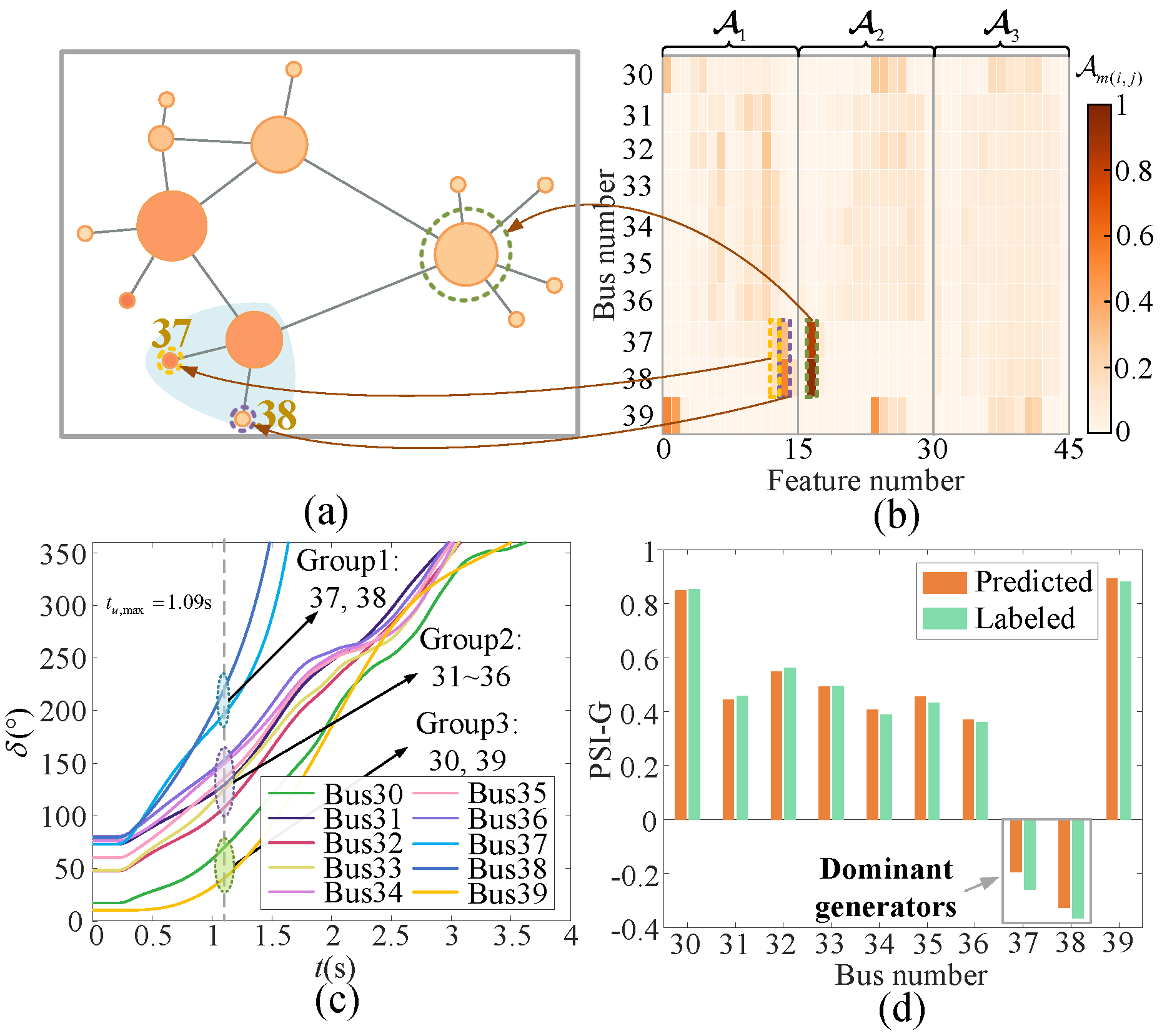
5.1. The Assistant Decision-Making of Generator
5.2. Loss Function
5.3. Definition of Evaluation Metrics
6. Case Studies
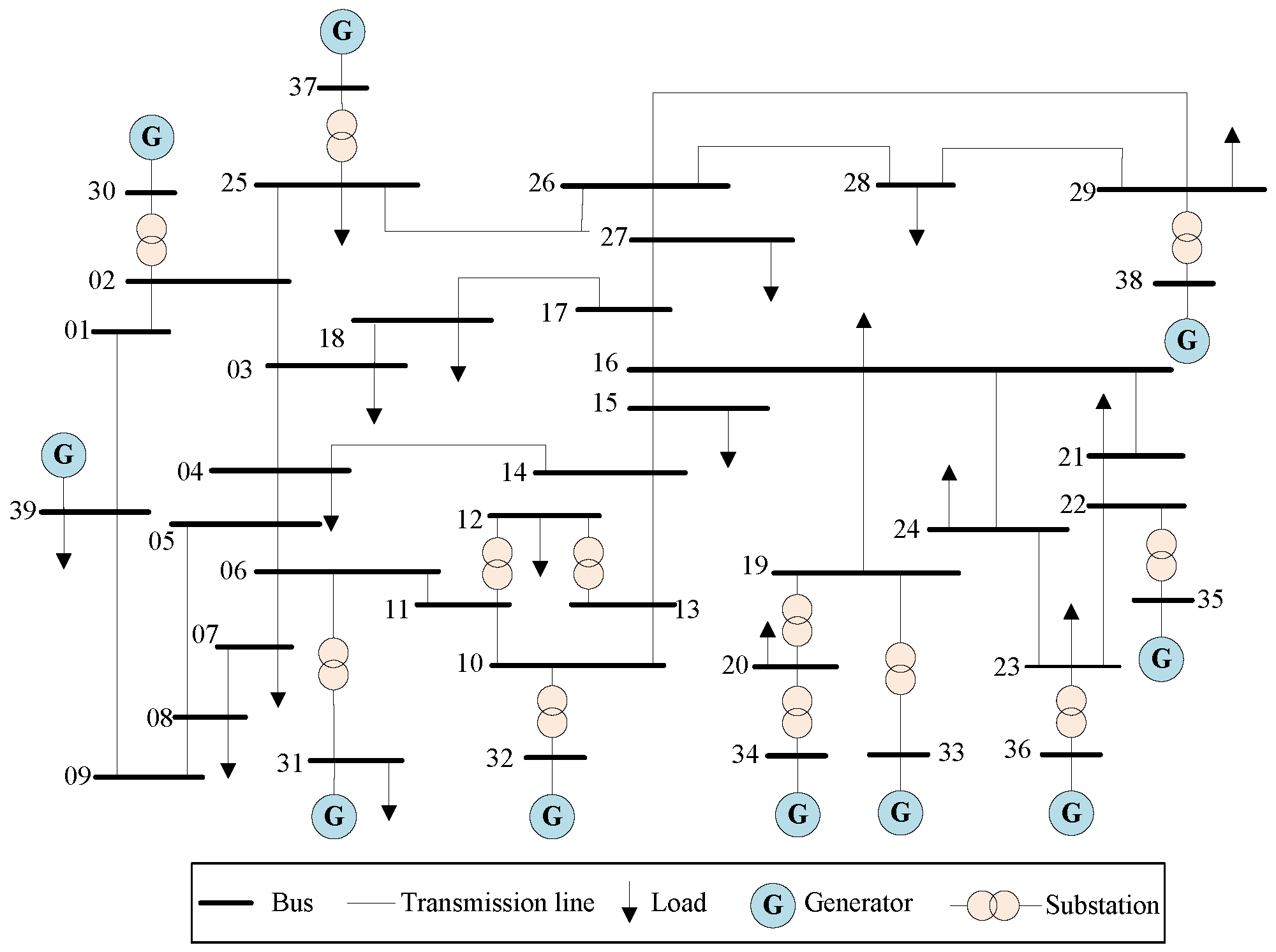
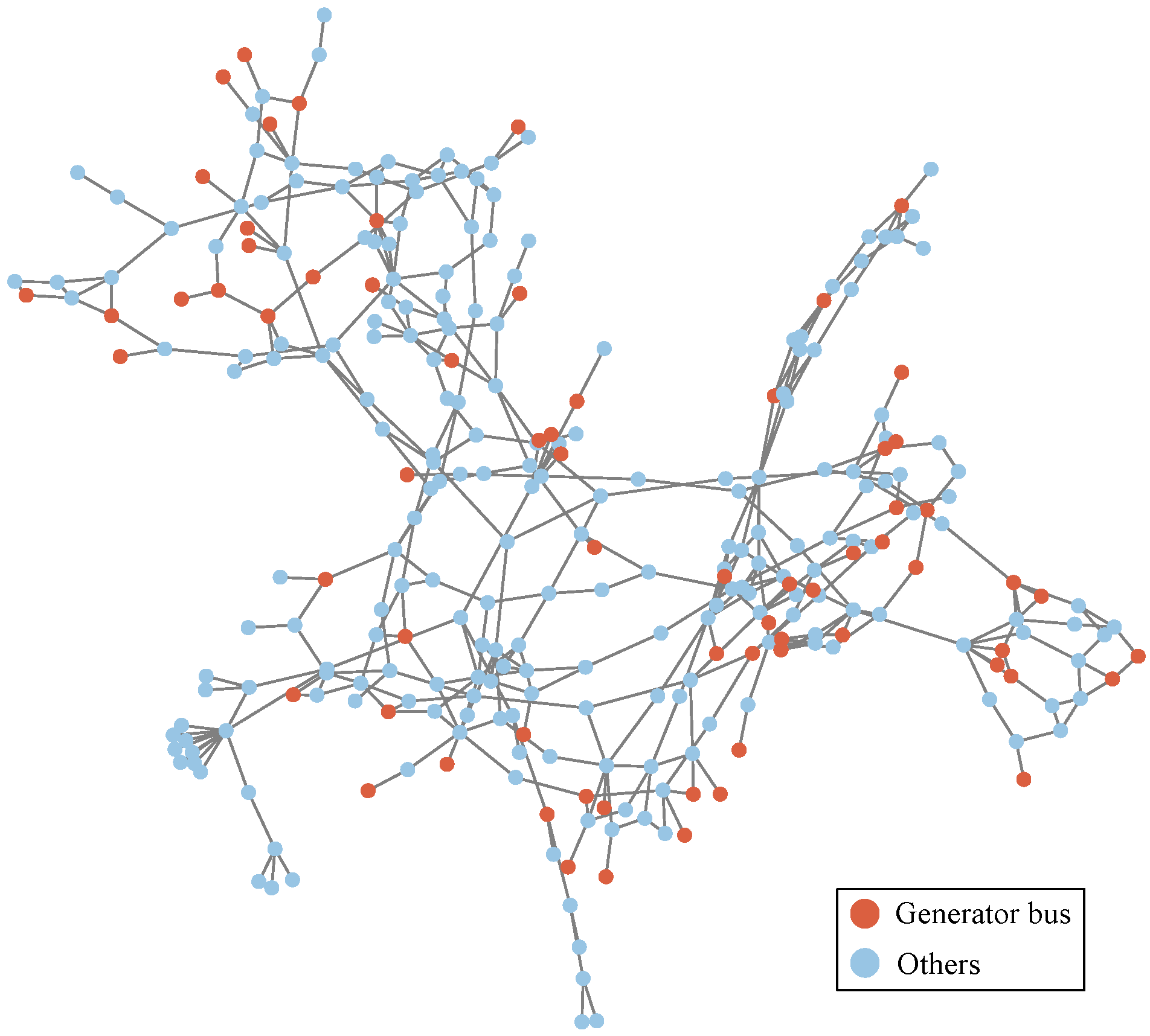
6.1. Test System and Model Setting
6.2. Comparisons with Existing GTSA Models
6.3. Pooling Methods and Structure Comparisons
6.4. Detailed Advantage Analysis of Sparse Hybrid Pooling
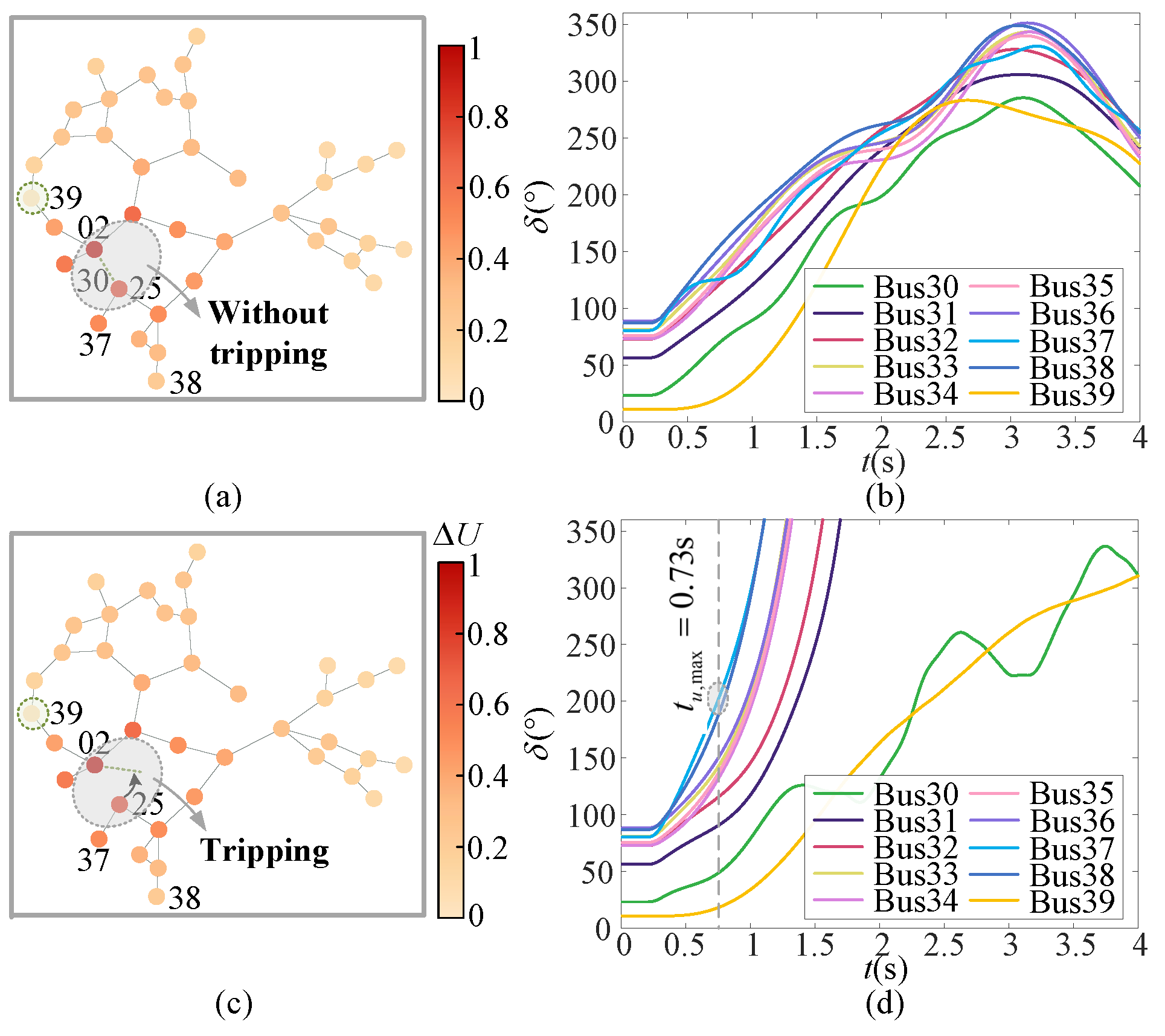
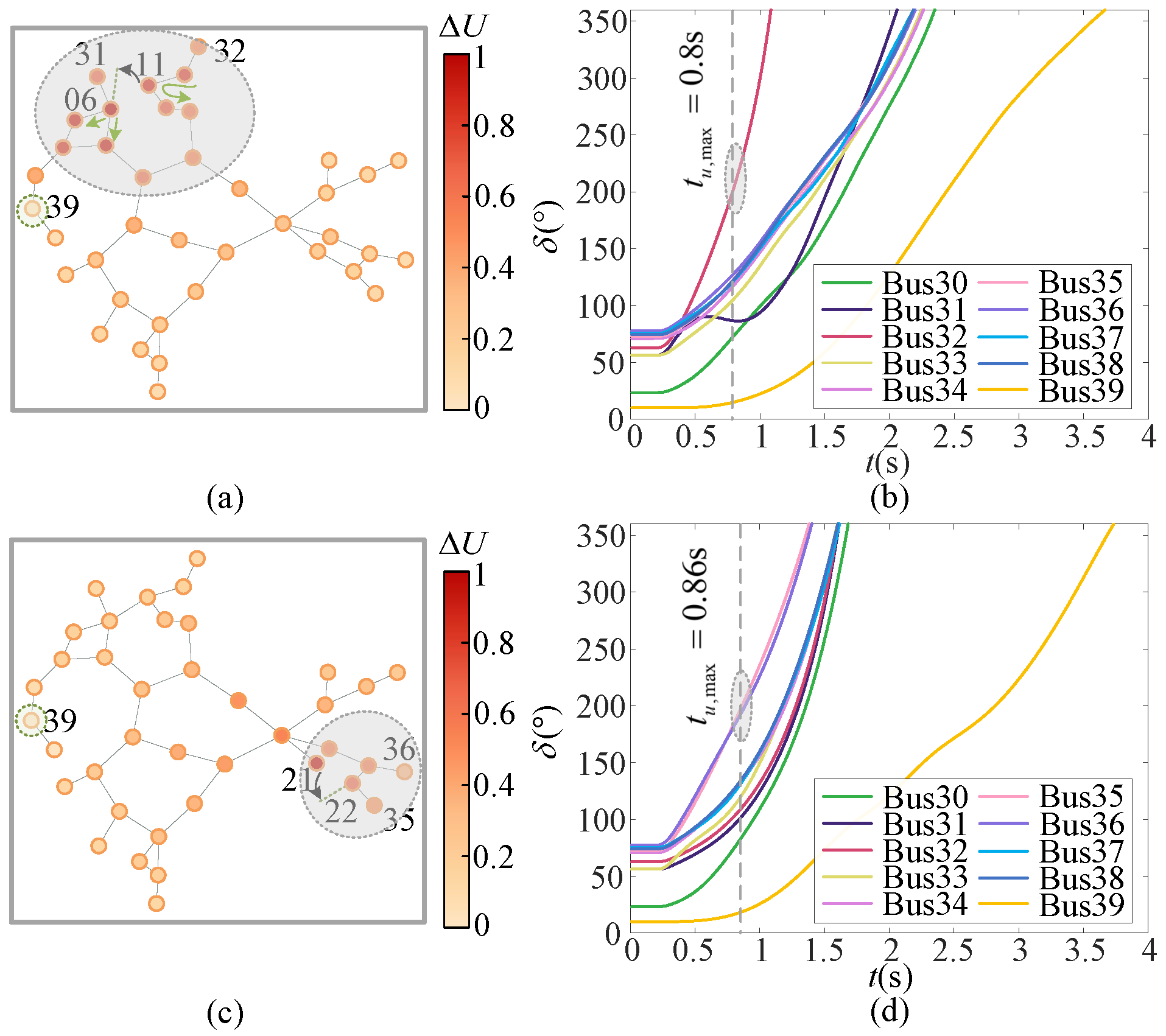
6.4.1. Ecap Visualization
6.4.2. Gap Visualization
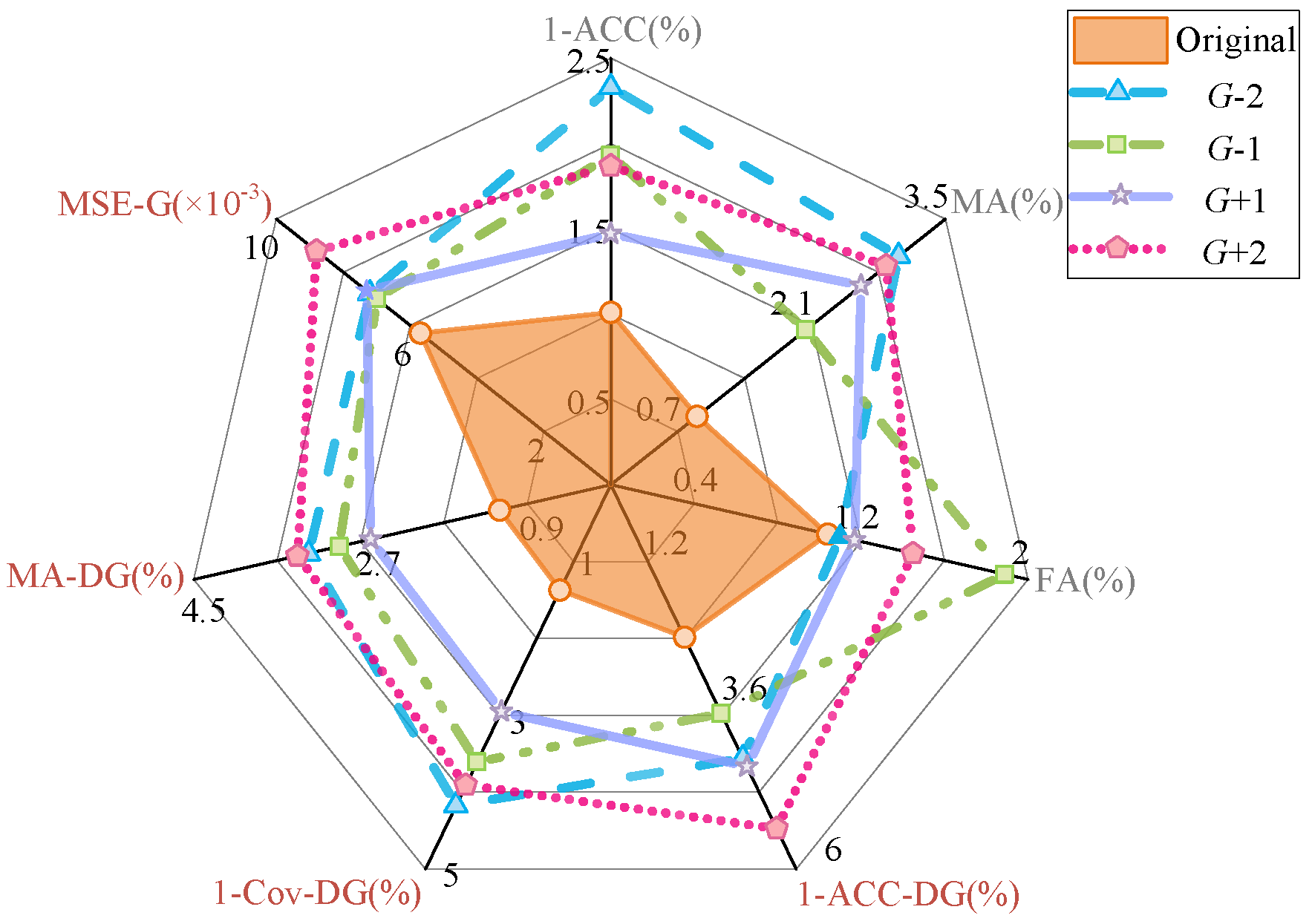
6.5. Robustness and Scalability to Generator-Scale Changes
6.5.1. Modified IEEE 39-Bus Systems
6.5.2. IEEE 300-Bus System
7. Conclusions
8. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| TDS | Time-domain simulation |
| TSA | Transient stability assessment |
| ML | Machine learning |
| GTSA | Generator-level transient stability assessment |
| SVM | Support vector machine |
| ANN | Artificial neural network |
| RF | Random forest |
| DL | Deep learning |
| CNN | Convolutional neural network |
| LSTM | Long short-term menmory |
| ViT | Vision Transformer |
| RGCN | Recurrent graph convolutional network |
| ECAP | Edge Contraction-based Attention Pooling |
| GAP | Global Attention Pooling |
| DGP | Dominant generator predictor |
| GPP | Generator perturbation predictor |
| ADM-G | Assistant decision-making of generator |
| ACC-DG | Accuracy of dominant generator sets |
| MA-DG | miss alarm of dominant generators |
| Cov-DG | Accuracy of dominant generator sets |
| The piece transient stability index of the generator | |
| N, | The number of buses, the number of those connected with generator in a power system |
| , | The state variables, algebraic variables |
| Parameterized topologies | |
| , | Input graphs and nodes |
| , | Input node feature matrix, adjacency matrix |
| The angle of the generator at the moment t | |
| The maximum angle difference among any two generator at the moment t | |
| The maximum relative angle difference | |
| The first time exceeds | |
| ,, | The generator set, dominant generator set, unstable generator set |
| , | The number threshold of generator, time window of the affinity propagation (AP) cluster |
| , | The similarity matrix, its element of the affinity propagation (AP) cluster |
| The generator pair at the moment t that accounts for | |
| The dominant status of the generator | |
| The TDS curves of the voltage phase of the chosen reference bus | |
| , | The instablity time and its normalized version of the generator |
| A constant that represents the maximum of all in the history data | |
| , | The mean, variance of all in the history data |
| The modulation factor of PSI-G | |
| The sigmoid function | |
| The LeakyReLu function | |
| The parameter to form an uncertain area | |
| , | The output matrix, its row vector of the graph in the graph convolution (“Conv”) layer |
| , | The (coarsened) system scale and feature dimension in the graph pooling (“Pool”) layer |
| , | The (coarsened) system scale and feature dimension in the ECAP layer |
| , | The node sets of the old graph to be merged in the ECAP layer, the node of the new graph in the ECAP layer |
| The number of attention heads of ECAP layers | |
| The parameter matrix of the attention head | |
| The attention coefficient from node j to node i of the head in the ECAP layer | |
| The edge score from node to node | |
| The 1st-order neighborhood set of the node in the graph | |
| The transformation matrix for the data-driven features | |
| , | The features of all the nodes, the generator nodes in the output coarsened graph |
| ,, | The parameter matrics to generate keys, queries and values |
| The attention matrix of the graph in the GAP | |
| , | The final representation(s) of all the generators, the generator |
| , | The function of DSP, GPP |
| , | The confidence level of , the prediction of |
| ∼ | The logical signals derived from the model prediction |
| ,, | The prediction of dominant generator, generator severity vector, system-level stability category after the ADM-G |
| ,,, | The loss functions concerning the whole model, DGP, GPP, sparsity |
References
- Obuz, S.; Ayar, M.; Trevizan, R.D.; Ruben, C.; Bretas, A.S. Renewable and energy storage resources for enhancing transient stability margins: A PDE-based nonlinear control strategy. Int. J. Elec. Power 2020, 116, 105510. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Hill, D.J.; Lam, A.Y.S.; Gu, J.; Li, V.O.K. Intelligent Time-Adaptive Transient Stability Assessment System. IEEE Trans. Power Syst. 2016, 33, 1049–1058. [Google Scholar] [CrossRef]
- Yan, R.; Geng, G.; Jiang, Q.; Li, Y. Fast transient stability batch assessment using cascaded convolutional neural networks. IEEE Trans. Power Syst. 2019, 34, 2802–2813. [Google Scholar] [CrossRef]
- Shi, Z.; Yao, W.; Zeng, L.; Wen, J.; Fang, J.; Ai, X.; Wen, J. Convolutional neural network-based power system transient stability assessment and instability mode prediction. Appl. Energy 2020, 263, 114586. [Google Scholar] [CrossRef]
- Lotufo, A.D.P.; Lopes, M.L.M.; Minussi, C.R. Sensitivity analysis by neural networks applied to power systems transient stability. Electr. Power Syst. Res. 2007, 77, 730–738. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Ji, L.; Yu, Z.; Lin, K.; Hao, L. Transient stability preventive control of power systems using chaotic particle swarm optimization combined with two-stage support vector machine. Electr. Power Syst. Res. 2018, 155, 111–120. [Google Scholar] [CrossRef]
- Liu, X.; Min, Y.; Chen, L.; Zhang, X.; Feng, C. Data-driven transient stability assessment based on kernel regression and distance metric learning. J. Mod. Power Syst. Cle. 2020, 9, 27–36. [Google Scholar] [CrossRef]
- Liu, Y.; Zhai, M.; Jin, J.; Song, A.; Zhao, Y. Intelligent Online Catastrophe Assessment and Preventive Control via a Stacked Denoising Autoencoder. Neurocomputing 2019, 380, 306–320. [Google Scholar] [CrossRef]
- Ren, J.; Chen, J.; Shi, D.; Li, Y.; Li, D.; Wang, Y.; Cai, D. Online multi-fault power system dynamic security assessment driven by hybrid information of anticipated faults and pre-fault power flow. Int. J. Electr. Power 2022, 136, 107651. [Google Scholar] [CrossRef]
- Wang, K.; Wei, W.; Xiao, T.; Huang, S.; Zhou, B.; Diao, H. Power system preventive control aided by a graph neural network-based transient security assessment surrogate. Energy Rep. 2022, 8, 943–951. [Google Scholar] [CrossRef]
- Huang, J.; Guan, L.; Su, Y.; Yao, H.; Guo, M.; Zhong, Z. A topology adaptive high-speed transient stability assessment scheme based on multi-graph attention network with residual structure. Int. J. Elec. Power 2021, 130, 106948. [Google Scholar] [CrossRef]
- Huang, J.; Guan, L.; Su, Y.; Yao, H.; Guo, M.; Zhong, Z. System-Scale-Free Transient Contingency Screening Scheme Based on Steady-State Information: A Pooling-Ensemble Multi-Graph Learning Approach. IEEE Trans. Power Syst. 2021, 37, 294–305. [Google Scholar] [CrossRef]
- Huang, J.; Guan, L.; Chen, Y.; Zhu, S.; Chen, L.; Yu, J. A deep learning scheme for transient stability assessment in power system with a hierarchical dynamic graph pooling method. Int. J. Electr. Power 2022, 141, 108044. [Google Scholar] [CrossRef]
- Guo, T.; Milanović, J.V. Online identification of power system dynamic signature using PMU measurements and data mining. IEEE Trans. Power Syst. 2015, 31, 1760–1768. [Google Scholar] [CrossRef]
- Frimpong, E.; Asumadu, J.; Okyere, P. Real time prediction of coherent generator groups. J. Electr. Eng. 2016, 16, 47–56. [Google Scholar]
- Siddiqui, S.A.; Verma, K.; Niazi, K.; Fozdar, M. Real-time monitoring of post-fault scenario for determining generator coherency and transient stability through ANN. IEEE Trans. Ind. Appl. 2017, 54, 685–692. [Google Scholar] [CrossRef]
- Mazhari, S.M.; Safari, N.; Chung, C.; Kamwa, I. A quantile regression-based approach for online probabilistic prediction of unstable groups of coherent generators in power systems. IEEE Trans. Power Syst. 2018, 34, 2240–2250. [Google Scholar] [CrossRef]
- Pavlatos, C.; Makris, E.; Fotis, G.; Vita, V.; Mladenov, V. Enhancing Electrical Load Prediction Using a Bidirectional LSTM Neural Network. Electronics 2023, 12, 4652. [Google Scholar] [CrossRef]
- Gupta, A.; Gurrala, G.; Sastry, P.S. An Online Power System Stability Monitoring System Using Convolutional Neural Networks. IEEE Trans. Power Syst. 2019, 34, 864–872. [Google Scholar] [CrossRef]
- Fang, J.; Liu, C.; Zheng, L.; Su, C. A data-driven method for online transient stability monitoring with vision-transformer networks. Int. J. Electr. Power 2023, 149, 109020. [Google Scholar] [CrossRef]
- Zhu, L.; Wen, W.; Li, J.; Hu, Y. Integrated Data-Driven Power System Transient Stability Monitoring and Enhancement. IEEE Trans. Power Syst. 2023, 39, 1797–1809. [Google Scholar] [CrossRef]
- Huang, J.; Guan, L.; Su, Y.; Yao, H.; Guo, M.; Zhong, Z. Recurrent Graph Convolutional Network-Based Multi-Task Transient Stability Assessment Framework in Power System. IEEE Access 2020, 8, 93283–93296. [Google Scholar] [CrossRef]
- Diehl, F.; Brunner, T.; Le, M.T.; Knoll, A. Towards graph pooling by edge contraction. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Xue, Y.; Van Custem, T.; Ribbens-Pavella, M. Extended equal area criterion justifications, generalizations, applications. IEEE Trans. Power Syst. 1989, 4, 44–52. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Baek, J.; Kang, M.; Hwang, S.J. Accurate Learning of Graph Representations with Graph Multiset Pooling. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
| Layer | IEEE 39-Bus System | IEEE 300-Bus System | ||
|---|---|---|---|---|
| DGP | GPP | DGP | GPP | |
| Graph embedding (input size, output size, head(s)) | ||||
| conv1 | (3 × 39 × 5, 3 × 39 × 16, 6) | (3 × 300 × 5, 3 × 300 × 16, 6) | ||
| ecap1 | (3 × 39 × 96, 3 × × 96, 6) | (3 × 300 × 96, 3 × × 101, 6) | ||
| conv2 | (3 × × 101, 3 × × 24, 6) | (3 × × 101, 3 × × 16, 6) | ||
| ecap 2 | (3 × × 144, 3 × × 149, 6) | (3 × × 96, 3 × × 101, 6) | ||
| conv3 | (3 × × 149, 3 × × 32, 6) | (3 × × 101, 3 × × 24, 6) | ||
| ecap3 | (3 × × 192, 3 × × 197, 6) | (3 × × 144, 3 × × 149, 6) | ||
| conv4 | (3 × × 192, 3 × × 48, 6) | (3 × × 49, 3 × × 24, 6) | ||
| ecap 4 | - | (3 × × 144, 3 × × 149, 6) | ||
| conv5 | - | (3 × × 149, 3 × × 32, 6) | ||
| Global attention pooling (input size, output size) | ||||
| gap | (3 × × 192, × 864) | (3 × × 149, × 576) | ||
| Downstream network (input size, output size) | ||||
| fc1 | (864,128) | (864,128) | (576,128) | (576,128) |
| fc2 | (128,16) | (128,16) | (128,16) | (128,16) |
| fc3 | (16,2) | (16,1) | (16,2) | (16,1) |
| System-Level | Generator-Level | ||||||
|---|---|---|---|---|---|---|---|
| Model | ACC | MA | FA | ACC-DG | Cov-DG | MA-DG | MSE-G |
| (%)↑ | (%)↓ | (%)↓ | (%)↑ | (%)↑ | (%)↓ | ()↓ | |
| SVM [14] | 92.21 | 18.65 | 5.40 | 88.38 | 65.09 | 32.68 | 18.4 |
| RF [17] | 92.12 | 25.28 | 4.04 | 89.25 | 58.88 | 47.63 | 19.7 |
| ANN [16] | 92.67 | 21.82 | 4.14 | 89.43 | 64.08 | 34.18 | 15.3 |
| CNN [19] | 91.02 | 12.31 | 8.25 | 88.09 | 73.10 | 17.91 | 22.6 |
| RGCN [22] | 94.11 | 7.35 | 5.57 | 91.99 | 84.70 | 14.31 | 12.9 |
| Proposed | 98.99 | 0.90 | 1.04 | 97.62 | 98.63 | 1.20 | 5.7 |
| System-Level | Generator-Level | ||||||
|---|---|---|---|---|---|---|---|
| Model | ACC | MA | FA | ACC-DG | Cov-DG | MA-DG | MSE-G |
| (%)↑ | (%)↓ | (%)↓ | (%)↑ | (%)↑ | (%)↓ | ()↓ | |
| 97.34 | 5.80 | 1.96 | 95.51 | 83.38 | 11.89 | 11.9 | |
| 98.37 | 3.05 | 1.32 | 96.53 | 91.87 | 6.91 | 6.7 | |
| →decoupled | 98.50 | 3.23 | 1.12 | 96.91 | 93.19 | 5.63 | 6.3 |
| Proposed | 98.99 | 0.90 | 1.04 | 97.62 | 98.63 | 1.20 | 5.7 |
| System-Level | Generator-Level | |||||
|---|---|---|---|---|---|---|
| ACC | MA | FA | ACC-DG | Cov-DG | MA-DG | MSE-G |
| (%)↑ | (%)↓ | (%)↓ | (%)↑ | (%)↑ | (%)↓ | ()↓ |
| 98.96 | 1.39 | 0.95 | 97.48 | 97.39 | 2.39 | 7.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Guan, L.; Su, Y.; Cai, Z.; Chen, L.; Li, Y.; Zhang, J. Generator-Level Transient Stability Assessment in Power System Based on Graph Deep Learning with Sparse Hybrid Pooling. Electronics 2025, 14, 1180. https://doi.org/10.3390/electronics14061180
Huang J, Guan L, Su Y, Cai Z, Chen L, Li Y, Zhang J. Generator-Level Transient Stability Assessment in Power System Based on Graph Deep Learning with Sparse Hybrid Pooling. Electronics. 2025; 14(6):1180. https://doi.org/10.3390/electronics14061180
Chicago/Turabian StyleHuang, Jiyu, Lin Guan, Yinsheng Su, Zihan Cai, Liukai Chen, Yongzhe Li, and Jinyang Zhang. 2025. "Generator-Level Transient Stability Assessment in Power System Based on Graph Deep Learning with Sparse Hybrid Pooling" Electronics 14, no. 6: 1180. https://doi.org/10.3390/electronics14061180
APA StyleHuang, J., Guan, L., Su, Y., Cai, Z., Chen, L., Li, Y., & Zhang, J. (2025). Generator-Level Transient Stability Assessment in Power System Based on Graph Deep Learning with Sparse Hybrid Pooling. Electronics, 14(6), 1180. https://doi.org/10.3390/electronics14061180






