Prediction of Dissolved Gases in Transformer Oil Based on CEEMDAN-PWOA-VMD and BiGRU
Abstract
1. Introduction
- In response to the high volatility and nonlinearity of the dissolved gases in transformer oil, a secondary decomposition approach is proposed. Specifically, the CEEMDAN decomposition method is applied for primary decomposition, then VMD secondary decomposition is utilized for the higher-complexity modal components.
- Since the key parameters of the VMD algorithm used in the secondary decomposition are dependent on subjective settings, it may lead to excessive reconstruction errors and a subsequent decrease in prediction accuracy. To address this issue, this paper proposes an improved WOA, which possesses strong global search capabilities, achieves optimized selection for the critical parameters of the VMD algorithm, and ensures the effectiveness of modal decomposition.
- Considering that WOA exhibits randomness in searching during the optimization process, which leads to fluctuations and uncertainties in the optimization, this study integrates WOA and the PPO algorithm, thereby effectively resolving the instability issues and enhancing the solution efficiency.
2. Primary Decomposition Based on CEEMDAN
- The signal is obtained by introducing different white noise sequences to , as shown in Equation (1).In the equation, is the initial time series signal; represents a random value following a standard normal distribution; and l is the number of experimental groups.
- Sequentially decompose each signal group using EMD, extract the first order component from each group, calculate their average, then obtain the first intrinsic mode function by Equation (2):The residual component at the initial phase is acquired by Equation (3).
- The j-th component after EMD is denoted as . On the basis of step (1), the remaining components of the (i − 1)-th stage are further decomposed to obtain the i-th , as follows:At this time, the remaining component obtained by decomposing i-th stage is
- Repeat step (3) until further decomposition is not possible, signifying the completion of the decomposition process. And the final residual term R(t) is obtained as follows:In Equation (6), I represents the number of mode components, and is finally decomposed as shown in Equation (7):The specific process is illustrated in Figure 1.
3. Secondary Decomposition Based on PWOA-VMD
3.1. Principle of VMD
3.2. Principle of WOA
3.2.1. Shrinking Encircling
3.2.2. Spiral Updating
3.2.3. Random Search
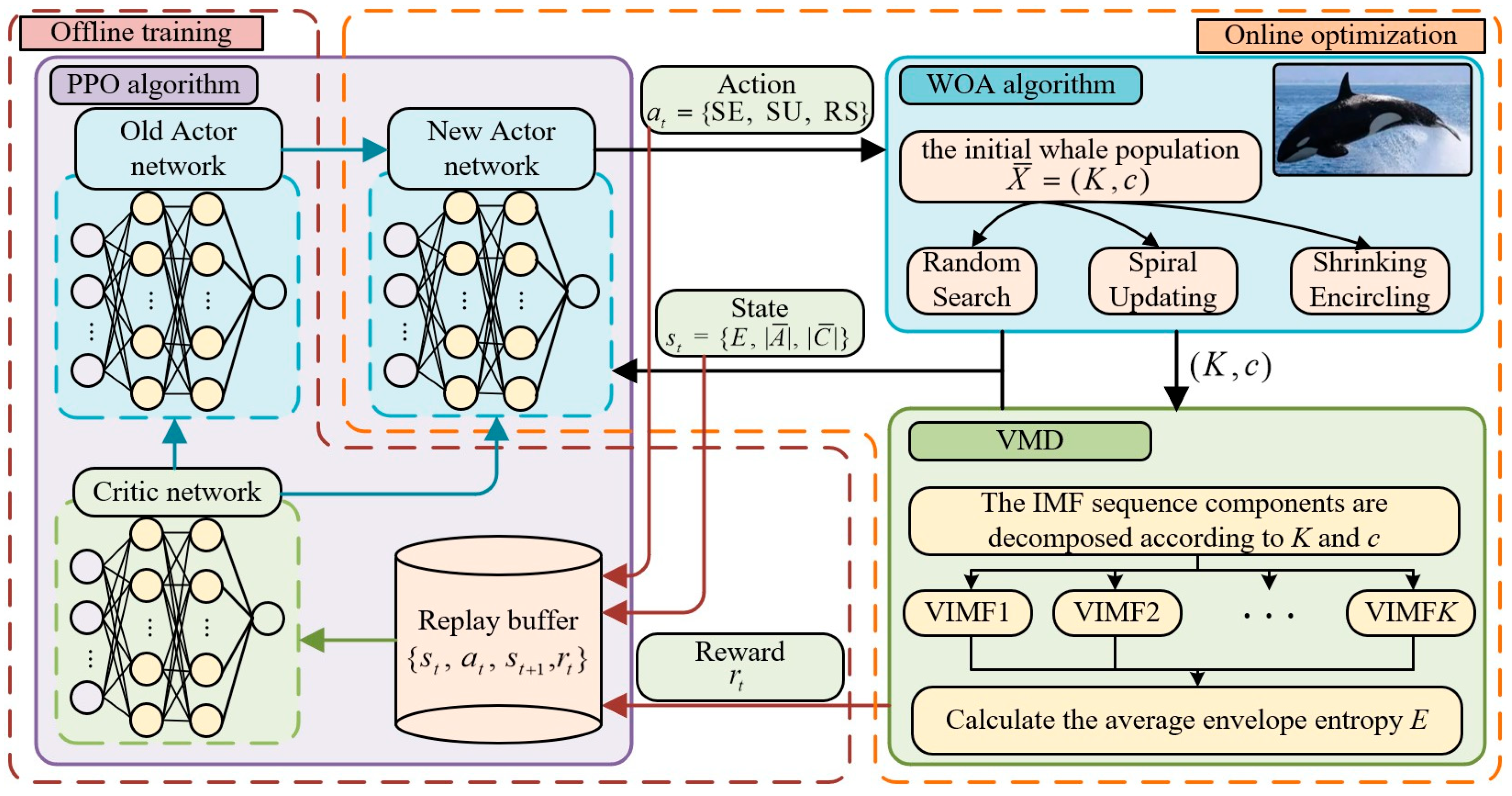
3.3. WOA Based on PPO Algorithm (PWOA)
3.3.1. The PPO Algorithm
3.3.2. Improve WOA Based on PPO
3.3.3. Markov Decision Process (MDP) for VMD Parameter Optimization Based on PWOA
- State space: The DRL algorithm’s observed state should supply sufficient information for the agent to make informed behavioral decisions at every iteration. In this article, in order to express the solution state of VMD through PWOA, the concept of envelope entropy is introduced. The envelope entropy reflects the sparsity of the signal, and its magnitude is inversely related to the periodicity of the signal. The greater the signal’s periodicity, the lower the envelope entropy. The average envelope entropy can be mathematically represented as follows:
- Action space: In each iteration of PPO, the agent is required to select the next action based on the present state. Likewise, in WOA, the agent must determine its hunting behavior according to the current circumstances. Consequently, the three hunting behaviors of WOA are correlated with the actions of the agent in PPO. Hence, the action space in this study is outlined as follows:
- Reward function: As the feedback of the environment to the action performed by the agent, it plays a key role in guiding the agent to select the best action. In this paper, the solution with a smaller envelope entropy is more favorable. Therefore, when the agent chooses an update action that reduces the envelope entropy, reward will be carried on; when it increases the envelope entropy, it should be punished. If the action has no effect on the envelope entropy, the reward value is set to zero. In summary, the definition of reward is as follows:
4. BiGRU Prediction Model
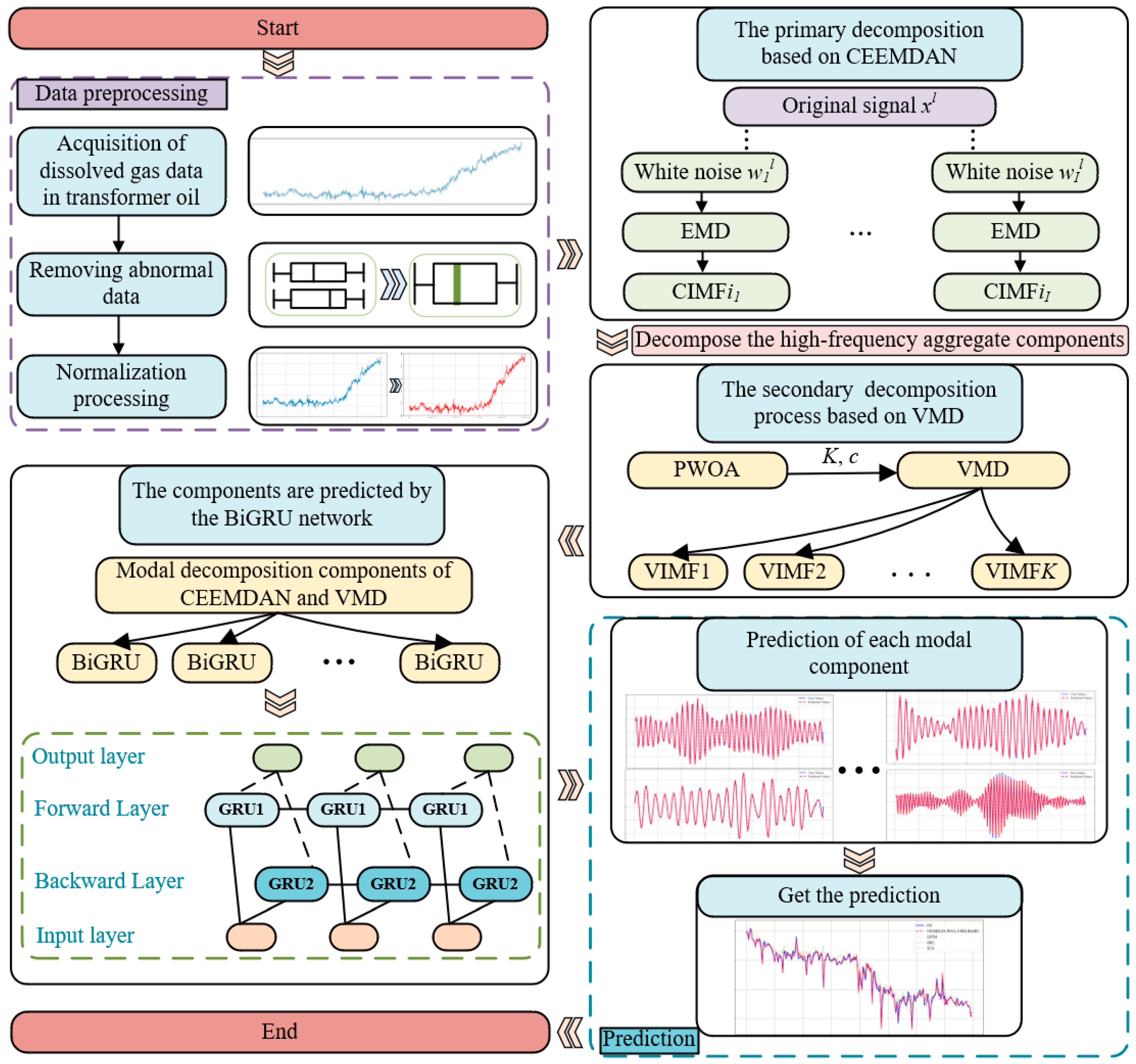
5. Prediction Process of Dissolved Gas in Transformer Oil Based on CEEMDAN-PWOA-VMD-BiGRU
- The original data of gas dissolved in the transformer oil are preprocessed, including Z-score outlier detection and linear interpolation. The specific equation is shown as follows:
- In the equation, represents the Z-score, represents the mean, and represents the standard deviation. If the calculated Z-score exceeds the predefined threshold, the data point is identified as an outlier.
- The preprocessed data is decomposed by CEEMDAN and the subsequences are obtained.
- The quantity of decomposition modes K of VMD and the penalty factor c are obtained by the PWOA, then the highly complex components of the subsequence are aggregated for VMD secondary decomposition to obtain the stable subsequence.
- The decomposition components of CEEMDAN and VMD are normalized.
- In the equation, represents the normalized value of ; and and represent the maximum and minimum values, respectively.
- The normalized data is sent to the BiGRU for forecasting, and the predictions of each component are combined to obtain the ultimate forecast results.
6. Case Study Analysis
6.1. CEEMDAN Decomposition of Gas Sequences
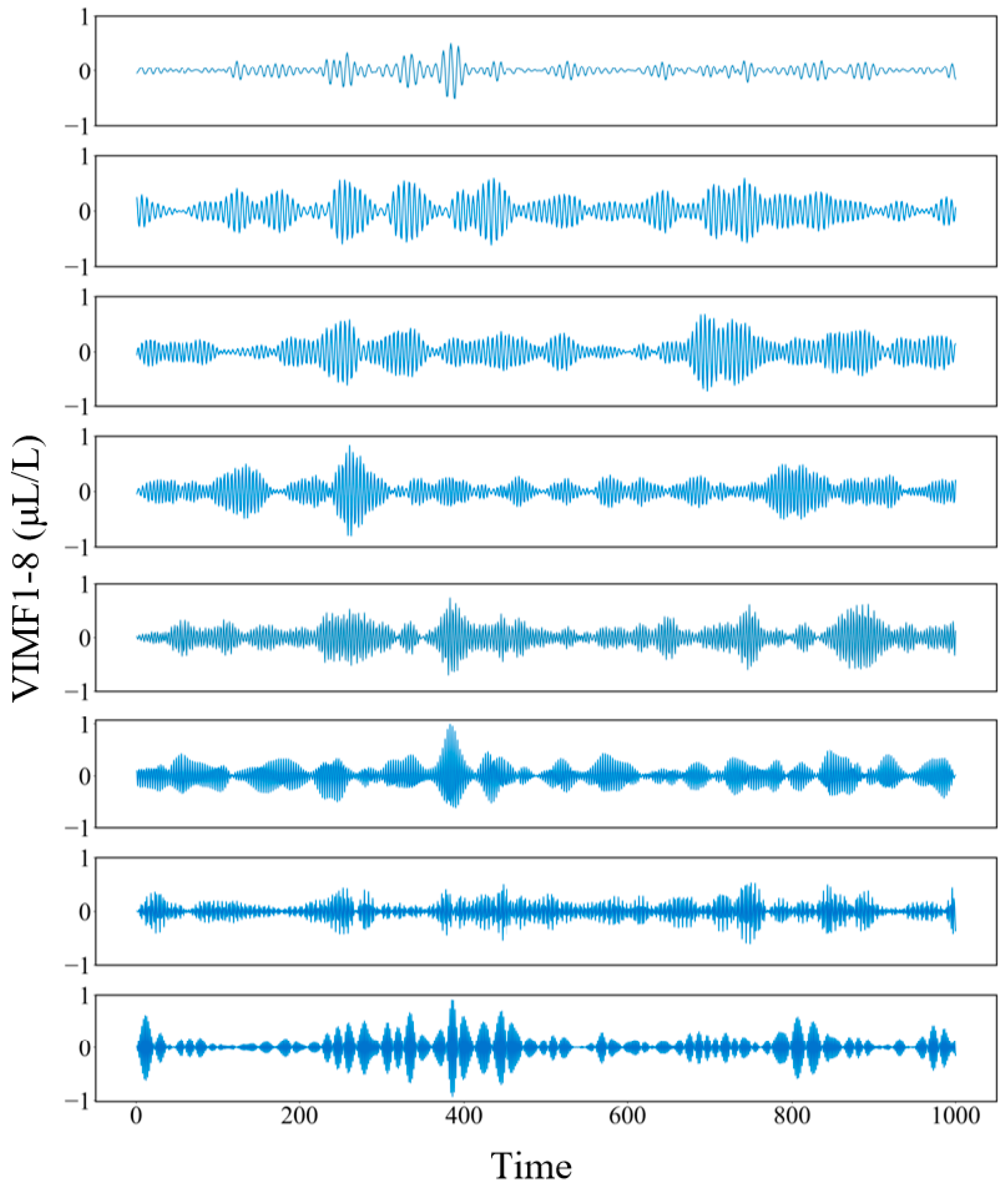
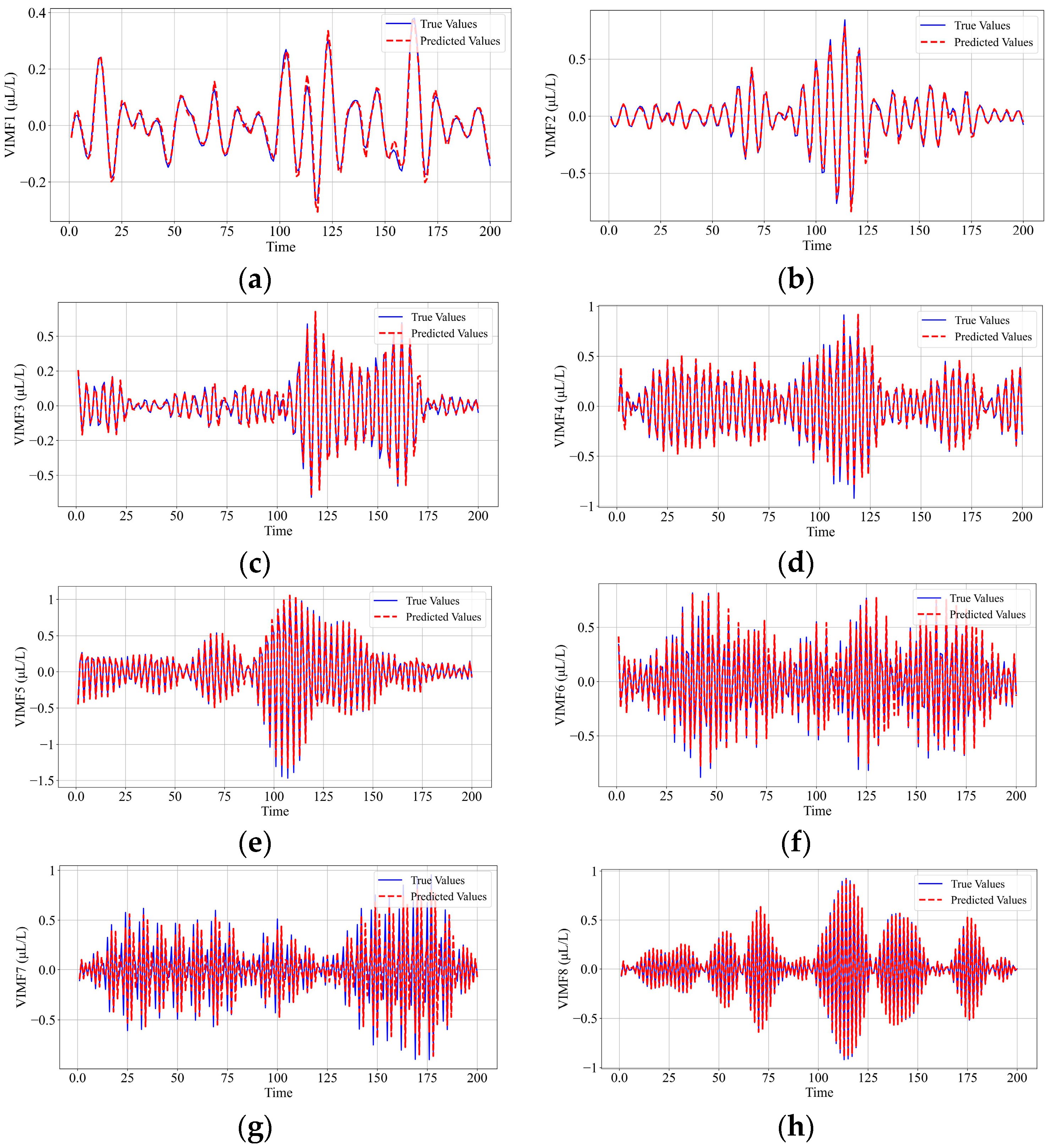
6.2. Secondary Decomposition by VMD of Gas Sequences
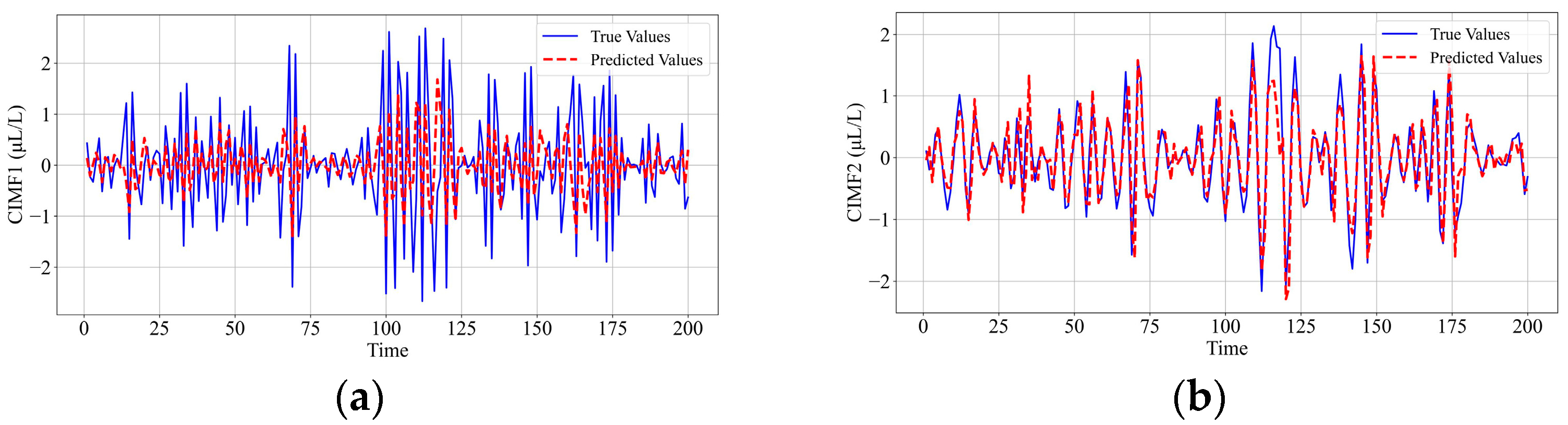
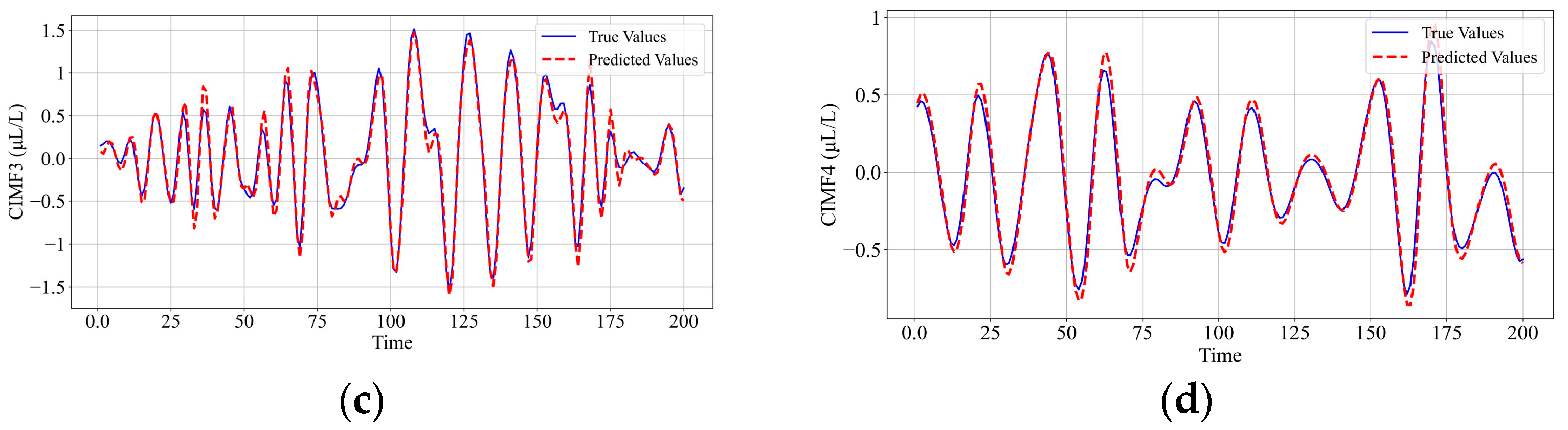
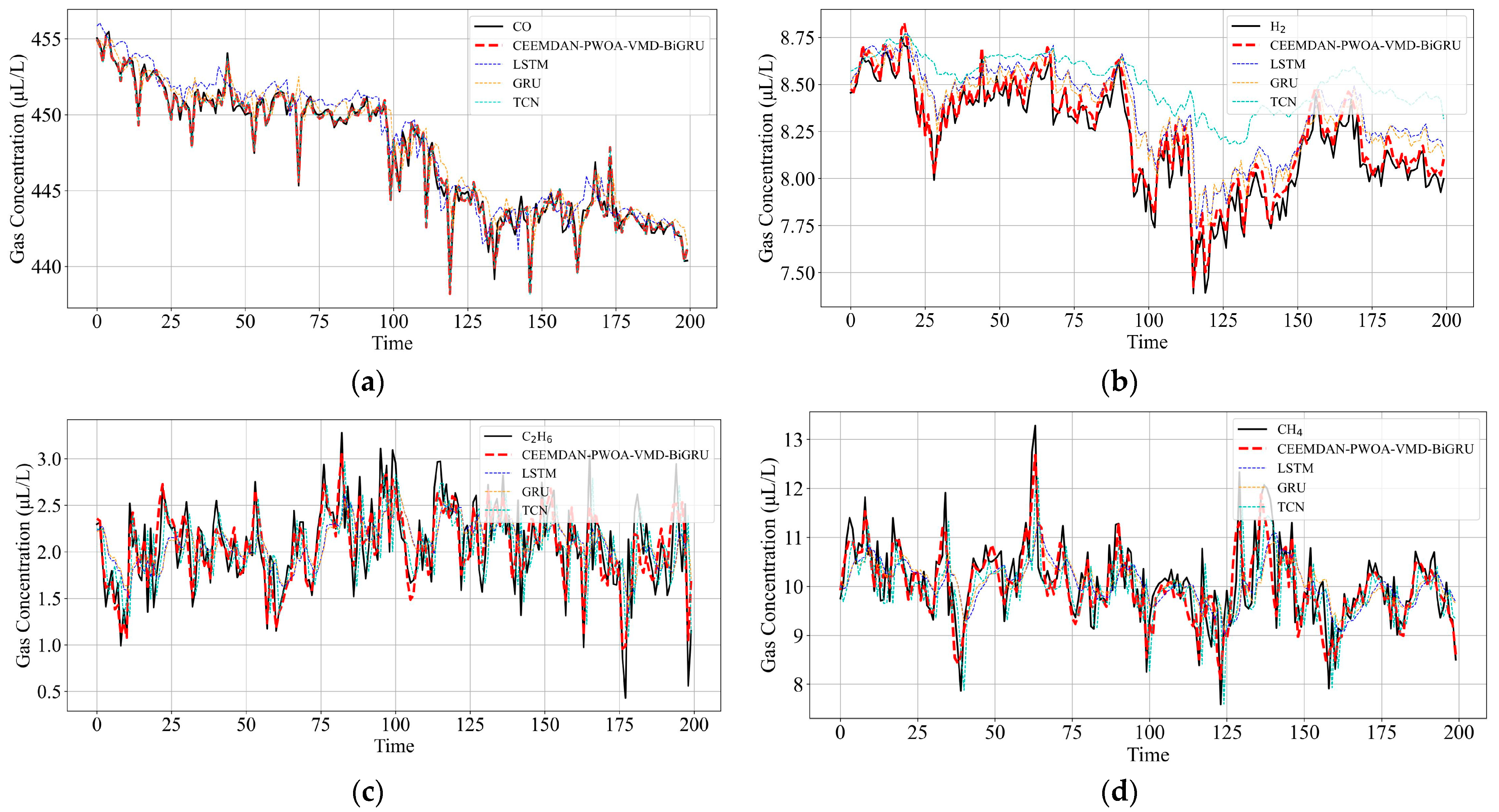
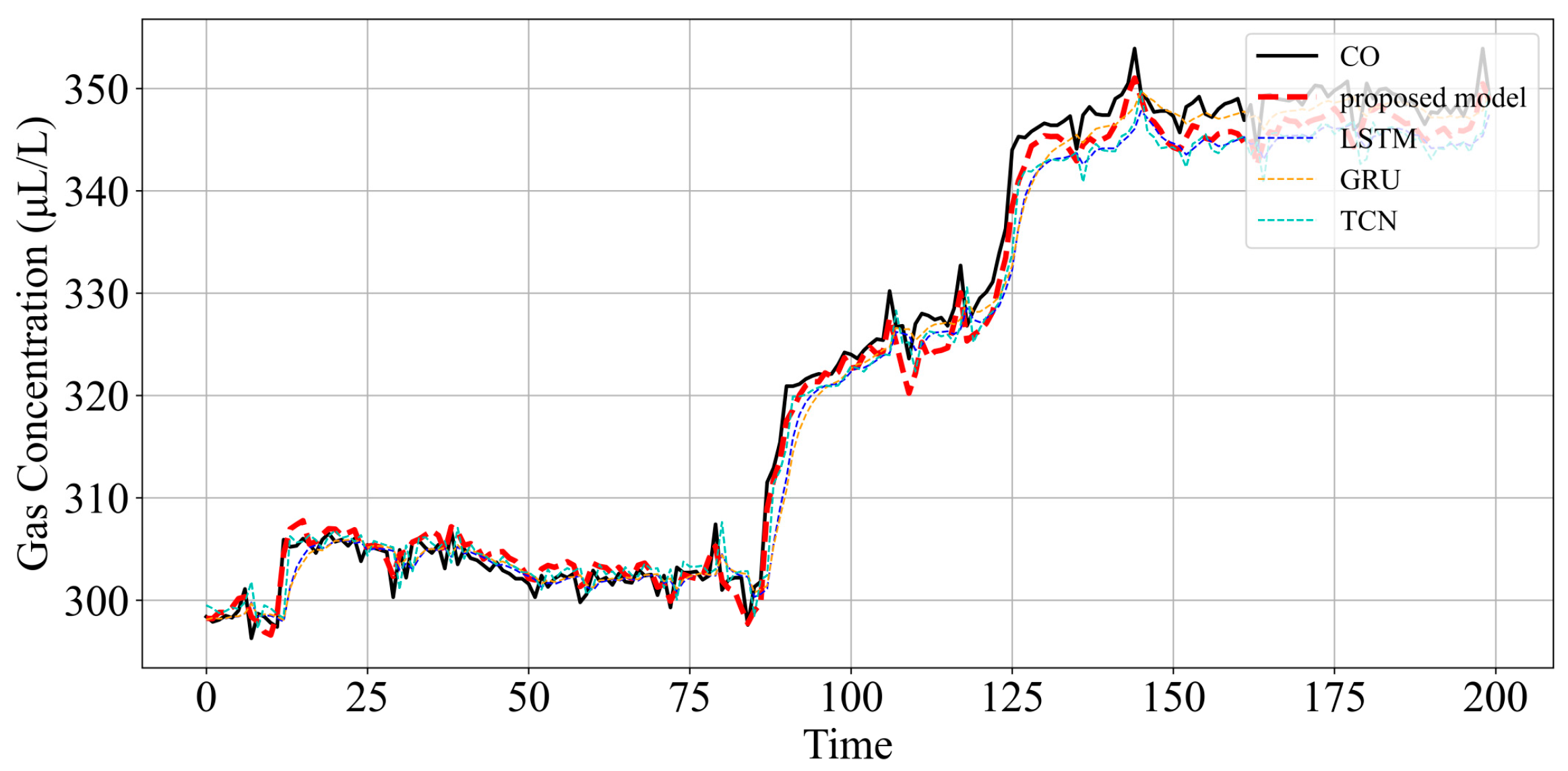
6.3. Analysis and Comparison of Testing Results
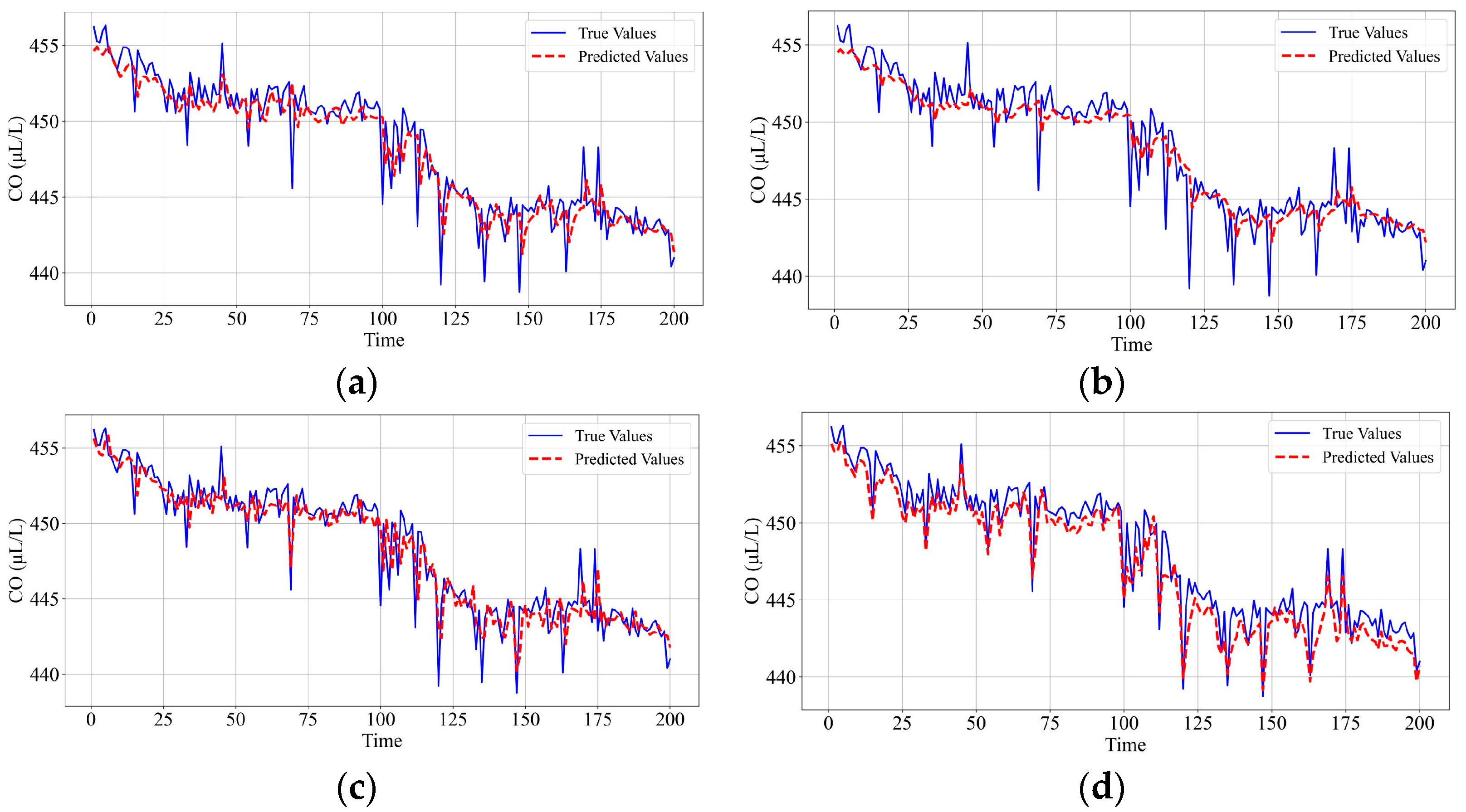
6.4. Experiment Analysis of Samples with Abnormal Change Trend
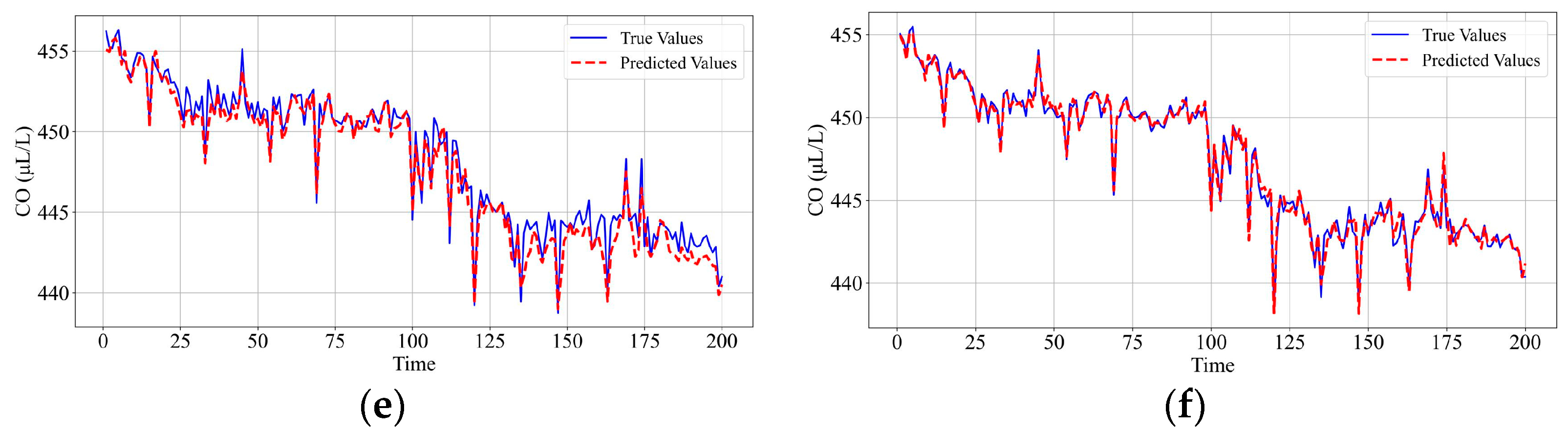
6.5. Ablation Study of the Prediction
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herath, T.; Wang, Z.D.; Liu, Q.; Wilson, G.; Hooton, R.; Raymond, T. Development of Trend Detection Technique for Dissolved Gas Analysis of Transmission Power Transformers. IEEE Trans. Power Deliv. 2025, 40, 332–342. [Google Scholar] [CrossRef]
- Guerbas, F.; Benmahamed, Y.; Teguar, Y.; Dahmani, R.A.; Teguar, M.; Ali, E.; Bajaj, M.; Dost Mohammadi, S.A.; Ghoneim, S.S.M. Neural Networks and Particle Swarm for Transformer Oil Diagnosis by Dissolved Gas Analysis. Sci. Rep. 2024, 14, 9271. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Kim, D.; Chan, K.Y.; Abu-Siada, A. Deep Machine Learning-Based Asset Management Approach for Oil- Immersed Power Transformers Using Dissolved Gas Analysis. IEEE Access 2024, 12, 27794–27809. [Google Scholar] [CrossRef]
- Pereira, F.H.; Bezerra, F.E.; Junior, S.; Santos, J.; Chabu, I.; Souza, G.F.M.d.; Micerino, F.; Nabeta, S.I. Nonlinear Autoregressive Neural Network Models for Prediction of Transformer Oil-Dissolved Gas Concentrations. Energies 2018, 11, 1691. [Google Scholar] [CrossRef]
- Elânio Bezerra, F.; Zemuner Garcia, F.A.; Ikuyo Nabeta, S.; Martha de Souza, G.F.; Chabu, I.E.; Santos, J.C.; Junior, S.N.; Pereira, F.H. Wavelet-Like Transform to Optimize the Order of an Autoregressive Neural Network Model to Predict the Dissolved Gas Concentration in Power Transformer Oil from Sensor Data. Sensors 2020, 20, 2730. [Google Scholar] [CrossRef]
- Lu, S.X.; Lin, G.; Que, H.; Li, M.J.J.; Wei, C.H.; Wang, J.K. Grey Relational Analysis Using Gaussian Process Regression Method for Dissolved Gas Concentration Prediction. Int. J. Mach. Learn. Cybern. 2019, 10, 1313–1322. [Google Scholar] [CrossRef]
- Xing, Z.; He, Y.; Wang, X.; Shao, K.; Duan, J. VMD-IARIMA-Based Time-Series Forecasting Model and Its Application in Dissolved Gas Analysis. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 802–811. [Google Scholar] [CrossRef]
- Wei, C.; Tang, W.; Wu, Q. Dissolved Gas Analysis Method Based on Novel Feature Prioritisation and Support Vector Machine. IET Electr. Power Appl. 2014, 8, 320–328. [Google Scholar] [CrossRef]
- He, J.; Huang, L.; Xiao, Y.; Li, W.; Yin, J.; Duan, Q.; Wei, L. Prediction Model of Continuous Discharge Coefficient from Tank Based on KPCA-DE-SVR. J. Loss Prev. Process Ind. 2024, 89, 105316. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Liu, J. MM-RNN: A Multimodal RNN for Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4101914. [Google Scholar] [CrossRef]
- Chen, T.; Guo, S.; Zhang, Z.; Yuan, Y.; Gao, J. A Method for Predicting Transformer Oil-Dissolved Gas Concentration Based on Multi-Window Stepwise Decomposition with HP-SSA-VMD-LSTM. Electronics 2024, 13, 2881. [Google Scholar] [CrossRef]
- Wang, S.; Shi, J.; Yang, W.; Yin, Q. High and Low Frequency Wind Power Prediction Based on Transformer and BiGRU-Attention. Energy 2024, 288, 129753. [Google Scholar] [CrossRef]
- Heddam, S.; Al-Areeq, A.M.; Tan, M.L.; Ahmadianfar, I.; Halder, B.; Demir, V.; Kilinc, H.C.; Abba, S.I.; Oudah, A.Y.; Yaseen, Z.M. New Formulation for Predicting Total Dissolved Gas Supersaturation in Dam Reservoir: Application of Hybrid Artificial Intelligence Models Based on Multiple Signal Decomposition. Artif. Intell. Rev. 2024, 57, 85. [Google Scholar] [CrossRef]
- Coşkun, M.; Gürüler, H.; Istanbullu, A.; Peker, M. Determining the Appropriate Amount of Anesthetic Gas Using DWT and EMD Combined with Neural Network. J. Med. Syst. 2015, 39, 173. [Google Scholar] [CrossRef]
- Heddam, S.; Vishwakarma, D.K.; Abed, S.A.; Sharma, P.; Al-Ansari, N.; Alataway, A.; Dewidar, A.Z.; Mattar, M.A. Hybrid River Stage Forecasting Based on Machine Learning with Empirical Mode Decomposition. Appl. Water Sci. 2024, 14, 46. [Google Scholar] [CrossRef]
- Melalkia, L.; Berrezzek, F.; Khelil, K.; Saim, A.; Nebili, R. A Hybrid Error Correction Method Based on EEMD and ConvLSTM for Offshore Wind Power Forecasting. Ocean Eng. 2025, 325, 120773. [Google Scholar] [CrossRef]
- Sahu, P.K.; Rai, R.N.; Patel, N. Deep Learning-Based Fault Classification of Rolling Bearings under Noisy Conditions Using CEEMD-VMD-IMF with Magnitude Scalogram Images. J. Mech. Sci. Technol. 2024, 38, 5281–5295. [Google Scholar] [CrossRef]
- Naraiah, R.P.; Kumar, P.N.; Dey, A. GNSS Multipath Error Analysis Based on Improved CEEMDAN and Detrended Fluctuation Analysis. J. Indian Soc. Remote Sens. 2025. [Google Scholar] [CrossRef]
- Ni, L.; Khim-Sen Liew, V. Carbon Emission Price Forecasting in China Using a Novel Secondary Decomposition Hybrid Model of CEEMD-SE-VMD-LSTM. Syst. Sci. Control Eng. 2024, 12, 2291409. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A Carbon Price Prediction Model Based on Secondary Decomposition Algorithm and Optimized Back Propagation Neural Network. J. Clean. Prod. 2020, 243, 118671. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H. A Denoising and Recognition Matching Algorithm of Projectile Signal in Infrared Light Screens Based on HOA-VMD. Microw. Opt. Technol. Lett. 2025, 67, e70166. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Z.; Yu, Y.; Liu, Y. Hybrid Energy Storage Power Allocation Strategy Based on Parameter-Optimized VMD Algorithm for Marine Micro Gas Turbine Power System. J. Energy Storage 2023, 73, 109189. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A. Prediction of Suspended Sediment Concentration Using Hybrid SVM-WOA Approaches. Geocarto Int. 2022, 37, 5609–5635. [Google Scholar] [CrossRef]
- Uzer, M.S.; Inan, O. Application of Improved Hybrid Whale Optimization Algorithm to Optimization Problems. Neural Comput. Appl. 2023, 35, 12433–12451. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, R.; Singh, V.P. Reinforcement Learning in Robotic Applications: A Comprehensive Survey. Artif. Intell. Rev. 2022, 55, 945–990. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative, Multi-Agent Games. arXiv 2022, arXiv:2103.01955. [Google Scholar]
- Ardila-Rey, J.; Rivera-Caballero, O.; Boya, C. Sample Entropy as a Performance Indicator of UHF Real Signal Denoising from Partial Discharges. IEEE Trans. Dielectr. Electr. Insul. 2025, 32, 1333–1342. [Google Scholar] [CrossRef]


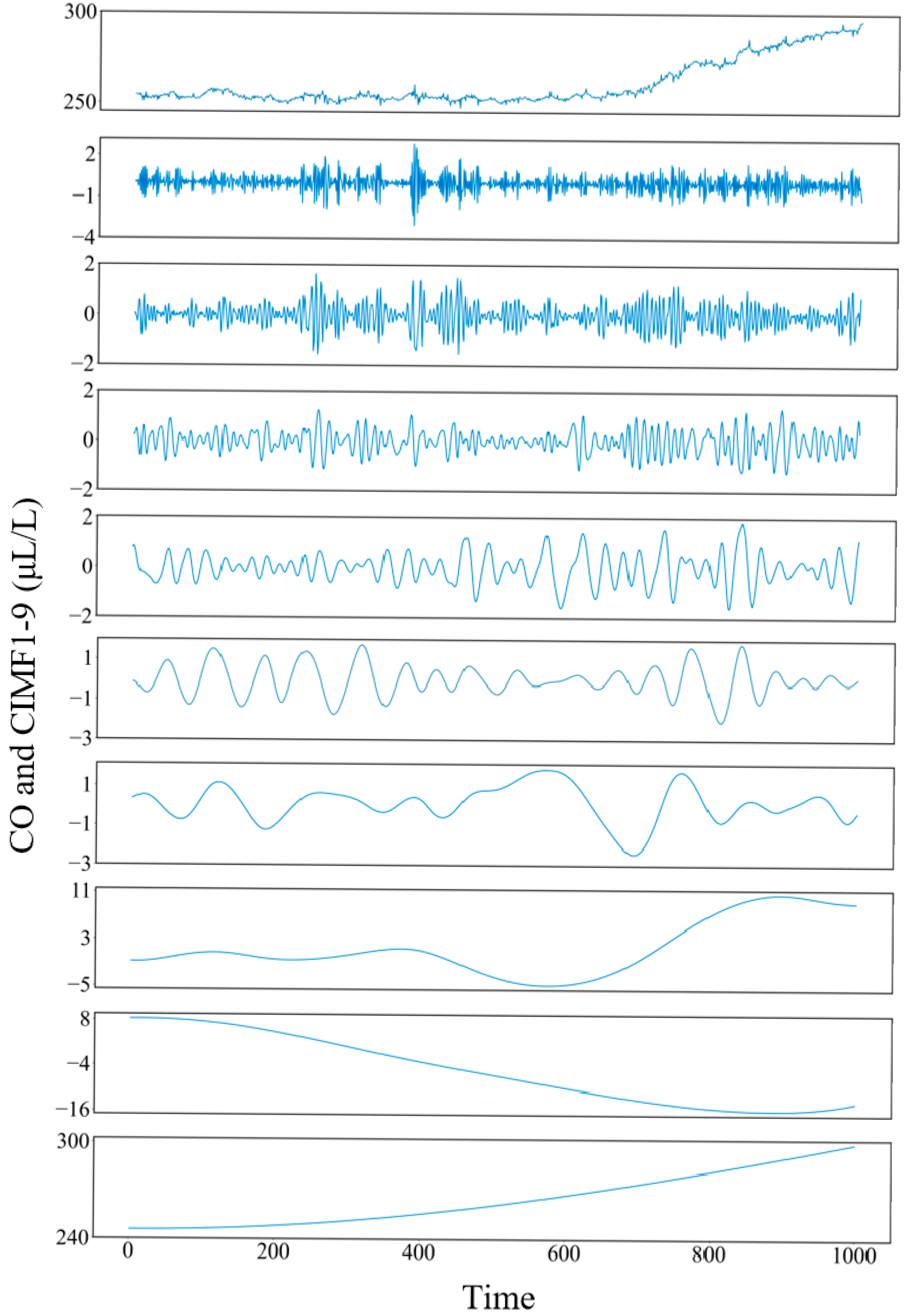
| Decomposed Components | Sample Entropy | Decomposed Components | Sample Entropy |
|---|---|---|---|
| CO | 1.9592 | CIMF5 | 0.3627 |
| CIMF1 | 1.1647 | CIMF6 | 0.2244 |
| CIMF2 | 0.7338 | CIMF7 | 0.1778 |
| CIMF3 | 0.5542 | CIMF8 | 0.1886 |
| CIMF4 | 0.5075 | CIMF9 | 0.010 |
| Decomposed Components | Sample Entropy | Decomposed Components | Sample Entropy |
|---|---|---|---|
| VIMF1 | 0.1783 | VIMF5 | 0.1318 |
| VIMF2 | 0.2817 | VIMF6 | 0.2717 |
| VIMF3 | 0.1934 | VIMF7 | 0.3559 |
| VIMF4 | 0.0914 | VIMF8 | 0.1836 |
| Algorithm Type | Parameters |
|---|---|
| CEEMDAN | Trials = 100, noise strength = 0.2 |
| TCN | Hidden dim = 8, hidden layers = 3, kernel size = 3, stride = 1, padding = 2, Adam optimizer, lr = 0.01 |
| GRU | Hidden dim = 256, hidden layers = 1, Adam optimizer, lr = 0.01 |
| LSTM | Hidden dim = 64, hidden layers = 1, Adam optimizer, lr = 0.01 |
| BiGRU | Hidden dim = 84, hidden layers = 1, Adam optimizer, lr = 0.01 |
| Model Type | CO | H2 | C2H6 | CH4 | ||||
|---|---|---|---|---|---|---|---|---|
| MAE (%) | MSE (%) | MAE (%) | MSE (%) | MAE (%) | MSE (%) | MAE (%) | MSE (%) | |
| proposed model | 3.64 | 2.18 | 0.54 | 0.05 | 1.92 | 0.58 | 3.25 | 1.86 |
| LSTM | 10.44 | 25.16 | 1.62 | 0.39 | 3.55 | 2.06 | 5.68 | 5.63 |
| GRU | 11.09 | 26.61 | 1.41 | 0.32 | 3.56 | 2.04 | 5.60 | 5.55 |
| TCN | 9.33 | 11.89 | 3.03 | 1.25 | 3.78 | 2.34 | 5.91 | 6.15 |
| Type of Model | MAE (%) | MSE (%) |
|---|---|---|
| proposed model | 3.00 | 0.125 |
| LSTM | 4.34 | 0.326 |
| GRU | 3.07 | 0.210 |
| TCN | 4.47 | 0.314 |
| Model Type | MAE (%) | MSE (%) |
|---|---|---|
| BiGRU | 11.06 | 25.60 |
| VMD-BiGRU | 16.86 | 36.81 |
| CEEMDAN-BiGRU | 9.46 | 15.43 |
| CEEMDAN-VMD-BiGRU | 8.47 | 12.65 |
| CEEMDAN-WOA-VMD-BiGRU | 6.13 | 7.85 |
| proposed model | 3.64 | 2.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; He, H.; Chen, H.; Liu, J.; Huang, S. Prediction of Dissolved Gases in Transformer Oil Based on CEEMDAN-PWOA-VMD and BiGRU. Electronics 2025, 14, 2370. https://doi.org/10.3390/electronics14122370
Peng X, He H, Chen H, Liu J, Huang S. Prediction of Dissolved Gases in Transformer Oil Based on CEEMDAN-PWOA-VMD and BiGRU. Electronics. 2025; 14(12):2370. https://doi.org/10.3390/electronics14122370
Chicago/Turabian StylePeng, Xinsong, Hongying He, Haiwen Chen, Jiahan Liu, and Shoudao Huang. 2025. "Prediction of Dissolved Gases in Transformer Oil Based on CEEMDAN-PWOA-VMD and BiGRU" Electronics 14, no. 12: 2370. https://doi.org/10.3390/electronics14122370
APA StylePeng, X., He, H., Chen, H., Liu, J., & Huang, S. (2025). Prediction of Dissolved Gases in Transformer Oil Based on CEEMDAN-PWOA-VMD and BiGRU. Electronics, 14(12), 2370. https://doi.org/10.3390/electronics14122370






