DualNetIQ: Texture-Insensitive Image Quality Assessment with Dual Multi-Scale Feature Maps
Abstract
1. Introduction
- Proposing a novel IQA method called DualNetIQ for texture-insensitive full reference IQA. Unlike existing IQA methods that employ a single deep feature extractor, the proposed method utilizes hybrid multi-scale feature maps selected from robust pre-trained CNNs models (VGG19 and SqueezeNet) to assess the quality of textured images effectively and withstand the effects of texture resampling under different distortion types. DualNetIQ makes a complete description of the textures and structures of the reference and the distorted images under different types of distortion. It addresses the limitations of similar existing models, particularly in handling various types of distortions.
- Proposing an efficient method for assessing the similarity between the reference and distorted images by optimally combining structure and texture similarity metrics utilizing the GWO algorithm, allowing the model to align closely with human perceptual judgement.
- Providing an extensive ablation study and comparative analysis against existing methods on five IQA datasets (LIVE [14], CSIQ [15], TID2013 [16], KADID-10k [17], and PIPAL [18]), one texture similarity dataset, SynTEX [4], and one perceptual similarity dataset, BAPPS [10]. These datasets encompass a wide range of distortions, including traditional synthetic artifacts and those created by modern image processing algorithms. The employment of such datasets provides a rigorous benchmark that confirms the adaptability and robustness of the DualNetIQ method across various evaluation scenarios.
2. Related Work
2.1. Traditional Full-Reference IQA Methods
2.2. Deep Learning-Based IQA Methods
3. Proposed Method
3.1. DualNetIQ Model
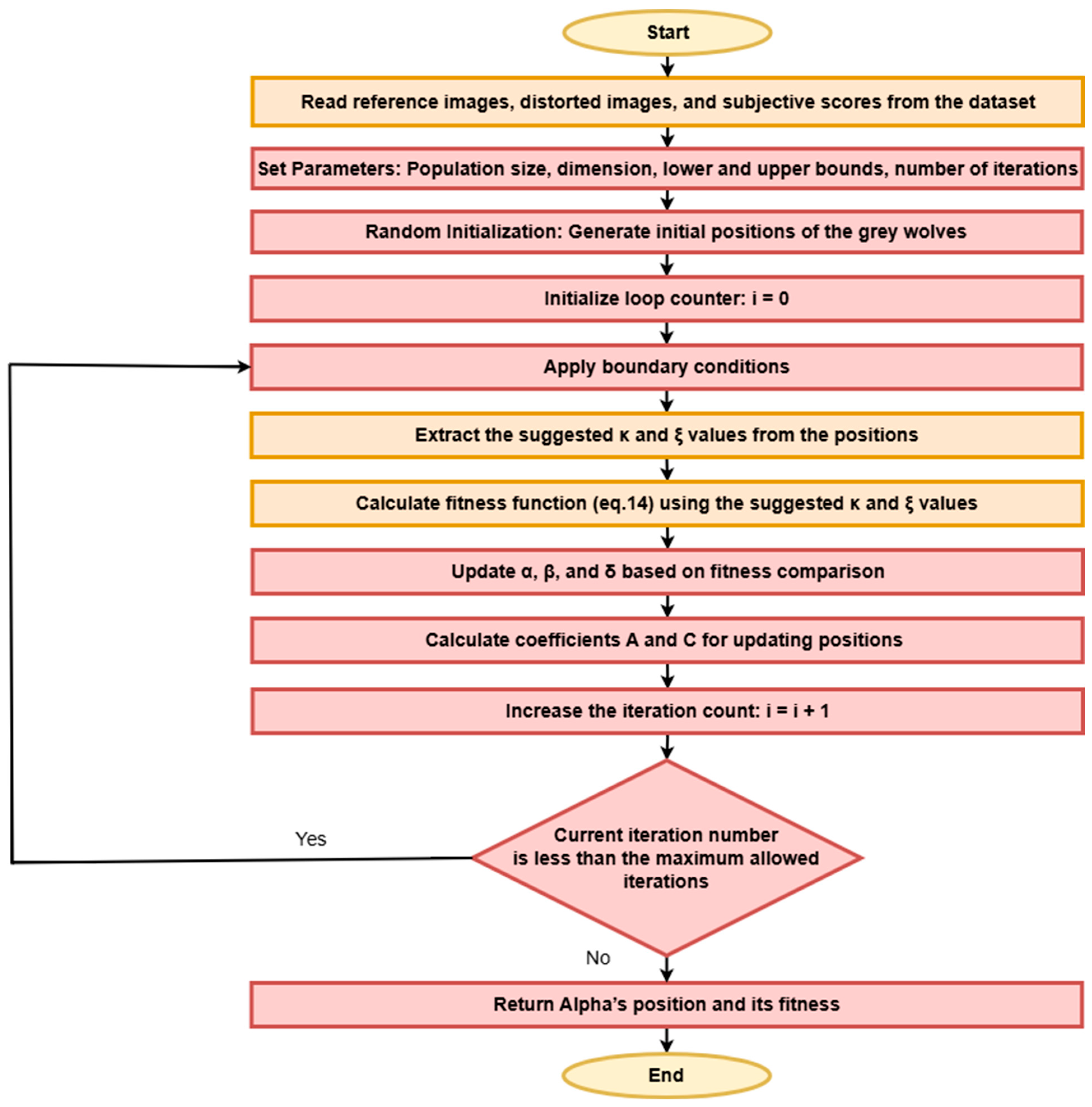
3.2. Optimal Combined Similarity Metric
3.3. Implementation of DualNetIQ
| Algorithm 1: Pseudocode of DualNetIQ | |
| 1 2 3 4 5 | Load tuned κ and ξ from files Load pretrained VGG19 and SqueezeNet models Define stages as sequential models for different layers of VGG19 and SqueezeNet Freeze model parameters Set mean and standard deviation for input normalization Define channel sizes list ([3,256,512,64,128,256,384,512]) |
| 6 7 8 9 10 11 12 13 14 15 | def forward_once(x): Normalize x using mean and std # Pass x through VGG19 stages Pass x through VGG19_stage1 -> h1 Pass h1 through VGG19_stage2 -> h2 # Pass x through SqueezeNet stages Pass x through SqueezeNet_stage1 -> h3 Pass h3 through SqueezeNet_stage2 -> h4 Pass h4 through SqueezeNet_stage3 -> h5 Pass h5 through SqueezeNet_stage4 -> h6 Pass h6 through SqueezeNet_stage5 -> h7 Return [x, h1, h2, h3, h4, h5, h6, h7] |
| 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | def forward(x, y, require_grad = False, batch_average = False): Normalize kappa and xi term1 = 0 term2 = 0 for i in range(len(channel_sizes)): x_mean, y_mean = Compute mean of features from x and y S1 = Compute similarity using x_mean, y_mean term1 += kappa[i] * S1 x_var, y_var = Compute variance of features from x and y S2 = Compute similarity using x_var, y_var term2 += xi[i] * S2 score = 1 − (term1 + term2).squeeze() if batch_average: return score.mean() else: return score |
3.4. Evaluation Metrics
4. Results and Discussion
4.1. Parameter Setting
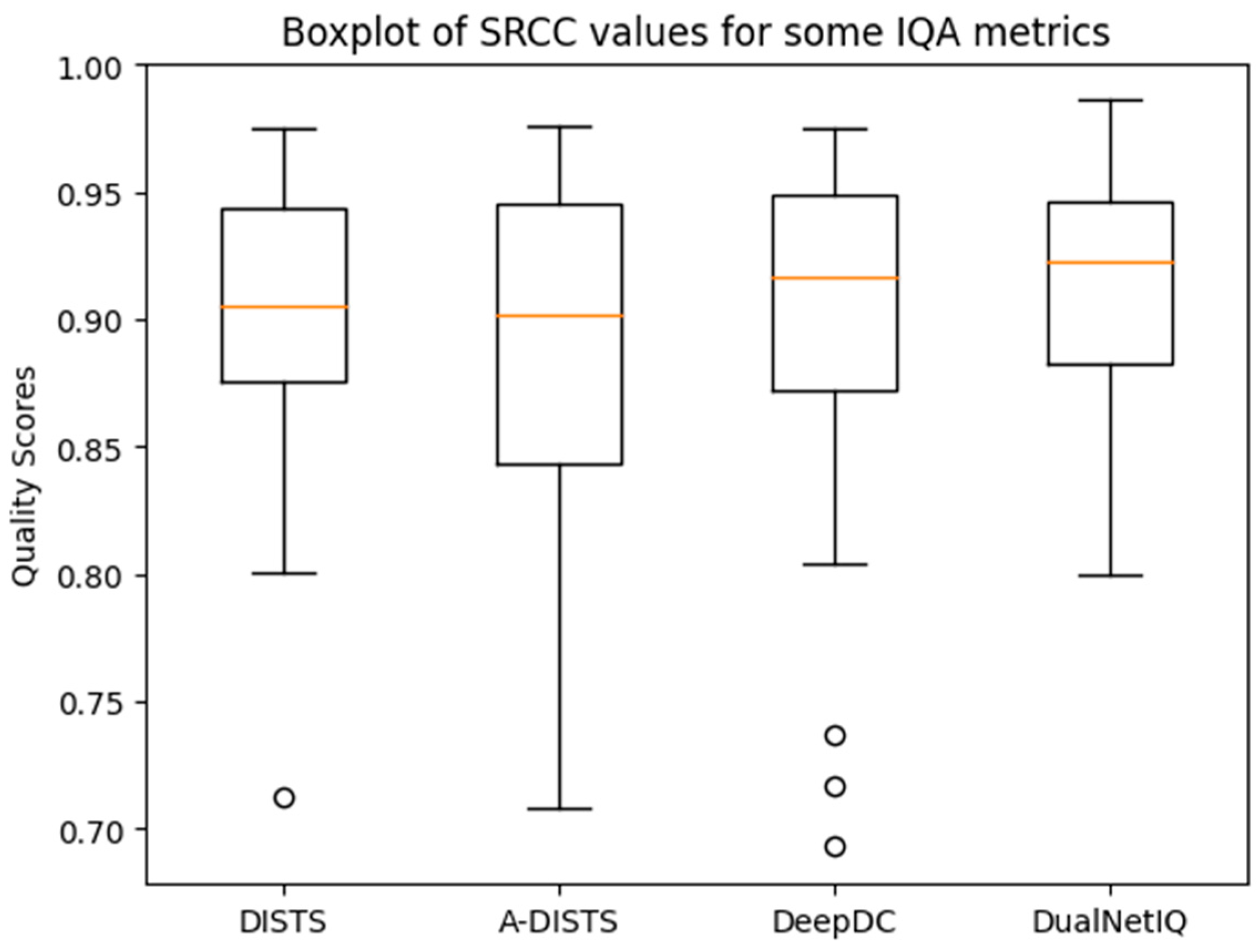
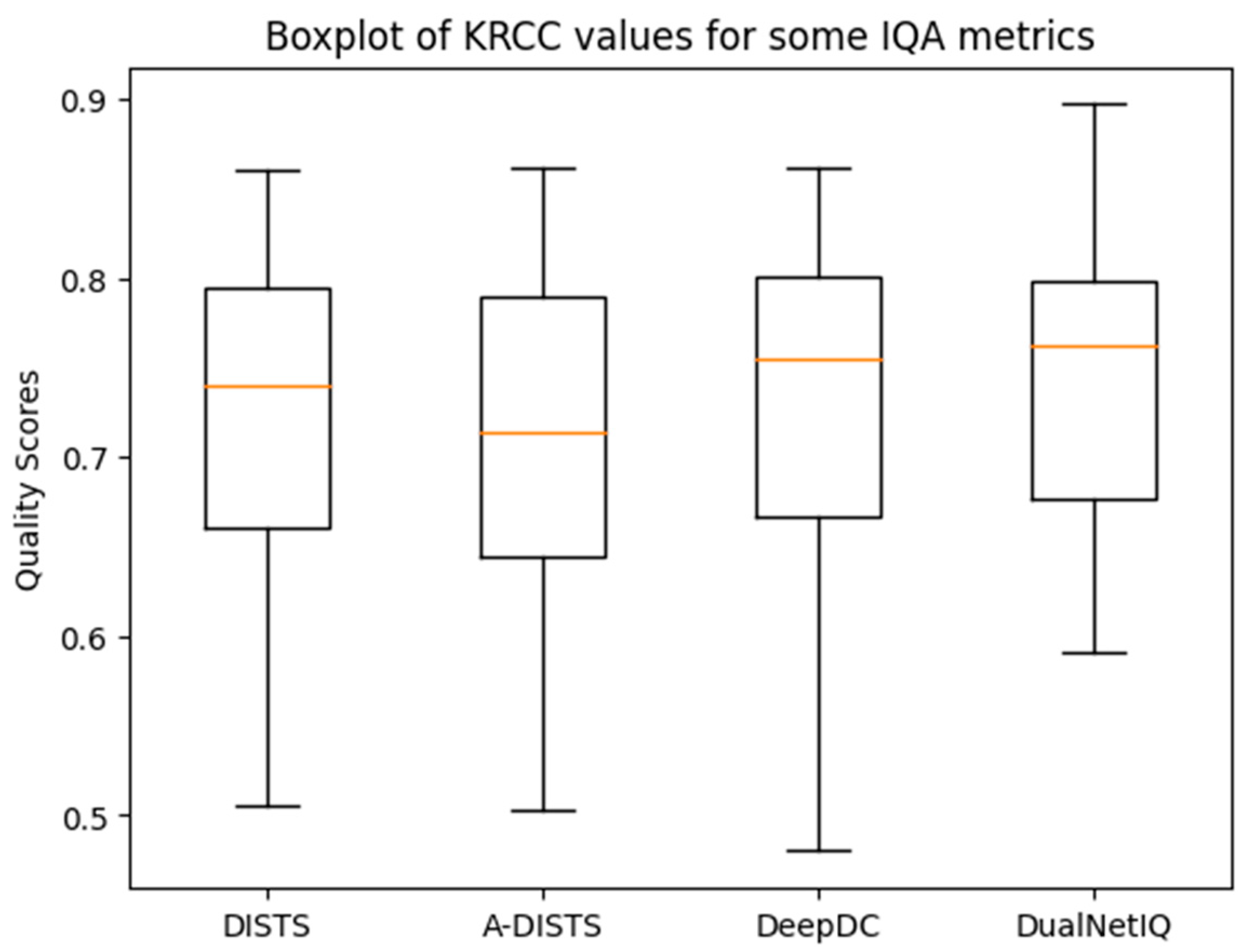
4.2. Performance in Quality Prediction and Texture Similarity
4.3. Performance on Perceptual Similarity Measurment
4.4. Performance Comparison Across Diversity of Distortion Types
4.5. Ablation Study
4.6. Complexity Comparison
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bosse, S.; Maniry, D.; Müller, K.R.; Wiegand, T.; Samek, W. Deep Neural Networks for No-Reference and Full-Reference Image Quality Assessment. IEEE Trans. Image Process. 2018, 27, 206–219. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Shi, Z.; Lu, Z.; Xie, S.; Chao, F.; Sui, Y. A Survey on Image Quality Assessment: Insights, Analysis, and Future Outlook. arXiv 2025, arXiv:2502.08540. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Golestaneh, S.A.; Subedar, M.M.; Karam, L.J. The effect of texture granularity on texture synthesis quality. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 9–13 August 2015; Volume 9599, pp. 356–361. [Google Scholar] [CrossRef]
- Efros, A.A.; Freeman, W.T. Image quilting for texture synthesis and transfer. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 341–346. [Google Scholar] [CrossRef]
- Wei, L.Y.; Levoy, M. Fast Texture Synthesis using Tree-structured Vector Quantization. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 479–488. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S. Deep Learning of Human Visual Sensitivity in Image Quality Assessment Framework. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1969–1977. [Google Scholar] [CrossRef]
- Varga, D. A Combined Full-Reference Image Quality Assessment Method Based on Convolutional Activation Maps. Algorithms 2020, 13, 313. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Y.; Li, P.; Tan, M.; Yu, J.; Zhu, Y. DeepSim: Deep similarity for image quality assessment. Neurocomputing 2017, 257, 104–114. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image Quality Assessment: Unifying Structure and Texture Similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2567–2581. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, B.; Zhu, L.; Wang, S.; Lin, W. DeepDC: Deep Distance Correlation as a Perceptual Image Quality Evaluator. arXiv 2023, arXiv:2211.04927v2. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Sheikh, H.R.; Wang, Z.; Cormack, L.; Bovik, A.C. Image and Video Quality Assessment Research at LIVE. Available online: http://live.ece.utexas.edu/research/quality/ (accessed on 3 October 2024).
- Chandler, D.M.; Larson, E.C. Most apparent distortion: Full-reference image quality assessment and the role of strategy. J. Electron. Imaging 2010, 19, 011006. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Jin, L.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Image database TID2013: Peculiarities, results and perspectives. Signal Process. Image Commun. 2015, 30, 57–77. [Google Scholar] [CrossRef]
- Lin, H.; Hosu, V.; Saupe, D. KADID-10k: A Large-scale Artificially Distorted IQA Database. In Proceedings of the 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), Berlin, Germany, 5–7 June 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Gu, J.; Cai, H.; Chen, H.; Ye, X.; Ren, J.; Dong, C. PIPAL: A Large-Scale Image Quality Assessment Dataset for Perceptual Image Restoration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Volume 16, pp. 633–651. [Google Scholar]
- Lin, W.; Li, D.; Xue, P. Discriminative Analysis of Pixel Difference towards Picture Quality Prediction. In Proceedings of the IEEE International Conference on Image Processing, Barcelona, Spain, 4–17 September 2003; Volume 3, pp. 193–196. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multi-Scale Structural Similarity For Image Quality Assessment. In Proceedings of the IEEE Asilomar Conference on Signals, System and Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar]
- Wang, Z.; Li, Q. Information content weighting for perceptual image quality assessment. IEEE Trans. Image Process. 2011, 20, 1185–1198. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P. Translation insensitive image similarity in complex wavelet domain. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Philadelphia, PA, USA, 23 March 2005; Volume 2. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, Y.; Li, H. VSI: A visual saliency-induced index for perceptual image quality assessment. IEEE Trans. Image Process. 2014, 23, 4270–4281. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, H.R.; Bovik, A.C. A Visual Information Fidelity Approach To Video Quality Assessment. In Proceedings of the First International Workshop on Video Processing and Quality Metrics for Consumer Electronics, Scottsdale, AZ, USA, 23–25 January 2005; Volume 7. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, J.; Wan, X.; Gong, Y.; Zheng, N. Image quality assessment using similar scene as reference. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Volume 9909, pp. 3–18. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2009, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]
- You, J.; Korhonen, J. Transformer For Image Quality Assessment. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 1389–1393. [Google Scholar] [CrossRef]
- Ke, J.; Wang, Q.; Wang, Y.; Milanfar, P.; Yang, F. MUSIQ: Multi-scale Image Quality Transformer. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 5128–5137. [Google Scholar] [CrossRef]
- Cheon, M.; Yoon, S.J.; Kang, B.; Lee, J. Perceptual image quality assessment with transformers. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Nashville, TN, USA, 19–25 June 2021; pp. 433–442. [Google Scholar] [CrossRef]
- Golestaneh, S.A.; Dadsetan, S.; Kitani, K.M. No-Reference Image Quality Assessment via Transformers, Relative Ranking, and Self-Consistency. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision, WACV 2022, Waikoloa, HI, USA, 3–8 January 2022; pp. 3989–3999. [Google Scholar] [CrossRef]
- Yang, S.; Wu, T.; Shi, S.; Lao, S.; Gong, Y.; Cao, M.; Wang, J.; Yang, Y. MANIQA: Multi-dimension Attention Network for No-Reference Image Quality Assessment. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Orleans, LA, USA, 19–20 June 2022; pp. 1190–1199. [Google Scholar] [CrossRef]
- Keshari, A.; Subudhi, B. Multi-Scale Features and Parallel Transformers Based Image Quality Assessment. arXiv 2022, arXiv:2204.09779. [Google Scholar]
- DIng, K.; Liu, Y.; Zou, X.; Wang, S.; Ma, K. Locally Adaptive Structure and Texture Similarity for Image Quality Assessment. In Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20–24 October 2021; pp. 2483–2491. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P. Maximum differentiation (MAD) competition: A methodology for comparing computational models of perceptual quantities. J. Vis. 2008, 8, 8. [Google Scholar] [CrossRef]
- Berardino, A.; Ballé, J.; Laparra, V.; Simoncelli, E.P. Eigen-Distortions of Hierarchical Representations. arXiv 2018, arXiv:1710.02266. [Google Scholar]
- Mady, H.; Agamy, A.; Aly, A.M.; Abdel-Nasser, M. A Comparative Analysis of CNN Feature Extractors and Parameter Tuning with Ray Tune Search Algorithms for Image Quality Assessment. Aswan Univ. J. Sci. Technol. 2024, 4, 132–148. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Wang, C.; Wu, Q.; Weimer, M.; Zhu, E. FLAML: A Fast and Lightweight AutoML Library. Proc. Mach. Learn. Syst. 2021, 3, 434–447. [Google Scholar]
- Rapin, J.; Teytaud, O. Nevergrad—A Gradient-Free Optimization Platform. Available online: https://GitHub.com/FacebookResearch/Nevergrad (accessed on 10 March 2025).
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1437–1446. [Google Scholar]
- Liaw, R.; Liang, E.; Nishihara, R.; Moritz, P.; Gonzalez, J.E.; Stoica, I. Tune: A Research Platform for Distributed Model Selection and Training. arXiv 2018, arXiv:1807.05118. [Google Scholar]
- Kennedy, J.; Eberhart, R.; bls gov. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Network, Perth, WA, Australia, 27 November–1 December 2002; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Watanabe, S. Tree-Structured Parzen Estimator: Understanding Its Algorithm Components and Their Roles for Better Empirical Performance. arXiv 2023, arXiv:2304.11127. [Google Scholar]
- Laparra, V.; Ballé, J.; Berardino, A.; Simoncelli, E.P. Perceptual image quality assessment using a normalized Laplacian pyramid. Electron. Imaging 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Prashnani, E.; Cai, H.; Mostofi, Y.; Sen, P. PieAPP: Perceptual Image-Error Assessment through Pairwise Preference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1808–1817. [Google Scholar]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient Magnitude Similarity Deviation: A Highly Efficient Perceptual Image Quality Index. IEEE Trans. Image Process. 2013, 23, 684–695. [Google Scholar] [CrossRef]
- Rehman, M.U.; Nizami, I.F.; Ullah, F.; Hussain, I. IQA Vision Transformed: A Survey of Transformer Architectures in Perceptual Image Quality Assessment. IEEE Access 2024, 12, 183369–183393. [Google Scholar] [CrossRef]

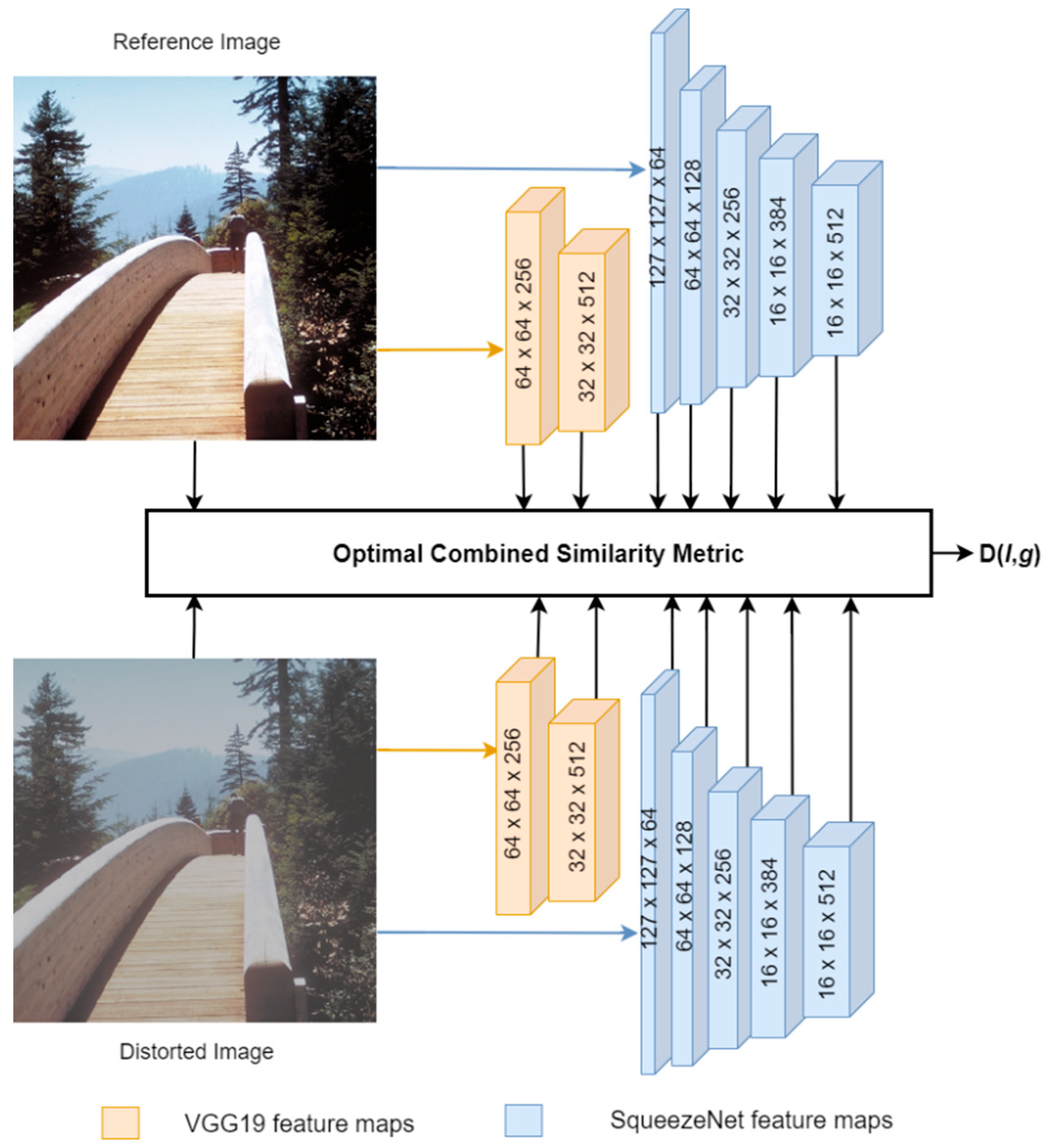
| Stage (i) | Description | Output Feature Dimension (ni) |
|---|---|---|
| 1 | Input image | 3 × 256 × 256 |
| 2 | VGG19 stage1: conv1_8 | 256 × 64 × 64 |
| 3 | VGG19 stage2: conv2_4 | 512 × 32 × 32 |
| 4 | SqueezeNet stage1: conv1_1 | 64 × 127 × 127 |
| 5 | SqueezeNet stage2: conv2_6 (fire1 + fire2) | 128 × 64 × 64 |
| 6 | SqueezeNet stage3: conv3_6 (fire3 + fire4) | 256 × 32 × 32 |
| 7 | SqueezeNet stage4: conv4_6 (fire5 + fire6) | 384 × 16 × 16 |
| 8 | SqueezeNet stage5: conv5_6 (fire7 + fire8) | 512 × 16 × 16 |
| Method | Quality Prediction | Texture Similarity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LIVE [14] | CSIQ [15] | TID2013 [16] | KADID-10k [17] | PIPAL [18] | SynTEX [4] | |||||||
| SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | |
| PSNR | 0.873 | 0.680 | 0.809 | 0.599 | 0.687 | 0.496 | 0.676 | 0.488 | 0.407 | 0.233 | 0.320 | 0.211 |
| SSIM [3] | 0.931 | 0.763 | 0.872 | 0.678 | 0.720 | 0.527 | 0.724 | 0.537 | 0.498 | 0.276 | 0.620 | 0.446 |
| MS-SSIM [20] | 0.951 | 0.805 | 0.906 | 0.730 | 0.786 | 0.605 | 0.826 | 0.635 | 0.552 | 0.291 | 0.632 | 0.454 |
| FSIMc [25] | 0.965 | 0.837 | 0.931 | 0.768 | 0.851 | 0.666 | 0.854 | 0.665 | 0.569 | 0.304 | 0.081 | 0.077 |
| VIF [24] | 0.964 | 0.828 | 0.911 | 0.743 | 0.677 | 0.518 | 0.679 | 0.507 | 0.443 | 0.261 | 0.606 | 0.492 |
| NLPD [49] | 0.937 | 0.778 | 0.932 | 0.769 | 0.800 | 0.625 | 0.812 | 0.623 | 0.469 | 0.255 | 0.606 | 0.464 |
| PieAPP [50] | 0.919 | 0.750 | 0.892 | 0.715 | 0.876 | 0.683 | 0.836 | 0.647 | 0.700 | 0.492 | 0.715 | 0.532 |
| LPIPS [10] | 0.932 | 0.765 | 0.876 | 0.689 | 0.670 | 0.497 | 0.843 | 0.653 | 0.573 | 0.323 | 0.663 | 0.478 |
| DISTS [11] | 0.954 | 0.811 | 0.939 | 0.780 | 0.830 | 0.639 | 0.887 | 0.709 | 0.624 | 0.433 | 0.923 | 0.759 |
| A-DISTS [36] | 0.955 | 0.812 | 0.942 | 0.796 | 0.836 | 0.642 | 0.890 | 0.715 | 0.622 | 0.431 | 0.760 | - |
| DeepDC [12] | 0.940 | 0.781 | 0.937 | 0.774 | 0.844 | 0.651 | 0.905 | 0.733 | 0.684 | 0.467 | 0.896 | 0.727 |
| DualNetIQ (ours) | 0.955 | 0.815 | 0.930 | 0.764 | 0.865 | 0.678 | 0.897 | 0.719 | 0.635 | 0.452 | 0.938 | 0.792 |
| Method | Synthetic Distortions | Distortions by Real-World Algorithms | All | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Traditional | CNN-Based | All | Super Resolution | Video Deblurring | Colorization | Frame Interpolation | All | ||
| Human | 0.808 | 0.844 | 0.826 | 0.734 | 0.671 | 0.688 | 0.686 | 0.695 | 0.739 |
| PSNR | 0.573 | 0.801 | 0.687 | 0.642 | 0.590 | 0.624 | 0.543 | 0.614 | 0.633 |
| SSIM [3] | 0.605 | 0.806 | 0.705 | 0.647 | 0.589 | 0.624 | 0.573 | 0.617 | 0.640 |
| MS-SSIM [20] | 0.585 | 0.768 | 0.676 | 0.638 | 0.589 | 0.524 | 0.572 | 0.596 | 0.617 |
| FSIMc [25] | 0.627 | 0.794 | 0.710 | 0.660 | 0.590 | 0.573 | 0.581 | 0.615 | 0.640 |
| VSI [23] | 0.630 | 0.818 | 0.724 | 0.668 | 0.592 | 0.597 | 0.568 | 0.622 | 0.648 |
| VIF [24] | 0.556 | 0.744 | 0.650 | 0.651 | 0.594 | 0.515 | 0.597 | 0.603 | 0.615 |
| NLPD [49] | 0.550 | 0.764 | 0.657 | 0.655 | 0.584 | 0.528 | 0.552 | 0.600 | 0.615 |
| GMSD [51] | 0.609 | 0.772 | 0.690 | 0.677 | 0.594 | 0.517 | 0.575 | 0.613 | 0.633 |
| DeepIQA [1] | 0.703 | 0.794 | 0.748 | 0.660 | 0.582 | 0.585 | 0.598 | 0.615 | 0.650 |
| PieAPP [50] | 0.727 | 0.770 | 0.746 | 0.684 | 0.585 | 0.594 | 0.598 | 0.627 | 0.659 |
| LPIPS [10] | 0.714 | 0.814 | 0.764 | 0.705 | 0.605 | 0.625 | 0.630 | 0.641 | 0.692 |
| DISTS [11] | 0.749 | 0.824 | 0.786 | 0.705 | 0.600 | 0.629 | 0.625 | 0.649 | 0.685 |
| DeepDC [12] | 0.757 | 0.825 | 0.796 | 0.712 | 0.608 | 0.631 | 0.626 | 0.655 | 0.692 |
| DualNetIQ (ours) | 0.739 | 0.832 | 0.797 | 0.719 | 0.606 | 0.648 | 0.631 | 0.661 | 0.693 |
| Noise Type | DISTS [11] | A-DISTS [36] | DeepDC [12] | DualNetIQ | ||||
|---|---|---|---|---|---|---|---|---|
| SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | |
| Quantization Noise | 0.831 | 0.644 | 0.799 | 0.62 | 0.872 | 0.682 | 0.862 | 0.672 |
| Gaussian Blur | 0.938 | 0.776 | 0.938 | 0.774 | 0.954 | 0.808 | 0.941 | 0.78 |
| Contrast Change | 0.488 | 0.335 | 0.433 | 0.289 | 0.472 | 0.297 | 0.472 | 0.303 |
| JPEG Compression | 0.904 | 0.702 | 0.907 | 0.709 | 0.917 | 0.725 | 0.921 | 0.736 |
| JPEG 2000 Compression | 0.944 | 0.795 | 0.945 | 0.797 | 0.949 | 0.801 | 0.946 | 0.798 |
| Additive Gaussian Noise | 0.877 | 0.677 | 0.858 | 0.651 | 0.868 | 0.667 | 0.883 | 0.688 |
| High-Frequency Noise | 0.878 | 0.659 | 0.872 | 0.651 | 0.879 | 0.663 | 0.895 | 0.677 |
| Impulse Noise | 0.713 | 0.506 | 0.708 | 0.503 | 0.693 | 0.48 | 0.8 | 0.591 |
| Image Denoising | 0.905 | 0.736 | 0.892 | 0.714 | 0.912 | 0.755 | 0.923 | 0.762 |
| Mean Shift | 0.801 | 0.594 | 0.801 | 0.598 | 0.737 | 0.538 | 0.804 | 0.604 |
| Change of Color Saturation | 0.814 | 0.612 | 0.839 | 0.644 | 0.717 | 0.518 | 0.836 | 0.642 |
| Multiplicative Gaussian Noise | 0.83 | 0.616 | 0.795 | 0.578 | 0.823 | 0.611 | 0.826 | 0.612 |
| CNN Model | Quality Prediction | Texture Similarity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LIVE [14] | CSIQ [15] | TID2013 [16] | KADID-10k [17] | SynTEX [4] | ||||||
| SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | SRCC | KRCC | |
| VGG19 | 0.954 | 0.813 | 0.941 | 0.786 | 0.833 | 0.648 | 0.896 | 0.718 | 0.928 | 0.773 |
| SqueezeNet | 0.953 | 0.812 | 0.896 | 0.714 | 0.858 | 0.668 | 0.881 | 0.695 | 0.930 | 0.778 |
| AlexNet | 0.942 | 0.797 | 0.900 | 0.716 | 0.833 | 0.640 | 0.860 | 0.666 | 0.892 | 0.713 |
| ResNet50 | 0.862 | 0.681 | 0.816 | 0.633 | 0.774 | 0.578 | 0.801 | 0.612 | 0.631 | 0.490 |
| VGG19 + SqueezeNet (DualNetIQ) | 0.955 | 0.815 | 0.930 | 0.764 | 0.865 | 0.678 | 0.897 | 0.719 | 0.938 | 0.792 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agamy, A.; Mady, H.; Esmaiel, H.; Al Ayidh, A.; Aly, A.M.; Abdel-Nasser, M. DualNetIQ: Texture-Insensitive Image Quality Assessment with Dual Multi-Scale Feature Maps. Electronics 2025, 14, 1169. https://doi.org/10.3390/electronics14061169
Agamy A, Mady H, Esmaiel H, Al Ayidh A, Aly AM, Abdel-Nasser M. DualNetIQ: Texture-Insensitive Image Quality Assessment with Dual Multi-Scale Feature Maps. Electronics. 2025; 14(6):1169. https://doi.org/10.3390/electronics14061169
Chicago/Turabian StyleAgamy, Adel, Hossam Mady, Hamada Esmaiel, Abdulrahman Al Ayidh, Abdelmageed Mohamed Aly, and Mohamed Abdel-Nasser. 2025. "DualNetIQ: Texture-Insensitive Image Quality Assessment with Dual Multi-Scale Feature Maps" Electronics 14, no. 6: 1169. https://doi.org/10.3390/electronics14061169
APA StyleAgamy, A., Mady, H., Esmaiel, H., Al Ayidh, A., Aly, A. M., & Abdel-Nasser, M. (2025). DualNetIQ: Texture-Insensitive Image Quality Assessment with Dual Multi-Scale Feature Maps. Electronics, 14(6), 1169. https://doi.org/10.3390/electronics14061169







