A Fast Calculation Method of the Time–Domain Coupling Characteristics Between Buildings and Electromagnetic Pulse Based on the Electromagnetic Parameter Equivalence of Reinforced Concrete

Abstract

With the development of pulse technology, reinforced concrete buildings are exposed to increasingly complex high-power electromagnetic pulse (EMP) environments, posing risks of functional degradation or destruction of indoor electronic equipment and systems. Therefore, it is imperative to assess the internal fields of buildings under EMP irradiation. The challenge lies in the multi-scale characteristics of reinforced concrete buildings, where fine grids are required for the accurate modelling of rebar, thereby consuming substantial computing resources. To address this challenge, this paper proposes a fast calculation method of the time–domain coupling characteristics between buildings and EMPs based on the electromagnetic parameter equivalence of reinforced concrete walls. The method first calculates the equivalent electromagnetic parameters from the S-parameters of the walls, which are then fitted into polynomial rational functions. Then, the auxiliary differential equation finite-difference time–domain (ADE-FDTD) method is used to analyze the time–domain coupling characteristics of reinforced concrete walls and buildings under EMP irradiation. The results show that the proposed method significantly enhances computational efficiency while maintaining high accuracy. Specifically, for a large two-story reinforced concrete building, the method achieves a 3.2-fold increase in computational speed and a 4.3-fold reduction in memory usage compared to conventional commercial software (CST Studio Suite 2022). This approach provides an effective solution for simulating the coupling characteristics between large reinforced concrete buildings and external EMPs.

1. Introduction

With the development of pulse technology and its application in diverse electromagnetic countermeasure scenarios, reinforced concrete buildings are inevitably exposed to increasingly severe high-power electromagnetic pulse (EMP) environments, leading to the risk of functional degradation or even destruction of various electronic devices, equipment, and systems inside the building [1,2]. Consequently, protective designs for sensitive indoor equipment and systems are essential to ensure their safe and stable operation. The premise of designing protection for sensitive equipment is assessing the field strength at the location of the equipment when the external high-power EMP is coupled. Therefore, there is an imperative need to analyze and calculate the time–domain coupling characteristics between the building and the external EMP environments.

Reinforced concrete structures have become the main building material and form of ground construction due to their long service life and low construction costs [3,4]. Some researchers have examined the electromagnetic wave transmission characteristics of reinforced concrete walls [5,6]. The shielding effectiveness (SE) of concrete blocks, concrete walls, and reinforced concrete walls in a shielded room is measured in [6]. Considering the protection requirements for indoor electronic devices, focusing solely on the electromagnetic coupling characteristics between a single wall and EMPs is often inadequate. Consequently, more researchers have been investigating the time–domain electromagnetic coupling characteristics of reinforced concrete buildings and external EMP environments. Currently, there are two main methods. One is the full-wave analysis method [7], which involves the precise modelling of the electromagnetic properties and geometric details of the reinforced concrete structure to accurately determine the electromagnetic field distribution. Although this approach provides highly accurate results, it has certain limitations, including computational challenges and low efficiency when addressing multi-scale structures such as reinforced concrete buildings. This is because the method demands fine grids to capture the detailed geometry of the steel bars and concrete, leading to significant computational resource consumption. To enhance computational efficiency, parallel techniques can be employed [8]. Another widely used approach is various approximations [9,10,11] or equivalent [12,13] modelling, which allows the use of coarse grids for calculations. In [9], the reinforced concrete wall is approximated as a homogeneous concrete material, and the characteristics of the electric field distribution inside a building with multiple rooms, as well as the electric field changes in the time domain at specific observation points, are calculated. In [12], a two-dimensional thin dielectric panel, exhibiting the same reflection and transmission characteristics as the wall, is used as an equivalent replacement for the reinforced concrete wall. This significantly reduces the number of grids required for calculation, allowing for an analysis of the electromagnetic field inside the building. In [13], the steel mesh embedded in the wall is considered as an equivalent thin metal sheet, in order to adopt coarse FDTD grids to decrease the number of meshes and improve computational efficiency. The study then calculates the internal current and electric field of a three-story building under the influence of lightning EMPs.

Currently, a key issue in equivalent modelling is the accurate extraction of the electromagnetic parameters of reinforced concrete structures. This is essential for using coarse grids to model the wall, thereby reducing the consumption of computing resources. This is crucial for calculating the time–domain electromagnetic coupling characteristics between electrically large buildings and external EMPs. The research hotspots on equivalent electromagnetic parameter extraction have mainly concentrated on the extraction and optimization of equivalent electromagnetic parameters for honeycomb-structured wave-absorbing materials [14] and metamaterials [15,16,17]. However, common electromagnetic parameter extraction methods are universal and can also be applied to extract equivalent electromagnetic parameters of reinforced concrete materials. Electromagnetic parameter extraction methods can be categorized into the two main types of resonant cavity methods [18] and network parameter methods [15,16]. The resonant cavity method offers high accuracy but is limited in that it primarily relies on the resonance frequency, where the frequency is the unknown variable. This makes it challenging to perform measurements across a broad frequency range. Among the network parameter methods, the Nicolson–Ross–Weir transmission–reflection (NRW T/R) method is the most commonly used due to its broadband capabilities and high precision. The NRW method and various improved methods developed to overcome its inherent multi-value and low-frequency limitations [17,19,20] have been widely used in the extraction of equivalent electromagnetic parameters of materials. Some researchers have focused solely on the equivalent relative permittivity of the measured material [21,22,23,24,25], which is not comprehensive enough for the research object in this paper that exhibits both electric and magnetic dispersion properties. In addition, some of the equivalent electromagnetic parameters obtained in the existing studies are single frequency data [23,24], which lack the equivalent electromagnetic parameter data across the wide frequency band that is of interest in our research. In recent years, machine learning has been applied to the inversion calculation of equivalent electromagnetic parameters due to its ability to effectively capture the nonlinear relationships between input and output parameters [14,26,27]. Nevertheless, intelligent algorithms require the input of data necessary for training.

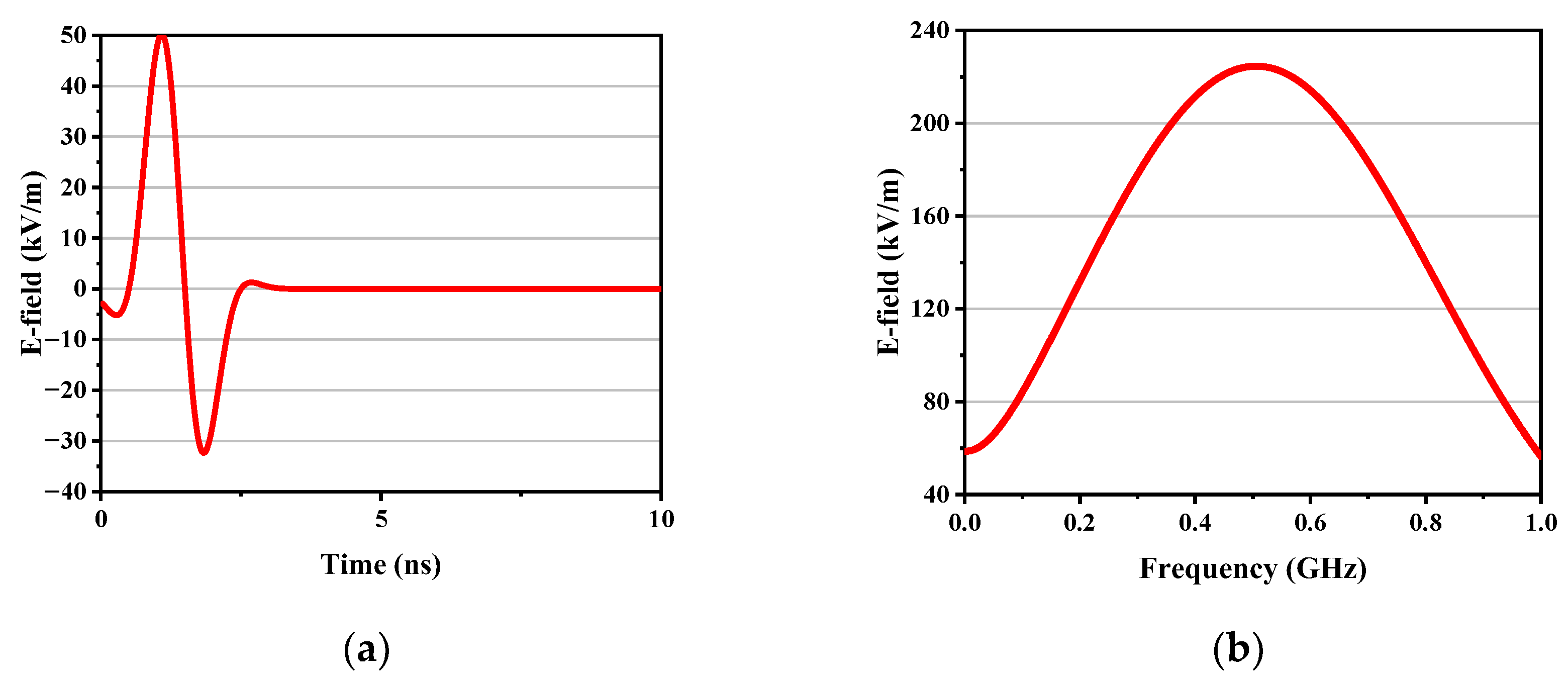
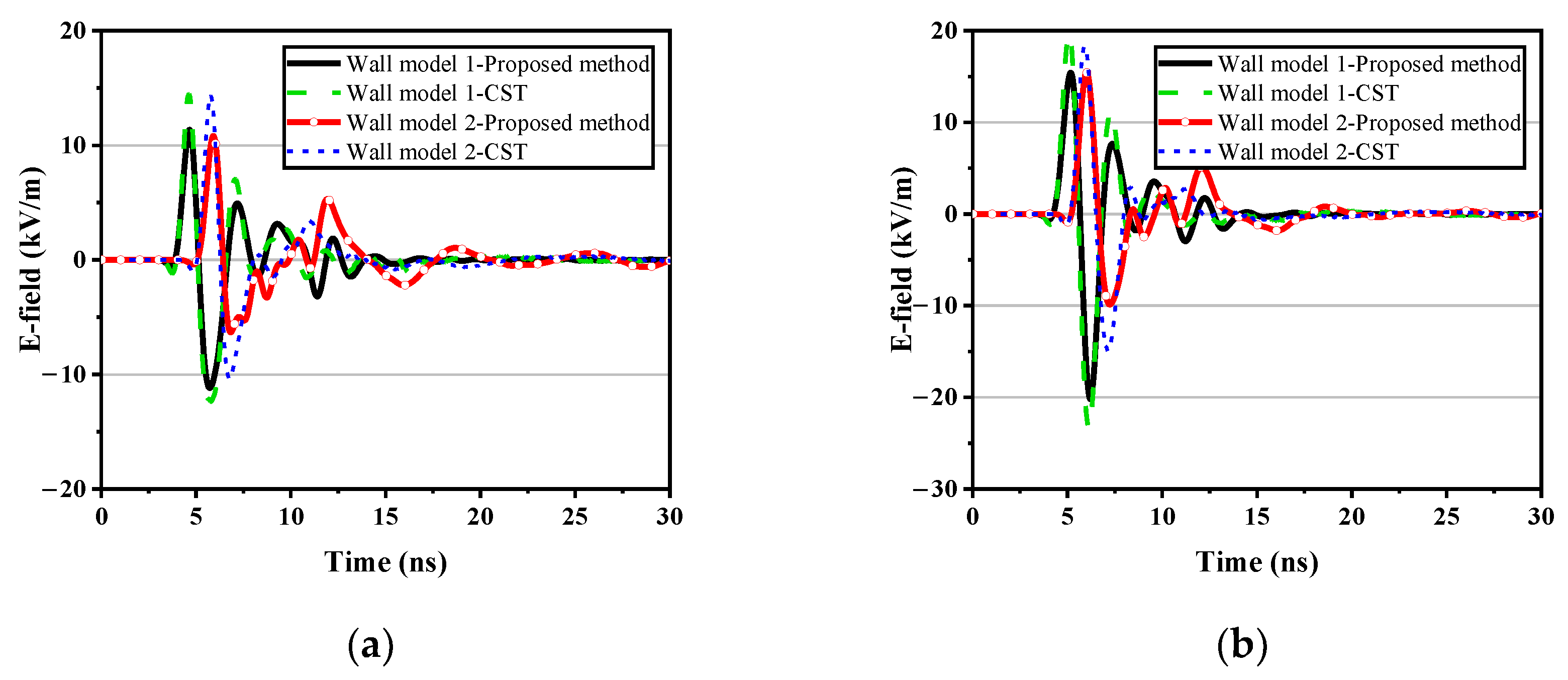
To address these challenges, this paper proposes a comprehensive simulation method for analyzing the electromagnetic coupling characteristics between buildings and external EMP environments, based on the electromagnetic parameter equivalence of reinforced concrete structures. The method begins by accurately extracting the dispersive equivalent electromagnetic parameters of the reinforced concrete structure, allowing the use of coarse grids in the simulation of the reinforced concrete wall. The auxiliary differential equation finite-difference time–domain (ADE-FDTD) method is then used to analyze the time–domain electromagnetic coupling characteristics of equivalent buildings under EMP irradiation based on the obtained electromagnetic parameters. The accuracy and efficiency of the proposed method are then verified by various simulations.

The rest of this paper is organized as follows. In Section 2, the proposed method for calculating the electromagnetic coupling characteristics between buildings and external EMP environments is described. In Section 3, several cases are carried out to validate the feasibility and effectiveness of the proposed integrated calculation method, and the calculation effect of the method is also discussed. Some conclusions are drawn in Section 4.

2. Description of the Integrated Simulation Method

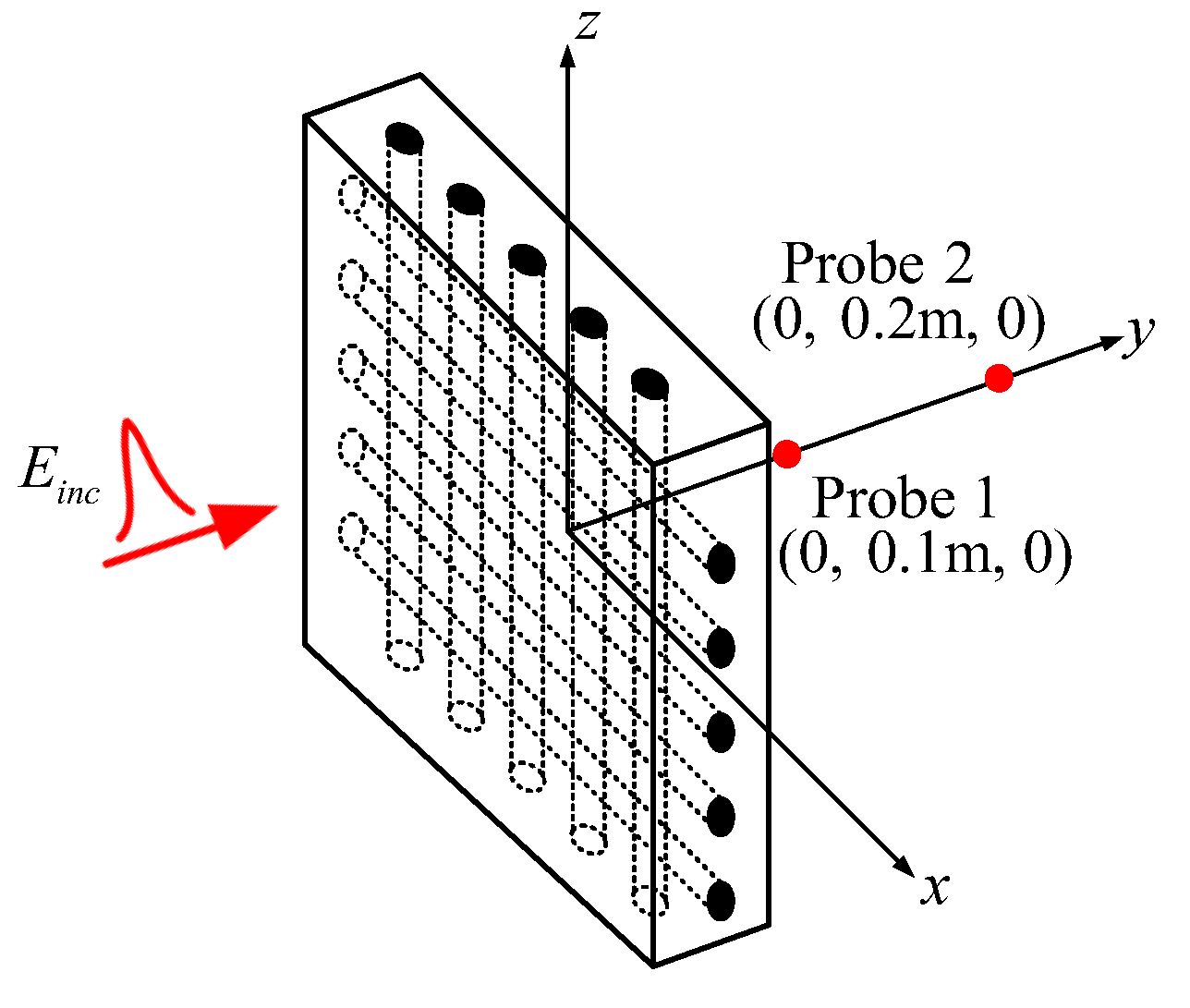
In practice, the diameter and arrangement period of the steel mesh, as well as the thickness of the walls, vary across different reinforced concrete buildings. Additionally, the diameter of the steel bars is in the order of millimeters, while the dimensions of the buildings generally range from several meters to a hundred meters. When calculating such a multi-scale problem, fine grids are often required to accurately simulate the rebar structure, which can consume a large amount of computing resources. To address this issue, this paper first accurately extracts the equivalent electromagnetic parameters of reinforced concrete structures based on their S-parameters, enabling the use of coarse grids to model reinforced concrete walls and reduce the consumption of computing resources. The dispersive equivalent electromagnetic parameters are then fitted into specific polynomial rational function forms by the vector fitting (VF) method. Finally, the ADE-FDTD method is used to analyze the time–domain coupling characteristics of reinforced concrete buildings under EMP irradiation, based on the derived electric and magnetic dispersive electromagnetic parameters. In conclusion, this paper proposes a comprehensive calculation method of the time–domain electromagnetic coupling characteristics between buildings and external EMP environments, which integrates the extraction of equivalent electromagnetic parameters, the VF method, and the ADE-FDTD method.

2.1. Equivalent Electromagnetic Parameter Extraction Method for Reinforced Concrete Material

When a plane wave irradiates a wall vertically, the S-parameters can be expressed by Equation (1) [28].

$$\begin{array}{l}{S}_{11}={\displaystyle \frac{\mathsf{\Gamma }(1-T^2)}{1-{\mathsf{\Gamma }}^2{T}^2}}\\ S_{21}={\displaystyle \frac{T(1-{\mathsf{\Gamma }}^2)}{1-{\mathsf{\Gamma }}^2{T}^2}}\end{array}$$

(1)

where $\mathsf{\Gamma }$ is the reflection coefficient and $T$ is the transmission coefficient.

If $K=(S_{11}^2-S_{21}^2+1)/(2S_{11})$ is set, Equation (2) is obtained.

$$\begin{array}{l}\mathsf{\Gamma }=K\pm \sqrt{K^2-1}(\left|\mathsf{\Gamma }\right|<1)\\ T={\displaystyle \frac{S_{11}+S_{21}-\mathsf{\Gamma }}{1-(S_{11}+S_{21})\mathsf{\Gamma }}}\end{array}$$

(2)

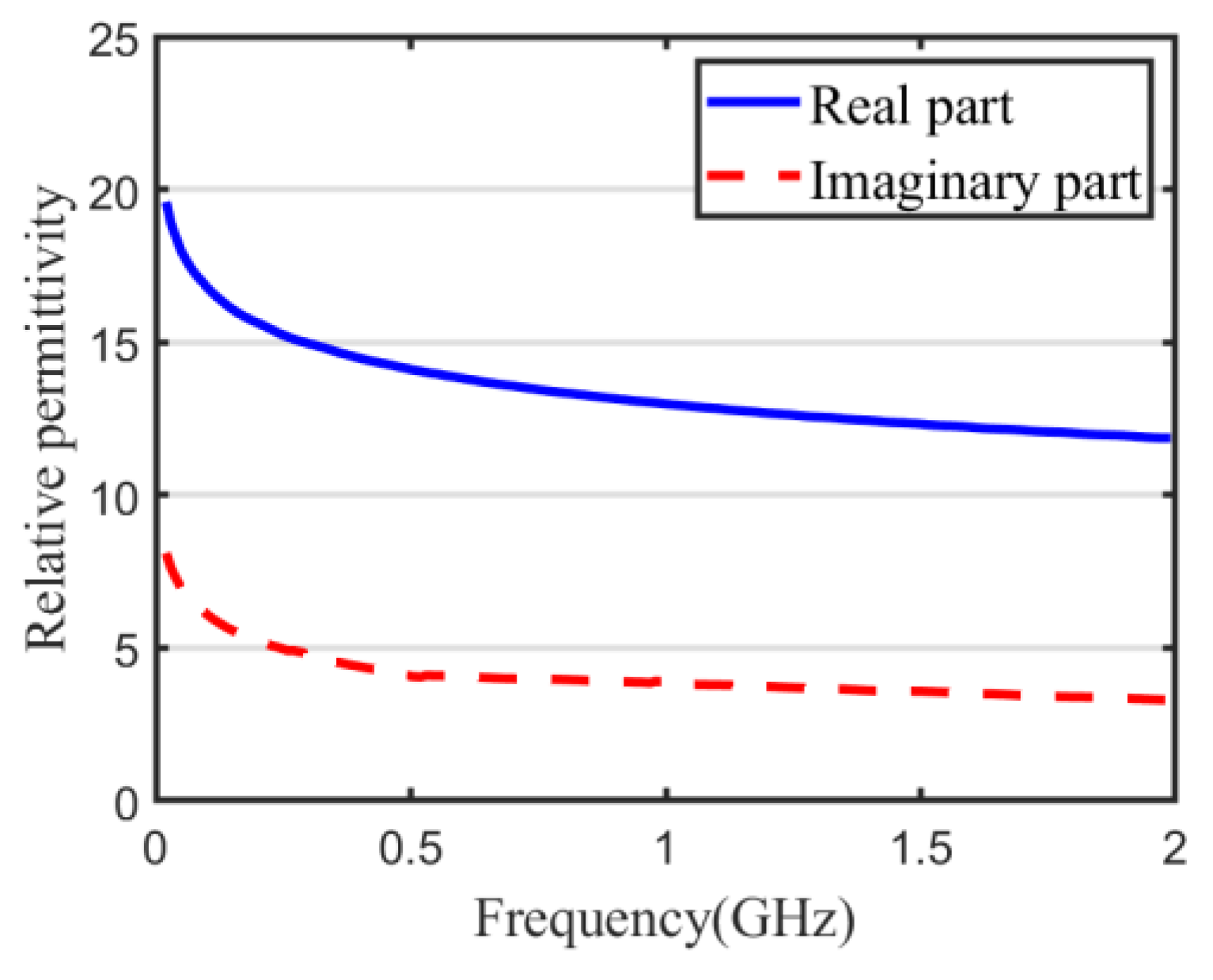
The equivalent relative permittivity ${\epsilon }_r$ and relative permeability ${\mu }_r$ can be calculated by Equation (3) [29].

$$\begin{array}{l}{\epsilon }_r={\displaystyle \frac{\gamma }{{\gamma }_0}}\left({\displaystyle \frac{1-\mathsf{\Gamma }}{1+\mathsf{\Gamma }}}\right)\\ {\mu }_r={\displaystyle \frac{\gamma }{{\gamma }_0}}\left({\displaystyle \frac{1+\mathsf{\Gamma }}{1-\mathsf{\Gamma }}}\right)\end{array}$$

(3)

where ${\gamma }_0$ is the propagation constant in the air; ${\gamma }_0=2\pi /{\lambda }_0$; $\gamma$ is the propagation constant in the wall; and $\gamma =\lg (1/T)/d$; $d$ is the thickness of the wall.

During the calculation process, the logarithmic operation of complex numbers has multivalued properties, resulting in periodic jumps in the imaginary part of the propagation constant $\gamma$, as shown in Equation (4). The derived equivalent electromagnetic parameters are correspondingly multivalued, as shown in Equation (3).

$$\gamma ={\displaystyle \frac{\lg (1/T)}{d}}=-\left[{\displaystyle \frac{\lg (|T|)}{d}}+j{\displaystyle \frac{2n\pi +\phi }{d}}\right](n=0,\pm 1,\pm 2\cdots )$$

(4)

In this regard, based on the theoretical premise that the imaginary part of the propagation constant $\gamma$ changes continuously with frequency, this paper unwraps the phase of the imaginary part of $\lg (1/T)$ for frequency point where the imaginary part of $\lg (1/T)$ jumps, overcoming the multi-valued issue.

Method for determining $n$:

(1)

In the low-frequency band, $n=0$, the imaginary part of $\lg (1/T)$ has a unique value;

(2)

In the high-frequency band, when the imaginary part of $\lg (1/T)$ jumps at a certain frequency point, it needs to be compensated by $2\pi$. This can be achieved by substituting $n+1$ for $n$ at the previous frequency point;

(3)

Repeating step 2 until the highest frequency is reached, ensuring the unique determination of the imaginary part of $\lg (1/T)$.

In this way, the unique determination of the propagation constant $\gamma$ is realized, and ultimately unique equivalent electromagnetic parameters are obtained.

2.2. Modelling of Equivalent Reinforced Concrete Structure in FDTD Method

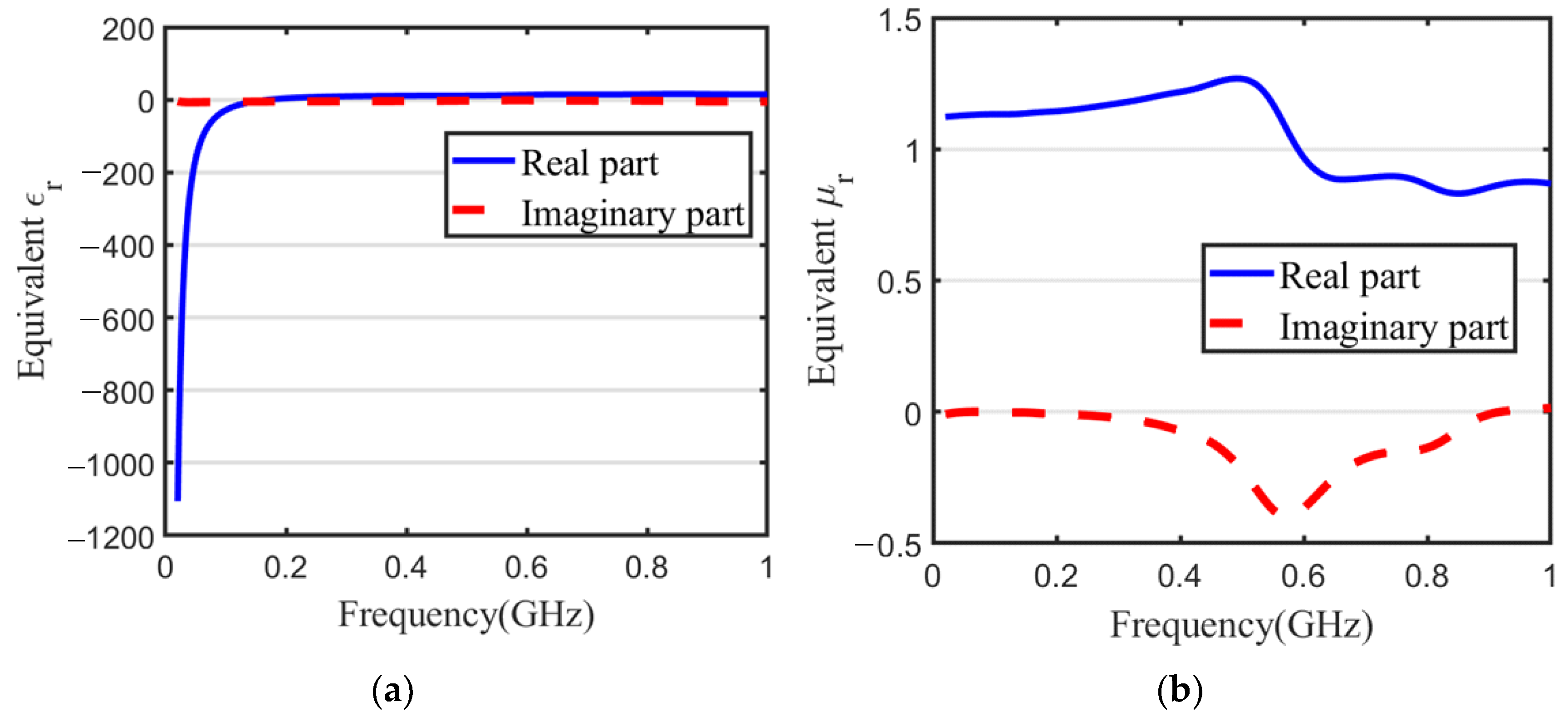
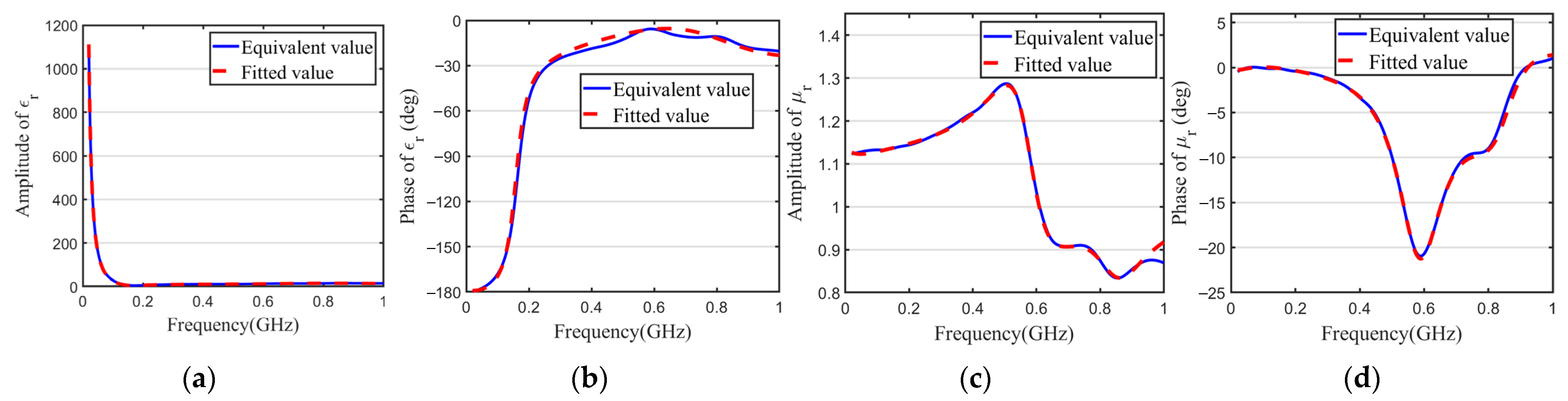
The equivalent electromagnetic parameters ${\epsilon }_r$ and ${\mu }_r$ obtained in Section 2.1 are just two sets of data in the frequency domain. In order to calculate them in the FDTD algorithm, it is necessary to convert the derived equivalent electromagnetic parameter data into a specific polynomial rational function form by the VF method [30]. The VF method is a mathematical fitting technique mainly used for rational function approximation of frequency–domain curves, enabling the data to be represented in a rational function form, as shown in Equation (5).

$$f(s)=m+se+{\displaystyle \sum _{n=1}^N\frac{r_n}{s-p_n}}$$

(5)

where $m$ and $e$ are real numbers and the residue $r_n$ and pole $p_n$ are real numbers or conjugate complex pairs.

By employing the VF method, the equivalent ${\epsilon }_r(\omega )$ and ${\mu }_r(\omega )$ are represented as Equation (6).

$$\left\{\begin{array}{c}{\epsilon }_r\left(\omega \right)={\epsilon }_r^{\prime }(\omega )-j{\epsilon }_r^{\prime \prime }(\omega )={\epsilon }_{\infty }+\chi (\omega )={\epsilon }_{\infty }+{\displaystyle \sum _{p=1}^P\frac{c_p}{j\omega -a_p}}+{\displaystyle \frac{c_p^{*}}{j\omega -a_p^{*}}}\\ {\mu }_r\left(\omega \right)={\mu }_r^{\prime }(\omega )-j{\mu }_r^{\prime \prime }(\omega )={\mu }_{\infty }+\chi (\omega )={\mu }_{\infty }+{\displaystyle \sum _{p=1}^P\frac{c_p}{j\omega -a_p}}+{\displaystyle \frac{c_p^{*}}{j\omega -a_p^{*}}}\end{array}\right.$$

(6)

where ${\epsilon }_{\infty }$ is the relative permittivity at infinite frequency whose value is equal to the value of the fitted data $m$; ${\mu }_{\infty }$ is the relative permeability at infinite frequency whose value is equal to the value of the fitted data $m$; both $a_p$ and $c_p$ can be complex numbers; and $a_p^{*}$ is the conjugate complex of $a_p$, and $c_p^{*}$ is the conjugate complex of $c_p$. The values of each set of $(a_p,c_p)$ are identical to those of the fitted data set $(p_n,r_n)$. It is important to note that when utilizing the VF method to fit ${\epsilon }_r(\omega )$ and ${\mu }_r(\omega )$, $e=0$ should be set.

Maxwell’s curl equation is shown in Equation (7).

$$\begin{array}{l}\nabla \times H=\epsilon {\displaystyle \frac{\partial E}{\partial t}}+\sigma E\\ \nabla \times E=-\mu {\displaystyle \frac{\partial H}{\partial t}}-{\sigma }_{m}H\end{array}$$

(7)

Its frequency domain form is shown in Equation (8).

$$\begin{array}{l}\nabla \times H(\omega )=j\omega {\epsilon }_0{\epsilon }_{r}E(\omega )+\sigma E(\omega )\\ \nabla \times E(\omega )=-j\omega {\mu }_0{\mu }_{r}H(\omega )-{\sigma }_{m}H(\omega )\end{array}$$

(8)

Taking the ADE-FDTD method to deal with the electric dispersion property of the reinforced concrete wall as an example [31], the first formula in Equation (6) is substituted into the first formula of Equations (8) and (9) is obtained.

$$\nabla \times H(\omega )=j\omega {\epsilon }_0{\epsilon }_{\infty }E(\omega )+\sigma E(\omega )+j\omega {\epsilon }_0{\displaystyle \sum _{p=1}^P(\frac{c_p}{j\omega -a_p}}+{\displaystyle \frac{c_p^{*}}{j\omega -a_p^{*}}})E(\omega )$$

(9)

Introduce auxiliary functions $J_p$ and ${\mathbf{J}}_p^{\prime }$, as shown in Equation (10).

$$\begin{array}{l}{J}_p(\omega )=j\omega {\epsilon }_0{\displaystyle \frac{c_p}{j\omega -a_p}}E(\omega )\\ {\mathbf{J}}_p^{\prime }(\omega )=j\omega {\epsilon }_0{\displaystyle \frac{c_p^{*}}{j\omega -a_p^{*}}}E(\omega )\end{array}$$

(10)

The relationship between $J_p$ and ${\mathbf{J}}_p^{\prime }$ is as follows:

$${\mathbf{J}}_p^{\prime }(\omega )=J_p^{*}(\omega )$$

(11)

where $J_p^{*}$ is the conjugate complex of $J_p$.

The time–domain form of the function $J_p$ (shown as the first formula in Equation (10)) is as follows:

$${\displaystyle \frac{d{J}_p(t)}{dt}}-a_p{J}_p(t)={\epsilon }_0{c}_p{\displaystyle \frac{dE(t)}{dt}}$$

(12)

Using the central difference approximation and the average value approximation for Equation (12), Equation (13) is obtained.

$${\displaystyle \frac{J_p^{n+1}-J_p^n}{\Delta t}}-a_p{\displaystyle \frac{J_p^{n+1}+J_p^n}{2}}={\epsilon }_0{c}_p{\displaystyle \frac{E^{n+1}-E^n}{\Delta t}}$$

(13)

Simplify Equation (13), the time–domain iterative formula of $J_p$ is obtained.

$$J_p^{n+1}=k_p{J}_p^n+{\beta }_p{\displaystyle \frac{E^{n+1}-E^n}{\Delta t}}$$

(14)

where $k_p={\displaystyle \frac{1+(a_p\Delta t)/2}{1-(a_p\Delta t)/2}}$, ${\beta }_p={\displaystyle \frac{{\epsilon }_0{c}_p\Delta t}{1-(a_p\Delta t)/2}}$.

Simplify Equation (9) using the conjugate relationship and convert it to time–domain form, so Equation (15) is obtained.

$$\nabla \times H={\epsilon }_0{\epsilon }_{\infty }{\displaystyle \frac{\partial E}{\partial t}}+\sigma E+{\displaystyle \sum _{p=1}^{P}2}\mathrm{Re}(J_p)$$

(15)

Using the central difference approximation and the average value approximation for Equation (15), then, Equation (16) is obtained.

$${[\nabla \times H]}^{n+{\displaystyle \frac{1}{2}}}={\epsilon }_0{\epsilon }_{\infty }{\displaystyle \frac{E^{n+1}-E^n}{\Delta t}}+\sigma {\displaystyle \frac{E^{n+1}+E^n}{2}}+{\displaystyle \sum _{p=1}^{P}2}\mathrm{Re}({\displaystyle \frac{J_p^{n+1}+J_p^n}{2}})$$

(16)

Substitute Equation (14) into Equation (16) to obtain the time–domain iterative formula for $E$.

$$\begin{array}{l}{E}^{n+1}={\displaystyle \frac{2{\epsilon }_0{\epsilon }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)-\sigma \Delta t}{2{\epsilon }_0{\epsilon }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)+\sigma \Delta t}}{E}^n+\\ {\displaystyle \frac{2\Delta t}{2{\epsilon }_0{\epsilon }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)+\sigma \Delta t}}\left\{{[\nabla \times H]}^{n+{\displaystyle \frac{1}{2}}}-\mathrm{Re}{\displaystyle \sum _{p=1}^P(}1+k_p)J_p^n\right\}\end{array}$$

(17)

Similarly, the time–domain iterative formula for $H$ is as follows:

$$\begin{array}{l}{H}^{n+1}={\displaystyle \frac{2{\mu }_0{\mu }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)-{\sigma }_m\Delta t}{2{\mu }_0{\mu }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)+{\sigma }_m\Delta t}}{H}^n-\\ {\displaystyle \frac{2\Delta t}{2{\mu }_0{\mu }_{\infty }+2{\displaystyle \sum _{p=1}^P\mathrm{Re}}({\beta }_p)+{\sigma }_m\Delta t}}\left\{{[\nabla \times E]}^{n+{\displaystyle \frac{1}{2}}}+\mathrm{Re}{\displaystyle \sum _{p=1}^P(}1+k_p)J_p^n\right\}\end{array}$$

(18)

where $k_p$, ${\beta }_p$, and $J_p$ in Equation (18) are calculated from ${\mu }_r$.

2.3. The Calculation Flow of the Method Proposed in This Article

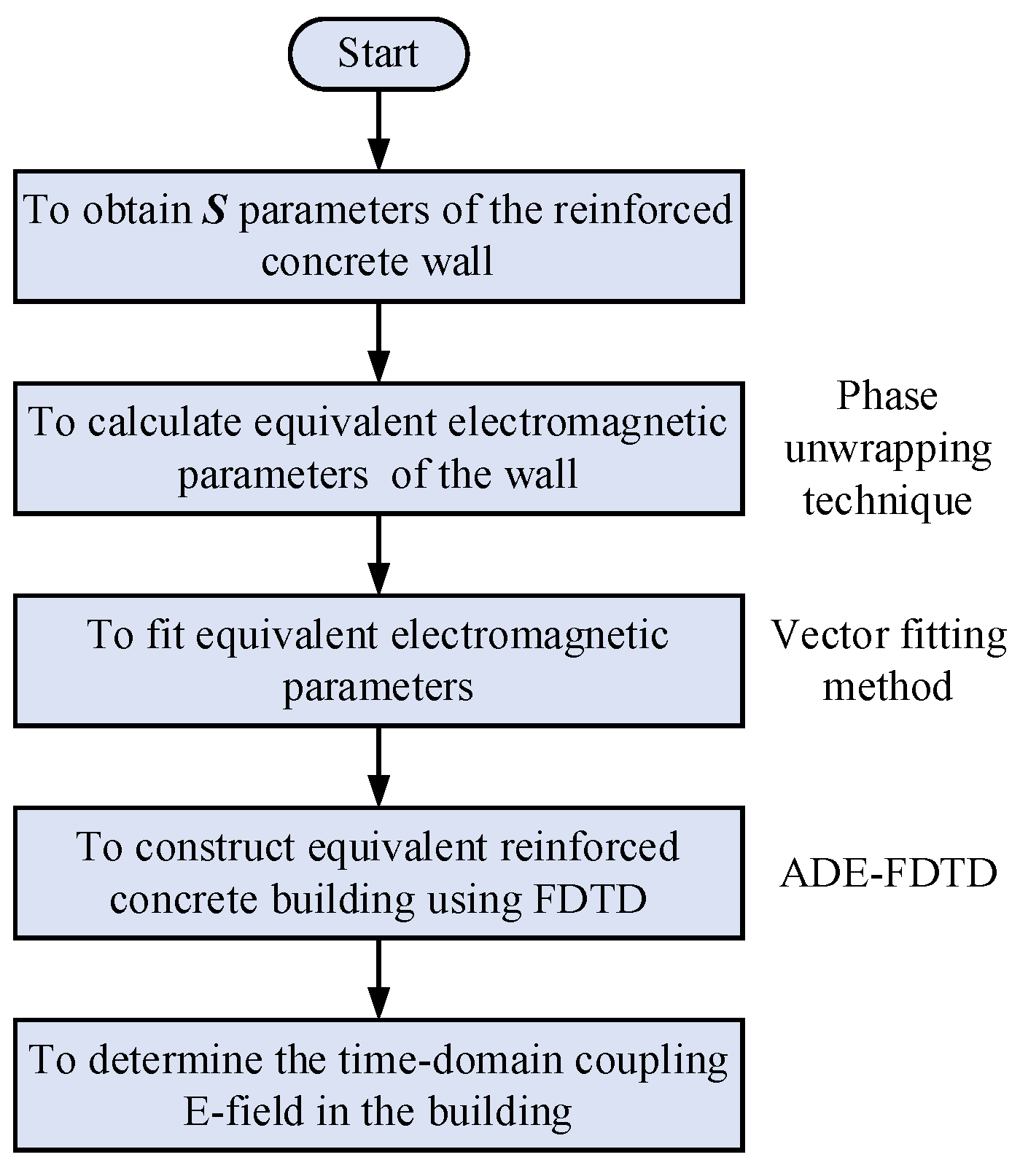
According to the above calculation, Figure 1 illustrates the calculation flow of the time–domain electromagnetic coupling characteristics between buildings and EMP environments based on the electromagnetic parameter equivalence of reinforced concrete structures. First, the S-parameters of the reinforced concrete wall are obtained by simulation [12] or measurement [32], and then the equivalent electromagnetic parameters are calculated. Next, the dispersive equivalent electromagnetic parameters are fitted into specific polynomial rational function forms. Finally, ADE-FDTD is used to analyze the time–domain electromagnetic coupling characteristics of equivalent buildings under EMP irradiation.

3. Algorithm Validation and Discussion

To verify the correctness and effectiveness of the method proposed in this paper, reinforced concrete walls with one-layered steel mesh and two-layered steel mesh, a one-story reinforced concrete room, and an electrically large two-story reinforced concrete building are selected as the objects of study in this section. The time–domain electromagnetic coupling characteristics are analyzed and calculated under the influence of external EMPs.

3.1. Verification of Coupling Characteristics Between Reinforced Concrete Wall and EMP Environments

3.1.1. Reinforced Concrete Wall with One-Layered Steel Mesh

The method is first validated by calculating the time–domain electromagnetic coupling characteristics between reinforced concrete walls with one-layered steel mesh (as shown in Figure 2). The diameter of the steel bar is $D=20\mathrm{mm}$, the arrangement period is $T=200\mathrm{mm}$, the conductivity of the lossy metal steel bar is $\sigma =1\times {10}^6\mathrm{S}/\mathrm{m}$, and the relative permeability is ${\mu }_r=1$. The geometric dimensions of concrete are as follows: $L=1\mathrm{m}$, $d=100\mathrm{mm}$ (defined as wall model 1) and $d=200\mathrm{mm}$ (defined as wall model 2), and the electromagnetic parameters of concrete are shown in Figure 3.

Taking the calculation process of the reinforced concrete wall with one-layered steel mesh and a thickness of 100 mm (wall model 1) as an example, the method described in Section 2.1 is used to calculate the equivalent electromagnetic parameters of the reinforced concrete wall model 1. The effect of the phase unwrapping technique is shown in Figure 4. The calculated equivalent electromagnetic parameters across the frequency range of 20 MHz⁻¹ GHz are shown in Figure 5, and the amplitudes of the S-parameters before and after equivalence are shown in Figure 6.

The VF method is then used to perform a polynomial fit of the equivalent electromagnetic parameters. The fitting results of ${\epsilon }_r$ and ${\mu }_r$ are shown in Figure 7, with the specific values displayed in

Table 1. The fitting values of equivalent ${\epsilon }_r$ of reinforced concrete wall model 1.

Parameter	Parameter Value After Fitting
${\epsilon }_{\infty }$	9.5932
$(a_1,c_1)$	$(-8.7696\times {10}^8,5.2216\times {10}^9)$
$(a_2,c_2)$	$(-1.6696\times {10}^9,7.5332\times {10}^9)$
$(a_3,c_3)$	$(-6.8016\times {10}^5+j1.3402\times {10}^7,2.5016\times {10}^8-j6.5959\times {10}^{11})$
$(a_4,c_4)$	$(-6.8016\times {10}^5-j1.3402\times {10}^7,2.5016\times {10}^8+j6.5959\times {10}^{11})$
$(a_5,c_5)$	$(-1.4654\times {10}^9+j5.0596\times {10}^9,8.1694\times {10}^9-j1.4404\times {10}^8)$
$(a_6,c_6)$	$(-1.4654\times {10}^9-j5.0596\times {10}^9,8.1694\times {10}^9+j1.4404\times {10}^8)$

and

Table 2. The fitting values of equivalent ${\mu }_r$ of reinforced concrete wall model 1.

Parameter	Parameter Value After Fitting
${\epsilon }_{\infty }$	1.0242
$(a_1,c_1)$	$(-1.8172\times {10}^8,2.9280\times {10}^6)$
$(a_2,c_2)$	$(-8.8550\times {10}^8,-2.4040\times {10}^7)$
$(a_3,c_3)$	$(-5.1040\times {10}^8+j3.5793\times {10}^9,1.2681\times {10}^7-j1.8869\times {10}^8)$
$(a_4,c_4)$	$(-5.1040\times {10}^8-j3.5793\times {10}^9,1.2681\times {10}^7+j1.8869\times {10}^8)$
$(a_5,c_5)$	$(-6.1268\times {10}^8+j5.2694\times {10}^9,-6.9169\times {10}^7-j4.4595\times {10}^7)$
$(a_6,c_6)$	$(-6.1268\times {10}^8-j5.2694\times {10}^9,-6.9169\times {10}^7+j4.4595\times {10}^7)$

.

After obtaining the equivalent electromagnetic parameters of the reinforced concrete structure, it can be treated as an equivalent homogeneous structure, as illustrated in Figure 8. The two-dimensional cross-section of the reinforced concrete structure reveals that fine grids are necessary to accurately capture the intricate geometry of the steel bars and concrete. However, after applying the equivalence, coarser grids can be employed in simulations, thereby significantly reducing computational resource consumption.

The equivalent FDTD modelling with coarse grids is then performed according to the method in Section 2.2. The modulated Gaussian pulse serves as a model for EMP environments, allowing for flexible adjustments to the waveform shape, as shown in Equation (19). It is mostly used to simulate the effects of EMP environments of different frequencies and amplitudes on equipment or systems in laboratory or simulation settings [33]. Considering that high-power EMP environments are typically characterized by high field strengths, a modulated Gaussian pulse with an amplitude of 50 kV/m and a center frequency of 0.5 GHz (as shown in Figure 9) is selected as the excitation source.

$$E(t)=E_0\cos (2\pi f_{0}t)\exp \left[-{\displaystyle \frac{4\pi {(t-t_0)}^2}{{\tau }^2}}\right]$$

(19)

When the excitation source vertically irradiates the reinforced concrete wall model 1, as illustrated in Figure 10, the time–domain electric field waveforms at observation points on the y = 0.1 m plane are calculated. The relative L2 norm error between the proposed method and the electromagnetic simulation software CST Studio Suite 2022 [34] is presented in Figure 11. This figure demonstrates that the relative L2 norm errors are generally less than 0.5 in the region close to the interior of the wall, indicating a good agreement between the proposed method and the CST 2022 simulation results. However, the errors in the edge region are relatively larger. This phenomenon may stem from boundary effects and discretization errors. Nevertheless, the overall error is still within an acceptable range, indicating that the proposed method can effectively simulate the electric field, particularly in the regions close to the interior of the model.

To provide a more detailed analysis of the time–domain coupling characteristics between the reinforced concrete wall and the EMP, the time–domain electric field waveforms at observation points P1 (0.1 m to the right of the wall center) and P2 (0.2 m to the right of the wall center) (as shown in Figure 12) are calculated and presented in Figure 13. This analysis is conducted for both reinforced concrete wall model 1 and model 2 under vertical irradiation from the excitation source, as illustrated in Figure 12. The calculation errors are given in

Table 3. Comparison of calculation errors.

Example	Coordinates of the Observation Point (m)	Maximum Relative Error (dB)	Mean Absolute Error (kV/m)
Wall model 1	P1 [0 0.1 0]	−5.8726	0.5614
	P2 [0 0.2 0]	−1.8308	0.6978
Wall model 2	P1 [0 0.1 0]	−0.1836	1.0043
	P1 [0 0.2 0]	−1.7735	0.9801

. It can be seen that the predicted time–domain electromagnetic coupling characteristics of reinforced concrete wall model 1 and model 2 are in good agreement with the data obtained from CST 2022, demonstrating high accuracy. Therefore, the method proposed in this paper is applicable to the analysis of the electromagnetic coupling characteristics between reinforced concrete walls of different thicknesses and external EMP environments. Furthermore, it can be found by comparison that the peak amplitude of the predicted electric field time–domain waveform observed at P1 behind wall model 1 is 11.35 kV/m, while the predicted peak amplitude of the electric field time–domain waveform observed at P1 behind wall model 2 is reduced to 10.82 kV/m. Therefore, when the same steel structure is included, the thicker the concrete wall is, the more obvious its shielding effect against the EMP.

Table 4. The comparison of calculation resources of wall model 1 and 2.

Example	Method	Mesh Number	Time (s)
Wall model 1	Proposed method	3,111,696	329
	CST	17,451,492	824
Wall model 2	Proposed method	4,148,928	388
	CST	17,937,684	898

compares the two methods in terms of the number of meshes and computing time. When calculating the time–domain coupling characteristics between reinforced concrete walls of two different thicknesses and external EMPs, the number of meshes required in this paper is reduced by approximately 5 times, while the calculation speed is increased by about 2.5 times compared to that of the CST 2022 simulation software. This demonstrates that the proposed method can enhance the computational efficiency and save computing resources, which is practically significant for the analysis of the time–domain coupling characteristics between reinforced concrete structures and external EMP environments.

3.1.2. Reinforced Concrete Wall with Two-Layered Steel Mesh

To further verify the universality of the method proposed in this paper, the time–domain electromagnetic coupling characteristic analysis between a reinforced concrete wall with two-layered steel mesh (defined as wall model 3) and external EMP environment is conducted, as shown in Figure 14. The geometric dimensions of reinforced concrete wall model 3 are 1 m × 1 m × 0.2 m. The arrangement of the steel mesh is the same as in the previous section, and the spacing between the layers of the two-layer steel mesh is 0.1 m.

When the modulated Gaussian pulse with an amplitude of 50 kV/m and a center frequency of 0.5 GHz vertically irradiates the reinforced concrete wall model 3, the predicted electric field time–domain waveforms at observation points P1 (0.1 m to the right of the center point of the wall) and P2 (0.2 m to the right of the center point of the wall) are shown in Figure 15. The comparison of computing resources of the wall model 3 used by the proposed method and the CST 2022 simulation is shown in

Table 5. The comparison of calculation resources of wall model 3.

Method	Mesh Number	Time (s)
Proposed method	5,186,160	388
CST	18,196,832	1586

. It can be observed that the predicted time–domain electromagnetic coupling characteristics of the reinforced concrete wall with two-layered steel mesh are in good agreement with the CST 2022 simulation results, demonstrating high accuracy and significant savings in computing resources. Therefore, the method proposed in this paper can effectively analyze the time–domain electromagnetic coupling characteristics of reinforced concrete walls with various reinforced concrete structures, demonstrating good universality.

In addition, Figure 15 also provides comparative information on the time–domain waveforms of the reinforced concrete wall two-layered steel mesh (wall model 3) and reinforced concrete wall one-layered steel mesh of the same thickness (wall model 2) at the same observation point. The comparison reveals that the predicted peak amplitude of the electric field time–domain waveform observed at P1 behind wall model 2 is 10.82 kV/m, while the predicted peak amplitude of the electric field time–domain waveform observed at P1 behind wall model 3 is reduced to 8.59 kV/m. The CST 2022 simulation results further indicate that the peak amplitude of the electric field in the time domain at the same observation point of wall model 3 is lower than that of wall model 2. Therefore, when the wall thickness is identical, the shielding effect of the reinforced concrete wall with two-layered steel mesh on EMP is more pronounced than that of the reinforced concrete wall with one-layered steel mesh.

3.2. Verification of Coupling Characteristics Between One-Story Reinforced Concrete Room and EMP Environments

In order to ensure the safe and stable operation of indoor electronic equipment and systems, the internal electromagnetic field of a reinforced concrete room under EMP irradiation is calculated using the method proposed in this paper. A reinforced concrete room with dimensions of 5 m × 4 m × 3 m, an internal floor height of 2.8 m, and a wall thickness of 0.1 m is selected as the object of study, as shown in Figure 16. The wall structure is the same as the reinforced concrete wall model 1 in Section 3.1.1. The size of the iron door is 1.25 m × 2 m, and the electromagnetic parameters of it are ${\epsilon }_r=1$, ${\mu }_r=1$, and $\sigma =1.04\times {10}^7\mathrm{S}/\mathrm{m}$. The size of the glass window is 2 m × 1.7 m, and the electromagnetic parameters of it are ${\epsilon }_r=5.1$, ${\mu }_r=1$, and $\sigma =0\mathrm{S}/\mathrm{m}$.

When a modulated Gaussian pulse with an amplitude of 50 kV/m and a center frequency of 0.25 GHz irradiates the room from the left side, the calculated electric field time–domain waveforms at observation points P1 (0, −1 m, 0), P2 (0, −0.5 m, 0), P3 (0, 0, 0) (the central point), and P4 (0, 1 m, 0) inside the room are in good agreement with the simulation results obtained from CST 2022, as shown in Figure 17. The calculation errors are given in

Table 6. Error of calculation.

Coordinates of the Observation Point (m)	Maximum Relative Error (dB)	Mean Absolute Error (kV/m)
P1 [0 −1 0]	−6.4515	0.9057
P2 [0 −0.5 0]	−4.1747	0.9434
P3 [0 0 0]	−3.0159	0.9509
P4 [0 1 0]	−5.7310	0.8488

. As can be seen from the figure, the maximum electric field time–domain peak amplitude at the four observation points is 20.29 kV/m, while the peak amplitude of the electric field gradually decreases to 16.2 kV/m along the direction of electromagnetic wave propagation.

Figure 18 shows the electric field spectra at the four observation points. It can be found that the spectral energy is mainly concentrated in the range of 0.1–0.4 GHz, which is consistent with the center frequency of the EMP (0.25 GHz), while the energy in the low- and high-frequency bands is relatively lower. Comparison of the spectral curves shows that the predicted results of the proposed method in the low-frequency band are in good agreement with the simulation results of CST 2022, but the difference between them increases with the increase in frequency. This phenomenon is related to the grid characteristics of the FDTD method: the grid size determines the highest frequency that can be accurately calculated. Typically, at least 10 grid cells per wavelength are required to ensure computational accuracy, so larger grid sizes will limit the accurate computational capability in the high-frequency range.

Table 7. The comparison of calculation resource of one-story reinforced concrete room.

Method	Mesh Number	Time (s)	Memory Usage (MB)
Proposed method	8,580,000	816	1339
CST	38,454,804	4404	3511

shows the comparison of the two methods in terms of the number of meshes, computing time, and memory usage. The proposed method exhibits significant improvements in computational efficiency and resource utilization, with a 4.5-fold reduction in the number of meshes, a 5.4-fold reduction in runtime, and a 2.6-fold reduction in memory usage. These results highlight the ability of the proposed method to achieve high computational accuracy while significantly saving computing resources, making it a practical and efficient solution for simulating the electromagnetic coupling characteristics between reinforced concrete buildings and external EMP environments.

3.3. Verification of the Coupling Characteristics Between Electrically Large Reinforced Concrete Building and EMP Environments

Finally, the time–domain electromagnetic coupling characteristics of an electrically large two-story reinforced concrete building are analyzed to verify the effectiveness of the proposed method. The geometric dimensions of the two-story reinforced concrete building are 5 m × 4 m × 5.3 m, with an internal floor height of 2.5 m. The wall structure is identical to the reinforced concrete wall model 1 described in Section 3.1.1. The schematic diagram of the electrically large two-story building with simplified wall structures is shown in Figure 19.

When a modulated Gaussian pulse with an amplitude of 50 kV/m and a center frequency of 0.25 GHz vertically irradiates the two-story reinforced concrete building from above, the predicted electric field time–domain waveforms and frequency responses at the central observation points P1 (0, 0, 3.95 m) and P2 (0, 0, 1.35 m) in the second- and first-floor rooms are shown in Figure 20 and Figure 21, respectively. The figures demonstrate that the predicted electric field time–domain waveforms are in good agreement with the CST 2022 simulation data, indicating that the method proposed in this paper can accurately reflect the time–domain coupling characteristics of electrically large buildings and external EMP environments. In particular, the predicted peak amplitude of the time–domain waveform observed at P1 is 20.32 kV/m, far exceeding that the peak amplitude at P2, which is 7.95 kV/m. Consequently, the room on the second floor may require enhanced protection to ensure the safe and stable operation of the sensitive equipment inside.

Table 8. The comparison of calculation resource of electrically large reinforced concrete building.

Method	Mesh Number	Time (s)	Memory Usage (MB)
Proposed method	10,255,808	1513	1905
CST	88,833,360	4872	8228

compares the two methods in terms of the number of meshes, computing time, and memory usage. In comparison to the CST 2022 simulation, the method proposed in this paper achieves approximately a 9-fold reduction in mesh complexity, a 3.2-fold improvement in computational speed, and a 4.3-fold reduction in memory usage. These results indicate that the proposed method offers higher efficiency and significantly lower memory requirements when dealing with electrically large buildings. It provides an effective approach for the analysis and calculation of electrically large structures, such as reinforced concrete buildings.

4. Conclusions

In this paper, aiming at the electromagnetic coupling problem between electrically large reinforced concrete buildings and external high-power EMP environments, we propose a fast calculation method of the time–domain coupling characteristics between large buildings and external EMP environments, based on the equivalence of the electromagnetic parameters of reinforced concrete structures. The equivalent electromagnetic parameters of the reinforced concrete structure are calculated based on its S-parameters. Subsequently, the dispersive equivalent electromagnetic parameters are fitted into specific polynomial rational function forms. Finally, ADE-FDTD is used to analyze the time–domain electromagnetic coupling characteristics of equivalent walls and buildings under EMP irradiation. The proposed method is validated by analyzing the influence of wall thickness and the number of layers of steel mesh on the shielding effect of the wall. Additionally, the time–domain electromagnetic coupling characteristics of a one-story reinforced concrete room and an electrically large two-story reinforced concrete building under external high-power EMP environments are further calculated. The results demonstrate that the proposed method requires less memory and provides improved computational efficiency. Specifically, the proposed method achieves approximately about 3.2 times improvement in computational speed and 4.3 times reduction in memory usage when calculating the coupling characteristics between the electrically large two-story reinforced concrete building and the external EMP environment, compared to the CST simulation. This study facilitates the efficient evaluation of the time–domain electromagnetic coupling characteristics between electrically large reinforced concrete buildings and EMPs and then evaluates the field strength at the locations of indoor electronic equipment, which can provide a reliable basis for the electromagnetic protection design of various indoor electronic equipment.