Abstract
The Internet of Things (IoT) enables remote monitoring of various environmental components through existing network infrastructures, thereby facilitating the integration of diverse computing systems. IoT systems encompass a wide range of devices and communication protocols, offering flexibility across various application domains. This adaptability makes IoT solutions particularly suitable for healthcare applications. For example, hospitals have implemented the Internet of Medical Things (IoMT) to collect and transmit patient data to healthcare professionals, as continuous monitoring is critical for patients in intensive care. Healthcare systems often demand high availability and have stringent performance requirements due to the necessity for rapid medical decision-making. However, the simultaneous assessment of performance and availability in IoMT systems is often overlooked. This paper introduces a modeling approach using stochastic Petri nets (SPNs) to evaluate both the availability and performance of IoMT systems. The approach also takes into account redundancy techniques, which may significantly improve system availability. The results highlight the practical feasibility of the proposed approach, demonstrating a reduction in downtime from 46.36 h to 0.21 h, while the response time remained constant. This indicates that the proposed modeling approach can enhance system availability without compromising performance. In addition, the proposed models adopt data collected from a real environment designed to support this approach. Furthermore, a sensitivity analysis was performed to identify the components that have a significant impact on system operation.
1. Introduction
The Internet of Medical Things (IoMT) [1] represents a significant advancement in healthcare by integrating Internet of Things (IoT) [2] technologies to enhance patient monitoring. IoMT devices are equipped with software, sensors, and communication technologies that enable seamless information exchange. Hospitals are increasingly adopting IoMT systems to improve patient data gathering and transmission, which is important for the continuous observation of critically ill patients [3]. This growing trend is proportional to global investments, which reached USD 217.34 billion in 2022 and may rise to USD 960.2 billion by 2030 [4].
Availability is a remarkable attribute of IoMT systems, as they must operate continuously due to the critical nature of patient data [5]. Performance is another prominent non-functional requirement, as delays in patient monitoring may lead to inaccurate diagnoses, posing significant risks to patient safety. However, ensuring high availability in IoMT systems remains a challenge, particularly in cloud-based and edge-based architectures, where network reliability, latency, and fault tolerance must be carefully managed to guarantee uninterrupted data transmission and real-time monitoring.
Performance and availability evaluations can be carried out using stochastic models to assess a system using distinct configurations before implementation [6]. Indeed, many works ([7,8,9,10,11]) have focused on evaluating the availability and performance of IoMT systems. However, an integrated assessment, namely, performability, is often overlooked. IoMT systems may have different processing demands based on data volume, which is influenced by the request rate and system capacity. The understanding of such an interaction is also important to deal with variation in the workload without compromising performance or availability [12].
Existing research has explored performance improvement and availability assurance in IoMT systems. However, these aspects are often examined in isolation, leading to incomplete understanding of the system under analysis. Performance evaluations usually focus on network efficiency, computational overhead, and resource allocation without considering the impact of failures or system resilience. However, availability analyzes emphasize primarily fault tolerance, redundancy mechanisms, and failover strategies without integrating real-time performance constraints. The lack of a unified framework to assess both dimensions simultaneously creates a research gap that limits the comprehensive understanding of IoMT systems.
Furthermore, prevailing approaches frequently fail to capture the dynamic and heterogeneous nature of IoMT ecosystems, where diverse medical devices, fluctuating network conditions, and complex cloud-edge interactions introduce intricate dependencies. Addressing these challenges requires the development of robust analytical models that incorporate stochastic behavior, predictive analytics, and adaptive mechanisms. Such models are essential to comprehensively evaluate the interplay between performance degradation and availability threats in real-world deployments, ensuring the reliability and efficiency of next-generation IoMT infrastructures.
This paper presents a modeling-based approach for the performance and availability assessment of IoMT systems to jointly evaluate the availability and performance of IoMT systems. The approach is an extension of a previous work [13], in which only a single device per layer could be represented. In this paper, we extend the model to deal with many devices in each layer, providing a finer assessment of the system configuration. In addition, the current work may incorporate an analysis of system capacity concerning the request rate.
The main contributions of this work are as follows.
- Joint Performance and Availability Assessment: The proposed SPN model enables a simultaneous evaluation of system performance and availability, considering key metrics such as the response time, throughput, and system uptime. This integrated approach provides a more comprehensive understanding of system behavior compared to traditional evaluation methods.
- Failure Impact Representation: The model explicitly incorporates failure scenarios, ensuring that when a system component becomes unavailable, all requests dependent on that layer are dropped. This enhances the accuracy of system reliability assessments by capturing the real impact of failures on service continuity.
- Sensitivity Analysis for Critical Component Identification: A sensitivity analysis is conducted to determine which hardware and software components have the most significant influence on overall system performance and availability. This information supports decision-making for system optimization and resource allocation.
- Dynamic System Behavior Simulation: The approach introduces flexibility by allowing for variations in request arrival rates, reflecting changes in workload conditions. This adaptability enables more realistic simulations, making the model suitable for evaluating different IoMT deployment scenarios and optimizing resource management strategies.
The SPN model focuses on an IoMT system deployed in a private cloud, considering both software and hardware components that constitute the system architecture. The technique can estimate system the response time, availability, and throughput. Furthermore, the approach explicitly considers the maximum number of requests the system can handle simultaneously. A sensitivity analysis is also adopted to identify the elements that most significantly affect system performance and availability.
This work adopts SPNs that offer a structured and graphical representation of systems. This makes them easier to model, visualize, and understand compared to Markov chains, which necessitate large state-transition matrices. Additionally, the graphical nature of SPNs allows modular modeling and the decomposition of complex systems.
This manuscript is organized as follows: Section 2 presents related work. Section 3 provides an overview of the prominent concepts for understanding the proposed approach. In Section 4, the methodology is explained. Section 5 describes the IoMT architecture, and Section 6 describes the performability model. Section 7 presents two case studies. Finally, Section 8 summarizes the contributions of the paper and presents future work.
2. Related Work
Studies have recently been conducted to evaluate the performance and availability of IoMT systems. Although availability is sometimes neglected, it remains a vital factor in ensuring their uninterrupted functionality. Dighriri [14] propose a remote health monitoring solution using IoMT. This approach integrates two software systems to assess a patient’s health condition as part of an intelligent edge-based IoMT system. The primary objective is to enhance system performance. The results indicate that using this method reduces bandwidth usage by 99% and decreases energy consumption by 92%.
Ilyas et al. [15] present a bidirectional approach aimed at enhancing real-time data transmission in IoT-based healthcare monitoring systems by minimizing latency and optimizing network usage. This method focuses on the efficient selection of connections between sensor devices and gateways, as well as the effective allocation of tasks to the fog node. The strategy was tested using the iFogSim tool within the Eclipse IDE, yielding results that demonstrated a 20% to 25% improvement over existing methods in terms of both network usage and latency.
Khan et al. [16] present an approach to optimize dynamic resource allocation and load balancing in IoT architectures. The proposed algorithm was evaluated using the iFogSim tool (version 3.0.3), and the results were compared with existing approaches. The results showed that the proposed technique outperforms existing methods, with a 45% reduction in delay, 37% lower energy consumption, and 25% lower bandwidth usage.
Rocha et al. [17] propose an SPN model that evaluates the performability of a multi-tier IoMT architecture, which includes edge, fog, and cloud layers. The model assesses the mean response time (MRT) metric by examining variations in the parameters that significantly influence the availability of a container and cloud processing capacity. The results indicate that allocating more resources to the cloud layer reduces both the mean response time and the drop rate, improving overall system performance.
Lisboa et al. [18] propose an e-health monitoring architecture that utilizes sensors along with cloud and fog infrastructure to analyze system availability. The study employs stochastic models to assess the impact of failures on the availability of the e-health system. It considers four different scenarios, revealing that sensors and fog devices significantly influence system availability. Sensitivity analysis indicates that the combination of fog and cloud technologies results in high availability.
In [19], the authors present stochastic Petri net models to assess the availability of wireless sensor networks (WSNs) in smart hospitals, taking into account power and server failures. The study focuses on three availability models, labeled A, B, and C, and examines the effects of power redundancy and server rejuvenation. The results show that model C, which features the optimal configuration, achieves an availability rate of 99.64%, reducing downtime by 21 h per year compared to the worst-case scenario. In addition, a sensitivity analysis identifies the most critical components affecting system availability, including the power supply and server aging.
Ilyas et al. [20] present a hybrid architecture for IoT-based healthcare systems that leverages device, fog, and cloud layers to enhance real-time data transmission and minimize latency and network usage. The strategy incorporates optimal fog node selection, dynamic load balancing, and task assignment to increase system efficiency. Simulations using an efficient scanning mechanism (ESM) and load balancing scheme for real-time monitoring data (LBRT) algorithms revealed substantial improvements in network usage and latency compared to current methods. The main goal of the study is to meet the non-functional requirements of IoT healthcare monitoring systems, particularly emphasizing data consistency and uninterrupted service delivery.
In [21], the authors introduce models that use continuous-time Markov chains to depict fault-tolerant IoT systems. The results demonstrate significant improvements in system availability, achieved by adding more devices to enhance redundancy and fault tolerance. In [22], the authors propose a method to evaluate the impact of load-balancing techniques on the performance of healthcare information systems. Their research employs stochastic reward networks to model the system. Analyzing both performance and availability is essential in IoMT environments to ensure that these systems meet the necessary requirements to provide quality healthcare to patients.
Hassan et al. [23] propose a fog computing-based remote patient monitoring system to reduce latency and network consumption in IoMT architectures. The authors integrated biosensors to collect and process surface electromyogram (sEMG) and electrocardiogram (ECG) signals in real-time and adopted the iFogSim simulator to validate the proposed approach. The results demonstrate that the proposed method reduces latency, network usage, and execution costs compared to cloud-based systems.
Said and Tolba [24] propose a large-scale IoMT architecture that improves communication between medical devices. It includes an architecture that integrates satellites, high-altitude platforms (HAPs), and the Internet to enhance coverage and applied clustering and data prioritization for better management. The authors evaluated the system using NS3 simulations, measuring delay, energy consumption, packet loss, throughput, and user coverage. The results showed significant improvements over traditional healthcare architectures, including a 19.211% reduction in delay, an 11.357% decrease in energy consumption, a 26.886% reduction in packet loss, a 22.999% increase in throughput, and a 10% increase in served users.
Table 1 presents a comparative summary of related works found in the literature on the availability and performance evaluation of IoMT systems. A comparative analysis of the strategies adopted in each paper and the key metrics of interest can be conducted through this table. Additionally, it highlights work that assesses performance and availability. Most studies focus only on evaluating availability [18,19,21] or performance [14,15,16,20,23,24], while only a few evaluate both the availability and performance [17,22] of IoMT architectures. Although these two last papers conducted an integrated evaluation of performance and availability, the authors did not conduct a validation process using a real testbed system, which may reduce confidence in the results.

Table 1.
Summary of related work.
Unlike previous studies, this paper presents an integrated modeling approach using SPN to simultaneously assess the performance and availability of IoMT systems with private cloud configurations. In addition, the proposed modeling approach explores different architecture configurations and considers various processing capacities. When a component fails and causes a layer to become unavailable, the requests for that layer are dropped. This modeling approach provides a more accurate representation of system behavior during failures. Additionally, this work introduces flexibility by allowing for adjustments to the request arrival rate, resulting in a more dynamic and adaptable simulation environment.
3. Background
This section presents key concepts to facilitate the comprehension of this work.
3.1. IoT Architecture
The IoT allows remote monitoring of environmental elements using existing network infrastructures, making it easier to connect distinct computer systems. Such an integration allows efficient data gathering, monitoring, and processing, which are essential for many applications, such as smart homes, healthcare, and agriculture. The IoT also facilitates dynamic and autonomous communication between devices, which is an important feature for operation in harsh locations [25].
A typical IoT architecture [26] (Figure 1) is generally structured into four distinct layers: device, communication, processing, and presentation. The device layer is responsible for data gathering and includes sensors, microcontrollers, and other hardware components that may monitor an environment, such as temperature, humidity, motion, or health metrics. These devices are the core of an IoT network, providing the essential raw data required for further analysis and decision-making.
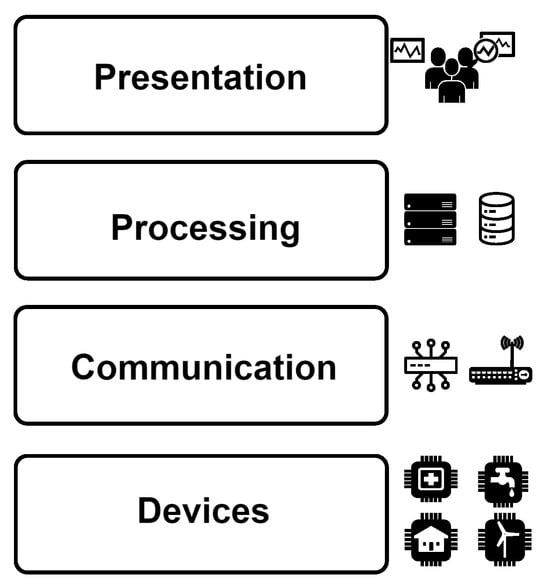
Figure 1.
IoT basic architecture.
The communication layer then acts as the channel in which data are transmitted from the devices to the next processing stages. This layer utilizes standard communication protocols to ensure secure and efficient data transfer to other systems [27]. The processing layer is responsible for managing, analyzing, and storing the collected data. The layer may perform data aggregation, filtering, and computation, often using cloud or edge computing. The processing layer transforms raw data into valuable insights, which can then be adopted to provide system services or trigger specific actions. In addition, the processing layer can incorporate machine learning algorithms, data analytics, and artificial intelligence to improve decision-making and automate responses to specific events or conditions.
Finally, the presentation layer provides an interface for users to interact with the IoT system. The layer includes dashboards, visualization tools, mobile applications, and web interfaces that present processed data.
3.2. Availability
IoMT systems frequently manage sensitive data, making availability a prominent attribute for these systems [28]. For example, a device failure may put a patient’s life at risk. Availability refers to the probability that a system is operational at a given moment. A widely used measure is the steady-state availability, which considers the system’s average time to failure and average time to repair. This metric provides a long-term evaluation of the system reliability by taking into account both the frequency of failures and the time required for recovery. Equation (1) presents how to compute the availability of the system. Equations (2) and (3) show how to compute MTTF and MTTR, respectively.
represents the cumulative distribution function (CDF), which quantifies the probability that a repair is completed within time t. Conversely, denotes the reliability function, describing the likelihood that a system operates without failure over a given time period t.
In SPN, time can be associated with transitions. Thus, MTTF and MTTR values can be associated to transitions to represent the system availability behavior. However, the inverse of the MTTF corresponds to the failure rate. The failure rate represents the probability that a failure can occur, while the MTTF corresponds to the interval between these failures. Therefore, MTTF corresponds to the inverse of the failure rate. For instance, if a transition has a failure rate of (lambda), MTTF is given by MTTF = 1/. This model is useful for estimating the system’s availability using SPNs. In addition, considering that the SPN models proposed in this work represent the mean system behavior, we can adopt the exponential distribution to represent the mean failure and repair activities.
3.3. Petri Nets
Petri nets (PNs) are a prominent modeling formalism, which are capable of representing many system features, such as concurrency, parallelism, asynchronous actions, and non-deterministic events [29]. A Petri net is a directed bipartite graph, in which places represent local conditions and transitions denote actions. Arcs connect places to transitions and vice versa. Tokens can reside in places, representing the state of the Petri net (i.e., marking). An inhibitor arc represents the absence of tokens in places, and the behavior of a Petri net is described by a token game, in which tokens are generated and consumed as transitions are fired.
The proposed approach adopts a PN extension, namely, stochastic Petri nets (SPNs), which adopt probabilistic delays for timed transitions or zero delays for immediate transitions. In addition, guard expressions are also adopted to provide support for additional firing rules of transitions. Figure 2 shows the basic elements of SPNs. A place (Figure 2a) is represented as a circle and contains tokens (Figure 2d) to represent the current state of the system. SPN models also adopt arcs (Figure 2b) to directly represent the token flow through the places. In addition, inhibitor arcs (Figure 2c) allow a transition to fire when no tokens are present in its input place. SPN models consider two types of transitions, timed (Figure 2e) and immediate transitions (Figure 2f). Timed transitions are represented as rectangles, and their fire represents a stochastic delay associated with them to allow the modeling of probabilistic events. Black rectangles represent immediate transitions, and these transitions can be fired instantly when enabled, taking zero (0) time to be executed. The term stochastic Petri nets (SPNs) broadly refers to various stochastic extensions of Petri nets. For clarity, we adopt the term SPN throughout this discussion. The state space of an SPN model can be mapped to a CTMC, with simulation serving as an alternative approach to constructing CTMCs [6].
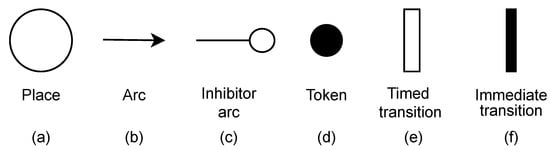
Figure 2.
Basic elements of SPNs.
An SPN model represents a system as a set of places (system states), transitions (events that change states), and tokens (markers indicating the current state). The transitions are associated with exponentially distributed firing rates, defining the probability and timing of state changes. The model is mathematically formulated as a CTMC, where the system’s behavior is captured by the state probability distribution over time. The transition rate matrix governs how probabilities evolve, allowing the evaluation of performance metrics such as availability, response time, and throughput.
Figure 3 illustrates an example of an SPN representing a device that can be operational or not. In this model, the places correspond to the states Up or Down, and the transitions Repair and Failure represent the actions that change the state of the model. A token in place indicates that the device is operational (Figure 3a); in this state, the transition Failure is enabled.
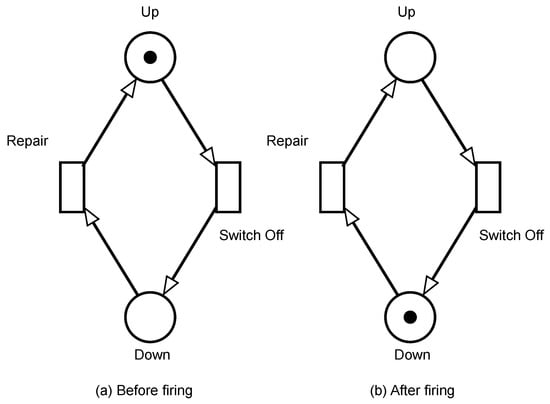
Figure 3.
An SPN model example.
The fire of such a transition consumes a token from the place UP and generates a token into the place Down, representing that the current state of the model has changed to failed. If the Repair transition is fired, the state depicted in Figure 3b is reached. The availability can be computed by the probability of having a token in the place Up, which is represented by the Equation (4) (in the Mercury [30] notation). The reader is redirected to [6] for more information on SPNs.
4. Methodology
Figure 4 illustrates the methodology adopted to evaluate the availability and performance of IoMT architectures utilizing a private cloud. The process begins with an in-depth analysis of system requirements to gain a comprehensive understanding of component behaviors and interactions. Subsequently, key metrics, such as availability, are established to enable a quantitative assessment of system operation.
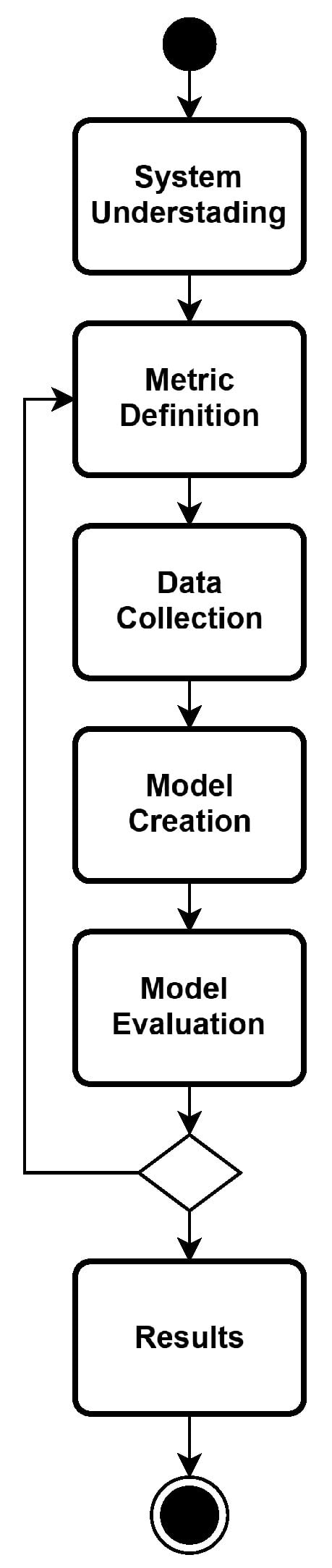
Figure 4.
Methodology.
The third step conducts a preliminary measurement of the system data. If an actual system is not at disposable, a prototype may be adopted or even data from datasheets or other works. Afterwards, a formal model (i.e., SPN) is created based on component interactions and the obtained data.
The fifth step corresponds to the model evaluation. For instance, a Design of Experiments (DoE) approach can be employed to systematically explore the effects of different model parameters. Another possibility is to evaluate the impact of the frequency of data collection on system performance and availability. If the respective results do not provide the expected estimates, the designer is redirected to the second step to review the defined metrics, collected data, and the model created. Finally, the last step of the methodology corresponds to the analysis of results. In addition, once the model has proven results, other system configurations can be analyzed.
5. IoMT Architecture
An IoMT architecture provides a guideline to integrate distinct hardware and software components to ensure continuous monitoring and transmission of patients’ physiological data. Additionally, IoMT systems must provide a small response time, as delays may affect medical decisions about a patient treatment.
Figure 5 depicts the adopted IoMT architecture [31], which comprises four distinct layers. The sensor layer contemplates devices responsible for obtaining physiological data from patients, which are then collected by the data gathering layer (e.g., microcontrollers). The data transmission layer includes network components to transmit sensor data over the public network (i.e., the Internet). Lastly, the private cloud layer deals with data storage for analysis of healthcare professionals, and such a layer also provides mechanisms for managing the cloud computing infrastructure, including virtual machines.
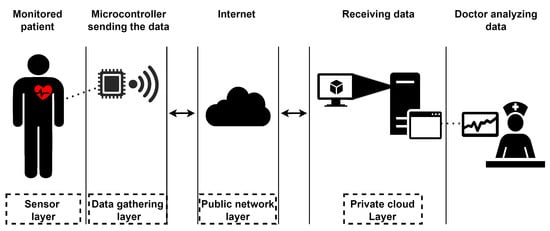
Figure 5.
IoMT architecture.
A private cloud infrastructure is essential for securely managing and storing sensitive patient information to ensure that it is protected by healthcare organizations. The failure of any component in this baseline architecture results in complete unavailability of the system. Therefore, this study proposes the development of extensions to improve the performance and availability of the architectures.
6. Performability Model
This section presents the proposed SPN model (Figure 6) for the joint evaluation of availability and performance (i.e., performability) of IoTM systems based on the previous architecture (Section 5). The conceived technique assumes the interaction between the layers and the respective devices, and the metrics of interest are response time, throughput, and system availability. In our model, we assume that upon device failure, all active requests on the affected device are immediately discarded. However, certain devices, such as network components, may attempt to retransmit messages until a predefined timeout period elapses, a factor not considered in this model. All timed transitions adopt the infinite server semantic [6], in which the firing rate of a transition is linearly increased in relation to its enabling degree. In addition, for the sake of explanation, the model is organized into two types of blocks: performance and availability.
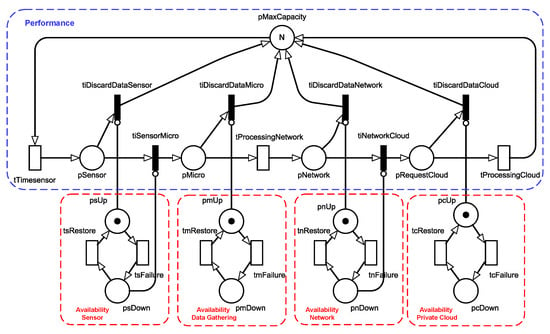
Figure 6.
Performability model.
Each layer has an availability block (in red), which represents the operational state of the respective devices. Place (e.g., ) indicates the layer (or components) is functioning, whereas place denotes the corresponding failure. Transition tXFailure (tXRestore) represents the failure (repair), and the associated delay is the device MTTF (MTTR).
Tokens in places psUp, pmUp, PnUp, and pcUP indicate the number of devices in the respective layer, which also denote the available resources to process and transmit the collected data in each layer. For instance, a token in place may indicate that the private cloud can deal with one request, and additional tokens (e.g., ) allow multiple requests simultaneously. The system is considered available only if all layers are operational. If any single layer fails, the entire system is in a failure state. The steady-state availability (A) can be estimated as .
The performance block (in blue) represents the communication between the architecture layers. Place pMaxCapacity indicates the system maximum capacity, which corresponds to the maximum number of requests that the system can handle at the same time. Each token represents one request, indicating the limit of active requests the system may manage.
Transition tTimesensor denotes the frequency at which data are collected from a sensor, and a token in pSensor place indicates the respective data are ready. Immediate transition tiSensorMicro represents the activity for a microcontroller to collect the sensor data. The sensor and microcontroller are connected to the same board, and, thus, the delay is assumed to be negligible. Transition tiSensorMicro has an inhibitor arc that prevents data acquisition when the sensor is not operational (pSensor). Transition also verifies if the layer components are down. In case of failure, the request is lost (i.e., is fired). The interactions with other layers have similar behavior. For instance, transition represents data transmission over the Internet, and transition denotes data storage and processing by the private cloud layer. Table 2 presents comprehensive descriptions of the model’s components. To improve clarity, equivalent elements in different blocks have been grouped, with descriptions provided for each representative element.

Table 2.
SPN model components.
In this work, the response time is the period for a patient’s physiological data (collected by a sensor) to arrive and be processed by the private cloud, considering the interaction of all layers. Little’s Law [6] is applied to estimate the mean response time, defined as the ratio between the average number of messages in the system and the processing throughput. Specifically, the average number of messages is determined by summing the expected number of requests across various system components, including sensors, microcontrollers, network infrastructure, and cloud processing. The processing throughput is derived from the expected number of cloud requests and the inverse of the average cloud processing time. Here, the expected number of requests in a given system component is represented by , while the firing rate of a transition, denoted as , corresponds to the time required for processing a request.
7. Case Study
This section presents two case studies that demonstrate the practical applicability of the conceived technique. The first case study evaluates the influence of the processing capacity on the IoMT architecture. The second case study focuses on assessing the impact of the data gathering frequency on system performance and availability. In this work, Mercury [30] has been adopted to evaluate the SPN models. In addition, the system capacity (N) is assumed to be 100, which is based on [13].
7.1. Case Study I
Understanding the relationship between resource capacity and system performance is essential for improving the operation of an IoT system. The influence of processing capacity is assessed by doubling the resources allocated to each layer.
A design of experiments (DoE) approach [32] is adopted. The factors are the places , , and , which represent the components of each layer. The levels denote the number of resources, which may vary from 1 to 2 in this experiment. In the proposed model, the levels are the marking (tokens) of such places. Table 3 shows the adopted values for MTTF and MTTR, which are based on [33,34,35]. The values for transitions tTimesensor, tNetwork, and tProcessingCloud are 1 s, 0.001 s, and 0.014133 s, respectively. Such values were taken from our previous work [13] in which measurement activities were conducted and validated in a real testbed system.

Table 3.
Input parameters.
The results are presented on the basis of the rank of effects. An effect, as defined by [32], represents the change in response resulting from a variation in a factor level. All effects are ranked in descending order, and the ranks are determined by the absolute values of the effects. Additionally, this study focuses on main effects and second-order interactions, as higher-order interactions are typically considered negligible. For each defined treatment, a specific combination of factor levels, a model is developed to conduct a steady-state analysis.
Table 4 depicts availability (A), downtime (), mean response time (R), and throughput () for each treatment. Downtime assumes a period of one year (8760 h), and throughput represents the number of requests per second (). Comparing treatment 1 (only 1 resource) with treatment 16 (2 resources in all layers), a significant difference is observed. System downtime is improved by 99.54%, reducing from 46.364 h to just 0.2112 h (12.672 min). Indeed, for all treatments in which the private cloud () has redundant components, downtime and availability considerably improve.

Table 4.
Case Study 1—Treatments and results.
For response time, there is an increase of 0.26%, indicating redundancy may minimally impact performance, as the difference is negligible. Throughput shows a slight improvement as redundancy is added. Table 5 presents the rank of effects. For availability, the most prominent factor is , which may increase availability to 0.00488, indicating the private cloud plays a remarkable role in reducing system downtime (i.e., 42 h may be reduced). Regarding response time, has the greatest influence, suggesting the sensor plays an important role in delaying system response. also stands out concerning throughput (effect of 0.004879 ), which highlights the importance of the cloud computing infrastructure in supporting the system capacity to efficiently handle requests. Some values are missing in Table 5, since they are too small (close to 0).

Table 5.
Case Study 1—Rank of effects.
Figure 7 presents the cumulative distribution of the average response time of a system, where the x-axis represents the average response time, and the y-axis shows the cumulative probability associated with these times. The curve suggests that as redundant equipment is added, the system experiences slight improvements in response, reducing variability and ensuring more predictable response times. The slope of the curve indicates the relative frequency of the observed response times, with the final portion showing that most times converge to similar values, reinforcing the idea of increased system stability with the introduction of redundancies.
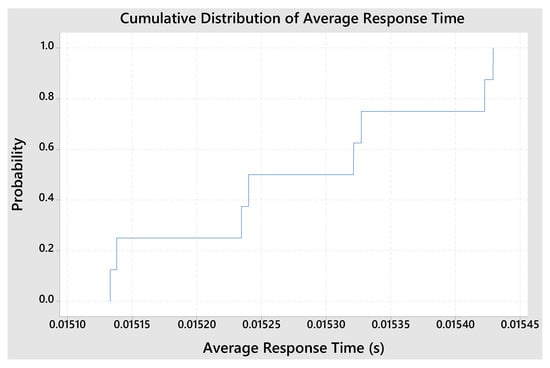
Figure 7.
Cumulative distribution of response time.
Figure 8 illustrates the cumulative distribution of availability, where the x-axis represents the availability of the system, and the y-axis shows the cumulative probability of achieving a given availability level. The curve indicates that as redundant equipment is added, the overall system availability improves, leading to higher reliability. Initially, there is a rapid increase in the cumulative probability, suggesting that a significant portion of the system operates within a certain availability range. As the availability approaches 1.0, the curve steepens, showing that a large proportion of observations achieve near-perfect availability. This trend confirms that redundancy contributes to increased stability and reliability, ensuring that system failures become increasingly rare.
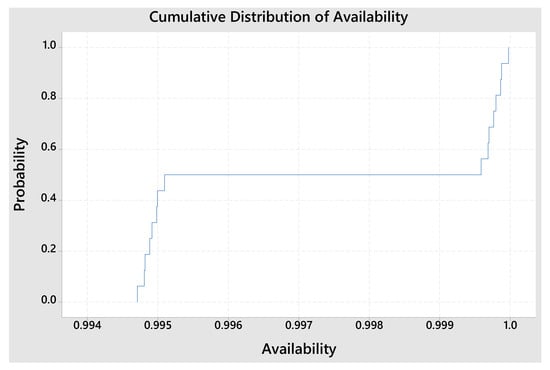
Figure 8.
Cumulative distribution of availability.
Figure 9 presents the response times for all treatments considered, where each treatment represents a configuration with varying levels of redundancy. The x-axis denotes the response time, while the y-axis lists the treatment numbers. This figure visually summarizes the distribution of response times by displaying key statistical measures: the box represents the interquartile range (IQR) (the middle 50% of the data), the line inside the box indicates the median, and the whiskers extend to the minimum and maximum values within 1.5 times the IQR. Outliers beyond this range are shown as individual points.
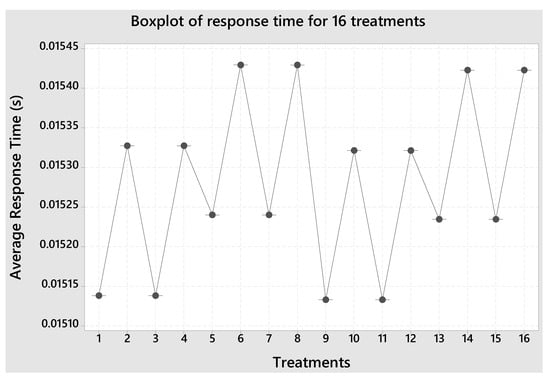
Figure 9.
Boxplot response time.
Observing the figure, as the treatment number increases, redundant equipment is added, contributing to a reduction in response time variability. In some cases, treatments with higher redundancy exhibit lower medians and narrower interquartile ranges, indicating improved performance and consistency. However, some treatments still show the presence of outliers, suggesting occasional higher response times due to external factors. The overall trend suggests that adding redundancy generally enhances system performance.
7.2. Case Study II
The frequency for data gathering is a remarkable non-functional requirement, as a shorter sampling period for the sensor data may provide a finer monitoring of patient health. However, the system may not be capable of properly dealing with a greater workload. A single factor () is assumed, which represents the delay for sampling a sensor. Two distinct experiments are carried out, which differ from the number of servers in the private cloud layer ( or ). For other transitions, the delays are the same as in the previous case study, and the metrics of interest are the response time and throughput.
Table 6 presents the results assuming one server (). For very short delays ( s and s), the response time (R) is approximately 0.01567 s. As the delay increases, the response time presents minimal variations, remaining around 0.01513, which suggests the system has a stable response, regardless of the sampling rate.

Table 6.
Results—mean response time and throughput size with 1 server.
On the other hand, throughput () has high values for short sampling periods ( s and s), which approximately contemplate 5805 requests per second, reflecting a high system demand. As the interval between sensor sampling increases, throughput considerably decreases. For 1 s, throughput decreases to 97.97 requests, and, for 6 s, throughput reaches its lowest value, 16.53 requests per second (). Indeed, with a smaller sampling frequency, the system processes fewer requests due to the reduction in the workload.
Table 7 presents the results assuming two servers (). The values are slightly better than Table 6, considering the response time. The major improvement is related to throughput, since the system is capable of dealing with a greater workload. For s, the system handles an additional 116 requests. However, when the sampling period is larger, additional servers do not provide further improvements. An extra server is a practical approach to improve system performance, but the acquisition cost and workload are trade-offs that should not be neglected.

Table 7.
Results—mean response time and throughput with 2 server.
7.3. Remarks
As presented, the results indicate redundant equipment can considerably reduce system downtime and increase throughput. Availability significantly improved with the addition of redundant devices, which is important for ensuring continuous patient monitoring. In case study 1, redundancy decreased downtime from 46.36 to 0.21 h. Such a reduction keeps the system operational for extended periods, which is important for healthcare systems.
In case study 2, a second server increased throughput (116 additional requests) for the highest workload, but no significant impact was presented in response time. Additional servers may effectively mitigate bottlenecks and ensure better scalability for high-demand configurations. Case studies demonstrated the proposed technique is an additional tool for designing IoMT systems, which may estimate prominent metrics without constructing a prototype or modifying a running system.
8. Conclusions
This work presented a modeling-based approach for the performance and availability assessment of IoMT systems. Distinct system designs can be assessed before making changes or implementing the actual system or prototype. Two case studies were presented to show the applicability of the conceived approach. The results demonstrate the influence of redundant equipment to improve availability and performance. High availability is a prominent non-functional requirement of IoMT systems due to the continuous patient monitoring, and the small response time may assure timing constraints are met. As future work, a tool will be developed to provide users with a simpler interface for using the formal model, making the solution accessible and practical for non-experts, such as infrastructure designers, who will not need extensive knowledge of the modeling process. Additionally, efforts will focus on extending the proposed SPN model to enhance scalability, enabling its application in larger healthcare settings, such as entire hospitals. Another possible direction of this work is to integrate machine learning techniques for predictive analytics to anticipate failures and proactively optimize resource allocation.
Author Contributions
Conceptualization, T.V.B.; formal analysis, T.V.B., G.C. and E.T.; Investigation, T.V.B.; methodology, T.V.B.; project administration, E.T. and G.C.; supervision, E.T and G.C.; validation, T.V.B.; visualization, T.V.B., G.C. and E.T.; writing—original draft, T.V.B., G.C., F.A. and E.T.; writing—review and editing, T.V.B., F.A., G.C. and E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to express their gratitude to the editors and anonymous reviewers of the journal for their contributions to this publication.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Valsalan, P.; Baomar, T.A.B.; Baabood, A.H.O. IoT based health monitoring system. J. Crit. Rev. 2020, 7, 739–743. [Google Scholar]
- Farahani, B.; Firouzi, F.; Chakrabarty, K. Healthcare iot. In Intelligent Internet of Things: From Device to Fog and Cloud; Springer: Berlin/Heidelberg, Germany, 2020; pp. 515–545. [Google Scholar]
- Verma, D.; Singh, K.R.; Yadav, A.K.; Nayak, V.; Singh, J.; Solanki, P.R.; Singh, R.P. Internet of things (IoT) in nano-integrated wearable biosensor devices for healthcare applications. Biosens. Bioelectron. X 2022, 11, 100153. [Google Scholar] [CrossRef]
- Research, P. Internet of Things in Healthcare Market. Available online: https://www.precedenceresearch.com/internet-of-things-in-healthcare-market (accessed on 10 September 2023).
- Xing, L. Reliability in Internet of Things: Current status and future perspectives. IEEE Internet Things J. 2020, 7, 6704–6721. [Google Scholar] [CrossRef]
- Maciel, P.R.M. Performance, Reliability, and Availability Evaluation of Computational Systems, Volume I: Performance and Background; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Wai, K.T.; Aung, N.P.; Htay, L.L. Internet of things (IoT) based healthcare monitoring system using NodeMCU and Arduino UNO. Int. J. Trend Sci. Res. Dev. (IJTSRD) 2019, 3, 755–759. [Google Scholar]
- Pokorni, S.J. Reliability and availability of the Internet of things. Vojnoteh. Glas. Tech. Cour. 2019, 67, 588–600. [Google Scholar] [CrossRef]
- Ruman, M.R.; Barua, A.; Rahman, W.; Jahan, K.R.; Roni, M.J.; Rahman, M.F. IoT based emergency health monitoring system. In Proceedings of the 2020 International Conference on Industry 4.0 Technology (I4Tech), Pune, India, 13–15 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 159–162. [Google Scholar]
- Athira, A.; Devika, T.; Varsha, K. Design and development of IOT based multi-parameter patient monitoring system. In Proceedings of the 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 862–866. [Google Scholar]
- Valentim, T.; Callou, G.; Vinicius, A.; França, C.; Tavares, E. Availability Assessment of Internet of Medical Things Architecture using Private Cloud. In Proceedings of the Anais do L Seminário Integrado de Software e Hardware; SBC: Ghaziabad, India, 2023; pp. 13–23. [Google Scholar]
- Dang, L.M.; Piran, M.J.; Han, D.; Min, K.; Moon, H. A survey on internet of things and cloud computing for healthcare. Electronics 2019, 8, 768. [Google Scholar] [CrossRef]
- Valentim, T.; Callou, G.; França, C.; Tavares, E. Availability and Performance Assessment of IoMT Systems: A Stochastic Modeling Approach. J. Netw. Syst. Manag. 2024, 32, 95. [Google Scholar] [CrossRef]
- Dighriri, M. Internet of Medical Things (Iotm) Based Sustainable Architecture For Health Monitoring System. In Proceedings of the 2023 1st International Conference on Innovations in High Speed Communication and Signal Processing (IHCSP), Bhopal, India, 4–5 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 17–20. [Google Scholar]
- Ilyas, A.; Mahfooz, S.; Mehmood, Z.; Ali, G.; ElAffendi, M. Two-Way Approach for Improved Real-Time Transmission in Fog-IoT-Based Health Monitoring System for Critical Patients. Comput. Syst. Sci. Eng. 2023, 46, 3815–3829. [Google Scholar] [CrossRef]
- Khan, S.; Shah, I.A.; Tairan, N.; Shah, H.; Nadeem, M.F. Optimal resource allocation in fog computing for healthcare applications. Comput. Mater. Contin 2022, 71, 6147–6163. [Google Scholar] [CrossRef]
- Rocha, F.; Nogueira, B.; Gonçalves, G.; Silva, F.A. Smart Hospital Patient Monitoring System Aided by Edge-Fog-Cloud Continuum: A Performability Evaluation Focusing on Distinct Sensor Sources. J. Netw. Syst. Manag. 2024, 32, 99. [Google Scholar] [CrossRef]
- da Silva Lisboa, M.F.F.; Santos, G.L.; Lynn, T.; Sadok, D.; Kelner, J.; Endo, P.T. Modeling the availability of an e-health system integrated with edge, fog and cloud infrastructures. In Proceedings of the 2018 IEEE Symposium on Computers and Communications (ISCC), Natal, Brazil, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 00416–00421. [Google Scholar]
- Silva, F.A.; Brito, C.; Araújo, G.; Fé, I.; Tyan, M.; Lee, J.W.; Nguyen, T.A.; Maciel, P.R.M. Model-driven impact quantification of energy resource redundancy and server rejuvenation on the dependability of medical sensor networks in smart hospitals. Sensors 2022, 22, 1595. [Google Scholar] [CrossRef] [PubMed]
- Ilyas, A.; Alatawi, M.N.; Hamid, Y.; Mahfooz, S.; Zada, I.; Gohar, N.; Shah, M.A. Software architecture for pervasive critical health monitoring system using fog computing. J. Cloud Comput. 2022, 11, 84. [Google Scholar] [CrossRef] [PubMed]
- Marcozzi, M.; Gemikonakli, O.; Gemikonakli, E.; Ever, E.; Mostarda, L. Availability evaluation of IoT systems with Byzantine fault-tolerance for mission-critical applications. Internet Things 2023, 23, 100889. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Fe, I.; Brito, C.; Kaliappan, V.K.; Choi, E.; Min, D.; Lee, J.W.; Silva, F.A. Performability evaluation of load balancing and fail-over strategies for medical information systems with edge/fog computing using stochastic reward nets. Sensors 2021, 21, 6253. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.R.; Ahmad, I.; Ahmad, S.; Alfaify, A.; Shafiq, M. Remote pain monitoring using fog computing for e-healthcare: An efficient architecture. Sensors 2020, 20, 6574. [Google Scholar] [CrossRef] [PubMed]
- Said, O.; Tolba, A. Design and evaluation of large-scale IoT-Enabled healthcare architecture. Appl. Sci. 2021, 11, 3623. [Google Scholar] [CrossRef]
- Islam, M.M.; Nooruddin, S.; Karray, F.; Muhammad, G. Internet of Things: Device Capabilities, Architectures, Protocols, and Smart Applications in Healthcare Domain. IEEE Internet Things J. 2022, 10, 3611–3641. [Google Scholar] [CrossRef]
- Jara, A.J.; Zamora, M.A.; Skarmeta, A.F. An architecture for ambient assisted living and health environments. In Proceedings of the International Work-Conference on Artificial Neural Networks, London, UK, 27–29 August 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 882–889. [Google Scholar]
- Rahmani, A.M.; Gia, T.N.; Negash, B.; Anzanpour, A.; Azimi, I.; Jiang, M.; Liljeberg, P. Exploiting smart e-Health gateways at the edge of healthcare Internet-of-Things: A fog computing approach. Future Gener. Comput. Syst. 2018, 78, 641–658. [Google Scholar] [CrossRef]
- Joyia, G.J.; Liaqat, R.M.; Farooq, A.; Rehman, S. Internet of medical things (IoMT): Applications, benefits and future challenges in healthcare domain. J. Commun. 2017, 12, 240–247. [Google Scholar] [CrossRef]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Silva, B.; Matos, R.; Callou, G.; Figueiredo, J.; Oliveira, D.; Ferreira, J.; Dantas, J.; Lobo, A.; Alves, V.; Maciel, P. Mercury: An integrated environment for performance and dependability evaluation of general systems. In Proceedings of the Industrial Track at 45th Dependable Systems and Networks Conference, DSN, Rio de Janeiro, Brazil, 22–25 June 2015; pp. 1–4. [Google Scholar]
- Vishnu, S.; Ramson, S.J.; Jegan, R. Internet of medical things (IoMT)-An overview. In Proceedings of the 2020 5th International Conference on Devices, Circuits and Systems (ICDCS), Piscataway, NJ, USA, 5–6 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 101–104. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Tang, D.; Kumar, D.; Duvur, S.; Torbjornsen, O. Availability measurement and modeling for an application server. In Proceedings of the International Conference on Dependable Systems and Networks, Florence, Italy, 28 June–1 July 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 669–678. [Google Scholar]
- Kim, D.S.; Machida, F.; Trivedi, K.S. Availability modeling and analysis of a virtualized system. In Proceedings of the 2009 15th IEEE Pacific Rim International Symposium on Dependable Computing, Shanghai, China, 16–18 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 365–371. [Google Scholar]
- Novacek, G. Tips for Predicting Product Reliability. Available online: https://circuitcellar.com/cc-blog/tips-for-predicting-product-reliability/ (accessed on 10 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).