Abstract
Radome stealth technology is a key research area in aircraft stealth design. Traditional aircraft stealth methods primarily focus on optimizing the shape to scatter radar waves and using absorbing materials to absorb radar waves. However, when these methods are applied to radomes, they can negatively impact antenna performance. By combining Frequency-Selective Surface (FSS) technology with radome design, it is possible to ensure good transmission performance for the antenna within its operating frequency range while simultaneously reducing the radar cross-section outside the operating frequency range, achieving an integrated design for both transmission and stealth. This paper outlines the technical approaches for radome stealth, reviews the research status of scattering stealth radomes and absorbing stealth radomes based on FSS both domestically and internationally, and provides an outlook on the future development of FSS radomes from the perspectives of omnidirectional broadband, conformal design, and intelligent control.
1. Introduction
The changing demands of modern military technology and advancements in radar detection technology have led to increasingly stringent performance requirements for radomes. Against this backdrop, stealth radome technology, which integrates both wave transmission and stealth functions, has gradually garnered widespread attention. Traditional radomes primarily serve a physical protection role, shielding antenna systems from environmental impacts. However, for new radomes applied in modern military technologies, in addition to the basic physical protection, they must also incorporate stealth capabilities to reduce the radar cross-section (RCS) of the antenna system, which acts as a strong scattering source [1]. Currently, conventional stealth design methods for aircraft primarily include shape-based stealth and the use of radar-absorbing materials [2,3,4,5]. Shape-based stealth design adjusts the aircraft’s profile to reflect radar waves in a direction away from the radar source, thereby effectively reducing the aircraft’s RCS. However, this method must also account for the aircraft’s aerodynamic performance, leading to certain limitations in RCS reduction. On the other hand, radar-absorbing materials can effectively absorb electromagnetic waves and suppress specular reflection, thus reducing the target’s RCS. However, while these materials absorb radar detection waves, they also absorb the electromagnetic waves emitted by the aircraft’s own antenna system, which can affect the normal operation of the antenna. These two stealth measures cannot be directly applied to radomes because, while considering stealth characteristics, the radome must also support the normal operation of the antenna system.
Frequency-Selective Surface (FSS) technology is one of the most promising solutions to this problem [6,7]. FSS is a two-dimensional infinite array structure made up of metal patch units or aperture metal units arranged periodically. It can transmit electromagnetic waves in specific frequency bands while reflecting waves outside these bands. Once conformed to the surface of the radome (Figure 1), electromagnetic signals within the passband of the FSS structure can pass through the radome freely. In contrast, out-of-band signals are reflected like they encounter metal, exhibiting specular reflection. This allows the antenna dome to achieve electromagnetic invisibility outside the passband. Furthermore, if electromagnetic loss structures are added to the FSS, it can absorb electromagnetic waves in the stopband. When FSS is applied to a radome, it not only enables the normal transmission of electromagnetic waves in the antenna system’s operating frequency band but also reflects or absorbs electromagnetic waves outside the operating band, resulting in an extremely low RCS and enhancing the radome’s out-of-band stealth performance [8,9]. Therefore, stealth radomes based on frequency-selective surfaces have significant application value.
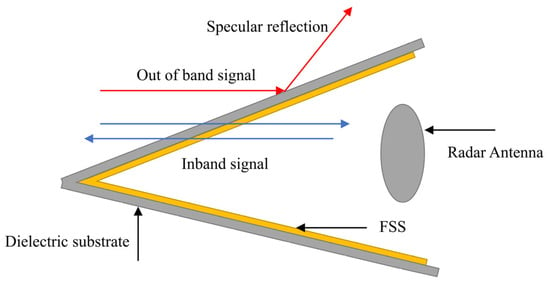
Figure 1.
Stealth principle of frequency-selective surface radome.
2. FSS Stealth Radome Based on Scattering Mechanism
2.1. Development History of FSS
In the study of monostatic RCS characteristics, planar metallic structures and curved metallic structures exhibit markedly distinct electromagnetic responses. When illuminated by radar waves, planar metallic structures generate strong specular reflections, leading to significant RCS enhancement. In contrast, curved metallic structures leverage their geometric curvature to convert incident electromagnetic waves into wide-angle scattering, effectively suppressing backscattering and achieving RCS reduction.
Building on this electromagnetic scattering mechanism, a curved radome conformally integrated with a FSS enables intelligent electromagnetic regulation: Within the operational band of the antenna, the FSS elements achieve impedance matching with incident waves, preserving the radome’s high transmissivity; out-of-band, the FSS-loaded structure mimics the behavior of a curved metallic surface, inducing multiple scattering mechanisms that drastically reduce backscattered RCS, thereby simultaneously fulfilling radar stealth and electromagnetic transmission requirements.
It is critical to emphasize that the stealth efficacy and wave-transparent performance of FSS radomes depend fundamentally on the comprehensive optimization of FSS unit geometries, array configurations, and material properties. Consequently, advancing research on high-performance FSS designs—characterized by wide-angle stability, strong frequency selectivity, and environmental adaptability—has emerged as a pivotal pathway for enhancing the multifunctional performance of next-generation stealth radomes [7].
With the rapid development of communication technology, the operating frequency bands and bandwidths of antenna systems have continuously expanded, placing higher demands on the transmission performance of radomes. The transmission performance of an FSS radome is primarily determined by the FSS itself, making the study of high-performance FSSs crucial. Since the 1960s, scholars such as Professor Munk in the United States have conducted in-depth research on the theory and design of FSS, as well as the application of FSS-based radomes [10,11,12]. In 1974, they successfully created the first conical FSS radome. Since then, FSS has received widespread attention and research. Professor Parker and other researchers at the University of Kent in the UK systematically studied FSS, proposed equivalent circuit theories for different FSS elements, and comprehensively explored the effects of various FSS parameters on transmission characteristics [13].
The design theory of FSS has become highly mature from its development since the last century. Starting from the initial simple unit designs, it has now evolved into various complex unit forms [14,15,16,17,18]. The structure of FSS has expanded from single-layer to multi-layer configurations [19,20], and it has even undergone a transition in structural dimensions from two-dimensional to 2.5-dimensional [21,22] and, eventually, to three-dimensional designs [23,24]. By combining various FSS design theories, current FSS can simultaneously achieve a range of excellent performances, such as multi-band transmission, wideband transmission, high incidence angle stability, and high selectivity. In 2023, Jiang et al. proposed a highly selective dual-band transparent FSS with a second-order response, where the center frequencies of the two operating bands were 3.06 GHz and 4.33 GHz, respectively [25]. In 2024, Ge et al. investigated a new design approach for a miniaturized FSS with ultra-wideband suppression, introducing parallel plate capacitors into the non-resonant FSS. The final unit cell size was 0.06 wavelengths, with angular stability maintained up to 60°, and a suppression bandwidth of 10–45 GHz [26]. In the same year, Li et al. achieved a wideband passband and sharp suppression band by adding rectangular polygonal lines and symmetric spiral structures in the middle layer. The relative bandwidth of the structure reached 141.4%, with a transition band of only 0.2 GHz [27].
When applied to radomes, FSS, by utilizing its filtering mechanism, can not only meet the resonant bandwidth required for the normal operation of antenna systems but also achieve high-pass transmission efficiency, deep stopband suppression, and high selectivity. Due to the high requirements for the polarization insensitivity and angular stability of FSS in the streamlined design of radomes, FSS is moving toward miniaturization, low profile, and multi-layer structures [28].
2.2. Multi-Frequency FSS
In the design of multi-frequency FSS, T. Wu and others from the California Institute of Technology (Caltech) were the pioneers in adopting concentric ring designs of different specifications, successfully constructing multi-frequency FSS structures and providing new ideas for multi-frequency FSS design [29,30]. In recent years, the rapid development of wireless communication has led to the widespread application of multi-frequency communication and multi-frequency detection technologies, and the research on multi-frequency FSS has also garnered significant attention. A single FSS unit structure typically generates only one resonant frequency point. To achieve multi-frequency transmission properties of FSS, various unit structures need to be combined. The combination design approaches mainly include planar structure design and multi-layer cascaded design, with the resulting structures being referred to as single-screen FSS and multi-screen FSS, respectively.
For single-screen FSS, multi-frequency selective properties can be achieved in two ways: one is by combining FSS units [31], and the other is by using fractal FSS units [32,33]. Combined FSS units are designed by arranging different types of FSS at certain intervals, utilizing the resonant frequency differences in various FSS units, so that the combined FSS can work at multiple frequency points. However, the design of combined FSS is more complex because the compatibility between different FSS units needs to be considered. A typical issue is that when two different types of FSS units are combined, it may result in an increase in the unit size, causing the grating lobe phenomenon to appear prematurely. In addition, it is necessary to ensure that the frequency response of high-frequency FSS units does not affect the stopband of low-frequency FSS units. In contrast, fractal FSS units are obtained by applying linear transformations (such as replication, scaling, or transformation) to simple FSS basic units. Since the initial and iterative units of fractal patterns are similar, fractal FSS exhibits multi-frequency resonance characteristics. Compared to combined FSS units, the advantage of fractal FSS units is that they can achieve multi-frequency selective performance while effectively reducing the unit spacing and delaying the appearance of grating lobes.
For multi-screen FSS, multi-frequency transmission performance can be achieved by cascading different single-screen FSSs with the addition of dielectric layers. Between 2008 and 2016, Professor Behdad and his colleagues in the United States designed various dual-frequency FSSs with second-order responses by embedding resonators of different shapes into metal patches and cascading them with line gratings or patch structures [34,35,36]. Indian scholar Varikuntla Krushna Kanth designed a dual-frequency FSS based on integrated waveguide cavities (SIWC) using waveguides of different shapes [37]. Professor Shen Zhongxiang and others from Nanyang Technological University in Singapore proposed a three-dimensional FSS design method, successfully realizing multi-frequency filtering in a three-dimensional FSS structure by reasonably designing multiple coupling methods in three-dimensional cavities (Figure 2) [38]. In Table 1, we compare the performance of multi-frequency FSS with different structures.
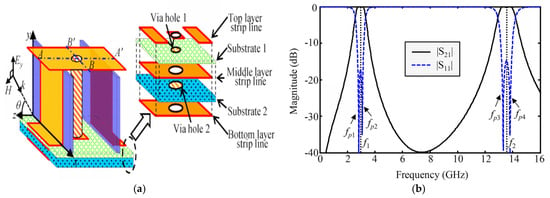
Figure 2.
Three-dimensional FSS: (a) structure; (b) S−parameter results. Reprinted with permission from ref. [38]. 2025 IEEE.

Table 1.
Comparison of transmission characteristics of three multi-frequency structure.
2.3. Broadband FSS
With the continuous development of modern integrated RF technology, the “integration” of airborne radar systems has been further advanced, and the demand for broadband FSS in radar domes has become increasingly urgent. The integrated RF systems of aircraft typically deploy multiple antenna systems within the limited space at the nose of the aircraft, including fire control radar, altimeter radar, data link radar, etc. Within a single radar dome of the airborne integrated RF avionics system, multiple antennas working at different frequency bands are installed, covering a broad spectrum of frequencies. The bandwidth extension of broadband FSS is typically achieved by superimposing multiple resonant frequency points, making its design approach similar to that of multi-frequency FSS. In fact, broadband FSS can be considered as a combination of multi-frequency FSS units with closely spaced resonant frequencies, so the design methods of multi-frequency FSS are also applicable to broadband FSS.
For planar structure design methods, the design of broadband FSS is similar to that of multi-frequency FSS, usually involving complex designs on the plane through rotations, combinations, folding, and splicing of metallic patches. This method can effectively reduce the coupling effects between the metallic patches, thereby decreasing the resonance strength and slowing down the frequency variation rate of the original frequency response curve. Specifically, this results in the lowest frequency of the passband shifting to lower frequencies, while the highest frequency of the passband extends to higher frequencies, thus effectively expanding the FSS transmission bandwidth. However, like the combination of units in multi-frequency FSS, this method still faces the problem of grating lobes. In 2016, Canadian scholar Arun Kesavan designed a single-layer FSS with a wide stopband based on the traditional Jerusalem cross element [39]. In the same year, Rabia Yahya from Bangkok University, Thailand, proposed a single-layer FSS design with a wide stopband based on the combination of square and circular rings (Figure 3) [40].
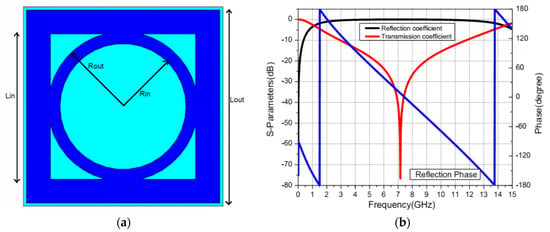
Figure 3.
The combined unit of square ring and circular ring: (a) structure; (b) S−parameter results. Reprinted with permission from ref. [40]. 2025 IEEE.
The principle of the multilayer cascade design method is similar to that of microwave filters to enhance bandwidth. By increasing the filter order, i.e., increasing the number of FSS layers, multiple adjacent passbands are merged and spliced, thus effectively expanding the operating bandwidth [41,42]. However, multilayer structures inevitably introduce insertion loss, and as the angle of incidence of the electromagnetic wave increases, the insertion loss within the passband also increases. Therefore, when using multilayer cascade designs for broadband FSS, it is essential to strictly control the number of layers in the FSS structure to ensure that the insertion loss within the passband remains within acceptable limits. Li Da and others proposed a low-profile broadband bandpass FSS, whose overall structure consists of three metallic layers [41]. Indian scholars Ramprabhu Sivasamy and others designed a three-dimensional broadband FSS based on concentric threaded cylinders [42]. In Table 2, we compare the performance of broadband FSS with three different structures.

Table 2.
Comparison of transmission characteristics of three broadband structure.
2.4. High-Selectivity FSS
High-selectivity FSS features a sharp cutoff characteristic and strong out-of-band suppression capability, enabling more effective differentiation between the electromagnetic waves transmitted by our antenna system and those detected by enemy radar. This helps reduce the out-of-band radar cross-section (RCS) of the radome while maintaining the normal operation of the antenna system, thereby improving the radar signature reduction and stealth performance of the radome. The mainstream approach to achieving high-selectivity FSS is to use a cascaded design of multiple FSS layers to achieve higher-order filtering characteristics [43,44,45,46,47,48]. From the perspective of equivalent circuits, as the number of cascaded layers increases, it is equivalent to increasing the order of the filter circuit, thereby enhancing the overall filtering performance of the FSS and making the frequency response curve steeper with higher selectivity.
In 2017, Muaad Hussein’s study proposed a low-profile second-order bandpass FSS by employing a three-layer non-resonant FSS cascade (Figure 4). This design successfully constructed the proposed FSS through two miniaturized resonant surfaces coupled by non-resonant inductive layers [43]. In 2019, Y. Feng introduced a novel aperture-coupled resonator FSS based on double-slot coupled rings in the Ka-band, significantly improving the selectivity of the FSS by using two adjacent transmission zeros generated by the coupled apertures [47].
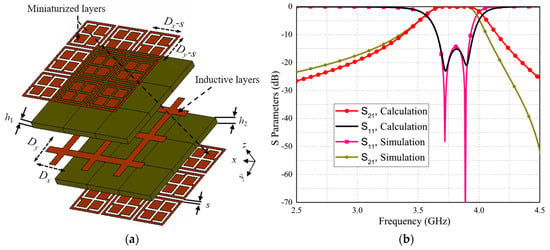
Figure 4.
Non-resonant high-selectivity FSS: (a) structure; (b) S−parameter results. Reprinted with permission from ref. [43]. 2025 IEEE.
In addition to the cascaded multi-layer FSS method, high-selectivity FSS can also be achieved by constructing resonant cavities [49,50] and using three-dimensional structures [51,52]. The construction of resonant cavities can leverage the cavity’s own resonance and quality factor (Q-value), combined with resonant structures such as patches, to generate more resonant points, thereby achieving higher-order passband or out-of-band transmission zeros to improve selectivity. The design of three-dimensional FSS is mainly based on transmission line theory for equivalent modeling, where elements in the equivalent circuit are constructed using forms such as longitudinal slots, thereby increasing resonance and achieving higher-order bandpass responses.
In 2021, Guo-Wen Che and other researchers stacked multiple layers of Substrate-Integrated Waveguide (SIW) cavities, adjusted the coupling between cavities using aperture modifications, and introduced internal metallic posts to adjust the cavity’s resonant frequency. This resulted in a third-order bandpass response with transmission zeros on both sides of the band, further enhancing selectivity [49]. In 2020, Wan-Ping Zhang and other researchers stacked slot-line units with printed metallic patches on both sides. The metallic patches on both sides of the slot-line could be equivalently modeled as inductors and capacitors in a parallel resonator, connected via metallic through-holes, forming a third-order bandpass filter circuit. This structure enabled the generation of a high-selectivity third-order bandpass response [51].
Although the construction of resonant cavities and three-dimensional structures can more easily achieve higher-order responses and out-of-band zeros, the size of the units is usually larger, making miniaturization difficult, and the structures are complex, posing challenges for practical application.
2.5. Angle-Stable FSS
For FSS applied to radomes, due to the streamlined structure of the radome itself, radar waves may not always incident perpendicularly onto the FSS but may instead strike at certain angles. Therefore, FSS needs to possess good angle stability to ensure that when radar waves incident at an angle onto the radome, the FSS can still effectively transmit waves within the operating frequency band and provide high suppression of the stopband. When the unit size is too large, if the electromagnetic waves are incident at a large angle, grating lobes will appear prematurely, adversely affecting the transmission characteristics. Moreover, an ideal FSS is an infinite periodic surface, but in practical applications the number of units should not be fewer than 20×20. However, when the FSS operates in low-frequency bands, excessively large unit sizes result in an overall large structure, thereby limiting the application of FSS in practical spaces. Miniaturized FSS is an effective solution to this problem [53]. Typically, the unit size of a simple FSS is half the wavelength of the operating frequency, while miniaturized FSS can reduce the unit size to a fraction of the operating wavelength, allowing the FSS to be effectively applied in limited spaces. There are many methods for miniaturizing FSS, with current main techniques including bending techniques, interdigitated structures [54,55,56,57], 2.5D techniques based on metallized vias [58,59], capacitive and inductive surface coupling techniques [19,60,61,62,63], and lumped parameter loading techniques [63,64,65,66], etc.
The bending technique involves bending metal lines to extend the metal paths within the unit, making the pattern denser. Essentially, this increases the electrical length of the pattern by bending it, thereby reducing the FSS unit size. From an equivalent circuit perspective, this greatly increases the unit’s equivalent inductance. The interdigitated technique involves adding cross-configured dipoles to the unit, which reduces the spacing between metal lines. From an equivalent circuit perspective, this significantly increases the unit’s equivalent capacitance. In the 1990s, Parker’s research group first proposed the bending method for miniaturization, with the designed curled square ring (Figure 5a) having a unit size of approximately 0.128λ0 [54]. While using the bending technique to reduce the FSS unit size, the bandwidth of the FSS also decreases. As a result, researchers extended the bending technique by introducing the interdigitated technique (Figure 5b), which further reduced the unit size while increasing the operating bandwidth [55]. The primary research direction for miniaturizing FSS using bending and interdigitated techniques has been in single-layer structures. In 2014, Yi-Min Yu and others from Taiwan proposed a 2.5D structure for FSS miniaturization [58]. This structure (Figure 5c) uses metallized vias to extend the current path, increasing the equivalent inductance and thereby lowering the resonant frequency. However, this method only reduces the unit size laterally, while the vertical profile remains relatively thick.
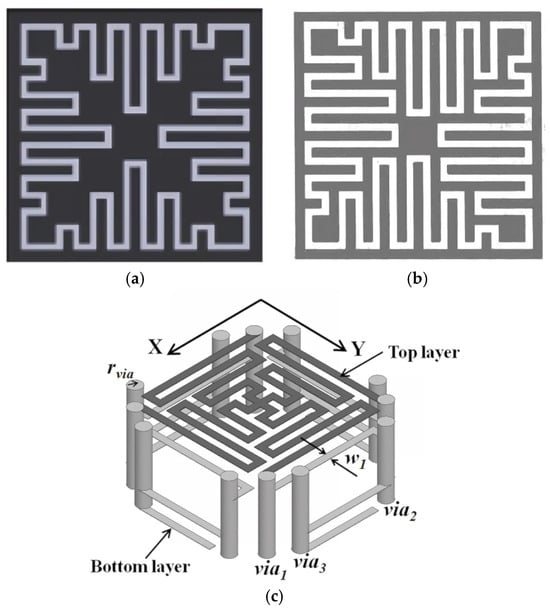
Figure 5.
Bending-based miniaturized FSS: (a) bended square ring unit, Reprinted with permission from ref. [54]. 2025 Institution of Electrical Engineers.; (b) interdigitated square ring unit, Reprinted with permission from ref. [55]. 2025 Institution of Electrical Engineers; (c) 2.5D miniaturized FSS unit. Reprinted with permission from ref. [58]. 2025 IEEE.
In 2006, Professor Behdad and his colleagues proposed a new method for miniaturizing FSS based on non-resonant FSS units [60]. In this method, metal patches are printed in a periodic arrangement on one side of the dielectric, while a line grid structure with the same periodicity as the metal patches is printed on the other side of the dielectric. The metal patch layer is equivalent to a capacitive surface, storing electric field energy, while the line grid layer is equivalent to an inductive surface, storing magnetic field energy. The coupling of the electromagnetic fields between the capacitive surface on one side and the inductive surface on the other side results in an equivalent parallel LC circuit, realizing the bandpass filtering performance of the FSS. Since this non-resonant FSS mainly relies on the electromagnetic field coupling between the capacitive and inductive surfaces to generate the filtering effect, the size of the FSS unit is not limited by the operating wavelength. Therefore, this method can significantly reduce the size of the FSS unit.
Both resonant FSS based on bending and interdigitated technologies, and non-resonant FSS based on the coupling of capacitive and inductive surfaces, generate equivalent capacitance and inductance through the metal structure of the unit itself. Compared to metal structures, lumped elements have larger equivalent capacitance and inductance. By loading lumped elements (capacitors and inductors), connecting them with metal wires, and arranging them periodically, an LC resonant array is formed, achieving the filtering effect and enhancing the miniaturization. Meanwhile, the frequency response is mainly controlled by the lumped parameters and the loading method, making it insensitive to the periodicity of the unit. In 2008, Liu Hui-Lai and his colleagues from the University of Sheffield in the UK designed an FSS with a unit period of 1/36 wavelength by introducing passive components such as capacitors and inductors into the metal patches [64]. However, this method faces challenges such as manufacturing difficulty, high losses, and poor durability, limiting its application scope. In Table 3, we compare the results achieved by four miniaturization techniques.

Table 3.
Comparison of transmission characteristics of four miniaturizing technique.
3. FSS Stealth Radome Based on Radar-Absorbing Mechanism
3.1. Development History of ATFSS
The method of reducing RCS through scattering reduction is only applicable to single-station RCS reduction. For multi-station RCS reduction, electromagnetic loss structures need to be incorporated into FSS, forming an absorptive/transmissive integrated FSS, commonly referred to as an Absorptive/Transmissive Frequency-Selective Surface (ATFSS). It still maintains good transmission performance within the passband while absorbing most of the reflected electromagnetic waves outside the passband, thus achieving multi-station RCS reduction [67].
In 1995, a U.S. patent first proposed the design concept of an ATFSS [68]. This patent added lossy dielectric to a bandpass FSS, allowing electromagnetic waves within the passband to pass through normally, while those outside the passband were absorbed and dissipated due to the lossy dielectric material, thereby achieving both absorption and transmission performance. However, this patent only presented the concept of the ATFSS design and did not provide any quantitative simulation or experimental results for absorption or transmission characteristics. It was not until 2012 that Filippo Costa, a scholar from the University of Pisa in Italy, combined square-ring resistive membrane elements and Jerusalem-slot elements (Figure 6) to design a low-frequency transmissive/high-frequency absorptive ATFSS [69] and proposed an analysis method based on an equivalent circuit model. The introduction of this ATFSS was of great significance to the development of absorptive/transmissive integrated radomes, laying the theoretical foundation for research on absorptive/transmissive integrated radomes. After that, many domestic and international teams joined the research on the ATFSS.
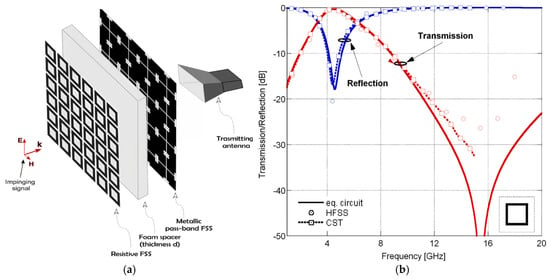
Figure 6.
ATFSS based on resistive membrane square-ring unit: (a) structure; (b) transmission/reflection results. Reprinted with permission from ref. [69]. 2025 IEEE.
3.2. Research Status of 2D ATFSS
The 2D ATFSS typically consists of a lossy layer and a bandpass FSS, where the lossy layer can be a high-impedance surface or an FSS with lumped resistances. For electromagnetic waves within the operating frequency band of the antenna system, both the lossy and FSS layers are almost transparent, ensuring the normal operation of the antenna system. However, for electromagnetic waves in the absorption band, the lower FSS acts like a metal plate that can fully reflect, ensuring that the incident waves passing through the lossy layer are reflected in-phase back to the lossy layer for reabsorption, thus achieving good out-of-band absorption performance. The ATFSS can be classified into three types based on the position of the transmission frequency band: (1) low-frequency transmission/high-frequency absorption [70,71]; (2) low-frequency absorption/high-frequency transmission [72,73,74]; (3) middle-frequency transmission/both ends absorption [75,76,77,78].
In 2015, Chen Qiang and his team proposed a miniaturized ATFSS, which consists of a metal low-pass FSS and a miniaturized resistive surface placed on top of it, achieving low-frequency transmission/high-frequency absorption performance [70]. In the same year, they controlled the current distribution on the structure by inserting lumped resistors as choke elements into the dipole-based lossy layer, making the ATFSS generate a passband with small insertion loss at high frequencies. The insertion of the lumped resistors corresponds to a quarter wavelength of the high-frequency transmission band. When high-frequency waves are incident, the impedance at the dipole’s end is infinite, and the current on it is weak, almost not resonating, and thus absorbs energy, allowing high-frequency waves to pass through the structure. When low-frequency waves are incident on the structure, the ends of the dipoles act like inductors, and the entire dipole resonates at low frequencies, generating strong currents that dissipate the low-frequency incident waves [72]. In 2019, Professor Fu Yun-Qi’s research group designed a dual-frequency ATFSS by inserting a dual-resonant structure into a metal dipole with resistive loading. This dual-frequency ATFSS has two passbands in the middle frequency range and can achieve absorption performance for both low and high frequencies [78]. In 2022, Ji et al. proposed a novel low-profile ATFSS, which flexibly adjusts the reflection phase by loading metal holes at the energy accumulation points of the induced electric field on the surface of a Jerusalem-type FSS, thereby disrupting the electric field distribution [79]. In 2025, Mu et al. introduced an ATFSS polarization conversion unit, consisting of resistive metasurface units, four frequency-selective surface units, and four cascaded polarization conversion metasurface units. This design achieved more than 10 dB RCS reduction within the 5.73–17.5 GHz frequency range [80].
3.3. Research Status of 3D ATFSS
The 3D ATFSS is based on resonant cavity theory, where multiple resonators are constructed and their coupling is controlled to generate passbands and absorption bands. In 2014, Li Bo et al. designed a 3D ATFSS by loading lumped resistors on one side of a microstrip line-based 3D bandpass FSS to construct multiple resonators [81]. The absorption characteristics of this ATFSS were obtained from the lossy resonators in the air region with resistive loading, while its high-selectivity bandpass performance was provided by the lossless resonators in the microstrip line substrate region. In 2016, Shen Zhong-Xiang et al. designed a dual-polarized ATFSS and provided a detailed explanation of the working principles and design methods of the 3D ATFSS [82]. The absorption in this ATFSS was realized by lossy resonators created by loading lumped resistors at the entrance of a short-circuited waveguide, while the high-selectivity transmission window was achieved by constructing lossless resonators through the insertion of metal posts in the parallel waveguide. In 2023, Yu et al. proposed an ATFSS with a hybrid 2D and 3D structure, where the 3D structure absorbs the fundamental mode and third-order mode, while the 2D structure absorbs the electromagnetic waves between the fundamental and third-order modes, providing a transmission window at the second-order mode. This design achieved wideband absorption performance [83]. In Table 4, we compare the performance of 2D ATFSS and 3D ATFSS.

Table 4.
Comparison of transmission characteristics of two structure.
4. Future Development Directions of FSS Stealth Radome
In modern warfare, aerospace weapons and equipment have become key factors influencing the outcome of battles. Omni-directional full-spectrum stealth, ultra-wideband frequency transmission, and high transmission are expected to be the key development directions for future radar radomes. Particularly, as countries continue to enhance their defense systems and capabilities for target reconnaissance, tracking, and strike, research on radome stealth technology has become a critical factor in determining whether a country will maintain a strategic advantage in future wars. Based on the current development status of FSS (Frequency-Selective Surface) theoretical design and the gradual improvement of curved conformal processing technologies, and considering the development trends of FSS radomes both domestically and internationally, the following future directions for FSS radome development are proposed.
4.1. Low-Frequency, Wide-Angle Stable FSS Radome
Currently, the operating frequency range of most FSS is limited to above 1 GHz, and their angular stability is only maintained up to 60°. This limitation arises because the unit size of FSS that transmit at lower frequencies is typically large, and at higher frequencies, grating lobes are easily formed, making miniaturization quite challenging. The main difficulty in improving angular stability lies in enhancing polarization stability. This is due to the fact that the bandwidth of the passband and the stopband exhibit opposite trends when the angle of incidence changes for TE and TM polarized waves, making it difficult to achieve polarization stability at large angles for FSS [84,85,86]. Figure 7 employs a bending approach to achieve miniaturization of the FSS, but the operating frequency range remains above 1 GHz, and since no improvement is made to the polarization stability, the angular stability remains limited to 60°. To achieve omni-directional full-spectrum stealth performance for future radar radomes, FSS that is stable at low frequencies and large angles will become a key research direction.
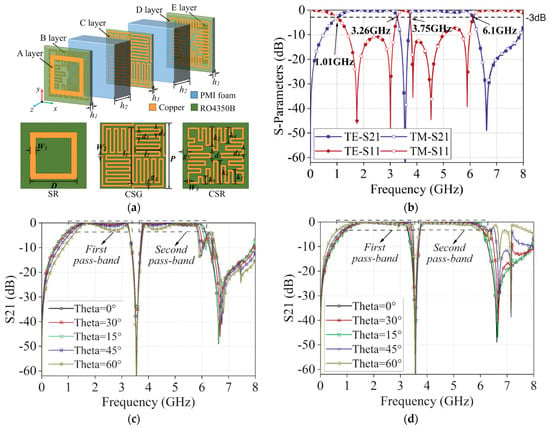
Figure 7.
Low-frequency, wide-angle stable FSS unit: (a) structure; (b) S−parameter; (c) angle stability of TE polarization; (d) angle stability of TM polarization. Reprinted with permission from ref. [86]. 2025 Dr. Mei Bi.
4.2. Conformal ATFSS Radome
The current performance of an ATFSS in terms of absorption and transmission is still far from meeting the requirements of actual equipment. There are common issues such as insufficient absorption bandwidth and transmission bandwidth, poor absorption performance, and instability of absorption and transmission performance under large angle incidence. Furthermore, there is a certain trade-off between absorption and transmission performance, which limits the practical application of an ATFSS [70,71,72,73]. In addition, the design of conformal ATFSS radomes is also quite challenging. The verification of the absorption and transmission performance of the ATFSS is typically performed using flat-panel prototypes, but applying them to actual engineering radomes requires conformal design. Compared to planar structures, curved ATFSS arrays must also account for issues such as truncation, bending, and scattering from edge elements. As indicated in the literature [87], the transmission coefficient decreases after conformal shaping. In the future, if an ATFSS is to be practically applied, exploring conformal design will be essential.
4.3. Smart FSS Radome
Airborne radar is typically in a non-operational state during extended cruising flight and only activates when approaching a target. Because of this, the cruising phase is the most vulnerable stage for the aircraft to be intercepted and tracked by enemy radars. Therefore, developing a smart radome to control the radar’s stealth status is particularly important. This would ensure that the radar remains in a stealth mode during the cruising phase and switches to a transmission mode during the terminal guidance phase. Active FSS is a key direction for realizing smart FSS radomes. By introducing active devices, such as PIN diodes or varactor diodes, into traditional FSS structures, the bias voltage or current can be controlled to adjust the resonant characteristics of the FSS [88,89]. Figure 8 illustrates a tunable square ring FSS, where each aperture contains a PIN diode spaced 90 degrees apart. By switching the diodes ON and OFF, the FSS can block or transmit waves in the 2.45 GHz frequency band. However, the addition of active devices inevitably leads to shifts in the resonant frequency and an increase in insertion loss. How to achieve an efficient and feasible smart FSS while maintaining FSS performance will be a key direction for the future development of FSS radomes.
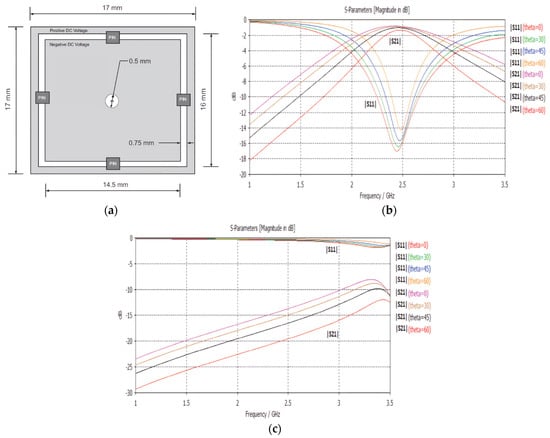
Figure 8.
Smart FSS: (a) structure; (b) S−parameter while the PIN diodes are in OFF state; (c) S−parameter while the PIN diodes are in ON state. Reprinted with permission from ref. [89]. 2025 IEEE.
5. Conclusions
In modern high-tech warfare, although detection methods such as infrared and acoustics have made significant progress and are increasingly being applied, radar technology remains the most effective detection means to date. It represents the primary threat to the battlefield survival and penetration capabilities of weapon platforms, such as aircraft. Radar stealth technology is an important means of enhancing the battlefield survivability and penetration ability of targets like aircraft. This paper provides an overview of the main techniques for radome stealth, discusses the FSS technology for improving the transmission performance of radomes, reviews the current research status of FSS stealth radomes both domestically and internationally, and offers an outlook on the future development trends of FSS radomes.
Author Contributions
Conceptualization, Y.-X.C., S.-J.W., M.L. and Y.-L.B.; methodology, Y.-X.C. and Y.-L.B.; investigation, Y.-X.C. and Y.-L.B.; writing—original draft preparation, Y.-X.C., S.-J.W., M.L. and Y.-L.B.; writing—review and editing, S.-J.W. and Y.-L.B.; visualization, Y.-X.C. and S.-J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62471099.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FSS | Frequency-Selective Surface |
| RCS | Radar Cross-Section |
| SIW | Substrate-Integrated Waveguide |
| ATFSS | Absorptive/Transmissive Frequency-Selective Surface |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
References
- Lu, G.; Zhang, J.; Yang, J.; Zhang, T.; Kou, Y. Status and development of frequency selective surface radome. Acta Phys. Sin. 2013, 62, 9–18. [Google Scholar]
- Ren, Z.; Chen, Y.; He, H. Design of a Broadband Stealth Radome. Telecommun. Eng. 2020, 60, 466–469. [Google Scholar]
- Zhou, P.; Guo, W.; Nie, T.; Teng, J.; Xu, Y. Improved Methods for Stealth of Low-Frequency Exposed Antenna. J. Ordnance Equip. Eng. 2017, 38, 117–119. [Google Scholar]
- Meng, Q.; Fan, J.; Shi, J.; Zhang, C.; Cheng, H. Research Status and Development Trend of Stealth Radome. China Textile Leader. 2018, S1, 108–112. [Google Scholar]
- Priyanka, R.R.; Sreeja, T.K. RCS Reduction Techniques: A Comparative Review. In Proceedings of the 2023 Annual International Conference on Emerging Research Areas: International Conference on Intelligent Systems (AICERA/ICIS), Kanjirapally, India, 16–18 November 2023; pp. 1–6. [Google Scholar]
- Jayakrishnan, V.M.; Liya, M.L. A Survey on Frequency Selective Surfaces in EM field. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; pp. 671–675. [Google Scholar]
- Katoch, K.; Jaglan, N.; Gupta, S.D. A Review on Frequency Selective Surfaces and its Applications. In Proceedings of the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019; pp. 75–81. [Google Scholar]
- Ye, Y. Research on Frequency Selective Surface Radomes. Master’s Thesis, Xidian University, Xi’an, China, 2021. [Google Scholar]
- Zhou, Q.; Shi, T. Research progress of broadband electromagnetic metamaterial absorber. J. Xi’an Univ. Posts Telecommun. 2021, 26, 29–35. [Google Scholar]
- Fenn, A.; Thiele, G.; Munk, B.A. Moment method analysis of finite rectangular waveguide phased arrays. IEEE Trans. Antennas Propag. 1982, 30, 554–564. [Google Scholar] [CrossRef]
- Luebbers, R.J.; Munk, B.A. Analysis of Thick Rectangular Waveguide Windows with Finite Conductivity. IEEE Trans. Microw. Theory Technol. 1973, 21, 461–468. [Google Scholar] [CrossRef]
- Pelton, E.; Munk, B.A. A streamlined metallic radome. IEEE Trans. Antennas Propag. 1974, 22, 799–803. [Google Scholar] [CrossRef]
- Parker, E.A.; Philips, B.; Langley, R.J. Analysis of coupling between a curved FSS and an enclosed planar dipole array. IEEE Microw. Guided Wave Lett. 1995, 5, 338–340. [Google Scholar] [CrossRef]
- Chang, T.K.; Langley, R.J.; Parker, E.A. An active square loop frequency selective surface. IEEE Microw. Guided Wave Lett. 1993, 3, 387–388. [Google Scholar] [CrossRef]
- Medina, F.; Mesa, F.; Marques, R. Extraordinary Transmission Through Arrays of Electrically Small Holes from a Circuit Theory Perspective. IEEE Trans. Microw. Theory Technol. 2008, 56, 3108–3120. [Google Scholar] [CrossRef]
- Rashid, A.K.; Shen, Z.; Li, B. An Elliptical Bandpass Frequency Selective Structure Based on Microstrip Lines. IEEE Trans. Antennas Propag. 2012, 60, 4661–4669. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Thin Bandstop Frequency-Selective Structures Based on Loop Resonator. IEEE Trans. Microw. Theory Technol. 2017, 65, 2298–2309. [Google Scholar] [CrossRef]
- Sivasamy, R.; Kanagasabai, M. A Novel Dual-Band Angular Independent FSS With Closely Spaced Frequency Response. IEEE Microw. Wireless Compon. Lett. 2015, 25, 298–300. [Google Scholar] [CrossRef]
- Momeni Hasan Abadi, S.M.A.; Behdad, N. A harmonic-suppressed miniaturized-element frequency selective surface with a second-order bandpass response. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 2054–2055. [Google Scholar]
- Li, Y. Study on Broadband Planar Reflectarrays and Multilayer Frequency Selective Surface and Their Applications. Master’s Thesis, Xidian University, Xi’an, China, 2015. [Google Scholar]
- Varikuntla, K.K.; Singaravelu, R. Design of a Novel 2.5D Frequency Selective Surface Element Using Fibonacci Spiral for Radome Application. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 1289–1291. [Google Scholar]
- Liang, L.; Pang, X.; Zhao, S. A 2.5D Miniaturized Wide Passband Frequency Selective Surface with High Selectivity. In Proceedings of the 2023 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar]
- Omar, A.A.; Shen, Z. Multiband High-Order Bandstop 3-D Frequency-Selective Structures. IEEE Trans. Antennas Propag. 2016, 64, 2217–2226. [Google Scholar] [CrossRef]
- Men, W.; Pang, X.; Zhao, S.; Ni, J.; Zhao, W.; Zhao, J.; Jiang, T. A Hybrid 2-D–3-D Wide Bandpass FSS with Angle stability Property. In Proceedings of the 2023 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Harbin, China, 15–18 July 2023; pp. 285–287. [Google Scholar]
- Jiang, B.; Hu, H.; Tian, J.; Lei, S.; Chen, M.; Chen, B. A Polarization-Insensitive Dual-Band FSS with High Selectivity and Independently Switchable Characteristics. IEEE Antennsa Wireless Propag. Lett. 2023, 22, 14–18. [Google Scholar] [CrossRef]
- Ge, J.; Hong, T.; Tang, J.; Jiang, W. Miniaturized FSS with Ultrawide Out-of-Band Suppression Based on Parallel-Plate Capacitor. IEEE Antennsa Wireless Propag. Lett. 2024, 23, 3892–3896. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Xi, Z. A Novel Frequency Selective Surface with UltraWideband and Broad Stopband for High Selectivity. In Proceedings of the 2024 IEEE 12th Asia-Pacific Conference on Antennas and Propagation (APCAP), Nanjing, China, 22–25 September 2024; pp. 1–2. [Google Scholar]
- Gao, Y.; Li, Y.; Zhao, L.; Huang, Z.; Sinkevich, E.; Mordachev, V. A Dual Bandstop FSS with Low Profile and High Polarization Stability for EMC. In Proceedings of the 2024 IEEE International Symposium on Antennas and Propagation and INC/USNC-URSI Radio Science Meeting (AP-S/INC-USNC-URSI), Firenze, Italy, 14–19 July 2024; pp. 2037–2038. [Google Scholar]
- Huang, J.; Wu, T.K.; Lee, S.W. Tri-band frequency selective surface with circular ring elements. IEEE Trans. Antennas Propag. 1994, 42, 166–175. [Google Scholar] [CrossRef]
- Wu, T.K. Four-band frequency selective surface with double-square-loop patch elements. IEEE Trans. Antennas Propag. 1994, 42, 1659–1663. [Google Scholar]
- Jia, H.; Gao, J.; Feng, X.; Sun, L. Novel Composite Element Frequency Selective Surface. Acta Opt. Sin. 2008, 8, 1596–1600. [Google Scholar]
- Puente-Baliarda, C.; Romeu, J.; Pous, R.; Cardama, A. On the behavior of the Sierpinski multiband fractal antenna. IEEE Trans. Antennas Propag. 1998, 46, 517–524. [Google Scholar] [CrossRef]
- Gianvittorio, J.P.; Romeu, J.; Blanch, S.; Rahmat-Samii, Y. Self-similar prefractal frequency selective surfaces for multiband and dual-polarized applications. IEEE Trans. Antennas Propag. 2003, 51, 3088–3096. [Google Scholar] [CrossRef]
- Al-Joumayly, M.A.; Behdad, N. Low-Profile, Highly-Selective, Dual-Band Frequency Selective Surfaces with Closely Spaced Bands of Operation. IEEE Trans. Antennas Propag. 2010, 58, 4042–4050. [Google Scholar] [CrossRef]
- Salehi, M.; Behdad, N. A Second-Order Dual X-/Ka-Band Frequency Selective Surface. IEEE Microw. Wireless Compon. Lett. 2008, 18, 785–787. [Google Scholar] [CrossRef]
- Gao, M.; Momeni Hasan Abadi, S.M.A.; Behdad, N. A Dual-Band, Inductively Coupled Miniaturized-Element Frequency Selective Surface with Higher Order Bandpass Response. IEEE Trans. Antennas Propag. 2016, 64, 3729–3734. [Google Scholar] [CrossRef]
- Krushna Kanth, V.; Raghavan, S. Dual-Band Frequency Selective Surface Based on Shunted SIW Cavity Technology. IEEE Microw. Wireless Compon. Lett. 2020, 30, 245–248. [Google Scholar] [CrossRef]
- Li, B.; Shen, Z. Dual-Band Bandpass Frequency-Selective Structures with Arbitrary Band Ratios. IEEE Trans. Antennas Propag. 2014, 62, 5504–5512. [Google Scholar] [CrossRef]
- Kesavan, A.; Karimian, R.; Denidni, T.A. A Novel Wideband Frequency Selective Surface for Millimeter-Wave Applications. IEEE Antennsa Wireless Propag. Lett. 2016, 15, 1711–1714. [Google Scholar] [CrossRef]
- Yahya, R.; Nakamura, A.; Itami, M. Compact single-layer UWB frequency selective surface. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, PR, USA, 26 June–1 July 2016; pp. 957–958. [Google Scholar]
- Hua, B. Research on Stability of Ultra-wideband Frequency Selective Surface. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Li, D.; Li, T.W.; Hao, R.; Chen, H.S.; Yin, W.Y.; Yu, H.C.; Li, E.P. A Low-Profile Broadband Bandpass Frequency Selective Surface with Two Rapid Band Edges for 5G Near-Field Applications. IEEE Electromagn. Compat. 2017, 59, 670–676. [Google Scholar] [CrossRef]
- Hussein, M.; Zhou, J.; Huang, Y.; Al-Juboori, B. A Low-Profile Miniaturized Second-Order Bandpass Frequency Selective Surface. IEEE Antennsa Wireless Propag. Lett. 2017, 16, 2791–2794. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Gao, X.; Guo, D.; Yang, R. A Band-Pass Frequency Selective Surface with Wideband Rejection Characteristic. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 1286–1288. [Google Scholar]
- Liu, N. Study on Rapid Design Method for High-Performance Frequency Selective Surface Radome. Ph.D. Thesis, Dalian University of Technology, Liaoning, China, 2019. [Google Scholar]
- Hong, T.; Wang, M.; Peng, K.; Zhao, Q.; Gong, S. Compact Ultra-Wide Band Frequency Selective Surface with High Selectivity. IEEE Trans. Antennas Propag. 2020, 68, 5724–5729. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, B. A Ka-band Frequency Selective Surface Based on Double-Opening Coupling Ring. In Proceedings of the 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Xie, J.; Li, B.; Lyu, Y.; Zhu, L. Single- and Dual-Band High-Order Bandpass Frequency Selective Surfaces Based on Aperture-Coupled Dual-Mode Patch Resonators. IEEE Trans. Antennas Propag. 2021, 69, 2130–2141. [Google Scholar] [CrossRef]
- Chen, G.W.; Wong, S.W.; Li, Y.; Chen, R.S.; Zhang, L.; Rashid, A.K.; Xie, N.; Zhu, L. High Roll-Off Frequency Selective Surface with Quasi-Elliptic Bandpass Response. IEEE Trans. Antennas Propag. 2021, 69, 5740–5749. [Google Scholar] [CrossRef]
- Chen, G.W.; Wong, S.W.; Li, Y.; Chen, R.S.; Zhang, L.; Rashid, A.K.; Xie, N.; Zhu, L. Bandpass FSS with Zeros Adjustable Quasi-Elliptic Response. IEEE Antennsa Wireless Propag. Lett. 2019, 18, 1184–1188. [Google Scholar]
- Zhang, W.; Li, B.; Zhu, L.; Lyu, Y.; Cheng, C. Stacked Slotline Structure-Based Unit Cell and Its Application for Synthesis of 3-D Bandpass Frequency-Selective Surfaces. IEEE Trans. Antennas Propag. 2020, 68, 7958–7968. [Google Scholar] [CrossRef]
- Li, B.; Huang, X.; Zhu, L.; Zhang, Y.; Tang, Y.; Lu, W.J.; Bo, Y. Bandpass Frequency Selective Structure with Improved Out-of-Band Rejection Using Stacked Single-Layer Slotlines. IEEE Trans. Antennas Propag. 2018, 66, 6003–6014. [Google Scholar] [CrossRef]
- Cui, Y. Design of Anular-Stable/Miniaturized/Wideband Aborptive Frequency Selective Surface. Master’s Thesis, Xidian University, Shanxi, China, 2021. [Google Scholar]
- Parker, E.A.; El Sheikh, A.N.A. Convoluted array elements and reduced size unit cells for frequency-selective surfaces. IEE Proc. H 1991, 138, 19–22. [Google Scholar] [CrossRef]
- Huang, F.; Batchelor, J.C.; Parker, E.A. Interwoven convoluted element frequency selective services with wide bandwidths. Electron. Lett. 2006, 42, 788–790. [Google Scholar] [CrossRef]
- Ynag, G.; Zhang, T.; Li, W.; Wu, Q. A Novel Stable Miniaturized Frequency Selective Surface. IEEE Antennsa Wireless Propag. Lett. 2010, 9, 1018–1021. [Google Scholar] [CrossRef]
- Zhao, P.; Zong, Z.; Wu, W.; Fang, D. A Convoluted Structure for Miniaturized Frequency Selective Surface and Its Equivalent Circuit for Optimization Design. IEEE Trans. Antennas Propag. 2016, 64, 2963–2970. [Google Scholar] [CrossRef]
- Yu, Y.; Chiu, C.; Chiou, Y.; Wu, T. A Novel 2.5-Dimensional Ultraminiaturized-Element Frequency Selective Surface. IEEE Trans. Antennas Propag. 2014, 62, 3657–3663. [Google Scholar] [CrossRef]
- Shi, Y.; Zhuang, W.; Tang, W.; Wang, C.; Liu, S. Modeling and Analysis of Miniaturized Frequency-Selective Surface Based on 2.5-Dimensional Closed Loop with Additional Transmission Pole. IEEE Trans. Antennas Propag. 2016, 64, 346–351. [Google Scholar] [CrossRef]
- Behdad, N.; Sarabandi, K. A Miniaturized Band-Pass Frequency Selective Surface. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 4171–4174. [Google Scholar]
- Behdad, N.; Al-Joumayly, M.A. A Generalized Synthesis Procedure for Low-Profile, Frequency Selective Surfaces with Odd-Order Bandpass Responses. IEEE Trans. Antennas Propag. 2010, 58, 2460–2464. [Google Scholar] [CrossRef]
- Al-Joumayly, M.A.; Behdad, N. A New Technique for Design of Low-Profile, Second-Order, Bandpass Frequency Selective Surfaces. IEEE Trans. Antennas Propag. 2009, 57, 452–459. [Google Scholar] [CrossRef]
- Gao, M.; Abadi, S.M.A.M.H.; Behdad, N. A Hybrid Miniaturized-Element Frequency Selective Surface with a Third-Order Bandpass Response. IEEE Antennsa Wireless Propag. Lett. 2017, 16, 708–711. [Google Scholar] [CrossRef]
- Liu, H.L.; Ford, K.L.; Langley, R.J. Design Methodology for a Miniaturized Frequency Selective Surface Using Lumped Reactive Components. IEEE Trans. Antennas Propag. 2009, 57, 2732–2738. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Zhang, C.; Fan, J.; Guo, D. A Design Method for Synthesizing Miniaturized FSS Using Lumped Reactive Components. IEEE Electromagn. Compat. 2018, 60, 536–539. [Google Scholar] [CrossRef]
- Liu, H.; Ford, K.L.; Langley, R.J. Novel Planar Band Pass Lump-Loaded Frequency Selective Surface. In Proceedings of the 2008 IEEE MTT-S International Microwave Workshop Series on Art of Miniaturizing RF and Microwave Passive Components, Chengdu, China, 14–15 December 2008; pp. 87–89. [Google Scholar]
- Meng, T. Research on Theory and Application Technology of the Metamaterial Radome. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2017. [Google Scholar]
- Arceneaux, W.S.; Akins, R.D.; May, W.B. Absorptive/Transmissive Radome. U.S. Patent 5,400,043, 21 March 1995. [Google Scholar]
- Costa, F.; Monorchio, A.; Langley, R.J. A Frequency Selective Radome with Wideband Absorbing Properties. IEEE Trans. Antennas Propag. 2012, 60, 2740–2747. [Google Scholar] [CrossRef]
- Chen, Q.; Bai, J.; Chen, L.; Fu, Y. A Miniaturized Absorptive Frequency Selective Surface. IEEE Antennsa Wireless Propag. Lett. 2015, 14, 80–83. [Google Scholar] [CrossRef]
- Bakshi, S.C.; Mitra, D.; Ghosh, S. A Frequency Selective Surface Based Reconfigurable Rasorber with Switchable Transmission/Reflection Band. IEEE Trans. Antennas Propag. 2019, 67, 1318–1322. [Google Scholar] [CrossRef]
- Chen, Q.; Bai, J.; Chen, L.; Fu, Y. Design of Absorptive/Transmissive Frequency-Selective Surface Based on Parallel Resonance. IEEE Trans. Antennas Propag. 2017, 65, 4897–4902. [Google Scholar] [CrossRef]
- Chen, Q.; Sang, D.; Guo, M.; Fu, Y. Miniaturized Frequency-Selective Rasorber with a Wide Transmission Band Using Circular Spiral Resonator. IEEE Trans. Antennas Propag. 2019, 67, 1045–1052. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Fu, J.; Chen, W.; Lv, B.; Song, M.; Denidni, T.A. A High-Transmittance Frequency-Selective Rasorber Based on Dipole Arrays. IEEE Access. 2018, 6, 31367–31374. [Google Scholar] [CrossRef]
- Shang, Y.; Shen, Z.; Xiao, S. Frequency-Selective Rasorber Based on Square-Loop and Cross-Dipole Arrays. IEEE Trans. Antennas Propag. 2014, 62, 5581–5589. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, W.; Gong, S. Design Bandpass Frequency Selective Surface Absorber Using LC Resonators. IEEE Antennsa Wireless Propag. Lett. 2017, 16, 2586–2589. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, S.; Monorchio, A.; Kong, X.; Wen, Y.; Huang, Z. A Miniaturized High-Selectivity Frequency Selective Rasorber Based on Subwavelength Resonance and Interdigital Resonator. IEEE Antennsa Wireless Propag. Lett. 2019, 18, 1833–1837. [Google Scholar] [CrossRef]
- Guo, M.; Chen, Q.; Sun, Z.; Sang, D.; Fu, Y. Design of Dual-Band Frequency-Selective Rasorber. IEEE Antennsa Wireless Propag. Lett. 2019, 18, 841–845. [Google Scholar] [CrossRef]
- Ji, K.; Cao, X.; Gao, J.; Yang, H.; Li, T.; Jidi, L.; Zhang, Z.; Lu, J. Design of Low Profile ATFSS and Antenna with In-Band and Out-of-Band RCS Reduction. IEEE Trans. Antennas Propag. 2022, 70, 11537–11547. [Google Scholar] [CrossRef]
- Mu, W.; Yuan, H.; Zhu, L.; Xu, G.; Hao, Z.; Li, L.; Cao, Q. An Ultrawideband Low-RCS Circularly Polarized Antenna Array Based on Hybrid Mechanism. IEEE Trans. Antennas Propag. 2025, 73, 254–265. [Google Scholar] [CrossRef]
- Li, B.; Shen, Z. Wideband 3D Frequency Selective Rasorber. IEEE Trans. Antennas Propag. 2014, 62, 6536–6541. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, J.; Li, B. 3-D Frequency Selective Rasorber: Concept, Analysis, and Design. IEEE Trans. Microw. Theory Technol. 2016, 64, 3087–3096. [Google Scholar] [CrossRef]
- Yu, W.; Cheng, M.; Yu, Y.; Wang, W.; Liu, L.; Luo, G.Q. Bandpass Absorptive Frequency-Selective Structures with Wide Absorption Bands Based on Hybrid 2-D and 3-D Structures. IEEE Trans. Antennas Propag. 2023, 71, 3183–3192. [Google Scholar] [CrossRef]
- Dang, T.; Tian, Y.; Wang, L.; Wang, G.; Zheng, H. Non-resonant multilayer cascading of frequency selective surface. Chin. J. Radio 2018, 33, 463–469. [Google Scholar]
- Wang, Y.; Chen, Y.; Mao, W. Design of a Miniaturized Band-pass Frequency Selective Surface Radome in Low Frequency. Telecommun. Eng. 2022, 62, 1526–1531. [Google Scholar]
- Li, Z.; Weng, X.; Yi, X.; Duan, W.; Li, K.; Bi, M.; Pan, T.; Lin, Y. A Miniaturized Ultrawideband Dual-Bandpass Frequency-Selective Surface with High Selectivity. IEEE Trans. Antennas Propag. 2024, 72, 6510–6519. [Google Scholar] [CrossRef]
- Zhu, J.; Cao, Q.; Fang, X.; Wang, Y. An Electromagnetic Performance Analysis and Design of Curved Frequency Selective Surface (C-FSS) Radome. J. Microw. 2019, 35, 69–74. [Google Scholar]
- Zhou, H.; Zhu, H.; Xu, J.; Di, Y.; Wang, G. Frequency Reconfigurable Frequency Selective Surface based on PIN diodes. In Proceedings of the 2024 International Symposium on Antennas and Propagation (ISAP), Incheon, Republic of Korea, 5–8 November 2024; pp. 1–2. [Google Scholar]
- Ibrahim, S.H.; Alsatti, K.S.; Hussaini, M.A.; Khan, J.; Kiani, G.I. Tunable FSS using PIN diodes and microcontroller. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 577–579. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).