Enhancing Domain-Specific Knowledge Graph Reasoning via Metapath-Based Large Model Prompt Learning

Abstract

Representing domain knowledge extracted from unstructured texts using knowledge graphs supports knowledge reasoning, enabling the extraction of accurate factual information and the generation of interpretable results. However, reasoning with knowledge graphs is challenging due to their complex logical structures, which require deep semantic understanding and the ability to address uncertainties with common sense. The rapid development of large language models makes them an option for solving this problem, with good complementary capabilities regarding the determinacy of knowledge graph reasoning. However, the use of large language models for knowledge graph reasoning also has challenges, including structural understanding challenges and the balance of semantic density sparsity. This study proposes a domain knowledge graph reasoning method based on a large model prompt learning metapath (DKGM-path), discussing how to use large models for the preliminary induction of reasoning paths and completing reasoning on knowledge graphs based on iterative queries. The method has made significant progress on several public reasoning question answering benchmark datasets, demonstrating multi-hop reasoning capabilities based on knowledge graphs. It utilizes structured data interfaces to achieve accurate and effective data access and information processing and can intuitively show the reasoning process, with good interpretability.

1. Introduction

In the realm of knowledge graphs, knowledge is stored in the form of numerous triplets, representing a structured and deterministic method of knowledge representation. The application of reasoning based on knowledge graphs is crucial for knowledge in various domains, as it provides accurate factual information and is renowned for its symbolic reasoning capabilities, which can generate interpretable results. For instance, a specialized concept in the field of healthcare management, namely “hospitalization splitting”, can be represented as shown in Figure 1. A knowledge graph can structurally store the key knowledge required to assess this concept (middle panel). Moreover, this structured conceptual knowledge can be utilized in a specific knowledge graph for medical information records (right panel), thereby facilitating the evaluation of specific cases.

However, constructing automatic reasoning based on domain knowledge graphs is challenging [1], as it requires handling complex logic and rules to ensure the accuracy and validity of the reasoning process. Traditional methods based on rules or representation learning struggle to adapt to the complexity of such systems, which often involve strong semantic understanding capabilities and in-depth comprehension of a vast amount of professional knowledge texts in order to correctly represent and process the relationships between entities. Moreover, automatic reasoning systems also need to be capable of dealing with uncertainty and ambiguity, as real-world domain knowledge is often incomplete and imprecise.

Therefore, to possess the ability to handle a large amount of complex semantics and represent the depth of domain knowledge, while also having sufficient common sense to fill in the missing reasoning logic in knowledge graphs, the rapidly developing large language models (LLMs) have emerged as a competitive solution in recent years.

Combining domain knowledge graphs with LLMs highlights their complementary strengths and weaknesses [1]. Therefore, integrating knowledge graphs into LLMs is a potential solution for automatic reasoning. This approach considers both reasoning capability and reliability. For example, LLMs are often criticized for lacking factual knowledge, which can lead to errors and hallucinations. These issues can be particularly harmful in fields like law, medical diagnosis, and legal judgments. In contrast, knowledge graphs can provide certain and retrievable factual knowledge. On the other hand, knowledge graph reasoning is based on rules and is deterministic but struggles to adapt to complex real-world tasks, while LLMs can offer reasoning capabilities based on complex patterns.

However, the use of LLMs for knowledge graph reasoning also faces several key challenges:

• Limited Structural Understanding: LLMs are trained primarily on unstructured text and lack the ability to fully comprehend the structured nature of knowledge graphs. This limitation hampers their ability to effectively navigate and reason over the complex relationships and entities within knowledge graphs.
• Inefficient Inference Paths: LLMs often struggle to identify and induce optimal reasoning paths, especially in multi-hop reasoning tasks. Their lack of structured reasoning capabilities can lead to inefficient or inaccurate inference, as they may not always select the most relevant paths for answering a query.
• Lack of Fact Verification: LLMs are known for their occasional factual errors and hallucinations, which can be particularly problematic when reasoning over knowledge graphs. Without a mechanism to verify the factual accuracy of their reasoning steps against the knowledge graph, these errors can propagate and affect the overall reliability of the reasoning process.
• Semantic Sparsity Discrepancy: Natural language, such as query task texts, typically exhibits low-density sparsity, which creates a significant difference in semantic space compared to the high-density structure of knowledge graphs. While LLMs have shown the ability to compensate for common sense deficiencies in natural language texts, they may still struggle when independently constructing a reasoning process based solely on the query target. This is primarily due to the limited information available for querying structured knowledge, which can lead to factual insufficiency and potential hallucinations. The challenge lies not in understanding the query intent, which LLMs are increasingly capable of, but in effectively constructing queries that align with the dense structure of knowledge graphs. This gap highlights the need for additional mechanisms to guide LLMs in accurately querying and utilizing structured knowledge.

To address these limitations, this study proposes a domain knowledge graph reasoning method based on a large model prompt learning metapath (DKGM-path). This method leverages the strengths of both LLMs and knowledge graphs by integrating structured reasoning paths and iterative queries to enhance the reasoning capabilities of LLMs. Specifically, DKGM-path employs prompt learning to guide the model in summarizing reasoning paths and in iteratively verifying them against the knowledge graph. This approach not only improves the accuracy and reliability of reasoning but also ensures that the reasoning process is interpretable and aligned with the factual knowledge stored in the knowledge graph.

2. Literature Review

Knowledge graphs (KGs) store structured knowledge as a set of triplets, which can be represented as

$$\mathrm{KG}=\left\{\right(h,r,t)\mid (h,r,t)\subseteq E\times R\times E\}$$

(1)

where E and R denote the sets of entities and relations, respectively. In this representation, h and t represent the instance entities, while r represents the relation between them. This triplet structure is fundamental for encoding knowledge in a structured manner.

Knowledge graphs can be divided into a schema layer and a data layer, both of which require certain constraints and specifications to form a logical framework. The schema layer represents the structure, hierarchy, and definition of knowledge categories, such as entities, relations, and attributes. It restricts the specific forms of knowledge in the data layer. The knowledge triplets in the data layer are regarded as units for storing specific data information. Therefore, knowledge graphs can typically be represented in the form of triplets:

$$G=\{E,R,F\}$$

(2)

where E represents the set of entities $\{e_1,e_2,\dots ,e_i\}$. An entity e is a basic element in a knowledge graph, referring to an objectively existing and distinguishable thing, including people, objects, or abstract concepts. R represents the set of relations $\{r_1,r_2,\dots ,r_j\}$, and a relation r indicates a certain connection between two different entities in the knowledge graph. F represents the set of facts $\{f_1,f_2,\dots ,f_k\}$, with each fact defined as a triplet $(h,r,t)\in F$, where h and t represent the instance entities, and r represents the relation between them. For example, basic types of facts can be represented as triplets $(\mathrm{entity},\mathrm{relation},\mathrm{entity})$, $(\mathrm{entity},\mathrm{attribute},\mathrm{value})$, etc.

Domain-specific knowledge graphs have long been used to represent knowledge in specific domains, such as medical, biological, and financial fields. Their development can be traced back to the 1960s with the emergence of semantic networks [2]. Over the years, these graphs have evolved to become more accurate and reliable, despite generally being smaller in scale compared to encyclopedic knowledge graphs. For instance, the Unified Medical Language System (UMLS) is a well-known domain-specific knowledge graph in the medical field, containing biomedical concepts and their relationships [3]. In other domains, such as finance, geology, biology, chemistry, and genealogy, domain-specific knowledge graphs have also been developed to address the unique needs of these fields. Recent advancements in neural networks have further enhanced the capabilities of domain-specific knowledge graphs by incorporating symbolic domain knowledge and improving their performance [4].

Knowledge reasoning is a significant research direction in the field of knowledge graphs. It involves the process of inferring unknown knowledge based on existing knowledge through logical rules, statistical methods, or machine learning techniques. Reasoning methods can be categorized into logical reasoning and non-logical reasoning. Logical reasoning includes deductive reasoning and inductive reasoning. Deductive reasoning is a process of reasoning from the general to the specific, while inductive reasoning is a process of reasoning from the specific to the general. Recent research progress includes three typical knowledge reasoning methods based on logical rules, embedding representations, and neural networks.

2.1. Rule-Based Knowledge Reasoning

The fundamental structure of knowledge graph reasoning enables the discovery of new facts using simple rules and features within the knowledge graph. These methods effectively leverage the symbolic representation of knowledge. In this context, they can operate with high accuracy and provide clear explanations for the reasoning outcomes. The early development of these methods set the tone for logical reasoning in knowledge graphs. The regularity of these methods is reflected in various aspects of their early basic research:

Classic logic-based knowledge reasoning refers to the direct use of first-order logic (FOL) and description logic to express rules formulated by experts. For instance, models based on probabilistic soft logic (PSL) are used to reason about the facts and confidence levels of candidates [5], as well as the applicability of methods for learning Markov logic network weights from a knowledge base (KB) in the presence of missing data [6].

Statistical knowledge reasoning applies machine learning techniques to automatically extract hidden logical rules from knowledge graphs and uses these rules for reasoning. These methods do not rely on expert-defined rules and can explain reasoning outcomes using automatically extracted logical rules. For example, methods based on association rule mining handle more complex and larger-scale knowledge graphs, including the high-confidence Horn rules mined by AMIE under incomplete evidence [7] or the extension of AMIE to AMIE+ through pruning strategies and approximations [8], as well as RDF2Rules, which mines multiple rules at once [9].

Graph-structure-based reasoning utilizes the structure of the graph as a feature for reasoning. For example, paths connecting entity pairs characterized by the target relationship are used to train a logistic regression model for each relationship, and then the trained logistic regression model is employed for knowledge graph reasoning [8]. Alternatively, a multi-task learning framework considers the correlations between different relationships, mines relationships with high relevance, and then performs multi-task learning to couple the predictions of these relationships [10]. Local structure reasoning uses local graph structures that are highly relevant to the reasoning as features for knowledge graph reasoning. Compared to reasoning based on global structures, this method focuses more on finer-grained features and has a lower computational cost. For example, methods that use breadth-first search to obtain subgraphs of target entities and then perform multi-feature extraction on the searched subgraphs to achieve reasoning [11], as well as methods that employ hierarchical random walk algorithms [12].

2.2. Representation Learning in Knowledge Reasoning

This study proposes a method based on metapaths and iterative reasoning to address the inference issues in domain knowledge graphs. The use of metapaths serves not only to decompose problems and facilitate reasoning by large language models in a chain-of-thought [13] manner but also to transform problems into triplets with the same semantic information density as the knowledge graph. Moreover, an iterative verification approach is employed during the generation process to ensure that entities and relationships truly exist in the graph, thereby enhancing the reliability of the reasoning process.

To overcome the limitations of text reasoning chains in knowledge graphs, where large language models may produce texts that are formally consistent with chain-of-thought prompts but logically ambiguous and not aligned with the actual connections in the knowledge graph, the method proposed in this study takes into account two key factors:

• The construction form of reasoning chain prompts: Relying solely on text reasoning chains is insufficient to fully stimulate large language models to generate reliable and authentic knowledge graph reasoning processes. Inspired by the triplet structure in knowledge graphs and the updating of graph nodes, structured features are used to construct metapaths to enhance prompts. A verification mechanism is repeatedly applied to update the generation results of metapaths, ensuring that they can more accurately guide the model in logical reasoning.
• Post-verification: Large language models typically cannot check the correctness of their reasoning processes on their own. After the reasoning process is completed, an external mechanism is needed for verification to ensure the accuracy of the reasoning results and to eliminate hallucinations.

By taking into account these two factors in a comprehensive manner, it can be ensured that large language models, when integrated with knowledge graphs, are capable of generating reasoning results that are not only accurate but also interpretable.

2.3. Integration of Knowledge Graphs and Large Language Models

Large language models (LLMs) have been widely adopted in various practical applications in recent years. For instance, ChatGPT, a chatbot based on LLMs, is capable of engaging in natural conversations with humans. To enhance the knowledge awareness of LLMs, several implementations integrating knowledge graphs have emerged. ERNIE 3.0 [14] and Bard incorporate knowledge graphs into chatbot applications to improve their performance. Firefly has developed a photo-editing application that allows users to edit images using natural language descriptions. Wikidata [15] and KO [16] are representative knowledge graph applications that provide external knowledge sources. OpenBG [17], designed for recommendation purposes, is another notable example of a knowledge graph. Additionally, Doctor.ai has developed a medical assistant that combines LLMs with knowledge graphs to offer medical advice.

The potential for unifying large language models and knowledge graphs has increasingly attracted the attention of researchers and practitioners. LLMs and knowledge graphs are inherently interconnected and can mutually enhance each other. In the context of knowledge graph-enhanced LLMs, knowledge graphs can be integrated into both the pre-training and inference stages of LLMs to provide external knowledge [18,19,20]. Moreover, knowledge graphs can be used to analyze LLMs and provide interpretability [21]. Conversely, in the context of LLM-enhanced knowledge graphs, LLMs have been applied to various knowledge graph-related tasks, such as knowledge graph embedding [22], knowledge graph completion [23], knowledge graph construction [24], knowledge graph-to-text generation [25], and knowledge graph question answering [26] to improve performance and facilitate the application of knowledge graphs.

2.4. LLMs for Knowledge Reasoning

Knowledge graph-enhanced LLMs focus on utilizing knowledge graphs to enable LLMs to effectively learn and memorize knowledge derived from their training corpora. However, the way LLMs memorize knowledge is based on probabilistic, parameterized models, which do not guarantee the accuracy of the memorized knowledge. Real-world knowledge is also dynamic, and the limitations of LLM training make it difficult to update the integrated knowledge without retraining the model. Therefore, a significant amount of research has been dedicated to keeping the knowledge space and the parameter space of LLMs separate and injecting knowledge during inference.

A straightforward approach is to employ a dual-tower architecture, where one independent module processes text input and another module handles the related knowledge graph input [27]. However, this method lacks interaction between text and knowledge. To address this, KagNet [21] proposed encoding the input knowledge graph first and then enhancing the text representation. MHGRN [28] uses the final LLM output of the input text to guide the reasoning process on the knowledge graph. However, both only designed unidirectional interaction between text and the knowledge graph. To solve this issue, QA-GNN [29] uses a graph neural network (GNN)-based model that jointly infers input context and knowledge graph information through message passing, representing the input text information as a special node and connecting it with other entities in the knowledge graph. Nevertheless, the text input is only summarized into a single dense vector, limiting the information fusion performance. Subsequently, JointLK [30] was proposed with a framework that achieves fine-grained interaction between any token in the text input and any knowledge graph entity through bidirectional attention mechanisms from the LLM to knowledge graph and vice versa. GreaseLM [31] employs deep and rich interactions between input text tokens and knowledge graph entities at each layer of the LLM.

Another category of methods proposed combining non-parametric and parametric modules to handle external knowledge, namely Retrieval-Augmented Generation (RAG). Given input text, RAG first searches for relevant knowledge graphs in the non-parametric module to obtain several documents. Then, RAG treats these documents as hidden variables z and inputs them into the output generator supported by the LLM as additional contextual information. Studies have shown that using different retrieved documents as conditions for different generation steps results in better performance than using a single document to guide the entire generation process [32]. RAG outperforms other purely parametric and non-parametric baseline models in open-domain question answering. Compared with other purely parametric baselines, RAG can also generate more specific, diverse, and factual text. Story-fragments [33] adds an extra module to determine significant knowledge entities and integrate them into the generator to improve the quality of generated long stories. EMAG [34] further improves on the efficiency of such systems by encoding external knowledge into key–value memory and utilizing fast maximum inner product search for memory queries. REALM [35] uses a novel knowledge retriever to help the model retrieve and focus on documents from a large corpus during the pre-training stage, successfully enhancing the performance of open-domain question answering. KGLM [36] uses the current context to select facts from the knowledge graph to generate factual sentences, and with the help of external knowledge graphs, KGLM can use out-of-domain vocabulary or phrases to describe facts.

2.5. Prompt-Based Knowledge Reasoning Methods

Prompt-based knowledge reasoning methods have emerged as significant approaches for enhancing the reasoning capabilities of LLMs by leveraging structured prompts. These methods aim to improve the accuracy and interpretability of reasoning results by guiding LLMs through carefully designed prompts. For instance, ReadPrompt [37] is a method that focuses on generating readable prompts to improve the reliability of knowledge probing in LLMs. It identifies meaningful sentences to serve as prompts, which are then used to assess the knowledge encoded within pre-trained language models (PLMs). The method achieves state-of-the-art performance on knowledge probing benchmarks and addresses the issue of misalignment between constructed prompts and knowledge, which is common in current prompting methods. KG prompting aims to better integrate the structure of knowledge graphs into LLMs by designing carefully crafted prompts. These prompts convert structured KGs into text sequences, which are then used as context inputs for LLMs. This allows LLMs to leverage the structure of the KG for reasoning. Methods like Mindmap [38] and ChatRule [39] use prompts to represent graph structures and relation paths, respectively, enabling LLMs to generate meaningful logical rules for reasoning.

However, these methods also face several limitations in the context of structured knowledge graph reasoning. For example, ReadPrompt primarily focuses on knowledge probing and may not be directly applicable to complex multi-hop reasoning tasks, where the structured nature of knowledge graphs and the need for iterative interaction are more pronounced. Methods like KG prompting require manual prompt design, which is labor-intensive and may not be scalable for large-scale knowledge graphs. Overall, while prompt-based knowledge reasoning methods have shown promise, they still face challenges in handling structured data, semantic mismatches, and the need for iterative interaction, which the DKGM-path method aims to address through the introduction of metapaths and multi-step iterative prompts.

3. Methodology

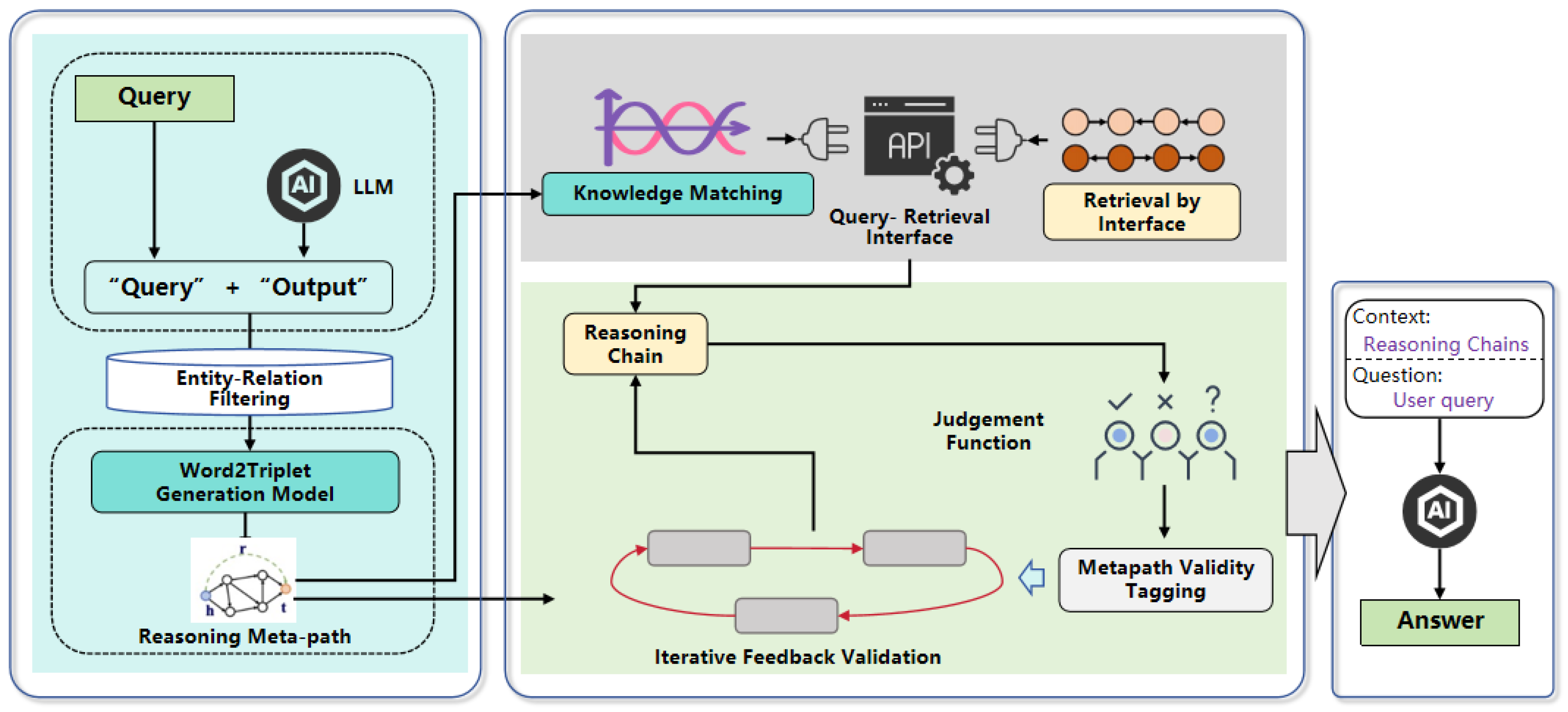
3.1. Proposed Framework

The DKGM-path method proposed in this study is clearly divided into three basic steps to complete the fundamental construction of the reasoning process. The proposed research framework is illustrated in Figure 2.

• In leveraging large language models to parse task prompts, several triplet examples are constructed as reasoning metapaths. These metapaths are verified and updated with the knowledge graph to obtain truly existing reasoning paths.
• The metapaths are used for iterative interaction between the large language model and the knowledge graph, promoting the step-by-step construction of reasoning by the large language model, and including the interpretation of prompts and evidence triplets extracted from the knowledge graph, namely a series of reasoning chains entirely drawn from within the knowledge graph.
• Algorithms for fact verification and loyalty verification are employed to ensure the reliability of the reasoning chains and to re-evaluate unreliable ones.

The DKGM-path method can be summarized into two main stages: the first stage involves retrieving relevant reasoning chains, and the second stage involves inferring answers and subsequent generation steps. The ultimate goal is to explicitly complete the knowledge graph retrieval and reasoning process of large language models and to utilize structured data interfaces to achieve accurate and effective data access and information processing. This enhances the factual reasoning ability and interpretability of large language models, thereby determining the next step or final outcome of the problem.

3.2. Construction and Verification of Reasoning Metapaths

Metapaths are constructed based on zero-shot prompts (prompts that do not require any labeled training data or prior domain-specific fine-tuning and rely entirely on the structured knowledge graph query feedback for the next step of reasoning) and are refined through iterative approximation and feedback validation to ensure that the metapaths represent genuine entities and relationships present within the knowledge graph.

3.2.1. Constructing Reasoning Metapaths Based on Zero-Shot Prompts

Drawing on insights from previous research on chain-of-thought prompts [13], the performance of large models in reasoning is contingent upon the fundamental principles of parsing task prompts. This suggests that the key challenge in constructing chain-of-thought prompts based on knowledge graphs lies in how to parse task text principles using structured triplets. Constructing metapaths, that is, by creating an example composed of a series of nodes and edges, to transform the original task text into a structured specific prompt will facilitate this process.

Specifically, inspired by the chain-of-thought approach, the method selects the original text as the basic input and connects specific prompt words to form a complete prompt. Through zero-shot prompts based on large models, a set of triplets is generated for each task question to formalize the basic logic of reasoning. For instance, to formally decompose the concept condition of “hospitalization splitting” from domain knowledge in a dataset, one can obtain several clear determination requirements such as (Patient A, discharge time, T1), (Patient A, admission time, T2), etc. The model is then required to generate an unstructured text explanation to assist in expressing the relationships between the triplets.

Applying the aforementioned steps to all task texts in the domain-specific knowledge graph yields multiple transformed original tasks denoted as $(Q_i,T_i,H_i)$. Here, $Q_i$ and $H_i$ represent the input query and prompt explanation for the i-th example, respectively, while $T_i$ signifies the list of generated triplets, comprising several basic logic triplets, i.e., $T_i={\left\{(s_{ij},r_{ij},o_{ij})\right\}}_j$, where $s_{ij}$, $r_{ij}$, and $o_{ij}$ correspond to the subject, relation, and object, respectively.

For example, consider a task question $Q_i$ asking to determine whether a patient’s hospitalization records are split correctly. The generated triplets $T_i$ could be [(Patient A, discharge time, T1), (Patient A, admission time, T2)], etc., and the prompt explanation $H_i$ might state “Check if the discharge time T1 of Patient A is before the admission time T2 to determine if the hospitalization records are split correctly”.

Specifically, when processing a given test query ${\widehat{Q}}_i$, it is first combined with a predefined prompt template E to form a new input sequence:

$$\widehat{i}=[E;{\widehat{Q}}_i]$$

(3)

This sequence is then fed into a large language model to generate the corresponding output sequence $\widehat{o}$, which contains the response to the test query.

Subsequently, the output sequence $\widehat{o}$ is converted back into the form of basic logic triplets to facilitate comparisons and evaluations with the triplets of the original task. This conversion process can be achieved through a parser P, designed analogously to the triplet error-checking validator in RuleHub, which is capable of identifying and extracting entities, relations, and objects from the output sequence, as well as verifying the structure and conflicts of the triplets to ensure that the results can be organized into a triplet list ${\widehat{T}}_i$:

$${\widehat{T}}_i=P\left(\widehat{o}\right)$$

(4)

Here, ${\widehat{T}}_i={\left\{({\widehat{s}}_{ij},{\widehat{r}}_{ij},{\widehat{o}}_{ij})\right\}}_j$ represents the transformed triplet list, where ${\widehat{s}}_{ij}$, ${\widehat{r}}_{ij}$, and ${\widehat{o}}_{ij}$ correspond to the entities, relations, and objects identified by the parser, respectively.

Ultimately, the transformed triplet list ${\widehat{T}}_i$ is obtained to represent the prompt metapath of the original task. Based on the principle of zero-shot prompt learning, the metapath predictions acquired by the method can be directly derived from the output of the large language model, serving as a formalized and structured interpretation of the task query text. Therefore, it can be used as a starting point for iteration and transformation into actual reasoning chains within the knowledge graph.

3.2.2. Feedback Validation of Reasoning Metapaths

To ensure the reliability of metapaths in guiding knowledge graph reasoning, after the construction pattern of the metapath is completed, a mechanism for validating the authenticity of the triplet nodes within the metapath and for updating and adjusting the nodes must be provided, ultimately generating a reliable metapath.

This study designed and trained a separate validation model to accomplish this step, with the specific training process as follows:

• Initialization: Select a triplet $(h,r,t)$ to be validated, where h is the head entity, r is the relation, and t is the tail entity. Initialize a vector representing the triple $\{{\mathbf{h}}_0,{\mathbf{r}}_0,{\mathbf{t}}_0\}$ and obtain the set S of all known triplets from the knowledge graph.
• Iterative Approximation: In each iteration, use the current triplet representation to predict the relation and check whether the triplet exists in the knowledge graph. Define an iterative process:

  $$\begin{array}{c}\mathrm{Existence}\mathrm{Check}=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{if}(h,r,t)\in S\hfill \\ \hfill 0,\hfill & \hfill \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

  (5)
• Feedback Validation: After each iteration, use a scoring function to evaluate the existence of the current triplet. Define a scoring function $f_v$:

  $$\begin{array}{c}{f}_v(h,r,t)=\parallel \mathbf{h}+\mathbf{r}-\mathbf{t}\parallel \end{array}$$

  (6)
  If the value of $f_v(h,r,t)$ is close to zero, the triplet is considered to exist.
• Set Loss Function: Construct a loss function to assess the existence of the current triplet:

  $$\begin{array}{c}L={\displaystyle \sum _{(h,r,t)\in S}}max(0,\gamma -f_v(h,r,t))\end{array}$$

  (7)
  Here, $\gamma$ is a set threshold representing the allowable error range. This threshold determines the minimum score required for a triplet to be considered valid. Specifically, if the scoring function $f_v(h,r,t)$ is less than $\gamma$, the triplet is considered to exist.
• Model Training: In each iteration, update the vector representation of the triplet using optimization algorithms such as stochastic gradient descent (SGD) to minimize the loss function:

  $$\begin{array}{c}{\mathbf{h}}_{n+1}={\mathbf{h}}_n-\alpha ·{\nabla }_{\mathbf{h}}L\\ {\mathbf{r}}_{n+1}={\mathbf{r}}_n-\alpha ·{\nabla }_{\mathbf{r}}L\\ {\mathbf{t}}_{n+1}={\mathbf{t}}_n-\alpha ·{\nabla }_{\mathbf{t}}L\end{array}$$

  (8)
  Here, $\alpha$ is the learning rate of the optimization algorithm, which controls the step size of each update during the training process.
• Final Validation: Input the triplet to be validated into the trained model and determine the existence of the triplet based on the output value of the scoring function. If $f_v(h,r,t)$ is less than the set threshold $\gamma$, then the triplet is considered to exist.
• Iteration Termination Condition: Set a threshold, and when the change in the output value of the scoring function is less than this threshold for several consecutive iterations, it can be considered that the existence of the triplet has reached a stable state, and the iteration can be stopped.
• Result Output: Finally, output the validation result to confirm whether the triplet $(h,r,t)$ exists in the knowledge graph.

3.3. Iterative Reasoning Steps on MetaPaths

Based on the generated knowledge reasoning metapaths, the method adopts an iterative “retrieve-reason” framework to support the reasoning of large language models on structured data. This framework collects reasoning evidence from structured knowledge graphs through interface calls (i.e., retrieval) and enables large language models to reason and solve user requirements based on the collected information (i.e., reasoning). It supports large language models in iteratively reasoning toward structured data with the help of external interfaces, gradually approaching the target of the given reasoning task query.

As mentioned earlier, more traditional methods treat the query target and the query method as two different “semantic spaces”, converting the query target into a format-compliant query statement, such as text-to-SQL. However, query languages, designed for the structure of knowledge graphs, do not possess complete semantic expression capabilities and always face the issue of different semantic spaces during the conversion process.

Therefore, the basic idea of iterative reasoning is to construct a two-step iterative framework:

• Utilize the interfaces of structured data to achieve precise and efficient data access and queries.
• Further leverage the reasoning capabilities of large language models to determine the next step of the question or the final result (solving the task).

These two steps are executed in sequence and iterated repeatedly. In this way, large language models can focus on solving reasoning tasks without having to consider the specific methods of querying structured data. Then, linearize them into text prompts, and finally input the prompts into the LLM for understanding and generation (selecting useful data for the next iteration or predicting the final answer to end the reasoning).

Specifically, these triplets are represented as $G=\left\{(e_1,r,e_2)\right|e_1,e_2\in E,r\in R\}$, where E and R represent the sets of entities and relations, respectively. The triplet $(e_1,r,e_2)$ indicates that there is a relation r between the head entity $e_1$ and the tail entity $e_2$. The reasoning process starts from a specific entity (i.e., a subject entity of the problem), and then jumps according to the relations until the answer is found. In this process, the LLM needs to be able to call the query interface of the knowledge graph, obtain and understand the adjacent relations of the current entity, reason to the adjacent triplets that have a specific relation with the current entity, and finally locate the answer entity.

3.3.1. Query Interface Design for Iterative Reasoning

Query languages, designed with the structure of knowledge graphs in mind, lack complete semantic expression capabilities and consistently face issues of differing semantic spaces during the conversion process, often leading to significant semantic loss or risks to fidelity.

This study employed an iterative reasoning method, where the entire reasoning process was designed using chains of thought, without the need for conversion into specific statements, thereby largely circumventing such risks. Consequently, the method initially employs two fundamental interface functionalities:

• Extract Neighboring Relations: For a given entity e, extract all adjacent relations.
• Extract Triplets: For a given head entity e and a set of relations $\left\{r\right\}$, extract all triplets that have a relation with e.

To implement these two basic functions and enable their invocation by large language models, the iterative framework utilizes API-based interface technology. This technology, by defining clear input and output specifications, allows large models to interact with knowledge graphs programmatically. Specifically, it typically relies on modern web service standards such as RESTful API or GraphQL, permitting large models to send queries via HTTP requests and receive response data in formats like JSON or XML.

Specifically, the process can be described with the following formulas:

• Extract Neighboring Relations: Define a function $f\left(e\right)$, where e represents the input entity, and the output of the function is the set of all adjacent relations of that entity. It can be represented as

  $$R_e=f\left(e\right)$$

  where $R_e$ is the set of relations for entity e. Define a function get_neighborhood(entity), which takes an entity as input and returns all neighboring relations of that entity.
• Extract Triplets: Define another function $g(e,r)$, where e is the head entity and r is the set of relations. The output of the function is the set of all triplets connected to entity e through relation r. Mathematically, it can be represented as

  $$T_{e,r}=g(e,r)$$

  where $T_{e,r}$ is the set of triplets corresponding to entity e and relation r.
• After obtaining the neighboring relations and triplets, the large language model can use these steps to assist the reasoning process:
  • Obtain neighboring relations: get_neighborhood(topic_entity).
  • Based on the specific relations needed, call the function to obtain triplets:
    get_triples(topic_entity, relation).
  • Use triplet data for reasoning to locate the answer entity: answer_entity = perform_reasoning(relevant_triples).

Through the iterative interface design, large language models can dynamically query the knowledge graph during the reasoning process to obtain necessary information to aid reasoning and answer generation. This design not only enhances the flexibility and accuracy of the model but also makes the reasoning process more transparent and interpretable.

3.3.2. Design of the Judgment Function

To control the iterative process of the framework, a judgment function needs to be constructed to determine whether the currently selected entity in the metapath is similar to a certain entity in the knowledge graph.

Specifically, the entity representations extracted from the context of the knowledge graph are denoted as

$$U=\{u_1,\dots ,u_{\left|U\right|}\}$$

(9)

where $u_i$ represents the relevant entities.

An encoding model $\mathrm{enc}\left(·\right)$ is utilized to encode the local entities $u_i$ in the knowledge graph as well as the entity E. Subsequently, the inner product similarity between the embedding vectors of $u_i$ and E is calculated. Entities with a similarity exceeding a predefined threshold $\delta \in [0,1]$ are considered to be a match. This linking process can be represented as

$$\begin{array}{c}\mathrm{sim}(u_i,e_j)=\left(\mathrm{enc}\left(u_i\right),\mathrm{enc}\left(e_j\right)\right),u_i\in U,e_j\in E,\\ u_i\leftrightarrow e_j\mathrm{if}{e}_j=arg{\displaystyle \underset{e_k\in E}{max}}\mathrm{sim}(u_i,e_k)\mathrm{and}\mathrm{sim}(u_i,e_j)>\delta \end{array}$$

(10)

where $\delta \in [0,1]$ is the threshold hyperparameter. The same encoding model $\mathrm{enc}\left(·\right)$ is used to embed each entity, and $(\mathrm{enc}\left(u_i\right),\mathrm{enc}\left(e_j\right))$ represents the inner product between the extracted entity and the knowledge graph entity, facilitating the linking of graph entities. Ultimately, the set of matched entities is denoted as $EQ$.

3.3.3. Iterative Verification from Metapath to Knowledge Graph

After completing the aforementioned two interface functionalities and the design of a judgment function, the iterative framework is now capable of utilizing the described functions to identify all entities adjacent to the current entity that conform to the metapath, thereby completing a single iteration from the metapath to an entity within one hop.

Specifically, based on the judgment of the metapath, an iterative step must be implemented that can find all entities adjacent to the current entity and that match the metapath pattern. Suppose there is a metapath pattern $P=(e_0,r_1,e_1,r_2,e_2,\dots ,r_n,e_n)$, where $e_i$ denotes entity types and $r_i$ denotes relation types. The objective is to locate all entities adjacent to the current entity $e_{\mathrm{current}}$ that have a relationship with $e_{\mathrm{current}}$ consistent with a portion of the metapath P. The specific implementation is as follows:

• Determine the Current Entity and Metapath’s Current Position
  • Define a function capable of receiving the current entity $e_{\mathrm{current}}$ and the metapath P as inputs to ascertain the current position $(e,r)$ in the metapath. This position will guide how to search for adjacent entities that match the metapath pattern from the current entity.
  • The common encoder TransE [40] is employed to accomplish this step, encoding entities and relations into vectors and predicting relationships between entities through vector operations. TransE is a translation-based embedding model that maps entities and relations in a knowledge graph into a low-dimensional vector space. Specifically, for a triplet $(h,r,t)$, where h is the head entity, r is the relation, and t is the tail entity, TransE models the relationship as a translation from h to t via r. Here, h, r, and t are the vector representations of the head entity, relation, and tail entity, respectively.
  • Utilize the principle of the encoder to determine the current entity and the current position of the metapath. Encode the current entity $e_{\mathrm{current}}$ and the entity type e in the metapath into vectors. Then, also encode the relation type r in the metapath into a vector. In this way, adjacent entities that match the metapath can be predicted and searched through vector operations.
  • Let ${\mathbf{e}}_{\mathrm{current}}$ be the vector representation of the current entity $e_{\mathrm{current}}$, $\mathbf{e}$ be the vector representation of the entity type e in the metapath, and $\mathbf{r}$ be the vector representation of the relation type r. The current position in the metapath can be determined with the following formula:

    $$\begin{array}{c}{\mathbf{e}}_{\mathrm{current}}+\mathbf{r}\approx \mathbf{e}\end{array}$$

    (11)
• Extract Adjacent Entities
  • After determining the current entity and the current position of the metapath, the next step is to extract all adjacent entities of the current entity. This step is the core of the iterative framework, as it involves retrieving from the knowledge graph other entities directly connected to the current entity.
  • Let ${\mathbf{e}}_{\mathrm{current}}$ be the vector representation of the current entity, and $\mathbf{r}$ be the vector representation of the relation type. The adjacent entities can be predicted with the following formula:

    $$\begin{array}{c}{\mathbf{e}}_{\mathrm{neighbor}}\approx {\mathbf{e}}_{\mathrm{current}}+\mathbf{r}\end{array}$$

    (12)
• Judge Whether Adjacent Entities Conform to the Metapath
  • After extracting the adjacent entities, it is necessary to determine whether these entities conform to the metapath pattern. This step involves verifying each adjacent entity to ascertain whether they are connected to the current entity through the relationship defined in the metapath.
  • In this step, the adjacent entities can be compared with the next entity type in the metapath to determine if they match.
  • Let ${\mathbf{e}}_{\mathrm{neighbor}}$ be the vector representation of the adjacent entity, and ${\mathbf{e}}_{\mathrm{next}}$ be the vector representation of the next entity type in the metapath. The conformity of the adjacent entity to the metapath can be verified with the following formula:

    $$\mathrm{is}\_\mathrm{match}=\mathrm{calculate}\_\mathrm{similarity}({\mathbf{e}}_{\mathrm{neighbor}},{\mathbf{e}}_{\mathrm{next}})>\mathrm{threshold}$$

    (13)
• Update the Metapath and Current Entity
  • After verifying whether the adjacent entities conform to the metapath, the metapath and current entity need to be updated for the next iteration. The adjacent entity that conforms to the metapath is set as the new current entity, and the metapath is updated to the next segment.
  • Let ${\mathbf{e}}_{\mathrm{new}\_\mathrm{current}}$ be the vector representation of the new current entity, and $P^{\prime }$ be the updated metapath. The metapath and current entity can be updated with the following formula:

    $$\begin{array}{c}{\mathbf{e}}_{\mathrm{new}\_\mathrm{current}}={\mathbf{e}}_{\mathrm{matched}\_\mathrm{neighbor}}\\ P^{\prime }=(e_1,r_2,e_2,\dots ,r_n,e_n)\end{array}$$

    (14)
• Repeat Iteration Until Metapath Ends
  • After updating the metapath and current entity, the aforementioned process must be repeated until all parts of the metapath have been traversed, or until no adjacent entities conforming to the metapath can be found. The principle of the encoder is utilized to determine when to stop the iteration. For example, a maximum number of iterations can be set, or the iteration can be halted when no adjacent entities conforming to the metapath are identified.
  • Let ${\mathbf{e}}_{\mathrm{final}}$ be the vector representation of the final current entity, and $P_{\mathrm{final}}$ be the final metapath. The condition to stop the iteration can be determined with the following formula:

    $$\begin{array}{c}\mathrm{stop}\_\mathrm{iteration}=P_{\mathrm{final}}=\varnothing \vee \max \_\mathrm{iterations}\end{array}$$

    (15)
• Serialization
  • Finally, construct an output function to serialize the output. That is, extract all entities from the knowledge graph obtained at each step.
  • As mentioned earlier, the extracted output must be transformed into a textual sentence comprehensible to large language models. For information from the knowledge graph, directly concatenate them into a long sentence marked by specific separation and boundary delimiters. The commonly adopted pattern is the following: “Here is… This is most relevant to answering the question.” The purpose of this prompt is to guide the LLM to select useful evidence (denoted as [X]) from the linearized extracted information (denoted as [Y]) based on the question (denoted as [Q]). Specifically, [X] represents the evidence selected by the model, [Y] represents the linearized extracted information from the knowledge graph, and [Q] represents the user’s question. For the final answer, the pattern followed is “Based on the question, please generate [Z].” Here, [Z] denotes the target result or answer. The purpose of this prompt is to predict the target result ([Z]) given the question ([Q]) and the linearized extracted information ([Y]) to obtain an exact answer.

3.3.4. Iterative Pattern Framework

Based on the aforementioned functions, the iterative framework regards all entities similar to those mentioned in the metapath as the topic entity $e_T$ and assumes that it is connected to a specific entity on the knowledge graph. Starting from the topic entity, the iterative process is executed:

• Call the metapath ‘Extract_Meta_Path($e_T$)’ based on the topic entity to extract candidate one-hop metapath relationships.
• Based on the similarity $\mathrm{sim}(u_i,e_j)$ with query annotations $Q_i,H_i$, linearize them to form input prompts. Then, utilize the large language model to select a useful set of relations $\left\{r\right\}$ based on the question.
• Based on the set of relations $\left\{r\right\}$, call the ‘Extract_Triples($e_T$, $\left\{r\right\}$)’ interface to collect triplets related to the head entity $e_T$ and the set of relations, which are added to the topic entity set $\left\{e_T\right\}$.

The method will iteratively repeat the above steps to complete multi-hop reasoning tasks, stopping the iteration when all candidate metapath entities have been selected or when the model determines that there are no relations in the set $\left\{r\right\}$ that conform, and generate the final answer based on the sets $\left\{e_T\right\}$ and $\left\{r\right\}$. These chains of entities and relations are defined as the “reasoning chain”.

In summary, this process iteratively applies the metapath pattern to gradually explore entities and relationships in the knowledge graph, ultimately identifying all entities connected to the initial entity via the specific metapath. The overall iterative steps can be represented as in Algorithm 1,

Algorithm 1 Iterative Framework for MetaPath

1: Input: Initial entity $e_{\mathrm{initial}}$, Metapath P  2: $e_{\mathrm{current}}\leftarrow e_{\mathrm{initial}}$  3: $P_{\mathrm{current}}\leftarrow P$  4: while  $P_{\mathrm{current}}\ne \varnothing$  do  5:     U←Extract_Meta_Path$\left(e_{\mathrm{current}}\right)$                 ▹ Extract one-hop metapath relations  6:     $U_{\mathrm{matched}}\leftarrow \varnothing$  7:     for $u\in U$ do  8:         if VerifyNeighbor($u,P_{\mathrm{current}}.\mathrm{entity}\_\mathrm{type}$) then  9:            $U_{\mathrm{matched}}\leftarrow U_{\mathrm{matched}}\cup \left\{u\right\}$ 10:         end if 11:     end for 12:     if $U_{\mathrm{matched}}=\varnothing$ then 13:         break                                                           ▹ No matching neighbors found 14:     end if 15:     $(P_{\mathrm{current}},e_{\mathrm{current}})\leftarrow$UpdatePathAndEntity$(U_{\mathrm{matched}},P_{\mathrm{current}})$;     ▹ Update metapath and current entity 16: end while 17: Output: Final entity set $\left\{e_{\mathrm{current}}\right\}$ and relation set $\left\{r\right\}$;     ▹ Form the reasoning chain

3.4. Post-Reasoning Verification

As mentioned earlier, large language models typically cannot check on their own whether their reasoning processes are correct, which necessitates the use of external mechanisms for verification. To mitigate these shortcomings, the method also incorporates fact verification and fidelity verification during the iterative process to, respectively, estimate whether the generated reasoning chains exist and whether the reasoning conforms to the task semantics, thereby enhancing the authenticity and reliability of the answers.

3.4.1. Fact Verification

The purpose of fact verification is to determine whether all the final output triplets come from the knowledge graph, avoiding the generation of incorrect reasoning chains or the combination of erroneous triplets.

First, define a function $f_v\left(r_{ij}\right|s_{ij},o_{ij},K)$ to represent the factuality of each piece of evidence.

Based on the subject $s_{ij}$ and object $o_{ij}$, check whether the generated relation $r_{ij}$ indeed exists in the knowledge base K. If the triplet $(s_{ij},r_{ij},o_{ij})$ exists in K, then $f_v\left(r_{ij}\right|s_{ij},o_{ij},K)=1$; otherwise, it is 0.

If a reasoning chain is found to contain a triplet that does not exist in the knowledge graph, that chain will be pruned. This pruning process is automated and performed by a program designed to verify the existence of each triplet in the knowledge graph.

3.4.2. Fidelity Verification

Fidelity verification: According to the definition in previous related work, if the reasoning process of a model can be accurately represented by an explanation, it can be called faithful. It is difficult to verify fidelity in previous knowledge reasoning work because there is a lack of sufficient direct evidence from the knowledge graph to understand the relationships between the items being explained.

Therefore, the method proposes a fidelity verification approach to identify such cases. Specifically, given a test query ${\widehat{Q}}_i$, a list of evidence ${\widehat{T}}_i$, and the final answer ${\widehat{A}}_i$, they are directly concatenated into a new sequence ${\widehat{H}}_i^{\prime }$. A pre-built sentence encoder is used to calculate the similarity between ${\widehat{H}}_i$ and ${\widehat{H}}_i^{\prime }$. This function is represented as $f_u\left({\widehat{H}}_i\right|{\widehat{H}}_i^{\prime }=[{\widehat{Q}}_i;{\widehat{T}}_i;{\widehat{A}}_i])=\mathrm{SimCSE}({\widehat{H}}_i,{\widehat{H}}_i^{\prime })$. Finally, for each question ${\widehat{Q}}_i$, a score $C_i$ ($0<C_i<1$) can be obtained, which indicates the reliability of the theory to the answer:

$$C_i=\gamma f_v\left(s_{ij}\right|r_{ij},o_{ij},K)+(1-\gamma )f_u\left({\widehat{H}}_i\right|{\widehat{H}}_i^{\prime }=[{\widehat{Q}}_i;{\widehat{T}}_i;{\widehat{A}}_i])$$

where $0<\gamma <1$ is a balancing factor, set to 0.5 by default, and $|{\widehat{T}}_i|$ is the number of triplets.

4. Experimental Results

To thoroughly evaluate the reasoning capabilities of DKGM-path on various domain structured knowledge graph datasets, this section comprehensively assesses the performance of the DKGM-path method on two distinct tasks: (1) question answering with reasoning and (2) multi-hop reasoning. The details of the datasets are outlined in Section 4.1, with the experimental setup. Section 4.2 presents the experimental results and comparisons with baseline methods to demonstrate the effectiveness of the proposed approach.

4.1. Data Preparation

4.1.1. Data Preparation for Question Answering with Reasoning

The experiments utilized two benchmark datasets, namely WebQuestionsSP (WebQSP) and ComplexWebQuestions (CWQ), for evaluation. WebQSP is a dataset designed for knowledge-based question answering, containing 4737 questions with full semantic parses in SPARQL queries and partial annotations for another 1073 questions. This dataset is derived from WebQuestions and provides a rich resource for evaluating the semantic parsing and reasoning abilities of models. Then, the CWQ is an extension of WebQSP, specifically designed to assess the ability of question answering systems to handle complex, multi-hop reasoning tasks. The dataset contains 34,689 complex question instances, each accompanied by a SPARQL query and relevant webpage snippets. The questions in CWQ require models to perform multiple steps of reasoning, involving various combinations of operations such as conjunction, disjunction, comparison, and superlatives. This complexity makes CWQ a challenging benchmark for evaluating advanced reasoning capabilities in question answering systems. The detailed data are presented in

Table 1. The benchmark datasets for question answering with reasoning.

Dataset	Total Question	Training	Testing
WebQSP	4737	3780	957
CWQ	34,689	27,734	3475

.

4.1.2. Data Preparation for Multi-Hop Reasoning

The experiments were conducted using two benchmark datasets, HOTPOT-QA and MUSIQUE, for evaluation. HOTPOT-QA is a large-scale, multi-hop question answering dataset constructed by researchers from Harvard University and Stanford University. It comprises approximately 100,000 questions that require information from at least two Wikipedia article paragraphs to answer. The HOTPOT-QA dataset is divided into two parts: bridge-type fact questions and comparison-type fact questions. The bridge-type questions require the model to aggregate information from different documents, while comparison-type questions necessitate the model to compare different aspects of two entities or events. The MUSIQUE dataset is a multi-hop reasoning dataset designed for complex question answering tasks, containing 25,000 questions that require two to four reasoning steps. The MUSIQUE dataset does not provide annotations for relevant sentences but offers supporting paragraph titles, question decomposition (breaking down multi-hop questions into simpler one-hop sub-questions), and intermediate answers for decomposed questions. This diversity makes MUSIQUE a more challenging multi-hop question answering dataset, requiring the model to not only find the correct answers but also understand the structure and reasoning path of the questions.

4.1.3. Data Preprocessing

The quality and consistency of data are crucial for the reasoning capabilities of knowledge graphs. To ensure the effectiveness and accuracy of the input data, we implemented preprocessing and cleansing procedures in our methodology. For input query texts, we designed a preprocessing pipeline to transform them into structured template forms. This process includes the following:

• Converting the query into a predefined template: “Here is the query……Please generate the initial nodes relevant to the query purpose”.
• Utilizing a small automatic verification program to check whether the generated triplets exist in the knowledge graph. This verification process is iterative, ensuring the accuracy of the initial nodes.
• During each hop of the iterative reasoning, the query results are transformed into the form “Here is… This is most relevant to answering the question.” to guide the model in finding the next relevant node.
• At the final answer generation stage, all relevant information is summarized and transformed into the template “Based on the question, please generate [Z].” to consolidate the results of all metapaths and obtain the final answer.
• The purpose of this preprocessing step is to structure natural language queries into clear templates, thereby enhancing the accuracy and efficiency of LLMs in the reasoning process.

4.2. Results and Analysis

4.2.1. Results for Reasoning Question Answering Task

Table 2. The results for question answering with reasoning task.

Methods	WebQSP		CWQ
	F1	Hits@1	F1	Hits@1
KV-Mem	34.5 ± 1.2	46.7 ± 1.5	15.7 ± 0.8	21.1 ± 1.0
Graft-Net	62.8 ± 1.0	67.8 ± 1.2	32.7 ± 1.5	36.8 ± 1.3
Topic Units	67.9 ± 0.9	68.2 ± 1.1	36.5 ± 1.4	39.3 ± 1.2
EmbedKGQA	-	66.6 ± 1.1	-	44.7 ± 1.3
NSM	68.7 ± 1.0	74.3 ± 1.2	44.0 ± 1.5	48.8 ± 1.3
UniKGQA	72.2 ± 0.8	77.2 ± 1.0	49.4 ± 1.4	51.2 ± 1.2
TextRay	60.3 ± 1.2	72.2 ± 1.3	33.9 ± 1.4	40.8 ± 1.5
DKGM-path	77.6 ± 0.7	78.4 ± 0.9	70.9 ± 1.0	72.2 ± 1.1

presents the comparative results of the DKGM-path method against various baseline models that have been fine-tuned with data supervision. The selected baseline models for comparison include KV-Mem [41], GraphNet [42], EmbedKGQA [43], and UniKGQA [26]. These models were chosen based on their established performance in the domain of question answering and their relevance to the tasks addressed by DKGM-path.The evaluation metrics used include F1 and Hits@1. F1 is the harmonic mean of precision and recall, measuring the balance between the two and providing an overall indication of the model’s accuracy in identifying relevant answers. Hits@1, on the other hand, measures the proportion of times the correct answer is ranked first among the model’s predictions, reflecting the model’s ability to prioritize the most accurate response.

In Table 2, our DKGM-path method demonstrates superior performance in reasoning question answering tasks, achieving an F1 score of 77.6% and Hits@1 of 78.4% on the WebQSP dataset, and an F1 score of 70.9% and Hits@1 of 72.2% on the CWQ dataset. These results highlight the robustness and effectiveness of our approach in handling complex question answering with reasoning task.

We compared DKGM-path against a variety of methods, categorizing them into memory-based models (KV-Mem, Graft-Net, Topic Units), embedding-based models (EmbedKGQA), and unified reasoning models (NSM, UniKGQA, TextRay). EmbedKGQA, an embedding-based model, achieved a Hits@1 of 66.6% on WebQSP and 44.7% on CWQ, showing better performance than memory-based models, such as KV-Mem, Graft-Net, and Topic Units, but still falling short compared to DKGM-path. Unified reasoning models like NSM, UniKGQA, and TextRay demonstrated stronger performance, with UniKGQA achieving the highest scores among them (F1: 72.2%, Hits@1: 77.2% on WebQSP; F1: 49.4%, Hits@1: 51.2% on CWQ). However, DKGM-path outperformed all these models, showcasing its advanced capabilities in aggregating and comparing information from different sources and effectively handling complex question answering with reasoning task.

To further evaluate the performance of our DKGM-path method, we introduced an additional baseline method for comparison. This baseline method utilized the original model (e.g., Llama2-7b) in a zero-shot manner to complete the aforementioned tasks. To ensure a fair comparison with the DKGM-path method, the same instructions used in the DKGM-path method were employed for this baseline method. The only difference was that the DKGM-path method had the capability to query structured knowledge graph data. In solving the extracted questions, we followed existing work and used the method of prompting the model to solve the problems, without utilizing a knowledge graph or applying any special processing to the questions.

Table 3. Comparison with baseline on reasoning question answering datasets.

Methods	WebQSP		CWQ
	F1	Hits@1	F1	Hits@1
Llama2-7b	61.8 ± 1.3	72.6 ± 1.4	64.0 ± 1.5	65.1 ± 1.6
DKGM-path	77.6 ± 0.7	78.4 ± 0.9	70.9 ± 1.0	72.2 ± 1.1

presents the comparative results.

It can be observed that, despite the original model achieving commendable results without additional domain-specific knowledge graphs, the method proposed in this chapter significantly enhances the accuracy and efficiency of reasoning by integrating the structured domain-specific information from knowledge graphs.

To further validate the effectiveness of our DKGM-path method, we conducted statistical significance tests comparing its performance against the baseline methods. The results indicate that the performance gains of DKGM-path over other baselines are statistically significant, with $p<0.05$ for both the WebQSP and CWQ datasets. This demonstrates the robustness and effectiveness of our approach in handling complex reasoning question answering tasks.

4.2.2. Results on Medical Domain Dataset

To further demonstrate the generalizability of our DKGM-path method, we conducted additional experiments on a medical domain dataset, namely Mediacalqa, obtained from the OpenKG platform. This dataset is specifically designed for concept-based question answering in the medical field and contains a rich set of medical entities and relations.

As shown in

Table 4. Comparison with baseline on medical domain dataset.

Methods	Mediacalqa
	F1	Hits@1
TextRay	48.5 ± 1.2	52.3 ± 1.3
NSM	54.2 ± 1.4	57.4 ± 1.4
Graft-Net	52.1 ± 1.0	55.3 ± 0.7
UniKGQA	58.4 ± 1.2	61.2 ± 1.0
DKGM-path	62.3 ± 1.3	65.4 ± 0.9

, DKGM-path significantly outperformed other baseline methods. This demonstrates the strong generalizability of our method to domain-specific knowledge graphs, even in the medical field where domain knowledge is highly specialized and complex.

4.2.3. Results for Multi-Hop Reasoning Task

Table 5. The results for the multi-hop reasoning task.

Methods	HotpotQA			MuSiQue
	Overall	Bridge	Comp.	Overall	2-Hop	3-Hop	4-Hop
Self-Ask	49.4 ± 1.2	45.3 ± 1.3	68.6 ± 1.5	16.2 ± 0.8	24.4 ± 1.0	8.8 ± 0.9	7.5 ± 0.8
IRCoT	56.2 ± 1.1	53.4 ± 1.2	69.6 ± 1.4	24.9 ± 1.0	31.4 ± 1.1	19.2 ± 1.2	16.4 ± 1.3
FLARE	56.1 ± 1.0	54.2 ± 1.1	64.4 ± 1.3	31.9 ± 1.2	40.9 ± 1.3	27.1 ± 1.4	15.0 ± 1.2
ProbTree	60.4 ± 0.9	59.2 ± 1.0	65.9 ± 1.2	32.9 ± 1.1	41.2 ± 1.2	30.9 ± 1.3	14.4 ± 1.1
DKGM-path	61.9 ± 0.8	60.7 ± 0.9	69.3 ± 1.0	33.8 ± 1.1	41.4 ± 1.2	29.1 ± 1.3	18.3 ± 1.2

presents the comparison results of our DKGM-path method with various baseline models for multi-hop reasoning tasks. Multi-hop reasoning employs four retrieval-enhanced methods similar to the DKGM-path method as baseline methods for comparison, including IRCoT[174], FLARE[175], ProbTree[176], and Self-Ask[177]. IRCoT alternates between retrieval-enhanced reasoning and reasoning-enhanced retrieval until the retrieved information is sufficient to answer the question. FLARE dynamically adjusts the timing of retrieval based on the confidence of reasoning and retrieves according to the upcoming reasoning sentences. ProbTree parses the question into a tree structure and uses logarithmic probability-based sub-problem aggregation to obtain the final answer. Self-Ask interleaves retrieval with the generation of subsequent sub-problems by triggering retrieval-enhanced generation before generating the next sub-problem.

Comparative experimental results show that, in terms of overall performance, DKGM-path outperforms Self-Ask, IRCoT, FLARE, and ProbTree on all datasets, only slightly lagging behind on a few sub-datasets such as Comp. This indicates that DKGM-path has a high accuracy in handling complex reasoning tasks. The mixed model of DKGM-path, which models the overall semantics and prompts reasoning, may be more effective in understanding the deep structure of questions and reasoning paths, and the step-by-step guidance of reasoning result generation may help generate more accurate reasoning paths, thereby improving overall performance.

On the Bridge sub-dataset, DKGM-path scored as high as 60.7. This may be because the reasoning paths involved in the Bridge dataset are relatively straightforward, and DKGM-path excels in capturing the semantics of direct reasoning paths. In contrast, although ProbTree performed best in the subsequent three-hop tasks, its performance on the Bridge dataset was not as good as that of DKGM-path, which may be because ProbTree’s tree-structured parsing method is not as effective as the mixed model in dealing with direct reasoning paths.

On the Comp. sub-dataset, DKGM-path’s performance was only slightly inferior to IRCoT, which may be attributed to IRCoT’s more effective alternation between retrieval-enhanced reasoning and reasoning-enhanced retrieval. IRCoT, through this dynamic retrieval and reasoning method, can more accurately locate and utilize relevant information to answer questions.

Overall, DKGM-path outperforms several state-of-the-art methods in multi-hop reasoning tasks, particularly in handling multiple reasoning steps. For instance, it achieves higher performance in two-hop and three-hop reasoning tasks compared to methods like Self-Ask, IRCoT, and FLARE. However, it is important to note that the performance gains are not uniformly significant across all sub-datasets. Statistical significance tests indicate that the improvements of DKGM-path over other baselines are statistically significant in most cases, with $p<0.05$, except for the Comparison sub-dataset, where the difference is marginal. This highlights the robustness of our approach in complex reasoning tasks while acknowledging areas for further improvement.

As shown in Figure 3, the performance changes of DKGM-path and the baseline methods on different reasoning hop numbers can be seen. It can be seen that the performance on multi-step reasoning tasks such as two-hop and three-hop tasks is better than that of IRCoT, indicating that DKGM-path may be more effective in dealing with multi-step reasoning. Only in the three-hop task, ProbTree is slightly better. This may be because ProbTree parses the problem into a tree structure and uses logarithmic probability-based sub-problem aggregation to improve accuracy in multi-hop reasoning tasks. However, in the subsequent four-hop reasoning task, DKGM-path’s performance is again better, indicating that DKGM-path’s step-by-step guidance of reasoning result generation can better maintain the coherence and accuracy of reasoning when dealing with more steps of reasoning. Statistical significance tests indicate that the improvements of DKGM-path over other baselines are statistically significant in most cases, with $p<0.05$, except for the Comparison sub-dataset, where the difference is marginal. This highlights the robustness of our approach in complex reasoning tasks while acknowledging areas for further improvement.

Overall, the performance of DKGM-path across multiple datasets demonstrates its effectiveness in understanding and generating reasoning paths. This validates that its hybrid model and prompt-based learning approach play a crucial role in capturing the semantics of reasoning paths and generating accurate reasoning results.

4.2.4. Ablation Studies

To further understand the contributions of each key component in the proposed DKGM-path method, we conducted an ablation study. The DKGM-path method integrates several critical components, including Metapath Construction (MPC), Iterative Verification (IV), and Post-Reasoning Checks (PRCs). Each of these components plays a unique role in enhancing the reasoning process over domain-specific knowledge graphs. By systematically removing each component and evaluating the performance, we can quantify their individual impacts on the overall reasoning capabilities of our method. We performed the ablation study on two benchmark datasets: WebQSP and CWQ. These datasets are widely used for evaluating question answering and reasoning capabilities. For each experiment, we removed one of the key components from the full model and measured the performance in terms of F1 score and Hits@1. The results are summarized in

Table 6. The results for question answering with reasoning task.

Methods	WebQSP		CWQ
	F1	Hits@1	F1	Hits@1
Full Model	77.6	78.4	70.9	72.2
w/o MPC	69.3	70.1	62.5	63.8
w/o IV	72.1	73.5	66.7	68.3
w/o PRC	74.8	75.6	68.9	70.1

.

• Metapath Construction (MPC): The metapath construction component is responsible for initializing the reasoning paths based on zero-shot prompts. Removing this component resulted in a significant drop in performance on both WebQSP (F1: 69.3) and CWQ (F1: 62.5). This indicates that metapath construction is crucial for guiding the model to focus on relevant entities and relationships, thereby improving the overall reasoning accuracy.
• Iterative Verification (IV): The iterative verification component ensures that the reasoning paths are refined and validated at each step. When this component was removed, the performance decreased to 72.1 on WebQSP F1 and 66.7 on CWQ F1. This suggests that iterative verification plays a vital role in refining the reasoning paths and ensuring their validity, especially in complex multi-hop reasoning tasks.
• Post-Reasoning Checks (PRCs): The post-reasoning checks, including fact verification and fidelity verification, ensure the reliability of the final reasoning results. Removing this component led to a moderate decline in performance (WebQSP F1: 74.8; CWQ F1: 68.9). This highlights the importance of post-reasoning checks in eliminating errors and hallucinations, thereby enhancing the robustness of the reasoning process.

The ablation study demonstrates that each component of the DKGM-path method contributes significantly to its overall performance. The metapath construction initializes the reasoning process effectively, iterative verification ensures the accuracy of reasoning paths, and post-reasoning checks enhance the reliability of the final results. The full model, with all components integrated, achieves the best performance, highlighting the synergistic effect of these components in enhancing domain-specific knowledge graph reasoning.

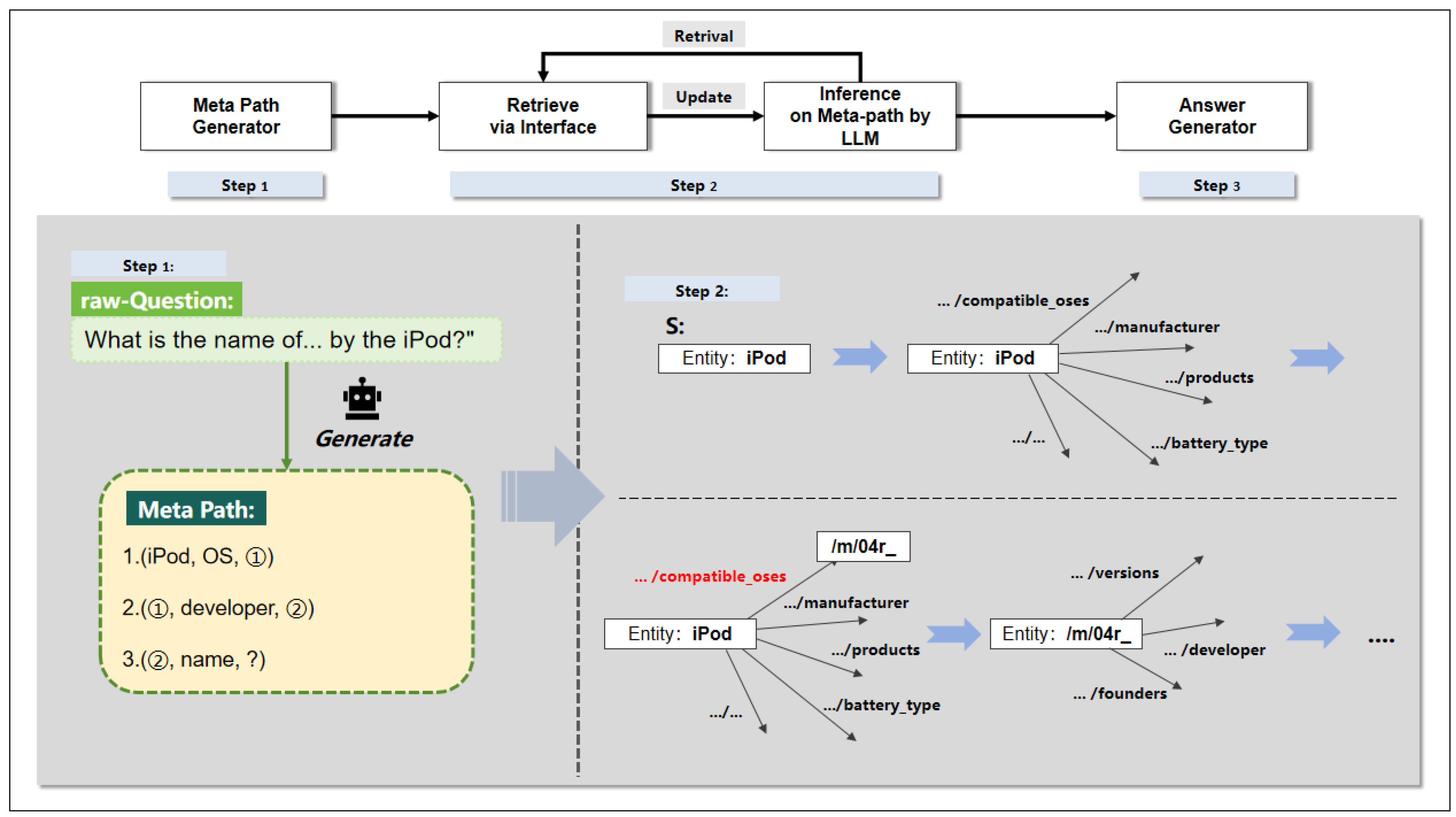
4.2.5. Case Study

To further parse and validate the working process of the DKGM-path method, we extracted a set of actual data from the dataset for the experimentation, verification, and demonstration of the intrinsic mechanisms of DKGM-path’s knowledge reasoning method. This also helped to showcase the interpretability of the methods presented in this section. The experiment randomly selected an example from the WebQSP dataset as a representative. In this case study, for a given question in the WebQSP dataset, three main parts need to be focused on: “rawQuestion”, which is the question to be answered; “sparql”, the SPARQL query annotated for the question, used to retrieve answers from the knowledge base; and “answer”, the annotated answer. We instructed DKGM-path to output intermediate states and answers, dissecting the process of how the method parses and answers a question. Figure 4 illustrates the basic process of generating metapath triples and step-by-step reasoning toward the answer in this case.

The basic process of this case study can be parsed as follows: Initially, the question “rawQuestion” is processed through a zero-shot prompting method, generating a metapath composed of a series of triples by the large model. This metapath determines the starting reasoning entity “iPod”, and through a knowledge graph retriever based on interfaces, the closest homonymous or similar entity iPod (MID: /m/02hrh0) to the reasoning entity is found. Subsequently, all adjacent entities and relationships of this entity are retrieved.

Then, the model will perform the following iterative steps:

• Prompt the model to judge all adjacent relationships based on the metapath, determining the most likely next-hop relationship that meets the metapath requirements, which is /computer/hardware_device/compatible_oses here. If there are multiple relationships that meet the conditions, multiple next-hop relationships will be obtained simultaneously.
• Move the starting point of the retriever to entity /m/02hrh0 according to the selected relationship, update the prompt template of the large model to reflect the current information obtained, and temporarily shield the effective metapath.
• Retrieve all adjacent relationships of entity /m/02hrh0 through the interface to obtain the next-hop relationship candidate list (the adjacent list of /m/02hrh0 is omitted here).
• Continue to update the prompt template of the large model and the metapath, and retrieve all adjacent relationships of entity /m/02hrh0 through the interface to obtain the next-hop relationship candidate list.
• Continuously perform iterative steps (1)–(4) until the judgment function determines that the current hop result can answer the question or all adjacent relationships cannot meet the conditions.
• Serialize all passed entities, connect them with the question, input them into the large language model, and output the final answer.

Ultimately, the case underwent three entity updates, as shown below. These updates were guided by the reasoning process, ultimately obtaining the correct answer:

• From entity /m/02hrh0 (iPod) to /m/04r_ (Mac OS) based on the relationship /computer/hardware_device/compatible_oses;
• From /m/04r_ (Mac OS) to /m/0k8z (Apple Inc.) based on the relationship /software/operating_system/developer;
• Finally, from /m/0k8z (Apple Inc.) to its name “Apple Inc.” based on the relationship /organization/name.

4.2.6. Prompt Study

Additionally, to further verify DKGM-path’s ability to construct and utilize prompts in multi-hop reasoning and to eliminate the interference brought by the large model’s own reasoning performance, following the relevant previous work, the experiment also used three different prompting methods for the reasoning control experiments, including the following:

• Direct Prompting: Prompting a large language model to directly predict the answer.
• Chain-of-Thought Prompting (CoT Prompting): Prompting a large language model to generate step-by-step explanations before providing the answer.
• One-step Retrieval (OneR): Enhancing chain-of-thought prompting by retrieving K paragraphs using the original complex question as a query. The retrieval method provided the large model with a paragraph retriever based on BM, retrieving the K highest-ranked paragraphs as reasoning context, where K was selected from 3, 5, 7. A comparison of the results from different prompts is shown in

  Table 7. Comparison of the effects of different prompting methods and DKGM-path in muti-hop reasoning.

  Methods	HotpotQA			MuSiQue
  	Overall	Bridge	Comp.	Overall	2-Hop	3-Hop	4-Hop
  Direct Promp.	38.9	37.5	45.3	15.6	16.4	16.2	12.6
  CoT Promp.	46.5	44.6	55.5	24.7	30.2	22.5	13.2
  OneR	55.3	52.9	66.5	16.4	22.1	10.6	10.4
  DKGM-path	61.9	60.7	69.3	33.8	41.4	29.1	18.3

  .

It can be observed that our DKGM-path method demonstrates significantly superior performance compared to more direct or simple retrieval-based prompting learning methods. This evidence supports the effectiveness of our proposed multi-step prompting and reasoning approach on structured knowledge graphs for multi-hop reasoning tasks. By comparing with these baseline methods, we can more accurately assess the validity of our proposed approach.

5. Discussion and Conclusions

The proposed domain knowledge graph reasoning method based on a large model prompt learning metapath (DKGM-path) has made significant strides in structured knowledge graph reasoning across various domains by integrating metapaths with multi-step iterative prompt learning for large language models. Traditional knowledge graph reasoning methods often struggle to stably acquire domain knowledge from knowledge graphs or ensure the reliability and interpretability of the knowledge due to the limitations and sparsity differences in the semantic space of knowledge graph reasoning tasks. DKGM-path addresses these limitations by introducing metapaths and constructing multi-step iterative prompts, thereby generating robust and interpretable reasoning process representations that can reliably acquire domain knowledge.

A key innovation of DKGM-path lies in its construction of metapaths and multi-step iterative prompts. Utilizing metapaths, DKGM-path can decompose complex reasoning tasks into a series of simpler sub-tasks, thereby reducing the difficulty of reasoning. Meanwhile, the multi-step iterative prompts enable the model to obtain the latest information in each step of reasoning, thereby improving the accuracy and reliability of reasoning. In addition, DKGM-path further ensures the accuracy and interpretability of reasoning results through means such as fact verification and loyalty verification.

Another important feature of DKGM-path is its full utilization of the structure of knowledge graphs. Through metapaths, the model can better understand and utilize the relationships and entities in knowledge graphs, thereby improving the depth and breadth of reasoning. In addition, DKGM-path also enables the model to dynamically interact with knowledge graphs through iterative prompts, thereby improving the flexibility and adaptability of reasoning.

However, DKGM-path also has some limitations. First, its multi-step iterative prompts may introduce certain computational complexity, which may limit its application in scenarios with high real-time requirements. Second, DKGM-path has certain dependencies on the quality and integrity of knowledge graphs. If there are errors or omissions in the knowledge graph, it may affect the accuracy of reasoning results. In addition, DKGM-path may face certain challenges when dealing with large-scale or dynamically evolving datasets, and further research is needed to explore how to expand its application scope.

Future research directions may include simplifying multi-step iterative prompts to reduce computational complexity; improving the construction and updating methods of knowledge graphs to enhance their quality and integrity; exploring distributed or online learning paradigms to expand the application of DKGM-path in large-scale or dynamically evolving datasets; and studying how to apply DKGM-path to cross-domain generalization problems to further improve its adaptability and generalizability. In summary, DKGM-path has made significant progress in structured knowledge graph reasoning by combining metapaths with multi-step iterative prompt learning for large language models, providing a solid foundation for future research.

6. Future Work

The DKGM-path method has shown remarkable potential in enhancing domain-specific knowledge graph reasoning with LLMs through the integration of structured knowledge graphs. Nevertheless, there are still several directions for future research that can further optimize the efficiency, scalability, and applicability of this approach.

DKGM-path is specifically designed to offer a framework that enables the combination of LLMs with domain-specific knowledge graphs, with the aim of facilitating automated reasoning based on domain knowledge. As it focuses on complex reasoning tasks within domain-specific contexts, its main priority lies in achieving high accuracy and interpretability rather than real-time performance. However, it should be noted that in some particular scenarios, for example, when it comes to the automated monitoring of relevant domain data, the capability of real-time processing may turn out to be a crucial factor that needs to be taken into account and improved in the future development of this method.

To address the computational overhead introduced by the multi-step iterative prompting strategy, future work will explore advanced model compression and optimization techniques. This includes investigating knowledge distillation methods to transfer the reasoning capabilities of large language models to smaller, more efficient architectures. Additionally, quantization and pruning techniques can be applied to reduce the model size and computational requirements while maintaining performance. These approaches will enable DKGM-path to be deployed in resource-constrained environments and improve its real-time capabilities.