Few-Shot Learning with Multimodal Fusion for Efficient Cloud–Edge Collaborative Communication
Abstract
1. Introduction
- We propose a novel framework that integrates few-shot learning with multimodal data fusion to achieve robust beam selection under data-limited conditions. By leveraging complementary features from RGB images, radar signals, and LiDAR data, the model effectively captures spatiotemporal features, enabling efficient and adaptive communication.
- The multimodal fusion approach enhances the model’s robustness against environmental variability and noise. By combining few-shot learning with multimodal inputs, the proposed method can quickly adapt to new scenarios, maintaining high accuracy in dynamic communication environments.
- By reducing the dependence on large-scale labeled datasets, the proposed framework optimizes computational efficiency, enabling real-time beam selection and satisfying the low-latency requirements of mmWave communication systems.
2. Related Works
2.1. Beam Selection Methods
2.2. Multimodal Fusion
2.3. Few-Shot Learning
3. System Model
3.1. Problem Formulation
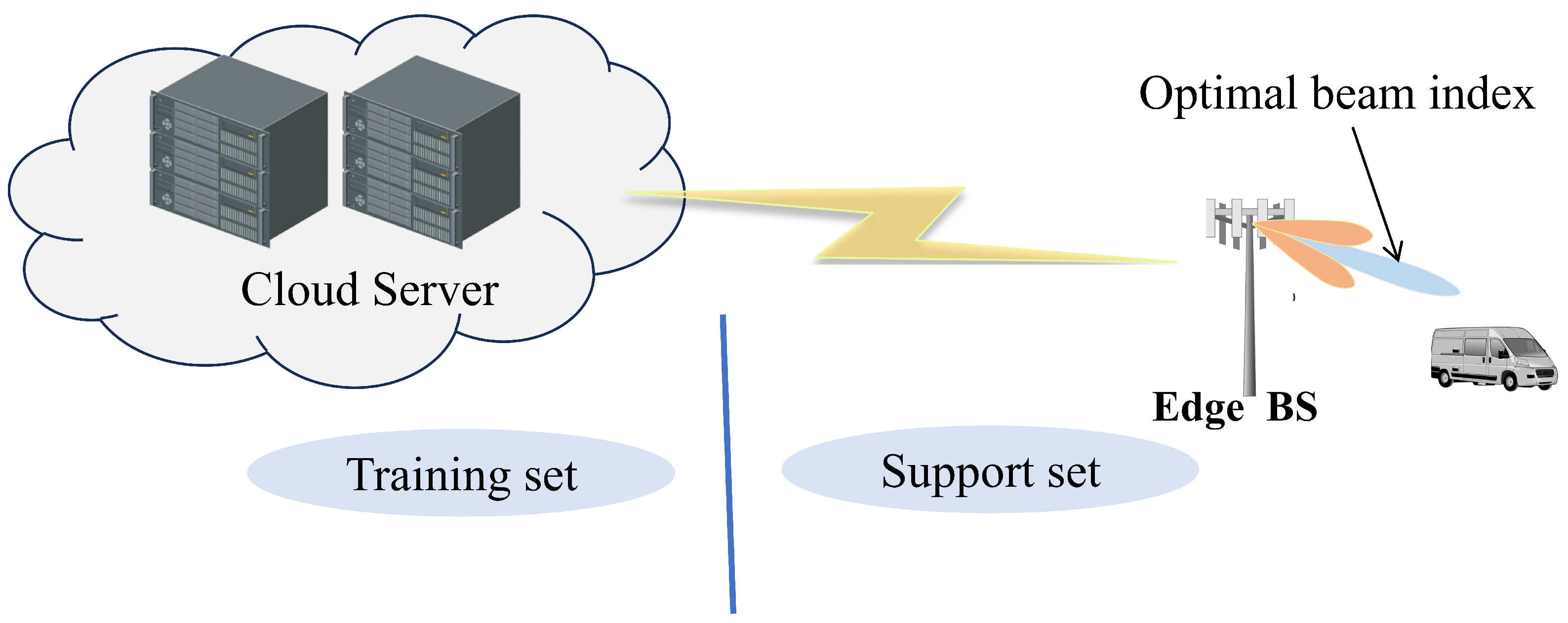
3.2. Cloud–Edge Collaboration Framework
3.2.1. Multimodal Input Layer
3.2.2. CNN for Feature Extraction
3.2.3. Transformer Module for Multimodal Fusion
3.2.4. Few-Shot Learning Module
3.2.5. Beam Selection Layer
3.2.6. Cloud–Edge Collaboration Mechanism
- Cloud Training Phase: The cloud server trains the multimodal fusion model and the relation network on the global dataset to generate a pre-trained model.
- Edge Inference Phase: The edge node receives the pre-trained model from the cloud and uses it to compare local test samples against the support set, determining the most suitable beam codeword for the given scenario.
3.3. Training and Optimization
Optimization of the Few-Shot Component
| Algorithm 1: Training procedure of C-way one-shot |
 |
4. Experiments and Discussion
4.1. Dataset and Settings
- mmWave Receiver: The system incorporates a 60 GHz phased array receiver equipped with a 16-element Uniform Linear Array (ULA), and the half-power beamwidth is 5°. This receiver supports a 64-beam codebook, enabling adaptive beamforming. It dynamically selects the optimal beam for communication, with the system outputting a 64-element vector that corresponds to the receiver power at each beam. This setup enables detailed 3D radar measurements, capturing essential information about the communication environment.
- Radar System: The radar used in the system is a FMCW radar. It features three transmit (Tx) antennas and four receive (Rx) antennas, operating within a frequency range of 76–81 GHz. The radar has a 4 GHz bandwidth, allowing a maximum range of approximately 100 m with a range resolution of 60 cm. The radar collects 3D complex I/Q radar measurements, which are stored in the format 4 × 256 × 128 (number of Rx antennas × samples per chirp × chirps per frame), providing rich environmental data for beam prediction.
- LiDAR: A LiDAR system is also employed for data collection, with a range of up to 40 m and a resolution of 3 cm. It features a 360° field of view (FoV) and provides point cloud sampling data. These data are crucial for detailed environmental mapping, thereby enhancing the overall dataset for beam prediction tasks.
4.2. Performance Evaluation
4.2.1. Impact of Different Transformer Modules on Beam Prediction Accuracy
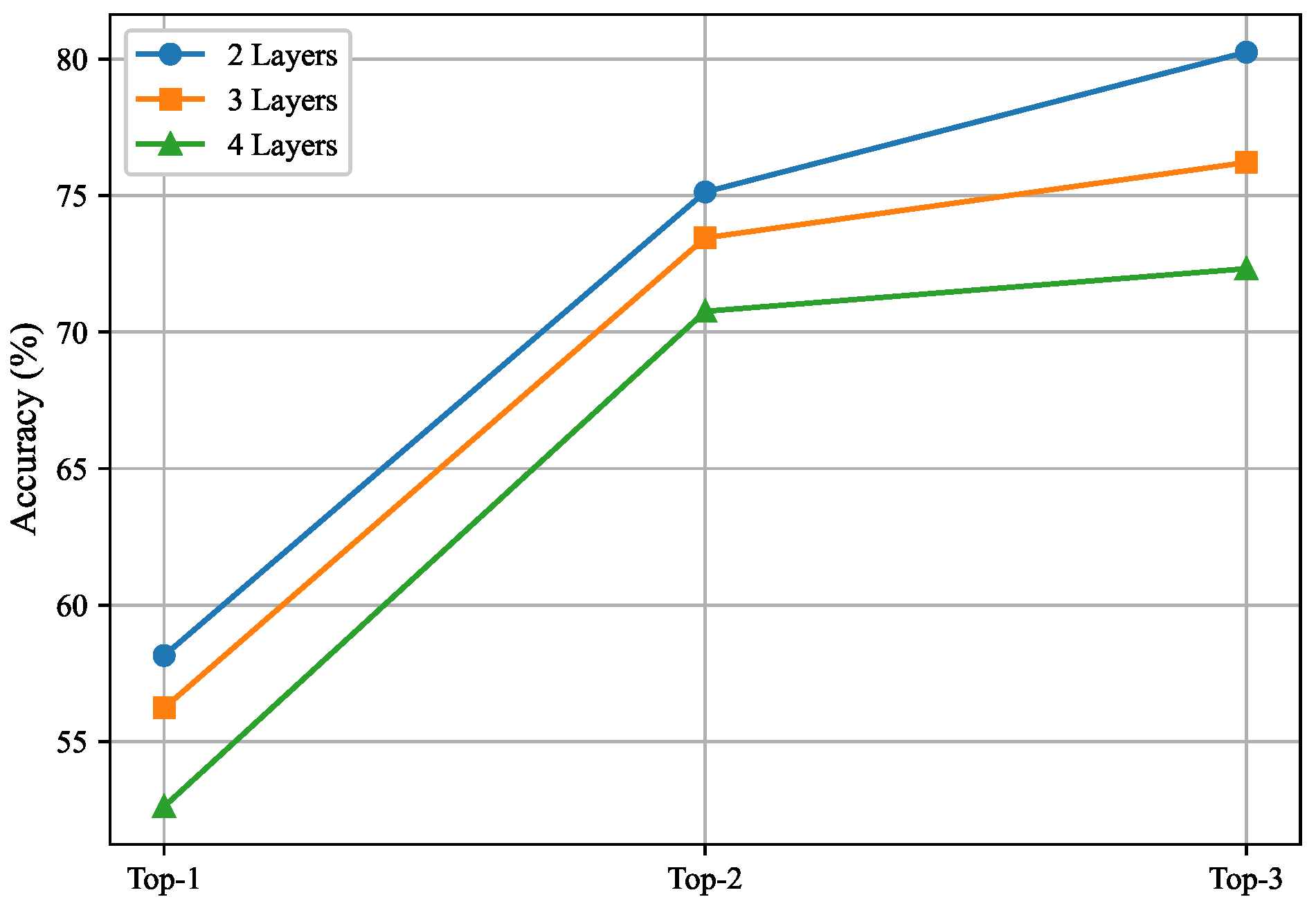
4.2.2. Impact of Convolutional Layer Count on Beam Prediction Accuracy
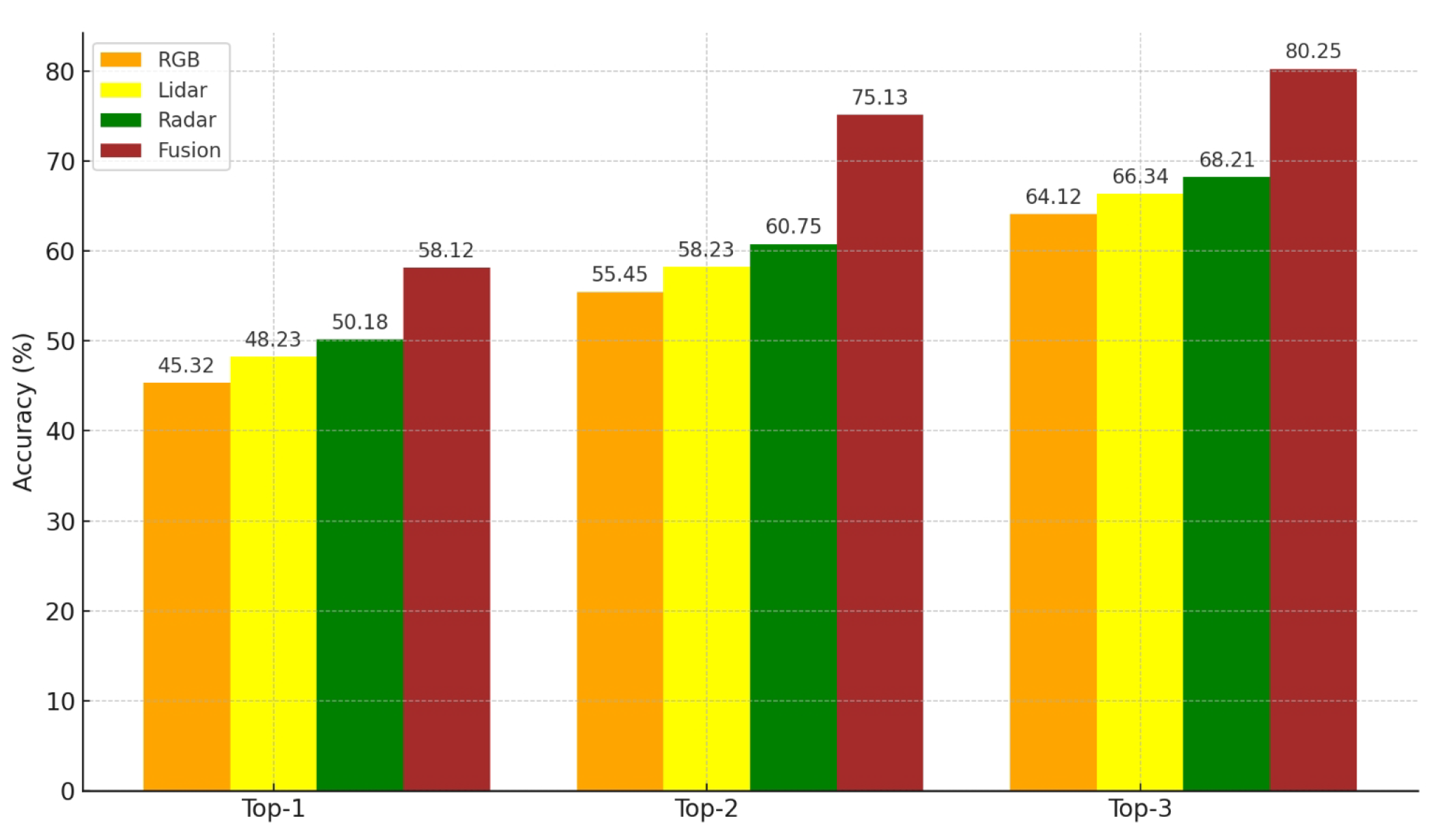
4.2.3. Impact of Multimodal Fusion on Beam Prediction Accuracy
4.2.4. Comparison
- Meta-SGD: Learns both the initial parameters and learning rates for each parameter, allowing the model to quickly adapt to new tasks. It is well suited for highly customized few-shot tasks.
- MAML: Optimizes the initial parameters so that the model can quickly adapt with few updates under few-shot conditions, making it adaptable to different model architectures.
- Fine-Tuning: Involves pre-training a model on a large dataset and then fine-tuning it on the target few-shot task. It performs best when the target task has similar characteristics to the source dataset.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Du, J.; Yuan, X.; Zhang, K. Differential Privacy-Based Location Privacy Protection for Edge Computing Networks. Electronics 2024, 13, 3510. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Pi, Z.; Khan, F. An introduction to millimeter-wave mobile broadband systems. IEEE Commun. Mag. 2011, 49, 101–107. [Google Scholar] [CrossRef]
- Roh, W.; Seol, J.Y.; Park, J.; Lee, B.; Lee, J.; Kim, Y.; Cho, J.; Cheun, K.; Aryanfar, F. Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results. IEEE Commun. Mag. 2014, 52, 106–113. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Heath, R.W.; Daniels, R.C.; Murdock, J.N. Wireless Communications: Principles and Practice; Pearson Education: New York, NY, USA, 2014. [Google Scholar]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Zhang, C. An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Leus, G.; Heath, R.W. Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Kaur, J.; Khan, M.A.; Iftikhar, M.; Imran, M.; Haq, Q.E.U. Machine learning techniques for 5G and beyond. IEEE Access 2021, 9, 23472–23488. [Google Scholar] [CrossRef]
- Fernando, N.; Shrestha, S.; Loke, S.W.; Lee, K. On Edge-Fog-Cloud Collaboration and Reaping Its Benefits: A Heterogeneous Multi-Tier Edge Computing Architecture. Future Internet 2025, 17, 22. [Google Scholar] [CrossRef]
- Ju, Y.; Cao, Z.; Chen, Y.; Liu, L.; Pei, Q.; Mumtaz, S. NOMA-Assisted Secure Offloading for Vehicular Edge Computing Networks with Asynchronous Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2627–2640. [Google Scholar] [CrossRef]
- Van Anh Duong, D.; Akter, S.; Yoon, S. Task Offloading and Resource Allocation for Augmented Reality Applications in UAV-Based Networks Using a Dual Network Architecture. Electronics 2024, 13, 3590. [Google Scholar] [CrossRef]
- Zhang, Y.; Osman, T.; Alkhateeb, A. Online beam learning with interference nulling for millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2024, 23, 5109–5124. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V. A deep learning approach for hybrid beamforming in multi-cluster millimeter-wave MIMO. IEEE Trans. Veh. Technol. 2019, 68, 4132–4141. [Google Scholar] [CrossRef]
- Dokhanchi, S.H.; Mysore, B.S.; Mishra, K.V.; Ottersten, B. A mmWave automotive joint radar-communications system. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1241–1260. [Google Scholar] [CrossRef]
- Elsanhoury, M.; Zhang, Y.; Farooq, M.U.; Otoum, Y. Precision positioning for smart logistics using ultra-wideband technology-based indoor navigation: A review. IEEE Access 2022, 10, 44413–44445. [Google Scholar] [CrossRef]
- Cheng, J.; Hao, F.; He, F.; Liu, L.; Zhang, Q. Mixer-based semantic spread for few-shot learning. IEEE Trans. Multimed. 2023, 25, 191–202. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 4077–4087. [Google Scholar]
- Sun, S.; Rappaport, T.S.; Heath, R.W., Jr.; Nix, A.; Rangan, S. Beamforming for millimeter-wave communications: An overview. IEEE Commun. Mag. 2018, 56, 124–131. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, W.; Wang, W.; Yang, L.; Zhang, W. Research challenges and opportunities of UAV millimeter-wave communications. IEEE Wirel. Commun. 2019, 26, 58–62. [Google Scholar] [CrossRef]
- Lim, S.H.; Kim, S.; Shim, B.; Choi, J.W. Deep learning-based beam tracking for millimeter-wave communications under mobility. IEEE Trans. Commun. 2021, 69, 7458–7469. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Charan, G.; Osman, T.; Hredzak, A.; Srinivas, N. DeepMIMO: A generic dataset for mmWave and massive MIMO applications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- González-Prelcic, J.; González-Prelcic, N.; Venugopal, K.; Heath, R.W. Channel Estimation and Hybrid Precoding for Frequency Selective Multiuser mmWave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2018, 12, 353–367. [Google Scholar] [CrossRef]
- Giordani, M.; Polese, M.; Roy, A.; Castor, D.; Zorzi, M. A tutorial on beam management for 3GPP NR at mmWave frequencies. IEEE Commun. Surv. Tutor. 2018, 21, 173–196. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Y.; Jin, D.; Su, L.; Vasilakos, A.V. A survey of millimeter wave communications (mmWave) for 5G: Opportunities and challenges. Wirel. Netw. 2015, 21, 2657–2676. [Google Scholar] [CrossRef]
- Zhou, Q.; Gong, Y.; Nallanathan, A. Radar-Aided Beam Selection in MIMO Communication Systems: A Federated Transfer Learning Approach. IEEE Trans. Veh. Technol. 2024, 73, 12172–12177. [Google Scholar] [CrossRef]
- Hur, S.; Kim, T.; Love, D.J.; Vook, J.; Ghosh, A. Millimeter wave beamforming for wireless backhaul and access in small cell networks. IEEE Trans. Commun. 2013, 61, 4391–4403. [Google Scholar] [CrossRef]
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A.Y. Multimodal deep learning. In Proceedings of the 28th International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011; pp. 689–696. [Google Scholar]
- Baltrušaitis, T.; Ahuja, C.; Morency, L. Multimodal machine learning: A survey and taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Stephen, K.; Sabitha, A.S. A systematic review on sensor fusion technology in autonomous vehicles. In Proceedings of the 2023 4th International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 20–21 July 2023; pp. 42–48. [Google Scholar] [CrossRef]
- Martin-Vega, F.J.; Aguayo-Torres, M.C.; Gomez, G.; Entrambasaguas, J.T.; Duong, T.Q. Key technologies, modeling approaches, and challenges for millimeter-wave vehicular communications. IEEE Commun. Mag. 2018, 56, 28–35. [Google Scholar] [CrossRef]
- Atrey, P.K.; Hossain, M.A.; El Saddik, A.; Kankanhalli, M.S. Multimodal fusion for multimedia analysis: A survey. Multimed. Syst. 2010, 16, 345–379. [Google Scholar] [CrossRef]
- Ramachandram, D.; Taylor, G.W. Deep multimodal learning: A survey on recent advances and trends. IEEE Signal Process. Mag. 2017, 34, 96–108. [Google Scholar] [CrossRef]
- Calhoun, V.D.; Adali, T. Feature-based fusion of medical imaging data. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-SGD: Learning to learn quickly for few-shot learning. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 3681–3691. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montréal, QC, Canada, 8 December 2014; pp. 3320–3328. [Google Scholar]




| Module | Input Size | Output Size |
|---|---|---|
| Image Enh. and Segmentation | ||
| Point Cloud Filtering | ||
| Angle + Speed FFT | ||
| Embedding Layer | ||
| 3D Module 1 | ||
| 3D Module 2 | ||
| Transformer Layer | ||
| 3D Module 3 | ||
| Transformer Layer | ||
| Pooling Layer | ||
| Summation Operation | 512 | |
| Feature Extraction Module | Test Data | - |
| Feature Sharing Module | Support Data | - |
| Concatenate Layer | 1024 | |
| FC Layer 1 | 1024 | 512 |
| FC Layer 2 | 512 | 256 |
| FC Layer 3 | 256 | 128 |
| FC Layer 4 | 128 | 32 |
| Relation Score | 32 | 1 (Scalar) |
| Parameter | Assignment |
|---|---|
| Training set | Scenarios 31, 32, 33, 34 |
| Support set | Scenarios 31, 32, 33, 34 |
| Test set | Scenarios 31, 32, 33, 34 |
| Number of samples | 120,000 |
| Number of support samples | One-shot: 1 × C, Q-shot: |
| C-way classification | 32 classes |
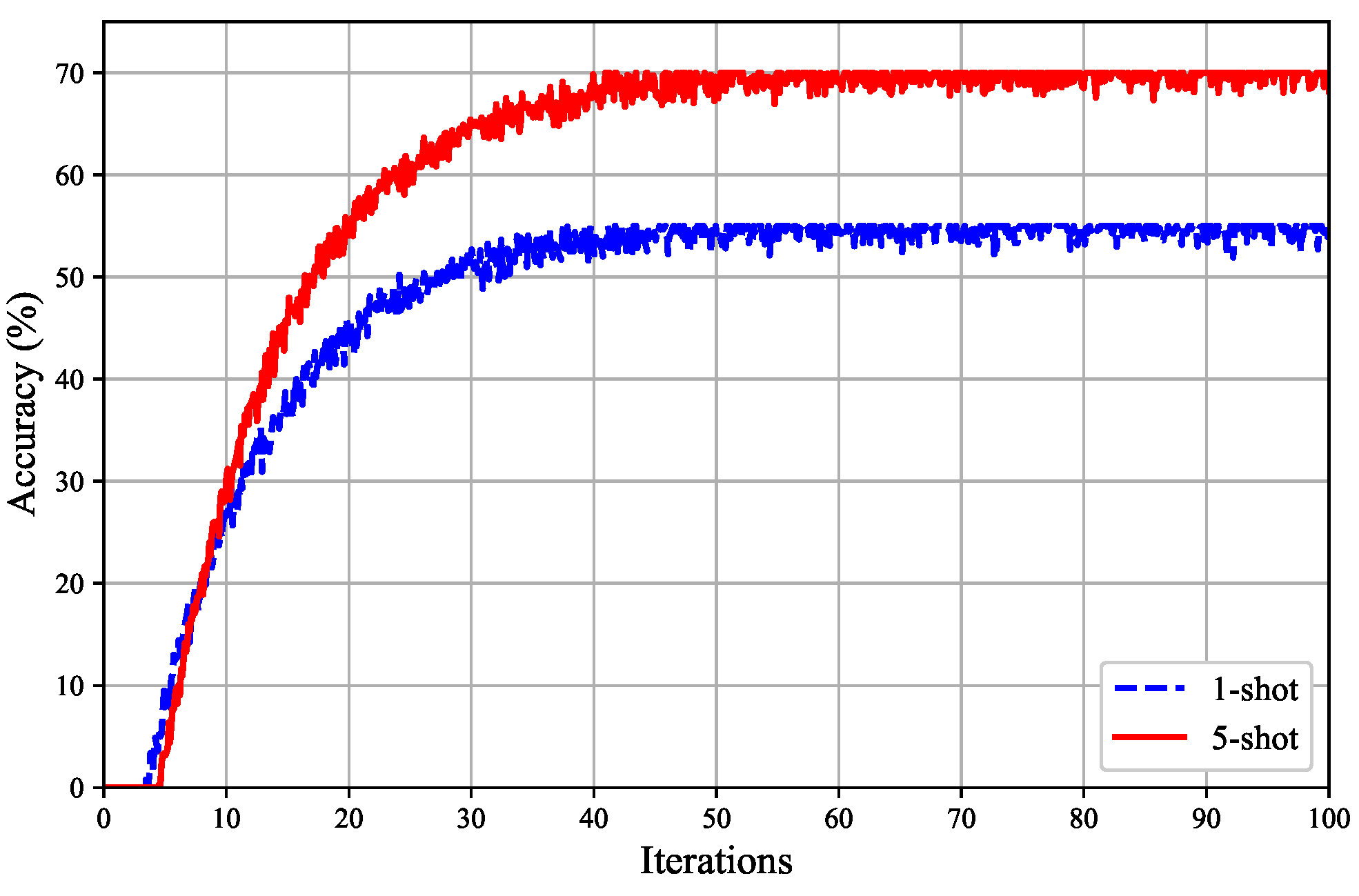
| Few-shot configurations | 1-shot, 5-shot |
| Input data dimensions |
| Algorithm | Time Complexity | Space Complexity | Convergence Speed | Scalability |
|---|---|---|---|---|
| Meta-SGD | Fast | Moderate | ||
| MAML | Moderate, task-dependent | Medium, affected by task count | ||
| Fine-Tuning | Slower | High, adaptable to various tasks | ||
| Relation Networks | Moderate | Moderate, adaptable to metric-based tasks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Liu, X.; Zhou, Q. Few-Shot Learning with Multimodal Fusion for Efficient Cloud–Edge Collaborative Communication. Electronics 2025, 14, 804. https://doi.org/10.3390/electronics14040804
Gao B, Liu X, Zhou Q. Few-Shot Learning with Multimodal Fusion for Efficient Cloud–Edge Collaborative Communication. Electronics. 2025; 14(4):804. https://doi.org/10.3390/electronics14040804
Chicago/Turabian StyleGao, Bo, Xing Liu, and Quan Zhou. 2025. "Few-Shot Learning with Multimodal Fusion for Efficient Cloud–Edge Collaborative Communication" Electronics 14, no. 4: 804. https://doi.org/10.3390/electronics14040804
APA StyleGao, B., Liu, X., & Zhou, Q. (2025). Few-Shot Learning with Multimodal Fusion for Efficient Cloud–Edge Collaborative Communication. Electronics, 14(4), 804. https://doi.org/10.3390/electronics14040804





