Elastic Balancing of Communication Efficiency and Performance in Federated Learning with Staged Clustering

Abstract

Clustered federated learning has garnered significant attention as an effective strategy for enhancing model performance in non-independent and identically distributed (non-IID) data scenarios. This approach improves model performance in such environments by calculating the similarity between users and clustering them into multiple groups. However, several challenges arise when implementing this method, particularly in balancing flexibility, communication costs, and model performance. To address these issues, this paper proposes a novel hierarchical federated learning framework that balances both network and model performance. The framework performs principal component analysis (PCA) on device-side image datasets to assess the similarity of private data across devices and, in conjunction with network performance measurements, dynamically adjusts communication strategies to minimize latency while ensuring stable model performance. By weighting similarity and communication metrics, the framework optimizes communication efficiency without significantly compromising model performance. To validate the proposed method’s effectiveness, we employed three publicly available datasets and compared it against four baseline methods. The experimental results demonstrate that SC-Fed (segmented clustering-federated learning) achieves a maximum accuracy improvement of 7.56% over baseline methods, while also reducing the average waiting time by 54.6%. These results indicate that the proposed algorithm significantly enhances the applicability and efficiency of clustered federated learning in practical training scenarios.

1. Introduction

In modern data-intensive fields such as computer vision [1,2], financial quantification [3], and power dispatching [4], federated learning stands out as a pivotal technological framework [5]. The primary advantage of federated learning is its ability to facilitate cross-institutional data sharing, thereby enhancing model generalization while preserving data privacy during collaborative processes [6,7,8]. Nonetheless, practical implementations of federated learning encounter the challenge of data heterogeneity [9,10,11,12] across clients. This heterogeneity encompasses notable variations in network resources, computing power, and data quality. To address these differences, federated learning algorithms must be crafted to strike a balance between resource limitations and performance metrics, which include communication overhead, computational efficiency, and prediction accuracy of the models. Specifically, these algorithms should be designed to optimize communication costs and computation time without compromising model performance, thereby accommodating the diverse resource conditions of various clients. To address these disparities, FL algorithms need to be designed to achieve a balance between resource constraints and performance metrics, which include but are not limited to communication overhead, computational efficiency, and model prediction accuracy. Specifically, FL algorithms must optimize communication costs and computation time, while ensuring model performance, to adapt to the resource conditions of different clients.

Clustered federated learning [13,14,15,16] has been demonstrated as an effective approach for managing non-independent and identically distributed (non-IID) data [17,18,19,20]. By clustering users based on their characteristics, this method allows devices with similar features to train within the same cluster, effectively adapting to the heterogeneity in computing and communication resources. Most current research focuses on optimizing single performance metrics, utilizing diverse model segmentation schemes and user selection strategies [21,22,23,24]. However, under multifactor conditions, existing federated learning algorithms lack quantitative and theoretical modeling of various metrics, making it challenging to balance model performance, communication efficiency, and privacy security [25,26,27,28].

The clustered federated learning problem in this context can be formulated as an optimization problem, with particular emphasis on balancing computational time and model performance [29,30]. An excessive number of clusters can reduce the flexibility of users within a cluster, while too few clusters may lead to improper partitioning of device data, adversely affecting model performance. This paper presents a theoretical model and designs an efficient and flexible clustered federated learning framework [31]. The framework ensures an elastic trade-off between model performance and training efficiency, enabling the determination of an optimal user grouping strategy within a limited time frame, thereby maintaining effectiveness in real-world federated learning environments.

Building on the federated clustered learning (FCL) framework [32,33,34], this paper introduces an enhanced federated learning approach that balances model performance with network communication capabilities. This approach utilizes a hierarchical clustering method for initial classification based on the data characteristics of user devices, aiming to mitigate the effects of non-IID data. Moreover, it incorporates an active selection strategy to balance communication and computation times, and adjusts batch sizes to ensure the fairness and effectiveness of user data in training [35,36,37,38]. Experimental results indicate that this method reaches the upper performance limit of the model more quickly and significantly reduces overall model training time compared to other federated learning baseline methods [5]. Specifically, the main contributions of our approach are as follows:

• By employing theoretical modeling that encompasses various factors such as non-IID data, network conditions, and computing resources, we have designed a simulation theoretical framework grounded in FCL.
• Building on clustered federated learning, this paper introduces a flexible hierarchical clustering-based federated learning method that optimizes the average training time per round without significantly impacting model accuracy. The method dynamically adjusts cluster weights based on an elastic weighting factor, adaptively balancing model performance and training efficiency, thereby ensuring the flexibility required for real-world federated learning applications.
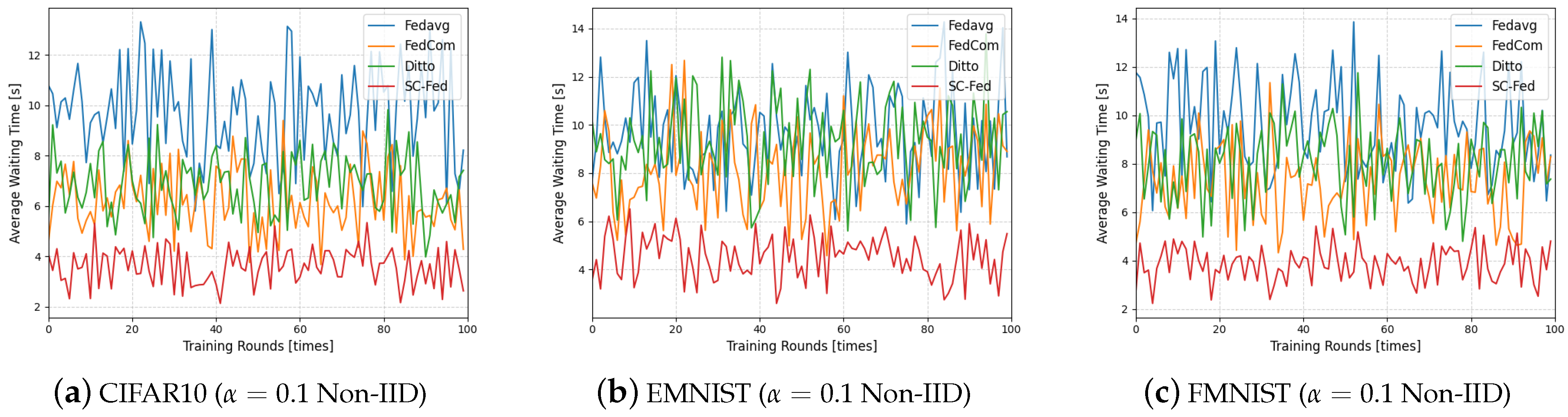
• Based on the theoretical framework and algorithm, this paper conducts comparative experiments with four baseline algorithms on three datasets. The experimental results demonstrate that our algorithm achieves higher model performance within the same time frame, while significantly reducing the average waiting time per training round.

The structure of the remaining sections of this paper is as follows: Section 2 presents an overview of existing methods. Section 3 provides a mathematical formulation of the hierarchical federated clustering algorithm in the non-IID scenario. Section 4 introduces our proposed solution, which balances communication efficiency and model accuracy. Section 5 validates the effectiveness of the method through experiments and compares it with several baseline algorithms. Section 6 summarizes the main contributions of the paper.

2. Related Work

While federated learning can address the issue of user data leakage during model training, the effectiveness of the training is closely tied to the distribution of user datasets. When user data is highly non-IID, the resulting model accuracy can be significantly compromised. To tackle this issue, researchers have proposed various methods such as FedAvg [39], FedProx [40], and SCAFFOLD [41]. Additionally, clustered federated learning (CFL) has also been shown to be an effective approach for addressing the challenges posed by non-IID data distributions.

Additionally, the computational and communication capabilities of user devices constrain model training, leading to a pronounced lag effect when resources are unevenly distributed. Many studies have addressed this issue by employing model compression techniques to adapt to the computational and communication capacities of individual user devices, thereby mitigating the lag effect. Notable examples include HeteroFL and FLANC, which aim to optimize training efficiency by tailoring models to the specific resource constraints of each device.

2.1. Personalized Federated Learning

Non-IID federated learning (FL) tackles the challenge of statistical heterogeneity across clients. The FedAvg algorithm [39], which employs a three-step protocol for federated training, often encounters issues such as client drift and slow convergence on non-IID data [42]. To address these, algorithms like FedProx [40] and FedDANE [43] have been developed. FedProx incorporates a proximal term in the local loss function to mitigate model heterogeneity, while FedDANE employs a federated Newton-type optimization method, adapting traditional distributed optimization for federated learning [44].

SCAFFOLD [41] and LFD [45] represent further advancements in addressing heterogeneity. SCAFFOLD aims to control variance and correct client update drift, and LFD extends stochastic full gradient descent with periodic averaging to manage non-convex optimization challenges in federated learning environments [46].

CFL [47] introduces a dynamic clustering approach, grouping clients based on the cosine similarity of their updates, which can enhance performance in diverse settings. In contrast, the IFCA algorithm [48] utilizes a fixed number of clusters, requiring clients to download all model options each round and select the best based on local accuracy.

2.2. Device Resources

Mobile and IoT devices are increasingly becoming the main computing resources for billions of users globally. These devices produce significant amounts of data that can be used to improve various applications [49]. With their growing computational power, the volume of locally stored data also rises. To ensure data privacy, FL is crucial for model training. FL [39,50] is a distributed machine learning framework that creates a global model by aggregating locally trained parameters without sharing local data. Addressing the diverse and dynamic computational and communication capabilities of heterogeneous clients is essential in this context.

However, the distribution of computational and communication resources among user devices is often uneven. Mobile devices [51], for example, have fewer resources compared to computers or servers, which have significantly more resources. Traditional FL involves sending local models with the same architecture as the global model to users for training, and then aggregating these local models on the server to form a single global model. In this approach, devices with varying resources receive identical local models for training. Due to the significant differences in computational resources, this can result in noticeable lag and decreased training efficiency.

To address the heterogeneity of user devices, Diao proposed HeteroFL [52], which adapts to varying computational and communication capacities by splitting the global model into several sub-models of different sizes. These heterogeneous local models enable local clients to contribute adaptively to the training of the global model, effectively addressing system heterogeneity and improving communication efficiency. Building on this, Mei introduced the FLANC algorithm [53], which employs low-rank decomposition to transform the model into two low-rank matrices, further reducing the resources required for model transmission by only transmitting these matrices instead of the entire model architecture.

3. Problem Statement

The set of clients is denoted as $\mathcal{C}=\{c_1,c_2,\dots ,c_N\}$, managed by a central server. Each client $c_i\in \mathcal{C}$ possesses its local dataset ${\mathcal{D}}_i={\left\{{\eta }_j\right\}}_{j=1}^{\left|{\mathcal{D}}_i\right|}$, where ${\eta }_j$ represents a data sample from ${\mathcal{D}}_i$. The loss function $\mathcal{L}(\theta ;\eta )$ evaluates the performance of the model $\theta$ on a data sample $\eta$. Therefore, the expected value of the loss function $\mathcal{L}(\theta ;\eta )$ over the data distribution ${\mathcal{D}}_i$ of client $c_i$ is defined as Equation (1):

$${\mathcal{F}}_D\left(\theta \right)={\mathbb{E}}_{\eta \sim {\mathcal{D}}_i}\left[\mathcal{L}(\theta ;\eta )\right]$$

(1)

For the global model, the loss function is a linear combination of the local loss functions of all $\mathcal{N}$ clients. The objective of FL is to train a high-quality model ${\theta }^{★}$ by minimizing the global loss function, which is defined as Equation (2):

$${\theta }^{★}:=\arg \underset{\theta }{min}\mathcal{F}\left(\theta \right)=\arg \underset{\theta }{min}\left({\displaystyle \frac{1}{\mathcal{N}}}\sum _{c=1}^{\mathcal{N}}{\mathcal{F}}_c\left(\theta \right)\right)$$

(2)

However, not all users participate in training in each round of federated learning. Suppose there are a total of H rounds of training. In each training round $h\in \{1,2,\dots ,H\}$, the parameter server (PS) randomly selects a subset of clients ${\mathcal{K}}_h\subseteq \mathcal{K}$ to participate in the training, where $|{\mathcal{K}}_h|=k$. The PS then sends the current global model ${\theta }_h$ to the selected clients. Each client $n\in {\mathcal{K}}_h$ updates the global model ${\theta }_h$ over its local dataset ${\mathcal{D}}_n$ for T iterations, with each update constituting one local iteration and T representing the local update frequency. Let ${\theta }_{(i,h)}^{\left(t\right)}$ denote the local model of client i at iteration t in round h. For the mini-batch stochastic gradient descent (SGD) algorithm, a local iteration can be expressed as Equation (3):

$${\theta }_h^{(t+1)}={\theta }_h^{\left(t\right)}-\lambda {\mathcal{F}}_c\left({\theta }_{(i,h)}^{\left(t\right)}\right)$$

(3)

where $\lambda$ is the learning rate. Finally, the PS collects the gradients from the participating clients and aggregates them into the latest global model for further training, as expressed by Equation (4):

$${\theta }_{h+1}={\displaystyle \frac{1}{|{\mathcal{K}}_h|}}\sum _{i\in {\mathcal{K}}_h}{\theta }_{(i,h)}^{\left(t\right)}$$

(4)

As shown in Equation (5), to obtain the characteristics of user datasets, this paper uses principal component analysis (PCA) for dimensionality reduction to acquire the main information vectors r $S_i=\{v_1,\dots ,v_r\}$. The experiment uses cosine distance to measure the similarity between user data.

$$M_{ij}=arccos\left({\displaystyle \frac{{\mathcal{S}}^i·{\mathcal{S}}^j}{\parallel {\mathcal{S}}^i\parallel \parallel {\mathcal{S}}^j\parallel }}\right)$$

(5)

Assuming there are n users in cluster i, the average cosine distance $M_i$ of this cluster is the average of the distances between each pair of these n users.

Evidently, an idealized federated learning system is not well suited for real-world environments. The heterogeneity of user devices, including variations in network conditions and computational capabilities, can impact the efficiency of FL training. Therefore, it is imperative to incorporate system performance parameters into the model. Assuming that the resources consumed for one local training iteration of the model are G and the computational capability of the client i is $u_i$, the time required for one local iteration in round h for the client i is given by Equation (6):

$$t_i^h={\displaystyle \frac{G\left({\theta }_i^h\right)}{u_i^h}}$$

(6)

In practical network environments, download bandwidth is typically significantly higher than upload bandwidth. Therefore, the time required to download the model is usually negligible, whereas the time required to upload the model is more significant. Let $b_i$ denote the upload bandwidth of user i, and let $P_i^h$ represent the model size of client i in round h. Consequently, the communication time for client i in round h can be expressed as Equation (7):

$$y_i^h={\displaystyle \frac{P_i^h}{b_i^h}}$$

(7)

Let ${\tau }_i^h$ denote the update frequency of client i in round h. A round of parameter updates requires ${\tau }_i^h$ instances of local training and one data upload. The total time for each user to complete a round of parameter updates is defined as Equation (8):

$$T_i^h={\tau }_i^h{t}_i^h+y_i^h$$

(8)

In a given training round, assume there are n users in the cluster $C_i$ and their update frequency is $\{{\tau }_1^h,\dots ,{\tau }_n^h\}$. For users participating in a round of model training, their average waiting time after completing the model training is calculated by Equation (9):

$${\mathcal{W}}_i={\displaystyle \frac{1}{n}}\sum _{i=1}^n(T_{\max }-{\tau }_i^h·y_i^h-t_i^h)$$

(9)

$$T_{\max }=\underset{i=1}{\overset{n}{max}}({\tau }_i^h·y_i^h+t_i^h)$$

Based on Equations (5) and (9), we have adopted a method grounded in Pareto optimality theory, with the goal of simultaneously minimizing the average cosine distance M and the average waiting time $\mathcal{W}$ among users. As shown in Equation (10), we have constructed a multi-objective optimization model to seek the optimal solution by reasonably clustering users.

$$\underset{\theta \in \mathbb{R}}{min}(w_1\mathcal{M}+w_2\mathcal{W})$$

(10)

$$\mathrm{st}.\left\{\begin{array}{c}{w}_1\gg w_2\hfill \\ {\mathcal{T}}^h\ge 0\hfill \\ {\mathcal{F}}_D\left(\theta \right)\ge 0\hfill \end{array}\right.$$

4. Overview and Implementation

In this chapter, we will introduce the algorithm content of this paper in three sections. The first section provides an overview of the algorithm, the second section details the algorithm process, and the third section presents the pseudocode of the algorithm.

4.1. Overview

The overall process of SC-Fed is illustrated in Figure 1, which consists of two main parts: the model training on the client side and the model aggregation on the server side, as detailed below.

To mitigate the adverse impact of highly non-IID data on model performance, this study employs an innovative approach: utilizing PCA to extract key features from client data and constructing feature matrices. By calculating the cosine similarity between feature matrices, we can quantify the similarity of client data and cluster clients based on these similarities.

Moreover, the experiment must account for the lag effect in model training caused by the heterogeneity of client resources. Clients with ample resources may experience prolonged idle times while waiting for resource-constrained clients, thereby affecting overall training efficiency. To address this issue, this paper proposes a client resource modeling method. By modeling each client’s resource status, the server can allocate appropriate update frequencies, balancing the model training time across clients and thereby reducing the average waiting time.

4.2. Model Training Process

Feature vector extraction based on PCA is a reliable and effective method. PCA performs coordinate transformation on matrix data, enabling dimensionality reduction of image matrices without loss, identifying the largest set of linearly independent vectors. Specifically, for a set of image data arranged row-wise, PCA can extract the r most representative principal component vectors, encapsulating the distribution and features of the images. By calculating the cosine similarity, the maximum similarity value between vectors can be obtained, constructing a similarity matrix. Based on matrix analysis, the optimal classification set $S=\{s_1,\dots ,s_k\}$ for any number of clusters k can be determined, where s is a set constructed from any number of c. This method aids in secondary clustering of subsequent system performance parameters.

To allocate an appropriate update frequency for each client, it is necessary to provide the server with information on the client’s computing and transmission resources. First, clients measure their network transmission rate using network measurement methods and determine their computing power by querying the local CPU and GPU usage. Second, clients upload their local computing and transmission resource data to the server. The server will calculate the model training frequency for client i in the current round based on the objective function described in Section 3, and determine the estimated completion time $m_i$ for the corresponding client. However, the data uploaded by the clients to the server may not be entirely accurate, and the clients’ computing resources $u_i$ and transmission resources $b_i$ are dynamically changing. It is necessary for the server to adjust the relevant data of the clients accordingly.

4.3. Implementation and Algorithm Description

As shown in Algorithm 1, for each user, use PCA to extract the top k principal component vectors $S_i$ from the user’s data $D_i$, and transmit them to the server (stp. 1). Measure the similarity between user data features $S_i$ using cosine distance and construct a similarity matrix M (stp. 2). Each user uploads their communication resource $b_i$ and computation resource $u_i$ to the server (stp. 3). Determine the optimal clustering $O_p$ based on the similarity matrix M, communication resource $b_i$, and computation resource $u_i$ (stp. 4). In each training round, clients train their models based on the update frequency (stp. 5). At the end of each training round, the server collects client models for aggregation (stp. 6).

Algorithm 1 PCA-based clustering algorithm with resource optimization

Require: Initial Model Parameters ${\theta }_0$, Learning Rate $\lambda$, Communication Rounds T, Number of Principal Components r, Clustering Number k 1: for each client $c_i$, $i\in \{1,2,\dots ,n\}$ do 2:       $S_i\leftarrow PCA(D_i,r)$ // Extract the main features of client data 3:       $Server\leftarrow S_i,u_i,b_i$ // Upload $S_i$, $b_i$ and $u_i$ to the server 4: end for 5: $M_{ij}={\displaystyle \frac{S_i·S_j}{\parallel S_i\parallel \parallel S_j\parallel }}$ // Calculate cosine similarity matrix 6: $O_p\leftarrow M_{ij},u_i,b_i$ // Obtain clustering groups $O_p$. 7: Parallel for each client clustering group $O_p$ 8: for $e\leftarrow 0$ to $T-1$ do 9:       $S_i\leftarrow PCA(D_i,r)$ // Extract the main features of client data 10:       $Client:{\theta }_h^{(t+1)}={\theta }_h^{\left(t\right)}-\lambda {\mathcal{F}}_c\left({\theta }_{(i,h)}^{\left(t\right)}\right)$ // Update model parameters ${\widehat{\theta }}_n\left(t\right)$ 11:       $Server:{\theta }_{h+1}={\displaystyle \frac{1}{|{\mathcal{K}}_h|}}{\sum }_{i\in {\mathcal{K}}_h}{\theta }_{(i,h)}^{\left(t\right)}$ //Model Aggregation 12:  end for 13:  end parallel

4.4. Datasets and Settings

This research focuses on image classification using the Fashion-MNIST [54], CIFAR-10 [55], and EMNIST [56] datasets to evaluate the proposed approach. Non-IID distributions are simulated by varying the Dirichlet distribution parameter ($\alpha =0.1$, $\alpha =1$, $\alpha =10$) with 100 users. PCA is employed to reduce the dimensionality of user datasets and extract key features. After validation, the number of principal components is set to three to balance information retention and computational efficiency.

This research focuses on image classification using the Fashion-MNIST [54], CIFAR-10 [55], and EMNIST [56] datasets to evaluate the proposed approach. Non-IID distributions are simulated by varying the Dirichlet distribution parameter ($\alpha =0.1$, $\alpha =1$, $\alpha =10$) with 100 users. Here, smaller $\alpha$ values increase data heterogeneity and non-IID nature, while larger $\alpha$ values make the distribution more uniform and closer to IID. PCA is employed to reduce the dimensionality of user datasets and extract key features. After validation, the number of principal components is set to three to balance information retention and computational efficiency.

To assess the efficacy of our SC-Fed method against state-of-the-art approaches, we conducted comparisons with various benchmark models. In scenarios involving a unified global model trained across all clients, we chose FedAvg [39] and Solo as our baselines. For more sophisticated personalization in federated learning, we compared our method against Ditto [57] and FedCom [58].

5. Experiment

In our experiments, we configured a setup with 20 users and varied the data distribution skew using the Dirichlet distribution with concentration parameters $\alpha =0.1$, $\alpha =1$, and $\alpha =10$ to simulate different levels of non-IID data. For all experiments, we used a gradient batch size of 128 and employed stochastic gradient descent (SGD) as the optimizer for local training.

We have evaluated SC-Fed against the aforementioned state-of-the-art benchmarks under the prevalent non-IID conditions characterized by Dirichlet label distribution. These conditions are designed to assess the resilience of the algorithms in scenarios involving data augmentation. We have documented the results from five experimental runs that cover both the validation precision of the ultimate user models across each dataset and the mean of these precisions.

As shown in

Table 1. Algorithm performance comparison. The maximum accuracy of the algorithms on datasets (CIFAR-10, FMNIST, EMNIST) with varying degrees ($\alpha$ = 0.1, 1, 10) of non-IID.

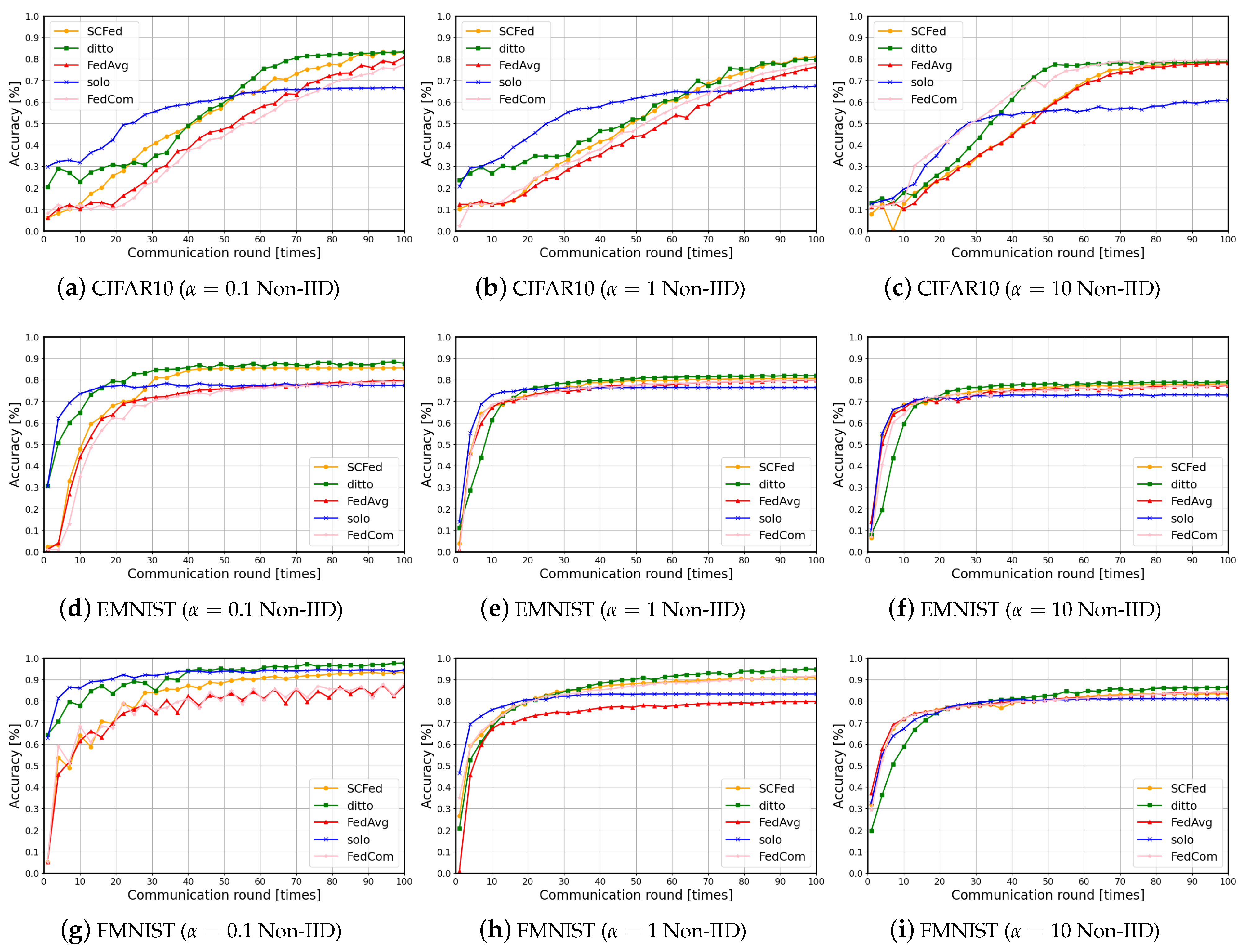
	Datasets	CIFAR-10			FMNIST			EMNIST
Algorithm		$\mathbf{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathbf{\alpha }=\mathbf{1}$	$\mathbf{\alpha }=\mathbf{10}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathbf{\alpha }=\mathbf{1}$	$\mathbf{\alpha }=\mathbf{10}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathbf{\alpha }=\mathbf{1}$	$\mathbf{\alpha }=\mathbf{10}$
Solo		0.66	0.67	0.60	0.94	0.83	0.81	0.76	0.76	0.73
FedAvg [39]		0.81	0.76	0.78	0.87	0.80	0.84	0.80	0.80	0.77
Ditto [57]		0.83	0.80	0.78	0.98	0.95	0.86	0.88	0.82	0.79
FedCom [58]		0.77	0.78	0.80	0.88	0.92	0.85	0.80	0.80	0.78
SC-Fed (Ours)		0.83	0.81	0.79	0.93	0.91	0.83	0.81	0.81	0.78

, the quantitative experimental results demonstrate that, across three varying degrees of non-IID settings on the CIFAR-10 dataset, the SC-Fed algorithm achieved average performance improvements of 7.53%, 7.09%, and 6.33% compared to the Solo, FedAvg, Ditto, and FedCom algorithms, respectively. On the Fashion-MNIST dataset, SC-Fed exhibited respective performance gains of 1.25%, 3.84%, and 1.20% under three distinct non-IID scenarios. Meanwhile, on the EMNIST dataset, SC-Fed achieved performance enhancements of 0%, 1.85%, and 1.60% across the three non-IID settings. The observations indicate that the performance improvement of the SC-Fed algorithm is relatively modest. This is primarily attributed to the optimization of communication efficiency while maintaining model performance, thereby providing robustness in communication performance for federated learning in real-world network scenarios.

Figure 2a presents the experimental results on the CIFAR-10 dataset under the highly non-IID setting ($\alpha =0.1$). The proposed SC-Fed method shows steady improvement, surpassing FedAvg, FedCom, and Solo, and achieving a final accuracy of approximately 82%. Before 50 communication rounds, Ditto performs worse than SC-Fed; however, it surpasses SC-Fed in accuracy after 50 rounds. The Solo method achieves the best performance initially, but its accuracy improves very slowly afterward, resulting in the worst final performance. FedCom consistently performs the worst throughout the training process. In Figure 2b, SC-Fed outperforms FedAvg and FedCom throughout the entire training process. Solo achieves the best performance in the early stages of training, but its model accuracy shows no significant improvement after 40 rounds, resulting in the worst final performance. SC-Fed achieves similar results to Ditto, although Ditto performs better in the early stages of training. In Figure 2c, SC-Fed performs similarly to FedAvg, while Ditto and FedCom achieve the best results. However, the Solo method continues to exhibit the worst performance.

Figure 2d–f present the experimental results on the EMNIST dataset under different non-IID settings ($\alpha =0.1$, $\alpha =1$, and $\alpha =10$). Under the highly non-IID setting ($\alpha =0.1$), shown in Figure 1, the proposed SC-Fed method demonstrates steady improvement, achieving a final accuracy of approximately 87%, comparable to Ditto. Solo performs the best before 30 communication rounds but shows a very slow improvement afterward, stabilizing at 78%, the lowest among all methods. FedAvg and FedCom achieve around 80% accuracy. In the moderately non-IID setting ($\alpha =1$), shown in Figure 2e, SC-Fed reaches a final precision of approximately 80%, similar to Ditto, FedAvg and FedCom. Solo performs best during the first 20 rounds but stabilizes at 75%. Finally, under the nearly IID setting ($\alpha =10$), shown in Figure 2c, SC-Fed, Ditto, FedAvg, and FedCom achieve similar final performances, converging at around 78%. Solo shows competitive performance in the early stages, achieving the highest accuracy within the first 20 rounds, but stabilizes at 72%. These results highlight the robustness and effectiveness of SC-Fed and Ditto across varying degrees of data heterogeneity.

The Figure 2g presents the experimental results on the FMNIST dataset under the highly non-IID setting ($\alpha =0.1$). Solo and Ditto achieve the best performance throughout the entire training process, while SC-Fed performs well. In contrast, FedCom and FedAvg exhibit the worst performance with significant fluctuations. Figure 2h presents the experimental results on the FMNIST dataset under the moderately non-IID setting ($\alpha =1$). SC-Fed and FedCom achieve similar final performances, both converging at approximately 85%. Solo performs best during the first 20 communication rounds, reaching the highest early accuracy, but improves only marginally afterward, stabilizing at around 82%. FedAvg converges to around 80%. Figure 2i presents the experimental results on the FMNIST dataset under the nearly IID setting ($\alpha =10$). SC-Fed, FedCom, and FedAvg achieve nearly identical final performances, converging at approximately 83%. Solo shows competitive performance in the early stages, but stabilizes at around 80% in the later stages, while Ditto remains the best effective, stabilizing at 87%.

The Figure 3a–c present the experimental results on the three datasets under non-IID settings ($\alpha =0.1$). In CIFAR-10 of Figure 3a, SC-Fed outperforms all baseline algorithms with the smallest average waiting time and the most stable performance. In EMNIST of Figure 3b, SC-Fed maintains a consistently lower average waiting time compared to the fluctuating results of FedAvg, FedCom, and Ditto. In FMNIST of Figure 3c, SC-Fed not only achieves the lowest waiting time but also demonstrates minimal variance, highlighting its robustness and efficiency. These results indicate the significant advantage of the SC-Fed algorithm in reducing communication delays and improving training efficiency in federated learning with heterogeneous data distributions.

6. Conclusions

To address the requirements of real-world federated learning environments, this paper proposes a balanced federated learning framework, SC-Fed, which leverages federated clustering to optimize model performance and training latency, effectively mitigating the non-IID problem in practical federated learning scenarios. Our approach aims to achieve elastic optimization of the average waiting time without significantly compromising model performance. Specifically, we validated the effectiveness of the algorithm using three publicly available datasets (EMNIST, FashionMNIST, and CIFAR10). The results show that the performance of the model of our federated learning framework exceeds the baseline algorithms by an average of 7.56%, while reducing the waiting time by 54.6%. This indicates that the framework for the federated learning algorithm is of practical significance in heterogeneous device environments.

Although the method shows promising results, we acknowledge certain unresolved challenges. The federated clustering framework based on PCA has been validated in terms of performance, but in pathological non-IID scenarios, the PCA-based clustering approach for user-device similarity still leaves room for improvement, as it does not capture shared knowledge across models but focuses solely on similarity-based knowledge. To address these challenges, future work will explore advanced PCA techniques such as incremental PCA (IPCA) and robust PCA (RPCA) to better handle data variability and noise, investigate hybrid clustering approaches that combine PCA with other methods like spectral clustering or hierarchical clustering to enhance clustering performance, and explore mechanisms for cross-model knowledge transfer using meta-learning or transfer learning to improve the generalization capability of the federated clustering framework. Furthermore, we will develop adaptive algorithms to dynamically adjust the local training frequency based on device computational load and data quality, thereby reducing the average waiting time.