DualAD: Exploring Coupled Dual-Branch Networks for Multi-Class Unsupervised Anomaly Detection

Abstract

Anomaly detection (AD) is crucial in various domains such as industrial inspection, medical diagnosis, and video surveillance. Previous advancements in unsupervised AD often necessitated training separate models for different objects, which can be inefficient when dealing with diverse categories in real-world scenarios. This paper addresses the recently proposed task of multi-class unsupervised anomaly detection (MUAD), which is more practical and challenging. We begin by reviewing the first MUAD framework, UniAD, and analyzing the characteristics of end-to-end feature reconstruction networks that can adapt to various backbone architectures. Building on these insights, we introduce a novel MUAD framework called DualAD. Our approach is based on the innovative design of a Coupled Dual-Branch Network (CDBN), which integrates a Wide–Shallow Network (WSN) with a Narrow–Deep Network (NDN), leveraging the strengths of both to achieve superior performance. We explore a fully transformer-based homogeneous design for the CDBN and introduce a more lightweight heterogeneous CDBN design that integrates a transformer with a Memory-Augmented Multi-Layer Perceptron (MMLP). Experimental results on the MVTec AD and VisA datasets demonstrate that DualAD outperforms the recent state-of-the-art methods and exhibits robust performance across various pre-trained backbone architectures.

1. Introduction

AD is a critical issue in the computer vision community, with extensive applications in industrial quality inspection, medical diagnosis, video surveillance, and other domains. In real-world scenarios, anomaly data are usually sparse and exhibit diverse patterns, posing a challenge for manually collecting adequately annotated anomaly samples. Therefore, current research in this field mainly focuses on unsupervised methods. As shown in Figure 1, in an unsupervised setting, AD models are trained on normal images to learn their distribution, aiming to detect and localize anomalies that deviate from it. Most existing unsupervised anomaly detection (UAD) methods are based on a single-class setting, where separate AD models are trained for each class. However, considering the diversity of categories and subtypes within individual categories in real-world anomaly detection scenarios, along with the significant memory and time consumption associated with running multiple models, this separate setting may be impractical. Therefore, a more realistic solution is to train a unified model capable of detecting anomalies across multiple classes of objects.

Recent UAD methods primarily rely on embedding and reconstruction techniques. Embedding-based approaches [1,2,3] typically utilize backbones pre-trained on ImageNet [4] to extract patch-level image features, constructing a prior distribution of normality. Reconstruction-based methods often follow an encoder–decoder framework to reconstruct input data. A prevalent approach combines reconstruction with embedding to perform feature-level reconstructions, which can be categorized into end-to-end reconstruction [5] and multi-stage reconstruction [6] depending on the strategy. While reconstruction-based methods are highly practical, as they detect anomalies by identifying anomalies in reconstruction errors without requiring complex training constraints or tricks, they suffer from the problem of the “identical shortcut” [5], where the model may learn tricks to reconstruct anomalies effectively. To mitigate this, enhancement strategies such as pseudo-anomalies [7] and memory mechanisms [8] are often introduced.

MUAD was first introduced in UniAD [5], which employs a pre-trained feature extractor along with a transformer-based [9] end-to-end feature reconstruction network. While UniAD has certain advantages, it relies on EfficientNet-b4 [10] as the feature extractor, which exhibits significantly lower-dimensional features compared to other commonly used pre-trained backbones, such as the ResNet series [11]. When using backbones with higher-dimensional features, significant dimensionality reduction can lead to severe and irrecoverable information loss, thereby constraining the accuracy of AD. To mitigate this, increasing the transformer’s embedding dimension is often necessary. However, the expansion of network capacity does not guarantee improved detection capabilities and can even lead to significant performance degradation. As shown in Figure 2, this issue arises when using WideResNet50 [11] (which extracts 1792-dimensional feature embeddings) instead of EfficientNet-b4’s 272-dimensional embeddings. The applicability of end-to-end reconstruction models across different feature extractor architectures remains largely unexplored.

Figure 1. (a) Task setup for unsupervised anomaly detection (UAD). During training, only normal sample images are used to train the model. In the testing phase, the model is tasked with distinguishing between normal and anomalous samples and identifying the location of any anomalies. (b) Single-class unsupervised anomaly detection (SUAD): a separate model is trained for each class to detect anomalies specific to that class. (c) Multi-class unsupervised anomaly detection (MUAD): a single unified model is trained to perform anomaly detection across multiple object classes (Figure created by the authors. Sample images are from the MVTec AD [12] dataset).

Figure 1. (a) Task setup for unsupervised anomaly detection (UAD). During training, only normal sample images are used to train the model. In the testing phase, the model is tasked with distinguishing between normal and anomalous samples and identifying the location of any anomalies. (b) Single-class unsupervised anomaly detection (SUAD): a separate model is trained for each class to detect anomalies specific to that class. (c) Multi-class unsupervised anomaly detection (MUAD): a single unified model is trained to perform anomaly detection across multiple object classes (Figure created by the authors. Sample images are from the MVTec AD [12] dataset).

To address the aforementioned issues, we propose a novel MUAD framework, namely DualAD. We begin by revisiting the UniAD framework, investigating how the transformer’s width and depth affect MUAD performance. Our findings indicate that a wider and shallower reconstruction network outperforms the default UniAD configuration in overall performance, while a deeper reconstruction network excels at capturing structural and semantic features. Based on these insights, we propose CDBN, which integrates a WSN and an NDN. Drawing inspiration from multi-head attention [9] and multi-stage feature fusion [6], the CDBN seamlessly integrates these two networks into a unified end-to-end reconstruction model, leveraging their strengths to achieve enhanced overall performance. Expanding on UniAD, we present a homogeneous CDBN design entirely based on the transformer. Additionally, we explore a more lightweight heterogeneous CDBN design that combines a transformer with an MMLP. Finally, we conduct extensive experiments on two well-known UAD public benchmark datasets, MVTecAD [12] and VisA [13], comparing our framework to recent state-of-the-art methods. The results confirm the superior performance of our framework, as well as its versatility across different pre-trained backbone architectures.

The main contributions of this paper are summarized as follows:

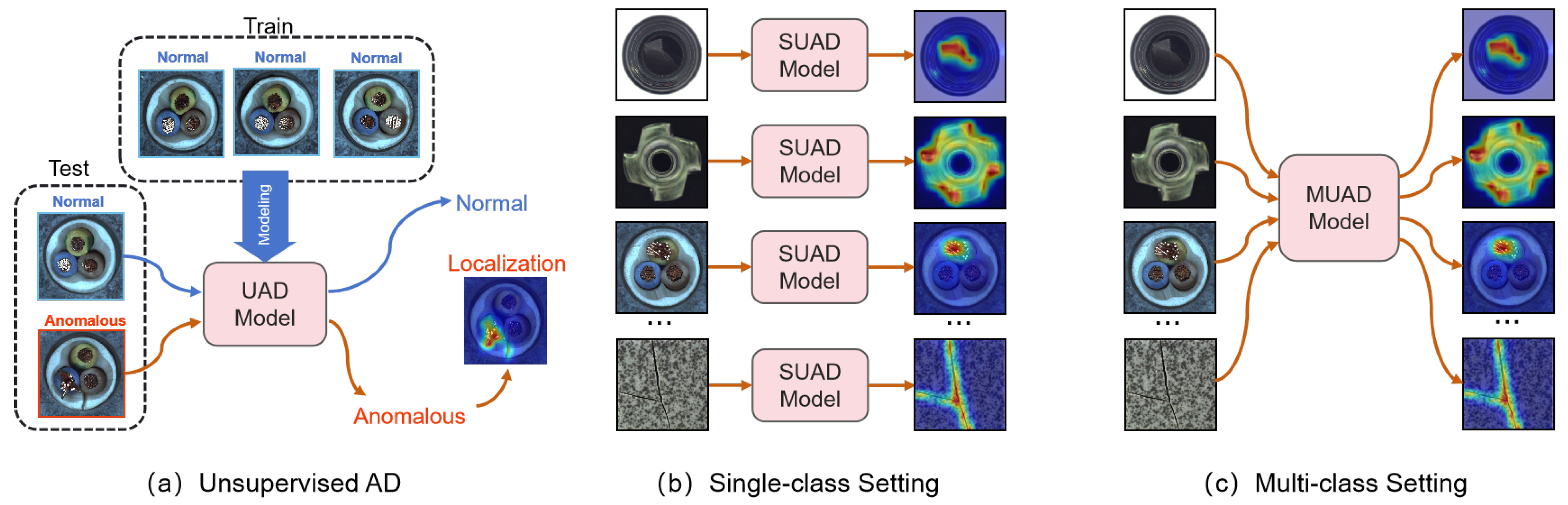
• We propose the DualAD, which tackles multi-class unsupervised anomaly detection tasks and explores a novel end-to-end feature reconstruction framework (see Section 3.3).
• We introduce the CDBN, which integrates a WSN and an NDN, leveraging their combined strengths to achieve superior overall performance (see Section 3.3.2).
• We present a homogeneous CDBN design entirely based on the transformer and explore a more lightweight heterogeneous design that combines a transformer with an MMLP (see Section 3.3.3).
• We conduct extensive experiments on the popular MVTec AD and VisA benchmark datasets, comparing our framework to recent state-of-the-art methods. The results demonstrate the superior performance of DualAD and its effectiveness across different pre-trained backbones (see Section 4).

The remainder of this paper is organized as follows: Section 2 reviews related work on UAD and recent advancements in MUAD. Section 3 outlines the materials and methods, including the task definition and setups, a revisit of transformer-based MUAD, and a detailed description of our proposed method, and the experimental setups. Section 4 presents the experimental results, offering quantitative comparisons with state-of-the-art methods on two public benchmark datasets, along with ablation studies. Section 5 discusses the key findings and limitations of our work, while Section 6 provides conclusions and highlights potential directions for future research.

2. Related Work

This section provides a comprehensive overview of existing research in UAD, with a particular focus on embedding-based and reconstruction-based methods, as well as recent developments in MUAD. We first discuss general approaches in UAD and then shift to more specific advancements in MUAD. The section is organized as follows: Section 2.1 covers general UAD methods, highlighting both embedding-based and reconstruction-based techniques, while Section 2.2 reviews the evolution of MUAD, detailing key contributions from prominent works.

2.1. Unsupervised Anomaly Detection

Embedding-based methods focus on modeling the deep feature representations of normal samples. Early efforts, such as those by Ruff et al. [14] and Yi et al. [15], extended classical one-class classification techniques like Support Vector Data Description (SVDD) [16] to deep features. Recent research tends to utilized features extracted from networks pre-trained on ImageNet [4] to construct the prior distribution of normal samples, often in conjunction with other methodologies. For example, the following:

(1)

Memory-based methods. These methods attempt to build prototype banks of pre-trained features for normal samples [1,17,18,19,20,21] and detect anomalies by matching against these normal templates. Roth et al. [1] directly compute the distance between the test sample and the most similar normal feature template to estimate the degree of anomaly. Liu et al. [19] and Gu et al. [20] enhance the input’s normality by matching with normal features. Zhang et al. [21] estimate the anomalous region by calculating the residual between the sample and the normal template, assisting the segmentation network’s decision. These methods are conceptually simple and effective. However, the cost of building prototype banks and the detection cost both increase with the number of categories, which limits their scalability in multi-class settings.

(2)

Normalizing flow-based methods. These methods seek to map the pre-trained features of normal samples to simpler probability distributions [2,22,23,24,25], such as multivariate Gaussian distributions. Rudolph et al. [22] first introduced normalizing flows for density estimation of multi-scale image features. However, this method primarily focuses on image-level anomaly detection. Gudovskiy et al. [23] enhanced anomaly localization by using conditional normalizing flows and introducing 2D hard positional encoding. Yu et al. [2] proposed a 2D normalizing flow and employed a vision transformer as the feature extractor for the first time. Lei et al. [25] introduced an anomaly localization paradigm based on normalizing flows and latent template comparison. These methods provide accurate density estimation for data, allowing for effective anomaly detection. However, they generally require significant computational resources for training, especially when dealing with high-dimensional data, leading to substantial training time and computational costs. Furthermore, these methods assume that the distribution of normal data is known and that the data must adhere to certain distributional properties. For more complex data distributions, the performance of the model may be affected.

(3)

Knowledge Distillation-based methods. These methods employ a pre-trained network as a teacher model, training a student model to learn its representation of normal samples [3,26,27,28], with anomalies being identified based on the output differences between the teacher and student models. Bergmann et al. [3] first utilized knowledge distillation for anomaly detection, which ensembles several student models trained on normal data at different scales. Wang et al. [27] introduced a pyramid feature matching mechanism between the teacher and student models, further improving anomaly localization efficiency and accuracy. Zhang et al. [28] proposed a denoising teacher-student network paradigm that enhanced the constraints on anomalous data. These methods are based on the assumption that a student network constrained only on the outputs of normal samples during training will generate different feature representations for anomalous samples compared to the teacher network. However, in practice, this assumption does not always hold true.

Reconstruction-based methods typically follow an encoder–decoder architecture and are based on the assumption that models trained solely on normal images cannot accurately reconstruct unseen anomalies, such as the surface staining of pills or the placement anomalies of transistors, as shown in Figure 3. These anomalies often differ significantly from their normal patterns. As a result, anomalies can be identified by comparing reconstruction errors with those of normal samples.

(1)

Image-level methods. These methods use the RGB pixels of the original image for reconstruction.The most basic approach involves autoencoders (AEs) [29,30,31], which map input images to latent space through an encoder and then reconstruct them via a decoder. The reconstruction is optimized by minimizing the difference between the original input and the output, typically using loss functions like Mean Squared Error (MSE). While these methods are conceptually simple, they face challenges in handling more complex scenarios. To improve reconstruction performance, generative models have been introduced. Variational autoencoders (VAEs) [32,33] learn the latent probabilistic distribution of the data, with the encoder outputting distribution parameters instead of a fixed latent vector. The loss function incorporates Kullback–Leibler (KL) divergence as a regularization term to constrain the latent space distribution. Generative Adversarial Networks (GANs) [34,35] employ adversarial training between a generator and a discriminator, where the generator learns the distribution of normal data, and the discriminator identifies outliers as potential anomalies. Diffusion-based methods [36,37,38] learn the data distribution through a series of noise addition and denoising steps to reconstruct inputs.

(2)

Feature-level methods. With the increasing popularity of embedding-based methods that leverage pre-trained networks for feature extraction, recent studies have introduced feature-level reconstruction techniques. These methods aggregate outputs from multiple stages of pre-trained networks and utilize different strategies for feature reconstruction. Methods by You et al. [5] and Lu et al. [39] employ end-to-end matching approaches, using an AE to reconstruct aggregated pre-trained features in a manner similar to image reconstruction. Meanwhile, Deng et al. [6], Zhang et al. [40], and He et al. [41] adopt multi-stage matching strategies, aggregating reconstruction differences between intermediate layers across multiple scales of the pre-trained network and decoder to assess anomaly severity.

Reconstruction-based methods are relatively easy to train and highly practical, but they are prone to the “identical shortcut” problem [5], where the model may learn techniques that effectively reconstruct anomalies, leading to ambiguous decision boundaries. To mitigate this issue, various enhancement strategies have been employed. Some methods augment reconstruction networks with memory mechanisms. Gong et al. [8] introduced the memory mechanism by adding a learnable memory module between the encoder and decoder. This module can be viewed as a dictionary organized in a matrix form, with each vector corresponding to a “word” in the dictionary. During training, the matrix parameters are jointly optimized with the AE to learn the feature patterns of normal data. The memory module is designed to reorganize abnormal features into normal ones, thereby improving the normality of the decoder’s output. Many subsequent methods have extended this design. For instance, Liu et al. [42] extended the memory module to multi-level features, while Hou et al. [43] used block-wise queries to prevent poor reconstruction of anomalous features due to limited anomaly patterns.

(3)

Enhancement strategies. Reconstruction-based methods are easy to train and demonstrate strong practicality; however, they are prone to the “identical shortcut” problem [5], where the model may learn specific techniques that effectively restore anomalies, resulting in ambiguous decision boundaries. To mitigate this issue, various enhancement strategies are employed. Some methods augment reconstruction networks with memory mechanisms. Gong et al. [8] introduce the memory mechanism by adding a learnable memory module between the encoder and decoder. This module can be viewed as a dictionary organized in a matrix form, with each vector corresponding to a “word” in the dictionary. During training, the matrix parameters are jointly optimized with the AE to learn the feature patterns of normal data. The memory module is designed to reorganize anomalous features into normal ones, thereby improving the normality of the decoder’s output. Many subsequent methods have extended this design. For instance, Liu et al. [42] extend the memory module to multi-level features, while Hou et al. [43] use block-wise queries to prevent poor reconstruction of anomalous features due to limited anomaly patterns. Furthermore, pseudo-anomalies can be added to the normal data for self-supervised training, helping to better model the normal distribution. Li et al. [44] generate anomalous images by randomly selecting a block from a normal image and pasting it into another region. Wyatt et al. [36] and Tien et al. [45] generate block-level image anomalies using simplex noise. Zavrtanik et al. [7,46] synthesize more realistic, shape-random image anomalies by combining Perlin noise with the Describable Textures Dataset [47]. In addition to adding pseudo-anomalies to the original images, Liu et al. [48] and You et al. [5] introduce anomalies at the feature level by adding Gaussian noise.

2.2. Multi-Class Unsupervised Anomaly Detection

Most existing unsupervised anomaly detection (UAD) methods are based on a single-class setting, where separate detection models are trained for each class. However, considering the diversity of categories in real-world scenarios and the variations among different subtypes within a single category, along with the significant memory and time consumption required to operate multiple models, this separate approach may not be practical. Therefore, a more feasible solution is to train a unified model capable of detecting anomalies across multiple object classes. The first MUAD framework, UniAD, was introduced by You et al. [5], who developed a unified model based on transformers [9] for end-to-end feature reconstruction. Subsequent research has advanced this framework: Lu et al. [39] integrated the VQ-Layer [49] into the transformer, while Jiang et al. [50] reduced inter-class interference through implicit neural representations [51] and class prompts. Other approaches have focused on exploring different reconstruction network architectures: Zhao et al. [52] proposed a CNN-based MUAD framework, He et al. [38] introduced a diffusion model, and Zhang et al. [40] proposed ViTAD, a multi-stage feature reconstruction framework entirely based on vision transformers. Furthermore, Ruan et al. [53] introduced MambaAD, which was the first to incorporate Mamba [41] into MUAD. However, these methods often rely on specific feature extractors, such as UniAD’s dependence on EfficientNet [10] and ViTAD’s reliance on vision transformers [54] as feature extractors. The applicability of reconstruction models across different feature extractor architectures remains largely unexplored.

3. Materials and Methods

3.1. Task Definition and Setups

Unsupervised Anomaly Detection. Image AD aims to identify samples or local patterns that significantly deviate from normal data. In the context of UAD, as illustrated in Figure 1a, the detection model is trained solely on normal images and is tasked with distinguishing between normal and anomalous samples during the testing phase, as well as identifying the locations of anomalies within the anomalous images. Depending on how the dataset is utilized, UAD can be categorized into two configurations:

Single-class Unsupervised Anomaly Detection. Under the SUAD setting, as illustrated in Figure 1b, a separate model is trained for each individual class to detect anomalies specific to that class. Formally, assume an AD dataset contains N classes, denoted as $\mathcal{C}=\{C_1,C_2,\cdots ,C_N\}$, each experiment focuses exclusively on a sub-dataset ${\mathcal{X}}_{C_i}=\{{\mathcal{X}}_{C_i}^{\mathrm{Train}},{\mathcal{X}}_{C_i}^{\mathrm{Test}}\}$ corresponding to a single class $C_i\in \mathcal{C}$, where ${\mathcal{X}}_{C_i}^{\mathrm{Train}}$ comprises all normal images available during the training phase ($\forall x\in {\mathcal{X}}_{C_i}^{\mathrm{Train}}:y_x=0$), with $y_x\in \{0,1\}$ denoting if an image x is normal 0 or anomalous 1, and ${\mathcal{X}}_{C_i}^{\mathrm{Test}}$ is defined as the set of samples at test time, which includes both normal and anomalous images ($\forall x\in {\mathcal{X}}_{C_i}^{\mathrm{Test}}:y_x\in \{0,1\}$).

Multi-class Unsupervised Anomaly Detection. Under the MUAD setting, as illustrated in Figure 1c, a unified model is trained to perform anomaly detection across multiple object classes. The sample set for each experiment $\mathcal{X}=\{{\mathcal{X}}^{\mathrm{Train}},{\mathcal{X}}^{\mathrm{Test}}\}$ covers all classes within $\mathcal{C}$. The training dataset ${\mathcal{X}}^{\mathrm{Train}}=\{{\mathcal{X}}_{C_1}^{\mathrm{Train}},{\mathcal{X}}_{C_2}^{\mathrm{Train}},\cdots ,{\mathcal{X}}_{C_N}^{\mathrm{Train}}\}$ contains the normal images from all classes that are available during training, with class information (i.e., category labels $\mathcal{C}$) not accessible. The test dataset ${\mathcal{X}}^{\mathrm{Test}}=\{{\mathcal{X}}_{C_1}^{\mathrm{Test}},{\mathcal{X}}_{C_2}^{\mathrm{Test}},\cdots ,{\mathcal{X}}_{C_N}^{\mathrm{Test}}\}$ includes both normal and anomalous images from test sample sets across all classes. The binary labels ($y_x$) and ground truth masks, indicating normal or anomalous images and pixels, are provided, enabling evaluation of the model’s binary classification capabilities at image level (anomaly detection) and pixel level (anomaly localization).

3.2. Revisiting Transformer-Based MUAD

In this section, we review the first MUAD framework, UniAD [5], and outline the motivation for the method proposed in this paper.

UniAD Framework. As shown in Figure 4, UniAD is composed of two main components: a pre-trained, parameter-frozen backbone (denoted as $\varphi$) and a transformer-based reconstruction network (denoted as $\psi$). The pre-trained backbone serves as a feature extractor, capturing features at multiple spatial scales, which are subsequently aggregated by a fuser F to form a sequence of feature tokens. The feature reconstruction network, which is the core of the framework, follows the standard architecture in vanilla transformer [9] and consists of an encoder ${\psi }^E$ and a decoder ${\psi }^D$. It effectively mitigates the “identical shortcut” issue by employing a neighbor-masked attention mechanism, introducing feature perturbations, and incorporating learnable queries into the decoder. The anomaly score map of the input image is generated by calculating the distance between the input feature tokens and the reconstructed feature tokens output by $\psi$. By default, UniAD uses an EfficientNet-b4 [10] as the pre-trained feature extractor, while the feature reconstruction network is made up of 4 encoder layers and 4 decoder layers, with the transformer embedding dimension set to 256.

Motivation for Exploring DualAD. Under the default setup, we noted that UniAD underperforms when using the ResNet [11] series pre-trained backbones [5]. To explore if this issue relates to network capacity, we increased the transformer’s embedding dimension and assessed the model’s detection and localization performance using image-level and pixel-level AUROC, while also tracking performance curves during training. As illustrated in Figure 2, a modest increase in the transformer dimension (from 256 to 512) does improve the performance to a certain degree. However, further increments lead to unstable training performance curves and significant performance degradation. Conversely, reducing the number of transformer layers (from 4 to 2 for both the encoder and decoder) helped restore and even enhance the detection performance.

To delve deeper into the cause of this phenomenon, we followed the method in [5] and additionally trained a decoder to reconstruct images from WideResNet50 features to facilitate the visualization of reconstructed features. As depicted in Figure 3, as the width of the reconstruction network increases, the expansion of parameters seems to make the network overly generalized. While the 1024-dimensional transformer effectively restores structural and semantic anomalies to the normal ones, it struggles with the reconstruction of more intricate and image-specific textural details. This leads the network to mistakenly identify the textures of normal images as anomalies. Conversely, reducing the depth of the reconstruction network allows for better recovery of image textures.

We contend that a key factor in enhancing the performance of feature reconstruction models on diverse pre-trained backbones is to minimize the loss of normal feature information during the reconstruction process, while effectively balancing the decision-making among structural, semantic, and image-specific textural anomalies. From a comprehensive performance perspective, wide and shallow networks appear to be better suited for MUAD tasks. The increased width allows the model to retain pre-trained feature information effectively, while the reduced depth helps prevent overgeneralization, thereby preserving the ability to discern textural anomalies. In contrast, deeper networks excel at understanding structural and semantic features. To harness the benefits of both configurations, we introduce the DualAD framework, which skillfully integrates a Wide–Shallow Network (WSN) with a Narrow–Deep Network (NDN). The WSN enhances the NDN by effectively preserving feature information, while the NDN improves the WSN’s ability to capture complex structural and semantic features, resulting in superior anomaly detection and localization performance.

3.3. Proposed Method

The DualAD framework is proposed for multi-class unsupervised anomaly detection, with Figure 4b and Figure 5 illustrating its two designs: homogeneous and heterogeneous. Overall, our proposed framework comprises two primary components: a Feature Extractor and a Coupled Dual-Branch Network (CDBN). The Feature Extractor aggregates multi-scale features to form a smooth sequence of feature tokens, while the CDBN is composed of a Wide–Shallow Network (WSN) and a Narrow–Deep Network (NDN), which are coupled together to facilitate end-to-end feature reconstruction. Based on the differences between the WSN and NDN architectures, we explore two CDBN designs for DualAD. The homogeneous design (Figure 4b), employs the Transformer for both the WSN and NDN. Conversely, the heterogeneous design (Figure 5) utilizes a Memory-Augmented MLP (MMLP) for the WSN, while retaining the same feature extractor and NDN structure as the homogeneous setup. Detailed descriptions of the framework are elaborated in the subsequent sections.

3.3.1. Feature Extractor

Similar to prior studies [5,40], the Feature Extractor retrieves feature tokens from the multi-scale outputs of the pre-trained backbone. Let $\varphi$ denote the pre-trained backbones, which include L stages $\{{\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_L\}$, and let $\mathcal{S}\subseteq \{1,2,\cdots ,L\}$ represent the set of selected stage indices. For an input image $\mathbf{x}\in {\mathbb{R}}^{H_{\mathrm{in}}\times W_{\mathrm{in}}\times 3}$, multi-scale features $\{{\mathbf{f}}_{{\varphi }_l}={\varphi }_l\left(\mathbf{x}\right)\mid l\in \mathcal{S}\}$ are extracted from $\varphi$, where ${\mathbf{f}}_{{\varphi }_l}\in {\mathbb{R}}^{H_l\times W_l\times C_l}$ represents the output feature map at stage l of $\varphi$, with the dimensions $H_l\times W_l$ and $C_l$ channels. To achieve spatial alignment of features, each ${\mathbf{f}}_{{\varphi }_l}$ is up-sampled to the resolution $H_u\times W_u$ of the largest feature map among those selected by $\mathcal{S}$, using an interpolation function u. These are then concatenated along the channel dimension to form a $C={\sum }_{l\in \mathcal{S}}{C}_l$ channels feature map ${\mathbf{f}}_u=\mathrm{cat}\left(\left\{u\left({\mathbf{f}}_{{\varphi }_l}\right)\mid l\in \mathcal{S}\right\}\right)\in {\mathbb{R}}^{H_u\times W_u\times C}$. Subsequently, ${\mathbf{f}}_u$ is downsampled to the input resolution of the reconstruction network by local patch aggregation. Specifically, ${\mathbf{f}}_u$ is partitioned into $(H_u/p)\times (W_u/p)$ non-overlapping patches, each of size $p\times p$. The $p^2$ embeddings within each patch are aggregated via average pooling to form the feature map ${\mathbf{f}}_{\mathrm{org}}\in {\mathbb{R}}^{H\times W\times C}$, where $H=H_u/p$ and $W=W_u/p$. Finally, ${\mathbf{f}}_{\mathrm{org}}$ is flattened into tokens of length $N=HW$, which constitute the input ${\mathbf{h}}_{\mathrm{org}}\in {\mathbb{R}}^{N\times C}$ for the feature reconstruction network.

The process described above can be summarized in the following pseudocode (Algorithm 1):

Algorithm 1: Feature Extraction Process

3.3.2. Coupled Dual-Branch Network for Feature Reconstruction

The Dual-Branch Coupled Network (CDBN) is composed of two sub-networks: a Wide–Shallow Network (WSN) and a Narrow–Deep Network (NDN), both consisting of an encoder and a decoder. The WSN has a larger network width to accommodate the high-dimensional properties of the pre-trained features, and with its shallower layers, as analyzed in Section 3.2, it is expected to have better overall anomaly detection and localization capabilities. Simultaneously, we employ a deeper NDN, which is positioned between the encoder and decoder of the WSN and is expected to further extract features from the WSN, enhancing the network’s discriminative capability on structural and semantic anomalies.

As shown in Figure 4 and Figure 5, we denote the encoder of WSN as ${\delta }^E$ and the decoder as ${\delta }^D$, while the encoder and decoder of NDN are denoted as ${\psi }^E$ and ${\psi }^D$, respectively. The original feature tokens ${\mathbf{h}}_{\mathrm{org}}$ are first fed into ${\delta }^E$ for preliminary feature extraction, resulting in WSN features ${\mathbf{h}}_{\mathrm{wsn}}={\psi }^E\left({\mathbf{h}}_{\mathrm{org}}\right)$.

Inspired by the idea of multi-head attention [9] and multi-scale feature fusion [6], we process ${\mathbf{h}}_{\mathrm{wsn}}$ in the NDN as follows. First, ${\mathbf{h}}_{\mathrm{wsn}}$ is split into $N_q$ feature heads $\mathcal{Q}=\{{\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_{N_q}\}$ to represent different aspects of ${\mathbf{h}}_{\mathrm{wsn}}$. Then, through an aggregation operation, the aggregated feature ${\mathbf{h}}_{\mathcal{Q}}$ is obtained (by default, summation is used, i.e., ${\mathbf{h}}_{\mathcal{Q}}={\sum }_{i=1}^{N_q}{\mathbf{q}}_i$). Next, ${\mathbf{h}}_{\mathcal{Q}}$ is fed into the NDN for further processing.

Following UniAD [5], the NDN adopts the standard architecture in vanilla transformer [9] and introduces neighbor masking in the attention calculation to prevent information leakage. Specifically, ${\mathbf{h}}_{\mathcal{Q}}$ is first fed into ${\psi }^E$ for further feature extraction, resulting in NDN features ${\mathbf{h}}_{\mathrm{ndn}}={\psi }^E\left({\mathbf{h}}_{\mathcal{Q}}\right)$. Subsequently, in each layer of ${\psi }^D$, ${\mathbf{h}}_{\mathrm{ndn}}$ is first fused with a feature head ${\mathbf{q}}_i\in \mathcal{Q}$ via a Multi-head Cross Attention (MCA) block (this implies that the number of layers in ${\psi }^D$ equals the number of feature heads K). Then, in the second MCA block, it is fused with the output of the previous decoder layer.

The fused features from each layer of ${\psi }^D$ are sent to a Feed-Forward Network (FFN) block for integration, producing hierarchical features. Finally, we obtain $N_q$ hierarchical output features from ${\psi }^D$, denoted as $\mathcal{Z}=\{{\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_{N_q}\}$, and concatenate them to form the hierarchical aggregated features ${\mathbf{h}}_{\mathcal{Z}}$ of the NDN, which are then fed into ${\delta }^D$ to obtain the final reconstructed feature tokens ${\mathbf{h}}_{\mathrm{rec}}$.

3.3.3. Memory-Augmented Heterogeneous CDBN

As shown in Figure 4, we explored the design of WSN and NDN with the same architecture—similar to UniAD, both are based on a transformer architecture and coupled together as described in Section 3.3.2, Additionally, to further verify the effectiveness of our CDBN network design, we explored another design scheme where WSN and NDN have different architectures. Specifically, we attempted to implement the encoder and decoder of WSN with a simpler network—a multilayer perceptron (MLP) for both. However, the problem with this simple design is the lack of a mechanism to suppress the “identical shortcut” [5] problem. Therefore, as depicted in Figure 5, we introduced multi-level memory modules [8] to suppress the anomalous information in WSN features.

Each level of the memory modules holds a memory bank $\mathbf{M}\in {\mathbb{R}}^{K\times C_M}$, defined as a real-valued matrix containing K memory items with a fixed embedding dimension $C_M$, which is explicitly used to record the prototypical normal patterns of WSN features during training. For ease of calculation, we set $C_M$ to be equal to the embedding dimension of the query vectors, which are feature heads ${\mathbf{q}}_i\in \mathcal{Q}$. Memory bank addressing is achieved through soft addressing, where the similarity between the query vector $\mathbf{e}\in {\mathbb{R}}^{C_M}$ and each memory item ${\mathbf{m}}_i\in {\mathbb{R}}^{C_M}(i\in \{1,2,\dots ,K\})$ is used as a weight. Specifically, each weight $w_i$ is calculated as follows:

$$w_i={\displaystyle \frac{exp\left(\frac{\mathbf{e}·{\mathbf{m}}_i}{{∥\mathbf{e}∥}_2{∥{\mathbf{m}}_i∥}_2}\right)}{{\sum }_{l=1}^{K}exp\left(\frac{\mathbf{e}·{\mathbf{m}}_l}{{∥\mathbf{e}∥}_2{∥{\mathbf{m}}_l∥}_2}\right)}},$$

(1)

where ${\sum }_{i=1}^K{w}_i=1$.

Then, based on the aggregated memory items weighted by $w_i$, the memory representation most related to the query $\mathbf{e}$ is retrieved and generated as $\widehat{\mathbf{e}}$:

$$\widehat{\mathbf{e}}=\sum _{i=1}^L{w}_i{\mathbf{m}}_i.$$

(2)

We aim to represent each query $\mathbf{e}$ during testing as the normal patterns recorded in the memory bank. However, through the linear combination of memory items, some anomalous features may also be restored well. To alleviate this issue, when calculating $\widehat{\mathbf{e}}$, we ignore those memory items with weights lower than the average value of ${\displaystyle \frac{1}{K}}$, performing sparse addressing such that only a small number of memory items are accessed each time.

3.3.4. Pseudo Anomalies

To mitigate the “identical shortcut” issue, we introduce perturbations to the feature tokens [5], encouraging the model to learn how to reconstruct the input features as normal ones. Specifically, during each iteration of the training phase, a noise token $ϵ\in {\mathbb{R}}^{N\times C}$ is generated for ${\mathbf{h}}_{\mathrm{org}}$, where each entry is sampled from an i.i.d. Gaussian distribution $\mathcal{N}(0,{\left(\alpha S\right)}^2)$. Here, S represents the instance-wise sample standard deviation of ${\mathbf{h}}_{\mathrm{org}}$ at the corresponding channel, and $\alpha$ is a noise scaling parameter. $ϵ$ is then added to ${\mathbf{h}}_{\mathrm{org}}$ to obtain the pseudo-anomalous feature tokens.

3.3.5. Training and Inference

The Mean Squared Error (MSE) is utilized to evaluate the reconstruction loss and to compute anomaly scores. To enhance the detection capabilities of features across various hierarchical levels, we employ a weighting mechanism that calculates the average value of channels originating from the same stage. Specifically, let ${\mathbf{f}}_{\mathrm{org}}^l\in {\mathbb{R}}^{H\times W\times C_l}$ denote the original feature map slice derived from the l-th stage of $\varphi$, and let ${\mathbf{f}}_{\mathrm{rec}}^l\in {\mathbb{R}}^{H\times W\times C_l}$ denote the corresponding reconstructed feature map slice. For each pair $({\mathbf{f}}_{\mathrm{org}}^l,{\mathbf{f}}_{\mathrm{rec}}^l)$, an anomaly map ${\mathbf{A}}_l$ is computed as follows:

$$\forall l\in \mathcal{S}{\mathbf{A}}_l={\displaystyle \frac{1}{C_l}}{∥{\mathbf{f}}_{\mathrm{rec}}^l-{\mathbf{f}}_{\mathrm{org}}^l∥}_2^2,\in {\mathbb{R}}^{H\times W}.$$

(3)

Training phase. After obtaining the anomaly maps $\{{\mathbf{A}}_l\mid l\in \mathcal{S}\}$ from each stage in $\mathcal{S}$, the reconstruction loss $\mathcal{L}$ is calculated by summing over these maps as follows:

$$\mathcal{L}={\displaystyle \frac{1}{HW}}\sum _{h=1}^H\sum _{w=1}^W\sum _{l\in \mathcal{S}}{\mathbf{A}}_l(h,w).$$

(4)

Inference phase. For pixel-level anomaly localization, we generate an anomaly score map ${\mathbf{S}}_{\mathrm{AL}}$ by further processing the anomaly maps across stages $\mathcal{S}$. This map assigns an anomaly score to each pixel of the input image. Specifically, ${\mathbf{S}}_{\mathrm{AL}}$ is represented as follows:

$${\mathbf{S}}_{\mathrm{AL}}=u\left(\prod _{l\in \mathcal{S}}\sqrt{{\mathbf{A}}_l}\right)\in {\mathbb{R}}^{H_{\mathrm{in}}\times W_{\mathrm{in}}},$$

(5)

where $\sqrt{{\mathbf{A}}_l}$ denotes the square root of ${\mathbf{A}}_l$, and u is a bilinear interpolation function that upsamples the element-wise product of $\sqrt{{\mathbf{A}}_l}$ to match the size of the input image.

The image-level anomaly detection result is obtained by computing the maximum value of the average-pooled ${\mathbf{S}}_{\mathrm{AL}}$, providing an overall anomaly score for the image.

3.4. Experimental Setup

In this study, experiments were conducted on two open-source UAD public benchmark datasets, MVTec [12] and VisA [13]. For the training phase, the model is trained on a single NVIDIA GeForce RTX 3080 10GB GPU for 1200 epochs with a batch size of 16. The initial learning rate is set to $1\times {10}^{-4}$ and is reduced by a factor of 0.1 after 1000 epochs. The AdamW optimizer [55] is used with a weight decay of $1\times {10}^{-4}$. For the inference phase, consistent with prior works [5,40,53], anomaly detection and localization results are presented as image-level and pixel-level anomaly scores, with detailed calculation methods provided in Section 3.3.5, rather than as binary classification or segmentation outputs. To assess the model’s performance, we utilized four threshold-independent metrics, covering both image-level and pixel-level evaluation. Each experiment is repeated three times, and intermediate performance results are reported. The specific experimental setups, including the datasets, evaluation metrics, and implementation details, are described below.

3.4.1. Datasets and Evaluation Metrics

MVTec-AD dataset [12] contains 10 object and 5 texture classes of real-world industrial products. Each class contains 60 to 320 color images with resolutions ranging from $700\times 700$ to $1024\times 1024$ pixels. The training set consists of 3629 anomaly-free images. The test set contains 1725 images, out of which 1258 are anomalous images with different defect types, and pixel-level annotations are provided for the corresponding defective regions. The remaining images in the test set are anomaly-free samples.

VisA dataset [13] comprises 10,821 high-resolution images, including 9621 normal images and 1200 anomalous images. The dataset includes 12 object classes, which are categorized into three different object types: complex structure, multiple instances, and single instance. The anomalous images contain various defects. Each type of defect has 5–20 images, and one image may contain multiple defects. The defects were manually generated to produce realistic anomalies.

Evaluation Metrics. Following prior works [3,7,13], we report the threshold-independent metrics including image-level Area Under the Receiver Operating Curve (${\mathrm{AUROC}}_{\mathrm{cls}}$), Average Precision (${\mathrm{AP}}_{\mathrm{cls}}$), F1-score at optimal threshold ($\mathrm{F}1{\max }_{\mathrm{cls}}$) to measure the performance of image-level anomaly detection and pixel-level localization. Besides, we report the pixel-level Area Under the Receiver Operating Curve (${\mathrm{AUROC}}_{\mathrm{sp}}$) to measure the performance of pixel-level localization).

3.4.2. Baselines and Backbones

We primarily use UniAD [5] as the baseline method for comparison. Additionally, we compare our approach with other recent state-of-the-art methods, including RD4AD [6], SimpleNet [48], ViTAD [40], DiAD [38], and MambaAD [53]. The selection of pre-trained backbone is crucial and is typically based on their demonstrated performance. In this study, all the backbones we use are selected from those employed as feature extractors in the recent state-of-the-art methods we are comparing against. Specifically, UniAD leverages a pre-trained EfficientNet-b4 [10] as its feature extractor, while RD4AD and SimpleNet utilize WideResNet50 [11], DiAD uses ResNet50 [11], MambaAD employs ResNet34 [11], and ViTAD [40] relies on ViT-S [54]. Among these pre-trained backbones, only ViT-S is trained using DINO [56] self-supervision, while the others are supervised models trained on ImageNet [4]. For the ResNet-based backbones (WideResNet50, ResNet34, and ResNet50), feature maps from stages 1 to 3 are selected (i.e., $\mathcal{S}=\left\{1,2,3\right\}$), while for EfficientNet-b4 and ViT-S, stages 1 to 4 are used (i.e., $\mathcal{S}=\left\{1,2,3,4\right\}$). Detailed stage information for the backbones is provided in

Table 1. Detailed stage information of the pre-trained backbones involved in this paper.

Backbone	Stages	Depths	Channels	Strides
Eff-b4	[1, 2, 3, 4, 5]	[1, 4, 5, 12, 10]	[24, 32, 56, 160, 448]	[2, 4, 8, 16, 32]
Res34	[1, 2, 3, 4]	[3, 4, 6, 3]	[64, 128, 256, 512]	[4, 8, 16, 32]
Res50	[1, 2, 3, 4]	[3, 4, 6, 3]	[256, 512, 1024, 2048]	[4, 8, 16, 32]
WRes50	[1, 2, 3, 4]	[3, 4, 6, 3]	[256, 512, 1024, 2048]	[4, 8, 16, 32]
ViT-S	[1, 2, 3, 4]	[3, 3, 3, 3]	[384, 384, 384, 384]	[16, 16, 16, 16]

. All evaluations are performed under the MUAD setting.

3.4.3. Implementation Details

All input images are resized to $224\times 224$. A pre-trained backbone, as detailed in Section 3.4.2, is utilized as the feature extractor. Feature maps from various stages are selected, aligned, and concatenated, then resized to a $14\times 14$ resolution to serve as the input pre-trained features for the reconstruction network. For instance, when using the WideResNet50 pre-trained backbone, features from stages 1 to 3 are selected, aligned, concatenated, and resized to create a 1792-channel feature map, which serves as the reconstruction target for the reconstruction network. In the default setting, the NDN is implemented using a transformer with an embedding dimension of 256, consisting of 4 encoder layers and 4 decoder layers. The input and output dimensions of WSN are set to 1024 by default. In the homogenous CDBN setup, the WSN is implemented using a transformer with 2 encoder layers and 2 decoder layers, while in the heterogeneous CDBN setup, the WSN is an MLP with 1 hidden layer, and the memory item number K is set to 196. For the primary experiments, WideResNet50 is used as the default pre-trained backbone, and the heterogeneous CDBN architecture is adopted, with the noise scale parameter $\alpha$ set to 3.2.

4. Results

4.1. Quantitative Comparisons with SoTAs on MVTec AD and VisA

We compared our method with several state-of-the-art approaches on both the MVTec AD and VisA datasets. The image-level and pixel-level quantitative comparison results for MVTec AD are presented in

Table 2. Comparison with SoTA methods on MVTec-AD dataset for multi-class anomaly detection with ${\mathrm{AP}}_{\mathrm{cls}}$/$\mathrm{F}1{\max }_{\mathrm{cls}}$ metrics.

Category		RD4AD [6]	UniAD [5]	ViTAD [40]	DiAD [38]	MambaAD [53]	Ours
		WRes50 (IN1K)	Eff-b4 (IN1K)	ViT-S (DINO)	Res50 (IN1K)	Res34 (IN1K)	WRes50 (IN1K)
Texture	Carpet	99.6/97.2	99.9/99.4	99.9/99.4	99.9/98.3	99.9/99.4	99.8/97.7
	Grid	99.4/96.5	99.5/97.3	99.9/99.1	99.8/97.7	100./100.	100./99.1
	Leather	100./100.	100./100.	100./100.	99.7/97.6	100./100.	100./100.
	Tile	99.3/96.4	99.8/98.2	100./100.	99.9/98.4	99.3/95.4	100./100.
	Wood	99.8/98.3	99.6/96.6	99.6/96.7	100./100.	99.6/96.6	99.9/98.3
Object	Bottle	99.9/98.4	100./100.	100./100.	96.5/91.8	100/100	100./100.
	Cable	89.5/82.5	95.9/88.0	99.1/95.7	98.8/95.2	99.2/95.7	99.4/96.7
	Capsule	96.9/96.9	97.8/94.4	99.0/95.5	97.5/95.5	98.7/94.5	99.5/96.9
	Hazelnut	69.9/86.4	100./99.3	99.9/98.6	99.7/97.3	100./100.	100./100.
	Metal Nut	100./99.5	99.9/99.5	99.9/98.4	96.0/91.6	100./99.5	100/98.9
	Pill	99.6/96.8	98.7/95.7	99.3/96.4	98.5/94.5	99.5/96.2	99.8/97.9
	Screw	99.3/95.8	96.5/89.0	97.0/93.0	99.7/97.9	97.9/94.0	99.1/95.8
	Toothbrush	99.9/94.7	97.4/95.2	99.6/96.8	99.9/99.2	99.3/98.4	98.5/95.2
	Transistor	95.2/90.0	98.0/93.8	98.3/92.5	99.6/97.4	100./100.	100./100.
	Zipper	99.9/99.2	99.5/97.1	99.3/97.1	99.1/94.4	99.8/97.5	99.5/97.5
Mean		96.5/95.2	98.8/96.2	99.4/97.3	99.0/96.5	99.6/97.8	99.7/98.3

and

Table 3. Comparison with SoTA methods on MVTec-AD dataset for multi-class anomaly detection with ${\mathrm{AUROC}}_{\mathrm{cls}}$/${\mathrm{AUROC}}_{\mathrm{sp}}$ metrics.

Category		RD4AD [6]	UniAD [5]	ViTAD [40]	DiAD [38]	MambaAD [53]	Ours
		WRes50 (IN1K)	Eff-b4 (IN1K)	ViT-S (DINO)	Res50 (IN1K)	Res34 (IN1K)	WRes50 (IN1K)
Texture	Carpet	98.5/99.0	99.8/98.5	99.5/99.0	99.4/98.6	99.8/99.2	99.4/99.0
	Grid	98.0/96.5	98.2/63.1	99.7/98.6	98.5/96.6	100./99.2	99.9/98.3
	Leather	100./99.3	100./98.8	100./99.6	99.8/98.8	100./99.4	100./99.1
	Tile	98.3/95.3	99.3/91.8	100./96.6	96.8/92.4	98.2/93.8	100./96.1
	Wood	99.2/95.3	98.6/93.2	98.7/96.4	99.7/93.3	98.8/94.4	99.6/95.8
Object	Bottle	99.6/97.8	99.7/98.1	100./98.8	99.7/98.4	100./98.8	100./98.4
	Cable	84.1/85.1	95.2/97.3	98.5/96.2	94.8/96.8	98.8/95.8	99.0/98.5
	Capsule	94.1/98.8	86.9/98.5	95.4/98.3	89.0/97.1	94.4/98.4	97.8/98.8
	Hazelnut	60.8/97.9	99.8/98.1	99.8/99.0	99.5/98.3	100./99.0	100./98.5
	Metal Nut	100./94.8	99.2/62.7	99.7/96.4	99.1/97.3	99.9/96.7	99.8/97.6
	Pill	97.5/97.5	93.7/95.0	96.2/98.7	95.7/95.7	97.0/97.4	98.6/98.7
	Screw	97.7/99.4	87.5/98.3	91.3/99.0	90.7/97.9	94.7/99.5	97.1/99.4
	Toothbrush	97.2/99.0	94.2/98.4	98.9/99.1	99.7/99.0	98.3/99.0	96.1/98.6
	Transistor	94.2/85.9	99.8/97.9	98.8/93.9	99.8/95.1	100./96.5	100./97.0
	Zipper	99.5/98.5	95.8/96.8	97.6/95.9	95.1/96.2	99.3/98.4	98.4/98.6
Mean		94.6/96.1	96.5/96.8	98.3/97.7	97.2/96.8	98.6/97.7	99.0/98.2

, while the results for the VisA dataset are shown in

Table 4. Comparison with SoTA methods on VisA dataset for multi-class anomaly detection with ${\mathrm{AP}}_{\mathrm{cls}}$/$\mathrm{F}1{\max }_{\mathrm{cls}}$ metrics.

Category		RD4AD [6]	UniAD [5]	ViTAD [40]	DiAD [38]	MambaAD [53]	Ours
		WRes50 (IN1K)	Eff-b4 (IN1K)	ViT-S(DINO)	Res50 (IN1K)	Res34 (IN1K)	WRes50 (IN1K)
Complex structure	PCB1	95.5/91.9	92.7/87.8	94.7/91.8	88.7/80.7	93.0/91.6	99.2/96.6
	PCB2	97.8/94.2	87.7/83.1	89.9/85.3	91.4/84.7	93.7/89.3	98.3/93.9
	PCB3	96.2/91.0	78.6/76.1	91.2/83.9	87.6/77.6	94.1/86.7	96.3/89.3
	PCB4	99.9/99.0	98.9/94.3	98.9.96.6	99.5/97.0	99.9/98.5	99.8/98.0
Multiple instance	Macaroni1	61.5/76.8	79.8/69.9	83.9/76.7	85.2/78.8	89.8/81.6	94.5/88.8
	Macaroni2	84.5/83.8	71.6/69.9	74.7/74.9	57.4/69.5	78.0/73.8	80.9/75.8
	Capsules	90.4/81.3	55.6/76.9	87.6/79.8	69.0/78.5	95.0/88.8	90.5/82.4
	Candle	92.8/86.0	94.0/86.1	91.2/83.7	9.0/87.6	96.9/90.1	97.0/91.3
Single instance	Cashew	95.8/90.7	92.8/91.4	94.2/86.1	95.7/89.7	97.3/91.1	99.0/94.8
	Chewing Gum	97.5/92.1	96.2/95.2	97.7/91.4	99.5/95.9	98.9/94.2	99.5/97.5
	Fryum	97.9/91.5	83.0/85.0	97.4/90.9	95.0/87.2	97.7/90.5	96.3/88.6
	Pipe Fryum	98.9/96.5	94.7/93.9	99.0/94.7	98.1/93.7	99.3/97.0	99.6/97.5
Mean		92.4/89.6	85.5/84.4	91.7/86.3	88.3/85.1	94.5/89.4	95.9/91.2

and

Table 5. Comparison with SoTA methods on VisA dataset for multi-class anomaly detection with ${\mathrm{AUROC}}_{\mathrm{cls}}$/${\mathrm{AUROC}}_{\mathrm{sp}}$ metrics.

Category		RD4AD [6]	UniAD [5]	ViTAD [40]	DiAD [38]	MambaAD [53]	Ours
		WRes50 (IN1K)	Eff-b4 (IN1K)	ViT-S(DINO)	Res50 (IN1K)	Res34 (IN1K)	WRes50 (IN1K)
Complex structure	PCB1	96.2/99.4	92.8/93.3	95.8/99.5	88.1/98.7	95.4/99.8	99.3/99.7
	PCB2	97.8/98.0	87.8/93.9	90.6/97.9	91.4/95.2	94.2/98.9	98.1/98.8
	PCB3	96.4/97.9	78.6/97.3	90.9/98.2	86.2/96.7	93.7/99.1	96.3/99.0
	PCB4	99.9/97.8	98.8/94.9	99.1/99.1	99.6/97.0	99.9/98.6	99.7/98.2
Multiple instance	Macaroni1	75.9/99.4	79.9/97.4	85.8/98.5	85.7/94.1	91.6/99.5	94.7/99.4
	Macaroni2	88.3/99.7	71.6/95.2	79.1/98.1	62.5/93.6	81.6/99.5	81.0/98.4
	Capsules	82.2/99.4	55.6/88.7	79.2/98.2	58.2/97.3	91.8/99.1	83.0/99.3
	Candle	92.3/99.1	94.1/98.5	90.4/96.2	92.8/97.3	96.8/99.0	96.6/99.0
Single instance	Cashew	92.0/91.7	92.8/98.6	87.8/98.5	91.5/90.9	94.5/94.3	97.9/99.2
	Chewing Gum	94.9/98.7	96.3/98.8	94.9/97.8	99.1/94.7	97.7/98.1	98.9/98.9
	Fryum	95.3/97.0	83.0/95.9	94.3/97.5	89.8/97.6	95.2/96.9	92.0/97.7
	Pipe Fryum	97.9/99.1	94.7/98.9	97.8/99.5	96.2/99.4	98.7/99.1	99.2/99.4
Mean		92.4/98.1	85.5/95.9	90.5/98.2	86.8/96.0	94.3/98.5	94.7/98.9

. It is evident that our proposed framework outperforms the second-best baseline Mamba [53] at image-level performance. However, the pixel-level performance is slightly weaker. We attribute this in part to the fact that, similar to UniAD [5], our end-to-end method downsamples the feature maps to a lower resolution for reconstruction, which may result in a loss of localization precision compared to multi-scale reconstruction-based [6,53] approaches. Additionally, the qualitative results, as shown in Figure 6, visualize the predictions of our model compared to UniAD.

4.2. Ablation Studies

Effectiveness on Different Pre-trained Backbones. To validate the effectiveness of our framework design across different feature extractors, we examined several popular pre-trained backbones used in recent state-of-the-art works, in addition to WideResNet50 used in our main experiments. These include ResNet34 and ResNet50 from the well-known ResNet [11] series, EfficientNet-B4 from the EfficientNet [10] series, and ViT-S from the vision transformer [54] series. Notably, WideResNet50, ResNet34, ResNet50, and EfficientNet-b4 are all supervised-trained on ImageNet1k [4], while ViT-S was selected based on DINO [56] self-supervised training. We tested the performance of both homogeneous (DualAD(Ho)) and heterogeneous (DualAD(He)) CDBN designs and reported the corresponding model complexity. As shown in

Table 6. Ablation studies on pre-trained backbones. The model complexity and performance metrics of the two proposed designs on four different backbones are reported.

Method		Params (M)	FLOPs (G)	Metrics
				${\mathrm{AUROC}}_{\mathrm{cls}}$	${\mathrm{AP}}_{\mathrm{cls}}$	$\mathrm{F}1{\max }_{\mathrm{cls}}$	${\mathrm{AUROC}}_{\mathrm{sp}}$
DualAD(Ho)	WRes50	137.3	24.1	98.8	99.6	97.9	98.1
	Res34	89.0	17.4	98.3	99.4	97.4	97.9
	Res50	98.0	18.2	98.3	99.3	97.6	97.9
	Eff-b4	86.7	15.3	98.8	99.6	98.0	98.0
	ViT-S	91.6	19.4	98.5	99.4	98.2	98.0
DualAD(He)	WRes50	97.5	15.5	99.0	99.7	98.3	98.2
	Res34	40.9	7.2	98.2	99.4	97.6	97.9
	Res50	54.2	9.6	98.3	99.4	97.8	98.1
	Eff-b4	37.5	4.8	98.7	99.6	98.2	98.1
	ViT-S	50.2	10.5	98.4	99.4	98.1	98.1

, our model’s performance under heterogeneous design is comparable to that under homogeneous design, while being more lightweight. Overall, our framework performs best with WideResNet50.

The Architecture Design of CDBN. We compared the performance of the reconstruction models under our proposed Coupled Dual-Branch Network (CDBN) architecture with that of single-branch architectures (i.e., using only transformer-based UniAD [5] or a single MMLP) across three pre-trained backbones, as shown in

Table 7. Ablation studies on architecture designs. Performance metrics ${\mathrm{AUROC}}_{\mathrm{cls}}$/${\mathrm{AP}}_{\mathrm{cls}}$/$\mathrm{F}1{\max }_{\mathrm{cls}}$/${\mathrm{AUROC}}_{\mathrm{sp}}$ are reported.

Method	Backbones
	WRes50	Eff-b4	ViT-S
${\mathrm{UniAD}}_{\mathrm{d}=256,\mathrm{l}=4}$	91.7/96.9/94.3/96.6	97.3/99.1/96.8/96.9	96.8/98.8/97.2/97.6
${\mathrm{UniAD}}_{\mathrm{d}=1024,\mathrm{l}=2}$	97.7/99.2/97.1/97.6	98.6/99.5/97.8/97.1	97.9/99.3/97.8/97.8
${\mathrm{UniAD}}_{\mathrm{DF}}$	96.1/98.7/95.9/97.3	98.2/99.3/97.5/97.0	97.7/99.1/97.6/97.7
MMLP	97.3/98.8/96.7/97.3	95.1/97.3/94.8/96.9	97.2/98.5/96.9/97.6
DualAD(Ho)	98.8/99.6/97.9/98.1	98.8/99.6/98.0/98.0	98.5/99.4/98.2/98.0
DualAD(He)	99.0/99.7/98.3/98.2	98.7/99.6/98.2/98.1	98.4/99.4/98.1/98.1

. The results demonstrate that UniAD with a 2-layer encoder–decoder and 1024 embedding dimensions consistently outperforms the UniAD with a 4-layer encoder–decoder and 256 embedding dimensions, which aligns with our analysis in Section 3.2. Additionally, both of our CDBN designs exhibit superior overall performance compared to single-branch architectures. Specifically, to further validate the effectiveness of our CDBN design, we also compared a simple decision fusion (DF) of UniAD models with a 2-layer encoder–decoder (1024 embedding dimensions) and a 4-layer encoder–decoder (256 embedding dimensions). As shown in Table 7, the results reveal that simple decision fusion between the two networks does not yield performance improvements, whereas our coupled dual-branch design more effectively leverages the strengths of both architectures, significantly enhancing overall performance.

Investigating the Impact of the Noise Scale. The scale of noise in feature perturbation controls the distance between the synthesized anomalous features and the reconstructed normal features. Specifically, an excessively large noise scale can make the model overly sensitive to noise, thereby impairing the reconstruction of normal features and leading to erroneous discrimination. On the other hand, a too-small noise scale can result in a blurred decision boundary. Moreover, due to differences among feature extractors, the impact of noise scale may vary. Figure 7 illustrates the influence of noise scale $\alpha$ on model performance when using different pre-trained backbones as feature extractors. From the overall performance curve changes, the selection of an appropriate noise scale appears to be related to the complexity of the model. For instance, implementations based on WideResNet50 and ViT-S require a larger noise scale compared to those based on ResNet34 and EfficientNet-b4 to achieve peak performance.

5. Discussion

In this work, we introduced DualAD, a novel framework for tackling multi-class unsupervised anomaly detection tasks through end-to-end feature reconstruction. We proposed the CDBN, which synergistically integrates a WSN with an NDN to harness their collective strengths, thereby enhancing overall performance. We proposed two CDBN designs: a homogeneous model based entirely on transformers, and a more lightweight heterogeneous design that integrates a transformer with an MMLP. Extensive experiments on the MVTec AD [12] and VisA [13] datasets demonstrated the effectiveness of DualAD, achieving state-of-the-art performance and showcasing its versatility across various pre-trained backbones with differing architectures.

While the results on existing benchmark datasets are promising, we recognize that several important challenges and limitations remain, which should be addressed in future work.

First, despite the excellent performance achieved on MVTec AD [12] and VisA [13], these datasets may not fully capture the diversity and complexity of real-world scenarios. Objects within the same category can exhibit greater variability in appearance than those in these datasets. The current model may not fully generalize to such diversity, and as a result, its applicability to more complex real-world anomaly detection tasks may be limited. If the model were to be applied to more diverse or challenging datasets, such as those with a greater variety of object textures or more noisy data, we hypothesize that performance could degrade, particularly in terms of detecting subtle anomalies. In this case, methods such as domain adaptation or the integration of category labels during training could help the model to better generalize to these real-world complexities, ensuring robustness across a broader range of scenarios.

Second, the scalability of the DualAD framework to larger datasets or real-time processing scenarios remains a significant challenge. The current model may face difficulties when applied to datasets with a substantially larger number of instances or when deployed in real-time environments where computational efficiency is crucial. If the framework were required to operate in such large-scale or real-time scenarios, we anticipate that the computational overhead would become a bottleneck. To mitigate this, future work could focus on optimizing the model’s architecture for faster inference or leveraging more efficient hardware for deployment.

Third, while anomaly detection technologies hold significant potential, their ethical implications must not be overlooked, particularly in sensitive fields such as medical diagnostics and video surveillance. The use of these technologies must comply with stringent privacy and security standards. Therefore, future research should also consider the ethical dimensions of anomaly detection, ensuring that models not only achieve high accuracy but also respect privacy regulations and ethical guidelines.

6. Conclusions

In this study, we introduced the DualAD framework, a promising solution for multi-class unsupervised anomaly detection that enhances performance and flexibility across various backbone architectures. Our extensive experiments highlight its potential to achieve state-of-the-art results on widely-used benchmark datasets, including MVTec AD [12] and VisA [13].

Despite these achievements, several challenges remain. In real-world scenarios, objects within each category often exhibit greater variability in appearance compared to the instances in the MVTec-AD and VisA datasets, which may hinder the model’s ability to generalize effectively. To address this limitation, future research could explore techniques such as domain adaptation or the integration of category labels during training. These strategies could enable the model to better capture the complex distribution patterns of multi-class data, offering a promising direction for further investigation. Moreover, future efforts should focus on improving the scalability and efficiency of the framework, while ensuring its alignment with privacy regulations and ethical standards.