1. Introduction
With the rise of industrialization and mechanization, dual-motor synchronous control systems have become prevalent in contemporary industrial production and manufacturing sectors, including robotics, electric vehicle drives, aerospace, and high-precision medical equipment. However, insufficient synchronization control accuracy can lead to decreased production efficiency, reduced equipment lifespan, diminished product quality, and even potential safety hazards. Therefore, enhancing the precision of synchronous control is of significant research importance and holds promising application prospects [
1,
2,
3].
The main reasons why synchronous errors in a dual-motor system are challenging to eliminate are as follows [
4,
5]:
The dual motor operates in different load environments due to the asymmetry of mechanical devices and fluctuations in external disturbance;
The uncertainty of the complex environment and the nonlinear characteristics of the dual-motor system;
There are issues related to model mismatch and parameter mismatch in the dual motors.
Therefore, it is essential to select an appropriate synchronous control strategy and design advanced error elimination algorithms to enhance the reliability and stability of dual-motor synchronous control. Currently, among the commonly used synchronous control strategies [
6], parallel control and master–slave control are classified as noncoupled and semi-coupled, respectively, resulting in the limited synchronization performance of dual motors when subjected to external disturbances. Although deviation coupling control can enhance synchronous performance, it requires substantial computational resources and involves a complex control structure, making it difficult to implement in dual-motor control systems. The cross-coupling control proposed by Koren [
7] compensates for the differences in synchronous speed between the two motors by adjusting the current reference values using a gain coefficient. This method effectively reduces speed errors in both motors and enhances the tracking performance of the dual-motor system.
To further enhance the performance of the synchronous controller, Liu et al. [
8], Chen et al. [
9], and Zhu et al. [
10] proposed the integration of PID control, fuzzy control, and vector control into the cross-coupling control strategy. This approach improved the synchronization performance of the dual-motor system to a significant extent. Although traditional PID control is widely utilized because of its straightforward and easily adjustable control structure, it has several drawbacks, including limited adaptability, low stability, and decreased control accuracy in complex environments. Furthermore, due to the inherent nonlinear characteristics of dual-motor systems, PID control is inadequate to satisfy its high synchronization performance requirements [
11]. Fuzzy control relies on the fuzzy rules established by researchers and experts to achieve high-precision control. However, this method requires a substantial number of operations and complex rule formulation, in addition to the challenge of parameter tuning [
12]. Vector control necessitates decoupling calculations, which presents challenges such as a high computational load and a complex control structure. Additionally, the effectiveness of traditional decoupling strategies in achieving dynamic decoupling is limited, which significantly exacerbates system perturbations and, as a result, reduces the system’s dynamic performance [
13]. Wu et al. [
14] replaced traditional PID control combined with cross-coupling control with fuzzy PID control, resulting in significant improvements in the system’s stability and dynamic performance. However, challenges remained regarding complex calculations and parameter tuning. Cao et al. [
15] used particle swarm optimization (PSO) to adjust the fuzzy PID parameters, enabling the real-time online tuning of the PID parameters. This approach further enhanced the system’s response speed and synchronization performance. Li et al. [
16] proposed a cross-coupling control method based on sliding mode control (SMC), which significantly enhanced the robustness of the system and reduced the speed synchronous error during the dynamic process. Nevertheless, a notable drawback is that the switching function in SMC can induce chattering, and its impact on the stability of the system requires further optimization. Yang et al. [
17] improved the response speed and robustness of the dual-motor synchronous control system by enhancing the approach rate of the nonsingular terminal sliding mode control (NTSMC). They also designed a sliding mode observer to implement feedforward compensation for system disturbances. Ultimately, the feasibility and effectiveness of the proposed scheme were validated through experimental results. Liu et al. [
18] adopted a global fast terminal sliding mode control (GFTSMC). Unlike traditional SMC, this approach does not include a switching term, which helps to eliminate chattering issues, decrease convergence time, and enhance tracking accuracy. Chen et al. [
19] utilized second-order sliding mode control (2-SMC) technology to propose a novel robust control strategy for dual-motor systems. They demonstrated that both the speed tracking error and the synchronous error of the dual-motor system can converge to zero. Zhao et al. [
20] combined nonsingular fast terminal sliding mode control (NFTSMC) with a variable gain neural network (NN) observer, utilizing the neural network to observe and compensate for nonlinear friction. This method effectively addresses the coupling issues associated with synchronization and tracking, ensuring that the dual-motor control system converges rapidly with minimal steady-state error. Xu et al. [
21] enhanced the cross-coupling control strategy through linear active disturbance rejection control (ADRC), achieving a high-precision control of the dual-motor synchronous control system. This improvement effectively mitigates challenges such as parameter variations and both internal and external disturbances that are likely to arise during the control process. Zou et al. [
22] proposed a high-order ADRC strategy to enhance the tracking performance and robustness of motors. They also introduced the Bandwidth Method (BM) to simplify the parameter tuning of the controller, and experimentally demonstrated the superiority of this method over the SMC strategy. Ding et al. [
23] designed funnel tracking control and sliding mode synchronous control strategies based on the Finite-Time Extended State Observer (FTESO). The tracking error was constrained by the funnel function and transformed into a new error term, which effectively limited both the transient and steady-state tracking error responses, thereby improving the speed of error elimination.
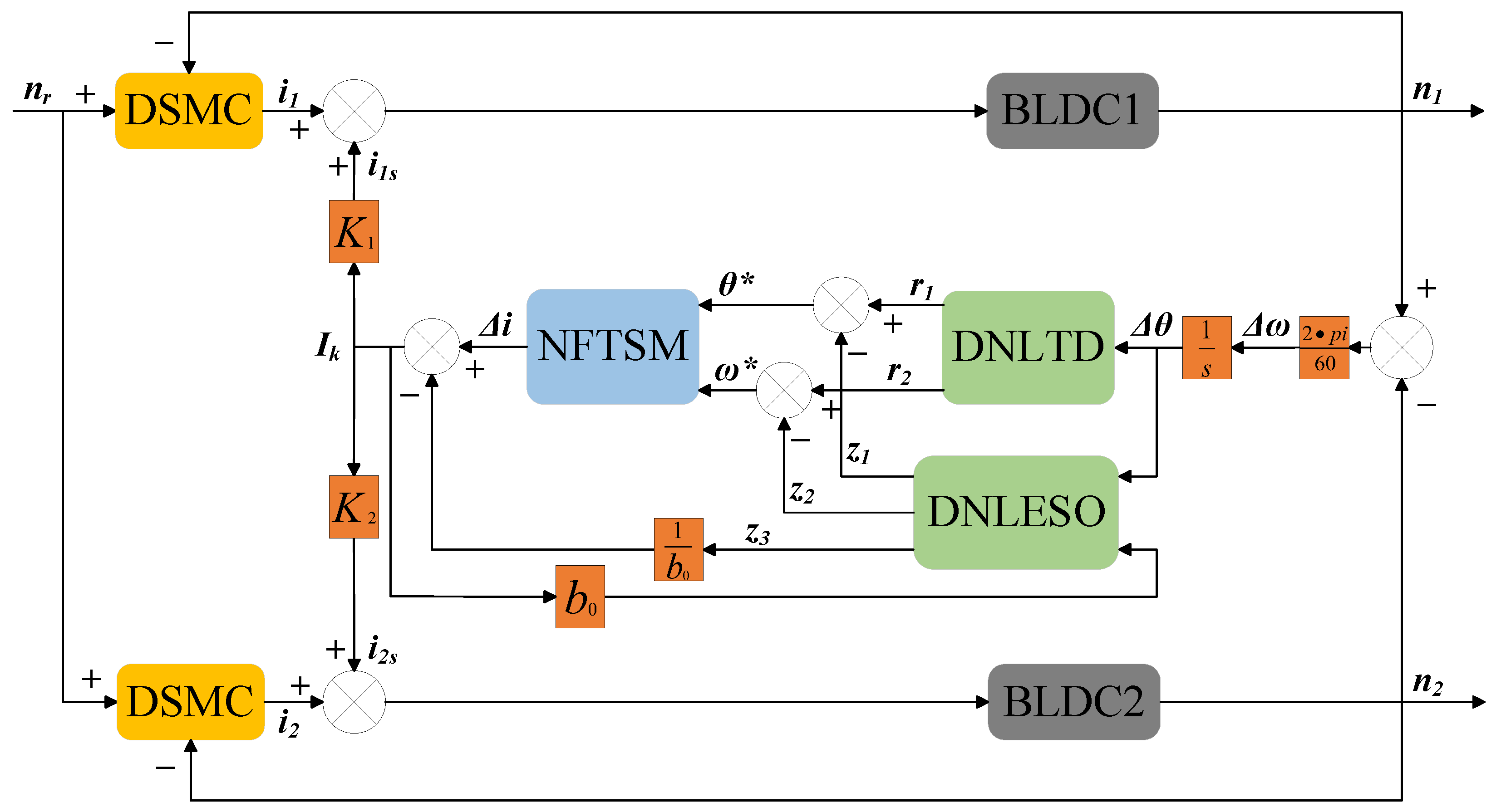
The research on the dual-motor synchronous control strategy significantly enhances the system’s robustness, providing both theoretical and practical value. However, several challenges remain to be addressed. Firstly, traditional control methods exhibit limitations when applied to nonlinear and discrete systems, which can adversely affect the system’s dynamic performance. Secondly, the approach rate in traditional sliding mode control incorporates a sign function, leading to the high-frequency switching of the controller, which negatively impacts stability. Furthermore, the fast terminal sliding mode method is susceptible to singularity issues and can induce sliding mode chattering, thereby compromising the convergence performance of the error. Lastly, the overly complex control structure results in high computational loads and complicates parameter tuning, ultimately affecting the system’s control efficiency. In response to the advantages and limitations of the control strategies discussed above, this paper proposes an ADRC-NFTSMC synchronous control strategy based on a cross-coupling control structure. This strategy is characterized by its rapid response speed, high synchronization accuracy, exceptional dynamic performance, and the elimination of chattering phenomena. It provides valuable insights and reference points for further research in this field. The main contributions of this paper are as follows:
A discrete sliding mode controller is designed to improve a single motor’s resistance to nonlinear disturbances. The saturation function is then used to optimize the approach rate, which reduces sliding mode chattering and enhances control smoothness.
To further enhance the system’s adaptability, DNLTD and DNLESO are designed to handle and compensate for uncertain external perturbations. This capability makes them more suitable for dual-motor synchronous control systems, given their discrete and nonlinear characteristics.
The design of NFTSMC enhances the robustness of the system by introducing an improved terminal attractor, which helps to avoid the singularity problem and reduces sliding mode chattering, all while improving the convergence speed of the sliding mode.
The improved ADRC-NFTSMC control strategy has been developed by integrating the cross-coupled control structure with the NFTSMC strategy optimized using DNLTD and DNLESO, resulting in enhanced synchronous control accuracy for the two-motor system.
The remainder of this paper is organized as follows: In the
Section 2, the mathematical model of the brushless direct current motor (BLDC) is established. In the
Section 3, an improved DSMC controller is designed for single-motor speed control, along with an analysis of system stability. In the
Section 4, an improved ADRC-NFTSMC is designed for dual-motor synchronous control, followed by a stability analysis of the system. In the
Section 5, anti-interference simulations for single-motor and dual-motor systems with different strategies are conducted. In the
Section 6, anti-interference experiments for single-motor and dual-motor systems with different strategies are performed. The
Section 7 provides a summary of the paper.
2. Mathematical Model of BLDC
This paper selects the BLDC as the subject of the experiment, operating in a star-shaped, three-phase, six-state control mode with two-phase conduction. To facilitate analysis, the motor model is simplified as follows, without compromising its accuracy [
24]:
Each stator core winding is evenly distributed and completely symmetrical according to a phase difference of 120°, with core saturation disregarded;
The air-gap magnetic field generated by the rotor’s permanent magnet is a uniformly distributed square wave, while the back electromotive force of the three-phase windings is a typical 120° trapezoidal wave;
The influence of the armature reaction of the stator winding is neglected, as are the effects of the commutation process and slot effects;
The magnetic circuit is not saturated, and there are no eddy currents or magnetic hysteresis loss;
The armature winding is uniformly and continuously distributed across the inner surface of the stator.
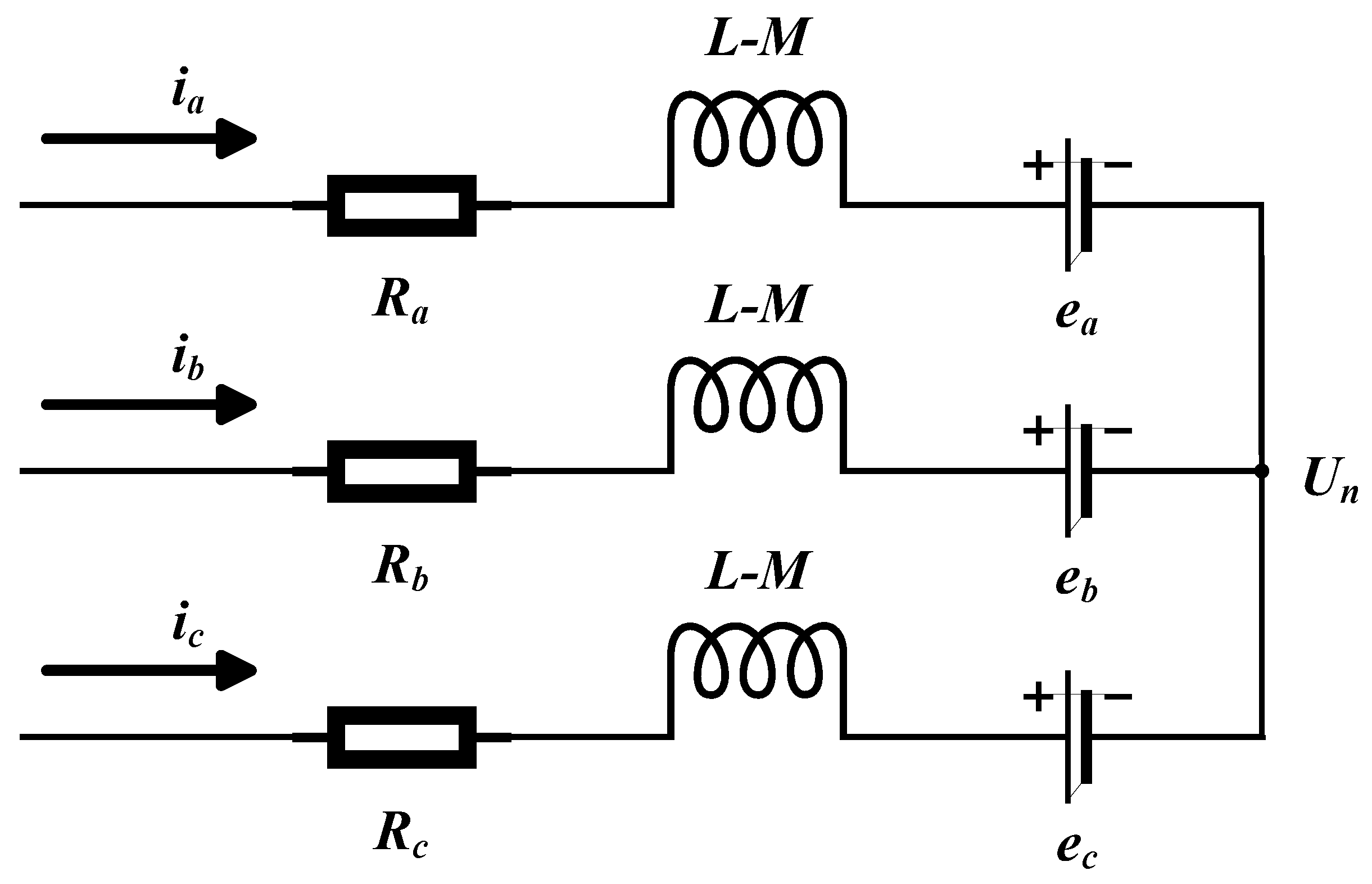
Based on the assumptions outlined above, the voltage balance equation for the stator’s three-phase windings in the BLDC system can be derived as follows [
25]:
where
represent the voltage of the three-phase stator windings (unit:
);
signify the resistance of the three-phase stator windings (unit:
);
indicate the phase current of the three-phase stator windings (unit:
);
denotes the self-inductance between each two-phase winding (unit:
);
represents the mutual inductance between each two-phase winding (unit:
);
signify the back electromotive force of the three-phase stator windings (unit:
); and
represents the midpoint voltage (unit:
).
Based on the complete symmetry and star connection of the three-phase windings in a BLDC, the following can be concluded:
Equation (1) can be derived from Equations (2) and (3) as follows:
Meanwhile, the equation for the midpoint voltage can be derived as follows:
The equivalent circuit diagram of the BLDC mathematical model can be derived from Equation (4), as illustrated in
Figure 1.
The equation for the electromagnetic torque generated by the stator winding is as follows:
During the 120° conduction and noncommutation process of the BLDC, the two-phase currents flowing through the three-phase windings are equal in magnitude but opposite in direction. Consequently, Equation (6) can be simplified as follows:
where
represents the electromagnetic torque of the motor (unit:
);
signifies the mechanical speed of the motor (unit:
);
denotes the motor torque constant (unit:
); and
represents the phase current of each phase winding (unit: A).
The mechanical motion equation for the BLDC is as follows:
where
represents the motor load torque (unit:
);
denotes the rotary inertia of the motor rotor (unit:
); and
indicates the motor damping coefficient (unit:
).
The equation for motor speed is as follows:
where
represents the motor speed (unit:
).
5. Simulation and Analysis
In order to verify the feasibility of the control algorithms designed in this paper, the simulation model of the dual-motor servo system was analyzed numerically using MATLAB/Simulink 2023b. The parameters of the BLDC motor are detailed in
Table 1, while the simulation parameters for the controller are presented in
Table 2.
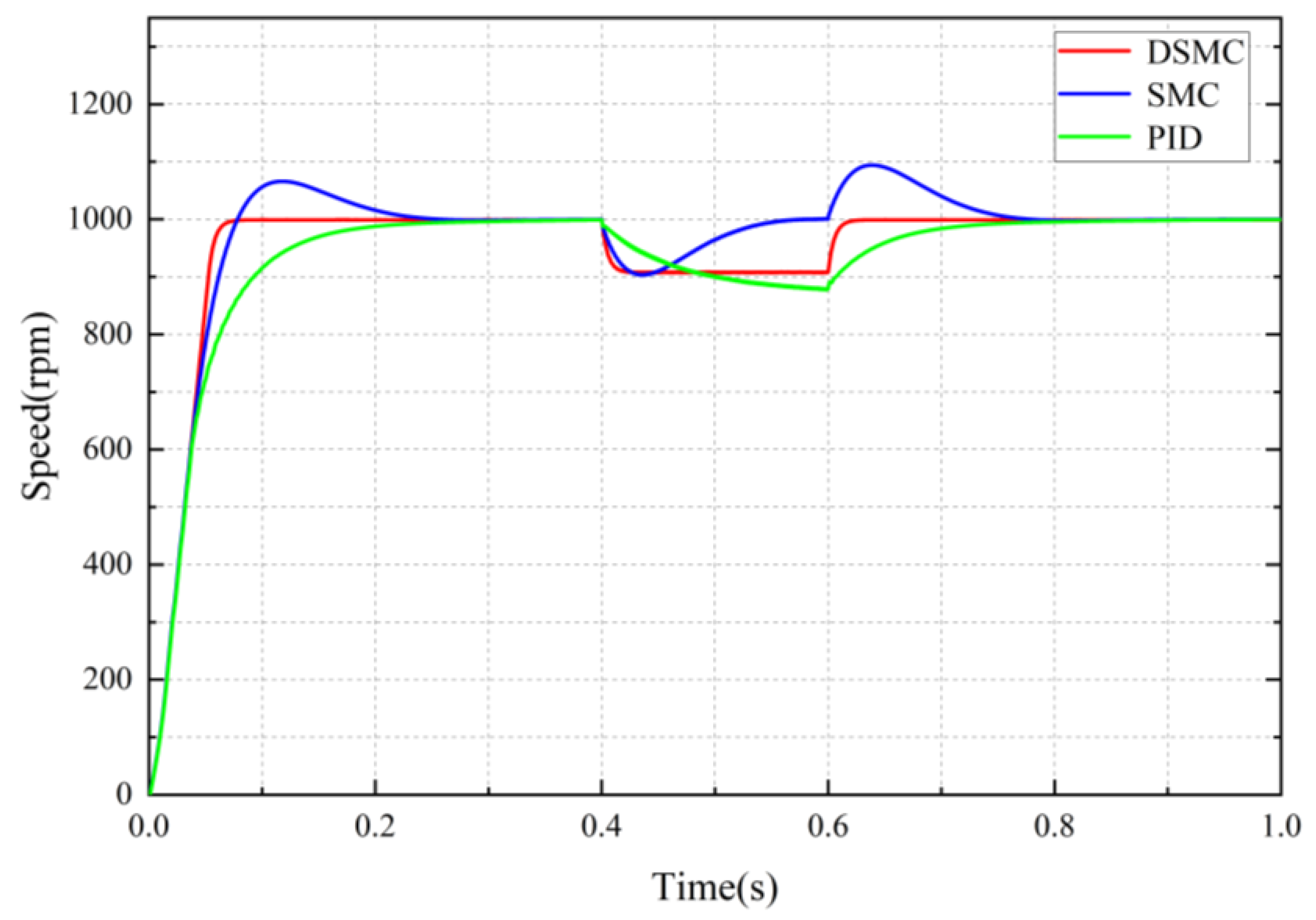
The tracking performance of the single motor is initially analyzed. The DSMC strategy proposed in this paper is then compared with the PID control strategy and the SMC strategy to evaluate the starting and dynamic performance of the single motor under different control strategies. Given an initial motor speed of 1000
, a load torque of 5
is suddenly applied at 0.4 s and lasts for 0.2 s.
Figure 5 and
Figure 6 illustrate the response speed curve and the tracking error curve of the single-motor system under different control strategies.
As illustrated in
Figure 5 and
Figure 6, the green curve denotes the motor speed under the PID control strategy, the blue curve indicates the motor speed under the SMC strategy, and the red curve represents the motor speed under the DSMC strategy.
As illustrated in the figure, the maximum overshoot of the motor under the SMC strategy is
, and it reaches a steady state at
. However, the motor’s starting time under both the PID and DSMC strategies is
and
, respectively. When a load of
is applied to the motor from
to
, the speed of the motor under the PID strategy does not converge, with a maximum tracking error of
, and it reaches a steady state again at
. The maximum motor speed tracking error with the SMC strategy is
, and the maximum overshoot is
after the load is removed at
, with steady state being achieved once more at
. The maximum motor speed tracking error using the DSMC strategy is
, and steady state is reached again at
.
Table 3 presents the performance of a single motor with different control strategies.
The simulation results indicate that the DSMC strategy used in this paper achieves a steady state at and , respectively, which is and faster than the SMC strategy at and , respectively, and and faster than the PID strategy at and , respectively. The maximum motor tracking error with the DSMC strategy is , representing a improvement compared to the PID strategy’s error of . Furthermore, it demonstrates a improvement over the SMC strategy’s error of , while effectively avoiding overshoot. It is evident that the response speed of the single motor utilizing the PID strategy is the slowest, indicating that the PID strategy has limited adaptability to the motor’s dynamic characteristics. Furthermore, the inability to achieve speed convergence when subjected to load variations suggests that the PID strategy exhibits poor robustness. In contrast, the response speed of the single motor under the SMC strategy is rapid; however, it experiences an overshoot phenomenon, indicating that the control smoothness and robustness of the SMC strategy are inadequate. Compared to the two previously mentioned control strategies, the DSMC strategy proposed in this paper enhances both the response speed and robustness of the motor, demonstrating superior control performance.
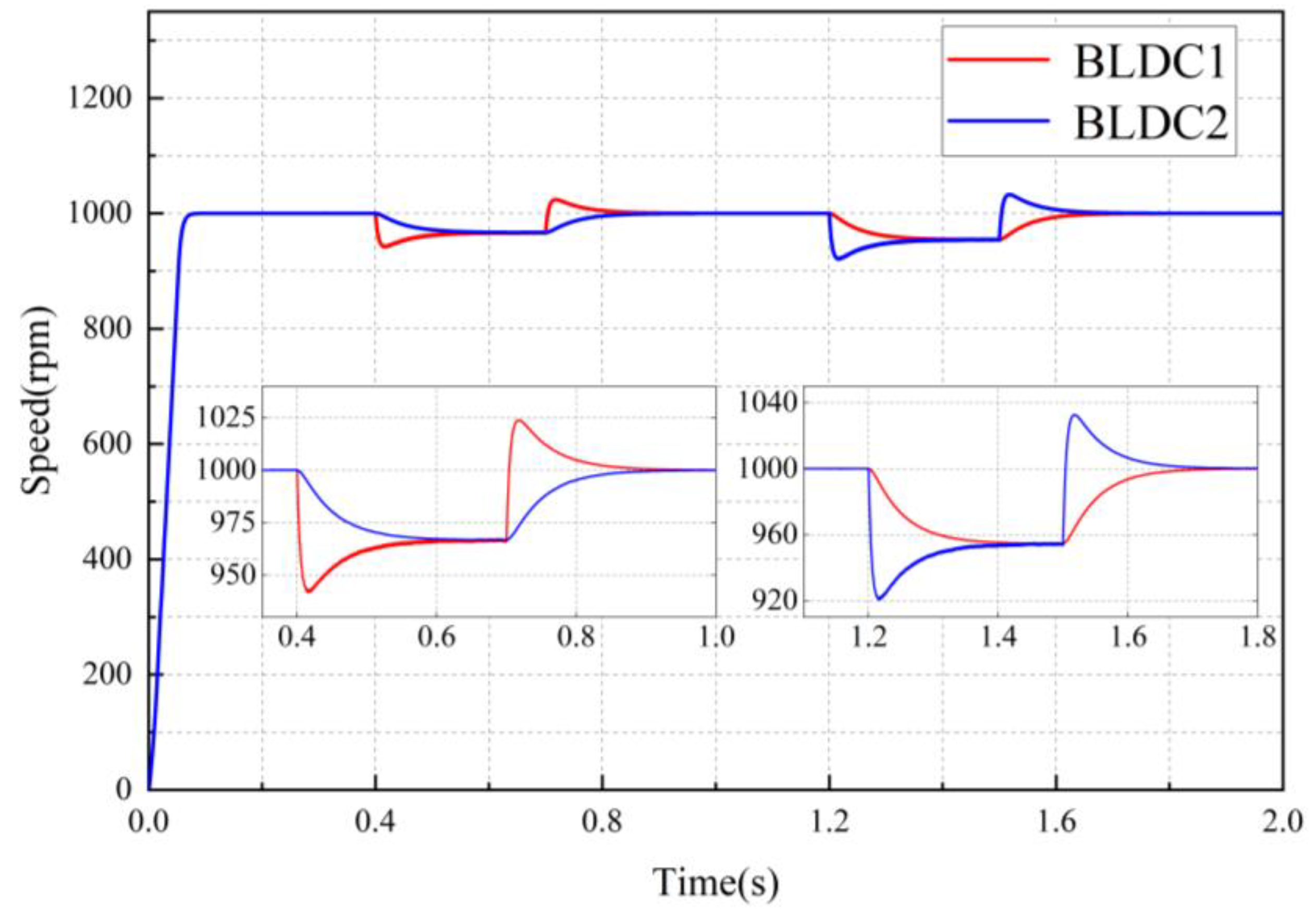
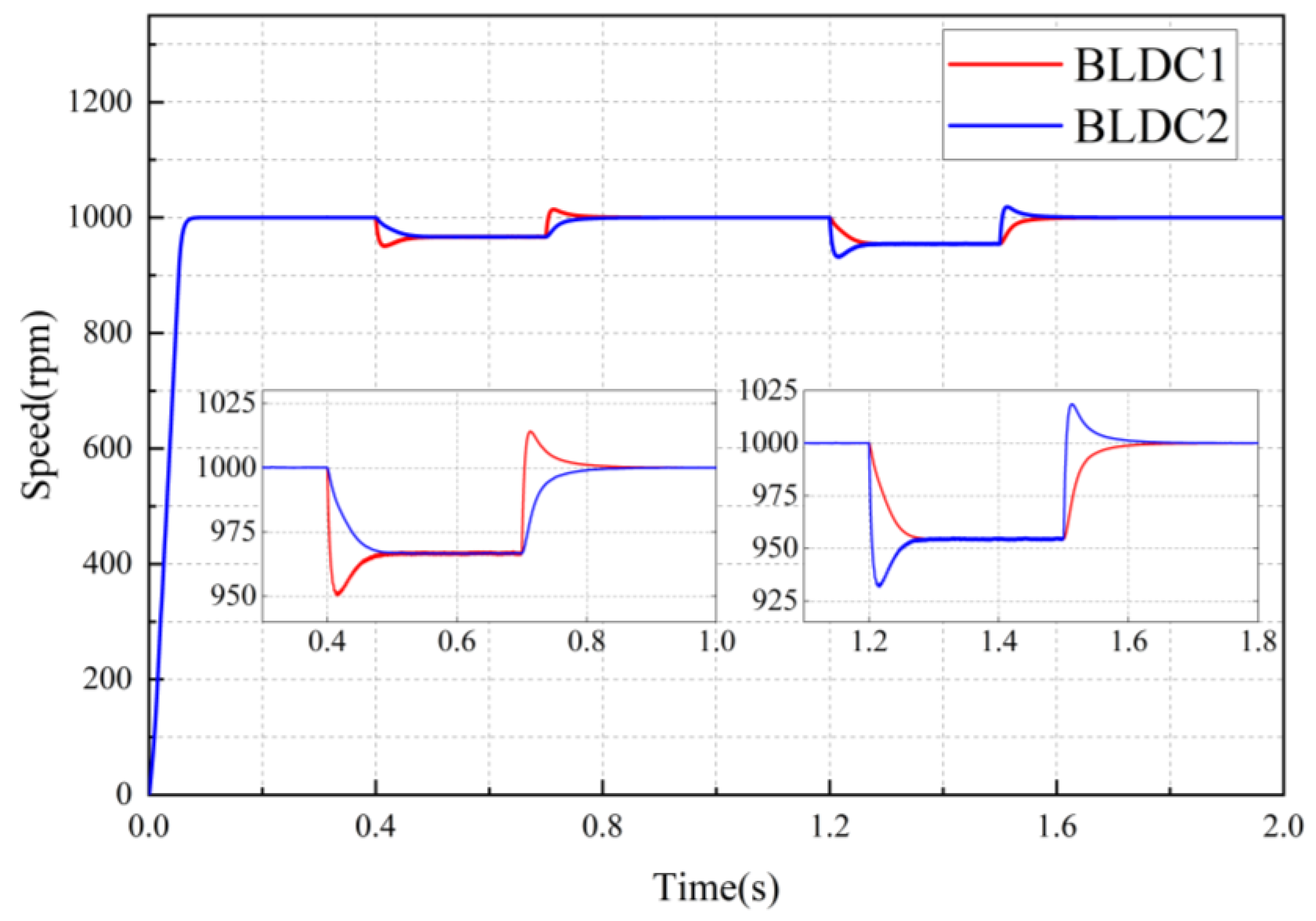
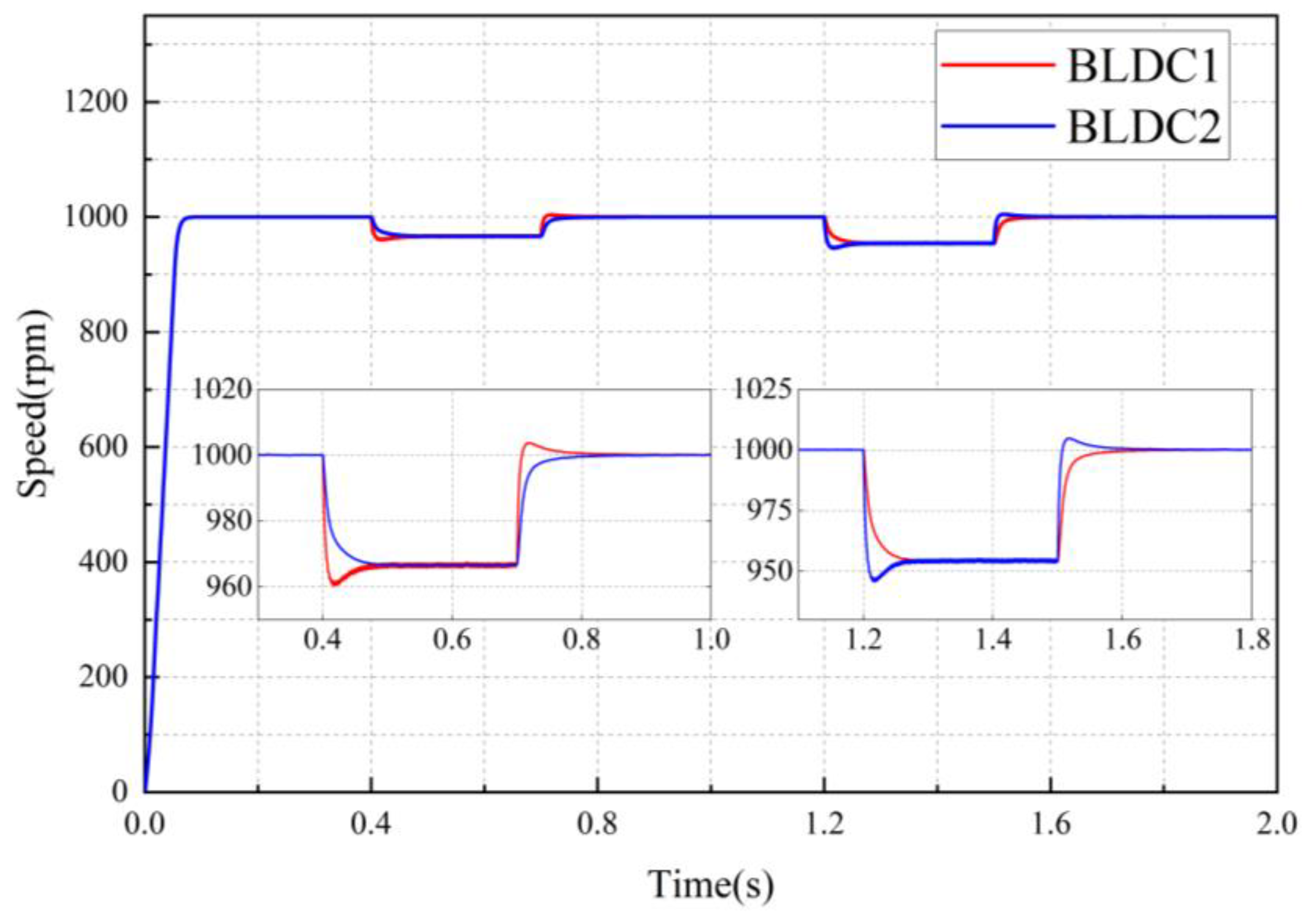
To assess the feasibility and effectiveness of the ADRC-NFTSMC synchronous control strategy proposed in this paper, a comparison is conducted with the SMC and NFTSMC strategies. With both motors starting at an initial speed of 1000
, a load torque of 2.5
is applied to BLDC1 at 0.4 s–0.7 s, while a load torque of 5
is applied to BLDC2 between 1.2 s–1.5 s.
Figure 7,
Figure 8 and
Figure 9 illustrate the speed curves of the dual-motor servo system under variable loads for the SMC, NFTSMC, and ADRC-NFTSMC strategies, respectively.
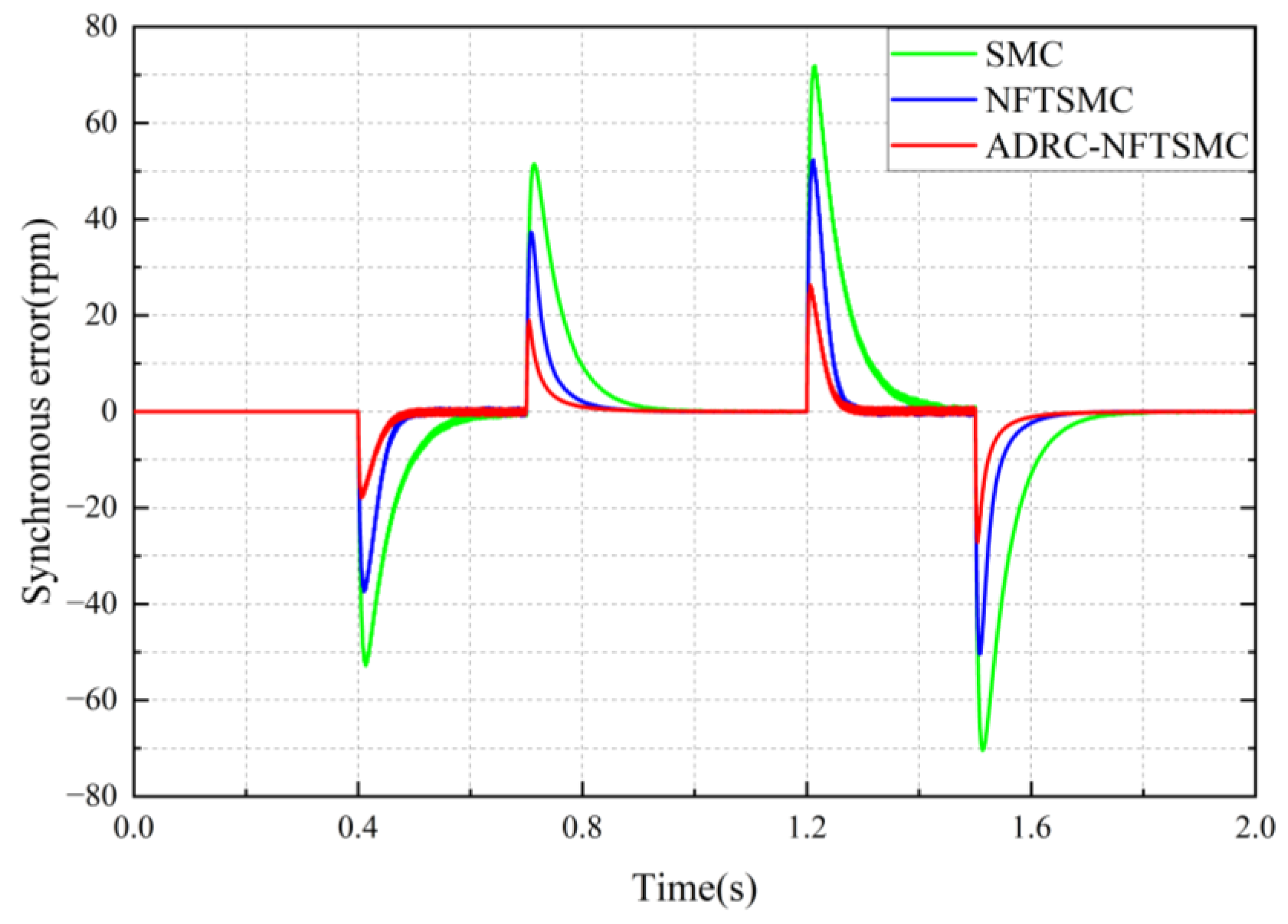
Figure 10 presents the synchronous error curve of the dual-motor servo system under these three synchronous control strategies with the same alternating load.
As illustrated in
Figure 10, the green curve represents the dual-motor synchronous error under the SMC strategy, the blue curve represents the dual-motor synchronous error under the NFTSMC strategy, and the red curve indicates the dual-motor synchronous error under the ADRC-NFTSMC strategy.
When the BLDC1 is subjected to a load torque of at , the maximum synchronous control error using the SMC strategy reaches , and the synchronous error converges to 0 at , and fluctuates back to a maximum of after the load is removed at , subsequently converging to 0 again at . The maximum synchronous control error using the NFTSMC strategy is . The synchronous error first converges to 0 at . After the load is removed at , the maximum fluctuation of the synchronous error remains , and the error converges to 0 again by . The maximum synchronous error of the ADRC-NFTSMC strategy is , with the error converging to 0 at . After the load is removed at , the maximum fluctuation of the synchronous error is , and the error converges to 0 again by .
When the BLDC2 is subjected to a load torque of
at
, the maximum synchronous control errors
for the SMC strategy, NFTSMC strategy, and ADRC-NFTSMC strategy are
,
, and
, respectively. The times
at which the synchronous error first converges to 0 are
,
, and
, respectively. After the load is removed at
, the maximum error
of synchronous control of the SMC strategy is
, which is approximately 1.4 times that of the NFTSMC strategy and 2.6 times that of the ADRC-NFTSMC strategy. The times
at which the synchronous error converges to 0 again are
,
, and
, respectively.
Table 4 presents the performance of the three control strategies under alternating load conditions.
The simulation results indicate that the maximum synchronous errors under the ADRC-NFTSMC strategy are and , respectively, following two sudden load changes. The system returns to a steady state at and , respectively. In comparison to the SMC strategy, the maximum synchronous errors of and increase by 65% and 64%, respectively, while the time taken to return to the steady state improves by and , with times of and , respectively. When compared to the NFTSMC strategy, the maximum synchronous errors of and increase by and , respectively, while the time to return to the steady state also increases by and , respectively, with times of and . It is evident that the NFTSMC strategy exhibits a faster error elimination speed and greater robustness than the SMC strategy; however, it still has some drawbacks when compared to the ADRC-NFTSMC strategy. Although the error elimination speeds of the two strategies are similar, the synchronous error produced by the dual-motor system under the ADRC-NFTSMC strategy, following two load disturbances, is smaller. This result demonstrates the superior robustness and dynamic control accuracy of the ADRC-NFTSMC strategy.
6. Experiments and Analysis
To further demonstrate the effectiveness of the control algorithm proposed in this paper, an experimental platform for dual-motor synchronous control was constructed, as illustrated in
Figure 11. This platform primarily consisted of a power supply module, upper computer, control and driver module, encoder, and the BLDC. The power supply was a 48 V DC source (Manufacturer: Jichuang Robotics Intelligent Technology Co., Ltd., Taian City, China), the encoder model was K3808-1000BM-C526 (Manufacturer: Haixi Information Technology Co., Ltd., Suqian City, China) with 2500 ppr, the driver model was KYDBL4850 (Manufacturer: Koya Electronic Technology Co., Ltd., Jinan City, China), and the control board model was STM32F407-Explorer-V2 (Manufacturer: Starwing Electronic Technology Co., Ltd., Guangzhou City, China). The control algorithm was compiled and implemented on this control board using Visual Studio 2019 software. The motor parameters are presented in
Table 1 of the simulation experiment, while the experimental parameters of the controller are provided in
Table 5. The compiled program was imported into the control module, where the encoder transmitted the motor motion signals to the control module for closed-loop control. Subsequently, the controller parameters were tuned based on the motor operating data recorded by the upper computer to achieve optimal control performance.
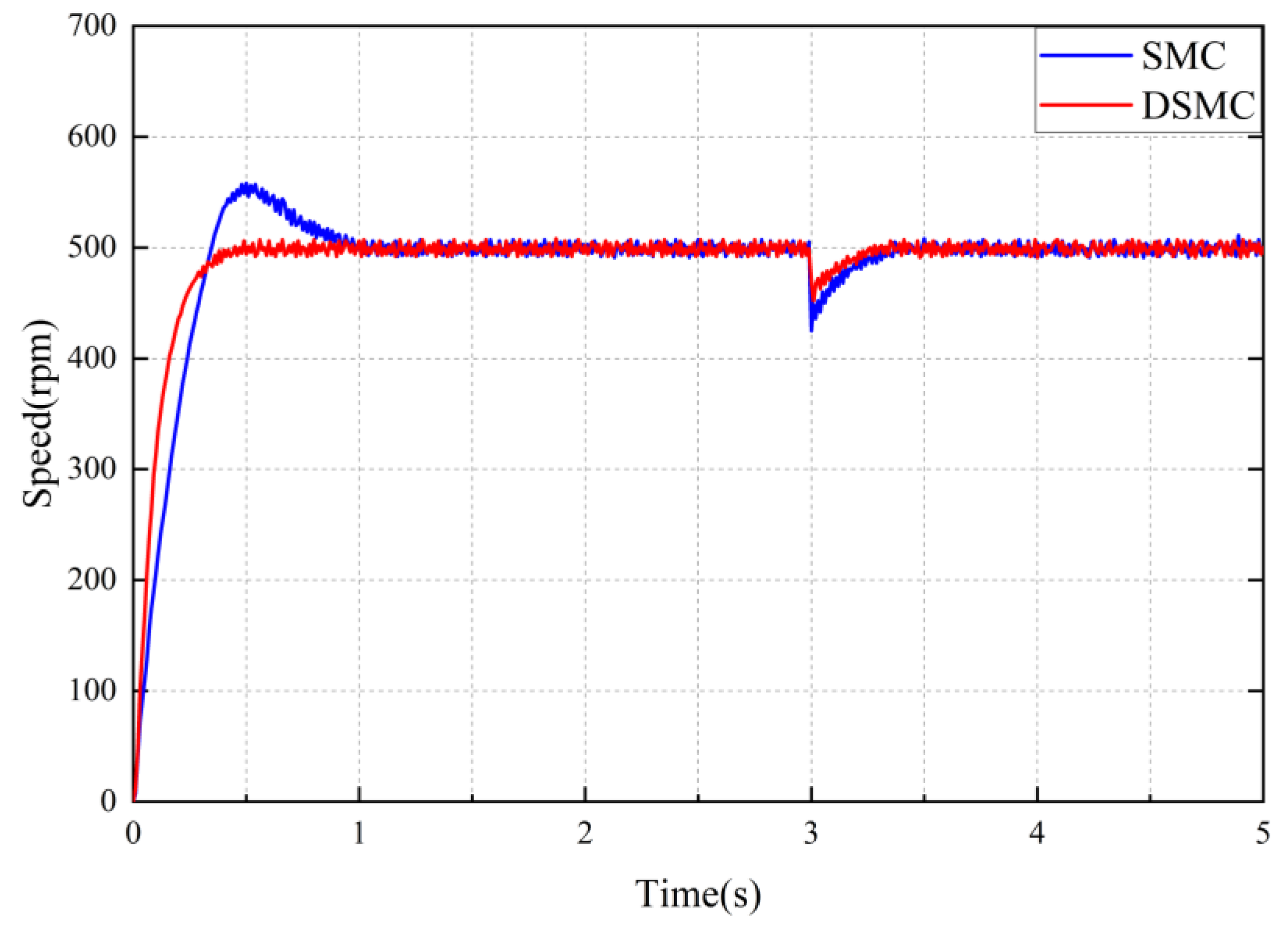
The performance comparison between the single-motor DSMC strategy and the SMC strategy is prioritized. Given that the motor’s reference speed is 500
and a load torque of 3
was applied at 3
, the speed curve of the single motor under different strategies is illustrated in
Figure 12, along with the tracking error curve presented in
Figure 13.
As illustrated in
Figure 12 and
Figure 13, the blue curve represents the motor speed under the SMC strategy, while the red curve represents the motor speed under the DSMC strategy.
The starting time
of the motor using the DSMC strategy is 0.547
shorter than that of the motor using the SMC strategy, and the motor using the SMC strategy exhibits an overshoot of
. As illustrated in
Figure 13, when a load torque of
is applied at
, the maximum fluctuations
in motor speed for the DSMC and SMC strategies are
and
, respectively, and the time
required to return to a steady state is
for the DSMC strategy and
for the SMC strategy.
Table 6 presents the performance of a single motor under different control strategies.
The experimental results indicate that the time required for the motor utilizing the DSMC strategy to reach a steady state is reduced by and compared to the motor employing the SMC strategy. Additionally, the robustness of the motor is improved by . Although the single motor using the SMC strategy does not experience overshooting during load perturbations, some overshooting still occurs during motor startup, accompanied by greater speed fluctuations during load disturbances. This indicates that the DSMC strategy provides superior robustness against disturbances. Furthermore, the motor controlled by the DSMC strategy demonstrates faster error convergence, demonstrating its superior dynamic control performance.
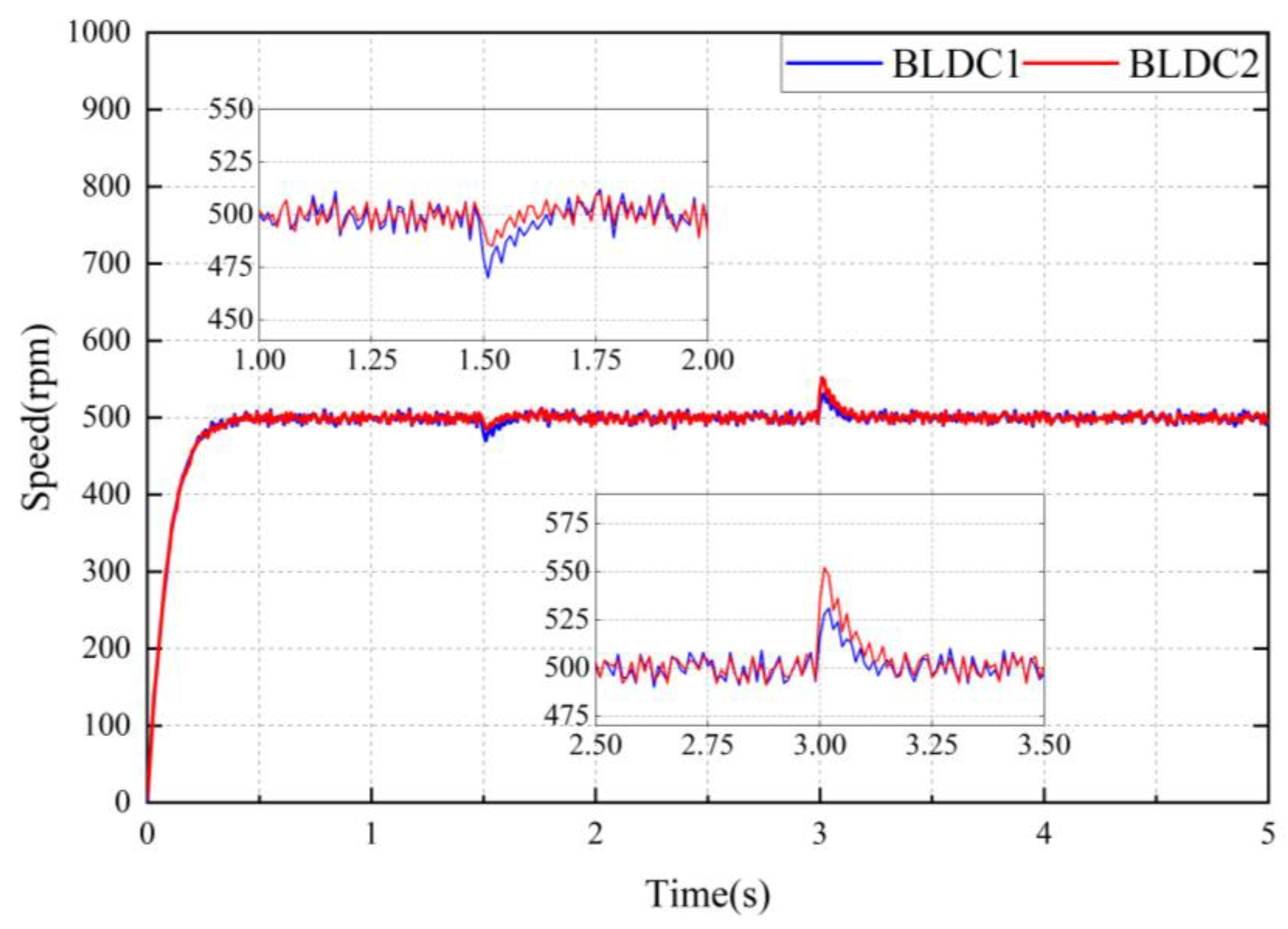
Next, the designed synchronous controller were analyzed experimentally, and the performance of the NFTSMC and ADRC-NFTSMC strategies is compared. Both motors were set to the same reference speed of
, a load torque of
was applied to BLDC1 at
, while a load torque of
was applied to BLDC2 at
. The synchronous error and response speed of the dual-motor system were then observed.
Figure 14 and
Figure 15 illustrate the speed curves of the dual-motor servo system under the NFTSMC and ADRC-NFTSMC strategies, respectively.
Figure 16 compares the synchronous errors of the dual-motor servo system under the two different control strategies.
As illustrated in
Figure 14,
Figure 15 and
Figure 16, the blue curve represents the dual-motor synchronous error under the NFTSMC strategy, while the red curve represents the dual-motor synchronous error under the ADRC-NFTSMC strategy.
When the BLDC1 is subjected to a load torque of at , the maximum synchronous control error of the dual-motor servo system using the NFTSMC strategy is , and the synchronous error converges to 0 at . In contrast, with the ADRC-NFTSMC strategy, the maximum synchronous control error is only , and the synchronous error converges to 0 at .
When the BLDC2 is subjected to a load torque of
at
, the maximum synchronous control errors
under the NFTSMC and ADRC-NFTSMC strategies are
and
, respectively, and the synchronous errors of the system converge to 0 again at
and
, respectively.
Table 7 presents the performance of the two control strategies under the same alternating load.
The experimental results indicate that the dual-motor system employing the ADRC-NFTSMC strategy enhances robustness by and response speed by compared to the dual-motor system utilizing the NFTSMC strategy. The dual-motor system with the NFTSMC strategy exhibits greater synchronous errors under identical load disturbances and a slower convergence speed for these errors. This clearly demonstrates that the ADRC-NFTSMC control strategy provides superior robustness and dynamic control performance, effectively improving both the response speed and synchronous control accuracy of the dual-motor system.