Wave Phase Coding Applied to Frequency-Shift Keying for Spectrally Efficient Underwater Optical Communication

Abstract

In the last decade, the advances in optoelectronics have led optical wireless communication to become an effective technology to transmit data in challenging environments like the underwater one. Unlike the well-established acoustic signaling, underwater optical communication enables high rates transmission even though they are limited to a shorter distance on the order of tens of meters. In fact, light propagation strongly suffers from attenuation caused by the channel. In such conditions, data transmission is typically based on modulation schemes providing high reliability at the expense of poor spectral efficiency. In this direction, herein we propose a novel modulation scheme that, by combining the principles of frequency and a novel phase modulation, referred to as wave phase coding, achieves a high spectral efficiency while maintaining a remarkable robustness to errors. Simulation results demonstrate that the proposed solution is able to achieve a convenient trade-off between spectral efficiency and reliability, outperforming both conventional schemes and hybrid techniques proposed in the literature.

1. Introduction

Approximately 70% of the Earth’s surface is covered by seas, oceans, and lakes, but the challenging accessibility of the underwater environment has long posed a significant obstacle for scientists and researchers seeking to understand its features and peculiarities. In this regard, technological advances over the past decades have proven to be fundamental in making the marine environment accessible for military and civilian applications, such as data collection, ocean exploration, coastal surveillance, and localization [1,2,3]. Many of these use cases require an underwater infrastructure that supports information exchange between entities acting as nodes of a network, such as sensors, Autonomous Underwater Vehicles (AUVs), buoys, and divers.

Contextually, the concept of the Internet of Underwater Things (IoUT) has been introduced as the latest technological frontier for monitoring and utilizing underwater environments [4,5]. Within this framework, underwater acoustic communication (UWAC) is now recognized as a well-established technology, enabling wireless data transmission over distances ranging from hundreds of meters to kilometers, but with poor performance in terms of rate [6,7,8]. Such a drawback is due to the narrow bandwidth of acoustic systems, the long propagation delay, and the effects of the channel, which degrade the signal quality and detection reliability [9]. So, part of the researchers’ interest has been recently oriented to the investigation of alternative and complementary solutions to deal with the challenges of underwater networks [10,11].

In the last decade, the development of efficient optical sources such as light-emitting diodes (LEDs) and laser diodes (LDs) has made wireless optics an attractive solution in various scenarios, including the emerging field of underwater optical communication (UWOC) [12]. By encoding the information through the fast modulation of the optical signal emitted by LEDs and leveraging the capability of a receiving photodetector (PD) to detect the signal intensity variations, it is possible to realize point-to-point links achieving high data rates on the order of megabits per second. Unfortunately, the propagation of light through the water medium is subject to attenuation, absorption, and scattering phenomena that limit the communication range to only tens of meters. Moreover, signal propagation is wavelength-dependent, and hence the water type and conditions lead the path loss to be different based on the portions of the visible light and ultraviolet spectrum exploited for UWOC [13,14]. The misalignment between transmitter and receiver may cause additional geometrical losses, impacting on the achievable transmission distance as well [15]. Therefore, the choice and implementation of an efficient transmission scheme that matches with the channel propagation properties results is one of the main challenges in UWOC.

1.1. State of the Art of Underwater Optical Signaling

As previously outlined, the performance of underwater communication systems is strictly dependent of the channel characteristics and properties. This is especially the case for UWOC, where modulation selection for transmission should provide a satisfactory trade-off between data rate and link reliability. Currently, the literature is mainly oriented to the investigation of single-carrier schemes thanks to their ease of implementation with respect to multi-carrier mechanisms. Aiming for low complexity, intensity modulation and direct detection (IM/DD) represent the category of simple and cost-effective modulation schemes typically used in optical communication, especially for short-range applications. The most widespread is On–Off Keying (OOK), characterized by a unitary spectral efficiency (SE) and providing a remarkable robustness to errors. The achievement of a data rate of hundreds of Mbits (up to Gbps) has been demonstrated in several experiments, considering a communication range up to 100 m [16,17]. In [18], a system based on OOK and a one-bit analog-to-digital converter is considered, with a novel deep learning-based architecture based on an autoencoder and generative adversarial network being proposed to equalize the channel and compensate the distortion due to quantization. Similarly to OOK, pulse amplitude modulation (PAM) works by modulating the intensity of a light pulse by potentially resorting to M different levels. So, SE is improved with respect to OOK, at the expense of a lower reliability and, therefore, a shorter achievable distance. The testing of a 4-PAM scheme is reported in [19], where a data rate of 3.8 Gbps is achieved over a 2 m link. In [20], a time-domain hybrid PAM realizes rate and distance adaptation over underwater optical wireless communications. PAM is a spectrally efficient scheme but power-inefficient. In the context of IM/DD approaches, pulse position modulation (PPM) provides essentially opposite performance, since it is oriented to high reliability at the expense of bandwidth inefficiency. An example of PPM applied to UWOC is given in [21], where an LD is employed as optical source in order to increase the directivity of the light beam and reduce the geometrical losses. In [22], a modified shortened PPM scheme is proposed to achieve a higher data rate with respect to the conventional PPM while maintaining robustness to errors. Several works present the performance analysis and comparison of IM/DD schemes, where it is possible to appreciate the trade-off between rate and reliability provided by the mentioned modulations [23,24,25,26].

As an alternative to IM/DD, coherent modulation and detection are considered in optical systems as well. In addition to intensity, coherent schemes allow the exploitation of other features of the optical carrier for data encoding, for instance phase and frequency. However, this is paid for in terms of receiver complexity that grows with respect to the IM/DD case. In this regard, quadrature amplitude modulation (QAM) is able to provide a high SE by increasing the size of the constellation, but the achievement of a satisfactory bit error rate (BER) is tied to the availability of a high signal-to-noise ratio (SNR) link [27]. Phase-shift keying (PSK) is another coherent modulation employable in UWOC. When the signaling vocabulary is binary, performance essentially follows the OOK behavior, but BER degrades when SE is increased through the use of a larger symbol vocabulary (as in PAM) [28,29]. Based on pure PSK, other derived modulations like differential PSK have been also considered for UWOC [30]. Differently from QAM and PSK, frequency-shift keying (FSK) is a coherent modulation showing remarkable robustness to errors but poor SE. This kind of scheme has been shown to be perfectly suited to UWOC, especially in scenarios characterized by strong channel turbulence [31].

Overall, the achievement of a high rate and reliable transmission is a fundamental challenge not only in UWOC, but in general in wireless optics, including both indoor and outdoor free-space communication. Furthermore, part of the research has also been devoted to the investigation of hybrid modulations that fruitfully combine the features of conventional schemes as, for example, in [32,33,34,35]. By specifically referring to the UWOC case, in [36], the principles of digital pulse interval modulation (DPIM) and polarization-shift keying (PolSK) have been merged together in order to realize a transmission mechanism exhibiting high reliability, as with PPM, but also improved SE competition with OOK. The authors in [37] investigate an adaptive modulation scheme for UWOC that, based on the SNR conditions, chooses the most fitting transmission scheme among PPM, DPIM, and dual-header pulse interval modulation (DH-PIM) to maintain the BER below the link performance constraint threshold. Finally, the results related to the testing of FSK combined with with subcarrier intensity modulation (SIM) and polarization division multiplexing (PDM) are presented in [38].

For the sake of completeness, it is worth mentioning another category of transmission schemes related to the so called spread-spectrum (SS) modulations, employable in those scenarios where reliability and link coverage are paramount with respect to data rate. Moreover, such strategies conveniently fit for those architectures suffering from hardware limitations, such as reduced source transmit power, low sensitivity of optical detectors, and poor system bandwidth. Anyway, while SS schemes have been largely investigated in the UWAC context, only a few works currently deal with the optical case [39,40].

1.2. Motivation and Goals

The literature review has highlighted how, in general, the most known and widespread modulation schemes show their own advantages and weaknesses related to reliability, achievable data rate, and detection complexity, as briefly summarized in

Table 1. Optical modulation scheme comparison at glance.

Modulation Scheme	Modulated Waveform Feature	Detection Type	Spectral Efficiency (bit/s/Hz)
OOK [16,17]	Amplitude	Direct	1
M-PAM [19]	Amplitude	Direct	${log}_{2}M$
L-PPM [21]	Position	Direct	${\displaystyle \frac{{log}_{2}L}{L}}$
M-QAM [27]	Amplitude and Phase	Coherent	${log}_{2}M$
N-FSK [31]	Frequency	Coherent	${\displaystyle \frac{{log}_{2}N}{N}}$
M-PSK [28,29]	Phase	Coherent	${log}_{2}M$
L-DPIM [36]	Position	Direct	${\displaystyle \frac{2{log}_{2}L}{L+3}}$
L-PPM/N-FSK/M-PAM [32]	Position, Frequency and Amplitude	Coherent	${\displaystyle \frac{{log}_2(L·N·M)}{N(1+(L-1\left)\beta \right)}}$
N-FSK/M-PSK [35]	Frequency and Phase	Coherent	${\displaystyle \frac{{log}_2(N·M)}{N}}$

. As a consequence, the exploration of hybrid transmission schemes seems to be a promising approach aimed to simultaneously accommodate different quality of service constraints characterizing the link. Such a goal is particularly true in UWOC, where the time variability of the channel poses additional challenges in the search for practical and effective solutions.

In this direction, this paper proposes the investigation of FSK modulation combined with a novel technique referred to as wave phase coding (WPC). The scheme is referred to as (K,N)-WPC-FSK, where K and N refer to the order associated with WPC and FSK, respectively. With WPC, each basic FSK symbol is subject to an additional modulation step that regards directly the cycles of the corresponding waveform. Such modification is performed through the use of particular wave phase codes, allowing the generation of an extended symbol vocabulary with respect to conventional FSK, resulting in a novel modulation scheme with improved SE. At the same time, by suitably choosing the wave phase codes, the orthogonality of symbols, typical of FSK, is preserved. In fact, simulation results demonstrate that, for a given SNR level, the proposed WPC-FSK is able to provide a higher SE than other modulations. In other words, with respect to known solutions, a certain data rate can be achieved with a lower quality channel. So, it follows that the same performance can be achieved but with lower power consumption. Furthermore, we discuss the implementation of a lightweight detector for WPC-FSK able to provide similar performance to the optimum detector but with lower computation effort.

The paper is organized as follows. In Section 2, we describe the system model, including the optical channel characterization and the basics of FSK. Section 3 introduces the proposed wave phase coding and its combining with FSK. Moreover, the principles of signal detection are proposed. Numerical results are presented and discussed in Section 4. Finally, conclusion is drawn is Section 5.

2. System Model

Let us consider an underwater point-to-point optical link, with the transmitter employing a modulated LED source, while the receiver is equipped with PD-based hardware for optical signal detection. Symbol emission is ruled by the proposed $(K,N)$-WPC-FSK scheme, and the propagation model can be described as follows:

$$y\left(t\right)=\rho x_{k,n}\left(t\right)\ast h\left(t\right)+w\left(t\right)$$

(1)

where $x_{k,n}\left(t\right)$ is a non-negative optical signal related to the WPC-FSK symbol emitted by the source considering the k-th wave phase code (k = 0, 1, ⋯, $K-$1) combined with the n-th FSK waveform (n = 0, 1, ⋯, $N-$1). Then, $h\left(t\right)$ is the channel impulse response, ∗ is the convolution operator, $\rho$ represents the PD responsivity (expressed in amperes/watts), $y\left(t\right)$ is the received signal resulting after optical-to-electrical conversion. Finally, $w\left(t\right)$ is the electrical background noise term, including those components related to dark current and shot and thermal noise [12]. Typically, the latter is prevalent, and hence the overall noise affecting the link can be characterized as an additive white Gaussian process with zero mean and variance ${\sigma }_w^2$.

2.1. The Optical Wireless Channel

In UWOC, signal propagation is typically considered as line of sight (LOS), with the multipath effect being negligible since potential echoes arriving at the receiver are significantly weaker than the main signal component. Anyway, the channel induces severe attenuation, absorption, and scattering that, as previously outlined, limit the communication performance in terms of range. The overall path loss is typically represented by a scalar gain following the Beer–Lambert law [12]:

$$h_{path}=e^{-c\left(\lambda \right)d}$$

(2)

where d is the propagation distance and c is the attenuation coefficient expressed as:

$$c\left(\lambda \right)=a\left(\lambda \right)+b\left(\lambda \right)$$

(3)

and representing the combined effect of absorption a and scattering b. As modeled in Equation (3), path loss is also a function of the wavelength $\lambda$. Moreover, the water quality and the presence of particles impact on the overall signal attenuation [13]. In fact, some values of $c\left(\lambda \right)$, $a\left(\lambda \right)$ and $b\left(\lambda \right)$ have been empirically calculated for different water types, as shown in

Table 2. Typical absorption and scattering coefficient values [13].

Water Type	a (${\mathbf{m}}^{-1}$)	b (${\mathbf{m}}^{-1}$)	c (${\mathbf{m}}^{-1}$)
Pure sea water	0.053	0.003	0.056
Clear ocean	0.069	0.08	0.151
Coastal ocean	0.088	0.216	0.305
Turbid harbor	0.295	1.875	2.170

.

By assuming the LED emission as Lambertian, signal propagation also undergoes geometrical losses that depend on both the link distance and the transmitter–receiver alignment accuracy. Due to the assumed LOS condition, such loss is modeled as a scalar gain as well [41]:

$$h_{LOS}=\left\{\begin{array}{ll}{\displaystyle \frac{(m+1)S_{\mathrm{pd}}}{2\pi d^2}}{cos}^m\left(\varphi \right)cos\left(\psi \right)g\left(\psi \right),& \psi \le \Psi \\ 0,& \psi >\Psi \end{array}\right.$$

(4)

where:

• m = $-ln2/ln(cos{\Phi }_{1/2})$ represents the Lambertian emission factor derived from the LED -3dB semi-angle;
• $S_{\mathrm{pd}}$ is the area of the PD;
• $\varphi$ and $\psi$ are the angle of radiance and incidence, respectively;
• $\Psi$ is the maximum incidence angle defining the PD field of view (FOV);
• g represents the angle-dependent gain of a potentially employable optical concentrator.

Hence, by merging Equations (2) and (4), the overall channel propagation model is given as:

$$h={\displaystyle \frac{(m+1)S_{\mathrm{pd}}}{2\pi d^2}}{cos}^m\left(\varphi \right)cos\left(\psi \right)g\left(\psi \right)e^{-c\left(\lambda \right)d}$$

(5)

being a positive and non-zero gain until the optical beam falls withing the receiver FOV, that is $\psi \le \Psi$.

2.2. WPC-FSK Signaling

Equation (1) introduces $x_{k,n}\left(t\right)$ as the generic waveform associated with the signal transmission according to (K,N)-WPC-FSK, whose features originate from FSK and the proposed WPC. The transmitter block diagram is shown in Figure 1. From the input serial bit stream, $lo{g}_{2}K$ are associated with the k-th wave phase code, while $lo{g}_{2}N$ bits are encoded in the n-th FSK waveform. Finally, the two signals are combined together to form the resulting WPC-FSK symbol.

By recalling the principles of N-FSK, the signal related to the n-th symbol is given, in the electrical domain, as:

$$s_n\left(t\right)=Asin\left(2\pi f_{n}t\right),0\le t\le T_s$$

(6)

where A is the amplitude of the signal, chosen so as to have a unitary energy symbol, $f_n$ is the frequency associated with the n-th symbol, with n = 0, 1,⋯, $N-$1, and $T_s$ is the signal duration. Furthermore, given $f_n$ and $T_s$ expressed in Hz and seconds, respectively, we have that:

$$C_n=f_n{T}_s$$

(7)

represents the number of cycles performed by the n-th sinusoidal waveform within the symbol time. The FSK waveform can also be organized as P chips of duration equal to $T_c$ (so, $T_s=P{T}_c$), each one gathering a different number of cycles $N_p^{\left(n\right)}$ based on the reference symbol frequency, so that $C_n=N_p^{\left(n\right)}P$.

The application of WPC considers the use of a code-like waveform that essentially applies chip by chip a phase shift equal to 0 or $\pi$ on the FSK waveform. Such a kind of wave phase code belongs to a vocabulary of K elements, the formation of which will be discussed in the next section and can be described in the time domain as:

$$z_k\left(t\right)=\sum _{p=0}^{P-1}{\alpha }_p^{\left(k\right)}rect\left({\displaystyle \frac{t-T_s/2-p{T}_s}{T_p}}\right)$$

(8)

that is a sequence of P squared semi-waves that, based on the value of ${\alpha }_p^{\left(k\right)}=\pm 1$, modifies the phase of the p-th chip of the FSK waveform by 0 (chip phase unchanged, ${\alpha }_p^{\left(k\right)}=1$) or by $\pi$ (chip phase inverted, ${\alpha }_p^{\left(k\right)}=-1$). An example of combining FSK and WPC is given in Figure 2, where an FSK symbol is divided into four chips and the considered wave phase codes operate by inverting the phase of the second and fourth chip.

The product of Equation (6) and Equation (8) still returns an electrical signal to be further converted in the optical domain. To this aim, we consider a bias current $I_b$ to be used in order to make the optical signal as non-negative, so we finally have:

$$x_{k,n}\left(t\right)=I_b+s_n\left(t\right)z_k\left(t\right)$$

(9)

with $I_b\ge A$ so as to guarantee that the FSK waveform is always non-negative. For the sake of completeness it is worth noting that, at the transmit side, the electro-optical conversion of the signal introduces some losses, known a priori and based on the hardware properties. Without loss of generality, Equation (9) describes a simplified signal model, assuming optical conversion as ideal. As further detailed, we highlight that the generic symbol of WPC-FSK is defined from the index pair $(k,n)$ related to the considered k-th WPC code and n-th FSK symbol, respectively.

3. Wave Phase Coding

The peculiarity of conventional FSK is the orthogonality of symbols, allowing a reliable signal detection even at low SNR. From theory, it is known that such a condition is achieved by a proper selection of the carrier frequencies associated with each FSK symbol [42]. The proposed WPC introduces a phase modification on the FSK waveform at the chip level, which my compromise the orthogonality of the resulting symbols. Hence, the shape of the FSK waveform must respect an additional constraint in order to let the WPC be applied without any consequence on symbol orthogonality. Specifically, it is requested that each chip of the n-th FSK symbol is composed of an integer number of wave cycles. It follows that a specific relationship between the FSK symbols’ frequency must be established. In this direction, it is sufficient to guarantee that the n-th symbol frequency doubles the frequency of the $(n-1)$-th symbol. So, once the fixed $f_0$ is associated with the FSK symbol with the lowest frequency, the frequency selection can be generalized as:

$$f_n=f_0·2^n,n=0,1,\cdots ,N-1$$

(10)

Furthermore, based on such a rule, we have that $f_0$ defines the maximum number of chips that the FSK waveform can be organized in. In fact, by recalling Equation (7), it follows that:

$$P\le C_0=f_0{T}_s$$

(11)

where P is maximized when each chip corresponds to a single wave cycle of the signal $s_0\left(t\right)$. So, Equations (10) and (11) impact the wave phase code length P, which as further detailed, reflects the vocabulary order of WPC.

3.1. WPC Properties

The application of WPC should provide an SE improvement with respect to conventional FSK while maintaining the same reliability level guaranteed by the orthogonality among symbols. This task is achieved by using a proper vocabulary of wave phase codes showing the mutual orthogonality condition as well. From Equation (8), we can express the generic k-th wave phase code in the chip time domain as the vector:

$${\mathbf{z}}_k=\left[{\alpha }_0^{\left(k\right)}{\alpha }_1^{\left(k\right)}...{\alpha }_p^{\left(k\right)}...{\alpha }_{P-1}^{\left(k\right)}\right]$$

(12)

with P elements equal to +1 or −1 depending on the phase modification to be applied to the corresponding FSK chip signal. In principle, there exist $2^P$ codes with such a structure, but only a subset of these retain the following property:

$${\mathbf{z}}_k^T{\mathbf{z}}_k=0,k\ne \ell ,$$

(13)

allowing the FSK symbols’ orthogonality to be preserved, with ${(·)}^T$ referring to the transpose operation. As each element of ${\mathbf{z}}_{\mathbf{k}}$ can be +1 or −1, it follows that the codes orthogonality in Equation (13) is achieved only if the codes length P is an even number. Furthermore, as shown in

Table 3. WPC vocabulary size as a function of the chips per symbol.

P	2	4	6	8	10	12	14	16
K	2	4	2	8	2	4	2	16

, the WPC vocabulary size K is maximized when P is a power of 2. In this case, K grows with P, as it typically happens with digital modulation constellation size.

So, by merging K-WPC and N-FSK, we obtain a novel modulation scheme with a richer symbol vocabulary and providing a higher SE given as:

$${\eta }_{WPC-FSK}={\displaystyle \frac{{log}_2(K·N)}{N}}$$

(14)

with ${log}_{2}K$ bits carried by the WPC and ${log}_{2}N$ bits encoded in the FSK waveform.

Table 4. Spectral efficiency (bit/s/Hz) for different WPC-FSK configurations.

$\mathit{N}\downarrow$  $\mathit{K}\to$	2	4	8	16	32
2	1	1.5	2	2.5	3
4	0.75	1	1.25	1.5	1.75
8	0.5	0.62	0.75	0.87	1
16	0.31	0.37	0.44	0.5	0.56
32	0.19	0.22	0.25	0.28	0.31

reports the achievable SE based on different configurations of the pair (K,N). Interestingly, it can be noted how the SE increases with K. The lower the FSK order N, the higher the SE. So, working with a low N allows the system to provide high data rate performance but at the expense of reliability that, as known from FSK theory [42], grows with N. Furthermore, we recall that K depends on P, the choice of which is function of the practical FSK waveform and frequency design. As shown in Table 4, the same SE can be achieved for different (K,N) configurations. So, the most suitable choice of N and K may be determined based on the performance and design constraints.

3.2. WPC-FSK Optimum Detector

The WPC-FSK symbol vocabulary is essentially composed of FSK-like waveforms with phase modulated at chip level according to the WPC. The use of orthogonal wave phase codes meeting Equation (13) allows the resulting WPC-FSK symbols to save the mutual orthogonality property as in conventional FSK. Hence, the optimum detection can be performed by following a matched filtering-based approach as in FSK, which returns:

$$r_{k,n}={\displaystyle \frac{1}{T_s}}{\int }_0^{T_s}{y}_e\left(t\right)x_{k,n}\left(t\right)dt$$

(15)

as the cross-energy measured between the reference WPC-FSK symbol $x_{k,n}\left(t\right)$ and the received electrical signal $y_e\left(t\right)$, obtained after optical-to-electrical conversion and bias removal from the received optical signal $y\left(t\right)$. Once all the possible $KN$ metrics are computed, the decision on the received symbol is taken as:

$$\widehat{k},\widehat{n}=\underset{k=0,\cdots ,N-1,n=1,\cdots ,N}{\mathrm{argmax}}\left|r_{k,n}\right|$$

(16)

representing the decided indexes related to the WPC and FSK, respectively.

Regarding the computational cost of the optimum detection, calculating the cross-energy value in Equation (15) requires sum-and-product operations that grow with the length of the WPC-FSK signals. In detail, the highest FSK frequency defines, according to the Nyquist theorem, the sampling frequency to be adopted at the receiver to achieve a reliable signal representation. So, given L as the number of samples describing each WPC-FSK symbol, we have that the computing of Equation (15) requires $(2L-1)$ sum/product operations. Equation (16) instead considers the computing of $NK$ metric comparisons. Hence, the total cost of optimum detection is:

$${\mathcal{C}}_{opt}=NK(2L-1)+NK=2NKL$$

(17)

3.3. WPC-FSK Chip-Level Detector

The construction of the WPC vocabulary based on Equation (13) shows that all the codes show an equal chip phase element within ${\mathbf{z}}_k$. This means that, for a certain chip $p^{\ast }$, we have ${\alpha }_{p^{\ast }}^{\left(k\right)}=1$ or ${\alpha }_{p^{\ast }}^{\left(k\right)}=-1$, $\forall k$. Such information can be exploited at the receiver since revealing that the received signal has the chip $p^{\ast }$ with the phase known a priori. For instance, refer to

Table 5. Wave phase code vocabulary associated with K = 2, 4, 8.

K = 2
$z_0$	+1	+1
$z_1$	+1	−1
K = 4
$z_0$	+1	+1	+1	+1
$z_1$	+1	+1	−1	−1
$z_2$	+1	−1	+1	−1
$z_3$	+1	−1	−1	+1
K = 8
$z_0$	+1	+1	+1	+1	+1	+1	+1	+1
$z_1$	+1	+1	+1	+1	−1	−1	−1	−1
$z_2$	+1	+1	−1	−1	+1	+1	−1	−1
$z_3$	+1	+1	−1	−1	−1	−1	+1	+1
$z_4$	+1	−1	+1	−1	+1	−1	+1	−1
$z_5$	+1	−1	+1	−1	−1	+1	−1	+1
$z_6$	+1	−1	−1	+1	+1	−1	−1	+1
$z_7$	+1	−1	−1	+1	−1	+1	+1	−1

reporting the wave phase code vocabulary associated with the cases of K = 2, 4, 8, where it is possible to verify that the first chip of all the codes is equal to +1.

In fact, by considering the chip waveform associated with different FSK signals, it is possible to compute:

$$r_{n,p}={\displaystyle \frac{1}{T_c}}{\int }_{p{T}_c}^{(p+1)T_c}{y}_e\left(t\right)s_{n,p^{\ast }}\left(t\right)dt$$

(18)

as the cross-energy related to the p-th chip of the received symbol. Given $s_{n,p^{\ast }}$ as the n-th FSK waveform windowed in the reference chip $p^{\ast }$ and by neglecting the effect of noise, we can have the following output:

• $r_{n,p}$ is equal to 0 when the frequency of the received signal y is different from the n-th frequency associated with $s_{n,p^{\ast }}$ (chip orthogonality);
• $r_{n,p}$ is strictly greater than 0 when y and $s_{n,p^{\ast }}$ have the same frequency and same phase;
• $r_{n,p}$ is strictly smaller than 0 when y and $s_{n,p^{\ast }}$ have the same frequency but opposite phase.

By applying Equation (18) for the P chips composing the received symbol, we obtain P chip cross-energy metrics that can be expressed in the form a [$1\times P$] vector:

$${\tilde{\mathbf{r}}}_n=\left[r_{n,0}{r}_{n,1}...r_{n,p}...r_{n,P-1}\right]$$

(19)

that can be exploited to compute the decision on the received symbol according to the maximum-likelihood criterion:

$$\widehat{k},\widehat{n}=\underset{k=0,...,N-1,n=1,...,N}{\mathrm{argmin}}{|{\tilde{\mathbf{r}}}_n-{\mathbf{z}}_{\mathbf{k}}|}^2.$$

(20)

The proposed chip-level detector performs essentially the same operations as the optimum one. The main difference relies on the fact that it computes a higher number of cross-energy values but on the shortest signal windows (that is, the chips). In fact, from the complexity point of view, we have that the cost associated with such a detector is:

$$\begin{array}{ll}{\mathcal{C}}_{chip-based}& =NP(2{\displaystyle \frac{L}{P}}-1)+NK(2P+1)+NK=\\ & =N(2L-P+2K(P+1))\end{array}$$

(21)

where the first term $NP(2{\displaystyle \frac{L}{P}}-1)$ is related to the computing of Equation (18), while the remaining part refers to the maximum-likelihood criterion in Equation (20).

4. Numerical Results

In this section, we provide a detailed performance investigation of the proposed WPC-FSK, discussing the SE improvement with respect to conventional FSK and the higher reliability than other schemes proposed in the literature. Furthermore, we evaluate the effectiveness of optimum and chip-level detectors both in terms of robustness to errors and computational cost. The analysis has been conducted through simulations performed in Matlab. The underwater optical channel has been modeled according to Equation (5) by considering typical opto-electronic hardware and propagation parameters taken from the literature. A detailed list is provided in

Table 6. Simulation parameters.

LED operating wavelength (λ)	430 nm
LED optical power	10 W
LED bandwidth	10 MHz
PD responsivity ($\rho$)	0.44 A/W
PD area ($S_{\mathrm{pd}}$)	1 ${\mathrm{cm}}^2$
Water type	Pure sea
Reference FSK frequency ($f_0$)	40 kHz
Symbol time ($T_s$)	0.4 ms

. In order to realize WPC with an order up to K = 16, we implement FSK with a frequency seed $f_0$ = 40 KHz, with the other symbol carriers being obtained following Equation (10).

The modulation reliability is expressed in terms of BER, evaluated on the transmission of ${10}^6$ random symbols at different levels of SNR per bit, referred to as $E_b/N_0$ and measured in dB. The SNR indicates the absolute quality of the link, thus including the potential effect of channel attenuation and fluctuation and geometrical losses due to transmitter–receiver misalignment.

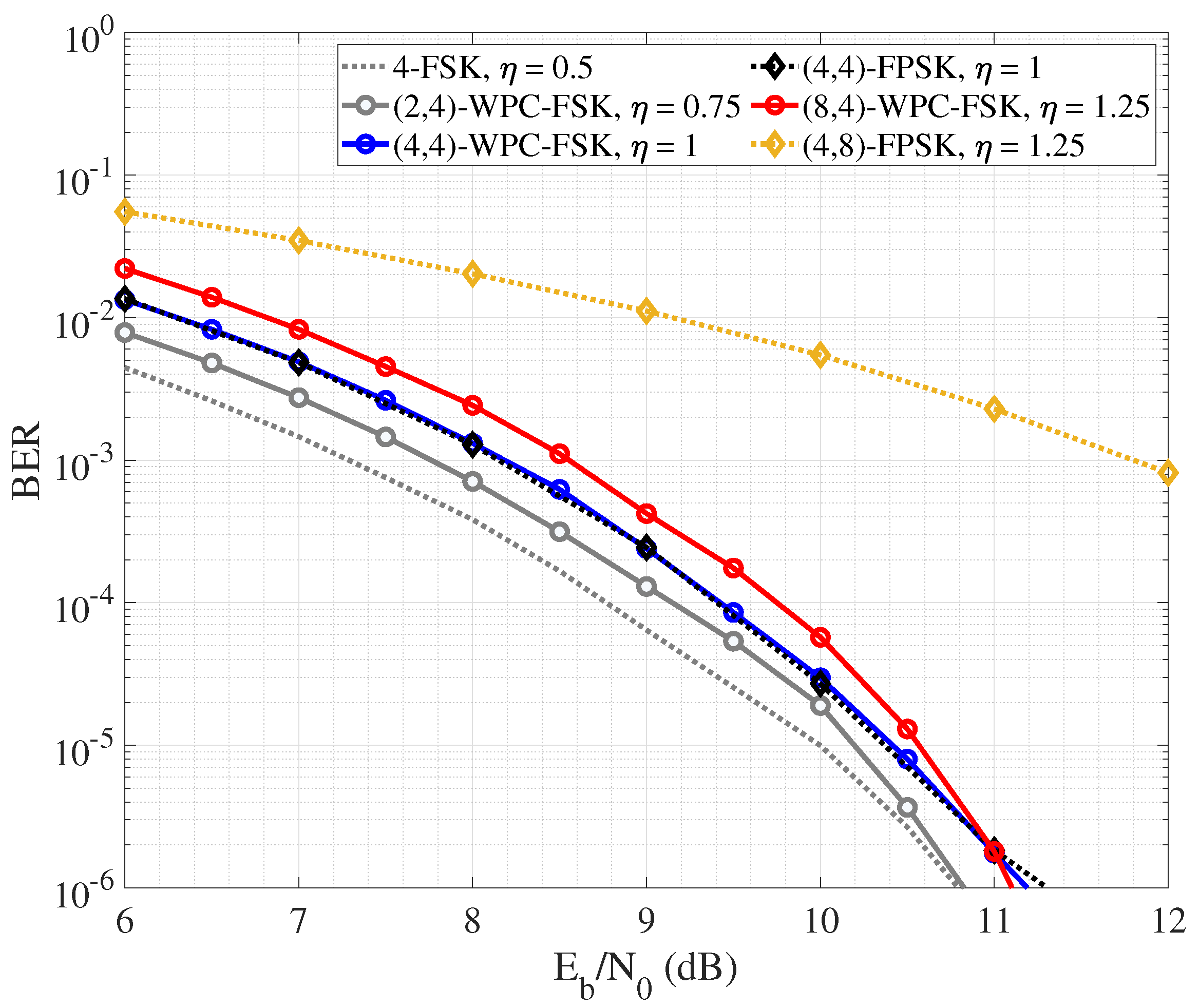
As WPC aims at improving the performance of conventional FSK, we initially set N = 4 and show the performance by considering the WPC order K as equal to 2, 4, and 8. Results are shown in Figure 3, where we also plot the performance of pure 4-FSK and hybrid N-FSK and M-PSK in [35], referred to as ($N,M$)-FPSK and chosen as a benchmark for exploiting phase modulation as we propose but in a different fashion. The legend of Figure 3 also highlights the SE of the mentioned schemes so as to let the reader appreciate the provided performance trade-off between rate and reliability.

In detail, it can be observed that 4-FSK outperforms WPC-FSK in terms of reliability by about 1 dB, even though guaranteeing a very low SE. From a different point of view, it means that, at the expense of a small transmit power increase, WPC-FSK is able to provide a doubled SE with respect to pure FSK. Furthermore, it is worth noting that the BER curves for ($4,4$)-WPC-FSK and ($4,4$)-FPSK follow the same behavior. On the other hand, regarding the cases with SE $\eta$ = 1.25 bit/s/Hz, ($8,4$)-WPC-FSK significantly outperforms ($4,8$)-FPSK. This is due to the fact that the increase in phase modulation order in FPSK leads the signal detection to be more prone to errors, while the proposed WPC applied to FSK exhibits a higher robustness.

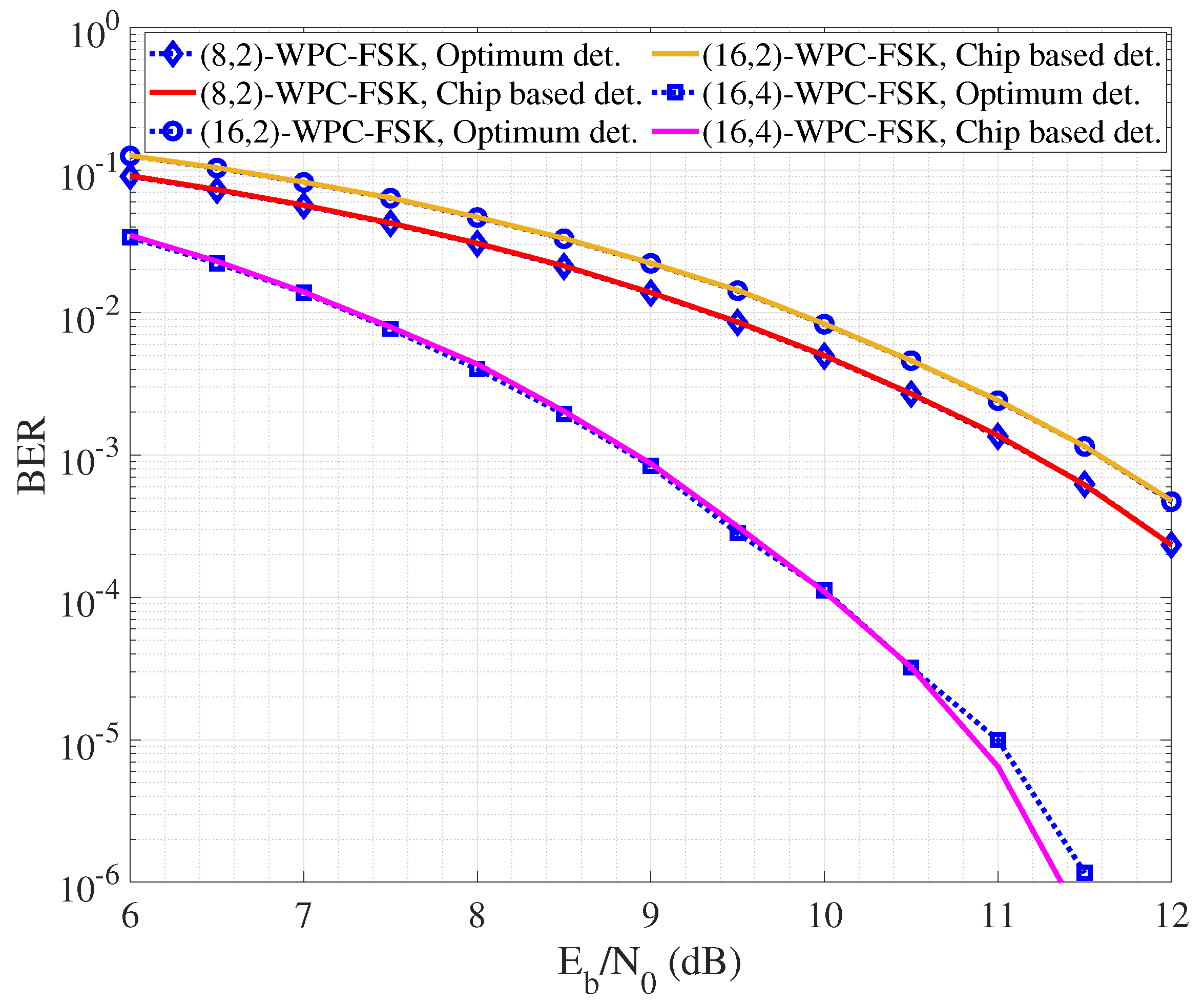
The BER performance of WPC-FSK in Figure 3 considers the use of the optimum detection given by Equations (15) and (16). Now, we evaluate the effectiveness of the proposed receiver relying on chip-based detection, realized by leveraging the properties of wave phase codes meeting the orthogonality property in Equation (13). To this aim, we consider the combinations of FSK and WPC in Table 4 providing SE strictly grater than 1 bit/s/Hz, which are ($4,2$)-WPC-FSK, ($8,2$)-WPC-FSK, and ($16,2$)-WPC-FSK. The reliability of optimum and chip-based detection is shown in in Figure 4.

Interestingly, it can be noted how, for each considered scheme, both the investigated detectors provide essentially the same performance. So, the only difference regards the required computation cost. In this direction, we introduce $\Gamma$ as the ratio between the costs ${\mathcal{C}}_{chip-based}$ and ${\mathcal{C}}_{opt}$. Furthermore, as shown in Table 3, since we consider for K only values that follow the power of 2, we have that $P=K$. So, by means of some mathematical manipulations, $\Gamma$ can be written as:

$$\begin{array}{ll}\Gamma & ={\displaystyle \frac{{\mathcal{C}}_{chip-based}}{{\mathcal{C}}_{opt}}}={\displaystyle \frac{N(2L-P+2K(P+1\left)\right)}{2KNL}}\\ & ={\displaystyle \frac{2L+2K^2+K}{2KL}}\end{array}$$

(22)

where it is possible to infer the independence from the FSK order N, while $\Gamma$ is only a function of the WPC order K and the number of samples L used for symbol representation at the receiver. For simulations, we consider different values of L to model the signal in the discrete domain.

Table 7. Detection cost ratio $\Gamma$ for different configurations of L and K.

$\mathit{L}\downarrow$  $\mathit{K}\to$	2	4	8	16	32
128	0.52	0.29	0.19	0.20	0.29
256	0.51	0.27	0.16	0.13	0.16
512	0.50	0.25	0.14	0.10	0.09
1024	0.50	0.25	0.13	0.08	0.06

shows how the configuration of L and K leads to different values of $\Gamma$.

Overall, $\Gamma$ is always lower than 1, thus meaning that the proposed chip-based detection requires a more lightweight computation than the optimum detection. For K = 2, the computational cost is halved, while it further decreases as K grows. Moreover, for low values of K the impact of L is negligible, while $\Gamma$ is minimized for high values of L and K.

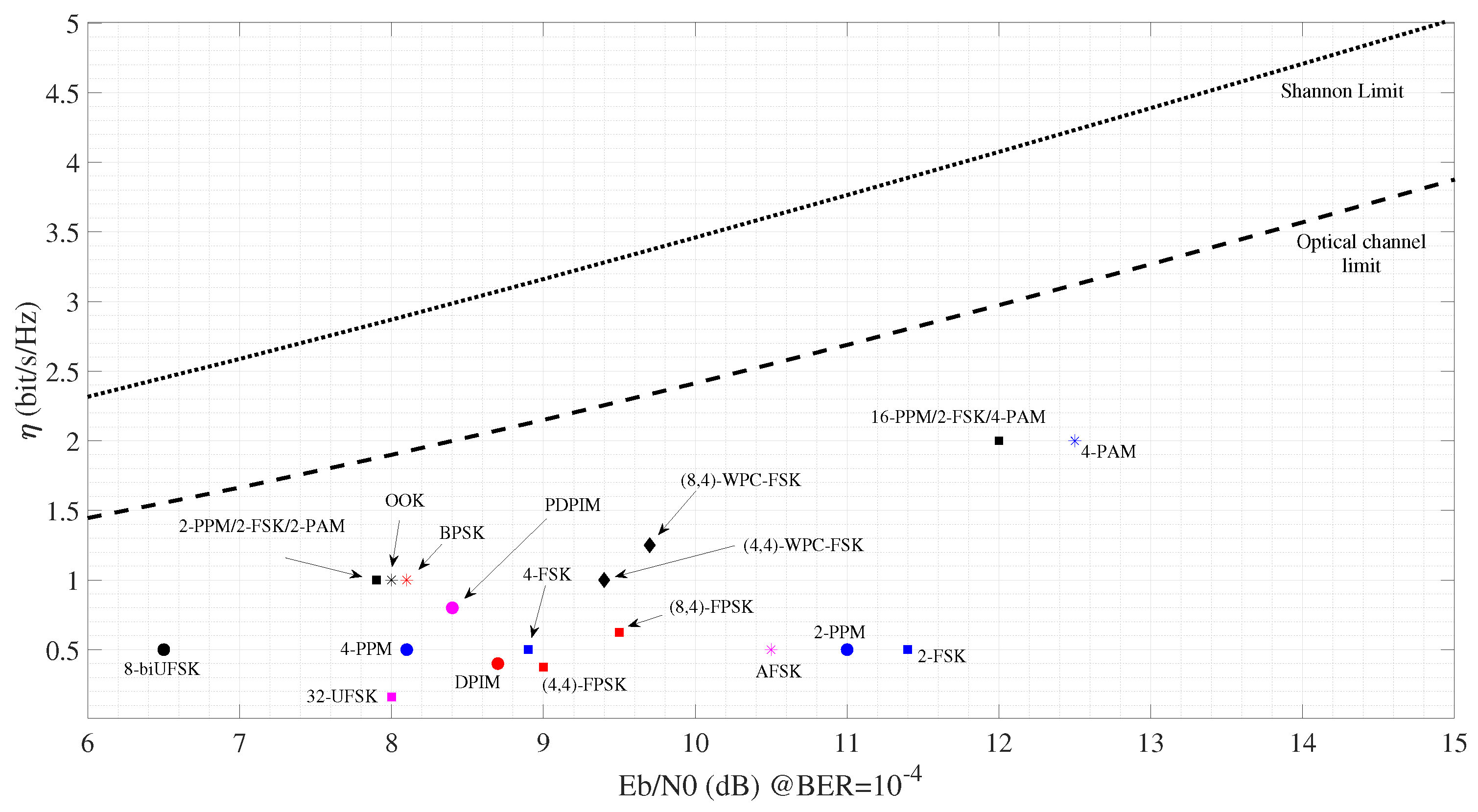
Finally, we conclude the analysis by providing a wider performance comparison among the proposed WPC-FSK and the other most widespread modulation schemes adopted in UWOC. Specifically, we map into a bi-dimensional space the performance of several transmission schemes, with each specifying two coordinates associated with the provided SE and the SNR per bit required to achieve a BER equal to ${10}^{-4}$. Figure 5 shows the performance comparison, including standard modulations like OOK, PSK, PPM, FSK, and PAM but also novel schemes proposed in the literature, such as Asymmetric Frequency-Shift Keying (AFSK) [33], DPIM and polarized-DPIM [36], hybrid PPM-FSK-PAM [32], unipolar and biorthogonal unipolar FSK (referred to as UFSK and biUFSK, respectively) [34], and FPSK [35].

In Figure 5, we also report the curves related to the classical Shannon limit so as to highlight how close to the maximum SE the considered schemes are. For the sake of completeness, we also plot the curve related to the optical channel limit, slightly different from the Shannon case but widely employed as a reference in optical communication [43]. The proposed WPC-FSK is well positioned in Figure 5; in fact, it provides an improved SE with respect to orthogonal modulations strictly oriented to reliability, at the expense of a slightly higher SNR per bit necessary to achieve the target BER. Of course, the achievement of high rates such as those with 4-PAM requires the use of high-order WPC, which may compromise the detection robustness. However, the performance of the considered WPC-FSK configuration is demonstrated to be satisfactory because it provides an SE greater than 1 with high reliability at a reasonable SNR. Furthermore, the points related to WPC-FSK in Figure 5 appear closer to the capacity limits than the largest part of the considered benchmark schemes.

5. Conclusions

Optical wireless communication has risen as a viable technology to enable high-rate data transmission in underwater environments. Unfortunately, the impairments induced by the channel make the UWOC link prone to errors, and hence the choice of an effective transmission scheme is crucial to guarantee good performance in terms of both rate and reliability. In this work, we introduced a novel modulation scheme referred to as WPC-FSK, which merges the intrinsic reliability of FSK with WPC to improve the SE while preserving the detection robustness. Simulation results have shown how the proposed technique is able to outperform conventional schemes like FSK and also other hybrid modulations proposed in the literature. The application of wave phase codes has demonstrated to have no impact on the FSK symbols’ orthogonality, thus saving the robustness to errors of this scheme. Based on such results, the use of WPC may be further investigated, for instance, to deal with multiuser scenarios where concurrent transmissions must be correctly separated at the receiver before detection. In addition, WPC may also be considered merged with other kinds of modulations, for instance, SS schemes.