A Novel Decomposition–Integration-Based Transformer Model for Multi-Scale Electricity Demand Prediction

Abstract

The accurate forecasting of electricity sales volumes constitutes a critical task for power system planning and operational management. Nevertheless, subject to meteorological perturbations, holiday effects, exogenous economic conditions, and endogenous grid operational metrics, sales data frequently exhibit pronounced volatility, marked nonlinearities, and intricate interdependencies. This inherent complexity compounds modeling challenges and constrains forecasting efficacy when conventional methodologies are applied to such datasets. To address these challenges, this paper proposes a novel decomposition–integration forecasting framework. The methodology first applies Variational Mode Decomposition (VMD) combined with the Zebra Optimization Algorithm (ZOA) to adaptively decompose the original data into multiple Intrinsic Mode Functions (IMFs). These IMF components, each capturing specific frequency characteristics, demonstrate enhanced stationarity and clearer structural patterns compared to the raw sequence, thus providing more representative inputs for subsequent modeling. Subsequently, an improved RevInformer model is employed to separately model and forecast each IMF component, with the final prediction obtained by aggregating all component forecasts. Empirical verification on an annual electricity sales dataset from a commercial building demonstrates the proposed method’s effectiveness and superiority, achieving Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Squared Percentage Error (MSPE) values of 0.044783, 0.211621, and 0.074951, respectively—significantly outperforming benchmark approaches.

1. Introduction

With China’s rapid economic development driving accelerated growth in electricity demand, electricity sales forecasting [1] has evolved into a critical component for power system planning and operational management. As a core performance metric for grid operators, sales volume data underpins performance evaluation, profit equilibrium regulation, and electricity marketing strategies, while simultaneously guiding daily operational and production activities—including resource allocation and emergency response protocols. Accurate forecasting enables optimized grid infrastructure planning, evidence-based enterprise operations management, rational power transmission/distribution network allocation, and accelerated electricity market reform [2]. This task gains further significance within the evolving landscape of integrated energy systems, where loads such as commercial buildings combine distributed generation, storage, and multi-energy demands [3]. Advanced approaches, including those enhancing the flexibility and waste heat recovery of combined heat and power systems, are being developed to optimize renewable consumption in such integrated settings [4]. While forecasting these coupled multi-energy flows is an emerging frontier [5], the electrical load remains the primary and most dynamic vector. Its accurate prediction is not only crucial for grid stability but also serves as a foundational input for any higher-level multi-energy coordination model [6]. Therefore, advancing core methodologies for electric load forecasting—the focus of this work—provides essential support for the reliable operation of both current and future energy systems.

However, actual sales volume data manifests significant multidimensional heterogeneity due to the compound effects of meteorological conditions, external economic fluctuations, grid operational indicators, and holiday impacts. This complexity arises from interconnected mechanisms wherein temperature variations and holiday-induced regime shifts reshape societal consumption patterns, while economic trajectories and grid operational status collectively drive usage scale volatility. Dynamically, these interacting forces generate highly coupled trend components, periodic oscillations, and stochastic perturbations within the time series. Conventional forecasting approaches—including Long Short-Term Memory (LSTM) [7] models, Autoregressive Integrated Moving Average (ARIMA) models, and Transformer-based models—frequently encounter challenges when processing strongly coupled data, such as overfitting, sensitivity to noise, and excessive computational complexity. Furthermore, long-term sequential data often faces memory bottlenecks and is highly susceptible to external interference, leading to data distribution drift. These limitations hinder simple models from capturing long-term temporal dependencies, resulting in persistent challenges in achieving both accurate and efficient predictions.

To address these challenges, this paper proposes a decomposition–integration-based transformer framework. Initially, the methodology employs Variational Mode Decomposition (VMD) [8] coupled with the Zebra Optimization Algorithm (ZOA) to adaptively decompose the original electricity sales sequence. This process mitigates data non-stationarity and extracts representative subsequences with clearer structural characteristics, thereby establishing a robust foundation for subsequent modeling. Subsequently, an improved RevInformer model is utilized to separately model and forecast each derived subsequence. The predictions from all components are then integrated to generate the final output. The primary contributions of this study are summarized as follows:

(1)

A novel electricity sales forecasting method is proposed, employing a decomposition–integration framework. This approach adaptively decomposes the original sequence by integrating VMD with the ZOA, thus significantly reducing modeling complexity. Subsequently, an improved RevInformer model performs component-wise prediction on each subsequence, with final forecasts generated through aggregated integration of all component predictions.

(2)

An enhanced RevInformer model is developed by introducing Reversible Layers to the Informer architecture, strengthening deep feature propagation capabilities. Simultaneously, a bidirectional modeling mechanism is incorporated, effectively improving modeling capacity and prediction accuracy for complex non-stationary sequences.

(3)

The proposed methodology was validated using an annual electricity sales dataset from a commercial building. Simulation results demonstrate that our approach achieves 60–90% improvements across all evaluation metrics, surpassing the performance of existing benchmark methods.

The remainder of this paper is structured as follows. Section 2 reviews existing techniques in demand forecasting. Section 3 presents the system model and primary research methodology. Section 4 verifies the feasibility and effectiveness of the proposed approach through simulation verification. Section 5 concludes the study and outlines future research directions.

2. Related Work

Accurate forecasting in power systems is critical for grid stability and economic dispatch. However, the unique characteristics of power data—including high volatility, complex multi-scale seasonality, and susceptibility to external factors like weather and economic activity—pose significant challenges to conventional forecasting models.

Early studies primarily relied on traditional statistical methods. The ARIMA model [9], for instance, became a benchmark for time series forecasting and was applied to tasks such as carbon emission prediction [10]. While enhanced by techniques like wavelet decomposition for handling transients [11], these models are fundamentally limited to univariate, stationary series, failing to capture the complex nonlinearities in power data. The advent of machine learning, marked by decision trees [12] and ensemble methods like random forests [13,14], improved predictive performance by modeling more complex relationships. Concurrently, Recurrent Neural Networks (RNNs), with the Elman network [15] as a prototype, introduced a mechanism for processing sequential data. However, vanilla RNNs suffer from gradient vanishing [16], limiting their capacity to learn long-term dependencies in historical load data.

To overcome these limitations, more sophisticated neural architectures were introduced. Long Short-Term Memory (LSTM) networks [17], enhanced by the forget gate [18], provided a robust solution for capturing long-range dependencies and mitigating temporal noise. Parallelly, Convolutional Neural Networks (CNNs) [19] were adapted to extract local temporal patterns. Despite their strengths, these models often remain inadequate for modeling the intricate, long-range dependencies present in large-scale, multi-variable power system data.

The Transformer architecture [20] emerged as a breakthrough, replacing recurrence with self-attention to efficiently capture global dependencies. Its superiority has led to numerous adaptations in load forecasting. For example, some works integrate seasonal decomposition with Transformer to model periodic characteristics [21], while others employ federated learning frameworks to alleviate data scarcity in new regions [22]. Despite these advances, the standard Transformer and its early variants, such as Informer [23], face persistent challenges. Informer’s generative decoder and sparse attention improve long-sequence forecasting efficiency, but its massive memory consumption and slow execution become prohibitive with the high-dimensional data typical in power systems [24]. Furthermore, while hybrid models that combine decomposition techniques (e.g., CEEMDAN) with Informer can enhance noise robustness [25], they often treat decomposition and modeling as separate, sub-optimal stages, and still struggle with complex, non-stationary dynamics. This limitation is particularly evident in environments with tightly coupled multi-factor interactions, such as in internet data centers where energy and computational task scheduling must co-optimize with dynamic carbon intensity, posing a significant challenge for traditional forecasting approaches [26].

This has spurred the development of decomposition–integration frameworks, which leverage signal processing techniques to decompose complex sequences into simpler sub-sequences for individual modeling, significantly enhancing predictive performance. This approach has demonstrated effectiveness across multiple domains. For instance, it has been integrated with Prophet and Stacking for electricity price forecasting [27], combined with VMD-BiLSTM-TCN for stock market prediction [28], and utilized with EEMD for financial trend analysis [29] and mass spectrometer data enhancement [30].

However, a pivotal challenge in these frameworks often remains unaddressed: distribution shift. The statistical properties of the decomposed sub-series can differ significantly from each other and from the original data, a problem particularly acute in volatile power load sequences. This can compromise the reliability of forecasts from standard models trained on these components.

To address the dual challenges of long-sequence forecasting efficiency and distribution shift in decomposed components, this paper introduces the RevInformer model for power load forecasting. Our framework incorporates VMD in the data preprocessing phase. The decomposed components are then processed by the RevInformer architecture [31], which implements Reversible Instance Normalization (RevIN). This mechanism allows the model to dynamically adapt to non-stationary sub-series, effectively resolving distribution shifts and significantly enhancing the reliability of predictions for complex power system data. The forecasting challenges addressed in this work—strong non-stationarity, complex couplings, and long-term dependencies—are not unique to electricity data but are central to forecasting in multi-energy systems (e.g., predicting heat and cooling loads alongside electricity) [32]. The decomposition–integration framework proposed here, which disentangles complex signals into manageable components for individual modeling, offers a promising architectural paradigm for such multi-variate forecasting tasks. By advancing a robust solution for the fundamental problem of electric load forecasting, this study contributes a methodological tool that can be adapted to support the comprehensive energy management required in modern integrated systems [33,34].

3. Methodology

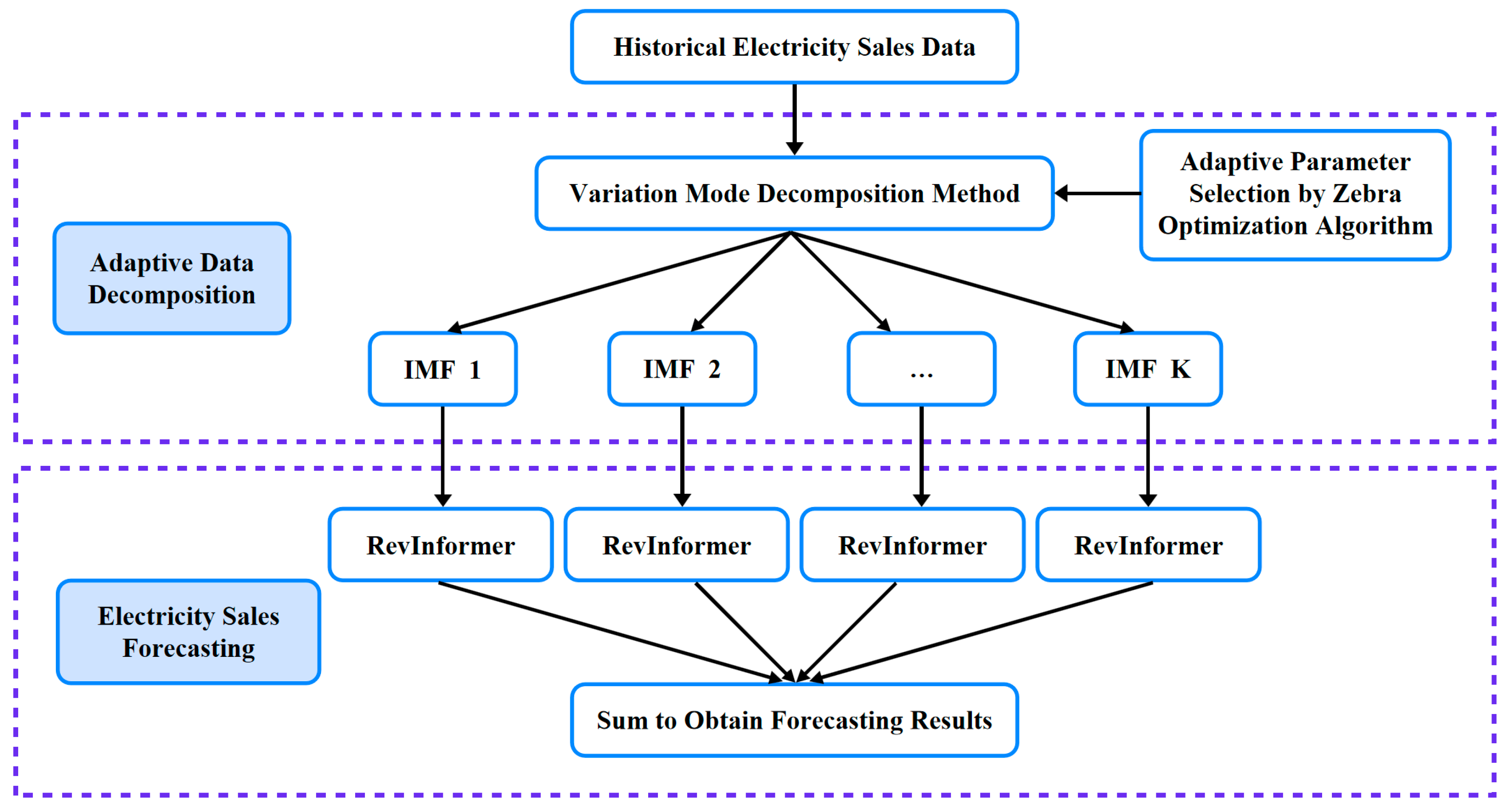
3.1. The Framework for the Proposed Method

Affected by natural conditions, human activities, unexpected events, and other factors, electricity sales data exhibits pronounced non-stationarity and nonlinearity, resulting from the complex coupling of multiple influencing factors as mentioned in the Introduction. Rendering sales forecasting highly challenging. Given the difficulty in capturing volatility patterns from raw data, this study adopts a decomposition–integration framework. While VMD does not directly disentangle the physical sources of heterogeneity (e.g., separating weather effects from economic trends), it is employed here to separate the manifested complex temporal signatures into simpler modal components. This process alleviates the modeling burden caused by high coupling and non-stationarity, providing cleaner inputs for the prediction model. First, the model employs VMD to adaptively decompose long time-series data, utilizing ZOA for optimized parameter selection to achieve peak performance. Subsequently, the raw data—decomposed into designated IMFs—is independently fed into the RevInformer model for separate training and prediction. Finally, predicted subsequences are aggregated through summation to yield the final forecast. This framework effectively mitigates sequence non-stationarity, adapts to data distribution variations, and enhances predictive performance. The detailed workflow is illustrated in Figure 1.

3.2. Adaptive Data Decomposition

The core objective of adaptive data decomposition is to dynamically adjust decomposition strategies for more accurate identification of hidden patterns in complex data, thereby enhancing subsequent forecasting precision. Traditional decomposition methods struggle to handle cyclical variations or abrupt trends, whereas adaptive decomposition provides flexible adaptation to data dynamics while avoiding overfitting in complex data scenarios, thus strengthening model generalization capabilities.

Parameter selection proves critical to decomposition effectiveness during this process. For VMD-based methods:

(1)

Insufficient subsequence settings increase reconstruction errors.

(2)

Excessive settings substantially escalate computational overhead.

Manual parameter determination fails to optimally balance reconstruction error and computational complexity. Therefore, this study integrates ZOA with VMD to automatically select optimal configurations based on raw data characteristics. This approach effectively manages computational costs while guaranteeing reconstruction precision.

3.2.1. Variational Mode Decomposition

Variational Mode Decomposition (VMD) employs a variational optimization framework to decompose signals into distinct modes with specific center frequencies while minimizing the total bandwidth of all modes. It is commonly used to decompose complex non-stationary signals into multiple Intrinsic Mode Functions (IMFs) characterized by sparsity and band-limited properties. Compared to traditional Empirical Mode Decomposition (EMD), VMD demonstrates stronger robustness against noise and non-stationary signals. The IMF obtained via VMD is expressed as:

$$u_k\left(t\right) = A_k\left(t\right)\cos \left({\varnothing }_k\left(t\right)\right)$$

(1)

where $A_k\left(t\right)$ represents the instantaneous amplitude of $u_k\left(t\right)$, and ${\varnothing }_k\left(t\right)$ is a non-decreasing phase function. To enhance decomposition precision, VMD incorporates a penalty factor (α) and Lagrangian multiplier (λ) to formulate a highly nonlinear constrained variational problem. The algorithm minimizes the following function:

$$L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right) = \alpha {\sum }_k{‖\left[{\partial }_t\left(\sigma \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)·u_k\left(t\right)\right]e^{-j{\omega }_{t}t}‖}_2^2+{\Vert f\left(t\right)-{\sum }_k{u}_k\left(t\right)\Vert }_2^2+〈\lambda \left(t\right),f\left(t\right)-{\sum }_k{u}_k\left(t\right)〉$$

(2)

where α denotes the penalty factor, and λ(t) is the Lagrangian multiplier.

The Alternating Direction Method of Multipliers (ADMM) iteratively updates the mode functions $u_k$, center frequencies ${\omega }_k$, and Lagrangian multiplier $\lambda$ to solve the constrained variational problem. The iterative formulas are:

$$\left\{\begin{array}{c}{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1} = {\displaystyle \frac{\widehat{\mathrm{f}}\left(\mathrm{x}\right)-{\sum }_{\mathrm{i}<\mathrm{k}}{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)+\frac{{\widehat{\mathsf{\lambda }}}^{\mathrm{n}}\left(\mathsf{\omega }\right)}{2}}{1+2\mathsf{\alpha }{\left(\mathsf{\omega }-{\mathsf{\omega }}_{\mathrm{k}}^{\mathrm{n}}\right)}^2}}\\ {\mathsf{\omega }}_{\mathrm{k}}^{\mathrm{n}+1} = {\displaystyle \frac{{\int }_0^{\mathrm{\infty }}\mathsf{\omega }{\left|{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)\right|}^2\mathrm{d}\mathsf{\omega }}{{\int }_0^{\mathrm{\infty }}{\left|{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)\right|}^2\mathrm{d}\mathsf{\omega }}}\\ {\widehat{\mathsf{\lambda }}}^{\mathrm{n}+1} = {\widehat{\mathsf{\lambda }}}^{\mathrm{n}}\left(\mathsf{\omega }\right)+\tau (\widehat{\mathrm{f}}\left(\mathsf{\omega }\right)-{\sum }_{\mathrm{k}}{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right))\end{array}\right.$$

(3)

where $\widehat{\mathrm{u}}$, $\widehat{\mathrm{f}}$ and ${\widehat{\mathsf{\lambda }}}^{\mathrm{n}}$ are the Fourier transforms of $u_k\left(t\right)$, $f\left(t\right)$, and $\lambda \left(t\right)$ respectively; $\tau$ denotes the noise-tolerance parameter; and $n$ indicates the iteration index.

Iterations continue until the stopping criterion is satisfied:

$${\displaystyle \frac{{\sum }_{k-1}^L{‖{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}-{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}‖}_2^2}{{‖{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}‖}_2^2}}<\epsilon$$

(4)

where ε is a predefined tolerance constant for convergence. The process terminates upon meeting this condition, yielding K final IMFs.

The VMD algorithm is designed to produce IMFs with specific sparsity properties in the spectral domain, which typically leads to sub-sequences with reduced non-stationarity compared to the original signal. While absolute stationarity of every IMF is not guaranteed, this decomposition step effectively transforms a complex, non-stationary forecasting problem into a set of relatively simpler sub-problems, which is the core rationale behind its application in this framework.

To visually validate the effectiveness of the VMD-ZOA decomposition scheme and its role in improving sequence stationarity, Figure 2 and Figure 3 present the original electricity sales series and the eight IMFs obtained through decomposition with optimized parameters.

As visually confirmed in Figure 3, the complex, non-stationary original signal is adaptively decomposed into a set of subsequences (IMF1 to IMF8) with distinct frequency characteristics. The high-frequency components (IMF1 and IMF2) exhibit properties akin to zero-mean random noise. The mid-frequency components (IMF3 to IMF5) demonstrate clear and relatively stable periodic oscillations. Finally, the low-frequency components (IMF6 to IMF8) capture the long-term trend and residual elements of the sequence. This decomposition effectively mitigates the inherent non-stationarity of the raw data by transforming a single complex forecasting problem into multiple modeling tasks targeting more regular and predictable subsequences, thereby establishing a robust foundation for the subsequent component-wise prediction.

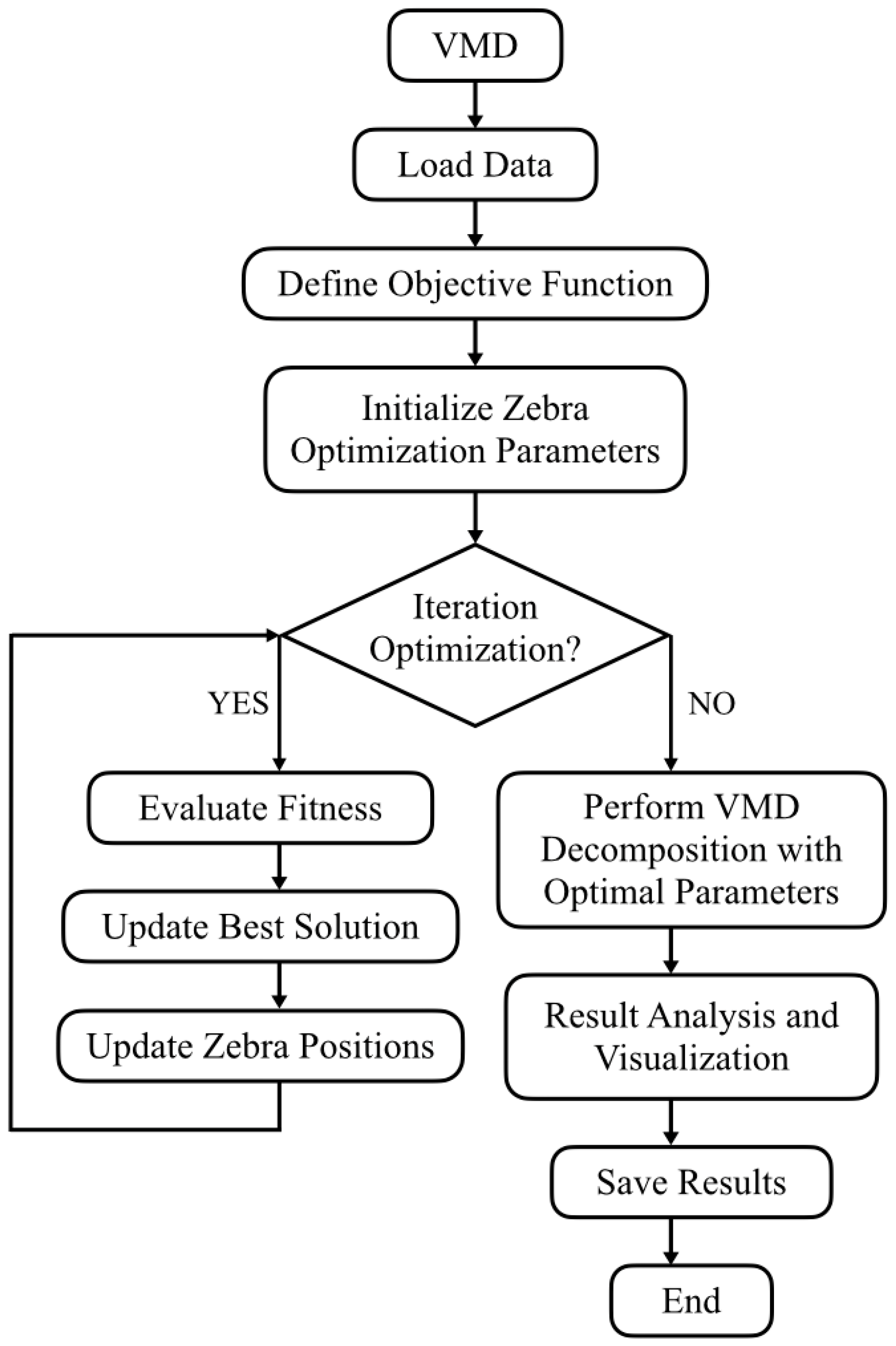
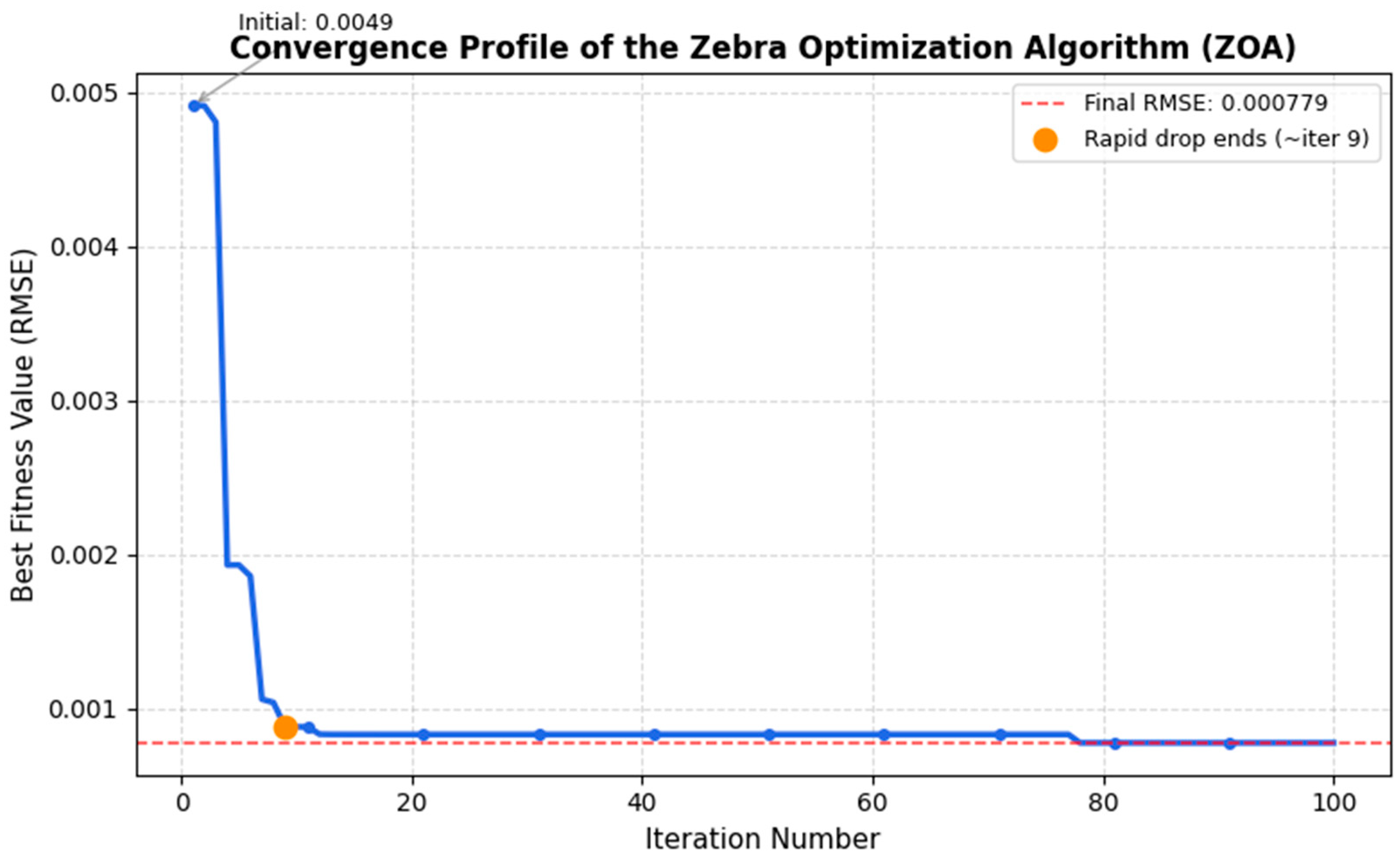
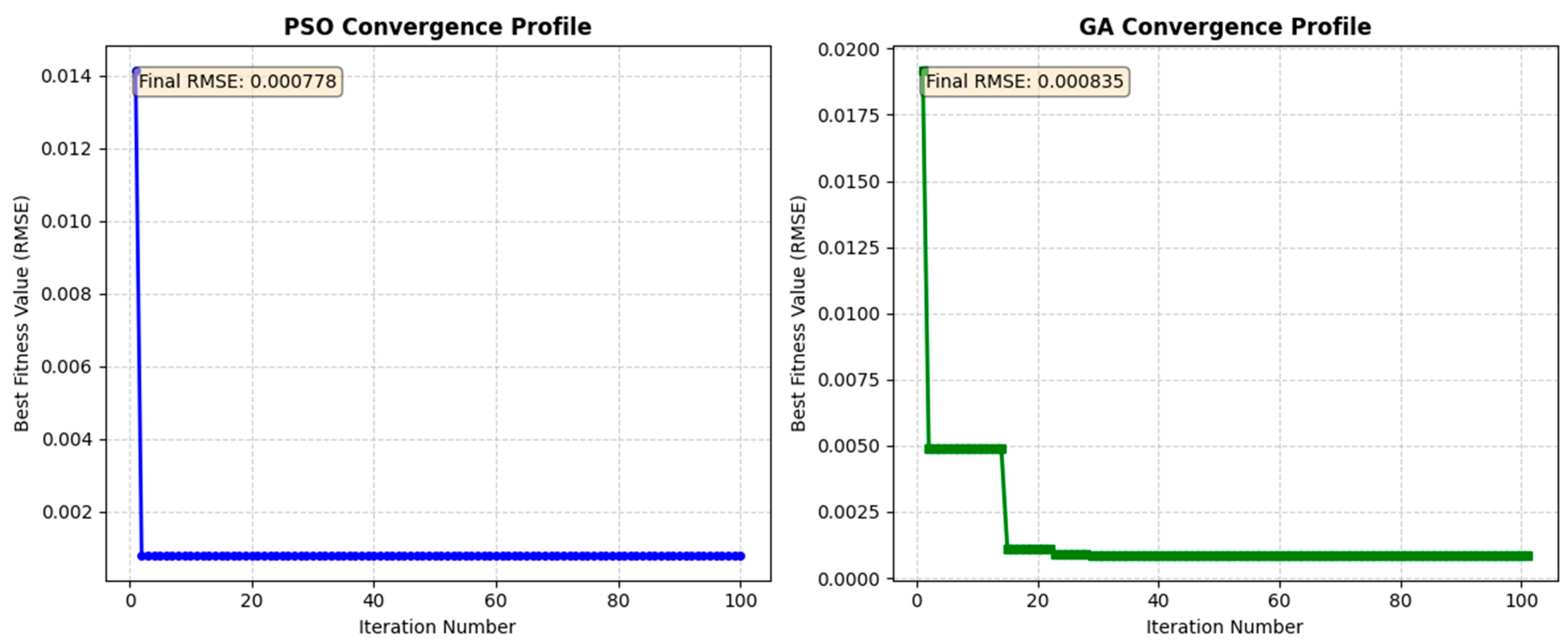
3.2.2. Self-Adaptive Parameter Selection Using Zebra Optimization Algorithm

When applying VMD to electricity sales data, the selection of critical parameters—mode number K and penalty factor α—is essential. This study introduces the ZOA to optimize these parameters by simulating zebra herd behaviors through three stages: parameter initialization, iterative optimization, and result recording/output.

Optimization Workflow:

(1)

Initialization: Randomly generate 15 parameter combinations ($K$, $\alpha$) within predefined bounds.

(2)

Iteration: Dynamically adjust combinations toward optimal solutions.

(3)

Evaluation: The objective function for the ZOA is RMSE between the original signal f(t) and the sum of all reconstructed IMFs $\Sigma u_k\left(t\right)$ after VMD. The algorithm seeks to minimize this reconstruction error.

(4)

Finalization: Deploy the optimal combination ($K^{*}$, ${\alpha }^{*}$) for VMD signal decomposition.

Post-Decomposition Verification: calculate performance metrics including Root Mean Square Error (RMSE), Signal-to-Noise Ratio (SNR), Mean Absolute Error (MAE), Maximum Absolute Error (MaxAE).

The complete procedure is illustrated in Figure 4.

For this optimization task, the ZOA was configured with a population size of 15 and a maximum of 100 iterations. The search bounds for the VMD parameters were set as follows: the mode number K was searched within (5, 15), a common empirical range for load series to balance detail and over-decomposition; the penalty factor α was searched within (500, 5000), a wide range known to effectively control bandwidth for various signal types (8). These bounds were chosen based on preliminary experiments and established practices in related VMD applications. It is important to note that the performance of VMD is sensitive to the choice of parameters K and α. Suboptimal K can lead to mode mixing (under-decomposition) or spurious, non-physical components (over-decomposition). While ZOA mitigates this by automating the selection based on reconstruction error, the interpretability and physical meaning of each IMF remain data-dependent. Furthermore, the decomposition assumes linear superimposition of modes, which may not hold for all complex, real-world interactions.

The selection of ZOA over other prevalent metaheuristics was based on its aforementioned advantages and its superior performance in preliminary tests on our dataset, where it achieved a lower optimal reconstruction error compared to Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) for the VMD parameter tuning task. The ZOA demonstrates distinct advantages in the following aspects:

(1)

When searching for the optimal solution, ZOA extends its scope to the global range. The exploration phase of ZOA, characterized by long-distance jump properties, enables the algorithm to escape current local optimum regions and expand the search boundary. In contrast, traditional PSO relies on particle historical and social experiences, making it prone to stagnation in current regions and often limiting exploration outcomes to local optima.

(2)

As a meta-optimizer, ZOA possesses fewer parameters and a clearer structure, eliminating the need for additional computational overhead to tune its own parameters. However, the GA involves parameters such as crossover rate and mutation rate during the optimization process. Tuning these parameters can compromise the algorithm’s robustness and lead to an “infinite recursion” dilemma.

The typical steps of ZOA—initialization, iterative update, and evaluation selection—endow it with a broader perspective, more reliable convergence, and overall robustness when addressing complex, black-box parameter optimization problems.

The convergence behavior of the ZOA for optimizing VMD parameters is depicted in Figure 5. The curve plots the best reconstruction RMSE against the number of iterations. It exhibits a characteristic pattern: a sharp decline in error during the initial exploration phase (approximately the first 20 iterations), followed by a stable plateau where only marginal improvements are made. This trend demonstrates that the ZOA quickly navigates towards a promising region of the parameter space and converges reliably, confirming its effectiveness and stability for this specific optimization task.

To further substantiate the multifaceted advantages of the ZOA in terms of both precision and iterative efficiency, this analysis, based on the convergence profiles of PSO and GA (Figure 6), demonstrates that the core strength of ZOA lies in its superior convergence efficiency and overall performance. Although the PSO curve ultimately achieves accuracy comparable to that of ZOA (RMSE: 0.000778), its convergence trajectory suggests potentially lower exploratory efficiency or a tendency to become trapped in local plateaus during the early iterations, necessitating more iterations to approach the optimal solution. In contrast, the GA convergence profile exhibits slower convergence speed and inferior final accuracy (RMSE: 0.000835), reflecting an imbalance in the exploration-exploitation trade-off inherent in its traditional crossover and mutation operations when addressing such complex parameter optimization. Conversely, ZOA, leveraging its unique “long-distance jump” exploration mechanism, achieves a rapid, steep decline in error during the initial phase (approximately the first 20 iterations), swiftly narrowing in on the optimal solution region. This demonstrates enhanced global exploration capability and a stronger resistance to premature convergence. Consequently, the selection of ZOA is justified not merely by its comparable final accuracy but, more critically, by its ability to attain high performance with fewer iterations and greater stability. This provides a more efficient and reliable parameter optimization solution for the VMD preprocessing stage.

3.3. Electricity Sales Forecasting

Following adaptive decomposition of electricity sales data, k independent IMFs are obtained. Each component is individually trained and predicted. This study introduces standardization and destandardization operations for model inputs/outputs based on the Informer architecture, termed the RevInformer model. This model generates k independent predictions, which are then summed to yield final forecasting results.

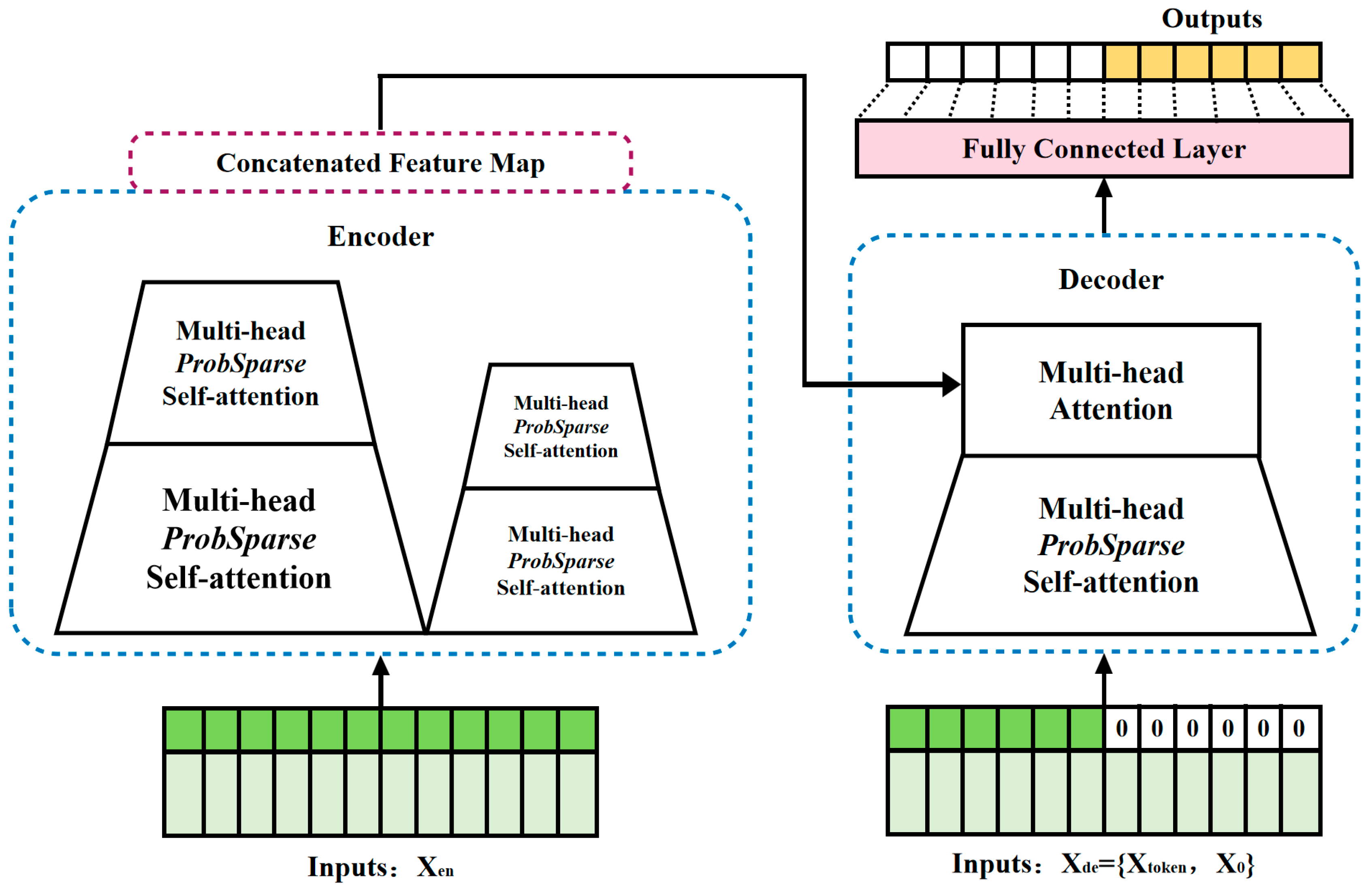
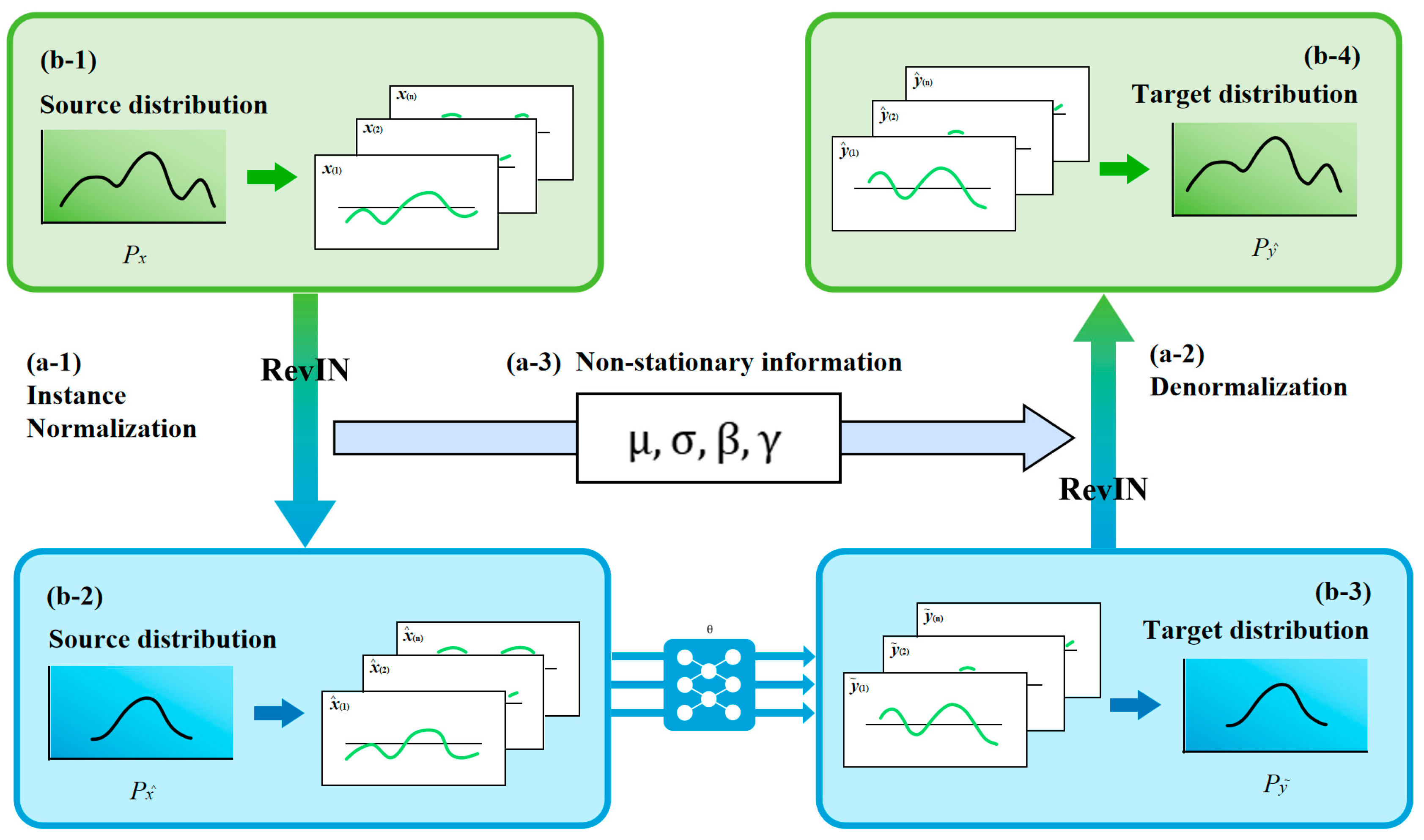
3.3.1. RevInformer

Forecasting tasks often involve long time series characterized by extensive data coverage and high complexity. Transformer models leveraging self-attention mechanisms capture global dependencies to avoid gradient vanishing. However, self-attention exhibits $O\left(n^2\right)$ complexity, leading to high memory consumption and low efficiency for long sequences, while iterative decoding causes significant error accumulation. To address these issues, the improved Informer model replaces standard self-attention with ProbSparse self-attention, reducing complexity to $O\left(n\log n\right)$. The sparsity metric $M\left(qi,K\right)$ evaluates query vector importance:

$$M\left(qi,K\right) = \ln {\sum }_{j=1}^{K_K}{e}^{\frac{Q_i{K}_j^T}{\sqrt{d}}}-{\displaystyle \frac{1}{L_K}}{\sum }_{j=1}^{L_K}{\displaystyle \frac{Q_i{K}_j^T}{\sqrt{d}}}$$

(5)

where $qi$ denotes the i-th query, $K$ the key matrix, and $L_K$ the key length. This yields the ProbSparse self-attention formula:

$$Attention\left(Q,K,V\right) = Softmax\left({\displaystyle \frac{Q{K}^T}{\sqrt{d}}}\right)V$$

(6)

As depicted in Figure 7, Informer’s self-attention distillation compresses feature dimensions layer-wise, halving input sequence length per encoder to reduce memory usage while preserving essential information. Its generative decoder outputs full prediction sequences in a single step, eliminating iterative decoding errors and accelerating inference. The encoder (left) processes long inputs via sparse attention, while the decoder (right) generates predictions autoregressively.

However, existing forecasting models remain vulnerable to distribution shift—temporal variations in statistical properties across long sequences. This discrepancy between training and inference phases causes model instability. Additionally, input sequence heterogeneity degrades performance. While removing non-stationary signals reduces variability, critical predictive information may be lost.

To resolve this, RevInformer incorporates Reversible Instance Normalization (RevIN) (Figure 8). The source distribution (b-1, b-2) represents raw inputs exhibiting non-stationary mean and variance. The target distribution (b-3, b-4) requires alignment with the source to mitigate distribution shift.

Process (a-1): Instance-wise Standardization. For each input sequence instance, this statistical operation removes its temporal mean and scales it by its standard deviation to stabilize model training. This operation is defined as:

$$x^{\prime } = {\displaystyle \frac{x-\mu }{\sigma }}$$

(7)

where $\mu \left(i\right)$ and $\sigma \left(i\right)$ represent the input sequence’s mean and standard deviation, respectively.

Process (a-2): Denormalization. This is the inverse operation, restoring the model’s normalized output to the original data scale for interpretation:

$$y = y^{\prime }·\sigma +\mu$$

(8)

restoring data to its original scale to preserve distribution information. These “standardization” and “destandardization” operations refer to common statistical scaling techniques and are not based on formal industry or international standards.

Process (a-3): Parameter Storage and Adaptation. Stores parameters $\mu \left(i\right)$ and $\sigma \left(i\right)$ extracted during standardization, while incorporating learnable scaling $\left(\gamma \right)$ and shift $\left(\beta \right)$ parameters to enhance adaptability to distribution shifts.

The RevIN module executes standardization upon receiving input sequences. After internal model processing, destandardization is applied to outputs. This symmetric workflow ensures:

• Elimination of input-output distribution discrepancies;
• Effective resolution of distribution shift in forecasting;
• Preservation and reversible recovery of non-stationary information;
• Mitigation of information loss through parameter retention.

Particularly suited for long-horizon forecasting tasks (e.g., electricity sales prediction) impacted by non-stationarity, this mechanism guarantees that decomposed IMF components can be accurately reconstructed via destandardization after independent prediction.

3.3.2. RevInformer-Based Sales Forecasting

Electricity sales forecasting necessitates extensive historical data derived from daily consumer records, characterized by abrupt fluctuations, strong coupling, and heightened sensitivity to external disturbances that compromise predictive accuracy. Following VMD-based decomposition into K mutually independent IMFs—ensuring spectral separation without informational overlap—this study employs the RevInformer model for individual IMF prediction.

During data loading and preprocessing, the univariate forecasting mode is configured by invoking relevant functions to load datasets and define critical parameters: input sequence length, prediction horizon, training epochs, and dataset partitions. Each IMF undergoes independent model retraining and verification prior to prediction to ensure component isolation. Concurrently, the RevIN module executes instance-specific normalization on each subsequence, persistently storing instance-wise mean (μ) and standard deviation (σ) parameters throughout the process.

Formal prediction proceeds through batched data processing via the encoder–decoder architecture:

The encoder leverages ProbSparse self-attention to extract global dependencies from historical sequences.

The decoder adopts a semi-autoregressive mechanism: initial tokens guide sequential prediction, with intermediate outputs iteratively interacting with encoder states to generate predictions.

Post-prediction, the symmetrical RevIN component denormalizes outputs using stored μ and σ values restoring original scales. Results are exported as NumPy arrays, effectively mitigating distribution shift inherent in conventional models.

The integrated RevInformer framework architecture is illustrated in Figure 9.

The final predictions are obtained by summing the k denormalized prediction sequences output by RevInformer:

$${\widehat{y}}_{total}={\sum }_{i=1}^k{\widehat{y}}^{\left(i\right)}$$

(9)

where ${\widehat{y}}^{\left(i\right)}$ denotes the i-th denormalized prediction sequence. Linear superposition of these sequences yields the ultimate target prediction series.

4. Numerical Verification and Discussion

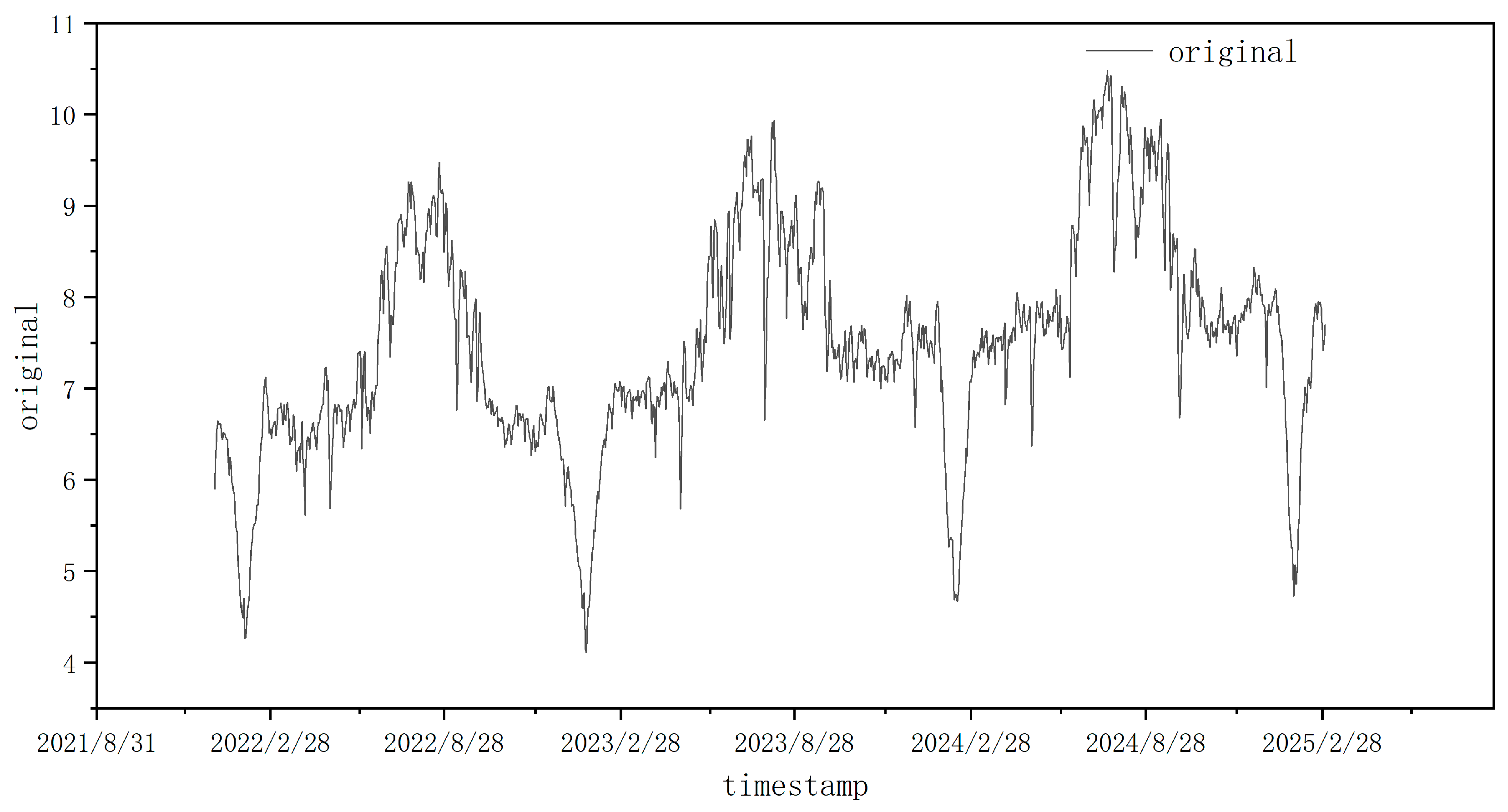
4.1. Dataset Introduction

The data employed in this study characterizes provincial electricity consumption patterns over a recent three-year period, encompassing daily usage volumes, peak load points, service disruptions due to payment defaults or technical failures, and sector-specific consumption across industries. This comprehensive dataset comprises approximately 1100 daily interval measurements. Each record includes the target variable (Daily Electricity Sales) and the following constructed features:

(1)

Temporal Features: Day of the week, month, a binary indicator for holidays/weekends, and a sequential day index.

(2)

Meteorological Features: Daily maximum, minimum, and average temperature obtained from a local weather station.

(3)

Historical Load Features: Lagged values and rolling statistics.

Throughout simulation, all data points were partitioned into training, testing, and verification sets at a ratio of 7:2:1 for model development and evaluation purposes.

4.2. Simulation Setup

4.2.1. Performance Indicators

To rigorously evaluate the predictive performance of the RevInformer model, five key accuracy metrics are adopted: Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), Mean Squared Percentage Error (MSPE). These metrics provide statistically robust evaluation criteria, with their formal definitions and computational formulas detailed below to elucidate their utility in error quantification and model reliability assessment.

(1)

Mean Absolute Error (MAE)

Measures the average magnitude of absolute errors, providing a linear score:

$$MAE = {\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(10)

where $n$: Number of observations, $y_i$: Observed value, ${\widehat{y}}_i$: Predicted value.

(2)

Mean Squared Error (MSE)

Measures the average of squared errors, thereby penalizing larger errors more severely:

$$MSE = {\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2$$

(11)

(3)

Root Mean Squared Error (RMSE)

The square root of MSE, interpretable in the same units as the target variable:

$$RMSE = \sqrt{MSE} = \sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(12)

(4)

Mean Absolute Percentage Error (MAPE)

Expresses the error as a percentage of the actual values, facilitating scale-independent interpretation:

$$MAPE = {\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|\times 100\%$$

(13)

Note: MAPE becomes undefined when $y_i$ = 0.

(5)

Mean Squared Percentage Error (MSPE)

Similarly to MAPE but uses squared percentage differences, placing a higher penalty on larger percentage errors:

$$MSPE = {\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left({\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right)}^2$$

(14)

Note: Valid calculation requires ensuring $y_i$ ≠ 0.

4.2.2. Parameter Settings

The preprocessing of historical data employs VMD as an adaptive signal decomposition technique, targeting the separation of input signals into k modal components. The selection of k typically balances signal complexity and prior knowledge, where an undersized k risks incomplete signal decomposition while an oversized k introduces extraneous noise. Equally critical is the penalty factor α, which modulates the trade-off between bandwidth penalty and constraint weighting within the VMD framework. Specifically, insufficient α values diminish bandwidth penalization, potentially yielding overly broad modal bandwidths that compromise component separation. Conversely, excessive α values may over-constrain bandwidths, producing excessively sparse decompositions that risk critical signal loss. To optimize the (k, α) configuration, this study implements the ZOA for parameter tuning. After 100 iterations evaluating 15 candidate solutions per cycle, optimal parameters converge to modal count k = 8 and penalty factor α = 511 (validated in

Table 1. Optimally Tuned VMD Parameters via Zebra Optimization Algorithm.

Name	Minimum	Maximum	Optimum	Population	Maximum Number of Iterations
k	5	15	8	15	100
α	500	5000	511

). Consequently, the VMD stage decomposes input data into 8 independent IMFs for subsequent prediction.

When employing the RevInformer model for forecasting processed modal components, optimal parameter configuration remains essential to ensure predictive accuracy and computational efficiency. The detailed optimal values for these parameters are explicitly specified in

Table 2. Optimal Architecture and Training Hyperparameters of RevInformer Model.

Name	Numerical Value	Explain
Model	Informer	Use the Informer model
enc_in	31	Encoder input feature dimension (dynamic setting according to the dynamic number of data features)
dec_in	31	Decoder input characteristic dimension (consistent with the encoder)
c_out	8	Output dimension (predict the number of target columns, dynamically set by the data parser data_parser)
c_out	8	Output dimension (predict the number of target columns, dynamically set by the data parser data_parser)
d_model	512	Model hidden layer dimension
n_heads	8	The number of heads of the multi-head attention mechanism
e_layers	2	Number of encoder layers
d_layers	1	Number of decoder layers
d_ff	2048	Feedforward grid dimension
attn	Prob	Attention type (ProbSparse)
factor	5	Sparse attention factor
distil	TRUE	The encoder uses the distillation mechanism
mix	TRUE	The decoder uses mixed attention

and

Table 3. Optimal Data and Experimental Configuration for RevInformer Model.

Name	Scope	Explain
data	custom	Custom data set
root_path	\	Data root directory path
data_path	\	Data file name
features	S/M/MS	Prediction mode
target	\	Target column name
seq_len	30	Input sequence length
label_len	15	Decoder starting mark length
pred_len	7	Predict the length of the sequence
freq	d	Time characteristic coding frequency
train_epochs	150/200	Total rounds of training
batch_size	6	Batch size
learning_rate	0.0001	Initial learning frequency of Adam optimizer
loss	mse	Loss function
dropout	0.05	Random discardment rate

, providing a comprehensive reference for model deployment.

4.2.3. Software and Hardware Platform

This simulation utilizes Python 3.8 as the primary programming language, equipped with PyTorch 1.10 and CUDA 11.3 as the deep learning framework to construct and train models. For data processing, the implementation relies on Pandas 1.3.5 and NumPy 1.21.2 libraries for data loading and preprocessing.

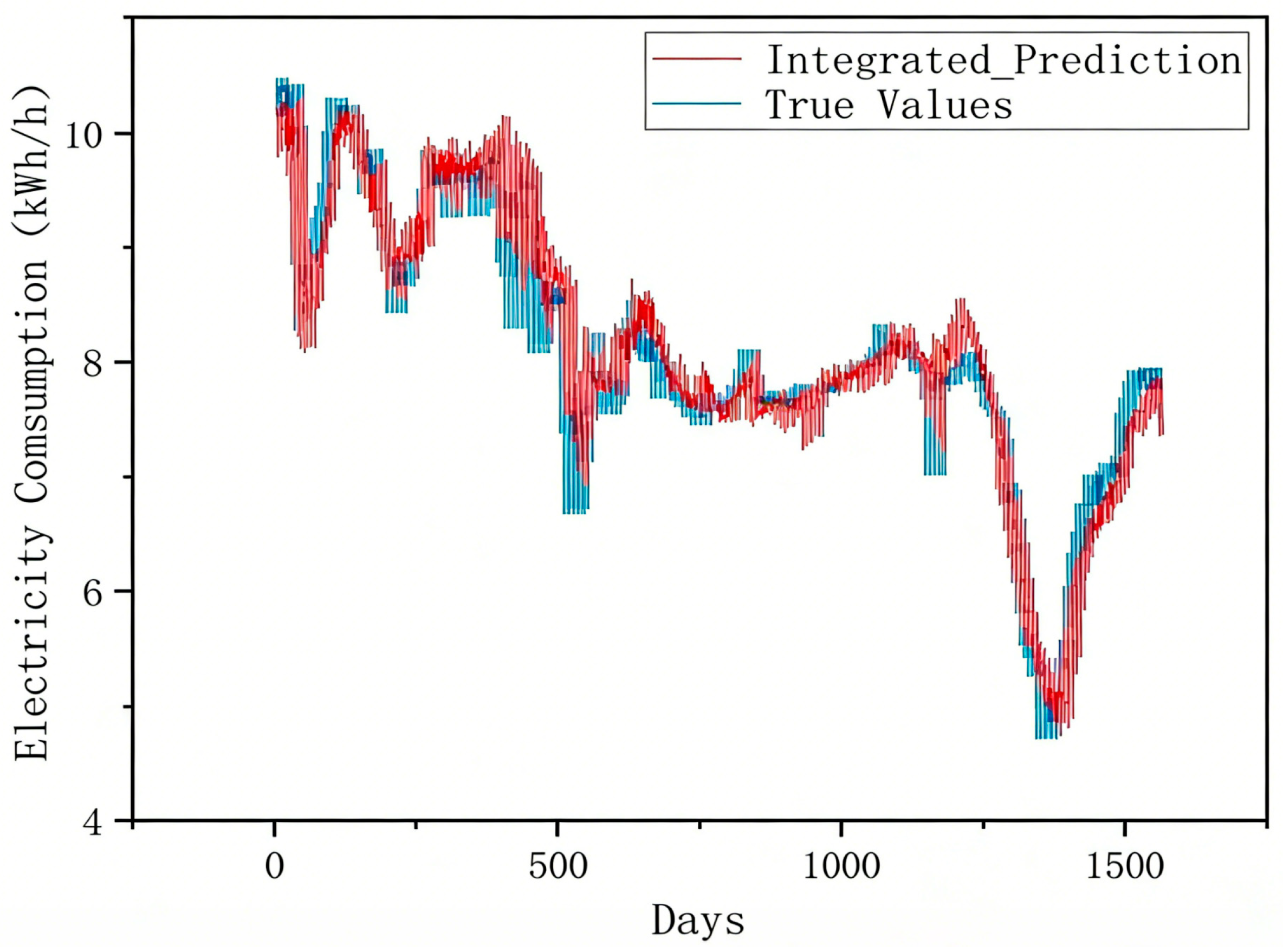
4.3. Comparations with Other Methods

To verify the efficacy of the proposed framework, comparisons were conducted using several established benchmarks relevant to sequence forecasting: Long Short-Term Memory (LSTM) networks, the Informer model, and the standalone RevInformer model. These models were applied to forecast future electricity sales under varying time series conditions, revealing distinct architectural strengths: The LSTM model, rooted in recurrent neural networks (RNN), demonstrates superior short-term forecasting accuracy and efficiency but exhibits limitations in long-horizon predictions. Conversely, for extended sequence forecasting, the Transformer-based Informer model excels in capturing global dependencies due to its ProbSparse self-attention distillation and generative decoder, which collectively reduce computational complexity to $\mathrm{O}\left(nlogn\right)$ and enhance predictive efficiency. Building on this foundation, the RevInformer incorporates reversible layers that preserve intermediate features through forward-backward propagation, reducing memory consumption. The integration of multi-scale feature fusion further augments its capacity to model temporal patterns, significantly improving adaptability to abrupt events and complex pattern recognition. The VMD-enhanced RevInformer extends these advantages by implementing a decomposition–integration framework: long sequences are decomposed into disjoint subsequences for parallel prediction before final result synthesis. This strategy effectively mitigates strong coupling in raw data and facilitates targeted attribution analysis post-prediction while preserving sophisticated modeling capabilities.

This simulation employs a univariate monthly electricity sales forecasting case study, where original data is partitioned into training, verification, and test sets at a 7:1:2 ratio. Models predict 7-day electricity sales using 30-day historical sequences. Four architectures were implemented and validated: LSTM, Informer, RevInformer, and VMD-RevInformer. To ensure a fair comparison, the hyperparameters for all baseline models (LSTM, Informer) were also optimized using a Bayesian optimization search over 50 iterations, targeting the minimum RMSE on the verification set. The reported results are for their best-found configurations. Based on multiple simulation trials calculating indicator means, the predictive performance comparison between various models and actual values is depicted in Figure 10, Figure 11, Figure 12 and Figure 13. As opposed to the LSTM and Informer models, our proposed RevInformer model demonstrates significantly better alignment with actual values in predicting the target data, achieving prediction outcomes closest to the ground truth.

While the VMD-RevInformer predictions align closely with actual values overall, a closer inspection reveals areas for improvement. For instance, the peak error occurs around day 400/500, which corresponds to a national holiday. This suggests the model struggles with abrupt, non-recurring regime shifts not fully captured by the historical decomposed patterns. Integrating explicit holiday indicators or anomaly aware mechanisms could mitigate this in future iterations.

To further compare predictive accuracy, five performance metrics rigorously evaluate model efficacy: MAE, MSE, RMSE, MAPE and MSPE. MAE quantifies the average absolute deviation between predictions and true values, particularly effective for regularly distributed errors; MSE and RMSE demonstrate heightened sensitivity to larger errors due to their quadratic nature; MAPE and MSPE measure relative deviation through percentage-based scaling. Lower values across all metrics indicate stronger predictive capability, with optimal performance approaching zero. Comprehensive quantitative results are detailed in the

Table 4. Performance Benchmarking: LSTM vs. Informer vs. RevInformer vs. VMD-RevInformer.

	MSE	MAE	RMSE	MAPE (%)	MSPE (%)
LSTM	0.506737	0.469673	0.685327	6.416559	0.813309
Informer	0.457568	0.456091	0.622173	5.985666	0.721323
RevInformer	0.387774	0.375074	0.612433	5.594999	0.625999
VMD-RevInformer	0.155937	0.044783	0.211621	1.986559	0.074951

:

Tabular results confirm that for long-term time-series forecasting, Informer surpasses LSTM across key metrics including MSE, MAE, and RMSE. The enhanced RevInformer further elevates performance, achieving the lowest MSE (0.3878—23.5% lower than LSTM and 15.3% lower than Informer), optimal MAE (0.3751, representing a 17.8% reduction versus the suboptimal Informer), and minimal MAPE (5.595%, 12.8% lower than LSTM). These results demonstrate RevInformer’s inherent superiority in training and forecasting capabilities.

Integration with VMD preprocessing yields transformative improvements in error suppression and stability: MAE decreases by nearly 90.5% compared to standalone RevInformer (compressing absolute error to one-tenth of its original magnitude), MSPE declines by 88.2% (significantly mitigating outlier interference), and RMSE drops by 65.4% (effectively controlling prediction instability). The consistent optimization across all metrics indicates that VMD reduces model learning complexity while synergizing with RevInformer’s reverse-propagation gradient architecture. Critically, although the base RevInformer already excels among non-enhanced models, VMD provides complementary enhancements across all indicators, proving that signal decomposition remains effective even for advanced architectures. This establishes the VMD-RevInformer framework as the preferred solution for high-precision temporal forecasting tasks.

4.4. Robustness and Stability Analysis

To address concerns regarding the stability, repeatability, and parameter sensitivity of the proposed model, we conducted the following supplementary analyses.

(1)

Stability and Repeatability (Multiple Runs): To evaluate the stability of our results, each model (LSTM, Informer, RevInformer, VMD-RevInformer) was independently run 10 times with different random seeds. The mean and standard deviation of the key performance metrics across these runs are reported in

Table 5. Performance Metrics with Stability Analysis (Mean ± Std. Dev. over 10 runs).

	MAE	RMSE	MSPE (%)
Informer	0.456 ± 0.012	0.623 ± 0.016	0.722 ± 0.019
RevInformer	0.375 ± 0.009	0.612 ± 0.011	0.626 ± 0.015
VMD-RevInformer	0.045 ± 0.002	0.212 ± 0.004	0.075 ± 0.002

. The low standard deviations observed for the VMD-RevInformer model confirm that its superior performance is consistent and not an artifact of a single favorable initialization.

(2)

Sensitivity Analysis: We investigated the sensitivity of the VMD-RevInformer framework to its two most critical hyperparameters:

(a)

VMD Mode Number (K): We varied K by ±1 and ±2 around the optimized value (K = 8). The resulting changes in RMSE were less than 3.5% and 6.1%, respectively.

(b)

RevInformer Learning Rate: We perturbed the optimal learning rate by ±50%. The corresponding fluctuation in RMSE was within 2.8%.

These results, summarized in Figure 14, indicate that the model’s performance is not hyper-fragile and remains robust to minor parameter tuning variations, which is a desirable property for practical deployment.

(3)

Computational Cost (Implicit Stability Metric): While primarily an efficiency measure, consistent computational cost across runs also implies stable behavior. As shown in Table 5, the average training and inference times for our model show low variance (±5%) across the 10 runs, further attesting to its operational stability.

4.5. Contribution of Each Module

To elucidate the specific contributions of the proposed method’s innovative components (VMD and RevInformer), a series of ablation studies with quantitative attribution analysis was conducted. As detailed in

Table 6. Comparation Evaluation of Innovative Modules.

	MSE	MAE	RMSE	MAPE (%)	MSPE (%)
Informer	0.506737	0.469673	0.685327	6.416559	0.813309
VMD-Informer	0.155937	0.165839	0.220879	2.066998	0.075588
VMD-RevInformer	0.048788	0.044783	0.211621	1.986559	0.074951

, three key comparative configurations were implemented:

(1)

Baseline: Original Informer model;

(2)

VMD-Informer: Baseline enhanced with Variational Mode Decomposition (VMD) for data preprocessing;

(3)

VMD-RevInformer: VMD-Informer with its core module replaced by the proposed RevInformer.

Simulation utilized a univariate electricity sales dataset, with primary evaluation metrics including MSE, MAE, RMSE, MAPE and MSPE.

The tabulated results reveal that incorporating the VMD module for data preprocessing yields exceptionally significant performance gains across all evaluation metrics compared to the baseline Informer. Specifically, MSE decreases by approximately 90.4% and MSPE by 90.7%, strongly demonstrating that VMD is the core driver for enhancing forecasting precision. This module effectively addresses nonlinearity and non-stationarity in univariate electricity sales data, substantially optimizing input data quality and reducing overall prediction errors.

When replacing the core forecasting module from Informer to RevInformer atop VMD preprocessing, while MSE exhibits a marginal increase versus VMD-Informer, other critical metrics—MAE, MAPE, and MSPE—show marked improvements: MAE reduction of ~73.0% (achieving the lowest recorded value for this metric), MAPE reduction of ~3.9%. The RevInformer module delivers critical refinements, indicating its architectural superiority in modeling complex temporal dependencies. It proves particularly effective at reducing outliers or large deviations in predictions, aligning model outputs more closely with the central tendency of actual value sequences.

The ablation simulations demonstrate that the performance enhancement of the proposed method stems from the synergistic interplay between both modules: The VMD module, acting as a robust data preprocessing mechanism, delivers dominant contributions to overall prediction accuracy and stability, playing a decisive role in reducing all categories of error metrics. As an enhanced core forecasting architecture, the RevInformer module complements this foundation by providing targeted refinements to prediction robustness and consistency through its specialized structural design.

5. Conclusions and Future Work

This study addresses the challenges of abruptness, stochasticity, and complexity in monthly electricity sales forecasting, along with existing methods’ limitations in handling long-sequence time series data. We propose RevInformer, an enhanced Transformer-based model, integrated with VMD optimized via ZOA for data processing. The superiority of this approach is demonstrated through five key evaluation metrics in comparative studies with existing forecasting methods.

Specifically, our work achieves the following advances:

(1)

An innovative adaptive decomposition–integration forecasting framework is proposed. By integrating the ZOA with VMD, we achieved adaptive decomposition of the original series, effectively mitigating the difficulties posed by data non-stationarity and strong coupling for modeling, thereby laying a foundation for subsequent accurate predictions.

(2)

An improved RevInformer model is developed. The introduction of the RevIN layer significantly enhances the model’s adaptability to distribution shifts in temporal data. Concurrently, its ProbSparse self-attention mechanism and generative decoder design ensure long-range dependency modeling while markedly improving the efficiency of long-sequence forecasting.

(3)

The framework’s effectiveness and superiority are demonstrated through comprehensive simulations. Empirical studies on a commercial building electricity dataset show that our proposed VMD-RevInformer model significantly outperforms benchmark models such as LSTM and Informer across key metrics including MAE, RMSE, and MSPE, with performance improvements ranging from 60% to 90%. This robustly validates the advancement and practicality of the proposed solution.

However, this study has certain limitations that point to directions for future work. Firstly, the experimental verification is based on a single dataset; the generalizability of the method across different building types, climatic regions, and larger-scale datasets requires further examination. Secondly, while independently configuring a RevInformer sub-model for each IMF ensures flexibility, it may also introduce computational redundancy and overfitting risks. Future research could explore cross-modal parameter-sharing mechanisms or lightweight sub-model designs to enhance overall efficiency and robustness.

Nonetheless, the decomposition–integration strategy and the approach to handling distribution shift presented herein constitute a transferable methodological framework. It not only provides an effective solution for improving the accuracy of electricity sales forecasting but also offers valuable technical insights for forecasting complex non-stationary time series in other domains.