Efficient Spiking Transformer Based on Temporal Multi-Scale Processing and Cross-Time-Step Distillation

Abstract

Spiking Neural Networks (SNNs) have drawn increasing attention for their event-driven and energy-efficient characteristics. However, achieving accurate and efficient inference within limited time-steps remains a major challenge. This paper proposes an efficient spiking Transformer framework that integrates cross-time-step knowledge distillation, multi-scale resolution processing, and attention-based token pruning to enhance both temporal modeling and energy efficiency. The cross-time-step distillation mechanism enables earlier time steps to learn from later ones, which improves inference consistency and accuracy, leading to better performance. Meanwhile, the multi-scale processing module dynamically adjusts input resolution and reuses features across scales, while the attention-based token pruning adaptively removes redundant tokens to reduce computational overhead. Extensive experimental results on static datasets (CIFAR-10/100 and ImageNet-1K) and dynamic event-based datasets (DVS128-Gesture and CIFAR10-DVS) demonstrate that the proposed method achieves higher accuracy and more than 1.4× inference speedup compared to baseline SNN–Transformer models. This framework provides a promising solution for developing energy-efficient and high-performance neuromorphic vision systems.

1. Introduction

With the rapid development of artificial intelligence, traditional Artificial Neural Networks (ANNs) have achieved remarkable results in tasks such as image classification and object detection. However, these networks often rely on fixed time steps and continuous activation functions, leading to limitations in handling highly dynamic, low-power scenarios, particularly in balancing computational resources and accuracy. Spiking Neural Networks (SNNs) [1], as the third generation of neural networks, have gradually become a research hotspot in brain-inspired computing and efficient artificial intelligence due to their biologically inspired spike-based information encoding and event-driven, low-power characteristics.

SNNs [2] simulate the spike firing mechanism of biological neurons, activating neurons only when input events occur, avoiding redundant computations in fixed time steps of traditional neural networks and significantly reducing power consumption. This mechanism not only aligns more closely with the operation of biological neural [3] systems but also adapts to the asynchronous event streams output by Dynamic Vision Sensors (DVSs) [4]. DVS cameras capture scene changes with microsecond-level temporal resolution, generating sparse spatiotemporal event streams [5].

However, the practical application of SNNs still faces several challenges [6]. The discrete spike-firing behavior of spiking neurons makes the network difficult to differentiate, which limits the direct use of traditional gradient-based optimization methods. Existing approaches such as surrogate gradients still have limitations in improving time-step efficiency and accuracy. In recent years, a number of low-power SNN studies have attempted to improve energy efficiency by reducing spike firing rates, designing more energy-friendly network structures, or integrating the characteristics of event cameras [7,8]. Examples include constant firing rate control, energy-efficient spiking convolution modules, and streaming inference frameworks tailored for DVS data. However, most existing pruning strategies mainly focus on the spatial dimension, while ignoring the dynamic properties of temporal spiking sequences. Although spatial pruning can reduce redundant tokens or features, temporal redundancy in spike sequences has not been effectively exploited, causing the inference process to remain fixed and time-consuming. Moreover, cross-time-step supervision, dynamic pruning, and multi-scale processing are often investigated separately, lacking a unified optimization framework. As a result, existing methods struggle to simultaneously address the requirements of temporal modeling, spatial compression, and adaptive resolution within a single architecture.

To address these issues, this paper proposes an SNN architecture incorporating a multi-time-step attention mechanism. By introducing the global spatiotemporal modeling capability of Transformer [9] and combining cross-time-step knowledge distillation, dual optimization of computational efficiency and key feature extraction is achieved. Additionally, a multi-scale image processing framework is designed to significantly reduce computational energy consumption through progressive feature reuse and dynamic pruning strategies. Experiments demonstrate that this method improves performance and efficiency on both static and dynamic datasets, providing a new technical pathway for SNNs in edge computing, visual analysis, and other scenarios.

The contributions of this paper are summarized as follows:

(1) Cross-time-step knowledge distillation for temporal optimization. We design a novel cross-time-step knowledge distillation strategy that transfers information from later to earlier time steps, which enables the model to learn more discriminative representations at earlier time-steps. This mechanism enhances temporal consistency and significantly improves inference accuracy.

(2) Multi-scale resolution processing with cross-scale feature reuse. A multi-scale processing framework is introduced to dynamically adjust image resolution during inference. By progressively reusing low-resolution features in higher-resolution stages, the proposed method achieves an effective balance between computational cost and classification performance.

(3) Attention-based token pruning for lightweight spiking transformers. We propose an attention-guided token pruning approach that adaptively removes less informative tokens using learnable thresholds. This mechanism reduces redundant computation and achieves significant inference speedup, while maintaining competitive accuracy across static and dynamic benchmarks.

(4) We evaluate the proposed method on three representative models, including Spikformer, S-D Transformer, and SGLFormer, and conduct extensive experiments on both static datasets (CIFAR-10/100 [10] and ImageNet-1K [11]) and dynamic datasets (DVS128-Gesture [12] and CIFAR10-DVS [13]). The results demonstrate that the proposed method not only achieves better performance but also significantly accelerates the model inference (more than $1.4\times$ speedup), which thus can further enhance the energy efficiency of SNNs.

2. Preliminaries

In this section, we introduce the basic components that are directly used in our method, including the LIF neuron and surrogate gradients, the formulation of knowledge distillation, and the spiking Transformer backbones.

2.1. Spiking Neural Networks

SNNs process information by simulating the spike firing mechanism of biological neurons. This network model abandons the continuous activation functions and fixed-time-step information processing of traditional ANNs, instead using discrete spike signals for information encoding and transmission. In SNNs, neuron activation and transmission are driven by spike events, meaning that neurons fire only when input signals reach a specific threshold. This mechanism gives SNNs sparse activation characteristics, effectively avoiding redundant computations at unnecessary times, thereby significantly reducing power consumption and improving computational efficiency.

Furthermore, the ability of SNNs to encode information along the temporal dimension is another highlight. Through spike intervals and frequencies, SNNs can carry rich information, demonstrating excellent spatiotemporal information representation capabilities. Neuron models such as the Integrate-and-Fire (IF) and Leaky Integrate-and-Fire (LIF) further enhance their ability to learn temporal patterns in input sequences [14]. In the LIF model, the membrane potential of a neuron gradually accumulates upon receiving synaptic input; once it exceeds the set threshold, the neuron fires a spike and resets the membrane potential.

Unlike the activation functions of traditional neural networks, SNNs use biologically inspired spiking neurons. The LIF neuron is a commonly used activation function in SNNs:

$$\begin{array}{c}V\left[t\right]=H\left[t\right]·(1-S\left[t\right])+V_{reset}·S\left[t\right],\\ S\left[t\right]=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}V\left[t\right]\ge V_{threshold}\hfill \\ 0,\hfill & \mathrm{if}V\left[t\right]<V_{threshold}\hfill \end{array}\right.,\\ H\left[t\right]=V[t-1]+{\displaystyle \frac{1}{\tau }}\left(X\left[t\right]-(V[t-1]-V_{reset})\right).\end{array}$$

(1)

$V\left[t\right]$ represents the membrane potential at time step t, $S\left[t\right]$ represents the spike firing state at time step t, $V_{\mathrm{threshold}}$ is the threshold voltage, $V_{\mathrm{reset}}$ is the reset voltage, $H\left[t\right]$ is an intermediate variable at time step t, and $\tau$ is the time constant. The membrane potential $V\left[t\right]$ is updated step by step based on the input $X\left[t\right]$. When $V\left[t\right]$ exceeds the threshold voltage $V_{\mathrm{threshold}}$, a spike is fired (i.e., $S\left[t\right]=1$), generating a spike feature map $S\left[t\right]$.

Training of Deep SNNs

In terms of training methods, SNNs face challenges due to the discreteness and non-differentiability of spike signals. Traditional backpropagation algorithms cannot be directly applied. To address the non-differentiability of SNNs [15], there are two main approaches to obtaining deep SNNs:

• ANN-to-SNN Conversion: Replaces activation functions like ReLU with spiking neurons and adds scaling operations such as weight normalization and threshold balancing to convert pre-trained ANNs into SNNs.
• Surrogate Gradients: Uses continuous differentiable functions to approximate the derivative of the step function, providing gradients during backpropagation. This allows direct training and handling of temporal data with only a few time steps, achieving good performance on both static and dynamic datasets [16].

A common surrogate gradient is the sigmoid function [17], as shown in Equation (2). Forward computation yields a 0–1 matrix, while backpropagation provides continuous gradient computation through the derivative of the sigmoid function as follows:

$$\begin{array}{c}{g}^{\prime }\left(x\right)=\alpha ·sigmoid\left(\alpha x\right)·(1-sigmoid\left(\alpha x\right))\end{array}$$

(2)

where a larger $\alpha$ makes the sigmoid closer to the step function, but the gradient range becomes narrower, requiring a trade-off between gradient strength and stability.

2.2. Knowledge Distillation

Knowledge distillation (KD) [18] is a technique for transferring knowledge from a large, complex model (teacher) to a smaller, simpler model (student). Let the teacher and student networks output the logits $z^{\mathrm{teacher}}\in {\mathbb{R}}^C$ and $z^{\mathrm{student}}\in {\mathbb{R}}^C$, respectively, for a given input sample, where C denotes the number of classes. Their softened class probability distributions, obtained via the softmax function with temperature parameter $\tau >0$, are defined as follows:

$$\begin{array}{c}\hfill p_i^{\mathrm{teacher}}={\displaystyle \frac{exp\left(z_i^{\mathrm{teacher}}/\tau \right)}{{\sum }_{j=1}^{C}exp\left(z_j^{\mathrm{teacher}}/\tau \right)}},p_i^{\mathrm{student}}={\displaystyle \frac{exp\left(z_i^{\mathrm{student}}/\tau \right)}{{\sum }_{j=1}^{C}exp\left(z_j^{\mathrm{student}}/\tau \right)}},\end{array}$$

(3)

where $p_i^{\mathrm{teacher}}$ and $p_i^{\mathrm{student}}$ represent the predicted probability of class i by the teacher and student models, respectively. The temperature $\tau$ controls the smoothness of the output distribution: higher values of $\tau$ produce softer probability distributions that reveal more information about the relative relationships among classes [19].

The student model is trained to minimize a distillation loss, which encourages its output distribution to match that of the teacher. A commonly used formulation is the Kullback–Leibler (KL) divergence between the softened teacher and student distributions:

$${\mathcal{L}}_{\mathrm{KD}}={\tau }^2\sum _{i=1}^C{p}_i^{\mathrm{teacher}}log{\displaystyle \frac{p_i^{\mathrm{teacher}}}{p_i^{\mathrm{student}}}},$$

(4)

where the factor ${\tau }^2$ compensates for the gradient scaling introduced by the temperature. In practice, this loss is often combined with the standard cross-entropy loss against the ground-truth labels to form the total training objective.

However, for SNNs, implementing knowledge distillation faces unique challenges [20,21,22,23,24]. The discrete spike characteristics and non-differentiability of SNNs limit the direct application of traditional knowledge distillation methods. To this end, researchers have explored strategies to introduce proxy losses between the continuous probability distribution output by the teacher model and the discrete spikes output by the student model, optimizing with surrogate gradients [25]. This method aims to maintain the event-driven and low-power characteristics of SNNs while enabling them to learn the teacher model’s advantages in feature extraction. Through this approach, the accuracy and generalization ability of SNNs in complex tasks are expected to be significantly improved, further promoting the practical application of SNNs.

2.3. Spiking Transformer

Transformer was initially designed for natural language processing but has also achieved great success in computer vision tasks, including image classification, object detection, and semantic segmentation. Unlike convolution-based models that primarily rely on inductive biases and focus on adjacent pixels, the Transformer structure uses self-attention mechanisms to globally capture relationships between spike features, thereby effectively improving performance.

To adopt the Transformer structure in SNNs, Zhou et al. [26] designed a novel spiking self-attention mechanism called Spiking Self-Attention (SSA). This mechanism uses sparse spike forms for Query, Key, and Value without softmax operations. The SSA computation process is as follows:

$$\begin{array}{c}Q=S{N}_Q\left(BN\left(X{W}_Q\right)\right),\\ K=S{N}_K\left(BN\left(X{W}_K\right)\right),\\ V=S{N}_V\left(BN\left(X{W}_V\right)\right),\\ SS{A}^{\prime }(Q,K,V)=SN\left(Q{K}^T{V}^{*}s\right),\\ SSA(Q,K,V)=SN\left(BN\left(Linear\left(SS{A}^{\prime }(Q,K,V)\right)\right)\right)\end{array}$$

(5)

where spike-form Query, Key, and Value are computed through learnable layers, sis a scaling factor, SNis the spiking activation layer, BNis the batch normalization layer, and Linearis the linear layer. SSA computation avoids multiplication operations, aligning with the characteristics of SNNs. Based on SSA, Zhou et al. designed Spikformer, which achieved 74.81% accuracy on ImageNet-1k, demonstrating excellent performance potential [27].

Zhou et al. [28] discussed the non-spiking computation issue caused by “addition after activation” shortcuts in Spikformer and proposed Spikingformer, which uses “pre-activation” shortcuts to avoid non-spiking computation in synaptic calculations. CML [29] specifically designed a downsampling structure for SNNs to address the imprecise gradient backpropagation in most advanced deep SNNs, achieving 77.64% accuracy on ImageNet, significantly improving the performance of Transformer-based SNNs.

Yao et al. [30] designed a spike-driven self-attention mechanism (SDSA) that linearly depends on the number of tokens and channels in terms of complexity, significantly reducing computational energy consumption. SDSA relies only on masking and addition operations, abandoning multiplication operations, reducing computational energy consumption by 87.2 times compared to SSA. Meanwhile, Zhang et al. [31] proposed SGLformer, which cleverly integrates Transformer and convolutional structures into SNNs to achieve efficient information processing at global and local scales. SGLFormer achieved a breakthrough top-1 accuracy of 83.73% on the ImageNet-1k dataset with 64 M parameters. Additionally, Zhou et al. [32] proposed QKFormer, which uses a novel hierarchical spiking Transformer structure, leveraging Q-K attention mechanisms to easily model the importance of token or channel dimensions while maintaining linear complexity. Through direct training, it achieved over 85% top-1 accuracy on ImageNet with 4 time steps, surpassing the performance of most ANN-based Transformer structures.

In summary, the fusion architecture of SNNs and Transformers not only inherits the biological plausibility and event-driven characteristics of SNNs but also incorporates the global modeling capability of Transformers, opening new avenues for developing low-power, high-performance neuromorphic computing systems, which are expected to play an important role in future edge computing and end-side models [33].

3. Proposed Method

The overall architecture of the proposed multi-scale SNN processing framework is shown in Figure 1. First, the input image undergoes multi-scale image processing: small-scale images are input and passed through LIF neurons to obtain spike feature maps, enhancing the representation of key information. Then, the model undergoes cross-time-step distillation, combined with KL divergence loss calculation [34], using information from subsequent time steps to guide feature learning in earlier time steps. At the final output layer, the current highest class probability is computed and compared with a confidence threshold: if the probability is below the threshold, a higher-resolution input mechanism is triggered, inputting higher-resolution images while reusing low-resolution feature information to achieve feature reuse; if the classification probability is above the threshold, the predicted classification is directly output.

3.1. Multi-Scale Resolution Processing

As shown in Figure 2, visual images are scaled down to the target size using bilinear interpolation to reduce subsequent computation. This process not only helps reduce interference from irrelevant information but also maintains the overall structure of the image, preserving features of key regions. The formula is expressed as follows:

$$\begin{array}{c}{\mathit{F}}_{\mathit{L}}=\mathrm{Conv}\left(\mathrm{Downsample}\left(I\right)\right)\in {\mathbb{R}}^{56\times 56\times C}\end{array}$$

(6)

In Equation(6), I is the original image and $F_L$ is the downscaled image. To ensure the clarity of visual features in the downscaled image, further preprocessing is performed, including grayscale enhancement and edge-preserving filtering, to maintain image clarity.

If the final classification probability of the small-scale image is below the threshold, a higher-scale image input is triggered. The low-scale image is upsampled first, and then feature reuse is performed. The formula is expressed as follows:

$$\begin{array}{c}{\mathit{F}}_L^{\prime }=Conv\left(Upsample\left({\mathit{F}}_L\right)\right)\\ {\mathit{F}}_{\mathrm{reuse}}={\mathit{F}}_{\mathit{H}}+\alpha {\mathit{F}}_L^{\prime }\end{array}$$

(7)

where cross-scale feature reuse is used to balance computational efficiency and classification accuracy. Taking ImageNet-1K as an example, a 56 × 56 low-resolution image is first input, and basic semantic information is obtained through conventional convolution and feature extraction. At this stage, computational load is small, and inference speed is fast. If the classification evaluation probability at the current resolution is low, higher-resolution processing is triggered, gradually introducing finer pixel details. When processing high-resolution images, features extracted at the low-resolution stage are reused and fused with current layer features after upsampling, preserving semantic information and enhancing feature expression capability. Finally, multi-time-step analysis integrates feature information from different resolutions, leveraging both global context information from low resolution and local details from high resolution to enhance classification accuracy.

3.2. Cross-Time-Step Distillation

As shown in Figure 3, the attention distribution at time step t + 1 serves as the teacher signal, guiding the attention distribution learning at time step t through KL divergence loss, enabling earlier time steps to focus on image features extracted by subsequent time steps.

The designed loss function is

$$\begin{array}{c}\mathrm{Loss}=\mathrm{CE}\left(y_T,y_{\mathrm{true}}\right)+{\displaystyle \sum _{t=1}^{T-1}}{\gamma }_t·\mathrm{KL}\left(y_{t+1}\parallel y_t\right)\\ \mathrm{KL}\left(y_{t+1}\parallel y_t\right)={\displaystyle \sum _i}{y}_{t+1}^{\left(i\right)}·log\left({\displaystyle \frac{y_{t+1}^{\left(i\right)}}{y_t^{\left(i\right)}}}\right)\end{array}$$

(8)

By combining cross-entropy and KL divergence, both final prediction accuracy and prediction consistency across time steps are optimized.

To strengthen the learning ability of earlier time steps, the model designs a gradually decaying loss weight strategy. As training progresses, the contribution of later time steps to the loss gradually increases, helping earlier time steps approach the final output more quickly. This progressively increasing guidance strategy not only accelerates the learning of earlier time steps but also reduces dependence on later time steps, thereby improving the prediction accuracy of earlier time steps. It is worth noting that the non-causal components of our method are used only during training for knowledge transfer, while the inference stage remains fully causal and does not rely on future information.

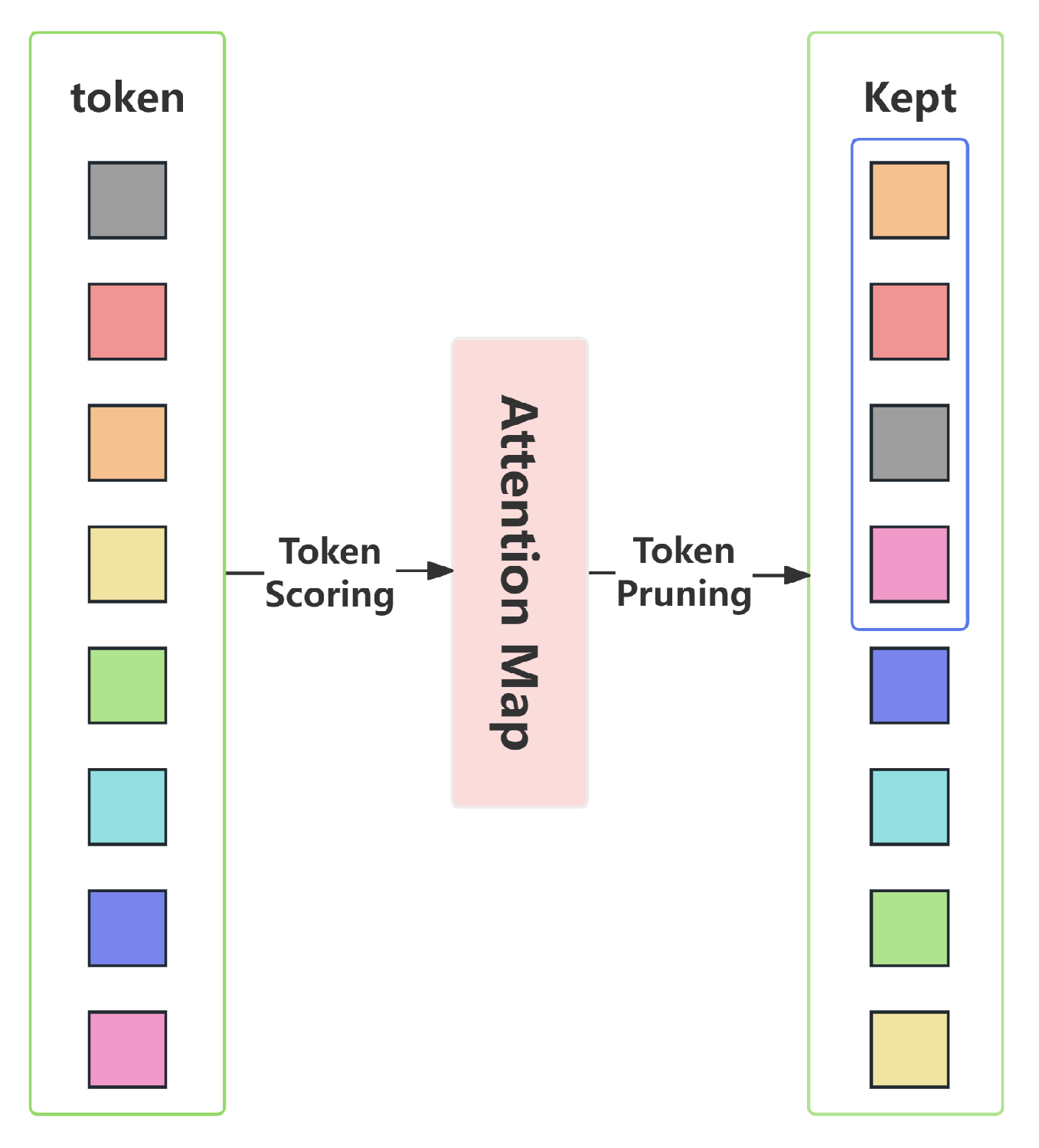
3.3. Attention-Based Token Pruning

For the Spike Transformer architecture, tokens are based on pixels rather than image patches, leading to excessive redundancy. The attention-based pruning strategy achieves finer computational resource allocation by evaluating token importance. As shown in Figure 4, by analyzing the importance scores of tokens in the attention mechanism, low-importance tokens are selectively pruned, retaining only tokens with scores exceeding $\gamma$ times the global maximum value ($\gamma \in (0,1)$). This design preserves key information for feature extraction while achieving a flexible balance between computational efficiency and model accuracy through the learnable parameter $\gamma$.

$$\begin{array}{c}{s}_i={\displaystyle \frac{1}{H}}{\displaystyle \sum _{h=1}^H}{\displaystyle \sum _{j=1}^N}softmax\left({\displaystyle \frac{Q{K}^{\top }}{\sqrt{d}}}\right)\\ T_{\mathrm{keep}}=\left\{i\mid s_i>\gamma ·max\left(s\right)\right\}\end{array}$$

(9)

As shown in Equation (8), token pruning is designed to further lightweight the model. Tokens with low attention scores are deemed less important, and a dynamic pruning strategy is used to reduce computation.

3.4. Multi-Scale Feature Fusion

To further reduce computational energy consumption, a multi-scale classification evaluation method is designed, as shown in Equation (9). By fusing the focused features of the current scale with the output results of the previous time step, a rich cross-scale feature input is formed.

$$\begin{array}{c}{F}_{\mathrm{fusion}}=\alpha F_t+\beta ·Conv\left(F_{t-1}\right)\end{array}$$

(10)

where $\alpha$ and $\beta$ are learnable fusion weights, $F_{t-1}$ is the feature map from historical time steps, and Conv represents convolutional computation. $F_{\mathrm{fusion}}$ is the fused image after multi-time-step processing. The system enhances global understanding of the target through this iterative fusion method. After outputting results at each time step, confidence evaluation is performed for each scale’s output results, as shown in Equation (10), to ensure the reliability of detection results.

$$\begin{array}{c}{C}_t=Linear\left(W_c·AvgPool\left(F_{\mathrm{fusion}}\right)+b_t\right)\end{array}$$

(11)

where $C_l$ is the final classification probability, Linear maps the dimension to the classification dimension, $W_c$ is the convolution operation, AvgPool is the average pooling of the output, and $b_i$ is the bias, defaulting to 0. If the maximum classification probability is above the set threshold, the prediction result is output; if the confidence is below the set threshold, a larger-scale image is input. Through this gradual increase in resolution, the model can model the target from coarse to fine granularity, gradually deepening feature representation and reducing initial computational complexity. During inference, the model determines whether to end inference early by judging the similarity between the current time step and the final time step, reducing unnecessary computational resource consumption and further improving overall inference efficiency.

4. Experiments and Results Analysis

4.1. Experimental Environment and Parameter Settings

The experiments were conducted on Ubuntu 20.04 using Python implementation. The network model was built with PyTorch 1.13.0, compiled with Python 3.7, and accelerated with CUDA 11.8 on 8 V100 GPUs. The hyperparameters set for ImageNet-1k are shown in

Table 1. Hyperparameter Settings.

Parameter	Value
Learning Rate	6 $\times {10}^{-4}$
Warm-up Epochs	5
Weight Decay	0.05
Batch Size	256
Epochs	200

.

4.2. Results on Static Datasets

We evaluate the proposed method on five mainstream models (Spikformer, Spike-driven Transformer, SGLFormer, Spike-driven Transformer, and QKFormer) on the CIFAR10, CIFAR100, and ImageNet-1K datasets [10,11]. CIFAR-10 is a common image classification dataset containing 60,000 32 × 32 color images divided into 10 classes, with 6000 images per class (50,000 for training, 10,000 for testing). It is often used for small-scale image classification tasks. CIFAR-100 is similar to CIFAR-10 but contains 100 classes with 600 images each, making it more challenging and suitable for complex image classification research. ImageNet-1K is a large-scale image classification dataset containing approximately 1.28 million images divided into 1000 classes, serving as a standard benchmark in computer vision for image classification. As shown in

Table 2. Performance Comparison on Static Datasets (%).

Algorithm Model	Dataset			Improvement
	CIFAR10	CIFAR100	ImageNet-1K
Spikformer [26]	95.51	78.21	74.81	-
Spikformer (Ours)	96.73	78.62	75.84	+1.22/+0.41/+1.03
S-D Transformer [28]	95.60	78.40	77.07	-
S-D Transformer (Ours)	96.82	79.12	78.62	+1.22/+0.72/+1.55
SGLFormer [31]	96.76	82.26	83.73	-
SGLFormer (Ours)	97.12	83.07	84.33	+0.36/+0.81/+0.60
S-D Transformer V2 [27]	96.86	81.36	80.02	-
S-D Transformer V2 (Ours)	97.37	82.07	80.75	+0.51/+0.71/+0.73
QKFormer [32]	96.18	81.15	84.22	-
QKFormer (Ours)	97.02	81.92	84.76	+0.84/+0.77/+0.54

, the improved model demonstrates significant performance improvements.

4.3. Results on Dynamic Datasets

DVS records scene changes in the form of asynchronous event streams, featuring high temporal resolution, low latency, and low power consumption, making it suitable for processing with SNNs and enabling efficient handling of sparse spatiotemporal data. The proposed improvements in this paper were validated on the DVS datasets DVS128-Gesture [12] and CIFAR10-DVS [13]. DVS128-Gesture is an event camera-based dynamic gesture recognition dataset containing 11 types of gestures, with data represented as event streams, commonly used in neuromorphic processing tasks. CIFAR10-DVS is a dynamic vision version of CIFAR-10, generated by capturing dynamic transitions of the original CIFAR-10 images using DVS, producing approximately 1000 event sequences per class for evaluating the performance of event-based neural networks in object classification tasks. The experimental results are shown in

Table 3. Performance Comparison on Dynamic Datasets (%).

Algorithm Model	DVS128-Gesture	CIFAR10-DVS
Spikformer [26]	98.30	80.90
Spikformer (Ours)	98.74	81.56
S-D Transformer [28]	99.30	80.00
S-D Transformer (Ours)	99.42	80.73
SGLFormer [31]	98.60	82.90
SGLFormer (Ours)	99.00	83.72

. All improved models demonstrated performance gains on both dynamic datasets.

The results indicate that the proposed improvements offer significant advantages in processing dynamic event stream data. The high temporal resolution of DVS128-Gesture enables the model to accurately capture continuous changes in gestures through a pulse-driven temporal attention mechanism, achieving an improved accuracy of nearly 99.5%. The dynamic blur challenge in CIFAR10-DVS is effectively mitigated by cross-time-step knowledge distillation. For instance, the improved version of SGLFormer achieves state-of-the-art performance of 83.72% by preserving key event features. The performance improvements on both dynamic datasets validate the generalization capability of the proposed method for event-driven scenarios, providing an efficient solution for dynamic vision tasks.

4.4. Ablation Study

To evaluate the contributions of each module, ablation studies were conducted using Spikformer as the baseline. The results in

Table 4. Ablation Study Results.

Module Configuration	CIFAR10 (%)	CIFAR100 (%)	Power (mJ)	Training Speed
Spikformer [26] (Baseline)	95.51	78.21	7.73	1.00×
+ Time-step Distillation	96.93	79.12	7.62	0.92×
+ Attention Pruning	95.21	77.92	6.82	1.38×
+ Classification Evaluation	94.11	76.37	5.11	2.42×
Full Model (Ours)	96.73	78.62	5.43	1.82×

demonstrate the impact of progressively introducing time step distillation, attention pruning, and the classification evaluation module on both model performance and computational efficiency, systematically validating the influence of each component.

4.4.1. Cross-Time-Step Knowledge Distillation

As shown in

Table 5. Computational Efficiency Comparison.

Algorithm Model	Power (mJ)	Training Speed	Inference Speed
Spikformer [26]	7.73	1.00×	1.00×
Spikformer (Ours)	5.43	1.82×	1.42×
S-D Transformer [28]	3.90	1.00×	1.00×
S-D Transformer (Ours)	3.37	2.01×	1.57×
SGLFormer [31]	13.04	1.00×	1.00×
SGLFormer (Ours)	10.47	1.97×	1.63×

, the time step distillation mechanism enhances classification accuracy by facilitating knowledge transfer between different time steps. Classification accuracy improved by 1.42% on CIFAR10 and 0.91% on CIFAR100, indicating that the model can better capture dynamic features and improve temporal information modeling through cross-time-step learning. However, the optimization in energy consumption was limited, with only a 0.11 mJ reduction, while training speed decreased by approximately 8%. This suggests that although time step distillation improves accuracy, the increased interaction between time steps may slightly reduce training efficiency.

4.4.2. Attention-Based Pruning

The attention pruning strategy significantly reduces power consumption and accelerates training. By dynamically pruning attention weights to eliminate redundant computations, the model’s classification accuracy decreased slightly by 0.30% on CIFAR10 and 0.29% on CIFAR100, but energy consumption was reduced by 0.91 mJ, and training speed increased by 38%. This indicates that reducing unnecessary computations in the attention mechanism can significantly enhance training and inference efficiency while maintaining accuracy. The dynamic attention pruning strategy greatly optimizes computational resource utilization, lowering power consumption and accelerating training, though minor accuracy degradation occurs on smaller datasets due to partial loss of feature information.

4.4.3. Multi-Scale Resolution Processing

The multi-scale resolution processing approach dynamically optimizes classification tasks by re-evaluating low-confidence samples at higher resolutions. On CIFAR10 and CIFAR100, classification accuracy decreased by 1.40% and 1.84%, respectively, but power consumption was significantly reduced by 2.62 mJ, and training speed increased by 142%. Although this module excels in ultra-low-power scenarios, the loss of feature information during high-resolution re-evaluation reduces the model’s ability to capture complex features, leading to an overall decline in accuracy. By triggering high-resolution re-evaluation for low-confidence samples, the module enables fast inference in low-power settings, but over-reliance on it weakens the model’s capacity to capture intricate features.

4.4.4. Comparison of Energy Consumption and Computational Complexity

The proposed improvements were validated on three baseline models, all with a final dimension of 384, and tested on ImageNet1k. As shown in Table 5, significant achievements were made in energy efficiency and computational efficiency. Spikformer performed most prominently, reducing power consumption by 29.8% to 5.43 mJ while maintaining a 1.82× training acceleration and a 1.42× inference acceleration, achieving a dual improvement in accuracy and energy efficiency. This indicates that pixel redundancy is a critical factor limiting SSA performance. SGLFormer reduced power consumption by 19.7% to 10.47 mJ while maintaining high accuracy and achieving a 1.97× training acceleration, with its dynamic classification evaluation strategy effectively balancing computational costs.

From a technical perspective, time step distillation and dynamic pruning are key to improving energy efficiency. These techniques effectively reduce computational complexity while maintaining or even enhancing model accuracy. For instance, SGLFormer achieved 84.33% accuracy on ImageNet1k with a 1.63× inference speedup, surpassing the performance of conventional optimization methods.

Integrating all modules achieves a balance between power consumption and training efficiency while maintaining improved accuracy. Time step distillation effectively compensates for the feature loss caused by attention pruning, and the dynamic classification evaluation strategy avoids redundant computations by activating high-resolution analysis, providing a solution that balances performance and efficiency for model deployment in resource-constrained scenarios.

5. Conclusions

In this work, we presented an efficient spiking Transformer architecture that enhances the temporal modeling and computational efficiency of SNNs. The proposed cross-time-step knowledge distillation mechanism enables earlier time steps to learn from later ones, which improves temporal consistency and overall inference accuracy. The multi-scale image processing framework further balances computational cost and performance through progressive feature reuse, while the attention-based token pruning dynamically eliminates redundant information to achieve efficient inference. Extensive experiments on both static and dynamic benchmarks verify that our approach achieves superior performance and over $1.4\times$ inference acceleration, which significantly enhances the energy efficiency of SNNs. These techniques enable temporal knowledge transfer and spatial feature selection in spiking CNNs, thereby improving their efficiency and overall performance. Future work will explore adaptive event encoding and hardware-level optimization to further improve real-time deployment on neuromorphic and edge computing devices.