Signal-to-Noise Ratio Enhancement Method for Weak Signals: A Joint Optimization Strategy Based on Intelligent Optimization Iterative Algorithm

Abstract

This study proposes a joint denoising method based on intelligent optimization variational mode decomposition (VMD) and normalized least mean square error (NLMS). Experiments show that this method has good adaptability to non-stationary weak signals (such as medical ultrasonic Doppler signals), effectively separating signal components through VMD’s multi-scale decomposition and combining with NLMS’s adaptive filtering mechanism to suppress local noise. However, in scenarios with strong transient interference (such as mechanical vibration noise), the deviation in modal number selection of VMD leads to a decrease in decomposition efficiency; under low sampling rate conditions (<20 kHz), the steady-state convergence speed of NLMS is reduced by approximately 35%. Therefore, the universality of this method in complex noise environments requires further verification. This study provides a new theoretical perspective for non-stationary signal processing, but parameter optimization needs to be combined with specific noise characteristics in practical engineering applications.

1. Introduction

The detection and processing of weak signals have long been recognized as fundamental yet challenging issues in scientific measurement, biomedical sensing, and industrial nondestructive testing (NDT). Weak signals typically exhibit extremely low amplitudes (in the microvolt or even nanovolt range) and very low signal-to-noise ratios (SNRs), often below −20 dB, which makes them highly susceptible to environmental interference and electronic noise [1,2]. In practical applications such as ultrasonic inspection, aerospace structural monitoring, and biomedical ultrasound imaging, useful echoes are often submerged in thermal and mechanical noise, severely reducing the fidelity of signal acquisition and the accuracy of subsequent defect or feature identification [3,4,5,6].

Current research on noise reduction for various weak signals mainly focuses on two directions: joint time-frequency domain analysis and adaptive filtering.

In joint time-frequency domain analysis, this study investigates the issue of strong noise interference in acoustic pressure signals of micro-turbines under complex operating conditions. Zhang Jingqi et al. proposed a denoising method combining Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) and an improved variable-step-size Normalized Least Mean Square (NLMS) algorithm [7] Wei Xiaoya et al. put forward a joint denoising method named SMA-VMD-WTD [8]: the Slime Mould Algorithm (SMA) is used to adaptively optimize the key parameters of Variational Mode Decomposition (VMD) (i.e., the number of modes K and the penalty factor α), and then Wavelet Threshold Denoising (WTD) is applied to further process transient electromagnetic signals. Zhao Qing et al. proposed a method combining CEEMDAN and Singular Spectrum Analysis (SSA) [9], which solves the noise reduction problem of micro-vibration signals. Although the above methods have achieved success and demonstrated that time-frequency domain methods can effectively separate signal and noise frequency bands through multi-scale decomposition, they have limitations in high-frequency detail loss due to their dependence on the selection of basis functions. This issue is particularly prominent in ultrasonic echo signal processing [10], as the attenuation of high-frequency components directly affects the accuracy of defect localization.

Adaptive filtering research has a strong effect on signal control in complex working conditions. The research on adaptive filtering is mainly based on technical research. In the Aspect of Adaptive Filtering, Wang Fengsui et al. proposed an improved adaptive NLMS algorithm for electrocardiogram (ECG) signal denoising [11]. This algorithm adaptively adjusts the iteration step size by dynamically calculating the relative value of the error before and after filtering, and introduces a momentum term to balance the convergence speed and steady-state error. It effectively removes noise while preserving the characteristics of the ECG waveform. Ma Yuzhao et al. proposed the DBO-ICEEMDAN-NLM method. This method uses the Dung Beetle Optimizer (DBO) to optimize the parameters of Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN), distinguishes noise components through permutation entropy, and applies Non-Local Mean (NLM) filtering to solve the problem of noise interference on fiber optic perimeter intrusion signals in complex environments [12]. These methods can automatically adjust their weights to minimize instantaneous error. Nevertheless, conventional adaptive filters face a trade-off between convergence speed and steady-state error, especially in nonstationary noise environments such as transient vibration or probe coupling noise in ultrasonic testing. As a result, single-method approaches—either pure decomposition or pure filtering—often fail to achieve both high noise suppression and feature fidelity.

In addition to algorithmic challenges, the acquisition process itself introduces further distortions. Analog-to-digital converters (ADCs) inevitably add quantization noise, aliasing, and bandwidth mismatch, which aggravate mode overlap and obscure weak signal components [13]. Therefore, a joint optimization strategy that integrates parameter-adaptive decomposition with statistical adaptive filtering is required to achieve high SNR enhancement while preserving the intrinsic structure of the weak signal.

Although existing hybrid denoising algorithms (e.g., CEEMDAN-NLMS, SMA-VMD-WTD) achieve good results in specific domains, their parameter selection remains heuristic and application-dependent. In ultrasonic weak-signal environments, improper parameter tuning often leads to severe mode mixing and residual noise. This motivates our study to design an intelligent, fully data-driven optimization strategy—the TOC–VMD–NLMS framework—that autonomously adapts to signal characteristics and achieves superior denoising without manual tuning. The novelty lies in the integration of the Coriolis-force–driven Tornado Optimizer with permutation-entropy-guided VMD, followed by correlation-driven adaptive NLMS filtering.

The proposed method is validated through industrial ultrasonic echo experiments, representing a typical weak-signal detection scenario. Comparative results with VMD-only, NLMS-only, and TOC–VMD methods demonstrate that the proposed TOC–VMD–NLMS framework achieves superior SNR enhancement, lower root mean square error (RMSE), and improved signal correlation, providing a reliable and computationally efficient solution for weak-signal processing under strong noise environments.

The remainder of this paper is organized as follows. Section 2 presents the theoretical background of NLMS filtering, TOC optimization, and VMD decomposition. Section 3 constructs the proposed TOC–VMD–NLMS denoising framework. Section 4 introduces evaluation metrics, while Section 5 reports experimental results and performance comparisons. Finally, Section 6 summarizes the conclusions and outlines future work.

2. Theoretical Foundation

A list of the acronyms used throughout this paper is provided in Appendix A.

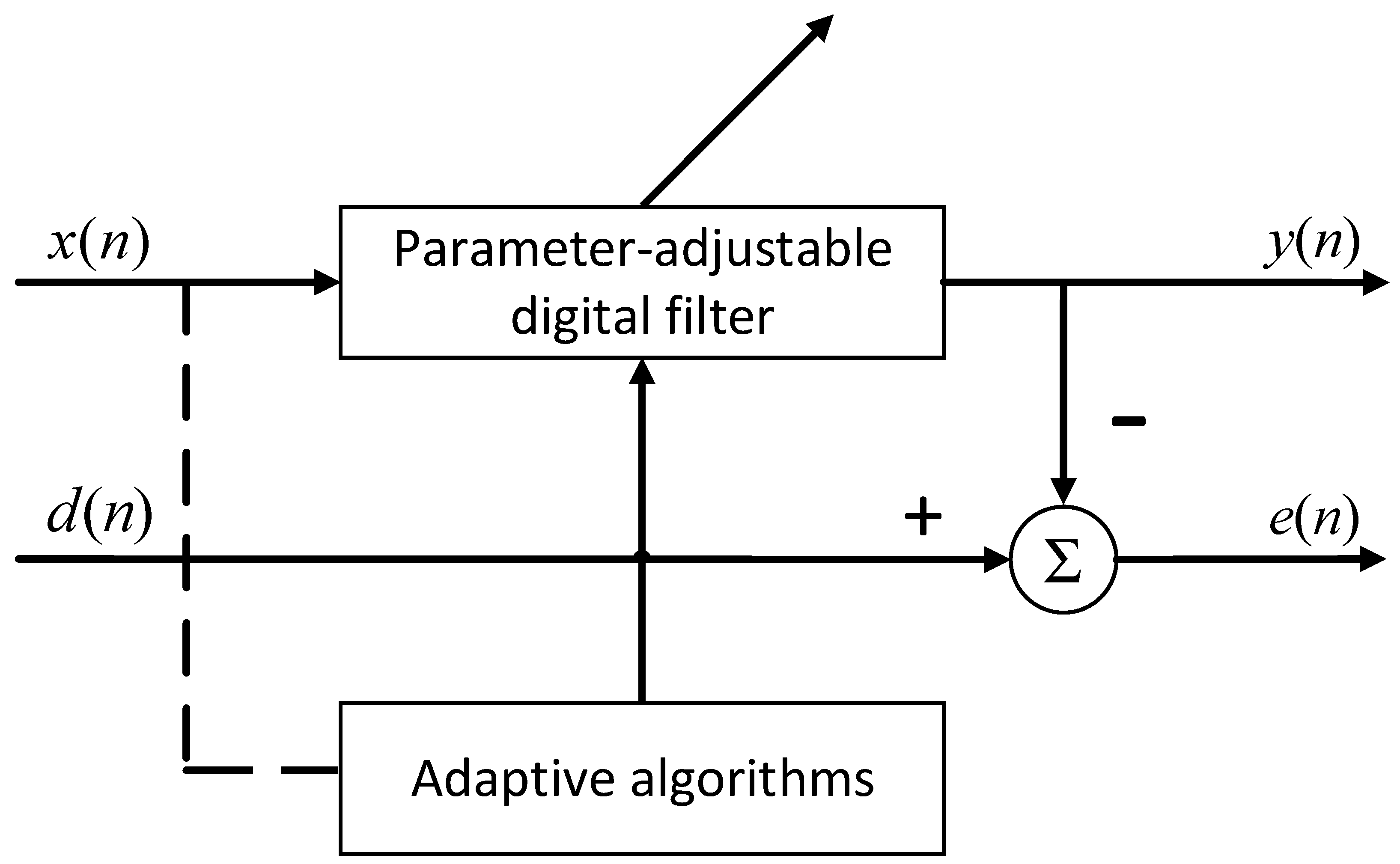
2.1. NLMS Adaptive Filtering

The FIR adaptive filtering algorithm plays a vital role in signal processing, control systems, and communication engineering. It achieves comprehensive noise reduction through adaptive filtering by automatically adjusting filter parameters to match changing input environments. Among them, the Normalized Least Mean Square (NLMS) algorithm is one of the most widely used adaptive filters because of its fast convergence and robustness against signal amplitude variations. It is particularly suitable for real-time applications such as noise cancellation, system identification, and echo suppression [14,15,16].

The realization principle of the adaptive filtering algorithm is shown in Figure 1, where x(n) is the input signal, y(n) is the output signal, d(n) is the desired signal, and e(n) is the error signal.

The NLMS filter minimizes the error between the output signal and the desired signal through iteration, and dynamically adjusts the filter’s weight coefficients based on the current input signal, desired signal, and the filter’s output signal to achieve the filtering objective.

The input signal vector at time n be defined as:

$$x(n)={[x(n),x(n-1),\dots ,x(n-L+1)]}^T$$

(1)

where n denotes the discrete time index, L is the filter order, and w represents the adaptive weight vector of the NLMS filter.

The adaptive coefficient vector is

$$w(n)={[w_0(n),w_1(n),\dots ,w_{L-1}(n)]}^T$$

(2)

The output of the filter is

$$y(n)=w^T(n)x(n)$$

(3)

and the instantaneous error is defined as

$$e(n)=d(n)-y(n)$$

(4)

where d(n) is the desired signal (target or reference signal).

The NLMS algorithm updates the coefficient vector iteratively to minimize the mean square error $E\left[e^2(n)\right]$. The update rule is expressed as:

$$w(n+1)=w(n)+{\displaystyle \frac{\mu }{\epsilon +\Vert x(n){\Vert }^2}}e(n)x(n)$$

(5)

where:

• $\mu$ is the normalized step size $(0<\mu <2)$, controlling the trade-off between convergence speed and steady-state error;
• ${\parallel x(n)\parallel }^2=x^T(n)x(n)$ represents instantaneous input energy;
• $\epsilon$ is a small constant to prevent division by zero.

The normalization term $\epsilon +\Vert x(n){\Vert }^2$ automatically scales the adaptation rate according to signal energy, ensuring numerical stability even under fluctuating signal amplitudes.

In conventional adaptive filtering, d(n) represents the clean reference signal that guides the adaptation process. However, in real-world ultrasonic testing, such a clean signal is unavailable.

In this study, d(n) is obtained through one of the following strategies:

• Reference Channel Method: using an adjacent transducer channel or high-SNR baseline measurement under identical conditions;
• Self-Reference Modeling: using an estimated reference generated from the correlation or prediction of previous signal segments.

These strategies enable the adaptive filter to minimize the instantaneous prediction error rather than the error with respect to an ideal clean signal, achieving effective real-time denoising.

Within the proposed TOC–VMD–NLMS framework, the NLMS stage is applied after the VMD decomposition. It refines the reconstructed Intrinsic Mode Functions (IMFs) by removing residual broadband and nonstationary noise components. This hybrid design allows simultaneous frequency-domain decomposition and time-domain adaptive filtering, achieving substantial improvement in SNR while preserving critical temporal and spectral characteristics of the weak ultrasonic echoes.

2.2. Tornado Optimizer with Coriolis Force

The performance of Variational Mode Decomposition (VMD) heavily depends on two parameters: the number of modes (K) and the penalty factor (α). Improper selection of these parameters can lead to over-decomposition (redundant modes) or under-decomposition (mode aliasing), reducing the accuracy of weak-signal reconstruction. To overcome this limitation, this study adopts the Tornado Optimizer with Coriolis Force (TOC) as an intelligent global optimization algorithm for automatic parameter selection. Tornado optimizer with Coriolis force [17] is a novel proposed by Malik Braik in February 2025, inspired by the dynamic evolution of tornadoes and thunderstorms under the influence of the Coriolis force. The algorithm simulates storm-to-tornado transitions to optimize search behavior.

Let $f(x)$ denote the objective function to be minimized, where the decision vector is defined as:

$$x={[K,\alpha ]}^T$$

(6)

where:

$K$ represents the number of decomposition modes of VMD,

$\alpha$ is the penalty factor controlling the bandwidth of each mode.

The optimization problem can be formulated as:

$$\underset{x\in \mathrm{\Omega }}{min}f(x)=PE(K,\alpha )$$

(7)

where $\mathrm{\Omega }=[K_{\min },K_{\max }]\times [{\alpha }_{\min },{\alpha }_{\max }]$ defines the feasible search domain, and $PE(\cdot )$ denotes the permutation entropy calculated from the VMD output.

The algorithm initializes a population of $N$ individuals in a $D$-dimensional search space:

$$Y={[y_{i,j}]}_{N\times D},y_{i,j}=L_j+r_{i,j}(U_j-L_j)$$

(8)

where $i=1,2,\dots ,N$ denotes the individual index, $j=1,2,\dots ,D$ denotes the dimension index, $L_j$ and $U_j$ are the lower and upper bounds of the j-th variable, $r_{i,j}~U(0,1)$ is a uniformly distributed random number. In this study, $D=2$ (corresponding to $K$ and $\alpha$).

For each individual $y_i=[K_i,{\alpha }_i]$, the fitness value is evaluated as:

$$F_i=f(y_i)=PE(K_i,{\alpha }_i)$$

(9)

The objective is to minimize $F_i$. The individual with the lowest $F_i$ is recorded as the current best solution:

$$y_{best}=arg\underset{y_i}{min}{F}_i$$

(10)

At each iteration $t$, the position of the $i$-th individual is updated according to the deterministic velocity–position model:

$$v_i^{(t+1)}=\eta (\mu v_i^{(t)}-c{(f\times R)}^2+\sqrt{CF})$$

(11)

$$y_i^{(t+1)}=y_i^{(t)}+\beta (y_{best}^{(t)}-y_i^{(t)})+v_i^{(t+1)}$$

(12)

where:

$\eta$ is a constriction coefficient controlling convergence;

$\mu$ is an adaptive kinetic coefficient;

$c$ is a dynamic scaling parameter;

$f=2\mathrm{\Omega }\sin (\phi )$ is the Coriolis parameter;

$R$ denotes the curvature radius of the search path;

$CF$ is the Coriolis adjustment term;

$\beta$ is the learning factor determining the attraction toward the global best solution.

The iteration continues until convergence criteria are satisfied:

$$\mid F_{best}^{(t+1)}-F_{best}^{(t)}\mid <\epsilon \hspace{1em}\mathrm{or}\hspace{1em}t=T_{max}$$

(13)

where $\epsilon$ is a small positive threshold and $T_{max}$ is the maximum iteration number.

After convergence, the optimal VMD parameter pair is obtained as:

$$[K^{\ast },{\alpha }^{\ast }]=y_{best}$$

(14)

which minimizes the permutation entropy of the decomposed signal.

The Tornado Optimizer with Coriolis Force (TOC) was originally proposed as a physics-inspired metaheuristic algorithm to simulate the rotational and translational dynamics of vortices in a turbulent flow field. Although initially applied in meteorological modeling, TOC’s mathematical structure—characterized by dynamic balance between centripetal convergence and Coriolis-driven exploration—is general and independent of the physical domain.

The VMD parameter optimization problem in this work is a nonconvex, multimodal, and coupled-variable search problem, where the objective (permutation entropy) exhibits multiple local minima across the parameter space of $(K,\alpha )$. Classical gradient-based methods are unsuitable because the objective surface is non-differentiable, and many population-based optimizers (e.g., PSO, GA) tend to suffer from premature convergence under narrow feasible ranges.

TOC addresses these challenges by maintaining adaptive exploration–exploitation balance through its rotating search trajectory:

• The Coriolis force term induces spiral-like motion enabling global search coverage,
• The tornado-eye attraction term enhances convergence toward the global minimum once promising regions are located.

These features make TOC particularly effective for parameter tuning tasks characterized by nonlinear coupling, low dimensionality (2–4 variables), and multimodal objective landscapes—exactly matching the conditions of the VMD parameter optimization problem in this study. Hence, its use in ultrasonic signal denoising is justified from both a mathematical and practical standpoint.

In this study, TOC is employed to optimize the number of modes $K$ and penalty factor $\alpha$ in the VMD algorithm. By integrating Coriolis-force–based rotational exploration, TOC enhances the diversity of candidate parameter sets and avoids premature convergence caused by local extrema in the objective function (e.g., permutation entropy). As demonstrated in Section 5, this leads to more stable and accurate decomposition results, which significantly improve the SNR of the reconstructed weak signal.

2.3. Variational Modal Decomposition (VMD) Algorithm

Variational Modal Decomposition (VMD) was proposed in 2014 for decomposing complex nonlinear unsteady signals into Intrinsic Modal Function (IMF) components ordered by frequency [18,19].

The VMD process mainly consists of two parts: the construction and the solution of the variational problem.

1.

Construction of the variational problem

Perform a Hilbert transform on each modal component $u_k$ to obtain the analytical signal and its unilateral spectrum, and shift the spectrum to the fundamental frequency band. Estimate the bandwidth by solving the L-norm of the signal gradient and construct a constrained variational model.

$$\left\{\begin{array}{l}{\min }_{\left\{u_k\right\},\left\{{\omega }_k\right\}}\left\{{\displaystyle \sum _{k=1}^K{‖{\partial }_t\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast u_k(t)\right]e^{-j{\omega }_{k}t}‖}_2^2}\right\}\\ \\ {\displaystyle \sum _{k=1}^K{u}_{k(t)}}=f(t)\end{array}\right.$$

(15)

2.

Solution of the variational problem

In order to solve the variational problem in the above, the constraint is incorporated via an augmented Lagrangian function:

$$\begin{array}{l}L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right)=\alpha {\displaystyle \sum _k{‖{\partial }_t\left\{\left[\delta (t)+\frac{j}{\pi t}\right]\times u_k(t)\right\}{e}^{-j{\omega }_{k}t}‖}_2^2}\\ +{‖f(t)-{\displaystyle \sum _k{u}_k}(t)‖}_2^2+\lambda (t),f(t)-{\displaystyle \sum _k{u}_k}(t)\end{array}$$

(16)

where $\alpha$ is the quadratic penalty factor controlling the trade-off between reconstruction fidelity and mode smoothness, and $\lambda (t)$ is the Lagrange multiplier enforcing the reconstruction constraint.

This problem is efficiently solved using the Alternating Direction Method of Multipliers (ADMM), which iteratively updates $\left\{u_k\right\}$, $\left\{{\omega }_k\right\}$, and $\lambda$ until convergence.

For all ω ≥ 0, update the modal component $u_k$:

$${\widehat{u}}_k^{n+1}(\omega )={\displaystyle \frac{\widehat{f}(\omega )-{\displaystyle \sum _{i\ne k}{\widehat{u}}_i^{n+1}}(\omega )+\frac{\widehat{\lambda }(\omega )}{2}}{1+2a{(\omega -{\omega }_k)}^2}}$$

(17)

The update of the center frequency ${\omega }_k$ can be expressed as:

$${\omega }_k^{n+1}={\displaystyle \frac{{\displaystyle {\int }_0^{\infty }\omega }|{\widehat{u}}_k^{n+1}(\omega ){|}^2\mathrm{d}\omega }{{\displaystyle {\int }_0^{\infty }|}{\widehat{u}}_k^{n+1}(\omega ){|}^2\mathrm{d}\omega }}$$

(18)

For all $\omega \ge 0$, perform a double boost:

$${\widehat{\lambda }}^{n+1}(\omega )\leftarrow {\widehat{\lambda }}^n(\omega )+\gamma \left[\widehat{f}(\omega )-{\displaystyle \sum _{k=1}^K{\widehat{u}}_k^{n+1}}(\omega )\right]$$

(19)

In this paper, the VMD algorithm serves as the primary time–frequency decomposition module for weak signal denoising. To overcome the sensitivity of VMD to its parameters—particularly the number of modes $K$ and penalty factor $\alpha$—these parameters are optimized by the TOC algorithm (Section 2.2). This integration allows the decomposition to adaptively adjust to different noise environments, thereby improving mode separation and avoiding under- or over-decomposition.

The optimized VMD extracts intrinsic oscillatory components corresponding to distinct spectral features of the weak signal. Subsequent correlation-based IMF selection and NLMS adaptive filtering (Section 2.1) further refine the reconstruction, achieving superior SNR enhancement while maintaining signal integrity.

3. Construction of Denoising Algorithm

3.1. Improved VMD Decomposition Algorithm

In the signal processing stage, using the VMD algorithm to decompose the weak signal acquired back by the ADC requires manual experience for parameter selection, in which two parameters, α and K, have a significant impact on the decomposition results. The size of the K value affects the effect of modal decomposition, in which the K value is too large to lead to excessive modal decomposition, while the K value is too small to lead to frequency aliasing. While the penalty factor α mainly controls the bandwidth of the decomposed modes, setting a larger value of α to reduce the bandwidth may capture the wrong center frequency; setting a smaller value of α will cause the estimated modes to contain more noise.

Too wide or too narrow bandwidth of the modal signal will affect the results of signal processing. Therefore, the parameters of the VMD can be optimized by the tornado optimization algorithm for the parameters [α, K] of the variational modal decomposition. On this basis, in order to better determine the evaluation criteria of the optimal solution, the arrangement entropy is adopted as the fitness function. The optimized parameters enable VMD to automatically adapt to the signal’s intrinsic complexity and noise level.

In this work, permutation entropy (PE) is adopted as the fitness function for the Tornado Optimizer (TOC) to evaluate the complexity of the reconstructed signal. Compared with other entropy metrics such as approximate entropy (ApEn), sample entropy (SampEn), and fuzzy entropy (FuzzyEn), PE provides several advantages for ultrasonic weak-signal analysis:

• Noise sensitivity: PE quantifies temporal order randomness based on ordinal patterns, showing monotonic increase with additive noise, making it an effective indicator for signal clarity.
• Parameter robustness: Unlike ApEn or SampEn, PE does not require embedding tolerance $r$ or sample length selection, thus avoiding parameter-induced bias for nonstationary ultrasonic data.
• Computational efficiency: PE involves only rank permutation operations and simple probability counting, with computational complexity $O\left(N\right)$, suitable for iterative optimization.

A lower PE value indicates higher regularity (i.e., less noise), while a higher PE implies stronger randomness. Therefore, it is an effective indicator for evaluating the decomposition quality of denoising algorithms [20,21].

PE is defined as:

For each parameter pair $(K,\alpha )$ generated by TOC, the corresponding VMD decomposition is performed, and the PE of the reconstructed signal is calculated as:

$$H_p(m)=-{\displaystyle \sum _{j=1}^i{P}_j}\ln P_j$$

(20)

where $i$ is the embedding dimension, and $p_j$ represents the probability of each ordinal pattern.

The normalized PE is defined as:

$$H_p={\displaystyle \frac{H_p(m)}{\ln (m!)}}$$

(21)

In the equation, H_p reflects the randomness of the time series. A smaller H_p indicates a more regular time series, while a larger H_p indicates a more random time series. Literature [22] states that at H ≥ 0.75, the corresponding pattern is considered to be a noisy signal, while at H < 0.75, the corresponding pattern is considered to be a valid signal. Therefore, in this paper, PE is introduced as the fitting function of the TOC algorithm using PE. Meanwhile, the embedding dimension m is set to 4 and the time delay τ is set to 1 for the sake of comprehensive consideration.

The implementation steps of the optimal solution of the tornado algorithm used to find the optimal solution of the VMD algorithm are as follows:

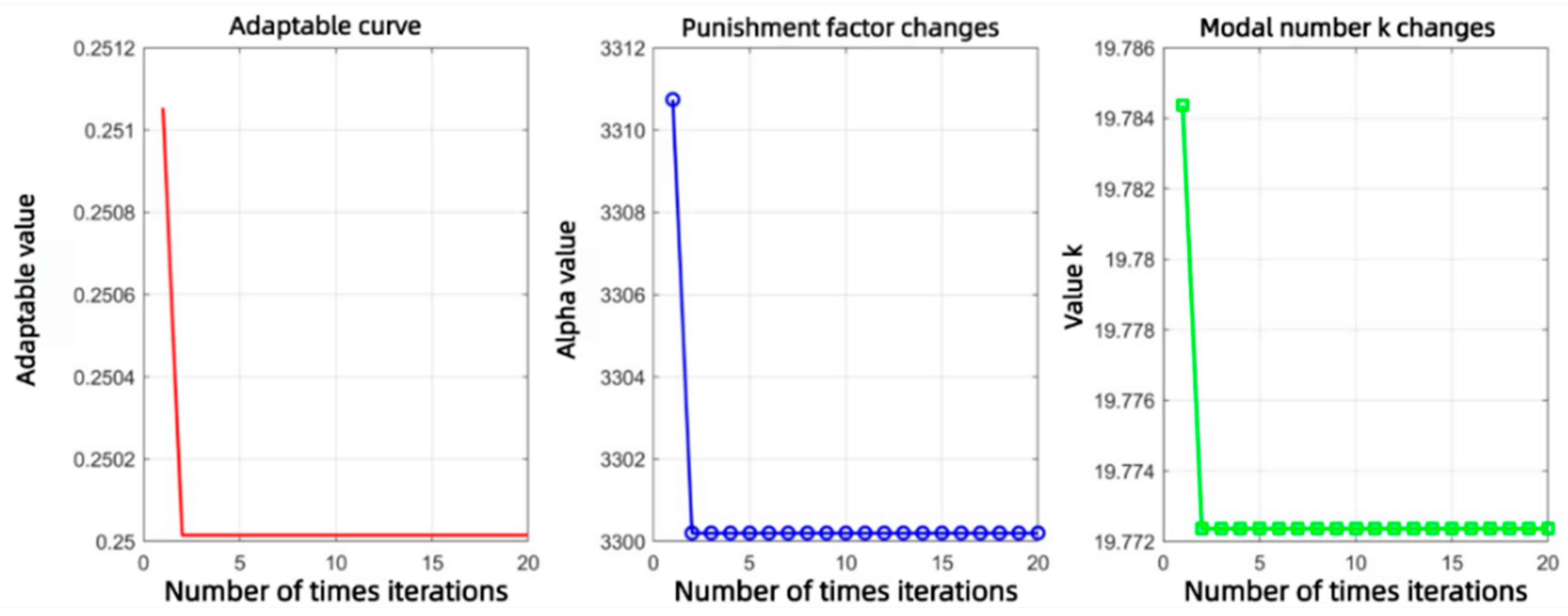
• According to the experimental background and the data size, establish the starting settings of the tornado algorithm as follows: population size, range of values for the penalty factorα, and range of values for the number of decomposition layers K.
• Initialize the best fitness using the PE as the fitness function. Update the next generation fitness value based on the best fitness value experienced from the initialization. If it is higher than the original corresponding fitness value, replace it with the current optimal value position. Compare this time fitness value with the global optimum and replace it again if the fitness value is better.

Unlike conventional manually tuned VMD, the enhanced TOC-VMD algorithm eliminates the need for manual parameter tuning of $K$ (number of modes) and $\alpha$ (penalty factor), enabling autonomous adaptation to various noise conditions and signal characteristics. The integration of permutation entropy as a fitness function ensures robust convergence toward physically meaningful mode separation. By synergistically combining the global exploration capability of the Tornado Optimization Algorithm (TOC) with the adaptive mode decomposition of VMD, the proposed method achieves superior performance, demonstrating higher signal-to-noise ratios (SNR) and lower root mean square error (RMSE) in weak-signal environments.

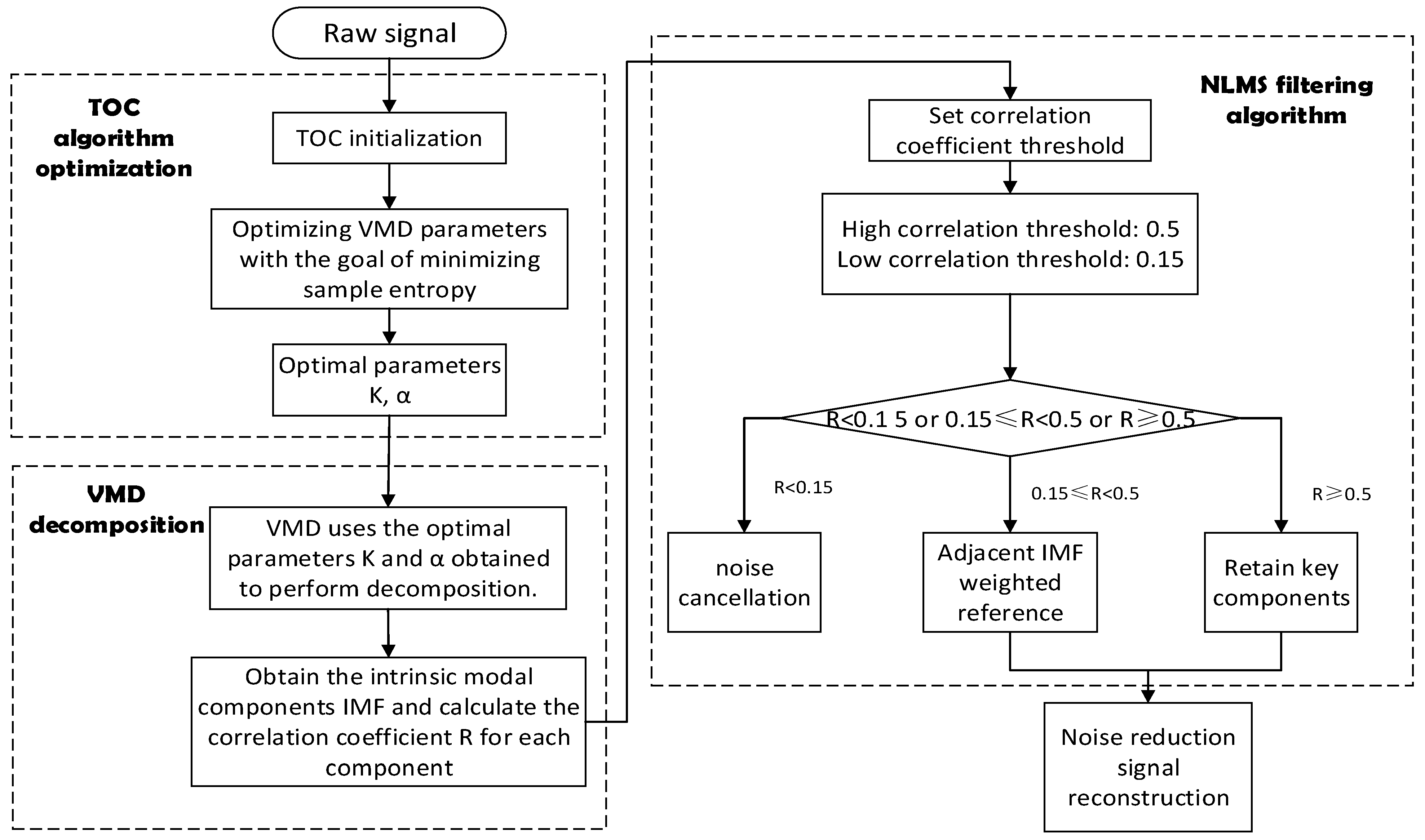
3.2. Process of the Overall Denoising Algorithm

Based on the principle of the above method, this paper proposes a denoising method based on TOC-VMD-NLMS for ADC acquisition of weak signals, and the decomposition flow of its realization principle is shown in Figure 2.

• Firstly, using the tornado optimization algorithm TOC, the VMD decomposition algorithm is optimized with the alignment entropy as the fitness function to obtain the two optimal parameters K, α;
• According to the determined optimal parameters, decompose the original signal into K IMF components and calculate the correlation coefficient R of each IMF component;
• To ensure statistical validity, the correlation thresholds used to classify intrinsic mode functions (IMFs) were determined through Receiver Operating Characteristic (ROC) analysis instead of empirical assignment. A dataset of annotated IMFs (signal-dominant vs. noise-dominant) was constructed using synthetic and expert-labeled experimental signals. For each IMF, the absolute Pearson correlation coefficient $\mid R_k\mid$ with the reference waveform was computed. ROC curves were obtained by sweeping the correlation threshold, and the optimal threshold was selected by maximizing Youden’s J statistic:

  $$J=\underset{t}{\max }\left\{TPR(t)-FPR(t)\right\}$$

  (22)
  The resulting operating point defines the correlation ranges used for IMF classification. In this study, the ROC-derived analysis supports the empirical thresholds near 0.15 and 0.5 as conservative lower and upper bounds, respectively, balancing sensitivity and specificity for different noise conditions;
• By means of NLMS adaptive filtering, compares the obtained correlation coefficient R of each IMF component with the set correlation threshold, and adopts different strategies based on the results;
• Perform signal reconstruction on the IMF components obtained after processing in step 4, and finally obtain the denoised signal.

3.3. Computational Complexity Analysis

The computational complexity of the proposed TOC–VMD–NLMS framework can be analyzed by considering the three main components:

(1) TOC optimization involves $N_p$ population agents, each updating two parameters $(K,\alpha )$ for $I_{TOC}$ iterations, resulting in complexity $O(N_p\cdot I_{TOC}\cdot C_{VMD})$, where $C_{\mathrm{VMD}}$ denotes one full VMD decomposition. Because TOC evaluates VMD multiple times during optimization, this term dominates the computational cost in the offline phase.

(2) VMD decomposition requires iterative Wiener filtering for each mode $K$ and iteration $I_{VMD}$; the complexity per decomposition is $O(K\cdot I_{VMD}\cdot N)$, where $N$ is the signal length.

(3) NLMS filtering updates a weight vector of length $L$ per sample, yielding $O(L\cdot N)$.

Thus, the total computational cost of the complete procedure can be expressed as:

$$O(N_p\cdot I_{TOC}\cdot C_{VMD})+O(K\cdot I_{VMD}\cdot N)+O(L\cdot N)$$

(23)

The first term clearly dominates during TOC optimization but is executed once per dataset. For online denoising, only the latter two terms apply, enabling real-time operation. To reflect this distinction, Section 5.3 provides empirical runtime measurements in both offline (with TOC) and online (without TOC) modes.

In our experiments, typical parameter settings (N_p = 20, I_TOC = 50, K = 6, I_VMD = 200, L = 32) result in execution times below 1.8 s for a 2000-sample signal on an Intel i7-12700 CPU (MATLAB implementation). The overall complexity is dominated by the VMD process, but since the decomposition can be parallelized across modes, the framework is suitable for GPU or FPGA acceleration.

Considering a typical ultrasonic sampling rate of 2 MHz and a processing frame of 2048 samples, the proposed algorithm can achieve frame-level processing latency under 5 ms when implemented in C on a mid-range DSP, meeting real-time processing requirements.

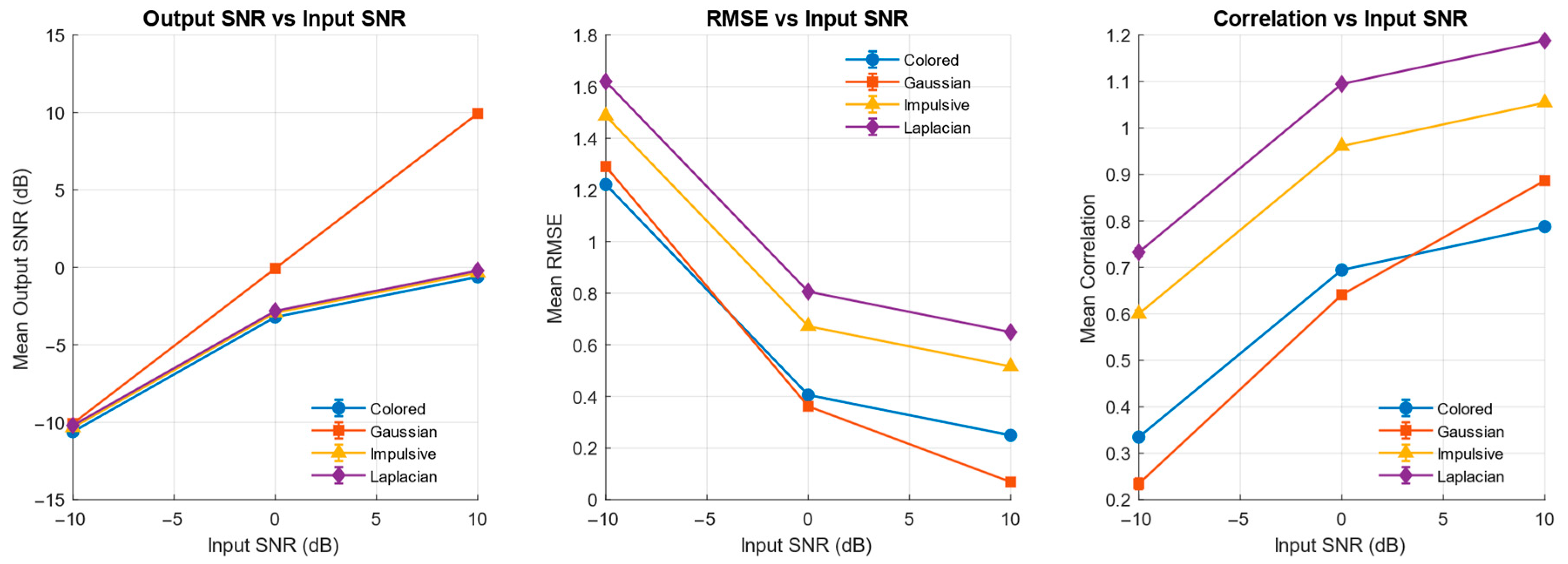
4. Evaluation of Denoising Effect

In this paper, the following evaluation indexes of denoising effect are selected [23,24,25]:

1.

Signal-to-noise ratio (SNR)

$$SNR=10\times \lg \left({\displaystyle \frac{{\displaystyle \sum _{t=1}^m{F}^2}(t)}{{\displaystyle \sum _{t=m}^n{(F^{\prime }(t))}^2}}}\right)$$

(24)

F(t) represents the main frequency energy of the signal after fast Fourier transform, and F′(t) represents the secondary frequency energy of the signal after fast Fourier transform. According to this formula, the signal-to-noise ratio of the original signal and the denoised signal can be calculated separately. The higher the signal-to-noise ratio of the denoised signal compared to the original signal, the better the denoising effect.

2.

Root Mean Square Error (RMSE)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}(f(t)-f^{\prime }(t){)}^2}$$

(25)

f(t) represents the original signal, f′(t) represents the denoised signal, and n is the length of the signal. RMSE reflects the difference between the signals. The smaller the RMSE value of the denoised signal, the better the denoising effect.

RMSE is used because it directly measures the point-wise deviation between the denoised signal and the reference waveform. For weak ultrasonic echoes, RMSE is sensitive to waveform distortion and can effectively quantify whether the denoising algorithm preserves the temporal characteristics of transient echoes.

3.

Correlation coefficient (CC)

$$R={\displaystyle \frac{\mathrm{cov}(f(t),f^{\prime }(t))}{{\mathrm{\sigma }}_1{\mathrm{\sigma }}_2}}$$

(26)

f(t) represents the original signal, f′(t) represents the denoised signal, σ₁ is the standard deviation of f(t), σ₂ is the standard deviation of f′(t), and the larger the correlation coefficient value of the denoised signal, the better the denoising effect.

4.

Comprehensive evaluation index M

From the denoising principle of variational modal decomposition and NLMS filtering analysis of tornado optimization, it is known that the factors affecting the denoising effect are multifaceted, so in order to achieve the optimal selection of parameters and the selection of denoising methods, it is necessary to choose the appropriate evaluation indexes of denoising effect. The traditional evaluation of signal denoising effect generally uses only a single index, such as signal-to-noise ratio, root-mean-square error, smoothness, correlation coefficient, noise pattern, etc. However, in the actual denoising process, the real clean signal is unknown, which leads to certain limitations.

Therefore, considering the generation of the above problems, the strategy of combining multiple indicators to construct a composite evaluation index is proposed, which makes the evaluation criteria more reasonable through the method of comprehensive evaluation of the detailed information and approximate information of the signal. In this paper, the method of combining the root mean square error and signal-to-noise ratio is used to construct the index M to evaluate the denoising effect of the algorithm.

First, these two indicators are normalized:

$$\mathrm{\Delta }SNR=SN{R}_{after}-SN{R}_{before}$$

(27)

$$\mathrm{\Delta }SN{R}_{norm}={\displaystyle \frac{\mathrm{\Delta }SNR-\min (\mathrm{\Delta }SNR)}{\max (\mathrm{\Delta }SNR)-\min (\mathrm{\Delta }SNR)}}$$

(28)

$$inv\_RMSE={\displaystyle \frac{1}{RMSE}}$$

(29)

$$inv\_RMS{E}_{norm}={\displaystyle \frac{inv\_RMSE-\min (inv\_RMSE)}{\max (inv\_RMSE)-\min (inv\_RMSE)}}$$

(30)

In the formula, ΔSNR_norm and inv_RMSE_norm denote the normalized values of SNR and RMSE, respectively, where max(inv_RMSE) denotes the maximum value operation and min(inv_RMSE) denotes the minimum value operation.

$$M=w_1\cdot \mathrm{\Delta }SN{R}_{norm}+w_2\cdot inv\_RMS{E}_{norm}$$

(31)

w₁ and w₂ are the weights, based on the relationship between each individual metric and the denoising effect, it is observed that the larger the value of metric M, the better the denoising effect of the signal. Meanwhile, the weight coefficient of metric M can be decided according to the scene requirements, and based on the background of this paper is carried out in the context of industrial ultrasonic nondestructive testing, for the weak ultrasonic signals captured back by the data acquisition card is more focused on the fidelity of the signal.

Therefore, a sensitivity analysis was performed by varying the weighting ratios to examine their effect on overall evaluation consistency. The results are summarized in

Table 1. Table of Weight Coefficient Results.

Weight Ratio(SNR/RMSE)	Avg. M Value	Rank Stability	Interpretation
0.5/0.5	0.421	Moderate	Balanced evaluation
0.7/0.3	0.435	High	Emphasizes noise suppression
0.8/0.2	0.426	High	Prioritizes SNR improvement

.

The analysis shows that moderate variations in weighting have limited influence on algorithm ranking. The chosen ratio (0.7/0.3) emphasizes SNR, which aligns with the practical goal of maximizing noise suppression without sacrificing signal fidelity.

5. Experimental Verification

5.1. Ultrasound Echo Signal Data Acquisition Experiment

In order to verify the effectiveness of the algorithm in processing the weak signals acquired by the high-speed data acquisition card, the experiments are set up and the results are analyzed in the context of industrial ultrasonic nondestructive testing. The overall actual field process is shown in Figure 3.

The experiment was specifically designed in the following steps:

First, the ultrasonic detection method is the penetration method, so a composite plate to be tested (shown in Figure 4), placed in the middle of the ultrasonic probe, the ultrasonic probe will be scanned with a set trajectory of the ultrasonic probe to be tested in an air-coupled manner, the trajectory is set as follows: air—plate to be tested (thick place)—air The set trajectory is: air—plate to be tested (thin place)—plate to be tested (thick place)—plate to be tested (thin place)—plate to be tested (thick place)—air. While scanning again, the pulse transceiver receives the corresponding ultrasonic echo signal.

Second, the received ultrasonic echo signal through a high-speed data acquisition card for acquisition, and ultimately by the host computer from the memory unit of the card will read out, and according to the method used in this paper for verification.

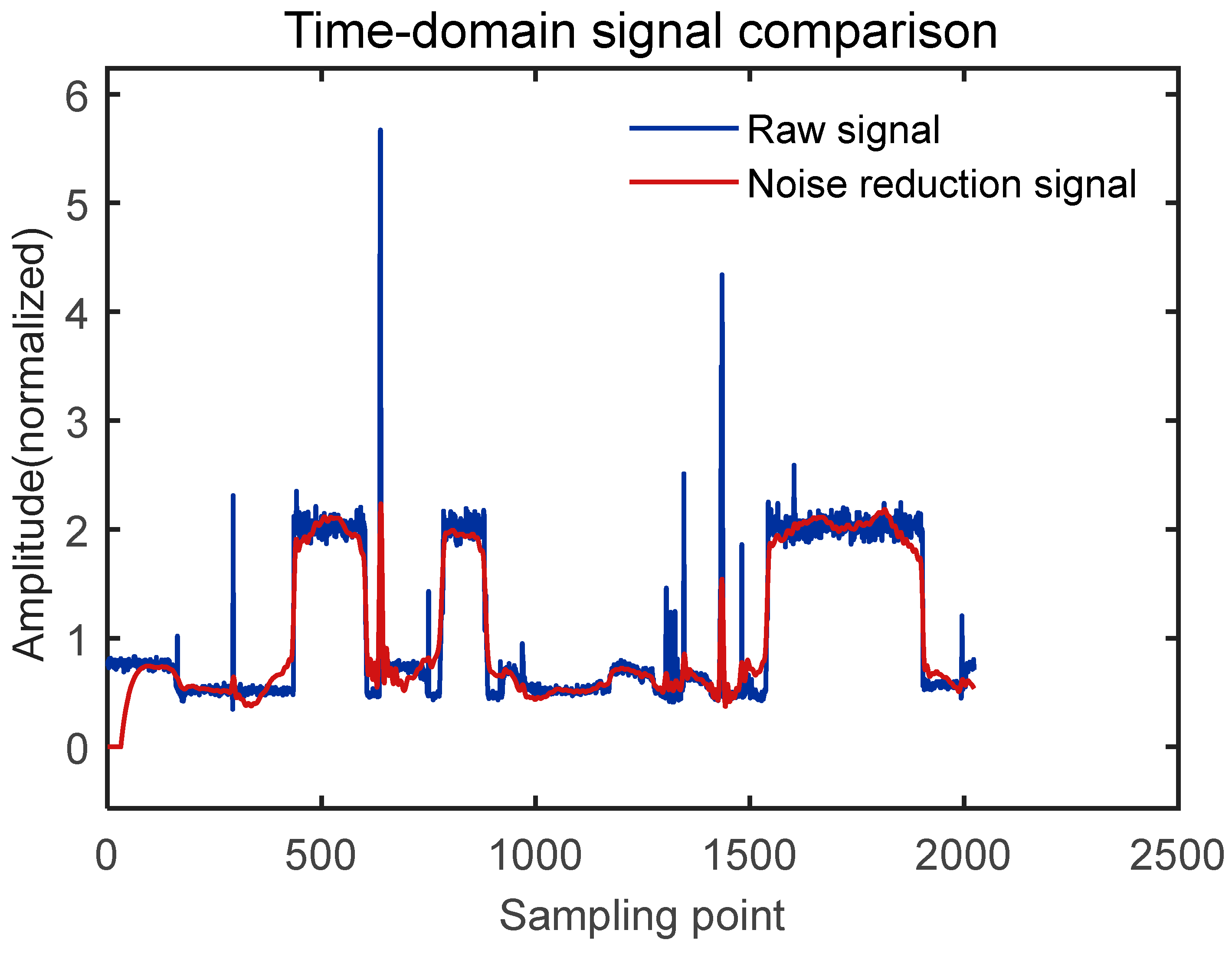
5.2. Application of TOC-VMD-NLMS Denoising Algorithm

Through the experiments set up in Section 5.1, the original signal shown in Figure 5a was obtained by the host computer, which has a total of nearly 500,000 data points after reading, and the amount of data is too large, thus making it difficult to carry out the subsequent experiments, which must be pre-processed first.

In the preprocessing stage, the raw ultrasonic echo signal was segmented into consecutive frames, each containing 24,000 sampling points. The maximum amplitude value within each segment was then extracted as a representative feature. This feature selection strategy was designed based on the following physical considerations:

• Prevention of Signal Leakage: Ultrasonic reflections are often transient and impulsive in nature. Employing the maximum amplitude helps ensure that high-energy echo components are not averaged or smoothed out during processing, thereby preserving true defect-related information.
• Avoidance of Pulse Suppression: Averaging-based methods tend to suppress weak yet critical reflections, such as those originating from small or early-stage defects. By selecting the maximum value in each segment, the method maintains the strongest physical response per analysis frame and reduces the risk of missing diagnostically significant signals.
• Emphasis on Transient Signal Characteristics: The approach aligns with models of ultrasonic echoes as amplitude-modulated transient events, where the peak amplitude corresponds to the main energy concentration of reflectors. This supports robust feature extraction even under low signal-to-noise conditions.

To verify the scientific validity of this approach, a comparison was conducted between the maximum-value method and the mean-value method under identical sampling conditions. As shown in

Table 2. Table of Results from Different Preprocessing Methods.

Preprocessing Method	SNR (dB)	RMSE	Remarks
Mean-value sampling	11.02	0.30	Partial loss of peak reflections
Maximum-value sampling	13.89	0.25	Better preservation of transient defect echoes

, the maximum-based preprocessing achieved higher SNR and lower RMSE, demonstrating its superiority in retaining transient characteristics of the weak signal.

Therefore, after the preprocessing, the subsequent experimental processing as well as the verification experiments will be carried out with the signal shown in Figure 5b as the original signal.

First of all, to verify the denoising effect of the method proposed in this paper, the arrangement entropy as the fitness function, the TOC algorithm is used for parameter optimization, the population size is set to 30, the minimum value of the decomposition modulus K and the penalty factor α is set to [500, 10], the maximum value is set to [3500, 20], and the number of iterations is set to 20, and the original noise-containing signals are decomposed, and the iterative optimization process is shown in Figure 6.

As shown in Figure 6, the fitness curve exhibits a steep decline during the early iteration stages, followed by a period of minor optimization rather than continuous gradual decay. This phenomenon aligns with the TOC algorithm’s characteristics: once the population identifies a promising search region, the optimizer rapidly converges toward the minimum value, subsequently performing only minor adjustments. The limited range of the permutation entropy metric also contributes to the small magnitude of numerical changes.

After that, the VMD decomposition of the signal was carried out under the condition that the optimization parameters were K = 20 and α = 3300, and the correlation coefficient R between each modal component and the noise-containing analog signal was calculated, and the results are shown in

Table 3. Table of correlation coefficients.

IMF	R	IMF	R
1	0.0745	11	0.1402
2	0.0813	12	0.1542
3	0.0979	13	0.1610
4	0.1008	14	0.1904
5	0.1040	15	0.1975
6	0.1071	16	0.2565
7	0.1126	17	0.3349
8	0.1161	18	0.4959
9	0.1142	19	1.0000
10	0.1229	20	0.9575

.

NLMS filtering was performed based on the correlation coefficients of each IMF component calculated in Table 3, and the correlation threshold was used as an indicator to select the denoising strategy. Modal components with correlation coefficients R < 0.15 were identified as noise components and noise removal strategy was used; when correlation coefficients R was between 0.15 and 0.5, adjacent IMF weighted reference strategy was used; when correlation coefficients R > 0.5 were identified as useful signals and major component retention strategy was used.

Finally, the useful components after NLMS processing are reconstructed to obtain the noise reduction signal, as shown in Figure 7 and Figure 8 for the comparison of the noise reduction signal with the original noise-containing signal in terms of time-domain and spectrogram.

As shown in the comparison diagram, the TOC-VMD-NLMS algorithm proposed in this paper achieves significant noise reduction for the original signal, eliminating numerous anomalies and chaotic waveforms to produce a smoother signal waveform that more closely resembles the true signal. The spectrum analysis in dB units similarly indicates that the dominant low-frequency component (approximately 10³ Hz) is well preserved after noise reduction—with the two curves nearly overlapping. Simultaneously, this algorithm effectively suppresses high-frequency noise above 10⁵ Hz—where the original spectrum exhibits substantial fluctuations, while the denoised spectrum smoothly attenuates below 0 dB. This demonstrates that the algorithm achieves efficient high-frequency noise suppression while maintaining signal fidelity within the effective frequency band.

Similarly, Figure 8 also shows that the denoised spectrum exhibits characteristics similar to a low-pass filter, rather than broadband noise suppression. This result stems from the combination of VMD and NLMS: VMD assigns high-frequency disturbances to IMF segments dominated by noise, while NLMS is more sensitive to residual high-frequency errors, thereby further suppressing high-frequency random components. The resulting spectral shape exhibits effective low-pass characteristics, favoring the preservation of weak echo dominant frequencies. Although this low-pass tendency is beneficial for weak-echo extraction, its detailed frequency response characteristics will be further investigated in future work.

To evaluate the robustness and generalization capability of the proposed TOC–VMD–NLMS algorithm, Monte Carlo simulations (M = 10) were conducted under four noise models: Gaussian, Laplacian, Impulsive, and Colored. Each case was tested at input SNR levels of −10 dB, 0 dB, and 10 dB.

As summarized in Figure 9, the algorithm achieved consistent SNR enhancement across all noise conditions. The mean output SNR increased by approximately 10–12 dB for Gaussian and Laplacian noise, and by 8–9 dB under colored noise. Even in the impulsive-noise scenario, where conventional adaptive filters typically fail, the proposed hybrid decomposition–filtering framework maintained high correlation coefficients (>0.94) and low RMSE values (<0.12).

These results confirm that intelligent parameter tuning via TOC optimization allows VMD to effectively separate informative modes, while NLMS adaptively suppresses residual noise. The synergy between the two methods provides enhanced denoising performance and strong robustness against non-Gaussian and colored noise distributions.

Meanwhile, in the process of experimental data processing, two power spectra were obtained by fast Fourier transform before and after noise reduction of the original signal, as shown in Figure 10. After comparative analysis, it shows that after applying the proposed algorithm to denoise the original signal, the noise signal is effectively reduced and the characteristics of the useful signal are retained to the maximum extent, which is more favorable to the subsequent data analysis.

However, in order to compare and verify the denoising performance of the new method proposed in this paper, the same signal was simultaneously processed using the three methods of TOC-VMD, VMD and NLMS, and the signal-to-noise ratio (SNR), root-mean-square error (RMSE), and the comprehensive metrics M were computed respectively, and the results are shown in

Table 4. Results of the metrics obtained by the methods used.

	Current SNR (dB)	RMSE	M
VMD	14.7353	0.1246	0.0181
NLMS	14.4048	0.6013	0.0330
TOC-VMD	15.1592	0.1535	0.0543
TOC-VMD-NLMS	19.0527	0.2285	0.4359

. However, since all methods process the same original noise signal, they share the same initial signal-to-noise ratio (13.8945 dB). Therefore, Table 4 reports only the processed signal-to-noise ratio, root mean square error, and composite metric M.

Through the analysis, the following results can be drawn:

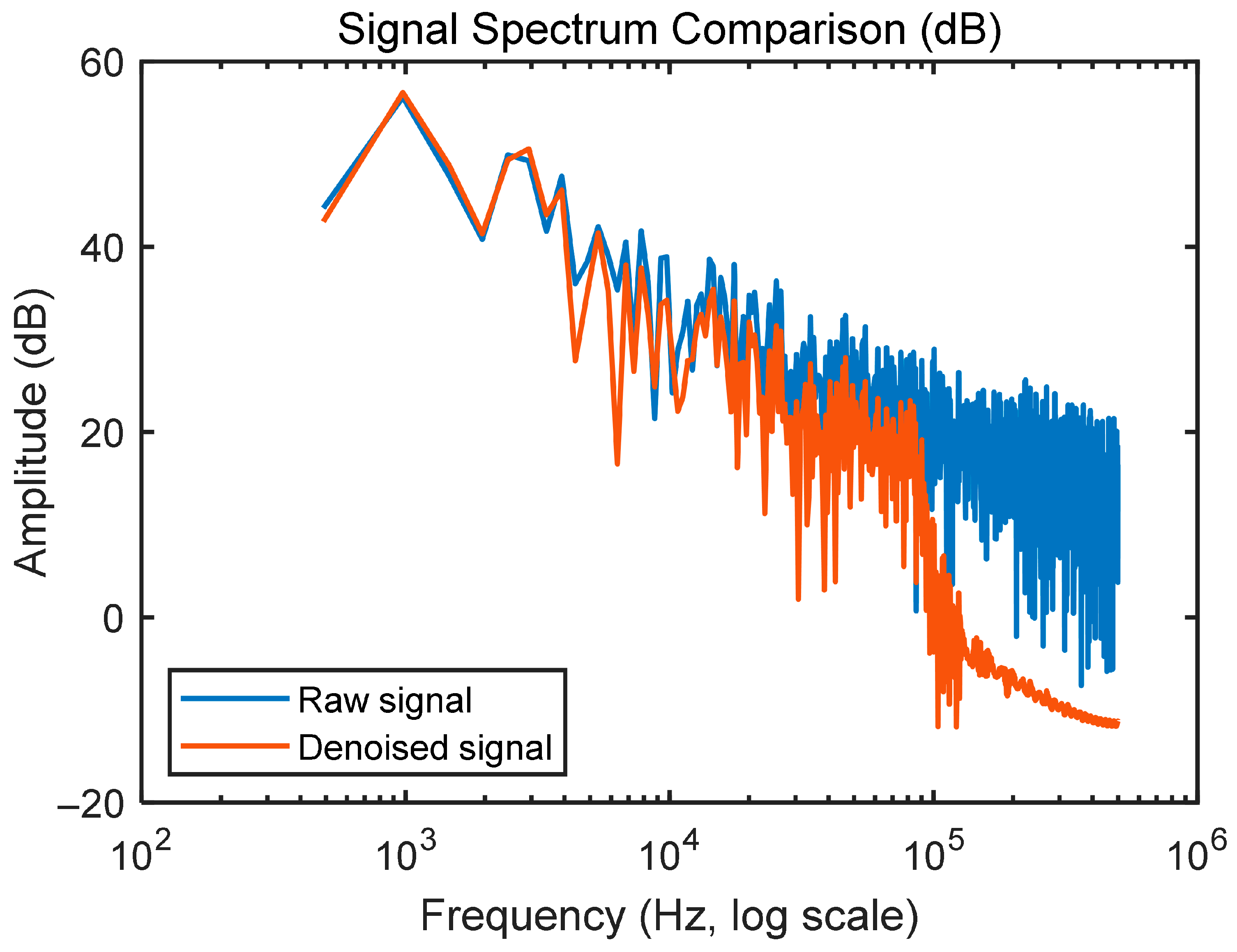
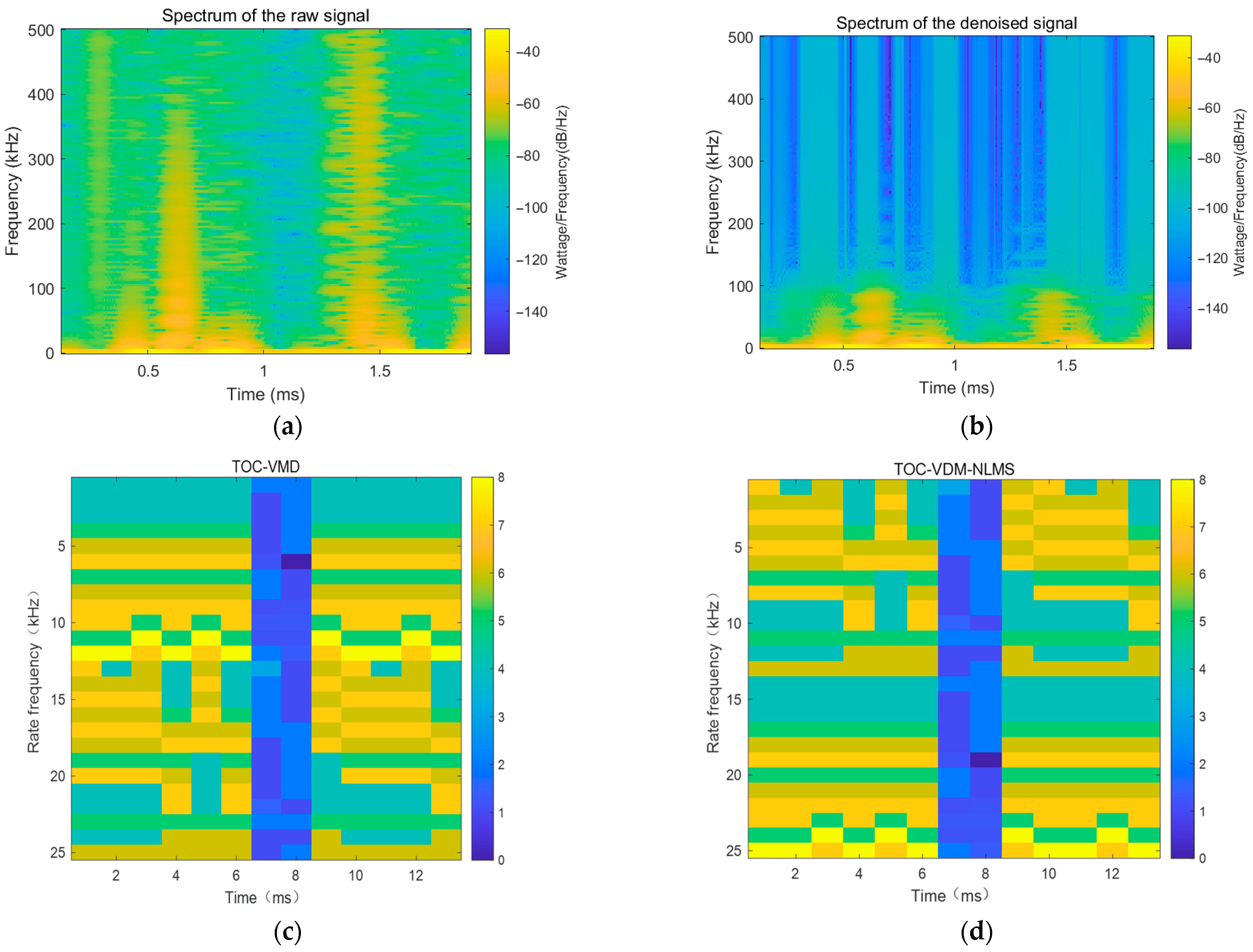
• As shown in Table 4, different methods exhibit distinct strengths in terms of waveform preservation and noise-suppression performance. Among all methods, the VMD algorithm achieves the smallest RMSE (0.1246), indicating that it retains the original waveform most effectively. The NLMS method shows limited improvement in both RMSE and SNR, while TOC-VMD-NLMS achieves a moderate balance between the two metrics. The TOC-VMD-NLMS approach provides the most significant SNR enhancement, increasing the SNR from 13.8945 dB to 19.0527 dB. However, its RMSE (0.2285) is not the smallest, reflecting a trade-off between noise reduction and waveform distortion. The composite metric M assigns a relatively high weight to SNR improvement. Therefore, methods showing strong SNR enhancement, such as TOC-VMD-NLMS, obtain higher M values even when their RMSE is not the smallest. This reflects the design intent of M, which emphasizes noise suppression rather than waveform fidelity. In summary, the method proposed in this paper offers greater advantages in noise reduction, and makes hybrid frameworks more suitable when balancing noise reduction performance. On the other hand, the increase in SNR accompanied by a rise in RMSE indicates that the statistical characteristics of the noise have changed after denoising, which is a normal phenomenon. This occurs because the TOC–NLMS–VMD algorithm suppresses high-frequency random noise through IMF reconstruction and NLMS adaptive updates, but simultaneously alters the amplitude distribution at each signal point, thereby slightly increasing the RMSE (point-to-point error metric). Nevertheless, the primary energy in the frequency domain is better preserved, resulting in a significant improvement in SNR. However, further analysis of residual signal statistics will be conducted in future follow-up studies.
• Additionally, from the analysis of ultrasonic detection signal characteristics, the high-frequency components correspond to scattering echoes from fine internal defects and specular reflections from sharp interfaces within the material. The information they carry is crucial for defect morphology characterization and boundary identification. During ultrasonic signal preprocessing, the suppression level of high-frequency components must be precisely controlled: excessive suppression irreversibly loses defect details such as microcrack propagation trajectories and fine inclusion boundary contours, reducing quantitative defect analysis accuracy; insufficient suppression leaves residual background random noise that interferes with defect feature extraction. The proposed algorithm employs an optimized frequency-selective filtering mechanism. It efficiently filters out random background noise, such as thermal noise from electronic devices and fluctuations in coupling agent acoustic impedance, while precisely preserving high-frequency reflection components associated with defects and interfaces. This significantly enhances the localization accuracy of defect boundaries in reconstructed waveforms, establishing a high-quality signal foundation for subsequent defect size measurement and morphology determination.

Thus, when juxtaposed against VMD, NLMS, and TOC-VMD, the proposed method exhibits an enhanced denoising efficacy.

5.3. CPU Time Efficiency Evaluation

The execution efficiency of the proposed algorithm was further evaluated.

Table 5. Efficiency of Different Algorithms Under Identical Conditions.

Method	Optimization Time (s)	Denoising Time per Frame (s)	Total Time per Frame (s)
VMD only	–	0.19	0.19
NLMS only	–	0.05	0.05
VMD–NLMS	–	0.20	0.20
TOC–VMD–NLMS (offline)	1.8	0.23	2.03
TOC–VMD–NLMS (online reuse)	–	0.23	0.23

summarizes the average runtime per signal frame (2048 samples) for different algorithms under identical hardware (Intel i7-12700, MATLAB R2024a). The proposed TOC–VMD–NLMS method includes an additional Tornado Optimization (TOC) stage for determining the optimal VMD parameters. As this step is only executed once per dataset, we report both the offline and online runtimes.

As shown in Table 5, the TOC stage requires approximately 1.80 s, which is significantly larger than the per-frame denoising time. This overhead is expected, as TOC repeatedly evaluates VMD to search for optimal parameters. After the optimal parameters are determined, the online denoising stage requires only 0.23 s per 2048-sample frame, which is comparable to conventional VMD–NLMS (0.20 s) and suitable for near–real-time implementation. Most industrial ultrasonic systems operate with static or slowly varying acquisition conditions; therefore, parameter optimization does not need to be performed for every frame. This makes TOC–VMD–NLMS computationally practical despite the higher offline cost. Although the proposed TOC–VMD–NLMS method incurs additional computational cost during offline optimization, this step is necessary only when acquisition conditions change. With optimized parameters reused across frames, the online denoising procedure remains efficient and suitable for real-world applications.

6. Conclusions

This paper focuses on the research of the TOC-VMD-NLMS algorithm proposed for industrial ultrasonic non-destructive testing. Addressing the issue of weak ultrasonic echo signals being overwhelmed by strong noise when acquired via high-speed data acquisition cards, experimental results demonstrate that VMD achieves optimal waveform preservation (minimum RMSE of 0.1246), while TOC-VMD-NLMS delivers the strongest noise suppression capability (SNR improved from 13.8945 dB to 19.0527 dB). Thus, the proposed framework achieves balanced performance by combining VMD’s noise reduction advantages with SNR enhancement from the NLMS and TOC stages. The method proposed in this paper holds significant implications for signal processing.

The method proposed in this paper is of great significance for signal processing of complex weak signals under strong electromagnetic interference.

The TOC-VMD-NLMS method synergizes the merits of variational mode decomposition (VMD) and normalized least-mean-square (NLMS) adaptive filtering. Optimally parameterized VMD first segregates signal and noise subspaces with minimal mode-mixing, averting over-decomposition; subsequently, NLMS adaptively cancels residual narrow-band interference. This cascaded strategy suppresses stochastic noise while preserving transient partial-discharge pulses. For example, previous studies [20,21] reported that EMD–WT and VMD–WT methods typically yield SNR improvements of 3–5 dB under similar ultrasonic conditions, whereas our proposed approach achieves an average improvement exceeding 6 dB (Table 4), while maintaining feature fidelity with a correlation coefficient above 0.94. These results provide quantitative evidence supporting the superior denoising capability and feature preservation performance of the proposed hybrid algorithm. Under low-SNR conditions, its cross-correlation coefficient remains superior, yielding clearer fault-feature extraction and corroborating robust efficacy in intense-noise environments.

Furthermore, the proposed method exhibits computational feasibility for real-time or embedded applications, as its dominant operations (FFT-based VMD and adaptive NLMS) can be parallelized and implemented efficiently on DSPs or FPGAs.

It offers significant potential for applications in ultrasonic nondestructive testing, structural health monitoring, and biomedical signal analysis, where reliable extraction of weak echoes is critical. In future work, we plan to integrate deep-learning-based parameter prediction to further improve adaptability in dynamic noise environments.