Velocity Ambiguity and Inter-Carrier Interference Suppression Algorithm in Stepped-Carrier OFDM Radar for ISAC

Abstract

Stepped-carrier orthogonal frequency division multiplexing (SC-OFDM) radar is an emerging low-cost alternative to standard OFDM radar for automotive applications due to providing high-range resolution at a low sampling rate. However, it is limited by inter-carrier interference (ICI) and velocity ambiguity in high-speed target detection. To address these issues, this paper proposes a two-step method for SC-OFDM radar. The method first applies multi-hypothesis Doppler compensation and leverages peak sidelobe ratio (PSLR) in the range profile as a distinguishing feature to estimate the target’s unambiguous velocity. Then, target signals are reconstructed into components free from ICI. Simulation results confirm the effectiveness of the proposed method. Compared to existing methods, this approach eliminates ICI without repeating OFDM symbols, thereby preserving communication data rate and enhancing suitability for integrated sensing and communication (ISAC) applications.

1. Introduction

Integrated sensing and communication (ISAC) systems employing orthogonal frequency division multiplexing (OFDM) waveforms are an active area of research in autonomous vehicles and unmanned aerial vehicle (UAV) networks [1,2,3]. OFDM-ISAC systems use a single hardware platform to realize wireless communication and radar sensing simultaneously, to improve system efficiency in terms of spectrum and cost. However, to achieve high-range resolution, OFDM-ISAC systems use a large bandwidth, which requires high sampling rates, thus imposing a serious challenge on hardware costs [4].

Researchers have explored some methods to lower sampling rates in OFDM radar [5,6,7,8]. Stepped-carrier OFDM (SC-OFDM) radar is a promising technique; it divides each OFDM symbol into subsymbols, which are transmitted at different carrier frequencies selected through linear [9], nonlinear [10], or random steps [11]. A modified discrete Fourier transform (DFT) corrects range migration errors induced by the stepping scheme and generates a high-resolution range–velocity (RV) map. However, the maximum unambiguous velocity $v_{\max }$ is reduced by the step number M compared to standard OFDM radar. To extend the unambiguous velocity range of SC-OFDM radar, a phase-jump method from velocity profiles has been proposed [12]. However, this method is constrained to single-target scenarios. For SC-OFDM radar with random frequency steps [13], modified DFT processing must be substituted with a more computationally intensive compressed sensing (CS) algorithm to extract range and velocity. Another approach based on variable cyclic prefix (CP) lengths [14] requires both waveform modifications and multi-frame post-processing, introducing additional latency that hinders real-time target detection.

Inter-carrier interference (ICI) is another inherent challenge for SC-OFDM radar in high-speed target detection, stemming from the OFDM waveform. When moving targets generate Doppler shifts, the orthogonality between subcarriers is disrupted, resulting in elevated range sidelobes and degraded detection performance [15,16]. To mitigate ICI-related losses, the conventional modified DFT method typically requires subcarrier spacing to exceed ten times the maximum Doppler shift [9,10,11]. However, increasing subcarrier spacing reduces the maximum unambiguous range. The all-cell Doppler correction (ACDC) scheme [17,18] mitigates ICI by repeating OFDM symbols, but this reduces the communication data rate. Additionally, multi-input multi-output (MIMO) radar methods mitigate ICI using the estimation of angle of arrival (AoA) [19,20], but they depend on accurate AoA estimation.

To overcome these limitations, we develop a two-step processing method for SC-OFDM radar. The proposed method combines multi-hypothesis Doppler compensation and ICI-free signal reconstruction to address both velocity ambiguity and ICI in multi-target scenarios. The key contributions of this work are as follows:

• Multi-Target Velocity Ambiguity Resolution: Our method effectively resolves velocity ambiguity in multi-target scenarios for SC-OFDM radar. In contrast, the phase-jump method only supports single-target scenarios [12]. Notably, our approach operates within a single frame, avoiding the multi-frame processing requirement of variable CP methods [14].
• Efficient ICI Mitigation: The proposed method mitigates ICI caused by moving targets, regardless of the presence of velocity ambiguity. Unlike the ACDC method [17,18], it avoids OFDM symbol repetition, thereby preserving the communication data rate, which is crucial for ISAC applications.

The rest of this paper is structured as follows: Section 2 describes the system model for SC-OFDM radar. Section 3 proposes a two-step method to resolve the velocity ambiguity and ICI. Section 4 shows the simulation results to verify the effectiveness of the proposed method. Section 5 concludes this paper.

Notation: Black bold letters represent matrices or vectors, ${\mathbf{A}}_{n,m,b}$ represents the $(n,m,b)$-th element of $\mathbf{A}$. $\mathbb{Z}$, $\mathbb{N}$, and $\mathbb{C}$ denote the sets of integer number, real number, and complex number, respectively. ${(·)}^{\mathrm{T}}$ and ${(·)}^{-1}$ represent transpose and inverse of matrix, respectively.

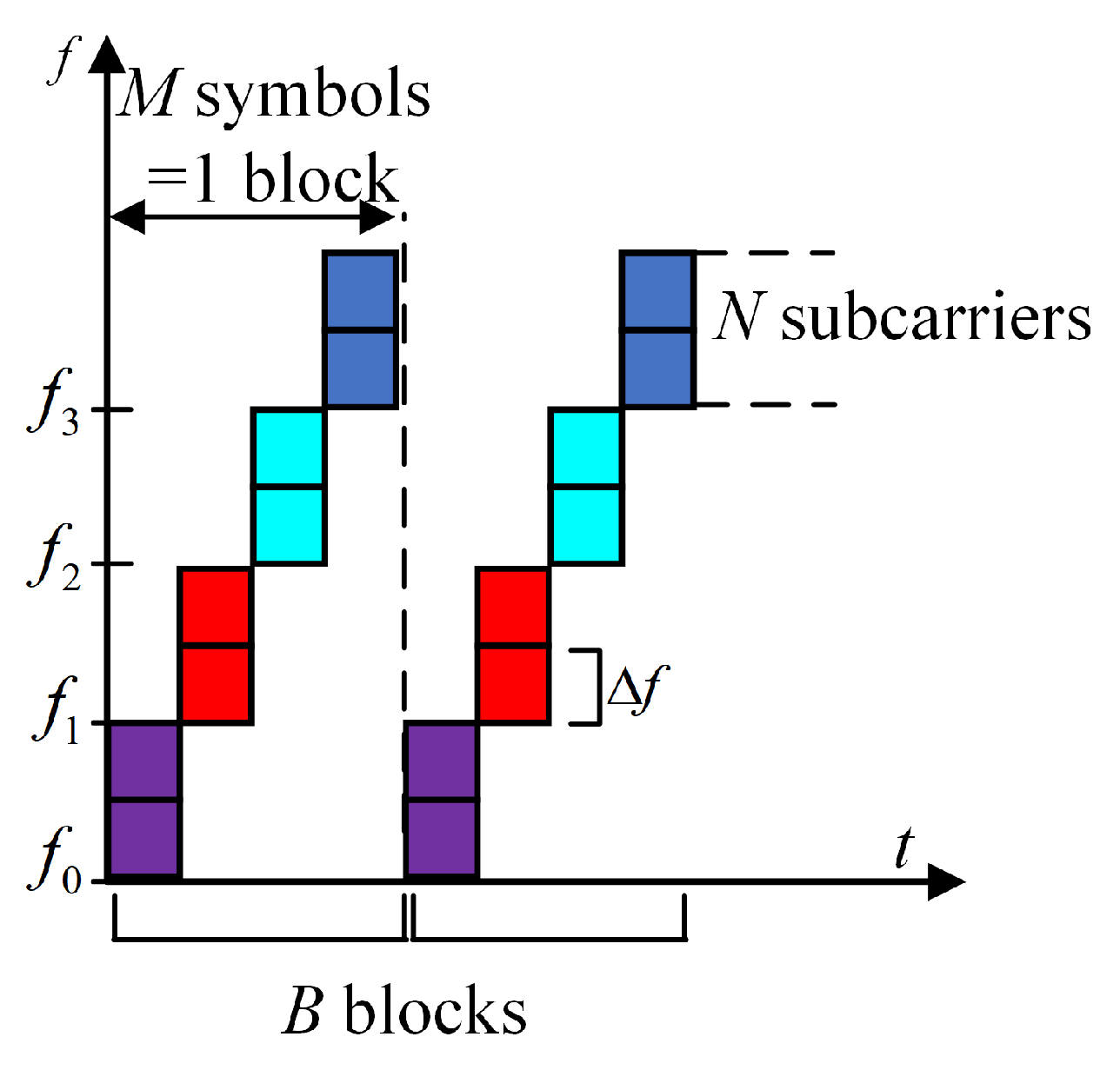
2. System Model

In this section, we first describe the signal model for SC-OFDM radar and then introduce the conventional modified DFT method that is used to jointly extract the range and velocity of targets.

2.1. Signal Model

Figure 1 presents the ratio-frequency (RF) time-frequency representation of the SC-OFDM signal. This signal transmits B blocks in the time domain, where each block is split into M symbols with a symbol duration of $T_s$. Each symbol occupies N subcarriers spaced at $\Delta f=1/T_s$ intervals. The m-th symbol is upconverted to an RF carrier frequency specified by $f_m=f_0+m{W}_0$, where $f_0$ denotes the lowest carrier frequency and $W_0=N\Delta f$ represents the baseband bandwidth. Thus, the RF bandwidth of SC-OFDM radar is $W_{\mathrm{RF}}=NM\Delta f$.

The resulting RF transmit signal for SC-OFDM radar is calculated as follows:

$$\begin{array}{c}\hfill x\left(t\right)=\sum _{b=0}^{B-1}\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{\mathbf{A}}_{n,m,b}{e}^{j2\pi (f_m+n\Delta f)t}\mathrm{rect}\left({\displaystyle \frac{t-mT-bMT}{T}}\right),\end{array}$$

(1)

where ${\mathbf{A}}_{n,m,b}$ is the modulated data on the subcarrier n, symbol m, and block b. $T=T_s+T_{\mathrm{cp}}$ is the total OFDM symbol duration, with $T_{\mathrm{cp}}$ being the CP duration. $\mathrm{rect}(t/T_s)$ is a rectangular window of duration $T_s$.

Consider P targets, each defined by a three-tuple $(R_p,v_p,{\alpha }_p)$, which represents the range, velocity, and reflection amplitude of the target p, respectively. The received signal after down-converting with $f_m$ is calculated as follows:

$$y\left(t\right)=\sum _{p=1}^P{\alpha }_{p}x(t-{\displaystyle \frac{2(R_p-v_{p}t)}{c}})e^{-j2\pi f_{m}t}.$$

(2)

where c is the speed of light.

By plugging (1) into (2), the received signal after sampling with $f_s=N\Delta f$ and removing CP is calculated as follows:

$$\begin{array}{cc}\hfill \mathbf{Y} = \left[y_{i,m,b}\right]& =\sum _{p=1}^P{\alpha }_p\sum _{n=0}^{N-1}{\mathbf{A}}_{n,m,b}{e}^{j2\pi {\displaystyle \frac{ni}{N}}}{e}^{-j2\pi (f_m+n\Delta f){\displaystyle \frac{2R_p}{c}}}{e}^{j2\pi {\displaystyle \frac{i{f}_{d,p}{T}_s}{N}}}\hfill \\ & \times e^{j2\pi (f_m+n\Delta f){\displaystyle \frac{2v_p(bM+m)T}{c}}}, i\in [0,N-1], m\in [0,M-1], b\in [0,B-1],\hfill \end{array}$$

(3)

where $f_{d,p}={\displaystyle \frac{2v_p{f}_0}{c}}$ is the Doppler shift of the target p. The third exponent corresponds to the intra-symbol Doppler effect, leading to ICI. The fourth exponent denotes inter-block and inter-symbol Doppler effects; the former is utilized for velocity estimation, and the latter induces range migration [9].

2.2. Conventional Modified DFT Method

SC-OFDM radar typically adopts the modified DFT method [9,10,11] to achieve the range and velocity estimations of targets, and its specific processing flow is illustrated in Figure 2. The detailed steps are described as follows.

Step 1: DFT and element-wise division. In (3), we first perform a DFT on $y_{i,m,b}$ along i-axis to obtain the frequency-domain signal, and then take element-wise division to eliminate the transmitted modulation symbols $\mathbf{A}$, resulting in the following:

$$\begin{array}{c}{\mathbf{H}}_{n,m,b}=\sum _{p=1}^P{\alpha }_p{e}^{-j2\pi (f_m+n\Delta f){\displaystyle \frac{2(R_p-v_p(bM+m)T)}{c}}}\hfill \\ \times (\underset{{\mathbf{H}}_{n,m,b}^{\mathrm{des}}}{\underbrace{s_N\left({\displaystyle \frac{{\widehat{f}}_{d,p}}{N}}\right)}}+\underset{{\mathbf{H}}_{n,m,b}^{\mathrm{ICI}}}{\underbrace{\sum _{u=0,u\ne n}^{N-1}{\displaystyle \frac{{\mathbf{A}}_{u,m,b}}{{\mathbf{A}}_{n,m,b}}}{s}_N\left({\displaystyle \frac{u-n+{\widehat{f}}_{d,p}}{N}}\right)}}),\hfill \end{array}$$

(4)

where $n\in [0,N-1]$, ${\widehat{f}}_{d,p}=f_{d,p}{T}_s$ denotes the normalized Doppler shift of the p-th target. $s_a\left(x\right)={\displaystyle \frac{sin\left(\pi ax\right)}{sin\left(\pi x\right)}}{e}^{j\pi (a-1)x}$, ${\mathbf{H}}^{\mathrm{des}}$ is the desired component, ${\mathbf{H}}^{\mathrm{ICI}}$ is the noise part of ICI.

Step 2: Modified DFT for velocity profile extraction. According to [9], to mitigate the inter-symbol Doppler effect and extract the velocity profile, a modified DFT is applied as follows:

$$\begin{array}{c}\hfill {\mathbf{V}}_{n,m,k}=\sum _{b=0}^{B-1}{\mathbf{H}}_{n,m,b}{e}^{-j2\pi {\displaystyle \frac{k(bM+m)}{BM}}},k\in [0,B-1].\end{array}$$

(5)

Substituting (4) into (5), the velocity estimate ${\widehat{v}}_p$ can be derived as follows:

$$\begin{array}{c}\hfill {\widehat{v}}_p={\displaystyle \frac{c{k}_0}{2f_{0}BMT}},k_0=0,\dots ,B-1.\end{array}$$

(6)

Step 3: IDFT for RV map generation. We define $u=mN+n$ in (5) and obtain ${\mathbf{Z}}_{u,k}={\mathbf{V}}_{n,m,k}$. Applying the range inverse DFT (IDFT) to the columns of $\mathbf{Z}$ yields the RV map

$$\begin{array}{cc}\hfill {\mathbf{G}}_{q,k}& =\sum _{u=0}^{MN-1}{\mathbf{Z}}_{u,k}{e}^{j2\pi {\displaystyle \frac{uq}{NM}}},q\in [0,MN-1]\hfill \\ \hfill & ={\mathbf{G}}_{q,k}^{\mathrm{des}}+{\mathbf{G}}_{q,k}^{\mathrm{ICI}},\hfill \end{array}$$

(7)

where ${\mathbf{G}}^{\mathrm{ICI}}$ is the noise component induced by ${\mathbf{H}}^{\mathrm{ICI}}$. The desired component contributed by ${\mathbf{H}}^{\mathrm{des}}$ is given by the following:

$$\begin{array}{c}\hfill {\mathbf{G}}_{q,k}^{\mathrm{des}}=\sum _{p=1}^P{\alpha }_p{s}_N\left({\displaystyle \frac{{\widehat{f}}_{d,p}}{N}}\right)s_B\left(f_{d,p}T-{\displaystyle \frac{k}{BM}}\right)s_{NM}\left({\displaystyle \frac{2R_p\Delta f}{c}}-{\displaystyle \frac{q}{NM}}\right),\end{array}$$

(8)

where $f_0\gg W_{\mathrm{RF}}$.

From the above processing, the range resolution $\Delta r$, maximum unambiguous range $r_{\max }$, velocity resolution $\Delta v$, and maximum unambiguous velocity $v_{\max }$ can be respectively derived as follows:

$$\begin{array}{cc}\hfill & \Delta r={\displaystyle \frac{c}{2MN\Delta f}},r_{\max }={\displaystyle \frac{c}{2\Delta f}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \Delta v={\displaystyle \frac{c}{2f_{0}MBT}},v_{\max }=\pm {\displaystyle \frac{c}{4f_{0}MT}}.\hfill \end{array}$$

(10)

Note that, the maximum unambiguous velocity $v_{\max }$ decreases inversely with M compared to standard OFDM radar. This may lead to velocity ambiguity in high-speed target scenarios. Additionally, the modified DFT method neglects the effect of ${\mathbf{G}}^{\mathrm{ICI}}$ when the normalized Doppler shift ${\widehat{f}}_{d,p}$ is below 0.1. As the target velocity increases, the ICI effect becomes more pronounced and non-negligible, thereby degrading the range profile performance.

3. Proposed Scheme

In this section, we build upon the ICI mitigation method for OFDM radar described in [21] and present a two-step method to mitigate velocity ambiguity and ICI for SC-OFDM radar. The principle and complexity of the proposed method are described as follows:

3.1. Step 1: Velocity Ambiguity Resolution by Multi-Hypothesis Doppler Compensation

Consider a moving target no matter the velocity ambiguity exists or not, its real velocity $v_r$ is expressed as follows:

$$v_r=v_0+2\kappa v_{\max },$$

(11)

where $v_0$ is the velocity ambiguity estimate output by the modified DFT, and $\kappa \in \mathbb{Z}$ is the velocity ambiguity number.

By substituting (11) into (3), the two exponents corresponding to $v_r$ satisfy the following:

$$\begin{array}{cc}\hfill & e^{j2\pi {\displaystyle \frac{2f_0(v_0+2\kappa v_{\max })i{T}_s/N}{c}}}=e^{j2\pi {\displaystyle \frac{2f_0{v}_{0}i{T}_s/N}{c}}}{e}^{j2\pi {\displaystyle \frac{\kappa i{T}_s}{NMT}}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & e^{j2\pi (f_m+n\Delta f){\displaystyle \frac{2(v_0+2\kappa v_{\max })(bM+m)T}{c}}}=e^{j2\pi (f_m+n\Delta f){\displaystyle \frac{2v_0(bM+m)T}{c}}}{e}^{j2\pi {\displaystyle \frac{\kappa m}{M}}}.\hfill \end{array}$$

(13)

From (12) and (13), it can be seen that velocity ambiguity introduces an additional two phase terms related to $\kappa$, written as follows:

$$\begin{array}{c}\hfill \Delta {\varphi }_1=e^{j2\pi {\displaystyle \frac{\kappa i{T}_s}{NMT}}},\Delta {\varphi }_2=e^{j2\pi {\displaystyle \frac{\kappa m}{M}}},\end{array}$$

(14)

which denote the intra-symbol and inter-symbol Doppler effects induced by the target velocity $2\kappa v_{\max }$, respectively.

To simultaneously mitigate the intra-symbol and inter-symbol Doppler effects mentioned above, we first construct a Doppler compensation matrix $\mathbf{D}\left(\kappa \right)\in {\mathbb{C}}^{N\times M}$, where the $(i,m)$-th element is given by the following:

$$\begin{array}{c}\hfill {\mathbf{D}}_{i,m}\left(\kappa \right)=e^{-j2\pi {\displaystyle \frac{\kappa iT}{NM{T}_s}}}{e}^{-j2\pi {\displaystyle \frac{\kappa m}{M}}},\kappa \in \{-N_a,\dots ,N_a\},\end{array}$$

(15)

where $N_a\in \mathbb{N}$ is the search ambiguity range, and the velocity ambiguity range expands from $v_{\max }$ to $(2N_a+1)v_{\max }$.

Before to performing conventional modified DFT processing, we multiply the received signal matrix $\mathbf{Y}$ by the compensation matrix $\widehat{\mathbf{D}}\left(\kappa \right)$ as follows:

$$\begin{array}{c}\hfill \widehat{\mathbf{Y}}\left(\kappa \right)=\mathbf{Y}·\widehat{\mathbf{D}}\left(\kappa \right),\end{array}$$

(16)

where $\widehat{\mathbf{D}}\left(\kappa \right)\in {\mathbb{C}}^{N\times M\times B}$, and its $(i,m,b)$-th element is defined as ${\widehat{\mathbf{D}}}_{i,m,b}\left(\kappa \right)={\mathbf{D}}_{i,m}\left(\kappa \right)$.

For each candidate ambiguity number $\kappa$, the conventional modified DFT method is applied to $\widehat{\mathbf{Y}}\left(\kappa \right)$ to generate the compensated RV map $\mathbf{G}\left(\kappa \right)$. Subsequently, CFAR detection is performed to extract potential targets from $\mathbf{G}\left(\kappa \right)$. The Doppler shift may cause target peak energy loss and elevated sidelobes in the range profile, resulting in a reduced peak sidelobe ratio (PSLR) [7]. For each potential target, if the selected $\kappa$ matches the true ambiguity number, the Doppler shift induced by the target’s velocity within the ambiguity region is fully compensated, and the range profile of the target exhibits the maximum PSLR.

Let L denote the number of detected targets. For the l-th target, its peak cell in $\mathbf{G}\left(\widehat{\kappa }\right)$ is denoted as $(q_l,k_l)$, where ${\widehat{\kappa }}_l$ is the ambiguity number corresponding to the target with the maximum PSLR, and $({\widehat{R}}_l,v_l)$ are the associated target estimates. The true velocity of the l-th target is thus calculated as follows:

$$\begin{array}{c}\hfill {\widehat{v}}_l=v_l+2{\widehat{\kappa }}_l{v}_{\max }.\end{array}$$

(17)

The proposed method increases the unambiguous velocity range from $v_{\max }$ to $(2N_a+1)v_{\max }$, in contrast to the phase-jump method described in [15]. The phase-jump method depends on the phase term $\Delta {\varphi }_2$ to extract the value of $\kappa$. The periodicity of $\Delta {\varphi }_2$, i.e., $e^{j2\pi {\displaystyle \frac{(\kappa +M)m}{M}}}=e^{j2\pi {\displaystyle \frac{\kappa m}{M}}}$, since $e^{j2\pi m}=1$ for all integers m, results in overlapping patterns between $\kappa$ and $\kappa \pm M$. Hence, the periodicity confines the phase-jump method to an unambiguous velocity range of only $(M-1)v_{\max }$. By contrast, the proposed method is free from this limitation.

3.2. Step 2: ICI Mitigation by Signal Reconstruction

To calculate the reflection amplitude of each target and reconstruct the target signal without ICI, all L targets’ cells in the RV map $\mathbf{G}$ are extracted as follows:

$$\begin{array}{c}\hfill \mathbf{p}={\left[{\mathbf{G}}_{q_0,k_0},{\mathbf{G}}_{q_1,k_1},\dots ,{\mathbf{G}}_{q_{L-1},k_{L-1}}\right]}^{\mathrm{T}}.\end{array}$$

(18)

The reflected signal from target l is then constructed as follows:

$$\begin{array}{cc}\hfill {\overline{\mathbf{Y}}}^l& =\left[{\widehat{y}}_{i,m,b}^l\right]=\sum _{n=0}^{N-1}{\mathbf{A}}_{n,m,b}{e}^{j2\pi {\displaystyle \frac{ni}{N}}}{e}^{-j2\pi (f_m+n\Delta f){\displaystyle \frac{2{\widehat{R}}_l}{c}}}\hfill \\ & \times e^{j2\pi (f_m+n\Delta f){\displaystyle \frac{2{\widehat{v}}_l(bM+m)T}{c}}}{e}^{j2\pi {\displaystyle \frac{2f_0{\widehat{v}}_{l}i{T}_s/N}{c}}},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{Y}}}^l& =\left[{\overline{y}}_{i,m,b}^l\right]=\sum _{n=0}^{N-1}{\mathbf{A}}_{n,m,b}{e}^{j2\pi {\displaystyle \frac{ni}{N}}}{e}^{-j2\pi (f_m+n\Delta f){\displaystyle \frac{2{\widehat{R}}_l}{c}}}\hfill \\ & \times e^{j2\pi (f_m+n\Delta f){\displaystyle \frac{2{\widehat{v}}_l(bM+m)T}{c}}},\hfill \end{array}$$

(20)

where ${\overline{\mathbf{Y}}}^l$ denotes the ICI-contaminated signal, while ${\widehat{\mathbf{Y}}}^l$ represents the ICI-decontaminated signal. Applying the modified DFT method to ${\overline{\mathbf{Y}}}^l$ yields the RV map ${\overline{\mathbf{G}}}^l$. All L targets’ cells are then extracted as follows:

$${\mathbf{q}}^l={[{\overline{\mathbf{G}}}_{q_0,k_0}^l,{\overline{\mathbf{G}}}_{q_1,k_1}^l,\dots ,{\overline{\mathbf{G}}}_{q_{L-1},k_{L-1}}^l]}^{\mathrm{T}}.$$

(21)

All L targets are combined into the matrix $\mathbf{Q}=[{\mathbf{q}}^0, {\mathbf{q}}^1,\dots , {\mathbf{q}}^{L-1}]$. The vector $\mathbf{p}$ is expressed as a linear combination of the columns of $\mathbf{Q}$, where the reflection amplitude vector $\widehat{\alpha }={[{\widehat{\alpha }}_0,{\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_{L-1}]}^{\mathrm{T}}$ serves as the coefficients. Therefore, $\widehat{\alpha }$ is given by the following:

$$\widehat{\alpha }={\left({\mathbf{Q}}^{\mathrm{T}}\mathbf{Q}\right)}^{-1}{\mathbf{Q}}^{\mathrm{T}}\mathbf{p}.$$

(22)

In the original received signal of (3), the ICI-contaminated signal is replaced with the reconstructed ICI-decontaminated signal. The final ICI-decontaminated signal ${\mathbf{Y}}_d$ is defined as follows:

$$\begin{array}{c}\hfill {\mathbf{Y}}_d=\mathbf{Y}-\sum _{l=0}^{L-1}{\widehat{\alpha }}_l{\overline{\mathbf{Y}}}^l+\sum _{l=0}^{L-1}{\widehat{\alpha }}_l{\widehat{\mathbf{Y}}}^l.\end{array}$$

(23)

3.3. Computation Complexity

We analyze the complexity of the proposed method as follows. Let W denote the CFAR window size. The complexity of velocity ambiguity resolution, CFAR algorithm, signal reconstruction, and reflection amplitude calculation are $\mathcal{O}\{(2N_a+1)NMBlog\left(N^{2}MB\right)\}$, $\mathcal{O}\left\{(2N_a+1)NMBW\right\}$, $\mathcal{O}\{LNMBlog\left(N^{2}MB\right)\}$, and $\mathcal{O}\left\{L^3\right\}$, respectively. Thus, its overall complexity is $\mathcal{O}\{(2N_a+1)NMB(log\left(N^{2}MB\right)+W)+LNMBlog\left(N^{2}MB\right)+L^3\}$. In contrast, the complexity of the conventional modified DFT method is $\mathcal{O}\left\{NMB(log\left(N^{2}MB\right)+W)\right\}$. Hence, the proposed method increases computational costs more than the conventional modified DFT method.

4. Simulation Results

In this section, we evaluate the performance of the proposed method through simulations. The transmitted modulation symbols are generated randomly using BPSK modulation, and the radar parameters are shown in

Table 1. SC-OFDM radar parameters.

Symbol	Parameter	Value
$f_0$	Carrier frequency $\left(\mathrm{GHz}\right)$	77
$W_0$	Basedband bandwidth $\left(\mathrm{MHz}\right)$	50
M	Number of symbols	4
N	Number of subcarriers	256
B	Number of blocks	128
$T_{\mathrm{cp}}$	Duration of CP ($\mu$s)	0.6

. The noise is modeled as additive white Gaussian noise (AWGN), and a Hamming window is applied to suppress sidelobe levels in both range and velocity dimensions.

The original unambiguous velocity is $v_{\max }=\pm 42.57\mathrm{m}/\mathrm{s}$ from (10). To address the range of potential relative velocities encountered in automotive environments [22], the search range for the velocity ambiguity number is defined as $\kappa \in \{-2,-1,0,1,2\}$, and the proposed method achieves a maximum unambiguous velocity of $\pm 212.85\mathrm{m}/\mathrm{s}$. Increasing $\kappa$ allows for the estimation of higher target velocities. Three targets are set as $R=[35,35,40]\mathrm{m}$, $v=[-110,40,135]\mathrm{m}/\mathrm{s}$, $\alpha =[0.6,1,0.3]$, and true ambiguity number $\kappa =[-1,0,2]$.

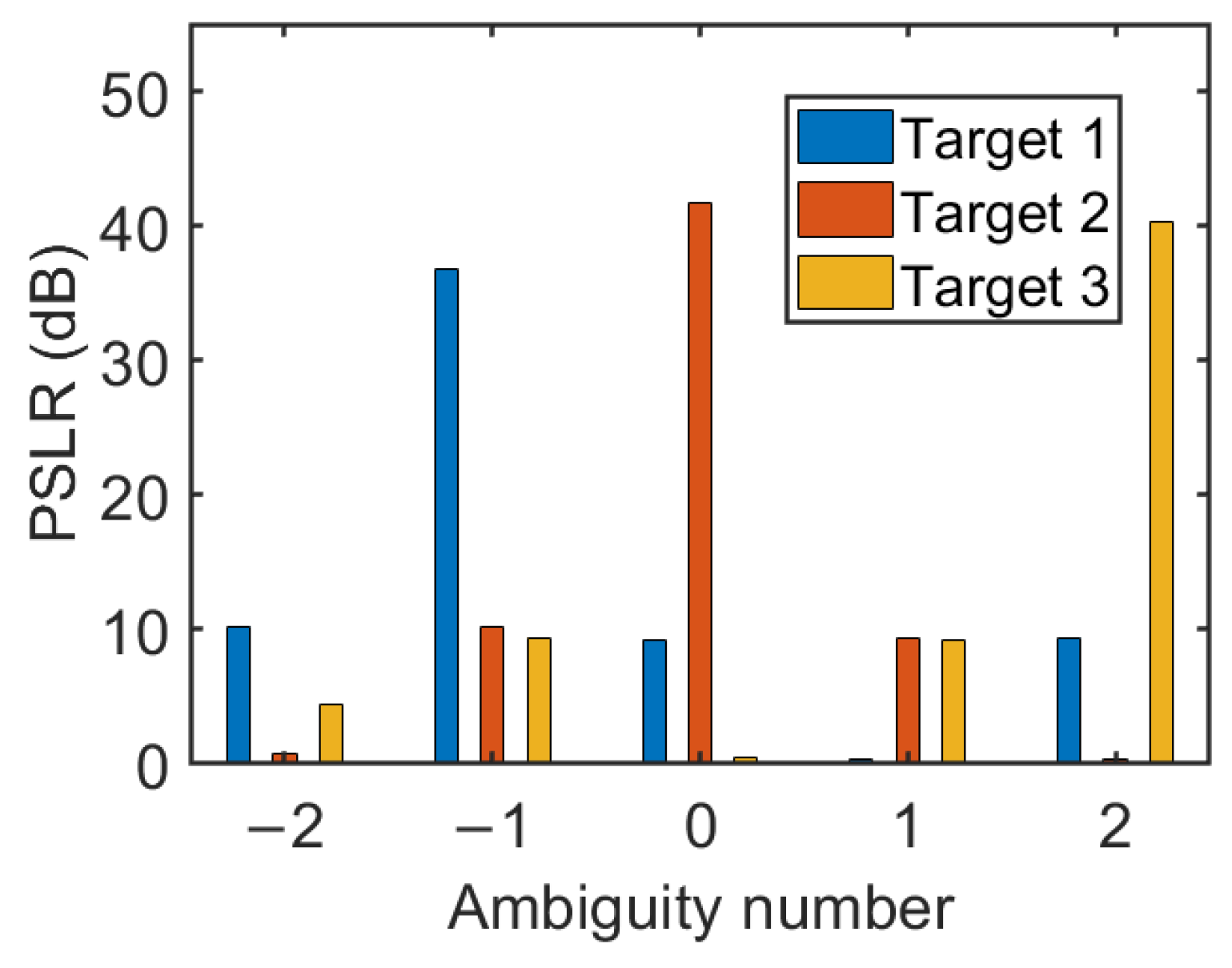
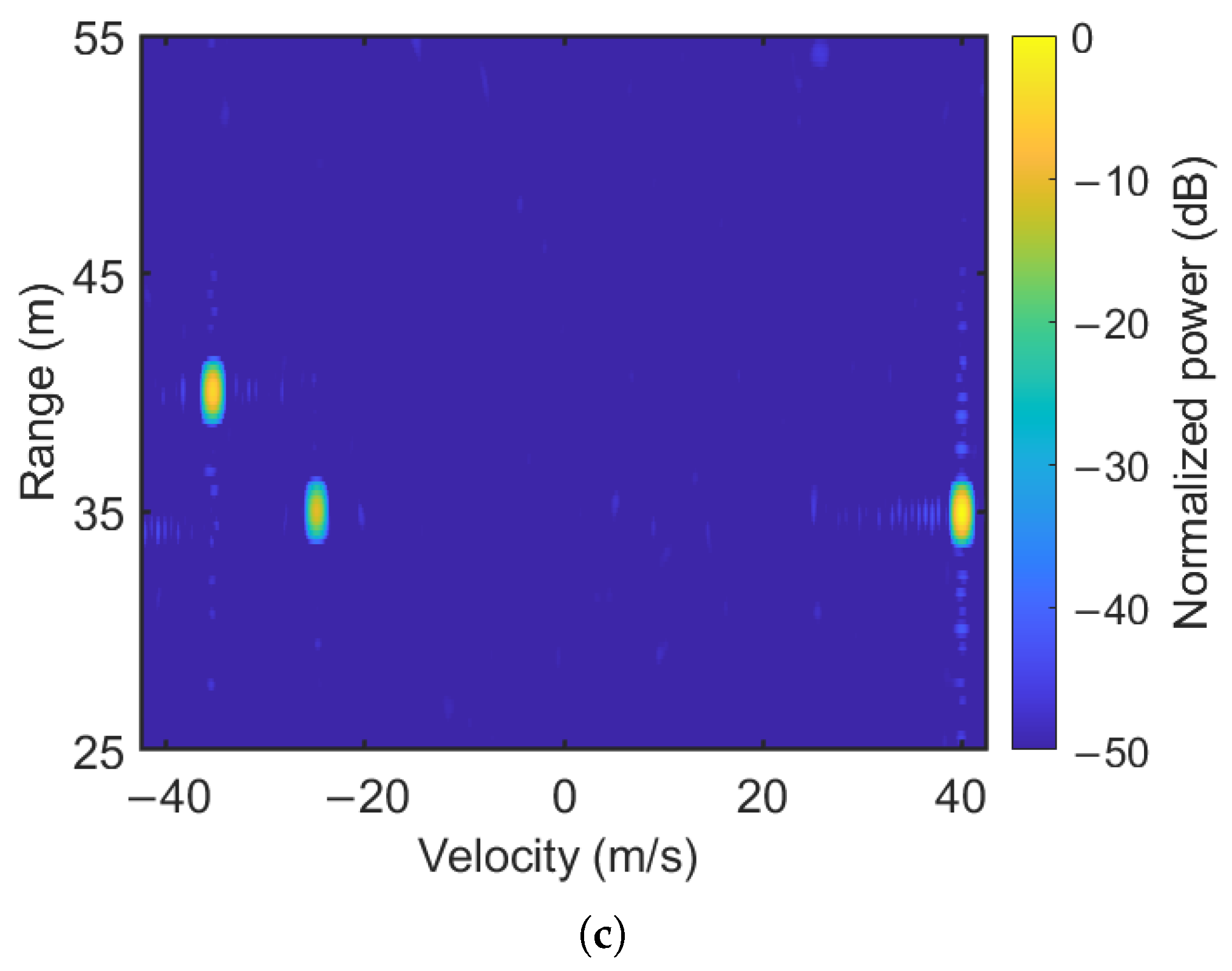
4.1. Velocity Ambiguity Mitigation Result

After 500 Monte Carlo simulations, Figure 3 presents the range PSLR of three targets versus ambiguity numbers $\kappa$ with a signal-to-noise ratio (SNR) of 10 dB at the input of the radar processing. We observe that applying the correct ambiguity number can maximize the range PSLR for each target; this is due to compensation of Doppler shift caused by target velocity $2\kappa v_{\max }$. Based on the PSLR maximization criterion, the estimated ambiguity numbers of the three targets are −1, 0, and 2, respectively, which are consistent with the true ambiguity numbers. This demonstrates that the proposed method can achieve accurate velocity ambiguity resolution in multi-target scenarios.

Figure 4 shows the probability of correct velocity ambiguity resolution $P_{\mathrm{success}}$ for three targets versus input SNR, where $P_{\mathrm{success}}$ is defined as the percentage of trials in which the estimated $\kappa$ matches the true value, and the input SNR varies from −40 dB to 10 dB in 5 dB increments. With the increased SNR, $P_{\mathrm{success}}$ for all targets approaches 1. Target 2 achieves $P_{\mathrm{success}}=1$ when SNR exceeds −25 dB, while Target 1 requires at least −15 dB. This difference is attributed to Target 2’s higher reflection amplitude, which increases signal strength and facilitates ambiguity resolution.

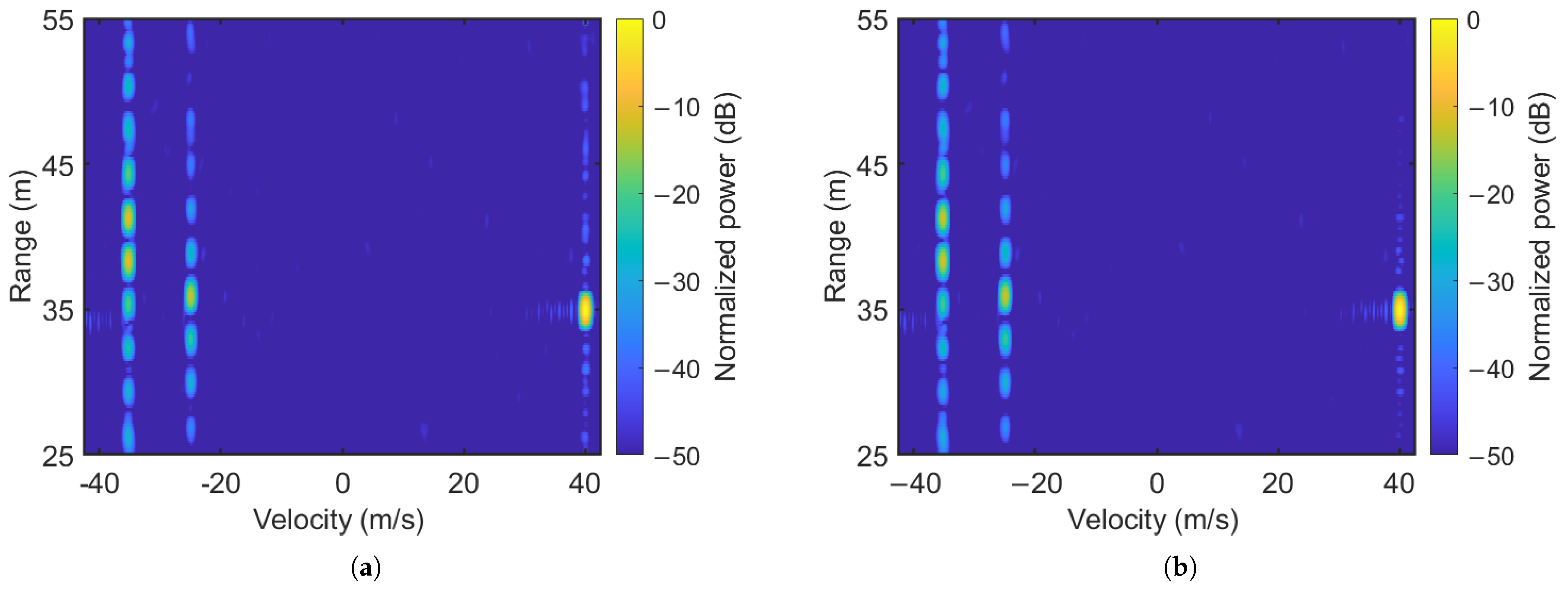
4.2. ICI Mitigation Result

Figure 5 shows the RV map generated by different methods, including the conventional modified DFT method [9] and the ACDC method [16]. We see that the RV map from the conventional method demonstrates elevated sidelobes for all three targets due to unsuppressed ICI. ACDC reduces the sidelobe for Target 2, as it effectively compensates for Doppler shifts for unambiguous-velocity targets. While the proposed methods provide substantial sidelobe suppression for each target, confirming successful compensation for Doppler shifts of targets with either unambiguous or ambiguous velocities.

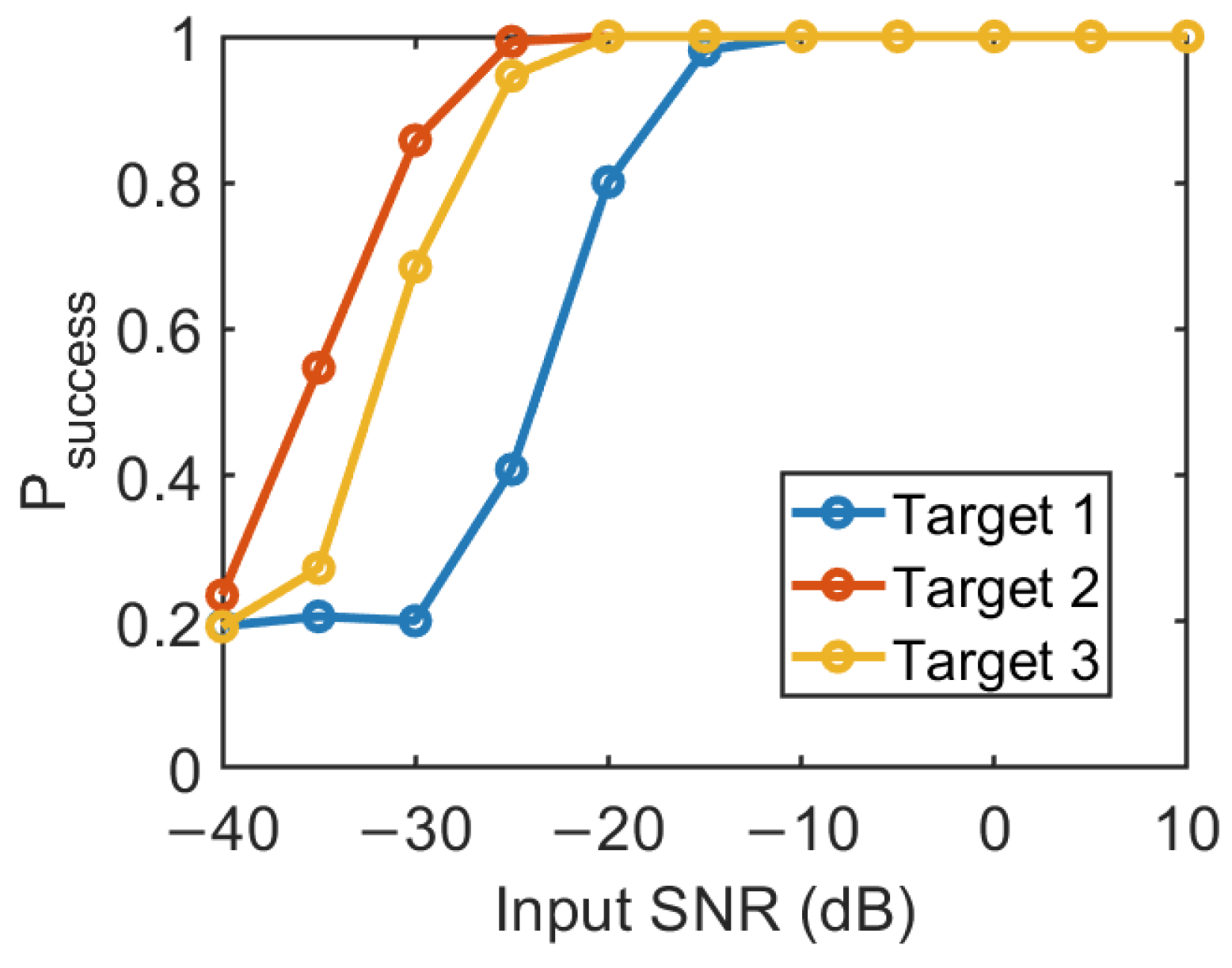
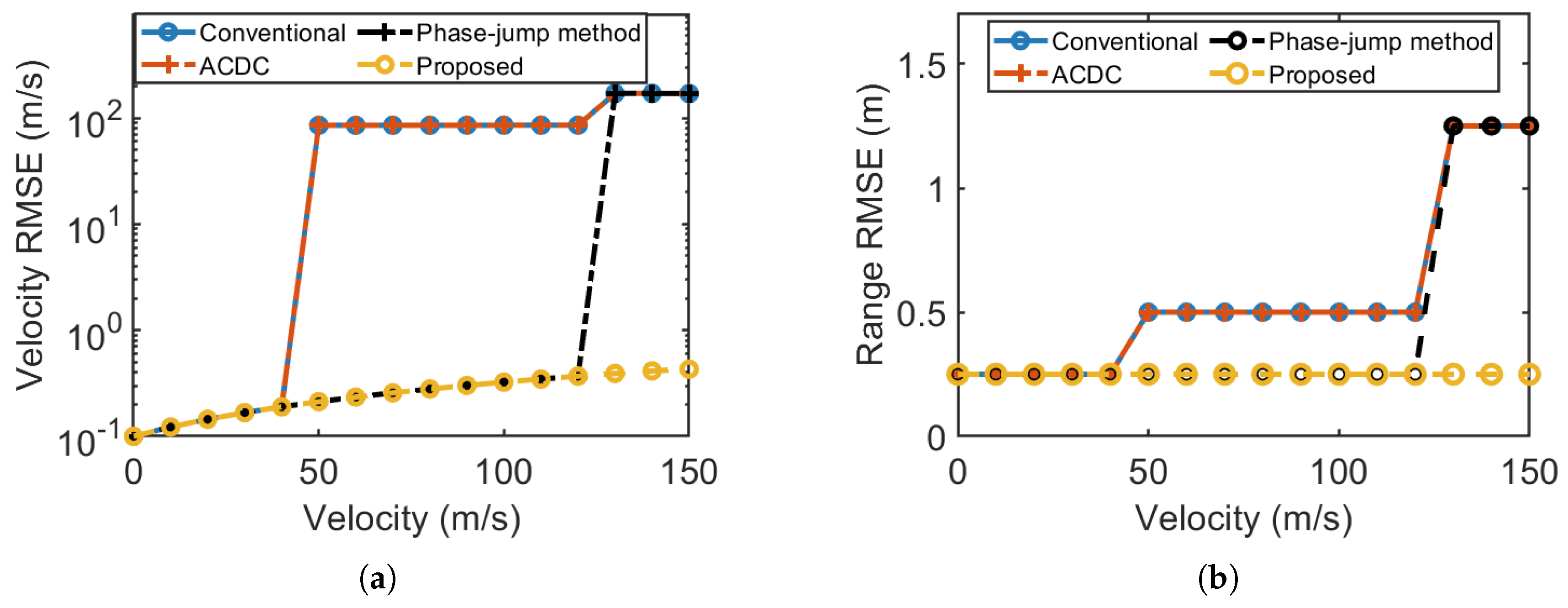
4.3. Robustness of the Proposed Method

To evaluate the robustness of the proposed method against target velocity, Target 2 was tested under a fixed range, with its velocity varied from 0 to 150 m/s at 10 m/s increments. Figure 6 presents the range of PSLR versus target velocity for different methods, including the conventional modified DFT method [9], the phase-jump method [12], and the ACDC method [17]. The key observations are summarized as follows:

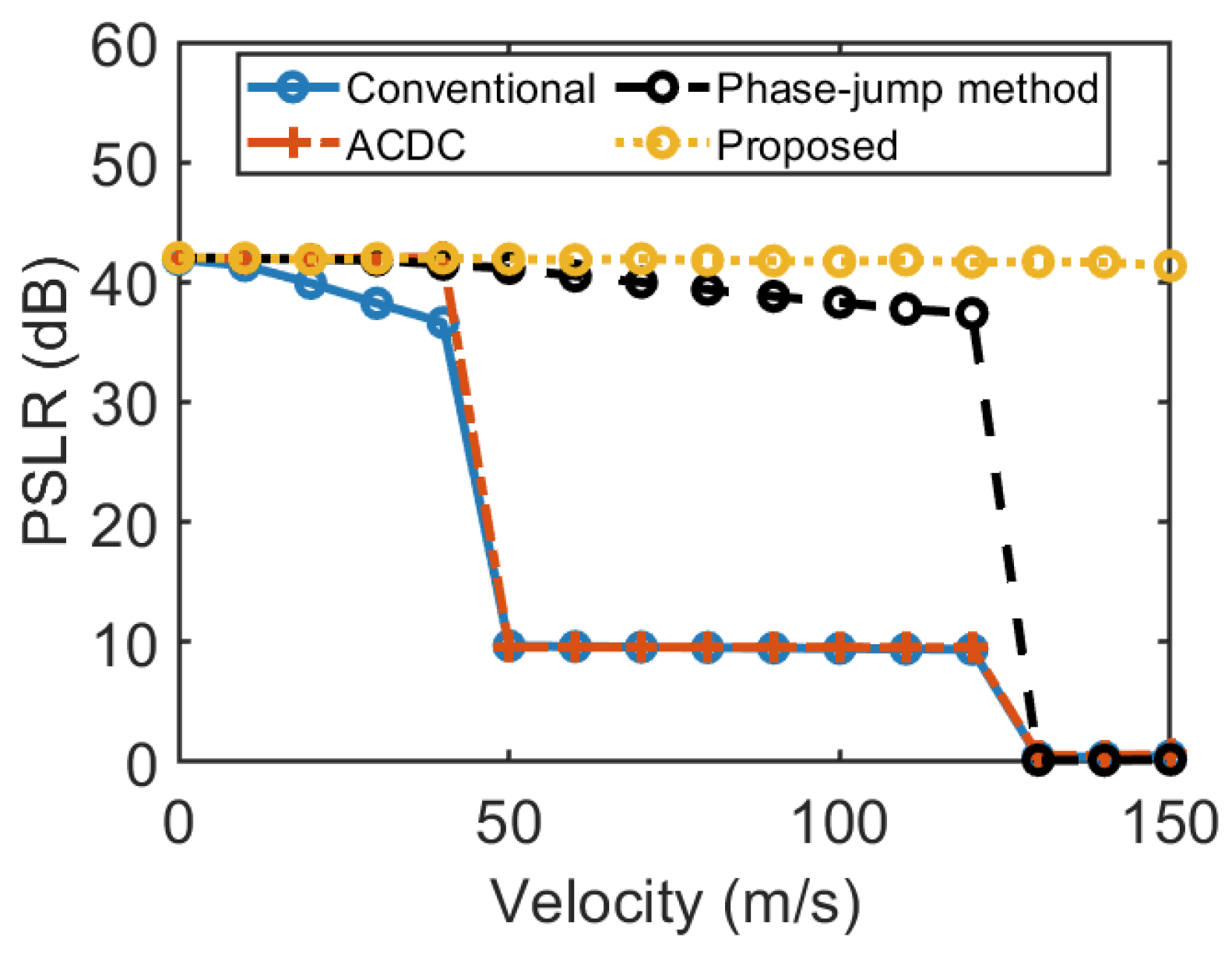
• The conventional method exhibits a gradual reduction in PSLR when $v \le v_{\max }$. When $v_{\max } < v \le 3v_{\max }$, PSLR drops to 9.8 dB. When $v>3v_{\max }$, PSLR falls to 0 dB. This decline results from the conventional method’s ability to mitigate only the inter-symbol Doppler effect for velocities up to $v_{\max }$. At higher velocities, both intra-symbol and inter-symbol Doppler effects are not compensated, causing substantial PSLR degradation.
• The ACDC method maintains a PSLR level similar to that of the proposed method when $v\le v_{\max }$, due to its capability to suppress both intra-symbol and inter-symbol Doppler effects in this velocity range. However, as v exceeds $v_{\max }$, its performance degrades inconsistently, reflecting the behavior of the conventional method. This is because the method does not compensate for Doppler effects at higher velocities.
• The phase-jump method exhibits a gradual reduction in PSLR when $v \le 3v_{\max }$. In contrast, when $v >3 v_{\max }$, the PSLR decreases sharply to 0 dB, mirroring the performance trends observed in the conventional method and the ACDC method. This is because the phase-jump method becomes ineffective when the target velocity surpasses $3v_{\max }$.
• Throughout the tested velocity range, the proposed method consistently maintains a PSLR of approximately 42 dB. This robust performance results from its ability to simultaneously suppress both intra-symbol and inter-symbol Doppler effects for targets with unambiguous and ambiguous velocities.

Figure 7 shows the root-mean-square error (RMSE) values of velocity and range estimations versus velocity. We observe that when $v \le v_{\max }$, all four methods yield identical estimation accuracy. When $v \le 3v_{\max }$, the phase-jump and proposed methods maintain consistent accuracy. However, when $v > 3v_{\max }$, the phase-jump method fails to provide accurate estimations due to unresolved velocity ambiguity, while the proposed method remains reliable.

5. Conclusions

This paper presents a novel method to eliminate ICI and velocity ambiguity in SC-OFDM radar. The proposed method employs a multi-hypothesis Doppler compensation to resolve velocity ambiguity in multi-target scenarios and eliminates ICI without lowering the data rate. Simulation results confirm that, compared with existing methods, the proposed approach demonstrates greater robustness against target velocity and improves the accuracy of range–velocity estimation.

However, the proposed method is limited to scenarios with overlapping targets that share an identical range–velocity cell in the range–velocity map. Future studies should analyze overlapping target separation through MIMO radar to explore the capabilities of SC-OFDM waveforms.