Research on Shear Mode Bidirectional Piezoelectric Energy Harvesting Structure Based on Underwater Vortex-Induced Vibration

Abstract

In order to solve the problem of continuous and stable energy supply of underwater sensor nodes, a shear mode bidirectional piezoelectric energy harvesting structure based on underwater vortex-induced vibration is proposed. The structure was investigated through fluid–solid and piezoelectric coupling numerical simulations using ANSYS 2020, and the relationship between the vibration mode, thickness, flow velocity, spacing diameter ratio of the bluff body and energy harvester (L/D) was studied. The vibration and piezoelectric characteristics of parallel and tandem energy harvesters were analyzed. The results verify that the piezoelectric material with d₁₅ mode has higher output power than that with d₃₃ and d₃₁ modes, under the same conditions, the output power has increased by 50%. When the flow velocity is 1.1 m/s, the bluff body is a wavy cylinder, the L/D is 2, and the maximum voltage and output power values generated by the energy harvesting structure are 56.97 V and 3.25 mW, respectively. Its power density reaches 1.35 mW/cm³, superior to similar-scale collectors reported in the recent literature. In the case of the double energy harvesting structure, it can capture vortex-induced vibration energy in both flow and lateral directions, thereby expanding the working bandwidth and improving the overall energy capture efficiency; the parallel output voltage is also the largest. When L/D is 1.5 and the flow velocity is 1.1 m/s, the maximum output voltage values of the upper and lower energy harvesting structures are 78.65 V and 83.05 V, respectively, and the corresponding output power is 6.19 mW and 6.90 mW. The above simulation results verify that the shear mode energy harvesting structure and its array can appropriately increase the open-circuit output voltage of the structure, which provides a new reference scheme for the study of underwater vortex-induced vibration piezoelectric energy harvesting structures.

1. Introduction

Underwater wireless sensor networks (UWSNs) are employed for data acquisition, disaster prevention, and navigation [1,2]. Given the challenge of battery replacement for nodes on the ocean floor, energy harvesting from vortex-induced vibrations using piezoelectric materials offers an effective solution for powering these sensors. Recent research has explored the conversion of vortex-induced vibration energy into electrical energy, including preliminary analyses and verifications of the underlying mechanisms and collection efficiency. Li et al. [3] proposed a new type of piezoelectric cantilever beam energy harvester based on vortex-induced vibration. The results verify that when the bluff body is a cylinder with a diameter of 0.02 m and a height of 0.05 m, and the ratio of the distance between the bluff body and the bluff body diameter is 2, the maximum voltage of the T-shaped piezoelectric cantilever energy harvester is 1.02 V. It provides a theoretical and experimental reference for energy collection in the wind. Kamenar et al. [4] discussed the solution of piezoelectric eels and hybrid turbines coupled with piezoelectric beams. The energy harvester is integrated into an autonomous wireless sensor node under real river conditions. After testing, the energy harvester successfully powered the entire sensor cluster. Abdelkefi [5] proposed a free resonant cylinder with piezoelectric patches on support rods aligned parallel or perpendicular to the tube’s axis. When water flows perpendicularly to the tube’s axis, vortex-induced vibrations cause transverse resonance, driving bending in the piezoelectric patches for energy conversion. Li et al. [6] developed a flexible circular tube energy harvester with an integrated piezoelectric beam, addressing sealing and corrosion issues. Laboratory tests of a 0.03 m diameter and 0.05 m height prototype yielded 1.46 mW power at 30.9 Hz and 1 MΩ resistance, with a water flow velocity of 1.1 m/s. Rong et al. [7] proposed a nested piezoelectric ring energy harvesting structure based on vortex-induced vibration. The result of the experimental test verifies that when the distance between the rigid bluff body and the energy harvesting structure is 0.07 m, the maximum voltage peak is 4.869 V. Jin et al. [8] proposed a piezoelectric energy harvester with a wavy cylinder with pits and hemispherical protrusions. Especially for the 5-column pit structure of 10 mm, the peak voltage can reach 47 V, the peak power can reach 1.21 mW, and the resistance is 800 kΩ, which is 0.57 mW higher than that of the wavy cylinder. Shi et al. [9] developed a hydrodynamic piezoelectric energy harvester inspired by fishtails, utilizing a forced separation topological vortex. The harvester with an elliptic cylinder (aspect ratio 2.5) achieved an output voltage of 38.4 V at 0.45 m/s water velocity, 21.5 times higher than a circular cylinder. Zhao et al. [10] proposed a system composed of an elastically supported wavy cylinder and a tuned mass damper (TMD) to improve energy harvesting efficiency. The results indicate that when the wavelength λz is greater than or equal to 3.6 times the diameter of the wave column (Dm), the performance of the corrugated column is better than that of the wavy cylinder, and reaches a peak at λz = 6.0 Dm and amplitude a = 0.25 Dm, which is increased by 70%. Shah [11] designed a series of cylindrical and piezoelectric thin films, systematically analyzed the influence of structural spacing on power generation performance, and found the optimal configuration. At a flow rate of 0.34 m/s and a spacing of 3 times the diameter of the cylinder, the power reaches 19.17 µW.

Current research on piezoelectric vibration energy harvesting predominantly utilizes d₃₃ and d₃₁ modes; however, d₁₅ mode has been shown to produce higher output power, A comparative analysis of the three primary piezoelectric modes, detailed in

Table 1. Comparison of piezoelectric modes.

Mode	Piezoelectric Constant (pC/N)	Deformation Mechanism	Energy Conversion Efficiency
d33	400–650	Thickness Extension/Compression	Moderate
d31	180–270	Transverse Bending/Compression	Lowest
d15	500–750	Shear	Highest

. For instance, Ren et al. [12] compared a PMN-PT cantilever harvester using shear mode (d₁₅) with one using thickness mode (d₃₁). Despite being only half the volume of the d₃₁ harvester, the d₁₅ device generates 8.3 times the output voltage and approximately 7 times the maximum output power. Malakooti [13,14] showed that d₁₅ mode provides better impedance-frequency response than d₃₁ mode for PZT piezoelectric cantilever beams, with significant variations in maximum output power across frequencies and impedances. Using Timoshenko beam theory, they developed a model indicating that shear mode harvesters generate about 50% more power than those in transverse modes. The exploration of d₁₅ mode with higher electrical constants and better suitability for underwater shear stress environment is still absent. In addition, existing designs mostly focus on unidirectional energy capture and fail to fully utilize the bidirectional vibration characteristics.

Based on this, this paper proposes a shear mode bidirectional piezoelectric energy harvesting structure based on underwater vortex-induced vibration and conducts numerical simulation to explore the vibration performance and piezoelectric characteristics of the energy harvesting structure under different conditions. The potential applications of this technology extend beyond powering static UWSN nodes. It could be deployed for long-term ocean monitoring tasks, such as providing power for sensors on autonomous underwater vehicles (AUVs), profiling floats, or mounting on underwater infrastructure for structural health monitoring, contributing to the development of self-powered systems in marine science and engineering.

2. Materials and Methods

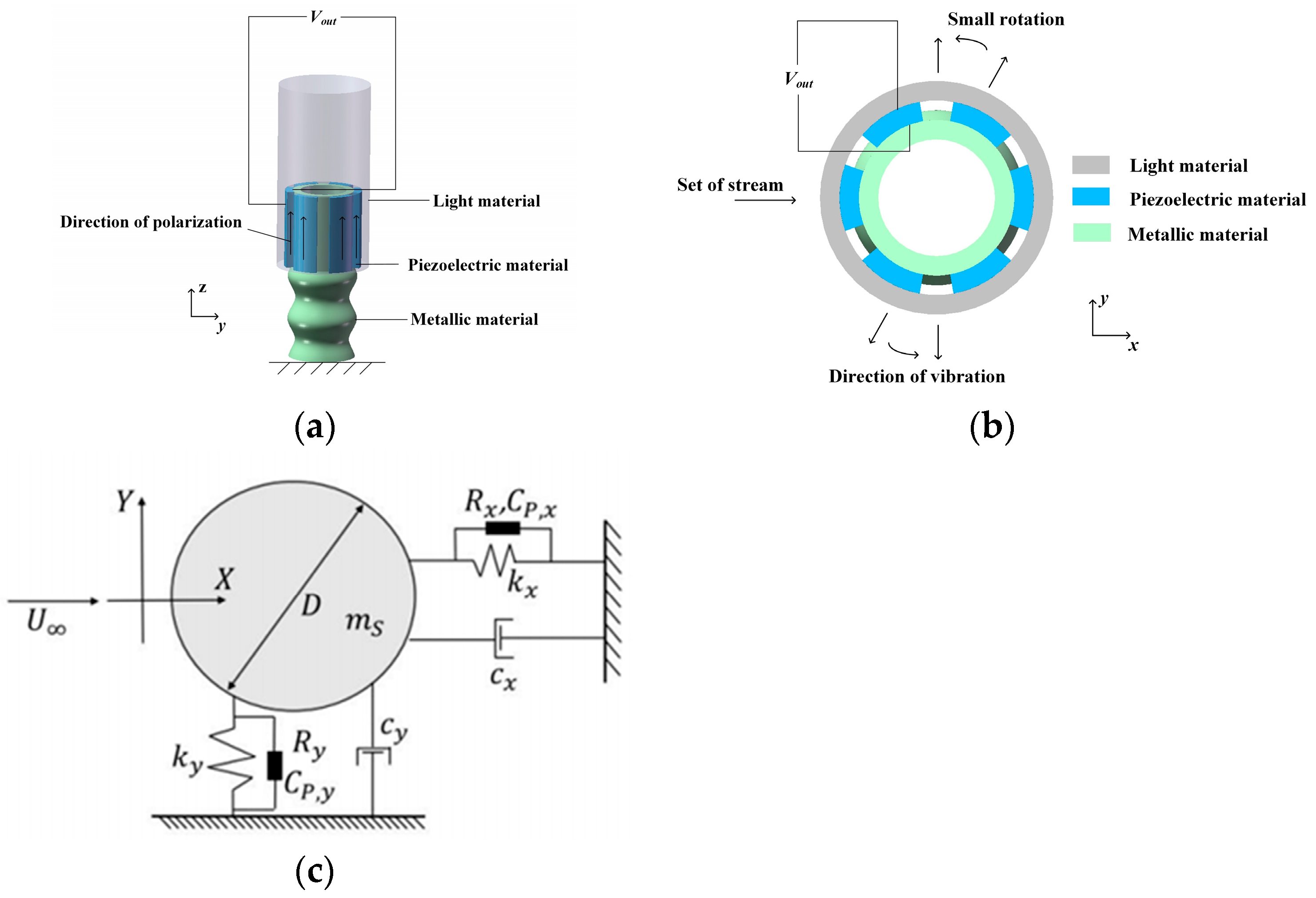
Figure 1a,b depict a bidirectional piezoelectric energy harvesting structure that operates in shear mode. This design harnesses vortex-induced vibrations of a tube to apply shear strain to a piezoelectric material, which is positioned between the tube and its support structure, thereby generating electrical charge. The high shear electromechanical coupling coefficient of the piezoelectric material facilitates efficient conversion of vibrational energy in both transverse and downstream directions into electrical energy, thereby improving energy conversion efficiency and expanding the operational bandwidth. Additionally, the piezoelectric material’s resilience to significant shear strain enhances its durability and extends its service life.

The bidirectional shear mode vortex-induced vibration piezoelectric energy harvester can be regarded as two independent piezoelectric energy harvesting systems in the transverse and downstream directions. The simplified electromechanical model is shown in Figure 1c. From the diagram, it can be seen that the flow direction is the x-axis direction; the tube is free vibration in the y direction; U_∞ is the flow velocity; D is the diameter of the tube; m_s is the mass of the tube; k_y and c_y are the elastic stiffness and equivalent damping in the transverse direction; k_x and c_x are the elastic stiffness and equivalent damping in the downstream direction; and R_x, R_y, C_p,x, C_p,y are the equivalent resistance and capacitance in two directions, respectively. Then, there is the following [15]:

$$(m_s+m_f){\displaystyle \frac{d^{2}X}{d{t}^2}}+c_x{\displaystyle \frac{dX}{dt}}+k_{x}X-{\theta }_x{V}_x={\displaystyle \frac{1}{2}}\rho U_{\infty }^{2}DL{C}_{x,v}$$

(1)

$${\displaystyle \frac{d^2{q}_x}{d{t}^2}}+{\in }_x{\omega }_f(q_x^2-1){\displaystyle \frac{d{q}_x}{dt}}+{(2{\omega }_f)}^2{q}_x={\displaystyle \frac{A_x}{D}}{\displaystyle \frac{d^{2}X}{d{t}^2}}$$

(2)

$$(m_s+m_f){\displaystyle \frac{d^{2}Y}{d{t}^2}}+c_y{\displaystyle \frac{dY}{dt}}+k_{y}Y-{\theta }_y{V}_y={\displaystyle \frac{1}{2}}\rho U_{\infty }^{2}DL{C}_{y,v}$$

(3)

$${\displaystyle \frac{d^2{q}_y}{d{t}^2}}+{\in }_y{\omega }_f(q_y^2-1){\displaystyle \frac{d{q}_y}{dt}}+{\omega }_f^2{q}_y={\displaystyle \frac{A_y}{D}}{\displaystyle \frac{d^{2}Y}{d{t}^2}}$$

(4)

$$C_{p,y}{\displaystyle \frac{d{V}_y}{dt}}+{\displaystyle \frac{V_y}{R_y}}+{\theta }_y{\displaystyle \frac{dY}{dt}}=0$$

(5)

$$C_{p,x}{\displaystyle \frac{d{V}_x}{dt}}+{\displaystyle \frac{V_x}{R_x}}+{\theta }_x{\displaystyle \frac{dX}{dt}}=0$$

(6)

Equations (1) and (3) are the linear oscillator equations for the vibration of an elastically supported tube in the x and y directions, respectively, where m_f denotes the potential added mass of the fluid; X and Y denote the displacement in x and y directions, respectively; t denotes the time; θ_x and θ_y denote the electromechanical coupling constant; ρ denotes the fluid density; L denotes the length of tube; V_x and V_y denote the electric tension; and C_x;v and C_y;v denote the force coefficient caused by the vortex shedding. Equations (2) and (4) are the wave characteristics of a vortex-induced vibration cylinder wake which satisfy the equation of van der Pol nonlinear oscillator, where ω_f is the vortex shedding frequency, ${\omega }_f=2\pi St{\displaystyle \frac{U_{\infty }}{D}}$, St is the Strouhal number; q_x, q_y represent wake variables; and ε_x, A_x, A_y, ε_y represent the parameters of the wake oscillator model. When the right side of (2) and (4) is 0, that is, the vibration frequency of the energy harvesting structure is equal to the vortex shedding frequency, the limit cycle periodic solution of the amplitude is obtained.

The working mechanism of different modes of the piezoelectric sheet [16]:

$$\epsilon ={\displaystyle \frac{D}{E}}$$

(7)

$$\left\{D\right\}=[d]\left\{T\right\}$$

(8)

$$Q=D\times S$$

(9)

$$F=T\times S$$

(10)

Equation (8) is the expression of the electromechanical relationship between piezoelectric materials. Under the condition of a certain external force, the electric displacement changes linearly with stress. Among them, {D} is the electric displacement tensor; [d] is the piezoelectric strain constant; and {T} is the stress tensor.

We use T, W, L to represent the length, width, and height of the piezoelectric material, respectively; then, the bottom area S = L × W. P represents the polarization direction, the field strength is E, and the voltage is V. Then, there is

$$E={\displaystyle \frac{V}{T}}$$

(11)

Combining the above equations, we can obtain

$$Q=F\times d$$

(12)

$$E={\displaystyle \frac{F\times d}{\epsilon \times L\times W}}$$

(13)

$$V=E\times T={\displaystyle \frac{F\times d\times T}{\epsilon \times L\times W}}$$

(14)

Again $\epsilon ={\epsilon }_r\times {\epsilon }_0$, $g={\displaystyle \frac{d}{{\epsilon }_r\times {\epsilon }_0}}$, there is

$$V={\displaystyle \frac{F\times g\times T}{L\times W}}$$

(15)

Among them, ε represents the dielectric constant, d represents the piezoelectric constant, and d is different under different vibration conditions. Commonly used modes include d₁₅, d₃₁, and d₃₃; the subscript next to the letter represents the polarization direction, and the second subscript represents the deformation direction. However, the piezoelectric constants of typical piezoelectric materials have the relationship d₁₅ > d₃₃ > d₃₁. It can be seen from Equation (15) that the output voltage of piezoelectric materials working in d₁₅ mode is higher than that of piezoelectric materials working in d₃₃ and d₃₁ modes.

According to Reference [17], there is an optimal load, which can maximize the output power of the energy harvesting structure, and the expression of the optimal load resistance is

$$R_{opt}=R_{\mathrm{x}}+R_y={\displaystyle \frac{1}{4{\omega }_{n,x}{C}_{p,x}}}+{\displaystyle \frac{1}{4{\omega }_{n,y}{C}_{p,y}}}$$

(16)

Among them, ${\omega }_{n,x}$ and ${\omega }_{n,y}$ represent the natural frequency. It can be seen from Equation (16) that the optimal load of the energy harvesting structure is only related to the natural frequency and internal capacitance of the structure itself. Therefore, after the natural frequency of the energy harvesting structure is determined, the optimal load resistance is also determined. The parameters in Table 1 are substituted into Equation (16), and the optimal load resistance is 1 MΩ. Therefore, the load resistance of 1 MΩ is connected in tandem in this experiment.

The total electric power equation is

$$P=P_{el,x}+P_{el,y}={\displaystyle \frac{V_x^2}{R_x}}+{\displaystyle \frac{V_y^2}{R_y}}$$

(17)

In order to simplify the calculation, the dimensionless parameters are defined:

$$U_{\mathrm{r}}={\displaystyle \frac{U_{\infty }}{f_{n,y}D}},f^{*}={\displaystyle \frac{{\omega }_{\mathrm{n},\mathrm{x}}}{{\omega }_{\mathrm{n},\mathrm{y}}}},{\theta }^{*}={\displaystyle \frac{{\theta }_x}{{\theta }_y}},m^{*}={\displaystyle \frac{m_s}{m_d}}{\sigma }_{1,x}={\displaystyle \frac{{\theta }_{\mathrm{x}}^2}{C_{p,x}(m_s+m_f){\omega }_{n,x}^2}},$$

$${\sigma }_{1,y}={\displaystyle \frac{{\theta }_y^2}{C_{p,y}(m_s+m_f){\omega }_{n,y}^2}},{\sigma }_{2,\mathrm{x}}={\displaystyle \frac{1}{C_{p,x}{R}_x{\omega }_{n,x}}},{\sigma }_{2,y}={\displaystyle \frac{1}{C_{p,y}{R}_y{\omega }_{n,y}}},$$

$$v_x={\displaystyle \frac{V_x}{V_0}},v_y={\displaystyle \frac{V_y}{V_0}}$$

The total energy harvesting efficiency is obtained as follows:

$$\eta ={\displaystyle \frac{4{\pi }^4}{U_r^3}}{\displaystyle \frac{{({\theta }^{*})}^2}{f^{*}}}(m^{*}+C_a)({\displaystyle \frac{{\sigma }_{2,x}}{{\sigma }_{1,x}}}{v}_x^2+{\displaystyle \frac{{\sigma }_{2,y}}{{\sigma }_{1,y}}}{v}_y^2)$$

(18)

where $U_r$ denotes the dimensionless fluid velocity, f_n,y = 0.62 Hz; m* indicates structural mass, where m_d represents the mass of fluid displaced by the cylinder; C_a denotes the additional mass of dimensionless fluid; and $v_x$ and $v_y$ represents the dimensionless electrical tension in two directions, respectively.

The coupled fluid–solid–piezoelectric simulation is governed by the following sets of equations:

Fluid Domain: The fluid flow is described by the incompressible Navier–Stokes equations, which govern the conservation of mass and momentum:

$$\nabla \cdot u=0$$

(19)

$${\displaystyle \frac{\partial u}{\partial t}}+(u\cdot \nabla )u=-{\displaystyle \frac{1}{\rho }}\nabla p+\nu {\nabla }^{2}u$$

(20)

where u is the fluid velocity vector, p is the pressure, ρ is the fluid density, and v is the kinematic viscosity.

Solid and Piezoelectric Domain: The piezoelectric material behavior is governed by the linear constitutive relations, which couple the mechanical and electrical fields:

$$\left\{T\right\}=[c^E]\left\{S\right\}-{[e]}^T\left\{E\right\}$$

(21)

$$\left\{D\right\}=[e]\left\{S\right\}+[{\epsilon }^S]\left\{E\right\}$$

(22)

where {T} and {S} are the stress and strain tensors, {D} and {E} are the electric displacement and electric field vectors, [c^E] is the elasticity matrix at constant electric field, [e] is the piezoelectric stress coefficient matrix, and [ε^S] is the dielectric permittivity matrix at constant strain.

3. Results and Discussion

According to the theoretical model of the shear mode bidirectional piezoelectric energy harvesting structure based on underwater vortex-induced vibration proposed in the previous section, the finite element analysis is used to simulate the fluid–solid coupling and piezoelectric coupling of the energy harvesting structure, respectively [18]. The vibration characteristics and output voltage are obtained, which proves the feasibility of the structure. A comparison of output voltage across three piezoelectric modes indicated that shear mode offers the highest power generation efficiency. On this basis, the optimal performance parameters are determined by changing the thickness of the piezoelectric sheet, the shape of the support, the flow velocity, the shape of the bluff body and L/D. In addition, by observing the changes in the flow field and the output voltage, the performance of the dual energy harvesting structure with tandem-parallel configuration in the fluid domain is analyzed.

Finite element simulation of the model based on ANSYS, mesh strategy: The fluid domain adopts a 5 mm tetrahedral mesh; In the solid domain, the piezoelectric sheet adopts a 1 mm regular hexahedral mesh, while the rest adopts a 2 mm regular tetrahedral mesh.

Boundary conditions: Select ‘Velocity Inlet’ as the inlet of the fluid domain, set the velocity as needed, and select ‘Pressure Outlet’ as the outlet and set it to 0; the boundary of the solid domain adopts fixed constraints; set one side of the piezoelectric material to zero voltage and the other side to the terminal.

3.1. Performance of Single Energy Harvester

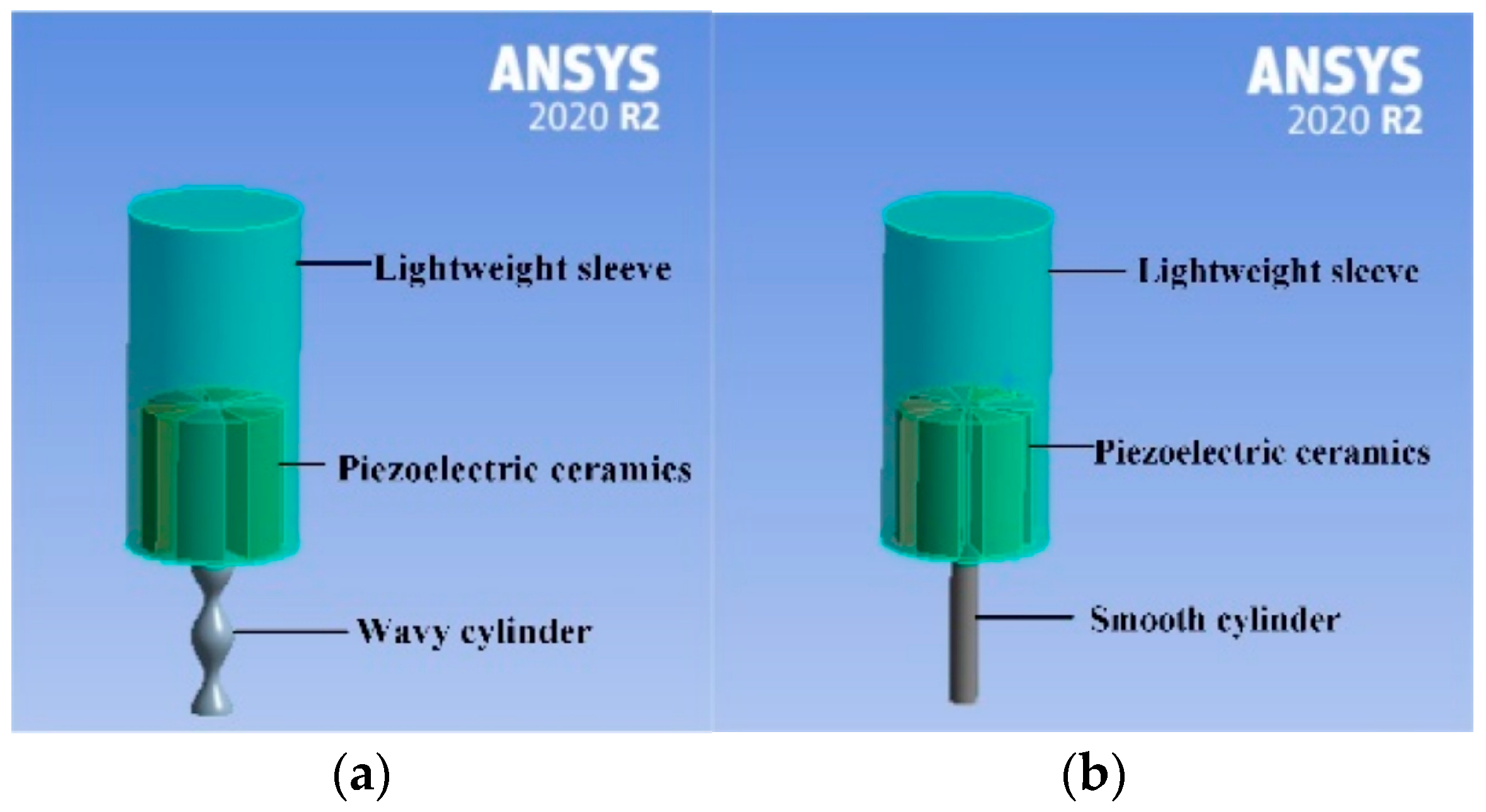
The numerical simulation analysis of single energy harvesting structure is completed. The three-dimensional geometric model is shown in Figure 2a. The specific parameters of the energy harvesting structure are shown in

Table 2. Specific parameter table of energy harvesting structure.

Name	Parameter	Value
Lightweight sleeve	Young’s modulus (E)	7 × 107 Pa
	Poisson’s ratio (ν)	0.3
	Outer diameter (D)	30 mm
Piezoelectric ceramics	Young’s modulus (E)	6 × 1011 N/m2
	Poisson’s ratio (ν)	0.36
	Density	7600 kg/m3
	Piezoelectric constant d31	−1.85 × 10−10 C/N
	Piezoelectric constant d33	4 × 10−10 C/N
	Piezoelectric constant d15	6.4 × 10−10 C/N
	Dielectric constant	1700
	Thickness	10 mm
Supports	Poisson’s ratio (ν)	0.34
	Young’s modulus (E)	1.1 × 1011 Pa
	Density	8300 kg/m3
	Diameter	5 mm
Bluff body	Young’s modulus (E)	1.93 × 1011 Pa
	Poisson’s ratio (ν)	0.31
	Density	7750 kg/m3

.

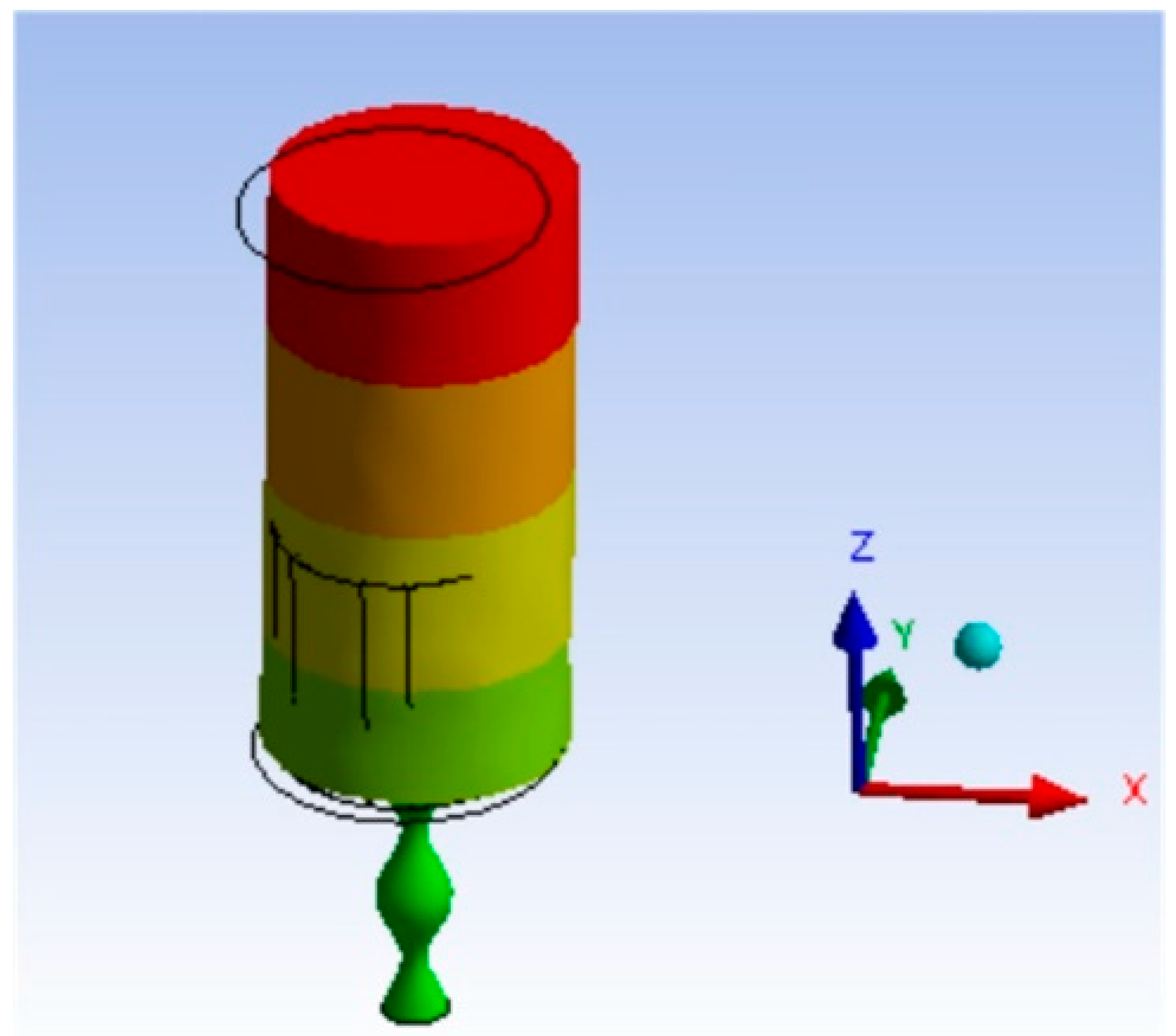
The trajectory of the piezoelectric energy harvesting structure in the fluid domain is shown in Figure 3. The black contour represents the original position of the energy harvesting structure. Compared with the current position, it is found that the energy harvesting structure is subjected to both the drag force in the downstream direction and the vortex lift force in the transverse direction. Vibration is generated in two directions, and its vibration form is reciprocating vibration in the transverse direction, accompanied by a small rotation in the downstream direction.

3.1.1. The Influence of Piezoelectric Mode on the Energy Harvesting Structure

Figure 4 shows the variation curves of the output voltage of the three piezoelectric modes with flow velocity. It can be seen from the diagram that the output voltage under different piezoelectric modes increases with the increase in the flow velocity. When the velocity is the same, the voltage of d₁₅ is the largest, followed by d₃₃, and the worst is the d₃₁. When the velocity is 1.1 m/s and the piezoelectric mode is in shear mode (d₁₅), the voltage generated by the energy harvesting structure is the largest, and the voltage amplitude is 34.88 V.

3.1.2. The Influence of the Thickness of the Piezoelectric Sheet and the Support Shape

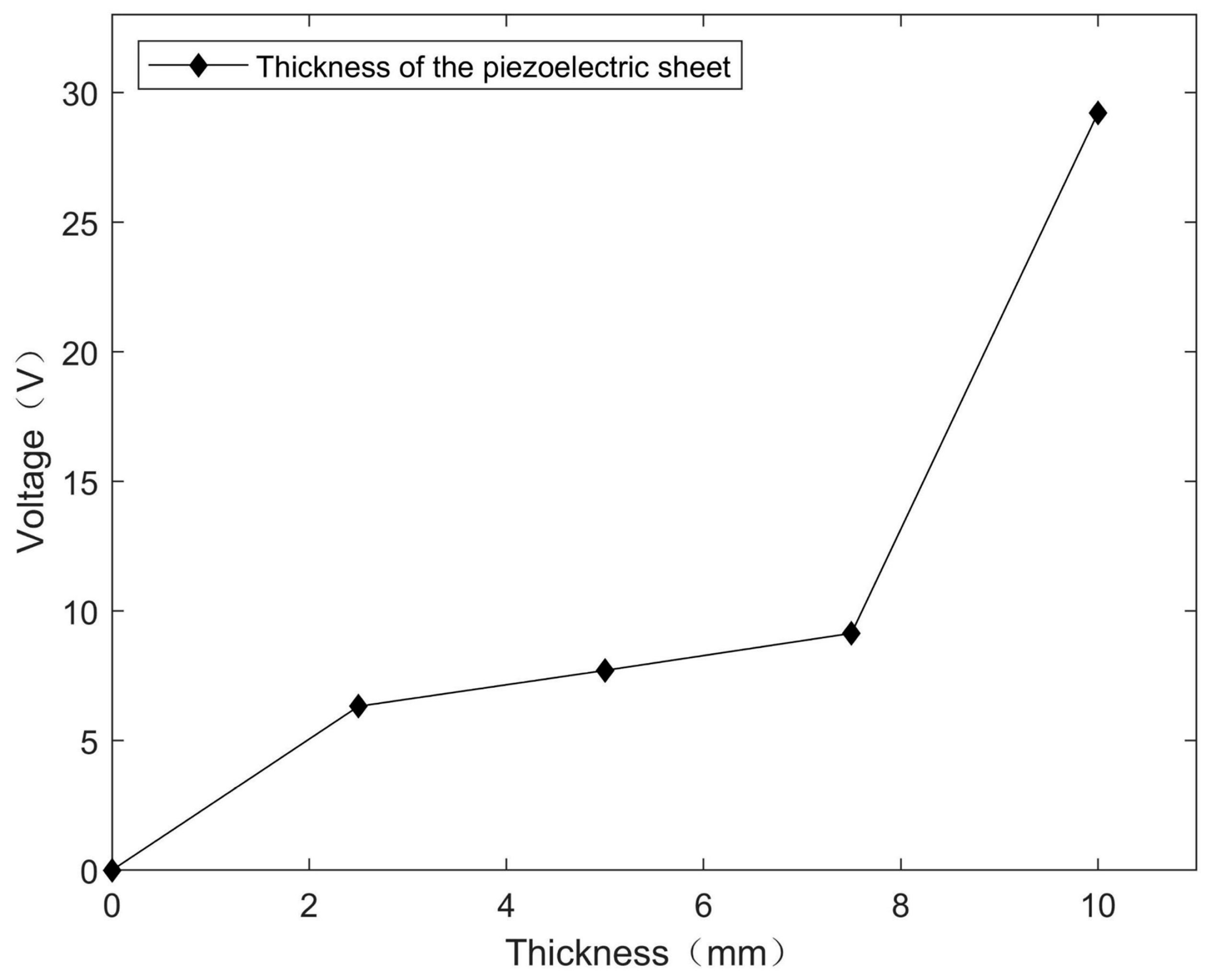
Figure 5 is the voltage change curve with the thickness of the piezoelectric sheet when the velocity is 1 m/s and the piezoelectric sheet working on the shear mode. From the diagram, it can be seen that the output voltage of the energy harvesting structure increases with the increase in the thickness of the piezoelectric sheet, reaching 29.21 V at 0.01 m.

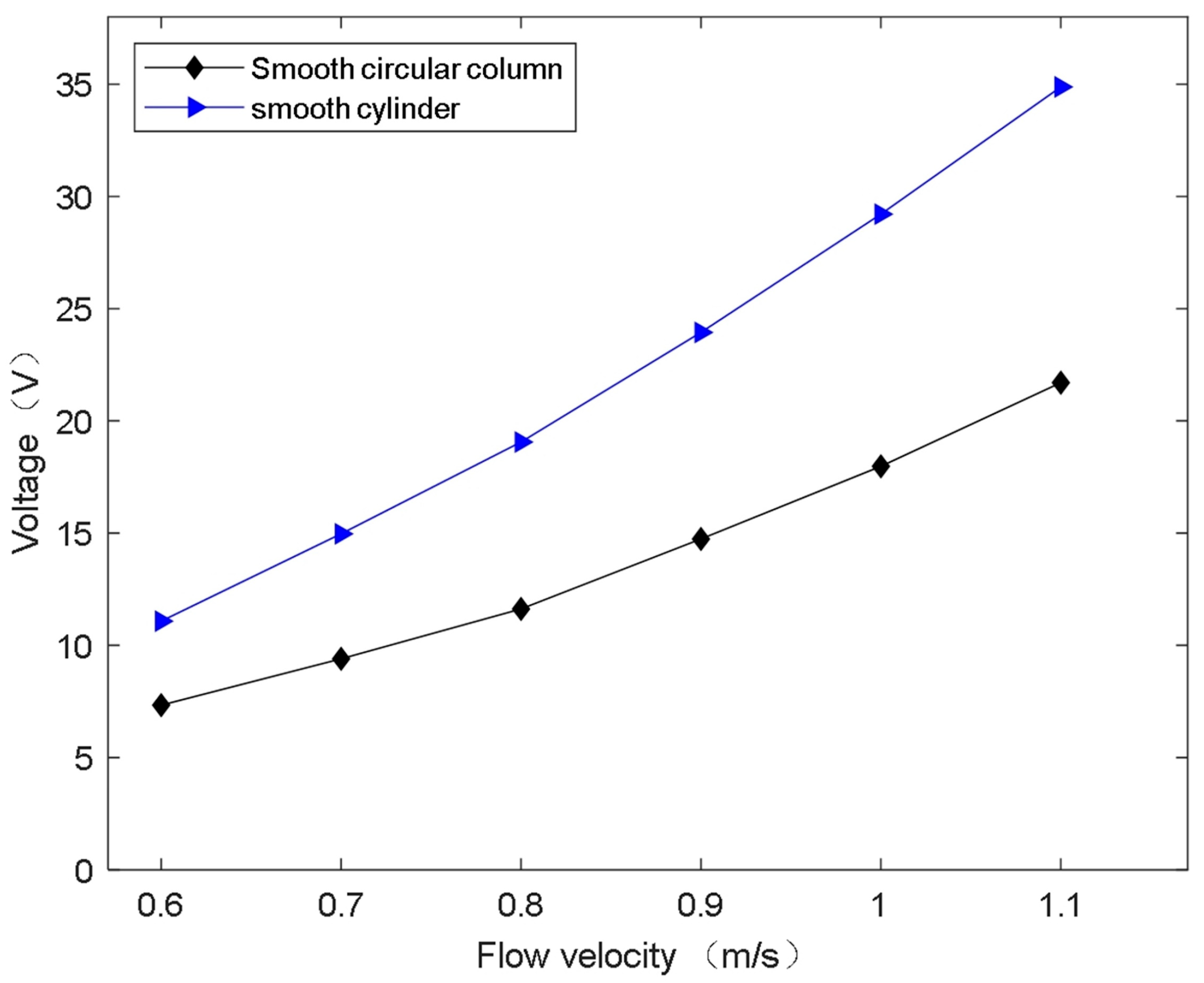
Figure 6 shows the voltage response of different supports as flow velocity varies. Using a piezoelectric sheet with a thickness of 0.01 m, the supports are either smooth or wavy cylinders, and the flow velocity ranges from 0.6 to 1.1 m/s. The results indicate that voltage increases with flow velocity, and for the same velocity, the wavy cylinder support generates higher voltage than the smooth cylinder support.

3.1.3. The Influence of Bluff Body and L/D Ratio

L is the distance between the bluff body and the center of energy harvesting structure, and the L/D is set to 2. The three-dimensional geometric model is shown in Figure 7a. The amplitude response variation law obtained by numerical simulation is shown in Figure 7b.

It can be seen from Figure 7b. The structural amplitude increases with the increase in the velocity. At low velocities, a long low-speed zone forms behind the bluff body, resulting in low energy density and minimal input energy, with most energy used for damping, thus small amplitude. As velocity increases, energy density rises, and the input energy surpasses damping losses, leading to larger amplitude vibrations.

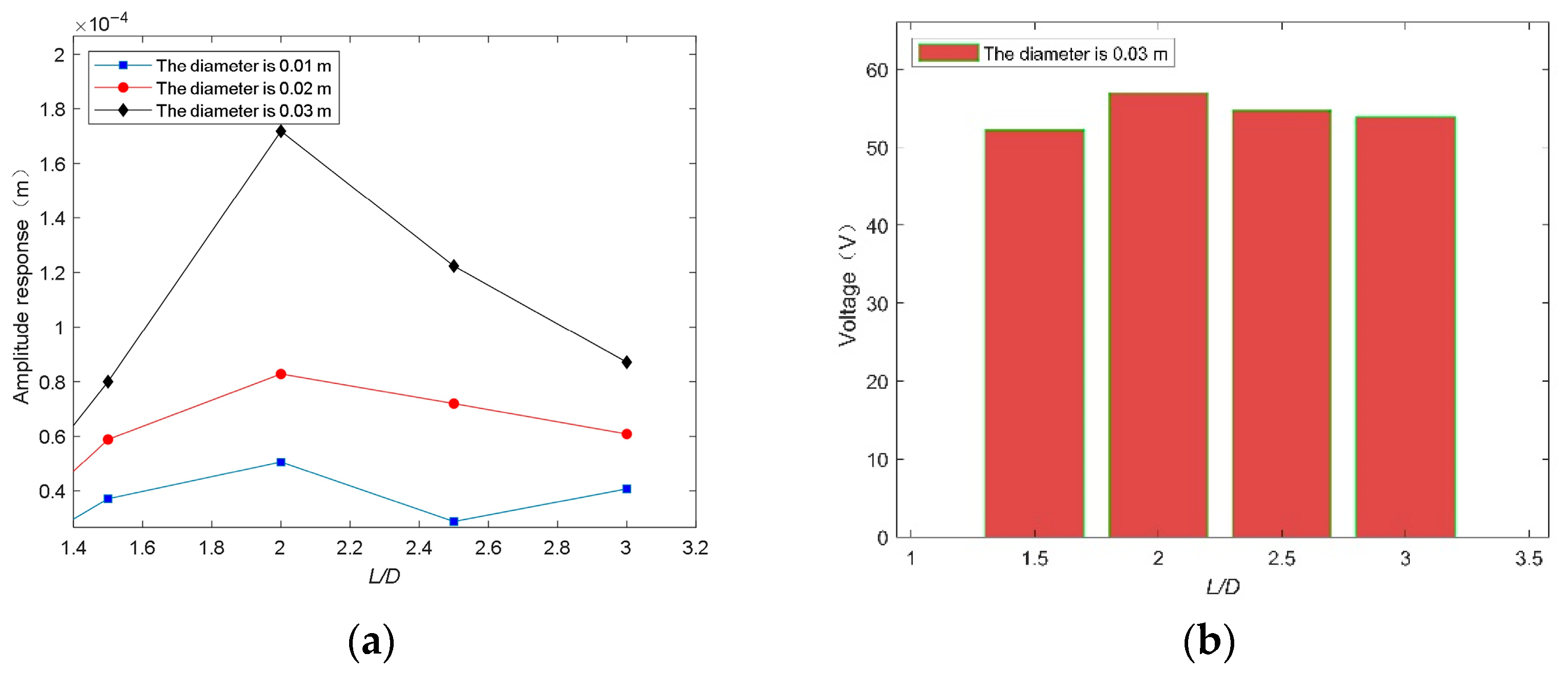
When the flow velocity is the same, the amplitude of the energy harvesting structure supported by wavy cylinder is larger than that by smooth cylinder. This is because when the bluff body is a wavy cylinder, hairpin vortices are formed on both sides of the wavy cylinder. Under the action of the hairpin vortex, a wider wake can be formed, and a larger force is generated on the energy harvesting structure, which increases the relative displacement between the two tubes, drives the piezoelectric sheets sandwiched in the middle to vibrate, and further produces a larger output voltage. When the flow velocity is 1.1 m/s and the bluff body is a wavy cylinder, the maximum amplitude generated by the energy harvesting structure is 1.72 × 10⁻⁴ m.

Figure 7c shows that the voltage of the structure behind different-shaped bluff bodies increases with flow velocity. When the bluff body is a wavy cylinder, the voltage is greater than that of the smooth cylinder. At a flow velocity of 1.1 m/s and the bluff body is a wavy cylinder, the voltage generated by the energy harvesting structure is the largest, the voltage amplitude is 56.97 V, corresponding to an output power of 3.25 mW according to Equation (17).

In the next part, the flow velocity is selected to be 1.1 m/s, and the diameters of the bluff body are changed to 0.01, 0.02, 0.03 m, respectively. The L/D is from 1.5 to 3, and the increment is 0.5. The influence of the three groups of bluff body on the amplitude is compared by simulation. The amplitude response and voltage of the energy harvesting structure is shown in Figure 8.

It can be seen from Figure 8a that when L/D is 2 and the diameter of the bluff body is 0.03 m, the maximum displacement amplitude of the energy harvesting structure is 1.72 × 10⁻⁴ m. Figure 8b is the voltage amplitude curve obtained by piezoelectric coupling simulation. It can be seen that the voltage response curve has similar changes corresponding with the displacement. The L/D has a certain influence on the performance of the piezoelectric energy harvesting device. Therefore, choosing a reasonable L/D will be more conducive to improving the output voltage of the energy harvesting structure.

3.1.4. Resonance Frequency Analysis

The energy harvesting efficiency is significantly enhanced when the vortex shedding frequency synchronizes with the natural frequency of the harvester structure. The vortex shedding frequency f_v can be estimated by the Strouhal number St:

$$f_v={\displaystyle \frac{St\cdot U}{D}}$$

(23)

where U is the flow velocity and D is the characteristic diameter of the bluff body. For the wavy cylinder bluff body with D = 30 mm at U = 1.1 m/s, and assuming S_t = 0.2, f_v = 7.33 Hz.

The natural frequency of the proposed harvester structure, obtained from modal analysis, was found to be f_n = 7.5 Hz. The close proximity between f_v and f_n explains the peak performance observed in our simulations. This frequency matching is crucial for maximizing the power generation of piezoelectric energy harvesters.

3.2. Performance of Dual Energy Harvester Array Configurations

3.2.1. Tandem Energy Harvesting Structure

Two energy harvesting structures with the same parameters are placed in tandem in the flow field. Under the action of fluid, the two energy harvesting structures generate vibration and output voltage, respectively. The energy harvesting structure near the inlet of the flow field is called the upstream structure, and the other is called the downstream structure. Taking the L/D as 2, the flow velocity is changed to 0.6–1.1 m/s, and the amplitude and voltage changes in the two energy harvesting structures are analyzed.

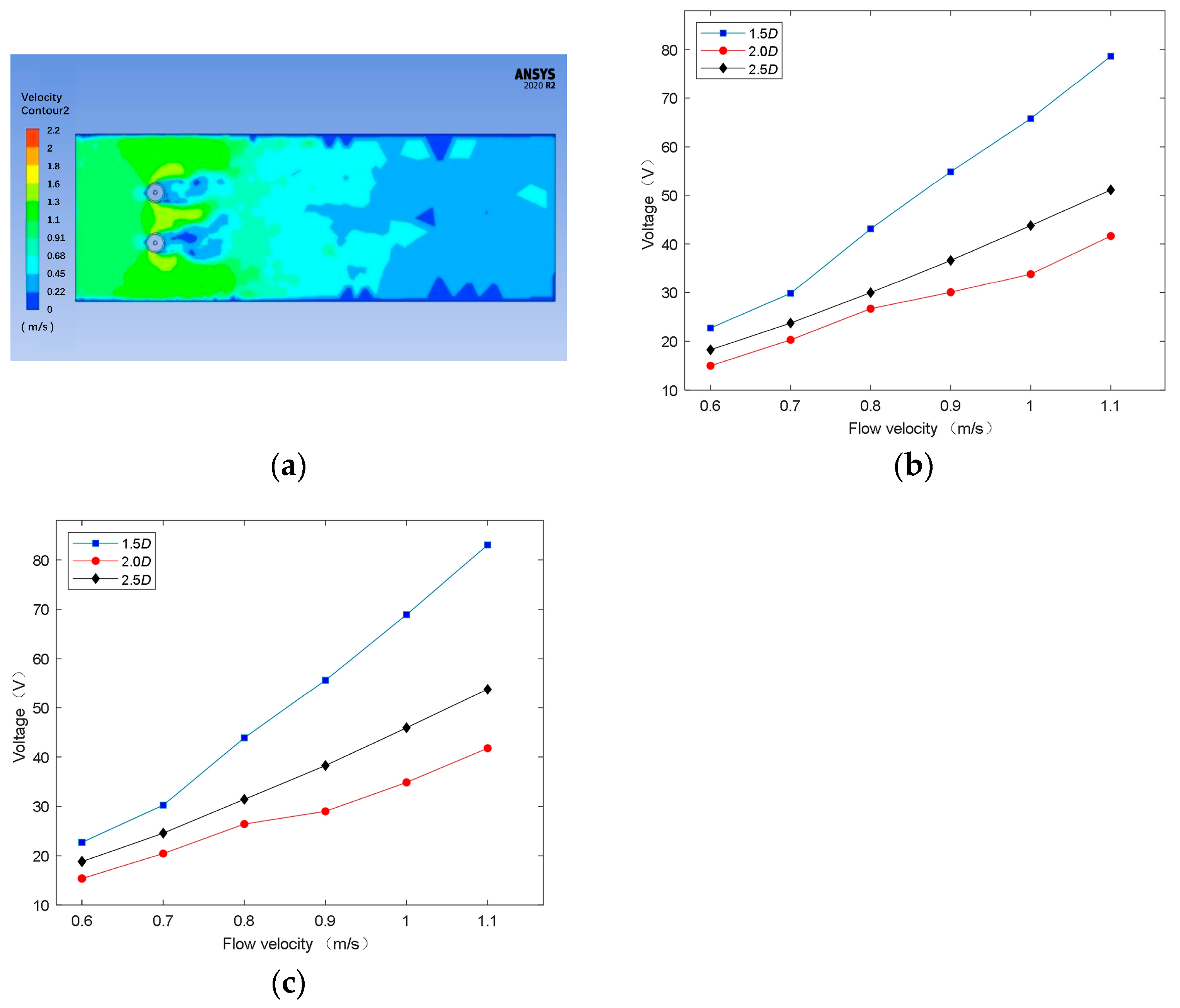
Figure 9a shows the velocity distributions of the fluid domain when the inlet velocity is 1.1 m/s and the L/D is 2. At this time, the vortex shedding from the upstream energy harvesting structure acts on the downstream structure, affecting its force and vibration amplitude.

Figure 9b,c are the vibration displacement of the upstream and downstream energy harvesting structure, respectively. The downstream structure is simultaneously subjected to the coupling effect between itself and the fluid, and the vortex shedding generated by the upstream structure. The superposition of the two vibration forms leads to the continuous change in its force, and the amplitude is much larger than the amplitude generated by the upstream energy harvesting structure.

From Figure 9d, it can be seen that the voltage generated by the downstream structure is greater than that generated by the upstream structure too. At 1.1 m/s of the velocity, the maximum output voltage of the upstream and downstream are 36.62 V and 48.95 V, respectively. According to Equation (17), the corresponding output power values are 1.34 mW and 2.40 mW, respectively.

From the comparison of Figure 8b and Figure 9d, it can be seen that the upstream and downstream energy harvesters of the double-structure tandem can convert the mechanical energy of the water flow into electrical energy, and then more electrical energy can be obtained.

3.2.2. The Parallel Energy Harvesting Structures

Two energy harvesting structures identical to the previous section are placed in parallel in the fluid domain. The energy harvester is called the upper energy harvesting structure in the top-down order, and the latter is the lower energy harvesting structure. The spacing between the upper and lower structures is adjusted to make L/D to be 1.5, 2, 2.5, respectively, and the amplitude response and power of the two energy harvesting structures are studied in the range of fluid velocity of 0.6–1.1 m/s.

Figure 10a shows the velocity distributions of the double parallel energy harvesting structure with a flow velocity of 1.1 m/s and L/D of 2.5. From the diagram, it can be seen that the vortexes behind the two energy harvesting structures move independently of each other.

From Figure 10b,c, it can be seen that the voltage generated by the upper and lower of the double parallel energy harvesting structure increases with the increase in L/D value. When L/D is 1.5 and the velocity is 1.1 m/s, the output voltage of the upper and lower structure reaches the peak values of 78.65 V and 83.05 V, respectively. According to Equation (17), the output power values are 6.19 mW and 6.90 mW, respectively. This is because when the distance between the two energy harvesting structures is small, the area of the fluid domain is small, resulting in an increase in the pressure difference, which in turn increases the vortex-induced force, accelerates the vibration of the two energy harvesting structures, and generates large amplitude and voltage. The simulations verify that the change in the L/D has a certain influence on the performance of the piezoelectric energy harvester. Therefore, choosing a reasonable L/D will be more conducive to improving the output voltage of the energy harvesting structure.

Table 3. Comparison of key performance metrics for different energy harvester configurations.

Structure	L/D	Max Power (mW)	Power Density (mW/cm3)
Single Harvester	2.0	3.25	1.35
Tandem (Upstream)	2.0	1.34	0.56
Tandem (Downstream)	2.0	2.40	1.00
Parallel (Upper)	1.5	6.19	2.58
Parallel (Lower)	1.5	6.90	2.86

provides the power density of various energy harvesting structures at a flow velocity of 1.1 m/s. The area of each piezoelectric sheet is 0.6 cm³, and the energy harvesting structure uses six piezoelectric sheets with a total volume of 2.4 cm³.

4. Experiments

To further validate the performance of the piezoelectric energy harvesting structure, this chapter will described the test that were conducted within a water circulation system. Firstly, the piezoelectric energy harvester was fabricated according to the simulation conditions, and the experimental platform is set up. Subsequently, experimental tests were carried out on a harvester with an upstream bluff body, and dual harvesters in both tandem and parallel configurations. The influence of parameters such as flow velocity, bluff body shape and size, and spacing ratio on the piezoelectric performance was investigated to determine the conditions for optimal power generation performance, thereby further exploring the feasibility of using the piezoelectric energy harvesting structure to power low-energy consumption electronic devices.

4.1. Design and Setup of the Experimental System

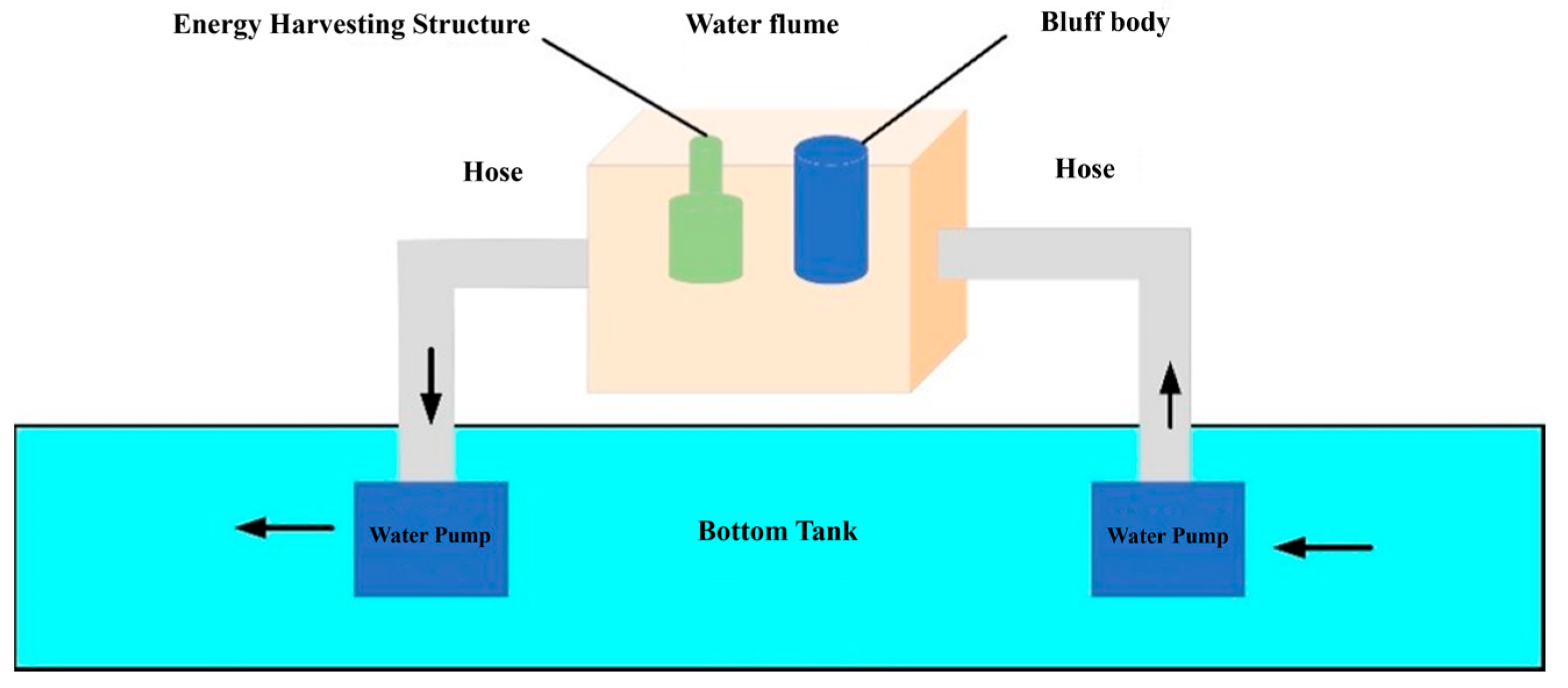
To test the energy harvesting structure in water flow, a water circulation experimental system was designed, as shown in Figure 11. This system mainly consists of a bottom water tank, an experimental water channel, a submersible pump, a digital oscilloscope, and a computer, forming a closed-loop water circulation experimental platform.

Based on the design requirements of the experimental platform, the water circulation experimental platform was set up. The specific experimental devices are shown in Figure 12.

4.2. Experiment of Single Energy Harvester

To further analyze factors affecting the power generation performance of the piezoelectric energy harvester, a bluff body was placed upstream of the harvester. Based on the numerical simulation conclusion that the optimal spacing between the harvester and the upstream bluff body is 2D, the bluff body was positioned accordingly.

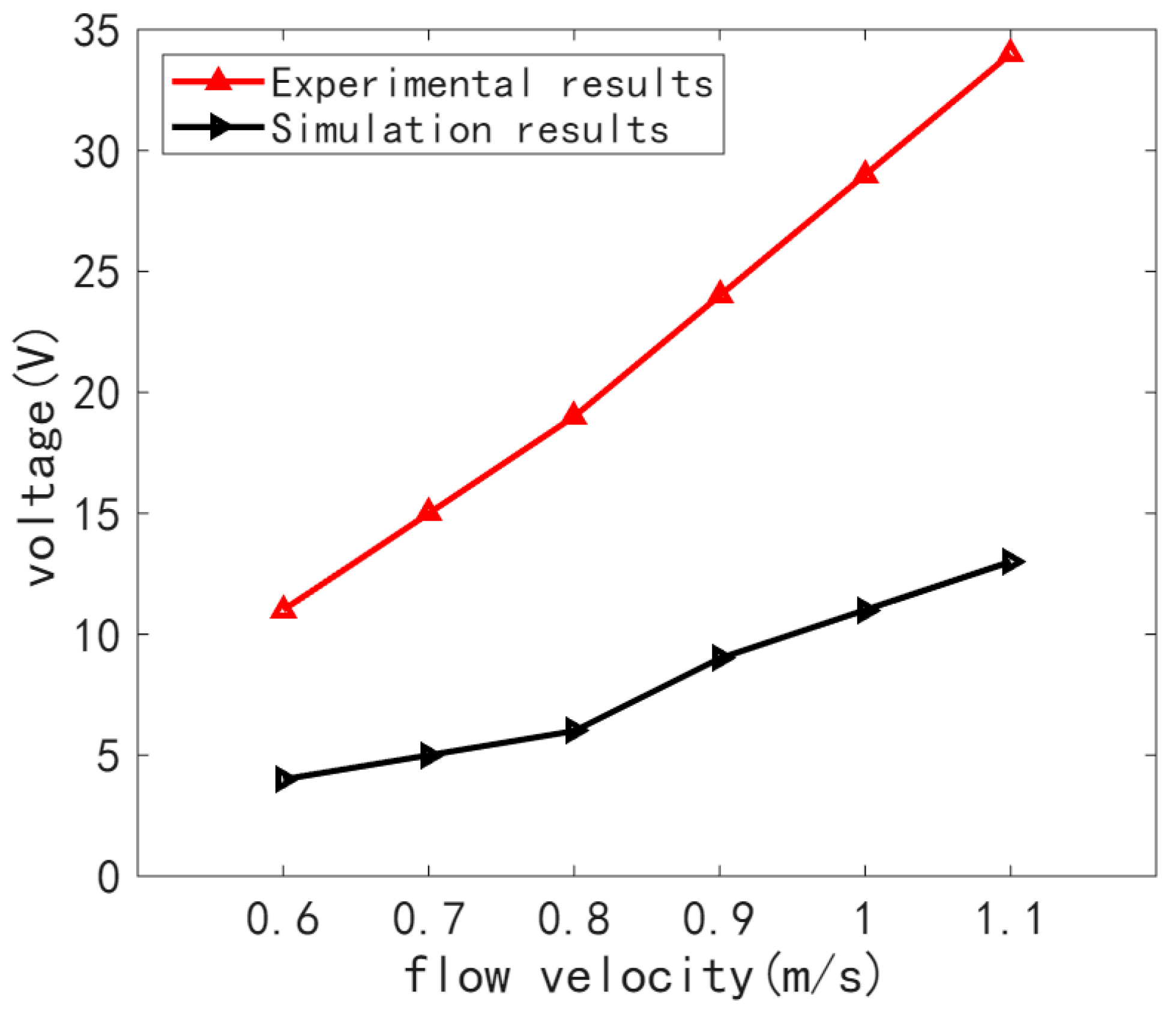
In the experiment, the flow velocity range was set from 0.6 m/s to 1.1 m/s, with an increment of 0.1 m/s. The output voltage of the harvester in series with the bluff body was systematically measured under these six different flow velocities. Based on this data, the curve shown in Figure 13 was plotted and compared with the simulation results.

Figure 13 shows the voltage variation trend of the energy harvester with an upstream bluff body at different flow velocities. It can be observed that as the flow velocity increases, the output voltage of the single harvester with an upstream bluff body shows a growing trend, consistent with the simulation results, reaching a maximum value of 12.4 V at 1.1 m/s. This is because the influence of the upstream bluff body on the harvester gradually strengthens with increasing flow velocity. The vortex shedding state of the fluid causes deformation of the piezoelectric material in the harvester, thereby generating voltage.

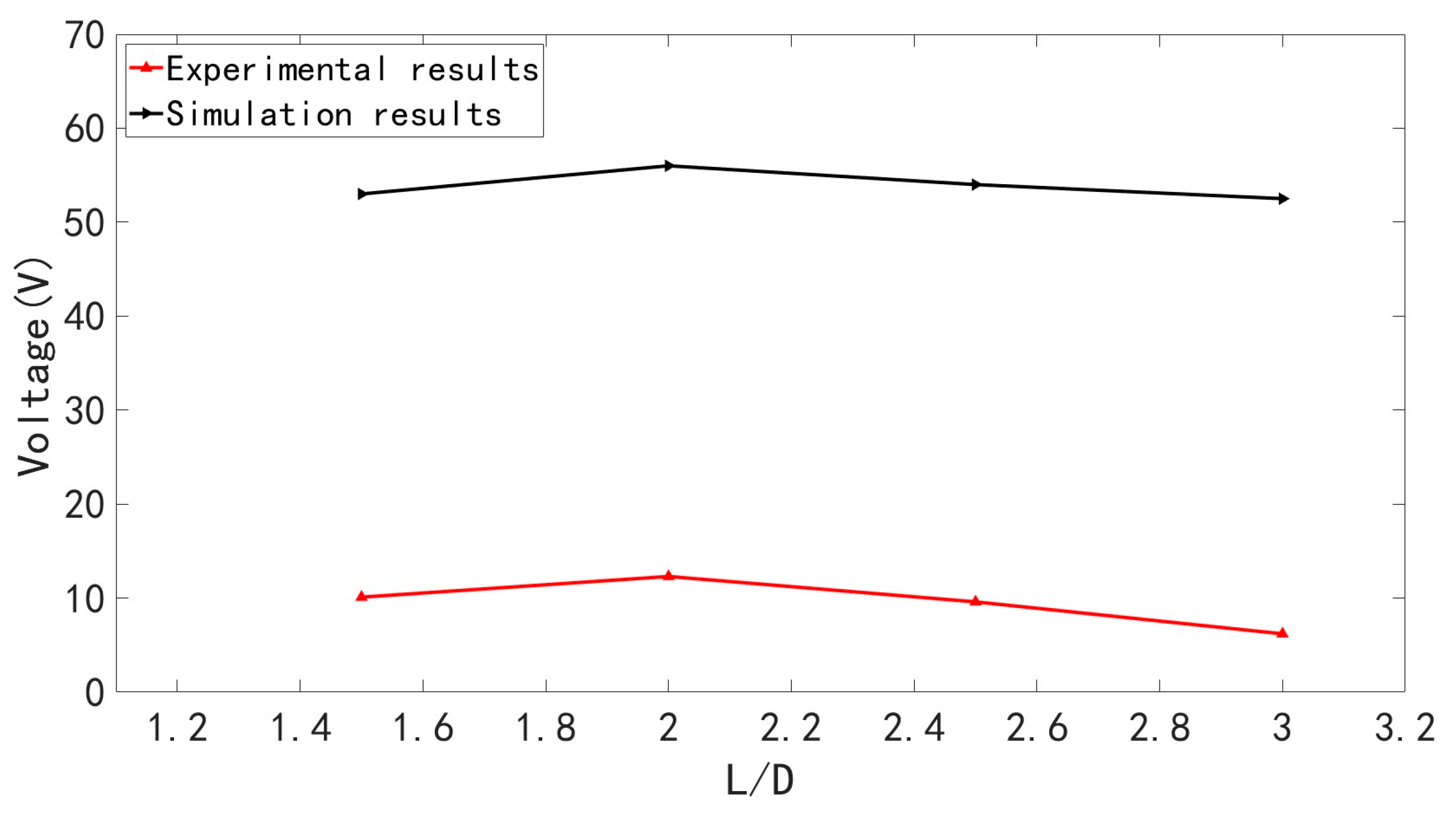
To investigate the influence of the spacing ratio L/D on the power generation performance when using a wavy cylinder as the bluff body. Based on the simulation conclusion that the wavy cylinder is one of the most effective bluff body shapes under known conditions, experiments were continued to validate and refine this conclusion.

In the experiment, the key parameters of the piezoelectric energy harvester remained unchanged to ensure the comparability of results under identical conditions. Specifically, the wavy cylindrical bluff body and the piezoelectric energy harvester were arranged in a tandem configuration at a flow velocity of 1.1 m/s. The L/D ratio was then gradually adjusted from 1.5 to 3, increasing by 0.5 each time, to observe the voltage output of the harvester under different settings. The results are shown in Figure 14.

The output voltage of the harvester initially increases and then decreases with increasing L/D, a phenomenon consistent with the numerical simulation results. When L/D < 1.5, the distance between the bluff body and the harvester is small, causing them to be perceived as a single entity, resulting in the formation of only one vortex street, and consequently, a relatively low output voltage under this condition. As the L/D value increases from 1.5 to 2.5, vortices appearing in-phase and anti-phase alternately emerge on both sides of the bluff body, known as the “coupled vortex street” state, which can generate a higher output voltage.

4.3. Experiment of Dual Energy Harvester Array Configurations

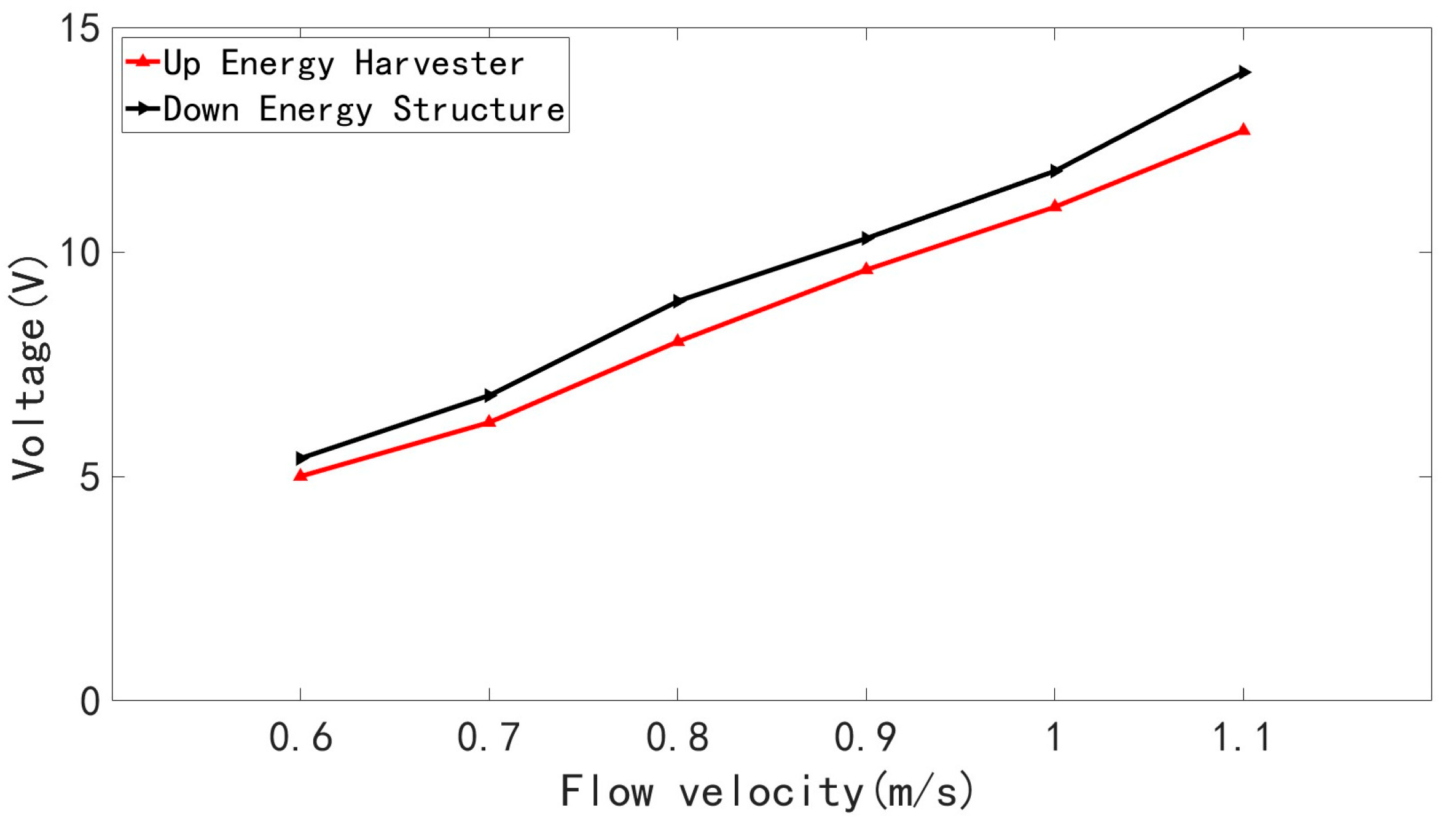
To further investigate the power generation performance of piezoelectric energy harvesters in a tandem configuration, two harvesters with identical parameters were placed sequentially in the experimental water channel for testing. The flow velocity was maintained constant at 1.1 m/s throughout the experiment. The results are shown in Figure 15.

Comparative analysis clearly verifies that under the same conditions, the output voltage variation trend of the tandem dual-harvester structure is consistent with the numerical simulation results. For the same type of harvester, the voltage generated by the downstream harvester is significantly higher than that generated by the upstream harvester.

Two piezoelectric energy harvesters with identical parameters were arranged in parallel in the experimental water channel. Based on the optimal configuration scheme determined from prior simulation results, L/D was set to 1.5. The flow velocity range was adjusted from 0.6 m/s to 1.1 m/s to investigate the output voltage of each harvester under different flow velocity conditions. The results are shown in Figure 16.

The results verify that the voltage values of both the upper and lower energy harvesters have a steady upward trend with the increase in water flow velocity. At a flow velocity of 1.1 m/s, the output voltage of the two energy harvesting structures reaches its maximum value, as shown in the numerical simulation results.

5. Conclusions

In this paper, a ‘fluid–solid–electric’ coupling mathematical model of a shear mode bidirectional piezoelectric energy harvesting structure based on underwater vortex-induced vibration was established. The numerical simulation was carried out. The change in the vibration displacement and the output voltage of the piezoelectric energy harvesting structure with the piezoelectric mode, thickness, flow velocity, bluff body and L/D was analyzed.

The results verify that under the same experimental conditions, the parallel array energy harvesting structure has the best power generation performance. When the flow velocity is 1.1 m/s and L/D = 1.5, the output voltage of the lower end energy harvesting structure is 83.05 V, and the average power is 6.90 mW after the load resistance of 1 MΩ is connected in tandem. In theory, it can meet the power supply requirements of simple chips with collection and forwarding functions. In order to further determine the practicability of the piezoelectric energy harvesting structure, the next step will be to test it experimentally, and then design and build a water cycle experimental system to verify the simulation results.