A Pipelined FPGA-Based Frame Synchronizer for Gaussian Noise Channels

Abstract

This paper presents a Field Programmable Gate Array (FPGA)-implementable Frame Synchronizer that overcomes deficiencies of existing synchronizers in the space communications industry and provides a pipelined approach to achieve improved performance in latency, performance in the presence of noise, and streamlined implementation complexity. Unlike a soft decision synchronizer, magnitude (soft) bits are not required from the demodulation stage, and only the sign bit is used, reducing the complexity and signal counts between the transceiver and the synchronizer. Improved performance in noise can be achieved by introducing a small observation window surrounding the candidate Attached Sync Marker (ASM) window to uncorrelated data around the ASM. Further improvement in the presence of noise is achieved by using two ASMs, effectively doubling the ASM length of observation, but with no increase in the ASM pattern length and using existing predefined ASM patterns, thus remaining compliant with the Consultative Committee for Space Data Systems (CCSDS) standards. A parallel and pipelined implementation without a state machine eliminates latency from search, verify, lock, and flywheel states and reduces the effects of cycle slips of traditional flywheel state machine synchronizers.

1. Introduction

The problems of transmitting digital information on space Radio Frequency (RF) channels have existed for decades. Recently, in the past five to ten years, with the advent of the emerging commercial space industry, for-profit companies now operate with extremely limited funding and drive opportunities to innovate for more efficient and cost-effective methods. Examples of these relatively new commercial endeavors include the commercial Starlink satellite constellations to address Internet availability in rural areas. Others include the recent Commercial Lunar Payload Services (CLPS) programs, such as the Nova-C project to land commercial payloads on the moon. Error correction and frame synchronization in communications links remain formidably challenging in the design of reliable and optimized communications for such systems to perform in noisy RF environments. Many of these commercial systems are restricted in available design resources. A further example is space projects in the nano-satellite industry, with low budget allocations [1]. However, the harsh space environments still exist for these systems as they have for historically government-funded programs, and therefore, they must also be mitigated by these newer commercial space industries.

Error correction methods, such as block Forward Error Correction (FEC) codes combined with a Frame Synchronizer (FS), remain part of system designs in these newer commercial space applications in order to mitigate communication errors and increase reliability. Historically, FEC codes have included Convolutional/Viterbi, Reed–Solomon (RS), and Turbo codes [2]. These error correction methods remain part of the palette available to the communications system designer, each with its own pros and cons [3]. In more recent years, Concatenated RS-Viterbi and Low-Density Parity Check (LDPC) have emerged as some of the higher performing FEC codes for RF communications, with LDPC approaching the Shannon channel capacity limit for error correction [4,5]. These more modern codes are block codes which require Frame Synchronizers to signal the start of downstream FEC processing and must also match, or surpass, the FEC performance levels in the presence of Additive White Gaussian Noise (AWGN).

A new commercial space industry has emerged to address the cost and schedule risk of space travel. Other industries are poised to benefit from improvements in RF communication innovation. Examples include distributed industrial settings, where facilities are located at long distances from each other. A distributed test facilities network may require real-time deterministic timing to synchronize interfaces among the various locations. Historically, Internet Protocol (IP) has been utilized for long-distant communications. However, IP introduces non-deterministic timing, as IP packetizing introduces variable latencies [6]. A long-distance data-distributed system requiring real-time deterministic timing can benefit from using RF channels with FEC error correction, via satellite hops, to minimize non-determinism latency. Examples include aircraft avionics testing, which may use a Distributed Systems Integration Laboratory (DSIL) architecture, to replace or augment a traditional centralized testing facility. Similar to spacecraft avionics, modern aircraft systems use multiple avionics vendors located at different locations around the nation. Each vendor traditionally uses their own local testing facility for their portion of avionics validation and verification. Integrating satellite hops with FEC error correction and synchronization can be utilized to create an early-phase distributed testing system among multiple vendors, early in the testing phases of the program. A high-reliable real-time communications testing architecture would benefit by using advanced FEC error correction and the frame synchronization method to provide distributed real-time integration testing.

Modern block FEC codes utilize Frame Synchronizers as part of the error correction process and have largely used flywheel state machines or simple-threshold detection in implementation. These traditional methods incur limitations in performance such as latencies during frame sync loss that cause otherwise correctable frames to be “thrown away” by not allowing downstream error correction to attempt the correction of bit errors during the re-acquire states. Further limitations include lowered throughput, as state machine implementations use decision making logic at each state in order to deduce state changes if needed. This logic adds combinational delays that reduce the clock speed of the synchronizer. In this paper, an alternative FS is presented for RF space communications systems that will reduce latency, improve performance in the presence of AWGN, and streamline implementation complexity. The FS is developed that can be implemented in Field Programmable Gate Arrays (FPGAs) and is scalable for space systems and other critical applications. The novelty of our improved system is in its pure linear pipelined and parallel implementation, without the use of a state machine. This architecture generates a Frame Synchronizer decision, or pulse, at every clock cycle, without latencies associated with state machine reacquisition states. Further, the pipelined structure can increase clock performance as there are no feedback loops, and there is an opportunity to increase clock frequency by increasing pipeline depth. Frame Synchronizers are ubiquitous in the literature in applications to not only space communications systems but Earth-based communications that utilize error correction codes to improve the Bit Error Rate (BER) performance of an RF system. Although this FS is initially targeted for space communications systems, it is applicable to any serial data communication systems that are prone to noisy AWGN channels, including factory and heavy industrial settings, critical medical equipment where high reliability and system availability are needed, Earth/ground-based systems utilizing satellite “hops” in their system, and other critical systems requiring high reliability.

The contributions of this paper are summarized below:

• Improved Throughput: In our Frame Synchronizer, improvements are presented to address the performance issues of latency, clock and data throughput, FEC opportunity loss, and implementation complexity. The approach uses deep pipelining and parallelism and removes state machine structures that are typical in the traditional Frame Synchronizers, thus increasing processing throughput.
• Improved Clock/Data Performance: A direct linear pipeline and parallelism allows the clock rate to increase proportionally to the depth of the pipeline structures. Further, operating several pipelined structures in parallel allows higher levels of complex operations without the latency in typical synchronizer state machine designs.
• Reduced Latency: A further benefit of a pure forward path pipelined structure is that there are no feedback paths to create “bubbles” in processing. Bubbles in this context are similar to processor instruction execution pipelines, where a process direction change, such as a branch instruction, causes a feedback or feedforward change of direction. Any partially processed pipeline stage function is thrown away, reducing the overall pipeline efficiency. In traditional FS, when a flywheel state machine synchronizer changes state from flywheel to search, a feedback path stops FEC code processing and returns to the starting “search” and “verify” states. During these states, FEC processing is suspended while frame synchronization lock is re-established. In our synchronizer, there is no state machine and thus there are no feedback paths, eliminating the FEC opportunity loss typical in flywheel FS state machines.
• Reduced Implementation Complexity: By implementing our Frame Synchronizer in a pure linear pipeline, with no feedback loops, and utilizing parallelism in combination, a symmetrical structure can be used in an FPGA, without requiring the complexity of a state machine. Parallelism and pipelining are good fits for FPGAs as they are fundamentally parallel processing devices. Although the resource utilization may increase, the implementation is still simpler as no state machine analysis is required. Once the pipeline starts and is operational, a Frame Sync decision (pulse) appears at the pipeline output every clock cycle without complex decision making typical of state machines.

The following is the structure of the remaining sections of our paper. In Section 2, we describe existing methods typically used in space system Frame Synchronizers and their FEC coding environments. The pros and cons of the prior art will be described. Section 3 describes our general Frame Synchronizer architecture. Section 4 describes the lower-level FPGA implementation details and describes the concepts and improvements in our synchronizer. Section 5 presents and discusses FPGA implementation synthesis results including resource utilization and timing performance estimates for a potential application to space applications. Section 6 concludes this paper.

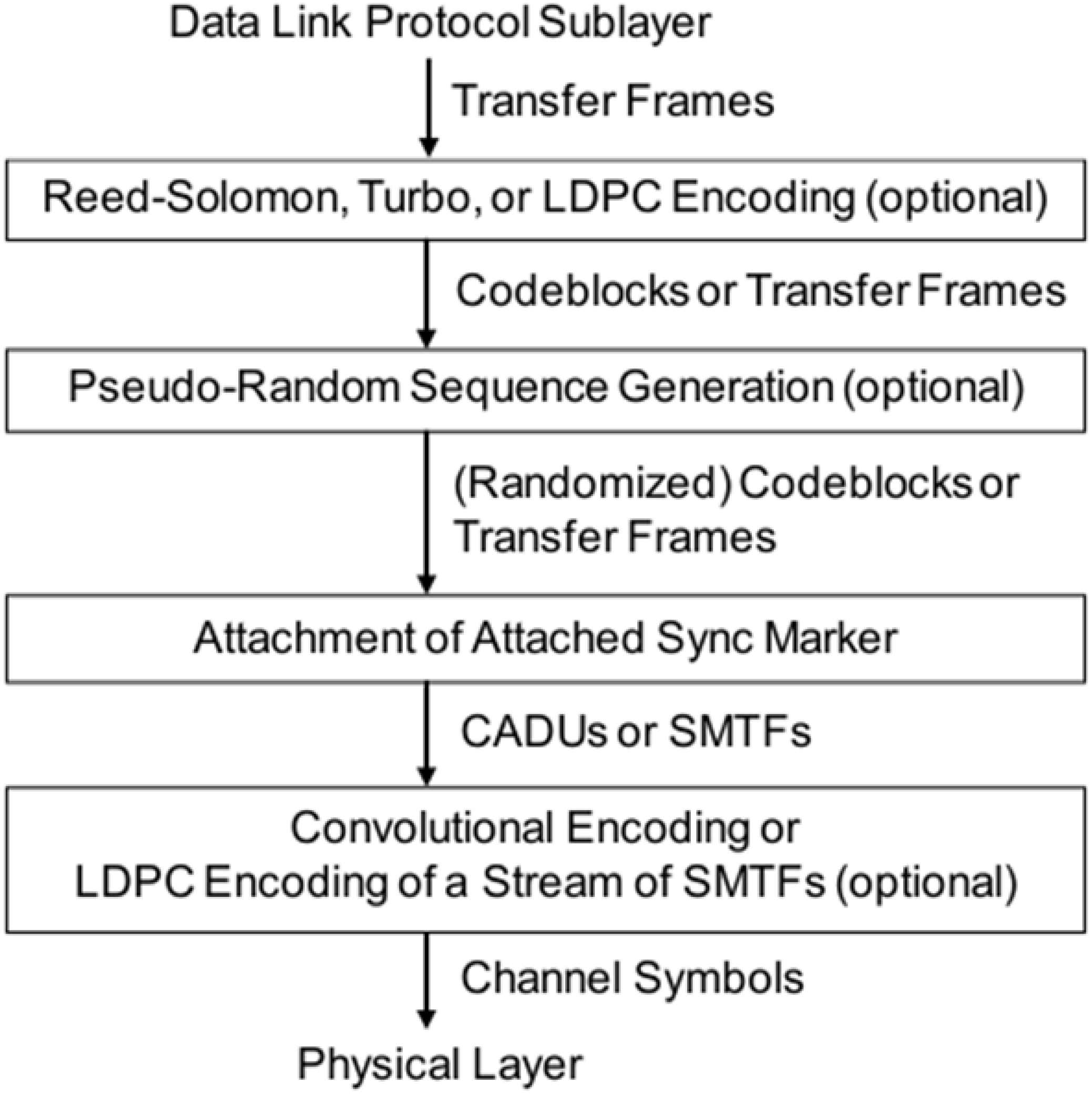
2. Background

Block FEC codes generate data streams with added parity bits prior to the modulation stage of the communications system. Other FEC codes, such as convolutional encoders combined with Viterbi decoders, can operate continuously without the addition of parity bits [7]. These types of codes modify the original data stream per the convolutional/Viterbi algorithms and can be implemented as non-block codes [8].

Contrarily, block FEC codes create blocks or frames of data and add redundant parity bits to the original data block. In a typical block code, the ASM pattern is inserted in front of the FEC-encoded block to create a frame of data. Examples include RS-encoded data. Block codes, where the original data block is unmodified and is appended with parity bits, are called systematic codes. These FEC block and systemic codes are ubiquitous in space communications systems and utilize Frame Synchronizers to signal the FEC decoder where to start the decoding process. In these space systems, the blocks are defined by the Consultative Committee for Space Data Systems (CCSDS), the international organization that governs space system communications standards [9].

2.1. Frame Synchronizers and Bit Error Rate

Frame Synchronizers for space systems have evolved since the 1960’s in parallel to the development of FEC codes, particularly block codes. Example block codes currently include RS, Low-Density Parity Check (LDPC) [10], Turbo codes, and concatenated RS with convolutional codes (where a combination of non-block and block codes are used together). Block codes during that time were limited by the scarce implementation resources available to the communications system designer. Digital devices of the time were limited and of simpler complexity, resulting in design techniques that could fit in a space-constrained environment. The fundamental problem, however, existed then as it does today, namely, designing a Frame Synchronizer strategy that can operate in a Gaussian noise space environment with higher BERs for a given space mission [11]. It is noted here that the focus in this paper is limited to AWGN channels, as in deep space missions, it is the primary channel type to model the extreme distances from spacecraft to Earth. The measure of bit errors uses a concept similar to the signal-to-noise ratio (SNR) but applied to transmission of bits in an RF system. As the SNR is a measure of relative signal power over noise power in an analog system, a similar measure of signal-to-noise in a digital signal transmitted in an RF channel is the Energy per Bit (Eb) over Noise Spectral Density (No) or Eb/No [12]. FEC codes are thus designed to improve error correction performance over varying BER levels or Eb/No and have been analyzed extensively in the literature [13]. Similarly, a Frame Synchronizer must also perform at low enough Eb/No levels to be able to correctly signal the start time of the coded blocks before sending those blocks to the FEC decoder for error correction processing.

2.2. Bit Transition Density and Clock Recovery

In a typical RF system, the bits to be transmitted are modulated onto a high frequency carrier wave creating “symbols” that are radiated over the air or vacuum, via an antenna. At the receiver, the carrier wave is received and then demodulated, reforming the bits that were originally transmitted [14]. Further, a secondary task of the receiver is to create or recovera clock based on the bit periods associated with those received symbols. This process creates a clock that is synchronous with the original transmitted data bit stream. The recovered clock is what drives the demodulator and any forthcoming digital logic in the system after the RF signal has been demodulated back into bits. The clock recovery is performed in a bit synchronizer as part of the demodulation process. These “bit syncs” require the original data stream to be “well-behaved”, a term informally used to say “have high bit transition density” [15]. In other words, the data stream at the source cannot have too many long spans of consecutive zeros or consecutive ones. Otherwise, a bit sync can introduce excessive jitter in the clock recovery process or not be able to recover the clock at all. High bit transition density is accomplished in the transmitter by randomizing the original baseband data stream, typically by a linear shift register that XOR’s the bit stream based on a predefined randomization polynomial.

CCSDS-relevant recommended standards for frame synchronization and coding are outlined in CCSDS Blue Book “TM Synchronization and Channel Coding” and are listed in

Table 1. CCSDS compliance requirements.

9.0	SYNCHRONIZATION
9.2	ATTACHED SYNC MARKER (ASM)
9.4	LOCATION OF ASM
10	PSEUDO-RANDOMIZER
11	TRANSFER FRAME LENGTHS

. The sections relevant to our Frame Synchronizer include Section 9.0, “Synchronization”, 9.2 “The Attached Sync Marker (ASM)”, where the patterns are defined for the various FEC coding schemes, and Section 9.4 “Location of ASM”, describing the location of ASM insertion relative to FEC coding fields. The randomization recommendations are defined in Section 10 “Pseudo-Randomizer”, which defines the polynomial to be used and its placement in a CCSDS-compliant system. Section 11 “Transfer Frame Lengths” details the size of the data fields, or Transfer Frames, for Reed–Solomon, Concatenated, Turbo, and LDPC FEC coding.

2.3. Randomization

It is noted here that the ASM pattern inserted into the bit stream at the transmitter is not typically randomized. However the remaining data, including any FEC parity bits, are randomized per CCSDS standards [16]. This ensures that at the receiver, the data stream at the clock recovery stage has adequate bit transition density. ASM patterns are already chosen to have strong bit transition density, for the same reasons mentioned before, to ensure good clock recovery at the receiver bit sync, and are therefore not randomized in the CCSDS standards. However, an additional rationale for not randomizing ASM patterns is that the forthcoming Frame Synchronizer will be attempting to correlate to the predefined ASM pattern. Thus if the ASM pattern is randomized, the Frame Synchronizer would never observe the original ASM pattern and not generate the necessary timing signals to the Forward Error Corrector. Figure 1 describes the Frame Synchronizer’s functional position relative to an FEC code, randomizer, and additional coding if necessary, as in the case of concatenated codes. The symbols are the final stage before the physical RF modulation and final presentation to the antenna.

2.4. Existing Frame Synchronizers

Most Frame Synchronizers perform the detection of a received ASM pattern after demodulation. These include the simple digital correlator, flywheel state machine, and optimum (soft decision) Frame Synchronizers. Although variations of these exist, the pros and cons of these three techniques are discussed here.

The simple digital correlator [17] operates by continuously observing a shifting serial bit window that is of the same width as the ASM pattern and monitors the received bits until a minimum (correlation threshold) number of correct bits match the predefined ASM pattern. Thresholds in frame synchronization are the number of correct bits from the receiver demodulator stage that match the predefined attached synchronization marker (ASM) pattern. The marker is appended at the source—the transmitter. The threshold is an agreed-upon minimum number of bits that must correctly match the ASM in order to declare that the ASM was detected at the receiver. As a Gaussian space channel will introduce more bits in error the farther the spacecraft is from Earth, some number of mismatches must be allowed. The threshold thus allows for both the acceptable mismatches and the minimum matches with the ASM. The threshold also changes depending on the distance from Earth; thus, it must be designed to be changed depending on where the spacecraft exists in different mission phases. These thresholds have historically been empirically determined by simulation and test prior to deployment of the spacecraft. This occurs at every clock cycle. For example, if the correlation threshold is chosen to allow for no more than 4 bits in error in the ASM pattern, and 3 bits or less in error are detected, then synchronization is declared, and the following Transfer Frame is sent to the FEC for decoding. If an ASM pattern is detected but with 5 bits in error, then the FS does not declare synchronization and the following Transfer Frame bits are discarded. The advantage of this system is its simplicity in implementation. However, it is not efficient as it can discard correctable frames, not allowing the FEC a chance to attempt correction of bit errors. This in a sense is a form of opportunity loss, where potential correctable errors do not get a chance to be corrected. This reduces the number of frames that could have been corrected, increasing the frame discard rate and reducing utilization of a given bandwidth of an RF system.

Flywheel state machine Frame Synchronizers [18] improve upon this and attempt to optimize the performance by allowing for some frames that normally would not pass the acceptable threshold test but still declare synchronization and allow the FEC to attempt bit error corrections. As shown in Figure 2, this is accomplished by allowing for ASM proclamation that is above the defined allowable bits in error to continue to be processed by the FEC, at the expected ASM position. A count of these ASM threshold exceptions is kept until the predefined unallowable flywheel exceptions have been reached. At that point, the state machine declares an unlocked state and re-starts a new search for an adequate (bit errors below the search threshold) ASM pattern. Once a certain number of sufficient matches of an ASM occur, synchronization is re-established, and new flywheel exceptions are allowed again. The term flywheel describes the process of allowing data to be accepted and processed with errors higher than the threshold for a limited number of frames. This allows the FEC to attempt to correct errors in blocks, whereas a simple digital correlator would not. As a result, less frames are discarded with the flywheel-based systems. However, the implementation is more complex as a state machine is required with search, check, lock, and flywheel states. There are no obvious optimal choices for state threshold settings, as each parameter offsets from the other state’s probability of optimal performance. Further, the process to go into a locked state requires multiple frames to be processed to traverse the search and check states before declaring lock. Thus, the improved efficiency in FEC processing comes at the cost of a longer re-start latency once the lock state is lost.

A third synchronizer is the “Optimum Frame Synchronization” method as described in James Massey’s seminal paper [19], which has been extensively analyzed and is currently used as the frame synchronization basis for modern lunar spacecraft [20]. The Massey approach is to improve performance in noise by processing not only the serial bit sequences but also the “soft decision bits” and surrounding random data to perform the ASM detection. Soft decision bits are the analog-to-digital (A/D)-converted magnitudes from the demodulator stage, not just the final demodulated bit (sign bit). This provides an estimate of confidence that the demodulated bit decision was correctly determined. Further, Massey shows that using two terms, the regular correlation (matching bits) term, and a second term that represents the energy of the surrounding data, 3 db better performance in coding gain is achieved as compared to the simpler digital correlation-only or flywheel approaches. The drawback is the increased complexity of implementation, as soft decision bits are required from the demodulator for processing, in addition to calculating the second term representing the surrounding data. Soft decision bits are the A/D conversion values from each bit, or symbol period, representing the demodulated signal at an RF receiver. It is the integration portion of the “integrate and dump” part of demodulation. Using soft decision bits rather than only the “final 1 or 0 bit” adds complexity to a spacecraft, as additional signals are needed between the receiver and the Frame Synchronizer. Further, FPGA complexity is also increased as processing of these soft bits is required.

Although other synchronizer techniques exist, these three approaches are typical in current space systems and are ubiquitous in the art. In order to be compliant with CCSDS space communications standards, these existing methods have been utilized for decades, as space systems must comply with CCSDS in order to be compliant with not only other spacecraft such as relay satellites but also with commercially available ground stations and other ground testing systems. Thus, very little deviation from these existing synchronization methods have been developed, which represents an opportunity for improvements.

The tradeoffs in Input/Output (IO) and complexity emerge after analyzing these traditional approaches. Both the digital correlator and flywheel state machine benefit from simple IO requirements, as only the demodulated bit, or the “sign bit”, is required as input from the radio receiver. This minimizes IO, harness mass, and harnessing complexity. The soft decision/optimum synchronizer has higher complexity as not only the sign bit is required but also the magnitude bits from the A/D converter from the receiver demodulator, increasing mass and complexity. The soft decision synchronizer is also increased in internal complexity, as an FPGA must calculate the two summations required in the algorithm, while the digital correlator calculates simple threshold comparisons. The benefit of the increased soft decision complexity is the 3 db improvement in Bit Error Rate [19].

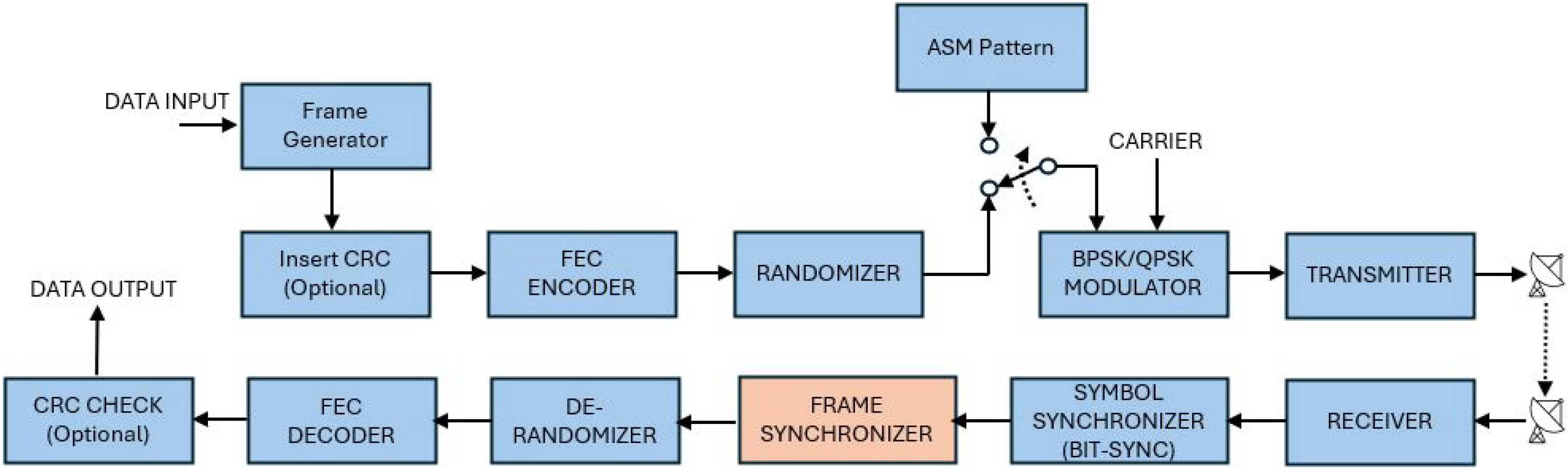
3. An Alternative Frame Synchronizer

An alternative Frame Synchronizer is now defined here, with reduced latency compared to the flywheel state machine approach, improved noise performance given a defined CCSDS-compliant ASM pattern, and reduced implementation complexity. The novelties in our improvements are, first and foremost, that a state machine is eliminated by implementing continuous forward pipelines with ASM pattern observation windows, with the observation width equal to the ASM width. As no “re-acquire” states exist, no temporary suspension of error correction exists, and downstream FEC processing is always active. Secondly, two ASM patterns are observed simultaneously, improving the confidence of ASM detection without latencies of using two state machine states. Further, no soft decision bits are required as in the optimal synchronizer, and only the sign bit is used, similarly to the simple digital correlator and flywheel synchronizers. And finally, implementation is a parallel and pipelined structure, which can increase throughput by increasing pipeline depth. A threshold, similar to the flywheel, is defined where the acceptable level of bit errors, or lower, is used to declare the detection of the ASM pattern.

This new synchronizer is placed to conform with existing space standards as defined by CCSDS. Figure 3 shows the position of the Frame Synchronizer relative to a Turbo FEC coding system, de-randomizer, and receiver demodulator subsystems. The diagram depicts a system using Binary Phase Shift Key (BPSK) modulation with Turbo FEC, but a Quadrature Phase Key system (QPSK) with any block FEC utilizes the same synchronizer placement and data flow. Both the transmit and receive systems are shown for completeness. Our alternative Frame Synchronizer complies with this CCSDS standard’s placement in the data flow. In a BPSK demodulator, two Frame Synchronizers would be needed to detect the two possible phase conditions. In the case of a QPSK system, four synchronizers could be utilized as four different phase possibilities can exist.

3.1. Random Data Around the ASM Marker

Figure 4 depicts the flow of serial data containing the block/frame of data, with ASM, Transfer Frame, and FEC Check Symbols comprising the data flow. A correlator would trigger a high correlation when the last bit of the ASM is detected in the observation window, represented by the long peaks in the bit flow. Note that at any bit-shifted position not at the ASM location, the likelihood is that approximately a 50% correlation is occurring. This is because in CCSDS-compliant systems, the data is randomized prior to modulation per CCSDS standards. A randomized stream is similar to what demodulated noise appears as, and there is reasonable likelihood that an ASM correlator would detect approximately 50% bit errors in the observed data stream. This has been observed in the laboratory using a BER Tester, where a BER of approximately 50% occurs when an observation window of the serial data is not correlated to the ASM pattern.

3.2. Parallel Three-Part Observation Windows

By implementing two additional observation windows of ASM length, shifted one-bit left and right from a center observation window, one can factor the likelihood of 50 percent correlation around the higher ASM correlation in the center window. This adds additional information in deciding whether a minimum correlation to the ASM pattern has occurred or not. Our Frame Synchronizer is comprised of three pipelines to implement these three windows, allowing parallel and pipelined processing simultaneously, one for each window. The general structure for the one-ASM case is shown in Figure 5.

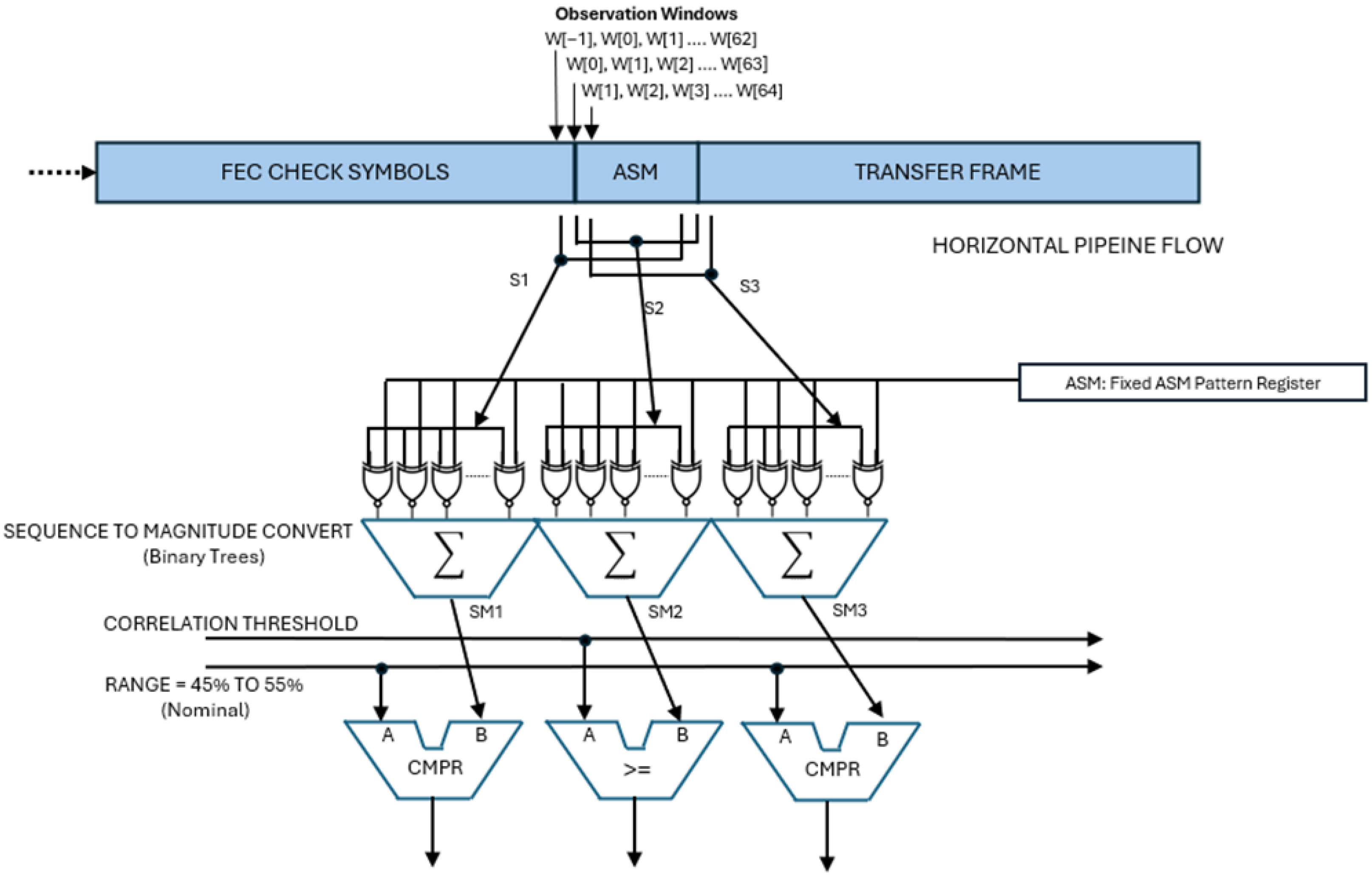
4. Implementation in an FPGA

For an FPGA-based Frame Synchronizer, the functions were divided into the following major sections: The horizontal pipeline and the vertical pipelines. The vertical pipeline consists of the Correlators, Sequence-to-Magnitude Converters (binary tree adders), and the threshold comparators. The details of these sections are described as follows.

4.1. Horizontal and Vertical Pipelines

At high signal levels (high Eb/No), the delta between shifted uncorrelated data and the correlated ASM location is high, and ASM correlation is easily detected. At lower Eb/No levels, as signal strength and noise floor levels approach similar levels, it becomes more difficult to differentiate the ASM peaks from the shifted uncorrelated data. The two adjacent observation sequences around the center are S1 and S3 with the center (ASM) window as S2. S1 and S3 will be uncorrelated (mismatched) to the ASM pattern and will result in approximately 50% BER. S2 will achieve a higher correlation when the ASM pattern appears. It is proposed here that the added confidence of using the surrounding uncorrelated information can allow for the lowering of the ASM threshold value, an increasing data rate, or lowering of transmit RF power, as the Frame Synchronizer will be able to perform in lower Eb/No environments. A pipelined multi-window observation structure that factors uncorrelated data is shown in Figure 6.

4.2. Sequence-to-Magnitude Conversion

In order to compare the number of bits in error from the correlator, or the number of bits above the ASM threshold value, a sequence-to-magnitude conversion must occur first. The three summers shown in Figure 6 are three pipelined binary trees, consisting of a chain of adders, which perform the sequence conversion. At each pipeline stage, adders become increasingly wider, until a final magnitude representing the number of 1’s in the original sequence with a magnitude computed at the output is reached. These binary trees, and the next-stage comparators, represent the startup time and pipeline latency. The multi-stage sequence-to-magnitude converter/binary tree is shown in Figure 7. This technique requires no feedback loops and is well suited to pipelined implementation.

4.3. Extending the Effective ASM Length

The proposed synchronizer factors the approximate 50 percent BER when not correlated to an ASM pattern and adds additional surrounding data to gain confidence in FS pattern detection. As CCSDS defines one ASM pattern per Transfer Frame, the ASM length is fixed. Extending the length of the fixed ASM pattern is an additional approach to more easily detect the sync marker in noisy environments, as the increased pattern length effectively increases the sample size of the ASM, thus increasing correlation confidence levels. In the CCSDS rate ½ LDPC code standard, a 64-bit ASM is fixed per the standard. In general, FEC sync words have been analyzed in the prior art to provide probabilities of correct frame lock, and also the probability of false lock [21]. A natural improvement would be to increase the ASM length and increase performance at increasing noise or Eb/No levels. This would improve frame lock performance in a noise channel, enabling either longer distances from Earth, lower required RF power levels, or a combination of both. Unfortunately, CCSDS does not allow for changing the ASM lengths or patterns if a space system is to be compliant to its standards.

However, a similar improvement effect can be used by extending the observation windows to accommodate two ASM patterns from two Transfer Frames, simultaneously and in parallel, without violating compliance with CCSDS standards. By extending the horizontal pipeline/shift register such that two ASM patterns are included, a similar effect to doubling a single ASM pattern is achieved. This provides a higher probability of successfully achieving a correlation threshold with a given Eb/No or signal strength levels. Although startup latency is increased to be able to observe two sync markers, efficiency is not reduced in throughput. The added length of the FS structure uses the frame length, two ASM lengths, and two additional bits to account for the two additional 50% BER observation windows. The two-ASM architecture is shown in Figure 8.

4.4. Alternative Observation Windows

Utilizing two observation windows surrounding a candidate ASM is based on the fact that a one-bit shifted correlation away from a candidate ASM location adds confidence by detecting an approximate 50 percent Bit Error Rate in the correlation comparator tests. Although ASM patterns are defined such that bit transition density is high, the patterns are not generated by a randomization process. A closer comparison to random data is accomplished by using the bits inside the Transfer Frame itself instead, as CCSDS defines a randomization polynomial for the data in the Transfer Frame. By adjusting the pipelines and observation windows to use the common Transfer Frame data between two ASM locations, a comparison with pseudo-randomized data is achieved instead. Figure 9 shows this alternative architecture, with the CCSDS randomized data observation windows adjacent to the two-ASM windows. Note that the randomized data is in the common frame encapsulated by the two ASM patterns.

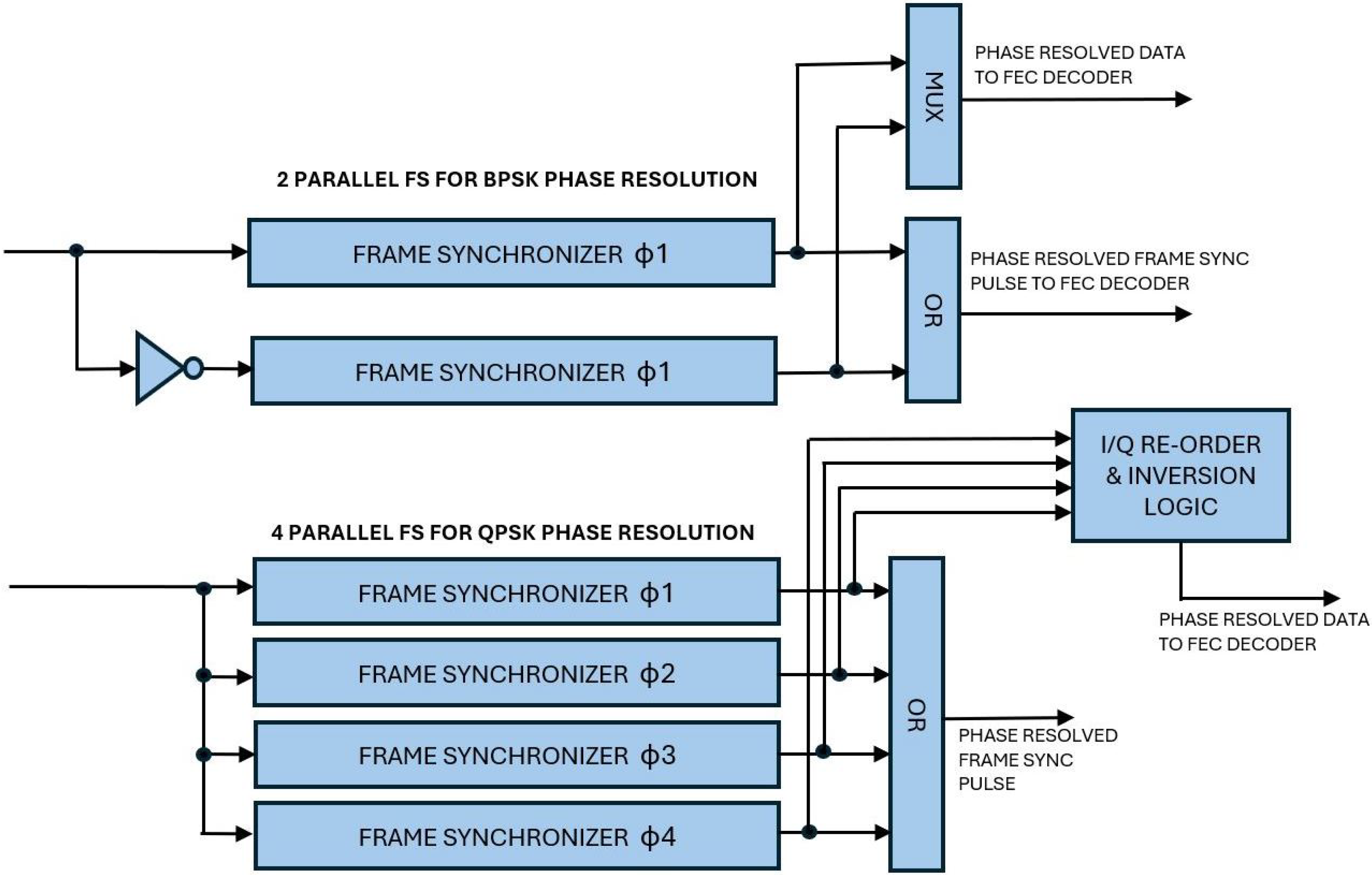
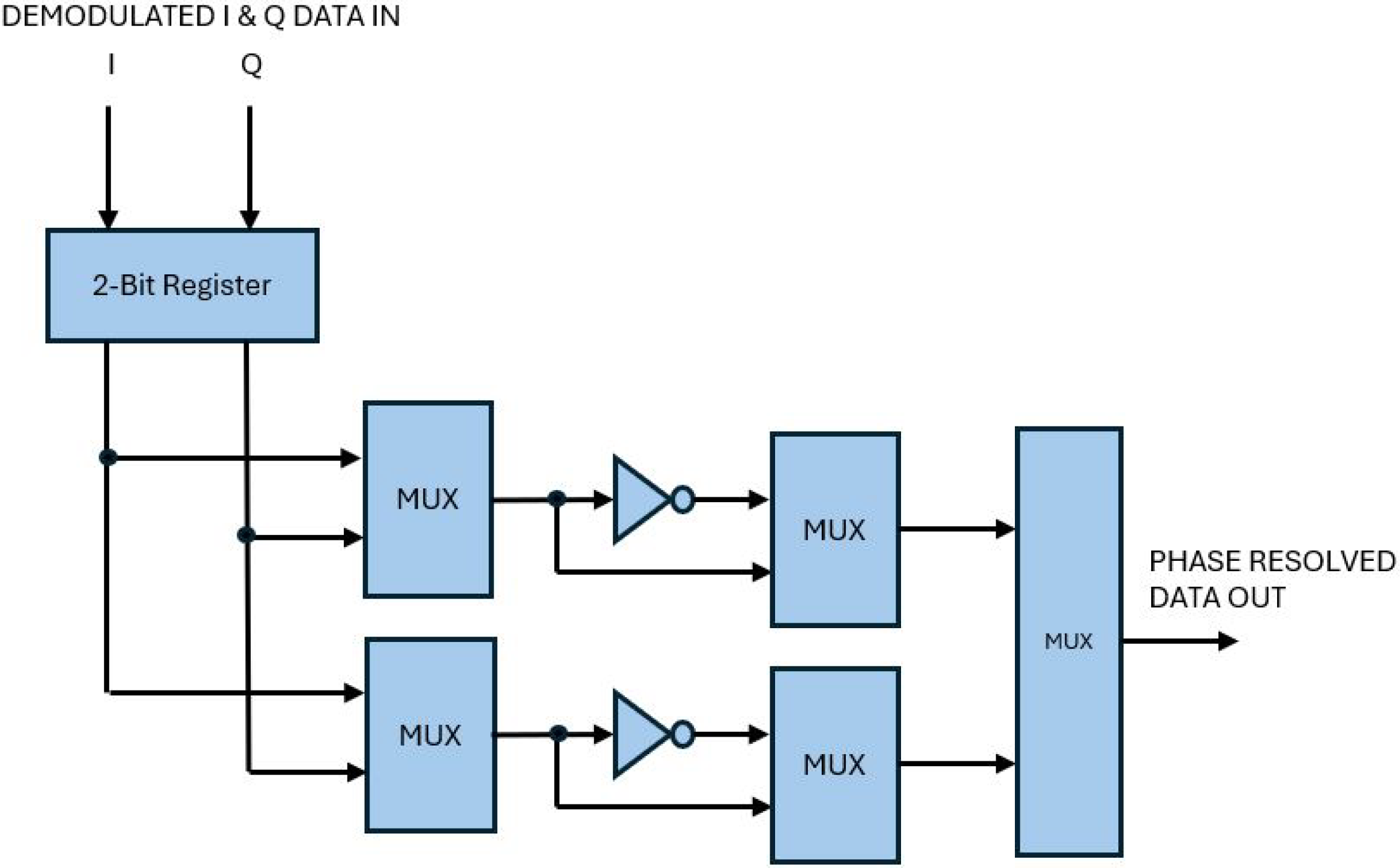
4.5. Phase Rotation Ambiguity Resolution

Up to this point, our alternative Frame Synchronizer has been described with the assumption that received data streams occur with only AWGN bit errors potentially occurring in the received data stream after traversing through a Gaussian channel, which may be correctable by the FEC decoder downstream. However, in space communications systems, the transmitter modulation and demodulation methods can introduce additional perturbations such as the incorrect reordering of received bits, the flipping of bit polarity (1’s becoming 0’s or 0’s becoming 1’s), or a combination of both inversion and reordering. This is in addition to bit errors that occur as natural “wrong decisions” that a receiver demodulator can make when Eb/No, or signal strength, is weakened by the natural effects of long transmit distances. Mitigation can be achieved by employing differential encoding prior to modulation. This solution, however, is not guaranteed when designing a new Frame Synchronizer into a spacecraft system that is already established and does not already utilize differential encoding.

4.6. BPSK and QPSK Modulation

With BPSK modulation, it is possible to have two states of ambiguity in the received demodulated data [22]. Either the received data stream demodulates to the correct polarity, or phase, of the original data stream, or all bits inverted, depicted in the top half of Figure 10. The two possible states, A and B, in the constellation diagram depict that either the demodulated data is true or inverted. The decision of either accepting the data or correcting the inversion is accomplished by having two parallel Frame Synchronizers, where one is processing the original data state of the bits and the second synchronizer is detecting an inverted version of the received data. This two-synchronizer system can determine which version of the data stream is correct and select the correct path to forward to the downstream FEC decoder. A second bypass path is used with a front-end inverter to create the inverted path.

Note that the “wrong” path will never achieve correlation, as all or most bits will be in the inverted state and will not trigger the correlation in the threshold comparators to create the final synchronization pulse. In this case, the parallel synchronizer will theoretically achieve correlation, assuming that the BER is below the desired error threshold. It is important to differentiate between bit errors as a result of Gaussian channel induced errors and phase ambiguity errors as each is caused by, and corrected by, different means.

The case for QPSK modulation is not as simple. QPSK demodulators can generate four different phase ambiguity states, as each radiated symbol represents two bits, such that four constellation rotations can occur at the receiver demodulator [22]. At the transmitter, QPSK defines two axes, I and Q, in a constellation diagram to represent two-bit symbols radiated by antenna over air or space. QPSK allows two bits to be transmitted over the air for every phase change in the same transmitted carrier signal. As such, doubling of RF bandwidth utilization is achieved since two bits are effectively transmitted simultaneously in the same RF bandwidth, where the two bit sequences are represented by four possible carrier phase changes.

However, a QPSK demodulator can incorrectly invert, and in addition, re-order the incoming two-bit symbol information, where the original constellation of possible states is changed from the original intended transmitted data stream. From the perspective of the Frame Synchronizer, four quadrants represent four different phase rotations that can occur, of which only one represents the correct data stream [23]. In addition to bit inversions as in BPSK, bit position swaps can also occur, shown in the bottom half of Figure 10. The four states of QPSK constellation ambiguity are depicted as A, B, C, and D in the constellation diagram, where only one state represents the original transmitted data, with the remaining three states having a combination of both bit re-orderings and bit inversions. A simple inverter is not sufficient to correct an incorrect phase rotation in QPSK because of the potential of bit re-ordering. However, unlike BPSK, instead of inverting the data stream, a simpler approach is to modify the ASM pattern being compared to the data stream, so that each ASM pattern represents the four possible constellation rotations. Four different ASM patterns can be used in four parallel synchronizers, such that each represents the possible phase-rotated versions of the original ASM pattern. Only one of the Frame Synchronizers will achieve correlation and generate frame sync pulses. The other three Frame Synchronizers can be ignored by selecting the only synchronizer generating the FS pulses. It is noted here that an active selection function can also be replaced by a simple “OR-ing” of the four FS pulses, as only one out of the four will be generating pulses. For QPSK, re-ordering and inverting to the correct state is necessary at the data stream to correct the data sequences. The correct phase rotation is subsequently forwarded to the downstream FEC decoder. This modified FS architecture with phase rotation correction is depicted in Figure 11. A solution for the data stream phase resolver is detailed in Figure 12 and can be pipelined to increase throughput. The data resolver selects which I and Q channel(s) should be reversed in order and which channel(s) should be inverted. Although multiple parallel Frame Synchronizers will increase FPGA resource usage, latency and throughput performance is optimized using the parallel approach.

5. Synthesis Results and Discussion

Test synthesis for the major sections of the Frame Synchronizer was performed using a development board with an Altera Cyclone-II FPGA and Freescale 68HC12 processor. The Cyclone-II FPGA was chosen because of its cost-effectiveness and because it has previous space legacy performing well under radiation environments on the International Space Station (ISS) [24]. This is a smaller class FPGA but can be used in designs for space environments at a commodity cost.

In order to estimate FPGA resource utilization and maximum clock frequency, the synchronizer elements were implemented and synthesized in stages. This allowed separate bottlenecks to be identified iteratively and allow for optimization, such as deepening of pipelines, to improve clock performance results. Three synthesis compilations were performed using the Altera Quartus compiler for the three major sections: the horizontal pipeline, the arithmetic paths consisting of the correlation adders, and the threshold comparators.

No Digital Signal Processing (DSP) blocks were needed for the compilations. Embedded Memory blocks were used at 2176 bits for the three compilations, as the same horizontal shift register is the same and is independent of vertical pipeline depths. Resource utilization and maximum clock frequency increases for the three synthesis cases were noted by adding pipeline stages.

Table 2. FPGA synthesis utilization, one-stage pipelining.

	PIPELINE STAGES	LOGIC ELEMENTS	COMBINATIONAL	REGISTERS	MEMORY BITS	FMAX (MHz)
Comparators	1	90	89	19	0	277
Adders	1	14	7	14	0	340
Horizontal Pipeline		1	1	0	2176	163

shows utilization and performance results for a one-stage pipeline. For the two-stage pipelined case, resources increased, and the added pipelining increased the maximum clock frequency increased to 336 MHz, as shown in

Table 3. FPGA synthesis utilization, two-stage pipelining.

	PIPELINE STAGES	LOGIC ELEMENTS	COMBINATIONAL	REGISTERS	MEMORY BITS	FMAX (MHz)
Comparators	2	96	92	27	0	336
Adders	2	24	7	21	0	340
Horizontal Pipeline		1	1	0	2176	163

. Additional clock frequency improvements were achieved with a three-stage pipeline implementation as shown in

Table 4. FPGA synthesis utilization, three-stage pipelining.

	PIPELINE STAGES	LOGIC ELEMENTS	COMBINATIONAL	REGISTERS	MEMORY BITS	FMAX (MHz)
Comparators	3	96	92	28	0	340
Adders	3	32	7	78	0	340
Horizontal Pipeline		1	1	0	2176	163

, with a maximum clock frequency increase to 240 MHz.

However, timing analysis results show that adding pipeline stages, although increasing clock performance to the arithmetic and threshold comparator sections, does not increase overall system performance, as the main bottleneck is not those sections but the horizontal shift register. In the rate 1/2 CCSDS LDPC case, the length of the overall parallel structure must accommodate a full 2112-bit Transfer Frame plus 128 bits for two 64-bit ASM observation windows. The built-in FPGA memory structures were thus utilized to maximize resource use efficiency rather than using fabric registers. A review of the timing analysis results indicates that the memory blocks (non-fabric) have a clock frequency upper limit of 163 MHz and cannot be pipelined. However, an analysis of this FPGA’s timing specification shows a potential clock doubling improvement by using fabric registers to increase the horizontal pipeline clock frequency above 163 MHz, as the internal global clock network is specified to a maximum of 402 MHz. A test synthesis was performed using fabric registers only for the horizontal pipeline, with a maximum clock frequency of 226 MHz, a 38% improvement over the memory block implementation. This clock frequency increase, however, would come at the cost of substantial use of fabric registers.

The Frame Synchronizer maximum clock frequency represents the maximum throughput of the entire FEC decoding system, since the frame sync pulse is the fundamental “heartbeat” driving the overall receiver forward correction system and downstream communications processing. Alternative solutions to increase throughput include using faster grade FPGAs. However, in the space-grade radiation-tolerant vendor space, faster FPGAs come at a significant cost, long lead times, and reduced radiation tolerance. Current lunar spacecraft such as Orion that utilize LDPC are operating with on-spacecraft FEC decoders at or below 20 Mbps [25]. Thus, 163 MHz clock performance is still a significant improvement over current spacecraft that utilize CCSDS-compliant LDPC decoders.

A quantitative analysis on the probabilities of correct lock, false lock, or quantifying effects from varying Eb/No or phase noise is beyond the scope of this paper. However, the fundamental advantage and improvement is presented that, unlike traditional state machine solutions, no seek, verify, lock, and flywheel states are used at all. The pipelined and parallel nature of the architecture means that once the horizontal and vertical pipelines are started and fully operational, a frame synchronization “yes or no” decision emerges at every clock cycle. Utilizing two ASM patterns, simultaneously at the two expected locations (the beginning and end of an FEC block), effectively doubles the ASM length for correlation, increasing the confidence of a frame “lock” decision for the FEC block in between, at every clock cycle. This ASM effective length extension increases the probability of differentiating ASM detection from uncorrelated or random data, compared to a one-ASM FS system. Using the additional knowledge that uncorrelated data when not aligned is approximately 50 percent in error further increases confidence in a frame sync assertion. In a traditional flywheel state machine synchronizer, it is possible to declare an invalid lock, or false lock, which would enable incorrect frames to be forwarded for downstream processing. Recovering from this erroneous state requires multiple flywheel states before detection and initiating a re-acquire state. In our synchronizer, there are no flywheel states, and a recovery from a false frame sync can occur immediately at the next valid threshold correlation.

An additional phenomenon addressed with our synchronizer is that on traditional state machine systems, cycle slips, or “bit slips” can occur and are associated with inadvertent QPSK constellation phase rotations. Not only can re-ordering or inversion of bits occur, but also bit time periods are lost or gained [26]. In the CCSDS rate 1/2 LDPC, as an example, a phase rotation can cause a gain or loss of a bit(s), where the block frame can become 2111 or 2113 bits in length, instead of the correct 2112 bit frame length during the slip. If this occurs during the lock state of a traditional state machine structure, incorrect sync lock can occur for several frames while in flywheel. The flywheel state will eventually decide that a loss of lock or bit slip was declared. But during the process of returning to the search state, several incorrect frames are sent to the FEC decoder, potentially allowing the acceptance of invalid frames downstream. If the communications link was a command link from Earth to the spacecraft, this could potentially be detrimental if the incorrect data was interpreted as a valid spacecraft command.

Contrarily, our synchronizer’s frame sync decision process is performed at every clock cycle; thus, if a BPSK or QPSK phase rotation cycle slip occurs and an incorrect frame is declared as valid and sent to the decoder, recovery from this condition is instant at the next clock cycle, instead of several CCSDS frames later, minimizing the potential for invalid command processing when compared to traditional flywheel-based systems. In this case, one of the remaining of the four synchronizer would correctly detect the ASM threshold, and the Data Phase Resolver would correct the I and Q channel ordering and inversion.

Existing state machine synchronizer-based FEC decoders also experience the “opportunity loss” phenomenon if the correlation thresholds of the various states are set overly conservative. This causes increasing frame discards and is referred to in the aggregate as the discard rate, or not allowing the opportunity for the downstream FEC decoder to attempt error corrections that may otherwise have been successfully decoded [27]. Our pipelined Frame Synchronizer is not affected from this effect as decisions on frame sync lock are determined at every clock cycle, without inherent frame discards from flywheels. It is observed that in a CCSDS-compliant space system, there are additional command verification stages downstream of the FEC decoder to validate that an incoming decoded command was on a valid list of allowable commands, mitigating the effects of potential erroneous decoded data. Thus, an erroneously decoded command message has an independent validity test before final execution to vet the Frame Synchronizer lock decisions. Based on the resource utilization results, our alternative synchronizer can feasibly be implemented on modern space-grade radiation-tolerant FPGAs. A full implementation of a three-stage pipelined two-ASM synchronizer would require quadrupling the threshold comparators and adders. Further, in a QPSK system, an additional quadrupling of resources would be needed to process the four states of phase rotation ambiguity. A first estimate of resource utilization would be 2064 Logic Elements, 1600 combinational elements, and 1696 registers. Memory bits would remain 2176 as the same horizontal pipeline register would generate the multiple vertical pipelines. An analysis of Microchip’s RTG4 family of rad-tolerant FPGA products shows that our utilization represents a very small percentage of FPGA internal resources. The RTG4-150 device includes 151,000 Logic/FF Elements, and 24,000 internal memory bits. On an RTG4150 FPGA, resource usage would leave an approximately 95% Logic/FF Elements margin and 93% memory bit margin.

6. Conclusions

An alternative FPGA-implementable Frame Synchronizer was presented that improves clock and data throughput performance by using parallel-pipelined processing. The architecture increases ASM detection in a given Eb/No level by factoring uncorrelated data when observing shifted correlation values surround the ASM and effectively doubling the ASM length by using two sync markers around a common FEC Transfer Frame. Implementation complexity is streamlined by the pipelined and parallel architecture, which produces a frame sync signal at every clock cycle not prone to state machine feedback loop latencies. This further reduces the opportunity loss associated by traditional state machine synchronizers as there are no frame discards associated with seek and verify states. By not requiring soft decision magnitudes and using only the final 1 or 0 demodulated bits, implementation complexity is further simplified. Applications to this Frame Synchronizer with FEC encoding can be applied to not only traditional spacecraft programs but also the newer emerging industries such as commercial space, distributed integration testing facilities where deterministic timing is needed, and nano-satellite industries.