Physical Layer Authentication Exploiting Multipath Delay Fingerprints in Millimeter-Wave Communication Systems

Abstract

To effectively address the issue of identity spoofing attacks in millimeter-wave (mmWave) systems, this paper proposes a physical layer authentication (PLA) mechanism that leverages multipath delay fingerprint features to enhance the system’s resilience to impersonation. A detailed mmWave channel model is constructed, and a precise method for estimating and extracting multipath delay features is developed. The device authentication task is formulated as a binary hypothesis testing problem, for which closed-form expressions for the probability of false alarm and the probability of detection are derived, providing a theoretical guarantee for the performance of the proposed scheme. Simulation results demonstrate that the proposed mechanism can effectively mitigate the threat of identity spoofing in mmWave communication environments.

1. Introduction

Millimeter-wave (mmWave) technology is a cornerstone of sixth-generation (6G) communication and future networks, offering advantageous characteristics such as high data rates, low latency, and receiver diversity [1]. The short wavelength of mmWave facilitates the integration of large antenna arrays into compact receiver form factors, leading to the development of mmWave Single-Input Multiple-Output (SIMO) systems. These systems represent a key enabling technology for a wide range of applications, including the Internet of Things (IoT) [2]. Compared to Multiple-Input Multiple-Output (MIMO) systems equipped with multiple antennas at both the transmitter and receiver ends, the SIMO architecture offers a more cost-effective and practical solution for many millimeter-wave applications, particularly in the IoT domain. This preference stems primarily from the fact that transmitting devices in IoT applications—such as sensors, wearables, or terminals—typically face extremely stringent constraints on size, cost, and power consumption. Integrating the multi-antenna arrays and corresponding RF chains required for MIMO systems onto these devices is often technically and economically infeasible. SIMO systems ingeniously address this challenge by shifting the system complexity to the receiver. The transmitter can maintain a minimalist design with a single antenna, thereby minimizing power consumption and hardware costs. The receiver, typically subject to less stringent constraints, can instead be configured with a large-scale multiple-output antenna array. This enables high receiver diversity gains, effectively countering the path loss and fading inherent in millimeter-wave channels, and ensuring reliable communication and signal quality. Therefore, the millimeter-wave SIMO system architecture discussed in this paper represents a critical and practical choice in balancing performance, cost, and power consumption constraints. However, the broadcast nature of wireless channels renders mmWave SIMO systems susceptible to spoofing attacks, where an illicit transmitter impersonates a legitimate entity to deceive the receiver, thereby gaining unauthorized access to execute further malicious activities. To mitigate this threat, device authentication has become a critical defense mechanism. Unlike higher-layer authentication schemes based on cryptography, physical layer authentication (PLA) verifies a transmitter’s identity by leveraging intrinsic physical layer characteristics, such as channel features and hardware fingerprints. PLA offers notable advantages, including high security, low complexity, and strong compatibility [3,4,5,6], making it a vital supplement to conventional cryptographic methods.

PLA is broadly categorized into hardware fingerprinting-based and channel-based authentication, distinguished by the exploited physical layer features [7]. Regarding hardware fingerprinting, Hou et al. [8] proposes a hypothesis-based authentication scheme that utilizes the time-varying carrier frequency offset (CFO) in dynamic environments. In the domain of channel-based authentication, Xiao et al. [6] utilized multiple landmarks to enhance transmitter resolution via received signal strength indicator (RSSI) features, subsequently proposing a logistic regression-based authentication scheme. Exploiting the sparse characteristics of the mmWave MIMO channel, the work in [9] extracts virtual angle of arrival (AoA) features from the virtual channel and formulates a binary hypothesis test to validate the transmitter.

While existing mechanism enhance wireless security, PLA in the context of mmWave SIMO systems remains underexplored. Such systems exhibit unique physical layer characteristics not present in conventional networks, particularly the multipath time delay features within the channel, which are highly suitable for identity validation. Accordingly, this paper introduces a novel PLA scheme for mmWave SIMO systems that leverages these distinctive delay characteristics. In particular, we first develop an efficient method to estimate and extract the requisite multipath time delay features. Subsequently, employing principles from statistical signal processing and hypothesis testing, we derive closed-form expressions for the key performance metrics of false alarm and detection probabilities. Finally, the practical effectiveness and robustness of the proposed authentication framework are validated through comprehensive simulations under a range of estimation conditions.

The rest of this paper is organized as follows. The system model and problem formulation are introduced in Section 2. Section 3 presents the proposed PLA scheme. The false alarm and detection probabilities are derived in Section 4. Section 5 provides the simulation results, and Section 6 concludes the paper.

2. Problem Formulation and System Model

2.1. Problem Formulation

This paper considers a canonical three-party model within an mmWave SIMO OFDM system. As shown in Figure 1, the model consists of the following entities: A legitimate transmitter Alice with a single antenna, who attempts to send data frames to the intended receiver; the intended receiver Bob, equipped with $N_r$ antennas, Bob’s objective is to accurately verify the identity of the incoming transmitter; and an illegitimate transmitter Eve who seeks to gain access to Bob by spoofing Alice’s identity, with the potential to launch subsequent advanced attacks [5,6,10]. It is assumed that the multipath delay estimation and authentication scheme employed by Bob is unknown to the adversary, Eve. However, certain public information, such as the frame format, may be accessible to Eve by analyzing the structure of intercepted signal frames due to the open nature of the wireless medium.

The authentication process is predicated on the reception of two consecutive signal frames. The first frame is presumed to have been authenticated as originating from Alice through a conventional upper-layer mechanism. During the reception of this initial frame, Bob executes the proposed delay estimation algorithm to extract multipath delay features from the channel. These features are then stored as a reference channel fingerprint for use in subsequent authentication challenges. This work does not consider the scenario of composite signals resulting from simultaneous transmissions by Alice and Eve. It is assumed that Bob’s receiver would discard any such collided frames. The system employs the CSMA/CA protocol to govern medium access and manage the transmission schedule.

2.2. Channel Model

A mmWave SIMO OFDM system is considered in this paper. The transmitter, Alice or Eve, has a single antenna, and the receiver Bob has $N_r$ antennas. Similar to [11], by considering the multipath delay feature, the mmWave SIMO OFDM channel vector at subcarrier d ($d=1,2,\dots ,D$) can be modeled as

$$\begin{array}{c}\hfill {\mathbf{h}}_d=\sum _{m=1}^M{\alpha }_m{e}^{-j2\pi f_d{\tau }_m}{\mathbf{a}}_d({\varphi }_m,{\theta }_m),\end{array}$$

(1)

where ${\alpha }_m$ denotes the complex amplitude of the m-th propagation path. ${\varphi }_m$ and ${\theta }_m$ are the azimuth and elevation angles of arrival of the m-th path, respectively. ${\mathbf{a}}_d({\varphi }_m,{\theta }_m)$ is the array response vector. $f_d$ is the frequency at the d-th subcarrier and $f_d=f_0+d{\Delta }_F$, where $f_0$ is the subcarrier frequency at the lower end of the band and ${\Delta }_F$ is the spacing between any two subcarriers. ${\tau }_m$ represents the time delay of the m-th propagation path.

The base station Bob exploits a hybrid uniform cylindrical array (UCyA), which consists of $N_1$ horizontal layers of uniform circular arrays (UCAs), each having $N_2$ antennas, i.e., $N_r=N_1{N}_2$. The radius of each UCA is represented by r. The vertical distance between any two adjacent UCAs is represented by h. Therefore, the array response vector is expressed by

$$\begin{array}{c}\hfill {\mathbf{a}}_d({\varphi }_m,{\theta }_m)={\mathbf{a}}_{1,d}\left({\theta }_m\right)\otimes {\mathbf{a}}_{2,d}({\varphi }_m,{\theta }_m),\end{array}$$

(2)

where

$$\begin{array}{c}{[{\mathbf{a}}_{1,d}\left({\theta }_m\right)]}_{n_1,1}=\hfill \\ \hspace{1em}\hspace{1em}{\displaystyle \frac{1}{\sqrt{N_1}}}\exp \left(-j{\displaystyle \frac{2\pi }{c}}{f}_{d}h\left(n_1-{\displaystyle \frac{N_1+1}{2}}\right)cos\left({\theta }_m\right)\right)\hfill \end{array}$$

(3)

$$\begin{array}{c}{[{\mathbf{a}}_{2,d}({\varphi }_m,{\theta }_m)]}_{n_2,1}=\hfill \\ \hspace{1em}\hspace{1em}{\displaystyle \frac{1}{\sqrt{N_2}}}\exp \left(j{\displaystyle \frac{2\pi }{c}}{f}_{d}rsin\left({\theta }_m\right)cos({\varphi }_m-{\phi }_{n_2})\right)\hfill \end{array}$$

(4)

are the array response vectors of the vertical and horizontal directions, respectively. $n_1=1,$$2,\dots ,N_1$ and $n_2=1,2,\dots ,N_2$ denote the index of the above array response vectors, respectively.

According to the characteristics of different random distributions, the multipath time delay is modeled as a Poisson distribution [12]. Thus, the time interval between any two adjacent multipath time delays obeys an independent and identical exponential distribution and can be expressed by

$$\begin{array}{c}\hfill q_i\left(t\right)={\tau }_{i+1}\left(t\right)-{\tau }_i\left(t\right),i=1,2,\cdots ,M-1.\end{array}$$

(5)

To model the time-varying characteristics between $q_i\left(t\right)$ and $q_i(t-1)$ more conveniently, Gaussian random variables can be used to model correlated exponential random variables [13]. Generally, an exponential random variable can be written as a sum of the squares of two independent Gaussian random variables. Thus, $q_i$ at time t and $t-1$ can be written equivalently and, respectively, as

$$\begin{array}{cc}\hfill q_i\left(t\right)& ={\left(q_{1,i}\left(t\right)\right)}^2+{\left(q_{2,i}\left(t\right)\right)}^2,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill q_i(t-1)& ={\left(q_{1,i}(t-1)\right)}^2+{\left(q_{2,i}(t-1)\right)}^2,\hfill \end{array}$$

(7)

where $q_{1,i}$ and $q_{2,i}$ are two independent Gaussian random variables with zero mean and variance ${\sigma }_q^2$, i.e., $q_{1,i}$, $q_{2,i}$∼$\mathcal{N}(0,{\sigma }_q^2)$. Further, $q_i$ is now an exponential random variable with parameter $\lambda ={\displaystyle \frac{1}{2{\sigma }_q^2}}$, i.e., $q_i\sim \exp \left({\displaystyle \frac{1}{2{\sigma }_q^2}}\right)$.

Similar to previous works [14,15], we use a first-order Gauss–Markov process to characterize time-varying multipath time delays [16,17], and therefore, $q_{1,i}$ and $q_{2,i}$ are mathematically expressed, respectively, as

$$\begin{array}{c}\hfill q_{1,i}\left(t\right)=\rho q_{1,i}(t-1)+\sqrt{(1-{\rho }^2){\sigma }_q^2}{u}_1(t-1),\end{array}$$

(8)

$$\begin{array}{c}\hfill q_{2,i}\left(t\right)=\rho q_{2,i}(t-1)+\sqrt{(1-{\rho }^2){\sigma }_q^2}{u}_2(t-1),\end{array}$$

(9)

where $\rho$ denotes the multipath time delay correlation coefficient. $u_1$ and $u_2$ are two independent Gaussian random variables with zero mean, i.e., $u_1,u_2\sim \mathcal{N}(0,{\sigma }_q^2)$.

The correlation coefficient $\rho$ is directly related to the channel coherence time, which is inversely affected by the Doppler spread caused by mobility. In practical scenarios, movement of the transmitter, receiver, or surrounding scatterers introduces non-static channel conditions. This mobility leads to a faster channel decorrelation over time, corresponding to a lower value of $\rho$. Therefore, our time-varying channel model inherently captures the statistical impact of mobility. A higher degree of mobility will widen the distribution of the channel variation between authentication attempts. This effect is explicitly accounted for in our theoretical performance analysis in Section 4, as the derivation of $P_f$ is directly dependent on $\rho$. A highly dynamic environment would naturally increase the dissimilarity between consecutive channel fingerprints, posing a greater challenge to the authentication system, which is a key aspect evaluated in our model.

2.3. Communication Model

Consider Bob receives a data frame from an unknown transmitter X. The aim of Bob is to verify the identity of the transmitter. We consider a hybrid front-end architecture as in [18]. By utilizing a hybrid beamformer, $\mathbf{W}\in {\mathbb{C}}^{N_r\times N_{DS}}$, on the received signal, ${\mathbf{r}}_d$, the final signal after beamforming is written as

$$\begin{array}{c}\hfill {\mathbf{y}}_d\left(t\right)={\mathbf{W}}^H{\mathbf{r}}_d\left(t\right)={\mathbf{W}}^H{\mathbf{h}}_d\left(t\right)s_d\left(t\right)+{\mathbf{W}}^H{\mathbf{n}}_d\left(t\right),\end{array}$$

(10)

where $s_d\left(t\right)$ is the transmitted signal at time t and subcarrier d. The average power is $p=\mathbb{E}\left\{\right|s_d\left(t\right){|}^2\}$. ${\mathbf{h}}_d\left(t\right)$ is the $N_r\times 1$ mmWave SIMO OFDM channel vector at time t and subcarrier d. $\mathbf{W}={\mathbf{W}}_{RF}{\mathbf{W}}_{BB}$ is a hybrid beamformer. ${\mathbf{W}}_{RF}\in {\mathbb{C}}^{N_r\times N_{RF}}$ is an analog combiner and ${\mathbf{W}}_{BB}\in {\mathbb{C}}^{N_{RF}\times N_{DS}}$ is a digital combiner. $N_{RF}$ and $N_{DS}$ denote the number of radio frequency chains and data streams, respectively. ${\mathbf{n}}_d\left(t\right)\in {\mathbb{C}}^{N_r\times 1}$ is the zero-mean additive white Gaussian noise (AWGN) with variance ${\sigma }_n^2$ at time t and subcarrier d, i.e., ${\mathbf{n}}_d\left(t\right)\sim \mathcal{CN}(0,{\sigma }_n^2\mathbf{I})$.

3. Identity Authentication Mechanism

3.1. Multipath Time Delay Estimation

By combining the received signals at all subcarriers, we have $\mathbf{y}=[{\mathbf{y}}_1,{\mathbf{y}}_2,\cdots ,{\mathbf{y}}_D]$. Then the vector form of $\mathbf{y}$ can be written as

$$\begin{array}{c}\hfill \mathrm{vec}\left(\mathbf{y}\right)=[\mathbf{\Phi }\diamond \mathbf{B}]\mathit{\alpha }+\mathrm{vec}\left(\mathbf{n}\right)=\mathbf{{\rm Y}}\mathit{\alpha }+\mathrm{vec}\left(\mathbf{n}\right),\end{array}$$

(11)

where $\mathbf{B}=[{\mathbf{W}}^H{\mathbf{a}}_0({\varphi }_1,{\theta }_1),\cdots ,{\mathbf{W}}^H{\mathbf{a}}_0({\varphi }_M,{\theta }_M)]$ is the effective spatial response matrix after receive beamforming, assuming a narrowband array response. Also, we have $\mathbf{n}={\mathbf{W}}^H[{\mathbf{n}}_1,{\mathbf{n}}_2,\cdots ,{\mathbf{n}}_D]$, ${[\mathbf{\Phi }]}_{d,m}=e^{-j2\pi f_d{\tau }_m}$, and $\mathit{\alpha }=s{[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_M]}^T$. $\mathbf{{\rm Y}}\in {\mathbb{C}}^{N_{DS}D\times M}$ is regarded as the space-time response matrix in [19] and characterizes the angles of arrival and multipath time delays. The covariance matrix of $\mathrm{vec}\left(\mathbf{y}\right)$ is calculated as

$$\begin{array}{cc}\hfill {\mathbf{R}}_{\mathrm{vec}\left(\mathbf{y}\right)}& =\mathbb{E}\left\{\mathrm{vec}\left(\mathbf{y}\right)\mathrm{vec}{\left(\mathbf{y}\right)}^H\right\}\hfill \\ & =\mathbf{{\rm Y}}{\mathbf{\Psi }}_{\alpha }{\mathbf{{\rm Y}}}^H+{\sigma }_n^2{\mathbf{I}}_{N_{DS}D},\hfill \end{array}$$

(12)

where ${\mathbf{\Psi }}_{\alpha }=\mathbb{E}\left\{\mathit{\alpha }{\mathit{\alpha }}^H\right\}$ is a diagonal matrix. Then, by using the eigenvalue decomposition (EVD) method on ${\mathbf{R}}_{\mathrm{vec}\left(\mathbf{y}\right)}$, ${\mathbf{R}}_{\mathrm{vec}\left(\mathbf{y}\right)}$ can be further rewritten as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbf{R}}_{\mathrm{vec}\left(\mathbf{y}\right)}& =[{\mathbf{V}}_s,{\mathbf{V}}_n]\hfill \\ & \times \left[\begin{array}{cc}{\mathbf{\Gamma }}_s& {\mathbf{0}}_{M\times (N_{DS}D-M)}\\ {\mathbf{0}}_{(N_{DS}D-M)\times M}& {\sigma }_n^2{\mathbf{I}}_{N_{DS}D-M}\end{array}\right]{[{\mathbf{V}}_s,{\mathbf{V}}_n]}^H\hfill \\ & ={\mathbf{V}}_s{\mathbf{\Gamma }}_s{\mathbf{V}}_s^H+{\sigma }_n^2{\mathbf{V}}_n{\mathbf{V}}_n^H\hfill \\ & ={\mathbf{V}}_s({\mathbf{\Gamma }}_s-{\sigma }_n^2{\mathbf{I}}_M){\mathbf{V}}_s^H+{\sigma }_n^2{\mathbf{I}}_{N_{DS}D},\hfill \end{array}\end{array}$$

(13)

where ${\mathbf{V}}_s\in {\mathbb{C}}^{N_{DS}D\times M}$ and ${\mathbf{V}}_n\in {\mathbb{C}}^{N_{DS}D\times (N_{DS}D-M)}$ denote the signal subspace and noise subspace, respectively. ${\mathbf{\Gamma }}_s\in {\mathbb{R}}^{M\times M}$ is a diagonal matrix.

From (12) and (13), we obtain

$$\begin{array}{c}\hfill {\mathbf{V}}_s=\mathbf{{\rm Y}}\mathbf{T},\end{array}$$

(14)

where $\mathbf{T}\in {\mathbb{C}}^{M\times M}$ is a full rank matrix.

We define the delay-selection matrix as ${\mathbf{U}}_E\triangleq \mathrm{diag}({\mathbf{U}}_{E,1},{\mathbf{U}}_{E,2},\cdots ,{\mathbf{U}}_{E,D})\in {\mathbb{R}}^{D\times N_{DS}D}$, where ${\mathbf{U}}_{E,d}={\mathbf{1}}_{N_{DS}}^T$. Then we obtain the delay-related submatrix ${\mathbf{{\rm Y}}}_E={\mathbf{U}}_E\mathbf{{\rm Y}}\in {\mathbb{C}}^{D\times M}$. We further define ${\tilde{\mathbf{U}}}_{D,d}\triangleq [{\mathbf{0}}_{1\times (d-1)},1,{\mathbf{0}}_{1\times (D-d)}]\in {\mathbb{R}}^{1\times D}$, then the delay-related submatrix associated with the subcarrier frequency $f_d$ can be written as ${\mathbf{{\rm Y}}}_{E,d}={\tilde{\mathbf{U}}}_{E,d}{\mathbf{{\rm Y}}}_E\in {\mathbb{C}}^{1\times M}$. Therefore, we obtain the relationship between the delay-related submatrices of each subcarrier frequency as

$$\begin{array}{c}\hfill {\mathbf{{\rm Y}}}_{E,\tilde{d}+1}={\mathbf{{\rm Y}}}_{E,\tilde{d}}{\mathbf{\Xi }}_E,\end{array}$$

(15)

where ${\mathbf{\Xi }}_E=\mathrm{diag}(e^{-j2\pi {\Delta }_F{\tau }_1},e^{-j2\pi {\Delta }_F{\tau }_2},\cdots ,e^{-j2\pi {\Delta }_F{\tau }_M})\in {\mathbb{C}}^{M\times M}$ and $\tilde{d}=1,2,\cdots ,D-1$.

Based on (14), we can calculate the delay-related submatrix for the subspace matrix at subcarrier frequency $f_d$ as

$$\begin{array}{c}\hfill {\mathbf{V}}_{E,d}={\tilde{\mathbf{U}}}_{E,d}{\mathbf{U}}_E{\mathbf{V}}_s={\mathbf{{\rm Y}}}_{E,d}\mathbf{T}.\end{array}$$

(16)

By substituting (15) into (16), we obtain

$$\begin{array}{c}\hfill {\mathbf{V}}_{E,\tilde{d}+1}={\mathbf{V}}_{E,\tilde{d}}{\mathbf{T}}^{-1}{\mathbf{\Xi }}_E\mathbf{T}={\mathbf{V}}_{E,\tilde{d}}{\mathbf{\Gamma }}_E.\end{array}$$

(17)

Then based on [20], we can estimate ${\widehat{\mathbf{\Gamma }}}_E={\mathbf{T}}^{-1}{\mathbf{\Xi }}_E\mathbf{T}={\mathbf{V}}_{E,\tilde{d}}^{†}{\mathbf{V}}_{E,\tilde{d}+1}$, each of which has a total of M eigenvalues, i.e., ${\lambda }_{E,\tilde{d},m}$. Therefore, the multipath time delay of the m-th path, ${\tau }_m$, is estimated as

$$\begin{array}{c}\hfill {\widehat{\tau }}_m={\displaystyle \frac{1}{D-1}}\sum _{\tilde{d}}^{D-1}\left[{\displaystyle \frac{jln({\lambda }_{E,\tilde{d},m})}{2\pi {\Delta }_F}}\right].\end{array}$$

(18)

From the estimated multipath time delay, we can calculate the time interval between any two adjacent multipath time delays as

$$\begin{array}{c}\hfill {\widehat{q}}_i\left(t\right)={\widehat{\tau }}_{i+1}\left(t\right)-{\widehat{\tau }}_i\left(t\right),i=1,2,\cdots ,M-1.\end{array}$$

(19)

By considering (6) and (7), the estimations of the two Gaussian random variables $q_{1,i}$ and $q_{2,i}$ can be generally formulated, respectively, as

$$\begin{array}{c}\hfill {\widehat{q}}_{1,i}\left(t\right)=q_{1,i}\left(t\right)+w_{1,i}\left(t\right),\end{array}$$

(20)

$$\begin{array}{c}\hfill {\widehat{q}}_{2,i}\left(t\right)=q_{2,i}\left(t\right)+w_{2,i}\left(t\right),\end{array}$$

(21)

where $q_{1,i}\left(t\right)$ and $q_{2,i}\left(t\right)$ are true values. $w_{1,i}\left(t\right)$ and $w_{2,i}\left(t\right)$ are independent estimation errors that both follow a zero-mean Gaussian distribution with equal variance ${\displaystyle \frac{{\sigma }_w^2}{2}}$ and are uncorrelated with ${\widehat{q}}_{1,i}\left(t\right)$ and ${\widehat{q}}_{2,i}\left(t\right)$, respectively. From (20) and (21), we can easily know that ${\widehat{q}}_{1,i}\left(t\right)$ and ${\widehat{q}}_{2,i}\left(t\right)$ are still two independent zero-mean Gaussian random variables with variance ${\sigma }_q^2+{\sigma }_w^2/2$, i.e., ${\widehat{q}}_{1,i}\left(t\right),{\widehat{q}}_{2,i}\left(t\right)\sim \mathcal{N}(0,{\sigma }_q^2+{\sigma }_w^2/2)$.

Therefore, the estimation of the time interval between any two adjacent multipath time delays at time t is expressed by

$$\begin{array}{c}\hfill {\widehat{q}}_i\left(t\right)={({\widehat{q}}_{1,i}\left(t\right))}^2+{({\widehat{q}}_{2,i}\left(t\right))}^2,i=1,2,\cdots ,M-1,\end{array}$$

(22)

where the time interval estimation ${\widehat{q}}_i\left(t\right)$ follows an exponential distribution with parameter ${\lambda }^{\prime }={\displaystyle \frac{1}{2{\sigma }_q^2+{\sigma }_w^2}}$, i.e., ${\widehat{q}}_i\left(t\right)\sim \exp ({\displaystyle \frac{1}{2{\sigma }_q^2+{\sigma }_w^2}})$.

3.2. Authentication Decision

Based on the estimated multipath time delay values, the authentication decision is formulated as a hypothesis testing problem. In detail, the binary hypothesis testing aims to compare the absolute difference in the estimated multipath time delays at time t and $t-1$ with a detection threshold. Define Z as

$$\begin{array}{c}\hfill Z\triangleq \sum _{i=1}^{M-1}|{\widehat{q}}_{X,i}\left(t\right)-{\widehat{q}}_{A,i}(t-1)|.\end{array}$$

(23)

According to the above analysis, we design the binary hypothesis test as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{H}_0:Z\le \eta ,\hfill \\ H_1:Z>\eta ,\hfill \end{array}\right.\end{array}$$

(24)

where subscript X and A denote an unknown transmitter (i.e., Alice or Eve) and Alice, respectively. Hypothesis $H_0$ indicates that the current transmitter is validated as the legitimate transmitter Alice, while hypothesis $H_1$ indicates that the current transmitter is validated as the illegitimate transmitter Eve. $\eta$ is a threshold for the designed hypothesis test. The threshold $\eta$ is a critical system parameter that dictates the practical trade-off between security and usability. Its value represents the sensitivity of the authentication decision. A low threshold makes the system highly sensitive to variations, increasing the probability of detection against an illegitimate user. However, this comes at the cost of increasing the probability of a false alarm, where the legitimate user is incorrectly rejected. A high threshold makes the system more lenient, decreasing the $P_f$ but simultaneously reducing the $P_d$, making it easier for an attacker to go undetected. The optimal choice of $\eta$ is not fixed; it is selected based on the desired operational performance, such as targeting a specific maximum $P_f$ (e.g., $P_f=0.01$, as used in our analysis in Section 5).

While the choice of $\eta$ sets the operating point, the performance that can be achieved at that point is directly related to the overall communication environment. Factors like channel conditions and the antenna geometry ($N_1,N_2,h,r$) influence the accuracy of the multipath delay estimation. Better channel conditions and a more effective antenna geometry lead to more accurate estimations, which in turn create a larger statistical separation between the $H_0$ and $H_1$ hypotheses. This improved separation results in a better Receiver Operating Characteristic curve, allowing the system to achieve a higher $P_d$ for any given $P_f$, as will be demonstrated in Section 4 and Section 5.

4. Theoretical Modeling of False Alarm and Detection Probabilities

4.1. False Alarm Probability

A false alarm occurs when the legitimate transmitter is incorrectly identified as the illegitimate transmitter. In the context of our hypothesis test, this corresponds to the event where the test statistic Z exceeds the threshold $\eta$, given that hypothesis $H_0$ is true. To derive the false alarm probability, we define ${\Lambda }_{q,H_0}$ as

$$\begin{array}{c}\hfill {\Lambda }_{q,H_0}\triangleq {\widehat{q}}_{A,i}\left(t\right)-{\widehat{q}}_{A,i}(t-1).\end{array}$$

(25)

Substituting (6) and (7) into (25), ${\Lambda }_{q,H_0}$ is obtained as

$$\begin{array}{cc}\hfill {\Lambda }_{q,H_0}& ={\widehat{q}}_{A,i}\left(t\right)-{\widehat{q}}_{A,i}(t-1)\hfill \\ & =\underset{Q_1}{\underbrace{({\widehat{q}}_{A,1,i}\left(t\right)-{\widehat{q}}_{A,1,i}(t-1))}}\times \underset{Q_2}{\underbrace{({\widehat{q}}_{A,1,i}\left(t\right)+{\widehat{q}}_{A,1,i}(t-1))}}\hfill \\ & +\underset{Q_3}{\underbrace{({\widehat{q}}_{A,2,i}\left(t\right)-{\widehat{q}}_{A,2,i}(t-1))}}\times \underset{Q_4}{\underbrace{({\widehat{q}}_{A,2,i}\left(t\right)+{\widehat{q}}_{A,2,i}(t-1))}}.\hfill \end{array}$$

(26)

By combining (8) and (20), the random variable $Q_1$ defined in (26) can be rewritten as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill Q_1& ={\widehat{q}}_{A,1,i}\left(t\right)-{\widehat{q}}_{A,1,i}(t-1)\hfill \\ & =(\rho -1)q_{A,1,i}(t-1)+\sqrt{(1-{\rho }^2){\sigma }_{q_A}^2}{u}_1(t-1)\hfill \\ & +w_{A,1,i}\left(t\right)-w_{A,1,i}(t-1).\hfill \end{array}\end{array}$$

(27)

From (27), because $q_{A,1,i}(t-1)$, $u_1(t-1)$, $w_{A,1,i}\left(t\right)$ and $w_{A,1,i}(t-1)$ are all zero-mean Gaussian random variables, $Q_1$ is also a zero-mean Gaussian random variable. Accordingly, we can know that $Q_2$, $Q_3$ and $Q_4$ are also zero-mean Gaussian random variables. Based on (27), we can derive the variances for $Q_1$, $Q_2$, $Q_3$ and $Q_4$ as

$$\begin{array}{c}\hfill {\sigma }_{Q_1}^2={\sigma }_{Q_3}^2=2{\sigma }_{q_A}^2(1-\rho )+{\sigma }_w^2,\end{array}$$

(28)

$$\begin{array}{c}\hfill {\sigma }_{Q_2}^2={\sigma }_{Q_4}^2=2{\sigma }_{q_A}^2(1+\rho )+{\sigma }_w^2.\end{array}$$

(29)

Let ${\sigma }_{H_0}^2=\sqrt{4{\sigma }_{q_A}^4(1-{\rho }^2)+4{\sigma }_{q_A}^2{\sigma }_w^2+{\sigma }_w^4}$. Following the derivation and approximation that ${\Lambda }_{q,H_0}$ follows a Laplace distribution, we have

$$\begin{array}{c}\hfill {\Lambda }_{q,H_0}\sim \mathrm{Laplace}(0,{\sigma }_{H_0}^2).\end{array}$$

(30)

Thus, the absolute value of ${\Lambda }_{q,H_0}$ follows an exponential distribution with scale parameter ${\sigma }_{H_0}^2$:

$$\begin{array}{c}\hfill |{\Lambda }_{q,H_0}|\sim \exp \left({\displaystyle \frac{1}{{\sigma }_{H_0}^2}}\right).\end{array}$$

(31)

Since Z is the sum of $M-1$ independent exponentially distributed random variables, it obeys a chi-square distribution with $2(M-1)$ degrees of freedom. Therefore, the PDF of Z under $H_0$ is expressed by

$$\begin{array}{cc}\hfill & f_{Z,H_0}\left(x\right)\hfill \\ & ={\displaystyle \frac{1}{2{\sigma }_{H_0}^2\Gamma (M-1)}}{\left({\displaystyle \frac{x}{2{\sigma }_{H_0}^2}}\right)}^{M-2}\exp \left(-{\displaystyle \frac{x}{2{\sigma }_{H_0}^2}}\right),x\ge 0,\hfill \end{array}$$

(32)

where $\Gamma (·)$ is the gamma function. Based on (32), the cumulative distribution function (CDF) of Z under $H_0$ is expressed by

$$\begin{array}{c}\hfill F_{Z,H_0}\left(x\right)=1-\exp \left(-{\displaystyle \frac{x}{2{\sigma }_{H_0}^2}}\right)\sum _{j=0}^{M-2}{\displaystyle \frac{1}{j!}}{\left({\displaystyle \frac{x}{2{\sigma }_{H_0}^2}}\right)}^j.\end{array}$$

(33)

Based on (33), the false alarm probability of our authentication scheme is expressed by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_f& =\mathrm{Pr}\left\{Z>\eta |H_0\right\}\hfill \\ & =1-F_{Z,H_0}\left(\eta \right)\hfill \\ & =\exp \left(-{\displaystyle \frac{\eta }{2{\sigma }_{H_0}^2}}\right)\sum _{j=0}^{M=2}{\displaystyle \frac{1}{j!}}{\left({\displaystyle \frac{\eta }{2{\sigma }_{H_0}^2}}\right)}^j.\hfill \end{array}\end{array}$$

(34)

4.2. Detection Probability

A detection occurs when the illegitimate transmitter is successfully identified and rejected by the system. This corresponds to the event where the test statistic Z exceeds the threshold $\eta$, given that hypothesis $H_1$ is true. To derive the detection probability, we define ${\Lambda }_{q,H_1}$ as

$$\begin{array}{c}\hfill {\Lambda }_{q,H_1}\triangleq {\widehat{q}}_{E,i}\left(t\right)-{\widehat{q}}_{A,i}(t-1).\end{array}$$

(35)

Similar to the derivation in Section 4.1, we let ${\sigma }_{H_1}^2={\sigma }_{q_E}^2+{\sigma }_{q_A}^2+{\sigma }_w^2$. We can obtain that $|{\Lambda }_{q,H_1}|$ is approximated by an exponential distribution with scale parameter ${\sigma }_{H_1}^2$:

$$\begin{array}{c}\hfill |{\Lambda }_{q,H_1}|\sim \exp \left({\displaystyle \frac{1}{{\sigma }_{H_1}^2}}\right).\end{array}$$

(36)

Therefore, the PDF of Z under $H_1$ is expressed by

$$\begin{array}{cc}\hfill & f_{Z,H_1}\left(x\right)=\hfill \\ & ={\displaystyle \frac{1}{2{\sigma }_{H_1}^2\Gamma (M-1)}}{\left({\displaystyle \frac{x}{2{\sigma }_{H_1}^2}}\right)}^{M-2}\exp \left(-{\displaystyle \frac{x}{2{\sigma }_{H_1}^2}}\right),x\ge 0,\hfill \end{array}$$

(37)

Based on (37), the CDF of Z under $H_1$ is expressed by

$$\begin{array}{c}\hfill F_{Z,H_1}\left(x\right)=1-\exp \left(-{\displaystyle \frac{x}{2{\sigma }_{H_1}^2}}\right)\sum _{j=0}^{M-2}{\displaystyle \frac{1}{j!}}{\left({\displaystyle \frac{x}{2{\sigma }_{H_1}^2}}\right)}^j.\end{array}$$

(38)

Based on (38), the detection probability of our authentication scheme is expressed by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_d& =\mathrm{Pr}\left\{Z>\eta |H_1\right\}\hfill \\ & =1-F_{Z,H_1}\left(\eta \right)\hfill \\ & =\exp \left(-{\displaystyle \frac{\eta }{2{\sigma }_{H_1}^2}}\right)\sum _{j=0}^{M-2}{\displaystyle \frac{1}{j!}}{\left({\displaystyle \frac{\eta }{2{\sigma }_{H_1}^2}}\right)}^j.\hfill \end{array}\end{array}$$

(39)

5. Simulation Results and Analysis

In this section, we conduct a series of numerical simulations to validate our theoretical derivations and evaluate the performance of the proposed PLA mechanism under various conditions. The simulation methodology is designed to model the authentication scenario described in Section 2.1. The time intervals between multipath delays, $q_{A,i}$, are modeled as exponential random variables, and their evolution between two consecutive frames (at time $t-1$ and t) is characterized using the first-order Gauss–Markov process. The channel for the illegitimate user, Eve, is generated independently using the same statistical model, but with a different variance for its delay components, as defined by the parameter $k_q$. To generate the performance metrics, we first simulate the reception of an authenticated frame from Alice at $t-1$ to store the reference fingerprint ${\widehat{q}}_{A,i}(t-1)$. Subsequently, we simulate a new frame at time t from an unknown transmitter X.

In the simulations, the system performance is evaluated under varying conditions. The SNR is defined as $\gamma =E_s/{\sigma }_n^2$, where $E_s$ denotes the average signal energy per symbol, and ${\sigma }_n^2$ represents the variance of the additive white Gaussian noise. Regarding the receiver configuration, the base station Bob employs a hybrid uniform cylindrical array (UCyA) as described in the system model. The specific geometry parameters for the UCyA used in our experiments are set as follows: the number of vertical layers is $N_1$, and the number of antennas per circular array is $N_2$, resulting in a total of $N_r$ receiving antennas. The radius of each circular array is set to r, and the vertical spacing between adjacent layers is h. The variance ratio of multipath delay components is denoted by $k_q={\sigma }_{qE}^2/{\sigma }_{qA}^2$, and is controlled by fixing ${\sigma }_{qA}^2$ while adjusting ${\sigma }_{qE}^2$, M represents the number of propagation paths, D is the number of subcarriers, $f_d$ is the frequency of each subcarrier, W is the system bandwidth, and $\rho$ represents the autocorrelation coefficient of adjacent multipath delay components. 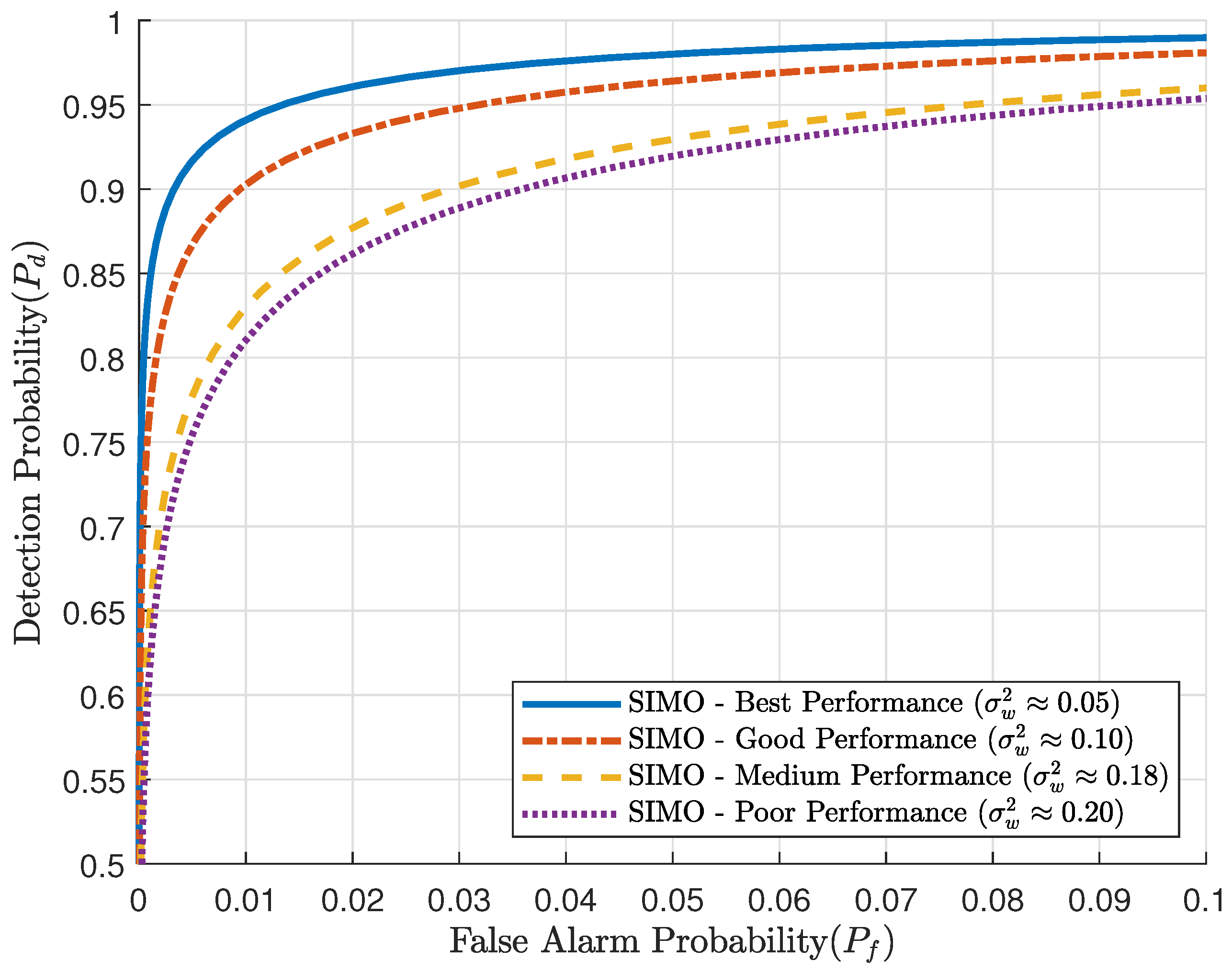Figure 2 illustrates the ROC curves of the proposed PLA scheme under varying conditions of multipath delay estimation error variance. The experimental setup is fixed with the following parameters: $M=16$, $k_q=2\mathrm{dB}$, $D=20$, $W=1.6\mathrm{GHz}$, and $\rho =0.9$. In the plot, the horizontal axis represents the probability of false alarm ($P_f$), and the vertical axis represents the probability of detection ($P_d$). Each curve corresponds to a specific value of ${\sigma }_w^2$, namely 0.05, 0.10, 0.15, and 0.20.

We first evaluate the impact of the multipath delay estimation error variance, ${\sigma }_w^2$. This parameter quantifies the accuracy of the feature extraction process itself. A lower ${\sigma }_w^2$ signifies a more precise estimation of the channel’s multipath delay features, which serve as the basis for the authentication decision. As this is a crucial parameter for the system’s performance, our first analysis is dedicated to isolating its effect. To clearly demonstrate this, the simulation process for Figure 2 treats ${\sigma }_w^2$ as an independent variable. We directly vary its value to model different levels of estimation quality, from “Best Performance” to “Poor Performance”. It is important to note that in a practical, real-world system, ${\sigma }_w^2$ would be a dependent variable; its value would be determined by other factors, most notably the SNR of the received signal. This relationship will be explored in the subsequent analysis for Figure 3.

It is clearly observable from the figure that ${\sigma }_w^2$ has a direct and significant impact on the performance of the authentication system. A lower value ${\sigma }_w^2$ indicates a more accurate estimation of the multipath delay features. As shown in Figure 2, the ROC curve corresponding to the smallest ${\sigma }_w^2$ is closest to the top left corner. This signifies that for a given false alarm probability $P_f$, the detection probability $P_d$ is maximized; conversely, for a given $P_d$, $P_f$ is minimized, which represents the optimal authentication performance. Although the figure directly illustrates the effect of ${\sigma }_w^2$, according to signal processing theory, the estimation error variance ${\sigma }_w^2$ is typically inversely proportional to the SNR of the received signal. Consequently, a lower ${\sigma }_w^2$ corresponds to a higher SNR, and vice versa. Therefore, the plot also implicitly demonstrates that higher SNR yields better performance.

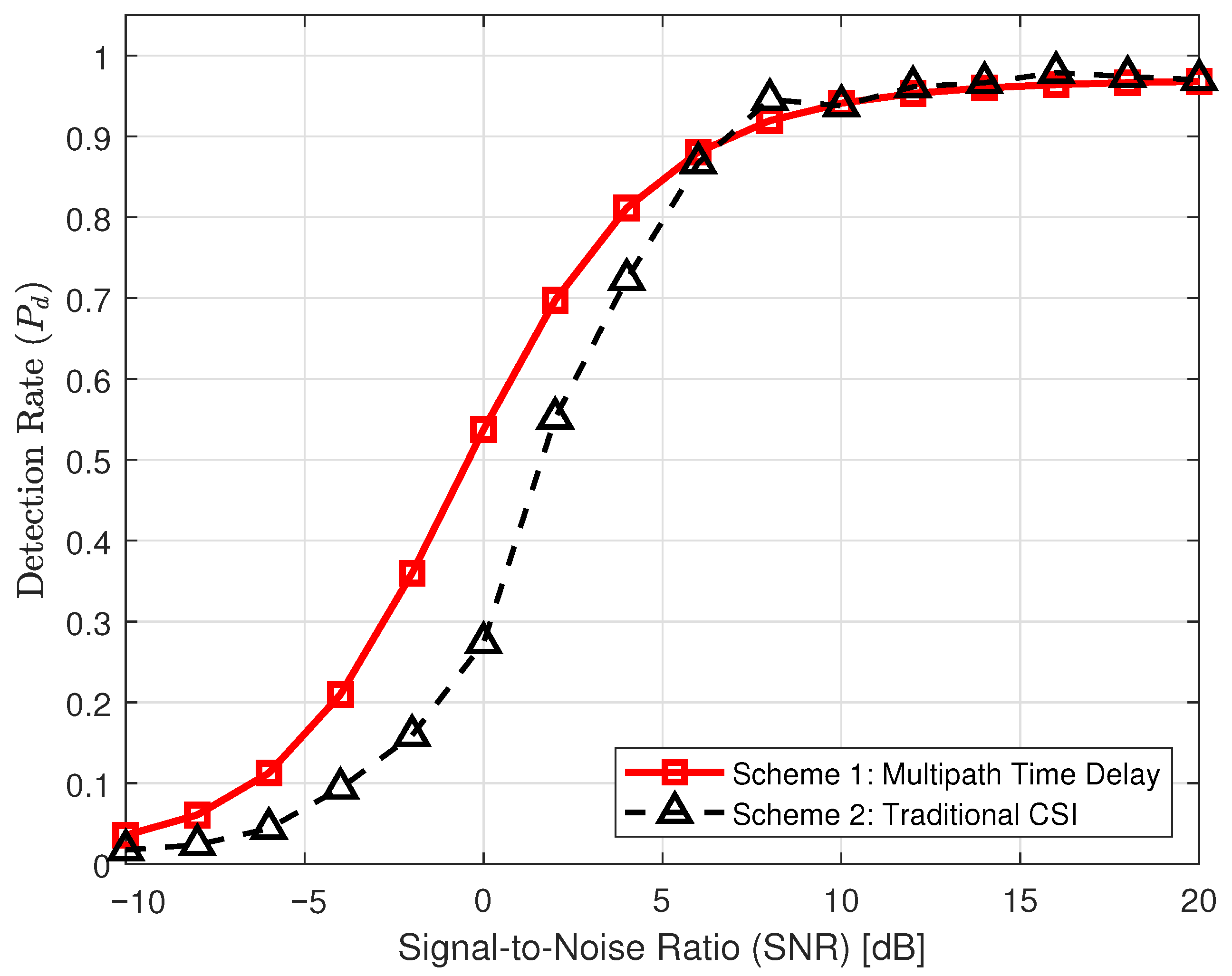
Figure 3 compares the detection performance of the traditional authentication scheme based on CSI in [21,22] with the authentication proposed based on multipath delay features in this paper, respectively. It illustrates the evolution of $P_d$ as a function of the SNR, given a fixed false alarm rate of $P_f=0.01$. As anticipated, the detection performance for both mechanisms improves monotonically with increasing SNR. This trend validates the theoretical expectation that higher signal quality minimizes noise interference, thereby enabling more accurate channel estimation and enhancing the distinctiveness of legitimate users. Notably, the proposed Scheme 1 (Multipath Time Delay) demonstrates superior robustness in low-SNR regimes compared to Scheme 2 (Traditional CSI). As shown in the plot, between −10 dB and 5 dB, Scheme 1 maintains a significant performance lead. For instance, at 0 dB, the multipath-based scheme achieves a $P_d$ of approximately 0.55, whereas the traditional CSI scheme reaches only 0.28. This advantage is attributed to the fine-grained nature of multipath delay features, specifically their differential and time-evolutionary characteristics, which are less sensitive to noise than the macroscopic holistic CSI correlations. Conversely, in high-SNR conditions (>10 dB), the performance of both methods converges and saturates near unity ($P_d\approx 1$), implying that both methods can effectively identify illegitimate users when the SNR is sufficiently high. This indicates that while traditional CSI is effective when signal quality is pristine, the proposed multipath delay approach offers a critical advantage in challenging, noise-limited environments.

To further evaluate the robustness of the proposed methodology, we investigated the impact of key system variables on the authentication performance. First, regarding the correlation coefficient $\rho$, which models the temporal stability of the channel, our analysis indicates that a higher $\rho$ significantly improves performance. As $\rho$ approaches 1, the legitimate channel becomes more correlated over time, reducing the variance of the test statistic Z under hypothesis $H_0$. Consequently, this lowers the False Alarm Probability ($P_f$) for a fixed threshold. Second, the system bandwidth W plays a critical role in the resolution of multipath delay estimation. An increase in bandwidth results in finer time-domain resolution. This enhanced resolution reduces the estimation error variance ${\sigma }_w^2$, thereby shifting the ROC curves toward the optimal upper-left corner. However, it is worth noting that increasing bandwidth imposes higher requirements on the hardware sampling rate and processing complexity. Third, the number of multipath components M contributes to the diversity of the fingerprint. As M increases, the degrees of freedom in the chi-square distribution of the test statistic increase. Theoretical analysis suggests that a larger M provides more distinctive features, improving the distinguishability between the legitimate user and the spoofer, provided that the additional paths can be accurately estimated. Moreover, in our proposed scheme, the antenna geometry indirectly, yet critically, influences the ROC curves through the channel estimation accuracy. The delay estimation algorithm relies on the effective SNR after beamforming. Specifically, the total number of antenna elements $N_r=N_1\times N_2$ determines the array gain. A larger array provides higher array gain, which effectively suppresses the noise variance ${\sigma }_n^2$ in the signal subspace. Therefore, while the geometric parameters ($h,r$) primarily determine the manifold structure for the Angle of Arrival resolution, the quantity of antennas is the dominant geometric factor enhancing the multipath delay authentication performance by minimizing estimation errors.

6. Conclusions

This paper addresses the issue of identity spoofing attacks in mmWave SIMO systems by proposing a PLA mechanism based on multipath delay fingerprint features. By constructing a channel model, designing an efficient feature extraction method, and establishing an authentication framework founded on hypothesis testing theory, the proposed scheme achieves effective differentiation between legitimate and spoofing devices. Furthermore, theoretical expressions for the false alarm rate and detection rate are derived to characterize the authentication performance. The efficacy of the scheme is systematically evaluated through simulations under various SNR and channel estimation error conditions. The results demonstrate that the proposed solution exhibits strong robustness and practicality while maintaining low communication overhead, thereby significantly enhancing the security of mmWave SIMO communication systems.

While the proposed scheme demonstrates strong robustness, it is important to discuss its limitations. Firstly, as noted in Section 2.1, our methodology assumes the absence of signal collisions, where the receiver discards collided frames. Developing a mechanism to authenticate reliably in the presence of such spoofing-by-collision attacks remains a significant challenge. Secondly, regarding mobility, our current work models the channel variation between two consecutive frames using a first-order Gauss–Markov process. This is effective for low-to-moderate mobility scenarios. However, in high-mobility environments, the channel may decorrelate significantly within a single transmission frame, not just between frames. This rapid intra-frame variation could degrade the accuracy of the channel feature estimation and subsequently increase the false alarm rate, as the reference fingerprint stored at time $t-1$ would become rapidly outdated. Analyzing and mitigating the impact of such high-speed movement is a critical limitation of the current study.

Future research will proceed in several directions to address these limitations. Firstly, we will investigate authentication mechanisms robust to signal collisions. Secondly, we will explicitly analyze the impact of high-mobility scenarios and develop more adaptive online mechanisms that can track rapid intra-frame channel variations, potentially by shortening the observation window or employing predictive tracking filters. Finally, we will explore multi-modal authentication that integrates diverse physical layer features to improve the overall identification accuracy.